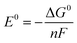View PDF VersionPrevious ArticleNext Article

Open Access Article
This Open Access Article is licensed under a
Creative Commons Attribution 3.0 Unported Licence
DOI: 10.1039/D2DT01150F (Paper) Dalton Trans., 2022, 51, 8618-8624

Computational comparison of Ru(bda)(py)2 and Fe(bda)(py)2 as water oxidation catalysts†

Ge Li and Mårten S. G. Ahlquist *
Department of Theoretical Chemistry & Biology, School of Engineering Sciences in Chemistry, Biotechnology and Health, KTH Royal Institute of Technology, 10691 Stockholm, Sweden. E-mail: ahlqui@kth.se

Received 13th April 2022 , Accepted 12th May 2022

First published on 17th May 2022

Abstract

Ru(bda)(py)2 (bda = 2,2′-bipyridine-6,6′-dicarboxylate, py = pyridine) has been a significant milestone in the development of water oxidation catalysts. Inspired by Ru(bda)(py)2 and aiming to reduce the use of noble metals, iron (Fe) was introduced to replace the Ru catalytic center in Ru(bda)(py)2. In this study, density functional theory (DFT) calculations were performed on Fe- and Ru(bda)(py)2 catalysts, and a more stable 6-coordinate Fe(bda)(py)2 with one carboxylate group of bda disconnecting with Fe was found. For the first time, theoretical comparisons have been conducted on these three catalysts to compare their catalytic performances, such as reduction potentials and energy profiles of the radical coupling process. Explanations for the high potential of [FeIII(bda)(py)2–H2O]+ and reactivity of [FeV(bda)(py)2–O]+ have been provided. This study can provide insights on Fe(bda)(py)2 from a computational perspective if it is utilized as a water oxidation catalyst.

Introduction

To satisfy the increasing demand for energy,1 catalytic water splitting could be a sustainable alternative by storing energy in chemical bonds with very high energy density. Many renewable forms of energy, including solar and wind, suffer from irregular supply. Consequently, efficient, stable, and large-scale energy storage is needed. Water splitting consists of two half reactions: water oxidation (2H2O → O2 + 4e− + 4H+) and proton reduction (4e− + 4H+ → 2H2). Compared to the latter, water oxidation typically requires harsh oxidizing conditions and undergoes transfers of four electrons and protons where multiple intermediates are formed, therefore water oxidation often has a limited reaction rate and is regarded as the bottleneck of the whole water splitting reaction.2 A wide range of water oxidation catalysts (WOCs) containing transition metals (TMs) have been synthesized to increase the rates, while keeping the overpotential low for the water oxidation reaction. Among them, molecular homogeneous WOCs mostly act as models to explore different reaction mechanisms and have thus attracted much attention owing to their advantages of well-defined structures, feasible characterization of intermediates, high reactive efficiency, and informative kinetic studies. Since the discovery of the first molecular WOC (blue dimer) by Meyer in 1982,3 Ru(bda)L2 (bda = 2,2′-bipyridine-6,6′-dicarboxylate, L = typically a nitrogen heterocycle such as pyridine) is another breakthrough in the history of homogeneous WOCs.4 Driven by CeIV, one variation Ru(bda)(isoquinoline)2,5 has achieved a turnover frequency that can be compared to the oxygen-evolving complex of photosystem II in vivo.6,7 Further modifications on L, like L = phthalazine, 6-fluoroisoquinoline, 6-bromophthalazine have achieved high turnover frequency (over 1000 s−1) and turnover number (over 100[thin space (1/6-em)]000) driven by CeIV.8,9 In addition to Ru-based WOCs, other WOCs based on the rare and expensive TM Ir, are also utilized in oxygen-evolving reactions.10,11 Precious noble TMs need to be substituted by cheaper, non-toxic and earth-abundant first-row TMs to realize economically and environmentally sustainable energy storage via water oxidation. For example, there have been noteworthy developments related to inexpensive first-row TM species, like Mn, Fe, Cu, Co, and Ni,12–17 among which Fe stands out because of its earth-abundance, no toxicity and special position located exactly above Ru in periodic table. Lloret-Fillol and co-workers stabilized Co, Fe, Mn, and Ni complexes with the same chelating tetradentate ligand and found that only Fe-based catalysts were active for water oxidation with high activity and stability using cerium ammonium nitrate or sodium periodate as sacrificial oxidants,18 and the ligand architectures with two available cis sites are key to the activity of these Fe-based WOCs.19 The groups of Collins and Bernhard in 2010 presented an efficient WOC of iron-centered tetraamido macrocyclic ligand (Fe-TAML) and its turnover frequency (TOF) exceeded 1.3 s−1 in unbuffered solution with ceric ammonium nitrate.13,20 Driven by the multinuclear characteristic of CaMn4O5 cluster in the photosystem II, a pentanuclear iron complex was synthesized and displayed efficient and robust catalytic performance for water oxidation with an extremely high turnover frequency of 1900 s−1 in an acetonitrile/water (10[thin space (1/6-em)]:[thin space (1/6-em)]1) mixed solution with Et4NClO4 (0.1 M), however, at a relatively high overpotential of 0.5 V.21,22 Fe-based WOCs progress fast considering its short history, together with its abundance, safety and same electronic configurations at same oxidation states as Ru, making Fe a promising alternative for Ru.

Herein, we used density functional theory (DFT) calculations on the key intermediates of Ru(bda)(py)2 and iron-based Fe(bda)(py)2 to assess how substituting Ru metal center with Fe and maintaining the bda and pyridine ligands affect the redox properties and the reactivity towards O–O bond formation. We focus on O–O reaction via radical coupling since that reaction mechanism is key to the extremely high rates of Ru(bda)L2 catalysts.

Computational details

All density functional theory (DFT) calculations were performed with Jaguar 10.3 program package23 by Schrödinger, LLC, New York, NY, 2019. Geometry optimizations were carried out using the B3LYP-D3 functional (Becke's three-parameter hybrid functional and the LYP correlation functional24 with adding the D3 version of Grimme's dispersion with the original D325 damping function) and the LACVP** basis set with effective core potentials on heavy atoms.26 Based on the optimized geometries, single-point calculations using different functionals (B3LYP-D3, B3LYP*-D327 and M06-L28) with a larger basis set LACV3P**++29 were performed. All tested functionals show the same preference that Fe species favor high spin states and Ru-contained complexes favor low spin states. As a result, all calculations were performed with B3LYP-D3 functional of higher accuracy. Frequency calculations with LACVP** were performed on optimized geometries to verify that the geometries correspond to the minima and to obtain the thermal corrections to Gibbs free energy. The solvation energies were estimated by adapting the Poisson Boltzmann Finite element method (PBF) implemented in Jaguar 10.3.30,31 The Gibbs free energies (G) are calculated at standard state of 1 M(aq) (and 1 atm for gaseous species) and the G of each species is defined as the following equation G = E(B3LYP-D3/LACV3P**++) + Gsolv + ZPE + H298 − T*S298 + 1.90 kcal mol−1 (a concentration correction to the solvation free energy when changing from 1 M(g) to 1 M(aq) that by default is calculated at 1 M(g) to 1 M(aq) in Jaguar). For water we used the hydration free energy of −2.05 kcal mol−1. To identify the transition states for O–O bond formation, we searched the potential energy surface by carrying out relaxed coordinate scans of the terminal O–O bond distance of the dimer at the antiferromagnetic open shell singlet state (RuV = O⋯O = RuV doublet–doublet or FeV = O⋯O = FeV quartet–quartet). The scan range of the O–O bond distance was from 2.8 Å to 1.1 Å. Frequency calculations were performed to confirm the obtained transition states and to acquire the thermal corrections for calculating Gibbs free energy.

TMs have different possibilities in spin states. Consequently, geometry optimizations on Fe(bda)(py)2 and Ru(bda)(py)2 at their different oxidative states were performed from low multiplicity to high, and the structures with lowest energies were further utilized to compute the Gibbs free energy. After obtaining the Gibbs free energy of every sub-reaction, the standard reduction potentials were calculated based on the Nernst equation under standard conditions (at 1 atm and 25 °C):

image file: d2dt01150f-t1.tif
where ΔG0 is the reactive Gibbs free energy under standard conditions; n is the number of electrons transferred in each sub-reaction; F is the Faraday constant, 96[thin space (1/6-em)]485 C mol−1; E0 is the standard reduction potential for the corresponding reaction. Standard hydrogen electrode (SHE) is used as the reference with an absolute electrode potential of 4.28 V.32,33 The experimental value of −270.28 kcal mol−1 is used as the Gibbs free energy of proton at 1 M, determined by Tissandier et al.34

Results and discussion

In the oxygen evolution reaction, catalysts need to undergo several oxidation steps before the formation of O–O bond. Table 1 shows the reduction potentials of the two metal complexes that are oxidized from low to high valence states. Firstly, the oxidation from MII(bda)(py)2 with a separate water to [MIII(bda)(py)2–H2O]+ requires potentials of 0.63 V for Fe(bda)(py)2 and 0.64 V for Ru(bda)(py)2, indicating facile oxidation for both Fe and Ru. Proton-coupled electron transfer (PCET) occurs in the next two sub-reactions when catalytic centers are oxidized from 3+ to 4+, then to 5+. The potentials of these two processes are 3.06 V and 2.41 V for Fe(bda)(py)2, and 1.29 V and 1.66 V for Ru(bda)(py)2. For the formation of FeIV(bda)(py)2[double bond, length as m-dash]O, the potential from [FeIII(bda)(py)2–H2O]+ is 3.22 V and the Gibbs free energy of deprotonation from [FeIV(bda)(py)2–OH]+ is 3.56 kcal mol−1. Both support that the FeIV(bda)(py)2[double bond, length as m-dash]O complex is less likely to form. Regarding the reduction potentials for Ru(bda)(py)2, all variations of Ru(bda)L2 WOCs have similar reduction potentials for these three sub-reactions. Based on the Pourbaix diagrams of Ru(bda)(4-picoline)2 and Ru(bda)(isoquinoline)2, the corresponding potentials locate approximately at 0.68 V, 1.19 V and 1.41 V at pH 0,4,5 which is consistent with our calculated potentials of Ru(bda)(py)2 catalyst.
Table 1 Reduction potentials of Fe(bda)(py)2 and Ru(bda)(py)2 in water oxidation reaction
Sub-reactions Potential (M = Fe) Potential (M = Ru)
a The reduction potential in the parenthesis is for the FeV/FeIV reaction involving the 6-coordinate [FeV(bda)(py)2−O]+.
[MIII(bda)(py)2-H2O]+ + e− → MII(bda)(py)2 + H2O 0.63 V 0.64 V
[MIV(bda)(py)2-OH]+ + e− + H+ → [MIII(bda)(py)2–H2O]+ 3.06 V 1.29 V
[MV(bda)(py)2-O]+ + e− + H+ → [MIV(bda)(py)2–OH]+ 2.41 V (2.00 Va) 1.66 V

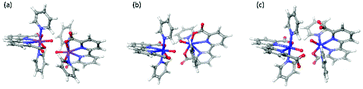
We found two different structures of [FeV(bda)(py)2–O]+, shown in Fig. 1. In a 6-coordinate [FeV(bda)(py)2–O]+ one carboxylate group of the bda ligand disconnects with Fe and the Gibbs free energy of 6-coordinate [FeV(bda)(py)2–O]+ is 9.4 kcal mol−1 lower than that of 7-coordinate [FeV(bda)(py)2–O]+. It is worth mentioning that for the more stable 6-coordinate [FeV(bda)(py)2–O]+, the broken bond between carboxylate group and Fe catalytic center reconnects when Fe is reduced to the FeII, FeIII and FeIV states, generating identical structures as the corresponding 7-coordinate Fe(bda)(py)2 species. Although the more stable 6-coordinate [FeV(bda)(py)2−O]+ decreased the FeV/FeIV reduction potential from 2.41 V to 2.00 V, FeII(bda)(py)2 still requires much higher potentials to be oxidized to FeV compared to RuII(bda)(py)2.


image file: d2dt01150f-f1.tif
Fig. 1 Optimized structures of [RuV(bda)(py)2–O]+ (a), [FeV(bda)(py)2–O]+ (b) and 6-coordinate [FeV(bda)(py)2–O]+ (c).

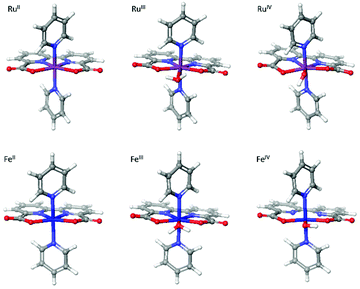
The newly-found 6-coordinate [FeV(bda)(py)2–O]+ will be discussed together with 7-coordinate [RuV(bda)(py)2–O]+ and [FeV(bda)(py)2–O]+. The three optimized [MV(bda)(py)2–O]+ structures are shown in Fig. 1 and all the optimized structures at MII, MIII, and MIV states are shown in Fig. 2. Unless otherwise specified, Fe(bda)(py)2 and Ru(bda)(py)2 represent 7-coordinate structures as shown in Fig. 1(b) and (a), respectively.


image file: d2dt01150f-f2.tif
Fig. 2 Structures of Ru(bda)(py)2 and Fe(bda)(py)2 at MII, MIII, MIV states.

Table 2 shows that Ru(bda)(py)2 complexes at different oxidation states are more stable when at low spin states, in agreement with earlier studies.35,36 In contrast, we found that Fe(bda)(py)2 species have lower energies at higher spin states. 6-coordinate [FeV(bda)(py)2−O]+ has the same spin multiplicity as [FeV(bda)(py)2−O]+. The energy differences of all species among different multiplicities are shown in Table S1.† High spin states are common for Fe-based organometallics,19,37–40 but less common for Ru.36

Table 2 Favorable spin multiplicity of different species
  Spin multiplicity   Spin multiplicity
a 6-coordinate [FeV(bda)(py)2–O]+ has the same spin multiplicity as 7-coordinate [FeV(bda)(py)2–O]+ but due to the spin localized on the dangling carboxylate the doublet and quartet are degenerate for the 6-coordinate species.
FeII(bda)(py)2 5 RuII(bda)(py)2 1
[FeIII(bda)(py)2–H2O]+ 6 [RuIII(bda)(py)2–H2O]+ 2
[FeIV(bda)(py)2–OH]+ 5 [RuIV(bda)(py)2–OH]+ 1
[FeV(bda)(py)2–O]+ 4a [RuV(bda)(py)2–O]+ 2

Calculations of highest occupied molecular orbitals (HOMO) and evaluations of pKa, have been carried out to clarify the rather high potential of the PCET process from [FeIII(bda)(py)2–H2O]+ to [FeIV(bda)(py)2–OH]+. As indicated in Table 3, the alpha HOMO energy of [FeIII(bda)(py)2–H2O]+ (−0.355 hartrees) is much lower than that of [RuIII(bda)(py)2–H2O]+ (−0.327 hartrees), indicating that the electrons are more tightly bound to Fe compared to Ru. Similarly, the pKa value for [FeIII(bda)(py)2–H2O]+ is 9.80, which is higher than that of [RuIII(bda)(py)2–H2O]+ (8.56). Both alpha HOMO energies and pKa demonstrate that it is more difficult for [FeIII(bda)(py)2–H2O]+ to abstract one electron as well as a proton compared to [RuIII(bda)(py)2–H2O]+. The alpha HOMO energy and pKa are also considered after one proton or one electron transfer of [MIII(bda)(py)2–H2O]+, respectively. The alpha HOMO energy and pKa value of [FeIII(bda)(py)2–OH] and [FeIV(bda)(py)2–H2O]2+ shows it is still harder to lose one electron and one proton after the deprotonation or oxidation of [FeIII(bda)(py)2–H2O]+.

Table 3 Alpha HOMO energy and pKa values for [MIII(bda)(py)2–H2O]+, [MIII(bda)(py)2–OH] and [MIV(bda)(py)2–H2O]2+
  Alpha HOMO energy (Hartree) pKa
[FeIII(bda)(py)2–H2O]+ −0.355 9.80
[RuIII(bda)(py)2–H2O]+ −0.327 8.56
[FeIII(bda)(py)2–OH] −0.219
[RuIII(bda)(py)2–OH] −0.191
[FeIV(bda)(py)2–H2O]2+ 1.32
[RuIV(bda)(py)2–H2O]2+ −3.59

Among all the intermediate species in water oxidation reaction, the [MV(bda)(py)2–O]+ species is the key intermediate since it is involved in O–O bond formation. Fig. 1 shows the optimized structures [RuV(bda)(py)2–O]+, [FeV(bda)(py)2–O]+ and 6-coordinate [FeV(bda)(py)2–O]+. The largest difference of these three structures is the broken bond between Fe and O of the right carboxylate group in 6-coordinate [FeV(bda)(py)2–O]+. More detailed differences of spin density distribution and structures are shown in Table 4. The numbering of related atoms in Table 4 is indicated in Fig. 3.


image file: d2dt01150f-f3.tif
Fig. 3 [MV(bda)(py)2–O]+ complexes included in the study (M = Fe or Ru) and numbering of atoms.
Table 4 Spin density on O1 and M2, angle of O3–M2–O4, bond distances of M2–O1, M2–O3 and M2–N7
  Spin density Angle (°) Bond distance (Å)
O1 M2 O3–M2–O4 M2–O1 M2–O3 M2–N7
a The distance in the parenthesis is between Fe2 and O4. b The distance in the parenthesis is between Fe2 and N8.
[RuV(bda)(py)2–O]+ 0.74 0.34 153.6 1.73 2.14 2.29
[FeV(bda)(py)2–O]+ 0.98 2.05 169.7 1.63 1.93 2.62
6-Coordinate [FeV(bda)(py)2–O]+ 0.95 1.08 139.4 1.63 1.91(3.58)a 1.98(2.11)b

As shown in Table 4, the total spin densities on the M2 and O1 are 3.03 and 1.08 for [FeV(bda)(py)2–O]+ and [RuV(bda)(py)2–O]+, respectively. For 6-coordinate [FeV(bda)(py)2–O]+, 2/3 of the total spin populates on the Fe2 and O1, and the other 1/3 spin is located on the dangling carboxylate group as shown in Fig. 4. The spin densities of Fe and Ru atoms are 2.05 and 0.34, respectively, which implies that the oxidation states of these two metal centers are closer to 4+ and the metal-oxos could also be termed as metal-oxyls [MIV(bda)(py)2–O˙]+.41 In addition, the dangling carboxylate group has one spin that is almost evenly shared by the two O atoms (O6: 0.50, O4: 0.55), which results in the spin distributions of the dangling carboxylate group shown in Fig. 4. The spin density distribution of degenerated 6-coordinate [FeV(bda)(py)2–O]+ at doublet state is shown in Fig. S1.† The detailed contributions of different atoms to the overall spin density of [MV(bda)(py)2–O]+ are shown in Table S2.† Regarding O3–M2–O4 angles and M2–N7 distances, [FeV(bda)(py)2–O]+ has the largest and appears less compact, and can be regarded as a pseudo 7-coordinate structure shown in Fig. 1(b). For the 6-coordinate [FeV(bda)(py)2–O]+, the disconnection between one carboxylate group and FeV catalytic center renders a more closely packed octahedral structure, such as the largely deceased distance of Fe2–N8 from 2.62 Å to 1.98 Å.


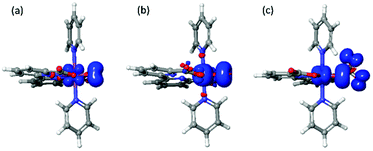image file: d2dt01150f-f4.tif
Fig. 4 Spin density distributions of [RuV (bda)(py)2–O]+(left), [FeV(bda)(py)2–O]+(middle) and 6-coordinate [FeV(bda)(py)2–O]+ (right) at an isovalue of 0.005 electrons per bohr3.

Ru(bda)L2 WOCs has been thoroughly investigated and the formation of O–O bond has been shown both experimentally and computationally to undergo an I2M pathway under homogeneous catalytic conditions.5,42,43 Despite that Fe-based complexes are more difficult to be oxidized, we still investigate its possibility of reacting via the efficient I2M pathway, to assess the reactivity of the FeV[double bond, length as m-dash]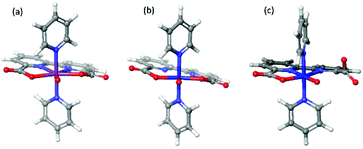O compared to RuV[double bond, length as m-dash]O. The two [MV(bda)(py)2–O]+ monomers have been placed in both parallel and vertical fashions (Fig. 5) to search for the most probable O–O coupling geometry. The parallel and vertical fashions mean that the angles between two bda ligands are 180° and 90° respectively. The comparisons of energy profiles of three different dimers when O atoms approach each other in the above two ways are presented in Fig. S2 of ESI.†


image file: d2dt01150f-f5.tif
Fig. 5 Radical coupling of [MV(bda)(py)2–O]+ dimer in the parallel (a) and vertical (b) orientations, pyridine ligands are omitted for clarity.

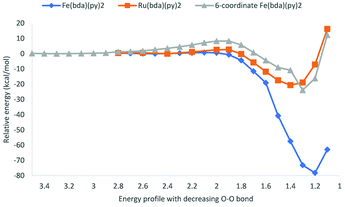
Potential energy surfaces were computed as the distance of O atoms in [MV(bda)(py)2–O]+ oxos decreases (Fig. 6). All the transition state structures and spin density distributions of them are shown in Fig. 7 and S3,† respectively. Transition states were located at the O–O distance of 1.9 Å, 2.1 Å and 2.0 Å for [RuV(bda)(py)2–O]+, [FeV(bda)(py)2–O]+ and 6-coordinate [FeV(bda)(py)2–O]+ dimers. All three dimers at transition states keep the antiferromagnetic open shell singlet state as shown in Fig. S3.† Notably, the degeneracy of doublet–doublet coupling and quartet–quartet coupling appears for the 6-coordinate [FeV(bda)(py)2–O]+ dimer, like the degeneracy of 6-coordinate [FeV(bda)(py)2–O]+ monomer at doublet and quartet states as shown in Fig. 4 and S1.† As shown in Table 5, the electronic activation energy for the RuV dimer is 2.2 kcal mol−1, which is in agreement with our previous study.36 For the [FeV(bda)(py)2–O]+ dimer, the electronic activation energy is low to 0.8 kcal mol−1 while the 6-coordinate [FeV(bda)(py)2–O]+dimer has the highest electronic energy barrier up to 8.3 kcal mol−1. After adding thermal corrections and solvation energies, the Gibbs activation free energies are 5.0, 2.4 and 8.7 kcal mol−1 for [RuV(bda)(py)2–O]+, [FeV(bda)(py)2–O]+ and 6-coordinate [FeV(bda)(py)2–O]+ dimers, respectively. The lower energy barrier of FeV dimer supports that [FeV(bda)(py)2–O]+ monomer is more reactive in the I2M mechanism owing to the unstable pseudo 7-coordinate [FeV(bda)(py)2–O]+ reactant. Comparing the different [MV(bda)(py)2–O]+ dimer systems, we found that the more stable 6-coordinate [FeV(bda)(py)2–O]+ dimer has a significanlty higher barrier in the I2M process than the RuV dimer. For [RuV(bda)(py)2–O]+ dimer, the whole system keeps a compact structure and the Ru metal center is tightly linked to bda ligand and two pyridine ligands. By contrast, the [FeV(bda)(py)2–O]+ is less compact and Fe tends to have a pseudo 7 coordination. The 6-coordinate octahedral [FeV(bda)(py)2–O]+ is stable in agreement with other reported Fe WOCs which typically prefer an octahedral Fe-based geometry.44 From this study and the synthesized Fe-based WOCs in published studies,13,18,44 we conclude that Fe does not form a coordination number of 7.


image file: d2dt01150f-f6.tif
Fig. 6 Energy profile of [MV(bda)(py)2–O]+ dimer with decreasing O–O distance.

image file: d2dt01150f-f7.tif
Fig. 7 Transition state structures of [RuV(bda)(py)2–O]+ dimer (a, O–O distance 1.9 Å), [FeV(bda)(py)2–O]+ dimer (b, O–O distance 2.1 Å) and 6-coordinate [FeV(bda)(py)2–O]+ dimer (c, O–O distance 2.0 Å).
Table 5 Electronic energy barrier, reaction energy and Gibbs free energy barrier of radical coupling
  Energy barrier ΔE‡ (kcal mol−1) Reaction energy ΔE‡ (kcal mol−1) Energy barrier ΔG‡ (kcal mol−1)
[RuV(bda)(py)2–O]+ 2.2 −20.6 5.0
[FeV(bda)(py)2–O]+ 0.8 −78.2 2.4
6-Coordinate [FeV(bda)(py)2–O]+ 8.3 −23.9 8.7

Concerning the electronic reaction energy of the three dimers, FeV dimer has a reaction energy of −78.2 kcal mol−1, which is much larger than those of RuV and 6-coordinate FeV dimer, −20.6 and −23.9 kcal mol−1 respectively. The large reaction energy of FeV dimer is due to two factors: (1) more energy is stored in FeV monomer since very high potentials are needed to reach that state (2) The reaction leads to direct generation of O2 that can be seen from the long distances (2.77 Å, 2.75 Å) between two pairs of Fe and O atoms indicated in Fig. 8(b).


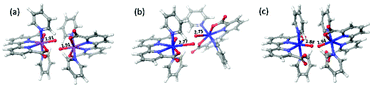image file: d2dt01150f-f8.tif
Fig. 8 Product structures of [RuV(bda)(py)2–O]+ dimer (a, O–O distance 1.4 Å), [FeV(bda)(py)2–O]+ dimer (b, O–O distance 1.2 Å) and 6-coordinate [FeV(bda)(py)2–O]+ dimer (c, O–O distance 1.3 Å).

Conclusions

We made a comparative study of the well-known Ru(bda)L2 catalyst to the iron analogue Fe(bda)L2. We found clear differences between the two systems. (1) The potentials for oxidizing the metal center up to the reactive MV[double bond, length as m-dash]O state was significantly higher for the Fe system compared to the Ru catalyst. We found that both the electrons and the protons are more tightly bound to Fe than Ru. (2) The Fe complex showed a preference for the high spin state for all oxidation states, while the Ru was more stable in the low spin state. This leads to lower tendency for Fe to form the unique 7-coordinate structure of Ru(bda)L2. The Fe structures that had a geometry resembling a 7-coordinate structure was found to be better described as pseudo-7-coordinate due to some very long metal ligand distances. This leads to the proposed reactive FeV[double bond, length as m-dash]O species rearranging to a more stable 6-coordinate structure. (3) While the pseudo-7-coordinate Fe structure could react via an I2M mechanism we found that the more stable 6-coordinate structure had a higher activation energy. Summing up these observations we conclude that replacing Ru with Fe requires a significant change in the ligand system. The bda with two additional pyridine type ligands lead to a system with high spin preference for iron which does not favor the 7-coordinate geometry and which leads to very high potentials for reaching the higher oxidation states.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by Vetenskapsrådet (2018-05396), the China Scholarship Council (CSC), and the Knut & Alice Wallenberg (KAW) project CATSS (KAW 2016.0072). The computations were enabled by resources provided by the Swedish National Infrastructure for Computing (SNIC) at National Supercomputer Center (NSC, Linköping University, Project numbers: SNIC2021/5-591, SNIC2022/22-3 and SNIC2021/22-854) and PDC Center for High Performance Computing (PDC-HPC, KTH, Royal Institute of Technology, Project number: SNIC2021/5-593) partially funded by the Swedish Research Council through grant agreement no. 2018-05973.

References

  1. J. Chow, R. J. Kopp and P. R. Portney, Science, 2003, 302, 1528 CrossRef PubMed.
  2. M. D. Kärkäs, O. Verho, E. V. Johnston and B. Åkermark, Chem. Rev., 2014, 114, 11863–12001 CrossRef PubMed.
  3. S. W. Gersten, G. J. Samuels and T. J. Meyer, J. Am. Chem. Soc., 1982, 104, 4029–4030 CrossRef CAS.
  4. L. Duan, A. Fischer, Y. Xu and L. Sun, J. Am. Chem. Soc., 2009, 131, 10397–10399 CrossRef CAS PubMed.
  5. L. Duan, F. Bozoglian, S. Mandal, B. Stewart, T. Privalov, A. Llobet and L. Sun, Nat. Chem., 2012, 4, 418–423 CrossRef CAS PubMed.
  6. Y. Umena, K. Kawakami, J.-R. Shen and N. Kamiya, Nature, 2011, 473, 55–60 CrossRef CAS PubMed.
  7. J. P. McEvoy and G. W. Brudvig, Chem. Rev., 2006, 106, 4455–4483 CrossRef CAS PubMed.
  8. L. Duan, C. M. Araujo, M. S. G. Ahlquist and L. Sun, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 15584 CrossRef CAS PubMed.
  9. L. Wang, L. Duan, Y. Wang, M. S. G. Ahlquist and L. Sun, Chem. Commun., 2014, 50, 12947–12950 RSC.
  10. N. D. McDaniel, F. J. Coughlin, L. L. Tinker and S. Bernhard, J. Am. Chem. Soc., 2008, 130, 210–217 CrossRef CAS PubMed.
  11. G. F. Moore, J. D. Blakemore, R. L. Milot, J. F. Hull, H.-E. Song, L. Cai, C. A. Schmuttenmaer, R. H. Crabtree and G. W. Brudvig, Energy Environ. Sci., 2011, 4, 2389–2392 RSC.
  12. J. Limburg, J. S. Vrettos, L. M. Liable-Sands, A. L. Rheingold, R. H. Crabtree and G. W. Brudvig, Science, 1999, 283, 1524–1527 CrossRef CAS PubMed.
  13. W. C. Ellis, N. D. McDaniel, S. Bernhard and T. J. Collins, J. Am. Chem. Soc., 2010, 132, 10990–10991 CrossRef CAS PubMed.
  14. S. M. Barnett, K. I. Goldberg and J. M. Mayer, Nat. Chem., 2012, 4, 498–502 CrossRef CAS PubMed.
  15. D. Wang and J. T. Groves, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 15579 CrossRef CAS PubMed.
  16. G. Zhu, E. N. Glass, C. Zhao, H. Lv, J. W. Vickers, Y. V. Geletii, D. G. Musaev, J. Song and C. L. Hill, Dalton Trans., 2012, 41, 13043–13049 RSC.
  17. Y. Han, Y. Wu, W. Lai and R. Cao, Inorg. Chem., 2015, 54, 5604–5613 CrossRef CAS PubMed.
  18. J. L. Fillol, Z. Codolà, I. Garcia-Bosch, L. Gómez, J. J. Pla and M. Costas, Nat. Chem., 2011, 3, 807–813 CrossRef CAS PubMed.
  19. F. Acuña-Parés, Z. Codolà, M. Costas, J. M. Luis and J. Lloret-Fillol, Chem. – Eur. J., 2014, 20, 5696–5707 CrossRef PubMed.
  20. M. Z. Ertem, L. Gagliardi and C. J. Cramer, Chem. Sci., 2012, 3, 1293–1299 RSC.
  21. M. Okamura, M. Kondo, R. Kuga, Y. Kurashige, T. Yanai, S. Hayami, V. K. K. Praneeth, M. Yoshida, K. Yoneda, S. Kawata and S. Masaoka, Nature, 2016, 530, 465–468 CrossRef CAS PubMed.
  22. R.-Z. Liao, S. Masaoka and P. E. M. Siegbahn, ACS Catal., 2018, 8, 11671–11678 CrossRef CAS.
  23. A. D. Bochevarov, E. Harder, T. F. Hughes, J. R. Greenwood, D. A. Braden, D. M. Philipp, D. Rinaldo, M. D. Halls, J. Zhang and R. A. Friesner, Int. J. Quantum Chem., 2013, 113, 2110–2142 CrossRef CAS.
  24. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
  25. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
  26. P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 299–310 CrossRef CAS.
  27. O. Salomon, M. Reiher and B. A. Hess, J. Chem. Phys., 2002, 117, 4729–4737 CrossRef CAS.
  28. Y. Zhao and D. G. Truhlar, J. Chem. Phys., 2006, 125, 194101 CrossRef PubMed.
  29. The LACV3P basis set is a triple-zeta contraction of the LACVP basis set developed and tested at Schrödinger, Inc.
  30. D. J. Tannor, B. Marten, R. Murphy, R. A. Friesner, D. Sitkoff, A. Nicholls, B. Honig, M. Ringnalda and W. A. Goddard, J. Am. Chem. Soc., 1994, 116, 11875–11882 CrossRef CAS.
  31. B. Marten, K. Kim, C. Cortis, R. A. Friesner, R. B. Murphy, M. N. Ringnalda, D. Sitkoff and B. Honig, J. Phys. Chem., 1996, 100, 11775–11788 CrossRef CAS.
  32. A. A. Isse and A. Gennaro, J. Phys. Chem. B, 2010, 114, 7894–7899 CrossRef CAS PubMed.
  33. C. P. Kelly, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2006, 110, 16066–16081 CrossRef CAS PubMed.
  34. M. D. Tissandier, K. A. Cowen, W. Y. Feng, E. Gundlach, M. H. Cohen, A. D. Earhart, J. V. Coe and T. R. Tuttle, J. Phys. Chem. A, 1998, 102, 7787–7794 CrossRef CAS.
  35. Q. Daniel, P. Huang, T. Fan, Y. Wang, L. Duan, L. Wang, F. Li, Z. Rinkevicius, F. Mamedov, M. S. G. Ahlquist, S. Styring and L. Sun, Coord. Chem. Rev., 2017, 346, 206–215 CrossRef CAS.
  36. T. Fan, S. Zhan and M. S. G. Ahlquist, ACS Catal., 2016, 6, 8308–8312 CrossRef CAS.
  37. R. Ezhov, A. K. Ravari and Y. Pushkar, Angew. Chem., Int. Ed., 2020, 59, 13502–13505 CrossRef CAS PubMed.
  38. A. Company, Y. Feng, M. Güell, X. Ribas, J. M. Luis, L. Que Jr. and M. Costas, Chem. – Eur. J., 2009, 15, 3359–3362 CrossRef CAS PubMed.
  39. Y.-Y. Li, L.-P. Tong and R.-Z. Liao, Inorg. Chem., 2018, 57, 4590–4601 CrossRef CAS PubMed.
  40. S. Hu, P. Xu, R.-X. Xu and X. Zheng, Inorg. Chem., 2021, 60, 7297–7305 CrossRef CAS PubMed.
  41. Y. Shimoyama and T. Kojima, Inorg. Chem., 2019, 58, 9517–9542 CrossRef CAS PubMed.
  42. S. Zhan, D. Mårtensson, M. Purg, S. C. L. Kamerlin and M. S. G. Ahlquist, Angew. Chem., Int. Ed., 2017, 56, 6962–6965 CrossRef CAS PubMed.
  43. D. W. Shaffer, Y. Xie and J. J. Concepcion, Chem. Soc. Rev., 2017, 46, 6170–6193 RSC.
  44. L. D. Wickramasinghe, R. Zhou, R. Zong, P. Vo, K. J. Gagnon and R. P. Thummel, J. Am. Chem. Soc., 2015, 137, 13260–13263 CrossRef CAS PubMed.

Footnote

† Electronic supplementary information (ESI) available: Details on energy differences among different multiplicities using different functionals, spin density contributions of [MV(bda)(py)2–O]+ monomers, spin density contributions of low-spin 6-coordinate [FeV(bda)(py)2–O]+ monomer and transition states of [MV(bda)(py)2–O]+ dimers, energy profiles of vertical and parallel radical coupling and Cartesian coordinates of all relevant structures. See DOI: https://doi.org/10.1039/d2dt01150f
This journal is © The Royal Society of Chemistry 2022