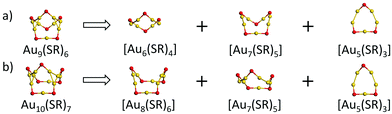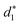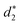View PDF VersionPrevious ArticleNext Article
 
DOI: 10.1039/D2CP00421F (Paper) Phys. Chem. Chem. Phys., 2022, 24, 15920-15924

New structural insights into the stability of Au22(SR)16 nanocluster under ring model guidance†

Wenhua Han a, Endong Wang *bc and Wen Wu Xu *a
aDepartment of Physics, School of Physical Science and Technology, Ningbo University, Ningbo, 315211, China. E-mail: xuwenwu@nbu.edu.cn
bSchool of Chemistry and Chemical Engineering, Liaoning Normal University, Dalian, 116029, China. E-mail: edwang@lnnu.edu.cn
cState Key Laboratory of Molecular Reaction Dynamics, Dalian Institute of Chemical Physics, Chinese Academy of Sciences, Dalian, 116023, China

Received 26th January 2022 , Accepted 13th June 2022

First published on 14th June 2022

Abstract

This study presents thorough structural insights into the stability of crystallized Au22(SAdm)16 (HSAdm = 1-adamantanethiol) nanocluster. With the recently developed Ring Model for describing the interaction between inner gold cores and outer protecting ligands in thiolate-protected gold nanoclusters, the experimental spontaneous transformation from the crystallized Au22(SAdm)16 to Au21(SAdm)15 could be well understood as structurally unfavorable for the current Au22(SAdm)16 and could also be attributed to the weaker aurophilic interaction between the inner Au4 core and the surrounding rings in Au22(SAdm)16 over that in Au21(SAdm)15. Furthermore, with the Ring Model and the grand unified model, two new Au22(SCH3)16 isomers with evident lower energies, higher HOMO–LUMO gaps as well as distinct optical properties over the available crystallized isomer were obtained. This study deepens the current knowledge on the structure of the Au22(SR)16 cluster from a new structural point of view and also confirms the validity as well as practicability of the Ring Model in understanding and predicting the stable structures of thiolate-protected gold nanoclusters.

Introduction

Understanding the structural stability of thiolate-protected gold nanoclusters is still a challenging task.1–4 Although numerous X-ray crystallography gold nanoclusters show high stability,5–8 several with low thermostability were also observed. For example, the experimentally crystallized Au38(PET)24 (referred as Au38T, PET = SC2H4Ph) nanoclusters can irreversibly transform to their another crystallized isomer Au38(PET)24 (referred as Au38Q) at 50 °C in toluene, indicating the low thermostablity of Au38T with respect to Au38Q.9 Besides, in principle, the 18-electron closed-shell Au44(2,4-DMBT)26 (2,4-DMBTH = 2,4-dimethylbenzenethiol) is expected to be more stable than 16-electron Au44(TBBT)28 (TBBTH = 4-tert-butylbenzenelthiol).10 Dynamic UV/vis/NIR spectra confirms that Au44(2,4-DMBT)26 can transform to other gold nanoclusters under 80 °C. Under the same conditions, similar transformation was not observed for Au44(TBBT)28, which indicates that Au44(2,4-DMBT)26 is actually less thermostable than Au44(TBBT)28 under 80 °C.10 In addition, Au22(SAdm)16 (SAdm = 1-adamantanethiol) was recently found to be metastable in a solution and can spontaneously transform into Au21(SAdm)15.11,12 These structural alternations clearly show that some crystallized thiolate-protected gold nanoclusters with low thermostability do exist. However, the structural insights on the geometrical transformation of these crystallized structures, and if there exists a more stable isomer, are yet to be unravelled.

Over the past decades, this field has seen tremendous progresses.13–20 Several models including divide and protect concept,13 superatom complex model,21 superatom network model,22 super valence bond model,23 polyhedra method,24 inherent structure rule,25 grand unified model (GUM)26 as well as Ring model27 have been developed to gain a better understanding of the stabilities of thiolate-protected gold nanoclusters. Among them, the Ring model was recently developed to describe the interfacial interaction between the inner gold cores and the outer protecting motifs of thiolate-protected gold nanoclusters. Several thiolate-protected clusters have been predicted via the Ring model, which demonstrates the usefulness in understanding the structural characters of ligand clusters.28,29 In the Ring model, thiolate-protected gold nanoclusters can be decomposed into several fusing or interlocking [Auq(SR)p] (q = 4–8, 10, 12, and 0 ≤ p ≤ q) rings. With the Ring model, this study presents new structural insights into the less thermostability of crystallized Au22(SAdm)16 with respect to the Au21(SAdm)15 nanocluster. Furthermore, another two isomeric structures of Au22(SR)16 (R = CH3) were obtained, which own lower relative energies and higher HOMO–LUMO gaps over the available crystallized structure.

Results and discussion

Structural understanding of Au22(SR)16via the Ring model and GUM model

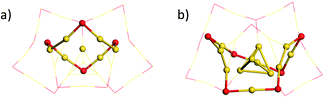
We first focused on the structural analysis of crystallized Au22(SR)16 and Au21(SR)15 (R = SAdm) nanoclusters in a straightforward manner following GUM. As shown in Fig. 1, GUM suggests that both clusters own one green-colored Au4(2e) elementary blocks and two blue-colored Au3(2e) elementary blocks as the kernel. Through the proper alignments of the core and the outer ligands, both Au22(SR)16 and Au21(SR)15 have one Au12(SR)9 part, which is made up of a Au4 block in green background and Au8(SR)9 ligand. Upon removing this Au12(SR)9 part from Au21(SR)15, a Au9(SR)6 cage can be seen, as shown in Fig. 1(a). Similarly, for Au22(SR)16, a Au10(SR)7 cage can be observed, as given in Fig. 1(b). Therefore, Fig. 1 shows that the main structural difference between crystallized Au22(SR)16 and Au21(SR)15 lies in the aforementioned two different sized cages, i.e. Au9(SR)6 cage for Au21(SR)15vs. Au10(SR)7 cage for Au22(SR)16.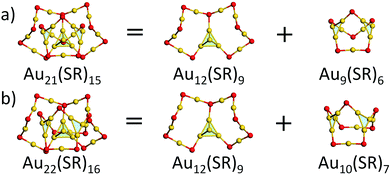
image file: d2cp00421f-f1.tif
Fig. 1 Geometric decompositions of (a) Au21(SR)15 and (b) Au22(SR)16 (R = SAdm). Au: yellow; S: red. The R groups are omitted for clarity.

With the Ring model, further analysis of the main structural difference between the Au9(SR)6 cage and the Au10(SR)7 cage was performed, as shown in Fig. 2. The Au9(SR)6 cage can be viewed as three rings [Au7(SR)5], [Au6(SR)4], and [Au5(SR)3] fusing together (Fig. 2(a)). The Au10(SR)7 cage can be viewed as three rings [Au8(SR)6], [Au7(SR)5], and [Au5(SR)3] fusing together (Fig. 2(b)). Therefore, the difference between the Au9(SR)6 cage of Au21(SR)15 and the Au10(SR)7 cage of Au22(SR)16 can be ascribed to the different rings fusing together.


image file: d2cp00421f-f2.tif
Fig. 2 Ring model-driven structural decomposition of (a) the [Au9(SR)6] ring of Au21(SR)15 and (b) [Au10(SR)7] ring of Au22(SR)16 into different rings. Au: yellow; S: red. The R groups are omitted for clarity.

With the increment of the radii of the ring, the Ring model suggests that the ring should properly match with the structures of the within this ring to maximize the interaction between the central structure and the outer ring.27 Summarized from the available crystal structures, the Ring model suggests that there should be one gold atom in the centre of the [Au5(SR)q] (1 ≤ q < 5) ring.27 For the [Au6(SR)q] (0 ≤ q ≤ 6) ring, one gold atom or one triangular Au3 should locate at the centre of the ring.27 For the [Au7(SR)q] (q = 4 and 5) ring, there is one tetrahedral Au4 located at the centre of the ring.27 For the [Au8(SR)q] (q = 4 and 8) ring, there should be two tetrahedral Au4 located at the centre of the rings.27

Based on the structural analysis of Fig. 1 and 2, special attention should be paid to the structural configurations of the Au9(SR)6 cage of Au21(SR)15 and Au10(SR)7 cage of Au22(SR)16 with the ring model. As given in Fig. 3, it can be found that the Au9(SR)6 cage of the Au21(SR)15 cluster one gold atom is located at the centre of [Au6(SR)4] ring, which satisfies the ring model. However, for the Au10(SR)7 cage of the Au22(SR)16 cluster, there is only one tetrahedral Au4 located at the centre of the [Au8(SR)6] ring, which conflicts with the Ring model, namely, two Au4 should exist within [Au8(SR)8] ring, as given in Table 1. Therefore, the experimental result could be ascribed to the confliction with the Ring model for the structural configuration in Au22(SR)16. For the [Au7(SR)5] ring and [Au5(SR)3] ring of both clusters, there is one tetrahedral Au4 located at the centre of the [Au7(SR)5] ring and one gold atom located below the centre of the [Au5(SR)3] ring, as given in Fig. S2 (ESI†), which is in accordance with the Ring model.


image file: d2cp00421f-f3.tif
Fig. 3 The structure locates at the centre of (a) the [Au6(SR)4] ring in the Au21(SR)15 cluster and (b) the [Au8(SR)6] ring in the Au22(SR)16 cluster. Au: yellow; S: red. The R groups are omitted for clarity.
Table 1 Inner structure of Au9(SR)6 cage in Au21(SR)15 and Au10(SR)7 cage in Au22(SR)16via the Ring model
[Au5(SR)3] [Au6(SR)4] [Au7(SR)5] [Au8(SR)6]
Au9(SR)6 cage Au Au Au4 —
Au10(SR)7 cage Au — Au4 Au4
Ring model Au Au/Au4 Au4 2Au4

In addition, the average distance between the gold atoms in tetrahedral Au4 and the gold atoms of three rings in the Au9(SR)6 cage in Au21(SR)15 (Fig. 2a) and the Au10(SR)7 cage in Au22(SR)16 (Fig. 2b) are also presented in Table 2. It can be found that the average Au–Au distances between Au4 and Au10(SR)7 cage in Au22(SR)16 are larger than those between Au4 and Au9(SR)6 cage in Au21(SR)15, which shows the weaker aurophilic interaction in Au22(SR)16 over that in Au21(SR)15. This also suggests the less thermostability of Au22(SR)16 than Au21(SR)15.

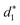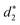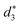Table 2 The average distance between the gold atoms in tetrahedral Au4 and the gold atoms of the surrounded rings. d1, d2 and d3 denote the average distance between the gold atoms in tetrahedral Au4 and the gold atoms of [Au7(SR)5], [Au6(SR)4], and [Au5(SR)3] rings in the Au9(SR)6 cage in Au21(SR)15, respectively. image file: d2cp00421f-t1.tif, image file: d2cp00421f-t2.tif and image file: d2cp00421f-t3.tif denote the average distances between the gold atoms in tetrahedral Au4 and the gold atoms of [Au8(SR)6], [Au7(SR)5], and [Au5(SR)3] rings in the Au9(SR)6 cage in Au21(SR)15, respectively. R is simplified as CH3
Au21(SR)15 Au22(SR)16
d 1 (Å) d 2 (Å) d 3 (Å)

image file: d2cp00421f-t4.tif

(Å)

image file: d2cp00421f-t5.tif

(Å)

image file: d2cp00421f-t6.tif

(Å)
2.980 3.030 2.762 3.368 3.223 2.949

Structural prediction of more stable isomers of Au22(SR)16

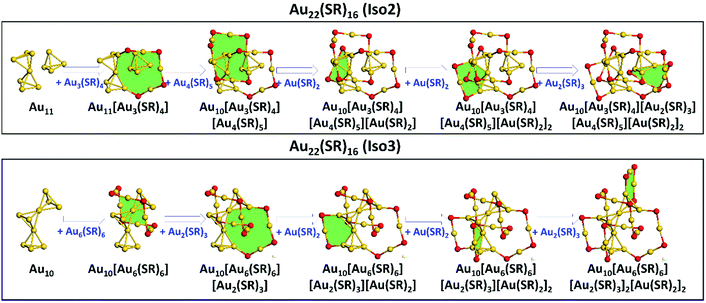
Based on the Ring model, we have obtained the structural insights into the less thermostability of Au22(SAdm)16 compared with Au21(SR)15, one may question if there exist more stable isomers of Au22(SR)16 with respect to the available crystallized structure (referred as Iso1 hereafter).

Recently, the GUM and Ring model have been used widely to predict the atomic structures of thiolate-protected gold nanoclusters, i.e., Au28+4n(SR)20+2n (n = 0–8) nanoclusters and Au15(SR)13 nanocluster with a new type of ligand [Au7(SR)7] ring.29,30 Here, the GUM together with the Ring model was employed to the structural predictions for Au22(SR)16. Based on GUM, two new Au11 and Au10 cores can be constructed by three packing or fusing tetrahedral Au4 units, as shown in Fig. 4. The Au11 core can be viewed as one bi-tetrahedron Au7 and one tetrahedron Au4 packing together, while the Au10 core can be viewed as three tetrahedron Au4 fusing together by sharing two gold atoms. Then, in accordance with the Ring model, the outer ligands were added to protect the newly constructed cores. For the Au11 core, two Au(SR)2, one Au2(SR)3, one Au3(SR)4, and one Au4(SR)5 ligands were added to surround the Au11 core via the formation of two [Au4(SR)2], one [Au4(SR)3], one [Au6(SR)4], and one [Au6(SR)5] rings (filled with green color in Fig. 4), which ultimately forms the whole structure of a new Au22(SR)16 isomer (referred as Iso2 hereafter). Following the same way, two Au(SR)2, two Au2(SR)3, and one Au6(SR)6 ligands can be added on the Au10 core via the formation of two [Au4(SR)2], one [Au4(SR)3], one [Au6(SR)3], and one [Au6(SR)6] rings (filled with green color in Fig. 4) to form the whole structure of another new Au22(SR)16 isomer (referred as Iso3). It should be noted that the [Au6(SR)6] ring has been confirmed in crystallized Au28(SR)22 nanoclusters.31


image file: d2cp00421f-f4.tif
Fig. 4 The structural predictions of two Au22(SR)16 isomers Iso2 (upper panel) and Iso3 (lower panel). Au: yellow; S: red. The rings were filled with green color. The R groups are omitted for clarity.

Further analysis on three Au22(SR)18 isomers via density functional theory calculations

To show the advantages of these two newly constructed isomers, density functional theory (DFT) calculations were performed to obtain the electronic properties of three Au22(SR)16 isomers with the Perdew–Burke–Ernzerhof (PBE) functional and the all-electron basis set 6-31G(d) for C, H, and S, pseudopotential basis set LANL2DZ for Au. In addition, Tao–Perdew–Staroverov–Scuseria functional (TPSS) and Becke's three parameter hybrid functional with the Lee–Yang–Parr correlation functional (B3LYP) were also employed to check the stabilities of Au22(SR)16 isomers. –CH3 was used as the outer organic ligand. All calculations were performed using the Orca package.32 Super-fast approximate TD-DFT implemented in the Orca package by Grimme et al. was used to obtain the UV-abs spectrum.33 As shown in Table 3, calculations using the three functionals (PBE, TPSS, and B3LYP) confirmed that both Iso2 and Iso3 had lower relative energies and larger HOMO–LUMO gaps (HL gaps) than the crystallized Iso1 with R = CH3. Frequency calculations showed that no imagination frequency existed, which confirmed the stability of these clusters. Calculations using the PBE functional showed that Iso2 was more stable than Iso1 by 0.17 eV, while Iso3 showed further stability with respect to Iso1 by 0.30 eV, which suggested the high stabilities of the predicted Iso2 and Iso3. Similar to the relative energy, taking the PBE functional as an example, Iso2 and Iso3 showed greater HOMO–LUMO gaps by 0.24 and 0.31 eV over Iso1, respectively. All the three functionals showed that Iso3 had the lowest relative energy and the largest HOMO–LUMO gap.
Table 3 Relative energies and HOMO–LUMO gaps of three Au22(SR)16 (R = CH3) isomers
Au22(SR)16 Relative energy (eV) HOMO–LUMO gap (eV)
PBE TPSS B3LYP PBE TPSS B3LYP
Iso1 0.30 0.25 0.21 1.66 1.59 2.75
Iso2 0.17 0.18 0.03 1.90 1.79 3.20
Iso3 0.00 0.00 0.00 1.97 1.96 3.20

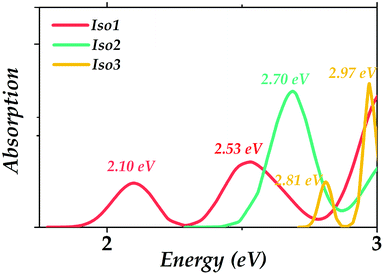
The calculated absorption spectra of the three Au22(SR)16 isomers are presented to compare with the experimental measurement and to obtain the optical absorption properties of the predicted isomers. PBE functional is widely known to cause a red-shift in the spectrum;34 herein, CAM-B3LYP was used to get the absorption spectra. Gaussian broadening was applied in obtaining the absorption spectra using the reorganization energy (Fig. S1, ESI†) as widths. It can be seen in Fig. 5 that the prominent absorption peaks of Iso1 (2.10, 2.53 eV) could well reproduce the experimental peaks (2.04, 2.66 eV), indicating the reliabilities of the theoretical methods employed in our simulations. In addition, the main absorption peak for Iso2 was 2.70 eV. Two absorption peaks for Iso3 included 2.81 eV and 2.97 eV.


image file: d2cp00421f-f5.tif
Fig. 5 Calculated optical absorption spectra for the three Au22(SR)16 (R = CH3) isomers.

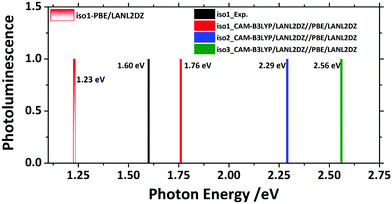
To show the optical emission properties of the three isomers, results on photoemission are also presented here, as can be seen in Fig. 6. Experimentally, Iso1 yielded emission at 1.60 eV from its first excited state. Fig. 6 and Fig. S1 (ESI†) showed that calculations using PBE functional gave 1.23 eV, which was significantly lower than the experimental one due to the lack of exact exchange.34 Thus, CAM-B3LYP functional was also used to rectify the emission spectrum, resulting in the emission peak (1.76 eV) that had a good agreement with the experiment (1.60 eV). Calculations showed that the emission peaks from the first excited state of Iso2 and Iso3 were 2.29 eV and 2.56 eV, respectively.


image file: d2cp00421f-f6.tif
Fig. 6 Photoluminescence spectra of the three Au22(SR)16 (R = CH3) isomers.

Conclusions

In summary, based on the recently developed Ring model, we presented new structural insights into the lower thermostability of Au22(SAdm)16 than Au21(SAdm)15. The violation of the Ring Model for the rings in Au22(SAdm)16 as well as the weaker aurophilic interactions between the Au4 core and surrounded rings in Au22(SAdm)16 led to the spontaneous transformation from Au22(SAdm)16 to Au21(SAdm)15. Further, with GUM and the Ring model, another two new Au22(SR)16 isomers with lower relative energies and higher HOMO–LUMO gaps over the crystallized isomer were predicted.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

W. W. X. was supported by Natural Science Foundation of China (Grant No. 11974195). E. W. thanks for the open fund of the state key laboratory of molecular reaction dynamics in DICP, CAS (SKLMRD-K202201).

References

  1. R. Jin, C. Zeng, M. Zhou and Y. Chen, Chem. Rev., 2016, 116, 10346–10413 CrossRef CAS PubMed.
  2. Z. Ma, P. Wang, L. Xiong and Y. Pei, WIREs Comput. Mol. Sci., 2017, 7, e1315 CrossRef.
  3. W. W. Xu, X. C. Zeng and Y. Gao, Acc. Chem. Res., 2018, 51, 2739–2747 CrossRef CAS PubMed.
  4. E. Wang and Y. Gao, J. Chem. Phys., 2021, 155, 044302 CrossRef CAS PubMed.
  5. X. Kang, Y. Li, M. Zhu and R. Jin, Chem. Soc. Rev., 2020, 49, 6443–6514 RSC.
  6. X. Kang and M. Zhu, Chem. Soc. Rev., 2019, 48, 2422–2457 RSC.
  7. X. Kang and M. Zhu, Chem. Mater., 2021, 33, 39–62 CrossRef CAS.
  8. X. Liu, W. W. Xu, X. Huang, E. Wang, X. Cai, Y. Zhao, J. Li, M. Xiao, C. Zhang, Y. Gao, W. Ding and Y. Zhu, Nat. Commun., 2020, 11, 3349 CrossRef CAS PubMed.
  9. S. Tian, Y.-Z. Li, M.-B. Li, J. Yuan, J. Yang, Z. Wu and R. Jin, Nat. Commun., 2015, 6, 8667 CrossRef CAS PubMed.
  10. L. Liao, S. Zhuang, C. Yao, N. Yan, J. Chen, C. Wang, N. Xia, X. Liu, M.-B. Li, L. Li, X. Bao and Z. Wu, J. Am. Chem. Soc., 2016, 138, 10425–10428 CrossRef CAS PubMed.
  11. Q. Li, S. Yang, T. Chen, S. Jin, J. Chai, H. Zhang and M. Zhu, Nanoscale, 2020, 12, 23694–23699 RSC.
  12. S. Chen, L. Xiong, S. Wang, Z. Ma, S. Jin, H. Sheng, Y. Pei and M. Zhu, J. Am. Chem. Soc., 2016, 138, 10754–10757 CrossRef CAS PubMed.
  13. H. Häkkinen, M. Walter and H. Grönbeck, J. Phys. Chem. B, 2006, 110, 9927–9931 CrossRef PubMed.
  14. D.-e Jiang, M. L. Tiago, W. Luo and S. Dai, J. Am. Chem. Soc., 2008, 130, 2777–2779 CrossRef CAS PubMed.
  15. C. M. Aikens, Acc. Chem. Res., 2018, 51, 3065–3073 CrossRef CAS PubMed.
  16. T. Higaki, Q. Li, M. Zhou, S. Zhao, Y. Li, S. Li and R. Jin, Acc. Chem. Res., 2018, 51, 2764–2773 CrossRef CAS PubMed.
  17. Q. Tang, G. Hu, V. Fung and D.-E. Jiang, Acc. Chem. Res., 2018, 51, 2793–2802 CrossRef CAS PubMed.
  18. K. L. D. M. Weerawardene, H. Häkkinen and C. M. Aikens, Annu. Rev. Phys. Chem., 2018, 69, 205–229 CrossRef CAS PubMed.
  19. P. Chakraborty, A. Nag, A. Chakraborty and T. Pradeep, Acc. Chem. Res., 2019, 52, 2–11 CrossRef CAS PubMed.
  20. Y. Pei, P. Wang, Z. Ma and L. Xiong, Acc. Chem. Res., 2019, 52, 23–33 CrossRef CAS PubMed.
  21. M. Walter, J. Akola, O. Lopez-Acevedo, P. D. Jadzinsky, G. Calero, C. J. Ackerson, R. L. Whetten, H. Grönbeck and H. Häkkinen, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 9157 CrossRef CAS PubMed.
  22. L. Cheng, Y. Yuan, X. Zhang and J. Yang, Angew. Chem., Int. Ed., 2013, 52, 9035–9039 CrossRef CAS PubMed.
  23. L. Cheng, C. Ren, X. Zhang and J. Yang, Nanoscale, 2013, 5, 1475–1478 RSC.
  24. A. Tlahuice-Flores, J. Phys. Chem. C, 2019, 123, 10831–10841 CrossRef CAS.
  25. Y. Pei, P. Wang, Z. Ma and L. Xiong, Acc. Chem. Res., 2019, 52, 23–33 CrossRef CAS PubMed.
  26. W. W. Xu, B. Zhu, X. C. Zeng and Y. Gao, Nat. Commun., 2016, 7, 13574 CrossRef CAS PubMed.
  27. W. Han, P. Liu, M. Zheng, X. C. Zeng and W. W. Xu, J. Phys. Chem. Lett., 2021, 12, 3006–3013 CrossRef CAS PubMed.
  28. L. Yang, Q. He, W. Han, P. Liu and W. W. Xu, Chem. Phys. Lett., 2021, 785, 139133 CrossRef CAS.
  29. P. Liu, W. Han, M. Zheng, W. Li, J. Ren, A. Tlahuice-Flores and W. W. Xu, J. Phys. Chem. A, 2021, 125, 5933–5938 CrossRef CAS PubMed.
  30. P. Liu, W. Han, M. Zheng and W. W. Xu, Nanoscale, 2020, 12, 20677–20683 RSC.
  31. Y. G. Srinivasulu, N. Goswami, Q. Yao and J. Xie, J. Phys. Chem. C, 2021, 125, 4066–4076 CrossRef CAS.
  32. F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108 CrossRef CAS PubMed.
  33. M. de Wergifosse and S. Grimme, J. Chem. Phys., 2018, 149, 024108 CrossRef PubMed.
  34. M. J. Alhilaly, M. S. Bootharaju, C. P. Joshi, T. M. Besong, A.-H. Emwas, R. Juarez-Mosqueda, S. Kaappa, S. Malola, K. Adil, A. Shkurenko, H. Häkkinen, M. Eddaoudi and O. M. Bakr, J. Am. Chem. Soc., 2016, 138, 14727–14732 CrossRef CAS PubMed.

Footnote

† Electronic supplementary information (ESI) available: Cartesian coordinates of two predicted Au22(SCH3)16 isomers included. See DOI: https://doi.org/10.1039/d2cp00421f
This journal is © the Owner Societies 2022