Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Self-adjusting binding pockets enhance H2 and CH4 adsorption in a uranium-based metal–organic framework†
Dominik P.
Halter
 ab,
Ryan A.
Klein
ab,
Ryan A.
Klein
 cd,
Michael A.
Boreen
cd,
Michael A.
Boreen
 ae,
Benjamin A.
Trump
d,
Craig M.
Brown
ae,
Benjamin A.
Trump
d,
Craig M.
Brown
 df and
Jeffrey R.
Long
df and
Jeffrey R.
Long
 *abg
*abg
aDepartment of Chemistry, University of California, Berkeley, CA 94720, USA. E-mail: jrlong@berkeley.edu
bMaterials Sciences Division, Lawrence Berkeley National Laboratory, Berkeley, CA 94720, USA
cChemistry and Nanoscience Department, National Renewable Energy Laboratory, Golden, CO 80401, USA
dCenter for Neutron Research, National Institute of Standards and Technology, Gaithersburg, MD 20899, USA
eChemical Sciences Division, Lawrence Berkeley National Laboratory, Berkeley, CA 94720, USA
fDepartment of Chemical Engineering, University of Delaware, Newark, DE 19716, USA
gDepartment of Chemical and Biomolecular Engineering, University of California, Berkeley, CA 94720, USA
First published on 27th May 2020
Abstract
A new, air-stable, permanently porous uranium(IV) metal–organic framework U(bdc)2 (1, bdc2− = 1,4-benzenedicarboxylate) was synthesized and its H2 and CH4 adsorption properties were investigated. Low temperature adsorption isotherms confirm strong adsorption of both gases in the framework at low pressures. In situ gas-dosed neutron diffraction experiments with different D2 loadings revealed a rare example of cooperative framework contraction (ΔV = −7.8%), triggered by D2 adsorption at low pressures. This deformation creates two optimized binding pockets for hydrogen (Qst = −8.6 kJ mol−1) per pore, in agreement with H2 adsorption data. Analogous experiments with CD4 (Qst = −24.8 kJ mol−1) and N,N-dimethylformamide as guests revealed that the binding pockets in 1 adjust by selective framework contractions that are unique for each adsorbent, augmenting individual host–guest interactions. Our results suggest that the strategic combination of binding pockets and structural flexibility in metal–organic frameworks holds great potential for the development of new adsorbents with an enhanced substrate affinity.
Introduction
Metal–organic frameworks are a class of chemically-robust, porous, and often rigid materials, composed of metal ions or clusters connected by bridging organic linkers.1–4 The physical and chemical properties of these materials are highly tunable based on choice of metal and linker, and thus metal–organic frameworks have been proposed for a wealth of applications,5–9 including catalysis,10–15 sensing,16–18 carbon capture,19–23 gas separations,24–26 and gas storage.27–31 Metal–organic frameworks have attracted particular interest as candidate gas storage materials for H2 and CH4 that could enable more efficient use of these energy carriers as cleaner fuel alternatives.32–38 However, significant advances are still needed to develop frameworks capable of maintaining interactions with these guests at ambient temperatures.39–41Two main strategies have been developed to achieve strong binding of H2 and CH4 in metal–organic frameworks. The first approach utilizes materials with coordinatively-unsaturated metal sites, which can polarize and strongly bind various guests.42,43 Representative of this materials class is the framework Ni2(m-dobdc) (m-dobdc4− = 4,6-dioxido-1,3-benzenedicarboxylate), which is currently the top performing material for ambient temperature, physisorptive H2 storage.33,34 The other strategy exploits tight binding pockets in small-pore frameworks, which can engage in multiple, weak interactions with guest molecules to achieve strong overall guest binding, analogous to shape-selective molecular recognition in enzymes.44 An example of how such cumulative dispersion forces can outperform strong interactions at open metal sites is the adsorption of CH4 in Cu2(btc)3 (HKUST-1, btc3− = 1,3,5-benzenetricarboxylate).45 This material exhibits open metal sites and binding pockets in direct competition for CH4 adsorption. Structural characterization of Cu2(btc)3 dosed with low pressures of CD4 confirmed that methane preferably adsorbs at the binding pockets inside small octahedral cages of the framework, rather than through direct interactions at the copper(II) open metal sites. The reason for this behavior is that the multiple interactions inside the pore give rise to a higher overall binding energy than that achieved with a CH4 molecule adsorbed at a single copper(II) center (−21.8 versus −9.4 kJ mol−1, respectively).45
Cumulative dispersion interactions between guest molecules and framework pockets decrease exponentially with the adsorbate–framework distances (F ∝ 1/r6), and therefore require a precise geometric fit between guest and binding pocket.46 For example, as a result of its smaller kinetic diameter relative to CH4,47 H2 preferentially binds at the open metal sites of Cu2(btc)3, rather than in the hexagonal pockets.48 The development of new frameworks with efficient binding pockets therefore requires precise optimization for each adsorbate of interest, although achieving this goal by structural design remains a significant challenge.
An alternative approach to circumvent the synthetic intricacy of developing materials with optimized guest–specific binding pockets, are materials that combine small binding pockets with moderate framework flexibility.49 Synthetic tuning can thus be used to design crude binding pockets, which are capable of self-adjusting in response to guest adsorption. Together, these design features could enable access to optimal binding pocket geometries for a variety of guests within the same material. Such molecular recognition often relies on initially weak host–guest interactions, highlighting the importance to precisely adjust the energy required for the deformation of a flexible framework and the energy released by guest adsorption.50–52
Flexibility is typically introduced into metal–organic frameworks by utilizing organic linkers with non-rigid stems, by interconnecting metals with non-chelating linkers, or by cross-linking two-dimensional frameworks with additional ditopic but weakly binding linkers.53–55 Prominent examples are M(OH)(bdc) (MIL-53; bdc2− = 1,4-benzenedicarboxylate; M = Fe, Cr, Sc, Al, or Ga)56–60 and M3(O)(OH)(H2O)2(bdc)3 (MIL-88; M = Fe, Cr).61 These frameworks undergo drastic geometric distortions upon guest adsorption, often referred to as framework swelling, which can induce a substantial unit cell volume increase of up to 74%, as shown for example by CO2 adsorption in Fe(OH)(bdc).62 Such large structural changes are too extreme to drive the subtle binding pocket adjustments sought here. One could instead envision limiting the flexibility of non-chelating bdc2− linkers by substantially increasing the number of metal–ligand bonds per metal node. A higher coordination number should limit structural rearrangements by causing steric encumbrance around the metal nodes and increase rigidity by further crosslinking the resulting material. Additionally, a higher ligand-to-metal ratio could result in smaller pore sizes and better binding pockets.
With their tendency to adopt high coordination numbers, actinides are well suited as metal nodes for the development of such materials.63 We chose depleted uranium to test our hypothesis, as it is only mildly radioactive and because a limited but growing number of uranium-based frameworks have already been reported and could guide the synthesis.64 Inspired by previous work on the synthesis of porous metal–organic frameworks from uranium(IV) and bdc2− linkers,65 we synthesized a new, three-dimensional U(bdc)2 phase (1) with permanent porosity and a moderate level of structural flexibility. Using a combination of gas adsorption studies and in situ powder neutron diffraction experiments, we demonstrate that this framework undergoes an adjustable contraction of its pores to accommodate and strongly bind H2 and CH4, with different levels of contraction and host–guest interactions for each molecule.
Results and discussion
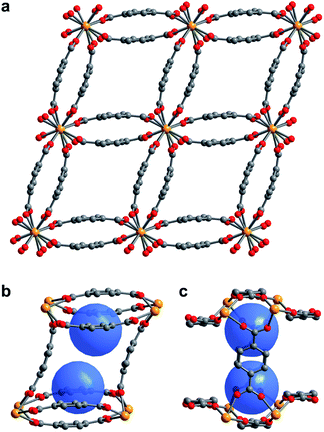
The compound U(bdc)2·4H2O (1–H2O) was synthesized through the reaction of UI4(1,4-dioxane)2 with H2bdc in N,N-dimethylformamide (DMF, <0.15% water content as received) at 140 °C under argon inside a Parr autoclave. After three days, the material was isolated in 79% yield as air-stable, thin emerald green needle-shaped crystals. Single crystal X-ray diffraction analysis was used to determine the structure of 1–H2O (Fig. 1), and selected bond distances and angles are given in Table S5 of the ESI.† We note that powder X-ray diffraction patterns collected for bulk samples of 1–H2O match the simulated pattern determined from single-crystal data, confirming the bulk purity of the crystalline material (see ESI, Fig. S7†).Compound 1–H2O crystallizes in the space group C2/c and features eight-coordinate uranium centers in a distorted square-antiprismatic environment. Each uranium(IV) is coordinated to one oxygen atom of eight different bdc2− linkers, and all linkers are coordinated to four different uranium ions in a bridging fashion. This motif results in an overall framework structure consisting of distorted parallelepipedal pores (Fig. 1a) formed by chains of uranium(IV) centers that propagate along the crystallographic c-axis (see ESI, Fig. S17†) and are bridged by bdc2− linkers bent in a concave and convex fashion.
Each pore is formed by two opposing, inwardly bent bdc2− linkers at the sides and is capped at the top and bottom by a bowl-shaped arrangement of three additional bdc2− linkers (Fig. 1b and c). The resulting geometry yields two identical binding pockets per pore that are ∼5 Å in diameter and related by an inversion center.
In the as-synthesized framework, each binding pocket is occupied by two disordered water molecules, yielding the composition U(bdc)2·4H2O, which was also confirmed by thermogravimetric analysis (see ESI, Fig. S6†). While disorder precluded modeling of any specific interactions, the guest water molecules are likely to engage in hydrogen bonding with each other and with the highly polarized U–O bonds. We note that the structure of the pores is such that guests could engage in a variety of additional interactions, including with the linker π-systems and arene C–H bonds.
Activated U(bdc)2 (1) was obtained by heating 1–H2O at 260 °C for 10 h under dynamic vacuum. Combustion analysis confirmed the empirical formula for 1 and the removal of guest water molecules. Nitrogen adsorption isotherms obtained at 77 K for four different samples revealed the activated material is permanently porous, with an average Langmuir surface area of 497 ± 6 m2 g−1 (see ESI, Fig. S1†). Powder X-ray diffraction analysis confirmed that 1 remains crystalline with a slightly different structure from that of its solvated analogue (see ESI, Fig. S7†). Interestingly, while many flexible frameworks contract or even fully collapse to a nonporous structure upon solvent removal,37,66–68 activation of 1–H2O to give 1 results in an expansion of the framework along the crystallographic b-axis, from 12.598(1) to 12.812(1) Å. This change results in an increase in the unit cell volume from 1887.4(3) to 1902.1(2) Å3, while retaining the C2/c space group. This behavior upon guest removal indicates that the framework binding pockets are indeed able to contract to improve interactions with adsorbates.
We sought to study the flexibility of 1 in more detail using H2 and CH4 (with kinetic diameters of 2.9 and 3.8 Å, respectively)18 as probe molecules of interest for potential gas storage applications. The low-pressure H2 adsorption isotherm for U(bdc)2 at 77 K exhibits an initial steep rise to ∼3.5 mmol g−1 at 115 mbar, which is indicative of the presence of strong adsorption sites (Fig. 2). We note that this loading corresponds to the theoretical capacity expected for adsorption of one H2 molecule per adsorption pocket (two per pore). With further increasing pressure, the quantity of adsorbed H2 increases very gradually to an apparent saturation value of ∼4.9 mmol g−1 at 1.2 bar. A dual site Langmuir model was used to fit independently H2 adsorption data collected at 77 and 87 K (see Section 3 of the ESI, Fig. S2 and Table S1†), and the Clausius–Clapeyron equation was then employed to calculate the isosteric heat (Qst) of H2 adsorption as a function of loading (Fig. 2, inset). For loadings up to 2.5 mmol g−1, H2 adsorbs exclusively at primary binding sites in the framework pockets (see below) to give a Qst of −8.6 kJ mol−1. Notably, this value is larger in magnitude than the H2 isosteric heat of adsorption in activated carbon materials (−5.0 to −6.4 kJ mol−1)69 and the majority of frameworks with coordinatively-saturated metal sites (−4.1 to −8.8 kJ mol−1).70
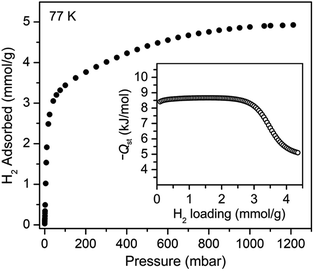 | ||
| Fig. 2 Hydrogen adsorption isotherm for 1, measured at 77 K. Inset: loading-dependent isosteric heat of adsorption (Qst) for H2 in 1. | ||
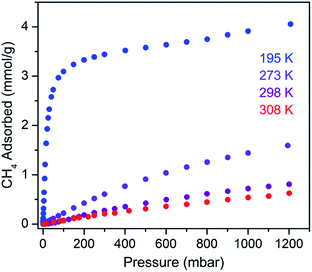
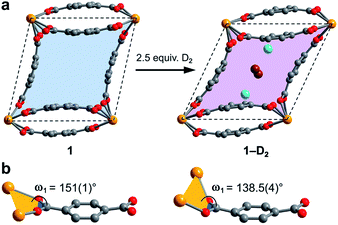
The CH4 adsorption isotherm for 1 obtained at 195 K exhibits a steep uptake similar to that characterized for H2 at low pressures, again indicative of strong interactions between CH4 and the binding pockets of the framework (Fig. 3). A dual site Langmuir model was used to simultaneously fit isotherm data collected at 195, 273, 298, and 308 K, and the Clausius–Clapeyron equation was then employed to calculate a value of Qst = −24.8 kJ mol−1 at low loadings (see ESI, Fig. S5†). Notably, this value surpasses that determined for Zn4O(bdc)3 (MOF-5; Qst = −12.3 kJ mol−1) and even values for frameworks with snugly fitting pore window, such as Cu2(btc)3 (Qst = −17.1 kJ mol−1), or strongly polarizing open metal cation sites, as in Ni2(dobdc) (dobdc4− = 2,5-dioxido-1,4-benzenedicarboxylate; Qst = −20.6 kJ mol−1).41,45 It is clear that the binding pockets in U(bdc)2 can strongly interact with both H2 and CH4, despite their different sizes, which suggests that the framework may distort or flex to optimize interactions with different guest molecules. In order to study the framework–guest interactions in more detail, we turned to in situ gas-dosing powder neutron diffraction. The powder neutron diffraction pattern of activated 1 at 9 K was first collected as a reference for gas dosing experiments (see ESI, Fig. S9†). Dosing with 0.3 equiv. of D2 per pore results in clear changes in the powder pattern, particularly visible at low values of scattering angle 2θ (Fig. 4 and S10†). Specifically, the reflections of 1 decrease in intensity while a second set of peaks arises, ascribed to a new crystalline phase 1–D2. Upon increasing the loading to 0.7 equiv. of D2, both phases are still present, although the peaks of 1 diminish further and the peaks of newly formed 1–D2 gain in intensity (Fig. 4 and S11†). The two phases coexist up to a loading of at least 1.5 equiv. D2 per pore (see ESI, Fig. S12†), and their interconversion is best followed by evaluating the high intensity, low angle peaks at 2θ ≈ 11.85° for 1 and at 2θ ≈ 12.63° for 1–D2 in Fig. 4. These data strongly suggest that cooperative effects drive an adsorbate-induced framework distortion from 1 to 1–D2. Such a mechanism is in contrast to a gradual and homogeneous uptake of D2, or a gradually changing degree of distortion depending on the D2-loading. As a result, before achieving saturation loading, some individual crystallites of the sample will be distorted, such that both binding pockets per pore are occupied with a D2 molecule, while others will remain in the activated structure of 1. At the highest D2 dosing level of 2.5 equiv. per pore, the diffraction pattern of the sample contains only reflections associated with 1–D2 (see ESI, Fig. S13†).
In situ powder neutron diffraction experiments were also carried out by dosing 1 with 0.7 and 1.5 equiv. of CD4 (Fig. S14 and S15†). The data from these experiments suggest a similar cooperative transformation from 1 to an adsorbed phase 1–CD4. Rietveld refinements were applied to all powder neutron diffraction data (see Section 6 in the ESI†) in order to elucidate adsorbate-induced structural deformations and characterize specific adsorption sites for D2 and CD4. Selected unit cell parameters determined for the different structures are summarized in Table 1. Based on unit cell volume, 1 contracts to a greater extent to accommodate D2 than it does in the presence of CH4.
| Sample | a (Å) | b (Å) | c (Å) | V (Å3) | φ 1 (°) | φ 2 (°) | ω 1 (°) | ω 2 (°) |
|---|---|---|---|---|---|---|---|---|
| 1 | 17.587(1) | 12.812(1) | 9.2999(5) | 1902.1(2) | 77.1(1) | 102.902(3) | 151(1) | 168.4(9) |
| 1–D2 (0.3 equiv.) | 18.361(7) | 11.35(1) | 9.335(2) | 1782(2) | 67.51(1) | 112.491(9) | 148.7(3) | 159.6(3) |
| 1–D2 (0.7 equiv.) | 18.402(3) | 11.324(5) | 9.333(1) | 1781.4(8) | 67.4(2) | 112.576(1) | 130(2) | 175(3) |
| 1–D2 (1.5 equiv.) | 18.456(1) | 11.233(1) | 9.3508(4) | 1775.8(2) | 66.86(6) | 113.143(1) | 141.4(8) | 170(1) |
| 1–D2 (2.5 equiv.) | 18.665(1) | 10.9486(8) | 9.3838(5) | 1754.5(2) | 65.03(6) | 114.973(1) | 138.5(4) | 174.9(5) |
| 1–CD4 (1.5 equiv.) | 18.031(1) | 11.9665(7) | 9.3206(4) | 1839.3(2) | 71.52(5) | 108.483(1) | 142(3) | 171.1(9) |
| 1–DMF | 18.2658(7) | 12.0252(5) | 9.3579(3) | 1865.6(1) | 71.63(4) | 108.373(1) | 166(11) | 164(4) |
Surprisingly, a structural comparison of 1 with 1–D2 and 1–CD4 reveals an almost constant coordination environment around the uranium nodes in each phase. The framework flexibility instead relies on a tilting of the parallelepipedal pores, which is clearly seen by comparing the pore geometries of 1 and 1–D2 dosed with 2.5 equiv. D2, as shown in Fig. 5a. Here, each structure is overlaid with an idealized parallelogram with corners defined by the uranium ions. Dosing with 2.5 equiv. of D2 results in a change of the idealized parallelogram angles, φ1 and φ2, from 77.1(1)° and 102.902(3)° in 1 to 65.03(6)° and 114.973(1)° in 1–D2. In order to accommodate this rearrangement, the two unique dihedral angles, ω1 and ω2, between the bdc2− O–C–O planes and the neighboring O–U⋯U–O planes adjust from 151(1)° and 168.4(9)° in 1 to 138.5(4)° and 174.9(5)° in 1–D2 (Fig. 5b).
The resulting hinge-type bending between the UO8 nodes and linkers is analogous to the change that occurs in the structure of the flexible framework Cr(OH)(bdc) upon water adsorption.53 In particular, water adsorption is accompanied by a unit cell volume decrease from 1486.1 to 1012.6 Å3, as well as a decrease of the symmetrical dihedral angles, ω, from 179.8° to 162.3°. The analogous idealized Cr⋯Cr⋯Cr angles φ1 and φ2 in Cr(OH)(bdc) change drastically from 75.9° and 104.2° (activated) to 44.8° and 135.2° (hydrated).56 Interestingly, in distinct contrast to 1, Cr(OH)(bdc) distorts very little upon interaction with D2 (<4 equiv. per pore), adopting a symmetric dihedral angle ω = 178.4° and Cr⋯Cr⋯Cr angles of 80.6° and 99.4°, concomitant with a very small unit cell volume increase to 1534.5 Å3.58,71 The change in the structure of 1 upon dosing with 2.5 equiv. of D2 results in a much more drastic change in unit cell volume, from 1902.1(2) to 1754.5(2) Å3. We rationalize that the greater deformation of 1 arises as a result of its better ability to enshroud H2 within its pores, which leads to a greater adsorption enthalpy (Qst = −8.6 kJ mol−1vs. −6.9 kJ mol−1 for Cr(OH)(bdc)),72 and a larger driving force for structural rearrangement. Thus, the smaller pores within the framework of 1 are able to optimize binding through multiple stabilizing interactions, whereas the comparably large pores of Cr(OH)(bdc) provide fewer contacts.
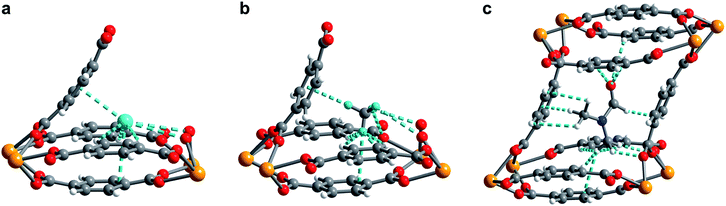
In order to elucidate the hydrogen binding sites in 1, we treated the D2 molecules as “super atoms” in our analysis of the diffraction data (see ESI, Section 6†).73,74 We first analyzed the structure of 1 loaded with 1.5 equiv. of D2 per pore (corresponding to less than one D2 per pocket) to enable an accurate structure determination in the absence of adsorbate–adsorbate interactions.75–77 As expected, the D2 super atoms were located in both binding pockets of each pore, with an occupancy of 75% per site. Each D2 super atom is situated within van der Waals contact distance of three H atoms of bdc2− linkers, the π-system of the outer pocket-capping bdc2− linker, and two oxygen atoms of the UO8 coordination polyhedron (Fig. 6a). The D2⋯H contact distances of 2.96(1), 2.98(1), and 3.15(2) Å indicate moderately strong van der Waals interactions.74,78,79 The distance from D2 to the centroid of the nearest benzene ring is 3.45(1) Å, which is indicative of a modest D2⋯π interaction,80 while the closest D2⋯O contact is 3.59(1) Å. In the structure of 1 dosed with 2.5 equiv. of D2, an additional D2 molecule was located in the center of the pore (site II, see Fig. 5a). The D2 molecules at site II are stabilized by four symmetry equivalent D2⋯D2 interactions at a distance of 3.10(1) Å, as well as by weak C–H⋯D2 contacts with the linkers (3.31(3) and 3.55(1) Å). As discussed above, in order to accommodate these interactions, the pores of 1 contract significantly around the D2 molecules, decreasing the unit cell volume by as much as 7.8% and shrinking the binding pocket diameter from 5.0 to 3.6 Å (see ESI, Section 6†). The crucial role of this structural distortion is further exemplified by considering a hypothetical D2 super atom at the fractional coordinates of site I in fully activated 1. In this environment, the D2···framework interactions are elongated beyond meaningful van der Waals contact distances (see ESI, Section 6†).
Rietveld refinement of in situ powder neutron diffraction data collected for 1 dosed with 1.5 equiv. of CD4 confirmed that the molecule occupies the same adsorption pocket as D2 (site I). Due to the larger size of CD4 relative to D2, a less pronounced contraction of the framework is sufficient to enable similar host–guest contacts. The unit cell volume of 1–CD4 contracts by 3.4% to 1839.3(2) Å3, resulting in a binding pocket diameter of 4.1 Å. Notably, the adsorbed CD4 molecules are well-ordered as a result of a large number of specific host–guest interactions (Fig. 6b). The nearest D···arene distances are 2.740(9) Å (side wall of the pore) and 3.407(8) Å (outer linker of bowl-shaped cap). These relatively short distances are consistent with those determined previously from studies of methane adsorption on benzene (2.1–3.8 Å) and support the characterized orientation of CD4 inside the pore of U(bdc)2.45,81–83 Additional D⋯H van der Waals contacts at 2.57(1), 2.69(2), and 2.81(2) Å stabilize and orient the adsorbed CD4 molecules within the binding pocket. Adsorbed CD4 further interacts with three O atoms of two independent UO8 nodes at distances of 3.10(2), 3.25(1), and 3.50(1) Å. Lastly, adsorbate–adsorbate interactions based on D⋯D contacts at 2.84(1), 3.10(1), and 3.20(1) Å stabilize CD4 inside each pore.84,85 Together, the wealth of stabilizing contacts explains the competitively high heat of adsorption (Qst = −24.8 kJ mol−1) for methane in U(bdc)2. It is worth noting that methane is also expected to occupy a second adsorption site at higher loadings, as seen for D2. This observation is supported by the CH4 adsorption data shown in Fig. 3. Here, initial steep uptake is associated with saturation of the binding pockets of site I until a loading of 3.5 mmol g−1. The onset of far more gradual CH4 uptake to 4.1 mmol g−1 at 1.2 bar suggests additional methane adsorption at a second, weaker binding site.
Finally, we sought to study the distortion of 1 in the presence of an even larger guest molecule and prepared crystals of 1–DMF by soaking the framework in dry DMF (kinetic diameter of 5.5 Å).86 The structure of 1–DMF was determined from Rietveld refinement of powder X-ray diffraction data obtained at 298 K (see ESI, Fig. S8†). The framework indeed contracts to optimize interactions with DMF, but the unit cell volume decreases by only 1.9% (compared to 7.8% and 3.4% in the cases of 2.5 equiv. D2 and 1.5 equiv. CD4, respectively) and the pocket diameter only decreases to 4.2 Å. While two molecules of the smaller guests D2 and CD4 can simultaneously occupy the two binding pockets in each pore, the larger DMF molecule occupies the whole pore space, bridging both pockets (Fig. 6c). As a result, DMF is stabilized by seven of the eight bdc2− linkers that form the surrounding pore. While precise contact distances are obscured by disorder of DMF over two positions in the structure, the general identity of host–guest interactions in 1–DMF is clear. In particular, DMF binds through eight H⋯H contacts, three C–H⋯π-interactions, three O⋯H contacts involving the carbonyl and arene C–H moieties, and interactions of two DMF C–H groups with O atoms of two UO8 nodes (all distances between 2 and 4 Å).
Conclusions
Porous adsorbents with small binding pockets can engage in strong, selective host–guest interactions, and are therefore of interest for applications including gas capture and storage. However, it remains a significant challenge to tune a binding pocket structure to optimize interactions with a specific target molecule. In this work, we show that combining moderate flexibility with small pores in the new flexible metal–organic framework U(bdc)2 (1) eliminates the need for precise tuning of pore geometry. Indeed, this material is capable of uniquely adjusting its pore and binding pocket geometry to optimize host–guest interactions in the presence of even very weakly adsorbing molecules, such as H2 and CH4. Temperature-dependent H2 and CH4 adsorption isotherms yielded isosteric heats of adsorption of −8.6 and −24.8 kJ mol−1 for H2 and CH4, respectively, confirming comparatively strong interactions of 1 with both gases, despite their different sizes. In situ powder neutron diffraction experiments with D2 and CD4 revealed that cooperative effects drive a spontaneous adjustment of the binding pockets in 1 to generate multiple stabilizing interactions between each adsorbate and the framework, which are not achieved without pore contraction. Altogether, our results demonstrate the utility of frameworks featuring self-adjusting binding pockets that can flex in response to different guest molecules. The design principles applied for our model material 1 are transferable to non-radioactive frameworks and suggest further exploration of such materials will be advantageous in the search for adsorbents with improved gas storage properties.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Hydrogen Materials – Advanced Research Consortium (HyMARC), established as part of the Energy Materials Network under the U. S. Department of Energy, Office of Energy Efficiency and Renewable Energy, Fuel Cell Technologies Office, under Contract DE-AC02-05CH11231. Powder X-ray diffraction data were collected on beamline 17-BM at the Advanced Photon Source at Argonne National Laboratory, which is supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences under Contract No. DE-AC02-06CH11357. Single-crystal X-ray diffraction data were collected at the Advanced Light Source beamline 12.2.1 at Lawrence Berkeley National Laboratory. The Advanced Light Source (ALS) is supported by the Director, Office of Science, Office of Basic Energy Sciences, of the U.S. DOE under Contract No. DE-AC02-05CH11231. D. P. H. thanks the Alexander von Humboldt Foundation for a Feodor Lynen Postdoctoral Research Fellowship. R. A. K. acknowledges research support from the U.S. Department of Energy, Office of Energy Efficiency and Renewable Energy, Fuel Cell Technologies Office, under Contract DE-AC36-08GO28308. We further thank Colin A. Gould for helpful discussions, Ari Turkiewicz for assistance with single-crystal X-ray diffraction, Henry Z. H. Jiang and Maria V. Paley for help with acquiring high resolution powder X-ray diffraction data, and Dr Katie R. Meihaus for editorial assistance.References
- H. Furukawa, K. E. Cordova, M. O'Keeffe and O. M. Yaghi, Science, 2013, 341, 1230444 CrossRef PubMed.
- N. Stock and S. Biswas, Chem. Rev., 2012, 112, 933 CrossRef CAS PubMed.
- M. Eddaoudi, J. Kim, N. Rosi, D. Vodak, J. Wachter, M. O'Keeffe and O. M. Yaghi, Science, 2002, 295, 469 CrossRef CAS PubMed.
- S. Yuan, L. Feng, K. Wang, J. Pang, M. Bosch, C. Lollar, Y. Sun, J. Qin, X. Yang, P. Zhang, Q. Wang, L. Zou, Y. Zhang, L. Zhang, Y. Fang, J. Li and H.-C. Zhou, Adv. Mater., 2018, 30, 1704303 CrossRef PubMed.
- T. Islamoglu, S. Goswami, Z. Li, A. J. Howarth, O. K. Farha and J. T. Hupp, Acc. Chem. Res., 2017, 50, 805 CrossRef CAS PubMed.
- W. Lu, Z. Wei, Z.-Y. Gu, T.-F. Liu, J. Park, J. Park, J. Tian, M. Zhang, Q. Zhang, T. Gentle, M. Bosch and H.-C. Zhou, Chem. Soc. Rev., 2014, 43, 5561 RSC.
- A. U. Czaja, N. Trukhan and U. Müller, Chem. Soc. Rev., 2009, 38, 1284 RSC.
- C. H. Hendon, A. J. Rieth, M. D. Korzyński and M. Dincă, ACS Cent. Sci., 2017, 3, 554 CrossRef CAS PubMed.
- A. Bétard and R. A. Fischer, Chem. Rev., 2012, 112, 1055 CrossRef PubMed.
- Q. Wang and D. Astruc, Chem. Rev., 2020, 120, 1438 CrossRef CAS PubMed.
- D. J. Xiao, E. D. Bloch, J. A. Mason, W. L. Queen, M. R. Hudson, N. Planas, J. Borycz, A. L. Dzubak, P. Verma, K. Lee, F. Bonino, V. Crocell, J. Yano, S. Bordiga, D. G. Truhlar, L. Gagliardi, C. M. Brown and J. R. Long, Nat. Chem., 2014, 6, 590 CrossRef CAS PubMed.
- S. A. Burgess, A. Kassie, S. A. Baranowski, K. J. Fritzsching, K. Schmidt-Rohr, C. M. Brown and C. R. Wade, J. Am. Chem. Soc., 2016, 138, 1780 CrossRef CAS PubMed.
- S. M. Cohen, Z. Zhang and J. A. Boissonnault, Inorg. Chem., 2016, 55, 7281 CrossRef CAS PubMed.
- Y.-B. Huang, J. Liang, X.-S. Wang and R. Cao, Chem. Soc. Rev., 2017, 46, 126 RSC.
- J. Lee, O. K. Farha, J. Roberts, K. A. Scheidt, S. T. Nguyen and J. T. Hupp, Chem. Soc. Rev., 2009, 38, 1450 RSC.
- L. E. Kreno, K. Leong, O. K. Farha, M. Allendorf, R. P. van Duyne and J. T. Hupp, Chem. Rev., 2012, 112, 1105 CrossRef CAS PubMed.
- M. G. Campbell, D. Sheberla, S. F. Liu, T. M. Swager and M. Dincă, Angew. Chem., Int. Ed., 2015, 54, 4349 CrossRef CAS PubMed.
- I. Stassen, N. Burtch, A. Talin, P. Falcaro, M. Allendorf and R. Ameloot, Chem. Soc. Rev., 2017, 46, 3185 RSC.
- K. Sumida, D. L. Rogow, J. A. Mason, T. M. McDonald, E. D. Bloch, Z. R. Herm, T.-H. Bae and J. R. Long, Chem. Rev., 2012, 112, 724 CrossRef CAS PubMed.
- T. M. McDonald, J. A. Mason, X. Kong, E. D. Bloch, D. Gygi, A. Dani, V. Crocellà, F. Giordanino, S. O. Odoh, W. S. Drisdell, B. Vlaisavljevich, A. L. Dzubak, R. Poloni, S. K. Schnell, N. Planas, K. Lee, T. Pascal, L. F. Wan, D. Prendergast, J. B. Neaton, B. Smit, J. B. Kortright, L. Gagliardi, S. Bordiga, J. A. Reimer and J. R. Long, Nature, 2015, 519, 303 CrossRef CAS PubMed.
- R. L. Siegelman, P. J. Milner, A. C. Forse, J.-H. Lee, K. A. Colwell, J. B. Neaton, J. A. Reimer, S. C. Weston and J. R. Long, J. Am. Chem. Soc., 2019, 141, 13171 CrossRef CAS PubMed.
- M. Ding, R. W. Flaig, H.-L. Jiang and O. M. Yaghi, Chem. Soc. Rev., 2019, 48, 2783 RSC.
- D. J. Babu, G. He, J. Hao, M. T. Vahdat, P. A. Schouwink, M. Mensi and K. V. Agrawal, Adv. Mater., 2019, 31, 1900855 CrossRef PubMed.
- B. R. Barnett, M. I. Gonzalez and J. R. Long, Trends Chem., 2019, 1, 159 CrossRef.
- H. Li, K. Wang, Y. Sun, C. T. Lollar, J. Li and H.-C. Zhou, Mater. Today, 2018, 21, 108 CrossRef CAS.
- D. E. Jaramillo, D. A. Reed, H. Z. H. Jiang, J. Oktawiec, M. W. Mara, A. C. Forse, D. J. Lussier, R. A. Murphy, M. Cunningham, V. Colombo, D. K. Shuh, J. A. Reimer and J. R. Long, Nat. Mater., 2020, 19, 517 CrossRef CAS PubMed.
- B. Li, H.-M. Wen, W. Zhou and B. Chen, J. Phys. Chem. Lett., 2014, 5, 3468 CrossRef CAS PubMed.
- R. E. Morris and P. S. Wheatley, Angew. Chem., Int. Ed., 2008, 47, 4966 CrossRef CAS PubMed.
- D. A. Reed, D. J. Xiao, H. Z. H. Jiang, K. Chakarawet, J. Oktawiec and J. R. Long, Chem. Sci., 2020, 11, 1698 RSC.
- S. Ma and H.-C. Zhou, Chem. Commun., 2010, 46, 44 RSC.
- I. Senkovska, E. Barea, J. A. R. Navarro and S. Kaskel, Microporous Mesoporous Mater., 2012, 156, 115 CrossRef CAS.
- P. García-Holley, B. Schweitzer, T. Islamoglu, Y. Liu, L. Lin, S. Rodriguez, M. H. Weston, J. T. Hupp, D. A. Gómez-Gualdrón, T. Yildirim and O. K. Farha, ACS Energy Lett., 2018, 3, 748 CrossRef.
- M. T. Kapelewski, S. J. Geier, M. R. Hudson, D. Stück, J. A. Mason, J. N. Nelson, D. J. Xiao, Z. Hulvey, E. Gilmour, S. A. FitzGerald, M. Head-Gordon, C. M. Brown and J. R. Long, J. Am. Chem. Soc., 2014, 136, 12119 CrossRef CAS PubMed.
- M. T. Kapelewski, T. Runčevski, J. D. Tarver, H. Z. H. Jiang, K. E. Hurst, P. A. Parilla, A. Ayala, T. Gennett, S. A. FitzGerald, C. M. Brown and J. R. Long, Chem. Mater., 2018, 30, 8179 CrossRef CAS PubMed.
- A. Ahmed, S. Seth, J. Purewal, A. G. Wong-Foy, M. Veenstra, A. J. Matzger and D. J. Siegel, Nat. Commun., 2019, 10, 1568 CrossRef PubMed.
- Y. He, W. Zhou, G. Qian and B. Chen, Chem. Soc. Rev., 2014, 43, 5657 RSC.
- J. A. Mason, J. Oktawiec, M. K. Taylor, M. R. Hudson, J. Rodriguez, J. E. Bachman, M. I. Gonzalez, A. Cervellino, A. Guagliardi, C. M. Brown, P. L. Llewellyn, N. Masciocchi and J. R. Long, Nature, 2015, 527, 357 CrossRef CAS PubMed.
- K. V. Kumar, K. Preuss, M.-M. Titirici and F. Rodríguez-Reinoso, Chem. Rev., 2017, 117, 1796 CrossRef CAS PubMed.
- M. D. Allendorf, Z. Hulvey, T. Gennett, A. Ahmed, T. Autrey, J. Camp, E. Seon Cho, H. Furukawa, M. Haranczyk, M. Head-Gordon, S. Jeong, A. Karkamkar, D.-J. Liu, J. R. Long, K. R. Meihaus, I. H. Nayyar, R. Nazarov, D. J. Siegel, V. Stavila, J. J. Urban, S. P. Veccham and B. C. Wood, Energy Environ. Sci., 2018, 11, 2784 RSC.
- M. P. Suh, H. J. Park, T. K. Prasad and D.-W. Lim, Chem. Rev., 2012, 112, 782 CrossRef CAS PubMed.
- J. A. Mason, M. Veenstra and J. R. Long, Chem. Sci., 2014, 5, 32 RSC.
- M. I. Gonzalez, J. A. Mason, E. D. Bloch, S. J. Teat, K. J. Gagnon, G. Y. Morrison, W. L. Queen and J. R. Long, Chem. Sci., 2017, 8, 4387 RSC.
- D. Denysenko, M. Grzywa, J. Jelic, K. Reuter and D. Volkmer, Angew. Chem., Int. Ed., 2014, 53, 5832 CrossRef CAS PubMed.
- P. G. Boyd, A. Chidambaram, E. García-Díez, C. P. Ireland, T. D. Daff, R. Bounds, A. Gładysiak, P. Schouwink, S. M. Moosavi, M. M. Maroto-Valer, J. A. Reimer, J. A. R. Navarro, T. K. Woo, S. Garcia, K. C. Stylianou and B. Smit, Nature, 2019, 576, 253 CrossRef CAS PubMed.
- Z. Hulvey, B. Vlaisavljevich, J. A. Mason, E. Tsivion, T. P. Dougherty, E. D. Bloch, M. Head-Gordon, B. Smit, J. R. Long and C. M. Brown, J. Am. Chem. Soc., 2015, 137, 10816 CrossRef CAS PubMed.
- D. G. Truhlar, J. Chem. Educ., 2019, 96, 1671 CrossRef CAS.
- N. Mehio, S. Dai and D.-e. Jiang, J. Phys. Chem. A, 2014, 118, 1150 CrossRef CAS PubMed.
- Y. Liu, C. M. Brown, D. A. Neumann, V. K. Peterson and C. J. Kepert, J. Alloys Compd., 2007, 446–447, 385 CrossRef CAS.
- A. P. Katsoulidis, D. Antypov, G. F. S. Whitehead, E. J. Carrington, D. J. Adams, N. G. Berry, G. R. Darling, M. S. Dyer and M. J. Rosseinsky, Nature, 2019, 565, 213 CrossRef CAS PubMed.
- Y. Gu, J.-J. Zheng, K.-I. Otake, K. Sugimoto, N. Hosono, S. Sakaki, F. Li and S. Kitagawa, Angew. Chem., Int. Ed., 2020 DOI:10.1002/anie.202003186.
- F.-X. Coudert, M. Jeffroy, A. H. Fuchs, A. Boutin and C. Mellot-Draznieks, J. Am. Chem. Soc., 2008, 130, 14294 CrossRef CAS PubMed.
- B. Chen, S. Xiang and G. Qian, Acc. Chem. Res., 2010, 43, 1115 CrossRef CAS PubMed.
- A. Schneemann, V. Bon, I. Schwedler, I. Senkovska, S. Kaskel and R. A. Fischer, Chem. Soc. Rev., 2014, 43, 6062 RSC.
- L. Sarkisov, R. L. Martin, M. Haranczyk and B. Smit, J. Am. Chem. Soc., 2014, 136, 2228 CrossRef CAS PubMed.
- J.-P. Zhang, H.-L. Zhou, D.-D. Zhou, P.-Q. Liao and X.-M. Chen, Natl. Sci. Rev., 2018, 5, 907 CrossRef CAS.
- C. Serre, F. Millange, C. Thouvenot, M. Noguès, G. Marsolier, D. Louër and G. Férey, J. Am. Chem. Soc., 2002, 124, 13519 CrossRef CAS PubMed.
- M. Vougo-Zanda, J. Huang, E. Anokhina, X. Wang and A. J. Jacobson, Inorg. Chem., 2008, 47, 11535 CrossRef CAS PubMed.
- G. Férey, M. Latroche, C. Serre, F. Millange, T. Loiseau and A. Percheron-Guégan, Chem. Commun., 2003, 2976 RSC.
- F. Millange, N. Guillou, M. E. Medina, G. Férey, A. Carlin-Sinclair, K. M. Golden and R. I. Walton, Chem. Mater., 2010, 22, 4237 CrossRef CAS.
- J. P. S. Mowat, S. R. Miller, A. M. Z. Slawin, V. R. Seymour, S. E. Ashbrook and P. A. Wright, Microporous Mesoporous Mater., 2011, 142, 322 CrossRef CAS.
- S. Surblé, C. Serre, C. Mellot-Draznieks, F. Millange and G. Férey, Chem. Commun., 2006, 284 RSC.
- N. Guillou, S. Bourrelly, P. L. Llewellyn, R. I. Walton and F. Millange, CrystEngComm, 2015, 17, 422 RSC.
- S. R. Daly, P. M. B. Piccoli, A. J. Schultz, T. K. Todorova, L. Gagliardi and G. S. Girolami, Angew. Chem., Int. Ed., 2010, 49, 3379 CrossRef CAS PubMed.
- E. A. Dolgopolova, A. M. Rice and N. B. Shustova, Chem. Commun., 2018, 54, 6472 RSC.
- C. Falaise, A. Assen, I. Mihalcea, C. Volkringer, A. Mesbah, N. Dacheux and T. Loiseau, Dalton Trans., 2015, 44, 2639 RSC.
- V. Bon, I. Senkovska, D. Wallacher, D. M. Többens, I. Zizak, R. Feyerherm, U. Mueller and S. Kaskel, Inorg. Chem., 2014, 53, 1513 CrossRef CAS PubMed.
- C. Mellot-Draznieks, C. Serre, S. Surblé, N. Audebrand and G. Férey, J. Am. Chem. Soc., 2005, 127, 16273 CrossRef CAS PubMed.
- M. K. Taylor, T. Runčevski, J. Oktawiec, M. I. Gonzalez, R. L. Siegelman, J. A. Mason, J. Ye, C. M. Brown and J. R. Long, J. Am. Chem. Soc., 2016, 138, 15019 CrossRef CAS PubMed.
- P. Bénard and R. Chahine, Langmuir, 2001, 17, 1950 CrossRef.
- L. J. Murray, M. Dincă and J. R. Long, Chem. Soc. Rev., 2009, 38, 1294 RSC.
- F. M. Mulder, B. Assfour, J. Huot, T. J. Dingemans, M. Wagemaker and A. J. Ramirez-Cuesta, J. Phys. Chem. C, 2010, 114, 10648 CrossRef CAS.
- F. Salles, D. I. Kolokolov, H. Jobic, G. Maurin, P. L. Llewellyn, T. Devic, C. Serre and G. Ferey, J. Phys. Chem. C, 2009, 113, 7802 CrossRef CAS.
- R. A. Pollock, J.-H. Her, C. M. Brown, Y. Liu and A. Dailly, J. Phys. Chem. C, 2014, 118, 18197 CrossRef CAS.
- H. Wu, W. Zhou and T. Yildirim, J. Am. Chem. Soc., 2007, 129, 5314 CrossRef CAS PubMed.
- D. Gygi, E. D. Bloch, J. A. Mason, M. R. Hudson, M. I. Gonzalez, R. L. Siegelman, T. A. Darwish, W. L. Queen, C. M. Brown and J. R. Long, Chem. Mater., 2016, 28, 1128 CrossRef CAS.
- K. Sumida, J.-H. Her, M. Dincă, L. J. Murray, J. M. Schloss, C. J. Pierce, B. A. Thompson, S. A. FitzGerald, C. M. Brown and J. R. Long, J. Phys. Chem. C, 2011, 115, 8414 CrossRef CAS.
- T. Runčevski, M. T. Kapelewski, R. M. Torres-Gavosto, J. D. Tarver, C. M. Brown and J. R. Long, Chem. Commun., 2016, 52, 8251 RSC.
- J. Luo, H. Xu, Y. Liu, Y. Zhao, L. L. Daemen, C. Brown, T. V. Timofeeva, S. Ma and H.-C. Zhou, J. Am. Chem. Soc., 2008, 130, 9626 CrossRef CAS PubMed.
- J. van Kranendonk and H. P. Gush, Phys. Lett., 1962, 1, 22 CrossRef CAS.
- V. K. Peterson, Y. Liu, C. M. Brown and C. J. Kepert, J. Am. Chem. Soc., 2006, 128, 15578 CrossRef CAS PubMed.
- S. Tsuzuki, K. Honda, T. Uchimaru, M. Mikami and K. Tanabe, J. Am. Chem. Soc., 2000, 122, 3746 CrossRef CAS.
- A. L. Ringer, M. S. Figgs, M. O. Sinnokrot and C. D. Sherrill, J. Phys. Chem. A, 2006, 110, 10822 CrossRef CAS PubMed.
- H. Wu, W. Zhou and T. Yildirim, J. Phys. Chem. C, 2009, 113, 3029 CrossRef CAS.
- E. Tsivion and M. Head-Gordon, J. Phys. Chem. C, 2017, 121, 12091 CrossRef CAS.
- S. Tsuzuki, T. Uchimaru and K. Tanabe, Chem. Phys. Lett., 1998, 287, 202 CrossRef CAS.
- J. E. ten Elshof, C. R. Abadal, J. Sekulić, S. R. Chowdhury and D. H. A. Blank, Microporous Mesoporous Mater., 2003, 65, 197 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Synthetic, analytical and crystallographic details. Single crystal X-ray crystallographic data was deposited in the Cambridge Crystallographic Data Centre database. CCDC 1996337. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0sc02394a |
| This journal is © The Royal Society of Chemistry 2020 |