Open Access Article
Open Access ArticleEnumeration of de novo inorganic complexes for chemical discovery and machine learning†
Stefan
Gugler
 ,
Jon Paul
Janet
,
Jon Paul
Janet
 and
Heather J.
Kulik
and
Heather J.
Kulik
 *
*
Department of Chemical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA. E-mail: hjkulik@mit.edu; Tel: +1 617 253 4584
First published on 4th July 2019
Abstract
Despite being attractive targets for functional materials, the discovery of transition metal complexes with high-throughput computational screening is challenged by the amount of feasible coordination numbers, spin states, or oxidation states and the potentially large sizes of ligands. To overcome these limitations, we take inspiration from organic chemistry where full enumeration of neutral, closed-shell molecules under the constraint of size has enriched discovery efforts. We design monodentate and bidentate ligands from scratch for the construction of mononuclear, octahedral transition metal complexes with up to 13 heavy atoms (i.e., metal, C, N, O, P, or S). From >11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 theoretical ligands, we develop a heuristic score for ranking a chemically feasible 2500 ligand subset, only 71 of which were previously included in common organic molecule databases. We characterize the top 20% of scored ligands with density functional theory (DFT) in an octahedral homoleptic ligand database (OHLDB). The OHLDB contains i) the geometry optimized structures of 1250 homoleptic octahedral complexes obtained from the enumerated pool of ligands and an open-shell transition metal (M(II)/M(III), M = Cr, Mn, Fe, or Co) and ii) the resulting high-spin/low-spin adiabatic electronic energy differences (ΔEH–L) obtained with hybrid DFT. Over the OHLDB, we observe structure–property (i.e., ΔEH–L) relationships different from those expected on the basis of ligand field arguments or from our prior data sets. Finally, we demonstrate how incorporating OHLDB data into artificial neural network (ANN) training improves ANN out-of-sample performance on much larger transition metal complexes.
000 theoretical ligands, we develop a heuristic score for ranking a chemically feasible 2500 ligand subset, only 71 of which were previously included in common organic molecule databases. We characterize the top 20% of scored ligands with density functional theory (DFT) in an octahedral homoleptic ligand database (OHLDB). The OHLDB contains i) the geometry optimized structures of 1250 homoleptic octahedral complexes obtained from the enumerated pool of ligands and an open-shell transition metal (M(II)/M(III), M = Cr, Mn, Fe, or Co) and ii) the resulting high-spin/low-spin adiabatic electronic energy differences (ΔEH–L) obtained with hybrid DFT. Over the OHLDB, we observe structure–property (i.e., ΔEH–L) relationships different from those expected on the basis of ligand field arguments or from our prior data sets. Finally, we demonstrate how incorporating OHLDB data into artificial neural network (ANN) training improves ANN out-of-sample performance on much larger transition metal complexes.
Design, System, ApplicationWe develop a strategy for octahedral transition metal complex design by enumerating potential ligands from scratch. Such complexes are relevant as molecular sensors and switches that can change their ground state spin in response to light, heat, or other stimuli. They are also models of catalytic active sites. We show how our de novo enumeration both produces complexes with novel electronic structure and provides training data that improves the baseline performance of our machine learning models (here, artificial neural networks) in out-of-sample tests. |
1. Introduction
Computational, first-principles (i.e., with density functional theory, DFT) high-throughput screening1–7 is an essential complement to experimental8–10 efforts in the discovery and design of molecules and materials. In recent years, machine learning (ML) property prediction models trained on first-principles simulation data have further accelerated this discovery process4,11–18 throughout chemistry,19–24 including for catalysis15,16,25,26 and materials.4,27–34 Unique challenges arise in applying these tools to the discovery of open shell transition metal complexes, despite their importance as selective catalysts35–43 and functional materials (e.g., molecular switches or sensors44–52). The theoretical chemical space of inorganic complexes is diverse and relatively unexplored due to the variable spin states, oxidation states, and coordination numbers feasible for each metal. The large sizes of inorganic complexes and limited applicability of more affordable semi-empirical53 or force field54,55 methods in open-shell transition metal chemistry also hinders the rapid computational exploration of this space.28To accelerate discovery in open-shell transition metal chemistry, we have developed4,17,27,28,56,57 ML models for predicting quantum mechanical properties (here, computed with DFT), including spin-splitting energies,17,27,56 redox or ionization potentials,28,56 metal–ligand bond lengths,17,28 frontier orbital energies,4 and reaction energetics.58 A key outstanding challenge for ML model improvement, especially in inorganic chemistry, is the generation of large data sets. While most organic chemistry ML models have been trained24,59–65 on large (>100k points) data sets19,66,67 of molecules consisting of up to 9 heavy (i.e., C, N, O, or F) atoms, the higher computational cost associated with the larger number of electrons and added complexity of open-shell wavefunctions have limited data set sizes for inorganic chemistry.28 Despite these limitations in data set size, ML models for inorganic chemistry on modest data sets are predictive to 1–3 kcal mol−1 as judged by test set errors.17,56 However, limited coverage of the wide range of chemical bonding in transition metal complexes means that ML model prediction error can rise rapidly (to ca. 6–10 kcal mol−1 (ref. 17 and 27)) when applied to complexes dissimilar from training data. Thus, an approach to efficiently increase data set diversity would benefit ML models in inorganic chemistry.
Here, we take inspiration from organic chemistry, where systematic enumeration of small, drug-like molecules68–73 paved the way for large data sets suitable for ML. However, the enumeration of possible inorganic complexes will necessarily differ from such prior organic enumerations, as the properties that make a molecule a good ligand for an inorganic complex (e.g., an unsaturated atom that can freely complex to a metal) are not the same as the characteristics that define closed-shell organic molecules. To construct such a set we note that, whether through ad hoc feature engineering17 or systematic feature selection,56 the most predictive and transferable feature sets for open-shell transition metal complex properties emphasize metal-local features. For spin-splitting energetics in particular, we found that the 24 most informative heuristic features obtained from feature selection28,56 were primarily (80%) comprised of properties from atoms within two bonds of the metal on the molecular graph. Thus, by selecting small ligands and systematically varying their properties, we expect to capture the most important variations needed to improve coverage for ML model training.
In this work, we enumerate de novo octahedral transition metal complex ligands, study properties of homoleptic complexes of these ligands with first-principles DFT simulation, and demonstrate the improvement of our inorganic ML models through the inclusion of this data. The rest of this work is as follows. In section 2, we describe our rules for enumerating monodentate and bidentate ligands composed of up to two and four heavy atoms, respectively. In section 3, we describe the Computational details of our simulation methodology. In section 4, we analyze the results of DFT geometry optimizations of homoleptic octahedral complexes built from these ligands and demonstrate how these data points improve ML model performance. Finally, in section 5, we provide our outlook and conclusions.
2. Enumerating inorganic complex ligands
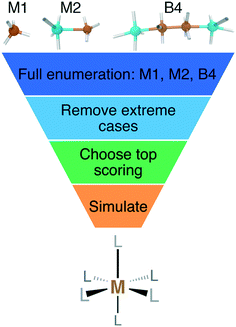
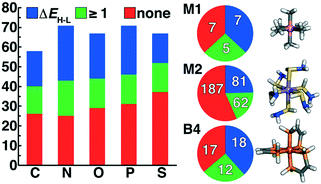
We enumerated candidate ligands from the elements C, N, O, P, or S, which were chosen i) for their abundance70,71,74 on earth and in organisms and ii) to enable comparison between isovalent compounds (i.e., N vs. P and O vs. S). Molecules were classified into three ligand types defined by the number of heavy (i.e., non-H) atoms: monodentate ligands with one (M1) or two (M2) heavy atoms and bidentate ligands with four heavy atoms (B4) created from joining two identical M2 heavy atom pairs, all of which were variably passivated with H atoms (Fig. 1). After enumeration of all theoretical ligands of these three types, we carried out two filtering steps, first excluding major violations of chemical bonding rules, then scoring the remaining cases and retaining the top-scoring ligands (Fig. 1). We penalized but did not exclude ligands that do not have octet valence or neutral charge, diverging from previous organic enumeration efforts69 that were not focused on ligand generation for inorganic chemistry. We did however remove any enumerated ligands with an odd number of electrons to avoid ligand noninnocence.75 Ligand scores were based on heuristic properties, i.e.: i) the number of H atoms bonded to any of the heavy atoms, h; ii) the charge, c; iii) the number of lone pairs, l; and iv) the number of valence electrons, v, as described next.2.1. M1 ligands
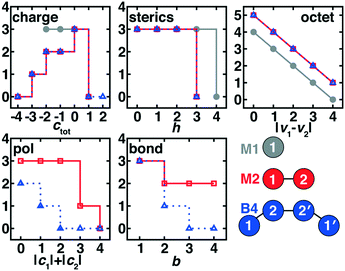
The simplest case corresponds to M1 ligands generated from a single heavy (i.e., C, N, O, P, S) atom with variable H atom passivation and charge. For initial enumeration, there were 5 possible heavy elements, we permitted 5 overall charge values, c, from −2 to 2 in an increment of 1, and we varied the number of H atoms added, h, over the range of 0 to 4. This combination produced 5 × 5 × 5 = 125 theoretical M1 ligands. After discarding ligands with an odd number of electrons and strongly positively charged ligands (i.e., retaining only −2 ≤ c ≤ 1), we obtained 50 ligands for the second filtering step.For M1 ligands, we assigned three scores, s, for the charge (scharge), sterics (i.e., presence of H atoms, ssterics), and accordance with the octet rule (soctet). We favored neutral and weakly negative ligands (scharge = 3 for −2 ≤ c ≤ 0) over positively charged ligands (scharge = 0 for c = 1), due to the fact that ligands will be complexed with positively charged metal centers (Fig. 2). We penalized h = 4 (ssterics = 0) passivation over all other choices (ssterics = 3) because large numbers of H atoms hinder the heavy atom from coordinating to the metal center (Fig. 2). We reduced the soctet of a valence, v, in proportion to its violation of the octet rule (Fig. 2):
| soctet = 4 − |8 − v| | (1) |
| stot = scharge + ssterics + soctet | (2) |
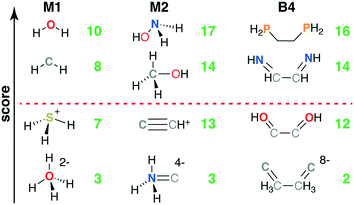
Common M1-type ligands in the spectrochemical series76 include OH−, H2O, and NH3, all of which were top scoring (i.e., stot = 10, Fig. 3 and ESI† Table S1). M1 ligands with stot = 8 that have been observed experimentally or invoked in the spectrochemical series include methylene77 (CH2) and elemental sulfur78 (Fig. 3). Still lower scores (i.e., stot = 7) arose primarily due to penalties for: i) steric repulsion, as in methane (CH4) or ii) charge, as in sulfonium (SH3+) and hydronium (OH3+) (Fig. 3). The lowest scoring ligand (stot = 3), OH42−, simultaneously violates steric and octet rules (Fig. 3). After filtering on score, we retained only the 29 M1 ligands with stot ≥ 8, all of which were neutral (9) or negatively charged (20, see ESI† Fig. S1).
2.2. M2 ligands
For initial enumeration of M2 ligands, two atoms of the 5 possible heavy elements were joined, the total charge was constrained overall (i.e., retaining only −4 ≤ ctot ≤ 4), and each atom was allowed to have between 0 and 4 passivating H atoms. The identities of the first and second atoms (i.e., indexed 1 and 2) were treated distinguishably because we defined the first atom as coordinating the metal, and we allowed the charges and passivating H atoms to vary between the two atoms. Thus, the initial theoretical space of M2 ligands was 5625, from 25 combinations of five types of atom 1 and 2 elements, 9 charge assignments, and 25 combinations of atom 1 and atom 2 H-atom passivation.In addition to eliminating ligands that produce odd numbers of electrons as in the M1 ligands, we also considered the expected bonding between the two heavy atoms in the ligand for filtering and scoring of the M2 ligands. To determine M2 candidate ligand bond order, we first assigned individual c1, c2 charges by choosing from all combinations that could produce the ctot value under constraint that the valence, v, of each ith atom was satisfied:
| vi = vei − ci − 2·li − hi | (3) |
| b = min (v1, v2) | (4) |
After assembling these M2 ligands, we discarded i) highly positively charged ligands (i.e., ctot > 1), ii) metal-coordinating heavy atoms (i.e., atom 1) with h > 3, and iii) ligands with b = 0 predicted between the two heavy atoms. We then scored the remaining 1171 ligands with scores adapted and augmented from the M1 case. In comparison to M1 charge scoring, the M2 ligand charge score was biased toward neutral ligands (scharge = 3 for ctot = 0) and weakly penalized intermediate, negatively charged ligands (scharge = 2 for ctot = −1 or −2, scharge = 1 for ctot = −3, see Fig. 2). Sterics of the M2 ligand were scored only for the metal-coordinating atom, but we penalized h = 3 or higher due to the presence of the second heavy atom (i.e., ssterics = 3 for h < 3, Fig. 2). The M2 soctet score was applied over atom 1 and 2 v values (Fig. 2):
| soctet = 5 − |v1 − v2| | (5) |
We introduced two bond-specific scores for the bond between the two heavy atoms in the M2 ligands: i) bond order, sbond and ii) charge polarization, spol. We already excluded b = 0 molecules, but in scoring we favored b = 1 (sbond = 3) weakly over b > 1 (sbond = 2) to avoid oversampling high bond-order, few-atom M2 ligands (Fig. 2). We disfavored unphysically ionic bonds in the present ligands by scoring highest the cases with low atom-wise charge assignment (spol = 3 for |c1| + |c2| ≤ 2), assigning intermediate scores for moderate polarization (spol = 1 for |c1| + |c2| = 3) and penalizing the highest formal charges (spol = 0 for |c1| + |c2| = 4, see Fig. 2). A total M2 ligand score was thus:
| stot = scharge + ssterics + soctet + sbond + spol | (6) |
The 55 highest scoring ligands (stot = 17) include the common metal-complexing ligands methylamine (NH2CH3),79 hydrogen peroxide (H2O2), and both hydroxylamine (NH2OH)80 and its experimentally-observed analogue, thiophosphinous acid81 (PH2SH, Fig. 3). Both reactive peroxide82 (O22−) and nitrosyl83 (NO−) (stot = 15) score highly as do stable small molecules such as N2 and HCN (stot = 16) and methanol (CH3OH) (O-coordinating stot = 17, C-coordinating stot = 14, see Fig. 3). Most M2-type ligands in the spectrochemical series84 have high scores (e.g., CN−, stot = 15 and CO, stot = 16), with NO+ (stot = 13) scoring the lowest due to its positive charge. Other stot = 13 ligands include sterically hindered ligands (e.g., NH3NH32−) or likely unstable, positively charged species, such as CCH+ (Fig. 3). The lowest score (stot = 3) was only assigned to 2 ligands when steric repulsion, octet rule violation, and unfavorable charges were all present in a single molecule (e.g., NH3C4−: soctet = 1, sbond = 2, all other scores are zero, see Fig. 3). From the scored subset of M2 ligands, we therefore retained the 494 M2 ligands with stot ≥ 14 for further characterization with DFT (sec. 4). Most of the retained ligands have single or double bonds between the two heavy atoms and are neutral or negatively charged (ESI† Fig. S2).
2.3. B4 ligands
We generated symmetric bidentate B4 ligands solely by joining two identical M2 ligands from the original pool of 5625 theoretical M2 ligands, and so there were also 5625 theoretical B4 ligands. To simplify our algorithmic approach, we did not remove hydrogen atoms or use fragments with unpaired electrons to generate B4 ligands, as might be done in an intuitive dimerization procedure. If an atom was labeled as the metal-coordinating atom (i.e., 1) in the M2 ligand, it remained so in the B4 ligands, and the identical atoms in the ligand were assigned the indices 1′ and 2′. To construct the B4 ligands from the M2 substituents, we defined the 2–2′ bond order (b2–2′) by reassigning the value for b1–2 (and equivalently b1′–2′, Fig. 2). This reassignment was necessary because the number of electrons and hydrogen atoms in the B4 ligand is simply twice that of the original M2 ligand. To determine the reassigned bond orders, we took the ctot from the parent M2 molecule and computed all possible ci and vi, requiring that v1 > 0 and v2 > 1, where vi was assigned from eqn (3).We next determined the b1–2 and b2–2′ bond orders simultaneously by iterating over allowed values between single and triple bonds:
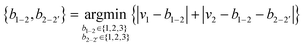 | (7) |
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH has b1–2 = 2 with c1 = −1 and c2 = 1. The resulting B4 ligand formed from two of these M2 ligands is NH2–CH
CH has b1–2 = 2 with c1 = −1 and c2 = 1. The resulting B4 ligand formed from two of these M2 ligands is NH2–CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH–NH2, which has the same net charge but neutral atom-wise charge assignments with b1–2 = b1′–2′ = 1 and b2–2′ = 2.
CH–NH2, which has the same net charge but neutral atom-wise charge assignments with b1–2 = b1′–2′ = 1 and b2–2′ = 2.
After assembling all theoretical B4 ligands, we discarded i) ligands with two consecutive double bonds or any cases with triple bonds that would be unable to form a 1–2–2′–1′ dihedral necessary to enable bidentate metal coordination, ii) strongly charged ligands with total charge (i.e., twice the charge of the original M2 ligand) higher than 4 or more negative than −8, iii) cases in which any bond orders were assigned to be zero, and iv) ligands with connecting atoms that had three or more passivating hydrogen atoms. These down-selection steps left a pool of 1356 B4 ligands suitable for further scoring with a five-component score similar to that applied to the M2 ligands. Both scharge and ssterics were unchanged from the M2 case but were evaluated, respectively, on the charge only of the original M2 fragment (i.e., half of the total B4 ligand charge) or a single relevant connecting atom (Fig. 2). The B4 soctet was also scored only for a single building block using eqn (5) but using the revised valency after charge redistribution (Fig. 2). After redistribution of charges, we scored a single 1–2 pair, penalizing strong polarization (spol = 0 for |c1| + |c2| > 1), favoring completely neutral atomic charges (spol = 2 for |c1| + |c2| = 0), and assigning an intermediate score (spol = 1) for slight polarization (i.e., |c1| + |c2| = 1, see Fig. 2). We also computed sbond only on the 1–2 bond and reduced it with respect to M2 scoring for higher bond orders (sbond = 3 for b = 1, sbond = 1 for b = 2, see Fig. 2).
The five B4 metrics were combined as in eqn (6) for a total score with a range of 2 to 16 across ligands retained for scoring (Fig. 1). Ethylenediamine (en, C2H8N2) is the only B4-type ligand in the spectrochemical series,84 and it has a maximum score (stot = 16) as does its phosphorus analogue, 1,2-ethanediyldiphosphine (C2H8P2, stot = 16, Fig. 3 and ESI† Table S4). Other common ligands that score highly include ethylene glycol (C2H6O2, stot = 16) and 1,2-ethanediimine (C2H4N2, stot = 14), which contains a bonding pattern analogous to that observed in the common bipyridine ligand (Fig. 3). Stable organic molecules that are sterically hindered and would make poor ligands, e.g., butane (C4H10, stot = 13), score more poorly than unstable but likely metal-coordinating molecules, e.g., tetraoxidane85 (H2O4, stot = 16, Fig. 3). Other molecules with intermediate scores (stot = 12) typically score lower due to a combination of steric hindrance, charge, and violations of the octet rule (e.g., S4, or HOC2OH, Fig. 3). The lowest scoring ligands are charged, have polarized bonds, and are octet violating (e.g., CCH3CH3C8−, stot = 2, Fig. 3). Following these holistic observations, we retained only the 47 B4 ligands with stot ≥ 14 for subsequent DFT calculations (ESI† Fig. S3).
2.4. Overall ligand analysis
From an original combinatorial space of 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 325 theoretical M1, M2, and B4 ligands, we scored 2577 ligands and identified the top 20% (570 ligands) as good candidates for DFT characterization (Fig. 1 and see sec. 4). The other 8748 ligands were eliminated prior to scoring due to disqualifications ranging from unpaired electrons on the ligand, zero bond order between heavy atoms or unsuitable bond order for bidentate coordination, high net positive charge that would prevent coordinating a positively charged metal, or strong steric repulsion from a high number of hydrogen atoms on the metal-coordinating atom that would prevent metal coordination. All such excluded ligands are provided in the ESI† and can be interpreted as scoring zero in comparison to the retained ligands that all score higher. We next compared characteristics of these ligands to molecules in other curated data sets that satisfy M1, M2, or B4 ligand definitions. We focused on three representative databases: ChEMBL;86 the generated database of enumerated organic molecules with up to 9 heavy atoms, GDB-9;69 and a database of experimentally and computationally characterized diatomic molecules, DiRef.87 Across these databases, 71 of the 2577 ligands were observed in at least one database, 17 occurred in more than one database, and most are diatomic molecules found only in DiRef87 (ESI† Table S5). The majority (55) of database ligands are M2 type, and 46 of these M2-type molecules are present twice in the enumerated ligand set, distinguished only by the metal coordinating atom and corresponding to a single chemical species. Thus, the 71 ligands identified in existing databases (DBs) are 48 chemically distinct species (ESI† Table S5).
325 theoretical M1, M2, and B4 ligands, we scored 2577 ligands and identified the top 20% (570 ligands) as good candidates for DFT characterization (Fig. 1 and see sec. 4). The other 8748 ligands were eliminated prior to scoring due to disqualifications ranging from unpaired electrons on the ligand, zero bond order between heavy atoms or unsuitable bond order for bidentate coordination, high net positive charge that would prevent coordinating a positively charged metal, or strong steric repulsion from a high number of hydrogen atoms on the metal-coordinating atom that would prevent metal coordination. All such excluded ligands are provided in the ESI† and can be interpreted as scoring zero in comparison to the retained ligands that all score higher. We next compared characteristics of these ligands to molecules in other curated data sets that satisfy M1, M2, or B4 ligand definitions. We focused on three representative databases: ChEMBL;86 the generated database of enumerated organic molecules with up to 9 heavy atoms, GDB-9;69 and a database of experimentally and computationally characterized diatomic molecules, DiRef.87 Across these databases, 71 of the 2577 ligands were observed in at least one database, 17 occurred in more than one database, and most are diatomic molecules found only in DiRef87 (ESI† Table S5). The majority (55) of database ligands are M2 type, and 46 of these M2-type molecules are present twice in the enumerated ligand set, distinguished only by the metal coordinating atom and corresponding to a single chemical species. Thus, the 71 ligands identified in existing databases (DBs) are 48 chemically distinct species (ESI† Table S5).
To simplify comparison of scores across the three ligand types, we obtained scaled scores, sscaled, between the minimum and maximum observed stot values within each ligand type:
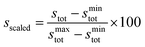 | (8) |
The scaled threshold for retention is lowest for M1 ligands (>71%) and highest for the B4 cases (>86%, see Fig. 4). Over all ligands, 75% (53 of 71 overall; 36 of 48 unique) of compounds found in DBs were above the relevant ligand cutoff (Fig. 4). The majority (13 of 18, 7 of 12 unique) of below-cutoff ligands are M2 type and correspond to positively charged diatomics from DiRef87 (e.g., NO+ and PS+ ESI† Table S5). Although such ligands are relevant for heteroleptic transition metal complexes, our focus on homoleptic octahedral complexes with high valent metals motivated penalizing positively charged ligands (see Fig. 2). Our restriction to octahedral complexes is motivated by their relevance in catalysis and functional materials, but study of heteroleptic or lower coordination number complexes in future work will motivate alternate scoring. The remaining database ligands below threshold typically exhibit steric hindrance (e.g., M1: CH4 or B4: C4H10, see Fig. 4). Conversely, known good inorganic ligands such as M1 ammonia, M2 methylamine, or B4 ethylenediamine are all among the top scoring database ligands (Fig. 4 and ESI† Table S5).
Overall, the enumeration recovered small molecules previously observed in other databases that are likely ligands in inorganic chemistry. Beyond validation of scoring heuristics, the large number of enumerated and retained ligands not present in other databases (i.e., around 90% or 517 of 570) suggests that our data set contains unique chemical bonding configurations. Thus, it will be useful to identify through first-principles DFT simulation the extent to which complexes could be formed from these ligands.
3. Computational details
Homoleptic, mononuclear octahedral transition metal complexes were generated from de novo ligands (sec. 2) with the molSimplify3 toolkit and molSimplify Automatic Design (mAD),4,27 which automated both structure and input file generation. The molSimplify3 code uses OpenBabel5,88 as a backend for force field-based transition metal complex preoptimization prior to first-principles simulation with DFT. DFT geometry optimizations were carried out using TeraChem89,90 using the B3LYP91–93 hybrid DFT functional. The default definition of B3LYP in TeraChem employs the VWN1-RPA94 form for the local density approximation correlation component. The LANL2DZ95 effective core potential was employed for transition metals with the 6-31G* basis for all other atoms. These choices were made due to the limited effect of a modest basis set on the relative energies of interest96 and to enable comparison to previously generated data sets.17,27,56All complexes were generated with four metals (M = Cr, Mn, Fe, and Co) in M(II) and M(III) oxidation states. The differences between high (H) and low (L) spin states, ΔEH–L, was computed as the electronic energy difference between the two geometry-optimized states (i.e., the adiabatic energy difference). This choice is motivated by the fact that spin-state change is slower than other processes (e.g., optical excitations) for which a vertical energy evaluation may be more appropriate. The high-spin/low-spin definitions for the metals studied in this work are: quintet-singlet for d6 Co(III)/Fe(II), sextet-doublet for d5 Fe(III)/Mn(II), quintet-singlet for d4 Mn(III)/Cr(II), and quartet-doublet for both d3 Cr(III) and d7 Co(II). Although thermodynamic and solvent corrections are known to be important in making direct comparison with experimental spin state ordering,97 the two corrections typically have compensating effects,96,97 and we therefore focused on relationships between ligand identity and DFT adiabatic, electronic ΔEH–L energies. All open-shell calculations (i.e., non-singlet spin states) were carried out with level shifting98 using spin-up and spin-down level shifts of 1.0 and 0.1 Ha, respectively. Geometry optimizations used the L-BFGS algorithm in translation rotation internal coordinates (TRIC)99 as implemented in TeraChem to the default tolerances of 4.5 × 10−4 Hartree/Bohr for the maximum gradient and 1 × 10−6 Hartree for the change in energy between steps.
4. Properties of de novo transition metal complexes
We next computed with DFT properties of homoleptic octahedral transition metal complexes containing the curated de novo ligands. Here, we focus on the high-spin to low-spin adiabatic energy splitting, ΔEH–L, of M(II) and M(III) (M = Cr, Mn, Fe, or Co) complexes, which we obtained with hybrid DFT for comparison to both prior DFT results and ML models17,27,56 (see sec. 3). Although quantitative spin-state assignment remains an outstanding challenge for DFT,97,100–106 with no one-size-fits-all functional for spin-state energetics motivating more advanced methods,107–109 ligand-dependent trends in relative spin-state ordering are expected to be less sensitive to method choice. From the 570 high-scoring ligands in sec. 2, we excluded 10 M1 and 164 M2 ligands with net −2 charge from calculation due to the high, negative complex charge (i.e., −9 or −10) of the homoleptic octahedral complex that cannot be treated well within approximate DFT.110,111 For the remaining 396 ligands, 16 combinations of metal, oxidation, and spin state mean that 6336 geometry optimizations were carried out for 3168 possible ΔEH–L evaluations (see sec. 3).To streamline and improve the quality of data ingested during high-throughput simulation3 of transition metal complexes, we recently introduced4 automated checks of geometry and properties of the wavefunction. The geometric checks, as outlined in ref. 4, focus on preservation of metal–ligand bond lengths in the coordination sphere, ligand detachment, and ligand distortion. In practice, all simulations run with mAD4 are run in 24 hour increments, with geometry checks being carried out at each resubmission as well as on the final optimized structure. From the 6336 initial geometry optimizations, 22% (1387) of all geometry optimizations completed successfully, a somewhat reduced success rate with respect to the range reported in our prior work on transition metal complexes.17,56,57 The majority of unsuccessful calculations corresponded to those that failed geometry checks initially (214 or 3%), during resubmission (3816 or 60%), or on the fully optimized structure (919 or 15%). Such ligand detachment or strong asymmetry in metal–ligand bond lengths can be attributed to Jahn–Teller distortion, which in extreme cases would lead to unstable transition metal complexes. Of all excluded calculations, 1537 exhibit strong bond asymmetry and 1037 exhibit ligand detachment, although many of these calculations had at least one other failure mode as well. Some cases showed bond rearrangement within the ligand, which could lead to an alternative feasible complex, but we judged success here as only cases where the original connectivity in the ligands was preserved.
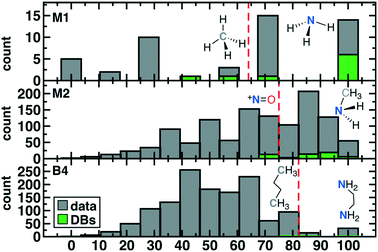
Over the 1387 converged complex results, completion rates are roughly evenly distributed over the M(II) (716) and M(III) (671) oxidation states as well as metals (Cr: 348, Mn: 341, Fe: 361, and Co: 337, see ESI† Fig. S4). Some bias is observed for successful convergence of low spin states (792 singlets or doublets) vs. their high spin counterparts (595 quartets, quintets, or sextets), likely due to the weaker bonding in high-spin complexes. Separating convergence by ligand reveals that of the 396 ligands we initially selected, only 185 converged successfully in at least one metal, oxidation state, or spin state (Fig. 5). The full ranges of retained scores are observed for successful ligands of all types, but the average score among the 185 ligand set is slightly higher than in the original 396 ligand set: M1 9.3 vs. 8.9 average score, M2 15.8 vs. 15.4 average score, and B4 15.7 vs. 15.4 average score. Because the applied geometry check penalized strong metal–ligand distortions or ligand detachment, 97% (1347) of optimized structures have metal–ligand bond asymmetries (i.e., the difference between maximum and minimum metal–ligand bond lengths) below 0.4 Å and 80% (1137) have differences below 0.2 Å (structures provided in the ESI†).
Dividing further by charge of the individual ligand, we observe that none of the 45 positively charged ligands of the M2 type in our original set led to a productive geometry optimization, further justifying our penalties on positively charged ligands during initial scoring (sec. 2). The highest success rate (37% or 77 of 210) is observed for neutral (M1, M2, or B4) ligands, but approximately 20% of the negatively charged ligands (29 of 141) also produced at least one stable complex. Of the 1387 converged geometries, we also discarded 134 for 〈S2〉 values that deviated from the anticipated value by more than 1 μB, as in prior work, to ensure limited symmetry breaking and localization of the spin on the metal. Finally, because ΔEH–L evaluation requires two successful geometry optimizations (the high-spin and low-spin states) of a given octahedral complex, a total of 343 new ΔEH–L evaluations were obtained for 106 unique ligands (see ESI† for all energies and structures).
In addition to being the most abundant ligands among the set selected for DFT characterization, N-coordinating ligands had the highest overall success rate, followed by P-coordinating ligands (Fig. 5 and ESI† Fig. S4). Generally, the second row analogues (P or S) of first row (N or O) complexes had lower overall success rates, but the final ligand set remained relatively balanced over all coordinating-atom types (Fig. 5). Because the majority of the selected ligand set is of the M2 type, this is also the greatest share of the successful ligands, but M2 ligands do not have the highest success rate (Fig. 5). For both M2 and B4 ligands, around 20% of ligands had at least one successful geometry optimization but no spin splitting energy pair, likely due to the greater flexibility of these ligands that increases the probability that at least one spin state fails to pass geometry checks. Within M1 ligand types, only 7 of the 19 retained ligands converged with spin-splitting energies, and most were complexes that are well known or that we had previously incorporated into ML data sets4,17,56,57 (e.g., NH3, PH3, H2S, and H2O). One exception was a Co(III) complex of the ammonia analogue, CH3− (Fig. 5). More diversity is observed in the successful B4 ligands, despite the relatively small size of the retained B4 ligand set, with the phosphorus analogue of the bipyridine core converging for multiple metal centers (Fig. 5). Finally, a large number of stable M2 ligand chemistries are observed for which spin-splitting energies were obtained, including a wide array of neutral (e.g., SHNH2) and negatively charged complexes (Fig. 5).
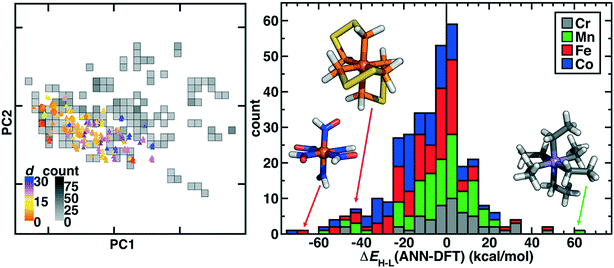
From the successfully converged complexes that make up our curated octahedral ligand database (OHLDB), we next quantified the extent to which these systematically enumerated complexes reflected chemistry divergent from the 1901 ΔEH–L values we had previously obtained for artificial neural network (ANN) model training.4,56 To compare diversity in the chemical structures, we featurized each new complex with the revised autocorrelation (RAC-155) representation56 (ESI† Text S1). The RAC-155 representation consists of products and differences of heuristic properties on the molecular graph and has shown good performance4,28,56,58,96 for predicting inorganic chemistry properties, including ΔEH–L. Although OHLDB complexes primarily lie within the convex hull of the first two principal components (PCs) in the RAC-155 representation, the overall Euclidean norm distance in feature space averaged over the ten nearest neighbors in existing data is quite large (>20) for a number of the complexes (Fig. 6). The complexes indeed fall outside the convex hull of the pre-existing data but do so especially at higher PCs (i.e., 7–8), where the first eight PCs generally contain the vast majority of the variance (89%, Fig. 6 and ESI† Fig. S5).
An alternative measure of data diversity is in property space, which we assessed first by determining if a previously trained RAC-155/ANN model112 could have predicted the ΔEH–L values exhibited by the OHLDB complexes (Fig. 6 and ESI† Table S6). Overall, although a large number of complexes were well predicted, significant (e.g., >60 kcal mol−1) over- and underestimations of ΔEH–L are indicative of limited prior knowledge by the ANN (mean absolute error, MAE = 14.3 kcal mol−1) of the chemistry of the OHLDB complexes (Fig. 6 and ESI† Table S6). Indeed, high error points are both chemically distinct and exhibit unexpected spin-state ordering, such as an Fe(II)(HNO)6 complex (ΔEH–L ANN: −17.1, DFT: 50.1 kcal mol−1), which contains an NO motif adjacent to the metal that had been absent from prior training complexes and is erroneously predicted by the ANN to be weak field in nature (Fig. 6). Similarly, no phosphorus-coordinating metal complexes and few sulfur-containing ligands had been in training data, leading to large errors for an Fe(II) complex with bidentate PH2SSPH2 ligands (ΔEH–L ANN: −27.8, DFT: 15.2 kcal mol−1, Fig. 6). Although phosphorus ligands are known to be low-spin directing, their absence from our training data means that accurate ANN predictions on such complexes cannot be expected. Finally, in some cases, the coordinating atom may be present in training data, but the chemistry is still unusual, as is the case for a strongly high-spin favoring Mn(III)(CH2CH3−)6 complex (Fig. 6). Although the ANN correctly predicts this complex to be high spin, it cannot predict the strong high-spin stabilization observed in the DFT calculation (ΔEH–L ANN: −11.8, DFT: −72.0 kcal mol−1) for this saturated, negatively charged carbon ligand that is distinct from other C-coordinating ligands (e.g., CO) in our prior training data sets.
Indeed, across a broad range of metals, oxidation states, and ligand coordinating atoms, the range of OHLDB ΔEH–L values exceeds that seen in our prior data sets (Fig. 7 and ESI† Fig. S6 and S7). Expected trends are observed, such as carbon- and phosphorus-coordinating complexes generally corresponding to low-spin-directing, strong field ligands, especially for Mn(II), Fe(II/III), or Co(II/III) complexes (Fig. 7 and ESI† Fig. S7). Although N-coordinating ligands generally form high-spin complexes, especially with Cr(II/III) or Mn(II/III) metals, notable exceptions are observed including low-spin Cr(II)(NSH)6 (ΔEH–L = 23.1 kcal mol−1) and Mn(II)(NNH2)6 (ΔEH–L = 20.6 kcal mol−1) complexes (Fig. 7). Given the dearth of low-spin Cr database complexes, the OHLDB therefore can be expected to enhance ML model predictions of ΔEH–L (Fig. 7).
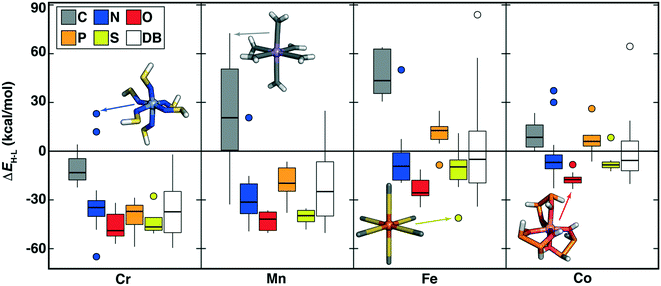 | ||
| Fig. 7 Boxplots of M(II) (M = Cr, Mn, Fe, or Co) ΔEH–L (in kcal mol−1) for ligands grouped by metal and by ligand-coordinating-atom (C in gray, N in blue, O in red, P in orange, and S in yellow, as shown in inset legend). Each box indicates the median by a horizontal line, the interquartile range (IQR), and whiskers indicate 1.5× the IQR. Here, DB (white boxplot) corresponds to range of ΔEH–L values from prior work in ref. 4 and 56 for the relevant metal, regardless of coordinating atom. | ||
Unsaturated carbon-coordinating ligands (e.g., CCH2 in Mn(II)(CCH2)6 ΔEH–L = 72.6 kcal mol−1) are known to be low-spin directing ligands but most were absent from our earlier data set, as were more unusual low-spin-directing ligands such as CHOH or CHNH2 (Mn(II) ΔEH–L = 47 to 62 kcal mol−1, Fig. 7). The sulfur-coordinated Fe(II) complexes in our new data set span from low-spin (e.g., monodentate SHOH: ΔEH–L = 11.0 kcal mol−1 or bidentate SC2H2S: ΔEH–L = 10.3 kcal mol−1) to high-spin (e.g., SC: ΔEH–L = −41.1 kcal mol−1), corresponding to a range that we had not observed in prior Fe(II) data (Fig. 7). Since sulfur is considered a soft element, low-spin sulfur complexes are somewhat surprising. Examination of the OHLDB confirms that the bidentate SC2H2S ligand also forms low-spin complexes with Fe(III) and Co(II/III) but forms high-spin complexes with Cr(II) and Mn(III) (see ESI†). Saturating the sulfur (i.e., SHC2H2SH) and the carbon backbone (i.e., SHC2H4SH) instead yields the expected, uniformly high-spin complexes regardless of metal center and oxidation state (see ESI†). Although oxygen-coordinating ligands are known to be weak-field, high-spin directing in nature, diverse ligand chemistry in the OHLDB yields, in addition to those previously observed, unexpectedly high-spin complexes e.g., Co(II)(OHP2H2OH)3 (ΔEH–L = −22.8 kcal mol−1, Fig. 7). This bidentate ligand and the isoelectronic OHS2OH ligand produce among the most high-spin-favoring Cr(II)/O-coordinating complexes (ΔEH–Lca. −49 to −52 kcal mol−1, see ESI†).
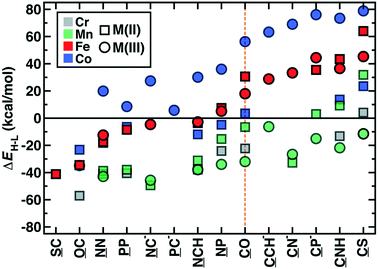
The OHLDB also enables examination of how isovalent and isoelectronic variations in ligands alter spin-state ordering (Fig. 8). Here, we focus on the widely-studied CO ligand and related isovalent and isoelectronic species, including those in the spectrochemical series76 (e.g., CN−) and other common molecules (e.g., HCN and N2, Fig. 8). Given ligand definitions, ΔEH–L can in principle be obtained for either orientation of asymmetric M2 ligands, but only 14 of these ligands in practice yielded at least one ΔEH–L value for any metal or oxidation state (Fig. 8). High-spin Fe(II) or Fe(III) complexes are formed from either homonuclear ligands (e.g., N2 and P2) or cases where the weaker-field element coordinates the metal (e.g., SC, OC), despite being isovalent or isoelectronic with low-spin directing CO (Fig. 8). These effects are not additive by element, where the NP ligand is low-spin directing, in spite of the high spin preferences of N2 and P2 (Fig. 8). Although CO is often invoked as one of the strongest field ligands (ΔEH–L = 20–30 kcal mol−1 for Fe(II) or Fe(III) complexes), five ligands form even more low-spin-favoring complexes, including those where O is replaced by anionic (e.g., CN−, CP−) or less electron withdrawing species (e.g., CCH−, CNH, or CS, Fig. 8). The trends observed for iron complexes generally hold for other metals, with Co(III) complexes exhibiting more low-spin bias for the same ligands, Mn(III) complexes remaining uniformly high spin, and all other metals and oxidation states generally residing within these two bounds (Fig. 8). Thus, a very wide range of ΔEH–L values (ca. −60 to +80 kcal mol−1) can be obtained simply by adjusting the charge and elemental identities in M2-type ligands isoelectronic or isovalent to a common ligand.
Finally, we considered the extent to which OHLDB data could be used to improve ML model predictions on large, diverse complexes112 by improving the chemical coverage of the ML model training data. We recently curated112 a 116 complex out-of-sample test set from the Cambridge Structural Database (CSD)113 for testing ΔEH–L predictions with a RAC-155/ANN model. Because the CSD complexes were chosen to be distinct from the 1901 complexes used in the training of the ANN, the CSD set ΔEH–L MAE of 8.6 kcal mol−1 was much poorer than set-aside test set errors (ca. 1–3 kcal mol−1 (ref. 17 and 56)) or uncertainty-controlled, out-of-sample prediction errors (ca. 4.5 kcal mol (ref. 27)). Notably, very high ΔEH–L prediction errors, either due to over or underestimation, were observed on the order of 20–50 kcal mol−1 (Fig. 9). Incorporating OHLDB data and retraining the RAC-155/ANN eliminated many of these highest error points and reduced CSD set MAE to 6.7 kcal mol−1 (Fig. 9, ESI† Text S1, Table S6, and Fig. S8 and S9). Despite the fact that most of the CSD complexes are much larger in size, significant improvements are observed for complexes that had metal-adjacent coordination environments present in the OHLDB but absent in our prior data, such as coordination by NO species (CSD ID: CEYSAA, Fig. 9). In most cases model performance improved, but for select complexes model performance remained the same or worsened slightly in a manner that is not dependent on the metal center (CSD ID: COBWEX, Fig. 9 and ESI† Fig. S9 and S10). Given that most of the CSD curated set112 is multidentate in nature, whereas the OHLDB is weighted toward monodentate ligands, further improvement could likely be achieved through continued systematic enumeration of a greater number of ligands of higher denticity.
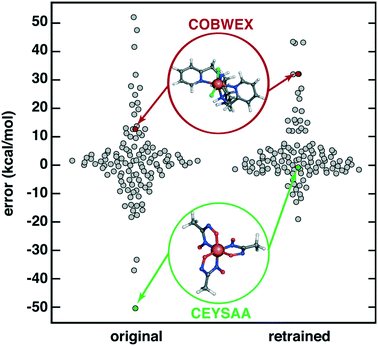 | ||
| Fig. 9 Swarm plot of RAC-155/ANN signed errors (in kcal mol−1) on an out-of-sample 116 CSD structure data set112 (original, left) and after retraining with OHLDB data (retrained, right). The single most improved (CSD ID: CEYSAA) and worsened (CSD ID: COBWEX) points are shown in green and red insets, respectively, and have data points colored in the same manner. | ||
5. Conclusions
We developed an approach for de novo ligand enumeration for the discovery of octahedral transition metal complexes. Our effort diverged from prior enumeration studies that had focused on neutral and stable organic molecules both by requiring that the individual ligands be smaller in size to form mononuclear octahedral transition metal complexes with no more than 13 heavy atoms as well as by relaxing prior constraints on charge or in satisfying the octet rule. From a space of over 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 theoretical monodentate or bidentate ligands comprised of C, N, O, P, or S heavy atoms, we identified a 2500-ligand subset for scoring. Based on analysis of ligand feasibility by score, we identified cutoffs and retained a high-scoring, 570-ligand subset as most promising for subsequent calculations. Only a small number (71 of over 2500) of our ligands were in prior databases, and most (75%) of those ligands remained within our high-scoring cutoff.
000 theoretical monodentate or bidentate ligands comprised of C, N, O, P, or S heavy atoms, we identified a 2500-ligand subset for scoring. Based on analysis of ligand feasibility by score, we identified cutoffs and retained a high-scoring, 570-ligand subset as most promising for subsequent calculations. Only a small number (71 of over 2500) of our ligands were in prior databases, and most (75%) of those ligands remained within our high-scoring cutoff.
We next characterized with DFT all of the feasible mononuclear, homoleptic octahedral transition metal complexes formed from combinations of the 396 ligands in complex with a choice of eight metal/oxidation state combinations in each of two spin states. Over the calculations that comprise the OHLDB, we obtained and analyzed nearly 350 spin-splitting energies. We observed unexpected combinations of metal/coordinating atom and spin-state ordering, including those that extended the ranges sampled in our prior databases of octahedral transition metal complexes. We showed how these complexes reflected chemical compositions previously absent from our machine learning (i.e., artificial neural network) models for predicting spin splitting. After enriching machine learning models with OHLDB data, we showed improved machine learning model prediction performance on an out-of-sample test set consisting of transition metal complexes much larger in size. We anticipate that the OHLDB will be a good testbed both for the application of high-scaling, correlated wavefunction theory methods and for representation development for machine learning in inorganic chemistry both in spin-splitting energy predictions and beyond.
Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
The authors acknowledge support by the Office of Naval Research under grant numbers N00014-17-1-2956 and N00014-18-1-2434 and a 2017 MIT Energy Initiative seed grant. H. J. K. holds a Career Award at the Scientific Interface from the Burroughs Wellcome Fund. This work was supported in part by an AAAS Marion Milligan Mason award (to H. J. K.). This work was carried out in part using computational resources from the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation grant number ACI-1548562. This work used the XStream computational resource, supported by the National Science Foundation Major Research Instrumentation program (ACI-1429830). The authors thank Adam H. Steeves for providing a critical reading of the manuscript.References
- S. Curtarolo, W. Setyawan, G. L. Hart, M. Jahnatek, R. V. Chepulskii, R. H. Taylor, S. Wang, J. Xue, K. Yang and O. Levy, AFLOW: An Automatic Framework for High-Throughput Materials Discovery, Comput. Mater. Sci., 2012, 58, 218–226 CrossRef CAS.
- S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, Python Materials Genomics (Pymatgen): A Robust, Open-Source Python Library for Materials Analysis, Comput. Mater. Sci., 2013, 68, 314–319 CrossRef CAS.
- E. I. Ioannidis, T. Z. H. Gani and H. J. Kulik, molSimplify: A Toolkit for Automating Discovery in Inorganic Chemistry, J. Comput. Chem., 2016, 37, 2106–2117 CrossRef CAS.
- A. Nandy, C. Duan, J. P. Janet, S. Gugler and H. J. Kulik, Strategies and Software for Machine Learning Accelerated Discovery in Transition Metal Chemistry, Ind. Eng. Chem. Res., 2018, 57, 13973–13986 CrossRef CAS.
- N. M. O'Boyle, M. Banck, C. A. James, C. Morley, T. Vandermeersch and G. R. Hutchison, Open Babel: An Open Chemical Toolbox, J. Phys. Chem. Lett., 2011, 3, 33 Search PubMed.
- T. J. Martínez, Ab Initio Reactive Computer Aided Molecular Design, Acc. Chem. Res., 2017, 50, 652–656 CrossRef PubMed.
- S. Luber, Recent Progress in Computational Exploration and Design of Functional Materials, Comput. Mater. Sci., 2019, 161, 127–134 CrossRef CAS.
- J. Caruthers, J. A. Lauterbach, K. Thomson, V. Venkatasubramanian, C. Snively, A. Bhan, S. Katare and G. Oskarsdottir, Catalyst Design: Knowledge Extraction from High-Throughput Experimentation, J. Catal., 2003, 216, 98–109 CrossRef CAS.
- S. Katare, J. M. Caruthers, W. N. Delgass and V. Venkatasubramanian, An Intelligent System for Reaction Kinetic Modeling and Catalyst Design, Ind. Eng. Chem. Res., 2004, 43, 3484–3512 CrossRef CAS.
- A. Corma, M. J. Díaz-Cabanas, M. Moliner and C. Martínez, Discovery of a New Catalytically Active and Selective Zeolite (ITQ-30) by High-Throughput Synthesis Techniques, J. Catal., 2006, 241, 312–318 CrossRef CAS.
- Y. Zhuo, A. Mansouri Tehrani and J. Brgoch, Predicting the Band Gaps of Inorganic Solids by Machine Learning, J. Phys. Chem. Lett., 2018, 9, 1668–1673 CrossRef CAS PubMed.
- S. De, A. P. Bartok, G. Csanyi and M. Ceriotti, Comparing Molecules and Solids across Structural and Alchemical Space, Phys. Chem. Chem. Phys., 2016, 18, 13754–13769 RSC.
- L. Ward, A. Agrawal, A. Choudhary and C. Wolverton, A General-Purpose Machine Learning Framework for Predicting Properties of Inorganic Materials, npj Comput. Mater., 2016, 2, 16028 CrossRef.
- G. Pilania, C. Wang, X. Jiang, S. Rajasekaran and R. Ramprasad, Accelerating Materials Property Predictions Using Machine Learning, Sci. Rep., 2013, 3, 2810 CrossRef PubMed.
- B. Meyer, B. Sawatlon, S. Heinen, O. A. von Lilienfeld and C. Corminboeuf, Machine Learning Meets Volcano Plots: Computational Discovery of Cross-Coupling Catalysts, Chem. Sci., 2018, 9, 7069–7077 RSC.
- X. Ma, Z. Li, L. E. K. Achenie and H. Xin, Machine-Learning-Augmented Chemisorption Model for CO2 Electroreduction Catalyst Screening, J. Phys. Chem. Lett., 2015, 6, 3528–3533 CrossRef CAS.
- J. P. Janet and H. J. Kulik, Predicting Electronic Structure Properties of Transition Metal Complexes with Neural Networks, Chem. Sci., 2017, 8, 5137–5152 RSC.
- Z. Li, N. Omidvar, W. S. Chin, E. Robb, A. Morris, L. Achenie and H. Xin, Machine-Learning Energy Gaps of Porphyrins with Molecular Graph Representations, J. Phys. Chem. A, 2018, 122, 4571–4578 CrossRef CAS.
- K. Yao, J. E. Herr, D. W. Toth, R. Mckintyre and J. Parkhill, The Tensormol-0.1 Model Chemistry: A Neural Network Augmented with Long-Range Physics, Chem. Sci., 2018, 9, 2261–2269 RSC.
- J. Behler, Perspective: Machine Learning Potentials for Atomistic Simulations, J. Chem. Phys., 2016, 145, 170901 CrossRef.
- J. S. Smith, O. Isayev and A. E. Roitberg, ANI-1: An Extensible Neural Network Potential with DFT Accuracy at Force Field Computational Cost, Chem. Sci., 2017, 8, 3192–3203 RSC.
- L. Zhang, J. Han, H. Wang, R. Car and E. Weinan, Deep Potential Molecular Dynamics: A Scalable Model with the Accuracy of Quantum Mechanics, Phys. Rev. Lett., 2018, 120, 143001 CrossRef CAS.
- S. Chmiela, A. Tkatchenko, H. E. Sauceda, I. Poltavsky, K. T. Schütt and K.-R. Müller, Machine Learning of Accurate Energy-Conserving Molecular Force Fields, Sci. Adv., 2017, 3, e1603015 CrossRef.
- F. A. Faber, L. Hutchison, B. Huang, J. Gilmer, S. S. Schoenholz, G. E. Dahl, O. Vinyals, S. Kearnes, P. F. Riley and O. A. Von Lilienfeld, Prediction Errors of Molecular Machine Learning Models Lower Than Hybrid DFT Error, J. Chem. Theory Comput., 2017, 13, 5255–5264 CrossRef CAS.
- B. R. Goldsmith, J. Esterhuizen, J. X. Liu, C. J. Bartel and C. Sutton, Machine Learning for Heterogeneous Catalyst Design and Discovery, AIChE J., 2018, 64, 2311–2323 CrossRef CAS.
- J. R. Kitchin, Machine Learning in Catalysis, Nat. Catal., 2018, 1, 230 CrossRef.
- J. P. Janet, L. Chan and H. J. Kulik, Accelerating Chemical Discovery with Machine Learning: Simulated Evolution of Spin Crossover Complexes with an Artificial Neural Network, J. Phys. Chem. Lett., 2018, 9, 1064–1071 CrossRef CAS.
- J. P. Janet, F. Liu, A. Nandy, C. Duan, T. Yang, S. Lin and H. J. Kulik, Designing in the Face of Uncertainty: Exploiting Electronic Structure and Machine Learning Models for Discovery in Inorganic Chemistry, Inorg. Chem., 2019 DOI:10.1021/acs.inorgchem.9b00109.
- S. Lu, Q. Zhou, Y. Ouyang, Y. Guo, Q. Li and J. Wang, Accelerated Discovery of Stable Lead-Free Hybrid Organic-Inorganic Perovskites via Machine Learning, Nat. Commun., 2018, 9, 3405 CrossRef.
- R. Yuan, Z. Liu, P. V. Balachandran, D. Xue, Y. Zhou, X. Ding, J. Sun, D. Xue and T. Lookman, Accelerated Discovery of Large Electrostrains in BaTiO3-Based Piezoelectrics Using Active Learning, Adv. Mater., 2018, 30, 1702884 CrossRef.
- B. Meredig, E. Antono, C. Church, M. Hutchinson, J. Ling, S. Paradiso, B. Blaiszik, I. Foster, B. Gibbons and J. Hattrick-Simpers, Can Machine Learning Identify the Next High-Temperature Superconductor? Examining Extrapolation Performance for Materials Discovery, Mol. Syst. Des. Eng., 2018, 3, 819–825 RSC.
- F. Ren, L. Ward, T. Williams, K. J. Laws, C. Wolverton, J. Hattrick-Simpers and A. Mehta, Accelerated Discovery of Metallic Glasses through Iteration of Machine Learning and High-Throughput Experiments, Sci. Adv., 2018, 4, eaaq1566 CrossRef.
- B. Sanchez-Lengeling and A. Aspuru-Guzik, Inverse Molecular Design Using Machine Learning: Generative Models for Matter Engineering, Science, 2018, 361, 360 CrossRef CAS.
- Q. Zhao and H. J. Kulik, Where Does the Density Localize in the Solid State? Divergent Behavior for Hybrids and DFT+U, J. Chem. Theory Comput., 2018, 14, 670–683 CrossRef CAS.
- K. D. Vogiatzis, M. V. Polynski, J. K. Kirkland, J. Townsend, A. Hashemi, C. Liu and E. A. Pidko, Computational Approach to Molecular Catalysis by 3d Transition Metals: Challenges and Opportunities, Chem. Rev., 2018, 119, 2453–2523 CrossRef PubMed.
- L. Grajciar, C. J. Heard, A. A. Bondarenko, M. V. Polynski, J. Meeprasert, E. A. Pidko and P. Nachtigall, Towards Operando Computational Modeling in Heterogeneous Catalysis, Chem. Soc. Rev., 2018, 47, 8307–8348 RSC.
- P. B. Arockiam, C. Bruneau and P. H. Dixneuf, Ruthenium(II)-Catalyzed C-H Bond Activation and Functionalization, Chem. Rev., 2012, 112, 5879–5918 CrossRef CAS PubMed.
- C. K. Prier, D. A. Rankic and D. W. C. MacMillan, Visible Light Photoredox Catalysis with Transition Metal Complexes: Applications in Organic Synthesis, Chem. Rev., 2013, 113, 5322–5363 CrossRef CAS.
- G. Rouquet and N. Chatani, Catalytic Functionalization of C(sp(2))-H and C(sp(3))-H Bonds by Using Bidentate Directing Groups, Angew. Chem., Int. Ed., 2013, 52, 11726–11743 CrossRef CAS.
- D. M. Schultz and T. P. Yoon, Solar Synthesis: Prospects in Visible Light Photocatalysis, Science, 2014, 343, 1239176 CrossRef.
- D. W. Shaffer, I. Bhowmick, A. L. Rheingold, C. Tsay, B. N. Livesay, M. P. Shores and J. Y. Yang, Spin-State Diversity in a Series of Co(Ii) PNP Pincer Bromide Complexes, Dalton Trans., 2016, 45, 17910–17917 RSC.
- C. Tsay and J. Y. Yang, Electrocatalytic Hydrogen Evolution under Acidic Aqueous Conditions and Mechanistic Studies of a Highly Stable Molecular Catalyst, J. Am. Chem. Soc., 2016, 138, 14174–14177 CrossRef CAS PubMed.
- M. Schilling, G. R. Patzke, J. Hutter and S. Luber, Computational Investigation and Design of Cobalt Aqua Complexes for Homogeneous Water Oxidation, J. Phys. Chem. C, 2016, 120, 7966–7975 CrossRef CAS.
- D. C. Ashley and E. Jakubikova, Ironing out the Photochemical and Spin-Crossover Behavior of Fe (II) Coordination Compounds with Computational Chemistry, Coord. Chem. Rev., 2017, 337, 97–111 CrossRef CAS.
- D. N. Bowman, A. Bondarev, S. Mukherjee and E. Jakubikova, Tuning the Electronic Structure of Fe(II) Polypyridines via Donor Atom and Ligand Scaffold Modifications: A Computational Study, Inorg. Chem., 2015, 54, 8786–8793 CrossRef CAS PubMed.
- A. Yella, H. W. Lee, H. N. Tsao, C. Y. Yi, A. K. Chandiran, M. K. Nazeeruddin, E. W. G. Diau, C. Y. Yeh, S. M. Zakeeruddin and M. Gratzel, Porphyrin-Sensitized Solar Cells with Cobalt (II/III)-Based Redox Electrolyte Exceed 12 Percent Efficiency, Science, 2011, 334, 629–634 CrossRef CAS PubMed.
- R. Czerwieniec, J. B. Yu and H. Yersin, Blue-Light Emission of Cu(I) Complexes and Singlet Harvesting, Inorg. Chem., 2011, 50, 8293–8301 CrossRef CAS.
- F. B. Dias, K. N. Bourdakos, V. Jankus, K. C. Moss, K. T. Kamtekar, V. Bhalla, J. Santos, M. R. Bryce and A. P. Monkman, Triplet Harvesting with 100% Efficiency by Way of Thermally Activated Delayed Fluorescence in Charge Transfer OLED Emitters, Adv. Mater., 2013, 25, 3707–3714 CrossRef CAS.
- P. S. Kuttipillai, Y. M. Zhao, C. J. Traverse, R. J. Staples, B. G. Levine and R. R. Lunt, Phosphorescent Nanocluster Light-Emitting Diodes, Adv. Mater., 2016, 28, 320–326 CrossRef CAS.
- M. J. Leitl, F. R. Kuchle, H. A. Mayer, L. Wesemann and H. Yersin, Brightly Blue and Green Emitting Cu(I) Dimers for Singlet Harvesting in Oleds, J. Phys. Chem. A, 2013, 117, 11823–11836 CrossRef CAS.
- C. L. Linfoot, M. J. Leitl, P. Richardson, A. F. Rausch, O. Chepelin, F. J. White, H. Yersin and N. Robertson, Thermally Activated Delayed Fluorescence (TADF) and Enhancing Photoluminescence Quantum Yields of Cu-I(Diimine)(Diphosphine)(+) Complexes-Photophysical, Structural, and Computational Studies, Inorg. Chem., 2014, 53, 10854–10861 CrossRef CAS.
- D. M. Zink, M. Bachle, T. Baumann, M. Nieger, M. Kuhn, C. Wang, W. Klopper, U. Monkowius, T. Hofbeck, H. Yersin and S. Brase, Synthesis, Structure, and Characterization of Dinuclear Copper(I) Halide Complexes with PAN Ligands Featuring Exciting Photoluminescence Properties, Inorg. Chem., 2013, 52, 2292–2305 CrossRef CAS PubMed.
- Y. Minenkov, D. I. Sharapa and L. Cavallo, Application of Semiempirical Methods to Transition Metal Complexes: Fast Results but Hard-to-Predict Accuracy, J. Chem. Theory Comput., 2018, 14, 3428–3439 CrossRef CAS PubMed.
- R. J. Deeth, The Ligand Field Molecular Mechanics Model and the Stereoelectronic Effects of d and S Electrons, Coord. Chem. Rev., 2001, 212, 11–34 CrossRef CAS.
- A. K. Rappé, C. J. Casewit, K. Colwell, W. A. Goddard III and W. Skiff, UFF, a Full Periodic Table Force Field for Molecular Mechanics and Molecular Dynamics Simulations, J. Am. Chem. Soc., 1992, 114, 10024–10035 CrossRef.
- J. P. Janet and H. J. Kulik, Resolving Transition Metal Chemical Space: Feature Selection for Machine Learning and Structure-Property Relationships, J. Phys. Chem. A, 2017, 121, 8939–8954 CrossRef CAS.
- C. Duan, J. P. Janet, F. Liu, A. Nandy and H. J. Kulik, Learning from Failure: Predicting Electronic Structure Calculation Outcomes with Machine Learning Models, J. Chem. Theory Comput., 2019, 15, 2331–2345 CrossRef CAS.
- A. Nandy, J. Zhu, J. P. Janet, C. Duan, R. B. Getman and H. J. Kulik, Machine Learning Accelerates the Discovery of Design Rules and Exceptions in Stable Metal- Oxo Intermediate Formation, 2019, chemRxiv, DOI:10.26434/chemrxiv.8182025.v1.
- C. R. Collins, G. J. Gordon, O. A. von Lilienfeld and D. J. Yaron, Constant Size Descriptors for Accurate Machine Learning Models of Molecular Properties, J. Chem. Phys., 2018, 148, 241718 CrossRef.
- B. Huang and O. A. von Lilienfeld, Communication: Understanding Molecular Representations in Machine Learning: The Role of Uniqueness and Target Similarity, J. Chem. Phys., 2016, 145, 161102 CrossRef PubMed.
- K. Yao, J. E. Herr, S. N. Brown and J. Parkhill, Intrinsic Bond Energies from a Bonds-in-Molecules Neural Network, J. Phys. Chem. Lett., 2017, 8, 2689–2694 CrossRef CAS PubMed.
- K. Hansen, F. Biegler, R. Ramakrishnan and W. Pronobis, Machine Learning Predictions of Molecular Properties: Accurate Many-Body Potentials and Nonlocality in Chemical Space, J. Phys. Chem. Lett., 2015, 6, 2326–2331 CrossRef CAS PubMed.
- K. Gubaev, E. V. Podryabinkin and A. V. Shapeev, Machine Learning of Molecular Properties: Locality and Active Learning, J. Chem. Phys., 2018, 148, 241727 CrossRef PubMed.
- P. Bjørn Jørgensen, K. Wedel Jacobsen and M. N. Schmidt, Neural Message Passing with Edge Updates for Predicting Properties of Molecules and Materials, 2018, arXiv e-prints [Online], https://ui.adsabs.harvard.edu/-abs/2018arXiv180603146B (accessed June 01, 2018).
- N. Lubbers, J. S. Smith and K. Barros, Hierarchical Modeling of Molecular Energies Using a Deep Neural Network, J. Chem. Phys., 2018, 148, 241715 CrossRef PubMed.
- R. Ramakrishnan, P. O. Dral, M. Rupp and O. A. Von Lilienfeld, Quantum Chemistry Structures and Properties of 134 Kilo Molecules, Sci. Data, 2014, 1, 140022 CrossRef CAS PubMed.
- J. S. Smith, O. Isayev and A. E. Roitberg, ANI-1, a Data Set of 20 Million Calculated Off-Equilibrium Conformations for Organic Molecules, Sci. Data, 2017, 4, 170193 CrossRef CAS.
- A. M. Virshup, J. Contreras-García, P. Wipf, W. Yang and D. N. Beratan, Stochastic Voyages into Uncharted Chemical Space Produce a Representative Library of All Possible Drug-Like Compounds, J. Am. Chem. Soc., 2013, 135, 7296–7303 CrossRef CAS PubMed.
- L. Ruddigkeit, R. van Deursen, L. C. Blum and J.-L. Reymond, Enumeration of 166 Billion Organic Small Molecules in the Chemical Universe Database GDB-17, J. Chem. Inf. Model., 2012, 52, 2864–2875 CrossRef CAS.
- R. W. Sterner and J. J. Elser, Ecological Stoichiometry: The Biology of Elements from Molecules to the Biosphere, Princeton University Press, 2002 Search PubMed.
- H. J. M. Bowen, Environmental Chemistry of the Elements, Academic Press, 1979 Search PubMed.
- T. Fink, H. Bruggesser and J.-L. Reymond, Virtual Exploration of the Small-Molecule Chemical Universe Below 160 Daltons, Angew. Chem., Int. Ed., 2005, 44, 1504–1508 CrossRef CAS.
- M. J. Wester, S. N. Pollock, E. A. Coutsias, T. K. Allu, S. Muresan and T. I. Oprea, Scaffold Topologies. 2. Analysis of Chemical Databases, J. Chem. Inf. Model., 2008, 48, 1311–1324 CrossRef CAS.
- S. B. Heymsfield, M. Waki, J. Kehayias, S. Lichtman, F. A. Dilmanian, Y. Kamen, J. Wang and R. N. Pierson, Chemical and Elemental Analysis of Humans in Vivo Using Improved Body Composition Models, Am. J. Physiol., 1991, 261, E190–E198 CAS.
- C. K. Jørgensen, Differences between the Four Halide Ligands, and Discussion Remarks on Trigonal-Bipyramidal Complexes, on Oxidation States, and on Diagonal Elements of One-Electron Energy, Coord. Chem. Rev., 1966, 1, 164–178 CrossRef.
- R. Tsuchida, Absorption Spectra of Co-ordination Compounds. I, Bull. Chem. Soc. Jpn., 1938, 13, 388–400 CrossRef CAS.
- W. A. Herrmann, C. Krüger, R. Goddard and I. Bernal, Transition Metal Methylene Complexes: III. Methylene (CH2), a Carbonyl Analogous Ligand; Crystal Structure of M-Methylenebis(Carbonyl-H5-Cyclopentadienylrhodium)(Rh—Rh), J. Organomet. Chem., 1977, 140, 73–89 CrossRef CAS.
- H. Vahrenkamp, Sulfur Atoms as Ligands in Metal Complexes, Angewandte Chemie International Edition in English, 1975, 14, 322–329 CrossRef.
- J. Miller, A. L. Balch and J. H. Enemark, Addition of Methylamine to Hexakis(Methyl Isocyanide)Iron(II). Formation of an Unusual Chelating Ligand, J. Am. Chem. Soc., 1971, 93, 4613–4614 CrossRef CAS.
- M. N. Hughes and K. Shrimanker, Metal Complexes of Hydroxylamine, Inorg. Chim. Acta, 1976, 18, 69–76 CrossRef CAS.
- P. Barbaro, M. Di Vaira, M. Peruzzini, S. Seniori Costantini and P. Stoppioni, Hydrolysis of Dinuclear Ruthenium Complexes [CpRu(PPh3)22(M,H1:1-L)][CF3SO3]2 (L=P4, P4S3): Simple Access to Metal Complexes of P2H4 and PH2SH, Chem. – Eur. J., 2007, 13, 6682–6690 CrossRef CAS.
- H. Mimoun, Transition-Metal Peroxides—Synthesis and Use as Oxidizing Agents, in Peroxides (1983), Wiley-Blackwell, 2010, pp. 463–482 Search PubMed.
- T. W. Hayton, P. Legzdins and W. B. Sharp, Coordination and Organometallic Chemistry of Metal−NO Complexes, Chem. Rev., 2002, 102, 935–992 CrossRef CAS.
- Y. Shimura and R. Tsuchida, Absorption Spectra of Co(III) Complexes. II. Redetermination of the Spectrochemical Series, Bull. Chem. Soc. Jpn., 1956, 29, 311–316 CrossRef CAS.
- D. J. McKay and J. S. Wright, How Long Can You Make an Oxygen Chain?, J. Am. Chem. Soc., 1998, 120, 1003–1013 CrossRef CAS.
- A. Gaulton, A. Hersey, M. Nowotka, A. P. Bento, J. Chambers, D. Mendez, P. Mutowo, F. Atkinson, L. J. Bellis, E. Cibrián-Uhalte, M. Davies, N. Dedman, A. Karlsson, M. P. Magariños, J. P. Overington, G. Papadatos, I. Smit and A. R. Leach, The ChEMBL Database in 2017, Nucleic Acids Res., 2017, 45, D945–D954 CrossRef CAS.
- P. F. Bernath and S. McLeod, Diref, a Database of References Associated with the Spectra of Diatomic Molecules, J. Mol. Spectrosc., 2001, 207, 287 CrossRef CAS PubMed.
- N. M. O'Boyle, C. Morley and G. R. Hutchison, Pybel: A Python Wrapper for the Openbabel Cheminformatics Toolkit, Chem. Cent. J., 2008, 2, 5 CrossRef PubMed.
- B. Pritchard and J. Autschbach, Theoretical Investigation of Paramagnetic NMR Shifts in Transition Metal Acetylacetonato Complexes: Analysis of Signs, Magnitudes, and the Role of the Covalency of Ligand–Metal Bonding, Inorg. Chem., 2012, 51, 8340–8351 CrossRef CAS PubMed.
- I. S. Ufimtsev and T. J. Martinez, Quantum Chemistry on Graphical Processing Units. 3. Analytical Energy Gradients, Geometry Optimization, and First Principles Molecular Dynamics, J. Chem. Theory Comput., 2009, 5, 2619–2628 CrossRef CAS.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- A. D. Becke, Density-Functional Thermochemistry. III. The Role of Exact Exchange, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- S. H. Vosko, L. Wilk and M. Nusair, Accurate Spin-Dependent Electron Liquid Correlation Energies for Local Spin Density Calculations: A Critical Analysis, Can. J. Phys., 1980, 58, 1200–1211 CrossRef CAS.
- P. J. Hay and W. R. Wadt, Ab Initio Effective Core Potentials for Molecular Calculations. Potentials for the Transition Metal Atoms Sc to Hg, J. Chem. Phys., 1985, 82, 270–283 CrossRef CAS.
- J. P. Janet, T. Z. H. Gani, A. H. Steeves, E. I. Ioannidis and H. J. Kulik, Leveraging Cheminformatics Strategies for Inorganic Discovery: Application to Redox Potential Design, Ind. Eng. Chem. Res., 2017, 56, 4898–4910 CrossRef CAS.
- S. R. Mortensen and K. P. Kepp, Spin Propensities of Octahedral Complexes from Density Functional Theory, J. Phys. Chem. A, 2015, 119, 4041–4050 CrossRef CAS PubMed.
- V. R. Saunders and I. H. Hillier, Level-Shifting Method for Converging Closed Shell Hartree-Fock Wave-Functions, Int. J. Quantum Chem., 1973, 7, 699–705 CrossRef.
- L.-P. Wang and C. Song, Geometry Optimization Made Simple with Translation and Rotation Coordinates, J. Chem. Phys., 2016, 144, 214108 CrossRef PubMed.
- T. Z. H. Gani and H. J. Kulik, Unifying Exchange Sensitivity in Transition Metal Spin-State Ordering and Catalysis through Bond Valence Metrics, J. Chem. Theory Comput., 2017, 13, 5443–5457 CrossRef CAS PubMed.
- E. I. Ioannidis and H. J. Kulik, Towards Quantifying the Role of Exact Exchange in Predictions of Transition Metal Complex Properties, J. Chem. Phys., 2015, 143, 034104 CrossRef PubMed.
- E. I. Ioannidis and H. J. Kulik, Ligand-Field-Dependent Behavior of Meta-GGA Exchange in Transition-Metal Complex Spin-State Ordering, J. Phys. Chem. A, 2017, 121, 874–884 CrossRef CAS PubMed.
- H. J. Kulik, M. Cococcioni, D. A. Scherlis and N. Marzari, Density Functional Theory in Transition-Metal Chemistry: A Self-Consistent Hubbard U Approach, Phys. Rev. Lett., 2006, 97, 103001 CrossRef PubMed.
- G. Ganzenmüller, N. Berkaïne, A. Fouqueau, M. E. Casida and M. Reiher, Comparison of Density Functionals for Differences between the High- (T2g5) and Low- (A1g1) Spin States of Iron(II) Compounds. IV. Results for the Ferrous Complexes [Fe(L)(‘NHS4’)], J. Chem. Phys., 2005, 122, 234321 CrossRef PubMed.
- A. Droghetti, D. Alfè and S. Sanvito, Assessment of Density Functional Theory for Iron (II) Molecules across the Spin-Crossover Transition, J. Chem. Phys., 2012, 137, 124303 CrossRef CAS PubMed.
- P. Verma, Z. Varga, J. E. Klein, C. J. Cramer, L. Que and D. G. Truhlar, Assessment of Electronic Structure Methods for the Determination of the Ground Spin States of Fe (II), Fe (III) and Fe (IV) Complexes, Phys. Chem. Chem. Phys., 2017, 19, 13049–13069 RSC.
- L. Wilbraham, P. Verma, D. G. Truhlar, L. Gagliardi and I. Ciofini, Multiconfiguration Pair-Density Functional Theory Predicts Spin-State Ordering in Iron Complexes with the Same Accuracy as Complete Active Space Second-Order Perturbation Theory at a Significantly Reduced Computational Cost, J. Phys. Chem. Lett., 2017, 8, 2026–2030 CrossRef CAS PubMed.
- Q. M. Phung, M. Feldt, J. N. Harvey and K. Pierloot, Toward Highly Accurate Spin State Energetics in First-Row Transition Metal Complexes: A Combined CASPT2/Cc Approach, J. Chem. Theory Comput., 2018, 14, 2446–2455 CrossRef CAS PubMed.
- C. Zhou, L. Gagliardi and D. G. Truhlar, Multiconfiguration Pair-Density Functional Theory for Iron Porphyrin with CAS, RAS, and DMRG Active Spaces, J. Phys. Chem. A, 2019, 123, 3389–3394 CrossRef CAS.
- M. C. Kim, E. Sim and K. Burke, Communication: Avoiding Unbound Anions in Density Functional Calculations, J. Chem. Phys., 2011, 134, 171103 CrossRef PubMed.
- F. Jensen, Describing Anions by Density Functional Theory: Fractional Electron Affinity, J. Chem. Theory Comput., 2010, 6, 2726–2735 CrossRef CAS PubMed.
- J. P. Janet, C. Duan, T. Yang, A. Nandy and H. J. Kulik, A Quantitative Uncertainty Metric Controls Error in Neural Network-Driven Chemical Discovery, chemrXiv, DOI:10.26434/chemrxiv.7900277.v2, 2019.
- C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, The Cambridge Structural Database, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171–179 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: SMILES strings and components of scores for M1, M2, and B4 ligands; details of M1, M2, and B4 ligand scoring along with properties of retained ligands; comparison of ligand scores to properties of ChEMBL, DiRef, and GDB-9 molecules; principal component analysis of OHLDB data and comparison to prior calculations; success rate of DFT calculations; spin-splitting properties of new complexes, including M(III) boxplot results; analysis of improvement in out-of-sample CSD ANN performance with retrained ANN (PDF). Geometry optimized structures and properties of OHLDB complexes; geometry optimized structures and properties of 1901 training complexes, geometry optimized structures and properties of 116 CSD test case complexes; ANN predictions on OHLDB structures; ANN predictions on CSD structures before and after retraining; ANN models, ANN models, weights and scaling information before and after retraining (ZIP). See DOI: 10.1039/c9me00069k |
| This journal is © The Royal Society of Chemistry 2020 |