Open Access Article
Open Access ArticlePrecise modulation of molecular weight distribution for structural engineering†
Rui
Tan
a,
Dongdong
Zhou
a,
Baolei
Liu
c,
Yanxiao
Sun
a,
Xinxin
Liu
a,
Zhuang
Ma
a,
Deyu
Kong
a,
Jinlin
He
 c,
Zhengbiao
Zhang
c,
Zhengbiao
Zhang
 c and
Xue-Hui
Dong
c and
Xue-Hui
Dong
 *ab
*ab
aSouth China Advanced Institute of Soft Matter Science and Technology, School of Molecular Science and Engineering, South China University of Technology, Guangzhou 510640, China. E-mail: xdong@scut.edu.cn
bState Key Laboratory of Luminescent Materials and Devices, South China University of Technology, Guangzhou 510640, China
cCollege of Chemistry, Chemical Engineering and Materials Science, Soochow University, Suzhou, 215123, China
First published on 29th October 2019
Abstract
As one of the most critical molecular parameters, molecular weight distribution has a profound impact on the structure and properties of polymers. Quantitative and comprehensive understanding, however, has yet to be established, mainly due to the challenge in the precise control and regulation of molecular weight distribution. In this work, we demonstrated a robust and effective approach to artificially engineer the molecular weight distribution through precise recombination of discrete macromolecules. The width, symmetry, and other characteristics of the distribution can be independently manipulated to achieve absolute control, serving as a model platform for highlighting the importance of chain length heterogeneity in structural engineering. Different from their discrete counterparts, each individual component in dispersed samples experiences a varied degree of supercooling at a specific crystallization temperature. Non-uniform crystal nucleation and growth kinetics lead to distinct molecular arrangements. This work could bridge the gap between discrete and dispersed macromolecules, providing fundamental perspectives on the critical role of molecular weight distribution.
Introduction
Molecular weight is one of the most fundamental parameters that define a macromolecule. Unlike most biomacromolecules of uniform size, synthetic macromolecules generally have an inherent heterogeneity in their chain length. Many behaviors of polymeric materials, such as viscosity, processability, crystallization, and self-assembly, depend not only on the average molecular weight, but also on the distribution of molecular weight.1 Minor changes in the distribution could significantly alter the content of each component, which may result in substantial differences in the physical properties.2 Although a few pioneering theoretical explorations3–7 and experimental studies8–14 have been conducted, the importance of molecular weight distribution in determining the structure and properties of macromolecules is, however, still unclear. There are mainly two obstacles: (i) precise control and quantitative modulation of molecular weight distribution is challenging;13,15,16 and (ii) molecular weight distribution is a complex parameter consisting of multiple variables such as distribution width, symmetry, shape, etc.17 The collective effect is very difficult to decouple to elucidate the independent contribution of each factor.12,18A polymer is essentially a mixture of macromolecules having the same repeat unit and consecutive degrees of polymerization. Average molecular weight (e.g. number average, Mn, or weight average, Mw) and dispersity (Đ, defined as Mw/Mn), measured typically by size exclusive chromatography (SEC), however, provide only indirect and oversimplified characteristics of the composition (i.e. arithmetic mean and relative breadth of the distribution).18 Samples with the same Mn and Đ do not necessarily have the same constitution.12 In principle, higher moments (such as skewness and kurtosis) containing information about symmetry, shape, etc. of a given distribution are also required.17,19 These critical quantities, however, are usually not included in Đ. Therefore, Đ is not a comprehensive description of molecular weight distribution.18 The use of Đ as a sole variable to represent the molecular weight distribution could thus be limited.
Technically, two approaches are usually adopted to modulate molecular weight distribution.20 One is to control the polymerization process. The development of living/controlled polymerization makes complicated molecular design and “narrow” molecular weight distribution possible.21–23 Recently, Fors13,24 and Cölfen15 further demonstrated initial attempts to control the shape of the molecular weight distribution by manipulating the initiation process, such as temporal control of the initiator addition, or spatial control of the initiator gradient. Though the molecular weight distribution can be regulated to some extent,25–27 precise control is not possible due to the essential statistical nature of chain growth. The batch-to-batch variation would severely impede further systematic studies. The second approach is to blend samples with different average molecular weights.28–30 Although this method is relatively simple and straightforward, the resultant blends suffer from complex compositions such as multimodal distributions, due to the intrinsic chain length heterogeneity of the blending stocks.
Precise control and modulation of molecular weight distribution is the prerequisite for quantitative and comprehensive exploration. Discrete polymers (Đ = 1) having a definite composition, sequence, and topology exhibit unique phase behaviors compared to their dispersed analogues,31,32 revealing high sensitivity of microstructures to the chain length heterogeneity.33–39 In this study, we will demonstrate a method for precisely tailoring the molecular weight distribution. By rationally blending discrete oligo-L-lactic acid (oLLA) according to certain distribution functions (such as the Schulz–Zimm distribution, Gaussian distribution, skew-normal distribution, etc.), we could artificially generate and regulate molecular weight distributions on demand (Scheme 1a). The content of each component is accurately defined, and the width, symmetry, shape, and other characteristics of molecular weight distribution could be independently engineered to achieve absolute control, bridging the gap between discrete and dispersed macromolecules. Crystallization behaviors of oLLAs with varied distributions are systematically studied and quantitatively compared (Schemes 1b and c), serving as a model example to reveal the detailed contribution of molecular weight distribution. This research work not only deepens the understanding of fundamental crystallization theory, but also provides a potential tunable molecular parameter for rational design of functional polymers with advanced properties.
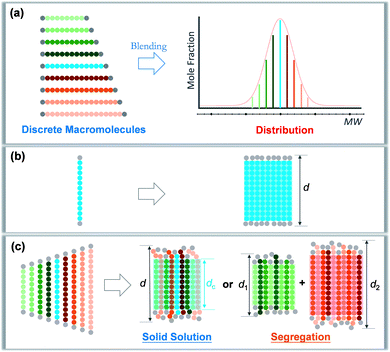 | ||
| Scheme 1 Modulation of molecular weight distribution via precisely blending discrete macromolecules (a) and proposed molecular packing of discrete (b) and dispersed (c) oLLAs upon crystallization. | ||
Results and discussion
Synthesis of discrete oLLAs
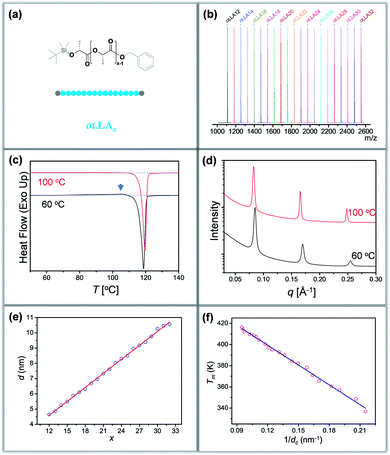
Discrete oLLAs were synthesized following an iterative growth route (Scheme S1, see the ESI† for details).40,41 The oligomers have tert-butyldimethylsilyl (TBDMS) and benzyl (Bn) groups as two protecting end groups, respectively (Fig. 1a). Discrete oLLAs with the number of repeat units ranging from 12 to 32 were prepared typically at the gram scale (labeled as oLLAx, where x refers to the number of repeat units). Their chemical structure was characterized by proton nuclear magnetic resonance (1H NMR, Fig. S1†). For each sample, matrix-assisted laser desorption/ionization time-of-flight mass spectrometry (MALDI-ToF MS) displays a single peak with molecular weight in good accordance with the calculated value, confirming the identity and discrete feature (Fig. 1b and S3†). Size exclusive chromatography (SEC) elution profiles show a certain instrumental spread though the samples have uniform size, which can be attributed to diffusion in the column (Fig. S2a†). Though no further attempt has been made, it should also be possible to prepare oLLA with higher molecular weight by taking advantage of the exponential growth approach. Detailed molecular information of the discrete oLLA library is summarized in Table S1.†Crystallization behaviors of discrete oLLAs
All the oLLA samples listed in Table S1† are crystalline solids at room temperature. It is well known that poly(L-lactic acid) has multiple crystal polymorphs, in which the α form with two 103 helical chains packed into an orthorhombic unit cell is the most common one.42 An α′ form has recently been recognized as a “disordered crystal” having the same 103 helical conformation but a loose packing structure, which is likely to be produced at low crystallization temperature (Tc).43,44 Similar behaviors were also recorded in the oligomers. As will be clarified later, discrete oLLAs assume α′ form and metastable α form crystals at relatively high supercooling. To avoid potential polymorphism and/or kinetic trapping, an isothermal crystallization process, with Tc being about 20 °C below the melting temperature (Tm) of each discrete oLLA, was adopted (see the ESI† for details).All the oLLAs that crystallized under the above-mentioned conditions are in the α crystal form, as confirmed by differential scanning calorimetry (DSC) and wide-angle X-ray diffraction (WAXD). In general, a single and sharp endothermic melting can be observed in the DSC thermograms (Fig. 1c, red), corresponding to the melting transition of oLLA crystals possessing highly ordered packing. Due to the low molecular weight nature, Tm is very sensitive to the chain length variation, covering a broad temperature range (Fig. S4 and Table S1†). Three characteristic diffraction peaks can be observed at 2θ = 14.8, 16.7, and 19.1° (Fig. S6b,† red), corresponding to (010), (110)/(200), and (203) planes of the orthorhombic unit cells of the α form crystal, with two 103 helical chains parallel to the c axis (also parallel to the normal of the lamellae).42
Small angle X-ray scattering (SAXS) patterns exhibit sharp scattering peaks with a ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4…, which are typical characteristics of a highly uniform lamellar structure (Fig. 1d and S5†).35 The lamellar thickness (d, determined by the primary peak of the SAXS pattern) increases as the number of repeat units increases, with a near-perfect linear correlation (Fig. 1e and Table S1†), indicating that all these crystals adopt an extended chain conformation (Scheme 1b).36 Extrapolating the linear fit to x = 0 gives the thickness of the amorphous layer (da = 0.91 nm, mainly the protecting group, assuming 100% crystallinity), and the thickness of the crystalline layer (dc) can thus be calculated accordingly (dc = d − da). The slope of the linear fit, on the other hand, indicates an increase of 0.307 ± 0.003 nm per monomeric residue, which is in good agreement with the crystal unit cell parameters.36
4…, which are typical characteristics of a highly uniform lamellar structure (Fig. 1d and S5†).35 The lamellar thickness (d, determined by the primary peak of the SAXS pattern) increases as the number of repeat units increases, with a near-perfect linear correlation (Fig. 1e and Table S1†), indicating that all these crystals adopt an extended chain conformation (Scheme 1b).36 Extrapolating the linear fit to x = 0 gives the thickness of the amorphous layer (da = 0.91 nm, mainly the protecting group, assuming 100% crystallinity), and the thickness of the crystalline layer (dc) can thus be calculated accordingly (dc = d − da). The slope of the linear fit, on the other hand, indicates an increase of 0.307 ± 0.003 nm per monomeric residue, which is in good agreement with the crystal unit cell parameters.36
For polymer lamellar crystals, the relationship between Tm and dc can be described by the Thomson–Gibbs equation (eqn (1))
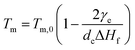 | (1) |
It should be noted that these extended chain crystals are not always under thermodynamic equilibrium. Typical α′ form crystals were produced when crystallized at a relatively low temperature, as revealed by a small exotherm in the DSC thermogram prior to the dominant melting peak (Fig. 1c and S5a,† indicated by an arrow, corresponding to an α′-to-α form transition). WAXD patterns further corroborate the formation of the α′ form crystal by a slight shift of the (110)/(200) and (203) diffractions toward lower angles, as well as the disappearance of (103) and other diffractions (Fig. S6b†). Other metastable states (i.e., ill-defined α form crystals) were also captured at large x and/or high supercooling, as indicated by the additional melting transitions in the DSC thermograms (Fig. S4†), attributed probably to kinetic trapping.42 Nevertheless, neither is the lamellar thickness nor the corresponding equilibrium Tm sensitive to the crystallization conditions (Fig. 1d and S5a†), due to extended chain conformation and very similar unit cells between α and α′ form crystals. The clear and quantitative correlations make this library of molecules a unique platform to reveal the profound importance of dispersity in polymer crystallization.
Modulation of molecular weight distribution
Blending discrete species according to specific recipes provides an effective and straightforward strategy to precisely manipulate the width and shape of the molecular weight distribution. As the simplest case, a symmetric distribution can be generated based on the Gaussian distribution (Scheme S2a†). For a given Đ and Mn, the molar content of each component (n(x)) can be determined using eqn (2) and (3)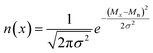 | (2) |
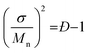 | (3) |
The resultant blends are characterized by SEC and MALDI-ToF MS. Here we take the oLLA22 series as an example. Minor adjustments of Đ can be clearly distinguished by SEC (Fig. 2a and S7†). Mn and Đ were experimentally calculated based on SEC profiles using the discrete oLLA library for calibration, exhibiting a constant average and an increasing dispersity (Table 1). Samples with low Đ generally have a near-perfect bell shape, while those with larger Đ show a tail on the low molecular weight side (Fig. S8a†). This deviation originates from the nonlinear correlation between the retention time and the molecular size (Fig. S2b†). It should be noted that the SEC curves in Fig. 2a are not a simple resemblance of the Gaussian distribution (Scheme S2a†), since they have different coordinate axes (molecular weight vs. retention time). In principle, a mathematical representation of the Gaussian distribution in the semilogarithmic coordinates (corresponding to retention time) would not be symmetric. Diffusion, however, would smooth the SEC traces, making them appear symmetric in the case of limited Đ. MALDI-ToF MS, on the other hand, provides improved resolution of the composition. Typical mass spectra are shown in Fig. 2c and S8c†. Each of the fractions in the formulation can be recognized, and their relative ratio can be clearly identified. Due to the difference of ionization efficiency, the intensity corresponding to each fraction might deviate from the actual composition. Nevertheless, a Gaussian distribution is evident in general, and resembles the mathematical calculation more appropriately. The same characteristics were also observed in the oLLA19 and oLLA24 series (Fig. S9 and S10†). Detailed characterization is summarized in Table S4.†
 | (4) |
 | ||
| Fig. 2 SEC traces (a and b) and the corresponding MALDI-ToF mass spectra (c and d) of symmetrically (a and c) and asymmetrically (b and d) dispersed oLLA22 series samples (Tables 1 and 2). For clarity, only Đ = 1.00–1.01 and α = ±2 are shown. See Fig. S8† for more data. | ||
| Samplea | M n | Đ | T c = 60 °C | T c = 100 °C | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| d | T m | ΔHmi | d 1 | T m,1 | ΔHm,1i | d 2 | T m,2 | ΔHm,2i | ||||
| a Sample label oLLAx(Đ), where x refers to the number of repeat units and Đ is the dispersity. b Number average molecular weight (Da) measured by SEC using the discrete oLLA library for calibration. c Dispersity measured by SEC using the discrete oLLA library for calibration. d Dispersity measured by MADLI-ToF. e Discrete oLLA22, adopted from Table S1. f Crystallization temperature (Tc). g Lamellar thickness, nm, calculated based on d = 2π/q*. h Melting temperature (°C), determined by DSC. i Heat of fusion (J g−1), determined by DSC. | ||||||||||||
| oLLA22e | 1807.8e | <1.0001e | 7.57 | 119.1 | 64.8 | 7.57 | 119.7 | 73.5 | — | — | — | |
| oLLA22(1.001) | 1800 | 1.003 c | 1.001d | 7.39 | 118.4 | 57.5 | 7.57 | 118.7 | 66.0 | — | — | — |
| oLLA22(1.003) | 1810 | 1.005 | 1.002 | 7.48 | 117.2 | 54.1 | 7.57 | 117.4 | 57.1 | — | — | — |
| oLLA22(1.005) | 1810 | 1.006 | 1.002 | 7.48 | 116.5 | 50.0 | 7.57 | 116.7 | 58.8 | — | — | — |
| oLLA22(1.007) | 1820 | 1.007 | 1.004 | 7.48 | 116.0 | 40.9 | 7.57 | 116.0 | 58.7 | — | — | — |
| oLLA22(1.01) | 1800 | 1.009 | 1.006 | 7.57 | 115.9 | 45.6 | 7.66 | 115.9 | 61.9 | — | — | — |
| oLLA22(1.02) | 1800 | 1.012 | 1.009 | 7.48 | 115.3 | 41.7 | 7.66 | 115.1 | 54.2 | — | — | — |
| oLLA22(1.04) | 1800 | 1.029 | 1.015 | 7.65 | 115.2 | 42.7 | 7.85 | 115.2 | 48.8 | 6.16 | 83.6 | 3.0 |
| oLLA22(1.06) | 1790 | 1.038 | 1.024 | 7.73 | 115.0 | 37.1 | 8.06 | 119.6 | 43.4 | 6.10 | 82.4 | 5.3 |
| oLLA22(1.10) | 1780 | 1.050 | 1.027 | 7.86 | 114.8 | 39.2 | 8.27 | 121.7 | 38.8 | 5.87 | 82.0 | 7.3 |
To generate an asymmetric molecular weight distribution, we adopted the skew-normal distribution (eqn (4)) as a proof of concept, by introducing an additional asymmetric parameter, α (Scheme S2b†).
The skew-normal distribution will be reduced to a Gaussian distribution (eqn (2)) when α = 0, while it will skew to higher or lower molecular weight when α is a positive or negative integer, respectively (Scheme S2b†). We prepared three sets of blending samples with fixed Mn (x = 19, 22, or 24) and Đ (Đ = 1.01), while tuning the value of α. Detailed compositions are listed in Table S3.†
Fig. 2b and d show the SEC traces and MALDI-ToF mass spectra of the resultant asymmetric oLLA22 series. Compared with a Gaussian distribution, clear deviations from a symmetric curve can be observed when α is not 0 (Fig. 2b). The SEC traces incline to the lower retention time (higher Mw) when α is positive, while they incline to the larger retention time (lower Mw) when α is negative. The initial change in the symmetry is apparent (e.g., from α = 0 to α = ±1), while a further increase in α generates a mild variation (Fig. S8†). It should be noted that the average molecular weight and dispersity inevitably drift when α is introduced, despite the fact that Mn and σ were set as constant in eqn (4). Using the discrete oLLA library for calibration, effective Mn and Đ were measured and the results are listed in Table 2, which fit well to calculations based on the constitution (see the ESI†). MALDI-ToF MS provides detailed information of the composition (Fig. 2d). Each individual peak can be assigned to the ingredient in the blending formulation. The relative abundance is proportional to the peak intensity qualitatively, resembling the features of the skew-normal distribution in general. The same characteristics were also recorded in the oLLA19 and oLLA24 series (Fig. S9 and S10 and Table S5†). The precise composition confirms the blending strategy as a robust and efficient approach in tailoring the width and shape of the molecular weight distribution.
| Samplea | M n | Đ | d | T m | ΔHmg | |
|---|---|---|---|---|---|---|
| a Sample label oLLAx(α), where x refers to the number of repeat units and α is the asymmetric parameter. b Number average molecular weight (Da) measured by SEC using the discrete oLLA library for calibration. c Dispersity measured by SEC using the discrete oLLA library for calibration. d Dispersity measured by MADLI-ToF. e Lamellar thickness, nm. f Melting temperature (°C), determined by DSC. g Heat of fusion (J g−1), determined by DSC. Tc = 80 °C. | ||||||
| oLLA22(−3) | 1650 | 1.007c | 1.003d | 7.06 | 109.4 | 51.6 |
| oLLA22(−2) | 1660 | 1.008 | 1.003 | 7.22 | 110.2 | 54.1 |
| oLLA22(−1) | 1680 | 1.009 | 1.005 | 7.30 | 112.1 | 55.4 |
| oLLA22(0) | 1800 | 1.009 | 1.006 | 7.57 | 116.0 | 60.8 |
| oLLA22(+1) | 1880 | 1.008 | 1.003 | 7.95 | 118.9 | 61.7 |
| oLLA22(+2) | 1900 | 1.008 | 1.003 | 8.06 | 119.8 | 64.3 |
| oLLA22(+3) | 1910 | 1.006 | 1.002 | 8.16 | 121.1 | 64.6 |
Effects of distribution width on crystallization
A synthetic polymer contains a collection of non-uniform macromolecules with size-dependent behaviors. The structure and properties are collective and synergistic outputs of each individual component. As for crystallization, organizing polymer chains into an ordered arrangement critically depends on supercooling (i.e., ΔT = Tm − Tc).46 Different from a discrete polymer with an explicit melting temperature, a dispersed polymer consists of multiple fractions, for which Tm usually covers a broad range of temperatures. As a result, at a specific crystallization temperature, each individual species may experience a varied degree of supercooling, leading to non-uniform nucleation and growth kinetics. As Đ increases, the disparity on supercooling may result in three possible scenarios during crystallization (Scheme 1c): (1) solid solution, that is polymer chains with different lengths co-crystallize homogeneously; (2) eutectic system, that is one (or some) component(s) crystallizes partially from miscible melts before reaching the eutectic point, beyond which the remaining melts co-crystallize; and (3) segregation, in which polymer chains separate into different domains based on chain length.47,48 Detailed molecular packing, however, has yet to be quantitatively explored due to the challenge in dispersity modulation.It can be envisioned that crystallization temperature plays vital role in the molecular arrangement. By defining the equilibrium melting temperature of the longest and shortest components of a dispersed sample as THm and TLm respectively, three temperature regions can be recognized: full crystallization (all the fractions participate in the crystallization) is expected when Tc < TLm (region I); partial crystallization takes place for TLm < Tc < THm (region II); and no crystallization occurs when Tc > THm (region III).
Take the symmetrically dispersed oLLA22 series (Table 1) as an example. The THm and TLm of each sample are listed in Table S6.† To systematically explore the crystallization behaviors, the oLLA22 series with varying Đ were isothermally crystallized at a set of temperatures (Tc = 60, 80, 100, and 110 °C) for sufficient time before cooling to room temperature. The as-prepared solids were then characterized by DSC, SAXS, and WAXD.
Different crystallization characteristics were recorded in region I and region II. In the case of Tc = 60 °C, all the samples are crystallized in region I. A set of sharp and equally spaced scattering peaks were observed for each sample, similar to the SAXS profile of discrete oLLA22 (Fig. 3a). The position of the peaks remains nearly constant (very slightly to the left), indicating that the lamellar thickness is not significantly affected by the chain length heterogeneity. The uniformity of the lamellae, on the other hand, diminishes as Đ increases, as revealed by the broadening of the primary peak (Fig. 3a). Similar behaviors were recorded at Tc = 80 °C.
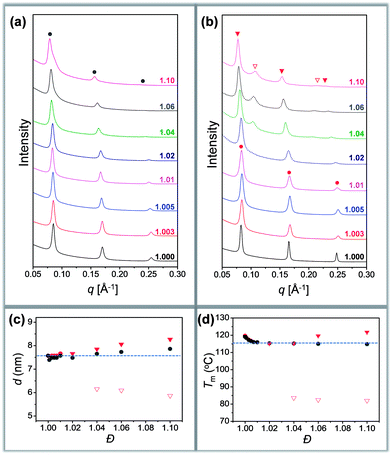 | ||
| Fig. 3 (a and b) SAXS patterns of oLLA22 series samples with varying Đ crystallized at 60 °C (a) and 100 °C (b): solid line (region I); dashed line (region II). (c and d) Relationship between lamellar thickness and Đ (c), and between melting temperature (Tm) and Đ (d): solid circles (region I); triangles (region II). Only Tc = 60 °C (grey) and 100 °C (red) are shown for clarity. See Fig. S11† for more data. | ||
In the case of Tc = 100 °C, oLLA22 series samples with Đ < 1.02 are still in region I, while those with Đ ≥ 1.02 enter region II. The former show essentially the same SAXS patterns as those of samples crystallized at 60 °C (Fig. 3b). For samples with Đ ≥ 1.02, an obvious shift of the peaks to the left was observed (Fig. 3b, solid red triangles), accompanied by the appearance of an additional set of equally spaced scattering peaks (Fig. 3b, open red triangles, not detected in the case of Đ = 1.02 due to the trace amount of low molecular weight fractions). Similar behaviors were recorded at Tc = 110 °C. The relationship between lamellar thickness (d) and Đ at different Tc is plotted in Fig. 3c (see Fig. S11† for more data).
We propose that oLLA chains align in an extended conformation perpendicular to the lamellar surface, unaffected by chain length heterogeneity or crystallization conditions. The detailed molecular packing, however, depends critically on both Tc and Đ. The uniform lamellae thickness in region I indicates that oLLAs co-crystallize homogeneously to form solid solutions (Scheme 1c). The existence of multiple populations of lamellae in region II, on the other hand, is due to the segregation of the oLLA chains with varying chain length: long chains crystallize, while short chains remain in the melt and crystallize upon further cooling to room temperature (Scheme 1c). No eutectic behavior was observed.
The resultant lamellae consist of alternating crystalline and amorphous layers. The overall lamellar thickness (d) is a sum of both contributions (d = da + dc), which can be calculated based on eqn (5)
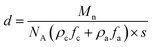 | (5) |
Detailed molecular packing is further revealed by DSC and WAXD. According to the proposed molecular arrangement, a single endothermic peak is expected in the DSC thermogram in region I, while two separate peaks are expected in region II, corresponding to each individual lamella population. This feature is generally followed (Fig. S12†). There, however, also exist some additional peaks, especially when Đ is relatively large. For example, the DSC curve of the discrete sample crystallized at 60 °C shows a sharp melting peak in the DSC thermogram. As Đ increases, an exothermic peak appears before the melting peak. The exotherm becomes broad as Đ further increases, followed by the melting process with multiple overlapping peaks (Fig. S12†). Though they look complicated, the characteristics have been well-recognized in the crystallization of PLLA, due to co-existence of multiple metastable crystals.44 The exotherm is attributed to the α′-to-α form transition (see WAXD data in Fig. S13†), while the latter corresponds to a series of melting–recrystallization processes. Metastable crystals (e.g., with defects included inside, varying crystal thickness, etc.) generated under non-uniform supercooling are continuously annealed and rearranged during the heating process, resulting in multiple endothermic peaks.44 The rearrangement, however, does not change the overall lamellar thickness (d), as confirmed by the SAXS patterns of samples annealed at elevated temperatures (Fig. S14†). By assuming the highest melting peaks as the equilibrium melting point of dispersed samples, the relationship between Tm and Đ was established (Fig. 3d). A depression of Tm, accompanied by a reduction of crystallinity (Table 1), was recorded as Đ increases, indicating the shrinking of the crystalline layer (dc). In the case of region II, an additional melting peak appears as expected, corresponding to the melting transition of the low molecular weight fractions (Fig. S12,† open triangle). All the data are summarized in Table 1. The DSC data (Fig. 3d) generally follow a similar trend to the SAXS results (Fig. 3c). Parallel studies on the oLLA19 and oLLA24 series samples show essentially the same behaviors (Table S4 and Fig. S15–S18†), further supporting our proposed molecular arrangement.
Effects of distribution symmetry on crystallization
The symmetry is another characteristic of molecular weight distribution dictating the composition. Our understanding in this area is, however, still in the primitive stage.12,13 The asymmetrically dispersed samples prepared in this work could provide a model system to elucidate the contribution of distribution symmetry.Take the oLLA22 series (Đ = 1.01, see Table 2) with varying skewness as examples. All these samples were isothermally crystallized at 80 °C (region I). A homogeneous solid solution forms under these conditions, as revealed by a set of equally spaced scattering peaks in the scattering profile (Fig. S19a†), as well as a single melting peak in the DSC thermogram (Fig. S19b†). Compared with the symmetrically dispersed counterpart, i.e. oLLA22(1.01), both lamellar thickness (d) and melting temperature (Tm) are significantly altered by variation of α (Table 2). In general, d and Tm increase simultaneously and monotonically when α > 0, while they decrease when α < 0 (Fig. 4). Similar behaviors were also recorded for the oLLA19 and oLLA24 series samples (Table S5† and Fig. S20 and S21†).
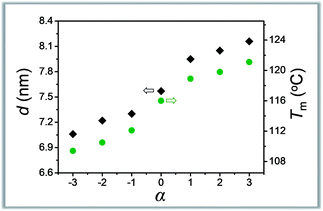 | ||
| Fig. 4 Plot of lamellar thickness (grey) and melting temperature (olive) of asymmetrically dispersed oLLA22 samples as a function of α. | ||
As revealed by eqn (5), d (as well as equilibrium Tm) is dictated by the average molecular weight. The shift of effective Mn results in the change of d and Tm in the same direction. On the other hand, samples with similar Mn and Đ but different symmetries [e.g., oLLA22(1.01, α = +2) vs. oLLA24(1.01)] exhibit similar lamellar thickness (Fig. S22a†). This, however, does not necessarily imply that the shape of the distribution has no impact on crystallization. On the one hand, lamellar thickness is an average property which is not sensitive to the heterogeneity of the chain length (neither width nor symmetry, eqn (5)). On the other hand, the samples involved in this section generally have relatively low dispersity (Đ = 1.01), which cannot generate appreciable differences. Nevertheless, a quite different melting transition was recorded (Fig. S22b†), indicating that detailed molecular packing is influenced by the symmetry of the distribution. We envision that the contribution of the asymmetric composition is more profound in the processes that depend critically on individual performance, especially crystallization kinetics. The details will be discussed in a separate study.
Conclusions
In this work, we established an efficient approach to modulate molecular weight distribution through precise recombination of discrete macromolecules. A series of dispersed oLLA samples were prepared accordingly with tailored average, width, and symmetry. The profound influence of molecular weight distribution on crystallization behaviors was quantitatively studied. Depending on crystallization temperature, oLLAs in dispersed samples adopt distinct molecular arrangements, i.e., solid solution or segregation, due to non-uniform nucleation and growth kinetics. The blending strategy is very robust, and can be extended to regulate the chain length heterogeneity of one or multiple blocks of block copolymers or polymers with complicated architectures. In principle, arbitrary distributions could be constructed at will, including those inaccessible through polymerization. It thus provides a unique model platform to elucidate the critical contribution of chain length heterogeneity to self-assembly and molecular dynamics, as well as properties of polymers.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (51773066), the Guangdong Innovative and Entrepreneurial Research Team Program (2016ZT06C322), and the Fundamental Research Funds for the Central Universities (2019XX04). We thank the staff of Beamline BL16B1 at the Shanghai Synchrotron Radiation Facility for assistance with the SAXS experiments.Notes and references
- D. W. van Krevelen and K. te Nijenhuis, Properties of Polymers, Elsevier, Amsterdam, 2009 Search PubMed.
- W. Zhang, X. Dong and S. Z. Cheng, Chem, 2019, 5, 492 CAS.
- L. Leibler, Macromolecules, 1980, 13, 1602 CrossRef CAS.
- D. M. Cooke and A.-C. Shi, Macromolecules, 2006, 39, 6661 CrossRef CAS.
- N. A. Lynd, M. A. Hillmyer and M. W. Matsen, Macromolecules, 2008, 41, 4531 CrossRef CAS.
- B. L. Peters, M. K. Salerno, T. Ge, D. Perahia and G. S. Grest, Phys. Rev. Lett., 2018, 121, 057802 CrossRef PubMed.
- P. K. Bommineni, N. Varela-Rosales, M. Klement and M. Engel, Phys. Rev. Lett., 2019, 122, 128005 CrossRef CAS PubMed.
- N. A. Lynd and M. A. Hillmyer, Macromolecules, 2005, 38, 8803 CrossRef CAS.
- N. A. Lynd and M. A. Hillmyer, Macromolecules, 2007, 40, 8050 CrossRef CAS.
- N. A. Lynd, A. J. Meuler and M. A. Hillmyer, Prog. Polym. Sci., 2008, 33, 875 CrossRef CAS.
- J. M. Widin, A. K. Schmitt, A. L. Schmitt, K. Im and M. K. Mahanthappa, J. Am. Chem. Soc., 2012, 134, 3834 CrossRef CAS PubMed.
- D. T. Gentekos, J. Jia, E. S. Tirado, K. P. Barteau, D.-M. Smilgies, R. A. Distasio and B. P. Fors, J. Am. Chem. Soc., 2018, 140, 4639 CrossRef CAS PubMed.
- D. T. Gentekos, L. N. Dupuis and B. P. Fors, J. Am. Chem. Soc., 2016, 138, 1848 CrossRef CAS PubMed.
- D. T. Gentekos and B. P. Fors, ACS Macro Lett., 2018, 7, 677 CrossRef CAS.
- A. Spinnrock and H. Cölfen, Angew. Chem., Int. Ed., 2018, 57, 8284 CrossRef CAS PubMed.
- X. Liu, C.-G. Wang and A. Goto, Angew. Chem., Int. Ed., 2019, 58, 5598 CrossRef CAS PubMed.
- A. Rudin, J. Chem. Educ., 1969, 46, 595 CrossRef CAS.
- S. S. Rane and P. Choi, Chem. Mater., 2005, 17, 926 CrossRef CAS.
- T. Ward, J. Chem. Educ., 1981, 58, 867 CrossRef CAS.
- R. Whitfield, N. P. Truong, D. Messmer, K. Parkatzidis, M. Rolland and A. Anastasaki, Chem. Sci., 2019, 10, 8724–8734 RSC.
- K. Matyjaszewski, Macromolecules, 2012, 45, 4015 CrossRef CAS.
- M. Ouchi and M. Sawamoto, Macromolecules, 2017, 50, 2603 CrossRef CAS.
- R. B. Grubbs and R. H. Grubbs, Macromolecules, 2017, 50, 6979 CrossRef CAS.
- V. Kottisch, D. T. Gentekos and B. P. Fors, ACS Macro Lett., 2016, 5, 796 CrossRef CAS.
- R. Whitfield, K. Parkatzidis, M. Rolland, N. P. Truong and A. Anastasaki, Angew. Chem., Int. Ed., 2019, 58, 13323 CrossRef CAS PubMed.
- Z. Wang, J. Yan, T. Liu, Q. Wei, S. Li, M. Olszewski, J. Wu, J. Sobieski, M. Fantin, M. R. Bockstaller and K. Matyjaszewski, ACS Macro Lett., 2019, 8, 859 CrossRef CAS.
- S. Domanskyi, D. T. Gentekos, V. Privman and B. P. Fors, Polym. Chem., 2019 10.1039/c9py00074g.
- Y. Matsushita, A. Noro, M. Iinuma, J. Suzuki, H. Ohtani and A. Takano, Macromolecules, 2003, 36, 8074 CrossRef CAS.
- A. Noro, M. Linuma, J. Suzuki, A. Takano and Y. Matsushita, Macromolecules, 2004, 37, 3804 CrossRef CAS.
- J. Neve, J. J. Haven, S. Harrisson and T. Junkers, Angew. Chem., Int. Ed., 2019, 58, 13869 CrossRef PubMed.
- J.-F. Lutz, M. Ouchi, D. R. Liu and M. Sawamoto, Science, 2013, 341, 1238149 CrossRef PubMed.
- J.-F. Lutz, J.-M. Lehn, E. Meijer and K. Matyjaszewski, Nat. Rev. Mater., 2016, 1, 16024 CrossRef CAS.
- B. Oschmann, J. Lawrence, M. W. Schulze, J. M. Ren, A. Anastasaki, Y. Luo, M. D. Nothling, C. W. Pester, K. T. Delaney, L. A. Connal, A. J. McGrath, P. G. Clark, C. M. Bates and C. J. Hawker, ACS Macro Lett., 2017, 6, 668 CrossRef CAS.
- B. van Genabeek, B. F. de Waal, B. Ligt, A. R. Palmans and E. Meijer, ACS Macro Lett., 2017, 6, 674 CrossRef CAS PubMed.
- B. van Genabeek, B. A. Lamers, B. F. de Waal, M. H. van Son, A. R. Palmans and E. Meijer, J. Am. Chem. Soc., 2017, 139, 14869 CrossRef CAS PubMed.
- B. A. Lamers, B. van Genabeek, J. Hennissen, B. F. de Waal, A. R. Palmans and E. Meijer, Macromolecules, 2019, 52, 1200 CrossRef PubMed.
- A. Das, K. Petkau-Milroy, G. Klerks, B. van Genabeek, R. P. Lafleur, A. R. Palmans and E. Meijer, ACS Macro Lett., 2018, 7, 546 CrossRef CAS PubMed.
- Y. Jiang, M. R. Golder, H. V. Nguyen, Y. Wang, M. Zhong, J. C. Barnes, D. J. Ehrlich and J. A. Johnson, J. Am. Chem. Soc., 2016, 138, 9369 CrossRef CAS PubMed.
- M. R. Golder, Y. Jiang, P. E. Teichen, H. V. Nguyen, W. Wang, N. Milos, S. A. Freedman, A. P. Willard and J. A. Johnson, J. Am. Chem. Soc., 2018, 140, 1596 CrossRef CAS PubMed.
- K. Takizawa, H. Nulwala, J. Hu, K. Yoshinaga and C. J. Hawker, J. Polym. Sci., Part A: Polym. Chem., 2008, 46, 5977 CrossRef CAS.
- B. van Genabeek, B. F. de Waal, M. M. Gosens, L. M. Pitet, A. R. Palmans and E. Meijer, J. Am. Chem. Soc., 2016, 138, 4210 CrossRef CAS PubMed.
- T. Kawai, N. Rahman, G. Matsuba, K. Nishida, T. Kanaya, M. Nakano, H. Okamoto, J. Kawada, A. Usuki, N. Honma, K. Nakajima and M. Matsuda, Macromolecules, 2007, 40, 9463 CrossRef CAS.
- J. Zhang, K. Tashiro, A. J. Domb and H. Tsuji, Macromol. Symp., 2006, 242, 274 CrossRef CAS.
- P. Pan, W. Kai, B. Zhu, T. Dong and Y. Inoue, Macromolecules, 2007, 40, 6898 CrossRef CAS.
- B. Kalb and A. Pennings, Polymer, 1980, 21, 607 CrossRef CAS.
- X. Tang, W. Chen and L. Li, Macromolecules, 2019, 52, 3575 CrossRef CAS.
- R. Zwiers, S. Gogolewski and A. Pennings, Polymer, 1983, 24, 167 CrossRef CAS.
- S. Z. D. Cheng and B. Wunderlich, J. Polym. Sci., Part B: Polym. Phys., 1986, 24, 577 CrossRef CAS.
- J. Yang, Y. Liang, J. Luo, C. Zhao and C. C. Han, Macromolecules, 2012, 45, 4254 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Synthesis and characterization of discrete and dispersed samples. See DOI: 10.1039/c9sc04736k |
| This journal is © The Royal Society of Chemistry 2019 |