Open Access Article
Open Access ArticleDissociation path competition of radiolysis ionization-induced molecule damage under electron beam illumination†
Zenghua
Cai
 a,
Shiyou
Chen
a,
Shiyou
Chen
 *ab and
Lin-Wang
Wang
*c
*ab and
Lin-Wang
Wang
*c
aState Key Laboratory of Precision Spectroscopy, Key Laboratory of Polar Materials and Devices (MOE), Department of Electronics, East China Normal University, Shanghai 200241, China. E-mail: chensy@ee.ecnu.edu.cn
bCollaborative Innovation Center of Extreme Optics, Shanxi University, Taiyuan, Shanxi 030006, China
cMaterials Sciences Division, Lawrence Berkeley National Laboratory, One Cyclotron Road, Mail Stop 66, Berkeley, CA 94720, USA. E-mail: lwwang@lbl.gov
First published on 24th September 2019
Abstract
Radiolysis ionization under electron beam illumination induces dissociation and damage of organic and biological molecules; thus, it is impossible to image the related materials by transmission electron microscopy (TEM). To understand the atomistic mechanism of radiolysis damage, we developed a systematical procedure based on real-time time-dependent density functional theory (rt-TDDFT) for simulating the radiolysis damage processes of molecules; this procedure can describe the ionization cross sections of the electronic states and the fast dissociation processes caused by hot carrier cooling and the Auger decay on deep levels. For the radiolysis damage of C2H6O2, our simulation unexpectedly showed that there is strong competition among three different dissociation paths, including fast dissociation caused by nonadiabatic cooling of the hot carrier; fast dissociation caused by Auger decay, which induces double ionization and Coulomb explosion; and slow dissociation caused by increased kinetic energy. As the energy of the incident electron beam changes, the time scales of these dissociation paths and their relative contributions to the molecule damage change significantly. These simulation results explain the measured mass spectra of the C2H6O2 dissociation fragments and also provide clear competition mechanisms for blocking these dissociation paths in the TEM imaging of organic and biological materials.
Introduction
The molecular dissociation and damage caused by electron beam illumination is a very important problem in transmission electron microscopy (TEM).1,2 From the perspective of electron scattering,2 we can categorize electron beam-induced radiation damage into two main classes: (1) elastic scattering, which includes knock-on displacement (atomic displacement),3 electrostatic charging4 and sputtering;5 and (2) inelastic scattering, which includes ionization damage (radiolysis),6 heating7 and hydrocarbon contamination.8 Among these different types of radiation damage, knock-on displacement is the most common elastic scattering damage, while radiolysis is the most common inelastic scattering damage.1,9 As discussed in ref. 9, knock-on displacement (where the electron beam gives its momentum and some of its energy to nuclei through Coulomb interactions) is predominant for conducting inorganic materials,10,11 while radiolysis (where the material is first ionized by the electron beam) can occur in organic materials and molecules as well as some inorganic systems, such as halides, oxides, hydrides, hydroxides, sulfides and silicates. Furthermore, radiolysis is important in many other processes, including electric discharge and breakdown in high voltage dielectric materials; degradation of polymers and organic electronic devices; excimer lasers; radiation damage of electronic devices in space; radiation chemistry; and biomedicine.12–15However, although radiolysis is highly important, its atomistic mechanism and detailed steps are often not clear. The challenges in studying radiolysis damage reside mainly in the complexity of the process. First, radiolysis-related phenomena can be divided into different situations. Usually, radiolysis involves the ionization of a single electron;1 however, a possible related process is that the excited electron is not transported all the way to the vacuum but is transited into higher antibonding states in the system. The ionized or excited electron can come from the valence state1 but can also come from the core level of the high energy electron beam. Additionally, in addition to the original ionization due to the high energy external electron beam, the ejected (ionized) electron itself can cause some secondary excitation with lower electron energy.1,9 This lower energy electron beam (LEEB) has a larger ionization cross section, although the secondary “beam” intensity will be much smaller compared to the original beam intensity in a TEM experiment. However, many experiments have revealed that small molecules can dissociate into different fragments under LEEB illumination.16–24 In this study, we will focus on the original ionization from the valence electron for molecular systems. Although this is only one path among all the possible electron beam damaging scenarios discussed above, it is a common and important path. For a high energy TEM beam, although ionization from the core level is also possible, its cross section is usually much smaller than that of the ionization from the valence electron. Although excitation to the empty antibonding state is also possible, due to the finite density of states of a molecule, its cross section is also smaller for a relatively high energy electron beam; thus, this possibility will be ignored in the current study. Our method is applicable to radiolysis caused by different electron beam energies; however, in order to compare our results with available experiments, we will focus on lower energy electron beam results. The lower energy electron beam results provide more sensitive dependence on the electron energy and thus provide a rich test ground for the calculated results. These low energy results are also relevant to secondary ionization, as discussed above.
In addition to the different situations discussed above, the main challenge for studying radiolysis is the possible complex subsequent steps following the initial ionization, i.e., the ionized molecule can have various dissociation paths depending on the original orbital from which the electron was ejected. As shown schematically in Fig. 1, at least three different processes can be expected: (i) if the ejected electron level is very shallow and close to the highest occupied molecular orbital (HOMO) level, a hot hole carrier will be formed; it will cool with relaxation of the hole to the HOMO, and the energy will be transformed into nuclear kinetic energy. Because the ejected electron level is very shallow, the energy from the hot hole relaxation will be small and cannot drive dissociation of the molecule in a short time scale. However, both the hot hole relaxation energy and the reorganization energy of the molecule (the structure of the molecule will be relaxed after an electron is ejected from one occupied state) will be converted into nuclear kinetic energy, which can still dissociate the molecule on a longer time scale; (ii) if the electron is ejected from a level that is slightly lower than the HOMO level, the energy released by hot hole relaxation is higher than in the above situation and will also be converted to nuclear kinetic energy, which may in turn dissociate the molecule; (iii) if the ejected electron level is very deep and much lower than the HOMO level, the large energy from the hot hole relaxation can induce an Auger process with another electron ejected to the vacuum, causing dissociation of the doubly ionized molecule via Coulomb explosion.
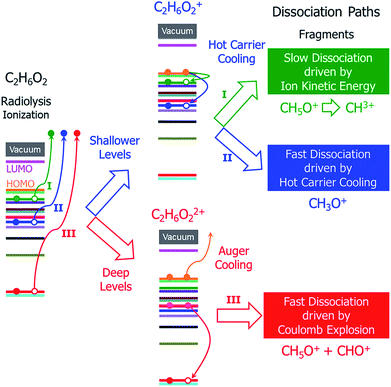 | ||
| Fig. 1 Schematic of the hot carrier decay processes on different electronic levels and the structural dissociation processes of C2H6O2 after radiolysis ionization. | ||
It is currently unclear which process is dominant in radiolysis damage and how the energy of the electron beam influences these processes. For example, mass spectroscopy measurements showed that the C2H6O2 molecule dissociates into different charged fragments under the illumination of incident electron beams with different kinetic energies; however, it is unknown how C2H6O2 is damaged and dissociates into these fragments. To control radiolysis damage, it will be tremendously helpful if we know what process is playing a dominant role and the time scales of these processes. The unclear mechanism of radiolysis damage hinders development in related areas, such as the application of TEM and high voltage dielectric material designs.
Ab initio simulation of the radiolysis damage process is an efficient and reliable method for studying atomistic mechanisms and the related detailed steps; however, because the three aforementioned dissociation processes have very different time scales, different ab initio methods are required. Ground state Born–Oppenheimer molecular dynamics (BO-MD) have often been used to simulate knock-on displacement damage;25,26 however, radiolysis is fundamentally a nonadiabatic process beyond the BO-MD description.27 Although there are quantum chemical calculations for nonadiabatic nuclear movement based on the potential energy surface (PES),27 they are seldom used to study molecule damage after radiolysis because the related energy potential is too complex to be mapped out in its entirety. In this work, we have developed a practical systematical framework for calculating radiolysis damage, including three modules:
Firstly, we simulated the hot carrier relaxation and the corresponding dissociation during the relaxation process. This was realized by real-time time-dependent density functional theory (rt-TDDFT) simulations. In recent years, we have seen a surge of the use of rt-TDDFT to study various nonadiabatic processes, including ion collisions on materials,28,29 dissipative processes in ion irradiation,30 carrier-multiplication-induced structural changes31 and plasmon excitation in nanowires.32,33 It is thus natural to attempt to use rt-TDDFT to describe the hot carrier decay after the initial ionization. Unfortunately, the original rt-TDDFT method following Ehrenfest dynamics does not satisfy the detailed balance rule. This causes the electronic degree of freedom to be overheated instead of cooled.34 In this work, we introduce a method which incorporates detailed balance in rt-TDDFT simulations and thus allows study of nonadiabatic hot carrier cooling. Using this modified rt-TDDFT method, we have simulated the hot carrier cooling process in the molecule and the possible fragmentation during this process.
Secondly, the times of the Auger process and the resulting secondary ionization were calculated and compared to the hot hole relaxation time in order to determine which process is dominant. This is necessary if the initial ionized orbital is sufficiently deep and has enough energy to cause secondary ionization. While the nonadiabatic process is induced by electron–phonon interaction, the Auger process is induced by electron–electron interaction. Currently, it is difficult to simulate the Auger process with rt-TDDFT. In this study, we developed an analytical formalism to calculate the Auger cross section with the Fermi-golden rule. We found that whenever energetically possible, the Auger process is extremely fast and is more efficient than nonadiabatic hot carrier decay.
Thirdly, a longer time scale dissociation process was studied according to the nuclear kinetic energies obtained from hot carrier cooling (calculated at the electronic ground state). This occurs if the initial fast nonadiabatic cooling process does not dissociate the molecule and the Auger second ionization does not occur. In C2H6O2, we found that this is the case when the initial ionization occurs at the two shallowest orbitals (the HOMO and below the HOMO). In these cases, we did not observe molecule breakdown during the rt-TDDFT simulations. However, thermodynamic energy analysis shows that the molecule can still break down eventually, albeit after overcoming some energy barriers.
Finally, in order to predict the profiles of the initial ionization on different orbital levels, we calculated the cross sections of the ionization rates for different kinetic energies of the illuminating electron beam.
We have used the above procedure to study the mechanisms behind the damage and have compared our results with experimentally observed mass spectroscopy results, especially at relatively low electron beam energies.16 We found that after taking into account all the above dissociation processes and ionization cross sections, we can explain some of the qualitative trends in the peaks observed by mass spectroscopy and understand the origins of different charged fragments. This provides previously unknown insights into the molecular breakdown process following ionization radiolysis.
Calculation methodology
All the first-principles calculations were carried out based on density functional theory (DFT) as implemented by the PWmat code, which uses the plane wave pseudopotential Hamiltonian and runs on graphics processing units (GPU).35,36 The generalized gradient approximation (GGA) to the exchange correlation functional in the Perdew–Burke–Ernzerhof (PBE)37 form was used with a 50 Ry cutoff energy for the plane wave basis. All the calculations were performed using a 10 Å × 10 Å × 10 Å cubic cell with one C2H6O2 molecule located at the center. A double box formalism (as implemented in PWmat) was used to calculate the Hartree energy with a truncated range Coulomb interaction; therefore, no image interactions existed due to the finite size of the periodic box.All the modules for calculating the ionization cross sections of the electronic states, the time for double ionization caused by the Auger decay of hot carriers on deep levels, and the thermodynamic dissociation energy costs of singly-ionized and doubly-ionized C2H6O2, as well as the rt-TDDFT method, including the detailed balance, were developed based on the PWmat code. The details will be described later.
It is worth commenting on the accuracy of the PBE exchange correlation functional in our DFT calculations. It is well known that PBE-calculated eigenenergies may have significant error when compared with experiments. Here, we chose PBE mostly based on computational efficiency considerations, especially when the plane wave basis set is used. The use of the plane wave basis set is important due to its variational flexibility in describing excited states and ejected electron states. However, the PBE eigenenergy error is mostly a concern for the analytical calculations of the ionization cross section and the Auger effect, where the eigenenergies are used for energy conservation. In the future, more advanced eigenenergy corrections can be used to further correct these energy errors. On the other hand, for rt-TDDFT simulations, the results may be more reliable. This is evidenced by the accurate optical absorption spectrum results from the rt-TDDFT simulations for small molecules. In these rt-TDDFT simulations, the transition rate is determined more by the total energy change upon a transition than by the eigenenergies. The total energy change is more like the ΔDFT calculations, which have been shown to be accurate for small molecules.39
Results and discussion
Cross sections of electron ejection on different levels
Perturbation formalisms exist to calculate the ionization cross sections caused by high velocity incident electrons, such as Bethe theory.38,39 For a low energy electron beam (at a few tens of eV, as in experiments), approximated formalisms exist to describe this cross section. One such formalism is the binary-encounter-dipole (BED) model,40 which takes into account the acceleration of the incident electron beam caused by nuclear attraction.40,41 Because this BED model changes to the Bethe theory40 at high electron energy, it should also be suitable for a high energy incident electron beam. In Fig. S4 of the ESI,† we show that the ionization cross sections of C2H6O2 illuminated by a 100 keV electron beam as calculated by the BED model and the Bethe formula are almost the same. Thus, in our study, the ionization cross sections for all the energy ranges (including the 100 keV) were calculated with the BED model (as shown in Fig. 3).In the BED model, an incident electron beam (with initial kinetic energy T) will be deflected by its Coulomb interaction with a valence electron (at energy E below vacuum) in the molecule and eject the valence electron into the vacuum with kinetic energy W. Then, the total cross section σ(t) for this ionization process can be calculated as:
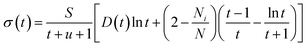 | (1) |
![[P with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0050_20d1.gif) 2〉/2me),
2〉/2me), ![[P with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0050_20d1.gif) is the momentum operator and me is the mass of the electron);
is the momentum operator and me is the mass of the electron);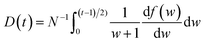 | (2) |
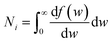 | (3) |
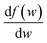 , we take the form of the differential oscillator strength in ref. 38. Using the same notation as above, we have
, we take the form of the differential oscillator strength in ref. 38. Using the same notation as above, we have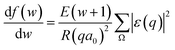 | (4) |
ε(q) = 〈ϕ1|exp(i![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) · ·![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) j)|ϕ0〉 j)|ϕ0〉 | (5) |
![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) = (
= (![[K with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004b_20d1.gif) 0 −
0 − ![[K with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004b_20d1.gif) 1) represents the change of the momentum of the electron beam between the incident electron (
1) represents the change of the momentum of the electron beam between the incident electron (![[K with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004b_20d1.gif) 0) and the deflected electron (
0) and the deflected electron (![[K with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004b_20d1.gif) 1). Ω represents all the possible final plane wave states of the ejected valence electron. As a result,
1). Ω represents all the possible final plane wave states of the ejected valence electron. As a result, 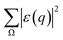 depends on w.
depends on w.
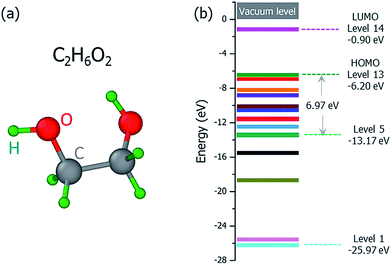
The ground state structure of the C2H6O2 molecule is shown in Fig. 2(a), and its molecular orbital energies calculated within DFT (PBE) are shown in Fig. 2(b). There are 13 occupied valence energy levels (2 electrons per level). The HOMO level is labeled as Level 13, and the deepest occupied valence level is labeled as Level 1. The valence electron ionization can occur at any one of these energy levels. After the ionization, the neutral C2H6O2 molecule becomes the ionized C2H6O2+ radical with one electron ejected to the vacuum, and all the final fragments come from this ionized radical; this is shown by mass spectroscopy experiments,16 where only charged fragments can be observed by mass spectroscopy.
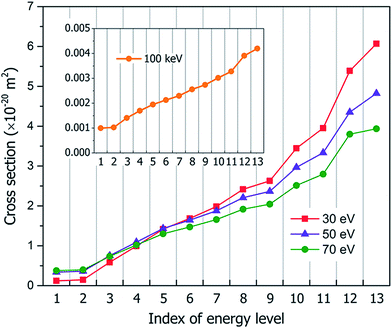
Fig. 3 shows our calculated cross sections for all levels under the illumination of different incident electron beams. The cross sections decrease monotonously from Level 13 to Level 1. This indicates that the electron in the HOMO level is most likely to be ejected into the vacuum (ionized). The predominant reason for this trend is the availability of the final states for the ejected electrons. For a shallow level, the number of the final states is much larger (the sum of Ω in eqn (4)), which leads to a larger cross section. Furthermore, the ionization cross section decreases as the energy of the incident electron beam increases, except for the very deep levels (Level 1–4) and very low incident electron beam energies, where energy conservation prevents the ionization of the very low energy levels. The smaller ionization cross section for the faster electron beam is due to the very short time in which it passes through the molecule, which prevents the electron from reacting or being ejected.
Molecule dissociation during hot hole carrier cooling
Following the initial ionization, we performed a rt-TDDFT simulation. A new rt-TDDFT algorithm was implemented.28 In this algorithm, the time-dependent electron wave function is expanded on the basis set of adiabatic states. These are the adiabatic states of the TDDFT Hamiltonian H(t) at time t, with the TDDFT charge density ρ(r,t), instead of the ground state charge density for a given atomic configuration {R} at time t. This procedure helps to reduce the original high dimensional problem to a small N-dimensional problem, where N is the number of adiabatic states included in the expansion. While the N adiabatic state wave functions are updated every Δt (∼0.1 fs) step, the N-dimensional problem is integrated within the [t, t + Δt] interval using a much smaller time step dt (∼0.1 attoseconds). However, because this integration is performed in a N × N Hamiltonian, it can be done quickly. The use of the adiabatic state not only allows us to significantly accelerate the simulation, but also enables us to introduce detailed balance and decoherence. As we know, the direct Ehrenfest dynamics does not satisfy the detailed balance. As a result, it can overheat the electronic system and thus cannot simulate the hot carrier cooling phenomenon.To restore the detailed balance for the transitions between the adiabatic state i and j, we developed an algorithm42 based on the occupation number O(i,t) of each adiabatic state ϕi; 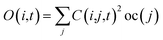 , oc(j) is the occupation of the time evolving state ψj in the rt-TDDFT, and it will not change with time. Note that
, oc(j) is the occupation of the time evolving state ψj in the rt-TDDFT, and it will not change with time. Note that 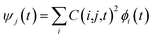 , where ψj follows the time-dependent Schrodinger equation ∂ψj/∂t = iHψj. During the time propagation, it is possible to define the change of the adiabatic state occupation as
, where ψj follows the time-dependent Schrodinger equation ∂ψj/∂t = iHψj. During the time propagation, it is possible to define the change of the adiabatic state occupation as
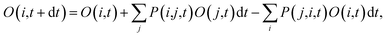 | (6) |
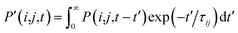 , where τij is the decoherence time between the two states i and j. This τij can be calculated based on the time fluctuations of Ei and Ej, as described in Section 1 of the ESI.† After the Boltzmann factor is applied to P′, O(i,t + dt) will be modified. A special algorithm was developed to change C(i,j,t) in
, where τij is the decoherence time between the two states i and j. This τij can be calculated based on the time fluctuations of Ei and Ej, as described in Section 1 of the ESI.† After the Boltzmann factor is applied to P′, O(i,t + dt) will be modified. A special algorithm was developed to change C(i,j,t) in 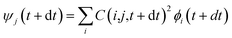 so that the desired renewed occupation O(i,t + dt) will be reproduced by the modified C(i,j,t + dt). This treatment of the detailed balance and decoherence time of rt-TDDFT is implemented in the PWmat code. Details about the calculation of the decoherence time are described in Section 1 of the ESI,† and the average of the values calculated using eqn (S1)† is τij = 2 fs. Our test calculations showed that the exact value of this decoherence time (within a factor of 2) does not affect our results significantly. Note that in our modified Ehrenfest dynamics with the Boltzmann factor and dephasing, our nuclear movement is not on the ground state energy surface but in a mean field excited state energy surface. Although we do not use energy surface hopping, some of the aspects (e.g., detailed balance) do have some commonality with the surface hopping dynamics.
so that the desired renewed occupation O(i,t + dt) will be reproduced by the modified C(i,j,t + dt). This treatment of the detailed balance and decoherence time of rt-TDDFT is implemented in the PWmat code. Details about the calculation of the decoherence time are described in Section 1 of the ESI,† and the average of the values calculated using eqn (S1)† is τij = 2 fs. Our test calculations showed that the exact value of this decoherence time (within a factor of 2) does not affect our results significantly. Note that in our modified Ehrenfest dynamics with the Boltzmann factor and dephasing, our nuclear movement is not on the ground state energy surface but in a mean field excited state energy surface. Although we do not use energy surface hopping, some of the aspects (e.g., detailed balance) do have some commonality with the surface hopping dynamics.
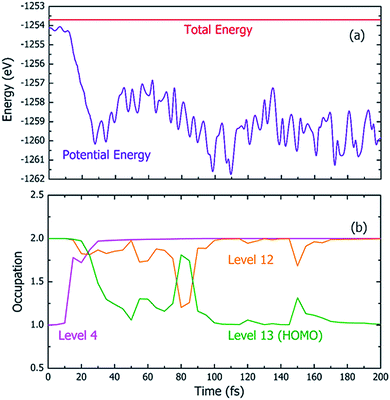
Fig. 4 shows one particular case of the rt-TDDFT simulation where one electron has been ejected from Level 4 at t = 0. Note that the initial ionization event is not an instantaneous process. Instead, it is a transition from the ground state to a many-body excited state (a higher energy many-body adiabatic state). To represent this higher-energy many-body adiabatic state under the DFT framework, we carried out a constraint DFT calculation at t = 0 with one electron removed from Level 4. In other words, ψj (t = 0) in our rt-TDDFT simulations are different from the Kohn–Sham orbitals at the neutral ground state. At t = 0, the nuclear kinetic energy of the molecule has a temperature of 350 K. As the electronic structure cools from the hot hole state, the released energy is converted to nuclear kinetic energy (which increases its temperature as the time increases), as shown in Fig. 4(a). While the occupation O(i,t) for Level 4 (i = 4) at t = 0 is 1, it returns to 2 very quickly (about 35 fs); then, the occupation of Level 13 (the HOMO level) decreases to 1 (about 100 fs), indicating that the hole has relaxed to the HOMO level. The full relaxation time of the hot hole on Level 4 is about 100 fs, as shown in Fig. 4(b).
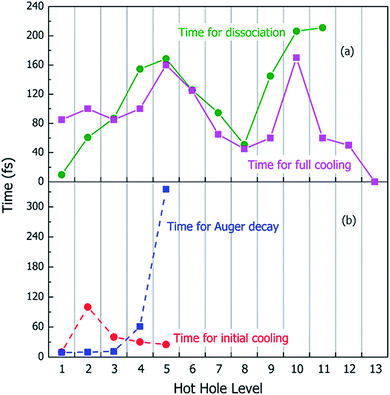
Using the above rt-TDDFT simulations, we systematically studied the hot hole relaxations and the corresponding molecule dissociation processes for all the initial ionization levels (Level 1–13). The total simulation time for each case was 300 fs. Although the initial kinetic energy of random atomic movements caused by the 350 K temperature can modify the results slightly, the overall different initial velocities do not change the results significantly. From the occupation changes during the rt-TDDFT simulation (e.g., in Fig. 4(b)), we can derive the times for the hot hole to cool from the initial ionization level to higher-energy levels. The results for the different initial ionization levels are shown in Fig. 5(a). The cooling times fall in the range from 40 fs to 160 fs.
During these simulations, we can also monitor whether the ionized molecule dissociates into different fragments. This is determined by the bond length changes of the molecule. When the atom–atom distance is beyond a certain cutoff and never comes back within a certain period, we can judge that the molecule has dissociated into small fragments, as described in Section 2 of the ESI.† The dissociation times for different ionization levels are also plotted in Fig. 5(a). The corresponding patterns of dissociation are listed in Table 1.
| Initial ionization level | Dissociation to different fragments |
|---|---|
| 1 | C2H6O2+ → C2H5O+ (CH3CHOH+) + OH |
| 2 | C2H6O2+ → C2H5O+ (CH2CH2OH+) + OH |
| 3–11 | C2H6O2+ → CH3O+ + CH3O |
| 12–13 | No dissociation observed |
As one can see from Fig. 5(a), remarkably, for most cases, the dissociation time and cooling time are close to each other. After the carrier cools, all its energy has been converted into kinetic energy of the molecule, and the system is in its electronic ground state. This means when the molecule is broken into two fragments during the hot hole cooling, it is the large kinetic energy increase (contributed by the hot hole cooling) at the electronic ground state which plays a significant role, rather than the hot hole on a certain level (e.g. the missing of any particular bond orbital). Another important fact is that for all these fast dissociations (ionizations 3–11), we only observed the breaking of the C–C bond, as shown in Table 1. This high probability of C–C bond breakdown is consistent with the high intensity of CH3O+ fragments observed in the mass spectrum shown in Fig. 6(a).
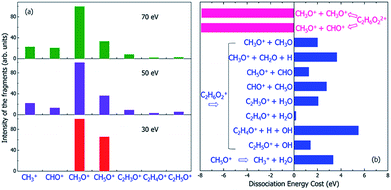 | ||
| Fig. 6 (a) The experimental mass spectra of the charged fragments from the dissociation of C2H6O2 molecule under the illumination of electron beams with different incident energies of 30, 50 and 70 eV, reproduced from ref. 16. (b) The calculated energy costs for the dissociation of the doubly-ionized C2H6O22+ and singly-ionized C2H6O2+ into different fragments. Negative dissociation energy means the dissociation is exothermic, while positive energy means the dissociation is endothermic. The dissociation energies were calculated according to the electronic ground state energies of the reaction species. | ||
When the initial ionization levels are Level 12, 13, or 1, 2, the process after ionization is quite different. Firstly, when the ionization occurs at Level 12 or 13 (HOMO level), no dissociation is observed during our simulation for 300 fs. The consequence of this will be discussed later in the last subsection of the Results and discussion.
Secondly, when the ionization occurs at Level 1 or 2, the dissociation occurs very quickly, before the hot hole is fully cooled. Especially for Level 1, the dissociation is extremely fast and happens in a few femtoseconds. For both Level 1 and 2, the dissociation patterns are different from those for the other levels. Here, the C–O bond is broken, and one OH group will move away. This results in a CH2–CH2 group in the case of Level 2. In the case of Level 1, a H is transferred from one C to another C, resulting in the formation of a CH3 group. These two processes are shown in Fig. S2(a and b) of the ESI,† respectively. Note that although the positively charged fragments of the two dissociations can both be denoted as C2H5O+, they actually have different structures. According to the rt-TDDFT simulations, we should observe the two different C2H5O+ fragments experimentally; however, the probability for the experimental observation of C2H5O+ is quite small according to the mass spectrum shown in Fig. 6(a). To explain this, we investigate the effects of the Auger process in the next section.
Double ionization and dissociation induced by ultra-fast Auger processes
When the initial ionization occurs at a deep level (Level 1, 2, 3, 4 or 5), the hot hole is deep enough in energy that one electron on a higher energy level can jump down to this level and emit one electron to the vacuum from another level in order to satisfy energy conservation. This is an Auger process. The lifetime τ of this Auger process can be calculated as43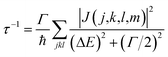 | (7) |
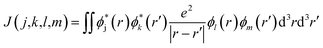 | (8) |
| ΔE = E(k) − E(m) + E(j) − E(l) | (9) |
For each original hot hole Level m, multiple Auger channels (j and k in eqn (7)) can occur. For example, for the hot hole on Level 2, up to 41 possible (j, k) channels of Auger processes were found, and their Auger rates were all calculated. All the possible channels of the Auger processes are listed in Table S1 of the ESI.† The total Auger rate was calculated from eqn (7) by summing up all the channels, as shown in Fig. 5(b). We can see that the Auger lifetime increases dramatically with the initial hot hole level. This is mainly due to the available density of states of the emitted state l for a deep initial level. The overall lifetimes of the Auger processes of Level 1, 2 and 3 are extremely fast, on the time scale of a few femtoseconds. They are all quicker than the initial hot hole cooling process caused by electron–phonon coupling. Here, to compare to the Auger process, we chose the initial cooling times of the hot holes during the rt-TDDFT simulations. This initial cooling time is defined as the time when the initial hot hole level is fully occupied instead of the full relaxation time for the hot hole to relax all the way to the HOMO level. As soon as the original hot hole level is occupied, the corresponding Auger process of that mth level in eqn (7) will no longer be possible. As shown in Fig. 5(b), for Level 1, 2 or 3, the Auger process is faster than the initial cooling time of the hot hole; thus, the Auger process and the secondary ionization (double ionization) will occur. On the other hand, for 4 and 5, the secondary ionization will not occur.
Because the Auger process occurs if a hot hole is formed on Level 1, 2 or 3, the singly-ionized C2H6O2+ will become the doubly-ionized C2H6O22+. This explains why the predicted fragments C2H5O+ for Level 1 and 2 in Table 1 (as a result of nonadiabatic decay) are not observed experimentally in Fig. 6(a). C2H6O22+ is not stable; the Coulomb explosion will break it into two fragments. From the pure energy consideration, it can have two different pathways of dissociation. One is into CH3O+ + CH3O+, and the other is into CH5O+ + CHO+. Both dissociation processes are exothermic, as shown by the calculated energy change of the dissociation in Fig. 6(b). The released energies are quite large and are both about 8 eV.
The first possible dissociation product of the doubly-ionized C2H6O22+ is CH3O+ + CH3O+; thus, only the fragment CH3O+ can be observed (because only charged fragments can be observed by mass spectroscopy), which is the same as the fragment CH3O+ for Level 3–11 in Table 1. This also explains the high intensity of CH3O+ observed in the mass spectrum shown in Fig. 6(a).
The second possible dissociation product of the doubly-ionized C2H6O22+ is CH5O+ + CHO+. However, according to Fig. 6(a), only the fragment CH5O+ is observed, and CHO+ is not observed in the mass spectrum when the electron beam energy is 30 eV; meanwhile, they are both observed when the electron beam energy is 50 or 70 eV. This indicates the CH5O+ in the 30 eV case must come from a different channel instead of from the doubly-ionized C2H6O22+. This is also consistent with the fact that for 30 eV, in comparison with the 50 and 70 eV cases, the initial ionization cross sections for Level 1 and 2 are very small, as shown in Fig. 3. Thus, the Auger effect will be small in the case of 30 eV. On the other hand, for 50 and 70 eV, the Auger effects are large, and we do see both CH5O+ and CHO+ in similar amplitudes due to the Auger process.
Slow thermodynamic dissociation of the singly-ionized molecule
If the initial ionization is on a high-energy level, such as Levels 12 and 13, no fragmentation is observed in our direct rt-TDDFT simulations, as shown in Table 1; meanwhile, there is also not enough energy for an Auger process to cause double-ionization-induced dissociation. However, the ionized C2H6O2+ can still dissociate because the nuclear kinetic energy increases during the hot hole relaxation and due to the structural reorganization after a hot hole is formed. The increased kinetic energy can overcome some of the dissociation energies, as shown in Fig. 6(b), and cause slow dissociation of the ionized C2H6O2+ from the thermodynamic point of view.In Fig. 6(b), the thermodynamic energy costs for the dissociation of C2H6O2+ into different fragments are calculated. The energy cost is defined as the change from the energy of the ionized C2H6O2+ at its ground state (after the hot hole has been cooled to the HOMO level) to the sum of the energies of all the fragments at their ground states (the whole system of all the fragments has one positive charge). The calculated energies of all the fragments in either neutral or +1 charged states are also listed in Table S2.† Compared to the energy of the ionized C2H6O2+ at its ground state, the total energies of the dissociated fragments are all higher; therefore, the energy costs of all the dissociation paths are positive, in the range from 0.2 eV to 5.5 eV.
Because the energy costs are all positive, additional energies are needed to drive these endothermic reactions. If the nuclear kinetic energy is high enough, these dissociations are still possible. This nuclear kinetic energy can come from two sources after an electron is ejected and a hot hole is formed: (i) the nonadiabatic decay and cooling of the hot hole carrier if the original ionization is at Level 1–12, which can convert the eigenenergy difference between the ionized energy level and the HOMO level to nuclear kinetic energy; and (ii) the reorganization energy of C2H6O2+ from the original unrelaxed structure of the neutral state (the structure immediately after ionization) to the ground state structure of C2H6O2+. Our calculations show that the reorganization energy can be as large as 0.7 eV for Levels 12 and 13. The energy from the hot carrier cooling increases significantly as the initial ionization level becomes deeper. The sum of the two energies increases from 0.7 eV to about 27 eV as the initial ionization level changes from Level 13 to Level 1. Therefore, the increased kinetic energy is close to the energy costs of the dissociation shown in Fig. 6(b); therefore, slow dissociation becomes possible. However, this slow thermally activated dissociation should be in competition with the direct fast nonadiabatic decay-caused dissociation observed in our rt-TDDFT simulation. As shown in Fig. 5(a), in this nonadiabatic process, the time for dissociation is correlated with the time for electronic cooling. This indicates that this dissociation is similar to a ballistic process. Therefore, if this dissociation is possible, the thermally activated slow process will not be competitive. As a result, the thermally activated process may only be relevant for Level 12 and 13 ionizations.
As discussed above, the peaks of CH5O+ and CHO+ under illumination of the 50 or 70 eV electron beams result from the dissociation of the doubly-ionized C2H6O22+ after the Auger process; however, only the peak of CH5O+ is observed for the 30 eV electron beam, which indicates that it is not caused by the Auger effect. However, the CH5O+ in the 30 eV case can be explained by the thermally activated slow process for Level 12–13 ionization through the C2H6O2+ → CH5O+ + CHO process, which has an energy cost of around 1.2 eV. The kinetic energy gain from Level 12 ionization is also around 1.2 eV, which is sufficient to cause the above dissociation but insufficient to cause the CH3O+ + CH3O dissociation (this process requires about 2.2 eV to occur). Because CH5O+ + CHO dissociation requires two H atoms to transfer from one C to another C, it will be slow and will only happen in the electronic ground state instead of during the fast hot hole cooling process. When the energy of the electron beam is low (e.g., 30 eV), the ionization on the higher energy levels (Level 12 or 13) has larger cross-sections, as shown in Fig. 3; therefore, this slow dissociation becomes more dominant, explaining the high CH5O+ peak in Fig. 5(a).
One remaining puzzle is the dissociation into C2H4O+ + H2O. According to our ground state energy calculations, the energy cost of this dissociation is rather small; thus, it should be possible, and the charged C2H4O+ fragment should be observed. However, no strong peak is observed experimentally for C2H4O+, as shown in Fig. 6(a). One possible reason is that due to the high barrier of this reaction, this dissociation path is very improbable, as claimed by Li et al.44 using electronic ground state calculations.
Finally, we note that we have yet to find the formation of CH3+ in our above analysis; however, the mass spectra show that CH3+ is formed under 50 or 70 eV electron beam illumination. We propose that the CH3+ arises from a secondary dissociation of CH5O+ into CH3+ and H2O, as first studied in ref. 16. This secondary dissociation requires a dissociation energy of about 3.3 eV, as shown in Fig. 6(b); therefore, in the 30 eV case, it cannot occur from CH5O+, which arises from dissociation due to Level 12 ionization, and very little kinetic energy should remain in CH5O+. However, large kinetic energy in CH5O+ is possible in the 50 and 70 eV cases because it arises from exothermic C2H6O22+ dissociation, which can release 8 eV kinetic energy, as shown in Fig. 6(b). This agrees with the experimental observation that CH3+ only appears in the 50 and 70 eV electron beam cases.
Putting together all the dissociation paths and their competitions, we have tentatively assigned the underlying mechanisms of the main peaks to different dissociation channels (paths) under the illumination of electron beams with different incident energies, as shown in Fig. 7. Note that our results can be verified by future time-resolved mass spectroscopy experiments to distinguish the fast and slow dissociation channels.
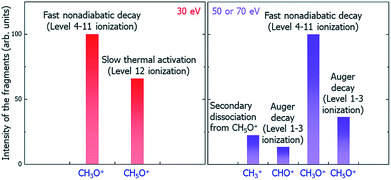 | ||
| Fig. 7 Schematic of the underlying mechanisms of the main peaks in different electron beam energy situations. | ||
Conclusions
In summary, we have developed a systematic procedure to study the whole radiolysis-induced molecule damaging process. This includes the initial ionization cross-section calculations of different electronic levels under the illumination of electron beams with different incident energies; the nonadiabatic hot carrier cooling calculation following the initial ionization and the associated molecule fragmentation by applying the newly developed rt-TDDFT method, which incorporates the detailed balance; the lifetime calculation of the Auger secondary ionization process; and the calculation of the thermodynamic dissociation energies at the final electronic ground state. Taking the dissociation processes of C2H6O2 molecule after the initial radiolysis ionization caused by LEEB illumination as an example, through systematical calculations using these methods and comparing the time scales and competitiveness of different dissociation paths, we have revealed the underlying mechanisms of the peaks of different charged fragments in the observed mass spectra. We are not at the level of predicting the quantitative value of the amplitude of each peak; however, we can tentatively assign the origin of each peak and predict the trend of its amplitude as a function of the illuminating electron beam energy. We found three categories of dissociation paths: the fast and ballistic dissociation during hot hole carrier cooling (CH3O+); the fast Coulomb explosion caused by secondary ionization due to the Auger effect (CH5O+, CHO+ for the 50 and 70 eV electron beams); the slow dissociation driven by the kinetic energy at the electronic ground state (CH5O+ for the 30 eV electron beam); and the secondary fragment decay from the initial decay fragments (CH3+ decayed from CH5O+ for the 50 and 70 eV electron beams). Our results explain all the main peaks in the experimentally observed mass spectra and their relative amplitudes and qualitative trends as a function of the electron beam energy. Our work demonstrates that it is now possible to use ab initio calculations to understand the complex underlying mechanisms of molecule damage under electron beam illumination in TEM experiments. The insights provided by the current work and the identification of different dissociation paths can help us to find solutions to mitigate the molecule damage problem in TEM experiments as well as in many other applications. The methods developed here can also be adopted for the study of defect formation or bond breaking processes in bulk materials under electron beam illumination.Conflicts of interest
There are no conflicts to declare.Acknowledgements
L. W. W. was supported by the US Department of Energy, Office of Science, Office of Basic Energy Sciences, Materials Sciences and Engineering Division under contract no. DE-AC02-05-CH11231 within the in situ TEM program (KC22ZH). H. C. and S. C. were supported by the National Natural Science Foundation of China (NSFC) under grant No. 61722402, 61574059 and 91833302, the National Key Research and Development Program of China (2016YFB0700700), Shanghai Academic/Technology Research Leader (19XD1421300), Fok Ying Tung Education Foundation (161060), the Fundamental Research Funds for the Central Universities and CC of ECNU. This work used the resources of the National Energy Research Scientific Computing Center.Notes and references
- R. F. Egerton, Ultramicroscopy, 2013, 127, 100 CrossRef CAS PubMed.
- R. F. Egerton, P. Li and M. Malac, Micron, 2004, 35, 399 CrossRef CAS PubMed.
- O. Ugurlu, J. Haus, A. A. Gunawan, M. G. Thomas, S. Maheshwari, M. Tsapatsis and K. A. Mkhoyan, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 113408 CrossRef.
- L. Reimer, U. Golla, R. Böngeler, M. Kässens, B. Schindler and R. Senkel, Optik, 1992, 92, 14 CAS.
- L. E. Thomas, Ultramicroscopy, 1985, 18, 173 CrossRef CAS.
- R. Henderson and R. M. Glaeser, Ultramicroscopy, 1985, 16, 139 CrossRef CAS.
- M. Liu, L. Xu and X. Lin, Scanning, 1994, 16, 1 CrossRef CAS.
- J. J. Hren, Barriers to AEM: Contamination and Etching, in Introduction to Analytical Electron Microscopy, Springer US, 1979 Search PubMed.
- R. F. Egerton, Microsc. Res. Tech., 2012, 75, 1550 CrossRef CAS PubMed.
- J. C. Meyer, C. O. Girit, M. F. Crommie and A. Zettl, Nature, 2008, 454, 319 CrossRef CAS PubMed.
- A. Hashimoto, K. Suenaga, A. Gloter, K. Urita and S. Iijima, Nature, 2004, 430, 870 CrossRef CAS PubMed.
- T. D. Märk and G. H. Dunn, Electron impact ionization, Springer Science & Business Media, 2013 Search PubMed.
- L. G. Christophorou, Electron-molecule interactions and their applications, Academic Press, 2013 Search PubMed.
- L. C. Pitchford, B. V. McKoy, A. Chutjian and S. Trajmar, Swarm studies and inelastic electron-molecule collisions, Springer Science & Business Media, 2012 Search PubMed.
- V. Garner, Biomedical applications|Gas chromatography-mass spectrometry, Academic Press, 2000 Search PubMed.
- M. Y. Mykyta, L. G. Romanova, A. M. Zavyilopulo and O. B. Shpenik, Ukr. J. Phys., 2011, 56, 116 CAS.
- D. Bouchiha, J. D. Gorfinkiel, L. G. Caron and L. Sanche, J. Phys. B: At., Mol. Opt. Phys., 2007, 40, 1259 CrossRef CAS.
- A. N. Zavilopulo, F. F. Chipev and L. M. Kokhtych, Nucl. Instrum. Methods Phys. Res., Sect. B, 2005, 233, 302 CrossRef CAS.
- R. Rejoub, C. D. Morton, B. G. Lindsay and R. F. Stebbings, J. Chem. Phys., 2003, 118, 1756 CrossRef CAS.
- J. E. Hudson, M. L. Hamilton, C. Vallance and P. W. Harland, Phys. Chem. Chem. Phys., 2003, 5, 3162 RSC.
- L. G. Christophorou and J. K. Olthoff, J. Phys. Chem. Ref. Data, 2000, 29, 267 CrossRef CAS.
- R. Völpel, G. Hofmann, M. Steidl, M. Stenke, M. Schlapp, R. Trassl and E. Salzborn, Phys. Rev. Lett., 1993, 71, 3439 CrossRef PubMed.
- F. L. Arnot, Nature, 1932, 129, 617 CrossRef CAS.
- L. Sanche, Mass Spectrom. Rev., 2002, 21, 349 CrossRef CAS PubMed.
- S. T. Skowron, I. V. Lebedeva, A. M. Popov and E. Bichoutskaia, Nanoscale, 2013, 5, 6677 RSC.
- T. Susi, J. Kotakoski, R. Arenal, S. Kurasch, H. Jiang, V. Skakalova, O. Stephan, A. V. Krasheninnikov, E. I. Kauppinen, U. Kaiser and J. C. Meyer, ACS Nano, 2012, 6, 8837 CrossRef CAS PubMed.
- B. F. E. Curchod and T. J. Martínez, Chem. Rev., 2018, 118, 3305 CrossRef CAS PubMed.
- Z. Wang, S.-S. Li and L.-W. Wang, Phys. Rev. Lett., 2015, 114, 063004 CrossRef CAS PubMed.
- G. Bi, J. Kang and L.-W. Wang, Phys. Chem. Chem. Phys., 2017, 19, 9053 RSC.
- R. Ullah, E. Artacho and A. A. Correa, Phys. Rev. Lett., 2018, 121, 116401 CrossRef CAS PubMed.
- J. Bang, Y. Y. Sun, X. Q. Liu, F. Gao and S. B. Zhang, Phys. Rev. Lett., 2016, 117, 126402 CrossRef PubMed.
- F. Ding, E. B. Guidez, C. M. Aikens and X. Li, J. Chem. Phys., 2014, 140, 244705 CrossRef PubMed.
- B. Peng, D. B. Lingerfelt, F. Ding, C. M. Aikens and X. Li, J. Phys. Chem. C, 2015, 119, 6421 CrossRef CAS.
- W. H. Miller and S. J. Cotton, J. Chem. Phys., 2015, 142, 131103 CrossRef PubMed.
- W. Jia, J. Fu, Z. Cao, L. Wang, X. Chi, W. Gao and L.-W. Wang, J. Comput. Phys., 2013, 251, 102 CrossRef.
- W. Jia, Z. Cao, L. Wang, J. Fu, X. Chi, W. Gao and L.-W. Wang, Comput. Phys. Commun., 2013, 184, 9 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- M. Inokuti, Rev. Mod. Phys., 1971, 43, 297 CrossRef CAS.
- M. Inokuti, Y. Itikawa and J. E. Turner, Rev. Mod. Phys., 1978, 50, 23 CrossRef CAS.
- Y.-K. Kim and M. E. Rudd, Phys. Rev. A: At., Mol., Opt. Phys., 1994, 50, 3954 CrossRef CAS PubMed.
- Y. K. Kim, W. Hwang and M. E. Rudd, AIP Conf. Proc., 1996, 381, 93 CrossRef CAS.
- J. Kang and L.-W. Wang, Phys. Rev. B, 2019, 99, 224303 CrossRef CAS.
- L.-W. Wang, M. Califano, A. Zunger and A. Franceschetti, Phys. Rev. Lett., 2003, 91, 056404 CrossRef PubMed.
- Y. Li and T. Baer, J. Phys. Chem. A, 2002, 106, 8658 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9sc04100a |
| This journal is © The Royal Society of Chemistry 2019 |