Open Access Article
Open Access ArticleScrutinizing metal–ligand covalency and redox non-innocence via nitrogen K-edge X-ray absorption spectroscopy†
James T.
Lukens‡
a,
Ida M.
DiMucci‡
 a,
Takashi
Kurogi
a,
Takashi
Kurogi
 b,
Daniel J.
Mindiola
b,
Daniel J.
Mindiola
 b and
Kyle M.
Lancaster
b and
Kyle M.
Lancaster
 *a
*a
aDepartment of Chemistry and Chemical Biology Cornell University, Baker Laboratory, Ithaca, NY 14853, USA. E-mail: kml236@cornell.edu
bDepartment of Chemistry, University of Pennsylvania, 231 South 34th Street, Philadelphia, PA 19104, USA
First published on 17th April 2019
Abstract
Nitrogen K-edge X-ray absorption spectra (XAS) were obtained for 19 transition metal complexes bearing bipyridine, ethylenediamine, ammine, and nitride ligands. Time-dependent density functional theory (TDDFT) and DFT/restricted open configuration interaction singles (DFT/ROCIS) calculations were found to predict relative N K-edge XAS peak energies with good fidelity to experiment. The average difference (|ΔE|) between experimental and linear corrected calculated energies were found to be 0.55 ± 0.05 eV and 0.46 ± 0.04 eV, respectively, using the B3LYP hybrid density functional and scalar relativistically recontracted ZORA-def2-TZVP(-f) basis set. Deconvolution of these global correlations into individual N-donor ligand classes gave improved agreement between experiment and theory with |ΔE| less than 0.4 eV for all ligand classes in the case of DFT/ROCIS. In addition, calibration method-dependent values for the N 1s → 2p radial dipole integral of 25.4 ± 1.7 and 26.8 ± 1.9 are obtained, affording means to estimate the nitrogen 2p character in unfilled frontier molecular orbitals. For the complexes studied, nitrogen covalency values correlate well to those calculated by hybrid DFT with an R2 = 0.92 ± 0.01. Additionally, as a test case, a well-characterized PNP ligand framework (PNP = N[2-P(CHMe2)2-4-methylphenyl]21−) coordinated to NiII is investigated for its ability to act as a redox non-innocent ligand. Upon oxidation of (PNP)NiCl with [FeCp2](OTf) to its radical cation, [(PNP)NiCl](OTf) (OTf = triflate), a new low-energy feature emerges in the N K-edge XAS spectra. This feature is assigned as N 1s to a PNP-localized acceptor orbital exhibiting 27 ± 2% N 2p aminyl radical character, obtained using the aforementioned nitrogen covalency calibration. Combined, these data showcase a direct spectroscopic means of identifying redox-active N-donor ligands and also estimating nitrogen 2p covalency of frontier molecular orbitals in transition metal complexes.
Introduction
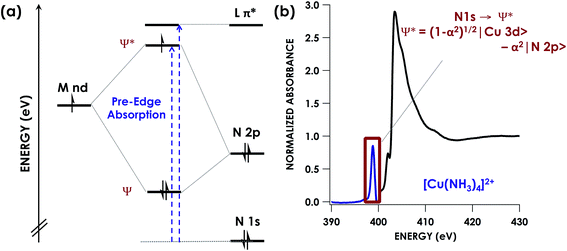
Numerous factors can complicate or otherwise invalidate the use of the oxidation state formalism to rationalize the properties of transition metal compounds. The “formal” oxidation state of a transition metal, assigned by assuming redox flexibility of the metal rather than its supporting ligands,1–4 is frequently found to be at odds with its “physical” oxidation state5—the experimental electronic population of d-orbitals at the metal center. Ligand redox non-innocence (RNI)6—the recognition that ligands such as nitric oxide (NO)7 and dithiolenes8 exist in multiple oxidation states—has established that consideration of simple complex charge is insufficient to determine the physical oxidation state of a metal. More recently, we explored how extreme metal–ligand covalency can lead to “inverted” bonding schemes in which ligand-localized, rather than metal-localized, molecular orbitals (MOs) serve as frontier orbitals. In these cases, the metal has a more reduced physical oxidation state than would have been expected from simple electron counting schemes.9,10 Ligand field inversion calls into question the propriety of assigning high physical oxidation states to late metals without experimental validation. In a more extreme paradigm, ligands are far more electronically pliable than transition metals, and thus only the ligands should be thought to have modulated charge, not the metal.4 Given the well-recognized relationship between transition metal electronic structure and function in synthetic and biological transformations, reliable methods to probe physical oxidation states and metal–ligand covalency are of high utility.Arguably the most direct tools to probe physical oxidation states are synchrotron-based X-ray absorption spectroscopies (XAS).11 These element-selective methods typically do not have restrictions on sample compositions and are sensitive to local charges at photo-absorbing elements, probing the energetics and compositions of unfilled frontier MOs. Metal K-edge (1s → valence) XAS is frequently used to establish whether the metal undergoes redox, although metal–ligand covalency, coordination environment, and other factors can confound interpretation.11
Alternatively, XAS can be used to directly probe ligand donor-atom electronics (Fig. 1). Ligand K-edge XAS has been developed for routine use in the case of S- and Cl-donor ligands,12,13 and efforts are underway to bring P-donors into the fold.14–17 These spectra may be readily interpreted to not only show whether ligands undergo redox, but also to afford estimation of ligand np orbital participation in bonding with transition metals. Moreover, computational protocols such as time-dependent density functional theory (TDDFT)18,19 and DFT/restricted open configuration interaction singles (DFT/ROCIS)20,21 have been developed that predict XAS with high fidelity, thus facilitating data interpretation.
K-edge XAS studies of transition metal complexes where lighter C-, O-, and N-donor ligands are probed are less common.22–24 This is likely due to the low (<1000 eV) excitation energies involved. Consequently, the spectroscopy at these soft X-ray energies requires ultrahigh vacuum conditions that impose restrictions on the types of samples that may be studied. Moreover, high absorption cross-sections at these energies frequently lead to significant photodamage. There are however, studies in the literature using N K-edge energy loss near edge structures spectra to investigate N containing transition metals. This technique can enable further interpretation of features seen in the X-ray absorption near edge structure (XANES) spectra and allow for investigation of the electronic structure and bonding of these species.25–27 In addition, studies using N K-edge on solids has been shown to provide information on changes in the local structure surrounding N atoms in these materials. However few studies exist involving the use of pre-edge features in N K-edge spectra to specifically inform covalency and electronic structure in transition metal species.28 Given emerging beamline technologies29 and the abundance of chemistry involving RNI N-donor ligands as either supporting ligands or as group-transfer moieties,30–32 we undertook a calibration study of N K-edge XAS. Herein, we show that DFT-based computational methods including TDDFT and DFT/ROCIS predict N K-edge XAS pre-edge features with high fidelity in the energy domain. Moreover, using [Cu(NH3)4]2+ and [Cu(en)2]2+ (en = ethylenediamine) as calibrants, we show that N K-edge XAS affords reliable estimation of relative N 2p contributions to bonding across and down the transition series of the periodic table. After calibration of the nitrogen covalency, we then showcase the ability of N K-edge XAS to identify RNI behaviour in a PNP pincer ligand (PNP = N[2-P(CHMe2)2-4-methylphenyl]21−) coordinated to Ni. Bearing a lone N atom and hence providing only one locus for N oxidation, the PNP ligand represents an ideal case to use N K-edge XAS to study RNI. Identification of an inner-sphere aminyl radical is achieved through direct observation and quantification of a N-localized vacancy formed upon oxidation.
Experimental
Samples of [Cu(NH3)4](SO4)·xH2O,33 [Ni(NH3)6]Cl2,34 [Cu(en)2](OTf)2·xH2O,35 [Ni(en)3]Cl2·xH2O,36 [Zn(en)3]Cl2·xH2O,37 [Fe(bpy)3](PF6)2,38 [Ru(bpy)3](BPh4)2,38 [Os(bpy)3](PF6)2,38 [Co(bpy)3](PF6)2,39 [Co(bpy)3](BF4)2(PF6),39 [Rh(bpy)3](PF6)3,40 [Mn(bpy)3](PF6)2,39 [Ni(bpy)3](PF6)2,39 [Zn(bpy)3](PF6)2,39 (nBu4N)[RuNCl4],41 (nBu4N)[OsNCl4],41 (nBu4N)[ReNCl4],42 PNPH, (PNP)NiCl, and [(PNP)NiCl](OTf)16 were prepared according to the published procedures. [Co(NH3)6]Cl3 and [Co(NH3)5Cl]Cl2 were purchased from Sigma Aldrich and used without further purification. Purity of compounds upon recrystallization was judged by elemental analysis analytical data, collected at the CENTC Elemental Analysis Facility at the University of Rochester. Samples were weighed with a PerkinElmer Model AD6000 Autobalance and their compositions were determined using a PerkinElmer 2400 Series II Analyzer.XAS data collection
All data were measured at the Stanford Synchrotron Radiation Lightsource (SSRL) under ring conditions of 3.0 GeV and 500 mA. All samples were prepared in an inert-atmosphere glovebox and were measured as solids. For Cu L2,3-edge and N K-edge measurements, samples were ground immediately prior to measurement to expose fresh surfaces. The sample stick was prepared in an anaerobic dry box, and immediately transferred under an argon atmosphere to high vacuum for measurement. Given the analytical purity of all materials tested, we have no reason to suspect any degradation that would confound sample identity. Moreover, scans were found to be superimposable as the sample surfaces were rasterized, precluding any localized contamination.N K-edge measurements were collected on the 31-pole wiggler beamline 10–1 with a 600 lines per mm spherical grating monochromator and 20 μm entrance and exit slits. Data were measured by monitoring the change in sample current through detection of the total electron yield (TEY). The drain current was normalized to incident photon flux with a gold-grid reference monitor. Incident beam energy was calibrated by comparison of the Ni L3 second order transition at 426.35 eV in a reference sample placed upstream of the sample chamber. Samples were maintained at room temperature under an ultra-high vacuum (10−9 Torr) during collection. Eight scans were measured and averaged for each compound. Normalization was carried out using PyMCA43 and data were processed with Igor 6.37. Background subtraction was achieved by fitting a line to the pre-edge region below 395.0 eV and subtracting from the entire spectrum. The post edge region above 410.0 eV was fit to a flattened polynomial and normalized to 1.0. Spectra were fit according to a pseudo-Voigt deconvolution of pre-edge and rising edge peaks.
Cu L2,3-edge XAS measurements were collected on the 31-pole wiggler beamline 10–1 with a 1000 lines per mm spherical grating monochromator and 29 μm entrance and exit slits. Data were measured by monitoring the change in sample current through detection of the total electron yield (TEY). The drain current was normalized to incident photon flux with a gold-grid reference monitor. Incident beam energy was calibrated to the L3 edge position at 930.65 eV of a (nmph)2[CuCl4] (nmph = N-methylphenethylammonium) standard spectra collected before and after each sample.44 Samples were maintained at room temperature under an ultra-high vacuum (10−9 Torr) during collection. Data were collected from 910.0 to 990.0 eV. Four scans were measured and averaged for each compound. Processing was done using PyMCA. Background subtraction was achieved by fitting a line to the pre-edge region below 925.0 eV and subtracting from the entire spectrum. The post edge region from 975.0 eV to 990.0 eV was fit to a line and normalized to 1.0. The edge jumps at L3 and L2 were subtracted using a statistics-sensitive non-linear iterative peak-clipping (SNIP) algorithm45 as implemented in PyMCA. Spectra were fit according to a pseudo-Voigt deconvolution of pre-edge and rising edge peaks with Igor 6.37.
Fitting procedures
An in-house developed, Monte-Carlo based, nonlinear least squares fitting algorithm46 was used to fit the N K-edge XAS spectra in Python using a common set of weights and bounds. A minimum of 100 initial fits were performed with a series of floating parameters, allowing for a maximum of 10 available peaks in the range of 395 to 415 eV with a full width at half max (FWHM) up to 3 eV. This allows for the fitting of both pre-edge and rising-edge peaks to Pseudo-Voight peaks as well as inclusion of the edge-jump step function. The edge function itself was constrained to having a range of 407 to 415 eV with a FWHM up to 5 eV. The pre-edge region of 395 to 402 eV was weighted 100 times more than the rising/post-edge 402–415 eV region in order to obtain minimal errors in pre-edge peak areas. Analysis of the histogram produced from the initial fits complied with the 50 best fits (according to the weighted R2) then allowed for further peak bounds to be set that led to the finalized fits, selected for the lowest R2. A more complete description of this fitting procedure is available in the ESI.†DFT calculations
Density Functional Theory (DFT) calculations were performed with version 4.002 of the ORCA software package.47 All spectra were calculated from crystallographic coordinates. Single-point energies were calculated by using the B3LYP48 functional. N K-edge XAS spectra were calculated using TDDFT49 and DFT/ROCIS21 methods. Calculations with hybrid functionals used the RIJCOSX algorithm to speed the calculation of Hartree–Fock exchange.50 The CP(PPP) basis set was used for 3d transition metals with a special integration accuracy (ORCA Grid7).51 The scalar relativistically recontracted ZORA-def2-TZVP(-f) basis set52 with ORCA Grid4 was used for all other atoms. Calculations included the zeroth-order regular approximation (ZORA)53 for relativistic effects as implemented by van Wüllen.54 Solvation was modeled with CPCM in an infinite dielectric.55 For the 5d transition metal atoms, the segmented all-electron relativistically contracted (SARC) basis set was used.56Results and discussion
Pre-edge energy predictions
We undertook a calibration of N K-edge XAS by obtaining spectra for 19 well-characterized coordination complexes. The N K-edge XAS library we constructed comprises a series of transition metal bipyridine, ethylenediamine, ammine, and nitride complexes (Table S1†). Representative spectra are shown in Fig. 2. To facilitate the calibration, crystallographic coordinates for these complexes were used in single-point hybrid DFT calculations using ORCA 4.0.47 All calculations were spin unrestricted and employed the B3LYP hybrid density functional,57,58 the ZORA-def2-TZVP(-f) basis set56 on all atoms, and the zeroth order regular approximation (ZORA)59 as a relativistic correction. Hartree–Fock mixing has previously been shown to give improved results in the calculation of light atom XAS over generalized gradient approximation functionals, meanwhile basis set choice has a small effect.60 Frontier MO diagrams were generated in all cases (Panel (c) Fig. S8–S25†). These single point DFT solutions were then used as starting points for TDDFT spectral simulations. Example TDDFT-calculated spectra are shown in Fig. 2a. Quasi-restricted orbitals were generated from the unrestricted DFT solutions and used as input for the DFT/ROCIS calculations. Example DFT/ROCIS-calculated spectra are shown in Fig. 2b.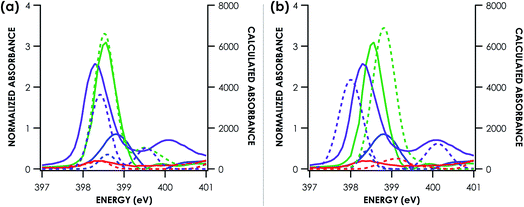 | ||
| Fig. 2 Example comparison of experimental (solid lines) and TDDFT calculated (a) and DFT/ROCIS calculated (b) (dotted lines) nitrogen K-edge XAS pre-edge features. Calculated spectra are shifted according to individualized fits seen in Fig. 3. Purple = (nBu4N)[RuNCl4]. Green = [Mn(bpy)3](PF6)2. Blue = [Cu(NH3)4](SO4). Red = [Zn(en)3]Cl2. | ||
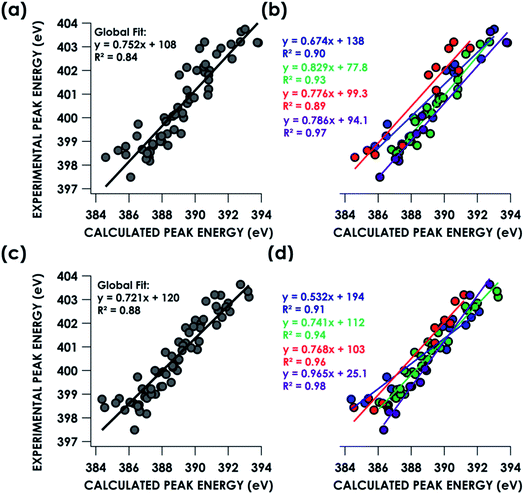
TDDFT and DFT/ROCIS simulations of core spectra (XAS and X-ray emission spectroscopy, XES) must be corrected for large systematic errors in calculating absolute core (e.g. 1s) potentials.18,19 Relative errors in frontier orbital energies are typically smaller. In the present case, a linear correction with a non-unity slope must be applied to align spectra calculated using either approach to experiment (Table 1). Points for this calibration were obtained by correlating predicted peaks below 405 eV to calculated peaks based on peak position, intensity and shape. Global correlation including all measured compounds affords good agreement between experimental and calculated pre-edge peak energies for spectra calculated using both the TDDFT (R2 = 0.84) and DFT/ROCIS (R2 = 0.88) methods (Fig. 3a and c). Fidelity of the calculations to experiment may also be expressed as the average value of the absolute magnitude of the difference between experiment and theory after a linear correction has been performed: |ΔE|.61 It should be noted that this is an average error and is only used to compare the accuracy of the calculations to one another. The absolute error for certain species – such as the en species – is much larger. From global consideration of the data, |ΔE| is 0.55 ± 0.05 eV and 0.46 ± 0.04 eV for TDDFT and DFT/ROCIS, respectively.
| Dataset | TDDFT slope | TDDFT intercept (eV) | TDDFT |ΔE| (eV) | DFT/ROCIS slope | DFT/ROCIS intercept (eV) | DFT/ROCIS |ΔE| (eV) |
|---|---|---|---|---|---|---|
| Global | 0.752 ± 0.042 | 108 ± 16 | 0.55 ± 0.05 | 0.720 ± 0.033 | 120 ± 13 | 0.46 ± 0.04 |
| NH3 | 0.674 ± 0.070 | 138 ± 27 | 0.42 ± 0.08 | 0.532 ± 0.052 | 194 ± 20 | 0.34 ± 0.07 |
| En | 0.776 ± 0.091 | 99 ± 35 | 0.57 ± 0.08 | 0.768 ± 0.058 | 102 ± 23 | 0.36 ± 0.05 |
| Bpy | 0.829 ± 0.047 | 78 ± 18 | 0.27 ± 0.05 | 0.741 ± 0.033 | 112 ± 13 | 0.28 ± 0.03 |
| N3− | 0.786 ± 0.048 | 94 ± 19 | 0.27 ± 0.09 | 0.965 ± 0.048 | 25 ± 19 | 0.26 ± 0.05 |
Decomposing the library-spanning correlations into individualized correlations distinguished by N-donor ligand class improves the correlations between experimental and calculated pre-edge peak energies, with R2 ≥0.9 in all cases (Fig. 3b and d). This translates to slightly smaller values for |ΔE| relative to the global fits. Via this treatment, TDDFT and DFT/ROCIS give similarly improved agreements between experiment and theory. Overall, the ca. ±0.5 eV error in peak energy prediction by either method is similar to what we have reported previously in calibration studies of Cr valence-to-core (V2C) XES61 and Cu K-edge XAS,62 and thus likely reflects a limit imposed by systematic errors endemic to hybrid DFT calculations of orbital energetics. A study examining calculated Kohn–Sham (KS) orbitals and eigenvalues using a variety of density functionals found a linear dependence, for both occupied and virtual orbitals, between KS orbital energies and either Hartree–Fock energies or experimental ionization potentials.63 The absolute energy differences, dependent on the functional used, were attributed to the electron self-interaction error in the Hartree term of the wavefunction approximation. Energy deviations are minimized using hybrid functionals, such as B3LYP, compared to “pure” density functionals such as BP86. However, relative energy level spacing was found to be inconsistent for the hybrid functionals, explaining the observed ca. ±0.5 eV error in peak energy predictions seen for a variety of calculated XAS and XES spectra.
Nitrogen 2p covalency calibration: an experimental estimate of the 1s2p transition dipole integral
Prediction of N K-edge XAS peak energies via these DFT-based methods can facilitate identification of N-donor RNI. For example, the appearance of new peaks assigned to transitions into ligand localized MOs can diagnose ligand-localized redox.31 However, assigning proper physical oxidation states can also require quantification of metal–ligand covalency. To this end, we explored the ability of N K-edge XAS to quantify N 2p character in unfilled frontier MOs comprising, or proximal to, the ligand field. This approach has been well developed by Solomon and co-workers for Cl and S K-edge XAS.12,13 The absorptivities (D0) of ligand K pre-edge XAS features are governed by eqn (1):64| D0 (L1s → Ψ*) = α2hIs/3n | (1) |
To this end, we used [Cu(NH3)4](SO4)·H2O and [Cu(en)2](OTf)2·H2O as calibrants. To estimate N 2s and 2p character in the frontier SOMOs (the Ψ* involved in the pre-edge band) we employed a combination of Cu L2,3-edge XAS and hybrid DFT calculations. Solomon, Cramer and co-workers showed44 that Cu L2,3-edge XAS spectroscopy is a direct probe of MO Cu 3d character. Using D4h (nmph)2[CuCl4] (nmph = methyl(2-phenylethyl)ammonium) as a standard with a covalency value of 61% Cu dx2−y2 character in the SOMO, determined through evaluation of hyperfine coupling constants from EPR,44,68 comparison of integrated peak areas (Table 2) from the Cu L2,3-edge spectra (Fig. 4) led to a determination of 68 ± 2% and 70 ± 2% Cu 3d character in the SOMOs of [Cu(NH3)4](SO4)·H2O and [Cu(en)2](OTf)2·H2O, respectively. These values accord with respective hybrid DFT values: 64% and 68% Cu. The remaining orbital parentage in the SOMO was then attributed to the σ-donating sp3 hybridized orbital, for which N 2s character is estimated by DFT at 15%. Subtracting this 15% N 2s contribution from the remaining 32% and 30% Ψ* orbital nitrogen character results in N 2p contributions of 27.2 ± 1.4% and 25.5 ± 1.4% for [Cu(NH3)4](SO4)·H2O and [Cu(en)2](OTf)2·H2O, respectively.
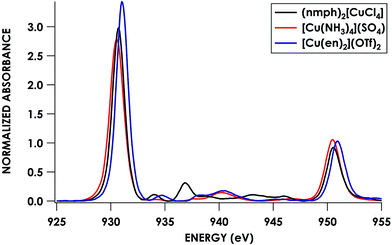 | ||
| Fig. 4 Cu L2,3-edge XAS spectra of CuII complexes: (nmph)2[CuCl4] (black), [Cu(NH3)4](SO4) (red), and [Cu(en)2](OTf)2 (blue). | ||
Returning to the N K-edge spectra, values of D0 corresponding to the first pre-edge features of these two compounds, 0.62 ± 0.05 and 0.50 ± 0.01 for [Cu(NH3)4](SO4)·H2O and [Cu(en)2](OTf)2·H2O, respectively, were obtained by least-squares fitting. Using the obtained values, an averaged value for Is of 25.4 ± 1.7 was obtained from eqn (1). This Is was used to obtain experimental N 2p percentages for the remaining compounds, defined henceforth as method A (Table 2). Alternatively, using solely hybrid DFT-calculated N 2p contributions (25.0% for both compounds), an Is of 26.8 ± 1.9 was obtained. This Is was used in method B.
As noted, S K-edge XAS has been extensively investigated and become routine for the use of extracting covalency parameters in a variety of S-containing coordination complexes. For S, Is was found to be heavily dependent on the charge of the S atom due to the variation of the S 1s/3p radial functions. Delocalization of electron density away from the S 3p orbital increases the effective nuclear charge on the S center, contracting the valence S 3p orbital, increasing the S 1s/3p overlap, and hence increasing the transition dipole integral. Upon metal complexation, electron donation from ligand to metal should further increase the value of the dipole integral. Solomon and co-workers have previously determined Is values for free S-containing ligands such as sulfide (Is = 6.54), thiolate (Is = 8.05),69 and dithiolene (Is = 9.15).12 For [Cu(MNT)]1− (MNT = maleonitriledithiolate), an Is of 14.1 was determined using the S K-edge XAS pre-edge intensity and the S character from 33S EPR. The authors were then able to formulate a linear correlation of the Is of S-containing ligands to the S K-edge 1s → 4p transition energy observed along the post-edge region.65 A further report by Wieghardt and co-workers studying an electron transfer series of rhenium tris(dithiolene) species revealed Is values ranging from 12.92 to 15.78 using the correlation developed by Solomon.67 However, they also established an alternative method of estimating covalency, determined through agreement between calculated and experimental S 3p character, by calibration of calculated dipole oscillator strengths to experimental peak intensities using a well-behaved standard. The discrepancy between the linear correlation method of Solomon and the TDDFT standard calibration method of Wieghardt was attributed to an error in the former method that fails to account for the differing degrees of overlap for transitions into σ and π orbitals that will alter the radial distortion and hence the value of Is. We however do not observe dramatic differences between either type of transition (σ vs. π). Moreover, we find that we can use one Is value to describe several different N ligand classes. This accords with the lower polarizability of the radially contracted 2p orbital of N compared to sulfur 3p, and we expect changes in the Is value to be less than the overall error of the analysis.
To our knowledge, this report details the first estimation of the Is for nitrogen containing ligands. The average Is value determined—25.4 ± 1.7 using [Cu(NH3)4](SO4)·H2O and [Cu(en)2](OTf)2·H2O as standards—is significantly larger than that for S-containing ligands. Considering the increased radial probability of an electron being closer to the nucleus in a 2p vs. 3p orbital, we expected the radial wave function overlap for N1s/2p to be significantly larger than that of S 1s/3p. Indeed, evaluating the radial overlap integrals of the form 〈R3,1|r|R1,0〉 or 〈R2,1|r|R1,0〉 (where Rn,l are the radial components of the hydrogen-like orbitals) as a function of the effective nuclear charge (Zeff), estimated using Slater's rules,70 of a valence 2p/3p electron, we see that the absolute value of the overlap is greater for N than S for all values of Zeff (Fig. S34†). A similar approach was taken by Neese and co-workers64 in examining the charge dependence of the transition dipole integral for S and Cl for varying 3pn (n = 0 to 6) configurations. They found that as the number of valence shell electrons increases, the dipole integral decreases due to a more diffuse 3p orbital, lowering the 1s/3p overlap. It was noted that the Zeff dependence on the dipole integral was minor. Evaluating the integral value for an effective 3p population from 5.22 to 5.69 only led to a 3% change for Cl and 5% for S.64 We encountered similarly small changes for N, with an 8% change in the magnitude of 〈R2,1|r|R1,0〉 over an effective 2p population from 5.2 to 5.7.
In the series of compounds studied and analyzed (Table 3), the acceptor orbitals participating in excitations giving rise to the lowest energy pre-edge feature span a range from ca. 9% N 2p to ca. 40% N 2p. These values were correlated to hybrid DFT-calculated % N 2p in acceptor orbitals identified via DFT/ROCIS. Nitrogen parentage values for acceptor orbitals used in TDDFT (UKS) and DFT/ROCIS (QRO) in general are found to be within 1–3% of each other for open-shell systems. For closed shell systems, the identity of unrestricted alpha and beta Kohn–Sham orbitals used for TDDFT results in equal parentage in quasi-restricted orbitals used for DFT/ROCIS. Excellent agreement (R2 = 0.92 ± 0.01) between experimental and calculated % N 2p was obtained using either method A or method B (Fig. 5). It should be noted that in order to obtain accurate covalency numbers according to eqn (1) using the standard Is values, it is helpful to use calculations to determine exactly how many acceptor orbitals are accessed. Calculated MO diagrams for all measured compounds are included in the ESI† to facilitate spectral analysis. For example, in simple cases such as [Cu(en)2](OTf)2·H2O and [Ni(NH3)6]Cl2, the pre-edge features at 399.4 and 398.6 eV, respectively, represent transitions into the metal-based σ* 3d dominated SOMOs that contain minor mixing with N 2p character; accordingly, h = 1 (Cu2+, d9) or h = 2 (Ni2+, d8) in these cases.
| Compounda | Total pre-edge area (D0) | #Absorbers (n) | #Holes (h) | Calc %N 2p (α2) | Experimental %N 2p (α2) method A | Experimental %N 2p (α2) method B |
|---|---|---|---|---|---|---|
| a Complete formulations including counterions given in the ESI. b Determined via Cu L2,3-edge XAS. c Determined via B3LYP/ZORA-def2-TZVP(-f) calculations. d Necessary to set n = 2 in order to account for absorption contributions from the nBu4N+ counterion. | ||||||
| [Co(NH3)5Cl]2+ | 1.21 ± 0.07 | 5 | 4 | 17 | 17.8 ± 1.6 | 16.9 ± 1.6 |
| [Ni(NH3)6]2+ | 0.29 ± 0.06 | 6 | 2 | 12 | 10.4 ± 2.3 | 9.9 ± 2.2 |
| [Cu(NH3)4]2+ | 0.62 ± 0.05 | 4 | 1 | 25 | 27.2 ± 2.8b | 25.0c |
| [Cu(en)2]2+ | 0.50 ± 0.01 | 4 | 1 | 25 | 25.5 ± 1.8b | 25.0c |
| [Zn(en)3]2+ | 0.17 ± 0.08 | 6 | 2 | 9 | 6.1 ± 2.9 | 5.8 ± 2.7 |
| [Mn(bpy)3]2+ | 1.89 ± 0.03 | 6 | 6 | 20 | 22.4 ± 1.5 | 21.2 ± 1.5 |
| [Fe(bpy)3]2+ | 1.87 ± 0.04 | 6 | 6 | 19 | 22.1 ± 1.6 | 20.9 ± 1.6 |
| [Co(bpy)3]2+ | 1.68 ± 0.05 | 6 | 6 | 21 | 19.8 ± 1.4 | 18.8 ± 1.4 |
| [Co(bpy)3]3+ | 2.01 ± 0.06 | 6 | 6 | 20 | 23.8 ± 1.7 | 22.5 ± 1.7 |
| [Ni(bpy)3]2+ | 2.47 ± 0.09 | 6 | 6 | 25 | 29.1 ± 2.2 | 27.6 ± 2.2 |
| [Zn(bpy)3]2+ | 2.0 ± 0.2 | 6 | 6 | 20 | 24.1 ± 2.5 | 22.8 ± 2.4 |
| [Ru(bpy)3]2+ | 1.82 ± 0.08 | 6 | 6 | 21 | 21.5 ± 1.7 | 20.4 ± 1.7 |
| [Rh(bpy)3]3+ | 2.00 ± 0.02 | 6 | 6 | 20 | 23.6 ± 1.6 | 22.3 ± 1.6 |
| [Os(bpy)3]2+ | 2.15 ± 0.09 | 6 | 6 | 20 | 25.4 ± 2.0 | 24.0 ± 2.0 |
| [ReNCl4]1– | 5.4 ± 0.2 | 2d | 4 | 30 | 32.1 ± 2.6 | 30.4 ± 2.5 |
| [OsNCl4]1– | 6.20 ± 0.06 | 2d | 4 | 34 | 36.6 ± 2.5 | 34.7 ± 2.5 |
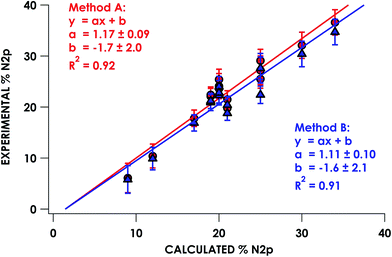 | ||
| Fig. 5 Correlation of experimentally derived N K-edge pre-edge acceptor orbital covalency with hybrid DFT-calculated N 2p character. | ||
The homoleptic metal bipyridine series of spectra are less intuitive. All species show a pronounced pre-edge feature whose energy ranges from 398.5 to 399.2 eV that arises due to excitations into three acceptor orbitals: LUMO, LUMO+1, LUMO+2. These are principally bpy π* MOs that all contain ca. 20% N 2p with the remaining electron density delocalized in the aryl rings. Transitions into the ligand field MOs, which calculations show comprise minor (ca. 10%) N 2p contributions, contribute only ca. 5% of the peak intensity and are thus obscured by the far more intense transitions involving bpy π* MOs. For the nitride series, there is an intense pre-edge feature around 398.3 eV common to all three species. For the Os and Re nitrides, there is a small side band feature to lower energy that DFT/ROCIS assigns to a transition into the π* M dxz/yz–N 2p LUMO and LUMO+1 that ranges from 30% N 2p ([ReNCl4]+) to 34% N 2p ([OsCl4]+). Of the 19 compounds studied, all but 3 were included in the N 2p covalency correlation. [Ni(en)3]Cl2, [Co(NH3)6]Cl3, and (nBu4N)[RuNCl4] were noted as significant outliers during covalency analysis, identified by a much lower experimental % N 2p covalency value than is predicted by TDDFT. Photodamage analysis (multiple scans on the same sample spot) (Fig. S7†) reveal a significant decrease in the intensity of the first pre-edge feature and these spectra were consequently removed from the covalency analyses. The susceptibility of compounds to damage by soft X-rays and the effect that this damage can have on spectral intensities underscores the importance of rigorous damage analysis during any experiment of this sort.
Application to inner-sphere nitrogen radicals: unmasking light-atom non-innocence
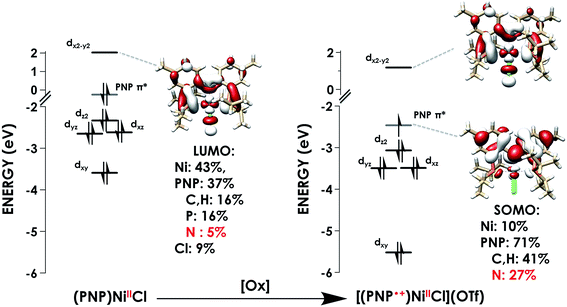
We subsequently applied the nitrogen covalency calibration developed herein to a system in which a Ni complex supported by a PNP pincer ligand is proposed, upon 1 e− oxidation, to maintain its NiII oxidation state while the ligand acts in a RNI fashion (Fig. 6). The preparation of the complexes used in this study, PNP = N[2-P(CHMe2)2-4-methylphenyl]2, (PNP)NiCl, and [(PNP)NiCl](OTf) have been reported previously.16 Through the use of EPR, UV-vis, XRD, and multi-edge XAS, it has been suggested that upon oxidation from (PNP)NiCl to [(PNP)NiCl](OTf), the electron hole that is formed resides primarily on the N contained within the PNP framework. This conclusion rested upon a few lines of indirect evidence: the observation of modest 14N superhyperfine coupling in the EPR and the lack of additional features in the Ni L3-edge and Cl K-edge XAS of (PNP)NiCl compared to [(PNP)NiCl](OTf). Only the P K-edge data displayed a minor new feature distinguishing (PNP)NiCl from [(PNP)NiCl](OTf), offering some evidence that the PNP ligand is oxidized in the latter compound. However, anisotropy in the g-values extracted from the EPR suggested some minor Ni 3d character in the singly-occupied MO of [(PNP)NiCl](OTf). | ||
| Fig. 6 HN[2 P(CHMe2)2-4-methylphenyl]2 pincer ligand (PNPH) and two oxidation states of (PNP)NiCl investigated using N K-edge XAS. | ||
Metal K-edge XAS has long been a standard method choice for determining whether or not a change in metal physical oxidation state (effectively, the d-electron count) attends a given redox event.71 For metal K-edge XAS, the weak pre-edge features observed are due to metal 1s to 3d transitions that are formally dipole forbidden but gain intensity through quadrupolar mixing with metal 4p and ligand p orbitals.71 Traditionally, the shift in the position of these metal 1s to 3d pre-edge features to higher energy upon complex oxidation has been attributed to an increase in effective nuclear charge at the metal center.72 Though, recently, that paradigm has been challenged. Metal K-edge XAS transitions involving ligand-localized acceptor orbitals as well as spectral shifts that arise from changes in coordination environment can complicate metal K-edge analysis.62,73–75
The Ni K-edge spectra (Fig. S33†) of (PNP)NiCl and [(PNP)NiCl](OTf) were thus first investigated to ascertain the metal oxidation state and hence inferred presence of a ligand radical. Only minor differences between the two spectra are observed. Both contain a weak pre-edge feature at 8332.1 eV assigned as the Ni 1s → Ni 3dx2−y2 LUMO transition. This feature falls within the range of ca. 8332 to 8333 eV generally observed for Ni 1s → 3d transitions seen in a variety of NiII as well as NiIII species.76–78 Higher energy features are observed at 8334.5 and 8335.8 eV for (PNP)NiCl and at 8334.7 and 8335.9 eV for [(PNP)NiCl](OTf). These can be assigned as Ni 1s → 4p and LMCT shakedown transitions.77 The near identical position of the pre-edge features seen in (PNP)NiCl and [(PNP)NiCl](OTf) suggests that upon 1 e− oxidation, the NiII center is likely maintained and the redox event can be tentatively assigned to the ligand backbone. This provides further support for the conclusions obtained by Mindiola and Szilagyi in 2008 when using the Ni L2,3-edge to probe electronic structure of these Ni PNP species following ligand-centered oxidation.16 The covalent nature of highly oxidized late, first-row transition metal complexes as well as the complicating factors stated above in assigning metal oxidation states solely on pre-edge shifts does not discredit some involvement of Ni 3d participation in the redox event, however. In contrast to metal K-edge XAS, N K-edge XAS contains pre-edge features observed due to dipole allowed transitions from N 1s → 2p orbitals where the peak intensity is directly correlated to the degree of N 2p character in the antibonding wavefunction.12 As detailed previously, this allows for the extraction of metal–ligand orbital covalency values from the integration of pre-edge peaks that can thus be used to assign primary parentage to the redox event and hence directly identify RNI.
Direct evidence of an N-localized radical is furnished by analysis of the N K-edge XAS spectra obtained for PNPH, (PNP)NiCl, and [(PNP)NiCl](OTf), which are shown in Fig. 7a. All three spectra exhibit similar high energy features at 401.0 and 401.5 eV (PNPH), 399.9 and 400.8 eV ((PNP)NiCl), and 399.9 and 401.0 eV ([(PNP)NiCl](OTf)) assignable to antibonding molecular orbitals (MOs) comprising N and aryl character. The spectra of metal complex (PNP)NiCl exhibits an additional absorption near 398.2 eV most plausibly assigned as N 1s → Ψ*, where Ψ* is the Ni 3d-based anti-bonding σ* lowest unoccupied molecular orbital (LUMO) which will comprise some N 2s/2p contribution. An analogous feature is present in the spectrum of [(PNP)NiCl](OTf) now at 398.6 eV, shifted to higher energy by 0.4 eV from that of (PNP)NiCl. We assign this feature to the analogous Ni 3dx2−y2-based MO. The N K-edge XAS of [(PNP)NiCl](OTf) most notably exhibits an additional intense absorption at 397.0 eV—the appearance of such a feature necessitates an additional N 2p-based vacancy. Given prior characterization, this feature plausibly corresponds to a transition from N 1s to the N-centered SOMO on the inner-sphere aminyl ligand. Additionally, our group has previously observed features to similar energy around 395 eV in a series of dipyrrin ligated iron imido/iminyl complexes corresponding to transitions into iminyl based nitrogen radicals.31
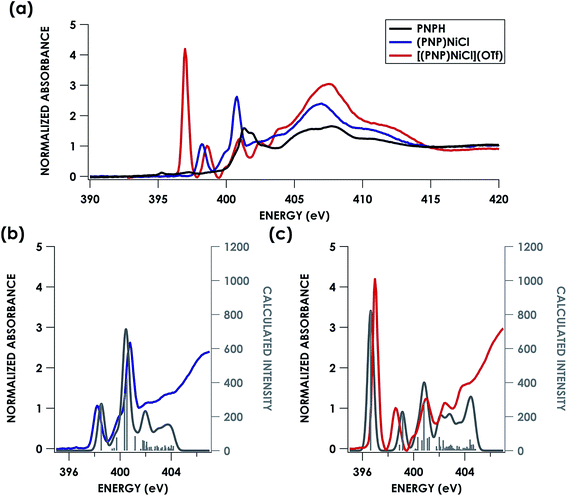 | ||
| Fig. 7 (a) Experimental N K-edge XAS of PNPH, (PNP)NiCl, and [(PNP)NiCl](OTf). Overlay of experimental (b) (PNP)NiCl (blue) and (c) [(PNP)NiCl](OTf) (red) with TDDFT calculated (grey) N K-edge XAS spectra with energies shifted according to individualized correlation plots seen in Fig. S26† with underlying orbital transitions plotted as sticks in grey. | ||
Turning next to spectral predictions in order to corroborate our assignment and gain further insights, the B3LYP TDDFT calculated spectra of (PNP)NiCl and [(PNP)NiCl](OTf) are also shown in Fig. 7b and c. TDDFT and DFT/ROCIS calculated spectra were first adjusted according to the global correlation seen in Fig. 3, giving |ΔE| = 0.57 eV for TDDFT and |ΔE| = 0.82 eV for DFT/ROCIS (full adjusted spectra seen in Fig. S26†). Shifting the calculated spectra according to only the homologous PNP donor class series correlation, a marginally better agreement is observed, with R2 = 0.85 and 0.72 and |ΔE| = 0.53 eV and 0.74 eV for TDDFT and DFT/ROCIS, respectively (Fig. S27†). In order to produce the most accurate energy adjustment for the calculated spectra to overlay with the experimental, it was necessary to create individualized energy correlation plots for each compound (PNPH, (PNP)NiCl, and [(PNP)NiCl](OTf)) (Fig. S28 and S29†). Further decomposing the PNP donor class into individual correlations separated by oxidation state of the ligand resulted in excellent agreement between experiment and theory with R2 = 0.99, 0.95, and 0.97 and |ΔE| = 0.01, 0.3, and 0.3 eV for PNPH, (PNP)NiCl, and [(PNP)NiCl](OTf), respectively, (TDDFT) and R2 = 0.99, 0.92, and 0.95 and |ΔE| = 0.02, 0.4, and 0.4 eV (DFT/ROCIS). As the TDDFT calculated spectra showed slightly better agreement, these spectra were chosen for the final comparison.
The first calculated pre-edge feature in (PNP)NiCl is predicted at 398.5 eV and is predicted to be a N 1s → Ni 3dx2−y2 LUMO transition in accord with our assignment. The LUMO for (PNP)NiCl comprises 43% Ni, 37% PNP (5% N), and 9% Cl character in good agreement with prior work which found 43% Ni, 44% PNP (8% N), and 13% Cl character in the LUMO.16 Higher-energy features at 399.7 and 400.4 eV are predicted as transitions into delocalized PNP π orbitals with negligible Ni and Cl participation, comparable to those seen in the calculated spectrum of the free ligand, PNPH (Fig. S30†). These assignments apply to the ca. 400 and 401 eV features observed in the experimental spectra of all three species.
The calculated LUMO in [(PNP)NiCl](OTf) comprises 42% Ni, 36% PNP (4% N), and 10% Cl character, comparable to that of (PNP)NiCl. However, the transition into the LUMO is now slightly overestimated by 0.5 eV at 399.1 eV, falling within, but representing the high end of the range of |ΔE| expected for XAS peak predictions. A new lower-energy transition at 396.6 eV, predicted as a transition from N 1s into the singularly unoccupied molecular orbital (SOMO), is observed. The SOMO acceptor orbital contains 10% Ni 3d and 71% PNP character, with 27% of the electron density localized on the nitrogen. In accord with the calculated spectra, the feature observed at 397.0 eV in the experimental spectrum of [(PNP)NiCl](OTf) can be assigned as the N 1s → aminyl radical-based SOMO transition. The majority of the electron density of the SOMO is delocalized on the π system of the PNP ligand. This indicates that upon oxidation from (PNP)NiCl to [(PNP)NiCl](OTf), the locus of oxidation has primarily occurred on the PNP ligand with the metal center maintaining a NiII oxidation state (Fig. 8). Furthermore, quantification of the nitrogen covalency using the method determined previously reveals 27 ± 2% N 2p (method A) and 25 ± 2% N 2p (method B) character of the SOMO of [(PNP)NiCl](OTf) as well as 4 ± 1% N 2p (method A and B) character present in the Ni dx2−y2 LUMO for (PNP)NiCl and [(PNP)NiCl](OTf). These values accord well with those calculated by TDDFT.
Conclusions
All told, this study affords a N K-edge XAS spectral library and example calibrations of band energy predictions using TDDFT and DFT/ROCIS. We note that the type of N-donor ligand may impede resolution of transitions into the d-orbital manifold in cases where N character is delocalized across the ligand π* orbital manifold, as in the case of bpy. Consequently, calibrated electronic structure calculations are valuable in making assignments. Finally, we were able to obtain reasonably precise, experimentally-grounded values of Is for estimation of % N 2p in acceptor orbitals localized to four commonly employed yet diverse classes of N-donor ligands. We present this correlation as a method for estimation of Is in other species, taking into consideration that the EPR-derived covalencies used as the basis calibration of the method derive from relativistic Hartree–Fock calculations of atomic parameters79 that are in turn used to relate superhyperfine coupling to % L np contributions. The general applicability of this value was demonstrated by quantifying N 2p character in an inner-sphere aminyl donor. This study should encourage use of N K-edge XAS as an additional means to determine physical oxidation states in transition metal complexes and to readily identify reactivity-defining N-radical ligands. The accessibility of this approach should accelerate accumulation of data that will furnish understanding within the chemical sciences concerning how RNI, ligand field inversion, and other formalism-defying electronic structures may impart unique reactivity.Conflicts of interest
There are no conflicts to declare.Author contributions
The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.Acknowledgements
We thank Prof. Jesper Bendix and Dr Theis Brock-Nannestad (U. Copenhagen) for samples of the nitride complexes. We thank Prof. Nandini Ananth (Cornell) for providing analytical expressions for radial overlap integrals. We thank Prof. Robert Szilagyi for helpful discussions. We thank Dr Richard Walroth (NASA-Ames) for development of the X-ray data fitting procedure used in this work. We acknowledge Dennis Nordlund (Stanford Synchrotron Radiation Lightsource, SSRL) for invaluable assistance with soft X-ray spectroscopy. K. M. L. acknowledges NSF (CHE-1454455), ACS PRF (55181-DNI6) and the A. P. Sloan Foundation for support. D. J. M. thanks the Chemical Sciences, Geosciences, and Biosciences Division, Office of Basic Energy Sciences, Office of Science, U.S. Department of Energy (DEFG02-07ER15893). T. K. thanks the JSPS for a postdoctoral fellowship. XAS data were obtained at SSRL, which is supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences under Contract No. DE-AC02-76SF00515. The SSRL Structural Molecular Biology Program is supported by the Department of Energy's Office of Biological and Environmental Research, and by NIH/HIGMS (including P41GM103393).References
- M. L. Green and G. Parkin, J. Chem. Educ., 2014, 91, 807–816 CrossRef CAS.
- G. Parkin, J. Chem. Educ., 2006, 83, 791 CrossRef CAS.
- M. Green, J. Organomet. Chem., 1995, 500, 127–148 CrossRef CAS.
- P. T. Wolczanski, Organometallics, 2017, 36, 622–631 CrossRef CAS.
- P. Chaudhuri, C. N. Verani, E. Bill, E. Bothe, T. Weyhermüller and K. Wieghardt, J. Am. Chem. Soc., 2001, 123, 2213–2223 CrossRef CAS PubMed.
- C. K. Jørgensen, Coord. Chem. Rev., 1966, 1, 164–178 CrossRef.
- J. Enemark and R. Feltham, Coord. Chem. Rev., 1974, 13, 339–406 CrossRef CAS.
- S. Sproules and K. Wieghardt, Coord. Chem. Rev., 2011, 255, 837–860 CrossRef CAS.
- R. Hoffmann, S. Alvarez, C. Mealli, A. s. Falceto, T. J. Cahill III, T. Zeng and G. Manca, Chem. Rev., 2016, 116, 8173–8192 CrossRef CAS PubMed.
- R. C. Walroth, J. T. Lukens, S. N. MacMillan, K. D. Finkelstein and K. M. Lancaster, J. Am. Chem. Soc., 2016, 138, 1922–1931 CrossRef CAS PubMed.
- S. N. MacMillan and K. M. Lancaster, ACS Catal., 2017, 7, 1776–1791 CrossRef CAS.
- E. I. Solomon, B. Hedman, K. O. Hodgson, A. Dey and R. K. Szilagyi, Coord. Chem. Rev., 2005, 249, 97–129 CrossRef CAS.
- T. Glaser, B. Hedman, K. O. Hodgson and E. I. Solomon, Acc. Chem. Res., 2000, 33, 859–868 CrossRef CAS PubMed.
- A. V. Blake, H. Wei, C. M. Donahue, K. Lee, J. M. Keith and S. R. Daly, J. Synchrotron Radiat., 2018, 25, 529–536 CrossRef CAS PubMed.
- K. Lee, H. Wei, A. V. Blake, C. M. Donahue, J. M. Keith and S. R. Daly, Dalton Trans., 2016, 45, 9774–9785 RSC.
- D. Adhikari, S. Mossin, F. Basuli, J. C. Huffman, R. K. Szilagyi, K. Meyer and D. J. Mindiola, J. Am. Chem. Soc., 2008, 130, 3676–3682 CrossRef CAS PubMed.
- C. M. Donahue and S. R. Daly, Comments Inorg. Chem., 2018, 38, 54–78 CrossRef CAS.
- S. DeBeer George and F. Neese, Inorg. Chem., 2010, 49, 1849–1853 CrossRef CAS PubMed.
- S. D. George, T. Petrenko and F. Neese, Inorg. Chim. Acta, 2008, 361, 965–972 CrossRef.
- M. Roemelt, D. Maganas, S. DeBeer and F. Neese, J. Chem. Phys., 2013, 138, 204101 CrossRef PubMed.
- M. Roemelt and F. Neese, J. Phys. Chem. A, 2013, 117, 3069–3083 CrossRef CAS PubMed.
- L. J. Giles, A. Grigoropoulos and R. K. Szilagyi, J. Phys. Chem. A, 2012, 116, 12280–12298 CrossRef CAS PubMed.
- J. Shearer, P. E. Callan, C. s. A. Masitas and C. A. Grapperhaus, Inorg. Chem., 2012, 51, 6032–6045 CrossRef CAS PubMed.
- S. G. Minasian, J. M. Keith, E. R. Batista, K. S. Boland, J. A. Bradley, S. R. Daly, S. A. Kozimor, W. W. Lukens, R. L. Martin and D. Nordlund, J. Am. Chem. Soc., 2013, 135, 1864–1871 CrossRef CAS PubMed.
- Y. Kihn, C. Mirguet and L. Calmes, J. Electron Spectrosc. Relat. Phenom., 2005, 143, 117–127 CrossRef CAS.
- A. Paxton, M. Van Schilfgaarde, M. MacKenzie and M. Craven, J. Phys.: Condens. Matter, 2000, 12, 729 CrossRef CAS.
- T. Yoshida, M. Yamamoto, M. Akatsuka, A. Ozawa, Y. Kato, S. Yagi and T. Tanabe, Surf. Interface Anal., 2018, 51, 46–50 CrossRef.
- M. Krbal, A. Kolobov, P. Fons, K. Mitrofanov, Y. Tamenori, B. Hyot, B. Andre and J. Tominaga, J. Alloys Compd., 2017, 704, 254–259 CrossRef CAS.
- C. J. Titus, M. L. Baker, S. J. Lee, H.-M. Cho, W. B. Doriese, J. W. Fowler, K. Gaffney, J. D. Gard, G. C. Hilton and C. Kenney, J. Chem. Phys., 2017, 147, 214201 CrossRef PubMed.
- A. R. Corcos, O. Villanueva, R. C. Walroth, S. K. Sharma, J. Bacsa, K. M. Lancaster, C. E. MacBeth and J. F. Berry, J. Am. Chem. Soc., 2016, 138, 1796–1799 CrossRef CAS PubMed.
- M. J. Wilding, D. A. Iovan, A. T. Wrobel, J. T. Lukens, S. N. MacMillan, K. M. Lancaster and T. A. Betley, J. Am. Chem. Soc., 2017, 139, 14757–14766 CrossRef CAS PubMed.
- P. Maire, M. Königsmann, A. Sreekanth, J. Harmer, A. Schweiger and H. Grützmacher, J. Am. Chem. Soc., 2006, 128, 6578–6580 CrossRef CAS PubMed.
- F. Mazzi, Acta Crystallogr., 1955, 8, 137–141 CrossRef CAS.
- R. Eßmann, G. Kreiner, A. Niemann, D. Rechenbach, A. Schmieding, T. Sichla, U. Zachwieja and H. Jacobs, Z. Anorg. Allg. Chem., 1996, 622, 1161–1166 CrossRef.
- Y. Inada, K. Ozutsumi, S. Funahashi, S. Soyama, T. Kawashima and M. Tanaka, Inorg. Chem., 1993, 32, 3010–3014 CrossRef CAS.
- S. P. Roe, J. O. Hill and R. J. Magee, Monatsh. Chem., 1991, 122, 467–478 CrossRef CAS.
- C. Muralikrishna, C. Mahadevan, S. Sastry, M. Seshasayee and S. Subramanian, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1983, 39, 1630–1632 CrossRef.
- E. M. Kober and T. J. Meyer, Inorg. Chem., 1982, 21, 3967–3977 CrossRef CAS.
- E. C. Constable, in Adv. Inorg. Chem., ed. A. G. Sykes, Academic Press, 1989, vol. 34, pp. 1–63 Search PubMed.
- A. Hauser, M. Maeder, W. T. Robinson, R. Murugesan and J. Ferguson, Inorg. Chem., 1987, 26, 1331–1338 CrossRef CAS.
- W. P. Griffith and D. Pawson, Dalton Trans., 1973, 1315–1320 RSC.
- U. Abram, M. Braun, S. Abram, R. Kirmse and A. Voigt, J. Chem. Soc., Dalton Trans., 1998, 231–238 RSC.
- V. A. Solé, E. Papillon, M. Cotte, P. Walter and J. Susini, Spectrochim. Acta, Part B, 2007, 62, 63–68 CrossRef.
- S. J. George, M. D. Lowery, E. I. Solomon and S. P. Cramer, J. Am. Chem. Soc., 1993, 115, 2968–2969 CrossRef CAS.
- M. Morháč and V. Matoušek, Appl. Spectrosc., 2008, 62, 91–106 CrossRef PubMed.
- R. C. Walroth, K. C. Miles, J. T. Lukens, S. N. MacMillan, S. S. Stahl and K. M. Lancaster, J. Am. Chem. Soc., 2017, 139, 13507–13517 CrossRef CAS PubMed.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS.
- F. J. Devlin, J. W. Finley, P. J. Stephens and M. J. Frisch, J. Phys. Chem., 1995, 99, 16883–16902 CrossRef CAS.
- E. K. U. Gross and W. Kohn, in Adv. Quantum Chem., ed. P.-O. Löwdin, Academic Press, 1990, vol. 21, pp. 255–291 Search PubMed.
- F. Neese, F. Wennmohs, A. Hansen and U. Becker, Chem. Phys., 2009, 356, 98–109 CrossRef CAS.
- F. Neese, Inorg. Chim. Acta, 2002, 337, 181–192 CrossRef.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- E. v. Lenthe, A. v. d. Avoird and P. E. S. Wormer, J. Chem. Phys., 1998, 108, 4783–4796 CrossRef.
- C. v. Wüllen, J. Chem. Phys., 1998, 109, 392–399 CrossRef.
- V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 102, 1995–2001 CrossRef CAS.
- D. A. Pantazis, X.-Y. Chen, C. R. Landis and F. Neese, J. Chem. Theory Comput., 2008, 4, 908–919 CrossRef CAS PubMed.
- P. Stephens, F. Devlin, C. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1992, 96, 2155–2160 CrossRef CAS.
- E. van Lenthe, A. van der Avoird and P. E. Wormer, J. Chem. Phys., 1998, 108, 4783–4796 CrossRef CAS.
- P. J. Lestrange, P. D. Nguyen and X. Li, J. Chem. Theory Comput., 2015, 11, 2994–2999 CrossRef CAS PubMed.
- S. N. MacMillan, R. C. Walroth, D. M. Perry, T. J. Morsing and K. M. Lancaster, Inorg. Chem., 2014, 54, 205–214 CrossRef PubMed.
- R. C. Walroth, J. W. Uebler and K. M. Lancaster, Chem. Commun., 2015, 51, 9864–9867 RSC.
- R. Stowasser and R. Hoffmann, J. Am. Chem. Soc., 1999, 121, 3414–3420 CrossRef CAS.
- F. Neese, B. Hedman, K. O. Hodgson and E. I. Solomon, Inorg. Chem., 1999, 38, 4854–4860 CrossRef CAS PubMed.
- R. Sarangi, S. DeBeer George, D. J. Rudd, R. K. Szilagyi, X. Ribas, C. Rovira, M. Almeida, K. O. Hodgson, B. Hedman and E. I. Solomon, J. Am. Chem. Soc., 2007, 129, 2316–2326 CrossRef CAS PubMed.
- S. E. Shadle, B. Hedman, K. O. Hodgson and E. I. Solomon, J. Am. Chem. Soc., 1995, 117, 2259–2272 CrossRef CAS.
- S. Sproules, T. Weyhermüller, R. Goddard and K. Wieghardt, Inorg. Chem., 2011, 50, 12623–12631 CrossRef CAS PubMed.
- A. A. Gewirth, S. L. Cohen, H. J. Schugar and E. I. Solomon, Inorg. Chem., 1987, 26, 1133–1146 CrossRef CAS.
- K. Rose, S. E. Shadle, T. Glaser, S. de Vries, A. Cherepanov, G. W. Canters, B. Hedman, K. O. Hodgson and E. I. Solomon, J. Am. Chem. Soc., 1999, 121, 2353–2363 CrossRef CAS.
- J. C. Slater, Phys. Rev., 1930, 36, 57 CrossRef CAS.
- P. Glatzel and U. Bergmann, Coord. Chem. Rev., 2005, 249, 65–95 CrossRef CAS.
- F. de Groot, Chem. Rev., 2001, 101, 1779–1808 CrossRef CAS PubMed.
- R. C. Walroth, J. T. Lukens, S. N. MacMillan, K. D. Finkelstein and K. M. Lancaster, J. Am. Chem. Soc., 2016, 138, 1922–1931 CrossRef CAS PubMed.
- N. C. Tomson, K. D. Williams, X. Dai, S. Sproules, S. DeBeer, T. H. Warren and K. Wieghardt, Chem. Sci., 2015, 6, 2474–2487 RSC.
- L. S. Kau, D. J. Spira-Solomon, J. E. Penner-Hahn, K. O. Hodgson and E. I. Solomon, J. Am. Chem. Soc., 1987, 109, 6433–6442 CrossRef CAS.
- N. D. Addison, H. Weiying, B. Shirin, C. Weiling, A. L. Jennifer and K. Pierre, Probing the Dichotomy of Square Planar d1 Complexes: Geometric and Electronic Structure of Nickel π-Complexes, 2018 Search PubMed.
- G. J. Colpas, M. J. Maroney, C. Bagyinka, M. Kumar, W. S. Willis, S. L. Suib, P. K. Mascharak and N. Baidya, Inorg. Chem., 1991, 30, 920–928 CrossRef CAS.
- R. Sarangi, M. Dey and S. W. Ragsdale, Biochemistry, 2009, 48, 3146–3156 CrossRef CAS PubMed.
- J. Morton and K. F. Preston, J. Magn. Reson., 1978, 30, 577–582 CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Orca input files and coordinates, fits to Cu L2,3-edge and N K-edge XAS spectra, experimental/calculated N K-edge XAS overlays and MO diagrams, experimental Ni K-edge XAS spectra, and radial overlap integral analysis. The following files are available free of charge. See DOI: 10.1039/c8sc03350a |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2019 |