Open Access Article
Open Access ArticleRevised values for the X23 benchmark set of molecular crystals†
Grygoriy A.
Dolgonos‡
 ,
Johannes
Hoja
,
Johannes
Hoja
 * and
A. Daniel
Boese
* and
A. Daniel
Boese
 *
*
Institute of Chemistry, University of Graz, Heinrichstraße 28/IV, 8010 Graz, Austria. E-mail: Adrian_Daniel.Boese@uni-graz.at; johannes.hoja@uni-graz.at
First published on 15th October 2019
Abstract
We present revised reference values for cell volumes and lattice energies for the widely used X23 benchmark set of molecular crystals by including the effect of thermal expansion. For this purpose, thermally-expanded structures were calculated via the quasi-harmonic approximation utilizing three dispersion-inclusive density-functional approximations. Experimental unit-cell volumes were back-corrected for thermal and zero-point energy effects, allowing now a direct comparison with lattice relaxations based on electronic energies. For the derivation of reference lattice energies, we utilized harmonic vibrational contributions averaged over four density-functional approximations. In addition, the new reference values also take the change in electronic and vibrational energy due to thermal expansion into account. This is accomplished by either utilizing experimentally determined cell volumes and heat capacities, or by relying on the quasi-harmonic approximation. The new X23b reference values obtained this way will enable a more accurate benchmark for the performance of computational methods for molecular crystals.
Introduction
Computational and theoretical chemistry has come a long way: whereas physics already became more and more of theoretical nature with the advent of quantum mechanics at the beginning of the last century, chemistry has undergone an increased transformation towards theory only within the last twenty to thirty years. The methods regularly used1,2 are classical ab initio methods, starting from a Hartree–Fock reference function, density functional theory (DFT), or semi-empirical methods which serve as an approximation to either one of the two families of methods.Post-Hartree–Fock methods are nowadays able to predict properties of molecular systems up to virtually any desired accuracy by systematically improving the correlation treatment together with the wave function representation. Unfortunately, the computational time required by these methods scales conventionally with n to the power of five or higher – with n being the number of electrons. However, there are many recent efforts to make methods such as coupled cluster with single, double, and perturbative triple excitations [CCSD(T)] inherently linear scaling.3–9 Still, important features such as analytical gradients for geometry optimizations are not yet available for these linear scaling methods. This implies that, even with computers getting much faster, we cannot calculate the properties of much larger systems.
For DFT methods, it is much easier to achieve inherent near-linear scaling.10–16 However, at this point there is a consensus that for DFT, while formally exact, an exact universal functional will not be available. This implies that the possibility for systematically improving DFT is missing, and convergence towards the highest accuracy can never be achieved. Finally, semi-empirical17,18 and density-functional tight-binding19 methods, which are even faster than DFT, are parameter dependent, have a smaller range of applicability, and are usually less accurate.
The situation is further complicated by the fact that for “periodic lattice problems”, post-Hartree–Fock methods are still under development20–23 and the computation with the so-called “gold standard” of quantum chemistry, CCSD(T), is not possible. Thus, until today, only DFT is commonly applied to predict solid-state properties of periodic systems such as molecular crystals. This directly implies that there is a lack of highly accurate reference values for periodic systems. Thus, for now such data has to be taken from experiment rather than computed with higher-level methods, introducing numerous deviations which can be found when comparing an experiment at finite temperature to an idealised model system within a computational model.
One of the main applications of the computational modelling of molecular crystals is organic crystal structure prediction. Therein, the goal is to predict the crystal-packing arrangement occurring in crystallization experiments solely based on the structural formula of the involved chemical unit. This is primarily achieved by calculating a thermodynamic stability ranking of a vast number of different possible structures. Many molecular crystals can crystallise in more than one crystal-packing arrangement or polymorph and their stabilities typically differ by only very few kJ mol−1.24 Therefore, very accurate relative polymorph stabilities would be needed in order to confidently describe polymorphic systems. The success of crystal-structure-prediction methods in predicting the correct polymorph structure of a molecular crystal among the thermodynamically most-stable structures was evaluated in several blind tests organized by the Cambridge Crystallographic Data Centre.25–30 However, these blind tests do not provide a direct benchmark for the accuracy of lattice energies.
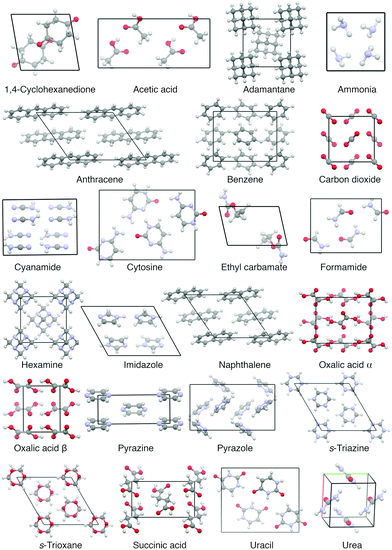
Currently, the most used benchmark set for lattice energies, which compiles a diverse set of experimentally well determined molecular crystals, is the so-called X23 dataset of Reilly and Tkatchenko.31 It extended upon the C21 set of Otero-de-la-Roza and Johnson32 and contains 23 rather small molecular crystals with rather rigid molecules (see Fig. 1). Therein, the reference values are experimentally measured sublimation enthalpies, which have been back-corrected for vibrational contributions—allowing a direct benchmark of static lattice energies. The vibrational contributions in ref. 31 were obtained by using the harmonic approximation, which allows a computationally affordable determination of vibrational (free) energies using electronic structure methods but ignores all anharmonic effects.
However, the unit cell of molecular crystals expands with increasing temperature and several properties are highly volume dependent.33 Vibrational contributions in the harmonic approximation are calculated at the minimum of the electronic energies. Hence, the used structures do not include any temperature effects, not even volumetric changes due to zero-point motion at a temperature of 0 K. The thermal expansion of a periodic system can be estimated via the so-called quasi-harmonic approximation (QHA), which has been recently used by several groups to study molecular crystals (including the original C21 publication).32–44
As new methods and density functionals are often developed by especially comparing to the X23 set of molecular crystals, improved reference values are direly needed going beyond the harmonic approximation for both lattice energies as well as cell volumes, even if they have been determined at low temperatures. In this contribution, we will address the effect of thermal expansion by utilizing dispersion-inclusive density functional theory.
First, we present new reference values for unit-cell volumes, which have been back-corrected for thermal expansion and zero-point vibrational effects in order to allow a direct benchmark of optimized structures at the minimum of the electronic energy. Second, we also present new reference values for lattice energies with harmonic vibrational contributions averaged over several density functional approximations, which minimizes the bias towards a certain density functional. Furthermore, we also discuss the effect of expansion on the lattice energies.
Computational methods
Calculation of crystal structures
All calculations were performed using the Vienna Ab Initio Simulation Package55–58 (VASP, version 5.4.1) in a similar manner as reported in our earlier publications.59,60 In all cases, the hard projector augmented-wave pseudopotentials61,62 were used along an energy cut-off of 1000 eV. The convergence criteria for the periodic structure relaxation correspond to 10−5 eV for the energy and to 5 × 10−3 eV Å−1 for the gradient. All optimizations were carried out using the so-called “standard” k-point grid defined in ref. 60. These fully relaxed structures are referred to as Vel, indicating that the unit-cell volume corresponds to the minimum of the electronic energy.
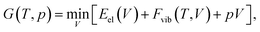 | (1) |
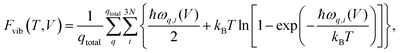 | (2) |
One way of obtaining the volume corresponding to a certain temperature is the usage of a Murnaghan equation-of-state (EOS) fit,63 as discussed in ref. 33. This requires the calculation of at least four vibrational free energies for different unit-cell volumes.
However, at zero temperature and by neglecting zero-point-energy effects, G(T,p) can easily be minimised by applying an external hydrostatic pressure during the cell relaxation. Throughout, we are investigating molecular crystals at ambient pressure. This makes the effect of the pV term on the unit-cell volumes negligible. Relaxations under an external pressure can be utilised to efficiently mimic thermal (vibrational) effects.32 The so-called thermal pressure pth related to the effect of Fvib at a temperature T can be calculated according to
 | (3) |
| Vrefel = Vexpl − ΔVQHAl, | (4) |
All periodic harmonic vibrational free energies were calculated via the finite displacement approach utilizing Phonopy.66 These calculations were performed by using supercells with minimal lengths larger than 12 Å, finite displacements of 0.01 Å, and a 1 × 1 × 1 k-grid. In contrast to geometry optimizations, these energy calculations were converged to 10−8 eV; all other VASP settings remain the same. The vibrational free energies were then evaluated within Phonopy using a 8 × 8 × 8 q-point mesh. At the Γ-point, no actual imaginary modes were present and the magnitude of the three acoustic modes was always smaller than 3 cm−1, and for every system except acetic acid even smaller than 1 cm−1. For all optimizations under an external hydrostatic pressure (−pth), gradients were converged to 2.5 × 10−3 eV Å−1.
For PBE+D3 we have also explored the role of different numerical differentiation procedures (see Table S2, ESI†) and super cell sizes (see Table S3, ESI†) on the obtained thermal pressure values. The resulting thermal pressure differences are not significant—leading in the worst case to a modification of the cell volume by only 0.5% compared to our standard approach. In addition, we have also calculated the unit cells corresponding to a temperature of 0 K with PBE+D3 by taking into account zero-point vibrational energies.
Since we want to discuss sublimation enthalpies at mostly room temperature later on, we have also calculated with PBE+D3 high-temperature unit cells via the QHA with volumes VQHAh corresponding to a temperature of 298 K in most cases. For the systems for which a solid phase at 298 K at ambient pressure does not exist, the temperature of the corresponding melting point/triple point67–70 was used (see Table S1, ESI†); in the case of carbon dioxide, the used temperature corresponds to the sublimation enthalpy measurement71 at the highest available temperature (207 K), since no local minimum can be found at larger thermal pressures.
| Vexph = Vexpl + VQHAh − VQHAl. | (5) |
Calculation of sublimation enthalpies
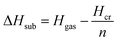 | (6) |
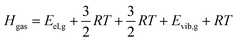 | (7) |
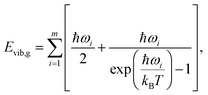 | (8) |
The enthalpy of the crystal Hcr consists of three terms: the electronic energy Eel,cr, the vibrational internal energy Evib,cr and a pV term:
| Hcr = Eel,cr + Evib,cr + pV | (9) |
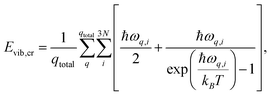 | (10) |
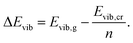 | (11) |
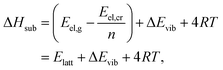 | (12) |
We have calculated the sublimation enthalpies of all X23 systems with PBE+D3, BLYP+D3, and RPBE+D3 at temperatures Tcalch (mostly 298 K, see Table S1, ESI†) using the respective fully optimized structures (at Vel). The periodic vibrational internal energies were calculated using Phonopy as described above. All molecular DFT calculations were performed in an empty periodic box of 17 Å in each dimension using VASP. The gas phase molecular structure was in most cases obtained by optimizing the molecular structure of the crystalline phase. However, in the case of oxalic acid we used a conformation with an intramolecular hydrogen bond, since this is significantly more stable than any conformation without a hydrogen bond. For succinic acid, we used a gauche conformer corresponding to conformer I in ref. 72. The molecular vibrational modes were calculated directly using VASP.
Based on the harmonic vibrational energies obtained this way, we have derived new reference values for lattice energies (Eref,HAlatt) according to
| Eref,HAlatt = ΔHexpsub − (ΔEavgvib + 4RT), | (13) |
For systems with Tcalch = 298 K, we used the ΔHexpsub values listed in ref. 31 except for naphthalene74 and cytosine.75 For the five systems where Tcalch < 298 K, the ΔHexpsub values were obtained as follows: for ammonia, carbon dioxide, and formamide we used the experimental value closest to Tcalch listed in ref. 76; for benzene we used the average of experimental values in ref. 76 within 5 K of Tcalch; for acetic acid we extrapolated both values listed in ref. 76 to 290 K viaeqn (3) therein using the experimentally determined heat capacity from ref. 77. Adamantane shows at 208 K a phase transition from the here considered tetragonal polymorph to a cubic polymorph, which is accounted for by adding the enthalpy of the phase transformation (3.2 kJ mol−1) to ΔHexpsub.78
| Eref,QHAlatt = Eref,HAlatt − ΔΔEQHAlatt − ΔΔEQHAvib = Eref,HAlatt − ΔΔEQHAsub. | (14) |
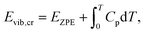 | (15) |
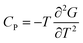 | (16) |
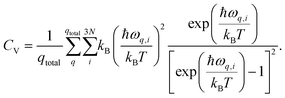 | (17) |
The resulting reference energies Eref,explatt were then obtained via
| Eref,explatt = Eref,HAlatt − ΔΔEexplatt − ΔΔEexpvib = Eref,HAlatt − ΔΔEexpsub, | (18) |
Results and discussion
Cell volumes
We start by investigating the volumetric expansion of all molecular crystals within the X23 data set31 when anharmonic effects are considered within the quasi-harmonic approximation (QHA). Therefore, we have first calculated the respective thermal pressures pth using PBE+D3, BLYP+D3, and RPBE+D3 (see Table 1). The used temperatures Tl correspond to the temperatures of the experimental crystal-structure determinations, preferably at low temperatures (see Table S1, ESI†).| System | T l | PBE+D3 | BLYP+D3 | RPBE+D3 | Ref. 32 |
|---|---|---|---|---|---|
| 1,4-Cyclohexanedione | 133 | 0.439 | 0.569 | 0.427 | 0.275 |
| Acetic acid | 40 | 0.197 | 0.302 | 0.211 | 0.201 |
| Adamantane | 188 | 0.536 | 0.728 | 0.507 | 0.343 |
| Ammonia | 2 | 0.402 | 0.443 | 0.384 | n/a |
| Anthracene | 16 | 0.235 | 0.386 | 0.252 | n/a |
| Benzene | 4 | 0.235 | 0.370 | 0.262 | n/a |
| Carbon dioxide | 6 | 0.190 | 0.260 | 0.159 | n/a |
| Cyanamide | 108 | 0.151 | 0.279 | 0.187 | 0.095 |
| Cytosine | 295 | 0.487 | 0.667 | 0.476 | 0.294 |
| Ethyl carbamate | 168 | 0.412 | 0.523 | 0.395 | 0.331 |
| Formamide | 90 | 0.324 | 0.436 | 0.319 | 0.137 |
| Hexamine | 15 | 0.310 | 0.462 | 0.317 | n/a |
| Imidazole | 123 | 0.191 | 0.354 | 0.185 | 0.267 |
| Naphthalene | 10 | 0.236 | 0.382 | 0.254 | 0.215 |
| Oxalic acid α | 295 | 0.628 | 0.753 | 0.601 | 0.496 |
| Oxalic acid β | 295 | 0.285 | 0.570 | 0.321 | 0.510 |
| Pyrazine | 184 | 0.472 | 0.594 | 0.461 | 0.252 |
| Pyrazole | 108 | 0.268 | 0.373 | 0.283 | 0.316 |
| s-Triazine | 295 | 0.740 | 0.878 | 0.738 | 0.531 |
| s-Trioxane | 103 | 0.426 | 0.549 | 0.397 | 0.661 |
| Succinic acid | 77 | 0.184 | 0.386 | 0.201 | n/a |
| Uracil | 295 | 0.388 | 0.480 | 0.439 | 0.398 |
| Urea | 12 | 0.374 | 0.461 | 0.389 | n/a |
The PBE+D3 and RPBE+D3 values are very similar, with a mean absolute relative deviation (MARD) of 7% and a maximum deviation of 24% (cyanamide). In contrast, BLYP+D3 yields significantly different thermal pressures than PBE+D3 with a MARD of 46%. For oxalic acid β and succinic acid, the BLYP+D3 thermal pressure is twice as large as the corresponding PBE+D3 value in both cases.
Our obtained thermal pressures are similar to the ones obtained by Otero-de-la-Roza and Johnson,32 although the latter are often smaller. However, a direct comparison of thermal pressures obtained with different methods does not provide significant insight since the resulting thermal expansion highly depends on the potential energy surface corresponding to the utilized method. For instance, as discussed below, BLYP+D3 yields significantly larger thermal pressures than PBE+D3, but very similar changes in cell volumes. Therefore, thermal pressure differences between density functionals are to be expected and cell volume changes are in fact the more important quantity for comparisons.
All thermal pressures in Table 1 approximate vibrational-free energy effects at the minimum of the electronic energy (Vel) and have been obtained in a cost-effective way via central finite differences using two unit cells with volumes of 0.95Vel and 1.05Vel, respectively. For PBE+D3 we have also investigated other schemes for determining the thermal pressure based on central, backward, and forward finite differences (see Table S2, ESI†).
From the ESI,† it can be seen that the central difference approach already yields accurate results since the addition of another two data points does not change the corresponding thermal pressure. Backward differences yield similar data in many cases and on average the thermal pressures are about 2% smaller.
For pyrazole and s-triazine, we have also calculated the thermal pressures at 1.05Vel utilizing central differences, resulting in slightly smaller thermal pressures compared to those listed in Table 1. For pyrazole, this thermal pressure difference leads to a modification of the unit-cell volume of 0.4%. While that modification is small, this approach might be more exact since we can expect a volumetric expansion of about 5% on average (see below).
In addition, we have also investigated the usage of larger supercells modifying the derived thermal pressures (see Table S3, ESI†). On average, the obtained thermal pressures change by 2.5% and the observed maximal difference was found to be 9% for uracil—leading to an alteration of the unit-cell volume by only 0.5%. Using larger supercells changes the vibrational free energy by only 0.1 kJ mol−1 on average and the largest observed difference amounts to 0.4 kJ mol−1 for cytosine. Therefore, our standard supercells provide sufficiently accurate results.
Furthermore, we have also validated the quality of the used thermal-pressure optimization by comparing with EOS fits. The comparison was performed for all systems with Tl other than room temperature utilizing the available PBE+D3 phonon calculations at Vel, VQHAh and the isotropically expanded/shrunk cell volumes of 0.9Vel, 0.95Vel, and 1.05Vel. The average difference in the resulting unit-cell volumes between the thermal pressure and EOS approaches amounts to only 0.3%, with a mean absolute difference of 0.4%, while all differences are smaller than 0.8%.
Note that the deviation between thermal pressure optimizations and EOS fits will likely increase with temperature since our derived constant thermal pressure corresponds to Vel. Therefore, evaluating the thermal pressure close to the expected thermally-expanded volume should provide better results at high temperatures.
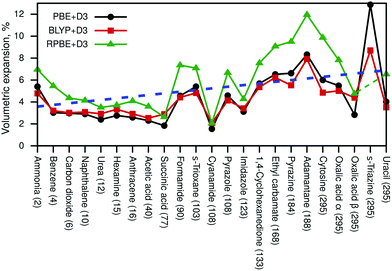
Next, we discuss the resulting volumetric expansions of the unit cells. This expansion includes thermal effects as well as zero-point energy effects. Fig. 2 shows the obtained expansions in % for all three density-functional approximations and the blue dashed line indicates the average expansion from 2 K to 295 K.
The numeric data compared to several literature values is available in Table S4 (ESI†). All resulting cell volumes are listed in Tables S5 and S6 (ESI†) contains all cell parameters for PBE+D3-optimised structures at Vel and VQHAl. The RPBE+D3 result for pyrazole was omitted in Fig. 2 and in the discussion later on due to an unrealistically large volumetric expansion of 27%. Based on all shown data points, the average expansion amounts to about 5%, while a linear fit (blue line) suggests that the expansion due to zero-point fluctuations amounts to about 3.6% and that thermal effects lead additionally to a percentage expansion of 0.01T. The volumetric expansion due to zero-point effects (at 0 K) was explicitly calculated with PBE+D3, leading to an average expansion of 2.4%.
It can be seen in Fig. 2 that PBE+D3 and BLYP+D3 yield very similar values for the volumetric expansion despite their differences in pth, while RPBE+D3 yields significantly larger values.
Moreover, we have compared our results with force-field data (FIT, W99rev6311P5) from Nyman et al.80 (see Table S4, ESI†). Unfortunately, the force-field results are quite scattered; several values are smaller than our DFT data, while some are significantly larger. In addition, the FIT force field yields even an unphysical negative volumetric expansion for cyanamide, suggesting that force fields might not be robust enough to properly deal with certain molecular crystals. Furthermore, our calculated values (especially PBE+D3 and BLYP+D3) agree very well with post-Hartree–Fock data from ref. 42 (acetic acid, carbon dioxide, imidazole).
Based on the obtained volumetric expansions corresponding to a temperature Tl, we can now provide a back-correction for experimental unit-cell volumes. The resulting reference values can then be directly compared with lattice relaxations minimising the electronic energy. Since the QHA works best at low temperatures due to minimal anharmonic effects, low-temperature experimental volumes were used when available. The average expansion of all three methods is used for the back-correction in order to minimize the influence of a single density functional. Note that a similar back-correction was presented for X23 in ref. 60 using the force-field data from Nyman et al.80
Table 2 displays the final new electronic reference values Vrefel. It can be seen that the values of Vrefel are on average 5% smaller than the experimentally determined volumes. Since our back-correction utilizes the average over three methods, we also supply an uncertainty for the new reference values, which amounts to the maximal difference from the average value in both directions. On average, this uncertainty in the unit-cell volume amounts to about 1.5%. Note that these uncertainties do not include the experimental error. Since the deviation of available experimental unit-cell volumes for the X23 set corresponding to the same temperature is typically below 1%, we expect the experimental error to be less than our average calculated error of 1.5% for X23. For some other molecular crystals, the spread of experimentally determined cell volumes can be much larger. This is for instance illustrated in ref. 44 for paracetamol (acetaminophen).
| System | T l/K | V expl/Å3 | V refel/Å3 |
|---|---|---|---|
| a RPBE+D3 result omitted due to unrealistically large thermal expansion. | |||
| 1,4-Cyclohexanedione | 133 | 279.6 | 262.5 ± 4.2 |
| Acetic acid | 40 | 297.3 | 288.8 ± 2.7 |
| Adamantane | 188 | 393.1 | 357.6 ± 10.6 |
| Ammonia | 2 | 128.6 | 121.5 ± 1.7 |
| Anthracene | 16 | 455.2 | 441.2 ± 4.0 |
| Benzene | 4 | 461.8 | 444.3 ± 7.1 |
| Carbon dioxide | 6 | 171.3 | 164.8 ± 2.1 |
| Cyanamide | 108 | 415.7 | 407.9 ± 1.4 |
| Cytosine | 295 | 472.4 | 440.3 ± 14.3 |
| Ethyl carbamate | 168 | 248.8 | 231.2 ± 4.9 |
| Formamide | 90 | 224.1 | 211.9 ± 4.7 |
| Hexamine | 15 | 332.4 | 321.6 ± 1.6 |
| Imidazole | 123 | 348.8 | 336.4 ± 2.7 |
| Naphthalene | 10 | 340.8 | 329.7 ± 2.6 |
| Oxalic acid α | 295 | 312.6 | 293.2 ± 6.1 |
| Oxalic acid β | 295 | 156.9 | 150.5 ± 1.9 |
| Pyrazine | 184 | 203.6 | 189.6 ± 4.8 |
| Pyrazole | 108 | 698.3 | 662.5 ± 11.3 |
| s-Triazine | 295 | 586.8 | 528.0 ± 12.8a |
| s-Trioxane | 103 | 616.5 | 580.7 ± 9.6 |
| Succinic acid | 77 | 239.3 | 233.3 ± 1.5 |
| Uracil | 295 | 463.4 | 442.0 ± 8.9 |
| Urea | 12 | 145.1 | 140.8 ± 0.9 |
Given the large effect of the back-correction, these new reference values should serve as new reference for benchmarking volumes obtained via minimization of electronic energies rather than the experimentally obtained cell volumes.
Lattice energies
After discussing cell volumes, we can turn to the calculation of new reference values for lattice energies. Reilly and Tkatchenko31 have back-corrected experimental sublimation enthalpies by removing vibrational contributions calculated with PBE+TS in the harmonic approximation. In addition, they have provided so-called semi-anharmonic values for some systems by utilizing experimental heat capacities.First, we discuss and compare our corresponding harmonic values calculated at Vel. Table 3 shows our ΔEvib + 4RT contributions obtained with PBE+D3, BLYP+D3, and RPBE+D3 as well as the PBE+TS results from ref. 31. Since the experimental sublimation enthalpies are typically extrapolated to the standard temperature 298 K, we have evaluated the ΔEvib + 4RT contributions in most cases at this temperature. However, for systems which do not exist in a solid form at 298 K, we have reduced the temperature (see Tcalch in Table 4). For completeness, vibrational contributions at 298 K for structures with Tcalch < 298 K are available in Table S7 (ESI†).
| System | Ref. 31 | PBE+D3 | BLYP+D3 | RPBE+D3 |
|---|---|---|---|---|
| a T = 290 K. b T = 195 K. c T = 279 K. d T = 207 K. e T = 276 K. | ||||
| 1,4-Cyclohexanedione | −7.5 | −6.1 | −7.9 | −6.2 |
| Acetic acida | n/a | −4.3 | −5.4 | −4.9 |
| Adamantane | −8.0/−11.0 | −4.9 | −8.3 | −6.2 |
| Ammoniab | n/a | −6.4 | −7.0 | −6.8 |
| Anthracene | −7.6/−10.9 | −6.3 | −9.3 | −6.7 |
| Benzenec | n/a | −5.2 | −6.7 | −5.7 |
| Carbon dioxided | n/a | −2.7 | −2.9 | −2.8 |
| Cyanamide | −4.2 | −3.6 | −4.6 | −3.9 |
| Cytosine | −6.4 | −5.5 | −7.3 | −5.9 |
| Ethyl carbamate | −7.6 | −6.1 | −7.6 | −6.3 |
| Formamidee | n/a | −6.9 | −7.9 | −7.3 |
| Hexamine | −9.9/−10.4 | −7.4 | −9.4 | −8.5 |
| Imidazole | −5.5 | −4.9 | −6.2 | −5.3 |
| Naphthalene | −7.9/−10.5 | −5.9 | −8.2 | −6.2 |
| Oxalic acid α | −4.7 | −2.3 | −3.5 | −3.2 |
| Oxalic acid β | −2.4 | −2.2 | −3.9 | −2.9 |
| Pyrazine | −5.0 | −6.3 | −7.3 | −6.3 |
| Pyrazole | −5.4 | −4.8 | −6.1 | −5.4 |
| s-Triazine | −6.0 | −5.4 | −6.3 | −5.6 |
| s-Trioxane | −8.3/−10.1 | −6.8 | −8.2 | −7.0 |
| Succinic acid | −4.3/−7.2 | −3.0 | −5.7 | −3.8 |
| Uracil | −6.5 | −5.6 | −7.1 | −6.0 |
| Urea | −6.6/−8.7 | −7.1 | −7.9 | −7.3 |
| System | T calch | ΔEavgvib + 4RT | ΔΔEQHAsub | ΔΔEexpsub |
|---|---|---|---|---|
| 1,4-Cyclohexanedione | 298 | −6.9 | −3.1 | −2.0 |
| Acetic acid | 290 | −4.9 | −1.2 | −1.1 |
| Adamantane | 298 | −6.9 | −3.5 | −3.4 |
| Ammonia | 195 | −6.7 | −0.1 | −0.8 |
| Anthracene | 298 | −7.5 | −1.8 | −1.0 |
| Benzene | 279 | −5.9 | −3.7 | −4.0 |
| Carbon dioxide | 207 | −2.8 | −2.8 | −0.5 |
| Cyanamide | 298 | −4.1 | −0.1 | −1.9 |
| Cytosine | 298 | −6.3 | −0.6 | −0.9 |
| Ethyl carbamate | 298 | −6.9 | −1.4 | −2.6 |
| Formamide | 276 | −7.4 | −0.9 | −2.1 |
| Hexamine | 298 | −8.8 | −2.2 | 0.5 |
| Imidazole | 298 | −5.5 | −0.5 | −3.4 |
| Naphthalene | 298 | −7.1 | −2.7 | −1.7 |
| Oxalic acid α | 298 | −3.4 | −0.8 | −1.6 |
| Oxalic acid β | 298 | −2.9 | −0.1 | −0.4 |
| Pyrazine | 298 | −6.2 | −1.9 | −1.7 |
| Pyrazole | 298 | −5.4 | −1.7 | −1.0 |
| s-Triazine | 298 | −5.8 | −2.7 | −1.1 |
| s-Trioxane | 298 | −7.6 | −2.1 | −0.8 |
| Succinic acid | 298 | −4.2 | −0.8 | −2.8 |
| Uracil | 298 | −6.3 | −0.2 | −0.7 |
| Urea | 298 | −7.2 | −0.9 | −1.1 |
For our DFT+D3 vibrational contributions (Table 3), we observe the following general trend: PBE+D3 < RPBE+D3 < BLYP+D3. The mean absolute deviation (MAD) of PBE+D3, BLYP+D3, and RPBE+D3 compared to the harmonic PBE+TS values amounts to 1.3, 0.8, and 0.9 kJ mol−1, respectively. Interestingly, PBE+D3 deviates the most from the PBE+TS results. All four methods show a good agreement with an average energy interval of 1.7 kJ mol−1. The worst agreement is found for adamantane, for which the maximal difference between the discussed methods amounts to 3.4 kJ mol−1—originating from the difference between the D3 and the Tkatchenko–Scheffler (TS) dispersion models.
Vibrational contributions turned out to be less pronounced for the small and rigid systems (e.g., carbon dioxide, cyanamide and two oxalic acids polymorphs), for which the conformational difference of a molecule between the gas-phase and the solid state is negligible. On the contrary, larger, conformationally flexible, and mostly nitrogen-containing systems are prone to large vibrational contributions (e.g., ammonia, urea, formamide, hexamine) on account of a different degree of planarization of nitrogen atoms in the crystal compared to that in the gas phase. Based on the average of the PBE+TS, PBE+D3, BLYP+D3, and RPBE+D3 results (ΔEavgvib + 4RT), we derive new harmonic reference values for lattice energies (Eref,HAlatt), which are listed in Table 5. Using the average over four methods should minimize the bias of the reference values towards a single density functional. The MAD between the ΔEavgvib terms and the harmonic PBE+TS results from Ref. 31 amounts to 0.5 kJ mol−1, with a maximum difference of 1.3 kJ mol−1 (oxalic acid α).
| System | ΔHexpsub | E ref,HAlatt | E ref,QHAlatt | E ref,explatt | Δ max |
|---|---|---|---|---|---|
| 1,4-Cyclohexanedione | 81.1 | 88.0 | 91.1 | 90.0 | 1.0 |
| Acetic acid | 67.7 | 72.6 | 73.7 | 73.6 | 0.6 |
| Adamantane | 61.6 | 68.5 | 71.9 | 71.8 | 2.0 |
| Ammonia | 31.2 | 37.9 | 38.1 | 38.7 | 0.3 |
| Anthracene | 101.9 | 109.4 | 111.2 | 110.4 | 1.8 |
| Benzene | 44.9 | 50.8 | 54.5 | 54.8 | 0.8 |
| Carbon dioxide | 26.1 | 28.9 | 31.7 | 29.4 | 0.1 |
| Cyanamide | 75.5 | 79.6 | 79.7 | 81.5 | 0.5 |
| Cytosine | 156.4 | 162.7 | 163.3 | 163.5 | 1.0 |
| Ethyl carbamate | 78.7 | 85.6 | 87.0 | 88.2 | 0.8 |
| Formamide | 71.7 | 79.1 | 80.0 | 81.1 | 0.5 |
| Hexamine | 75.8 | 84.6 | 86.8 | 84.1 | 1.4 |
| Imidazole | 81.4 | 86.9 | 87.4 | 90.4 | 0.7 |
| Naphthalene | 72.6 | 79.7 | 82.4 | 81.3 | 1.2 |
| Oxalic acid α | 93.7 | 97.1 | 97.9 | 98.8 | 1.3 |
| Oxalic acid β | 93.6 | 96.5 | 96.5 | 96.8 | 1.1 |
| Pyrazine | 56.3 | 62.5 | 64.4 | 64.3 | 1.2 |
| Pyrazole | 72.4 | 77.8 | 79.5 | 78.8 | 0.7 |
| s-Triazine | 55.7 | 61.5 | 64.2 | 62.6 | 0.5 |
| s-Trioxane | 56.3 | 63.9 | 66.0 | 64.6 | 0.8 |
| Succinic acid | 123.1 | 127.3 | 128.0 | 130.1 | 1.5 |
| Uracil | 129.2 | 135.5 | 135.7 | 136.2 | 0.8 |
| Urea | 93.8 | 101.0 | 102.0 | 102.1 | 0.7 |
As estimated uncertainty Δmax for our calculated reference values, we utilize the maximal difference between a specific method and the average ΔEavgvib. Note that this error estimation does not include any error of the underlying experimental reference data. Estimating the experimental error of sublimation enthalpies is a non-trivial task. Here, we would have to rely on the differences between very few reported experimental values.
Concerning the systems in the X23 set, Roux et al.74 have analysed the experimental measurements for aromatic hydrocarbons and estimate the error in their recommended sublimation enthalpy to be 0.2, 0.3, and 1.3 kJ mol−1 for benzene, naphthalene, and anthracene, respectively. Emelyanenko et al.75 have estimated the error for cytosine to be 2.0 kJ mol−1. As worst-case scenario, for 1,4-cyclohexanedione and adamantane, the maximum deviation between two experiments is 9 and 10 kJ mol−1, respectively. As the average of the experimentally available data is typically used as reference, we can assume that the error in the experimental sublimation enthalpies can become as large as 5 kJ mol−1 in certain cases.
The effect of thermal expansion is completely neglected in the harmonic approximation. Therefore, we also investigate the importance of anharmonic effects for the reference values of lattice energies. We have obtained thermally expanded unit cells corresponding to Tcalchvia the QHA using PBE+D3. This allows us to determine the change in lattice energy upon thermal expansion (ΔΔEQHAlatt) and the corresponding modification of the vibrational energy (ΔΔEQHAvib). Both terms are listed in Table S8 (ESI†) and are aggregated to ΔΔEQHAsub (see Table 4), which describes the total effect of including thermal expansion into the description of sublimation enthalpies. Based on eqn (14), we have derived a second set of reference values (Eref,QHAlatt), which is shown in Table 5. It can be seen that accounting for thermal expansion within the QHA leads to an average modification of reference values by only 1.6 kJ mol−1. In comparison, the average of all ΔEvib + 4RT terms amounts to 6 kJ mol−1. This implies that the corrections for the sublimation enthalpies (ΔEvib + 4RT + ΔΔEQHAsub) are in all cases closer to the semi-anharmonic values of Reilly and Tkatchenko31 compared to ΔEvib + 4RT.
Furthermore, in order to evaluate the quality of the used QHA, we derive a third set of reference values (Eref,explatt) by utilizing experimental unit-cell volumes and experimental heat capacities when available (see Table S1, ESI†). The corresponding correction to the harmonic values is labelled ΔΔEexpsub (see Table 4) and the resulting reference lattice energies are given in Table 5. It can be seen that the ΔΔEQHAsub and ΔΔEexpsub values are in most cases in good agreement having a MAD of only 1.0 kJ mol−1. We observe no systematic differences, as the mean deviation is only 0.1 kJ mol−1. The deviations exceed 2 kJ mol−1 for carbon dioxide, hexamine, and imidazole. In the first two cases, these differences originate mainly from the large ΔΔEQHAlatt contributions, suggesting that the QHA significantly overestimates the thermal expansion at Tcalch in these cases. Indeed, for carbon dioxide the QHA leads at 207 K to a thermal expansion (without zero-point energy effects) of 21%, while the experimentally observed thermal expansion between 6 and 205 K amounts to only 9%.81 Due to this overestimation of the thermal expansion, we believe that the Eref,explatt reference energies provide a more consistent picture than the Eref,QHAlatt values. Therefore, we recommend using the Eref,explatt reference values, the second last column in Table 5, as new X23b lattice-energy benchmark values. Nevertheless, the QHA is able to yield accurate results in many cases and allows the efficient account for thermal expansion even for large molecular crystals.
Note that we have utilized atom-pairwise dispersion models throughout this paper. As dispersion interactions are not strictly pairwise additive, many-body dispersion interactions can become important for some systems, especially when large and flexible molecules are involved.82–84 Such interactions can be captured by the many-body dispersion (MBD) model.85,86 The X23 set, however, involves mainly small and rigid molecules and only small differences between the D3 and MBD dispersion models have been reported.59,60
Fig. 3 summarizes the sublimation enthalpy back-corrections of our new X23b (Eref,explatt) reference values compared to the original C21 and X23 values. For C21, we observe a MAD of 2.8 and a maximal deviation of 6.2 kJ mol−1, respectively, compared to the new X23b. Our values agree much better with the X23 reference values (including some anharmonic estimates) with a MAD of 1.4 kJ mol−1 and a maximum deviation of 3.5 kJ mol−1. We note that while the new X23b lattice-energy benchmark values are on average rather similar to previous reference data, the maximum deviations are large enough to be of importance for certain systems.
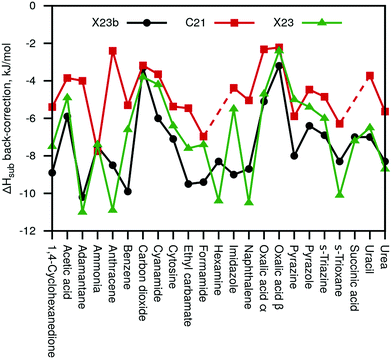 | ||
| Fig. 3 Calculated sublimation enthalpy back-corrections of our new X23b reference data compared with the back-corrections of the original C21 paper32 and the X23 paper31 (including semi-anharmonic values). | ||
Conclusions
We have derived new reference values of cell volumes and lattice energies for the X23 set of molecular crystals by back-correcting the respective experimental cell volumes and sublimation enthalpies for vibrational contributions. For this purpose, the quasi-harmonic approximation (QHA) was utilized in order to model the thermal expansion of the considered molecular crystals. Based on the average expansion described by three different dispersion-inclusive density functional approximations (PBE+D3, BLYP+D3, and RPBE+D3), we have created a new reference data set for unit-cell volumes, which can be directly compared to lattice relaxations minimizing the electronic energy. This back-correction is crucial and rather large, since it decreased the reference volumes on average by 5% compared to low-temperature experimental values due to zero-point and thermal effects. It has been found that PBE+D3 and BLYP+D3 typically provide a better description of the thermal volumetric expansion compared to high-level estimates than RPBE+D3. Our description of thermal-expansion effects is also more uniform than those typically obtained with empirical force fields.In the second part, we have focused on the back-correction of sublimation enthalpies for vibrational contributions. First, we have provided a harmonic correction like the one presented by Reilly and Tkatchenko.31 However, the presented harmonic back-correction herein amounts in all but five cases to the average of our PBE+D3, BLYP+D3, and RPBE+D3 results and the PBE+TS values obtained by Reilly and Tkatchenko. Since we are averaging over three distinct density-functional approximations and two dispersion models (in case of PBE), the resulting reference data is less biased towards the method employed. Furthermore, we have included the change in electronic and vibrational energy due to thermal expansion in our back-correction. In one case, we relied entirely on the QHA, while another back-correction was performed by utilizing experimentally obtained unit-cell volumes and heat capacities. In many cases, these two approaches lead to very similar results, but for a few systems we observe differences exceeding 2 kJ mol−1, which is mainly due to the overestimation of the thermal expansion by the QHA at larger temperatures.
The average effect of thermal expansion for sublimation enthalpies amounts to 1.6 kJ mol−1 and is therefore less pronounced than for the unit-cell volumes reported. However, these effects could still be crucial for molecular crystals with complex polymorphic energy landscapes. Note that sublimation enthalpies—in contrast to free energies—do not include entropic effects. Vibrational free energies are mainly determined by low-frequency vibrations, which in turn are modified by the thermal expansion of a crystal. Therefore, the effect of thermal expansion is likely more pronounced for Helmholtz free energies. Moreover, accounting for thermal expansion can be crucial for several properties, for instance low-frequency vibrational spectra or elastic constants.33
Since our back-corrections involve the average over several density-functional approximations, we have estimated an uncertainty of our reference values based on the maximal observed difference from the average. However, the overall accuracy of our new reference data depends on the accuracy of the underlying experimental measurements and used theoretical approximations. For some systems, the error in the underlying experimental sublimation enthalpies can be as large as 5 kJ mol−1 and more accurate experimental data would be desirable. Nevertheless, our new revised X23b reference values constitute a consistent high-level estimate and will further enable a more consistent benchmark and development of computational methods for molecular crystals.
Conflicts of interest
There are no conflicts to declare.Notes and references
- W. Kohn, Rev. Mod. Phys., 1999, 71, 1253–1266 CrossRef CAS.
- J. A. Pople, Angew. Chem., Int. Ed., 1999, 38, 1894–1902 CrossRef CAS.
- T. Korona, D. Kats, M. Schütz, T. B. Adler, Y. Liu and H.-J. Werner, in Linear-Scaling Techniques in Computational Chemistry and Physics: Methods and Applications, ed. R. Zalesny, M. G. Papadopoulos, P. G. Mezey and J. Leszczynski, Springer, Netherlands, Dordrecht, 2011, pp. 345–407 Search PubMed.
- J. Yang, G. K.-L. Chan, F. R. Manby, M. Schütz and H.-J. Werner, J. Chem. Phys., 2012, 136, 144105 CrossRef PubMed.
- F. Neese, A. Hansen and D. G. Liakos, J. Chem. Phys., 2009, 131, 064103 CrossRef PubMed.
- C. Hättig, D. P. Tew and B. Helmich, J. Chem. Phys., 2012, 136, 204105 CrossRef PubMed.
- S. Saebø and P. Pulay, J. Chem. Phys., 2001, 115, 3975–3983 CrossRef.
- J. E. Subotnik, A. Sodt and M. Head-Gordon, J. Chem. Phys., 2006, 125, 074116 CrossRef PubMed.
- P. Constans, P. Y. Ayala and G. E. Scuseria, J. Chem. Phys., 2000, 113, 10451–10458 CrossRef CAS.
- J. C. Burant, M. C. Strain, G. E. Scuseria and M. J. Frisch, Chem. Phys. Lett., 1996, 248, 43–49 CrossRef CAS.
- J. Kussmann, M. Beer and C. Ochsenfeld, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2013, 3, 614–636 CAS.
- C. A. White, B. G. Johnson, P. M. W. Gill and M. Head-Gordon, Chem. Phys. Lett., 1994, 230, 8–16 CrossRef CAS.
- S. Manzer, P. R. Horn, N. Mardirossian and M. Head-Gordon, J. Chem. Phys., 2015, 143, 024113 CrossRef PubMed.
- E. A. Toivanen, S. A. Losilla and D. Sundholm, Phys. Chem. Chem. Phys., 2015, 17, 31480–31490 RSC.
- E. Rudberg, E. H. Rubensson and P. Sałek, J. Chem. Theory Comput., 2011, 7, 340–350 CrossRef CAS PubMed.
- M. A. Watson, Y. Kurashige, T. Nakajima and K. Hirao, J. Chem. Phys., 2008, 128, 054105 CrossRef PubMed.
- J. J. P. Stewart, J. Mol. Model., 2013, 19, 1–32 CrossRef CAS PubMed.
- P. O. Dral, X. Wu, L. Spörkel, A. Koslowski, W. Weber, R. Steiger, M. Scholten and W. Thiel, J. Chem. Theory Comput., 2016, 12, 1082–1096 CrossRef CAS PubMed.
- M. Elstner, D. Porezag, G. Jungnickel, J. Elsner, M. Haugk, T. Frauenheim, S. Suhai and G. Seifert, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 7260–7268 CrossRef CAS.
- L. Maschio, D. Usvyat, M. Schütz and B. Civalleri, J. Chem. Phys., 2010, 132, 134706 CrossRef PubMed.
- M. Del Ben, J. Hutter and J. VandeVondele, J. Chem. Theory Comput., 2012, 8, 4177–4188 CrossRef CAS PubMed.
- G. H. Booth, A. Grüneis, G. Kresse and A. Alavi, Nature, 2012, 493, 365–370 CrossRef PubMed.
- S. Suhai and J. Ladik, J. Phys. C: Solid State Phys., 1982, 15, 4327–4337 CrossRef CAS.
- A. J. Cruz-Cabeza, S. M. Reutzel-Edens and J. Bernstein, Chem. Soc. Rev., 2015, 44, 8619–8635 RSC.
- J. P. M. Lommerse, W. D. S. Motherwell, H. L. Ammon, J. D. Dunitz, A. Gavezzotti, D. W. M. Hofmann, F. J. J. Leusen, W. T. M. Mooij, S. L. Price, B. Schweizer, M. U. Schmidt, B. P. van Eijck, P. Verwer and D. E. Williams, Acta Crystallogr., Sect. B: Struct. Sci., 2000, 56, 697–714 CrossRef CAS PubMed.
- W. D. S. Motherwell, H. L. Ammon, J. D. Dunitz, A. Dzyabchenko, P. Erk, A. Gavezzotti, D. W. M. Hofmann, F. J. J. Leusen, J. P. M. Lommerse, W. T. M. Mooij, S. L. Price, H. Scheraga, B. Schweizer, M. U. Schmidt, B. P. van Eijck, P. Verwer and D. E. Williams, Acta Crystallogr., Sect. B: Struct. Sci., 2002, 58, 647–661 CrossRef PubMed.
- G. M. Day, W. D. S. Motherwell, H. L. Ammon, S. X. M. Boerrigter, R. G. Della Valle, E. Venuti, A. Dzyabchenko, J. D. Dunitz, B. Schweizer, B. P. van Eijck, P. Erk, J. C. Facelli, V. E. Bazterra, M. B. Ferraro, D. W. M. Hofmann, F. J. J. Leusen, C. Liang, C. C. Pantelides, P. G. Karamertzanis, S. L. Price, T. C. Lewis, H. Nowell, A. Torrisi, H. A. Scheraga, Y. A. Arnautova, M. U. Schmidt and P. Verwer, Acta Crystallogr., Sect. B: Struct. Sci., 2005, 61, 511–527 CrossRef CAS PubMed.
- G. M. Day, T. G. Cooper, A. J. Cruz-Cabeza, K. E. Hejczyk, H. L. Ammon, S. X. M. Boerrigter, J. S. Tan, R. G. Della Valle, E. Venuti, J. Jose, S. R. Gadre, G. R. Desiraju, T. S. Thakur, B. P. van Eijck, J. C. Facelli, V. E. Bazterra, M. B. Ferraro, D. W. M. Hofmann, M. A. Neumann, F. J. J. Leusen, J. Kendrick, S. L. Price, A. J. Misquitta, P. G. Karamertzanis, G. W. A. Welch, H. A. Scheraga, Y. A. Arnautova, M. U. Schmidt, J. van de Streek, A. K. Wolf and B. Schweizer, Acta Crystallogr., Sect. B: Struct. Sci., 2009, 65, 107–125 CrossRef CAS PubMed.
- D. A. Bardwell, C. S. Adjiman, Y. A. Arnautova, E. Bartashevich, S. X. M. Boerrigter, D. E. Braun, A. J. Cruz-Cabeza, G. M. Day, R. G. Della Valle, G. R. Desiraju, B. P. van Eijck, J. C. Facelli, M. B. Ferraro, D. Grillo, M. Habgood, D. W. M. Hofmann, F. Hofmann, K. V. J. Jose, P. G. Karamertzanis, A. V. Kazantsev, J. Kendrick, L. N. Kuleshova, F. J. J. Leusen, A. V. Maleev, A. J. Misquitta, S. Mohamed, R. J. Needs, M. A. Neumann, D. Nikylov, A. M. Orendt, R. Pal, C. C. Pantelides, C. J. Pickard, L. S. Price, S. L. Price, H. A. Scheraga, J. van de Streek, T. S. Thakur, S. Tiwari, E. Venuti and I. K. Zhitkov, Acta Crystallogr., Sect. B: Struct. Sci., 2011, 67, 535–551 CrossRef CAS PubMed.
- A. M. Reilly, R. I. Cooper, C. S. Adjiman, S. Bhattacharya, A. D. Boese, J. G. Brandenburg, P. J. Bygrave, R. Bylsma, J. E. Campbell, R. Car, D. H. Case, R. Chadha, J. C. Cole, K. Cosburn, H. M. Cuppen, F. Curtis, G. M. Day, R. A. DiStasio Jr., A. Dzyabchenko, B. P. Van Eijck, D. M. Elking, J. A. Van Den Ende, J. C. Facelli, M. B. Ferraro, L. Fusti-Molnar, C. A. Gatsiou, T. S. Gee, R. De Gelder, L. M. Ghiringhelli, H. Goto, S. Grimme, R. Guo, D. W. M. Hofmann, J. Hoja, R. K. Hylton, L. Iuzzolino, W. Jankiewicz, D. T. De Jong, J. Kendrick, N. J. J. De Klerk, H. Y. Ko, L. N. Kuleshova, X. Li, S. Lohani, F. J. J. Leusen, A. M. Lund, J. Lv, Y. Ma, N. Marom, A. E. Masunov, P. McCabe, D. P. McMahon, H. Meekes, M. P. Metz, A. J. Misquitta, S. Mohamed, B. Monserrat, R. J. Needs, M. A. Neumann, J. Nyman, S. Obata, H. Oberhofer, A. R. Oganov, A. M. Orendt, G. I. Pagola, C. C. Pantelides, C. J. Pickard, R. Podeszwa, L. S. Price, S. L. Price, A. Pulido, M. G. Read, K. Reuter, E. Schneider, C. Schober, G. P. Shields, P. Singh, I. J. Sugden, K. Szalewicz, C. R. Taylor, A. Tkatchenko, M. E. Tuckerman, F. Vacarro, M. Vasileiadis, A. Vazquez-Mayagoitia, L. Vogt, Y. Wang, R. E. Watson, G. A. De Wijs, J. Yang, Q. Zhu and C. R. Groom, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 439–459 CrossRef CAS PubMed.
- A. M. Reilly and A. Tkatchenko, J. Chem. Phys., 2013, 139, 024705 CrossRef PubMed.
- A. Otero-de-la-Roza and E. R. Johnson, J. Chem. Phys., 2012, 137, 054103 CrossRef CAS PubMed.
- J. Hoja, A. M. Reilly and A. Tkatchenko, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2017, 7, e1294 Search PubMed.
- A. Erba, J. Maul and B. Civalleri, Chem. Commun., 2016, 52, 1820–1823 RSC.
- J. G. Brandenburg and S. Grimme, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 502–513 CrossRef CAS.
- J. G. Brandenburg, J. Potticary, H. A. Sparkes, S. L. Price and S. R. Hall, J. Phys. Chem. Lett., 2017, 8, 4319–4324 CrossRef CAS PubMed.
- J. Nyman and G. M. Day, Phys. Chem. Chem. Phys., 2016, 18, 31132–31143 RSC.
- J. Hoja, H.-Y. Ko, M. A. Neumann, R. Car, R. A. DiStasio Jr. and A. Tkatchenko, Sci. Adv., 2019, 5, eaau3338 CrossRef PubMed.
- J. Hoja and A. Tkatchenko, Faraday Discuss., 2018, 211, 253–274 RSC.
- N. Raimbault, V. Athavale and M. Rossi, Phys. Rev. Mater., 2019, 3, 053605 CrossRef CAS.
- C. Červinka, M. Fulem, R. P. Stoffel and R. Dronskowski, J. Phys. Chem. A, 2016, 120, 2022–2034 CrossRef.
- Y. N. Heit and G. J. O. Beran, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 514–529 CrossRef CAS.
- Y. N. Heit, K. D. Nanda and G. J. O. Beran, Chem. Sci., 2016, 7, 246–255 RSC.
- J. McKinley and G. J. O. Beran, Faraday Discuss., 2018, 211, 181–207 RSC.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS.
- A. D. Becke, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 38, 3098–3100 CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- B. Hammer, L. B. Hansen and J. K. Nørskov, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 7413–7421 CrossRef.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- A. D. Becke and E. R. Johnson, J. Chem. Phys., 2005, 123, 154101 CrossRef.
- E. R. Johnson and A. D. Becke, J. Chem. Phys., 2005, 123, 024101 CrossRef.
- E. R. Johnson and A. D. Becke, J. Chem. Phys., 2006, 124, 174104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS.
- L. Goerigk, A. Hansen, C. Bauer, S. Ehrlich, A. Najibi and S. Grimme, Phys. Chem. Chem. Phys., 2017, 19, 32184–32215 RSC.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. A. Dolgonos, O. A. Loboda and A. D. Boese, J. Phys. Chem. A, 2018, 122, 708–713 CrossRef CAS.
- O. A. Loboda, G. A. Dolgonos and A. D. Boese, J. Chem. Phys., 2018, 149, 124104 CrossRef.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- F. D. Murnaghan, Proc. Natl. Acad. Sci. U. S. A., 1944, 30, 244–247 CrossRef CAS.
- J. H. Smith and A. I. M. Rae, J. Phys. C: Solid State Phys., 1978, 11, 1761–1770 CrossRef CAS.
- R. D. Chirico, S. E. Knipmeyer and W. V. Steele, J. Chem. Thermodyn., 2003, 35, 1059–1072 CrossRef CAS.
- A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5 CrossRef CAS.
- R. C. Wilhoit, J. Chao and K. R. Hall, J. Phys. Chem. Ref. Data, 1985, 14, 1–175 CrossRef CAS.
- L. A. K. Staveley, L. Q. Lobo and J. C. G. Calado, Cryogenics, 1981, 21, 131–144 CrossRef CAS.
- J. B. Hudson, W. B. Hillig and R. M. Strong, J. Phys. Chem., 1959, 63, 1012–1016 CrossRef CAS.
- H. G. M. De Wit, C. G. De Kruif and J. C. Van Miltenburg, J. Chem. Thermodyn., 1983, 15, 891–902 CrossRef CAS.
- R. M. Stephenson and S. Malanowski, Handbook of the Thermodynamics of Organic Compounds, Springer, Netherlands, Dordrecht, 1987 Search PubMed.
- N. Vogt, M. A. Abaev, A. N. Rykov and I. F. Shishkov, J. Mol. Struct., 2011, 996, 120–127 CrossRef CAS.
- A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 073005 CrossRef PubMed.
- M. V. Roux, M. Temprado, J. S. Chickos and Y. Nagano, J. Phys. Chem. Ref. Data, 2008, 37, 1855–1996 CrossRef CAS.
- V. N. Emel’yanenko, D. H. Zaitsau, E. Shoifet, F. Meurer, S. P. Verevkin, C. Schick and C. Held, J. Phys. Chem. A, 2015, 119, 9680–9691 CrossRef PubMed.
- W. Acree and J. S. Chickos, J. Phys. Chem. Ref. Data, 2010, 39, 043101 CrossRef.
- J. F. Martin and R. J. L. Andon, J. Chem. Thermodyn., 1982, 14, 679–688 CrossRef CAS.
- P. J. van Ekeren, A. C. G. van Genderen and G. J. K. van den Berg, Thermochim. Acta, 2006, 446, 33–35 CrossRef CAS.
- A. Togo, L. Chaput, I. Tanaka and G. Hug, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 174301 CrossRef.
- J. Nyman, O. S. Pundyke and G. M. Day, Phys. Chem. Chem. Phys., 2016, 18, 15828–15837 RSC.
- I. N. Krupskii, A. I. Prokhvatilov, A. I. Erenburg and A. S. Barylnik, Fiz. Nizk. Temp., 1982, 8, 533–541 CAS.
- A. Ambrosetti, N. Ferri, R. A. DiStasio Jr. and A. Tkatchenko, Science, 2016, 351, 1171–1176 CrossRef CAS PubMed.
- A. Ambrosetti, D. Alfè, R. A. DiStasio Jr. and A. Tkatchenko, J. Phys. Chem. Lett., 2014, 5, 849–855 CrossRef CAS PubMed.
- A. M. Reilly and A. Tkatchenko, Chem. Sci., 2015, 6, 3289–3301 RSC.
- A. Tkatchenko, R. A. DiStasio Jr., R. Car and M. Scheffler, Phys. Rev. Lett., 2012, 108, 236402 CrossRef PubMed.
- A. Ambrosetti, A. M. Reilly, R. A. DiStasio Jr. and A. Tkatchenko, J. Chem. Phys., 2014, 140, 18A508 CrossRef PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Additional tables with calculated structural and thermodynamic quantities for all systems of the X23 data set. See DOI: 10.1039/c9cp04488d |
| ‡ Current address: Institute of Solid State Physics, Graz University of Technology, Petersgasse 16, 8010 Graz, Austria. |
| This journal is © the Owner Societies 2019 |