Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Influence of polar co-solutes and salt on the hydration of lipid membranes†
Amanuel
Wolde-Kidan
 a,
Quoc Dat
Pham
a,
Quoc Dat
Pham
 b,
Alexander
Schlaich
b,
Alexander
Schlaich
 c,
Philip
Loche
c,
Philip
Loche
 a,
Emma
Sparr
a,
Emma
Sparr
 b,
Roland R.
Netz
a and
Emanuel
Schneck
b,
Roland R.
Netz
a and
Emanuel
Schneck
 *d
*d
aFachbereich Physik, Freie Universität Berlin, Arnimallee 14, 14195 Berlin, Germany
bDivision of Physical Chemistry, Chemistry Department, Lund University, P.O. Box 124, 22100 Lund, Sweden
cUniversité Grenoble Alpes, CNRS, LIPhy, 38000 Grenoble, France
dBiomaterials Department, Max Planck Institute of Colloids and Interfaces, 14476 Potsdam, Germany. E-mail: schneck@mpikg.mpg.de
First published on 18th July 2019
Abstract
The influence of the co-solutes TMAO, urea, and NaCl on the hydration repulsion between lipid membranes is investigated in a combined experimental/simulation approach. Pressure–hydration curves obtained via sorption experiments reveal that the repulsion significantly increases when the membranes are loaded with co-solutes, most strongly for TMAO. As a result, the co-solutes retain additional water molecules and therefore provide membranes with a fluid and more physiological environment. The experimental data are quantitatively reproduced in complementary solvent-explicit atomistic molecular dynamics simulations, which yield the chemical potential of water. Simulation analysis reveals that the additional repulsion arises from the osmotic pressure generated by the co-solutes, an effect which is maximal for TMAO, due to its unfavorable interactions with the lipid headgroup layer and its extraordinarily high osmotic coefficient.
1 Introduction
Lipid membranes in water experience a strong mutual repulsion at separations below 2–3 nm.1,2 This so-called hydration repulsion plays an essential biological role as it creates a barrier against close membrane contacts and thereby suppresses uncontrolled membrane adhesion and fusion.3 In addition, it provides lipid membrane systems with the fluid environment required for vital functioning. Under dry conditions, however, dehydration due to osmotic stress can affect lipid self-assembly with far-reaching consequences. For example, dehydration-induced phase transitions, which shift the membrane state from fluid to gel-like,4,5 have been associated with altered barrier functions of the human stratum corneum (SC), the outermost layer of the skin.6 The SC is only a few micrometers thick and formed by dead corneocyte cells embedded in a lipid multilamellar matrix, where the bilayers are arranged parallel to the skin surface.7 It exhibits very low permeability for hydrophilic and hydrophobic molecules.8In nature, protection against osmotic stress is commonly achieved by the release of small polar co-solutes with low vapor pressure, sometimes referred to as osmolytes.9,10 These molecules serve to retain the physiological, fluid state of membrane systems in low humidity conditions. This strategy is taken by algae and higher plants, which produce small carbohydrates and polyols, like glycerol.11,12 Similarly, insects and higher animals rely on glycerol, urea, and trimethylamine-N-oxide (TMAO), among others.13,14 The human skin contains a mixture of small polar compounds that is referred to as the “natural moisturizing factor” (NMF), comprising free amino acids, derivatives thereof, lactic acid, urea, and glycerol.15,16 The manifestation of NMF components in the SC is well documented, and their presence is considered crucial to maintain softness and pliability.16,17 In fact, defective skin conditions and certain skin diseases, for example winter xerosis and atopic dermatitis, are associated with decreased NMF levels in the SC.18,19
Previous studies on urea, glycerol, and small carbohydrates have shown that these molecules act as non-volatile substitutes of water molecules, thereby protecting self-assembled structures that are otherwise only present in more hydrated conditions.20–22 More recently, it was shown that TMAO, in contrast to urea, exhibits unfavorable interactions with lipid headgroups and is therefore preferentially expelled from membrane multilayers via precipitation at very dry conditions23 or by partitioning into the excess aqueous medium when present.24 In a wide range of dehydrating osmotic pressures, however, both urea and TMAO remain confined between the membrane surfaces.23
In the present work, we investigate the influence of co-solutes on the hydration repulsion between lipid membranes, the interfacial force that ultimately governs the hydration level of membrane systems subject to osmotic stress.1 Pressure–hydration curves obtained via sorption calorimetry and sorption balance experiments of phospholipid multilayers containing defined amounts of urea, TMAO, and of the salt NaCl reveal that the repulsion can be dramatically enhanced, depending on the chemistry of the co-solute (for chemical structures see Fig. 1A). The effect of TMAO is 2–3 times stronger than that of urea or NaCl. The pressure–hydration curves are quantitatively reproduced in solvent-explicit atomistic molecular dynamics (MD) simulations, which precisely yield the chemical potential of water25,26 (for a simulation snapshot see Fig. 1B). Detailed analysis of the simulation results provides the physical explanation for the observed repulsion enhancement: additional repulsion arises from the osmotic pressure generated by the co-solutes, an effect which is amplified for TMAO, due to its unfavorable interactions with the membrane surfaces and its extraordinarily high osmotic coefficient. For high enough TMAO weight fractions, the thermodynamics of membrane dehydration is dominated by the dehydration of the confined TMAO solution.
While the fluidizing effect of small polar co-solutes has so far been mainly attributed to their ability to substitute water molecules,21,22 the enhancement of the hydration repulsion identified and explained in the present work demonstrates that co-solutes can additionally have a moisturizing effect in the literal sense: at dry conditions, i.e., depressed water chemical potential, they retain additional water molecules and therefore provide membranes with a fluid and more physiological environment.
2 Materials and methods
2.1 Sample preparation
The phospholipids dimyristoylphosphatidylcholine (DMPC) and palmitoyl-oleoyl-phosphatidylcholine (POPC) were purchased from Avanti Polar Lipids, Inc. (Alabaster, AL). Urea and TMAO were obtained from Sigma-Aldrich and NaCl from VWR. The samples were prepared so that the co-solute–lipid mass fraction (of urea, TMAO or NaCl) in the dry samples, Ψlipcosol = mcosol/(mcosol + mlip), was fixed while the water content in terms of the number of water molecules per lipid nw = Nw/Nlip is variable. The samples were mixed together by the use of a mortar and pestle to produce a fine powder, which was then subjected to drying under vacuum with a 3 Å molecular sieve for at least 24 hours. According to earlier reports,27,28 this drying procedure removes all water from the lipid sample. The dry samples were then loaded into the measurement device under a stream of dry N2.2.2 Sorption calorimetry measurements
A double twin isothermal microcalorimeter was used to study the thermodynamics of the water vapor sorption.29 The instrument involves a two-chamber calorimetric cell, with a sorption chamber that contains the dry sample and a vaporization chamber in which liquid water is injected to start the sorption experiment. The chambers are connected by a tube. Water vaporizes in the vaporization chamber and diffuses through the tube to the sorption chamber where it is absorbed by the sample. The calorimetric cell is inserted into a double twin isothermal microcalorimeter that separately measures thermal powers released or absorbed in the two chambers. The data for each experiment were recorded for ca. 14 days at T = 27 °C. The experimental setup can be considered a continuous titration of an initially dry sample with water vapor.29 Using this method, one can simultaneously monitor the water uptake in terms of nw, the partial enthalpy of water, and the relative humidity hrel, which is then converted into the water chemical potential as Δμ = −RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(hrel/100), where R is the gas constant.
ln(hrel/100), where R is the gas constant.
In addition, osmotic coefficients Φ of TMAO, urea and NaCl can be determined from the water chemical potential in aqueous solutions at various co-solute concentrations, using the following equation30
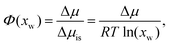 | (1) |
2.3 Sorption microbalance measurements
Sorption balance measurements were performed using an Aquadyne DVS microbalance device from Quantachrome Instruments. The dry samples were placed on pans in the device and exposed to a stream of nitrogen at controlled relative humidity hrel. The balance measured the mass gain or loss over time with a weight reading every 5 s. Experiments started with drying steps, where hrel was brought as closely as possible to zero for 240–5000 min at 40 °C and then for 180–5000 min at 27 °C. After the drying, the experiments continued subsequently with a ramp of hrel steps at T = 27 °C, where each step was performed for 180–5000 min. The condition for the next step to be engaged after the minimum step duration was that the weight change per min was less than 0.0001% of the starting mass. The total weight of water and dry sample at each hrel step was obtained from the final plateau values of the weight recorded after each change in hrel and immediately before the next hrel step. Sorption isotherms were constructed based on the water content as a function of hrel.2.4 Simulations
Using the GROMACS 2016.4 package,31 planar lipid bilayers with Nlip = 72 lipid molecules (36 in each leaflet) were simulated at various hydration levels and with various co-solute contents. For a simulation snapshot see Fig. 1B. Periodic boundary conditions were imposed in all directions, effectively representing infinite stacks of hydrated lipid bilayers. Unless stated otherwise, the Berger lipid forcefield32 was employed in combination with SPC/E water33 and thermodynamically optimized forcefields for TMAO,34 urea35 and NaCl.36 In order to investigate forcefield effects, selected simulations were repeated with the CHARMM36 forcefield for lipids and ions37,38 in combination with the TIP3P water model39,40 (see Section 3.3.5). Simulations were run in the NpT-ensemble at T = 300 K and atmospheric pressure of p = 1 bar. Temperature was controlled using the velocity re-scaling thermostat41 with a time constant of τT = 0.5 ps, while for the pressure the Berendsen barostat42 was used with semi-isotropic pressure coupling with a time constant of τp = 1 ps and a compressibility of κ = 4.5 × 10−5 bar−1. The timestep was Δt = 2 fs. Charge interactions were modeled using the particle-mesh-Ewald (PME) method43 and van der Waals interactions were described by Lennard-Jones potentials shifted to zero at the cut-off. For both, electrostatics and van der Waals interactions, a cut-off radius of rc = 0.9 nm was used. Starting configurations for the different hydration levels were generated by step-wise dehydration of a highly hydrated bilayer (nw = 25) and subsequent equilibration for 10 ns. All data points represent averages over five independently dehydrated systems. For density profiles and observables derived thereof data were gathered from 10 ns production runs of each of the five systems, amounting to a total of 50 ns.The repulsive pressure Π was obtained from the shift Δμ in the water chemical potential according to eqn (2). To determine μ = μex + μid, its excess and ideal contributions, μex and μid = kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(ρwΛ3NA/Mw), were measured independently, where ρw is the water density, Λ ≈ 0.0237 nm is the thermal wavelength of water at T = 300 K and NA is Avogadro's number. While μ by definition is constant over the simulation volume in thermal equilibrium, μex and μid are not. Due to the inhomogeneous water distribution perpendicular to the membrane surface, μex(z) and μid(z) via ρw(z) are functions of the perpendicular coordinate, z. As a consequence, μex and μid have to be evaluated at the same z position in the simulation box to determine μ. While μid trivially follows from ρw, μex was determined via a computationally efficient combination of two approaches, the test particle insertion44 for the Lennard-Jones contribution and the thermodynamic integration with multi-state Bennet acceptance ratio analysis45 for the Coulomb contribution. The thermodynamic integration involved 18 λ-steps of at least 10 ns duration each, amounting to a total simulation time of at least 5 × 18 × 10 ns = 900 ns per data point, or 7.2 μs per pressure–distance curve. The water chemical potential of the bulk reference μ0 was approximated by averaging values obtained at the three largest hydration levels (nw = 19, 22, and 25).
ln(ρwΛ3NA/Mw), were measured independently, where ρw is the water density, Λ ≈ 0.0237 nm is the thermal wavelength of water at T = 300 K and NA is Avogadro's number. While μ by definition is constant over the simulation volume in thermal equilibrium, μex and μid are not. Due to the inhomogeneous water distribution perpendicular to the membrane surface, μex(z) and μid(z) via ρw(z) are functions of the perpendicular coordinate, z. As a consequence, μex and μid have to be evaluated at the same z position in the simulation box to determine μ. While μid trivially follows from ρw, μex was determined via a computationally efficient combination of two approaches, the test particle insertion44 for the Lennard-Jones contribution and the thermodynamic integration with multi-state Bennet acceptance ratio analysis45 for the Coulomb contribution. The thermodynamic integration involved 18 λ-steps of at least 10 ns duration each, amounting to a total simulation time of at least 5 × 18 × 10 ns = 900 ns per data point, or 7.2 μs per pressure–distance curve. The water chemical potential of the bulk reference μ0 was approximated by averaging values obtained at the three largest hydration levels (nw = 19, 22, and 25).
Interaction free energies were computed by integrating the change in the water chemical potential as 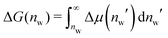 . The enthalpic contribution was computed from the system's total enthalpy as ΔH(nw) = H(nw) − (H(nmaxw) − (nmaxw − nw)·dHw/dNw), where nmaxw = 25. From independent simulations of bulk water we determined dHw/dNw = −38.67 kJ mol−1 (see Fig. S1 in the ESI†).
. The enthalpic contribution was computed from the system's total enthalpy as ΔH(nw) = H(nw) − (H(nmaxw) − (nmaxw − nw)·dHw/dNw), where nmaxw = 25. From independent simulations of bulk water we determined dHw/dNw = −38.67 kJ mol−1 (see Fig. S1 in the ESI†).
Osmotic coefficients were determined by measuring the change in water chemical potential Δμ in simulations of bulk co-solute solutions at various concentrations. The corresponding values for the osmotic coefficients Φ were then calculated using eqn (1).
3 Results and discussion
TMAO and urea are commonly-studied co-solutes, due to their abilities to stabilize and destabilize, respectively, the native fold of proteins.46 In phospholipid bilayer systems, TMAO has been shown to be repelled from the lipid headgroup region, while urea has a slight affinity for the bilayer surface.23 Here, the effect of TMAO and urea as well as NaCl on the hydration of phospholipid multilayers is investigated. Two lipid species, one with saturated chains and one with partially unsaturated chains, dimyristoyl-phosphatidylcholine (DMPC) and palmitoyl-oleoyl-phosphatidylcholine (POPC), respectively, are studied. First, the experimental data obtained via sorption calorimetry and sorption balance are presented. This is followed by a description of the simulation results and their comparison with the experimental data. Finally, the underlying mechanisms identified through simulation analysis are discussed.3.1 Co-solute influence on the hydration repulsion: experiments
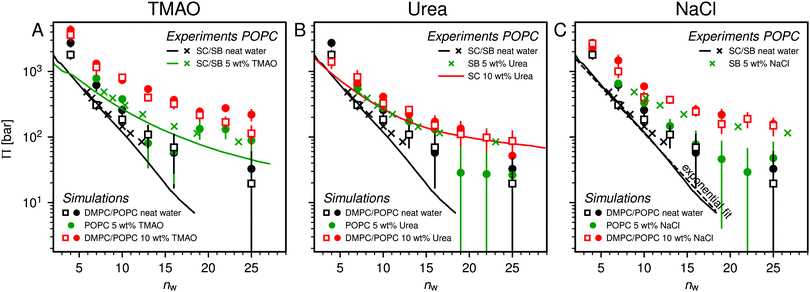
Fig. 2 shows the relationships between the dehydrating osmotic pressure Π and the hydration level nw as obtained in sorption experiments for samples composed of POPC lipids with varying amounts of co-solutes (data for DMPC lipids are shown in Fig. S3 in the ESI†). The dehydrating osmotic pressure follows from the shift in the water chemical potential, Δμ (see Methods section), as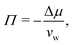 | (2) |
| Dw = 2nwv0w/Alip, | (3) |
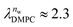 and
and 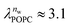 in units of nw. For areas per lipid of Alip ≈ 0.60–0.65 nm2 (see Fig. 4), this corresponds to decay lengths of λDMPC ≈ 0.21 nm and λPOPC ≈ 0.29 nm, in agreement with the literature.47,48 The addition of co-solutes significantly increases both strength and range of the repulsion. The increase in the hydration level nw for a fixed osmotic pressure upon co-solute addition clearly demonstrates that the presence of co-solutes leads to the retention of additional water molecules for a given humidity level. The strength of this effect is monotonic in the added co-solute mass fraction, as seen for TMAO in panel A, but it is not simply proportional to the co-solute concentration. Instead, the repulsion is amplified more strongly for TMAO, although the added mass fraction corresponds to a lower co-solute concentration compared to the other co-solutes with a smaller molar mass. The results in Fig. 2 demonstrate that co-solutes have a pronounced influence on the hydration repulsion between lipid membranes, which is however strongly dependent on the co-solute chemistry. The underlying physical mechanisms are discussed in the following on the basis of the results obtained with complementary MD simulations.
in units of nw. For areas per lipid of Alip ≈ 0.60–0.65 nm2 (see Fig. 4), this corresponds to decay lengths of λDMPC ≈ 0.21 nm and λPOPC ≈ 0.29 nm, in agreement with the literature.47,48 The addition of co-solutes significantly increases both strength and range of the repulsion. The increase in the hydration level nw for a fixed osmotic pressure upon co-solute addition clearly demonstrates that the presence of co-solutes leads to the retention of additional water molecules for a given humidity level. The strength of this effect is monotonic in the added co-solute mass fraction, as seen for TMAO in panel A, but it is not simply proportional to the co-solute concentration. Instead, the repulsion is amplified more strongly for TMAO, although the added mass fraction corresponds to a lower co-solute concentration compared to the other co-solutes with a smaller molar mass. The results in Fig. 2 demonstrate that co-solutes have a pronounced influence on the hydration repulsion between lipid membranes, which is however strongly dependent on the co-solute chemistry. The underlying physical mechanisms are discussed in the following on the basis of the results obtained with complementary MD simulations.
3.2 Comparison between experiments and simulations
Over the last few years we have demonstrated that dehydrating osmotic pressures in atomistic MD simulations can be determined via precise measurements of the water chemical potential μ as a function of the hydration level.25,26 In analogy to the experimental procedure, the osmotic pressure follows from Δμ = μ − μ0 according to eqn (2). In the simulations the reference chemical potential in pure bulk water is μ0 = −48.3 kJ mol−1 and the partial molecular volume of water, vw, is found to be approximately equal to v0w ≈ 0.0304 nm3 for all hydration levels (see ESI†). The main simulation results are reported for the Berger lipid forcefield, which is known to quantitatively reproduce pressure–distance curves between lipid bilayers,26 and which uses the SPC/E water model, for which also the co-solute forcefields have been optimized.34–36As seen in Fig. 2, the pressure vs. hydration data obtained in the simulations are in near-quantitative agreement with the corresponding experimental data on POPC. While the agreement between simulations and experiments for lipid membranes in pure water has been demonstrated earlier,26,47 we here show that the simulations also accurately reproduce the effect of added TMAO and urea. This agreement lends credibility to the employed forcefields and simulation methodology and motivates further analysis of the simulation trajectories as discussed below. In the case of NaCl the simulations significantly underestimate the added repulsion, which must likely be attributed to shortcomings in the forcefield regarding the interaction of Na+ with the membrane surfaces (see Section 3.3.5). The simulation data for DMPC are also shown in Fig. 2. They are very similar to the ones obtained with POPC and, as shown in the ESI,† agree with the experiments, but only within the limits of their comparability. Namely, DMPC at low hydration levels undergoes a phase transition from fluid to gel-like, which is not captured on the time scale of the MD simulations.5 Moreover, phase separation of co-solutes from the lipid phase, which was reported experimentally earlier for low hydration levels,23 by construction cannot occur in the MD simulations which involve only a single bilayer. Generally, it should be noted that simulations of POPC or DMPC multilayers loaded with as much as 10 wt% co-solutes for the same reasons do not always have an experimental counterpart, especially at very low hydration. They are nonetheless helpful to elucidate the physical mechanisms underlying the experimentally observed effects.
3.3 Simulation analysis
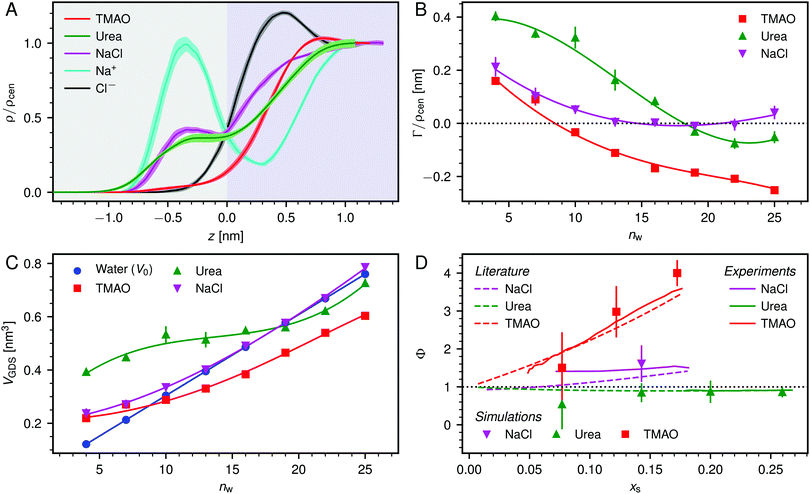 | ||
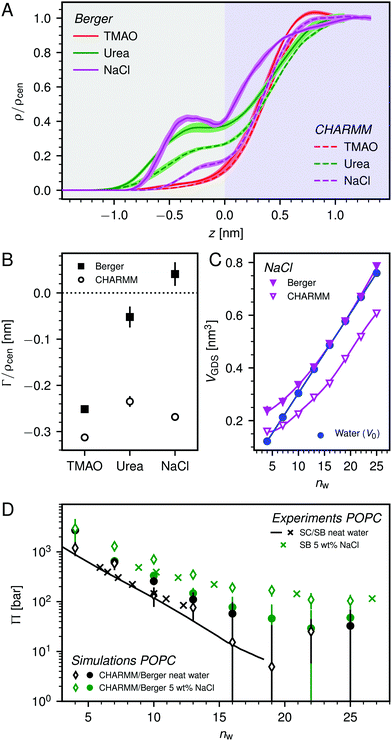
| Fig. 3 (A) Normalized density profiles of the co-solutes perpendicular to the membrane surface at high hydration (POPC, nw = 25). The profiles are averaged over five independent simulations with 10 wt% of co-solutes. Shaded areas indicate standart errors of the mean. The background color indicates the location of the lipid bilayer (grey) and the water slab (purple) in the Gibbs dividing surface definition (see main text). (B) Hydration-dependent surface excess for the different co-solutes as computed from eqn (4). (C) Volume per lipid effectively accessible to the co-solutes, VGDS = Alip·DGDS/2, as a function of the hydration level. Lines show cubic smoothing splines. (D) Concentration-dependent osmotic coefficients from the experimental literature49–51 and the corresponding values from sorption experiments and simulations obtained in the present work. Data are plotted over the solute mole fraction xs = 1 − xw for clarity. The dotted horizontal line indicates ideal behavior (Φ = 1). | ||
Preferential accumulation or depletion of the respective solutes at the membrane surface is quantified in terms of the surface excess Γ, which is computed from the co-solute density profiles as
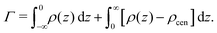 | (4) |
The hydration-dependent values of Γ, normalized by ρcen, are shown in Fig. 3B. TMAO is strongly repelled from the membrane surface for almost all hydration levels. Urea is weakly repelled from the membrane surface at high hydration levels but attracted at low hydration. The surface excess of NaCl is significantly positive, especially at low hydration levels, where we stress again that this result is specific to the Berger forcefield.
The volume per lipid effectively accessible to the co-solutes is VGDS = AlipDGDS/2, where DGDS = Dw − 2zGDS. The Gibbs dividing surface for the co-solutes, zGDS, is defined as the z-position for which Γ would vanish and is computed as
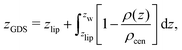 | (5) |
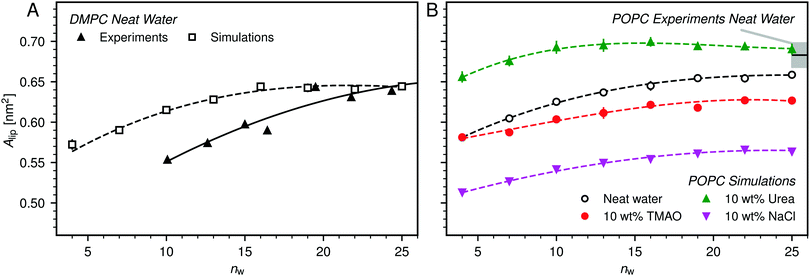 | ||
| Fig. 4 (A) Average area per lipid, Alip, in DMPC membranes without added co-solutes as a function of the hydration level, as reported in the experimental literature48 and as obtained from the simulations in the present work. (B) Influence of 10 wt% TMAO, urea, or NaCl on Alip as observed in simulations of POPC bilayers. Experimental data for fully hydrated POPC bilayers in neat water is shown for comparison, with the shaded area indicating the experimental uncertainty.52 Lines are guides to the eye. | ||
Fig. 4B shows the hydration dependence of Alip in presence of co-solutes as obtained in the simulations with POPC bilayers. It is seen that TMAO significantly decreases Alip, by about 2 to 3 Å2, while urea increases Alip by a comparable increment, depending on the hydration level. NaCl has the strongest effect. It decreases Alip by about 7 to 8 Å2 for all hydration levels. A simple Gibbs adsorption model, associating a positive surface excess with an increase in Alip and a negative surface excess with its decrease, qualitatively predicts the effect of TMAO and urea at most hydration levels. This model however neglects co-solute-induced variations in the lipid chemical potential and is thus of limited predictive power. In fact, it fails to predict the NaCl-induced decrease of Alip, which is in line with earlier indirect experimental evidence55,56 and can be attributed to a condensation due to local charge compensation.54,57
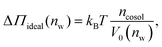 | (6) |
 | ||
| Fig. 5 Pressure–hydration curves Π(nw) of PC membranes with and without added 10 wt% TMAO (panel A), urea (panel B), and NaCl (panel C) as obtained in the simulations. Black solid lines represent exponential fits to the simulation data for POPC without added co-solutes. Dotted and solid red lines indicate the predictions of theoretical models for POPC simulations, neglecting (eqn (6)) and accounting (eqn (7)) for effective volume and osmotic coefficient effects, respectively. Theoretical predictions are only shown for hydration levels for which the co-solute concentration is below the solubility limit. Panel (D) shows the influence of the effective volume and of the osmotic coefficient individually. | ||
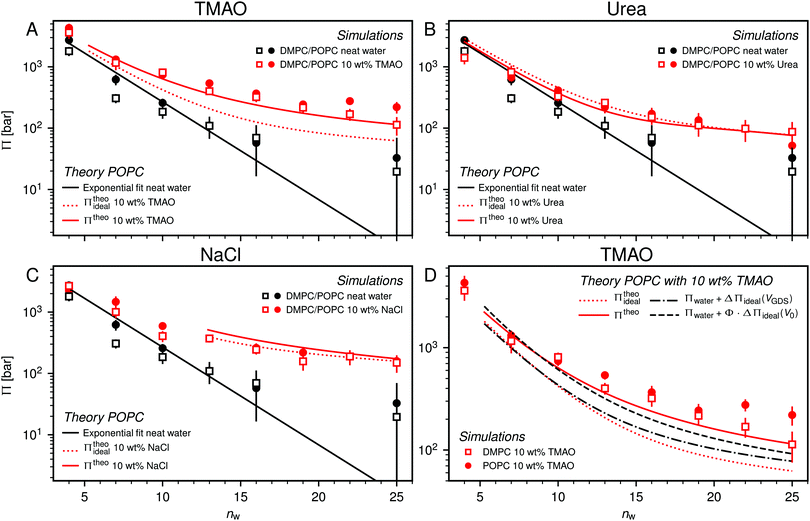
One necessary refinement directly follows from one of our earlier conclusions: the effective volume accessible to the co-solutes, VGDS, deviates significantly from that of the solvent, V0, meaning that eqn (6) needs to be augmented by a correction factor V0/VGDS. Another refinement concerns the co-solute osmotic coefficients, Φ, which substantially deviate from the ideal behavior (Φ = 1) assumed in eqn (6). Fig. 3D shows osmotic coefficients of urea, TMAO, and NaCl in a wide concentration range, determined in independent simulations and experiments as described in the Methods section. The data are in good agreement with experimental data from the literature for urea,50 TMAO,49 and NaCl,51 indicated in the figure with lines. Literature values were either computed from the reported water activity using eqn (1) or the given relation between the osmotic coefficients and the solute molality b(xw) was used directly (for details see ESI†). The solution's osmotic coefficient and the more commonly used co-solute's activity coefficient γ, are related through the Gibbs–Duhem equation as 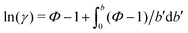 where b is the molal concentration. The agreement between simulations and experimental data for TMAO and urea in Fig. 3D is expected because the simulation forcefields have been developed with the aim to reproduce osmotic coefficients.34,35 The investigated co-solutes display different deviations from ideality: ΦTMAO deviates the strongest, enhancing its osmolyte-capabilities, and ΦNaCl is slightly larger than unity which is typical for salts. Finally, urea forms near-ideal solutions in water.
where b is the molal concentration. The agreement between simulations and experimental data for TMAO and urea in Fig. 3D is expected because the simulation forcefields have been developed with the aim to reproduce osmotic coefficients.34,35 The investigated co-solutes display different deviations from ideality: ΦTMAO deviates the strongest, enhancing its osmolyte-capabilities, and ΦNaCl is slightly larger than unity which is typical for salts. Finally, urea forms near-ideal solutions in water.
Augmentation of eqn (6) by the co-solute osmotic coefficients and their accessible volume yields
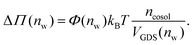 | (7) |
With these refinements, the theoretically predicted osmotic pressures Πtheo = Πwater + ΔΠ fit well to the simulation data (see Fig. 5). Remaining deviations likely originate from the neglect of other effects such as additional electrostatic repulsion in the case of NaCl58 or other altered contributions to the perpendicular equation of state.59 Overall, the agreement between eqn (7) and the simulation data demonstrates that the co-solutes' osmotic pressure is at the heart of the increase in the repulsion. Closer inspection (Fig. 5D) reveals that the osmotic coefficient is the dominant correction at low hydration, while excluded-volume and osmotic coefficient effects are equally important at higher hydration. It becomes clear that TMAO leads to the strongest repulsion because it exhibits unfavorable interactions with the membrane surfaces and at the same time a remarkably high osmotic coefficient. TMAO and the lipids' PC headgroups both have a dipolar/hydrophobic architecture. The high osmotic coefficient and the pronounced depletion at the membrane surfaces therefore likely have the same physical origin previously termed dipolar/hydrophobic frustration.34
Fig. 6A shows the enthalpy/entropy decomposition for DMPC membranes interacting across neat water, where the methodology described earlier25 was used. It is seen that the repulsion is of entropic origin at larger hydration but crosses over to an enthalpy-driven regime at low hydration. The addition of co-solutes significantly increases the magnitude of both contributions as well as their antagonistic interplay. Fig. 6B exemplarily shows the enthalpy/entropy decomposition of the free energy associated with the dehydration of membranes loaded with 10 wt% TMAO, for which the effect is most pronounced and for which complementary thermodynamic information is available.34 The repulsion is seen to be enthalpic throughout the entire separation range. The entropic contribution is of opposite sign but sub-dominant.
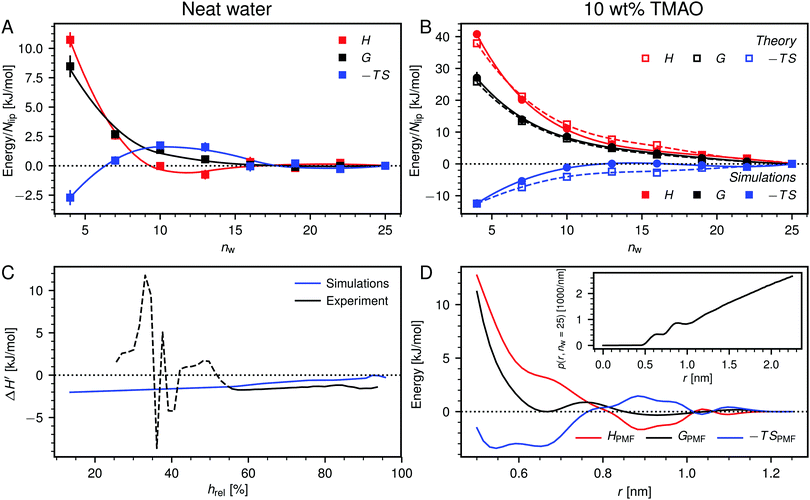 | ||
| Fig. 6 (A) Decomposition of the dehydration free energy, G(nw), in DMPC membrane simulations without added co-solutes into enthalpic and entropic contributions, H(nw) and −TS(nw), respectively. Lines are guides to the eye. (B) Same decomposition for DMPC membranes loaded with 10 wt% TMAO. Open squares are theoretical predictions according to eqn (8). (C) Comparison between experiments and simulations of POPC lipids, regarding the change ΔH′ in the differential hydration enthalpy H′ = dH/dnw due to addition of 5 wt% TMAO. The comparison is only valid for humidities above hrel ≈ 55% (indicated with a solid line style). (D) Potential of mean force, GPMF(r), for the TMAO–TMAO interaction in bulk solutions and its enthalpic and entropic contributions, HPMF(r) and −TSPMF(r), respectively. The TMAO–TMAO center-to-center radial distance is denoted with r. Data are reproduced from the literature.34 Inset: Normalized TMAO–TMAO distance distribution p(r,nw) in DMPC membranes loaded with 10 wt% TMAO at nw = 25. | ||
In Fig. 6C we compare experimental and simulation data for the change 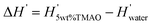 in the differential enthalpy of hydration H′ = dH/dnw when loading POPC membranes with 5 wt% TMAO. The comparison is valid only for relative humidities above hrel ≈ 55%, because in the humidity range below that threshold (indicated with a dashed line style), TMAO forms a separate phase and POPC undergoes a phase transition in the experiments. In the meaningful humidity range (indicated with a solid line style), the simulation data semi-quantitatively agree with the experiments. In fact, the agreement looks even better when ΔH′ is plotted as a function of the hydration level nw (see Fig. S5 in the ESI†). One should keep in mind, however, that in this representation, the water chemical potential deviates between experiments and simulations.
in the differential enthalpy of hydration H′ = dH/dnw when loading POPC membranes with 5 wt% TMAO. The comparison is valid only for relative humidities above hrel ≈ 55%, because in the humidity range below that threshold (indicated with a dashed line style), TMAO forms a separate phase and POPC undergoes a phase transition in the experiments. In the meaningful humidity range (indicated with a solid line style), the simulation data semi-quantitatively agree with the experiments. In fact, the agreement looks even better when ΔH′ is plotted as a function of the hydration level nw (see Fig. S5 in the ESI†). One should keep in mind, however, that in this representation, the water chemical potential deviates between experiments and simulations.
The pairwise mutual repulsion between TMAO molecules in water was reported to be of enthalpic origin34 (see Fig. 6D) and the dehydration of TMAO-loaded membranes is associated with a reduction in the average TMAO/TMAO distance. The enthalpic character of the repulsion between TMAO-loaded membranes can therefore be attributed to the enthalpic character of the TMAO/TMAO mutual repulsion. In fact, the interaction thermodynamics appear dominated by the dehydration of the confined TMAO solution. To take this concept to a quantitative level, the dehydration thermodynamics of TMAO-loaded lipid membranes is approximated in the following as a linear combination of the dehydration thermodynamics of pure membrane dehydration (Gtheolip, Htheolip, and Stheolip) and of the thermodynamics of the TMAO/TMAO pairwise interaction (GtheoTMAO, HtheoTMAO, and StheoTMAO),
| Gtheo(nw) = Gtheolip(nw) + K·GtheoTMAO(nw) | (8a) |
| Htheo(nw) = Htheolip(nw) + K·HtheoTMAO(nw) | (8b) |
| Stheo(nw) = Stheolip(nw) + K·StheoTMAO(nw), | (8c) |
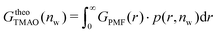 | (9a) |
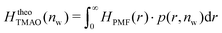 | (9b) |
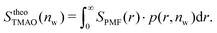 | (9c) |
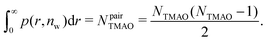 | (10) |
Fig. 7D shows a comparison between experimental pressure–distance curves (POPC loaded with 5 wt% NaCl) and those predicted by the Berger-based and CHARMM36-based forcefield combinations. It is apparent that, especially at larger membrane separations, the added repulsion due to the presence of NaCl is better captured by the CHARMM36-based forcefield combination. This difference can be partially attributed to the difference in VNaClGDS (see Fig. 7C and eqn (7)). It should be noted, however, that the bulk activity coefficient of the NaCl forcefield used in the CHARMM36-based forcefield combination deviates significantly from the experimental behavior (see Fig. S9 in the ESI†). So the CHARMM36 results in Fig. 7 should be considered carefully.
Selected simulations with a CHARMM36-based forcefield combination (i.e., with the CHARMM36 lipid forcefield and TIP3P water) were also performed for the co-solutes TMAO and urea and compared to the results obtained with the Berger-based forcefield combination. As shown in Fig. 7A and B, the influence of the forcefield is practically negligible for TMAO, the osmolyte most extensively discussed in the present work. For urea the agreement between the two forcefield combinations is only qualitative and consistent only with regard to the negative sign of the surface excess (see Fig. 7B). It is, however, important to note that irrespective of any forcefield effects on the quantitative level, all simulations reproduce the repulsion-enhancement due to the presence of co-solutes at least semi-quantitatively (see Fig. 2). More importantly, the physical insights into the repulsion mechanisms are gained from a self-consistent comparison between the simulation results and a theoretical model involving parameters determined with the same forcefields.
4 Conclusions
By combining sorption calorimetry and sorption balance experiments with molecular dynamics simulations, the influence of TMAO, urea, and NaCl on the hydration repulsion between stacked phospholipid membranes was investigated. All these co-solutes are found to enhance the repulsion. For a given level of dehydrating osmotic stress, the presence of co-solutes leads to the retention of a higher hydration level in terms of number of water molecules per lipid or per membrane area. The co-solutes therefore do not only substitute for water molecules but additionally have a moisturizing effect in the literal sense. The simulations, which accurately yield the chemical potential of water, quantitatively reproduce the experimental data and provide detailed insight into the mechanism by which the co-solutes enhance the hydration repulsion.The osmotic pressure generated by the co-solutes confined in the aqueous layer between the membrane surfaces is identified as the source of the additional repulsion. The strength of this effect is found to be strongly dependent on the preferential interaction of the co-solutes with the membrane surfaces and on the osmotic coefficient of the confined co-solute solution. For high enough co-solute contents, the thermodynamics of membrane dehydration is dominated by the thermodynamics of the dehydration of the co-solute solution. With that, the simulations provide the explanation for the remarkably strong moisturizing effect of the osmolyte TMAO, which exhibits highly unfavorable interactions with the membrane surfaces and at the same time a high osmotic coefficient.
In an earlier study by Sukenik et al.,24 TMAO was reported to dehydrate bilayer systems under excess water conditions when TMAO is in a phase-separated aqueous phase. Here we show that the trend is reversed in the absence of excess water, which is the relevant boundary condition in the stratum corneum. This complete reversal of the effect of a co-solute depending on the imposed boundary conditions demonstrates that the same type of co-solute can be used by nature for both moisturizing and dehydrating purposes. In fact, this reversal can be identified also in the data reported by Sukenik et al., where TMAO enhances the hydration repulsion at the highest applied osmotic pressures. Based on the insights gained in our present work, this observation suggests that under these conditions TMAO partitions at least partially into the lipid multilayers, where it contributes to the repulsion via the same mechanisms described above.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
E. Schneck acknowledges support by the Max Planck Society and by the German Research Foundation (DFG) via Emmy-Noether grant (SCHN 1396/1). The DFG is gratefully acknowledged also for financial support (R. R. N. and A. W.-K.) via grant SFB1078. E. Sparr and Q. D. P. acknowledge support by the Swedish Research Council (VR), both through regular grants and the Linnaeus Center of Excellence “Organizing molecular matter”. We thank Lars Wadsö and Vitaly Kocherbitov for help with the sorption calorimetry measurements. We kindly acknowledge Håkan Wennerström for fruitful discussions. Open Access funding provided by the Max Planck Society.References
- V. A. Parsegian, N. Fuller and R. P. Rand, Proc. Natl. Acad. Sci. U. S. A., 1979, 76, 2750–2754 CrossRef CAS PubMed.
- J. Israelachvili and H. Wennerström, Nature, 1996, 379, 219 CrossRef CAS PubMed.
- R. Lipowsky, Nature, 1991, 349, 475 CrossRef CAS PubMed.
- J. Ulminus, H. Wennerstrom, G. Lindblom and G. Arvidson, Biochemistry, 1977, 16, 5742–5745 CrossRef CAS PubMed.
- B. Kowalik, T. Schubert, H. Wada, M. Tanaka, R. R. Netz and E. Schneck, J. Phys. Chem. B, 2015, 119, 14157–14167 CrossRef CAS PubMed.
- E. Sparr and H. Wennerström, Biophys. J., 2001, 81, 1014–1028 CrossRef CAS PubMed.
- P. M. Elias, J. Controlled Release, 1991, 15, 199–208 CrossRef CAS.
- R. Schulz, K. Yamamoto, A. Klossek, R. Flesch, S. Hönzke, F. Rancan, A. Vogt, U. Blume-Peytavi, S. Hedtrich and M. Schäfer-Korting, et al. , Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 3631–3636 CrossRef CAS PubMed.
- K. B. Storey and J. M. Storey, Physiol. Rev., 1988, 68, 27–84 CrossRef CAS PubMed.
- P. H. Yancey, J. Exp. Biol., 2005, 208, 2819–2830 CrossRef CAS PubMed.
- G. O. Kirst, Annu. Rev. Plant Physiol. Plant Mol. Biol., 1990, 41, 21–53 CrossRef CAS.
- I. J. Vereyken, V. Chupin, A. Islamov, A. Kuklin, D. K. Hincha and B. de Kruijff, Biophys. J., 2003, 85, 3058–3065 CrossRef CAS PubMed.
- K. N. Barton, M. M. Buhr and J. S. Ballantyne, Am. J. Physiol., 1999, 276, R397–R406 CAS.
- U.-B. Ramløy, Hum. Reprod., 2000, 15, 26–46 CrossRef PubMed.
- M. Hara and A. Verkman, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 7360–7365 CrossRef CAS PubMed.
- A. V. Rawlings, I. R. Scott, C. R. Harding and P. A. Bowser, J. Invest. Dermatol., 1994, 103, 731–740 CrossRef CAS PubMed.
- S. Björklund, J. M. Andersson, Q. D. Pham, A. Nowacka, D. Topgaard and E. Sparr, Soft Matter, 2014, 10, 4535–4546 RSC.
- C. Katagiri, J. Sato, J. Nomura and M. Denda, J. Dermatol. Sci., 2003, 31, 29–35 CrossRef CAS PubMed.
- S. Kezic, G. O'Regan, N. Yau, A. Sandilands, H. Chen, L. Campbell, K. Kroboth, R. Watson, M. Rowland and W. Irwin McLean, et al. , Allergy, 2011, 66, 934–940 CrossRef CAS PubMed.
- J. H. Crowe, L. M. Crowe and D. Chapman, Science, 1984, 223, 701–703 CrossRef CAS PubMed.
- F. O. Costa-Balogh, H. Wennerström, L. Wadsö and E. Sparr, J. Phys. Chem. B, 2006, 110, 23845–23852 CrossRef CAS PubMed.
- A. Nowacka, S. Douezan, L. Wadsö, D. Topgaard and E. Sparr, Soft Matter, 2012, 8, 1482–1491 RSC.
- Q. D. Pham, A. Wolde-Kidan, A. Gupta, A. Schlaich, E. Schneck, R. R. Netz and E. Sparr, J. Phys. Chem. B, 2018, 122, 6471–6482 CrossRef CAS PubMed.
- S. Sukenik, S. Dunsky, A. Barnoy, I. Shumilin and D. Harries, Phys. Chem. Chem. Phys., 2017, 19, 29862–29871 RSC.
- E. Schneck, F. Sedlmeier and R. R. Netz, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 14405–14409 CrossRef CAS PubMed.
- M. Kanduč, A. Schlaich, A. H. de Vries, J. Jouhet, E. Maréchal, B. Demé, R. R. Netz and E. Schneck, Nat. Commun., 2017, 8, 14899 CrossRef PubMed.
- A. Nilsson, A. Holmgren and G. Lindblom, Biochemistry, 1991, 30, 2126–2133 CrossRef CAS PubMed.
- T. McIntosh, A. Magid and S. Simon, Biochemistry, 1987, 26, 7325–7332 CrossRef CAS PubMed.
- N. Markova, E. Sparr, L. Wadsö and H. Wennerström, J. Phys. Chem. B, 2000, 104, 8053–8060 CrossRef CAS.
- R. A. Robinson and R. H. Stokes, Electrolyte Solutions, Dover Publications, Incorporated, 2nd revised edition, 1959 Search PubMed.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindah, SoftwareX, 2015, 1-2, 19–25 CrossRef.
- O. Berger, O. Edholm and F. Jähnig, Biophys. J., 1997, 72, 2002–2013 CrossRef CAS PubMed.
- H. J. C. Berendsen, J. R. Grigera and T. P. Straatsma, J. Phys. Chem., 1987, 91, 6269–6271 CrossRef CAS.
- E. Schneck, D. Horinek and R. R. Netz, J. Phys. Chem. B, 2013, 117, 8310–8321 CrossRef CAS PubMed.
- S. Weerasinghe and P. E. Smith, J. Phys. Chem. B, 2003, 107, 3891–3898 CrossRef CAS.
- L. X. Dang, J. Am. Chem. Soc., 1995, 117, 6954–6960 CrossRef CAS.
- J. B. Klauda, R. M. Venable, J. A. Freites, J. W. O'Connor, D. J. Tobias, C. Mondragon-Ramirez, I. Vorobyov, A. D. MacKerell and R. W. Pastor, J. Phys. Chem. B, 2010, 114, 7830–7843 CrossRef CAS PubMed.
- R. M. Venable, Y. Luo, K. Gawrisch, B. Roux and R. W. Pastor, J. Phys. Chem. B, 2013, 117, 10183–10192 CrossRef CAS PubMed.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- S. R. Durell, B. R. Brooks and A. Ben-Naim, J. Phys. Chem., 1994, 98, 2198–2202 CrossRef CAS.
- G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101 CrossRef PubMed.
- H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS.
- B. Widom, J. Chem. Phys., 1963, 39, 2808 CrossRef CAS.
- C. H. Bennett, J. Comput. Phys., 1976, 22, 245 CrossRef.
- T.-Y. Lin and S. N. Timasheff, Biochemistry, 1994, 33, 12695–12701 CrossRef CAS PubMed.
- B. Kowalik, A. Schlaich, M. Kanduč, E. Schneck and R. R. Netz, J. Phys. Chem. Lett., 2017, 2869–2874 CrossRef CAS PubMed.
- L. J. Lis, M. McAlister, N. Fuller, R. P. Rand and V. A. Parsegian, Biophys. J., 1982, 37, 657–665 CAS.
- E. S. Courtenay, M. W. Capp, C. F. Anderson and M. T. Record, Biochemistry, 2000, 39, 4455–4471 CrossRef CAS PubMed.
- R. H. Stokes, Aust. J. Chem., 1967, 20, 2087–2100 CrossRef CAS.
- A. R. G. Lang, Aust. J. Chem., 1967, 20, 2017–2023 CrossRef CAS.
- N. Kučerka, S. Tristram-Nagle and J. F. Nagle, J. Membr. Biol., 2006, 208, 193–202 CrossRef PubMed.
- A. Schlaich, B. Kowalik, M. Kanduč, E. Schneck and R. R. Netz, Phys. A, 2015, 418, 105–125 CrossRef CAS.
- R. A. Böckmann, A. Hac, T. Heimburg and H. Grubmüller, Biophys. J., 2003, 85, 1647–1655 CrossRef.
- A. Catte, M. Girych, M. Javanainen, C. Loison, J. Melcr, M. S. Miettinen, L. Monticelli, J. Määttä, V. S. Oganesyan, O. H. S. Ollila, J. Tynkkynen and S. Vilov, Phys. Chem. Chem. Phys., 2016, 18, 32560–32569 RSC.
- G. Pabst, A. Hodzic, J. Štrancar, S. Danner, M. Rappolt and P. Laggner, Biophys. J., 2007, 93, 2688–2696 CrossRef CAS PubMed.
- R. Vácha, S. W. Siu, M. Petrov, R. A. Böckmann, J. Barucha-Kraszewska, P. Jurkiewicz, M. Hof, M. L. Berkowitz and P. Jungwirth, J. Phys. Chem. A, 2009, 113, 7235–7243 CrossRef PubMed.
- H. I. Petrache, T. Zemb, L. Belloni and V. A. Parsegian, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 7982–7987 CrossRef CAS PubMed.
- E. Leontidis, A. Aroti, L. Belloni, M. Dubois and T. Zemb, Biophys. J., 2007, 93, 1591–1607 CrossRef CAS PubMed.
- L. Sapir and D. Harries, Curr. Opin. Colloid Interface Sci., 2015, 20, 3–10 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9cp01953g |
| This journal is © the Owner Societies 2019 |