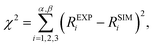Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Elucidating the alkaline oxygen evolution reaction mechanism on platinum†
M.
Favaro
abc,
C.
Valero-Vidal
ad,
J.
Eichhorn
c,
F. M.
Toma
 c,
P. N.
Ross
e,
J.
Yano
bf,
Z.
Liu
gh and
E. J.
Crumlin
c,
P. N.
Ross
e,
J.
Yano
bf,
Z.
Liu
gh and
E. J.
Crumlin
 *ad
*ad
aAdvanced Light Source, Lawrence Berkeley National Laboratory, One Cyclotron Rd, Berkeley, CA 94720, USA. E-mail: ejcrumlin@lbl.gov
bJoint Center for Artificial Photosynthesis, Lawrence Berkeley National Laboratory, One Cyclotron Rd, Berkeley, CA 94720, USA
cChemical Sciences Division, Lawrence Berkeley National Laboratory, One Cyclotron Rd, Berkeley, CA 94720, USA
dJoint Center for Energy Storage Research, Lawrence Berkeley National Laboratory, One Cyclotron Rd, Berkeley, CA 94720, USA
eMaterials Sciences Division, Lawrence Berkeley National Laboratory, One Cyclotron Rd, Berkeley, CA 94720, USA
fMolecular Biophysics and Integrated Bioimaging Division, Lawrence Berkeley National Laboratory, One Cyclotron Rd, Berkeley, CA 94720, USA
gState Key Laboratory of Functional Materials for Informatics, Shanghai Institute of Microsystem and Information Technology, Chinese Academy of Sciences, Shanghai 200050, People's Republic of China
hDivision of Condensed Matter Physics and Photon Science, School of Physical Science and Technology, ShanghaiTech University, Shanghai 200031, China
First published on 7th March 2017
Abstract
Understanding the interplay between surface chemistry, electronic structure, and reaction mechanism of the catalyst at the electrified solid/liquid interface will enable the design of more efficient materials systems for sustainable energy production. The substantial progress in operando characterization, particularly using synchrotron based X-ray spectroscopies, provides the unprecedented opportunity to uncover surface chemical and structural transformations under various (electro)chemical reaction environments. In this work, we study a polycrystalline platinum surface under oxygen evolution conditions in an alkaline electrolyte by means of ambient pressure X-ray photoelectron spectroscopy performed at the electrified solid/liquid interface. We elucidate previously inaccessible aspects of the surface chemistry and structure as a function of the applied potential, allowing us to propose a reaction mechanism for oxygen evolution on a platinum electrode in alkaline solutions.
Introduction
With the world's energy utilization increasing, new solutions are required to satisfy the energy demand while minimizing the environmental impact. To meet this challenge, new technologies must be improved to achieve sustainable energy conversion and consumption.1,2 Fuel cells and electrolyzers3 constitute a promising candidate towards the clean conversion of chemical energy into electricity and electricity into chemical energy, respectively. However, their current use is still partially limited by several factors, such as the limited efficiency and stability of the low cost alternatives to platinum (Pt) for the electrocatalysis of oxygen reduction and evolution reactions (ORR and OER, respectively).4,5 In order to enhance the catalytic performance of next generation fuel cells and electrolyzers, it is necessary to obtain a comprehensive understanding of the chemistry and electronic structure of the catalyst and the reaction intermediates/products under realistic operating conditions.6,7 In particular, Pt has been used as a model system to provide surface chemical and structural transformation insights under various (electro)chemical reaction environments.8–23 Ultimately, the scope of these studies is to expedite the development of novel and cost-effective catalysts with tailored physical/chemical properties, capable of achieving, if not surpassing, the Pt electrocatalytic performance.8,24–27Previous studies have been conducted to indentify the role of Pt oxides in the oxygen evolution reaction pathway (also known as oxygen discharge).8,24–26 Krasilshchikov24,26,28 demonstrated that at high overpotentials the corresponding current density (Tafel slope 120 mV dec−1) depends exponentially on the thickness of the Pt surface oxide. Other studies report much higher Tafel slopes (up to 160 mV dec−1)13,24,26 in both acidic and alkaline environments. Such an increase is often attributed to an increase of the surface oxide layer thickness and Pt dissolution.13,15–26,29 In alkaline media, the reversible binding of a hydroxide ion (OH−) coupled to a one electron oxidation is thought to precede the removal of one proton and one electron to form surface oxide species.30 This hypothesis has been mostly supported so far by surface structure and chemical characterizations far from operando conditions,6,31,32 thereby limiting an unambiguous investigation of the role of Pt oxides in the oxygen evolution catalytic cycle. Moving towards realistic operating conditions, Arrigo et al. recently studied Pt nanoparticles deposited on an acidic-polymer membrane using ambient pressure X-ray photoelectron spectroscopy (APXPS) in a humidified (solid/gas interface) environment.27 The authors found that the first stage of Pt oxidation involves the formation of a surface Pt oxide27,33 where atomic oxygen (O) is weakly bound to Pt (Pt–O).27,34
However, the detailed chemistry, structure, and dynamics of the surface oxide(s) on Pt at an electrified solid/liquid interface as a function of the applied potential and during oxygen evolution as a function of time still remains unclear. A definitive chemical speciation of such species and their role in the reaction pathway has not been completely achieved yet, in particular on Pt surfaces in alkaline conditions.
To achieve a molecular-level comprehension of the OER mechanism, we studied a polycrystalline Pt electrode surface under anodic conditions in an alkaline electrolyte, by means of operando APXPS performed with “tender” X-rays (hν = 4 keV) directly at the electrified solid/liquid interface.35,36 We report the speciation of porous Pt surface oxides as a function of applied potential, thereby elucidating the differences between thermodynamic predictions (Pourbaix diagrams)37 and the actual surface composition under polarization. Moreover, we study the Pt surface chemistry as a function of time during oxygen evolution, thereby observing the evolution of the different Pt oxidation states (as well as their spatial localization in the near-surface region) under non-equilibrium conditions (initial transient) and upon reaching steady state conditions. Based on these findings, we propose an OER mechanism in terms of a catalytic (Tolman) cycle38 for the various oxidized Pt species. We show that the rate-determining step is constituted by activated Pt sites selectively binding OH−. In addition, by coupling the experimental results with numerical simulations of the photoelectron intensity, we reveal that the active sites during OER are located in the sub-surface region, whereas Pt oxides such as Pt(II)O and Pt(IV)O2 are present in the high-surface outer layer and are not actively contributing to the oxygen evolution.
Results
Probing the solid/liquid interface
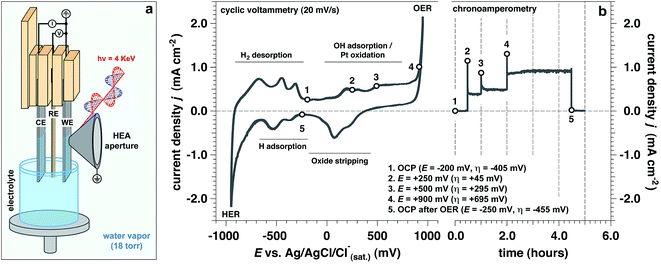
Operando measurements (defined here as a function of the applied potential at a solid/liquid interface) were performed on a polished polycrystalline Pt working electrode (WE) in 1.0 M KOH electrolyte interface using “tender” X-rays (hν = 4 keV) for APXPS,35–40 as depicted in Fig. 1a. The “dip and pull” procedure35–40 enabled us to simultaneously probe ∼21 nm of the aqueous electrolyte and ∼10 nm of the Pt WE using photoelectron spectroscopy, while undergoing electrochemical reactions at the solid/liquid electrified interface. In our three-electrode electrochemical cell,34 we used a polycrystalline Pt foil as the counter electrode (CE) and a Ag/AgCl/Cl(sat.)− as the reference electrode (RE). All potentials are reported with respect to this RE, unless otherwise stated.In order to study the evolution of the current density as a function of applied potential and time (by holding the applied potential at a constant value), we performed both cyclic voltammetry (CV) and chronoamperometry (CA) measurements (Fig. 1b), respectively. We explored different potentials along the anodic branch of the CV from open circuit potential (OCP) up to +900 mV (OER conditions, see Fig. 1b). In addition, the reversibility of the Pt surface chemistry and structure was assessed by returning back to OCP after OER conditions, defined as “OCP after OER”. The overpotential (η) has been computed using the standard Nernstian potential for water oxidation for a pH equal to 13.9 (+205 mV vs. Ag/AgCl/Cl(sat.)−).
To approximate the current density of the thin electrolyte layer under operando conditions formed by the “dip & pull” procedure, we conducted a separate electrochemical experiment that preserved the same “dip & pull” geometries, we masked the bottom of the electrode that was immersed in the bulk electrolyte and compared to an unmasked electrode (see schematization reported in ESI Fig. 1†). The thickness of electrolyte layer on the Pt WE was equal to 21.3 nm. This value was calculated via the inverse Beer–Lambert relation using the attenuation of the Pt 4f core level signal passing from hydrated conditions (saturated environment before “dip & pull” procedure) to the final solid/liquid interface configuration.31,36 We have determined that a bulk (unmasked) current density of about 1.0 mA cm−2 at +900 mV (overpotential η = +695 mV, OER conditions) corresponds to ca. 0.3 mA cm−2 in the nanometric-thick electrolyte layer on the WE surface (ESI Fig. 1b†). This is due to the predominant contribution of the current rising from the part of the WE immersed in the bulk electrolyte. This observation was reaffirmed by electrochemical impedance spectroscopy (EIS) measurements which extracted the polarization resistance (Rp) for the masked and unmasked configurations (see ESI Fig. 2 and 3, Tables 1 and 2 and Discussion 1 for further details†). The ratio between the two configurations polarization resistances (unmasked to masked) is equal to 3.37, thereby confirming that the total current density associated with the thin electrolyte film was about a third of the overall measured current.
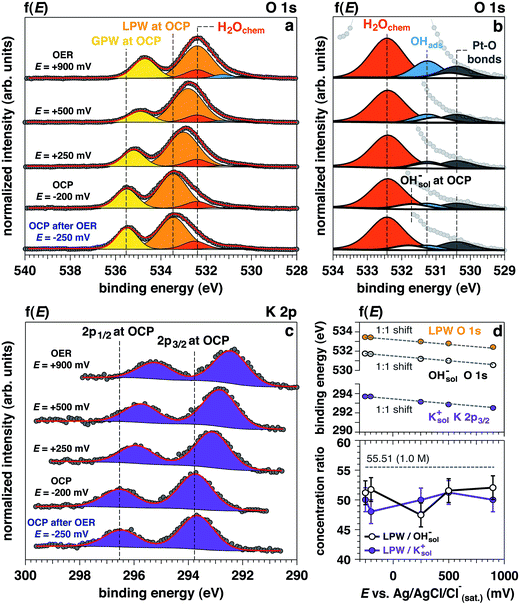
Upon establishing current flow within the nanometric electrolyte layer, we can use the XPS data in Fig. 2 to confirm the applied potential directly at the probing location.35–39 O 1s and K 2p core levels as a function of the applied potential are reported in Fig. 2a–c, respectively. In particular, Fig. 2b reports a magnification of the O 1s multipeak fitting procedure for the low BE tail. Notably, at different applied potentials, the area of the OHsol− (hydroxide ions in solution) and K 2p (solely depicting the K+ ions in solution) spectral feature remains constant throughout the experiment. Indeed, the liquid phase water (LPW)/OHsol− and LPW/K 2p concentration ratio is equal to 51.4 ± 2.1 as the applied potential is changed from OCP to OER conditions (Fig. 2d). Our measurement is therefore in agreement with the expected value for a 1.0 M electrolyte concentration, which is 55.51 water to one KOH.
The binding energy (BE) trends of the O 1s LPW, OHsol− and K 2p3/2 core levels present in the liquid layer as a function of the applied potential is reported in Fig. 2d. The BEs for elements in the electrolyte (BEelectrolyte) obey the relation:
| BEelectrolyte = BE0 − eE | (1) |
E is the applied potential and BE0 is the BE measured in absence of an applied potential. According to eqn (1), the aforementioned core levels shift toward lower BEs with respect to the Fermi level of the sample (grounded to the analyzer, see schematization reported in Fig. 1a) for applied anodic potentials, thereby confirming that potential control is achieved in the measuring spot (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 shift).
1 shift).
From the O 1s low BE tail in Fig. 2b, it is possible to observe that the area of the Pt–O component (centered at 530.4 eV) increases as well as the adsorbed OH− (OHabs− at 531.3 eV).
Finally, the area of the chemisorbed water component (H2Ochem centered at 532.4 eV) also remains constant as the potential changes from OCP to +500 mV, with an increase under OER at +900 mV. Interestingly, upon removing the potential (“OCP after OER”), the peak area does not appreciably change. Such observation is consistent with an increase of the electrode surface area under catalytic conditions, which will be detailed in a following section.
Evolution of Pt surface chemistry as a function of the applied potential
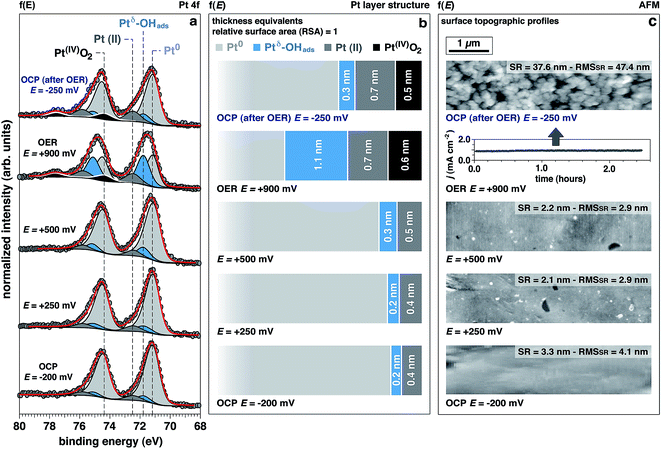
The Pt 4f spectra (Fig. 3) can be de-convoluted into four different spectral components: metal Pt (71.2 eV), Ptδ–OHads (71.8 eV), Pt(II) (72.5 eV), and Pt(IV) (74.6 eV).27,41 Among these different components, Ptδ–OHads provides insights into the OER mechanism at the Pt/electrolyte interface.As proposed by Krasilshchikov28 and Damjanovic,24,26 it is well-accepted that under alkaline conditions the OER on Pt starts with the nucleophilic attack of OH− ion on Pt followed by a fast electron transfer to the metastable configuration where OH− is then chemisorbed on an “activated” platinum site (Ptδ).24,26 The formal positive charge of the Ptδ (set between Pt metal and Pt(II)) in the Ptδ–OHads active site, as suggested by Wagner et al.,42 could explain the spectral position of its corresponding photoelectron peak, centered between the metal and Pt(II) spectral components.
Interestingly, while the integrated area of this component remains unchanged with applied potentials below the OER threshold, it drastically increases under OER conditions. This finding is supported by a similar trend observed in the O 1s spectrum for the OHabs− (Fig. 2a and b). At OCP after OER, the intensity of this component is comparable to the initial OCP state. This reversibility suggests that the formation of this component is driven by high overpotentials (i.e. under OER conditions). Since oxygen evolution in alkaline environments is proceeded by the deprotonation of adsorbed OH−, we conclude that the observed spectral feature, Ptδ–OHads, is representing the active species in the OER catalytic cycle.
Together with Ptδ–OHads, the amount of Pt(II) species increases with the applied potentials, where we observe a sharp increase once the potential is raised to +900 mV (OER conditions). Under this applied potential, the formation of Pt(IV)O2 oxide becomes prominent concurrently with the previously discussed Pt species (Fig. 3).
Understanding the surface and sub-surface structure of Pt electrode under OER conditions
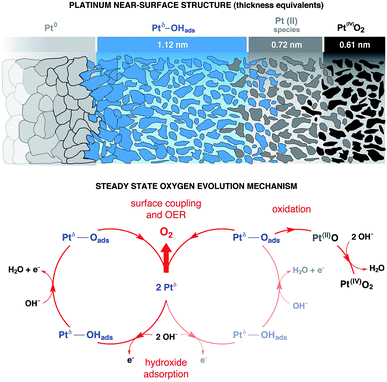
Using numerical simulations of the individual Pt component photoelectron attenuation (averaged over a 300 μm-diameter surface area region, equal to the analyzer cone aperture), we were able to qualitatively determine the surface and sub-surface structure as a function of the applied potential (Fig. 3b). We evaluated a wide range of Pt species configurations ranging in thickness and relative locations, finding that the structure that best matches with the experimental data is constituted by stacked layers of Pt species. In an effort to simplify the simulations, dense layers referred to as “equivalent thickness” are used to represent the actual porosity of the Pt electrode upon OER reconstruction (see detailed explanations about the numerical procedure reported in the Experimental section and ESI Fig. 4†). At OCP and increasing the potential to +500 mV, the Pt WE possesses a sub-surface domain of Ptδ–OHads and an outer (electrolyte facing) layer of Pt(II), present in the form of Pt(II)(OH)2 and Pt(II)O. Under OER conditions at +900 mV, the outermost layer presents an additional layer of Pt(IV)O2, while the Ptδ–OHads increases significantly. The spatial continuity between the Pt(II) and the Pt(IV) layers is ensured by an interfacial region of mixed Pt(II, IV) oxides. As reported in literature,24,25,27,43,44 our data and simulations confirm that the highly electroactive layer constituted by Ptδ–OHads is localized sub-surface, between the metal substrate and a overlayer constituted by Pt(II) and Pt(IV) species.The evolution of the outer surface morphology as a function of the applied potential was studied by ex situ AFM (Fig. 3c). The surface undergoes a clear reconstruction upon OER conditions transitioning from a flat metallic surface at OCP and low applied potentials (as confirmed by the low surface roughness (SR) values) to a high surface area oxidic system after catalytic conditions, characterized by a much higher SR then the pristine surface. Therefore, we believe that the so-called “gelly structure” reported in literature for Pt surfaces under OER conditions in acidic electrolytes,27,43,44 also occurs when the reaction is driven in alkaline environments. Using the previously described simulations, we can investigate the chemistry of the mesoporous (“gelly”) structure, which is composed of a Pt(IV)O2 outer layer and an inner layer (on top of the Ptδ–OHads active phase) constituted by a mixture of Pt(II) phases consisting of Pt(II)(OH)2 and Pt(II)O.
Experimental surface observations compared to thermodynamics predictions
Interestingly, the measured Pt electrode properties differ drastically from the predicted Pt/H2O Pourbaix diagram45 (ESI Fig. 5†). In alkaline conditions (pH 13.9, KOH 1.0 M) at the OCP, Pt should partially oxidize to a Pt(II)(OH)2 phase. Upon increasing the potentials to +250 mV, +500 mV, and +900 mV (+447 mV, +697 mV, and +1097 mV vs. normal hydrogen electrode, respectively), the only thermodynamically stable phase the Pourbaix diagram predicts is Pt(IV)O2.On the other hand, the experimental results clearly shows that up to +500 mV Ptδ–OHads and Pt(II) species are present on the surface (Fig. 3). Notably, the Pt(IV) spectral component is eventually observed only under the OER potential (+900 mV), therefore at a much higher potentials than the thermodynamically predicted in the Pourbaix diagram at the same pH. Such a deviation can be due to kinetic effects that are not taken into account in a merely thermodynamic investigation of the stability of Pt phases. In addition, at OCP after OER, the surface chemistry exhibits a partial chemical hysteresis. While the Ptδ–OHads feature decreases (as a result of the potential removal, as previously discussed), it is still possible to observe both Pt(II) and Pt(IV) spectral fingerprints. On the contrary, the Pourbaix diagram predicts only Pt(II) (present as Pt(II)(OH)2) as the stable phase at this pH value.
Pt surface chemistry evolution under OER conditions
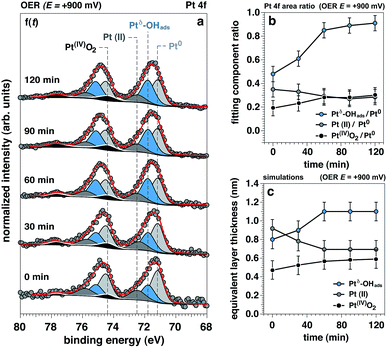
The time evolution of the Pt 4f spectrum and accompanying Pt0-normalized integrated areas of the Pt spectral components under OER conditions at +900 mV is reported in Fig. 4a and b, respectively. The same time evolution for the O 1s and K 2p core levels is reported in ESI Fig. 6,† together with the ionic concentration and the thickness of the electrolyte layer determined as a function of the observation time. Between 0 to 60 minutes under OER conditions we can observe the initial transitions for Ptδ–OHads, Pt(II), and Pt(IV) before stabilizing and reaching steady state conditions (>60 minutes). During this period, it can be seen that the Ptδ–OHads/Pt0 and Pt(IV)/Pt0 ratios increase accompanied by a slight decrease of the Pt(II)/Pt0 ratio with respect to time, Fig. 4b. Using our previously established layered model, we used numerical simulations to estimate the respective “equivalent thicknesses” for each Pt phase (i) and retrieve their in-depth localization as a function of time under catalytic conditions (ii) (Fig. 4c).Proposed Pt structure under catalytic conditions and OER mechanism in alkaline environments
We can now propose a more complete mechanism for platinum OER under alkaline conditions (Fig. 5) by combining our steady state and dynamic information detailed in Fig. 3 and 4 with previous literature. The mesoporosity27,43,44 of the Pt electrode (as seen in Fig. 3c and reported in ref. 27, 43 and 44) is present throughout the near surface structure, and it is composed of 3 regions. Moving from the Pt0 substrate to the outer surface, we have demonstrated the presence of Ptδ–OHads, Pt(II) species (Pt(II)(OH)2 and Pt(II)O) and Pt(IV)O2. As proposed by Krasilshchikov28 and Damjanovic24,26 for oxygen evolution on Pt in alkaline conditions, the formation of the Ptδ–OHads phase is promoted by the nucleophilic attack of hydroxide ions to the metal Pt surface, followed by a fast electron transfer to the metastable configuration where OH− is chemisorbed on an “activated” platinum site (Ptδ).24,26 Overall, this can be rationalized by a mixed electrostatic and thermodynamic effect. As the potential applied to the WE becomes more anodic, the local increase of hydroxyl concentration (within the inner Helmholtz layer, IHL) becomes more pronounced. At the same time the high positive potential at the electrode surface lowers the Pt/OH− surface binding energy whilst the high pH value (13.9) decreases the electrochemical potential of the electrolyte,46 thereby favoring the activation of the Pt surface via hydroxyl adsorption followed by the electron transfer and the consequent formation of the Ptδ–OHads species.47–49 The final surface coupling and deprotonation of the adsorbed OH− leads to the evolution of oxygen. Interestingly, as it can be seen from the time trends reported in Fig. 4b and c, only when a considerable amount of Ptδ–OHads is present on the sub-surface region the surface coupling process and the consequent O2 evolution can occur. This result is extremely important since it directly shows a kinetic limitation that contributes to the observed OER overpotential. The proposed mechanism is schematically represented in Fig. 5.It is important to consider the possibility for Pt(IV) dissolution in the form of a Pt(IV) aquocomplex as indicated by the Pourbaix diagram. Based on our data, we do not observe any Pt dissolution during the potentiostatic measurements. However, one must consider that reversing (or removing) potentials could induce Pt dissolution on the order of tens of nM as reported by Lopes et al.15 The reported dissolution rates are considerably below the detection limit of the APXPS (about 100 mM). Therefore, although we would not be able to detect this process, a Pt dissolution cannot be excluded.50,51
Conclusions
This study revealed the complexity and significant surface chemical reconstruction that takes place on a Pt electrode, in particular on the nature of Ptδ–OHads species, and its crucial role on the OER mechanism. Our findings show that the presence of Ptδ–OHads is triggered by potentials within the OER region: upon removing the applied potential, the concentration of this species drops to similar values observed for the initial OCP whilst the Pt(II) and Pt(IV) oxides chemistries remained essentially unchanged. This observation, together with the fact that the OER in alkaline conditions occurs via the oxidation of the hydroxyl, allows us to conclude that the Ptδ–OHads constitutes the actual rate determining species for oxygen evolution. The combination of APXPS, AFM, and numerical simulations allowed us to provide new insights into the chemical structure of the Pt electrode under OER conditions, showing that the Ptδ–OHads layer is located sub-surface. The presence of the Ptδ–OHads layer leads to the formation of a high surface area oxidic outer layer in which OH− need to diffuse in order to activate the oxygen evolution.This observation allows us to propose that the applied overpotential (above the thermodynamic oxidation potential of water) has two main effects. First, it positively polarizes the electrode surface, which lowers the binding energy of hydroxyl ions and increase their adsorption rate. Second, the OH− may electrostatically be driven through the oxidic porous passivation layer.52 Therefore, from the experimental observations reported here we provide motivation for reevaluating the kinetic limitations (overpotentials) of OER on Pt to take into account both adsorption/electron transfer rate and mass transport effects through the modified electrode under catalytic conditions.
Moreover, we have elucidated the differences between thermodynamic predictions of the Pt phase stability and the actual surface chemistry under polarization. The high chemical sensitivity of XPS probing the solid/liquid electrified interface has allowed us to re-interpret the Pourbaix diagram of Pt. Thus motivating the need for these types of operando experiments and the development of new thermodynamic, kinetic, and computational models for electrified interfaces under realistic operating conditions.53 Expanding this experimental strategy for the study of different materials and catalytic reactions under operando conditions,31,32,54 will open a path for new discoveries that will deepen our knowledge towards the accelerated development of novel tailored materials.
Experimental
Dip & pull method and operando measurements
The three electrodes were mounted into a PEEK electrode housing that was attached to a multi-axis manipulator. Electrical feedthrough within the manipulator connected the WE, RE, and CE to an external potentiostat/galvanostat (Biologic SP 300) to perform operando electrochemistry measurements. During the operation, the WE and the analyzer front cone were commonly grounded.Prior its introduction into the experimental chamber, the electrolyte (KOH 1.0 M aqueous solution) was outgassed for at least 30 min at low pressure (around 10 Torr) in a dedicated off-line chamber. Then, once the manipulator (Fig. 1a) and the outgassed electrolyte were placed into the APXPS experimental chamber, the pressure was carefully lowered down to the water vapor pressure (between 16 and 20 Torr, at r.t.).
To create a solid/liquid interface (WE/electrolyte), all three electrodes were immersed into the electrolyte. Then they were slowly extracted from the electrolyte solution by rising the manipulator at a constant vertical rate. Following this procedure, a thin layer of liquid electrolyte film is formed on the Pt electrode (typical values ranges between 10 and 30 nm); the three electrodes were then positioned at the focal point of the analyzer, giving the possibility of performing XPS investigation of the solid/liquid interface as a function of the applied potential. During the measurements, the bottom parts of the electrodes were kept into the bulk electrolyte, in order to ensure electrical continuity between the thin electrolyte layer on the WE surface and the bulk electrolyte itself.
Electrochemical measurements
The chemicals employed here were high purity reagents and they were used as received without further operations. MilliQ water (DI, ρ = 18.2 MΩ cm) and potassium hydroxide (KOH, 99.99%, Aldrich) were used as solvent and supporting electrolyte, respectively.The working (WE) and counter electrodes (CE, Pt polycrystalline foils, 99.99%, thickness 0.5 mm, Aldrich) were polished to a mirror finish with silicon carbide papers of decreasing grain size (Struers, grit: 2400 and 4000). The samples were then cleaned by two cycles of ultrasonic treatment in a mixture of MilliQ water/ethanol (Aldrich, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) for 10 min. A third ultrasonic cleaning was then conducted in pure MilliQ water for 15 min, followed by a thoroughly rinsing and drying in N2 stream. As reference electrode (RE), a miniaturized leakless Ag/AgCl/Cl(sat.)− RE (ET072-1, eDAQ) was used (standard electrode potential
1) for 10 min. A third ultrasonic cleaning was then conducted in pure MilliQ water for 15 min, followed by a thoroughly rinsing and drying in N2 stream. As reference electrode (RE), a miniaturized leakless Ag/AgCl/Cl(sat.)− RE (ET072-1, eDAQ) was used (standard electrode potential 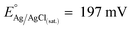 with respect to the normal hydrogen electrode, NHE). All the potentials reported in this work are referred to this RE unless differently stated.
with respect to the normal hydrogen electrode, NHE). All the potentials reported in this work are referred to this RE unless differently stated.
An electrochemical cleaning procedure was conducted by holding the Pt WE at −1200 mV (within the HER region) for 30 minutes, in order to obtain a pure metallic surface and a homogeneous surface, increasing in this way the experimental reproducibility. The cleaning procedure was stopped after reaching the current open circuit potential (OCP) of the cell from the cathodic side. The data acquisition started only when the OCP reached a stable value over the observation time (about 30 minutes). All the voltammetric measurements were conducted at a scan rate of 20 mV s−1.
Electrochemical impedance spectroscopy (EIS) measurements were carried out with the aim of electrochemically evaluate the interfacial properties of the solid/liquid interface. EIS measurements were conducted by measuring the response in current after applying to the WE a sinusoidal wave of potential of 10 mV peak-to-peak voltage amplitude, at OCP (−200 mV) and OER conditions (+900 mV). The frequency of the sinusoidal potential wave was ranging from 105 Hz to 5 mHz, scanning 10 frequencies per decade.
Beamline 9.3.1 and APXPS experimental details
Beamline 9.3.1 at Advanced Light Source (ALS, Lawrence Berkeley National Laboratory) is equipped with a bending magnet and a Si (111) double crystal monochromator (DCM) having a total energy range between 2.0 keV and 7.0 keV (“tender” X-ray range). The minimal spot size at the beamline is 0.7 mm (v) × 1.0 mm (h).For the data acquisition, the pass energy of the Scienta analyzer (R4000 HiPP-2) was set to 200 eV, using a step of 100 meV and a dwell time of 300 ms. Under these conditions, the total resolution (X-rays and analyzer) was equal to about 250 meV at room temperature (r.t.) and at 4 keV. The measurements were taken using a photon energy of 4 keV at r.t. and in normal emission (NE), at a pressure in the experimental chamber matching the water vapor tension at r.t., between 16 and 18 Torr. The detection stage in the analyzer (multichannel plate, MCP) was under high vacuum conditions (∼10−7 Torr) throughout the all experiment, thanks to the differentially pumped electrostatic lens system based on four independent pumping stages. To limit the evaporation from the electrochemical cell we place a larger outgassed solution buffer in the analysis chamber to facilitate the fully humidified environment at room temperature. The calibration of the binding energy (BE) scale was carried out using the Au 4f photoelectron peak as reference (4f7/2 BE = 84.0 eV) as well as the Fermi edge, from a clean gold polycrystalline surface measured under all the investigated experimental conditions.
All the fit reported in this work have been carried out using a Doniach–Šunjić shape for the Au and Pt 4f photoelectron peaks, whereas a symmetrical Voigt function (G/L ratio ranging from 85/15 to 75/25) was used to fit the O 1s photoelectron peaks (after Shirley background subtraction).36 During the fitting procedure, the Shirley background was optimized as well together with the photoelectron intensity of the spectral components, increasing in this manner the precision and reliability of the fitting procedure.36,55,56 The χ2 minimization was ensured by the use of a nonlinear least squares routine, with increased stability over simplex minimization.36,55,56
Atomic force microscopy characterization
AFM measurements were performed under ambient condition using a Bruker Dimension Icon AFM and rectangular silicon cantilevers (RFESP-75, Bruker). Nanometer scale lateral resolution images of surface topography were acquired in peak force (PF) tapping mode at 2 kHz modulation with a PF amplitude of 150 nm. The linear scan rate was set to 0.3 Hz with scan resolution of 256 samples per line. For the applied peak force a maximum value of 40 nN was used to avoid damaging the sample or wearing the tip.Data processing of the raw images was performed using customized Igor procedures.
Numerical simulations of the photoelectron intensity
The numerical simulations of the photoelectron intensity were developed used SESSA software. Technical details and examples of the potentialities of this tool can be found in ref. 57–60.From observations already reported in literature about the oxidic surface structure of Pt under OER conditions,27,44 the simulations were built adopting a conformal layer-by-layer structure “buried” underneath an electrolyte (KOH 1.0 M) film characterized by an average thickness of 21.3 ± 0.9 nm. Three crucial aspects needs to be highlighted:
- The simulations were performed using net and well-defined layer/layer interfaces. This is an approximation of the real configuration, where most likely gradients and mixed regions may exist at the layer/layer interfaces. However, the spatial extension of such regions are typically of about 1–2 nm, a dimension that is typically difficult to access and discriminate with tender X-rays. Therefore, the approximation used here is reasonable at the light of the features offered by the APXPS technique;
- The simulations were conducted by using the well-known growth modes: layer-by-layer or Frank-Van der Merwe, layer-island or Stranski–Krastanov and island formation or Volmer–Weber.61,62 Moreover, for a chosen model, we have investigated different spatial localization of the oxidized Pt chemistries (see summary reported in ESI Fig. 4†). The model that fitted better with the experimental simulations was found by using a chi-square (χ2) statistical test. The quantities used for its evaluation were the Ptδ–OHads/Pt0 (R1), Pt (II)/Pt0 (R2) and Pt(IV)O2/Pt0 (R3) ratios, determined experimentally through the multipeak fitting procedure of Pt 4f photoelectron peak (EXP) and from the numerical simulations (SIM). Therefore:
For the final evaluation of model/configuration, the space of parameters was explored using a variational principle: for each model, the minimum value of the χ2 was achieved by properly adjusting the layer thickness of the different oxidized Pt species. This procedure allows to determine both the structure and the corresponding configuration (layer thicknesses) that best match with the experimental results;
- The relative surface area (RSA) for the top most layer in the calculations have been derived directly from the experimental ex situ AFM surface characterizations reported in Fig. 3.
Author contributions
The manuscript was written through contributions of all authors. M. F. planned and executed the operando APXPS experiments and the numerical simulations, evaluated the data and drafted the manuscript. E. J. C. and Z. L. conceived and supervised the study and drafted the manuscript. C. V. V. performed the EIS analysis, while J. E. performed the AFM characterizations. P. N. R., J. Y. and F. M. T. gave general advisory and actively participated in drafting the manuscript. All authors have given approval to the final version of the manuscript.Conflict of interest
The authors declare no competing financial interests.Acknowledgements
This work was partially supported through the Office of Science, Office of Basic Energy Science (BES), of the U.S. Department of Energy (DOE) under award no. DE-SC0004993 to the Joint Center for Artificial Photosynthesis (JCAP), a DOE Energy Innovation Hub. This work was also supported by the National Natural Science Foundation of China (11227902). The Advanced Light Source is supported by the Director, Office of Science, Office of Basic Energy Sciences, of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231. J. E. and F. M. T acknowledge support by the Laboratory Directed Research and Development Program of Lawrence Berkeley National Laboratory under U.S. Department of Energy contract number DE-AC02-05CH11231.References
- N. S. Lewis and D. G. Nocera, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 15729–15735 CrossRef CAS PubMed.
- J. R. McKone, N. S. Lewis and H. B. Gray, Chem. Mater., 2013, 26, 407–414 CrossRef.
- L. Carrette, K. A. Friedrich and U. Stimming, Fuel cells, 2001, 1, 5–39 CrossRef CAS.
- W. Yu, M. D. Porosoff and J. G. Chen, Chem. Rev., 2012, 112, 5780–5817 CrossRef CAS PubMed.
- Z. Chen, D. Higgins, A. Yu, L. Zhang and J. Zhang, Energy Environ. Sci., 2011, 4, 3167–3192 CAS.
- R. Schlögl, Angew. Chem., Int. Ed., 2015, 54, 3465–3520 CrossRef PubMed.
- B. K. Carpenter, J. N. Harvey and A. J. Orr-Erwing, J. Am. Chem. Soc., 2016, 138, 4695–4705 CrossRef CAS PubMed.
- B. E. Conway and T. C. Liu, Langmuir, 1990, 6, 268–276 CrossRef CAS.
- N. M. Markovic, H. A. Gasteiger and P. N. Ross, J. Phys. Chem., 1996, 100, 6715–6721 CrossRef.
- V. Stamenkovic, B. S. Mun, K. J. J. Mayrhofer, P. N. Ross, N. M. Markovic, J. Rossmeisl, J. Greeley and J. K. Nørskov, Angew. Chem., Int. Ed., 2006, 118, 2963–2967 CrossRef.
- W. Sheng, H. A. Gasteiger and Y. Shao-Horn, J. Electrochem. Soc., 2010, 157, B1529–B1536 CrossRef CAS.
- I. E. L. Stephens, A. S. Bondarenko, F. J. Perez-Alonso, F. Calle-Vallejo, L. Bech, T. P. Johansson, A. K. Jepsen, R. Frydendal, B. P. Knudsen, J. Rossmeisl and I. Chorkendorff, J. Am. Chem. Soc., 2011, 133, 5485–5491 CrossRef CAS PubMed.
- T. Reier, M. Oezaslan and P. Strasser, ACS Catal., 2012, 2, 1765–1772 CrossRef CAS.
- I. E. L. Stephens, A. S. Bondarenko, U. Grønbjerg, J. Rossmeisl and I. Chorkendorff, Energy Environ. Sci., 2012, 5, 6744–6762 CAS.
- P. P. Lopes, D. Strmcnik, D. Tripkovic, J. G. Connell, V. Stamenkovic and N. M. Markovic, ACS Catal., 2016, 6, 2536–2544 CrossRef CAS.
- D. Strmcnik, M. Uchimura, C. Wang, R. Subbaraman, N. Danilovic, D. Van der Vliet, A. P. Paulikas, V. Stamenkovic and N. M. Markovic, Nat. Chem., 2013, 5, 300306 CrossRef PubMed.
- P. Hernandez-Fernandez, F. Masini, D. N. McCarthy, C. E. Strebel, D. Friebel, D. Deiana, P. Malacrida, A. Nierhoff, A. Bodin, A. M. Wise, J. H. Nielsen, T. W. Hansen, A. Nilsson, I. E. L. Stephens and I. Chorkendorff, Nat. Chem., 2014, 6, 732–738 CAS.
- D. Strmcnik, K. Kodama, D. Van Der Vliet, J. Greeley, V. R. Stamenkovic and N. M. Markovic, Nat. Chem., 2009, 1, 466–472 CrossRef CAS PubMed.
- D. Strmcnik, V. Tripkovic, D. Van Der Vliet, K.-C. Chang, V. Komanicky, H. You, G. Karapetrov, J. P. Greeley, V. R. Stamenkovic and N. M. Markovic, J. Am. Chem. Soc., 2008, 130, 15332–15339 CrossRef CAS PubMed.
- L. Gan, C. Cui, M. Heggen, F. Dionigi, S. Rudi and P. Strasser, Science, 2014, 346, 1502–1506 CrossRef CAS PubMed.
- M. Escudero-Escribano, P. Malacrida, M. H. Hansen, U. G. Vej-Hansen, A. Velazquez-Palezuela, V. Tripkovic, J. Schiøtz, J. Rossmeisl, I. E. L. Stephens and I. Chorkendorff, Science, 2016, 352, 73–76 CrossRef CAS PubMed.
- P. P. Lopes, D. Strmcnik, J. S. Jirkovsky, J. G. Connell, V. Stamenkovic and N. M. Markovic, Catal. Today, 2016, 262, 41–47 CrossRef CAS.
- L. F. Sallum, E. R. Gonzalez and J. M. Feliu, Electrochem. Commun., 2016, 72, 83–86 CrossRef CAS.
- A. Damjanovic, A. Dey and J. O. 'M. Bockris, Electrochim. Acta, 1966, 11, 791–814 CrossRef CAS.
- D. Gilroy and B. E. Conway, Can. J. Chem., 1968, 46, 875–890 CrossRef CAS.
- I. V. Birss and A. Damjanovic, J. Electrochem. Soc., 1987, 134, 113–117 CrossRef.
- R. Arrigo, M. Hävecker, M. E. Schuster, C. Ranjan, E. Stotz, A. Knop-Gericke and R. Schlögl, Angew. Chem., Int. Ed., 2013, 52, 1–6 CrossRef PubMed.
- A. L. Krasilshchikov, Zh. Fiz. Khim., 1963, 37, 531 CAS.
- N. Danilovic, R. Subbaraman, K.-C. Chang, S.-H. Chang, Y. J. Kang, J. Snyder, A. P. Paulikas, D. Strmcnik, Y.-T. Kim, D. Myers, V. Stamenkovic and N. M. Markovic, J. Phys. Chem. Lett., 2014, 5, 2474–2478 CrossRef CAS PubMed.
- Y. Surendranath, M. W. Kanan and D. G. Nocera, J. Am. Chem. Soc., 2010, 132, 16501–16509 CrossRef CAS PubMed.
- E. J. Crumlin, Z. Liu, H. Bluhm, W. Yang, J. Guo and Z. Hussain, J. Electron Spectrosc. Relat. Phenom., 2015, 42, 264–273 CrossRef.
- H.-J. Lewerenz, M. F. Lichterman, M. H. Richter, E. J. Crumlin, S. Hu, S. Axnanda, M. Favaro, W. Drisdell, Z. Hussain, B. S. Brunschwig, A. Nilsson, A. Bell, N. S. Lewis and D. Friebel, Electrochim. Acta, 2016, 211, 711–719 CrossRef CAS.
- Y. T. Law, S. Zafeiratos, S. G. Neophytides, A. Orfanidi, D. Costa, T. Dintzer, R. Arrigo, A. Knop-Gericke, R. Schloegl and E. R. Savinova, Chem. Sci., 2015, 6, 5635–5642 RSC.
- Z. Zhu, F. Tao, F. Zheng, R. Chang, Y. Li, L. Heinke, Z. Liu, M. Salmeron and G. A. Somorjai, Nano Lett., 2012, 12, 1491–1497 CrossRef CAS PubMed.
- S. Axnanda, E. J. Crumlin, B. Mao, S. Rani, R. Chag, P. G. Karlsson, M. O. M. Edwards, M. Lundqvist, R. Moberg, P. N. Ross, Z. Hussein and Z. Liu, Sci. Rep., 2015, 5, 9788 CrossRef CAS PubMed.
- M. Favaro, B. Jeong, P. N. Ross, J. Yano, Z. Hussain, Z. Liu and E. J. Crumlin, Nat. Commun., 2016, 7, 12695 CrossRef CAS PubMed.
- M. Pourbaix, National Association of Corrosion Engineers, 1974 Search PubMed.
- C. A. Tolman, Chem. Soc. Rev., 1972, 1, 337–353 RSC.
- M. F. Lichterman, S. Hu, M. H. Richter, E. J. Crumlin, S. Axnanda, M. Favaro, W. Drisdell, Z. Hussein, T. Mayer, B. S. Brunschwig, N. S. Lewis, Z. Liu and H.-J. Lewerenz, Energy Environ. Sci., 2015, 8, 2409–2416 CAS.
- A. Eilert, F. Cavalca, F. S. Roberts, J. Osterwalder, C. Liu, M. Favaro, E. J. Crumlin, H. Ogasawara, D. Friebel, L. G. M. Pettersson and A. Nilsson, J. Phys. Chem. Lett., 2017, 8, 285–290 CrossRef CAS PubMed.
- V. A. Saveleva, V. Papaefthimiou, M. K. Daletou, W. H. Doh, C. Ulhaq-Buillet, M. Diebold, S. Zaiferatos and E. R. Savinova, J. Phys. Chem. C, 2016, 120, 15930–15940 CAS.
- F. T. Wagner and T. E. Moylan, Surf. Sci., 1987, 191, 121–146 CrossRef CAS.
- M. Peuckert and H. Ibach, Surf. Sci., 1984, 136, 319–326 CrossRef CAS.
- A. E. Bolzan and A. J. Arvia, J. Electroanal. Chem., 1994, 375, 157–162 CrossRef CAS.
- The thermodynamic predictions of the stability of the different Pt species as a function of applied potential and pH have been determined by simulating the corresponding Pourbaix diagram with the Materials Project facility A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002 CrossRef; A. Jain, G. Hautier, S. P. Ong, C. Moore, C. Fischer, K. Persson and G. Ceder, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 045115 CrossRef.
- P. Daubinger, J. Kieninger, T. Unmüssig and G. A. Urban, Phys. Chem. Chem. Phys., 2014, 16, 8392–8399 RSC.
- G. B. Fisher and B. A. Sexton, Phys. Rev. Lett., 1980, 44, 683–686 CrossRef CAS.
- A. V. Melo, W. E. O'Grady, G. S. Chottiner and R. W. Hoffman, Appl. Surf. Sci., 1985, 21, 160–167 CrossRef CAS.
- S. Yamamoto, H. Bluhm, K. Andersson, G. Ketteler, H. Ogasawara, M. Salmeron and A. Nilsson, J. Phys.: Condens. Matter, 2008, 20, 184025 CrossRef.
- T. Binninger, R. Mohamed, K. Waltar, E. Fabbri, P. Levecque, R. Kötz and T. J. Schmidt, Sci. Rep., 2015, 5, 12167 CrossRef CAS PubMed.
- H. Dau, C. Limberg, T. Reier, M. Risch, S. Roggan and P. Strasser, ChemCatChem, 2010, 2, 724–761 CrossRef CAS.
- J. Yang, J. K. Cooper, F. M. Toma, K. A. Walczak, M. Favaro, J. W. Beeman, L. H. Hess, C. Wang, C. Zhu, S. Gul, J. Yano, C. Kisielowski, A. Schwartzberg and I. D. Sharp, Nat. Mater. DOI:10.1038/nmat4794.
- F. M. Toma, J. K. Cooper, V. Kunzelmann, M. T. McDowell, J. Yu, D. M. Larson, N. J. Borys, C. Abelyan, J. W. Beeman, K. M. Yu, J. Yang, L. Chen, M. R. Shaner, J. Spurgeon, F. A. Houle, K. A. Persson and I. D. Sharp, Nat. Commun., 2016, 7, 12012 CrossRef PubMed.
- M. Favaro, W. S. Drisdell, M. A. Marcus, J. M. Gregoire, E. J. Crumlin, J. A. Haber and J. Yano, ACS Catal., 2017, 7, 1248–1258 CrossRef CAS.
- S. Evans, Surf. Interface Anal., 1991, 17, 85–93 CrossRef CAS.
- J. Muñoz-Flores and A. Herrera-Gomez, J. Electron Spectrosc. Relat. Phenom., 2012, 184, 533–541 CrossRef.
- W. Smekal, W. S. M. Werner and C. J. Powell, Surf. Interface Anal., 2005, 37, 1059–1067 CrossRef CAS.
- S. Techane, D. R. Baer and D. G. Castner, Anal. Chem., 2011, 83, 6704–6712 CrossRef CAS PubMed.
- W. S. M. Werner, M. Chudzicki, W. Smekal and C. J. Powell, Appl. Phys. Lett., 2014, 104, 233106 CrossRef.
- W. S. M. Werner, W. Smekal, T. Hisch, J. Himmelsbach and C. J. Powell, J. Electron Spectrosc. Relat. Phenom., 2013, 190, 137–143 CrossRef CAS.
- H. Brune, H. Röder, C. Boragno and K. Kern, Phys. Rev. Lett., 1994, 73, 1955–1958 CrossRef CAS PubMed.
- K. Bromann, H. Brune, H. Röder and K. Kern, Phys. Rev. Lett., 1995, 75, 677–680 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ta00409e |
| This journal is © The Royal Society of Chemistry 2017 |