Effects of temperature-induced lattice distortion and phase evolution on electromagnetic wave absorption in high-entropy powders
Hailing
Yang
ab,
Ji
Zou
 *ac,
Neng
Zhang
bd,
Lin
Li
ab,
Jingjing
Liu
b,
Haibin
Ma
a,
Weichao
Bao
d,
Wei
Ji
a,
Weimin
Wang
ac and
Zhengyi
Fu
*ac,
Neng
Zhang
bd,
Lin
Li
ab,
Jingjing
Liu
b,
Haibin
Ma
a,
Weichao
Bao
d,
Wei
Ji
a,
Weimin
Wang
ac and
Zhengyi
Fu
 ac
ac
aState Key Laboratory of Advanced Technology for Materials Synthesis and Processing, Wuhan University of Technology, Wuhan, 430070, China. E-mail: ji.zou@whut.edu.cn; Tel: +86-(027)-87884448
bSchool of Materials Science and Engineering, Wuhan University of Technology, Wuhan, 430070, China
cHubei Longzhong Laboratory, Xiangyang 441000, Hubei, China
dState Key Laboratory of High Performance Ceramics, Shanghai Institute of Ceramics, Shanghai 200050, China
First published on 22nd October 2025
Abstract
High entropy transition metal diborides (HEBs) have garnered significant attention in various fields due to their excellent thermal stability, oxidation resistance, and electromagnetic wave absorption (EMA) properties. Nevertheless, the mechanism underlying their EMA enhancement remains incompletely understood. In this study, (Ti, Zr, Hf, Nb, Ta)B2 powder, a baseline material for HEBs, was synthesized through a sol–gel method using inorganic salts as metal sources. By systematically varying the synthesis temperature (1400 °C, 1650 °C, and 1800 °C, designated as MB14, MB16, and MB18, respectively), HEB powders with varied degrees of solid solution were successfully prepared. Compared to ZrB2, the impedance matching and reflection loss (RL) of MB14 had slightly improved due to the element solid solution and the presence of the byproduct hexagonal BN which encapsulated diboride powders. MB18 achieved a minimum RL value of −34.79 dB at 17.84 GHz with a thickness of 3.8 mm, and an effective absorption bandwidth (EAB) of 1.12 GHz. As the synthesis temperature increased, the lattice distortion caused by multi-principal elements became more pronounced, which not only regulated impedance matching by reducing the dielectric constant but also induced various dielectric loss mechanisms. Therefore, for HEBs, processing parameters should be optimized to suppress phase separation, thereby enhancing their EMA performance.
Introduction
Currently, with the rapid development of radar detection and communication technology, there is an increasingly urgent demand for electromagnetic wave absorption (EMA) materials in the aerospace industry, stealth technology, and high-temperature electromagnetic protection applications.1–3 Although traditional EMA materials (such as ferrites, polymer-based composites, and carbon matrix composites) exhibit superior electromagnetic dissipation performance, they also suffer from impedance mismatch, structural instability and insufficient oxidation resistance at high temperatures.4–6 In particular in applications involving key structures of hypersonic vehicles such as engine exhaust nozzles and nose cones, the development of materials that combine efficient broadband electromagnetic wave absorption with good mechanical properties and oxidation/ablation resistance would demonstrate high multifunctional potential. Such capabilities are expected to offer designers broader design space for the integration of structure and function.5,7,8In recent years, high-entropy diboride (HEB) ceramics have demonstrated exceptional tunable properties and high-temperature stability due to their unique high-entropy effects (including lattice distortion, sluggish diffusion, and “cocktail” effects), offering new insights for the design of EMA materials.7,9–11 Beyond their intrinsic layered structure of alternating boron and transition metal atoms that enables high conductivity and conductive loss,9,12 the multi-principal components synergy further enhances the dielectric/magnetic loss capability via tailored electronic structures and defect concentrations.10,11,13 In contrast to conventional single-element borides, which often suffer from limited tunability in impedance matching, single loss mechanism, and inadequate wave absorption performance, high-entropy borides demonstrate significant superiority.3,9,14 Numerous studies have focused on modulating the EMA properties of HEBs. One strategy is through composition and microstructure design to induce multiple interfaces or dielectric/magnetic heterostructures, which could simultaneously improve impedance matching and promote multiple internal reflections of electromagnetic waves within the materials.15,16 Gong et al.16 successfully prepared (V, Ti, Ta, Nb)B2-SiC composite powders with uniformly dispersed SiC whiskers via a milling-assisted boro/carbothermal reduction route, achieving a minimum reflection loss (RLmin) of −44.9 at a thickness of 4.4 mm. Another aspect mainly focuses on modifying the intrinsic properties of materials, such as adjusting elemental composition, and increasing the number of principal elements.11,13,17 Zhang et al.9 demonstrated that the introduction of magnetic Cr element into (Zr, Hf, Nb, Ta)B2 significantly enhanced the impedance matching of the resulting (Zr, Hf, Nb, Ta, Cr)B2 material through optimized complex permittivity and complex permeability. This strategy achieved the expansion of effective absorption bandwidth (EAB) from 7.6 GHz to 11.0 GHz, attaining a RLmin of −56.2 dB (8.48 GHz, 2.63 mm).
Although HEB powders have made significant progress as promising EMA materials, most investigations have focused on single-phase HEB powders. Moreover, powders synthesized at different temperatures exhibit significant differences in phase composition and morphology, and the underlying mechanism by which these variations affect EMA performance remains unclear. On the one hand, high temperatures facilitate the solid solution process and induce lattice distortions within the particles, which may enhance their EMA performance.18,19 On the other hand, as the absorber size is reduced from micron-scale to nano-scale, the high surface area nano-absorbers contain abundant surface atoms and numerous dangling bonds, which enhance particle activity and interfacial polarization. Consequently, high temperature induced grain growth may degrade their EMA performance.3,20,21 Nevertheless, the relative contribution of these two mechanisms in enhancing the EMA performance of high-entropy borides requires further investigation.
Compared with the conventional powder mixing based boro/carbothermal reduction route, the sol–gel process facilitates atomic-level mixing and generates high-surface-area nanopowders at low temperatures, providing an efficient synthetic strategy for HEB powders.22 Herein, ZrB2 and (Ti, Zr, Hf, Nb, Ta)B2 powders were synthesized using a sol–gel method, and the effects of synthesis temperatures on their electromagnetic wave absorption properties were investigated, along with the underlying absorption mechanisms.
Experimental
Zr(NO3)4·5H2O (AR, Shanghai Macklin Biochemical Technology Co., Ltd., Shanghai, China), HfCl4 (99.5%), NbCl5 (99%), TaCl5 (99%) and C16H36O4Ti (99.0%) (Shanghai Aladdin Biochemical Technology Co., Ltd., Shanghai, China) were used as five metal sources. Boric acid (H3BO3, AR) and sucrose (C12H22O11, AR) (Sinopharm Chemical Reagent Co., Ltd., Shanghai, China) were used as boron and carbon sources. Acetylacetone (acac) (C5H8O2, AR, Sinopharm Chemical Reagent Co., Ltd., Shanghai, China) was used as the chelating agent. Five equimolar metal salts and the chelating agent, acac, were dissolved in alcohol to obtain a yellow transparent sol. With a molar ratio of M![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) B
B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C = 1
C = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4
4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5.5, H3BO3 and C12H22O11 were dissolved in water and then dropped into the above sol. The mixture was continuously stirred at 80 °C in a reflux device until a uniform sol was achieved, then further stirred until nearly all the water had evaporated. After drying at 110 °C, the precursor with brown color was obtained. Finally, as-ground powders were further pyrolyzed at 1400 °C, 1650 °C, and 1800 °C for 1.5 hours to obtain boride powders with different degrees of solid solution, named MB14, MB16, and MB18, respectively.
5.5, H3BO3 and C12H22O11 were dissolved in water and then dropped into the above sol. The mixture was continuously stirred at 80 °C in a reflux device until a uniform sol was achieved, then further stirred until nearly all the water had evaporated. After drying at 110 °C, the precursor with brown color was obtained. Finally, as-ground powders were further pyrolyzed at 1400 °C, 1650 °C, and 1800 °C for 1.5 hours to obtain boride powders with different degrees of solid solution, named MB14, MB16, and MB18, respectively.
The morphology and elemental analyses of precursors and pyrolysis products were performed using a field-emission scanning electron microscope (FESEM, SU8230, Hitachi, Japan). The composition of pyrolysis powders was determined by X-ray diffraction (XRD, Empyrean series 3, Netherlands) with Cu Kα radiation (k = 0.15406 nm). Element compositions and chemical states were examined by X-ray photoelectron spectroscopy (XPS, ESCALAB 250Xi, Thermo Fisher, USA). Detailed microstructure and local elemental mappings of powders were measured using a scanning transmission electron microscope (STEM, TalosF200S, Thermo Fisher, USA). The atomically resolved HAADF images were characterized using a Spherical Aberration Corrected Transmission Electron Microscope (ACTEM, Spectre300, Thermo Fisher, USA). The intensity (∼1200) and center (∼600) of atomic sites in denoised images were determined using the CalAtom software with a multiple-ellipses fitting method.23 Displacement separation analysis was employed to further ascertain the atomic displacement by determining the ideal lattice atomic positions through Fourier space filtering, and the corresponding strain maps were generated by the geometric phase analysis.24 According to ASTM D7449, the electromagnetic (EM) parameters of as-synthesized powders were determined using a vector network analyzer (VNA, N5234A, Agilent, USA) using a coaxial method in the frequency range of 2.0–18.0 GHz, and annular samples (Φout = 7.00 mm, Φin = 3.04 mm) prepared by mixing and pressing as-synthesized powders and paraffin at a mass ratio of 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3.
3.
Results and discussion
Calcined powders were vacuum heat treated at various temperatures to obtain diboride powders with varying degrees of solid solution. As shown in Fig. 1a, the XRD pattern exhibited dual-phase (HEB1 & HEB2) in MB14. Although both phases exhibited the AlB2-type structure, differences in their lattice parameters gave rise to two distinct sets of diffraction peaks. A comparison with five standard single-phase boride patterns revealed that the diffraction peaks of HEB1 were positioned closer to those of TiB2, TaB2, and NbB2, while the diffraction peaks of HEB2 were closer to ZrB2 and HfB2. TEM and corresponding EDS mapping (Fig. 2) further confirmed their compositional inhomogeneity, with HEB1 predominantly enriched in Ti, Ta, and Nb, while HEB2 exhibited higher concentrations of Zr and Hf in agreement with previous reports.18 As the temperature increased to 1650 °C, the diffraction peaks progressively converged. Rietveld refinement of the XRD patterns was conducted to analyze the phase evolution (Fig. 1). Using the (Nb1/3Ta1/3Ti1/3)B2 and (Zr1/2Hf1/2)B2 models for HEB1 and HEB2, respectively (Fig. 1b), the analysis showed that increasing the temperature caused the progressive dissolution of the larger atomic radius Zr and Hf atoms from HEB2 into HEB1. This dissolution resulted in the expansion of the lattice parameters of HEB1 (Fig. 1c). A single-phase HEB was finally achieved at 1800 °C, exhibiting a theoretical density of 8.164 g cm−3 and lattice parameters (a = 3.1138 Å, c = 3.3934 Å), they are all larger than the corresponding values in the original HEB1 (7.698 g cm−3, a = 3.0859 Å, c = 3.3135 Å). | ||
| Fig. 1 (a) XRD patterns of diboride powders synthesized at 1400 °C, 1650 °C, and 1800 °C, compared with reference patterns of single-phase borides (TiB2 (ICDD: 00-035-0741), ZrB2 (ICDD: 00-034-0423), HfB2 (ICDD: 00-038-1398), NbB2 (ICDD: 00-035-0742), TaB2 (ICDD: 00-038-1462)), (b) and (c) Rietveld refinement of XRD patterns in Fig. 1a, (d) corresponding XPS spectra of B 1s and Zr 3d in as-synthesized powders. | ||
 | ||
| Fig. 2 SEM, TEM with corresponding EDS maps and HR-TEM analysis, grain size distribution maps of MB14 (a–c, k), MB16 (d–f, l), and MB18 (g–j, m). | ||
XPS spectra of B 1s in MB14, MB16 and MB18 are compared as shown in Fig. 1d. Two peaks of 192.71 eV and 187.86 eV (Fig. 1d) in MB14 could be attributed to B–O (192 eV) and B–M bonds, which might originate from B2O3 and HEB, respectively.18,25 Additionally, the peak between them, located at 190.88 eV, was similar to the position of B 1s (190.9 eV) in hBN.26 The formation of it had been attributed to the decomposition products of nitrate that could react with B2O3 and C.18,27 The relative intensity of the BN peak in XPS spectra decreased at 1650 °C and disappeared completely at 1800 °C. TEM further demonstrated the formation of BN in MB14, and the EDS mappings (Fig. 2b) indicated that the dark region corresponded to the HEB particles, while the bright region, characterized by a thin sheet morphology, was identified to be hBN. In particular, Fig. 2c showed that hBN nanostructures encapsulated the HEB particles, forming a typical core–shell structure. The lattice spacing of 3.32 Å belonged to the (002) crystal plane of hBN and the lattice spacing of 3.30 Å was in accordance with the (001) crystal plane of HEB powders, and two grains are tightly bonded. With increasing pyrolysis temperature, due to the decomposition in vacuum, less amounts of hBN were detected in MB16, and no residual hBN was observed in MB18, which is consistent with the XPS results. Obviously, the dual-phase MB14 powder consisted predominantly of fine spherical particles (Fig. 2a). With increasing temperature, MB16 powders (Fig. 2d and e) developed into a short columnar morphology, accompanied by an increase in median particle size (d50) from 142.84 nm to 214.68 nm (Fig. 2k and l), while retaining their dual-phase structure according to the XRD. These results suggested that grain growth was kinetically favored over complete solid-solution formation at 1650 °C. In contrast, MB18 demonstrated a uniform spherical morphology with homogeneous elemental distribution of all five constituent metals, and their d50 increased to 678.17 nm (Fig. 2m). A selected area electron diffraction pattern along the [101] axis presented a single-crystal hexagonal structure (Fig. 2i). The corresponding HRTEM image demonstrated the periodic lattice structure of the synthesized powder, with a lattice spacing of 2.68 Å for the (100) crystal plane (Fig. 2j). This finding corroborated the XRD results (Fig. 1a), demonstrating successful synthesis of a phase-pure HEB at 1800 °C.
Complex permittivity (εr = ε′ − jε″) and complex permeability (μr = μ′ − jμ″) of HEB powders were used to investigate the EM properties. The real part ε′ and μ′, respectively, reflect the storage capability of electric and magnetic energy, whereas the imaginary parts of ε″ and μ″ represent the loss capability.28 Based on the transmission line theory and the metal backplane model, the electromagnetic wave absorption (EMA) performance of materials is evaluated using reflection loss (RL) values (eqn (1)), which assess the reflection intensity of EM waves at the surface of materials.9,29 Impedance matching (Z = |Zin/Z0|) is also a crucial parameter to evaluate the transmission performance of EMA materials, which could be derived from eqn (2).30,31
 | (1) |
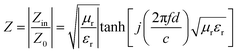 | (2) |
The EMA performance of materials depends on both their dielectric/magnetic loss capabilities and impedance matching characteristics.3,33 As illustrated in Fig. 3, ZrB2 exhibited high ε′ and ε″, which indicated its excellent dielectric loss capability without considering impedance matching. For high entropy powders, the complex permittivity decreased in the order MB16 > MB14 > MB18, which was primarily attributed to their electrical conductivity.3,34 With the increase in temperature, atomic disorder in the powders gradually increased, causing enhanced electron scattering and electrical resistivity, which subsequently caused a decrease in conductivity.35,36 Remarkably, the single-phase MB18 exhibited the lowest values of ε′ and ε″ due to the conductivity of 3.3 × 106 S m−1 significantly lower than that of ZrB2 (2.17 × 107 S m−1).3,34,36 MB14 exhibited lower complex permittivity than MB16 due to the presence of BN and finer grain size-induced interfacial scattering (Fig. 2b, c and k), which collectively suppressed the formation of a continuous conductive network. For all the obtained powder, μ′ was close to 1 and μ″ approached 0 (Fig. 3c and d), and the value of tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δμ (Fig. 3g) fluctuated around 0.02, indicating that ZrB2 and (Ti, Zr, Hf, Nb, Ta)B2 were lacking magnetism.37 This indicated that the loss mechanisms of all samples were dominated by the dielectric loss, and the order of dielectric loss capability decreased in the order ZrB2 > MB16 > MB14 > MB18 based on complex permittivity and tan
δμ (Fig. 3g) fluctuated around 0.02, indicating that ZrB2 and (Ti, Zr, Hf, Nb, Ta)B2 were lacking magnetism.37 This indicated that the loss mechanisms of all samples were dominated by the dielectric loss, and the order of dielectric loss capability decreased in the order ZrB2 > MB16 > MB14 > MB18 based on complex permittivity and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δε (Fig. 3a, b and e). Attenuation constant α represents the dissipative electromagnetic capability, the equation is as follows:
δε (Fig. 3a, b and e). Attenuation constant α represents the dissipative electromagnetic capability, the equation is as follows:
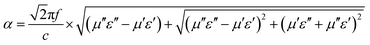 | (3) |
Generally, the α value exhibits a positive correlation with the attenuation capacity of the absorber.28,38 As illustrated in Fig. 3h, the α values of all samples follow the same order as their complex permittivity (ε′ and ε″). However, the electromagnetic wave absorption performance showed the opposite trend as shown in RL maps (Fig. 4). ZrB2 exhibited the worst EMA performance, with RL values predominantly exceeding −2 dB and a minimum RL of merely −2.15 dB. Although the dual-phase MB14 (RLmin = −9.05 dB) and MB16 (RLmin = −2.76 dB) powders demonstrated marginally improved EMA capabilities compared to ZrB2, their performance remained insufficient for practical applications. Obviously, the EMA performance of MB18 with single-phase was significantly enhanced, achieving an optimal RL value of −34.79 dB at 17.84 GHz with a matching thickness of 3.8 mm, indicating an effective absorption of 99.9%, and the EAB was 1.12 GHz. The performance enhancement was primarily attributed to improved impedance matching. As shown in Fig. 4(a3)–(d3), due to the significant mismatch between ε′ and μ′, as well as between ε″ and μ″, ZrB2 showed the worst impedance matching of 0.14. While MB14 and MB16 showed slight improvements but remained below 0.5 and 0.2, respectively, MB18 achieved optimal matching (0.8–1.2) at 13–18 GHz. According to Weston's theorem, when εr is approximately equal to μr, the material exhibits better impedance matching, and the zone back-scattered field is around zero, which facilitates the plane electromagnetic wave into the interior of the absorber.14,38 Due to ZrB2 with higher conductivity, a continuous conduction current was formed on the surface, obstructing the entry of electromagnetic waves into the material.9,38 The increase in temperature promoted the high-entropy transformation of powders, leading to a reduction in complex permittivity, which enhanced impedance matching and consequently improved EMA performance. As depicted in Fig. 4(e1)–(e3), all RL peaks shift toward higher frequency regions with decreasing thickness, which can be explained by the 1/4 wavelength model as described in eqn (4):39,40
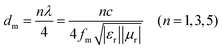 | (4) |
Atomic-resolution HAADF-STEM images (Fig. 5) were collected and analyzed to elucidate the mechanism for EMA performance. As the temperature increased, more atoms gradually dissolved into the solid solution, which was manifested by the atomic intensity contrast. Atomic-resolution images along the [100] zone axis from (Ta, Nb)-rich region of MB14 and MB16 samples were selected based on Fig. 2 for comparison. Notably, the full width at half maximum (FWHM) of the Gaussian-fitted intensity curves increased from 0.287 at 1400 °C to 0.318 at 1650 °C and further rose markedly to 0.739 at 1800 °C (Fig. 5(a2)–(c2)). The observed broadening indicated enhanced atomic solid solubility at higher temperatures, confirming complete overcoming of the solvation energy barrier at 1800 °C. Therefore, atomic displacement and strain distribution images revealed that MB18 exhibited the highest average atomic displacement (8.74 pm) compared to MB14 and MB16, accompanied by significant lattice distortion regions at εxx and εyy with a strain rate ≥2%. Theoretically, in the absence of BN formation, the lattice strain was expected to increase with the temperature due to the enhanced solid solubility. It was confirmed by comparing the nearly BN-free dual-phase MB16 with the single-phase MB18, which revealed a significant increase in lattice distortion. However, MB14 exhibited a larger mean atomic displacement (7.33 pm) compared to MB16 (5.27 pm), with particularly pronounced lattice distortion along the [001] direction (εxx). One possible explanation was the poor crystallinity of the nano MB14 powder (Fig. 2a), leading to structural disorder, while the MB16 powder (Fig. 2d), demonstrated improved crystallinity through grain growth, resulting in reduced atomic disorder. Additionally, as illustrated in Fig. 2c, the epitaxial growth of BN (002) on HEB (001) caused partial replacement of B atoms in HEB particles by N atoms, thereby increasing the lattice distortion rate in the [001] direction (Fig. 5(a3) and (a4)). Stronger lattice distortion and enhanced electron localization may reduce the free electron density, leading to a decrease in ε′ (Fig. 3a).41 Concurrently, enhanced electron scattering reduced conductivity, thereby diminishing ε″, and the increased lattice distortion functioned as effective polarization centers, promoting electromagnetic energy dissipation.9,42 As-observed lattice distortion degree was in an order of MB18 > MB14 > MB16, which was inversely correlated with the complex permittivity. This point is consistent with the proposed mechanism. Furthermore, the averaged particle sizes in MB14 (142.84 nm) and MB16 are 142.84 nm and 214.68 nm, which are much finer than that of MB18 (678.17 nm). Finer particles are expected to favor interfacial polarization due to their high surface energy and abundant dangling bonds.20,21 However, single-phase MB18, with the largest averaged particle size (678.17 nm), exhibited superior electromagnetic wave absorption (EMA) performance. This indicates that lattice distortion induced by high-temperature synthesis plays a more dominant role in determining EMA properties than the effect of particle refinement. Dielectric loss comprises not only the conduction loss related to conductivity, but also the Debye relaxation loss dominated by the dipole polarization.43 As shown in Fig. 3f, compared to pure ZrB2, MB14 exhibited two Cole–Cole semicircles, which may be attributable to interfacial polarization induced by the heterogeneous BN@HEB core–shell structure and lattice distortions resulting from elemental solid solution. In contrast, MB16 exhibited fewer semicircles owing to the missing of hBN coating and improved HEB crystallinity. Remarkably, MB18 displayed more semicircles, suggesting the coexistence of multiple polarization mechanisms, which can be linked to the formation of abundant boundary defects due to N-atom substitution at B sites in the near-surface HEB structure during BN decomposition (Fig. 2h), as well as enhanced polarization relaxation resulting from pronounced lattice distortion. Although the increased particle size of single-phase high-entropy powders at elevated temperature reduced interfacial polarization loss, the lattice distortion induced by high-entropy effects optimized impedance matching and enhanced dipole polarization, collectively resulting in superior electromagnetic wave absorption (EMA) performance compared to poor-solid-solubility borides (MB14 and MB16).
Conclusions
In summary, precursor powders obtained using a the sol–gel method were heat-treated at different temperatures, successfully synthesizing (Ti, Zr, Hf, Nb, Ta)B2 powders with identical nominal composition but varying degrees of solid solution. Compared to ZrB2, high entropy effects effectively modulated microwave absorption properties. The increased synthesis temperature induced both lattice distortion and particle growth, yet the former had a greater impact on their electromagnetic wave absorption. Consequently, the single-phase (Ti, Zr, Hf, Nb, Ta)B2 synthesized at 1800 °C achieved a good combination of properties, including a minimum reflection loss of −34.79 dB at 17.84 GHz with a matching thickness of 3.8 mm, and an effective absorption bandwidth of 1.12 GHz. When the synthesis temperature was reduced, all these properties degraded.Author contributions
All authors contributed to this article. Sample preparation: H. L. Yang; XRD and XPS measurements: H. L. Yang and L. Li; TEM and HAADF-STEM measurements: N. Zhang and W. C. Bao; methodology: J. Zou, W. C. Bao; writing – original version preparation: H. L. Yang and J. Zou; supervising review and editing: J. Zou, J. J. Liu, and W. Ji; project administration, supervision, and funding acquisition: J. Zou, H. B. Ma, W. M. Wang, and Z. Y. Fu. All authors gave approval for the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Data availability
All data supporting the findings of this study are available from the corresponding author upon reasonable request.Acknowledgements
This work was financially supported by the National Natural Science Foundation of China (52332003, 52293373, 52022072 and 52202067), the Hubei Provincial Natural Science Foundation of China (Distinguished Young Scholars 2022CFA042) and Independent Innovation Projects of the Hubei Longzhong Laboratory (2022ZZ-10).References
- C. S. Ma, W. B. Yu, G. Z. Ma and H. D. Wang, Crit. Rev. Solid State Mater. Sci., 2022, 48, 726–753 CrossRef.
- M. Zhang, M. S. Cao, Q. Q. Wang, X. X. Wang, W. Q. Cao, H. J. Yang and J. Yuan, J. Mater. Sci. Technol., 2023, 132, 42–49 CrossRef CAS.
- X. Jian, W. Tian, J. Li, L. J. Deng, Z. W. Zhou, L. Zhang, H. P. Lu, L. J. Yin and N. Mahmood, ACS Appl. Mater. Interfaces, 2019, 11, 15869–15880 CrossRef CAS PubMed.
- Y. J. Zhang, C. Y. Liu, X. R. Zhao, M. H. Yao, X. F. Miao and F. Xu, J. Magn. Magn. Mater., 2020, 494, 165828 CrossRef CAS.
- C. Wang, V. Murugadoss, J. Kong, Z. F. He, X. M. Mai, Q. Shao, Y. J. Chen, L. Guo, C. T. Liu, S. Angaiah and Z. H. Guo, Carbon, 2018, 140, 696–733 CrossRef CAS.
- J. M. Qi, C. B. Liang, K. P. Ruan, M. K. Li, H. Guo, M. K. He, H. Qiu, Y. Q. Guo and J. W. Gu, Natl. Sci. Rev., 2025, nwaf394 CrossRef.
- W. M. Zhang, B. Zhao, N. Ni, H. M. Xiang, F. Z. Dai, S. J. Wu and Y. C. Zhou, J. Mater. Sci. Technol., 2021, 87, 155–166 CrossRef CAS.
- Y. Wang, S. H. Yi, X. Sun, W. Y. Yang, L. Lu, S. N. Guo, G. B. Ji and Z. H. Xiao, Mater. Today Nano., 2025, 29, 100572 CrossRef CAS.
- W. M. Zhang, F. Z. Dai, H. M. Xiang, B. Zhao, X. H. Wang, N. Ni, R. Karre, S. J. Wu and Y. C. Zhou, J. Adv. Ceram., 2021, 10, 1299–1316 CrossRef CAS.
- J. T. Zhang, W. L. Wang, Z. X. Zhang, J. Q. Chen, X. N. Sun, G. X. Sun, Y. J. Liang, G. F. Han and W. B. Zhang, J. Alloys Compd., 2023, 966, 171593 CrossRef CAS.
- S. Y. Zeng, Q. Y. Chen, Q. J. Chen, X. Y. Wang, P. Sun, C. C. Liu, T. Zhu, Y. Zhu, W. L. Zhang, Y. Z. Wang and N. Jiang, Mater. Today Commun., 2025, 43, 111670 CrossRef CAS.
- M. Mallik, A. J. Kailath, K. K. Ray and R. Mitra, J. Eur. Ceram. Soc., 2012, 32, 2545–2555 CrossRef CAS.
- F. C. Gu, W. Wang, H. Meng, Y. W. Liu, L. Zhuang, H. L. Yu and Y. H. Chu, Matter, 2025, 8, 102004 CrossRef CAS.
- F. Qin and C. Brosseau, J. Appl. Phys., 2012, 111, 061301 CrossRef.
- J. Y. Cheng, H. B. Zhang, Y. F. Xiong, L. F. Gao, B. Wen, H. Raza, H. Wang, G. P. Zheng, D. Q. Zhang and H. Zhang, J. Materiomics, 2021, 7, 1233–1263 CrossRef.
- Y. B. Gong, Z. G. Yang, X. G. Wei, S. L. Song and S. Q. Ma, J. Mater. Sci., 2022, 57, 9218–9230 CrossRef CAS.
- C. C. Liu, Q. Y. Chen, P. Sun, X. Y. Wang, S. Y. Zeng, Q. J. Chen, T. Zhu, Y. Zhu, W. L. Zhang, H. Song, Y. Z. Wang, K. Nishimura, H. S. Liu and N. Jiang, J. Adv. Ceram., 2025, 14, 9221030 CrossRef CAS.
- H. L. Yang, J. Zou, Z. M. Xiong, J. J. Liu, W. M. Wang and Z. Y. Fu, J. Mater. Sci. Technol., 2024, 178, 133–142 CrossRef CAS.
- Z. G. Yang, Y. B. Gong, S. L. Song, G. Yu and S. Q. Ma, J. Asian Ceram. Soc., 2021, 9, 1275–1281 CrossRef.
- H. Y. Nan, F. Luo, H. Y. Jia, H. W. Deng, C. H. Wang and Q. Chen, J. Mater. Sci.: Mater. Electron., 2022, 33, 16488–16500 CrossRef CAS.
- H. L. Zhu, Y. J. Bai, R. Liu, N. Lun, Y. X. Qi, F. D. Han and J. Q. Bi, J. Mater. Chem., 2011, 21, 13581 RSC.
- Y. Yang, J. Q. Bi, X. C. Gao, K. N. Sun, L. J. Qiao, G. D. Liang and H. Y. Wang, Ceram. Int., 2023, 49, 19523–19527 CrossRef CAS.
- Q. Zhang, L. Y. Zhang, C. H. Jin, Y. M. Wang and F. Lin, Ultramicroscopy, 2019, 202, 114–120 CrossRef CAS.
- W. Wang, S. X. Liu, Y. Wang, B. H. Jia, Y. Huang, L. Xie, B. B. Jiang and J. Q. He, Sci. Adv., 2024, 10, eadp4372 CrossRef CAS PubMed.
- A. R. Burke, C. R. Brown, W. C. Bowling, J. E. Glaub, D. Kapsch, C. M. Love, R. B. Whitaker and W. E. Moddeman, Surf. Interface Anal., 2004, 11, 353–358 CrossRef.
- L. J. Ci, L. Song, C. H. Jin, D. Jariwala, D. X. Wu, Y. J. Li, A. Srivastava, Z. F. Wang, K. Storr, L. Balicas, F. Liu and P. M. Ajayan, Nat. Mater., 2010, 9, 430–435 CrossRef CAS PubMed.
- A. Aydoğdu and N. Sevinç, J. Eur. Ceram. Soc., 2003, 23, 3021–3034 CrossRef.
- Y. Guo, H. S. Long, Z. Q. Wang, S. J. Luo, L. Xu, C. T. Liu, C. Y. Shen and H. Liu, Adv. Compos. Hybrid Mater., 2025, 8, 207 CrossRef CAS.
- M. Green and X. B. Chen, J. Materiomics, 2019, 5, 503–541 CrossRef.
- H. Sun, R. C. Che, X. You, Y. S. Jiang, Z. B. Yang, J. Deng, L. B. Qiu and H. S. Peng, Adv. Mater., 2014, 26, 8120–8125 CrossRef CAS.
- J. Jin, H. S. Long, H. Liu, Y. Guo, T. T. Bai, B. B. Xu, M. A. Amin, H. Qiu, M. H. Helal, C. T. Liu, C. Y. Shen, Z. M. El-Bahy and Z. H. Guo, Nano Res., 2024, 17, 7290–7300 CrossRef CAS.
- Y. X. Xia, W. W. Gao and C. Gao, Adv. Funct. Mater., 2022, 32, 2204591 CrossRef CAS.
- G. Z. Wang, Z. Gao, S. W. Tang, C. Q. Chen, F. F. Duan, S. C. Zhao, S. W. Lin, Y. H. Feng, L. Zhou and Y. Qin, ACS Nano, 2012, 6, 11009–11017 CrossRef CAS PubMed.
- S. Q. Guo, Y. Kagawa, T. Nishimura, D. H. Chung and J. M. Yang, J. Eur. Ceram. Soc., 2008, 28, 1279–1285 CrossRef CAS.
- E. W. Neuman, M. Thompson, W. G. Fahrenholtz and G. E. Hilmas, J. Eur. Ceram. Soc., 2021, 41, 7434–7441 CrossRef CAS.
- Q. Liu, L. Xu, J. Zou, J. Liu, S. Qiu, W. Ji, W. Wang and Z. Fu, Compos. Pt. B-Eng., 2024, 287, 111868 CrossRef CAS.
- Y. Q. Bai, B. Zhong, Y. L. Yu, M. Wang, J. Zhang, B. Zhang, K. X. Gao, A. M. Liang, C. Y. Wang and J. Y. Zhang, npj 2D Mater. Appl, 2019, 3, 32 CrossRef.
- X. S. Qi, J. L. Xu, Q. Hu, Y. Deng, R. Xie, Y. Jiang, W. Zhong and Y. W. Du, Sci. Rep., 2016, 6, 28310 CrossRef CAS.
- Y. Wu, Y. Zhao, M. Zhou, S. J. Tan, R. Peymanfar, B. Aslibeiki and G. B. Ji, Nano-Micro Lett., 2022, 14, 171 CrossRef CAS PubMed.
- S. Gupta and N. H. Tai, Carbon, 2019, 152, 159–187 CrossRef CAS.
- Z. F. Zou, L. Xu, J. Zou, S. H. Qiu, J. J. Liu, W. Ji, W. W. Wu, Z. H. Han, W. M. Wang and Z. Y. Fu, J. Mater. Sci. Teechnol., 2026, 242, 226–237 CrossRef.
- S. H. Qiu, J. Zou, J. J. Liu, Q. L. He, J. J. Xie, Y. C. Zhou, W. Ji, W. M. Wang and Z. Y. Fu, Acta Mater., 2025, 288, 120817 CrossRef CAS.
- X. T. Chen, Z. D. Wang, M. Zhou, Y. Zhao, S. L. Tang and G. B. Ji, Chem. Eng. J., 2023, 452, 139110 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2026 |



