Open Access Article
Open Access ArticleIonic organic terahertz crystals: a perspective on design and solid-state phonon absorption
O-Pil
Kwon
 *a and
Mojca
Jazbinsek
*a and
Mojca
Jazbinsek
 *b
*b
aDepartment of Molecular Science and Technology, Ajou University, Suwon 16499, Korea. E-mail: opilkwon@ajou.ac.kr
bInstitute of Computational Physics, Zurich University of Applied Sciences (ZHAW), 8401 Winterthur, Switzerland. E-mail: mojca.jazbinsek@zhaw.ch
First published on 28th August 2024
Abstract
Ionic organic nonlinear optical crystals have been established as efficient terahertz (THz) wave generators with a high generated THz power and a very wide bandwidth and can also be used as ultra-broad THz detectors. In this perspective, we discuss various design strategies to obtain high-performance ionic organic THz crystals. The introduction of aromatic coulombic interaction groups and acentric head-to-tail cation–anion assembly groups, as well as the control of the van der Waals volume of aromatic ions, are common to many top-level ionic organic THz crystals. Solid-state molecular and phonon vibrations of these crystals strongly influence the characteristics of THz generation and detection, in addition to their optical and nonlinear optical properties. The THz vibrational modes depend on the chemical structure, intermolecular interaction ability, crystal structure, void volume, and crystal density of organic THz crystals. To give a perspective on the future design of optimized ionic organic THz crystals and the influence of their phonon modes on ultra-broadband THz applications, we discuss both the structural factors that influence these modes and their specific influence on THz optical properties.
1. Ionic organic THz crystals
Organic nonlinear optical materials are very promising for diverse terahertz (THz) applications as well as for high-speed optical modulators for telecommunications.1–17 Achieving second-order optical nonlinearity in organic materials requires a well-aligned, non-centrosymmetric molecular ordering of nonlinear optical chromophores, which is mainly the case in two types of materials: poled polymers and self-assembled single crystals. In poled polymers, highly polar chromophores are non-centrosymmetrically aligned from a randomly oriented state by an additional poling process with a strong electric field, e.g., few kV cm−1, applied above the glass transition temperature. This can lead to very large second-order nonlinear optical susceptibilities, enabling for example electro-optic coefficients of a few hundred pm V−1.8–12 However, it is extremely challenging to achieve long lifetimes of poled polymer devices due to: (i) a strong tendency to randomize the orientation of highly polar chromophores towards centrosymmetric molecular order, and (ii) a limited photochemical stability when using high-power lasers.18,19 For THz applications in addition, it is difficult to fabricate thick poled films with an in-plane poling direction that is optimal for efficient THz generation and detection.On the other hand, organic nonlinear optical crystals have several advantages compared to poled polymers, but there are other challenges. In organic nonlinear optical crystals, (i) there is no need for a poling process due to non-centrosymmetric self-assembly of chromophores in the crystalline state, (ii) there are no issues with temporal stability due to chromophore reorientation, at least below the lowest phase transition temperature (mostly melting temperature), and (iii) the photochemical stability is relatively high due to the high density (i.e., low oxygen content), resulting in a high damage threshold, important for THz applications. However, only few types of chromophores self-assemble with a non-centrosymmetric molecular order in the crystalline state. Most push–pull chromophores with high molecular optical nonlinearity – consisting of a long π-conjugated bridge and various polar substituents – result in a centrosymmetric crystal structure. For example, at present, all chromophores that lead to poled polymer systems with record-high electro-optic coefficients beyond 100 pm V−1 crystallize in centrosymmetric arrangements or have difficulty crystallizing. Although first organic nonlinear optical crystals were already reported four to five decades ago,20–23 designing organic crystals with a large macroscopic optical nonlinearity is still challenging. In this perspective, we discuss the design strategies to achieve highly efficient nonlinear optical organic crystals, mainly targeting the specific requirements for THz applications.
THz applications may require different crystal and optical characteristics to high-speed integrated optics. Both applications profit from a large macroscopic second-order optical nonlinearity. For example, the THz wave generation efficiency and the THz detection sensitivity increase with the effective second-order nonlinear optical susceptibility and the electro-optic coefficient.4 On the other hand, the involved frequency ranges are distinguishable: while the modulation frequencies in integrated optics are currently still in the sub-THz range, they may extend to several THz to tens of THz for THz-specific applications, such as THz spectroscopy and imaging. For both applications also the materials properties at optical and (near-)infrared wavelengths are important, defining the best velocity-matching conditions. The origins of optical characteristics such as refractive index, absorption coefficient and their dispersion are different at optical and THz frequencies as illustrated in Fig. 1.24 Consequently, although both applications are based on second-order optical nonlinearity, the design strategies for organic crystals for THz applications may have both similarities and differences compared to those for integrated optics.2–12
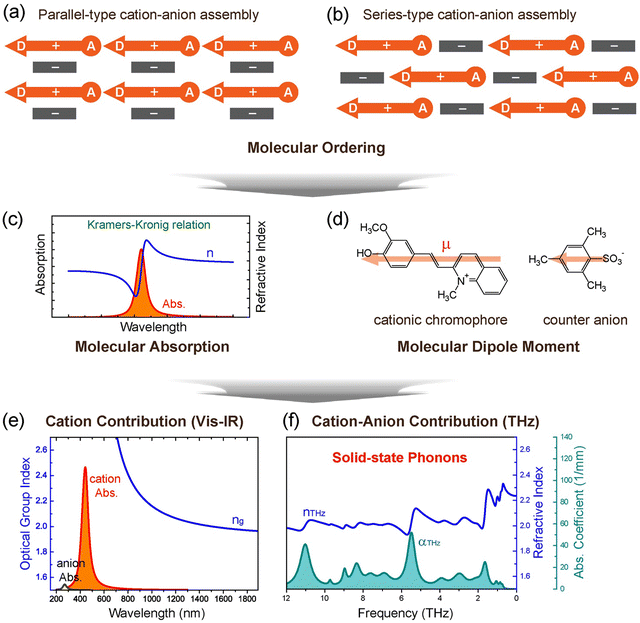 | ||
| Fig. 1 Schematics of the design strategy for benchmark ionic organic THz crystals, self-assembly of nonlinear optical cationic chromophores and counter anions. Non-centrosymmetric molecular ordering with a high order parameter, based on (a) parallel- and (b) series-type cation–anion assembly. (c) Correlation between the molecular absorption and the refractive index via the Kramers–Kronig relation. (d) Dipole moment of chromophores and anions. (e) and (f) Different contribution of cations and anions to the optical properties and solid-state molecular phonon vibrations of crystals (HMQ-TMS crystals in this example). Reproduced and adapted with permission.24 Copyright 2023, Wiley-VCH. | ||
Organic THz crystals can generate intense THz waves with high optical-to-THz conversion efficiency and broad bandwidth, by using two different approaches for optical pumping, either based on optical rectification of femtosecond laser pulses25–31 or difference frequency generation of nanosecond or picosecond laser pulses.32–37 For efficient THz wave generation and detection, good phase matching between optical and THz frequencies, as well as low absorption in both optical and THz frequency ranges are required. The optical characteristics in (near-)infrared and THz frequency ranges strongly depend on the chemical structure and their crystal characteristics such as molecular ordering features and crystal density (Fig. 1). The optimal thickness of organic THz crystals is often in the range of 0.1–1.0 mm for broadband THz applications (a few mm for narrowband THz applications), while for integrated optics, thin films and microstructures with thickness in the range of 0.1–10 μm are required.2–12
Therefore, to develop high-performance THz organic crystals, the design strategy should simultaneously target (i) large second-order nonlinear optical susceptibility resulting from non-centrosymmetric ordering of highly nonlinear chromophores with a high order parameter, (ii) low absorption in optical and THz frequency ranges; e.g. a strong suppression of molecular phonon vibrations for low THz self-absorption, (iii) good phase matching between optical and THz pulses, (iv) optimal thickness in the (sub-)millimeter scale, and (v) good bulk single-crystal growth ability with high optical quality and large-area plate-shape morphology.
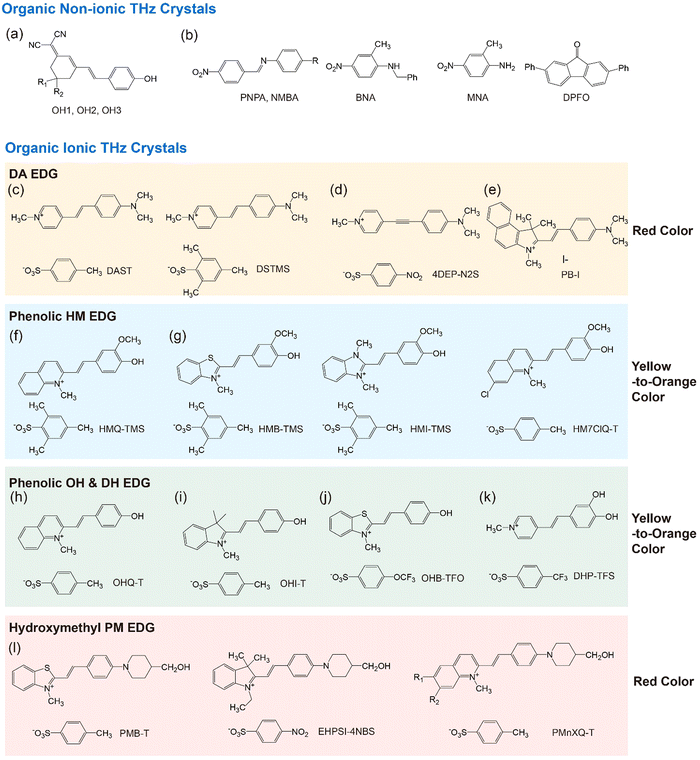
Organic THz crystals can be classified into two types, based on either non-ionic or ionic chromophores (Fig. 2).38–58 For both types, main supramolecular interactions are intermolecular (and interionic) secondary bonds such as hydrogen bonds, face-to-face and edge-to-face π–π interactions, and halogen bonds. In ionic organic THz crystals, strong coulombic interactions are additionally formed. Both non-ionic and ionic organic THz crystals may exhibit excellent THz wave generation performance: e.g., strong THz electric field of few MV cm−1 and ultra-broad bandwidth of over 15 THz.2–7 Each organic THz crystal, even within the same type (non-ionic or ionic), has different THz wave generation characteristics, strongly depending on their intrinsic material properties, crystal orientation and size, as well as extrinsic optical parameters of laser systems such as the pulse width, repetition rate, pump fluence and wavelength. Note that in many cases the melting temperature of ionic organic THz crystals (typically above 200 °C) is higher than that of non-ionic organic THz crystals. A higher melting temperature is beneficial for high environmental stability and reduced thermal stress during optical pumping.
During the last two decades, several new organic THz (and nonlinear optical) crystals have been developed.2–7,37–40,43–67 Many of those new crystals are presented in Fig. 2, including also a few crystals reported before 2000.38–58 For both non-ionic and ionic THz crystals, even a small change of the chemical structure often leads to a radical change in the crystal structure. In most cases, it is presently still not possible to predict the resulting crystal structures based on the chemical structure alone. For example, when modifying the chemical structure of non-ionic polyene OH1 crystals, only two analogous crystals, OH2 and OH3 that exhibit a similar non-centrosymmetric molecular ordering feature with high order parameter have been identified (Fig. 2(a)),38–40 while other analogous derivatives exhibited different crystal structures or even centrosymmetric crystal structures.
In terms of chemical structure, a greater number of ionic than non-ionic organic THz crystals based on highly nonlinear styryl-type chromophores have been reported during the last two decades (Fig. 2). Ionic organic THz crystals often allow larger changes of the chemical structure of the corresponding chromophores to achieve a similar non-centrosymmetric molecular ordering with a high order parameter. For example, when the chemical structure of the quinolinium electron withdrawing group (EWG) of the cationic chromophore in ionic HMQ-TMS (Fig. 2(f)) crystals is modified to benzothiazolium, benzimidazolium, and halogenated quinolinium EWGs, the resulting crystals HMB-TMS, HMI-TMS, HM7ClQ-T (Fig. 2(g)) exhibit similar molecular ordering features with a high order parameter.48–51 In addition, changing the chemical structure of only anions in many cases also results in a similar crystal structure: e.g., for DAST and DSTMS crystals (Fig. 2(c)).44,45 This is attributed to introducing strong coulombic interactions in ionic organic THz crystals. We note here that although some of the ionic organic THz crystals with chemical structure modification result in similar molecular ordering features, their intrinsic material parameters such as the optical and physical properties, solid-state molecular phonon vibrations, melting temperature, crystal density, and crystal growth properties can still be substantially different. This can lead to largely different THz characteristics.
In the following Section 2, we discuss the details of the design strategy commonly observed in benchmark ionic organic THz crystals with a high order parameter. In Section 3, we discuss the solid-state molecular phonon vibrations of organic THz crystals that depend on the chemical structure, intermolecular interaction ability, crystal structure, void volume, and crystal density. In addition, we discuss the influence of molecular phonons on the characteristics of THz generation and detection. This gives a perspective on the future design of optimized ionic organic THz crystals and the influence of their phonon modes on THz applications.
2. Design of ionic organic THz crystals
2.1 Introducing strong intermolecular interaction groups
Organic THz crystals must achieve a non-centrosymmetric ordering of nonlinear optical chromophores to exhibit a second-order optical nonlinearity. The perfectly parallel alignment of chromophores in the crystalline state (or a high order parameter) is challenging due to the difficulty of predicting the crystal structure. This is because long π-conjugated (ionic and non-ionic) chromophores with various polar substituents (e.g., electron donating groups (EDGs) and EWGs) create complex intermolecular interactions such as hydrogen bonds, halogen bonds, van der Waals interactions, face-to-face and edge-to-face π–π interactions, and ion–π interactions. Among various design strategies, inducing strong intermolecular (interionic) interactions for highly polar chromophores is very attractive to overcome the centrosymmetric tendency in the crystalline state.In this perspective, a high order parameter roughly refers to the value of the order parameter cos3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θp of above ∼0.8, for which the molecular ordering angle θp of chromophores is less than ∼20 degrees. The molecular ordering angle θp of chromophores is as usually defined as the angle between the main charge transfer axis of the chromophores and the polar axis of the crystal.68
θp of above ∼0.8, for which the molecular ordering angle θp of chromophores is less than ∼20 degrees. The molecular ordering angle θp of chromophores is as usually defined as the angle between the main charge transfer axis of the chromophores and the polar axis of the crystal.68
In many benchmark ionic organic THz crystals with a high order parameter (e.g., Fig. 2(c)–(l)), two interionic interaction groups commonly appear: (i) aromatic coulombic interaction groups and (ii) acentric head-to-tail cation–anion assembly groups. The combination of aromatic cationic chromophores and aromatic counter anions have shown to be an efficient design strategy to obtain (close-to) perfectly parallel alignment of cationic chromophores with a high order parameter. For example, DAST and DSTMS crystals are based on the pyridinium-based 4-(4-(dimethylamino)styryl)-1-methylpyridinium (DAS) cation and benzenesulfonate anion, 4-methylbenzenesulfonate (T) and 2,4,6-trimethylbenzenesulfonate (TMS), respectively (Fig. 2(c)).44,45 Their strongest interionic interactions are aromatic coulombic interactions between Ar(+) cation of pyridinium EWG on DAS cations and Ar–SO3− on benzenesulfonate anions. With DAS cationic chromophores, introducing various aromatic sulfonates (benzenesulfonates, naphthalene-sulfonates, thiophene-sulfonates) result in non-centrosymmetric crystal structures with a high order parameter.69,70
However, the approach based only on using aromatic coulombic interaction groups (e.g., between Ar(+) and Ar–SO3−) is rather limited for developing new ionic organic THz crystals, which was shown by an additional chemical modification of the DAS cationic chromophore. As the chemical structure of the N-methyl pyridinium based DAS cation was modified, most cases resulted in centrosymmetric crystal structures or non-centrosymmetric structures with a low order parameter. One of the exceptional cases is the 4DEP cationic chromophore with a triple bond instead of a double bond in the DAS cation. New crystals based on 4DEP with benzenesulfonate anions (Fig. 2(d)) resulted in a desired high order parameter.46
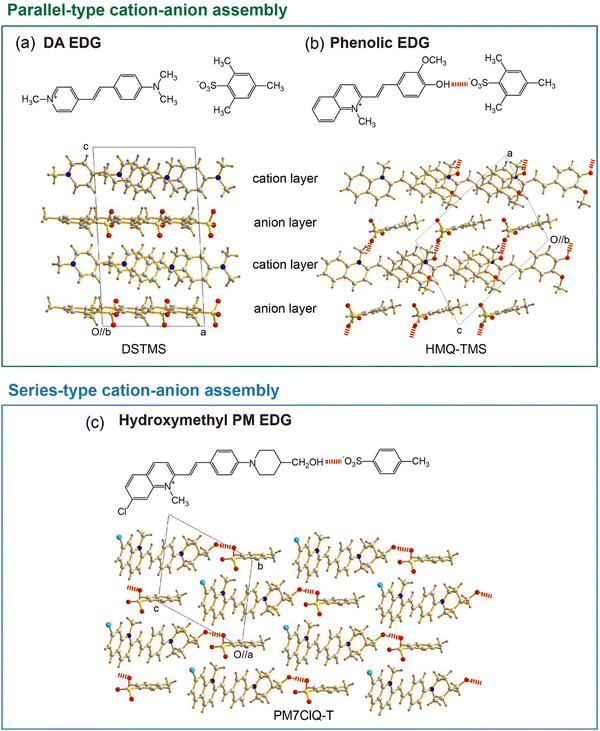
Besides using aromatic coulombic interaction groups, introducing acentric head-to-tail cation–anion assembly groups has been identified as an efficient design strategy for obtaining efficient organic THz ionic crystals. Ionic organic THz crystals in Fig. 2(c)–(e)44–47 are based on 4-(dimethylamino)phenyl (DA) EDG that does not have strong hydrogen bond capability. In contrast, introducing phenolic or hydroxymethyl groups on EDGs into cationic chromophores (Fig. 2(f)–(l))48–58 shows a strong tendency to form optimal non-centrosymmetric molecular ordering with high order parameter, based on the acentric head-to-tail cation–anion assembly with strong hydrogen bond between –OH⋯−O3S–Ar groups (Fig. 3(b) and (c)). For example, in HMQ-TMS crystals (Fig. 2(f)), phenolic 4-hydroxy-3-methoxyphenyl (HM) EDG-based HMQ cations form a strong hydrogen bond with the TMS anion (Fig. 3(b)), in addition to aromatic coulombic interactions. Upon changing the chemical structure of HMQ cationic chromophores by using both different EWGs (Fig. 2(g)) as well as different EDGs, phenolic 4-hydroxyphenyl (OH) and 3,4-dihydroxyphenyl (DH) EDGs (Fig. 2(h)–(k)), optimal non-centrosymmetric ordering with a high order parameter was obtained.
Interestingly, introducing acentric head-to-tail cation–anion assembly groups based on phenolic EDGs (HM, OH and DH EDGs) results in a molecular assembly comparable to DSTMS and DAST crystals with DA EDG. For example, in DSTMS crystals (Fig. 3(a)), a parallel-type cation–anion assembly can be identified, in which the cation and anion layers alternate (Fig. 1(a)). The phenolic EDG-based crystals in Fig. 2(f)–(k) also exhibit a parallel-type cation–anion assembly (e.g., Fig. 3(b) for HMQ-TMS crystals).
Another groups on cationic chromophores, which also promote acentric head-to-tail cation–anion assembly, are based on hydroxymethyl groups; e.g., 2-(4-(4-(hydroxymethyl)piperidin-1-yl)phenyl) (PM) EDG. Fig. 2(l) shows examples of hydroxymethyl piperidino-phenyl PM EDG-based crystals.56–58 Note that PM EDG groups exhibit a stronger electron donating strength compared to phenolic EDGs (HM, OH and DH EDGs). This leads to an enhanced molecular optical nonlinearity accompanied with a narrower HOMO–LUMO bandgap (red shifted absorption edge), which is reflected in a changed color of the crystals (Fig. 2). PM EDG-based crystals also exhibit optimal non-centrosymmetric ordering with a high order parameter (Fig. 3(c)),58,71 like phenolic EDG-based crystals. However, the type of molecular arrangement is different; they form the so-called series-type cation–anion assembly (Fig. 1(b)). In this assembly, instead of forming distinguishable cation and anion layers, cations and anions are arranged in series of cation–anion pairs (see Fig. 3(c) for PM7ClQ-T crystals).
Therefore, introducing aromatic coulombic interaction groups (e.g., between Ar(+) and Ar–SO3−) and acentric head-to-tail cation–anion assembly groups (e.g., phenolic HM, OH, and DH EDGs and hydroxymethyl PM EDG) are highly potential design strategies for developing new ionic organic THz crystals. Introducing different cation–anion assembly EDG groups often results in either parallel or series-type cation–anion assemblies. In addition, different cation–anion assembly EDG groups result in a different color of the corresponding crystals ranging from yellow to red, which for example leads to different phase matching conditions for THz wave generation and detection.
2.2 Control of the van der Waals volume
Regardless of the introduction of strong intermolecular interaction groups, the control of the van der Waals volume of cations and anions is important for developing optimized ionic organic THz crystals. The van der Waals volume is relevant for various aspects of the design and the performance of these crystals. First, bigger cationic chromophores may need bigger molecular anions for obtaining the required non-centrosymmetric crystal structure with a high order parameter. For example, the PMPR cationic chromophore (Fig. 4(a))72 is bigger than the widely used cationic chromophores of organic THz ionic crystals in Fig. 2(c)–(l). The two aromatic ring-based MO anion is bigger than anions with a single aromatic ring in Fig. 2(c)–(l). The MO anion results in a non-centrosymmetric crystal structure with the PMPR cationic chromophore (Fig. 4(a)), while all tested anions with a single aromatic ring led to centrosymmetric crystal structures with PMPR.72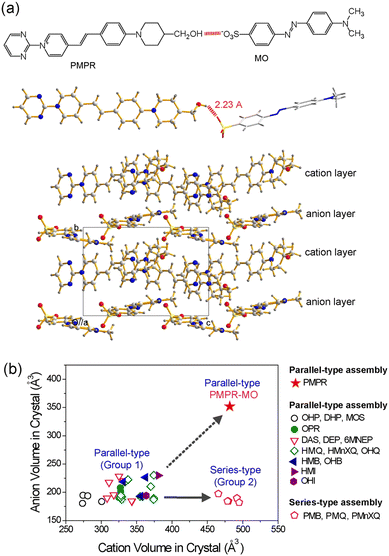 | ||
| Fig. 4 Schematic of van der Waals volume matching between the cationic chromophores and counter anions in benchmark organic THz crystals. (a) Large PMPR cation matching with the large MO anion that results in a high order parameter. Note that although PMPR cation possesses hydroxymethyl PM EDG, PMPR-MO crystals exhibit a parallel-type cation–anion assembly. (b) A relatively narrow relative ratio of the crystallographic volume of molecular cations and anions in non-centrosymmetric ionic organic crystals. Reproduced and adapted with permission.72 Copyright 2023, Wiley-VCH. | ||
Second, depending on the specific assembly type, only a narrow ratio of the van der Waals volume of cationic chromophores, Vcation relative to that of molecular anions, Vanion resulted in high order parameter in crystals (see group 1 and group 2 in Fig. 4(b)).72 For example, in crystals based on the OHQ cationic chromophore, high order parameter crystals were only obtained for the relative ratio of Vanion/Vcation of 0.57–0.66.73 When smaller or larger anions were combined with OHQ cations, the result was either a centrosymmetric crystal structure or a drastic reduction of the order parameter (Fig. 5(a)).74 The yellow-highlighted region in Fig. 5(a) illustrates the optimal van der Waals volume of anions for the OHQ cationic chromophores. Different cationic chromophores show a different range of the optimal volume ratio Vanion/Vcation (Fig. 4(b)).
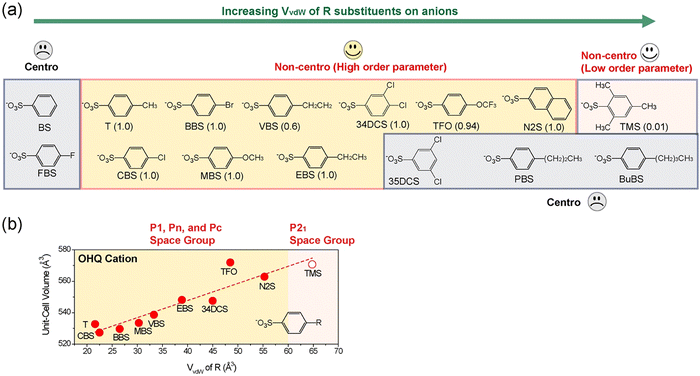 | ||
| Fig. 5 (a) Schematic trend of the crystal structure characteristics of OHQ-based crystals with various counter anions with different van der Waals volume, VvdW of R substituents. (b) The corresponding volume of a cation–anion pair (unit-cell volume divided by the crystallographic Z number) as a function of van der Waals volume, VvdW of R substituents. Reproduced and adapted with permission.74 Copyright 2023, Wiley-VCH. | ||
Third, the unit-cell volume (the volume of a cation–anion pair) linearly increases with the van der Waals volume of anions in high order parameter crystals having (pseudo-)isomorphic and sometimes non-isomorphic crystal structures (e.g., OHQ-based crystals showing parallel-type cation–anion assembly in Fig. 5(b)). A similar behavior was observed in another ionic organic THz crystals with series-type cation–anion assembly (PM7ClQ-based crystals in Fig. 2(l)).74
In summary, to develop new ionic organic THz crystals with a high order parameter, the first step may be to find (or design) a non-centrosymmetric core structure by introducing strong intermolecular interaction group into molecular cations and anions, as well as introducing acentric head-to-tail cation–anion assembly groups. Careful selection of the van der Waals volume ratio between cation and anion is also important in this step. After obtaining a desired non-centrosymmetric core structure (of cationic chromophores and counter anions), the introduction of different anions within the optimal van der Waals volume is very attractive for controlling (and fine tuning) the optical, THz and other physical properties of ionic organic crystals.
3. Solid-state phonon absorption
3.1 Origin and suppression design of solid-state phonons
The origins of solid-state phonon vibrations in organic THz crystals are different from those in inorganic crystals. The constituents of inorganic THz crystals are mostly sphere shape, e.g. monoatomic ions, while the constituents of organic THz crystals are more complex non-sphere and rod-shaped long molecules, typical for chromophores. Consequently, solid-state molecular phonon vibrations of ionic organic THz crystals are rather complex. THz phonon absorption occurs due to changes of polarization by molecular vibrations in crystals, rather than changes of the dipole moment as for molecules in gas phase.75 In THz crystals based on chromophores of the stilbene-type, e.g., the styryl quinolinium HMQ cation in HMQ-TMS crystals, the solid-state molecular phonon vibrations consist of entire molecular vibrational motions of HMQ cations (translation, rotation, and twisting), intramolecular vibrational motions of different parts of HMQ cations (e.g., phenolic EDG and quinolinium EWG separately), and intramolecular vibrational motions of substituents (e.g., hydroxyl, methoxy, and N-methyl groups). In addition, the vibrational motions of the HMQ cations are simultaneously correlated to those of the TMS anions.75In ionic organic THz crystals with a parallel-type cation–anion assembly (e.g., HMQ-TMS, OHQ-T, and DAST), the vibrational motions originate from entire molecules, parts of molecules, and substituents. The entire molecular translations and rotations (ET/ER) appear at lower frequencies of about <2 THz. Intramolecular vibrations (IMs) appear at higher frequencies >5 THz. The mixed motions of ET/ER/IM vibrations appear in the middle frequency range of about 2–5 THz.75,76 These frequency ranges were slightly different for different organic THz ionic crystals investigated, but only a few of them have been thoroughly analyzed so far. It should be noted that theoretical calculations of phonon modes in organic THz crystals with a series-type cation–anion assembly have not been reported yet.
For organic THz crystals, low absorption in the THz frequency range (i.e., low self-absorption) is highly beneficial for THz applications such as THz wave generation and detection.4 While in certain THz frequency ranges these crystals can have very low absorption, for ultra-broad THz applications it is practically impossible to completely avoid solid-state phonon vibrations. If the vibration strength is not too high, these crystals can still have a sufficiently high efficiency for applications, even in ranges with phonon vibrations. The solid-state molecular phonon vibrations of organic THz crystals depend on many factors: (i) the chemical structure (and substituents), (ii) the characteristics of intermolecular interactions, (iii) the crystal structure with molecular ordering features, (iv) the void volume, and (v) the crystal density. For suppressing solid-state molecular phonon vibrations of organic THz crystals, few design strategies have been suggested. Fig. 6 shows two strategies identified, lattice hardening and local-motion hardening.55,73,76,77
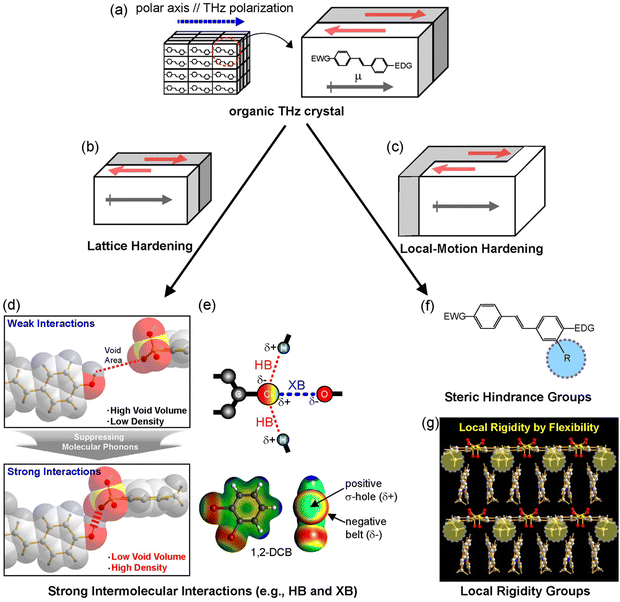 | ||
| Fig. 6 Schematics of strategies for suppressing phonon vibrations of (a) benchmark organic THz crystals: (b) lattice hardening by (d) and (e) introducing strong intermolecular interaction groups and (c) local-motion hardening by (f) introducing steric hindrance group and (g) local rigidity group with a high conformational freedom. Reproduced and adapted with permission.55,73,76,77 Copyright 2022 and 2023, Wiley-VCH. | ||
The lattice hardening approach relies on tight packing of entire molecules (or parts of molecules/substituents). This could be achieved by introducing a rigid chemical structure for both cations and anions, avoiding flexible (aliphatic) groups, introducing strong intermolecular interaction capable groups for hydrogen bonds, halogen bonds, and π–π interactions (Fig. 6(d) and (e)), as well as introducing heavier groups.55,77–79 When successful, the resulting crystals will have a low void volume and a high crystal density. For example, DHP-TFS crystals (Fig. 2(k)) possess several strong intermolecular interaction capable groups acting as hydrogen bond donor and acceptor sites: dihydroxy group on phenyl ring, trifluoro group, and sulfonate group. DHP-TFS crystals simultaneously exhibit one of the highest crystal densities and the lowest void volume, which leads to a very low absorption in the THz frequency range.55
The local-motion hardening could be achieved by inducing steric hindrance to restrain molecular vibrations. The bigger substituents may prevent the surrounding motions (Fig. 6(f)). For example, methoxy (–OCH3) substituent of HMQ cation in HMQ-TMS crystals (Fig. 2(f)) is bigger than the –H substituent of the OHQ cation in OHQ-T crystals (Fig. 2(g)). A comparison of the solid-state phonon modes in HMQ-TMS and OHQ-T crystals using periodic density functional theory has shown that a larger substituent prevents the slipping vibration of the cationic chromophores in the crystalline state.75,76 The local-motion hardening could also be achieved by introducing a flexible conformational group with a high conformational freedom. The resulting out-of-plane conformation of the substituent resulted in local rigidity (see yellow circles in Fig. 6(g)), which led to a reduction of the void volume of the resulting crystals.73
3.2 Understanding the influence of solid-state phonons on THz characteristics
There are several intrinsic characteristics that need to be considered when considering a new nonlinear optical material for THz wave generation and detection. A high second-order nonlinearity, achieved for organic crystals when chromophores with a high first hyperpolarizability self-assemble with a high order parameter, as discussed in Section 2, is a prerequisite for efficient THz applications. Another requirement is good phase matching, achieved when the group index ng of the pump optical beam (Fig. 1(e)) is as close as possible to the THz refractive index nTHz (Fig. 1(f)). This requirement is then considered when choosing an optimal pump optical wavelength, where in addition there should be no considerable absorption at this wavelength to achieve a high damage threshold. For organic nonlinear optical crystals, this is usually achieved in the entire infrared range above ∼800 nm (Fig. 1(e)), but few additional weak absorption bands in the infrared may need to be considered as well.Finally, the self-absorption of the crystals (Fig. 7(a) and (e)), although unavoidable in the THz range, should possibly be as low as possible to be able to use thicker crystals for an increased THz wave generation and detection efficiency. The generated THz electric field in a relatively thick organic crystal leads to several dimples in the broadband spectrum (Fig. 7(c)). Since many research groups employ an inorganic electro optic crystal for THz wave detection (such as ZnTe, Fig. 7(b) and (d)), the finally detected THz spectrum may be in addition considerably limited (Fig. 7(d)). Much broader spectrum has been obtained by using organic crystals also as detectors or employing other detection techniques as discussed in more detail in ref. 4.
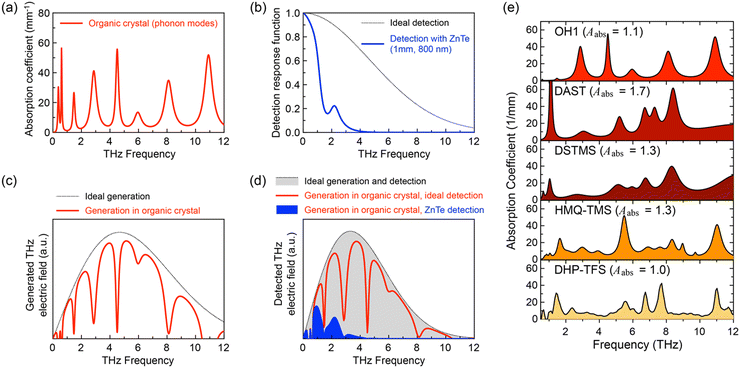 | ||
| Fig. 7 The influence of phonon modes on THz wave generation by optical rectification and electro-optic sampling detection using an 80-fs pulsed laser source (schematics): (a) phonon modes model for a typical organic nonlinear optical crystal. (b) Ideal detection response function and the detection response function for the most widely used inorganic crystal ZnTe, limited by a very strong phonon mode at 5.3 THz. (c) Ideal THz wave generation spectrum and the spectrum generated by an organic crystal with absorption modes as in (a). The panel (d) shows the schematics of a typical THz spectrum for an ideal generation and detection material (grey dotted curve, perfect phase matching and no absorption), using an organic crystal as generator and an ideal detector (solid red curve) and by using a ZnTe detector (blue curve), which is considerably cutting the wideband spectrum generated by the organic crystal. (e) Experimental absorption spectra of various materials, reproduced with permission.55 Copyright 2022, Wiley-VCH. | ||
Fig. 8 shows the influence of the most important extrinsic parameters on the THz spectra generated by optical rectification, the pump laser wavelength and the crystal thickness, along with the intrinsic crystal parameters. For the simulated spectra, the measured optical and THz parameters an ionic organic crystal HMQ-TMS shown in Fig. 1(e) and (f) were considered using literature models for THz wave generation.4,25,75 The spectral bandwidth of the ideal spectra with perfect phase matching and no THz self-absorption (black dotted curves) are limited by the length of the pump pulses, which are here considered short enough (80 fs) to cover the range of the measured material parameters of HMQ-TMS up to 12 THz. When phase matching is approximately satisfied in a broad range like at 1500 nm (ng = 2.00 ∼ nTHz, see Fig. 1(e) and (f)), the THz absorption spectrum alone can well predict the resulting spectrum. In this case, the difference between the realistic spectrum (solid black curve) and the approximate spectrum (red dashed curve) is practically negligible (Fig. 8(a) and (b)). At 1140 nm (ng = 2.09), the phase matching is slightly worse at higher THz frequencies, therefore the generated spectral amplitude in a crystal of 0.5 mm thickness drops considerably above the frequency of the largest phonon mode at 5.5 THz (Fig. 8(c)). For a thin crystal (0.1 mm), the realistic spectrum is however still close to the approximate spectrum (solid black and red dashed curves in Fig. 8(d)). At the wavelength of 800 nm that is approaching the optical absorption resonance, the group index increases considerably to ng = 2.41 (Fig. 1(e)) and the phase matching is satisfactory only below the first larger phonon mode at 1.6 THz. In this case, the phase matching plays a dominant role in the resulting spectra, also when considerably reducing the crystal thickness (Fig. 8(e) and (f)).
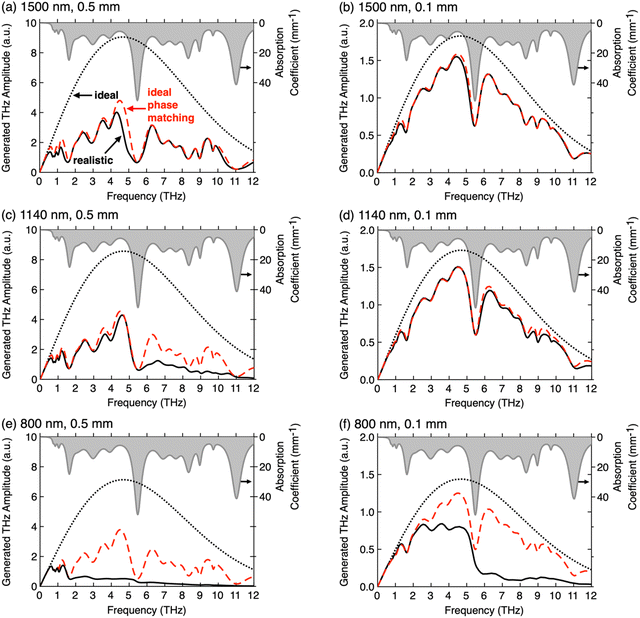 | ||
| Fig. 8 The influence of the pump laser wavelength, (a) and (b) 1500 nm, (c) and (d) 1140 nm, (e) and (f) 800 nm, and the thickness of the generation crystal, (a), (c) and (e) 0.5 mm, (b), (d) and (f) 0.1 mm, on the THz spectra generated by optical rectification in ionic organic THz crystal HMQ-TMS. The optical and the THz properties of HMQ-TMS as shown in Fig. 1(e) and (f) were considered in the model. The THz phonon-mode absorption dispersion is included in each plot (grey, right scale). For all theoretical THz generation spectra, transform-limited pump pulses with a length of 80 fs were considered. Each panel includes three spectra: (i) the ideal spectrum (black dotted curve) that assumes no THz absorption and perfect phase matching, nTHz = ng at each pump wavelength; (ii) the spectrum considering THz absorption but still perfect phase matching (red dashed curve); and (iii) the realistic spectrum considering both the THz absorption and the THz refractive index dispersion from Fig. 1(f). (a)–(d) Reproduced and adapted with permission.75 Copyright 2021, Wiley-VCH. | ||
Fig. 8 clearly shows that thinner crystals will in any case lead to smoother THz spectra, considerably less affected by the THz phonon and vibrational modes. However, the generation efficiency will also considerably decrease (note the different scale for the generated THz amplitude in Fig. 8). Therefore, when using organic THz crystals for various applications, careful selection of the optimal extrinsic parameters is required. Often, the main limitation presents the available pump laser sources on the market and their price, quality, and size. Therefore, it is often desired that the optical and the THz properties of the organic crystals are fine-tuned for the best performance at the specific pump optical wavelength. For example, blue shift of the absorption maximum in the optical range (Fig. 1(e)) will improve the phase matching at shorter pump optical wavelengths, accompanied with the shift of the crystal color from red to yellow. Note however that this may also affect all other optical and physical properties, including the nonlinear optical susceptibility and the solid-state THz phonon and vibrational resonances.
4. Outlook
In this perspective, we discuss various design strategies focused on ionic organic THz crystals and the possibilities to suppress their intrinsic phonon vibrations. In addition, we discuss the influence of solid-state molecular phonons on the characteristics of THz generation and detection spectra. The ionic organic THz crystals often allow relatively large changes of their chemical structure to achieve a high order parameter with modified optical, THz and other physical properties. For obtaining both a non-centrosymmetric crystal structure with a high order parameter and suppressed phonon vibrations in the crystalline state, controlling intermolecular (and interionic) interactions and van der Waals volume is very important. We also discuss the important influence of solid-state phonon and vibrational modes on broadband THz spectra and the main parameters that need to be considered for optimizing the performance of ionic organic THz crystals for practical applications.While this perspective primarily centers on ionic organic THz crystals rather than their non-ionic counterparts, it is important to note that this emphasis does not imply a superiority of the former for applications. Ionic and non-ionic crystals each offer their own advantages with different material characteristics that can be beneficial depending on specific application requirements or available pump laser sources. Designing new organic nonlinear optical crystals continues to progress for obtaining large macroscopic optical nonlinearity, including increasing the length of the π-conjugation bridge and introducing various substituents.24,66,67,80–82 In addition, further development of design strategies aimed at improving both ionic and non-ionic organic THz crystals for THz applications is still desired.
Data availability
No primary research results have been included and no new data were generated as part of this perspective.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has been supported by the Ministry of Trade, Industry and Energy (MOTIE) and Korea Institute for Advancement of Technology (KIAT) through the International Cooperative R&D program (no. P0026100) funded by the Ministry of Science, ICT & Future Planning, Korea, and Swiss Innovation Agency (Innosuisse) grant no. 108.968 INT-EE, Switzerland.Notes and references
- A. Schliesser, N. Picque and T. W. Hänsch, Nat. Photonics, 2012, 6, 440–449 CrossRef CAS.
- J. A. Fülöp, S. Tzortzakis and T. Kampfrath, Adv. Opt. Mater., 2019, 8, 1900681 CrossRef.
- S. Kannan, A. Sekar and K. Sivaperuman, J. Mater. Chem. C, 2020, 8, 16668 RSC.
- S. J. Kim, B. J. Kang, U. Puc, W. T. Kim, M. Jazbinsek, F. Rotermund and O. P. Kwon, Adv. Opt. Mater., 2021, 9, 2101019 CrossRef CAS.
- S. Mansourzadeh, T. Vogel, A. Omar, T. O. Buchmann, E. J. R. Kelleher, P. U. Jepsen and C. J. Saraceno, Opt. Mater. Express, 2023, 13, 3287–3308 CrossRef CAS.
- Y. Yang, X. Zhang, Z. Hu and Y. Wu, Crystals, 2023, 13, 144 CrossRef CAS.
- X. Mu, K. Xu, J. Ma, T. Wang, X. Feng, Y. Zhai, F. Xuan, L. Cao and B. Teng, J. Mater. Sci.: Mater. Electron., 2024, 35, 388 CrossRef CAS.
- L. R. Dalton, P. A. Sullivan and D. H. Bale, Chem. Rev., 2010, 110, 25–55 CrossRef CAS PubMed.
- M. Wang, Y. Chen, S. Zhang, L. Dong, H. Yao, H. Xu, K. Chen and J. Wu, J. Mater. Chem. C, 2023, 11, 11107 RSC.
- J. Liu, C. Ouyang, F. Huo, W. He and A. Cao, Dyes Pigm., 2020, 181, 108509 CrossRef CAS.
- J. Wu, Z. Li, J. Luo and A. K.-Y. Jen, J. Mater. Chem. C, 2020, 8, 15009 RSC.
- L. Yu, Y. Wang, S. Zhan, D. Chen, S. Wang and M. Zhang, J. Mater. Chem. C, 2023, 11, 1226 RSC.
- X. You, P. Wang, Y. Tan, Y. Li, J. Wang, Z. Li, Y. Ao and M. Li, Mater. Today Chem., 2024, 37, 101971 CrossRef CAS.
- L. R. Dalton, P. Gunter, M. Jazbinsek, O. P. Kwon and P. A. Sullivan, Organic Electro-Optics and Photonics: Molecules, Polymers and Crystals, Cambridge University Press, Cambridge UK, 2015 Search PubMed.
- D. Venkatakrishnarao, E. A. Mamonov, T. V. Murzina and R. Chandrasekar, Adv. Opt. Mater., 2018, 6, 1800343 CrossRef.
- S. Semin, X. Li, Y. Duan and T. Rasing, Adv. Opt. Mater., 2021, 9, 2100327 CrossRef CAS.
- R. Shi, X. Han, J. Xu and X. H. Bu, Small, 2021, 17, 2006416 CrossRef CAS PubMed.
- D. Rezzonico, S. J. Kwon, H. Figi, O. P. Kwon, M. Jazbinsek and P. Günter, J. Chem. Phys., 2008, 128, 124713 CrossRef PubMed.
- M. Cigáň, A. Gáplovský, I. Sigmundová, P. Zahradník, R. Dedic and M. Hromadová, J. Phys. Org. Chem., 2011, 24, 450–459 CrossRef.
- C. Bosshard, M. Bosch, I. Liakatas, M. Jager and P. Gunter, Nonlinear Optical Effects and Materials, ed. P. Gunter, Springer-Verlag, Berlin, 2000, ch. 3 Search PubMed.
- H. S. Nalwa, T. Watanabe and S. Miyata, Nonlinear Optics of Organic Molecules and Polymers, ed. H. S. Nalwa and S. Miyata, CRC Press, 1997, ch. 4 Search PubMed.
- D. S. Chemla and J. Zyss, Nonlinear Optical Properties of Organic Molecules and Crystals, Academic Press, Orlando, 1987, vol. 1 Search PubMed.
- Nonlinear Optical Properties of Organic and Polymeric Materials ACS Symposium Series, ed. D. J. Williams, 1983, vol. 233 Search PubMed.
- B. R. Shin, I. C. Yu, U. Puc, W. T. Kim, W. Yoon, C. Kim, H. Yun, D. Kim, M. Jazbinsek, F. Rotermund and O. P. Kwon, Adv. Opt. Mater., 2023, 11, 2201420 CrossRef CAS.
- A. Schneider, M. Neis, M. Stillhart, B. Ruiz, R. U. A. Khan and P. Günter, J. Opt. Soc. Am. B, 2006, 23, 1822–1835 CrossRef CAS.
- S. R. Tripathi, K. Murate, H. Uchida, K. Takeya and K. Kawase, Appl. Phys. Express, 2013, 6, 072703 CrossRef.
- J. Li, R. Rana, L. Zhu, C. Liu, H. Schneider and A. Pashkin, Opt. Express, 2021, 29, 22494–22503 CrossRef PubMed.
- B. Liu, H. Bromberger, A. Cartella, T. Gebert, M. Först and A. Cavalleri, Opt. Lett., 2017, 42, 129–131 CrossRef CAS PubMed.
- B. Urbanek, M. Möller, M. Eisele, S. Baierl, D. Kaplan, C. Lange and R. Huber, Appl. Phys. Lett., 2016, 108, 121101 CrossRef.
- C. Rader, Z. B. Zaccardi, S. H. E. Ho, K. G. Harrell, P. K. Petersen, M. F. Nielson, H. Stephan, N. K. Green, D. J. H. Ludlow, M. J. Lutz, S. J. Smith, D. J. Michaelis and J. A. Johnson, ACS Photonics, 2022, 9, 3720–3726 CrossRef CAS.
- H. Zhao, Y. Tan, T. Wu, G. Steinfeld, Y. Zhang, C. Zhang, L. Zhang and M. Shalaby, Appl. Phys. Lett., 2019, 114, 241101 CrossRef.
- Z. Wang, Y. Wang, H. Li, M. Ge, D. Xu and J. Yao, Opt. Express, 2023, 31, 39030 CrossRef CAS PubMed.
- X. Cai, T. Xie, Q. Ruan, P. Pan, S. Chen, J. Luo, H. Fu, D. Chen and S. Gao, Opt. Laser Technol., 2022, 150, 107912 CrossRef CAS.
- C. Bernerd, P. Segonds, J. Debray, J. F. Roux, E. Hérault, J. L. Coutaz, I. Shoji, H. Minamide, H. Ito, D. Lupinski, K. Zawilski, P. Schunemann, X. Zhang, J. Wang, Z. Hu and B. Boulanger, Opt. Mater. Express, 2020, 10, 561–576 CrossRef.
- H. Uchida, S. R. Tripathi, K. Suizu, T. Shibuya, T. Osumi and K. Kawase, Appl. Phys. B: Lasers Opt., 2013, 111, 489–493 CrossRef CAS.
- A. Majkić, M. Zgonik, A. Petelin, M. Jazbinsek, B. Ruiz, C. Medrano and P. Günter, Appl. Phys. Lett., 2014, 105, 141115 CrossRef.
- M. Gao, J. Zhang, X. Zhang, D. Xu, Z. Hu, J. Yao and Y. Wu, Cryst. Growth Des., 2021, 21, 3153–3157 CrossRef CAS.
- O. P. Kwon, S. J. Kwon, M. Jazbinsek, F. D. J. Brunner, J. I. Seo, C. Hunziker, A. Schneider, H. Yun, Y. S. Lee and P. Günter, Adv. Funct. Mater., 2008, 18, 3242–3250 CrossRef CAS.
- O. P. Kwon, M. Jazbinsek, H. Yun, J. I. Seo, J. Y. Seo, S. J. Kwon, Y. S. Lee and P. Günter, CrystEngComm, 2009, 11, 1541–1544 RSC.
- O. P. Kwon, S. J. Kwon, M. Jazbinsek, J. Y. Seo, J. T. Kim, J. I. Seo, Y. S. Lee and P. Günter, Chem. Mater., 2011, 23, 239–246 CrossRef CAS.
- G. A. Valdivia-Berroeta, Z. B. Zaccardi, S. K. F. Pettit, E. S. H. Ho, B. W. Palmer, M. J. Lutz, C. Rader, B. P. Hunter, N. K. Green, C. Barlow, C. Z. Wayment, D. J. Ludlow, P. Petersen, S. J. Smith, D. J. Michaelis and J. A. Johnson, Adv. Mater., 2022, 34, 2107900 CrossRef CAS PubMed.
- H. Hashimoto, Y. Okada, H. Fujimura, M. Morioka, O. Sugihara, N. Okamoto and R. Masushima, Jpn. J. Appl. Phys., 1997, 36, 6754–6760 CrossRef CAS.
- M. Savoini, L. Huber, H. Cuppen, E. Abreu, M. Kubli, M. J. Neugebauer, Y. Duan, P. Beaud, J. Xu, T. Rasing and S. L. Johnson, ACS Photonics, 2018, 5, 671–677 CrossRef CAS.
- S. R. Marder, J. W. Perry and W. P. Schaefer, Science, 1989, 245, 626–628 CrossRef CAS PubMed.
- Z. Yang, L. Mutter, M. Stillhart, B. Ruiz, S. Aravazhi, M. Jazbinsek, A. Schneider, V. Gramlich and P. Günter, Adv. Funct. Mater., 2007, 17, 2018–2023 CrossRef CAS.
- G. A. Valdivia-Berroeta, L. K. Heki, E. A. McMurray, L. A. Foote, S. H. Nazari, L. Y. Serafin, S. J. Smith, D. J. Michaelis and J. A. Johnson, Adv. Opt. Mater., 2018, 5, 1800383 CrossRef.
- H. Chen, Q. Ma, Y. Zhou, Z. Yang, M. Jazbinsek, Y. Bian, N. Ye, D. Wang, H. Cao and W. He, Cryst. Growth Des., 2015, 15, 5560–5567 CrossRef CAS.
- J. H. Jeong, B. J. Kang, J. S. Kim, M. Jazbinsek, S. H. Lee, S. C. Lee, I. H. Baek, H. Yun, J. Kim, Y. S. Lee, J. H. Lee, J. H. Kim, F. Rotermund and O. P. Kwon, Sci. Rep., 2013, 3, 3200 CrossRef PubMed.
- S. H. Lee, J. Lu, S. J. Lee, J. H. Han, C. U. Jeong, S. C. Lee, X. Li, M. Jazbinsek, W. Yoon, H. Yun, B. J. Kang, F. Rotermund, K. A. Nelson and O. P. Kwon, Adv. Mater., 2017, 29, 1701748 CrossRef PubMed.
- D. Kim, W. T. Kim, J. H. Han, J. A. Lee, S. H. Lee, B. J. Kang, M. Jazbinsek, W. Yoon, H. Yun, D. Kim, S. van Bezouw, J. Campo, W. Wenseleers, F. Rotermund and O. P. Kwon, Adv. Opt. Mater., 2020, 8, 1902099 CrossRef CAS.
- S. I. Kim, W. T. Kim, J. H. Seok, M. Jazbinsek, W. Yoon, I. C. Yu, H. Yun, D. Kim, F. Rotermund and O. P. Kwon, Adv. Opt. Mater., 2020, 8, 1901840 CrossRef CAS.
- S. H. Lee, B. J. Kang, J. S. Kim, B. W. Yoo, J. H. Jeong, K. H. Lee, M. Jazbinsek, J. W. Kim, H. Yun, J. Kim, Y. S. Lee, F. Rotermund and O. P. Kwon, Adv. Opt. Mater., 2015, 3, 756–762 CrossRef CAS.
- J. Shi, Y. He, F. Liang, X. Zhang, D. Xu, J. Yao, G. Zhang, Z. Hu, J. Yao and Y. Wu, J. Mater. Chem. C, 2020, 8, 4226–4233 RSC.
- M. H. Shin, W. T. Kim, S. I. Kim, S. J. Kim, I. C. Yu, S. W. Kim, M. Jazbinsek, W. Yoon, H. Yun, F. Rotermund and O. P. Kwon, Adv. Sci., 2020, 7, 2001738 CrossRef CAS PubMed.
- G. E. Yoon, J. H. Seok, U. Puc, B. R. Shin, W. J. Yoon, H. S. Yun, D. W. Kim, I. C. Yu, F. Rotermund, M. Jazbinsek and O. P. Kwon, Adv. Sci., 2022, 9, 2201391 CrossRef CAS PubMed.
- S. C. Lee, B. J. Kang, J. A. Lee, S. H. Lee, M. Jazbinsek, W. J. Yoon, H. S. Yun, F. Rotermund and O. P. Kwon, Adv. Opt. Mater., 2018, 6, 1701258 CrossRef.
- G. A. Valdivia-Berroeta, E. W. Jackson, K. C. Kenney, A. X. Wayment, I. C. Tangen, C. B. Bahr, S. J. Smith, D. J. Michaelis and J. A. Johnson, Adv. Funct. Mater., 2020, 30, 1904786 CrossRef CAS.
- B. R. Shin, I. C. Yu, U. Puc, W. T. Kim, W. J. Yoon, C. Y. Kim, H. S. Yun, D. W. Kim, M. Jazbinsek, F. Rotermund and O. P. Kwon, Adv. Opt. Mater., 2023, 11, 2201420 CrossRef CAS.
- W. Zhang, Z. Wang, X. Zhang, Y. Wang, D. Xu, Z. Hu, J. Yao and Y. Wu, Cryst. Growth Des., 2022, 22, 3311–3318 CrossRef CAS.
- R. Shi, Z. Han, P. Cheng, M. Xin and J. Xu, Cryst. Growth Des., 2022, 22, 3998–4004 CrossRef CAS.
- G. A. Valdivia-Berroeta, L. K. Heki, E. W. Jackson, I. C. Tangen, C. G. Bahr, S. J. Smith, D. J. Michaelis and J. A. Johnson, Optica, 2019, 44, 4279–4282 CAS.
- M. Gao, X. Zhang, Y. Guo, J. Yao, G. Zhang, Z. Hu and Y. Wu, CrystEngComm, 2020, 22, 6444–6447 RSC.
- J. Shi, F. Liang, Y. He, X. Zhang, Z. Lin, D. Xu, Z. Hu, J. Yao and Y. Wu, Chem. Commun., 2019, 55, 7950–7953 RSC.
- H. Barhum, C. McDonnell, T. Alon, R. Hammad, M. Attrash, T. Ellenbogen and P. Ginzburg, ACS Appl. Mater. Interfaces, 2023, 15, 8590–8600 CrossRef CAS PubMed.
- J. Ogawaa, S. Okadaa, Z. Glavchevab and H. Nakanishi, J. Cryst. Growth, 2008, 310, 836–842 CrossRef.
- H. Liang, Q. Fu, Y. Wu, X. Zhang and P. Liu, Adv. Funct. Mater., 2024, 2406804 CrossRef.
- R. Zhao, T. Zhu, S. Wang, C. Jarrett-Wilkins, A. M. Najjarian, A. J. Lough, S. Hoogland, E. H. Sargent and D. S. Seferos, Chem. Sci., 2022, 13, 12144–12148 RSC.
- S. H. Lee, M. Jazbinsek, C. P. Hauri and O. P. Kwon, CrystEngComm, 2016, 18, 7180–7203 RSC.
- Z. Yang, M. Jazbinsek, B. Ruiz, S. Aravazhi, V. Gramlich and P. Günter, Chem. Mater., 2007, 19, 3512–3518 CrossRef CAS.
- Z. Yang, S. Aravazhi, A. Schneider, P. Seiler, M. Jazbinsek and P. Günter, Adv. Funct. Mater., 2005, 15, 1072–1076 CrossRef CAS.
- J. H. Seok, D. J. Kim, W. T. Kim, S. J. Kim, W. J. Yoon, G. E. Yoon, I. C. Yu, M. Jazbinsek, S. W. Kim, H. S. Yoon, D. W. Kim, F. Rotermund and O. P. Kwon, Adv. Opt. Mater., 2021, 9, 2100324 CrossRef CAS.
- S. J. Kim, I. C. Yu, D. J. Kim, M. Jazbinsek, W. J. Yoon, H. S. Yun, D. W. Kim, F. Rotermund and O. P. Kwon, Adv. Funct. Mater., 2023, 33, 2209915 CrossRef CAS.
- D. J. Kim, I. C. Yun, M. Jazbinsek, C. Y. Kim, W. J. Yoon, H. S. Yun, S. W. Kim, D. W. Kim, F. Rotermund and O. P. Kwon, Adv. Opt. Mater., 2023, 11, 2300807 CrossRef CAS.
- B. R. Shin, U. Puc, Y. J. Park, D. J. Kim, C. W. Lee, W. J. Yoon, H. S. Yun, C. Y. Kim, F. Rotermund, M. Jazbinsek and O. P. Kwon, Adv. Sci., 2023, 10, 2304767 CrossRef CAS PubMed.
- J. T. Kim, Y. C. Park, J. H. Seok, M. Jazbinsek and O. P. Kwon, Adv. Opt. Mater., 2021, 9, 2001521 CrossRef CAS.
- C. W. Lee, U. Puc, J. T. Kim, M. Jazbinsek and O. P. Kwon, Adv. Opt. Mater., 2023, 2302689 Search PubMed.
- B. R. Shin, I. C. Yu, M. Jazbinsek, W. J. Yoon, H. S. Yun, S. W. Kim, D. W. Kim, F. Rotermund and O. P. Kwon, Adv. Opt. Mater., 2023, 11, 2202027 CrossRef CAS.
- S. H. Lee, B. J. Kang, B. W. Yoo, S. C. Lee, S. J. Lee, M. Jazbinsek, H. S. Yun, F. Rotermund and O. P. Kwon, Adv. Funct. Mater., 2017, 27, 1605583 CrossRef.
- B. R. Shin, I. C. Yu, M. H. Shin, M. Jazbinsek, F. Rotermund and O. P. Kwon, APL Mater., 2023, 11, 011101 CrossRef CAS.
- G. A. Valdivia-Berroeta, K. C. Kenney, E. W. Jackson, J. C. Bloxham, A. X. Wayment, D. J. Brock, S. J. Smith, J. A. Johnson and D. J. Michaelis, J. Mater. Chem. C, 2020, 8, 11079–11087 RSC.
- A. Arul and J. V. Ramaclus, CrystEngComm, 2023, 25, 2534–2545 RSC.
- S. Shang, R. Li, L. Ping, W. Luo, M. Hai, Z. Yang, D. Wang, H. Cao and W. He, CrystEngComm, 2019, 21, 5626–5632 RSC.
| This journal is © The Royal Society of Chemistry 2024 |