 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Theoretical predictions of alkali hexazirconate (A2Zr6O13, A = Li, Na, And K) as candidates for alkali ion batteries†
José. R.
Fernández-Gamboa
 *ab,
Frederik
Tielens
*ab,
Frederik
Tielens
 b and
Yohandys A.
Zulueta
b and
Yohandys A.
Zulueta
 a
a
aDepartamento de Física, Facultad de Ciencias Naturales y Exactas, Universidad de Oriente, CP: 90500, Santiago de Cuba, Cuba. E-mail: Jose.Ramon.Fernandez.Gaboa@vub.be; jrfernandez@uo.edu.cu
bGeneral Chemistry (ALGC) – Materials Modelling Group, Vrije Universiteit Brussel, CP: 1050, Pleinlaan 2, Brussels, Belgium
First published on 28th October 2024
Abstract
As the demand for advanced energy storage materials continues to grow, it is essential to conduct new research to discover alternative materials for use in batteries. Therefore, this work delves into the potential of new materials for use as alternative electrodes for Li-ion and alkali ion batteries, specifically alkali hexazirconates such as A2Zr6O13 (where A represents Li, Na, and K). Utilizing advanced atomistics simulations, our objective is to conduct a comprehensive assessment of their structural, electronic, and mechanical properties. The results indicate the insulating behavior of A2Zr6O13 materials, with calculated lattice parameters closely aligned with previous studies. Mechanical property analysis reveals greater susceptibility of Li2Zr6O13 and Na2Zr6O13 to compression along the x and y axes than along the z-axis. Furthermore, their ductile behavior and Young's modulus, in alignment with lithium and sodium hexazirconates, suggests their potential in alkaline ion batteries. Electrochemical performance shows Li2Zr6O13 and Na2Zr6O13 present two stable phases during charge and discharge, leading to a plateau in the open cell voltage profile at 1.3 and 2.9 V and theoretical capacity of 69.68 mA h g−1 and 66.89 mA h g−1, respectively. Comparative analysis unearths distinctions in mechanical and electronic properties among Li, Na, and K variants, aiding in the precise tailoring of materials. In conclusion, this study emphasizes the potential of alkali hexazirconates such as A2Zr6O13as alternative electrode materials, showcasing notable mechanical stability and derived properties rendering them promising candidates for advancements in energy storage applications.
1 Introduction
Titanium oxide-based materials have been the subject of extensive investigation due to their potential applications as electrodes in lithium-ion batteries, photocatalysts, and semiconductor devices. Within this family, the oxides belonging to Andersson–Wadsley family (A2O·nTiO2, where A denotes an alkali cation and 1 ≤ n ≤ 6) have garnered significant attention. These materials have captured the interest of researchers owing to their diverse compositions and variations in microstructure, providing an excellent platform for exploring the relationship between their structure and properties. Among these compounds, the members with n = 6, particularly the alkali hexatitanate A2Ti6O13, have been extensively studied for a broad range of potential applications, including their effectiveness as electrodes in energy storage devices.1–6In the structure of alkali hexatitanate, three TiO6 octahedral units are edge-shared to form a foundational building block. This block is then connected to identical units both above and below, creating a ribbon-like structure. These ribbons further interconnect through corner-sharing, resulting in a [Ti6O13]2− framework that forms a tunnel. The results reported by different authors clearly prove the stability of the A2Ti6O13 hexatitanate tunnel structure for ion exchange reactions.4,5,7–9 Lattice parameters were only little affected by the successive Na+, Li+, H+ ion exchange process with retention of the basic [Ti6O13]2− skeleton framework. This unique structure establishes a one-dimensional (1D) pathway for ion flow, holding promising applications in ion batteries and ion exchange processes.4,5,7,8
The utilization of theoretical design and state-of-the-art first-principles simulation methods has witnessed a notable surge. This approach is becoming increasingly essential for expediting the discovery of new materials, offering substantial accuracy in understanding structures and electronic properties. This computational methodology has proven successful in diverse material design applications, including alkali-ion batteries.6,8
Atomistic simulations play a pivotal role in unveiling the fundamental properties of materials. Notably, investigations into the structures of Li2Ti6O13, Li2Sn6O13,6,7 and more recently, Li2Zr6O13, have identified the latter as a promising candidate electrode material for Li-ion batteries with similar crystal structure and electronic properties of titanium counterpart.7,10
In our previous study an in-depth analysis of the energy profiles associated with potential reactions for synthesizing A2Zr6O13(A = Na+, Li+, K+).10 By scrutinizing the energetic disparities between reactants and product constituents, they evaluated ion exchange reactions involving Li/K, Li/Na, and K/Na, revealing their energy-efficient potential. This investigation resulted in the successful study of structural, electronic and thermodynamics stability, of previously unidentified materials, namely A2Zr6O13(A = Na+, Li+, K+), positioning them as promising candidates for energy storage applications in ion batteries.7,10
While the structural and electronic properties of these materials were extensively studied in a prior work,7,10 an essential aspect that has not been explored is the mechanical/elastic properties. Understanding these properties is crucial for assessing the stability of electrodes in batteries. Therefore, a comprehensive investigation into the mechanical/elastic properties is imperative to provide a holistic understanding of the material's suitability for electrochemical applications. In this study, a comprehensive investigation into the structural, electronic, and mechanical properties of Li2Zr6O13, as well as the newly discovered compounds Na2Zr6O13 and K2Zr6O13, was conducted through a combination of classical simulations and density functional theory (DFT) calculations. This work significantly enhances our comprehension of these materials, emphasizing their promise for energy storage applications. It encourages continued exploration, fostering advancements in alkaline ion battery technology.
2 Methodology
The compounds under consideration fall into the category of 1D type structures, specifically A2Zr6O13 (where A can be Li+, Na+, or K+). These structures are characterized by a substantial specific surface area and structural anisotropy, as detailed in a previous work.7The crystal structure of alkali hexazirconate, denoted as A2Zr6O13 with A being Li+, Na+, or K+, is depicted in Fig. 1a. The A2Zr6O13 compound comprises interconnected [Zr6O13]−2 frameworks, held together by alkali ions and oxygen in square planar hybridization.
In this context, the A2Zr6O13 compounds, along with their Ti-containing counterparts, are considered interactive partners. This collaborative perspective is informed by the premise that the ion-exchange reactions involving these compounds hold promise for generating diverse structures with distinct properties. These insights contribute to the foundation for exploring the potential applications and unique characteristics of Na2Zr6O13 and K2Zr6O13 structures in the context of ion-exchange synthesis.
The procedures employed in discovering superior negative electrodes for high-performance batteries are not only arduous but also financially demanding, primarily resulting from the dependence on empiricism. A method to circumvent these obstacles is through density functional theory (DFT) computations to predict structural, electronic properties and other fundamental variables crucial for battery materials’ development. This methodology presents a perspective to researchers seeking to enhance negative electrodes for high-performance batteries. It facilitates the prompt and meticulous identification of materials capable of enhancing battery output. As technology progresses and computational power expands, we anticipate DFT and other computational methodologies to continue revolutionizing battery research and promote superior energy storage solutions.
In this study, DFT computations are conducted to explore the structural and electronic characteristics of the targeted structures. The CASTEP computer code, a reliable tool for first-principles calculations, is utilized for the DFT calculations.11 The calculations employ the generalized gradient approximation with the Perdew–Burke–Ernzerhof formulation.12 Additionally, norm-conserving pseudopotentials are applied, with a plane-wave energy cutoff set at 750 eV. The electronic configurations considered are A-ns1, O-2s2 2p4, and Zr-5s2 5p2.
Convergence thresholds for self-consistent computations and geometry optimizations are set at 10−6 eV per atom, with a maximum force limit of 10−3 eV Å−1. The quasi-Newton algorithm is employed for geometry optimization, allowing simultaneous relaxation of internal coordinates and lattice parameters while preserving crystal symmetry. The criteria for convergence include stress and atomic displacements of 5 × 10−2 GPa and 5 × 10−4 Å, respectively.13 A Γ-centered Monkhorst–Pack scheme is employed for sampling the Brillouin zone. Specifically, a k-point set of 7 × 7 × 3 along the reciprocal representation is utilized for the A2Zr6O13 structures. This approach is instrumental in obtaining the total and projected density of states (DOS and PDOS, respectively) in their reciprocal conventional representation.
The employed rigorous computational approach ensures a detailed exploration of the structural and electronic properties of the materials under consideration. This approach aims to provide valuable insights for the development of high-performance battery electrodes, contributing to advancements in energy storage technologies.
The monoclinic systems under investigation, namely Na2Zr6O13 and K2Zr6O13, exhibit a conventional cell containing 42 atoms with a space group of C2/m, which was employed for bulk calculations. In comparison to the crystal structure of Li2Zr6O13, slight modifications are introduced in the crystal structures of Na2Zr6O13 and K2Zr6O13 by displacing the Na/K atoms from the Li positions within the fractional coordinate system.
Lattice static calculations, employing the force-field approach implemented in the GULP code,14 complement our exploration of the structural properties. The interatomic potential parameters, defining the ionic interactions within the force field, are sourced from the literature. Coulombic forces handle long-range interactions, while short-range interactions are represented by Buckingham-type potentials. To account for ion polarization in O–O interactions, a shell model is introduced.15
In the shell model, each ion is conceptualized as a positively charged core and a negatively charged shell connected by a spring with a spring constant, denoted as k. The sum of the core–shell charge equals the formal charge of each ion. The Broyden–Fletcher–Goldfarb–Shanno (BFGS) approach is employed to update the cell parameters and fractional positions of the equilibrium A2Zr6O13 lattice structures.
The atomistic simulations conducted in this study, which incorporate density functional theory (DFT) computations to validate force field calculations, have emerged as a robust methodology for accurately predicting the relevant properties of ionic compounds.5,15,16 The utilization of force field calculations is deemed indispensable in determining the thermochemical properties of these materials due to the computationally expensive nature of quantum calculations for large supercells. The synergy between these computational techniques significantly enhances our understanding and prediction capabilities regarding the structural and mechanical aspects of the studied materials.
The investigation into the relative distribution of lithium vacancies involves systematically generating all symmetrically inequivalent configurations in a 1 × 4 × 1 supercell. This exploration spans intermediate compositions of AxZr6O13, where x varies from 0 to 2.0. The identification of these inequivalent configurations is accomplished through the site occupancy disorder code (SOD), following the procedure outlined by other authors.17,18 This methodology, proven effective in previous studies is employed to describe the distribution of species over crystal sites.8
In this procedure, all possible configurations within the designated supercell are initially generated, with the assumption that each configuration can be uniquely defined by specifying substitution sites within a parent structure. Subsequently, we select and fully relax the atomic positions and volume the inequivalent configurations from the complete ensemble. The criteria for determining equivalence between two configurations rely on the presence of an isometric transformation capable of converting one configuration into another. The symmetry group of the parent structure, along with internal translations within the supercell, provides a list of potential symmetry operations. This approach remains valid as long as the symmetry of each configuration is preserved during the relaxation process. Any deviation from symmetry during relaxation would indicate the existence of additional configurations beyond those initially considered.
To assess the thermodynamic stability of the pseudo-binary phases of AxZr6O13, the above hull energy is employed.19 All computational analyses, including the construction of phase diagrams, were conducted using the Python Materials Genomics (pymatgen) software library.20 This approach enables a comprehensive exploration of the thermodynamic landscape and aids in determining the stable compositions and phases under varying conditions.
3 Results and discussion
3.1 Structural and electronic properties
In all examined cases, the A2Zr6O13 compositions (where A = Li+, Na+, K+) demonstrate a monoclinic crystal structure within the C2/m space group. The initiation of these calculations relied on structural data previously presented by the authors in a prior study,7 during the geometry optimization process, the structures underwent relaxation.The crystal structure is characterized by zigzag chains composed of triple-edge-shared [ZrO6] octahedra. These octahedra, in turn, form one-dimensional rectangular tunnels that serve as host sites for the alkaline A atoms.
The findings of this study, incorporating cell parameters derived from both density functional theory (DFT) and classical force-field approaches, are systematically presented in Table 1. Significant observations emerge concerning the approximately 5% variations in cell parameters obtained through both computational methods.
| Structures | a (Å) | b (Å) | c (Å) | β (°) | |
|---|---|---|---|---|---|
| Li2Zr6O13 | DFT | 16.389 | 3.976 | 9.934 | 98.853 |
| FF | 16.511 | 3.892 | 9.82 | 97.489 | |
| % | 0.74 | −2.10 | −1.11 | −1.38 | |
| DFT | 17.355 | 3.993 | 9.857 | 99.326 | |
| Na2Zr6O13 | FF | 17.388 | 3.908 | 9.818 | 98.970 |
| % | 0.18 | −2.15 | −0.39 | −0.35 | |
| DFT | 18.247 | 3.999 | 9.815 | 100.721 | |
| K2Zr6O13 | FF | 17.342 | 3.908 | 9.818 | 98.938 |
| % | −4.9 | −2.2 | 0.03 | −1.7 | |
Table 1 establishes a clear correspondence between the structural parameters of the investigated Li2Zr6O13, Na2Zr6O13, and K2Zr6O13structures and those reported in existing literature, primarily derived from density functional theory (DFT) investigations.7 Our analysis further reveals that the cell parameters obtained through the force field methodology for all scrutinized structures in this study exhibit only minor deviations, not exceeding 5%, when compared with values derived from rigorous DFT calculations. Notably, these calculated cell parameters consistently fall within the established range documented in previous works.7 This alignment with literature values adds confidence to the reliability of the force field simulations in capturing the essential structural features of the alkali hexazirconate compounds, providing a valuable and computationally efficient tool for exploring their properties.
Table 2 shows the octahedral volume, average bond length, and bond angle variance of the three octahedral types (labeled 1, 2 and 3, respectively in Fig. 1b) forming the simulated A2Zr6O13 structures. The influence of A-site cations (Li, Na, K) on the distortion of octahedra in the monoclinic A2Zr6O13 system can be assessed by examining the volume (V), average bond length (L), and bond angle variance (Ω) for each octahedral type.21 In Li2Zr6O13, the octahedra exhibit the smallest volumes and shortest bond lengths, with volumes ranging from 11.81 Å3 to 11.87 Å3 and a average bond length from 2.09 Å to 2.14 Å. Conversely, in K2Zr6O13, the octahedra display the largest volumes and larger bond lengths, with volumes from 11.87 Å3 to 12.26 Å3 and average bond length from 2.12 Å to 2.15 Å. This trend suggests that larger A-site cations lead to an increase in both the volume and bond lengths of the octahedra.
| Compound | Octahedral 1 | Octahedral 2 | Octahedral 3 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| V (Å) | L (Å) | Ω (o2) | V (Å) | L (Å) | Ω (o2) | V (Å) | L (Å) | Ω (o2) | |
| Li2Zr6O13 | 11.84 | 2.09 | 153.56 | 11.87 | 2.14 | 175.34 | 11.81 | 2.12 | 157.94 |
| Na2Zr6O13 | 11.96 | 2.13 | 172.18 | 11.95 | 2.13 | 159.65 | 12.10 | 2.13 | 125.85 |
| K2Zr6O13 | 12.10 | 2.15 | 203.77 | 11.87 | 2.12 | 144.30 | 12.26 | 2.14 | 140.48 |
Furthermore, the bond angle variance, which indicates octahedral distortion, also varies with the size of the A-site cation. For octahedral 1, the bond angle variance increases significantly from 153.56°2 in Li2Zr6O13 to 203.77°2 in K2Zr6O13, indicating a greater distortion with larger cations. In octahedral 2, however, the distortion decreases from 175.34°2 in Li2Zr6O13to 144.30°2 in K2Zr6O13. Octahedral 3 shows a more complex behavior, with the bond angle variance decreasing from Li (157.94°2) to Na (125.85°2) and then increasing again for K (140.48°2).
In comparison, the octahedral parameters in Li2Ti6O13 are distinctly different.7 The volumes are considerably smaller, ranging from 10.30 Å3 to 10.43 Å3, and the bond lengths are consistently shorter at 2.02 Å3 for all octahedra. The bond angle variances are also lower, with values of 111.60°2, 128.96°2, and 141.47°2 for octahedra 1, 2, and 3, respectively. Note that the Ω variation is not directly correlated with the unit cell parameters.22 These lower values suggest that the Ti-containing octahedra are less distorted compared to their Zr counterparts.
These structural differences likely have significant implications for the mechanical properties of these materials. The increased distortion and larger volumes in the Zr-containing structures may lead to higher internal stress and lower overall structural stability, potentially resulting in lower hardness and greater susceptibility to deformation under mechanical load. Conversely, the smaller volumes and lower distortion in the Ti-containing structures suggest a more stable and rigid framework, which could translate to higher hardness and better mechanical strength. Thus, replacing Zr by Ti in the A2Ti6O13 systems likely reduces the mechanical robustness of the material.
In order to prove the possible existence and practical application of a compound, it is advisable to disclose the thermodynamic stability. The thermodynamics stability of A2Zr6O13 is evaluated evaluating by examining the standard molar enthalpy. Considering the thermodynamic cycle to form the A2Zr6O13 compounds as follows:
| A2O(s) + 6ZrO2(s) → A2Zr6O13(s) | (1) |
As the thermodynamics of the binary decomposition of Li2Zr6O13 into A2O and ZrO2 follows the Hess Law,23 the ΔfHm is evaluated from the total energy (E) derived from DFT computations, taking as the starting point the total energy difference upon formation from their binary blocks and the available experimental data of ΔfHm of A2O and ZrO2. Then, the standard molar formation enthalpy (ΔfHm) is evaluated by:
| ΔfHm(A2Zr6O13) = ΔrHm(A2Zr6O13) + ΔfHm(A2O) + 6ΔfHm(ZrO2) | (2) |
| ΔrHm(A2Zr6O13) = E(A2Zr6O13) − E(A2O) − 6E(ZrO2) | (3) |
Table 3 collects the values of ΔrHm of A2Zr6O13 and other tunnel structures for comparison. The thermodynamics stability of the partner structure to form the Li2Ti6O13 structure via Na/Li ion exchange was previously studied.6 In a previous work, the thermodynamic stability of A2B6O13 (B = Ti, Sn) was proven delivering their respective standard molar enthalpy of formation.5,24 The values of the standard formation enthalpy of A2B6O13 are comparable with those for A2Zr6O13 compounds. The more negative is ΔfHm the more stable is the compound against decomposition. In this sense, the A2Zr6O13 structures have high thermodynamic stability, highlighting that the new compound Na2Zr6O13 has the highest value of standard molar enthalpy of formation.
The evaluation of ionic–electronic properties is a crucial criterion in assessing materials for electrode applications, with the band gap serving as a key indicator of electronic characteristics.7,27 In this study, electronic band structures for A2Zr6O13 compounds were meticulously computed using identical density functional theory (DFT) parameters. The comprehensive density of states (DOS) and projected density of states were extracted employing the interpolation integration method, with a modest broadening factor of 0.01 eV. The resulting band structures provide a detailed insight into the electronic behavior of the alkali hexazirconates, revealing the distribution of electronic states and the presence of band gaps.
Fig. 2 portrays the density of states (DOS), intricately highlighting the contributions from individual constituents within the Li2Zr6O13, Na2Zr6O13, and K2Zr6O13 structures. A salient feature across all samples is the notable accumulation of DOS proximate to the Fermi level, a characteristic trait shared by semiconductor materials. This accumulation signifies the presence of electronic states available for conduction and valence band formation, crucial for understanding the materials’ electronic behavior. The band gap, representing the energy range devoid of electronic states, is discernible in the DOS plots, with its magnitude providing insights into the materials’ electrical conductivity. These electronic structure analyses contribute to a comprehensive understanding of the alkali hexazirconates, aiding in the assessment of their suitability for electrode applications in energy storage systems.
 | ||
| Fig. 2 Band structure and density of states of (a) Li2Zr6O13, (b) Na2Zr6O13, and (c) K2Zr6O13 compounds, respectively. (d) DOS of Alkali ions in each A2Zr6O13. | ||
In each structure, Zr species predominantly contribute to the conduction band, while the valence region is primarily governed by oxygen species. Alkali ions, conversely, exhibit relatively minor contributions to the electronic properties. Notably, K-ion emerges as the principal contributor to the conduction region as shown in the Fig. 2(d), resulting in a diminished energy band gap of 3.72 eV in K2Zr6O13, compared to approximately 4.32 eV for Li2Zr6O13 and 4.26 eV for Na2Zr6O13, respectively.
Notably, K-ions contribute more significantly to the valence and conduction bands, as shown in Fig. 2(d), resulting in a lower energy band gap of 3.72 eV in K2Zr6O13, compared to 4.32 eV for Li2Zr6O13 and 4.26 eV for Na2Zr6O13. This can be attributed to the differences in ionic radii among the alkali ions (0.76, 1.02, and 1.38) Å for Li+, Na+, and K+, respectively.28 For instance, the larger K-ion generally increases the average bond length in K2Zr6O13 lattice structure, consequently affecting the cell parameters as described in Table 1. Larger ions increase the distance between atoms in the crystal lattice, which can reduce the overlap between atomic orbitals, leading to a smaller splitting of energy levels and thus a smaller band gap. Additionally, the octahedral distortion discussed in Table 2 for reflects the influence of the large K-ion on the crystal structure. These distortions can alter the electronic structure and affect the band gap.
It is important to note that while classical pseudopotentials have been employed in this study to approximate ground state properties, their precision tends to wane when estimating band gaps in semiconductors and insulating materials. This can potentially lead to an underestimation of up to 40%, with variations contingent on the specific material being investigated.29 Additionally, for alternative hybrid functionals such as HSE06, HSE03, and Hubbard approximations, the band gap value relies on supplementary parameters essential for aligning with experimental data. However, in light of the absence of experimental data for K2Zr6O13, Na2Zr6O13, and Li2Zr6O13, coupled with the recognized tendency of DFT to underestimate band gap calculations,6,16,30,31 the energy gap values presented herein are to be regarded as conservative lower bounds.
The band structures depicted in Fig. 2, accompanied by density of states (DOS) analysis, offer a comprehensive overview of the electronic characteristics of Li2Zr6O13, Na2Zr6O13, and K2Zr6O13 in their ground states. The graphical representations convincingly establish the insulating nature of these compounds, emphasizing sizable energy bands located near the Fermi level. The observed insulating properties of Li2Zr6O13, Na2Zr6O13, and K2Zr6O13 may pose limitations on their direct use in electronic devices and energy storage systems, as enhanced electronic conductivity is typically desired for applications influencing the rate capability of composite electrodes in ion batteries.32 However, in practical scenarios, the rate capability may not be solely governed by the electronic conductivity of these compounds, given the potential utilization of nano-sized particles with carbon coating. The versatile nature of these materials, coupled with the ability to fine-tune their properties, presents various opportunities to enhance their performance in multiple technological applications.
3.2 Mechanical properties
Mechanical properties, together with analysis of the mechanical stability, are important keys to evaluate the feasibility of an unknown compound. The elastic constants describe the mechanical stiffness of the material with respect to deformation. Elastic constants can be estimated within a simulation by subjecting the optimized structure to a given strain pattern and then performing energy minimization with fixed cell parameters on the resulting atomic configurations and solving Hookes law.The calculation of single-crystal elastic constants can be performed using the stress–strain method from first-principles calculations. In a monoclinic structure, there are 13 independent elastic constants. These constants can be divided into two categories: those related to elasticity in length (C11, C22, and C33), and those related to elasticity in shape (C44, C55, C66, C12, C13, C15, C23, C25, C35, and C46).
There are 13 independent elastic constants, nonzero, elastic constants with both models as would be expected according to Neumanns rules.6,9,33
 | (4) |
For a stable monoclinic structure, the independent elastic constants should satisfy the criteria which are given by the following relations:6,9,33
| 2Cii > 0, | (5a) |
| [C11 + C22 + C33 + 2(C12 + C13 + C33)] > 0, | (5b) |
| (C33C55 − C352) > 0, | (5c) |
| (C44C66 − C462) > 0, | (5d) |
| (C22 + C33 − 2C23) > 0, | (5e) |
| [C22(C33C55 − C352) + 2C23C25C35 − C232C55 − C252C33] > 0, | (5f) |
| 2[C15C25(C33C12 − C13C23) + C15C35(C22C13 − C12C23) + C25C35(C11C23 − C12C13)] − [(C22C33 − C232)C152 + (C11C33 − C132)C252 + (C11C22 − C122)C352 + gC55] > 0 | (5g) |
| C ij (GPa) | Li2Zr6O13 | Na2Zr6O13 | K2Zr6O13 | |||
|---|---|---|---|---|---|---|
| DFT | FF | DFT | FF | DFT | FF | |
| C 11 | 173.417 | 228.868 | 190.891 | 260.242 | 102.781 | 242.044 |
| C 12 | 61.439 | 75.493 | 68.675 | 83.358 | 50.399 | 80.849 |
| C 13 | 98.460 | 124.441 | 99.774 | 125.951 | −187.667 | 120.527 |
| C 15 | 7.069 | 13.094 | 7.731 | 8.630 | 0.829 | 8.614 |
| C 22 | 180.802 | 199.100 | 183.587 | 201.813 | 180.842 | 197.799 |
| C 23 | 71.449 | 84.795 | 67.353 | 78.475 | −52.316 | 78.003 |
| C 25 | 4.364 | 2.438 | 4.064 | 1.782 | −0.351 | 1.393 |
| C 33 | 254.614 | 348.984 | 216.510 | 318.618 | −35.011 | 313.790 |
| C 35 | 15.042 | 23.503 | 14.753 | 6.745 | 50.964 | 9.244 |
| C 44 | 30.870 | 31.927 | 32.254 | 41.383 | −6.047 | 42.452 |
| C 46 | 5.240 | 4.160 | 6.776 | 3.879 | 32.270 | 4.259 |
| C 55 | 49.912 | 62.055 | 46.781 | 69.237 | 45.383 | 68.404 |
| C 66 | 7.759 | 23.777 | 2.625 | 17.704 | 7.386 | 20.986 |
The elastic constants reflect the material's ability to withstand deformation subjected to external pressure. Fig. 3 illustrates the variation in elastic constants (measured in GPa) concerning the alkali ion A (Li and Na). The results indicate that the elasticity components in the direction of length (C11, C22, and C33) are significant, while the elasticity components in the direction of shape are below 100 GPa. As such, the focus remains predominantly on C11, C22, and C33.
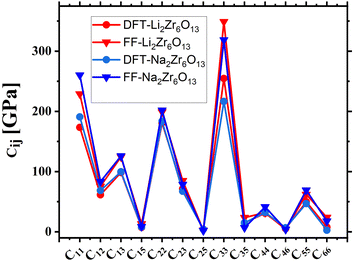 | ||
| Fig. 3 Calculated elastic constants by DFT and force field for the hexazirconate A2Zr6O13 (A = Li, Na). | ||
The hexazirconate materials is incompressible stress along of the principals axis x, y and z, that in monoclinic system are directly related with crystallographic axis a, b and c, respectability. The structures Li2Zr6O13 and Na2Zr6O13 present the values of C11 and C22 smaller that C33, see Fig. 3, this mean that these materials is more easy to compress along to axis C11 and C22 that C33. However, in the case of Li2Zr6O13 the value of C22 is minor that C11 this can be associated to with the location of the Li atom on the xz plane of the 8-atom oxygen cage. Note that the elastics constant increase with the atomics number of the alkaline ions. The elastics constant obtained by force field in all cases studied in this paper is high that the obtained by DFT calculations as show in the Fig. 3.
If compare the elastic constants along of x, y and z axis with Li2Ti6O13 and Na2Ti6O13 studied by Zulueta and Simalaotao,9,15 the hexazirconates and hexatitanates present similar value of C33 that suggest that the change of Ti by Zr no affect the elastic properties along of z axis. However, our materials are more resistant to deformation along the x and y axis that the heaxtitanate studied in previously work by Zulueta and Simalaotao.9,15
It is feasible to determine various material properties such as bulk, shear and Youngs modulus, based on the elastic constants. These results are presented in Table 5, where a comparison is made between the properties computed using DFT and the force field (FF) methods. The elastic constants obtained by force field (in all cases studies in this work) are higher than those obtained through DFT calculations.
| Convenium | Li2Zr6O13 | Na2Zr6O13 | ||
|---|---|---|---|---|
| DFT | FF | DFT | FF | |
| Bulk modulus | ||||
| Voigt | 119.05 | 149.60 | 118.06 | 142.97 |
| Reuss | 112.41 | 115.73 | 114.95 | 131.54 |
| Hill | 115.73 | 142.96 | 116.50 | 137.26 |
| Shear modulus | ||||
| Voigt | 42.87 | 56.36 | 40.01 | 58.45 |
| Reuss | 21.18 | 22.36 | 5.22 | 22.82 |
| Hill | 32.02 | 39.36 | 22.61 | 40.64 |
| Youngs modulus | ||||
| x | 128.20 | 81.61 | 136.17 | 85.88 |
| y | 152.30 | 80.60 | 152.84 | 78.25 |
| z | 188.03 | 265.46 | 155.77 | 244.82 |
The calculated elastic properties of monoclinic Li2Zr6O13 and Na2Zr6O13 are comprehensively presented, encompassing bulk modulus (B), shear modulus (G), and Young's modulus (E) in Table 5. Utilizing both density functional theory (DFT) and force field (FF) methodologies, the Voigt and Reuss approximations, along with the Hill average, were employed to delineate upper and lower bounds on the effective elastic modulus of the polycrystalline materials. Specifically focusing on the bulk modulus, Li2Zr6O13 and Na2Zr6O13 consistently exhibit similar resistance to volume changes under hydrostatic pressure. Notably, when compared to their Ti counterparts, these materials demonstrate small bulk modulus values.6,9,15 This observation holds true for both DFT and FF approaches, indicating a heightened compressibility of Li2Zr6O13 and Na2Zr6O13 in response to hydrostatic pressure, thereby providing valuable insights into their mechanical behavior.
The shear modulus, a critical indicator of a material's resistance to shear deformation, reveals distinctive mechanical disparities between monoclinic Li2Zr6O13 and Na2Zr6O13. Through the application of both density functional theory (DFT) and force field (FF) calculations, Li2Zr6O13 consistently exhibits higher shear modulus values than its sodium counterpart, as evidenced by both Voigt and Reuss approximations. This implies that Li2Zr6O13 demonstrates superior resistance to shape changes induced by tangential forces, emphasizing its enhanced ability to withstand shear deformations compared to Na2Zr6O13. However, it is noteworthy that in both cases, the shear modulus of the Ti counterpart significantly surpasses that of the studied materials,6,9,15 underscoring the distinctive mechanical behavior of the titanium-based compound.
Young's modulus, also known as the modulus of elasticity, measures the stiffness of a solid material. It quantifies a material's ability to resist deformation when subjected to an axial or tensile load. In simpler terms, Young's modulus describes how much a material stretches or compresses when a force is applied along its length.6,9,34 The young modulus in the direction y is equal to hexazirconate of lithium and sodium, this suggests that in this type of structure, the young modulus in this direction is not affected by the alkaline metals. Compared with the hexatitanatium of lithium and sodium are more resistant to deformations in both cases.9
The brittleness and ductility of materials can be analyzed using different mechanical properties, as mentioned, including the ratio of the bulk modulus to the shear modulus (B/G ratio). These parameters provide insights into how a material will behave under different types of stress. If the Pugh's Criterion (B/G ratio) is less than 1.75, the material is considered brittle, otherwise is ductile.6,9,15,16 This criterion suggests the materials studies in this work are ductile, these materials have a relatively high ability to deform under stress, this properties is essential to the use of these materials in alkaline ions batteries.
3.3 Thermodynamical stability and open cell voltage
A material is thermodynamically stable under a given set of conditions if its energy cannot be lowered by rearranging its atoms. Energy lowering can arise from two distinct mechanisms: (1) phase separation (decomposition) into competing materials with the same average composition or (2) phase transition to an alternative crystal structure (polymorph) at fixed composition.35 In the case of some lithium materials used in batteries exhibit stable phases at intermediate lithium concentrations, such as lithium-vacancy orderings in intercalation materials or different atomic ordering in alloys.36 In principle, if computed using atomistic simulation is possible determinate all intermediate possible phases and using a formalism of convex Hull we can determinate the pseudobinary stable phases for study materials. However the number of combinations to generate lithium vacancy is huge and impossible to calculate using atomistic simulations.The intermediate phases in the system belong to the same host structure, i.e., lithium ions and vacancies occupy a common sublattice. Although this general problem of finding the distribution of a species over available lattice sites can be solved using site occupancy disorder (SOD) program to identify the inequivalent configurations and reduce significantly the number of calculations. However, to construct the above Hull diagram we used the force field validate before because the size of the supercell 1 × 4 × 1 and the number the inequivalent configurations are impractical to be computed used DFT.
In order to determine equilibrium concentrations of pseudo-binary phases, it is imperative to compare energies of nonequivalent configurations within an appropriate supercell. The probability of a given configuration (m) is contingent upon not only its energy (Em), but also its degeneracy (Ωm), and can be expressed mathematically as:
 | (6) |
By utilizing this formula, we can subsequently calculate the energy of the system in configurational equilibrium as the average shown in the following equation:
 | (7) |
The computed energy at 300 K for various pseudobinary phases of AxZr6O13 (A = Li and Na, and x = 0 to 2) using canonical distributions is depicted in Fig. 4. The plot illustrates the Hull energies, and notably, both cases exhibit only two stable phases when lithium ions and vacancies are generated within the material. This characteristic is of paramount importance for materials intended for use in secondary batteries. The stability of these phases ensures that the materials do not decompose into other phases with lower open cell voltage during the cyclic charge and discharge processes. This stability is a key factor in the long-term performance and reliability of the materials in practical battery applications.
 | ||
| Fig. 4 Formation energies of pseudobinary phases for (a) LixZr6O13 and (b) NaxZr6O13 at 300 K, respectively. | ||
The stability of battery electrodes is directly associated with the number of plateau regions observed in the open cell voltage curve during the discharge process. Unlike materials such as Li2Ti6O13 and NaTi6O13, which exhibit multiple plateaus indicative of transitions to pseudobinary phases during Ti oxidation and reduction, our investigated materials, Li2Zr6O13 and Na2Zr6O13, demonstrate a simplified behavior with only two stable phases, resulting in a consistent discharge curve. The open cell voltage, a crucial parameter reflecting the absence of corrosion reactions, is determined by the difference in chemical potentials of A ions in the cathode (μAcath) and the anode (μAan, where A = Li, Na), as described by the equation:5,37
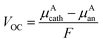 | (8) |
 | (9) |
To assess the energetic cost of Li-intercalation and the change in internal energy of the A2Zr6O13 structure, a supercell with dimensions of 1 × 4 × 1 is utilized to remove alkaline ions, and the total energy is obtained through force field (FF) calculations. The change in reaction energy (ΔEA) of Li-intercalation between A2Zr6O13 and A2−xZr6O13 can be calculated using eqn (10):
| ΔEA = E(A2Zr6O13) − [E(A2−xZr6O13) + xE(A)] | (10) |
The theoretical capacity (Q) can be evaluated by using the Faraday law:34,38–41
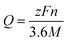 | (11) |
The open cell voltage of the stable phase of Li2Zr6O13 and Na2Zr6O13 is determined to be 1.3 V and 2.9 V, with a theoretical capacity of 69.68 mA h g−1 and 66.89 mA h g−1, respectively. The higher open cell voltage and lower theoretical capacity of Na2Zr6O13 compared to Li2Zr6O13 can be attributed to the larger ionic radius (1.02 Å) and greater mass of the Na ion relative to the Li ion (0.76 Å). In addition, Na+/Na has higher reduction potential (−2.71 V) than Li+/Li (−3.04 V). These values are comparable to experimental results obtained for Ti-based counterparts by other authors.1,4
Bearing in mind the properties disseminated in this manuscript, we hope that these outstanding properties motivate further experimental syntheses and investigations of A2Zr6O13 compounds, leading to practical applications in current and future alkali-ion batteries.
4 Conclusion
In this study, we conducted a comprehensive assessment of the structural, electronic, and mechanical properties of Li2Zr6O13, as well as the previously unreported compounds Na2Zr6O13 and K2Zr6O13, utilizing classical simulations and density functional theory (DFT) calculations. The structural and mechanical properties were determined through force-field methods, validated by subsequent DFT computations. Notably, the lattice parameters obtained through DFT calculations closely align with previous research findings, affirming the efficacy of the force field approach in modeling such materials.The electronic band structure analysis revealed that Li2Zr6O13 and Na2Zr6O13 exhibit insulator behavior with indirect band gap energies of 4.3 eV, while K2Zr6O13 demonstrates semiconducting properties with a band gap energy of 3.7 eV. However, it's important to note that K2Zr6O13 was found to be mechanically unstable, leading us to discontinue its study. On the other hand, Li2Zr6O13 and exhibit mechanical properties with C11 and C22 smaller than C33, indicating greater susceptibility to compression along the x and y axes than along the z-axis. This ductile behavior, coupled with a Young's modulus similar to hexazirconates of lithium and sodium, suggests their potential in alkaline ion batteries, where the ability to deform under stress is essential. In terms of electrochemical performance, Li2Zr6O13 and Na2Zr6O13 present only two stable phases during the charge and discharge process, resulting in a plateau region in the open cell voltage profile at 1.3 and 2.9 V and theoretical capacity of 69.68 mA h g−1 and 66.89 mA h g−1, respectively. This contrasts with hexatitanates, which exhibit multiple plateau regions, highlighting a distinctive property that may influence the performance of alkaline ion batteries. In this study does not only improve our understanding of the structural and electronic properties of Li2Zr6O13, Na2Zr6O13, and K2Zr6O13 but also underscores the potential applications of the identified materials in energy storage. Future research may delve deeper into optimizing the electrochemical performance of these compounds and exploring additional compositions for further advancements in alkaline ion battery technology.
Author contributions
JR. Fernández-Gamboa: conception, data acquisition and interpretation, original draft preparation, editing, review. Frederik Tielens: data analysis, editing, review. Yohandys A. Zulueta: conception, project supervision, manuscript editing and review. All authors reviewed the manuscript.Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
This project received support from the Flemish Development Cooperation through the Flemish Interuniversity Council-University Cooperation for Development (VLIR-UOS) as part of an Institutional University Cooperation program with Universidad de Oriente in Santiago de Cuba, Cuba. FT wishes to acknowledge the VUB for support, among other through a Strategic Research Program awarded to his group. Computational resources and services were provided by the Shared ICT Services Centre funded by the Vrije Universiteit Brussel, the Flemish Supercomputer Center (VSC) and FWO. To Prof. Ricardo Grau Crespo for providing the SOD code and for useful comments.Notes and references
- J. C. Peréz-Flores, A. Kuhn and F. García-Alvarado, ECS Meeting Abstracts, 2010, MA2010-03, 280.
- J. C. Pérez-Flores, C. Baehtz, M. Hoelzel, A. Kuhn and F. García-Alvarado, Phys. Chem. Chem. Phys., 2012, 14, 2892–2899 RSC.
- J. Pérez-Flores, A. Kuhn and F. García-Alvarado, J. Power Sources, 2011, 196, 1378–1385 CrossRef.
- K. Kataoka, J. Awaka, N. Kijima, H. Hayakawa, K.-I. Ohshima and J. Akimoto, Chem. Mater., 2011, 23, 2344–2352 CrossRef CAS.
- Y. A. Zulueta, P. Geerlings, F. Tielens and M. T. Nguyen, J. Phys. Chem. C, 2019, 123, 24375–24382 CrossRef CAS.
- Y. A. Zulueta and M. T. Nguyen, Phys. Status Solidi B, 2018, 255, 1700669 CrossRef.
- J. Fernández-Gamboa, F. Tielens and Y. A. Zulueta, Mater. Sci. Semicond. Process., 2022, 152, 107074 CrossRef.
- J. Fernández-Gamboa, F. Tielens and Y. A. Zulueta, Mater. Sci. Semicond. Process., 2024, 173, 108144 CrossRef.
- K. Simalaotao, T. Thanasarnsurapong, T. Maluangnont, K. Phacheerak and A. Boonchun, J. Phys. D: Appl. Phys., 2023, 56, 385303 CrossRef CAS.
- J. R. Fernández-Gamboa, Y. A.-Zulueta, M. P. Pham-Ho, F. Tielens and M. T. Nguyen, Rev. Cubana Quim., 2023, 35, 390–404 Search PubMed.
- S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr. - Cryst. Mater., 2005, 220, 567–570 CrossRef CAS.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406 CrossRef PubMed.
- B. G. Pfrommer, M. Côté, S. G. Louie and M. L. Cohen, J. Comput. Phys., 1997, 131, 233–240 CrossRef CAS.
- J. D. Gale and A. L. Rohl, Mol. Simul., 2003, 29, 291–341 CrossRef CAS.
- Y. A. Zulueta, M. Froeyen and M. T. Nguyen, Comput. Mater. Sci., 2017, 136, 271–279 CrossRef CAS.
- Y. A. Zulueta, P. Geerlings, F. Tielens and M. T. Nguyen, J. Solid State Chem., 2019, 279, 120930 CrossRef CAS.
- R. Grau-Crespo, S. Hamad, C. R. A. Catlow and N. H. de Leeuw, J. Phys.: Condens. Matter, 2007, 19, 256201 CrossRef.
- V. Fotopoulos, R. Grau-Crespo and A. L. Shluger, Phys. Chem. Chem. Phys., 2023, 25, 9168–9175 RSC.
- R. S. Kingsbury, A. S. Rosen, A. S. Gupta, J. M. Munro, S. P. Ong, A. Jain, S. Dwaraknath, M. K. Horton and K. A. Persson, npj Comput. Mater., 2022, 8, 1–11 CrossRef.
- S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, Comput. Mater. Sci., 2013, 68, 314–319 CrossRef CAS.
- N. W. Thomas, Acta Crystallogr., Sect. B: Struct. Sci., 1989, 45, 337–344 CrossRef.
- M. Fleet, Mineral. Mag., 1976, 40, 531–533 CrossRef.
- J. M. Seddon and J. D. Gale, Thermodynamics and statistical mechanics, Royal Society of Chemistry, 2001, vol. 10 Search PubMed.
- Y. A. Zulueta and M. T. Nguyen, Chapter One - Defect mechanisms and transport properties of electrodes and solid-state electrolytes for alkali-ion batteries, Elsevier, 2023, vol. 19, pp. 1–43 Search PubMed.
- M. Holzinger, A. Benisek, W. Schnelle, E. Gmelin, J. Maier and W. Sitte, J. Chem. Thermodyn., 2003, 35, 1469–1487 CrossRef CAS.
- H. Manyu, L. Yimin, L. Chunguang and L. Xia, Phys. B, 2012, 407, 2811–2815 CrossRef.
- M. Schlüter and L. J. Sham, in Advances in Quantum Chemistry, ed. P.-O. Löwdin, Academic Press, 1990, vol. 21 of Density Functional Theory of Many-Fermion Systems, pp. 97–112 Search PubMed.
- R. D. Shannon, Acta Crystallogr., Sect. A: Found. Crystallogr., 1976, 32, 751–767 CrossRef.
- J. P. Perdew, Int. J. Quantum Chem., 2009, 28, 497–523 CrossRef.
- Y. A. Zulueta Leyva and M. T. Nguyen, Phys. Status Solidi B, 2019, 256, 1800568 CrossRef.
- M. G. Medvedev, I. S. Bushmarinov, J. Sun, J. P. Perdew and K. A. Lyssenko, Science, 2017, 355, 49–52 CrossRef CAS PubMed.
- Y. Orikasa, Y. Gogyo, H. Yamashige, M. Katayama, K. Chen, T. Mori, K. Yamamoto, T. Masese, Y. Inada and T. Ohta, et al. , Sci. Rep., 2016, 6, 26382 CrossRef CAS PubMed.
- S. T. Murphy, P. Zeller, A. Chartier and L. Van Brutzel, J. Phys. Chem. C, 2011, 115, 21874–21881 CrossRef CAS.
- Y. A. Zulueta, R. Mut, S. Kaya, J. A. Dawson and M. T. Nguyen, J. Phys. Chem. C, 2021, 125, 14947–14956 CrossRef CAS.
- C. J. Bartel, J. Mater. Sci., 2022, 57, 10475–10498 CrossRef CAS.
- A. Urban, I. Matts, A. Abdellahi and G. Ceder, Adv. Energy Mater., 2016, 6, 1600488 CrossRef.
- M. Saiful Islam and C. A. J. Fisher, Chem. Soc. Rev., 2014, 43, 185–204 RSC.
- A. Van der Ven, Z. Deng, S. Banerjee and S. P. Ong, Chem. Rev., 2020, 120, 6977–7019 CrossRef CAS PubMed.
- M. Aydinol, A. Kohan and G. Ceder, J. Power Sources, 1997, 68, 664–668 CrossRef CAS.
- G. Chaney, A. Ibrahim, F. Ersan, D. Çakr and C. Ataca, ACS Appl. Mater. Interfaces, 2021, 13, 36388–36406 CrossRef CAS PubMed.
- X. Zhao, P. Wang, E. Lv, C. Wu, K. Ma, Z. Gao, I. D. Gates and W. Yang, Appl. Surf. Sci., 2021, 569, 151050 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ma00254g |
| This journal is © The Royal Society of Chemistry 2024 |

