Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Simulations of photoinduced processes with the exact factorization: state of the art and perspectives
Lea Maria
Ibele
a,
Eduarda
Sangiogo Gil
ab,
Evaristo
Villaseco Arribas
ac and
Federica
Agostini
 *a
*a
aUniversité Paris-Saclay, CNRS, Institut de Chimie Physique UMR8000, Orsay, 91405, France. E-mail: federica.agostini@universite-paris-saclay.fr
bInstitute of Theoretical Chemistry, University of Vienna, Währinger Straße 17, 1090 Vienna, Austria
cDepartment of Physics, Rutgers University, Newark 07102, New Jersey, USA
First published on 4th October 2024
Abstract
This perspective offers an overview of the applications of the exact factorization of the electron–nuclear wavefunction to the domain of theoretical photochemistry, where the aim is to gain insights into the ultrafast dynamics of molecular systems via simulations of their excited-state dynamics beyond the Born–Oppenheimer approximation. The exact factorization offers an alternative viewpoint to the Born–Huang representation for the interpretation of dynamical processes involving the electronic ground and excited states as well as their coupling through the nuclear motion. Therefore, the formalism has been used to derive algorithms for quantum molecular-dynamics simulations where the nuclear motion is treated using trajectories and the electrons are treated quantum mechanically. These algorithms have the characteristic features of being based on coupled and on auxiliary trajectories, and have shown excellent performance in describing a variety of excited-state processes, as this perspective illustrates. We conclude with a discussion on the authors' point of view on the future of the exact factorization.
1 Introduction
Photochemical and photophysical phenomena in molecular systems occur around us at every moment. Light absorption initiates the chemical reactions at the basis of photosynthesis in plants,1 activates the isomerization of the retinal chromophore in rhodopsin culminating in animal vision,2 and converts provitamin D into vitamin D in our body.3 For technological and medical applications, the goal of understanding these and similar phenomena is the design of systems that function as well as nature itself, to produce photovoltaic current upon absorption of light,4 to label biological cells carrying diseases to the human body,5 or to produce light in a clean and efficient way via electroluminescence in organic light emitting diodes.6 Understanding and controlling the behavior of matter in all these situations require a deep knowledge of the fundamental quantum-mechanical laws governing the complex interplay of the molecules with light and with their environment at the microscopic scale over time scales ranging from femtoseconds to nanoseconds.In this rich landscape of molecular processes and systems, the field of quantum molecular dynamics has sparkled in recent years.7 Great progress has been achieved at the more fundamental, theoretical level as well as from the point of view of the algorithms/software developments and applications. Many novel ideas have been proposed, motivated by the challenges encountered when simulating complex organic materials4,6,8–10 and biological systems,3,9,11,12 or when investigating phenomena over long time scales to look at slow processes such as fluorescence13,14 or vibrational relaxation, or when creating hybrid light–matter states in the strong coupling regime in optical and plasmonic microcavities.15–19
Simulating photochemical and photophysical processes in molecular systems requires to describe the interplay of electronic and nuclear dynamics, possibly with the explicit inclusion of light, and, in particular, accounting for excited-state effects, i.e., the so-called nonadiabatic or beyond-Born–Oppenheimer effects.20 For excited-state processes, on-the-fly molecular-dynamics simulations are perhaps the most widely used approaches, allowing one to access complex systems over reasonably long time scales up to few tens of picoseconds. Aiming to solve the time-dependent Schrödinger equation and to approximate the fundamental quantity of interest, i.e., the time-dependent molecular wavefunction,21 these methods rely on the support of various kinds of trajectories to mimic the nuclear dynamics under the effect of the electronic ground state and the (necessary) excited states. Ranging from quantum to classical, the nuclear evolution can be treated using:
• trajectory-basis functions, generally used to evolve Gaussian wavepackets by integrating ordinary differential equations that in some cases closely resemble Hamilton's equations,22–33
• quantum,34–42 coupled,43–47 auxiliary48,49 trajectories, retaining fully or partially the quantum character of the overall dynamics,
• semiclassical methods combined with the path-integral formulation of the quantum-mechanical propagator,11,50–55
• independent classical trajectories,9,47,56–84 allowing one to access efficiently large systems of “experimental complexity”, even if, sometimes, at the cost a losing accuracy.
In on-the-fly simulations, the other aspect of the problem, i.e., the electrons, enters the nuclear evolution in a somehow static way, as the necessary properties, such as energies, gradients, nonadiabatic couplings, spin–orbit couplings, or transition dipole moments, are determined (on-the-fly) along the trajectories at the visited nuclear geometries. In addition, using an ab initio or a semi-empirical or an analytical description of the electronic Hamiltonian, the most suitable electronic representation for the problem at hand and for the methodology chosen for the simulations needs to be chosen, e.g., the adiabatic vs. the diabatic representation.
It is worth mentioning here that other classes of methodologies exist to simulate nonadiabatic dynamics, such as approaches based on the density-matrix formalism10,85–93 or on quantum wavepackets propagation,94–99 but will not be covered in this perspective.
As it is clear from the above discussion, the field of quantum molecular dynamics is extremely vast. Consequently, this perspective will only discuss the impact that theoretical developments based on the exact factorization of the electron–nuclear wavefunction100,101 had in this domain so far, and will present our viewpoint on some promising avenues for the future of the exact factorization.
In molecular systems, the standard theoretical construction to go beyond the Born–Oppenheimer approximation102 and to account for non-adiabatic effects arising from the coupled electron–nuclear nature of these systems, is the Born–Huang representation103 of the molecular wavefunction.21 This is an exact representation of the electron–nuclear wavefunction as a linear combination of the so-called adiabatic states, i.e., the eigenstates of the electronic Hamiltonian at each nuclear geometry. An alternative to the Born–Huang representation is the exact factorization, which expresses the electron–nuclear wavefunction as the product of a marginal nuclear amplitude and a conditional electronic amplitude, parametrically dependent on the nuclear configuration.100 The exact factorization can be extended to any multicomponent many-body wavefunction, since no assumption is made on the physical properties of the subsystems to identify the marginal and the conditional amplitudes, e.g., the small electron–nuclear mass ratio usually invoked in the Born–Oppenheimer approximation.
The exact factorization depicts a photochemical reaction in terms of the dynamics of nuclei and electrons, offering a reformulation of the quantum dynamics of a molecule that is free from concepts such as static potential energy surfaces, conical intersections,104–107 and electronic transitions.56 Specifically, it was formulated in 2010 by Gross and co-workers to tackle the problem of describing the nonadiabatic dynamics of electrons and nuclei in a molecule (H2+ in that case) under the effect of an external laser pulse.100,108 This work proposed to analyze and to simulate the coupled dynamics of electrons and nuclei in nonadiabatic conditions employing the time-dependent potential energy surface and the time-dependent vector potential, which are concepts arising purely from the dynamics of the electrons even in the absence of external time-dependent fields. These time-dependent potentials provided an original tool to rethink our way of looking at nonadiabatic processes: in the Born–Huang framework, nuclear wavepackets (blue and pink shaded areas in Fig. 1 represent the modulus squared of the wavepackets) evolve under the effect of static electronic potential energy surfaces (blue and pink curves in Fig. 1 represent the energies of the ground state and the first excited state as functions of a one-dimensional nuclear coordinate) and exchange amplitude in the regions where the energies are close, thus accounting for electronic nonadiabatic transitions; in the eye of the exact factorization, the evolution of a single nuclear wavefunction (purple-colored areas in Fig. 1 represent the modulus squared of the wavefunction) is driven by a single time-dependent (scalar and vector) potential incorporating the dynamical effects of the electrons (the purple curve in Fig. 1, i.e., the time-dependent potential energy surface, changes in time but its shape is reminiscent of the shapes of the blue and pink curves of the upper panels).
The introduction of the time-dependent potentials in the framework of the exact factorization, along with a natural analogy with classical electromagnetism, lends itself to the introduction of the concept of a classical force,109,110 that is uniquely defined in the framework of the exact factorization. The concept of a classical force goes hands in hands with that of trajectories:111 in this way, the formalism has been employed successfully and largely in the domain of quantum molecular dynamics and of on-the-fly simulations.48,112–114 Perhaps, this is the field where the exact factorization made the most progress and proposed the most interesting developments, some of which will be discussed in this perspective.
The time-dependent version of the exact factorization followed previous work based on the stationary Schrödinger equation.115–119 We refer the reader to ref. 119–128 for an overview of the topics tackled by various authors employing the time-independent formulation of the exact factorization. In addition, alternative viewpoints have been proposed to study electron–nuclear,126,129–134 electron–electron135–139 and photon–electron–nuclear140–145 systems.
In this perspective, we will focus on the theoretical and on the algorithmic aspects of the exact factorization of the electron–nuclear wavefunction. The formulation of the theory will be briefly recalled in Section 2 and we will describe the coupled-trajectory and auxiliary-trajectory algorithms derived from it to simulate nonadiabatic processes in Section 3. Some applications of the exact factorization and of these algorithms are presented in Section 4. Section 5 presents a brief overview of recent work on the dynamics of photon–electron–nuclear systems employing the exact-factorization framework. Our conclusions are discussed in Section 6.
2 The exact factorization framework
A non-relativistic quantum-mechanical system comprised of two sets of interacting particles, with coordinates r and R, can be described by the Hamiltonian Ĥ(r, R), which can be written asĤ(r, R) = ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) (R) + ĤBO(r, R) (R) + ĤBO(r, R) | (1) |
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) (R) the kinetic energy of the particles identified by the coordinates R, in our case the nuclei, and with ĤBO(r, R) the sum of the remaining terms, i.e., the kinetic energy of the particles identified by the coordinates r, in our case the electrons, and all the interactions. In the electron–nuclear problem, ĤBO(r, R) is usually referred to as Born–Oppenheimer (BO) Hamiltonian, which explains our choice of labelling this term with the subscript “BO”. When describing the interaction of a molecule with (classical) light, as in the case of a laser pulse146–149 or a continuous-wave laser,150–156 an additional time-dependent term may appear in the Hamiltonian, which can be expressed as
(R) the kinetic energy of the particles identified by the coordinates R, in our case the nuclei, and with ĤBO(r, R) the sum of the remaining terms, i.e., the kinetic energy of the particles identified by the coordinates r, in our case the electrons, and all the interactions. In the electron–nuclear problem, ĤBO(r, R) is usually referred to as Born–Oppenheimer (BO) Hamiltonian, which explains our choice of labelling this term with the subscript “BO”. When describing the interaction of a molecule with (classical) light, as in the case of a laser pulse146–149 or a continuous-wave laser,150–156 an additional time-dependent term may appear in the Hamiltonian, which can be expressed as ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) (r, R, t) = −
(r, R, t) = −![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_char_e0b3.gif) (r, R)·E(t) in the dipole approximation. In this case, the interaction potential
(r, R)·E(t) in the dipole approximation. In this case, the interaction potential ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) (r, R, t) depends on
(r, R, t) depends on ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_char_e0b3.gif) (r, R), the molecule electric dipole moment, and on E(t), the external time-dependent electric field. In some situations,157–167 the relativistic correction due to the geometry-dependent spin–orbit coupling ĤSOC(x, R) can be included in the system Hamiltonian, where the variable x = [r,σ] accounts for the electronic spin σ as well as for the electronic positions r.
(r, R), the molecule electric dipole moment, and on E(t), the external time-dependent electric field. In some situations,157–167 the relativistic correction due to the geometry-dependent spin–orbit coupling ĤSOC(x, R) can be included in the system Hamiltonian, where the variable x = [r,σ] accounts for the electronic spin σ as well as for the electronic positions r.
The time-dependent Schrödinger equation (TDSE) with Ĥ(r, R) dictates the evolution of the wavefunction Ψ(r, R, t) as
 | (2) |
| Ψ(r, R, t) = χ(R, t)Φ(r, t; R) | (3) |
 | (4) |
 | (5) |
Eqn (4) is itself a TDSE where the coupling to the dynamics of Φ(r, t; R) is expressed in terms of a time-dependent vector potential (TDVP)
| Aν(R, t) = 〈Φ(t; R)| − iħ∇νΦ(t; R)〉r | (6) |
 | (7) |
The TDVP encodes information about the momentum field of the nuclei, since
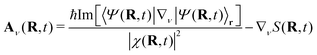 | (8) |
Note that the product form of the wavefunction Ψ(r, R, t) is invariant under the phase transformations ![[capital Phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0db.gif) (r, t; R) = exp[(i/ħ)θ(R, t)]Φ(r, t; R) and
(r, t; R) = exp[(i/ħ)θ(R, t)]Φ(r, t; R) and ![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) (R, t) = exp[(−i/ħ)θ(R, t)]χ(R, t). Thus, under these transformations, the TDVP and TDPES transform as well, as standard gauge potentials, namely Ãν(R, t) = Aν(R, t) + ∇νθ(R, t) and
(R, t) = exp[(−i/ħ)θ(R, t)]χ(R, t). Thus, under these transformations, the TDVP and TDPES transform as well, as standard gauge potentials, namely Ãν(R, t) = Aν(R, t) + ∇νθ(R, t) and ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (R, t) = ε(R, t) + ∂tθ(R, t), and eqn (4) and (5) are form-invariant.
(R, t) = ε(R, t) + ∂tθ(R, t), and eqn (4) and (5) are form-invariant.
Eqn (5) yields the evolution of Φ(r, t; R), where the coupling to the dynamics of eqn (4) is provided by
 | (9) |
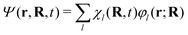 | (10) |
 | (11) |
 ). Third, it allows to somehow partition the nuclear wavefunction, which does not contain any information about the adiabatic states because it is a purely nuclear quantity, into adiabatic contributions.
). Third, it allows to somehow partition the nuclear wavefunction, which does not contain any information about the adiabatic states because it is a purely nuclear quantity, into adiabatic contributions.
While attempts have been made to solve exactly eqn (4) and (5),168,169 the most interesting developments of the exact factorization of the electron–nuclear wavefunction focused on introducing the quantum-classical perspective within this framework, such that the nuclear dynamics is ultimately approximated using classical-like trajectories while the electronic dynamics is treated quantum mechanically.39,41,43,112,170–176 The quantum-classical perspective naturally emerges in the exact factorization, since the classical limit of eqn (4) simply means to interpret the TDVP and TDPES as standard (classical) electromagnetic potentials producing a classical force on the nuclei.111 The main efforts in this context have been devoted, then, to the calculation and approximation of the TDVP and of the TDPES from the solution of the quantum-mechanical electronic eqn (5). To this end, extensive work has been devoted to analyze the TDVP and TDPES in model situations, such as in photo-activated processes,109,110,177 in relaxation dynamics through conical intersections,147,178–180 in the presence of quantum interferences,181 under the effect of an external time-dependent field,100,108,147,150,182–185 or including spin–orbit coupling.113,186 Those numerical analyses, together with theoretical developments focusing on understanding the behavior of the equations in some limiting cases, e.g., the adiabatic limit,187 or on resolution strategies of the nuclear equation, e.g., using semiclassical techniques188 or the method of characteristics,111,169 yielded various trajectory-based schemes readily applicable to on-the-fly molecular-dynamics simulations, as we will present now.
3 Trajectory-based methods for nonadiabatic dynamics in molecules
The exact factorization of the electron–nuclear wavefunction Ψ(r, R, t), especially thanks to the TDVP and TDPES, has been remarkably useful for understanding how the quantum-classical perspective is introduced starting from the quantum formulation of the dynamical problem, once eqn (4) and (5) are given. However, accurately and efficiently calculating the electronic TDVP and TDPES in the course of a quantum molecular-dynamics simulation requires to develop algorithms43,44,46,48,49,150,171,186,189,190 and software112,191–194 exploiting the strengths of current quantum-chemistry techniques for on-the-fly dynamics. With this idea in mind, let us present and compare the various quantum-classical schemes that have been introduced in recent years to simulate nonadiabatic (photochemical) processes.In general, the quantum-classical perspective on the exact factorization requires to replace the concept of a quantum nuclear wavefunction with an ensemble of trajectories. Formally, this is done by replacing in the equations R, a 3Nn-dimensional vector, with Nn the number of nuclei of the system, with the symbol Rα(t). Here, α = 1, …, Ntr labels the trajectories, that have to be many in order to reproduce the delocalization of the nuclei in configuration space, and for each α and at each time t, Rα(t) is a 3Nn-dimensional vector. The trajectory-based nuclear dynamics can be simply summarized using Hamilton's equations
 | (12) |
| Ṗαν(t) = Fαν(t) | (13) |
The trajectories can be assimilated to a moving grid: while in the quantum treatment the value of a function f(R, t) can be determined at time t at any point R, in the quantum-classical treatment only the values f(Rα(t), t) are accessible. Clearly, for a very large number of trajectories Ntr, information is not lost when going from the quantum to the quantum-classical treatment. It is important to note that, in order to evaluate how functions of the type f(Rα(t), t) evolve, only total time-derivatives can be computed instead of partial time-derivatives.
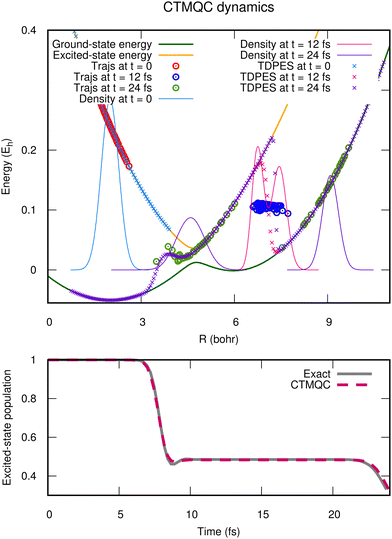
Aiming to develop on-the-fly procedures to solve the exact-factorization equations by exploiting quantum chemistry, the electronic wavefunction is expanded in the adiabatic basis, as shown in eqn (11). Therefore, the expression 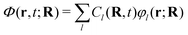 is inserted in eqn (5) to derive a set of evolution equations for the expansion coefficients Cl(R, t). Following from the above observations, when the idea of trajectories is introduced, the electronic eqn (5) is affected as well, and the evolution of the coefficients is ultimately expressed as a total time-derivative Ċl(Rα(t),t) = Ċαl(t).
is inserted in eqn (5) to derive a set of evolution equations for the expansion coefficients Cl(R, t). Following from the above observations, when the idea of trajectories is introduced, the electronic eqn (5) is affected as well, and the evolution of the coefficients is ultimately expressed as a total time-derivative Ċl(Rα(t),t) = Ċαl(t).
The key quantity arising in such a quantum-classical formulation of the electron–nuclear dynamics is the so-called quantum momentum. In eqn (5), the operator Û[Φ, χ] depends on the nuclear wavefunction, and, when it is expressed in polar form in terms of its modulus |χ| (or  ) and phase S, one gets
) and phase S, one gets
 | (14) |
 , which appears as a purely imaginary correction. The quantum momentum encloses information about the spatial delocalization of the nuclear density, and this information has to be recovered even when trajectories are used to mimic the nuclear dynamics. Therefore, the non-local character of the quantum nuclear density is encoded in the quantum momentum, that is why the algorithms derived from the exact factorization require either a coupled-trajectory scheme43,44 or an auxiliary-trajectory scheme.42,48
, which appears as a purely imaginary correction. The quantum momentum encloses information about the spatial delocalization of the nuclear density, and this information has to be recovered even when trajectories are used to mimic the nuclear dynamics. Therefore, the non-local character of the quantum nuclear density is encoded in the quantum momentum, that is why the algorithms derived from the exact factorization require either a coupled-trajectory scheme43,44 or an auxiliary-trajectory scheme.42,48
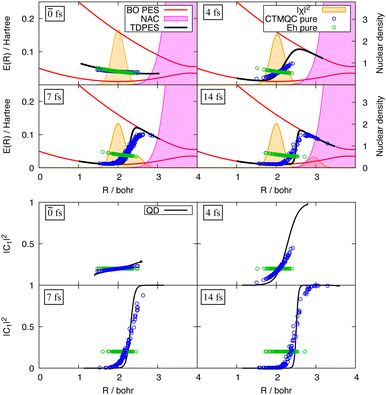
In general, the exact-factorization-based algorithms derived so far can be viewed as variations of the Ehrenfest scheme or of the surface-hopping method, where the effect of the quantum momentum is included. The advantage of these particular formulations is twofold: first, since Ehrenfest and surface hopping are the most widely-used approaches for simulations of photochemical processes, they are well-understood by the community and are implemented in many codes; second, it is easy to show how the corrections related to the inclusion of the quantum momentum cure the major drawbacks of both approaches, i.e., the mean-field character of Ehrenfest174 and the overcoherence problem of surface hopping.59,66,195 To demonstrate this second point, we find instructive to show here, for a simple model case, the performance of Ehrenfest dynamics and of surface hopping. Similarly to the scheme of Fig. 1, we use a one-dimensional two-electronic-state model defined by the green and orange potential energy curves reported in the upper panels of Fig. 2. The dynamics is initiated in the excited state with a Gaussian wavepacket centered at R = 2 bohr, whose density is represented as light-blue curves in both upper panels of the figure. The dynamics proceeds with such a photo-excited wavepacket moving towards the right and crossing the region where the energies of the ground and of the excited states are close. There, a nonadiabatic event takes place and the wavepacket branches, following partially the ground-state potential and partially the excited-state potential. This behavior can be verified at t = 12 fs, when the magenta nuclear density presents two peaks, attesting to the fact that the potential energy curves with different slopes drive the dynamics. Later on, at t = 24 fs, the nuclear density, represented in purple, is completely delocalized, with the portion on the right associated to the ground state while the portion on the left crosses once again the nonadiabatic region after being reflected by the barrier on the far right of the excited state potential curve.
The mean-field character of the Ehrenfest approach is not able, by construction, to capture with trajectories the dynamics just described, characterized by a final density that proceeds along diverging paths. This is very clearly represented by the circles in the upper left panel of Fig. 2, that show the positions of the Ehrenfest trajectories at the same time snapshots of the density, along with the potential energy felt by those trajectories, whose gradient is used to compute the force. The absence of the splitting in the distribution of trajectories yields wrong nuclear dynamics, and, consequently, it is not surprising that the population of the excited state (lower left panel of Fig. 2) at the end of the simulated dynamics is not correctly reproduced by Ehrenfest. The surface-hopping approach cures the mean-field problem of Ehrenfest. Specifically, the trajectories follow at all times either one or the other potential energy, that is why the circles on the right panel of Fig. 2 are distributed always either on the ground-state or on the excited-state energy curve. Surface-hopping trajectories correctly reproduce the splitting of the nuclear density since a hopping algorithm allows them to change instantaneously the potential that drives their dynamics (so-called, active state), with high probability in the region of strong nonadiabaticity. Nonetheless, the disconnect between the potential (or the force) that drives the dynamics of the trajectories and the evolution of the electronic coefficients (similarly to the Ċαl(t) above) can be source of disagreement between the two ways of estimating the electronic populations: one way is to count the fraction of trajectories in each state, while the other is via the coefficients. A surface-hopping procedure is internally consistent if these two ways of calculating the electronic populations yield the same or a similar result, as it should. When this is not the case, the algorithm suffers from overcoherence. This is clearly shown at the final times of the dynamics simulated with the fewest-switches surface-hopping algorithm56 (without decoherence corrections) and reported in the lower right panel of Fig. 2, where the purple-dashed and blue-continuous curves diverge. The small discrepancy between the exact curve (gray) and the curve calculated from the fraction of trajectories (blue) is probably due to the limited statistics, as only 2000 trajectories are used in this simulation. Note that many authors have devoted their efforts towards understanding and curing the problem of overcoherence in surface hopping45,59,66,72,196–202 (as well as in Ehrenfest75,203), since usually a surface-hopping simulation needs to account for decoherence corrections. Here, however, we show in Fig. 2 results obtained without including decoherence simply to explain the issue and to justify the need to go beyond the original algorithm.
Various algorithms based on the exact factorization are capable to circumvent naturally at the same time the mean-field and overcoherence issues of Ehrenfest and surface hopping thanks to the presence of the quantum momentum. In the past few years, different groups introduced different flavours of quantum-classical algorithms: the coupled-trajectory mixed quantum-classical (CTMQC) scheme was developed by Gross and coworkers in 2015,43 and as the name says, it employs an ensemble of coupled trajectories to mimic the nuclear dynamics; later on, the method surface hopping based on the exact factorization (SHXF) was introduced by Min and coworkers in 2018,48 aiming to use a surface-hopping scheme to mitigate the problems related to the large computational cost of CTMQC by evolving independent trajectories and adopting auxiliary trajectories when necessary; with a similar purpose, in 2021, Pieroni and Agostini developed the coupled-trajectory Tully surface hopping (CTTSH),44 which uses the idea of surface hopping within a coupled-trajectory procedure; Ha and Min proposed in 2022 an independent-trajectory version of CTMQC, named Ehrenfest dynamics based on the exact factorization (EhXF),49 which requires auxiliary trajectories similarly to SHXF; aiming to alleviate the issue of non-conservation of the total energy in CTMQC, Villaseco Arribas and Maitra introduced in 2023 a variation of the algorithm, i.e., CTMQC-E,190,204 by imposing energy conservation over the ensemble of trajectories, following a similar idea that in EhXF is imposed at the single-trajectory level; in a similar spirit, Blumberger and coworkers developed in 2023 CTMQC-(E)DI,46 where a double-intercept (DI) idea is introduced in CTMQC and in CTMQC-E to cure numerical instabilities encountered in CTMQC(-E) when calculating the quantum momentum and, thus, greatly improving energy and norm conservation; in 2024 Maitra and coworkers, inspired by the work of Martens,201 developed the quantum-trajectory surface-hopping based on the exact factorization (QTSH-XF),42 where a phase-space approach combined with the exact factorization cures the frustrated hops and velocity rescaling issues that SHXF inherits from surface hopping; an assessment of various exact-factorization-based algorithms, i.e., those based on auxiliary trajectories, along with their implementation in the Libra package205 has been recently presented by Han and Akimov.194 Currently, to the best of our knowledge, the available open-source codes able to perform exact-factorization-based calculations are PyUNIxMD,193 developed in the group of Min and interfaced with various quantum-chemistry packages, G-CTMQC,206 developed by our group and interfaced with the QuantumModelLib library of analytical potentials,207 and Libra,194 which for the moment only allows calculations with model potentials; CTTSH has been recently implemented in MOPAC-PI.208,209
As an example of the structure of the equations defining the CTMQC algorithm43,173 as a variation of the Ehrenfest scheme, let us show the following electronic and nuclear (force) equations
| Ċαl(t)|CTMQC = Ċαl(t)|Ehr + Ċαl(t)|qm | (15) |
| Fαν(t)|CTMQC = Fαν(t)|Ehr + Fαν(t)|qm | (16) |
| Ċαl(t)|CTTSH = Ċαl(t)|TSH + Ċαl(t)|qm | (17) |
| Fαν(t)|CTTSH = Fαν(t)|TSH | (18) |
To give an idea of the performance of the exact factorization, we show in Fig. 3 how CTMQC works in the situation described in Fig. 2. The delocalization of the distribution of trajectories is correctly reproduced by CTMQC, especially as it shown by the circles at the final simulated time t = 24 fs (green circles). Such a delocalization seems to appear more slowly than in the quantum dynamics, as the distribution of trajectories at t = 12 fs (blue circles) suggests. However, it is interesting to note how a single potential is able to yield different forces in different portions of space so as to induce the splitting of the distribution of trajectories (that is not possible to achieve in Ehrenfest while in surface hopping it is only possible by introducing the hopping idea). In this simple case, the TDPES can be calculated exactly, and it is shown in Fig. 3 as crosses at times t = 0 (light-blue crosses), t = 12 fs (magenta crosses) and t = 24 fs (purple crosses). Only at the intermediate time shown in the figure, the distribution of CTMQC trajectories along the potential that drives their dynamics, i.e., the blue circles, does not follow the TDPES, i.e., the magenta crosses, confirming, as observed previously, that CTMQC trajectories reproduce the splitting of the nuclear density with some delay. Nonetheless, such a delay does not affect significantly the population of the excited state (lower panel in Fig. 3) which perfectly agrees with the reference (gray line) all along the dynamics.
 | ||
| Fig. 3 Same as in Fig. 2 but for the CTMQC algorithm (using 1000 trajectories). | ||
3.1 Exact-factorization-based surface-hopping approaches
Among the various trajectory-based algorithms derived from the exact factorization and listed in the previous section, those that adopt a surface-hopping flavor have shown to be the most promising for molecular applications in photochemistry. Surface hopping is a widely-used, numerically-efficient, (almost) black-box and largely-implemented64,193,205,206,208,210–212 algorithm, thus it is easy to use as a starting point for new developments, either theoretical or computational. In addition, some analyses109,110 performed on the features of the TDPES and of the TDVP as well as their role in the dynamics draw interesting connections with surface hopping, motivating our efforts for combining it with the exact-factorization idea. Therefore, CTTSH and SHXF stand out as alternative choices to (standard) surface hopping, which ultimately has to be always cured with at least one of the many decoherence-correction schemes.59,66The main reason for moving away from CTMQC, which can be considered as the algorithm rigorously derived from the exact factorization, and for turning towards surface-hopping-based approaches is the computational advantage of the latter. Specifically,
• CTMQC requires the calculation of the nonadiabatic coupling vectors at all times. They are 3Nn-dimensional vectors for each pair of adiabatic states, and account for the spatial variation of the electronic states as functions of the nuclear coordinates. Their calculation is computationally expensive, but in surface hopping (i) only their projections along the nuclear velocity, which is a scalar quantity, is needed at all times, and (ii) depending on the implementations, they are calculated in full dimensionality only after a trajectory hop occurs.
• CTMQC potentially yields unstable long-time dynamics if the trajectories cross multiple times (the same) regions of configuration space with strong nonadiabaticity44,213 or in the case of quantum interferences.181,214 This happens because the algorithm, ultimately, produces a nuclear dynamics driven by an approximate TDPES. Such TDPES becomes noisy in the situations just mentioned, but in surface hopping this problem is naturally circumvented because the nuclear dynamics takes place on the adiabatic surfaces.
• CTMQC does not guarantee energy conservation, either along a single trajectory or over the ensemble of coupled trajectories, which is mainly due to the approximate nature of the quantum momentum used in the equations. This problem is partially alleviated in CTMQC-E by modifying the expression of the nuclear forces by imposing energy conservation a posteriori over the ensemble of trajectories. In surface hopping, instead, energy conservation is natural when the trajectories evolve adiabatically and is enforced on each trajectory when a hop occurs.
Both surface-hopping-based algorithms, i.e., CTTSH and SHXF, have been employed for calculations of molecular properties, as will be discussed in Section 4.2. The basic equations are the same, as both methods follow the same electronic evolution equation (eqn (17)), nuclear propagation scheme (eqn (18)) and fewest-switches hopping probability,44,56 but differ in the way they reconstruct the nuclear density for computing the quantum momentum (eqn (14)).
In CTTSH the quantum momentum is computed by approximating the nuclear density as a sum of Gaussians centered at the position of the trajectories and by adjusting this analytical expression by finding a modified expression guaranteeing that when averaged over the ensemble of coupled trajectories, the populations of the adiabatic states do not change if the nonadiabatic couplings are zero.112,173,177,209,215 The modified expression is used by default, unless it diverges numerically, in which case it is replaced by the analytical expression.
SHXF, instead, is an independent-trajectory approach, thus the quantum momentum has to be constructed with the support of auxiliary trajectories.48 In this case, frozen Gaussians are centered at the positions of these auxiliary – non-physical – trajectories such that the quantum momentum can be approximated locally using an analogous expression as the analytical expression used in CTTSH. SHXF is less computationally demanding than CTTSH since each physical trajectory can be propagated independently form the others, and the auxiliary trajectories are associated only to the electronic states that are coupled nonadiabatically to the active state. The auxiliary trajectories are launched when non-active electronic states become populated, with initial positions chosen to be the same as the position of the physical trajectory and with initial velocities determined by imposing that each auxiliary trajectory has the same kinetic or the same total energy of the physical trajectory. After they are created and associated to a certain electronic state, the auxiliary trajectories change positions with a velocity that at each time step is calculated by rescaling in all directions the velocity of the physical trajectory. The rescaling factor is determined by imposing energy conservation using the potential of the corresponding electronic state at the position of the physical trajectory. This procedure avoids additional electronic-structure calculations, namely the energy and the gradient of the electronic state(s) at the position of the corresponding auxiliary trajectories.
In Fig. 4 and 5, we summarize the steps of CTTSH and of SHXF. Fig. 4 shows that the procedure starts at time t = 0 with the sampling of the initial conditions (ICs) for the trajectories and the initialization of the electronic coefficients. Then, the electronic structure is computed at the positions of all trajectories, a task that can be performed in parallel, thus simultaneously for each trajectory. Note that in the scheme in Fig. 4 a thick gray arrow indicates a set of tasks, one for each trajectory, that can be performed in parallel. In CTTSH, the quantum momentum is calculated only once using information collected for all trajectories, therefore this task cannot be parallelized (it is indicated as a thin gray arrow). After the calculation of the quantum momentum, the nuclear trajectories and the electronic coefficients are propagated in time and the probability for a surface hop is determined, eventually imposing energy conservation if the hop is successful; these tasks can be parallelized over the trajectories. The procedure is repeated from the electronic-structure calculations at the new trajectories positions and iterated until the final time tmax of the simulation. Fig. 5 shows that all tasks can be performed in parallel, thus all steps in the scheme representing the algorithm are indicated as thin gray arrows. In addition, the calculation of the quantum momentum in SHXF is performed only after the auxiliary trajectories are created on the non-active states that are nonadiabatically coupled to the active state.
While the computational cost of SHXF is the same as “standard” surface hopping, CTTSH is more expensive. From the electronic-structure perspective, in addition to what is done in SHXF, CTTSH requires calculating the gradients of all electronic states involved in the dynamics (which is similar to ab initio multiple spawning27 after the trajectories start spawning, if the stochastic-selection idea216–218 is not applied, or to the augmented-fewest-switches surface hopping197). Note that, even though the calculation of the quantum momentum scales as Ntr2, it does not require additional electronic-structure information.
In ref. 209 we compared CTTSH to surface hopping and to a “synchronized” version of surface hopping using MOPAC-PI.208 This code uses a semi-empirical Floating Occupation Molecular Orbitals-Configuration Interaction (FOMO-CI) electronic structure approach, which is computationally very efficient, thus the time-limiting step in the overall dynamics is not the electronic structure, as it would be when using ab initio methods. The comparison was performed on the trans-azobenzene photodynamics using two electronic states, with ensembles of 10, 20 and 30 trajectories propagated for 50 fs (500 time steps) with computations carried out on a machine equipped with an Intel Xeon CPU E5-2450 0 with 32 CPUs, 2 sockets, 8 cores per package, and 2 threads per core. In surface hopping, the total time of the simulation was calculated as the sum of the time used in each trajectory. For CTTSH and “synchronized” surface hopping, the trajectories run synchronized in parallel using the same Message Passing Interface (MPI) strategy, but in the “synchronized” version of surface hopping, the quantum momentum is not calculated. The most significant time-consuming factor in CTTSH is the communication among processes necessary for the computation of quantum momentum. In Table 1 it is showed that the time spent on communication and synchronizing trajectories is significant, however, we expect that if a more expensive electronic-structure method was employed, the higher computational time required to perform CTTSH simulations would be less pronounced.
Apart from an efficient parallelization for the simultaneous propagation of CTTSH trajectories, there are indeed some ways to make the algorithm affordable for molecular studies: using a local diabatization scheme for the evolution (see Section 3.2), such that the nonadiabatic couplings are not needed for the propagation;194,208 using an efficient approach for the electronic structure information alternative to ab initio methods, as done with semi-empirical models or by building on-the-fly a database of nuclear configurations where the electronic structure is explicitly computed or by employing linear vibronic coupling models or with machine learning.208,210–212
3.2 General observations on nonadiabatic dynamics with trajectories
It is important to mention here that, in general, the outcome of a nonadiabatic quantum molecular-dynamics simulation strongly depends not only on the algorithm used to propagate nuclear and electronic dynamics, but also (i) on the choice of the initial conditions, (ii) on the representation used for the electronic problem, and, perhaps mainly, (iii) on the electronic-structure approach employed to determine electronic properties on-the-fly along the trajectories.219 Since the application of the exact factorization in the domain of photochemistry is independent of point (iii), below, we will briefly discuss only points (i) and (ii), as they have been analyzed precisely in the framework of the exact factorization.113,145,150,180 In relation to point (iii) above, some ideas have been developed in the context of the time-independent formulation of the exact factorization by Requist and Gross in ref. 120. There, it was proposed that the electronic equation, equivalent to eqn (5) but for the stationary solutions of the electron–nuclear Hamiltonian, is expressed and solved using density functional theory220,221 and some test studies were reported.121 In addition, Min and coworkers recently recast the exact factorization in such a way that a trajectory-based scheme can be made operational in combination with real-time time-dependent density functional theory.189An adequate preparation of the initial state of the system, point (i) above, depends on the process under investigation or on the experiment that one wants to simulate, and, thus, a general “recipe” for the correct procedure does not exist. Our group addressed this issue in earlier work focusing independently either on the nuclear180 or on the electronic145 aspects within the exact-factorization framework, but the problem has been discussed in the literature by other authors.222–228 The choice of initial conditions, namely the nuclear positions and momenta together with the electronic coefficients/populations at the initial time, can affect the calculated dynamics and observables, like photoproducts, lifetimes, and quantum yields, in many different ways. The dependence on the initial nuclear distribution might result more severe for the exact-factorization-based coupled-trajectory methods than for other approaches, since properly reconstructing the nuclear density along the dynamics is crucial to compute the quantum momentum that enters the expression of the classical force, in CTMQC (16), and of the evolution equation of the electronic coefficients, in CTMQC (15) and in CTTSH (17).
On the one hand, in recent work on the photo-isomerization dynamics of trans-azobenzene using CTTSH (see Section 4.2), it was necessary to freeze some high-energy internal vibrations while performing the initial harmonic Wigner sampling to avoid creating highly energetic trajectories: due to the limited number of affordable CTTSH trajectories (100 and 150 coupled trajectories were used) in such a large nuclear configuration space (of 72 dimensions), the energetic trajectories were rapidly separating in space and needed to be decoupled from the rest of the ensemble for numerical convenience, essentially reducing CTTSH to standard surface hopping. With a similar idea in mind, in order to avoid ensembles, or bundles, of trajectories that dramatically diverge in configuration space, the independent bundle approximation (IBA) was proposed using CTMQC.44 The IBA consists in organizing Ntr trajectories in n bundles each containing ntr trajectories, such that Ntr = n × ntr, where the ntr trajectories are grouped in the bundles according to their initial kinetic energy (or potential energy, or total energy, etc.). On the other hand, the initialization of the electronic dynamics in a pure adiabatic state is the commonly-accepted practice for photochemical studies, since with a femtosecond laser pulse it is possible to target the excitation of a low-lying electronic state. Nonetheless, photo-ionization with an attosecond laser pulse, broadly distributed in energy, is capable of creating a coherent superposition of electronic states (see Section 4.3). For applications in attochemistry, then, the way of creating such a superposition should be adapted to the used simulation method as well as to the observables under investigation, as discussed in ref. 145.
Point (ii) above concerns the theoretical representation adopted to describe the electronic dynamics. When aiming to simulate the ultrafast relaxation process of a photo-excited system via conical intersections or avoided crossings between electronic states of the same spin multiplicity, i.e., internal conversions, the Hamiltonian given in eqn (1) is able to fully capture this dynamics. Therefore, usually, the adiabatic representation is employed, formed by the eigenstates of the electronic Hamiltonian, i.e., ĤBO(r, R) in eqn (1). In this representation, a peculiar parametric dependence on the nuclear configuration R appears, as consequence of the dependence of ĤBO on R, and stimulates steadily interests in various communities due to its potential relation with geometric phases229–239 (see Section 4.1). The form of the electronic Hamiltonian ĤBO is diagonal in this representation and the coupling between pairs of electronic states is encoded in the nonadiabatic coupling vectors – connecting two electronic states via the nuclear displacement operator. Due to the very localized nature of these nonadiabatic coupling vectors, local diabatization schemes are often employed to solve the electronic evolution equation locally in the diabatic basis, designed to capture even with a finite integration time step the localized degeneracy region between two electronic states along the nuclear evolution. When describing processes as intersystem crossings involving electronic states with different spin multiplicity, the spin–orbit coupling ĤSOC(x, R), with x = r, σ, has to be included in the molecular Hamiltonian to open spin-forbidden relaxation pathways upon photo-excitation. In such situations, the question presents itself as to whether the spin-diabatic or the spin-adiabatic representation is most suited for the simulations.113,158,186,240 The former is composed by the eigenstates of ĤBO, and the pairs of electronic states are coupled either via the nonadiabatic coupling vectors or via the spin–orbit couplings, depending on the spin multiplicity; the latter is formed by the eigenstates of ĤBO + ĤSOC, and the couplings between pairs of states becomes fully of nonadiabatic character. Also in this case, the literature presents various options depending on the algorithm and on the code employed for the simulations. Dynamics in the presence of spin–orbit coupling was analyzed based on CTMQC113,186 and pointed out that, while at the exact-factorization level there is no difference between the two representations, as expected, the approximations underlying the CTMQC algorithm perform better in the spin-adiabatic basis than in the spin-diabatic basis. A very similar issue is encountered when an external laser field is added to the molecular Hamiltonian, i.e., ĤBO(r, R) + Ĥext(r, R, t), since now the ideas of field-adiabatic or field-diabatic bases can be introduced.241 Also in this case, authors discussed this point in relation to various trajectory-based algorithms for nonadiabatic dynamics, and in the context of the exact factorization only the particular case of a periodic drive was considered, and CTMQC was combined with the Floquet formalism,150 designed to solve a TDSE with a Hamiltonian that is periodic in time.
4 Studies of electron–nuclear dynamics based on the exact factorization
This section of the perspective provides an overview of the variety of dynamical problems that have been tackled using the exact factorization. In the following sections, we will demonstrate the flexibility of the formalism in describing different effects and different properties, often providing new insights into the studied processes or new understanding of the theory.First, in Section 4.1, we will report on a dynamics in the vicinity of a conical intersection in a Jahn–Teller model, recently engineered in a quantum simulator.239 In this study, it was discussed the fundamental difference between the concept of topological phases due to the presence of conical intersections that arise in the Born–Huang representation of the dynamics and the concept of dynamics-induced geometric phase that is independent of the underlying theoretical representation used to analyze the dynamics. Then, in Section 4.2, we report on various applications of exact-factorization-based algorithms to study the dynamics of molecules induced by the creation of a vibrational wavepacket produced by photoexcitation. In Section 4.2.1, we describe in some detail the work of our group that employs a coupled-trajectory scheme, in particular, the photo-isomerization process of trans-azobenzene upon nπ* and ππ* excitation with CTTSH in full dimensionality using the semi-empirical FOMO-CI electronic structure method with the reparametrized semi-empirical electronic-structure model AM1. The results of CTTSH dynamics are compared to surface hopping w/o accounting for decoherence corrections. In Section 4.2.2, an overview of the auxiliary-trajectory scheme SHXF is provided, highlighting the works of Min and of Maitra on a large variety of molecular systems and properties. Finally, in Section 4.3, we discuss a recent analysis reported on the different strategies to initialize the dynamics simulated by various trajectory-based procedures for excited-state dynamics in a model potential upon creation of a coherent superposition of electronic states,145 usually referred to as electronic wavepacket. Such an electronic wavepacket can be created by an attosecond laser pulse, and the ensuing dynamics is usually simulated using the (multi-trajectory) Ehrenfest method, whose performance in comparison to CTMQC have been discussed.
4.1 Low-energy dynamics at a conical intersection
As discussed in the previous sections, the exact factorization provides a fundamentally different picture of photochemistry if compared to the Born–Huang representation, as it introduces a single time-dependent potential governing the nuclear evolution, in the form of a TDPES and a TDVP, bypassing concepts such as multiple static adiabatic potential energy surfaces, conical intersections104–106,234,236,239,242–244 and nonadiabatic couplings.245When a dynamical process is studied in the Born–Huang representation, conical intersections appear ubiquitous in molecules: since the electronic Hamiltonian depends on the nuclear positions, its eigenstates, i.e., the adiabatic states, and its eigenvalues, the adiabatic potential energy surfaces, are functions of the nuclear positions as well. Conical intersections are regions of degeneracy of the adiabatic energies, where the correlation between electrons and nuclei manifests a singular behavior resulting in the divergence of the nonadiabatic couplings. In this picture, conical intersections give rise to topological phenomena of great interest for photochemistry and for low-energy molecular collisions or dissociations,231–235,238,246,247 which are related to geometric phases and often referred to as molecular Aharonov-Bohm effects.237,248,249
In the light of the broad interest of the physical-chemistry and chemical-physics communities in conical intersections and geometric phases, several studies employing the exact factorization147,178,179,250,251 have been conducted on prototypical situations of coupled electron–nuclear dynamics in the vicinity of conical intersections. Overall, these works concluded that in the studied cases, the time-dependent potentials do not reflect the singular behavior of the adiabatic potential energy surfaces and nonadiabatic couplings at the positions of the conical intersections. Hence, the signatures of conical intersections (seem to) disappear in the eye of the exact factorization. These studies raised the question as to whether it is possible to identify observable effects related to conical intersections without relying on the Born–Huang, or any other theoretical, representation, since physical observables are independent of the representation. This question is strictly related to a longstanding debate about the possibility of providing experimental evidence of effects directly related to geometric phases in molecules.232,233,235,238,239,246,247
Particular cases of geometric phases, which are those usually encountered in molecular processes within the Born–Huang representation, are the topological phases. When an electronic adiabatic eigenstate is slowly varied along a closed path in nuclear configuration space encircling the conical intersection, the corresponding wavefunction picks up a phase, in addition to the dynamical phase arising from the Schrödinger equation: if the phase depends on the geometry of the path, it is called geometric, whereas if it depends on the winding number of the path around the conical intersection, it is called topological. For a real-valued adiabatic wavefunction, the topological phase is γ = 0 or π and the phase factor is eiγ = ±1, yielding a change of sign of the electronic wavefunction when transported along the path. This idea of adiabatic transport of the electronic wavefunction in nuclear space implies the BO approximation. In an explicitly dynamical formulation, the BO approximation states that the molecular wavefunction is
| ΨBO(r,R, t) = ϕBO(r; R)χBO(R, t) | (19) |
 | (20) |
The topological phase within the BO approximation γBO(Γ) is defined as the circulation of the corresponding vector potential along the path Γ that encloses the conical intersection,
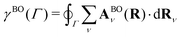 | (21) |
 | (22) |
Preliminary studies on geometric phases in the exact factorization were conducted by Gross and coworkers employing its static formulation and drew different conclusions depending on the systems that were considered.124,125,257 In ref. 124, for instance, it was shown that, in the studied model for proton coupled-electron transfer, the concept of topological phase was merely a consequence of the BO approximation. Thus, it completely disappeared in the framework of the exact factorization, only to reappear as a topological quantity in the limit of infinite nuclear mass, i.e., the BO limit. Instead, in ref. 125, a model of a pseudorotating triatomic molecule258 was used to show that the topological phase reverts to a geometric quantity if the system manifests a degenerate ground state, even within the exact factorization. These studies suggest, then, that the topological phase of the Born–Huang representation becomes geometric in particular cases related to degeneracies of the full Hamiltonian, while neither topological nor geometric phases appear otherwise. Later on, to shed some light on the time-dependent picture of geometric phases in the exact factorization and to relate theoretical observations to experiments, our group investigated the dynamics generated by the E⊗e Jahn–Teller Hamiltonian recently engineered in a trapped-ion quantum simulator.239 The experiment allowed to directly image the evolution of the nuclear density at the conical intersection in order to detect directly the signature of the conical intersection. The working hypothesis was that, since the real-valued electronic wavefunction changes sign when transported around the conical intersection, in order to yield a single-valued molecular wavefunction, the nuclear wavefunction in eqn (19) needs to change sign as well. Therefore, the nuclear wavefunction has to develop a node or a zero-density line, which are indications of destructive interferences caused by the geometric phase. However, this hypothesis relies on the BO approximation and, as shown in ref. 250, it cannot be verified when employing the exact factorization.
In ref. 250 and 251, the exact quantum dynamics was simulated using the same Hamiltonian as in ref. 239 and compared to the BO approximation, by calculating and analyzing the nuclear density, the TDPES and the TDVP of the exact factorization. Overall, the observations allowed to discard all traces of singularities or destructive interferences related to topological-phase effects. As an example, let us discuss here the TDPES in Fig. 6, which is shown as colour map at three times along the dynamics. First, in the left panel, the nuclear density (depicted as black contour lines) approaches the location of the conical intersection (indicated by a red cross at the origin X, Y = 0, 0) at 0.24 ms; then, in the central panel, the density has reached the location of the conical intersection at 0.69 ms; finally, at 1.35 ms, the density has passed the origin X, Y = 0, 0 and exhibits a depletion along the line X > 0, Y = 0. In particular at this last time, it is interesting to observe that the TDPES develops a barrier-like feature along Y = 0 for X > 0. However, while the height and width of this barrier change over time, it remains finite and does not diverge. Thus, this barrier induces a depletion of the nuclear density along Y = 0 but cannot cause a node in the corresponding nuclear wavefunction. Indeed, a finite (strictly larger than 10−5), yet small, amount of nuclear density is always present in the region X > 0, Y = 0, attesting to the fact that there is no nodal line formed and thus, no topological-phase effect induced in the nuclear dynamics.
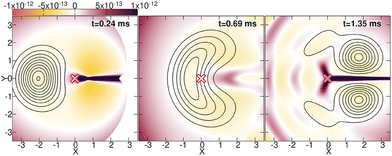 | ||
| Fig. 6 The color maps show the TDPES at different times along the simulated dynamics of the E⊗e Jahn–Teller model of ref. 239. The contour lines show the nuclear density at the same times. The cross at X, Y = 0, 0 indicates the position of the conical intersection. Reprinted with permission from J. Phys. Chem. Lett., 2023, 14 (51), 11625–11631. Copyright 2023 American Chemical Society. | ||
As indicated in eqn (7), the geometric phase arising in the exact factorization is calculated using the TDVP. While the TDVP is a gauge-dependent quantity, its curl and its circulation are not, thus they are physical observables. In Fig. 7, we show the curl of the TDVP at three different times along the simulated dynamics, and we compare it to the curl of the nonadiabatic coupling vectors of the Born–Huang representation. Note that in the particular case of a two-state system with real adiabatic eigenstates, γBO(Γ) of eqn (21) can be calculated by replacing ABOν(R) with the nonadiabatic coupling vectors. Therefore, we find instructive to compare the two quantities, i.e., the curl of the TDVP and the curl of the coupling, that give rise to the geometric phases. In Fig. 7 it is clear that the two quantities are qualitatively different, one being smooth everywhere in space and the other presenting a particular behavior only at the location of the conical intersection. Furthermore, we observe that the TDVP is not irrotational and, thus, cannot be eliminated by a suitable choice of gauge. It is clearly dependent on the dynamics of the electron–nuclear system while the nonadiabatic coupling vector is an intrinsic property of the system Hamiltonian itself.
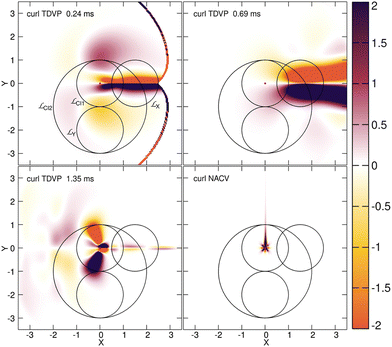 | ||
| Fig. 7 The color maps show the curl of the TDVP at different times along the simulated dynamics of the E⊗e Jahn–Teller model of ref. 239 and the curl of the nonadiabatic coupling vectors (NACV) for the same model. The circles show the paths along which the line integrals of eqn (21) and (22) are performed. Reprinted with permission from J. Phys. Chem. Lett., 2023, 14 (51), 11625–11631. Copyright 2023 American Chemical Society. | ||
The geometric phases, γBO(Γ) and γ(Γ,t), have been calculated from eqn (21) and (22), respectively, and are reported in Table 2. We used different paths Γ, namely ΓCI1 and ΓCI2 encircling the position of the conical intersection, and ΓX and ΓY that do not encircle the position of the conical intersection. The paths are shown in Fig. 7. Table 2 shows that in the adiabatic representation, namely for γBO(Γ), a value close to π is obtained only for ΓCI1 and ΓCI2, and that we find a value much smaller, i.e., close to zero, along the other paths. Using the TDVP, all the values change with time and with the path. Therefore, our numerical calculations show that the result of the integral in eqn (22) depends on the behavior and on the dynamics of the TDVP, i.e., the smooth function to be integrated, as well as on the geometry of the chosen path: γ(Γ, t) is a geometric phase. Instead, the integral of the nonadiabatic coupling vectors used to determine eqn (21) over the same paths chosen for eqn (22) only depends on the winding number of the path(s) around the point of singularity of the function to be integrated: γBO(Γ) is a topological phase. Thus, in ref. 250 we introduced the concept of dynamics-induced geometric phase to indicate γ(Γ, t), a concept that arises in the exact factorization. The dynamics-induced geometric phase is not a topological feature but rather caused and governed by the dynamics of the system, in stark contrast with the topological, path-independent phase that arises only in the adiabatic representation.
| 0.24 ms | 0.69 ms | 1.35 ms | Adiabatic | |
|---|---|---|---|---|
| Γ CI1 | −0.0209 | 0.0265 | 0.0506 | 3.12 |
| Γ CI2 | −0.794 | 2.05 | −0.00973 | 3.12 |
| Γ X | 0.00269 | 0.0624 | 0.000178 | −0.00281 |
| Γ Y | −0.758 | 0.157 | 0.188 | 0.000581 |
4.2 Dynamics induced upon creation of a vibrational wavepacket
In Section 4.2.1, we report on our recent study of the photodynamics of trans-azobenzene using CTTSH, whereas in Section 4.2.2 we present some examples of the work by Min and by Maitra with SHXF.In ref. 209, the photoisomerization dynamics was investigated upon nπ* and ππ* excitation, describing and comparing a two-state dynamics and a three-state dynamics, respectively. The semi-empirical FOMO-CI method was used to evaluate the electronic properties required for the on-the-fly dynamics, entering the evolution equation of the electronic coefficients (17) and the expression of the force needed for the nuclei classical propagation (18). The semi-empirical FOMO-CI method demonstrates high computational efficiency and reasonable accuracy when properly parameterized, making it suitable for computing multiple trajectories for medium to large molecular systems over time scales of up to a few picoseconds.
In CTTSH the force for the propagation of the nuclear trajectories is the same as in TSH, whereas CTTSH includes an additional term in the propagation of electronic coefficients that depends on quantum momentum, as shown in eqn (17). TSH is known to suffer from a systematic issue termed “overcoherence”, arising from the disconnect between the evolution of electrons and nuclei. Throughout time, the nuclei evolve on a single adiabatic potential energy surface and are allowed to hop to another surface at any time based on a stochastic algorithm. Therefore, on the one hand, the nuclear dynamics is governed by a single electronic states, while, on the other hand, the electronic evolution remains always coherent along a trajectory and yields a superposition of adiabatic states along that trajectory. CTTSH, thanks to the coupled-trajectory term of eqn (17), improves the description of quantum decoherence compared to TSH as it accounts in the electronic evolution equation for information about the spatial delocalization of the trajectories. This information is encoded in quantum momentum (14), which is related to the spatial variation of the nuclear density. Then, the nuclear density needs to be constructed from the distribution of trajectories, and this is done in CTTSH, as in CTMQC, with a sum of normalized Gaussians centered at the positions of trajectories. Therefore, at a given time t, the positions of all the trajectories need to be “shared” among the trajectories to construct the nuclear density and, thus, the trajectories cannot be evolved independently. From a practical standpoint, this is the main drawback of CTTSH when compared to standard TSH. For an efficient performance of CTTSH, a parallelized implementation using MPI was employed in ref. 209 (see Table 1). Despite the additional computation required for the quantum momentum, the runtime of our parallelized implementation is similar to that of a standard TSH approach, as all other calculations are performed in parallel. Furthermore, a local diabatization algorithm was utilized within the framework of the Runge–Kutta integrator to bypass the computation of the expensive and sometimes unavailable nonadiabatic coupling vectors.
This work on the photodynamics of trans-azobenzene demonstrated that, in CTTSH, the accuracy of the approximation of the nuclear density is crucial for a proper description of the quantum momentum and, consequently, for a correct account of decoherence effects in the electronic dynamics. Indeed, reconstructing the nuclear density for a polyatomic molecule is much more challenging than for a few-dimensional system. Therefore, we proposed four variants of the CTTSH method depending on the set of nuclear coordinates considered to construct the quantum momentum and depending on the approaches used to determine the widths of the Gaussian functions. The implementations of CTTSH can be summarized as follows:
1. CTTSH-FGAC (CTTSH with Frozen Gaussians and All Coordinates): in this approach, we utilize frozen Gaussians and all coordinates contribute to the calculation of the quantum momentum.
2. CTTSH-TGAC (CTTSH with Thawed Gaussians and All Coordinates): in this approach, we employ Gaussians whose widths change over time, and all coordinates contribute to the calculation of the quantum momentum.
3. CTTSH-FGLA (CTTSH with Frozen Gaussians and List of Active Atoms): in this approach, we utilize frozen Gaussians and only “active atoms”, whose list is provided as an input, contribute to the calculation of the quantum momentum.
4. CTTSH-TGLA (CTTSH with Thawed Gaussians and List of Active Atoms): in this approach, we utilize thawed Gaussians and only “active atoms” contribute to the calculation of the quantum momentum.
To assess the performance of these four flavours of CTTSH implementations, we compared our numerical results with TSH and TSH corrected with the inclusion of overlap-based decoherence corrections200 (TSH-ODC).
The minimum energy path on the S1 potential energy surface of azobenzene connects the trans (and cis) geometries to the S1/S0 conical intersection, located at approximately 95° of torsion of the CNNC dihedral. Consequently, nonadiabatic transitions to S0 in isolated trans-azobenzene occur predominantly in this region or slightly before, within a CNNC range of 90 to 120°. During the decay to S0, this molecule can isomerize to cis-azobenzene. The partial‡ photoisomerization quantum yields Φnπ* calculated using all four CTTSH methods, TSH, and TSH-ODC for the trajectories starting in the nπ* state are shown in the second column of Table 3. The calculated Φnπ* values are consistent across methods, are in agreement with each other and in good agreement with experimental results, which fall within the range of 20–32%.259–266 It is worth noting that trajectories with faster decay predominantly remain in the trans configuration after relaxing to the ground state, whereas slower trajectories have a higher probability of undergoing photoisomerization. In the third column of Table 3, we report the values of the partial photoisomerization quantum yields Φππ* upon ππ* excitation. The lower photoisomerization quantum yield after ππ* excitation has been previously discussed.267–269 It is related to an exception to Kasha's rule, resulting from a competition between “reactive” and “unreactive” internal conversion at the S1/S0 conical intersection, i.e., between internal conversion with photoisomerization or without photoisomerization, respectively. Both processes require a certain degree of progress along the CNNC torsional coordinate. However, the unreactive S1 → S0 internal conversion process can occur earlier (i.e., farther from the 90° midpoint of the torsional pathway) if more vibrational energy is available, as is typically the case with ππ* excitation. TSH-ODC, CTTSH-FGAC, and CTTSH-TGAC approaches presented photoisomerization quantum yields for ππ* in a very good agreement with the ones reported experimentally (0.09–0.16), whereas TSH, CTTSH-FGLA, and CTTSH-TGLA were unable to do so. These last three approaches showed higher or equivalent photoisomerization quantum yields for ππ* and nπ* excitation. However, it is important to emphasize that only approximately 40% of the trajectories for the TSH and CTTSH-TGLA methods successfully reached the ground state by the end of our simulations. Therefore, it is challenging to attribute a “precise” quantum yield in such cases. In addition, our simulations show that when using only the CNNC atoms for the calculations of the quantum momentum, the number of hops and back-hops between S1 and S2 increases if compared to the other CTTSH implementations. Thus, it is our interpretation that the non-satisfactory account of decoherence in the thawed-Gaussian method combined with the increased number of hops and back-hops in the list-of-active-atoms option bring the trajectories to explore regions of configuration space where the molecule isomerizes with higher probability.
| Method | Φ nπ* | Φ ππ* |
|---|---|---|
| CTTSH-FGAC | 0.22 ± 0.04 | 0.11 ± 0.04 |
| CTTSH-FGLA | 0.19 ± 0.03 | 0.19 ± 0.05 |
| CTTSH-TGAC | 0.23 ± 0.04 | 0.13 ± 0.04 |
| CTTSH-TGLA | 0.20 ± 0.04 | 0.38 ± 0.08 |
| TSH | 0.18 ± 0.04 | 0.17 ± 0.05 |
| TSH-0DC | 0.22 ± 0.03 | 0.13 ± 0.04 |
Fig. 8 shows the populations of the ground state S0 (in red) and of the excited state S1 (in blue) as functions of time for the simulation starting after the nπ* excitation. The four panels refer to the four flavors of CTTSH implementations presented above. Fig. 9 reports the analogous quantities calculated using TSH and TSH-ODC. In Fig. 8 and 9, the thick lines represent the populations calculated as the fraction of trajectories in a given electronic state m, namely as the ratio Fm(t) = Nm(t)/Ntr, where Nm(t) is the number of trajectories for which the active state at time t is m, and Ntr is the total number of trajectories; the thin lines represent the electronic population estimated as the average Pm(t) over the trajectories of |Cαm(t)|2, where Cαm(t) are the electronic coefficients along the trajectory α. In general Fm(t) ≠ Pm(t), and the difference is particularly severe if decoherence effects are important and not accounted for, like observed for TSH in Fig. 9. The decoherence corrections used in TSH-ODC are designed to restore the internal consistency of the TSH procedure in an ad hoc manner, resulting in Fm(t) ≃ Pm(t), as seen in Fig. 9. Instead, we note a remarkably good agreement across implementations of CTTSH with respect to the electronic populations evaluated as Fm(t) or as Pm(t). Internal consistency, thus Fm(t) ≃ Pm(t), is correctly achieved with CTTSH when utilizing frozen Gaussians (fixed widths) all along the simulated dynamics, instead, the agreement between Fm(t) and Pm(t) decreased over long times when thawed Gaussians (variable widths) are employed to calculate quantum momentum. This happens because, as the trajectories become delocalized in space, the widths of the individual Gaussians used for reconstructing the nuclear density increase. Consequently, the quantum momentum, which is evaluated as the spatial derivative of the density, decreases, leading to a reduced effect of decoherence. Nevertheless, we believe that by significantly increasing the number of coupled trajectories, we can attain an accurate representation of the nuclear distribution in configuration space without requiring a substantial increase in Gaussian width. In an ideal scenario, each trajectory would be strongly coupled to several others, making the nuclear density almost insensitive to variations in Gaussian widths within a reasonable range. However, achieving this would necessitate a much larger number of trajectories than the 100–150 (total number of trajectories used in this study) that can currently be accommodated on a single computing node, with the required number increasing with the number of coordinates.
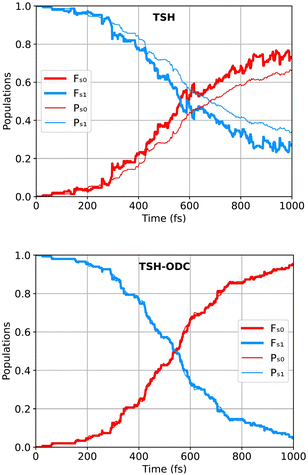 | ||
| Fig. 9 Same as in Fig. 8 but for TSH and TSH-ODC. Reprinted with permission from J. Chem. Theor. Comput., 2024, 20 (2), 580–596. Copyright 2024 American Chemical Society. | ||
In order to assess the performance of various surface-hopping procedures, including SHXF, Maitra and coworkers presented an in-depth analysis of the photodynamics of ethylene, fulvene and the methaniminium cation employing ab initio multiple spawning as benchmark.277 Specifically, the work analyzed various decoherence-correction schemes, which are found to operate in very different ways on the individual trajectories while yielding comparable results when averaged over the trajectories. In addition, the choice of the velocity-rescaling algorithm as well as the influence of nuclear time step for the propagation were studied as they were found to have an equally, if not more, important role on electronic and nuclear properties compared to the decoherence correction. Finally, Maitra and coworkers showed that the new mechanism for electronic transitions given by the quantum momentum in the exact-factorization based methods, and in particular SHXF, goes beyond a mere decoherence correction. The quantum-momentum induced effects were shown to be essential to capture the dynamics of the uracil cation as it is driven by a three-state conical intersection. This cannot be correctly captured using corrections to the electronic coefficients that involve only a pair of states (active and non active state).114,278
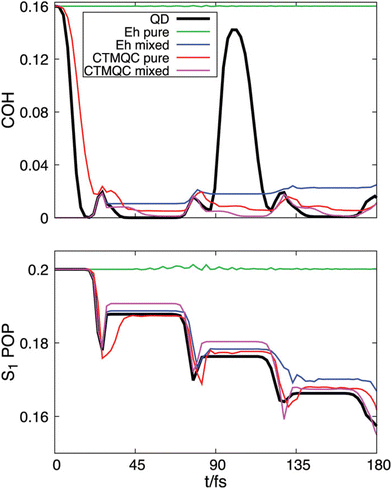
4.3 Dynamics induced upon creation of an electronic wavepacket
The creation of an electronic wavepacket can be achieved following the interaction of a molecule with an attosecond laser pulse279–282 that ionizes the molecule. Such a photoionization is able to trigger an ultrafast process that implies electronic charge redistribution coupled to the nuclear motion. The ultimate goal of the emerging field of attochemistry71 is to be able to control the evolution of such a wavepacket that implies the control of chemical reactivity, which is potentially achievable by tuning the electronic coherences among the states which are coupled via a second probe pulse or via the nuclear dynamics.An accurate description of electron–nuclear correlation effects, including coherence and decoherence, is essential for understanding and controlling the products of a photochemical reaction. However, the theoretical description of these processes presents several well-known challenges, and in ref. 145 we focused on the problem of the initialization of the electronic dynamics in trajectory-based simulations. The initial conditions for the classical-like nuclear dynamics {Rαν, Pαν} are often sampled from the (harmonic) Wigner distribution of the ground state nuclear wavepacket assuming vertical excitation or from a classical Boltzmann distribution at some given temperature.180 However, several options can be proposed for the initialization of the electronic dynamics via the electronic coefficients {Cαk(0)} when more than one electronic state needs to be populated to initiate the nonadiabatic simulations. In ref. 145, we defined and distinguished two situations, a pure state, where all trajectories carry the same set of electronic coefficients at the initial time, and a mixed state, where each trajectory is allowed to carry a different initial superposition of electronic states in such a way that the ensemble-average electronic populations at the initial time reproduces the “expected” population distribution of the molecular wavefunction after the pulse, i.e., 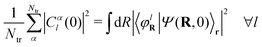 . Our work aimed to assess the performance of Ehrenfest and CTMQC in describing the nonadiabatic dynamics initiated by the creation of an electronic wavepacket distinguishing the two cases of a pure state and of a mixed state. We used a model system for our calculations, described by a two-electronic-state one-nuclear-mode Hamiltonian that consists, in the diabatic representation, of two coupled one-dimensional harmonic oscillators displaced in position and energy. The initial condition for the quantum dynamics is chosen as a coherent superposition of 80% and 20% of the ground state and of the excited state, respectively.
. Our work aimed to assess the performance of Ehrenfest and CTMQC in describing the nonadiabatic dynamics initiated by the creation of an electronic wavepacket distinguishing the two cases of a pure state and of a mixed state. We used a model system for our calculations, described by a two-electronic-state one-nuclear-mode Hamiltonian that consists, in the diabatic representation, of two coupled one-dimensional harmonic oscillators displaced in position and energy. The initial condition for the quantum dynamics is chosen as a coherent superposition of 80% and 20% of the ground state and of the excited state, respectively.
For such a model system, reference results can be provided by solving exactly the TDSE. Turning to the trajectory-based calculations, in the pure state, the initial electronic state for all trajectories is described by  and
and  whereas in the mixed state 80% of the trajectories are initialized by {C(α)0(0)} = 1 and the remaining 20% by {C(β)0(0)} = 1. Here, the index α runs over 80% of the trajectories, and β runs over the remaining 20%.
whereas in the mixed state 80% of the trajectories are initialized by {C(α)0(0)} = 1 and the remaining 20% by {C(β)0(0)} = 1. Here, the index α runs over 80% of the trajectories, and β runs over the remaining 20%.
Fig. 10 shows the electronic excited state population and the electronic coherence as functions of time. Surprisingly, we observe that starting with a pure state in Ehrenfest dynamics yields negligible net population transfer with the ground and excited state remaining coherent throughout the dynamics. This behavior is in stark contrast with the expected result predicted by the quantum dynamics (QD) simulation. On the other hand, CTMQC captures both the population and coherence behavior in very good agreement with the reference. Note that all methods miss the recoherence just after 90 fs that, unlike the other recoherences, occurs far from the nonadiabatic coupling region. Details on this mechanism are discussed in ref. 283.
Let us focus on the first decoherence event occurring within the first 20 fs, during which the excited-state nuclear wavepacket moves away from the trapped ground state wavepacket before entering a region of strong nonadiabatic coupling. This situation represents the first step after a molecule gets excited via the laser pulse. Fig. 11 shows time snapshots of the exact nuclear density and the spatially-resolved energies (upper panel) and excited state populations (lower panel) during this event. We observe that Ehrenfest trajectories evolve in a mean-field surface which has 80% ground state character, and their electronic populations (and coherences) do not change away from regions of strong nonadiabaticity. Conversely, the quantum momentum term accounted for in the CTMQC equation of motion (15) induces both a branching of the electronic coefficients and a splitting of the trajectory distribution achieving decoherence. We now direct our attention to the mixed-state results, where both Ehrenfest and CTMQC capture the periodic population transfers, with Ehrenfest deviating from the reference at ∼120 fs. In terms of coherences, both methods cannot account for the initial decoherence, because in a mixed state the coherences are zero initially. However, after this first decoherence event, CTMQC captures the behavior of the indicator of coherence quite well, even though it misses the large recoherence at 90 fs as pointed out earlier; instead, Ehrenfest remains overcoherent after the first increase of coherence at ∼25 fs.
In summary, this work pointed out that the problem of the initialization of the electronic dynamics is critical when trajectory-based methods are used to simulate the dynamics triggered by an ultrashort laser pulse that creates an electronic wavepacket. We presented two strategies: a pure state and a mixed state. We tested these concepts in the simulation of the nonadiabatic dynamics of two-state electronic wavepacket in a one-dimensional model system. The pure state seems the natural choice for both Ehrenfest and CTMQC since all trajectories are associated to the same coherent superposition of electronic states. However, Ehrenfest performs very poorly, and if the mixed state is used instead, the population behavior greatly improves but the coherences, and consequently coherence-dependent observables such as the electronic current-density,145 will be wrong from the very beginning. On the other hand, CTMQC starting from a pure state accurately captures both populations and coherences behavior. The quantum momentum is essential to capture those events at the spatially-resolved level, which is key to predict the right dynamics when regions of nonadiabatic electron–nuclear coupling are encountered.
5 Photon–electron–nuclear systems: the future of the exact factorization?
Little over a decade ago, the field of polaritonic chemistry started to emerge as an innovative way to steer photochemical reactions by creating hybrid light–matter states, i.e., the polaritons.284–286 The strong-coupling regime between the molecular excitations and confined light can be achieved in optical and plasmonic cavities as it scales inversely with the volume of the cavity and is proportional to the dipole moment of the molecule.17,287–304 The modifications of the photochemical landscape underlying a cavity-free molecular process are achieved when the bare electronic energies are altered by the coupling to the photons and produce the polaritonic states, whose energies, in turn, are affected by the number of molecules in the cavity. Theoretical modeling of polaritonic chemistry clearly requires a quantum-mechanical treatment of the coupled photon–electron–nuclear (PEN) problem and the extension of state-of-the-art simulation techniques for molecular dynamics to treat light as an intrinsic variable of the process rather than as an external field.The fields of physical chemistry and chemical physics have sparkled with ideas for novel developments to study processes in the strong light–matter coupling regime, reformulating in cavities concepts such as the BO approximation305–307 and nonadiabatic dynamics.15,18,19,144,302,303,308–310 In this respect, the exact factorization appears to be an extremely well adapted formalism to gain new insights into the correlated PEN dynamics and to develop simulation algorithms, in the spirit of similar efforts using surface hopping and the Ehrenfest scheme.
Maitra and coworkers,141 as well as Tokatly and coworkers,140 laid the basis for the conception of the exact-factorization formalism to treat the PEN wavefunction. Specifically, the factored form of the wavefunction Ψ(r, R, t) = χ(R, t)Φ(r, t; R) has been generalized and used to analyze various kinds of problems, like photon–electron dynamics, with Ψ(r,q,t) = χ(q,t)Φ(r, t; R) interpreting q as the photon displacement and r as the electronic coordinate, or the full PEN dynamics, by interpreting R as the nuclear coordinates and introducing the polaritonic coordinates r, q. Maitra's preliminary work demonstrates that different factorizations yield complementary information on the fundamental interpretation of the PEN problem,142–144,311 as well as, perhaps most importantly, on the directions to follow to introduce approximations for an efficient computational treatment. For instance, employing the factorization Ψ(r, q, t) = χ(q, t)Φ(r, t; q), it was observed that even though the free-photon Hamiltonian is harmonic in the photon displacement coordinate and the light–matter coupling is bilinear in the nonrelativistic dipole approximation, the q-TDPES is far from harmonic. Therefore, a quasi-classical trajectory-based representation of the photon displacements and conjugated momenta should be carefully assessed and does not guarantee reproducing correctly the quantum dynamics. Specifically, the limitations of the multi-trajectory Ehrenfest approach have been discussed in the light of the different forces guiding the photon-displacement dynamics within such a mean-field theory and the exact factorization.144 Furthermore, the factorization Ψ(r, R, q, t) = χ(R, t)Φ(r, q, t; R) was used to introduced the TDPES as an alternative tool to the polaritonic surfaces to interpret how photochemical reactivity is affected by the cavity in a model proton coupled-electron transfer.142,311 Such an exact factorization naturally inspires simulations based on the coupled-trajectory schemes presented in previous sections, similarly to what the community already proposed using, for instance, surface hopping308 or ab initio multiple spawning312 and in the spirit of the Floquet-based CTMQC150 method discussed briefly in Section 3.2. Nonetheless, this possibility has not been yet investigated.
Despite Maitra's observations on the difficulties in capturing correctly the photon dynamics using classical Ehrenfest trajectories, the exact factorization has the potential to shed light into alternative approximations of the PEN quantum dynamics where the photon displacements and momenta are treated with trajectories, perhaps within a CTMQC-like scheme. In the presence of many cavity modes143 or even when envisaging to employ the formalism of the exact factorization to study the vibrational strong-coupling regime,313–315 such a treatment might represent the only valuable route for efficient and accurate simulations, at the cost of rethinking the underlying approximations of CTMQC and similar algorithms. Developments in this direction are currently ongoing in our group and preliminary results have been reported elsewhere.316
6 Conclusions
This Perspective provided an overview of the application of the exact factorization of the electron–nuclear wavefunction in the domain of photochemistry. After a brief presentation of the fundamental theory at the quantum-mechanical level, we introduced the concept of classical-like trajectories to be used to approximate the nuclear dynamics coupled to the quantum electronic dynamics and to derive algorithms for quantum molecular dynamics. Key concepts arising in the exact factorization are the time-dependent vector potential and time-dependent potential energy surface that completely account for the effect of the electronic ground and excited states on the nuclear dynamics. These time-dependent potentials can be interpreted classically such that the concept of classical nuclear force naturally arises. Another key ingredient of the exact-factorization equations is the quantum momentum, that tracks the spatial delocalization of the nuclear density, or equivalently of the distribution of classical trajectories, such that quantum-decoherence effects can be reproduced in the coupled-trajectory or auxiliary-trajectory schemes derived from the exact factorization. In this respect, we discussed previous work where the time-dependent potentials and the quantum momentum have shown their power in interpreting and simulating dynamical processes in the presence of strong nonadiabatic effects.We concluded this perspective with some observations on the future of the exact factorization. In particular, we discussed some recent work in the field of polaritonic chemistry based on the introduction of the photon–electron–nuclear wavefunction together with some avenues for the extension to photochemistry in cavities of the algorithms discussed in the course of this perspective.
Data availability
No primary research results, software or code have been included and no new data were generated or analysed as part of this review.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the ANR Q-DeLight project, grant no. ANR-20-CE29-0014 of the French Agence Nationale de la Recherche, by a public grant from the Laboratoire d'Excellence Physics Atoms Light Matter (LabEx PALM) overseen by the French National Research Agency (ANR) as part of the “Investissements d'Avenir” program (reference: ANR-10-LABX-0039-PALM), and by the Chateaubriand Fellowship from the Mission Scientifique et Technologique of the Embassy of France in the United States.Notes and references
- A. Chenu and G. D. Scholes, Ann. Rev. Phys. Chem., 2015, 66, 69–96 CrossRef CAS PubMed.
- S. Gozem, H. L. Luk, I. Schapiro and M. Olivucci, Chem. Rev., 2017, 117, 13502–13565 CrossRef CAS PubMed.
- J. W. Snyder Jr., B. F. E. Curchod and T. J. Martínez, J. Phys. Chem. Lett., 2016, 7, 2444–2449 CrossRef PubMed.
- H. Tamura and I. Burghardt, J. Am. Chem. Soc., 2013, 135, 16364–16367 CrossRef CAS PubMed.
- M. Gao, F. Yu, C. Lv, J. Choo and L. Chen, Chem. Soc. Rev., 2017, 46, 2237–2271 RSC.
- Y. Olivier, J.-C. Sancho-Garcia, L. Muccioli, G. D'Avino and D. Beljonne, J. Phys. Chem. Lett., 2018, 9, 6149–6163 CrossRef CAS PubMed.
- L. González and R. Lindh, Quantum Chemistry and Dynamics of Excited States: Methods and Applications, John Wiley & Sons, Chichester, 2020 Search PubMed.
- H. Oberhofer, K. Reuter and J. Blumberger, Chem. Rev., 2017, 117, 10319–10357 CrossRef CAS PubMed.
- K. Takatsuka, Bull. Chem. Soc. Jpn., 2021, 94, 421–1477 CrossRef.
- A. Kelly, Faraday Discuss., 2020, 221, 547–563 RSC.
- G. Tao and W. H. Miller, J. Phys. Chem. Lett., 2010, 1, 891–894 CrossRef CAS.
- L.-M. Ibele, P. A. Sanchez-Murcia, S. Mai, J. J. Nogueira and L. González, J. Phys. Chem. Lett., 2020, 11, 7483–7488 CrossRef CAS PubMed.
- S. Mukherjee, M. Kar, M. Bhati, X. Gao and M. Barbatti, Theor. Chem. Acc., 2023, 142, 85 Search PubMed.
- M. Pérez-Escribano, J. J. G. Granucci and D. Escudero, J. Chem. Phys., 2023, 158, 124104 CrossRef PubMed.
- J. Fregoni, G. Granucci, E. Coccia, M. Persico and S. Corni, Nat. Commun., 2018, 9, 4688 CrossRef CAS PubMed.
- M. Ruggenthaler, N. Tancogne-Dejean, J. Flick, H. Appel and A. Rubio, Nat. Rev. Chem., 2018, 2, 0118 CrossRef CAS.
- J. Feist, J. Galego and F. J. Garcia-Vidal, ACS Photonics, 2018, 5, 205–216 CrossRef CAS.
- H. L. Luk, J. Feist, J. J. Toppari and G. Groenhof, J. Chem. Theory Comput., 2017, 13, 4324–4335 CrossRef CAS PubMed.
- B. Gu, Y. Gu, V. Y. Chernyak and S. Mukamel, Acc. Chem. Res., 2023, 56, 2753–2762 CrossRef CAS PubMed.
- F. Agostini and B. F. E. Curchod, Philos. Trans. R. Soc., A, 2022, 380, 20200375 CrossRef PubMed.
- F. Agostini and B. F. E. Curchod, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2019, 9, e1417 Search PubMed.
- G. A. Worth and I. Burghardt, Chem. Phys. Lett., 2003, 368, 502–508 CrossRef CAS.
- T. Ma, M. Bonfanti, P. Eisenbrandt, R. Martinazzo and I. Burghardt, J. Chem. Phys., 2018, 149, 244107 CrossRef PubMed.
- G. Richings, I. Polyak, K. E. Spinlove, G. A. Worth, I. Burghardt and B. Lasorne, Int. Rev. Phys. Chem., 2015, 34, 269–308 Search PubMed.
- B. Lasorne, M. A. Robb and G. A. Worth, Phys. Chem. Chem. Phys., 2007, 9, 3210–3227 RSC.
- G. A. Worth, M. A. Robb and I. Burghardt, Faraday Discuss., 2004, 127, 307–323 RSC.
- B. F. E. Curchod and T. J. Martínez, Chem. Rev., 2018, 118, 3305–3336 CrossRef CAS PubMed.
- B. Mignolet and B. F. E. Curchod, J. Chem. Phys., 2018, 148, 134110 CrossRef PubMed.
- D. V. Makhov, W. J. Glover, T. J. Martínez and D. V. Shalashilin, J. Chem. Phys., 2014, 141, 054110 CrossRef PubMed.
- D. V. Shalashilin, Faraday Discuss., 2011, 153, 105–116 RSC.
- A. J. Jenkins, K. E. S. M. Vacher and G. A. W. M. A. Robb, J. Chem. Phys., 2018, 149, 094108 CrossRef PubMed.
- M. Vacher, M. J. Bearpark and M. A. Robb, Theor. Chem. Acc., 2016, 135, 187 Search PubMed.
- V. M. Freixas, A. J. White, T. Nelson, H. Song, D. V. Makhov, D. Shalashilin, S. Fernandez-Alberti and S. Tretiak, J. Phys. Chem. Lett., 2021, 12, 2970–2982 CrossRef CAS PubMed.
- R. E. Wyatt, Quantum dynamics with trajectories: introduction to quantum hydrodynamics, Springer Science & Business Media, 2005, vol. 28 Search PubMed.
- R. E. Wyatt and E. R. Bittner, J. Chem. Phys., 2000, 113, 8898–8907 CrossRef CAS.
- B. Poirier, Chem. Phys., 2010, 370, 4–14 CrossRef CAS.
- B. F. E. Curchod, I. Tavernelli and U. Rothlisberger, Chimia, 2012, 4, 174 CrossRef PubMed.
- B. Gu and S. Garashchuk, J. Phys. Chem. A, 2016, 120, 3023–3031 CrossRef CAS PubMed.
- B. Gu and I. Franco, J. Chem. Phys., 2017, 146, 194104 CrossRef PubMed.
- G. Albereda and I. Tavernelli, Quantum Chemistry and Dynamics of Excited States: Methods and Applications, John Wiley & Sons, 2021 Search PubMed.
- L. Dupuy, F. Talotta, F. Agostini, D. Lauvergnat, B. Poirier and Y. Scribano, J. Chem. Theory Comput., 2022, 18, 6447–6462 CrossRef CAS PubMed.
- L. Dupuy, A. Rikus and N. T. Maitra, J. Phys. Chem. Lett., 2024, 15, 2643–2649 CrossRef CAS PubMed.
- S. K. Min, F. Agostini and E. K. U. Gross, Phys. Rev. Lett., 2015, 115, 073001 CrossRef PubMed.
- C. Pieroni and F. Agostini, J. Chem. Theory Comput., 2021, 17, 5969 CrossRef CAS PubMed.
- C. C. Martens, J. Phys. Chem. Lett., 2016, 7, 2610–2615 CrossRef CAS PubMed.
- A. Dines, M. Ellis and J. Blumberger, J. Chem. Phys., 2023, 159, 234118 CrossRef CAS PubMed.
- S. Gómez, E. Spinlove and G. Worth, Phys. Chem. Chem. Phys., 2023, 26, 1829–1844 RSC.
- J.-K. Ha, I. S. Lee and S. K. Min, J. Phys. Chem. Lett., 2018, 9, 1097–1104 CrossRef CAS PubMed.
- J.-K. Ha and S. K. Min, J. Chem. Phys., 2022, 156, 174109 CrossRef CAS PubMed.
- W. H. Miller, J. Chem. Phys., 2012, 136, 210901 CrossRef PubMed.
- G. Trenins and J. O. Richardson, J. Chem. Phys., 2022, 156, 174115 CrossRef CAS PubMed.
- R. Conte and M. Ceotto, Quantum Chemistry and Dynamics of Excited States: Methods and Applications, John Wiley & Sons, 2021 Search PubMed.
- A. Scheidegger, N. V. Golubev and J. J. L. Vaní'ček, Chimia, 2023, 77, 201 CrossRef CAS PubMed.
- S. Malpathak, M. S. Church and N. Ananth, J. Phys. Chem. A, 2022, 126, 6359–6375 CrossRef CAS PubMed.
- S. Kundu and N. Makri, Annu. Rev. Phys. Chem., 2022, 73, 349–375 CrossRef CAS PubMed.
- J. C. Tully, J. Chem. Phys., 1990, 93, 1061 CrossRef CAS.
- J. C. Tully, Faraday Discuss., 1998, 110, 407 RSC.
- J. R. Mannouch and J. O. Richardson, J. Chem. Phys., 2023, 158, 104111 CrossRef CAS PubMed.
- M. Persico, G. Granucci and D. Accomasso, Comprehensive Computational Chemistry, Elsevier, Oxford, 1st edn, 2024, pp. 273–292 Search PubMed.
- A. Akimov, Comprehensive Computational Chemistry, Elsevier, 2022 Search PubMed.
- M. Barbatti, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 620–633 CAS.
- T. R. Nelson, S. Fernandez-Alberti, A. E. Roitberg and S. Tretiak, J. Chem. Phys., 2013, 138, 224111 CrossRef PubMed.
- M. Richter, P. Marquetand, J. González-Vázquez, I. Sola and L. González, J. Chem. Theory Comput., 2011, 7, 1253–1258 CrossRef CAS PubMed.
- S. Mai, P. Marquetand and L. González, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1370 Search PubMed.
- R. Crespo-Otero and M. Barbatti, Chem. Rev., 2018, 118, 7026–7068 CrossRef CAS PubMed.
- J. E. Subotnik, A. Jain, B. Landry, A. Petit, W. Ouyang and N. Bellonzi, Annu. Rev. Phys. Chem., 2016, 67, 387–417 CrossRef CAS PubMed.
- J. Suchan, J. Janos and P. Slavícěk, J. Chem. Theory Comput., 2020, 16, 5809–5820 CrossRef CAS PubMed.
- A. K. Belyaev, C. Lasser and G. Trigila, J. Chem. Phys., 2014, 140, 224108 CrossRef PubMed.
- D. A. Fedorov and B. G. Levine, J. Phys. Chem. Lett., 2019, 10, 4542–4548 CrossRef CAS PubMed.
- L. Wang, A. Akimov and O. V. Prezhdo, J. Phys. Chem. Lett., 2016, 7, 2100–2112 CrossRef CAS PubMed.
- I. C. D. Merritt, D. Jacquemin and M. Vacher, J. Phys. Chem. Lett., 2021, 12, 8404–8415 CrossRef CAS PubMed.
- Y. Shu and D. G. Truhlar, J. Chem. Theory Comput., 2023, 19, 380–395 CrossRef CAS PubMed.
- T. R. Nelson, S. Fernandez-Alberti and S. Tretiak, Nat. Comput. Sci., 2022, 2, 689–692 CrossRef PubMed.
- J. Qiu, X. Bai and L. Wang, J. Phys. Chem. Lett., 2018, 9, 4319–4325 CrossRef CAS PubMed.
- J. Xu and L. Wang, J. Phys. Chem. Lett., 2020, 11, 8283–8291 CrossRef CAS PubMed.
- C. Stopera, T. V. Grimes, P. M. McLaurin, A. Privett and J. A. Morales, Adv. Quantum Chem., 2013, 66, 113–194 CrossRef CAS.
- S. M. Parker and C. J. Schiltz, J. Chem. Phys., 2020, 153, 174109 CrossRef CAS PubMed.
- S. Ghosh, S. Giannini, K. Lively and J. Blumberger, Faraday Discuss., 2020, 221, 501–525 RSC.
- X. Yang, M. Manathunga, S. Gozem, J. Léonard, T. Andruniów and M. Olivucci, Nat. Chem., 2022, 14, 441–449 CrossRef CAS PubMed.
- A. Kelly, J. Chem. Phys., 2019, 150, 204107 CrossRef PubMed.
- J. Spencer, L. Scalfi, A. Carof and J. Blumberger, Faraday Discuss., 2016, 195, 215–236 RSC.
- S. J. Cotton and W. H. Miller, J. Chem. Phys., 2019, 150, 104101 CrossRef PubMed.
- J. F. K. Halliday and E. Artacho, SciPost Phys., 2022, 12, 020 CrossRef.
- P. Chakraborty and S. Matsika, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2024, 14, e1715 CAS.
- S. Bonella, G. Ciccotti and R. Kapral, Chem. Phys. Lett., 2010, 484, 399–404 CrossRef CAS.
- W. C. Pfalzgraff, A. Montoya-Castillo, A. Kelly and T. E. Markland, J. Chem. Phys., 2019, 150, 244109 CrossRef PubMed.
- E. R. Bittner and P. J. Rossky, J. Chem. Phys., 1995, 103, 8130–8143 CrossRef CAS.
- H. Kim, A. Nassimi and R. Kapral, J. Chem. Phys., 2008, 129, 084102 CrossRef PubMed.
- D. F. Coker and L. Xiao, J. Chem. Phys., 1995, 102, 496–510 CrossRef CAS.
- S. Bonella and D. F. Coker, J. Chem. Phys., 2005, 122, 194102 CrossRef CAS PubMed.
- F. Gay-Balmaz and C. Tronci, J. Phys. A: Math. Theor., 2023, 56, 144002 CrossRef.
- A. J. Dunnett and A. W. Chin, Entropy, 2021, 23, 77 CrossRef PubMed.
- A. Chin, E. Mangaud, V. Chevet, O. Atabek and M. Desouter-Lecomte, Chem. Phys., 2019, 525, 110392 CrossRef CAS.
- H.-D. Meyer, U. Manthe and L. S. Cederbaum, Chem. Phys. Lett., 1990, 165, 73–78 Search PubMed.
- A. J. M. H. Beck, G. A. Worth and H.-D. Meyer, Phys. Rep., 2000, 324, 1–105 CrossRef.
- G. A. Worth, H.-D. Meyer, H. Koeppel, L. S. Cederbaum and I. Burghardt, Int. Rev. Phys. Chem., 2008, 27, 569 Search PubMed.
- H.-D. Meyer, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 351–374 Search PubMed.
- D. Lauvergnat and A. Nauts, Spectrochim. Acta, Part A, 2014, 119, 18–25 CrossRef CAS PubMed.
- S. Sasmal and O. Vendrell, J. Chem. Phys., 2022, 157, 134102 CrossRef CAS PubMed.
- A. Abedi, N. T. Maitra and E. K. U. Gross, Phys. Rev. Lett., 2010, 105, 123002 CrossRef PubMed.
- F. Agostini and E. K. U. Gross, Eur. Phys. J. B, 2021, 94, 179 CrossRef CAS.
- M. Born and R. Oppenheimer, Ann. Phys., 1927, 84, 457–484 Search PubMed.
- M. Born and K. Huang, The Dynamical Theory of Crystal Lattices, Clarendon Press, Oxford, 1954 Search PubMed.
- G. A. Worth and L. S. Cederbaum, Annu. Rev. Phys. Chem., 2004, 55, 127–158 CrossRef CAS PubMed.
- W. Domcke and D. R. Yarkony, Annu. Rev. Phys. Chem., 2012, 63, 325–352 CrossRef CAS PubMed.
- S. Matsika and P. Krause, Annu. Rev. Phys. Chem., 2011, 62, 621 CrossRef CAS PubMed.
- S. Matsika and D. R. Yarkony, J. Am. Chem. Soc., 2003, 125, 10672–10676 CrossRef CAS PubMed.
- A. Abedi, N. T. Maitra and E. K. U. Gross, J. Chem. Phys., 2012, 137, 22A530 CrossRef PubMed.
- A. Abedi, F. Agostini, Y. Suzuki and E. K. U. Gross, Phys. Rev. Lett., 2013, 110, 263001 Search PubMed.
- F. Agostini, A. Abedi, Y. Suzuki, S. K. Min, N. T. Maitra and E. K. U. Gross, J. Chem. Phys., 2015, 142, 084303 CrossRef PubMed.
- F. Agostini, I. Tavernelli and G. Ciccotti, Eur. Phys. J. B, 2018, 91, 139 CrossRef.
- S. K. Min, F. Agostini, I. Tavernelli and E. K. U. Gross, J. Phys. Chem. Lett., 2017, 8, 3048–3055 CrossRef CAS PubMed.
- F. Talotta, S. Morisset, N. Rougeau, D. Lauvergnat and F. Agostini, Phys. Rev. Lett., 2020, 124, 033001 CrossRef CAS PubMed.
- P. Vindel-Zandbergen, S. Matsika and N. T. Maitra, J. Phys. Chem. Lett., 2022, 13, 1785–1790 CrossRef CAS PubMed.
- G. Hunter, Int. J. Quantum Chem., 1975, 9, 237–242 CrossRef CAS.
- D. M. Bishop and L. M. Cheung, Chem. Phys. Lett., 1977, 50, 172–174 CrossRef CAS.
- G. Hunter, Int. J. Quantum Chem., 1981, 19, 755–761 Search PubMed.
- R. Lefebvre, J. Chem. Phys., 2015, 142, 214105 CrossRef CAS PubMed.
- N. I. Gidopoulos and E. K. U. Gross, Philos. Trans. R. Soc., A, 2014, 372, 20130059 CrossRef PubMed.
- R. Requist and E. K. U. Gross, Phys. Rev. Lett., 2019, 117, 193001 CrossRef PubMed.
- C. Li, R. Requist and E. K. U. Gross, J. Chem. Phys., 2018, 148, 084110 Search PubMed.
- L. Lacombe and N. T. Maitra, Phys. Rev. Lett., 2020, 124, 206401 Search PubMed.
- E. K. U. G. Ryan Requist, Phys. Rev. Lett., 2019, 127, 116401 Search PubMed.
- S. K. Min, A. Abedi, K. S. Kim and E. K. U. Gross, Phys. Rev. Lett., 2014, 113, 263004 CrossRef PubMed.
- R. Requist, F. Tandetzky and E. K. U. Gross, Phys. Rev. A, 2016, 93, 042108 CrossRef.
- R. Requist, C. R. Proetto and E. K. U. Gross, Phys. Rev. B, 2019, 99, 165136 CrossRef CAS.
- L. S. Cederbaum, J. Chem. Phys., 2013, 138, 224110 CrossRef PubMed.
- L. S. Cederbaum, Chem. Phys., 2015, 457, 129 CrossRef CAS.
- Y. Suzuki, A. Abedi, N. T. Maitra, K. Yamashita and E. K. U. Gross, Phys. Rev. A: At., Mol., Opt. Phys., 2014, 89, 040501(R) CrossRef.
- A. Schild, F. Agostini and E. K. U. Gross, J. Phys. Chem. A, 2016, 120, 3316 CrossRef CAS PubMed.
- A. Scherrer, F. Agostini, D. Sebastiani, E. K. U. Gross and R. Vuilleumier, Phys. Rev. X, 2017, 7, 031035 Search PubMed.
- C. Li, R. Requist and E. K. U. Gross, Phys. Rev. Lett., 2022, 128, 113001 Search PubMed.
- R. Martinazzo and I. Burghardt, Phys. Rev. Lett., 2022, 128, 206002 CrossRef CAS PubMed.
- R. Martinazzo and I. Burghardt, arXiv, 2023, preprint, arXiv:2310.08766v1 [physics.chem-ph] DOI:10.48550/arXiv.2310.08766.
- A. Schild and E. K. U. Gross, Phys. Rev. Lett., 2017, 118, 163202 CrossRef PubMed.
- J. Kocák and A. Schild, Phys. Rev. Res., 2020, 2, 043365 CrossRef.
- S. Giarrusso, P. Gori-Giorgi and F. Agostini, ChemPhysChem, 2024, 25, e202400127 CrossRef CAS PubMed.
- S. Giarrusso and F. Agostini, arXiv, 2024, preprint, arXiv:2408.06038v3 [physics.chem-ph] DOI:10.48550/arXiv.2408.06038.
- J. Kock, E. Kraisler and A. Schild, J. Phys. Chem. Lett., 2021, 12, 3204–3209 CrossRef PubMed.
- A. Abedi, E. Khosravi and I. Tokatly, Eur. Phys. J. B, 2018, 91, 194 CrossRef.
- N. M. Hoffmann, H. Appel, A. Rubio and N. Maitra, Eur. Phys. J. B, 2018, 91, 180 CrossRef.
- L. Lacombe, N. M. Hoffmann and N. T. Maitra, Phys. Rev. Lett., 2019, 123, 083201 CrossRef CAS PubMed.
- N. M. Hoffmann, L. Lacombe, A. Rubio and N. T. Maitra, J. Chem. Phys., 2020, 153, 104103 CrossRef CAS PubMed.
- B. Rosenzweig, N. M. Hoffmann, L. Lacombe and N. T. Maitra, J. Chem. Phys., 2022, 156, 054101 CrossRef CAS PubMed.
- E. Villaseco Arribas, N. T. Maitra and F. Agostini, J. Chem. Phys., 2024, 160, 054102 CrossRef CAS PubMed.
- B. Mignolet and B. F. E. Curchod, J. Phys. Chem. A, 2019, 123, 3582 CrossRef CAS PubMed.
- L. M. Ibele, B. F. E. Curchod and F. Agostini, J. Phys. Chem. A, 2022, 126, 1263–1281 CrossRef CAS PubMed.
- T. Fiedlschuster, J. Handt, E. K. U. Gross and R. Schmidt, Phys. Rev. A, 2017, 95, 063424 CrossRef.
- T. Fiedlschuster, J. Handt and R. Schmidt, Phys. Rev. A, 2016, 93, 053409 CrossRef.
- M. Schirò, F. G. Eich and F. Agostini, J. Chem. Phys., 2021, 154, 114101 CrossRef PubMed.
- G. Jolicard and O. Atabek, Phys. Rev. A: At., Mol., Opt. Phys., 1992, 46, 5845–5855 CrossRef CAS PubMed.
- X. He, O. Atabek and A. Giusti-Suzor, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 5586–5594 CrossRef CAS PubMed.
- A. Giusti-Suzor and F. H. Mies, Phys. Rev. Lett., 1992, 68, 38638729 CrossRef PubMed.
- L. J. Frasinski, J. Plumridge, J. H. Posthumus, K. Codling, P. F. Taday, E. J. Divall and A. J. Langley, Phys. Rev. Lett., 2001, 86, 2541–2544 CrossRef CAS PubMed.
- P. H. Bucksbaum, A. Zavriyev, H. G. Muller and D. W. Schumacher, Phys. Rev. Lett., 1990, 64, 1883–1886 CrossRef CAS PubMed.
- A. Giusti-Suzo, X. He, O. Atabek and F. H. Mies, Phys. Rev. Lett., 1990, 64, 515–518 CrossRef PubMed.
- F. Talotta, S. Morisset, N. Rougeau, D. Lauvergnat and F. Agostini, J. Phys. Chem. A, 2021, 125, 6075 CrossRef CAS PubMed.
- B. F. E. Curchod, C. Rauer, P. Marquetand, L. González and T. J. Martínez, J. Chem. Phys., 2016, 144, 101102 CrossRef PubMed.
- L. Favero, G. Granucci and M. Persico, Phys. Chem. Chem. Phys., 2013, 15, 20651 RSC.
- J. S. Garcáa, F. Talotta, F. Alary, I. M. Dixon, J.-L. Heully and M. Boggio-Pasqua, Molecules, 2017, 22, 1667 CrossRef PubMed.
- A. J. Atkins, F. Talotta, L. Freitag, M. Boggio-Pasqua and L. González, J. Chem. Theory Comput., 2017, 13, 4123–4145 Search PubMed.
- F. Talotta, M. Boggio-Pasqua and L. González, Chem. – Eur. J., 2020, 26, 11522–11528 CrossRef CAS PubMed.
- F. Talotta, J.-L. Heully, F. Alary, I. M. Dixon, L. González and M. Boggio-Pasqua, J. Chem. Theory Comput., 2017, 13, 6120–6130 CrossRef CAS PubMed.
- I. Tavernelli, B. F. E. Curchod and U. Rothlisberger, Chem. Phys., 2011, 391, 101–109 CrossRef CAS.
- M. Richter, P. Marquetand, J. González-Vázquez, I. Sola and L. González, J. Phys. Chem. Lett., 2012, 3, 3090–3095 CrossRef CAS PubMed.
- G. Capano, M. Chergui, U. Rothlisberger, I. Tavernelli and T. J. Penfold, J. Phys. Chem. A, 2014, 118, 9861–9869 CrossRef CAS PubMed.
- G. Cui and W. Thiel, J. Chem. Phys., 2014, 141, 124101 CrossRef PubMed.
- G. H. Gossel, L. Lacombe and N. T. Maitra, J. Chem. Phys., 2019, 150, 154112 Search PubMed.
- F. Talotta, F. Agostini and G. Ciccotti, J. Phys. Chem. A, 2020, 124, 6764–6777 CrossRef CAS PubMed.
- F. Agostini, A. Abedi, Y. Suzuki and E. K. U. Gross, Mol. Phys., 2013, 111, 3625–3640 CrossRef CAS.
- F. Agostini, A. Abedi and E. K. U. Gross, J. Chem. Phys., 2014, 141, 214101 CrossRef PubMed.
- A. Abedi, F. Agostini and E. K. U. Gross, Europhys. Lett., 2014, 106, 33001 Search PubMed.
- F. Agostini, S. K. Min, A. Abedi and E. K. U. Gross, J. Chem. Theory Comput., 2016, 12, 2127–2143 CrossRef CAS PubMed.
- F. Agostini, Eur. Phys. J. B, 2018, 91, 143 CrossRef.
- L. M. Ibele, C. Pieroni, F. Talotta, B. F. Curchod, D. Lauvergnat and F. Agostini, Comprehensive Computational Chemistry, Elsevier, Oxford, 1st edn, 2024, pp. 188–211 Search PubMed.
- Y. Suzuki and K. Watanabe, Phys. Rev. A, 2016, 94, 032517 CrossRef.
- E. V. Arribas, F. Agostini and N. T. Maitra, Molecules, 2022, 27, 4002 CrossRef PubMed.
- B. F. E. Curchod and F. Agostini, J. Phys. Chem. Lett., 2017, 8, 831–837 CrossRef CAS PubMed.
- F. Agostini and B. F. E. Curchod, Eur. Phys. J. B, 2018, 91, 141 CrossRef.
- C. Pieroni, E. Marsili, D. Lauvergnat and F. Agostini, J. Chem. Phys., 2021, 154, 034104 CrossRef CAS PubMed.
- B. F. E. Curchod, F. Agostini and E. K. U. Gross, J. Chem. Phys., 2016, 145, 034103 CrossRef PubMed.
- E. Khosravi, A. Abedi and N. T. Maitra, Phys. Rev. Lett., 2015, 115, 263002 CrossRef PubMed.
- Y. Suzuki, A. Abedi, N. T. Maitra and E. K. U. Gross, Phys. Chem. Chem. Phys., 2015, 17, 29271–29280 RSC.
- E. Khosravi, A. Abedi, A. Rubio and N. T. Maitra, Phys. Chem. Chem. Phys., 2017, 19, 8269–8281 RSC.
- T. Fiedlschuster, J. Handt, E. K. U. Gross and R. Schmidt, Phys. Rev. A, 2017, 95, 063424 CrossRef.
- F. Talotta, S. Morisset, N. Rougeau, D. Lauvergnat and F. Agostini, J. Chem. Theory Comput., 2020, 16, 4833–4848 CrossRef CAS PubMed.
- F. G. Eich and F. Agostini, J. Chem. Phys., 2016, 145, 054110 CrossRef CAS PubMed.
- F. Agostini, S. K. Min and E. K. U. Gross, Ann. Phys., 2015, 527, 546–555 CrossRef CAS.
- D. Han, J.-K. Ha and S. K. Min, J. Chem. Theory Comput., 2023, 19, 2186–2197 CrossRef CAS PubMed.
- E. Villaseco Arribas and N. T. Maitra, J. Chem. Phys., 2023, 158, 161105 CrossRef CAS PubMed.
- F. Agostini, B. F. E. Curchod, R. Vuilleumier, I. Tavernelli and E. K. U. Gross, Handbook of Materials Modeling, Springer, Netherlands, 2018, pp. 1–47 Search PubMed.
- B. F. E. Curchod, F. Agostini and I. Tavernelli, Eur. Phys. J. B, 2018, 91, 168 CrossRef.
- I. S. Lee, J. Ha, D. Han, T. I. Kim, S. W. Moon and S. K. Min, J. Comput. Chem., 2021, 42, 1755–1766 CrossRef CAS PubMed.
- D. Han and A. V. Akimov, J. Chem. Theory Comput., 2024, 20, 5022–5042 CrossRef CAS PubMed.
- G. Granucci and M. Persico, J. Chem. Phys., 2007, 126, 134114 CrossRef PubMed.
- N. Shenvi, J. E. Subotnik and W. Yang, J. Chem. Phys., 2011, 134, 144102 CrossRef PubMed.
- J. E. Subotnik and N. Shenvi, J. Chem. Phys., 2011, 134, 024105 CrossRef PubMed.
- H. M. Jaeger, S. Fischer and O. V. Prezhdo, J. Chem. Phys., 2012, 137, 22A545 CrossRef PubMed.
- G. Granucci and M. Persico, J. Chem. Phys., 2007, 126, 134114 CrossRef PubMed.
- G. Granucci, M. Persico and A. Zoccante, J. Chem. Phys., 2010, 133, 134111 CrossRef PubMed.
- C. C. Martens, J. Phys. Chem. A, 2019, 123, 1110–1128 CrossRef CAS PubMed.
- C. Zhu, S. Nangia, A. W. Jasper and D. G. Truhlar, J. Chem. Phys., 2004, 121, 7658 CrossRef CAS PubMed.
- M. P. Esch and B. G. Levine, J. Chem. Phys., 2020, 153, 114104 CrossRef CAS PubMed.
- E. Villaseco Arribas, L. M. Ibele, D. Lauvergnat, N. T. Maitra and F. Agostini, J. Chem. Theory Comput., 2023, 19, 7787–7800 CrossRef PubMed.
- A. V. Akimov, J. Comput. Chem., 2016, 37, 1626–1649 CrossRef CAS PubMed.
- F. Agostini, E. Marsili, F. Talotta, C. Pieroni, E. Villaseco Arribas, L. M. Ibele and E. Sangiogo Gil, G-CTMQC, 2024, accessed in June, https://gitlab.com/agostini.work/g-ctmqc Search PubMed.
- D. Lauvergnat, QuantumModelLib, 2024, accessed in June, https://github.com/lauvergn/QuantumModelLib Search PubMed.
- G. Granucci, M. Persico, D. Accomasso, E. Sangiogo Gil, S. Corni, J. Fregoni, T. Laino, M. Tesi and A. Toniolo, MOPAC-PI: a program for excited state dynamics simulations based on nonadiabatic trajectories and semiempirical electronic structure calculations, 2024, https://gitlab.com/granucci/mopacpi.git Search PubMed.
- C. Pieroni, E. Sangiogo Gil, L. M. Ibele, M. Persico, G. Granucci and F. Agostini, J. Chem. Theory Comput., 2024, 20, 580–596 CrossRef CAS PubMed.
- G. A. Worth, K. Giri, G. W. Richings, I. Burghardt, M. H. Beck, A. Jäckle and H.-D. Meyer, The QUANTICS Package, Version 2.0, University College London, London, UK, 2020 Search PubMed.
- S. Mai, D. Avagliano, M. Heindl, P. Marquetand, M. F. S. J. Menger, M. Oppel, F. Plasser, S. Polonius, M. Ruckenbauer, Y. Shu, D. G. Truhlar, L. Zhang, P. Zobel and L. González, SHARC3.0: Surface Hopping Including Arbitrary Couplings – Program Package for Non-Adiabatic Dynamics, 2023https://sharc-md.org/ Search PubMed.
- M. Barbatti, M. Bondanza, R. Crespo-Otero, B. Demoulin, P. O. Dral, G. Granucci, F. Kossoski, H. Lischka, B. Mennucci, S. Mukherjee, M. Pederzoli, M. Persico, M. Pinheiro Jr, J. Pittner, F. Plasser, E. S. Gil and L. Stojanovic, J. Chem. Theory Comput., 2022, 18, 6851 CrossRef CAS PubMed.
- L. M. Ibele and B. F. E. Curchod, Phys. Chem. Chem. Phys., 2020, 22, 15062 RSC.
- G. Granucci and M. Persico, Chem. Phys. Lett., 1995, 246, 228–234 CrossRef CAS.
- D. L. Audrey Pollien, E. Villaseco Arribas and F. Agostini, Mol. Phys., 2024, e2378960 CrossRef.
- B. F. E. Curchod, W. J. Glover and T. J. Martínez, J. Phys. Chem. A, 2020, 124, 6133–6143 CrossRef CAS PubMed.
- L. M. Ibele, Y. Lassmann, T. J. Martínez and B. F. E. Curchod, J. Chem. Phys., 2021, 154, 104110 CrossRef CAS PubMed.
- Y. Lassmann and B. F. E. Curchod, J. Chem. Phys., 2021, 154, 211106 CrossRef CAS PubMed.
- J. Janoš and P. Slavíček, J. Chem. Theory Comput., 2023, 19, 8273–8284 CrossRef PubMed.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B 864 CrossRef.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A 1133 CrossRef.
- S. Kube, C. Lasser and M. Weber, J. Comput. Phys., 2009, 228, 1947–1962 CrossRef CAS.
- M. Barbatti and K. Sen, Int. J. Quantum Chem., 2015, 116, 762–771 CrossRef.
- T. Plé, S. Huppert, F. Finocchi, P. Depondt and S. Bonella, J. Chem. Phys., 2019, 151, 114114 CrossRef PubMed.
- F. Kröninger, C. Lasser and J. J. L. Vaní’ček, Front. Phys., 2023, 11, 1106324 CrossRef.
- J. Suchan, D. Hollas, B. F. E. Curchod and P. Slavíček, Faraday Discuss., 2018, 212, 307 RSC.
- C. Pieroni, F. Becuzzi, L. Creatini, G. Granucci and M. Persico, J. Chem. Theory Comput., 2023, 19, 2430–2445 CrossRef CAS PubMed.
- D. Avagliano, E. Lorini and L. González, Philos. Trans. R. Soc., A, 2022, 380, 20200381 CrossRef PubMed.
- H. C. Longuet-Higgins, U. Öpik, M. H. L. Pryce and R. Sack, Proc. R. Soc. A, 1958, 244, 1–16 CAS.
- M. V. Berry, Proc. R. Soc. London, Ser. A, 1984, 392, 45–57 Search PubMed.
- S. C. Althorpe, F. Fernández-Alonso, B. D. Bean, J. D. Ayers, A. E. Pomerantz, R. N. Zare and E. Wrede, Nature, 2002, 416, 67–70 CrossRef CAS PubMed.
- J. C. Juanes-Marcos, S. C. Althorpe and E. Wrede, Science, 2005, 309, 1227–1230 CrossRef CAS PubMed.
- B. K. Kendrick, J. Hazra and N. Balakrishnan, Phys. Rev. Lett., 2015, 115, 153201 CrossRef CAS PubMed.
- C. Xie, C. L. Malbon, D. R. Yarkony, D. Xie and H. Guo, J. Am. Chem. Soc., 2018, 140, 1986–1989 CrossRef CAS PubMed.
- D. Yuan, Y. Guan, W. Chen, H. Zhao, S. Yu, C. Luo, Y. Tan, T. Xie, X. Wang, Z. Sun, D. H. Zhang and X. Yang, Science, 2018, 362, 1289–1293 CrossRef CAS PubMed.
- C. Xie, C. L. Malbon, H. Guo and D. R. Yarkony, Acc. Chem. Res., 2019, 52, 501–509 CrossRef CAS PubMed.
- E. Cohen, H. Larocque, F. Bouchard, F. Nejadsattari, Y. Gefen and E. Karimi, Nat. Rev. Phys., 2019, 1, 437–449 CrossRef.
- D. Yuan, Y. Huang, W. Chen, H. Zhao, S. Yu, C. Luo, Y. Tan, S. Wang, X. Wang, Z. Sun and X. Yang, Nat. Commun., 2020, 11, 3640 CrossRef CAS PubMed.
- C. H. Valahu, V. C. Olaya-Agudelo, R. J. MacDonell, T. Navickas, A. D. Rao, M. J. Millican, J. B. Pérez-Sánchez, J. Yuen-Zhou, M. J. Biercuk, C. Hempel, T. R. Tan and I. Kassal, Nat. Chem., 2023, 15, 1503–1508 CrossRef CAS PubMed.
- S. Mai, P. Marquetand and L. González, Int. J. Quantum Chem., 2015, 115, 1215–1231 CrossRef CAS.
- B. Mignolet, B. F. E. Curchod and T. J. Martínez, J. Chem. Phys., 2016, 145, 191104 CrossRef PubMed.
- T. J. Martinez, Nature, 2010, 467, 412–413 CrossRef CAS PubMed.
- W. Domcke and D. Yarkony, Annu. Rev. Phys. Chem., 2012, 63, 325 CrossRef CAS PubMed.
- D. R. Yarkony, Rev. Mod. Phys., 1996, 68, 985 CrossRef CAS.
- M. Baer, Beyond Born-Oppenheimer: Electronic nonadiabatic coupling terms and conical intersections, John Wiley & Sons, Inc., 2006 Search PubMed.
- J. Hazra, B. K. Kendrick and N. Balakrishnan, J. Phys. B: At. Mol. Phys., 2016, 49, 194004 CrossRef.
- D. Yuan, S. Yu, W. Chen, J. Sang, C. Luo, T. Wang, X. Xu, P. Casavecchia, X. Wang, Z. Sun, D. H. Zhang and X. Yang, Nat. Chem., 2018, 10, 653–658 CrossRef CAS PubMed.
- C. A. Mead, Chem. Phys., 1980, 49, 23–32 CrossRef CAS.
- C. A. Mead and D. G. Truhlar, J. Chem. Phys., 1979, 70, 2284 CrossRef CAS.
- L. M. Ibele, E. Sangiogo Gil, B. F. E. Curchod and F. Agostini, J. Phys. Chem. Lett., 2023, 14, 11625–11631 CrossRef CAS PubMed.
- L. M. Ibele and F. Agostini, J. Phys. Chem. A, 2024, 128, 3672–3684 CrossRef CAS PubMed.
- M. Baer, S. H. Lin, A. Alijah, S. Adhikari and G. D. Billing, Phys. Rev. A: At., Mol., Opt. Phys., 2000, 62, 032506 CrossRef.
- S. Adhikari, G. D. Billing, A. Alijah, S. H. Lin and M. Baer, Phys. Rev. A: At., Mol., Opt. Phys., 2000, 62, 032507 CrossRef.
- B. Sarkar and S. Adhikari, J. Chem. Phys., 2006, 124, 074101 CrossRef PubMed.
- B. Sarkar and S. Adhikari, Int. J. Quantum Chem., 2009, 109, 650–667 CrossRef CAS.
- A. K. Paul, S. Sardar, B. Sarkar and S. Adhikari, J. Chem. Phys., 2009, 131, 124312 Search PubMed.
- R. Requist, C. R. Proetto and E. K. U. Gross, Phys. Rev. A, 2017, 96, 062503 CrossRef.
- P. B. Allen, A. G. Abanov and R. Requist, Phys. Rev. A: At., Mol., Opt. Phys., 2005, 71, 043203 CrossRef.
- J. Ronayette, R. Arnaud, P. Lebourgeois and J. Lemaire, Can. J. Chem., 1974, 52, 1848–1857 CrossRef CAS.
- G. Gauglitz and S. Hubig, J. Photochem., 1985, 30, 121–125 CrossRef CAS.
- P. Bortolus and S. Monti, J. Phys. Chem., 1979, 83, 648–652 CrossRef CAS.
- N. Siampiringue, G. Guyot, S. Monti and P. Bortolus, J. Photochem., 1987, 37, 185–188 CrossRef CAS.
- A. W. Adamson, A. Vogler, H. Kunkely and R. Wachter, J. Am. Chem. Soc., 1978, 100, 1298–1300 CrossRef CAS.
- H. Rau and E. Lueddecke, J. Am. Chem. Soc., 1982, 104, 1616–1620 CrossRef CAS.
- H. Rau, J. Photochem., 1984, 26, 221–225 CrossRef CAS.
- V. Ladányi, P. Dvořák, J. Al Anshori, L. Vetráková, J. Wirz and D. Heger, Photochem. Photobiol. Sci., 2017, 16, 1757–1761 CrossRef PubMed.
- C. Ciminelli, G. Granucci and M. Persico, Chem. – Eur. J., 2004, 10, 2327–2341 CrossRef CAS PubMed.
- A. Nenov, R. Borrego-Varillas, A. Oriana, L. Ganzer, F. Segatta, I. Conti, J. Segarra-Marti, J. Omachi, M. Dapor, S. Taioli, C. Manzoni, S. Mukamel, G. Cerullo and M. Garavelli, J. Chem. Phys. Lett., 2018, 9, 1534–1541 CrossRef CAS PubMed.
- J. K. Yu, C. Bannwarth, R. Liang, E. G. Hohenstein and T. J. Martínez, J. Am. Chem. Soc., 2020, 142, 20680–20690 CrossRef CAS PubMed.
- M. Filatov, S. K. Min and K. S. Kim, J. Chem. Theory Comput., 2018, 14, 4499–4512 CrossRef CAS PubMed.
- M. Filatov, S. K. Min and K. S. Kim, Mol. Phys., 2019, 117, 1128–1141 CrossRef CAS.
- M. Filatov, M. Paolino, S. K. Min and K. S. Kim, J. Phys. Chem. Lett., 2018, 9, 4995–5001 Search PubMed.
- M. Filatov, M. Paolino, S. K. Min and C. H. Choi, Chem. Commun., 2019, 55, 5247 Search PubMed.
- M. Filatov(Gulak), M. Paolino, D. Kaliakin, M. Olivucci, E. Kraka and S. K. Min, Commun. Phys., 2024, 7, 219 CrossRef.
- M. Filatov, S. K. Min and C. H. Choi, Phys. Chem. Chem. Phys., 2019, 21, 2489–2498 RSC.
- T. I. Kim, J.-K. Ha and S. K. Min, Top. Curr. Chem., 2022, 380, 1–27 CrossRef PubMed.
- P. Vindel-Zandbergen, L. M. Ibele, J.-K. Ha, S. K. Min, B. F. E. Curchod and N. T. Maitra, J. Chem. Theory Comput., 2021, 17, 3852–3862 CrossRef CAS PubMed.
- E. V. Arribas, P. Vindel-Zandbergen, S. Roya and N. T. Maitra, Phys. Chem. Chem. Phys., 2023, 25, 26380 RSC.
- F. Krausz and M. Ivanov, Rev. Mod. Phys., 2009, 81, 163–234 CrossRef.
- F. Lépine, M. Y. Ivanov and M. J. J. Vrakking, Nat. Photonics, 2014, 8, 195–204 CrossRef.
- M. Nisoli, P. Decleva, F. Calegari, A. Palacios and F. Martn, Chem. Rev., 2017, 117, 10760–10825 CrossRef CAS PubMed.
- A. Palacios and F. Martn, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2020, 10, e1430 CAS.
- N. T. Maitra and E. Villaseco Arribas, arXiv, 2024, preprint, arXiv:2405.00649 [physics.chem-ph] DOI:10.48550/arXiv.2405.00649.
- J. A. Hutchison, T. Schwartz, C. Genet, E. Devaux and T. W. Ebbesen, Angew. Chem., Int. Ed., 2012, 51, 1592 CrossRef CAS PubMed.
- S. Wang, T. Chervy, J. George, J. A. Hutchison, C. Genet and T. W. Ebbesen, J. Phys. Chem. Lett., 2014, 5, 1433 CrossRef CAS PubMed.
- T. W. Ebbesen, Acc. Chem. Res., 2016, 49, 2403 CrossRef CAS PubMed.
- L. A. Martínez-Martínez, M. Du, R. F. Ribeiro, S. Kéa-Cohen and J. Yuen-Zhou, J. Phys. Chem. Lett., 2018, 9, 1951 CrossRef PubMed.
- M. Du, L. A. Martínez-Martínez, R. F. Ribeiro, Z. Hu, V. M. Menon and J. Yuen-Zhou, Chem. Sci., 2018, 9, 6659 RSC.
- L. A. Martínez-Martínez, R. F. Ribeiro, J. Campos-González-Angulo and J. Yuen-Zhou, ACS Photonics, 2018, 5, 167 CrossRef.
- R. T. Grant, P. Michetti, A. J. Musser, P. Gregoire, T. Virgili, E. Vella, M. Cavazzini, K. Georgiou, F. Galeotti, C. Clark, J. Clark, C. Silva and D. G. Lidzey, Adv. Opt. Mater., 2016, 4, 1615 CrossRef CAS.
- V. C. Nikolis, A. Mischok, B. Siegmund, J. Kublitski, X. Jia, J. Benduhn, U. Hörmann, D. Neher, M. C. Gather, D. Spoltore and K. Vandewal, Nat. Commun., 2019, 10, 3706 CrossRef PubMed.
- P. Vasa and C. Lienau, ACS Photonics, 2018, 5, 2 CrossRef CAS.
- D. G. Baranov, M. Wersäll, J. Cuadra, T. J. Antosiewicz and T. Shegai, ACS Photonics, 2018, 5, 24 Search PubMed.
- J. T. Hugall, A. Singh and N. F. van Hulst, ACS Photonics, 2018, 5, 43 CrossRef CAS.
- E. Orgiu, J. George, J. A. Hutchison, E. Devaux, J. F. Dayen, B. Doudin, F. Stellacci, C. Genet, J. Schachenmayer, C. Genes, G. Pupillo, P. Samori and T. W. Ebbesen, Nat. Mater., 2015, 14, 1123 CrossRef CAS PubMed.
- J. Fregoni, F. J. Garcia-Vidal and J. Feist, ACS Photonics, 2022, 9, 1096–1107 CrossRef CAS PubMed.
- J. Galego, F. J. Garcia-Vidal and J. Feist, Phys. Rev. X, 2015, 5, 041022 Search PubMed.
- J. Galego and F. J. G.-V. J. Feist, Phys. Rev. Lett., 2017, 119, 136001 CrossRef PubMed.
- T. E. Li, A. Nitzan and J. E. Subotnik, J. Chem. Phys., 2021, 154, 094124 CrossRef CAS PubMed.
- T. E. Li, A. Nitzan and J. E. Subotnik, J. Chem. Phys., 2022, 156, 134106 CrossRef CAS PubMed.
- M. R. Fiechter, J. E. Runeson, J. E. Lawrence and J. O. Richardson, J. Phys. Chem. Lett., 2023, 14, 8261–8267 CrossRef CAS PubMed.
- E. Hulkko, S. Pikker, V. Tiainen, R. H. Tichauer, G. Groenhof and J. J. Toppari, J. Chem. Phys., 2021, 154, 154303 CrossRef CAS PubMed.
- R. H. Tichauer, J. Feist and G. Groenhof, J. Chem. Phys., 2021, 154, 104112 CrossRef CAS PubMed.
- R. H. Tichauer, D. Morozov, I. Sokolovskii, J. J. Toppari and G. Groenhof, J. Phys. Chem. Lett., 2022, 13, 6259–6267 CrossRef CAS PubMed.
- J. Flick, H. Appel, M. Ruggenthaler and A. Rubio, J. Chem. Theory Comput., 2017, 13, 1616–1625 CrossRef CAS PubMed.
- M. R. Fiechter and J. O. Richardson, J. Chem. Phys., 2024, 160, 184107 CrossRef CAS PubMed.
- E. W. Fischer and P. Saalfrank, J. Chem. Theory Comput., 2023, 19, 72157229 CrossRef PubMed.
- J. Fregoni, G. Granucci, M. Persico and S. Corni, Chem, 2020, 6, 250–265 CAS.
- O. Vendrell, Phys. Rev. Lett., 2018, 121, 253001 CrossRef CAS PubMed.
- M. Kowalewski, K. Bennett and S. Mukamel, J. Phys. Chem. Lett., 2016, 7, 2050 CrossRef CAS PubMed.
- P. Martinez, B. Rosenzweig, N. M. Hoffmann, L. Lacombe and N. T. Maitra, J. Chem. Phys., 2021, 154, 014102 CrossRef CAS PubMed.
- B. Rana, E. G. Hohenstein and T. J. Martínez, J. Phys. Chem. A, 2023, 128, 139–151 CrossRef PubMed.
- A. Thomas, J. George, A. Shalabney, M. Dryzhakov, S. J. Varma, J. Moran, T. Chervy, X. Zhong, E. Devaux, C. Genet, J. A. Hutchison and T. W. Ebbesen, Angew. Chem., Int. Ed., 2016, 55, 11462–11466 CrossRef CAS PubMed.
- T. E. Lia, J. E. Subotnik and A. Nitzan, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 18324–18331 CrossRef PubMed.
- A. Z. Lieberherr, S. T. E. Furniss, J. E. Lawrence and D. E. Manolopoulos, J. Chem. Phys., 2023, 158, 234106 CrossRef CAS PubMed.
- E. Sangiogo Gil, D. Lauvergnat and F. Agostini, J. Chem. Phys., 2024, 161, 084112 CrossRef CAS PubMed.
Footnotes |
| † According to Stokes' theorem, the circulation of the TDVP along Γ is equal to the flux of the curl of the TDVP across a surface whose boundary is Γ. Therefore, this proves again that γ(Γ, t) is a physical gauge-independent observable. |
| ‡ Note that the photosisomerization is termed “partial” because the photoisomerization quantum yield is calculated only for the molecules that reached the ground state by the end of the trajectory. |
| This journal is © the Owner Societies 2024 |

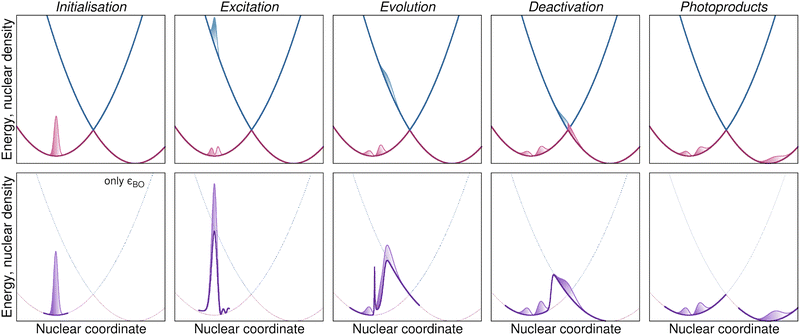
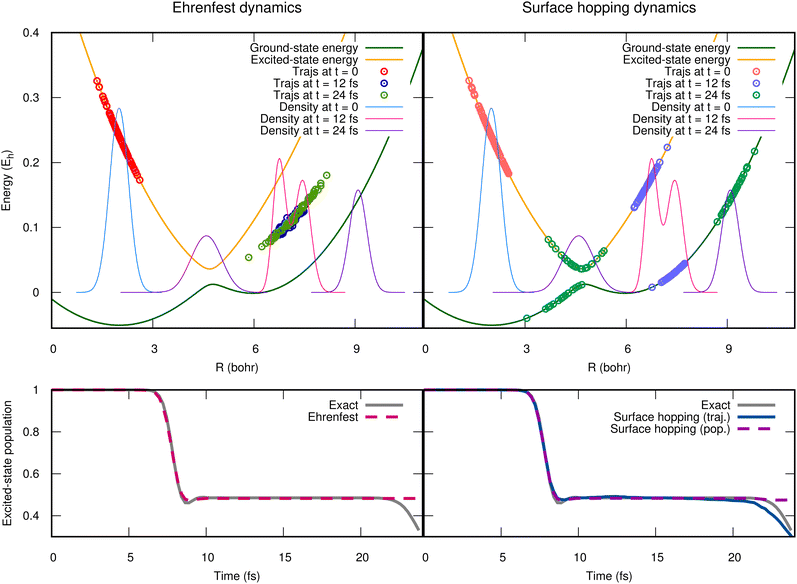
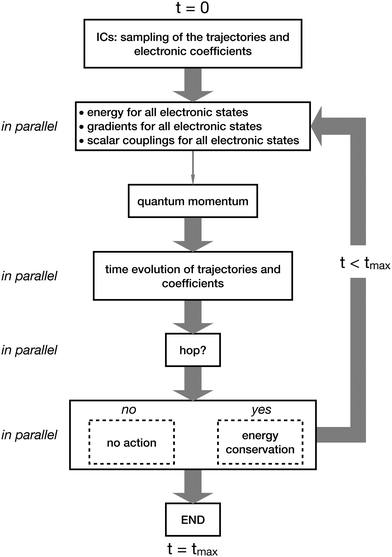
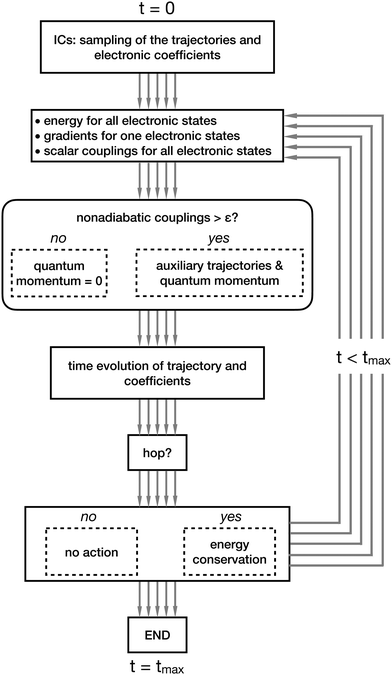
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 640.2
640.2