Trans vs. cis: a computational study of enasidenib resistance due to IDH2 mutations

Abstract

Isocitrate dehydrogenase 2 (IDH2) is a homodimeric enzyme that plays an important role in energy production. A mutation R140Q in one monomer makes the enzyme tumourigenic. Enasidenib is an effective inhibitor of IDH2/R140Q. A secondary mutation Q316E leads to enasidenib resistance. This mutation was hitherto only found in trans, i.e. where one monomer has the R140Q mutation and the other carries the Q316E mutation. It is not clear if the mutation only leads to resistance when in trans or if it has been discovered in trans only by chance, since it was only reported in two patients. Using molecular dynamics (MD) simulations we show that the binding of enasidenib to IDH2 is indeed much weaker when the Q316E mutation takes place in trans not in cis, which provides a molecular explanation for the clinical finding. This is corroborated by non-covalent interaction (NCI) analysis and DFT calculations. Whereas the MD simulations show a loss of one hydrogen bond upon the resistance mutation, NCI and energy decomposition analysis (EDA) reveal that a multitude of interactions are weakened.

---

1 Introduction

Drug resistance is a major clinical challenge, especially in cancer, bacterial, viral, fungal and parasitic diseases. In modern drug design, drugs are developed to bind molecular targets (most often proteins) with high specificity and affinity. Mutations that develop in the drug target upon treatment are a major cause for resistance.^1,2 Understanding the cause for drug resistance is essential for combating it and developing better drugs. Insights from physical chemistry can be highly useful in this respect. For example, in a study of resistance mutations to dasatinib that targets the protein ABL1, it was found that three such mutations have different mechanisms whereby resistance was driven by enthalpy, entropy or a combination of those.³ Other studies, theoretical and experimental, pointed to the importance of kinetics in enabling drug resistance.^4–7

IDH2 is a homodimeric enzyme that, upon mutations in residues Arg¹⁴⁰ or Arg¹⁷² leads to the formation of (R)-2-hydroxyglutarate (2HG), a metabolite which is not normally formed in the body. Accumulation of 2HG can drive several cancers. Specifically, a mutation R140Q in one of the two copies of the enzyme is associated with acute myeloid leukaemia (AML).⁸ Treatment with enasidenib, which specifically targets IDH2/R140Q over the wild-type enzyme, has been shown effective in such cases.^9,10 Secondary mutations in IDH2, Q316E and I319M have been observed in patients treated by enasidenib and were suggested to cause drug resistance.^10–12 Of note, AML is a rare disease and mutations in IDH2 are only observed in a subset of patients, thus reports on resistance mutations to enasidenib were few.

Interestingly, in the two cases where resistance mutations were reported, the resistance mutation was in trans to the activating R140Q mutation.¹² However, no mechanism was suggested to explain this finding. Moreover, the small number of patients that were hitherto subjected to treatment with enasidenib and for which data on resistance is available is not enough to conclude whether or not mutations must be in trans. Due to the scarcity of clinical information, computational studies can be insightful to examine if the binding of the drug is indeed weakened in trans but not in cis. We therefore employed molecular dynamics (MD) simulations to study the binding of enasidenib to IDH2/R140Q and to IDH2/R140Q/Q316E in cis and in trans. We have further studied the binding by examining how the drug binds to its nearby environment using density functional theory (DFT), non-covalent interactions (NCI) analysis and energy decomposition analysis (EDA) to gain physical insights on the binding of the drug in the single and double mutants.

2 Computational methods

2.1 Structure preparation

Structure preparations were conducted in CHARMM-GUI solution builder.^13–15 The crystal structure for R140Q-mutated IDH2 (PDB id 5I96¹⁶) was downloaded from Protein Data Bank (PDB).¹⁷ This structure had the R140Q mutation on both chains (A and B, each representing one monomer). Residue Gln¹⁴⁰ was modified back to Arg on chain A. Residues 43 to 449 were included in the analysis as these were visible in both chains. The systems were prepared by removing everything except the protein, enasidenib, the cofactor NADPH and calcium ions. Residue 316 was either (1) not modified (2) modified in cis to Glu, i.e. in chain B or (3) modified in trans to Glu. A cubic water box was applied with distance 12 Å from the protein. To mimic the conditions in cells, the systems were neutralized and simulated in a KCl solution (0.15 mol dm⁻³). The pressure was kept at 1 bar during the simulations.

2.2 MD simulations setup and forcefield

The simulations employed CHARMM36¹⁸ as force field for the protein and CGENFF¹⁹ for the drug. Water molecules were simulated with the TIP3P²⁰ model. GROMACS version 2022.3^21,22 was used throughout all of the protein simulations. Particle–mesh Ewald (PME) was used to treat long-range electrostatic interactions.²³ The temperature was kept constan at T = 310 K by the velocity rescaling thermostat²⁴ (τ_t = 0.1 ps). In order to constrain hydrogen bonds the LINCS constraint algorithm was used.²⁵ The SETTLE algorithm²⁶ was employed to constrain the water molecules. The cut-off distance for Coulomb and van der Waals interactions was set to 1.2 nm. The vdW potential was smoothly switched off starting at a distance of 1.0 nm between atoms.

The energy minimization procedure was run until maximum force was below 1000 kJ mol⁻¹ nm⁻¹ on every atom. Following this, a 20 ps simulation with positional restraints on solute atoms was performed as the first step towards system equilibration. The restrains were removed and a second equilibration simulation was carried out for 5 ns. Finally a 100 ns production simulation was run. Each system (wt and two mutants) was simulated in quadruplicate.

The pressure was kept constant by use of C-rescale algorithm²⁷ during equilibration and the Parrinello–Rahman algorithm²⁸ during production runs. The production simulations were carried out at the PDC high-performance computer system at KTH, Sweden.

2.3 Analysis of the MD simulations

The analysis was performed in GROMACS. Visual molecular dynamics (VMD)²⁹ was used for visualization. Median and maximal root mean square deviations (RMSD) values are given in the ESI.† Analysis of the structural similarity between the monomers was performed as follows. Firstly, ten equally-spaced structures were extracted from each simulation for each monomer, yielding overall 40 structures. These were thereafter aligned in pairs on their Cα atoms using the gmx confrms tool that only accepts single structures as input (no trajectories).

2.4 Estimation of the protein–drug binding free energies with linear interaction energy

Estimation of the protein–drug binding energies were performed here to supplement the finding from MD simulations. To this aim, we used the linear interaction energy (LIE) method, which has been developed to estimate free energies of binding from interaction energies calculated from MD simulations.³⁰ LIE was preferred over more sophisticated enhanced sampling methods such as the use of pulling simulations³¹ or non-equilibrium simulations^32–34 due to its simplicity, stability and lower computational cost.

The free energy is estimated as:³⁵

ΔG_b ≈ α(〈E^l–p_vdW〉 − 〈E^l–s_vdW〉) + β(〈E^l–p_Coul〉 − 〈E^l–s_Coul〉) + γ (1)

α, β and γ are parameters, whereas E^l–p and E^l–s are the ligand–protein and ligand–solvent interaction energies (vdW or Coulomb). In practice, interaction energies are averaged from simulations of drug bound to a protein and in solvent giving the 〈E〉 values in Eq. 1. A simulation of the drug in solvent was ran separately, using the same number of water molecules as in the simulations of the complex, to calculate the E^l–s values. From Linear Response Theory, β = 0.5.³⁰α = 0.16 had been used when LIE was developed and was used here as well. We tuned γ to reproduce the Gibbs energy of binding enasidenib to the R140Q mutant. The energy was estimated as the median value from the measurements of IC50 reported in the BindingDB database,³⁶ yielding −8.9 kcal mol⁻¹ (corresponding to an IC50 of 262 nM). Using the extracted value of γ, the binding energies were calculated for the R140Q/Q316E mutants. The relative error was calculated by estimating the standard deviations for the E^l–p_vdW and E^l–p_Coul energies and dividing these by the corresponding averages to get the relative error. The larger of these values was multiplied by the calculated free energy, as in Eqn 2 (σ in this equation refers to the standard deviation).

2.5 DFT calculations of the binding free energy of the drug and adjacent residues

The method for the binding energy calculations was described in ref. 3 and 37. A highly simplified model was used where the protein, drug and complex assumed the exact same conformation and only residues hydrogen bonding to the drug were considered. This neglects many important interactions while also reduces artifacts from strain to the protein. To build the DFT models, five snapshots from each simulation were extracted at equidistant time intervals (20, 40, 60, 80 and 100 ns) for a total of 20 energy calculations for each mutation. The residues were truncated and hydrogens were added at specific positions (Table 1 and Fig. 1). Avogadro version 1.2.0³⁸ was used for this purpose.

Table 1 Positions of added hydrogens for the DFT calculations

	R140Q/Q316E^cis
Gln^316	Truncated at ATOM 4408 CG, valence filled
Glu^316	Truncated at ATOM 4408 CG, valence filled
	R140Q/Q316E^trans
Glu^316	Truncated at ATOM 10852 CG, valence filled
Gln^316	Truncated at ATOM 10850 CG, valence filled

---

Fig. 1 Enasidenib in complex with R140Q mutated IDH2. PDB id 5I96. (a) A schematic view of the binding site for R140Q/Q316E^cis. (b) Enasidenib's positions at the interface between the two chains of the protein. (c) Enasidenib at the binding site.

Once the structures were prepared, geometry optimization was carried out in ORCA version 5.0.4^39,40 with the M06 functional⁴¹ and the def2-SV(P) basis set⁴² with the solvent (water) represented as PCM.⁴³ During optimization, heavy atoms were fixed to their initial positions. After the optimization was finished, binding free energy calculations were conducted. These calculations were performed with ωB97X-D/def2-TZVP/SMD.^42,44,45 Basis set superposition error (BSSE) was included. The binding energy was then obtained by the relations:

ΔG_bind = G_complex − (G_enasidenib + G^R140Q/Q316E_IDH2) (3)

and

ΔG_bind = G_complex − (G_enasidenib + G^R140Q_IDH2) (4)

where G_complex, G_enasidenib, G^R140Q_IDH2 and G^R140Q/Q316E_IDH2 are the electronic ground state free energies in SMD for each quantity. ΔG was taken as the arithmetic mean value of the 20 energy values for each mutation. ΔΔG was then calculated by

2.6 Energy decomposition analysis

Energy decomposition analysis (EDA) was performed in XEDA⁴⁶ using GKSEDA^47–49 at the ωB97X-D/def2-TZVP level of theory in gas phase. The calculation matches the PCMEDA method⁴⁸ which uses a set of energy calculations to divide the interaction energies between two or more monomers in a complex into contributions from electrostatics, exchange, repulsion, polarisation, desolvation, correlation and dispersion. The desolvation components were calculated separately in ORCA^39,40 since PCMEDA assumes the same cavity size for all atoms, which might be inappropriate for protein–drug interactions.³ Small differences between values calculated with XEDA and ORCA occur due to the different grids employed by the two packages and (to a small extent) since ORCA employs the RIJCOSX approximation.

2.7 Extracting representative structures from the simulations

Representative structures for further analysis were generated by clustering all snapshots in the trajectory using gmx cluster. The Gromos algorithm⁵⁰ was used for clustering with a cutoff of 0.15 nm. The central structure of the most occupied cluster was selected as representative.

2.8 Non-covalent interactions

The NCI analysis was performed in NCI plot version 4.⁵¹ The structures were taken from clustering analysis (vide supra) and include only the same representations as used in the DFT calculations. The NCI analysis for each of these structures was then plotted in the same figure using MATLAB version R2022b.

3 Results

3.1 Molecular dynamics simulations clearly indicate reduced protein–drug binding in trans but not in cis

The extensive sampling afforded by MD simulations enabled us to follow on of the number of hydrogen bonds and contacts between the drug and the protein (Table 2). These values revealed a very clear effect of the mutation in trans, which led to a loss of two hydrogen bonds and ∼30 protein–drug contacts. As an additive force-field was used in the MD simulations, it could be expected that the loss of hydrogen bonds would contribute to the electrostatic contribution to the binding energy becoming less favourable, whereas the loss of contacts can be expected to make the Lennard-Jones (LJ) contribution less favourable. Interestingly, analysis of the interaction energies shows only a change in electrostatics (Table 3). Furthermore, despite an overall lower number of hydrogen bonds when Gln³¹⁶ was mutated in cis, the interaction energies of the cis mutant were very similar to those observed in the wild type. This suggests that the cis mutation does not lead to resistance.

Table 2 Average number of hydrogen bonds between enasidenib and IDH2 for the different mutations from MD simulations

Measurement	R140Q	R140Q/Q316E^cis	R140Q/Q316E^trans
a The deviations from average are smaller than 0.1 for the hydrogen bonds and 1.0 for the contacts and are hence not shown.
IDH2-drug H-bonds^a	3.9	3.0	1.7
IDH2-drug contacts^a	493	497	464

---

Table 3 Protein–drug interaction energies calculated from MD simulations of IDH2 with enasidenib (values in kcal mol⁻¹ with standard deviations for the interaction energies and error estimations for ΔΔG_b in parentheses). ΔΔG_b is the Gibbs energy difference for drug binding calculated with LIE

Measurement	R140Q	R140Q/Q316E^cis	R140Q/Q316E^trans
Coul-SR	−24.1 (3.8)	−25.3 (6.9)	−14.3 (2.9)
LJ-SR	−45.7 (2.9)	−46.6 (3.1)	−45.3 (3.3)
ΔΔGb	0	−0.1 (2.0)	+2.5 (1.4)

---

Examining the hydrogen bonds involving residue 316 shows some difference between the mutants in cis and trans (Table 4). In the IDH2 R140Q variant, Residue Gln³¹⁶ is hydrogen bonded to residues Asp³¹², Gly³¹³ and Leu³²⁰ in the first monomer (with arginine in position 140) and to Asp³¹² and Leu³²⁰ in the second. Notably in the cis mutant, the carboxylate of Glu³¹⁶ accept a hydrogen bond from Trp³⁰⁶ whereas in the trans mutant, it forms a salt bridge with Arg¹⁴⁹. This is one structural reason for the reduction in hydrogen-bonding capacity between the trans mutant and the drug.

Table 4 Average number of hydrogen bonds involving residue 316 and selected protein residues in the simulations. Only residues with average number of hydrogen bonds above 0.1 are shown

Variant	Residue 140 in monomer	Residue 316 in monomer	H-Bonding residue	No. of H-bonds^a
a The deviations from average are smaller than 0.1 for the hydrogen bonds and are hence not shown.
R140Q	Arg^140	Gln^316	Asp^312	1.4
			Gly^313	0.6
			Leu^320	0.9
	Gln^140	Gln^316	Asp^312	1.3
			Leu^320	0.9
Cis	Arg^140	Gln^316	Asp^312	0.8
			Leu^320	0.9
	Gln^140	Glu^316	Asp^312	0.9
			Leu^320	0.9
			Trp^306	1.0
Trans	Arg^140	Glu^316	Gly^313	0.3
			Leu^320	0.4
			Arg^149	1.1
	Gln^140	Gln^316	Asp^312	1.1
			Leu^320	1.0

---

Linear interaction energy (LIE)³⁵ was used to approximate the free energy change upon mutation based on MD simulations. In agreement with the reported difference in interaction energies, the results (Table 3) show essentially no difference between the R140Q/Q316E^cis mutant and the R140Q IDH2 variant. The R140Q/Q316E^trans mutant show decreased binding of about 2.5 kcal mol⁻¹.

3.2 Structural changes observed in the molecular dynamics simulations explain the reduced binding upon trans mutation

To examine the structural changes between the different IDH2 variants as observed in the simulations, we start by examination of the opening of the active site. In crystal structures of IDH, the opening of the active site is measured by the distances between the residues that correspond to Ile⁷⁵ in one monomer and Leu²⁵⁰ in the other in human IDH1.⁵² In human IDH2, these residues are Ile¹¹⁶ and Leu²⁹⁸. In the crystal structure, these distances are 2.20 and 1.99 nm. The distribution of the distances in the simulations of IDH2/Arg¹⁴⁰|IDH2/Gln¹⁴⁰ (apo structure) show two somewhat asymetric openings with maxima at 2.10 and 1.99 nm (Fig. 2A, black lines). The active site becomes closer at the narrow side when Gln³¹⁶ is mutanted in cis (Fig. 2A, red lines, maxima at 2.10 and 1.70 nm). The trans-mutant shows a wider opening at the wide side (Fig. 2A, blue, with maxima at 2.40 and 2.00 nm). Only small changes are observed when the drug is bound to the R140Q variant or cis monomer (Fig. 2B, black and red lines). When residue 316 is mutanted in trans, both sides tend to be closed (with maxima of their distance distributions at 1.90 nm), but one distribution is much wider (Fig. 2B, blue; the solid line shows a wider distribution). Overall, the trans mutant shows considerable deviations from the original variant, especially when the drug is bound to it.

Fig. 2 Distance distribution for the opening of the active site in IDH, as calculated from the distance between the Cα atoms of residues Ile¹¹⁶ and Leu²⁹⁸. M1 is monomer 1 and M2 is monomer 2, referring to the location of Ile¹¹⁶. (a) Apo IDH2. (b) Drug-bound IDH2.

The structure of IDH protein also includes a back-cleft that can be in a closed (active) or open (inactive) state.⁵² The opening of the back cleft was defined by residues Met¹⁹⁹ and His³⁴² on each monomer in IDH1. The corresponding residues in IDH2 are Tyr²³⁸ and His³⁸¹. Unlike the active site opening, the back cleft opening was rather similar in all simulations (Fig. S1, ESI†).

Given that the opening of the active site between the monomers has been modified in the drug resistant trans mutant but the opening of the back cleft within the monomers did not, we have also carried out an analysis wherein the monomers were aligned with each other. This analysis also shows that the deviation between the monomers is about 0.25 nm in the free and 0.22 nm in the drug-bound state, showing a larger similarity in the latter case except for the trans mutant where it is ∼0.25 nm regardless of the drug-binding (Table 5). The deviations between the monomers can be smaller than the overall root mean square deviation (RMSD) for the whole complex (Table S1, ESI†) because the values for the whole complex require the alignment of the two dimers together.

Table 5 Root mean square deviations between monomer 1 and monomer 2 (averages over 40 calculations). Values are averages in nm with standard deviations in parentheses corresponding to the last significant digit, i.e. 0.24(5) means that the average is 0.24 nm and the standard deviation 0.05 nm

Protein	RMSD
R140Q apo	0.24(5)
Cis apo	0.25(5)
Trans apo	0.25(6)
R140Q holo	0.22(4)
Cis holo	0.22(5)
Trans holo	0.25(6)

---

3.3 NCI analysis reveals differences in the trans mutant

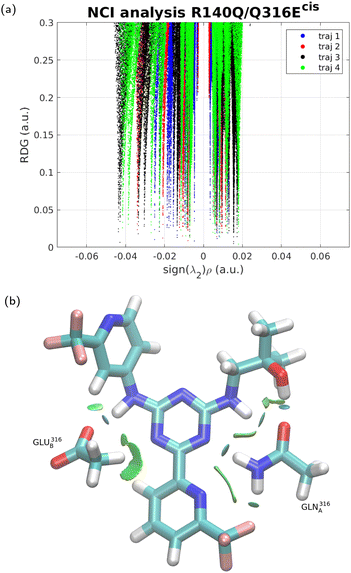
To further examine the difference between the three forms of the IDH protein in terms of binding to the inhibitor, NCI interaction analysis⁵¹ was performed for each of the four trajectories in each case, and the results are shown in Fig. 3–5. In NCI analysis, repulsive interactions are shown by positive values along the X-axis and attractive ones by negative values. The results show little if any difference between IDH2/R140Q and IDH2/R140Q/Q316E^cis. The IDH2/R140Q/Q316E^trans variant displays slightly smaller repulsion interactions with respect to the other two variants, and clearly less emphasized attraction (no interaction with sign(λ₂) < −0.04), corroborating the findings from the MD simulations.

Fig. 3 NCI analysis for the interaction between enasidenib IDH2 mutant R140Q. The analysis was performed separately on four independent MD trajectories. An example of the structure from one run is shown in frame (b), with areas of interaction in green. (a) Reduced density gradient. (b) Structural plot.

Fig. 4 NCI analysis for the interaction between enasidenib IDH2 mutant R140Q/Q316E^cis. The analysis was performed separately on four independent MD trajectories. An example of the structure from one run is shown in frame (b), with areas of interaction in green. (a) Reduced density gradient. (b) Structural plot.

Fig. 5 NCI analysis for the interaction between enasidenib IDH2 mutant R140Q/Q316E^trans. The analysis was performed separately on four independent MD trajectories. An example of the structure from one run is shown in frame (b), with areas of interaction in green. (a) Reduced density gradient. (b) Structural plot.

3.4 DFT calculations of interaction energies and energy decomposition analysis of the drug binding

The interaction energies calculated from the MD simulations do not include quantum mechanical (QM) effects. To this end, we approximated the binding free energies using small model of the binding site with full DFT, following our earlier studies that showed the reliability of such approach.^3,53 The results (Table 3) were in agreement with the interaction energies calculated in the MD simulations and clearly show that the binding free energy becomes much less favourable upon Q316E mutation in trans but not in cis (Table 6).

Table 6 Binding free energies (kcal mol⁻¹) estimated for a binding site model of IDH2 with enasidenib. The values were calculated with DFT for the R140Q, R140Q/Q316E^cis (cis) and R140Q/Q316E^trans (trans) mutants. CI = confidence interval. The QM calculations were performed in ORCA^39,40 using the ωB97X-D functional,⁴⁵ the def2-TZVP basis set⁴² and the solvent model SMD.⁴⁴ The values were calculated from 20 snapshot structures taken from the MD simulations

	ΔG^R140Q (n = 20)	ΔG^cis (n = 20)	ΔG^trans (n = 20)
Mean	−17.6 (3.6)	−16.1 (3.6)	−9.7 (2.0)
CI (95%)	[−19.3, −15.9]	[−17.8, −14.4]	[−10.6, −8.8]

---

	ΔΔG^trans–cis	ΔΔG^cis–R140Q	ΔΔG^trans–R140Q
	+6.3	+1.6	+7.9
CI (95%)	[4.5, 8.3]	[−0.8, 3.8]	[6.0, 9.8]

---

Analysis of the MD simulations suggests that the reduced affinity of the drug to the Q316E^trans mutant is due to loss of electrostatic interactions (Table 3). To get further insights into the different contributions and consider interactions that are not represented in the forcefield, we decomposed the energies calculated by DFT using the PCMEDA approach^47–49 (Fig. 6). The contribution of favourable electrostatics is indeed much reduced for the complex with the Q316E^trans mutant even in EDA. However, the EDA calculation reveal a more complex picture, where in effect all interactions are reduced, negative and positive, which is in agreement with the NCI calculations. The binding of the drug is dominated by electrostatics and polarization regardless of the mutation.

Fig. 6 Energy decomposition analysis for the interaction between enasidenib and the IDH2 mutants R140Q, R140Q/Q316E^cis and R140Q/Q316E^trans. PCMEDA was performed in each case for a structure where the interactions energies were the largest in absolute value. EL – electrostatics, EX + REP − exchange + repulsion, POL – polarization, DISP – dispersion, CORR – DFT correlation, DES – desolvation, TOT – total. EDA calculations in gas phase were performed in XEDA⁴⁶ and desolvation was calculated using ORCA.^39,40

4 Discussion

In this study we show, using MD simulations, that the previous finding of a resistance mutation Q316E in trans in two patients upon treatment with enasidenib is likely due to the protein–drug interaction rather than the small number of patients. MD simulations, NCI analysis and DFT calculations all show that the mutation in trans, i.e. in a different copy of the dimer than the activating mutation R140Q, leads to less favourable protein–drug interactions. The MD simulations show clearly that a hydrogen bond is lost between the drug and the protein, and that the electrostatic interaction is weakened. EDA analysis shows that this is the results of a weakening of multiple interactions (electrostatics, polarization, correlation and dispersion).

Analysis of the MD simulations showed modifications to the opening of the active site in the mutated IDH upon the Q316E mutation in trans. It remains to be seen if these changes might also affect the catalytic efficiency of the enzyme. In the apo structure, the two monomers are somewhat asymetric (RMSD of ∼0.25 nm between them) without clear changes when IDH2 was mutated. This indicates that modifications are mainly in the bound structure, which might make it more difficult to design drugs that would overcome resistance due to the Q316E mutation. On the other end, a comparison of the mutants reveal that maintaining the hydrogen bonds between the protein and the drug is a crucial aspect. Finally, this study suggests that any efforts to curb drug resistance in a dimeric structure should consider on which monomer the mutations take place.

Author contributions

Erik Arvidsson: investigation. Erik Lindahl: investigation, methodology, visualization, writing – original draft, writing – review & editing. Ran Friedman: conceptualization, data curation, funding acquisition, investigation, methodology, project administration, resources, supervision, writing – review & editing.

Data availability

All procedures are detailed in the article. Input files for energy calculations, EDA and NCI are freely available at: https://dx.doi.org/10.6084/m9.figshare.25205792.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Most calculations were performed on resources provided by the Swedish National Infrastructure for Computing (SNIC) at PDC, partially funded by the Swedish Research Council through grant agreement no. 2018-05973. EDA calculations were performed on the Xiamen Atomistic Computing Suite (XACS).

Notes and references

1. R. Friedman, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 12, e1563.
2. N. Kurt Yilmaz and C. A. Schiffer, Chem. Rev., 2021, 121, 3235–3237.
3. M. J. Dávila-Rodrguez, T. S. Freire, E. Lindahl, I. Caracelli, J. Zukerman-Schpector and R. Friedman, Chem. Commun., 2020, 56, 6727–6730.
4. G. Jindal, D. Mondal and A. Warshel, J. Phys. Chem. B, 2017, 121, 6831–6840.
5. P. S. Georgoulia, G. Todde, S. Bjelic and R. Friedman, Biochim. Biophys. Acta, Gen. Sub., 2019, 1863, 732–741.
6. P. S. Georgoulia, S. Bjelic and R. Friedman, FEBS J., 2020, 287, 3200–3220.
7. I. Choudhuri, A. Biswas, A. Haldane and R. M. Levy, J. Phys. Chem. B, 2022, 126, 10622–10636.
8. R. Chowdhury, K. K. Yeoh, Y.-M. Tian, L. Hillringhaus, E. A. Bagg, N. R. Rose, I. K. H. Leung, X. S. Li, E. C. Y. Woon, M. Yang, M. A. McDonough, O. N. King, I. J. Clifton, R. J. Klose, T. D. W. Claridge, P. J. Ratcliffe, C. J. Schofield and A. Kawamura, EMBO Rep., 2011, 12, 463–469.
9. E. S. Kim, Drugs, 2017, 77, 1705–1711.
10. E. M. Stein, C. D. DiNardo, A. T. Fathi, D. A. Pollyea, R. M. Stone, J. K. Altman, G. J. Roboz, M. R. Patel, R. Collins, I. W. Flinn, M. A. Sekeres, A. S. Stein, H. M. Kantarjian, R. L. Levine, P. Vyas, K. J. MacBeth, A. Tosolini, J. VanOostendorp, Q. Xu, I. Gupta, T. Lila, A. Risueno, K. E. Yen, B. Wu, E. C. Attar, M. S. Tallman and S. de Botton, Blood, 2019, 133, 676–687.
11. E. M. Stein, C. D. DiNardo, D. A. Pollyea, A. T. Fathi, G. J. Roboz, J. K. Altman, R. M. Stone, D. J. DeAngelo, R. L. Levine, I. W. Flinn, H. M. Kantarjian, R. Collins, M. R. Patel, A. E. Frankel, A. Stein, M. A. Sekeres, R. T. Swords, B. C. Medeiros, C. Willekens, P. Vyas, A. Tosolini, Q. Xu, R. D. Knight, K. E. Yen, S. Agresta, S. de Botton and M. S. Tallman, Blood, 2017, 130, 722–731.
12. A. M. Intlekofer, A. H. Shih, B. Wang, A. Nazir, A. S. Rustenburg, S. K. Albanese, M. Patel, C. Famulare, F. M. Correa, N. Takemoto, V. Durani, H. Liu, J. Taylor, N. Farnoud, E. Papaemmanuil, J. R. Cross, M. S. Tallman, M. E. Arcila, M. Roshal, G. A. Petsko, B. Wu, S. Choe, Z. D. Konteatis, S. A. Biller, J. D. Chodera, C. B. Thompson, R. L. Levine and E. M. Stein, Nature, 2018, 559, 125–129.
13. S. Jo, T. Kim, V. G. Iyer and W. Im, J. Comput. Chem., 2008, 29, 1859–1865.
14. B. R. Brooks, C. L. Brooks, 3rd, A. D. Mackerell, Jr, L. Nilsson, R. J. Petrella, B. Roux, Y. Won, G. Archontis, C. Bartels, S. Boresch, A. Caflisch, L. Caves, Q. Cui, A. R. Dinner, M. Feig, S. Fischer, J. Gao, M. Hodoscek, W. Im, K. Kuczera, T. Lazaridis, J. Ma, V. Ovchinnikov, E. Paci, R. W. Pastor, C. B. Post, J. Z. Pu, M. Schaefer, B. Tidor, R. M. Venable, H. L. Woodcock, X. Wu, W. Yang, D. M. York and M. Karplus, J. Comput. Chem., 2009, 30, 1545–1614.
15. J. Lee, X. Cheng, J. M. Swails, M. S. Yeom, P. K. Eastman, J. A. Lemkul, S. Wei, J. Buckner, J. C. Jeong, Y. Qi, S. Jo, V. S. Pande, D. A. Case, C. L. I. Brooks, A. D. J. MacKerell, J. B. Klauda and W. Im, J. Chem. Theory Comput., 2016, 12, 405–413.
16. K. Yen, J. Travins, F. Wang, M. D. David, E. Artin, K. Straley, A. Padyana, S. Gross, B. DeLaBarre, E. Tobin, Y. Chen, R. Nagaraja, S. Choe, L. Jin, Z. Konteatis, G. Cianchetta, J. O. Saunders, F. G. Salituro, C. Quivoron, P. Opolon, O. Bawa, V. Saada, A. Paci, S. Broutin, O. A. Bernard, S. de Botton, B. S. Marteyn, M. Pilichowska, Y. Xu, C. Fang, F. Jiang, W. Wei, S. Jin, L. Silverman, W. Liu, H. Yang, L. Dang, M. Dorsch, V. Penard-Lacronique, S. A. Biller and S.-S. M. Su, Cancer Discovery, 2017, 7, 478–493.
17. H. M. Berman, J. Westbrook, Z. Feng, G. Gilliland, T. N. Bhat, H. Weissig, I. N. Shindyalov and P. E. Bourne, Nucleic Acids Res., 2000, 28, 235–242.
18. R. B. Best, X. Zhu, J. Shim, P. E. Lopes, J. Mittal, M. Feig and A. D. Mackerell, J. Chem. Theory Comput., 2012, 8, 3257–3273.
19. K. Vanommeslaeghe, E. Hatcher, C. Acharya, S. Kundu, S. Zhong, J. Shim, E. Darian, O. Guvench, P. Lopes, I. Vorobyov and A. D. Mackerell, J. Comput. Chem., 2010, 31, 671–690.
20. W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935.
21. D. Van Der Spoel, E. Lindahl, B. Hess, G. Groenhof, A. E. Mark and H. J. C. Berendsen, J. Comput. Chem., 2005, 26, 1701–1718.
22. M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1–2, 19–25.
23. T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092.
24. G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101.
25. B. Hess, H. Bekker, H. J. C. Berendsen and J. G. E. M. Fraaije, J. Comput. Chem., 1997, 18, 1463–1472.
26. S. Miyamoto and P. A. Kollman, J. Comput. Chem., 1992, 13, 952–962.
27. M. Bernetti and G. Bussi, J. Chem. Phys., 2020, 153, 114107.
28. M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190.
29. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14(33–38), 27–28.
30. J. Åqvist, C. Medina and J.-E. Samuelsson, Protein Eng., Des. Sel., 1994, 7, 385–391.
31. J. A. Lemkul and D. R. Bevan, J. Phys. Chem. B, 2010, 114, 1652–1660.
32. S. Kim, H. Oshima, H. Zhang, N. R. Kern, S. Re, J. Lee, B. Roux, Y. Sugita, W. Jiang and W. Im, J. Chem. Theory Comput., 2020, 16, 7207–7218.
33. V. Gapsys, A. Yildirim, M. Aldeghi, Y. Khalak, D. van der Spoel and B. L. de Groot, Commun. Chem., 2021, 4, 61.
34. T. S. Freire, I. Caracelli, J. Zukerman-Schpector and R. Friedman, Phys. Chem. Chem. Phys., 2023, 25, 6175–6183.
35. H. Gutiérrez-de Terán and J. Åqvist, Linear Interaction Energy: Method and Applications in Drug Design, Springer, New York, 2011, vol. 819, pp. 305–323.
36. T. Liu, Y. Lin, X. Wen, R. N. Jorissen and M. K. Gilson, Nucleic Acids Res., 2007, 35, D198–D201.
37. B. Oruganti, E. Lindahl, J. Yang, W. Amiri, R. Rahimullah and R. Friedman, J. Biol. Chem., 2022, 298, 102238.
38. M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, J. Cheminf., 2012, 4, 17.
39. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 2, 73–78.
40. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1606.
41. Y. Zhao and D. G. Truhlar, J. Chem. Phys., 2006, 125, 194101.
42. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297.
43. S. Miertuš, E. Scrocco and J. Tomasi, Chem. Phys., 1981, 55, 117–129.
44. A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396.
45. J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620.
46. Z. Tang, Y. Song, S. Zhang, W. Wang, Y. Xu, D. Wu, W. Wu and P. Su, J. Comput. Chem., 2021, 42, 2341–2351.
47. P. Su, H. Liu and W. Wu, J. Chem. Phys., 2012, 137, 034111.
48. P. Su, Z. Jiang, Z. Chen and W. Wu, J. Phys. Chem. A, 2014, 118, 2531–2542.
49. P. Su, Z. Tang and W. Wu, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2020, 10, e1460.
50. X. Daura, K. Gademann, B. Jaun, D. Seebach, W. F. van Gunsteren and A. E. Mark, Angew. Chem., Int. Ed., 1999, 38, 236–240.
51. R. Boto, F. Peccati, R. Laplaza, C. Quan, A. Carbone, J.-P. Piquemal, Y. Maday and J. Contreras-García, J. Chem. Theory Comput., 2019, 16, 4150–4158.
52. X. Xu, J. Zhao, Z. Xu, B. Peng, Q. Huang, E. Arnold and J. Ding, J. Biol. Chem., 2004, 279, 33946–33957.
53. R. Friedman, J. Phys. Chem. B, 2021, 125, 2251–2257.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp01571a

---