Local reactivity descriptors to decipher the electrochemical hydrogenation of unsaturated carboxylic acids

Abstract

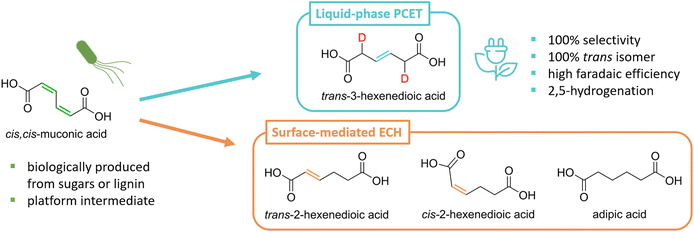
The decarbonization of chemical manufacturing is a multifaceted challenge that requires technologies able to selectively convert CO₂-sequestering feedstocks using renewable energy. The electrochemical conversion of biomass is well-positioned to address this need. However, the electroactivity of biobased molecules that carry multiple redox centers remains challenging to predict and control. For instance, cis,cis-muconic acid, a conjugated dicarboxylic acid, is electrohydrogenated to trans-3-hexenedioic acid (t3HDA) with excellent yield and stereoselectivity while free energy calculations predict mixtures of 2- and 3-hexenedioic acids. To decipher this discrepancy, we studied the electrohydrogenation of C4 and C6 unsaturated acids, diacids, and their esters, and tied the observed product distributions to the electronic structure of the parent molecules. We show that the electrohydrogenation of the three isomers of muconic acid proceeds through a hydrogenating proton-coupled electron transfer (PCET) in the α position of the carboxylic acids and invariably yields t3HDA as the sole product. The selectivity can be explained by the electron-withdrawing effect of the carboxylic acid groups and the resulting perturbation of the local electron density that promotes the 2,5-hydrogenation over the thermodynamically-preferred 2,3-hydrogenation. This electronic perturbation is reflected in the computed Fukui indices, which can serve as local reactivity descriptors to predict product distributions not captured by calculated reaction thermochemistry. In addition to predicting the electroactivity of other unsaturated acids, this approach can provide insights into homogeneous electrochemical processes that may coexist with surface-mediated electrocatalytic transformations.

---

Introduction

Chemical manufacturing is the third largest industrial emitter of greenhouse gases after the steel and cement industries, contributing 1 Gt of CO₂ each year.^1,2 Therefore, curbing these emissions represents a major challenge that can only be addressed through a multi-pronged approach combining CO₂-sequestering carbon feedstocks, renewable energy, and breakthrough technologies. Electrochemistry is ideally suited to address this challenge as it uses electrons to drive chemical reactions, overcoming the need for toxic chemicals, heat, and pressure for most transformations. Careful selection and pairing of the organic transformations taking place at the anode and cathode can also produce excess electricity, allowing energy-demanding thermochemical reactors to be replaced by energy-generating electrolyzers.^3–5

The past few years have seen breakthroughs in the electrosynthesis of various commodity chemicals from CO₂, including formic acid, ethylene, and ethylene oxide.^6–13 Progress in the electro-conversion of biomass has also enabled the synthesis of C3–C6 compounds—e.g., higher alkenes, furanics, phenolics, and diacids—with good yields and faradaic efficiencies.^5,14–20 Electrochemical hydrogenation (ECH) plays an increasingly important role in these transformations as unsaturated functionalities, in particular carbonyl (C=O) and alkenyl (C=C) groups, are ubiquitous in biobased molecules whether derived from lignocellulosic biomass or produced using microbial cell factories.

Notable biobased platform molecules include unsaturated (di)carboxylic acids—fumaric, levulinic, itaconic, and muconic acids—that can be hydrogenated to produce monomers key to the manufacture of polyamides and polyesters.^15,21–25 Their ECH is typically performed using the same platinum-group metal catalysts as for thermocatalytic hydrogenations (TCH).^16,18 However, surface-mediated ECH presents several important advantages over TCH: (i) hydrogen is generated in situ from water instead of supplied by H₂; (ii) the reaction proceeds under ambient conditions with reduced mass transfer limitations as H* is generated directly at the surface of the catalyst; and (iii) the various modes of electric current delivery—potentiostatic, galvanostatic, rapid alternating polarity, etc.—offer additional degrees of freedom to common reaction parameters such as temperature and pressure to finely control selectivity.^16,20,26

In contrast to TCH, ECH can also proceed in the absence of a platinum group metal catalyst, albeit through a different reaction pathway that involves concerted or sequential proton-coupled electron transfers (PCET) in solution. This approach is particularly valuable to process feedstocks containing biogenic impurities that can irreversibly poison metal catalysts at ppm levels.²⁷ For instance, fermentation broths present nitrogen- and sulfur-containing amino acids that deactivate common hydrogenation catalysts like Pd/C and Pt/C at concentrations as low as 50 ppm.^27–30 Such deactivation is suppressed in the case of liquid-phase PCET as the reaction is not mediated by the electrode surface.

Our group has recently demonstrated that cis,cis-muconic acid (ccMA) produced from sugars or lignin monomers using metabolically-engineered microorganisms can be directly hydrogenated in its fermentation broth through PCET by reusing the broth's inorganic salts and water as electrolyte and hydrogen sources.^27,31–33 This process intensification strategy minimizes chemical waste and improves process economics.³² The reaction produces the corresponding monounsaturated trans-3-hexenedioic acid (t3HDA) with excellent yield, stereoselectivity, and faradaic efficiency at an estimated cost of $1.75 kg⁻¹, close to adipic acid's 10 years average price of $1.60 kg⁻¹.^27,34 Like adipic acid, t3HDA can be used as a monomer to manufacture polyesters and polyamides, and its double bond can be leveraged to enable the design of polymeric materials with performance advantages. For instance, t3HDA's double bond can be used to tether pendant groups and build in desired properties like hydrophobicity and flame retardancy without compromising the mechanical properties of the parent polymer.^23,35

The selectivity observed for the liquid-phase PCET hydrogenation of ccMA is unexpected as TCH and surface-mediated ECH produce mixtures of the cis and trans isomers of 2- and 3-hexenedioic acids as intermediates to adipic acid (Scheme 1). This selectivity could not be explained theoretically, as the computational tools needed to quantitatively predict the chemoselectivity of electrochemical reactions are underdeveloped. Linear correlations have been established between molecules’ lowest unoccupied molecular orbital (LUMO) energies, electron affinities, and redox potentials.^36–38 However, the tools available do not provide information on the reactivity of individual redox sites within a molecule.

Scheme 1 cis,cis-Muconic acid produced biologically from sugars or lignin monomers can be hydrogenated to produce a variety of commodity and specialty monomers. While surface-mediated electrochemical hydrogenation (ECH) produces mixtures of hexenedioic acids and adipic acid, the liquid-phase proton-coupled electron transfer (PCET) hydrogenation generates trans-3-hexenedioic acid as the sole product. H/D isotopic tracing revealed that the reaction proceeds through a 2,5-hydrogenation pathway (deuterium atoms in red).

Herein, we address this gap by studying experimentally and theoretically the liquid-phase ECH of C=C in biobased chemicals with multiple redox sites. We compare the selectivity of the reaction for C4–C6 monoacids, diacids, and their esters at different pH to correlate redox activity and chemoselectivity with the substrate's molecular structure and protonation state. This work highlights how neighboring electron-donating and withdrawing functional groups alter the hydrogenation of C=C and control the selectivity of the PCET process. It also highlights how thermochemistry fails to predict the observed selectivity and how, instead, the electrophilicity of the carbon atoms captured by Fukui indices explains the experimental results.

Results and discussion

Thermochemistry of the proton-coupled electron transfer hydrogenation of cis,cis-muconic acid

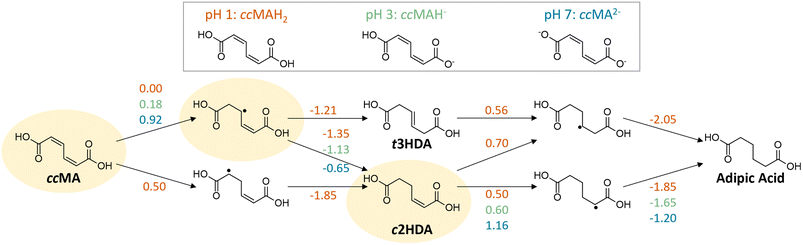
H/D isotopic tracing studies have previously demonstrated that the PCET hydrogenation of ccMA in the absence of a metal catalyst follows a 2,5-hydrogenation pathway with t3HDA as the sole product.²⁷ Deuterium atoms were selectively added to the carbon atoms next to the carboxylic acid groups (α positions) to form the corresponding β,γ-unsaturated diacid (Scheme 1). The selectivity to t3HDA was not influenced by common reaction parameters such as pH, electrolyte, applied potential, current, or charge passed. It was also unaffected by the nature of the muconic acid isomer, as cis,cis- and cis,trans-muconic acid gave identical results.^27,32 Therefore, we initiated the present study with a computational investigation of the reaction thermochemistry for the sequential hydrogen addition (H⁺|e⁻ pair) to ccMA in an attempt to explain the observed selectivity.

As can be seen in Fig. 1, the first H-addition to fully protonated ccMA is expected to take place on the carbon atom in the α position of the carboxylic acid. This addition has a reaction free energy of 0.00 eV at −0.48 V vs. Ag/AgCl, which is more favorable than addition at the β carbon by 0.50 eV at pH 1. The subsequent hydrogenation on the β carbon to form cis-2-hexenedioic acid (c2HDA), the 2,3-hydrogenation product, is energetically favored (ΔG = −1.35 eV) over the 2,5-hydrogenation that would yield t3HDA (ΔG = −1.21 eV). The calculations also revealed that further hydrogenation is disfavored by the energy barrier for the third proton–electron addition, such that the reaction may not readily occur at moderate potentials without a catalyst. Therefore, either c2HDA or a mixture of c2HDA and t3HDA were expected through PCET, which is inconsistent with the corresponding experiments as t3HDA was the only product detected.

Fig. 1 Changes in free energy (eV) for the sequential addition of H⁺|e⁻ pairs to cis,cis-muconic acid (ccMA) to form the hydrogenated hexenedioic acid and adipic acid products. Energetics are presented at −0.48 V vs. Ag/AgCl, the potential at which ccMA hydrogenation at pH 1 is calculated to have ΔG = 0.00 eV. The highlighted path shows the corresponding intermediates and products predicted by free energy calculations; t3HDA is formed experimentally.

pH dependence of the proton-coupled electron transfer hydrogenation of cis,cis-muconic acid

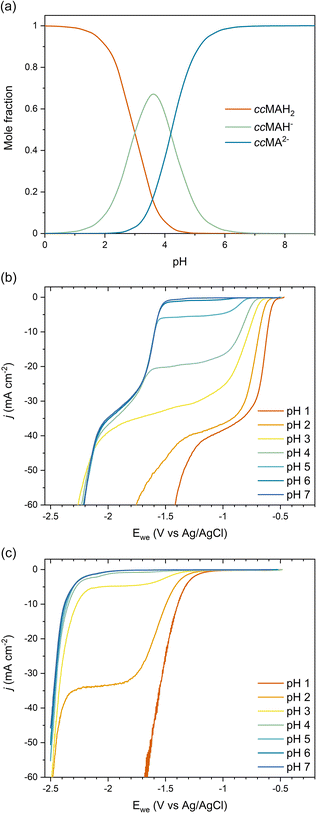
As COOH is a strong electron-withdrawing group, we hypothesized that the carboxylic acid functionalities in ccMA increase the electrophilicity of the carbon atoms in α positions (C2 and C5) and thereby favor the 2,5-hydrogenation pathway to t3HDA through kinetic control. To test this hypothesis, we studied the pH dependence of ccMA's electrohydrogenation using linear sweep voltammetry (LSV). COO⁻ is a weaker electron-withdrawing group than COOH and, therefore, the deprotonation of ccMA with increasing pH was expected to decrease the electrophilicity of the C2 and C5 carbon atoms, causing the onset to shift to more cathodic potentials (more negative voltages). Arguably, increasing the pH also lowers the availability of H₃O⁺, which serves as a hydrogen source for the PCET reaction. However, the contributions of these two effects to the reaction's onset potential can be untwined by (i) knowing the equilibrium concentrations of the organic species in solution and, (ii) understanding the pH dependence of PCET processes. Therefore, we started this part of the work by studying the role of pH on ccMA speciation, HER, and PCET hydrogenation.

The speciation diagram for ccMA revealed that diprotic, monoprotic, and deprotonated ccMA (for clarity labeled ccMAH₂, ccMAH⁻, and ccMA²⁻ in Fig. 2a) coexist near pH 3.5 but that diprotic muconic acid and deprotonated muconate dianions are the dominant species below pH 3 and above pH 5, respectively. This speciation and the absence of any side reactions (e.g., coupling) enabled us to identify the onset potentials of the various compounds when increasing pH from 1 to 7 and understand how reactivity changes with the protonation state of the molecule (Fig. 2b). At pH 1, protonated ccMA (ccMAH₂) exhibited an onset potential at −0.57 V vs. Ag/AgCl that can be easily distinguished from the reduction of hydronium ions to H₂via the acidic Volmer–Heyrovsky mechanism at −1.38 V (Fig. 2b and c).³⁹ At around pH 2–3, mass transfer limitations depleted MA species and hydronium ions near the cathode's surface giving rise to a diffusional plateau that is also visible in the polarization curves collected for the blank electrolytes between ca. −1.5 and −2.2 V (Fig. 2c). Above pH 3, new onset potentials appeared at −1.55 V and −2.18 V (Fig. 2b), corresponding to the hydrogenation of ccMA dianions and water reduction following the alkaline Volmer–Heyrovsky mechanism, respectively. Increasing the pH further from 3 to 7 shifted the onset potential for water reduction by less than −0.10 V, in good agreement with the literature on HER.^40,41

Fig. 2 (a) Speciation diagram for ccMA calculated for pK_a1 = 3.0 and pK_a2 = 4.2; ccMAH₂, ccMAH⁻, and ccMA²⁻ correspond to diprotic, monoprotic, and fully deprotonated species. (b and c) pH-Dependent current–potential polarization curves on Pb RDE for 0.1 M K₂SO₄/H₂SO₄ (b) with 0.5 g L⁻¹ccMA and (c) without ccMA.

The lack of distinct onset potential for the hydrogenation of the monoprotic acid (ccMAH⁻) is likely due to the pK_a values for ccMA being too close to distinguish the two deprotonation events. This observation is consistent with prior attempts to titrate ccMA.⁴² Alternatively, kinetic modeling performed for the isomerization of ccMA to ctMA provided ranges of possible pK_a values for ccMA, namely, 2.8 < pK_a1 < 4.4 and 4.2 < pK_a2 < 5.0 at 22.5 °C.⁴² These values and the corresponding speciation diagram (Fig. 2a) explain the decrease in current observed for the plateau at −1.6 < E_we < −1.0 V with increasing pH (Fig. 2b). Specifically, the current changed only slightly at pH 1–2 because ccMAH₂ was the only species in solution and the reaction was not limited by [H₃O⁺]; the reaction was solely limited by the diffusion of ccMAH₂ under these conditions. At pH 3, the drop in [ccMAH₂] and [H₃O⁺] concentrations caused more substantial changes to the LSVs and their independent contributions were estimated from the polarization curves for the blank electrolyte. As Fig. 2c revealed a transition from proton reduction to water reduction for HER at pH 3, H₂O was expected to also become the main source of hydrogen for ECH at this pH. Therefore, pH and [H₃O⁺] were not expected to play any role in the change in current observed at −1.6 < E_we < −1.0 V at pH > 3. This implies that current was controlled by the mass transport of ccMAH₂ and ccMAH⁻ for 3 < pH < 5. Above pH 5, ccMA²⁻ became the dominant species, which suppressed the diffusional plateau at −1.6 < E_we < −1.0 V and gave a single onset potential for ECH at −1.55 V. A new diffusional plateau also appeared at −2.2 < E_we < −1.6 V corresponding to the mass transport of ccMA²⁻.

We further investigated the involved reaction mechanism(s) by analyzing the polarization curves relative to the reversible hydrogen electrode (RHE) and standard hydrogen electrode (SHE). Fig. 3a shows a perfect overlap under the RHE scale for the first onset potential in the LSVs collected at pH 1–3. This overlap reveals that the shift observed in Fig. 2b follows the Nernst equation and corresponds to a change of 59 mV per pH unit.⁴³ It also supports a PCET process involving an equal number of protons and electrons as:

E(RHE) = E(Ag/AgCl) + 0.197 + 0.059 × (m/n) × pH (1)

with m/n corresponding to the number of protons (m) divided by the number of electrons (n) transferred.⁴³ In contrast, the second onset potential at −1.55 V was found to overlap under the SHE scale for pH 5–7 (Fig. 3b). This overlap indicates kinetics independent of pH and suggests that electron transfer is the rate-limiting step.

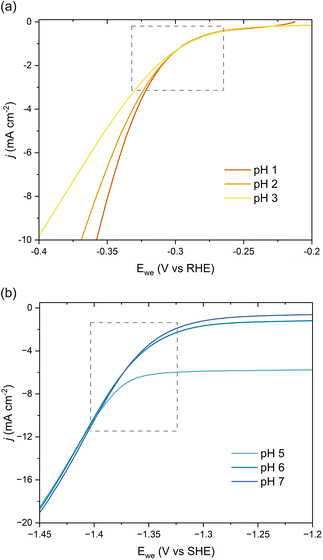Fig. 3 pH-Dependent current–potential polarization curves on Pb RDE for 0.5 g L⁻¹ccMA relative to (a) RHE and (b) SHE scales.

Overall, these experiments show that the transition from strong (COOH) to weaker (COO⁻) electron-withdrawing groups causes a nearly 1 V shift to stronger (more negative) reduction potentials with increasing pH. Admittedly, the deprotonation of ccMA also makes it more difficult for the substrate to approach the cathode due to the electrostatic repulsion between the negatively charged electrode and the muconate dianion. In Marcus theory, this additional work impacts the activation energy of the reaction. To address this point, we extended the dataset to other unsaturated diacids and their methyl esters.

Proton-coupled electron transfer hydrogenation of fumaric acid, maleic acid, and their esters

Since unsaturated C5 diacids are rarely available from biomass but C4 diacids (maleic and fumaric acids) were identified as bio-derived platform intermediates for the synthesis of commodity and specialty chemicals like succinic acid,²⁵ we selected them to extend our dataset (Fig. 4). The polarization curves recorded for maleic acid (Fig. 4a) and fumaric acid (Fig. 4b) were consistent with the results obtained for ccMA. At pH 1, the LSVs were dominated by the hydrogenation of the diacids (−0.58 V for both maleic and fumaric acids) and HER through proton reduction (−1.43 V and −1.52 V, respectively). At pH 6–7, the hydrogenation of the maleate and fumarate dianions were observed at −2.08 V and −1.72 V, respectively, while HER through water reduction took place at −2.40 V. Interestingly, LSVs recorded at pH 3 and 4 for maleic acid showed an additional onset potential at −0.88 V (Fig. 4a). We assigned it to the hydrogenation of the monoprotic acid and explain the absence of the corresponding onset potential for fumaric acid by the difference in pK_a values for the two compounds. The two carboxylic groups in fumaric acid have similar acidity with pK_a1 = 3.03 and pK_a2 = 4.57, similar to ccMA. In contrast, intramolecular hydrogen bonding in maleic acid delays the second deprotonation event and, as a result, pK_a1 = 1.9 and pK_a2 = 6.07. The difference between pK_a1 and pK_a2 has a profound impact on the species in solution, as can be inferred from the speciation diagrams in Fig. S1.† Monoprotic maleic acid (acid monoanion) is the dominant species in electrolytes at 3 < pH < 5 and the only species in solution at pH 4, making it possible to capture its independent reduction potential in LSVs. The significant concentration of the monoanion at pH 6 (Fig. S1b†) also explains why maleic acid is the only compound presenting a diffusional plateau between ca. −1.2 V and −2.0 V at this pH.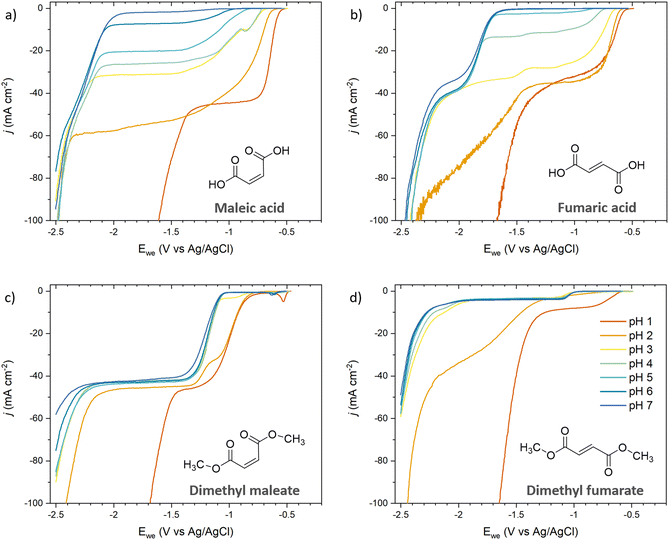

Fig. 4 pH-Dependent current–potential polarization curves on Pb RDE for (a) maleic acid, (b) fumaric acid, (c) dimethyl maleate, and (d) dimethyl fumarate. The same colors were used for all figures for clarity and the legend is shown in Fig. 4d.

Maleate and fumarate methyl esters were studied in order to further understand the role of pH when protonation and deprotonation of the carboxylic groups can be excluded (Fig. 4c and d). For both esters, the current–potential curves shifted by −0.25 V and −0.40 V for the maleate and fumarate methyl esters, respectively, when increasing pH from 1 to 7. The shift in overpotential was swift and occurred around pH 2–3, which is consistent with a transition from H₃O⁺ to H₂O as a hydrogen source for ECH. Surprisingly, the curves did not show the expected Nernstian shift of 0.059 mV per pH that was observed for the diacids at low pH. The most likely explanation is that the reaction is kinetically controlled by the charge transfer rather than by proton transfer for the esters. This interpretation is consistent with the higher overpotential measured at pH 1 for the maleate and fumarate esters (−0.87 V and −0.60 V, respectively) compared to the diacids (−0.58 V), and esters being weaker electron-withdrawing groups than carboxylic acids.

To this point, it can be concluded that the concentration of hydronium ions and the transition from H₃O⁺ to H₂O as a source of hydrogen play a relatively modest role on the ECH of unsaturated diacids, with a shift in overpotential on the order of −0.25 V when increasing the pH from 1 to 7. In contrast, the deprotonation of terminal carboxylic groups had a more pronounced effect evidenced by a −1.0 V shift to higher overpotentials. These experimental values are consistent with the computed change in hydrogenation energetics when increasing pH (Fig. 1). Considering the same intermediates along the energetically favored pathway from ccMA to adipic acid at pH 1, the free energies for ccMA initial hydrogenation shifted by 0.18 eV from pH 1 to 3, and by 0.92 eV from pH 1 to 7. Experimentally, the onset potentials for ECH were also found to follow the trend COOH > COOR ≫ COO⁻, which is in line with the electron-withdrawing capacity of these terminal groups (COOH > COOR ≫ COO⁻). Overall, they increased the electrophilicity of carbon atoms in α positions and thereby played a critical role in the kinetics of the ECH reaction. In the case of ccMA, these effects may also kinetically control the selectivity to t3HDA by facilitating the 2,5- over the 2,3-hydrogenation pathway.

Proton-coupled electron transfer hydrogenation of sorbic acid and crotonic acid

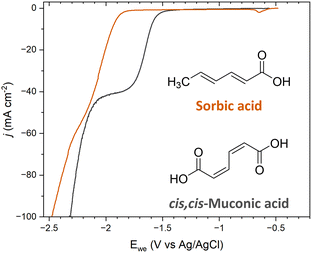
The ECH of sorbic acid (SA) was investigated to further probe the role of terminal carboxyl groups on selectivity. SA is a C6 diunsaturated carboxylic acid with a molecular structure that resembles ccMA, with the exception that SA has only one terminal carboxylic acid; a methyl functionality (–CH₃) replaces the second –COOH. This molecule was specifically chosen because the methyl moiety is an electron-donating group, i.e., a group with opposite electronic inductive effects compared to COOH. Therefore, we expected substantial changes in reactivity for both sides of the molecules, and obvious differences in selectivity for the ECH of SA compared to ccMA during bulk electrolysis.

Polarization curves were recorded at pH 7 for both ccMA and SA to avoid any contributions from [H₃O⁺] and/or differences in the protonation state of the molecules. As can be seen in Fig. 5, a 0.35 mV shift to higher overpotentials was observed for SA compared to ccMA, which is consistent with a lower electrophilicity for the carbon atom next to the methyl group and deactivation of the γ,δ-double bond. Similar results were obtained when comparing the polarization curves of SA (trans,trans-2,4-hexadienoic acid) and of trans,trans-muconic acid (Fig. S2†).

Fig. 5 Current–potential polarization curves on Pb RDE for 5 g L⁻¹ solutions of sorbic acid and cis,cis-muconic acid at pH 7. The onset potential for the hydrogenation reaction shifted by 0.35 mV, from −1.55 V for cis,cis-muconic acid to −1.90 V for sorbic acid.

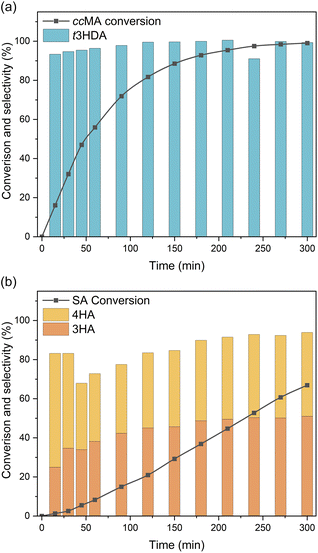
Bulk electrolysis was carried out to investigate the role of terminal groups on ECH selectivity. As ccMA and SA present very different onset potentials, we carried out these experiments under kinetic control by applying a constant current density of 100 mA cm⁻². Unsurprisingly, the bulk electrolysis of ccMA produced t3HDA with 100% selectivity (Fig. 6a). In contrast, the bulk electrolysis of SA gave two distinct isomers (Fig. 6b), 3-hexenoic acid (3HA) and 4-hexenoic acid (4HA). The selectivity of the reaction and absence of any other products such as 2-hexenoic acid (2HA) and hexanoic acid was confirmed by ¹H NMR and HSQC NMR (Fig. S3 and S4†).

Fig. 6 Conversion and selectivity achieved for the bulk electrolysis of (a) cis,cis-muconic acid (ccMA), and (b) sorbic acid (SA) in a divided flow reactor operated at a constant current of 100 mA cm⁻². ccMA only produced trans-3-hexenedioic acid (t3HDA) while SA produced 3-hexenoic acid (3HA) and 4-hexenoic acid (4HA).

Both hexenoic products formed with a 3HA : 4HA ratio of approximately 1 : 1 during most of the experiment, which indicates the coexistence of parallel PCET reaction pathways and the absence of any isomerization between 3HA and 4HA. Interestingly, the reaction proceeded through 2,5- and 2,3-addition of hydrogen to form 3HA and 4HA, respectively, but there was no sign of 4,5-addition that would yield 2-hexenoic acid (2HA). This observation suggests that the first H⁺|e⁻ pair was likely added to C2 (in α of COOH) due to the electron-withdrawing effect of the carboxylic acid. In the absence of a second terminal COOH, like in ccMA, there is no preferred position for the addition of the second H⁺|e⁻ pair and, therefore, 2,3- and 2,5-additions proceed simultaneously. The observed selectivity also suggests that electron-donating groups like –CH₃ may completely suppress the reactivity of neighbouring C=C. This contrasts with the reactivity of carbonyl-containing compounds where isolated C=O were proven to react even if isolated, e.g., in glucose or levulinic acid.⁴⁴

To further assess the role of the terminal –CH₃ group on reactivity, we studied the hydrogenation of crotonic acid, a C4 unsaturated acid with a molecular structure similar to maleic and fumaric acids. Crotonic acid was specifically chosen because the molecule presents a single C=C bond advantageously positioned between terminal –COOH and –CH₃ groups. As anticipated, ¹H NMR revealed no conversion even after 2 hours of bulk electrolysis at high current density (200 mA cm⁻²), see Fig. S5.† These results confirm the role of –CH₃ in compensating the electron-withdrawing effect of COOH observed for the C4 diacids (maleic and fumaric acid), suppressing all electroactivity for this conjugated monoacid.

Local reactivity descriptors to computationally predict selectivity for the proton-coupled electron transfer hydrogenation of conjugated acids and diacids

Our initial calculations showed that reaction free energies were insufficient to explain the observed selectivity in the ECH of ccMA (vide supra). Analogous calculations for the ECH of sorbic acid (Fig. S6†) were also unable to capture the selectivity to the observed products, as the calculations suggested the most favorable formation of 2HA rather than the experimentally-observed 3HA and 4HA mixture. These results clearly indicate the insufficiency of free energies as a selectivity descriptor.

Our experimental results revealed that liquid-phase PCET hydrogenation reactions are primarily controlled by charge transfer in the case of unsaturated (di)acids, i.e., by a molecule's ability to accept electrons during sequential electron and proton transfers. Therefore, we expected that the onset potential for ECH should be correlated with the energy of the molecule's LUMO based on Koopman's theorem, as reported in a similar fashion for other electrochemical reactions.^36–38 Building on this concept, we computed the LUMO energies for ccMA, SA, and their respective ECH reaction intermediates.

The LUMO energy of ccMA was computed to be 0.825 eV (Fig. S7†). The LUMO energies of the subsequent hydrogenation intermediates and products are all similar, ranging from 1.267 eV to 1.312 eV. Interestingly, the α-hydrogenated intermediate, through which t3HDA can form, has a slightly lower LUMO energy (1.287 eV) than the alternative β-hydrogenated radical (1.294 eV) that only yields c2HDA. The LUMO energy of t3HDA is also lower than that of c2HDA (1.267 eV vs. 1.312 eV).

The calculated LUMO energy of SA was 1.260 eV (Fig. S8†); this higher value than ccMA correlates with the more negative onset potential for the ECH of SA compared to ccMA. The singly-hydrogenated intermediates capable of forming the experimentally-observed products have again lower LUMO energies (1.264 eV and 1.278 eV) than the other intermediates (1.288 eV and 1.296 eV). Moreover, 3HA and 4HA have lower LUMO energies than the 2HA product that is not observed experimentally (1.278 eV and 1.274 eV vs. 1.309 eV, respectively).

The LUMO energies qualitatively agree with the selectivity observed for the bulk electrolysis of ccMA and SA (Fig. 6); however, this analysis has limited quantitative insight and does not provide the atomic-level detail required to understand the effects of electron-withdrawing groups (i.e., –COOH vs. –CH₃) on molecular reactivity. As the hydrogenation of C=C involves primarily the 2p orbitals of the corresponding carbon atoms, we also compared the LUMO 2p_z eigenvalues of the reactants and various reaction intermediates (Fig. S9†). Baran and coworkers recently used these LUMO coefficients to rationalize the exceptional selectivity observed for the reduction of carbonyl groups in molecules with multiple redox centers using rapid alternating polarity (rAP).⁴⁵ In this case, we do not find strong correlations between the 2p_z eigenvalues and the experimentally-observed products (Fig. S9†). For ccMA, the initial elementary hydrogenation at the α position, which can lead to the formation of t3HDA, would occur at a site with a LUMO coefficient of 0.12 (in contrast to −0.11 at the β position). However, the subsequent hydrogenation would have to occur at a site with LUMO coefficient of −0.01 to yield t3HDA, instead of at a site with a coefficient of 0.15. Similar issues are observed for the LUMO coefficients in the SA reaction network: the β-carbon has the highest coefficient (0.15), though addition at that position would preclude formation of the experimentally-observed 3HA. The LUMO coefficients therefore fail to explain the product distributions obtained experimentally.

We speculate that the discrepancy with prior works (e.g., Baran) comes from the sequence of events involved in the hydrogenation of unsaturated acids. Specifically, our experiments showed a much stronger impact of pH on inductive effects (1.0 V shift to higher overpotentials when transitioning from COOH to COO⁻) than on hydrogen source (0.25 to 0.40 V shift when transitioning from H₃O⁺ to H₂O as a hydrogen source). This suggests that the ability of a carbon atom to accept an electron, hence its electrophilicity, and the molecule's ability to form a “stable” intermediate may be better captured using Fukui functions.

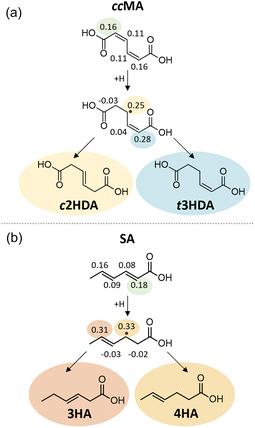
The Fukui function describes changes in the electronic charge density of a molecule due to addition or removal of an electron from the system; a higher value of the Fukui function indicates a more reactive site within the molecule. Our Fukui function analysis indicated that the hydrogenation of ccMA at one of the α carbons (Fukui index 0.16) is more favorable than at the β position (0.11), allowing formation of the intermediate leading to t3HDA due to the electron-withdrawing nature of the –COOH functionality (Fig. 7a). The Fukui index for the subsequent hydrogenation at the δ position (0.28) is more positive than that for the β position (0.25); while the two sites are linked by a resonance structure, the electron-withdrawing nature of the –COOH group near the δ position again improves the electrophilicity of that site, rationalizing the formation of t3HDA observed experimentally instead of c2HDA. The Fukui function analysis also explains the formation of 3HA and 4HA from SA (Fig. 7b). The Fukui-preferred addition at the α position (0.18, favored due to the proximity to –COOH over 0.16 at the δ position near –CH₃) yields an intermediate capable of forming only 3HA or 4HA (not 2HA), the only products observed experimentally. That intermediate formed by α hydrogenation shows a slight preference for formation of 4HA based on the Fukui indices of the respective carbon atoms (0.33 vs. 0.31), once again driven by the electrophilicity of the site nearest the –COOH functionality. Overall, the atomic-scale detail offered by the Fukui function demonstrated the strongest connections to the observed experimental product distributions, providing atomic-level insights into the effects of molecular geometry and inductive effects on the reactivity of conjugated (di)acids.

Fig. 7 Fukui function values of (a) cis,cis-muconic acid (ccMA) and (b) sorbic acid (SA). Included are the intermediates formed by hydrogenation at the Fukui-predicted most favorable sites of ccMA and SA (green) and the products formed by hydrogenating at the Fukui-predicted favorable sites of those intermediates.

Conclusion

Electrosynthesis is poised to play a vital role in the technological revolution that will decarbonize the chemical industry and implement green chemistry principles in chemical manufacturing. ECH reactions are of particular importance as they embrace water as a source of green hydrogen to substitute grey H₂ produced through methane steam reforming, an energy-intensive and CO₂-emitting process. However, the broad implementation of this technology requires descriptors and computational tools to predict reaction pathways and selectivity.

The polarization curves recorded for unsaturated C4 and C6 (di)acids and esters, and the selectivity observed during bulk electrolysis revealed that the source of hydrogen (H₃O⁺ or H₂O) has a limited impact on the overpotential of the ECH reaction (∼0.25 V vs. Ag/AgCl) and no effect on its selectivity. In contrast, the deprotonation of terminal groups with increasing pH increased the overpotential by about 1.0 V due to carboxylates (COO⁻) being weaker electron withdrawing groups than carboxylic acids (COOH). Substituting a terminal –COOH by –CH₃, an electron-donating group, in sorbic acid further shifted the onset potential and promoted the formation of both 3-hexenoic acid and 4-hexenoic acid, i.e., the 2,5- and 2,3-addition products, while only 2,5-hydrogenation was observed for ccMA. Lowering the distance between –CH₃ and C=C in crotonic acid completely suppressed ECH.

Computed free energies fail to predict the preferred reaction pathways and selectivity for these transformations, likely due to the inductive effects of terminal carboxylic acids on charge transfer during the addition of H⁺|e⁻ pairs. To account for these effects, we computed LUMO energies and LUMO 2p_z eigenvalues, but found they provided at best qualitative information on molecular reactivity. Computations ultimately demonstrated the utility of Fukui indices in describing the selectivity of ECH for both ccMA and SA, providing accurate local descriptors for predicting liquid-phase PCET transformations.

These advancements will benefit ECH beyond the molecules studied in the present work. In particular, Fukui indices provide a fast and reliable approach to predict reactivity and selectivity based on electronic structure calculations of only the reactant molecule. Moreover, the same approach can be applied to discriminate liquid-phase PCET hydrogenation and surface-mediated hydrogenation pathways that may coexist in electrocatalytic systems. Last, the local descriptors identified through this work are not unique to PCET processes; they are applicable to other electro-organic redox transformations governed by electron transfer.

Experimental

Chemicals

cis,cis-Muconic acid (98%, Acros Organics), trans,trans muconic acid (98%, Sigma-Aldrich), maleic acid (98%, Sigma-Aldrich), fumaric acid (98%, Sigma-Aldrich), dimethyl maleate (98%, Sigma-Aldrich), dimethyl fumarate (98%, Sigma-Aldrich), trans-3-hexenedioic acid (98%, Tokyo Chemical Industries), sorbic acid (98%, Sigma-Aldrich), crotonic acid (98%, Sigma-Aldrich), deuterium oxide (99.9% D, Sigma-Aldrich), dimethylmalonic acid (TraceCERT® grade for qNMR, Sigma-Aldrich), sulfuric acid (99.9%, Fisher Scientific), and potassium sulfate (>99%, Sigma-Aldrich) were used as-received. Ultrapure water with a resistivity of 18.2 MΩ cm at 20 °C (Barnstead™ E-Pure™) was used for all experiments.

Electrochemical measurements

Linear sweep voltammetry (LSV) was performed in a conventional 100 mL three-electrode cell using a BioLogic VSP-300 potentiostat (BioLogic, France). The cell was equipped with a 5 mm lead (Pb) rotating disk working electrode, Ag/AgCl reference electrode, and a platinum wire counter electrode (Pine Research Instrumentation, Durham, NC). Fresh solution was prepared before each measurement by dissolving the desired amount of organic reagent in 100 ml of either 0.1 M H₂SO₄ for experiments at pH 1 or 0.1 M K₂SO₄ for experiments at pH 7. Upon dissolution, the pH was corrected to the desired value with a few drops of 1 M H₂SO₄ or 1 M KOH. This method was slightly modified for ccMA solutions at low pH as this diacid is prone to isomerization to ctMA and intramolecular cyclization to form the corresponding muconolactone under acidic conditions. To prevent these undesired reactions, ccMA was dissolved in DI water and, upon complete dissolution, concentrated H₂SO₄ was added to achieve a final electrolyte concentration of 0.1 M. Each solution was purged with ultrapure Argon (grade 5.0) for 15 minutes prior to LSV and a blanket of flowing Argon was maintained for the duration of the experiment. Potentiostatic electrochemical impedance spectroscopy (PEIS) was first conducted to determine the uncompensated resistance of the solution (R_s), and 90% iR-compensation was applied for all measurements. The potential was then scanned from the open circuit potential (OCP) to −2.5 V vs. Ag/AgCl at 50 mV s⁻¹. The rotation speed of the working electrode was maintained at 1600 rpm using a Pine Research Instrumentation MSR rotator.

Bulk electrolysis was carried out using a two-compartment Micro Flow Cell® reactor purchased from ElectroCell (Amherst, NY). The reactor was equipped with a Pb plate working electrode, platinized titania counter electrode, and the two compartments were separated by a Nafion membrane. Each electrode had an exposed surface area of 10 cm². The reactions were performed galvanostatically at a current density of j = −100 mA cm⁻² using 100 ml of solution that was looped through the reactor at 180 ml min⁻¹ using a Fisherbrand™ GP1000 pump (ThermoFisher). These experiments were conducted at pH 7 as the solubility of organic acids is drastically reduced at low pH. Aliquots of 600 μL were withdrawn every 15 minutes for the first hour, then every 30 minutes for an additional 4 hours.

Product analysis

Product identification and quantification was carried out by ¹H NMR using a Bruker AV III 600 MHz spectrometer. Each sample was dried under air and the remaining solid was redissolved in a deuterium oxide solution containing 1 g L⁻¹ of dimethylmalonic acid as an internal standard. The weights of the dried and reconstituted samples were recorded. The corresponding weight fractions and integration of the proton peaks were combined to calculate conversion and selectivity. A more detailed explanation of the quantitative NMR (qNMR) method is available online.⁴⁶¹³C–¹H HSQC NMR spectra were recorded to confirm the structure of the reaction products.

Theoretical calculations

All quantum chemical calculations were performed using the GAUSSIAN 09 software package.⁴⁷ Molecular visualizations were performed using the Avogadro software.⁴⁸ The molecular structures were optimized using “very tight” convergence criteria in solution (water) using the SCRF (self-consistent reaction field) and the solvation model density (SMD).^49,50 Geometry optimizations, free energies, and LUMO energies were calculated using the highly accurate CBE-QB3 composite method.⁵¹ As the CBS-QB3 method is a composite method that includes geometry optimization, LUMO coefficients and Fukui functions were evaluated through single point calculations using the B3LYP functional^52,53 and the 6-311++G(d,p) basis set.^54,55

The computational hydrogen electrode (CHE) theory proposed by Nørskov and coworkers was utilized in this work to account for the effects of applied potential.⁵⁶ Through this method, the reversible hydrogen electrode (RHE) was taken as a computational reference, with hydrogen gas in equilibrium with protons and electrons at a potential of 0.0 V_RHE. Since the proton source at low pH (H₃O⁺) costs no energy for the hydrogenation using CHE, the potential-dependent change in free energy for an elementary hydrogenation step (A + 0.5H₂ ↔ AH) was therefore calculated as:

ΔG = G_AH − G_A − 0.5G_H2 + |e|U_RHE (2)

where G_AH, G_A and G_H2 are the free energies of AH, A, and gas-phase hydrogen, respectively, e is the electron charge, and U_RHE is the applied cell potential vs. RHE. For neutral media (pH 7), the free energy cost associated with the water dissociation to provide protons was taken into account following a recent procedure by Abild-Pedersen and coworkers.⁵⁷ Following this method, using an assumed symmetry factor β = 0.5, the free energy for hydrogenation steps at pH 7 and −0.48 V vs. Ag/AgCl is corrected by adding 0.30 eV to the CHE-calculated value.

The pH-dependent potential values reported in this work are provided relative to the Ag/AgCl refence electrode according to the following equation:

E_Ag/AgCl = E_RHE − 0.197 V − 0.059 V × pH.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This material is based upon work supported in part by the National Science Foundation under grant number 2132200. The research reported in this paper is also partially supported by the HPC@ISU equipment at Iowa State University, some of which has been purchased through funding provided by the National Science Foundation under MRI grant numbers 1726447 and 2018594. The authors acknowledge Deep M. Patel for fruitful discussions.

References

1. International Energy Agency, Tracking Clean Energy Progress 2023, https://www.iea.org/reports/tracking-clean-energy-progress-2023, Accessed July 19, 2023.
2. I. A. Bashmakov, L. J. Nilsson, A. Acquaye, C. Bataille, J. M. Cullen, S. de la Rue du Can, M. Fischedick, Y. Geng and K. Tanaka, 2022: Industry, in IPCC, 2022: Climate Change 2022: Mitigation of Climate Change. Contribution of Working Group III to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change, ed. P. R. Shukla, J. Skea, R. Slade, A. Al Khourdajie, R. van Diemen, D. McCollum, M. Pathak, S. Some, P. Vyas, R. Fradera, M. Belkacemi, A. Hasija, G. Lisboa, S. Luz and J. Malley, Cambridge University Press, Cambridge, UK and New York, NY, USA, 2022.
3. H. Liu, T.-H. Lee, Y. Chen, E. W. Cochran and W. Li, Green Chem., 2021, 23, 5056–5063.
4. H. Liu and W. Li, Curr. Opin. Electrochem., 2021, 30, 100795.
5. S. Verma, S. Lu and P. J. A. Kenis, Nat. Energy, 2019, 4, 466–474.
6. Z. J. Schiffer and K. Manthiram, Joule, 2017, 1, 10–14.
7. R. Xia, S. Overa and F. Jiao, JACS Au, 2022, 2, 1054–1070.
8. D. S. Mallapragada, Y. Dvorkin, M. A. Modestino, D. V. Esposito, W. A. Smith, B.-M. Hodge, M. P. Harold, V. M. Donnelly, A. Nuz, C. Bloomquist, K. Baker, L. C. Grabow, Y. Yan, N. N. Rajput, R. L. Hartman, E. J. Biddinger, E. S. Aydil and A. D. Taylor, Joule, 2023, 7, 23–41.
9. W. R. Leow, Y. Lum, A. Ozden, Y. Wang, D.-H. Nam, B. Chen, J. Wicks, T.-T. Zhuang, F. Li, D. Sinton and E. H. Sargent, Science, 2020, 368, 1228–1233.
10. Y. Li, A. Ozden, W. R. Leow, P. Ou, J. E. Huang, Y. Wang, K. Bertens, Y. Xu, Y. Liu, C. Roy, H. Jiang, D. Sinton, C. Li and E. H. Sargent, Nat. Catal., 2022, 5, 185–192.
11. M. Chung, K. Jin, J. S. Zeng and K. Manthiram, ACS Catal., 2020, 10, 14015–14023.
12. H. Shin, K. U. Hansen and F. Jiao, Nat. Sustain., 2021, 4, 911–919.
13. T. Li, H. Liu, J. Yu, Y. Chen, W. Huang and W. Li, Green Chem., 2023, 25, 1982–1990.
14. S. Jung and E. J. Biddinger, Energy Technol., 2018, 6, 1370–1379.
15. F. J. Holzhäuser, J. Artz, S. Palkovits, D. Kreyenschulte, J. Büchs and R. Palkovits, Green Chem., 2017, 19, 2390–2397.
16. S. A. Akhade, N. Singh, O. Y. Gutiérrez, J. Lopez-Ruiz, H. Wang, J. D. Holladay, Y. Liu, A. Karkamkar, R. S. Weber, A. B. Padmaperuma, M.-S. Lee, G. A. Whyatt, M. Elliott, J. E. Holladay, J. L. Male, J. A. Lercher, R. Rousseau and V.-A. Glezakou, Chem. Rev., 2020, 120, 11370–11419.
17. B. Hoff, J. Plassmeier, M. Blankschien, A.-C. Letzel, L. Kourtz, H. Schröder, W. Koch and O. Zelder, Angew. Chem., Int. Ed., 2021, 60, 2258–2278.
18. F. W. S. Lucas, R. G. Grim, S. A. Tacey, C. A. Downes, J. Hasse, A. M. Roman, C. A. Farberow, J. A. Schaidle and A. Holewinski, ACS Energy Lett., 2021, 6, 1205–1270.
19. H. Liu, D. M. Patel, Y. Chen, J. Lee, T.-H. Lee, S. D. Cady, E. W. Cochran, L. T. Roling and W. Li, ACS Catal., 2022, 12, 14072–14085.
20. A. S. May and E. J. Biddinger, ACS Catal., 2020, 10, 3212–3221.
21. I. Khalil, G. Quintens, T. Junkers and M. Dusselier, Green Chem., 2020, 22, 1517–1541.
22. G. C. Hayes and C. R. Becer, Polym. Chem., 2020, 11, 4068–4077.
23. S. Abdolmohammadi, D. Gansebom, S. Goyal, T.-H. Lee, B. Kuehl, M. J. Forrester, F.-Y. Lin, N. Hernández, B. H. Shanks, J.-P. Tessonnier and E. W. Cochran, Macromolecules, 2021, 54, 7910–7924.
24. P. Carter, J. L. Trettin, T.-H. Lee, N. L. Chalgren, M. J. Forrester, B. H. Shanks, J.-P. Tessonnier and E. W. Cochran, J. Am. Chem. Soc., 2022, 144, 9548–9553.
25. I. Bechthold, K. Bretz, S. Kabasci, R. Kopitzky and A. Springer, Chem. Eng. Technol., 2008, 31, 647–654.
26. Y. Kwon, K. J. P. Schouten, J. C. van der Waal, E. de Jong and M. T. M. Koper, ACS Catal., 2016, 6, 6704–6717.
27. M. N. Dell'Anna, M. Laureano, H. Bateni, J. E. Matthiesen, L. Zaza, M. P. Zembrzuski, T. J. Paskach and J.-P. Tessonnier, Green Chem., 2021, 23, 6456–6468.
28. Z. Zhang, J. E. Jackson and D. J. Miller, Bioresour. Technol., 2008, 99, 5873–5880.
29. T. J. Schwartz, R. L. Johnson, J. Cardenas, A. Okerlund, N. A. Da Silva, K. Schmidt-Rohr and J. A. Dumesic, Angew. Chem., Int. Ed., 2014, 53, 12718–12722.
30. T. J. Schwartz, Z. J. Brentzel and J. A. Dumesic, Catal. Lett., 2015, 145, 15–22.
31. M. Suástegui, J. E. Matthiesen, J. M. Carraher, N. Hernandez, N. Rodriguez Quiroz, A. Okerlund, E. W. Cochran, Z. Shao and J.-P. Tessonnier, Angew. Chem., Int. Ed., 2016, 55, 2368–2373.
32. J. E. Matthiesen, M. Suástegui, Y. Wu, M. Viswanathan, Y. Qu, M. Cao, N. Rodriguez Quiroz, A. Okerlund, G. Kraus, D. R. Raman, Z. Shao and J.-P. Tessonnier, ACS Sustainable Chem. Eng., 2016, 4, 7098–7109.
33. J. E. Matthiesen, J. M. Carraher, M. Vasiliu, D. A. Dixon and J.-P. Tessonnier, ACS Sustainable Chem. Eng., 2016, 4, 3575–3585.
34. J. Rios, J. Lebeau, T. Yang, S. Li and M. D. Lynch, Green Chem., 2021, 23, 3172–3190.
35. S. Abdolmohammadi, N. Hernández, J.-P. Tessonnier and E. W. Cochran, Bioadvantaged Nylon from Renewable Muconic Acid: Synthesis, Characterization, and Properties, in Green Polymer Chemistry: New Products, Processes, and Applications, American Chemical Society, Washington, DC, 2018, vol. 1310, ch. 22, pp. 355–367.
36. E. J. Lynch, A. L. Speelman, B. A. Curry, C. S. Murillo and J. G. Gillmore, J. Org. Chem., 2012, 77, 6423–6430.
37. J. C. Ortiz-Rodríguez, J. A. Santana and D. D. Méndez-Hernández, J. Mol. Model., 2020, 26, 70.
38. R. Fedorov and G. Gryn’ova, J. Chem. Theory Comput., 2023, 19, 4796–4814.
39. P. S. Lamoureux, A. R. Singh and K. Chan, ACS Catal., 2019, 9, 6194–6201.
40. D. Strmcnik, M. Uchimura, C. Wang, R. Subbaraman, N. Danilovic, D. van der Vliet, A. P. Paulikas, V. R. Stamenkovic and N. M. Markovic, Nat. Chem., 2013, 5, 300.
41. O. Jung, M. N. Jackson, R. P. Bisbey, N. E. Kogan and Y. Surendranath, Joule, 2022, 6, 476–493.
42. J. M. Carraher, T. Pfennig, R. G. Rao, B. H. Shanks and J.-P. Tessonnier, Green Chem., 2017, 19, 3042–3050.
43. S. Horvath, L. E. Fernandez, A. M. Appel and S. Hammes-Schiffer, Inorg. Chem., 2013, 52, 3643–3652.
44. L. Xin, Z. Zhang, J. Qi, D. J. Chadderdon, Y. Qiu, K. M. Warsko and W. Li, ChemSusChem, 2013, 6, 674–686.
45. Y. Kawamata, K. Hayashi, E. Carlson, S. Shaji, D. Waldmann, B. J. Simmons, J. T. Edwards, C. W. Zapf, M. Saito and P. S. Baran, J. Am. Chem. Soc., 2021, 143, 16580–16588.
46. Sigma-Aldrich, Quantitative NMR - Technical Details and TraceCERT® Certified Reference Materials, https://www.sigmaaldrich.com/content/dam/sigma-aldrich/docs/Sigma-Aldrich/Brochure/1/qnmr-brochure-rjo.pdf, Accessed July 19, 2023.
47. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision E.01, Gaussian, Inc., Wallingford CT, 2013.
48. M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, J. Cheminf., 2012, 4, 17.
49. A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 4538–4543.
50. A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396.
51. J. A. Montgomery Jr., M. J. Frisch, J. W. Ochterski and G. A. Petersson, J. Chem. Phys., 1999, 110, 2822–2827.
52. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
53. P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627.
54. A. D. McLean and G. S. Chandler, J. Chem. Phys., 1980, 72, 5639–5648.
55. K. Raghavachari and G. W. Trucks, J. Chem. Phys., 1989, 91, 1062–1065.
56. J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jónsson, J. Phys. Chem. B, 2004, 108, 17886–17892.
57. H.-J. Peng, M. T. Tang, J. Halldin Stenlid, X. Liu and F. Abild-Pedersen, Nat. Commun., 2022, 13, 1399.

---

Footnotes

† Electronic supplementary information (ESI) available: Additional electrochemical results, NMR spectra of reactants and products, additional DFT energetics and analyses. See DOI: https://doi.org/10.1039/d3gc02909c

‡ These authors contributed equally to this work.

---