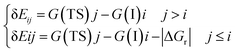Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Photochemical CO2 conversion on pristine and Mg-doped gallium nitride (GaN): a comprehensive DFT study based on a cluster model approach†
Valeria
Butera
 *a and
Hermann
Detz
ab
*a and
Hermann
Detz
ab
aCEITEC – Central European Institute of Technology, Brno University of Technology, Purkyňova 123, Brno 612 00, Czech Republic. E-mail: butera@vutbr.cz
bCenter for Micro- and Nanostructures & Institute of Solid State Electronics, TU Wien, 1040 Vienna, Austria
First published on 6th October 2021
Abstract
The photochemical reduction of carbon dioxide (CO2) into methanol is very appealing since it requires sunlight as the only energy input. However, the development of highly selective and efficient photocatalysts is still very challenging. It has been reported that CO2 can be spontaneously activated on gallium nitride (GaN). Moreover, the photocatalytic activity for CO2 conversion into methanol can be drastically enhanced by incorporating a small amount of Mg dopant. In this work, density functional theory (DFT) based on a cluster model approach has been applied to further explore the photocatalytic activity of bare GaN towards CO2 adsorption and conversion. We extended the investigation of Mg-doping replacing one Ga atom with Mg on three different sites and evaluated the consequent effects on the band gaps and CO2 adsorption energies. Finally, we explore different routes leading to the production of methanol and evaluate the catalytic activity of bare GaN by applying the energetic span model (ESM) in order to identify the rate-determining states which are fundamental for suggesting modifications that can improve the photocatalytic activity of this promising material.
Introduction
The chemical transformation of carbon dioxide (CO2) into chemicals and fuel has been receiving growing attention since it can potentially mitigate the negative environmental impact of increasing greenhouse gas emissions in the atmosphere and furnish a new renewable carbon source.1–7 In previous studies, we focused on homogeneous catalytic CO2 conversion to cyclic carbonates8,9 and methanol10 using sustainable alkali halide–glycol complexes and Ru-complexes, respectively. Recently, our focus has been on photochemical CO2 reduction since it requires sunlight as the only energy input. Significant attention has been paid to this subject in recent years, and substantial advances in the hydrogenation of CO2 to hydrocarbons and oxygenates have been achieved. Among these products, methanol is one of the most desired since it can be used as a liquid fuel-like renewable energy source and a chemical feedstock for other useful chemicals. Due to the high thermodynamic stability of the CO2 molecule, the first step of its reduction involves the adsorption and its consequent activation on the photocatalyst surface. Various semiconductor photocatalysts, including oxides, oxynitrides, sulfides, and phosphides, have been investigated over the last few decades.11–18 It has been observed that the presence of oxygen vacancies in metal oxide surfaces dominates the CO2 adsorption.19,20 However, this adsorption is hindered by the adsorption of O2, which occupies the vacancies leading to an inactive surface. Moreover, metal oxide semiconductors generally exhibit a large band gap, which limits the absorption of the visible and infrared solar spectrum. Therefore, it is of both fundamental and practical interest to explore alternative photocatalysts that can harvest a large part of the solar spectrum and can lead to spontaneous activation of the CO2 molecule.In this regard, the thermodynamically stable wurtzite-structure gallium nitride (GaN) has been proposed as a promising material for the reduction of highly stable CO2 molecules due to its unique electronic and optical properties. GaN has a wide band gap of 3.4 eV which can be tuned to absorb nearly the entire solar spectrum by alloying it with In and Al. Mi and collaborators21 have demonstrated the photochemical reduction of CO2 to CH3OH, CO, and CH4 with sunlight by a joint experimental and computational study based on periodic boundary condition (PBC) calculations. The authors also discovered that, with the incorporation of Mg dopant, the rate of CO2 reduction to CH3OH, CH4, and CO is enhanced nearly 50-fold due to the reduced surface potential barrier and the enhanced adsorption of CO2 molecules on the surface of the nanowire. In a very recent study, Liu and co-workers22 demonstrated that bulk GaN is an efficient catalyst for the selective direct hydrogenation of CO2 to DME, and DME was rigorously revealed as the primary product. The authors have performed DFT calculations using PBC methods in order to investigate the details of the reaction conversion mechanism. According to the authors, the reaction proceeds through the formation of adsorbed H2COH* species which can be hydrogenated to methanol or dissociate to CH2* and OH*. The energy barrier involved in the former process is calculated to be ∼1 eV, which is higher than the latter. Their DFT results well explain why DME rather than methanol is formed as the primary product on GaN surfaces, i.e. the difficult hydrogenation of CH2OH* to CH3OH* and the unfavourable formation of CH3O*. The CO2 photoreduction to hydrocarbons requires the presence of H+ species which can be formed by water oxidation on GaN surfaces or via the dissociation of hydrogen molecules (H2). In this regard, the hydrogen evolution reaction23–26 represents a competing reaction.
Calculations based on a cluster model approach have some advantages over PBC methods, such as the use of hybrid functionals at a lower computational cost, that allows for a highly accurate description of electronic properties; the ability to add/subtract a charge carrier without suffering from interactions with similar charge carriers due to periodic boundary conditions,27,28 which makes cluster approaches suitable for the study of charged systems. Thanks to the reduced size, a cluster approach can be used to intercept all the stationary points, including the more complex transition states, involved in the catalytic cycle and to determine the rate determining states.29–31 On the other hand, a PBC approach allows for the investigation of extended surfaces and provides an accurate description of the structural properties of the surface and molecular adsorbates. The complementarity of the two computational methods can therefore lead to an in-depth understanding of the structure–property relationship.32
In this work, we have used DFT calculations based on a cluster model approach in order to further explore the photocatalytic activity of bare GaN towards CO2 conversion. Based on the findings reported by Mi and collaborators,21 we have extended the investigation of Mg-doping replacing one Ga atom with Mg on three different sites and evaluated the consequent effects on the band gaps and CO2 adsorption energies. This provides a more realistic picture of the stochastic distribution of dopant atoms within the crystal and on its surface. Based on the results published by Liu and co-workers,22 we have explored different routes leading to the production of methanol that could potentially involve lower energy barriers. The catalytic activity of bare GaN has been evaluated by applying the energetic span model (ESM)33,34 in order to identity the rate-determining states and to suggest modifications that can improve the photocatalytic activity of this promising material. Eventually, the influence of Mg-doping at different sites on the catalytic CO2 conversion into methanol has been investigated. As will be discussed in more detail in the next sections, the reliability of the selected cluster models has been confirmed by the good agreement of the geometric parameters, that include calculated bond distances and angles, compared to the ones reported in ref. 21. Moreover, similar trends of the adsorption energies using the two different computational approaches have been computed, which further support the potential use of the selected cluster models to determine adsorption energies as a valid alternative to the more extended surfaces used in PBC calculations. The stability of the pure and Mg-doped GaN clusters has also been evaluated and the details are discussed in the ESI.† Therefore, these models can be used for further investigations allowing a better understanding of the photocatalytic activity of GaN-based materials at a notably reduced computational cost.
Results and discussion
GaN cluster selection and CO2 adsorption
Two different cluster models have been selected in this study: A_GaN built up of three Ga–N moiety rows and 2 layers for a total number of 58 atoms; B_GaN, including four Ga–N moiety rows and three layers (112 atoms). Both the optimized structures are shown in Fig. 1. For the sake of simplicity, throughout the text, all the structures labeled with “A” and “B” will refer to the smaller and bigger size cluster models, respectively, while “GaN” and “Mg” will be used to indicate the pristine and Mg-doped models, respectively. To identify the three different studied doping sites, the superscripts “surf”, “FL” and “bulk” will be adopted to refer to the surface, first layer and bulk, respectively.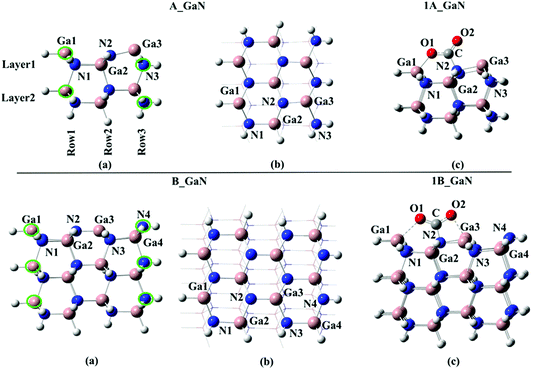 | ||
| Fig. 1 Top: (a) side and (b) top view of the A_GaN cluster model and (c) 1A_GaN intermediate; bottom: (a) side and (b) top view of the B_GaN cluster model and (c) 1B_GaN intermediate. | ||
As the first step of our investigation, we have focused on the adsorption of CO2 on the surface of both the cluster models. The relative adsorption energies, E(CO2)ads, are calculated as:
| E(CO2)ads = Ecluster+CO2 − Ecluster − ECO2 | (1) |
| A_GaN | B_GaN | Ref. 21 | |
|---|---|---|---|
| B3LYP/6-31+G** | B3LYP/6-31+G** | PBC | |
| Ads energy (eV) | −2.11 | −2.05 | −1.76 |
| C–N2 (Å) | 1.475 | 1.418 | 1.41 |
| O1–Ga1 (Å) | 1.918 | 2.323 | 2.24 |
| O2–Ga3 (Å) | 2.793 | 2.081 | 2.10 |
| Ga1–N2–Ga3 (°) | 170.4 | 167.0 | |
| O1–C–O2 (°) | 123.8 | 129.4 | 128.3 |
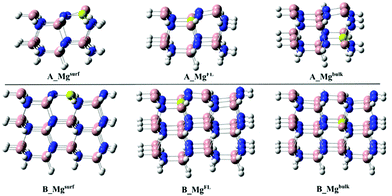
The effect of Mg-doping on the CO2 adsorption energies has been evaluated on both the A_GaN and B_GaN models. Three different doping positions have been considered as shown in Fig. 2, while the corresponding adsorption energies are reported in Table 2. Mi et al.21 computed an adsorption energy of −2.48 eV for CO2 on the Mg-doped GaN surface. The doping site considered by the authors can be compared to our A_Mgsurf and B_Mgsurf systems, whose calculated adsorption energies are 3.23 and 3.12 eV for 1A_Mgsurf and 1B_Mgsurf, respectively. According to those results, our cluster models tend to overestimate the adsorption energies giving more negative values. However, both the methods show a much stronger CO2 adsorption energy in the presence of the Mg dopant which corresponds to 0.7 eV for the PBC calculations in ref. 21, and 1.1 eV for our cluster model calculations.
| 1A_Mgsurf | 1B_Mgsurf | 1A_MgFL | 1B_MgFL | 1A_Mgbulk | 1B_Mgbulk |
|---|---|---|---|---|---|
| 3.23 | 3.12 | 2.95 | 2.54 | 2.65 | 2.29 |
As shown in Table 2, the stronger adsorption of the CO2 molecule in the presence of the Mg dopant is particularly enhanced when Mg replaces a gallium atom of the surface as in A_Mgsurf and B_Mgsurf in Fig. 2.
On the other hand, when Mg occupies a “bulk-like” position (A_Mgbulk and B_Mgbulk in Fig. 2), the calculated adsorption energy is much more similar to the undoped case. For a better understanding of the influence of Mg doping on the adsorption energy, the total adsorption energy, Eads, of CO2 on the B_Mg clusters has been decomposed into two main contributions, i.e., interaction and distortion energies:
| Eads = Eint + Edist | (2) |
The interaction energy, Eint, is given by the difference between the energy of the whole system and that of the single components taken at the final geometry of the adsorbed state, thus accounting for the bare electronic effects occurring at the adsorbate–surface interface:
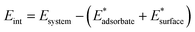 | (3) |
 | (4) |
As seen in Table 3, a positive contribution of about 4 eV, due to the distortion of the bare and Mg-doped GaN as a consequence of the CO2 adsorption, has been calculated. Moreover, the positive deformation energy confirms also that the CO2 molecule is activated upon coordination, changing from a linear structure to a bent one. On the other hand, the very negative terms of the interaction energy indicate a strong interaction between the CO2 molecule and the surface favoring the overall adsorption process. Particularly, following the same trend of the adsorption energy, the interaction energy becomes stronger when the cluster models are doped with Mg, and a more negative interaction energy is calculated when Mg replaces a surface Ga atom as in 1B_Mgsurf, while a more positive value is obtained for the “bulk-like” replacement. Therefore, the replacement of Mg on the surface will lead to a stronger interaction energy and an overall stronger adsorption energy.
| 1B_GaN | 1B_Mgsurf | 1B_MgFL | 1B_Mgbulk | ||||
|---|---|---|---|---|---|---|---|
| E int | E dist | E int | E dist | E int | E dist | E int | E dist |
| −5.94 | 3.89 | −6.95 | 3.83 | −6.63 | 4.10 | −6.22 | 3.93 |
Methanol production: The adsorption energies of one methanol molecule on the selected cluster models have been calculated and the corresponding values are reported in Table 4. Thanks to the agreement between the small and big cluster models on the computed CO2 adsorption energies, only the small clusters have been considered.
| AMeOH_GaN | AMeOH_Mgsurf | AMeOH_MgFL | AMeOH_Mgbulk | |
|---|---|---|---|---|
| E | −1.69 | −1.52 | −1.53 | −1.54 |
| Ga–O | 2.009 | 2.006 | 2.012 | 2.013 |
These values show that the adsorption of the methanol molecule is less strong (more positive) than that of CO2 for the bare and Mg-doped clusters. However, the methanol adsorption energy on A_GaN is slightly higher than the Mg-doped cases. The adsorption mode of the methanol molecule on the GaN is not particularly influenced by the Mg doping. Moreover, very similar adsorption energies have been calculated for the Mg-doping at the three different sites (see Table 4). Our calculations show that the adsorption of CO2 on pristine A_GaN is 0.42 eV stronger than that of methanol (see Tables 1 and 4). This difference increases when the Mg-doped clusters are taken into account and it becomes 1.71, 1.42 and 1.11 eV (see Tables 2 and 4) for A_Mgsurf, A_MgFL and A_Mgbulk, respectively. In other words, replacing one Ga atom with Mg favors the CO2 adsorption (particularly when a surface Ga atom is replaced) but has no influence on the methanol adsorption facilitating its release.
Band gaps and HOMO/LUMO orbitals
For all six Mg-doped and two bare GaN clusters, the band gaps have been calculated as the energy difference between the Lowest Unoccupied Molecular Orbital (LUMO) and Highest Occupied Molecular Orbital (HOMO). The computed band gap of the pristine B_GaN is 3.5 eV which is very similar to the experimental one (3.4 eV). According to our results, reported in Table 5, the presence of Mg lowers the band gap. This effect is much enhanced when Mg replaces a surface Ga as in B_Mgsurf. Even though the smaller A_GaN and A_Mg models dramatically underestimate the band gaps, the obtained trend confirms that calculated with the bigger cluster model.| A_GaN | B_GaN | A_Mgsurf | B_Mgsurf | A_MgFL | B_MgFL | A_Mgbulk | B_Mgbulk |
|---|---|---|---|---|---|---|---|
| 1.24 | 3.52 | 0.59 | 2.49 | 1.13 | 3.29 | 1.15 | 3.27 |
The band gaps can also be derived from the gap between the photoemission (PES) and inverse-photoemission (IPES) energy levels.27,35 It is indeed possible to compute the electron affinity/ionization potential of pristine and Mg-doped GaN by the addition/removal of an electron from the neutral system. This would be analogous to the measurement of the fundamental gap arising from the PES/IPES process, as explained in more detail in the ESI.† By applying this method to the smaller cluster models, A_GaN and A_Mgsurf, we obtain band gap values of 2.86 and 2.27 eV, respectively. Even though these values still underestimate the band gaps, they give more realistic values showing that the smaller clusters can be used for qualitative analysis at a very reduced computational cost.
Fig. 3 shows the HOMO orbitals of the B_GaN and B_Mg clusters. The HOMO orbital of the pristine GaN is localized on the bottom-left part of the cluster. On the other hand, when the surface Ga atom is replaced with Mg, as in B_Mgsurf, the HOMO orbital involves mostly the atoms of the surface layer. A more extended character of the HOMO orbital is calculated in the case of Mg-doping as in B_MgFL and B_Mgbulk. The analysis of the LUMO orbitals, instead, shows a very similar character of the LUMO for all the studied clusters. For this reason, in Fig. 4 only the undoped case is shown.
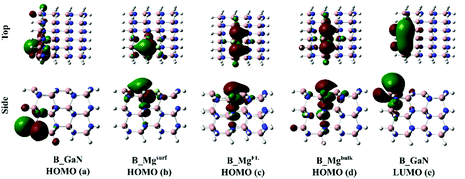 | ||
| Fig. 3 Top and side view of the HOMO orbitals of B_GaN (a), B_Mgsurf (b), B_MgFL (c) and B_Mgbulk (d); top and side view of the LUMO orbital of the pristine B_GaN (e). | ||
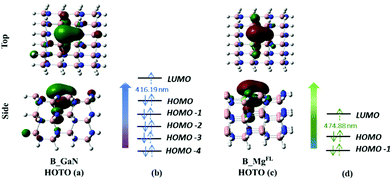 | ||
| Fig. 4 Top and side view of the HOTO of B_GaN (a) and B_MgFL (c) cluster models; canonical orbitals involved in the transition to the first excited state of B_GaN (b) and B_MgFL (d). | ||
Therefore, both the “A” and “B” cluster models have underlined the spontaneous coordination of the CO2 molecule on the pristine and Mg-doped surfaces and its consequent activation is thanks to the formation of a strong C–N single bond. Moreover, both the “A” and “B” clusters confirm that replacing a surface Ga atom with Mg leads to stronger (more negative) adsorption and interaction energies, along with notably reducing the band gap.
Absorption spectra
TD-DFT, which is a popular tool for computing the electronic excitation energies and the properties related to the optical spectra,36–38 has been used to investigate the light absorption of pure and Mg-doped GaN materials determining their vertical electronic absorption energies of optical transitions. The corresponding simulated spectra are shown in the ESI,† while the main excitation energies and the related oscillator strengths are listed in Table 6.| B_GaN | B_Mgsurf | B_MgFL | B_Mgbulk | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| eV | nm | f | eV | nm | f | eV | nm | f | eV | nm | f | |
| ES1 | 2.98 | 416.2 | 0.0143 | 1.86 | 666.3 | 0.0033 | 2.61 | 474.9 | 0.0135 | 2.63 | 471.6 | 0.0237 |
| ES2 | 3.06 | 405.7 | 0.0114 | 2.36 | 525.6 | 0.0446 | 2.67 | 463.5 | 0.0167 | 2.71 | 456.8 | 0.0018 |
| ES3 | 3.08 | 402.1 | 0.0020 | 2.65 | 467.2 | 0.0102 | 2.85 | 434.7 | 0.0118 | 2.88 | 429.7 | 0.0036 |
| ES4 | 3.25 | 381.8 | 0.0038 | 2.68 | 461.8 | 0.0050 | 2.92 | 425.1 | 0.0061 | 2.95 | 420.1 | 0.0115 |
| ES5 | 3.28 | 377.6 | 0.0006 | 2.70 | 458.9 | 0.0217 | 2.95 | 419.9 | 0.0040 | 3.00 | 412.7 | 0.0188 |
We report all excitations falling in the energy interval in terms of wavelengths between ∼700–350 nm (corresponding to ∼1.8–3.5 eV). This energy interval includes the visible spectrum (400–700 nm). The main difference between pristine and Mg-doped clusters is that the inclusion of Mg leads to absorption features at lower energies and this effect is particularly evident for the B_Mgsurf cluster which includes a Mg surface atom: pure GaN shows peaks that are located at about 3 eV, which means ∼400 nm in the visible region of violet light, and some further peaks are present out of the visible window (less than 400 nm); on the other hand, the presence of Mg shifts the absorption up to 666.32 nm, extending the range of the absorption of visible light and, consequently, improving the photocatalytic performance of gallium nitride.
The analysis of the TD-DFT calculations underlines that in the first excited state for both B_Mgsurf and B_Mgbulk the HOMO–LUMO transition dominates with a transition coefficient of about 0.70. In the case of B_MgFL, two transitions are involved: the HOMO−1 → LUMO and HOMO → LUMO, with transition coefficients of 0.6 and 0.4, respectively (see Fig. 4d). Eventually, in the B_GaN cluster, several transitions contribute to the first excited state with very similar coefficients (see Fig. 4b). In these two latter cases, examining the relevant canonical orbitals is not particularly helpful and therefore the analysis of the Natural Frontier Orbitals (NTOs) has been performed and the corresponding Highest Occupied Transition Orbitals (HOTOs) are shown in Fig. 4a and c for B_GaN and B_MgFL, respectively.
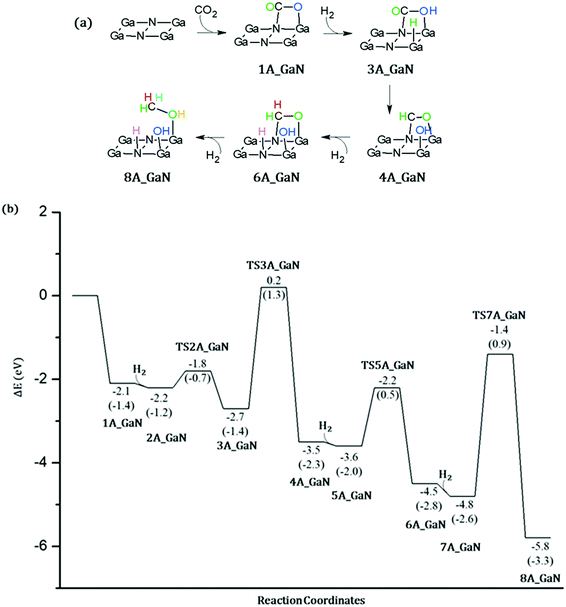
CO2 conversion on A_GaN
As the first step of our investigation of the CO2 conversion into methanol, we have considered the coordination of: (a) a CO2 molecule followed by the coordination of a hydrogen molecule (mechanism 1, Fig. 5) and (b) a hydrogen molecule followed by CO2 (mechanism 2, Fig. 6). For a direct comparison with the adsorption energy given in the previous section, the electronic energies calculated at B3LYP/6-31+G** will be discussed while comparing the reaction mechanisms. However, free energies are also reported in the Potential Energy Surfaces (PESs) and they will be discussed in more detail in the next section where the energetic span model will be applied in order to identify both the rate-determining intermediate, TDI, and the rate-determining transition state, TDTS.![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O double bond. Therefore, these results show that this mechanism does not lead to the formation of acetaldehyde. Eventually the third molecule of hydrogen is added to the system which remains uncoordinated as in 7A_GaN. The last transition state, TS7_GaN, of the proposed mechanism involves the hydrogenation of the coordinated H2CO thanks to the breaking of the H–H bond and the formation of both CH and OH. The calculated imaginary frequency is −1307.49i cm−1 and the involved activation barrier with respect to 7A_GaN is 3.44 eV. Eventually, the 8A_GaN intermediate is formed in which the methanol molecule is coordinated via a Ga–OH bond whose calculated distance is 1.951 Å, while a hydrogen bond is also formed between the hydrogen of the methanol and the oxygen of the adsorbed OH, whose distance is 1.423 Å. This intermediate lies at 4.4 eV below the reaction asymptote.
O double bond. Therefore, these results show that this mechanism does not lead to the formation of acetaldehyde. Eventually the third molecule of hydrogen is added to the system which remains uncoordinated as in 7A_GaN. The last transition state, TS7_GaN, of the proposed mechanism involves the hydrogenation of the coordinated H2CO thanks to the breaking of the H–H bond and the formation of both CH and OH. The calculated imaginary frequency is −1307.49i cm−1 and the involved activation barrier with respect to 7A_GaN is 3.44 eV. Eventually, the 8A_GaN intermediate is formed in which the methanol molecule is coordinated via a Ga–OH bond whose calculated distance is 1.951 Å, while a hydrogen bond is also formed between the hydrogen of the methanol and the oxygen of the adsorbed OH, whose distance is 1.423 Å. This intermediate lies at 4.4 eV below the reaction asymptote.
It is important to note that the stabilization energies of the last intermediates (8A_GaN and 16A_GaN) of the proposed catalytic cycles are much more negative than the ones discussed in the previous section (AMeOH_GaN and AMeOH_Mg). Since the adsorption mode of the methanol molecule is the same, the more negative stabilization energies are due to the presence of more adsorbed species in the former case. Therefore, in order to get a more realistic view, the coverage effect should be investigated on a more extended surface, which will be the focus of our further investigation.
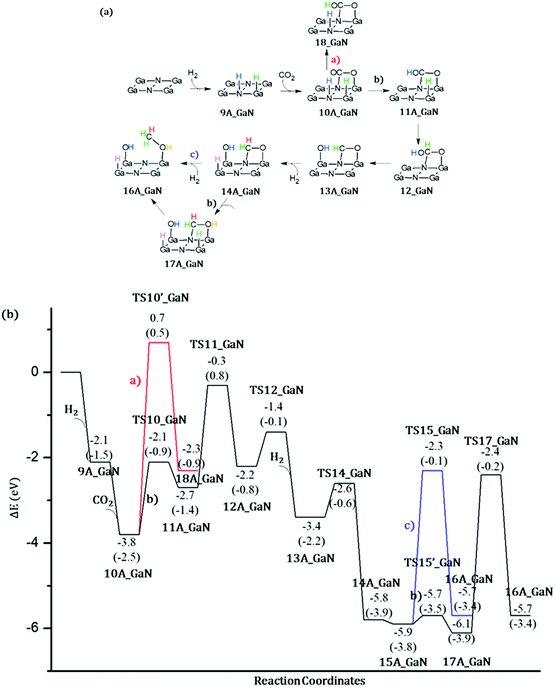
Energetic span model and rate determining states: According to the energetic span model (ESM), the turnover frequency (TOF) can be derived from electronic-structure calculations by identifying the energetic span of the cycle, δE, which is defined as the energy difference between the points of highest and lowest energy along the reaction profile corresponding to the complete catalytic cycle. Kozuch and Shaik33 extended this model including the ΔGr of the reaction and defining δEij as:
Therefore, if the j-th transition state lies after the i-th intermediate, then δEij is just the energy difference between them; if the j-th transition state precedes the i-th intermediate, then δEij is their energy difference minus the ΔGr. The highest δEij corresponds to the energy span of the cycle connecting the TOF-determining intermediate (TDI) and the TOF-determining transition state (TDTS). By applying this method to the potential energy surface of Fig. 5 and considering the free energies given in parentheses, we can identify 6A_GaN as the TDI and TS5A_GaN as the TDTS with a corresponding δE of 3.7 eV. Therefore, the rate determining state involves the last hydrogenation for the production of methanol. The same δE, involving very similar structures of TDI and TDTS, is calculated when the (c) route of the potential energy surface in Fig. 6 is considered. Along the (b) route, the application of the ESM leads to the identification of the rate-determining states, which involve the formation of the third C–H bond and the consequent production of methanol. Therefore, our calculations show that the last step leading to the methanol formation is the most challenging. Interestingly, no difference in terms of energy barrier has been found between the hydrogenation of the adsorbed H2CO species with an approaching inactivated hydrogen molecule, and the transfer of an adsorbed hydrogen atom. This is due to the very strong bonds that the adsorbed species establish with the GaN surface atoms that prevent easy bond breaking/formation. The application of the ESM to the mechanism proposed by Liu and collaborators22 leads to a δE of 3.3 eV. In their investigation, the TDI is the intermediate in which the CO2 molecule is activated on GaN as the bent COO* species while H2 is adsorbed dissociatively on Ga–N Lewis pairs (an intermediate that can be compared to our 10A_GaN). The TDTS of the catalytic cycle proposed by Liu and collaborators22 is the transition state associated to the C–H bond formation via an adsorbed hydrogen transfer to the H2COH* (comparable to TS17_GaN). Therefore, their study also identifies the last step of the methanol production as the rate-determining state. The authors indeed suggest that the dissociation of CH2OH* into CH2* (which is further hydrogenated to CH3*) and OH* is significantly more favorable than the formation of methanol, explaining why their experimental findings show that methanol is not the primary product of the CO2 hydrogenation.
Even though we were not able to identify an alternative mechanism for the methanol production involving lower energy barriers, our investigation furnishes a wider picture of the possible conversion route which contributes to a deeper understanding of the complex reaction mechanism. Moreover, the application of the ESM allows us to identify the rate determining states which is key information for the development of catalysts with improved performances.
Experimental
All the calculations have been performed using a cluster model approach. Two cluster models of 58, A_GaN, and 112, B_GaN, atoms have been carved out from the crystallographic structure of wurzite GaN, cutting along the (100) plane. We retained the cluster's overall zero spin and neutral charge by passivating with capping H atoms only those dangling bonds of our cluster that would have formed covalent bonds to Ga or N atoms in a bulk surface structure. The capping H atoms along with the outermost N and Ga atoms, underlined in green in Fig. 1, have been kept fixed while the rest of the atoms were allowed to relax. These optimizations were performed at the B3LYP39 level of theory as implemented in the Gaussian 16 quantum chemistry package13,40 and using the LANL2DZ14,41 pseudo potential for Ga atoms and the fully electron basis sets 6-31G for N and H. To check the accuracy of the selected computational protocol, preliminary tests were performed using the more accurate double hybrid PBE0DH15,42 functional that combines exact HF exchange with an MP2-like correlation to a DFT calculation. Moreover, the Counterpoise error as implemented in Gaussian 16 software has been evaluated. These results, whose details can be found in the ESI,† have confirmed the reliability of the B3LYP functional, which was therefore selected in our study. Frequency calculations have been done to check the nature of the stationary points (minimum and transition state). In order to obtain more accurate adsorption energy values, single-point calculations using the more extended 6-31+G** basis sets, except for Ga, on the fully optimized geometry, have also been performed and the obtained energies will be discussed throughout the text (unless differently specified). To evaluate the influence of Mg on CO2 adsorption, we replaced the three-coordinated Ga(+3) atom on the surface of the pristine A_GaN and B_GaN cluster models by Mg(+2), leading to the formation of A_Mg and B_Mg clusters, whose net charge is −1.Conclusions
In this work, DFT calculations based on a cluster model approach have been used to explore the photocatalytic activity of bare GaN towards CO2 conversion. Two different cluster models have been selected: A_GaN built up of three Ga–N moiety rows and 2 layers for a total number of 58 atoms and B_GaN, including four Ga–N moiety rows and three layers (112 atoms). We extended the investigation of the Mg-doping effect considering three different doping sites. Our calculations have shown that the CO2 molecule spontaneously coordinates on the pristine and Mg-doped surfaces for both the selected cluster models. This coordination implies the consequent activation of CO2 thanks to the formation of a strong C–N single bond and the change from the CO2 linear structure to a bent one. The activation of the CO2 molecule upon coordination is also confirmed by a similar positive contribution of about 4 eV for all the investigated cases related to its deformation along with the distortion of the bare and Mg-doped GaN clusters as a consequence of the CO2 adsorption. On the other hand, both the clusters confirm that replacing a surface Ga atom with Mg leads to stronger (more negative) adsorption and interaction energies. The most negative interaction energy is calculated when Mg replaces a surface Ga atom as in 1B_Mgsurf, while the more positive values are obtained for the “bulk-like” replacement. Therefore, the replacement of Mg on the surface leads to a stronger interaction energy and an overall stronger adsorption energy.Small pristine A_GaN and Mg-doped A_Mg clusters have been used to calculate the adsorption energies of one molecule of methanol which is the final product of the catalytic cycle. The calculated values have shown that the adsorption of a methanol molecule is less strong (more positive) than that of CO2 with the bare A_GaN showing a stronger MeOH adsorption energy. The adsorption mode of the methanol molecule on GaN is not particularly influenced by the Mg doping and doping sites, as underlined by the very similar calculated adsorption energies. The highest difference between CO2 and the MeOH adsorption energy of 1.71 eV was calculated when the two molecules were adsorbed on the A_Mgsurf cluster. Therefore, our calculations show the important contribution of replacing one surface Ga atom with Mg, which favors the CO2 adsorption and its consequent activation, but has no influence on the methanol adsorption facilitating its release.
Using the bigger cluster models, the band gaps have been calculated as the difference between the HOMO/LUMO orbital energies. The calculated band gap of 3.52 eV obtained for the pure B_GaN cluster is in good agreement with the experimental band gap (3.4 eV). Our calculations show that Mg-doping contributes to decrease the band gaps and this effect is particularly important in the case of B_Mgsurf for which a band gap value of 2.49 eV has been calculated. On the other hand, the small cluster models tend to drastically underestimate the band gaps even though they confirm the trend and, therefore, they could be used for a qualitative analysis.
TD-DFT has been used to calculate the vertical electronic absorption energies at optical wavelengths for the pure and Mg-doped GaN model clusters. The main difference between pristine and Mg-doped clusters is that the inclusion of Mg leads to absorption features at lower energies and this effect is particularly evident for the B_Mgsurf cluster which includes a Mg surface atom: pure GaN shows peaks that are located at about 3 eV, which means ∼400 nm in the visible region of violet light, and some further peaks are present out of the visible window (less than 400 nm); on the other hand, the presence of Mg shifts the absorption up to 666.32 nm extending the range of the absorption of visible light and, consequently, improving the photocatalytic performance of gallium nitride.
Thanks to the agreement of the two size cluster models, the smaller and less computationally demanding A_GaN was selected for the investigation of CO2 conversion into methanol. The catalytic activity of bare GaN was evaluated by applying the energetic span model in order to identify the rate-determining states. Following the proposed mechanism 1, the rate determining state involves the last hydrogenation for the production of methanol with a computed δE of 3.7 eV. The same δE, involving very similar structures of TDI and TDTS, is calculated when the (c) route is considered. Along the (b) route the application of the ESM leads to the identification of the rate-determining states which involve the formation of the third C–H bond and the consequent production of methanol. Therefore, our calculations show that the last step leading to methanol formation is the most challenging.
Therefore, the selected cluster models can be used for further investigations allowing a better understanding of the photocatalytic activity of GaN-based materials at a notably reduced computational cost.
Author contributions
V. B. performed the DFT simulations and analysis. Both the authors contributed to the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The Computational work was supported by The Ministry of Education, Youth and Sports from the Large Infrastructures for Research, Experimental Development and Innovations Project “e-Infrastructure CZ – LM2018140”. CzechNanoLab project LM2018110 funded by MEYS CR is gratefully acknowledged for the financial support of the measurements/sample fabrication at CEITEC Nano Research Infrastructure. This work was also supported by the Ministry of Education, Youth and Sports of the Czech Republic through the e-INFRA CZ (ID: 90140).Notes and references
- B. Aurianblajeni, M. Halmann and J. Manassen, Photo-reduction of carbon-dioxide and water into formaldehyde and methanol on semiconductor-materials, Sol. Energy, 1980, 25, 165–170 CrossRef CAS.
- D. Canfield and K. W. Frese, Reduction of carbon-dioxide to methanol on n-GaAs and p-GaAs and p-InP: Effect of crystal-face, electrolyte and current-density, J. Electrochem. Soc., 1983, 130, 1772–1773 CrossRef CAS.
- O. K. Varghese, M. Paulose, T. J. LaTempa and C. A. Grimes, High-rate solar photocatalytic conversion of CO2 and water vapor to hydrocarbon fuels, Nano Lett., 2009, 9, 731–737 CrossRef CAS PubMed.
- J. R. Cabrero-Antonino, R. Adam and M. Beller, Catalytic reductive N-alkylations using CO2 and carboxylic acid derivatives: Recent progress and developments, Angew. Chem., Int. Ed., 2019, 58, 2–21 CrossRef PubMed.
- S. Kar, A. Goeppert and G. K. S. Prakash, Integrated CO2 capture and conversion to formate and methanol: Connecting two threads, Acc. Chem. Res., 2019, 52, 2892–2903 CrossRef CAS PubMed.
- Q.-W. Song, Z.-H. Zhou and L.-N. He, Efficient, selective and sustainable catalysis of carbon dioxide, Green Chem., 2017, 19, 3707–3728 RSC.
- S. Samanta and R. Srivastava, Catalytic conversion of CO2 to chemicals and fuels: the collective thermocatalytic/photocatalytic/electrocatalytic approach with graphitic, Mater. Adv., 2020, 1, 1506–1545 RSC.
- V. Butera, N. Russo, U. Cosentino, C. Greco, G. Moro, D. Pitea and E. Sicilia, Computational insight on CO2 fixation to produce styrene carbonate assisted by a single-center aluminum(III) catalyst and quaternary ammonium salts, ChemCatChem, 2016, 8, 1167 CrossRef CAS.
- V. Butera and H. Detz, Cyclic carbonate formation from epoxides and CO2 catalyzed by sustainable alkali halide–glycol complexes: A DFT study to elucidate reaction mechanism and catalytic activity, ACS Omega, 2020, 5(29), 18064–18072 CrossRef CAS PubMed.
- V. Butera and H. Detz, Hydrogenation of CO2 to methanol by the diphosphine–ruthenium(II) cationic complex: A DFT investigation to shed light on the decisive role of carboxylic acids as promoters, Catal. Sci. Technol., 2021, 11, 3556–3397 RSC.
- L. Wang, Y. Dong, T. Yan, Z. Hu, A. A. Jelle, D. M. Meira, P. N. Duchesne, J. Y. Y. Loh, C. Qiu, E. E. Storey, Y. Xu, W. Sun, M. Ghoussoub, N. P. Kherani, A. S. Helmy and G. A. Ozin, Black indium oxide a photothermal CO2 hydrogenation catalyst, Nat. Commun., 2020, 11, 2432 CrossRef CAS PubMed.
- A. Fujishima and K. Honda, Electrochemical photolysis of water at a semiconductor electrode., Nature, 1972, 238, 37–38 CrossRef CAS PubMed.
- M. Halmann., Photoelectrochemical reduction of aqueous carbon-dioxide on p-type gallium-phosphide in liquid junction solar-cells, Nature, 1978, 275, 115–116 CrossRef CAS.
- T. Inoue, A. Fujishima, S. Konishi and K. Honda, Photoelectrocatalytic reduction of carbon dioxide in aqueous suspensions of semiconductor powders, Nature, 1979, 277, 637–644 CrossRef CAS.
- R. Vogel, P. Hoyer and H. Weller, Quantum-sized PbS, CdS, Ag2S, Sb2S3, and Bi2S3 particles as sensitizers for various nanoporous wide-bandgap semiconductors, J. Phys. Chem., 1994, 98, 3183–3188 CrossRef CAS.
- S. N. Habisreutinge, L. S. Mende and J. K. Stolarczyk, Photocatalytic reduction of CO2 on TiO2 and other semiconductors, Angew. Chem., Int. Ed., 2013, 52, 7372–7408 CrossRef PubMed.
- Y. F. Xu, P. N. Duchesne and L. Wang, et al., High-performance light-driven heterogeneous CO2 catalysis with near-unity selectivity on metal phosphides, Nat. Commun., 2020, 11, 5149 CrossRef CAS PubMed.
- Y. Wang, Y. Tian, L. Yan and Z. Su, DFT study on sulfur-doped g-C3N4 nanosheets as a photocatalyst for CO2 reduction reaction, J. Phys. Chem. C, 2018, 122(14), 7712–7719 CrossRef CAS.
- S. Funk, B. Hokkanen, E. Johnson and U. Burghaus, Effect of oxygen vacancy sites on CO2 adsorption dynamics: The case of rutile (1 × 1)-TiO2(110), Chem. Phys. Lett., 2006, 422, 461–465 CrossRef CAS.
- T. L. Thompson, O. Diwald and J. T. Yates, CO2 as a probe for monitoring the surface defects on TiO2(110) – temperature programmed desorption, J. Phys. Chem. B, 2003, 107, 11700–11704 CrossRef CAS.
- B. AlOtaibi, X. Kong, S. Vanka, S. Y. Woo, A. Pofelski, F. Oudjedi, S. Fan, M. G. Kibria, G. A. Botton, W. Ji, H. Guo and Z. Mi, Photochemical carbon dioxide reduction on Mg-doped Ga(In)N nanowire arrays under visible light irradiation, ACS Energy Lett., 2016, 1, 246–252 CrossRef CAS.
- C. Liu, J. Kang, Z.-Q. Huang, Y.-H. Song, Y.-S. Xiao, J. Song, J.-X. He, C.-R. Chang, H.-Q. Ge, Y. Wang, Z.-T. Liu and Z.-W. Liu, Gallium nitride catalyzed the direct hydrogenation of carbon dioxide to dimethyl ether as primary product, Nat. Commun., 2021, 12, 2305 CrossRef CAS PubMed.
- J. K. Nørskov, T. Bligaard, A. Logadottir, J. R. Kitchin, J. G. Chen, S. Pandelov and U. Stimming, Trends in the exchange current for hydrogen evolution, J. Electrochem. Soc., 2005, 152, J23–J26 CrossRef.
- Y. Zhao, C. Chang, F. Teng, Y. Zhao, G. Chen, R. Shi, G. I. N. Waterhouse, W. Huang and T. Zhang, Defect-engineered ultrathin δ-MnO2 nanosheet arrays as bifunctional electrodes for efficient overall water splitting, Adv. Energy Mater., 2017, 7, 1700005 CrossRef.
- Y. Zhao, S. Zhang, R. Shi, G. I. N. Waterhouse, J. Tang and T. Zhang, Two-dimensional photocatalyst design: A critical review of recent experimental and computational advances, Mater. Today, 2020, 34, 78–91 CrossRef CAS.
- J. Greeley, T. F. Jaramillo, J. Bonde, I. Chorkendorff and J. K. Nørskov, Computational high-throughput screening of electrocatalytic materials for hydrogen evolution, Nat. Mater., 2006, 5, 909 CrossRef CAS PubMed.
- V. Butera and M. C. Toroker, Electronic properties of pure and Fe-doped β-Ni(OH)2: New insights using density functional theory with a cluster approach, J. Phys. Chem. C, 2016, 120, 12344–12350 CrossRef CAS.
- V. Butera and M. C. Toroker, Practical cluster models for a layered β-NiOOH material, Materials, 2017, 10, 480 CrossRef PubMed.
- V. Butera, Y. Tanabe, T. Miyazawa, T. Fujitani, M. Kayanuma and Y.-K. Choe, Mechanistic investigation on ethanol-to-butadiene conversion reaction over metal oxide clusters, Int. J. Quantum Chem., 2021, 121, e26494 CrossRef CAS.
- V. Butera, N. Fukaya, J.-C. Choi, K. Sato and Y.-K. Choe, Alkoxysilane production from silica and dimethylcarbonate catalyzed by alkali bases: A quantum chemical investigation of the reaction mechanism, Inorg. Chim. Acta, 2018, 482, 70–76 CrossRef CAS.
- M. D’Arienzo, L. Gamba, F. Morazzoni, U. Cosentino, C. Greco, M. Lasagni, D. Pitea, G. Moro, C. Cepek, V. Butera, E. Sicilia, N. Russo, A. B. Munoz-Garcia and M. Pavone, Experimental and theoretical investigation on the catalytic generation of environmentally persistent free radicals from benzene, J. Phys. Chem. C, 2017, 121, 9381–9393 CrossRef.
- V. Butera, A. Massaro, A. B. Muñoz-García, M. Pavone and H. Detz, d-Glucose Adsorption on the TiO2 Anatase (100) Surface: A Direct Comparison Between Cluster-Based and Periodic Approaches, Front. Chem., 2021, 9, 716329 CrossRef PubMed.
- S. Kozuch and S. Shaik, How to conceptualize catalytic cycles? The energetic span model, Acc. Chem. Res., 2010, 44, 101–110 CrossRef PubMed.
- S. Kozuch, A refinement of everyday thinking: the energetic span model for kinetic assessment of catalytic cycles, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 795–815 CAS.
- N. Alidoust and E. A. Carter, First-principles assessment of hole transport in pure and Li-doped NiO, Phys. Chem. Chem. Phys., 2015, 17, 18098–18110 RSC.
- A. D. Laurent, C. Adamo and D. Jacquemin, Dye chemistry with time-dependent density functional theory, Phys. Chem. Chem. Phys., 2014, 16, 14334–14356 RSC.
- C. Adamo and D. Jacquemin, The calculations of excited-state properties with time-dependent density functional theory, Chem. Soc. Rev., 2013, 42, 845 RSC.
- S. Wu, J. Žurauskas, M. Domański, P. S. Hitzfeld, V. Butera, D. J. Scott, J. Rehbein, A. Kumar, E. Thyrhaug, J. Hauer and J. P. Barham., Hole-mediated photoredox catalysis: Tris(p-substituted)biarylaminium radical cations as tunable, precomplexing and potent photooxidants, Org. Chem. Front., 2021, 8, 1132–1142 RSC.
- A. D. Becke, Density-functional thermochemistry. III. The role of exact exchange, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford, CT, 2016 Search PubMed.
- (a) T. H. Dunning, Jr. and P. J. Hay, Modern theoretical chemistry, ed. H. F. Schaefer, III, Plenum, New York, 1977, vol. 3, pp 1–28 Search PubMed; (b) P. J. Hay and W. R. Wadt, Ab initio effective core potentials for molecular calculations – potentials for the transition-metal atoms Sc to Hg, J. Chem. Phys., 1985, 82, 270–283 CrossRef CAS; (c) W. R. Wadt and P. J. Hay, Ab initio effective core potentials for molecular calculations. Potentials for main group elements Na to Bi, J. Chem. Phys., 1985, 82, 284–298 CrossRef CAS; (d) P. J. Hay and W. R. Wadt, Ab initio effective core potentials for molecular calculations – Potentials for K to Au including the outermost core orbitals, J. Chem. Phys., 1985, 82, 299–310 CrossRef CAS.
- (a) J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed; (b) J. P. Perdew, K. Burke and M. Ernzerhof, Errata: Generalized gradient approximation made simple, Phys. Rev. Lett., 1997, 78, 1396–1399 CrossRef CAS; (c) C. Adamo and V. Barone, Toward reliable density functional methods without adjustable parameters: The PBE0 model, J. Chem. Phys., 1999, 110, 6158–6169 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1qm01118a |
| This journal is © the Partner Organisations 2021 |