Electrostatic effects in N-heterocyclic carbene catalysis: revealing the nature of catalysed decarboxylation†
Received
28th September 2021
, Accepted 26th October 2021
First published on 26th October 2021
Abstract
Quantum chemistry is used to investigate the nature of protonated N-heterocyclic carbene (NHC·H+) catalysed decarboxylation recently reported by Zhang et al. (ACS Catal., 2021, 11, 3443–3454). Our results show that there are strong electrostatic effects within the NHC·H+ catalysed decarboxylation, and these dominate hydrogen bonding. At the same time, energy decomposition analyses and comparison between the original NHC·H+ catalyst and a truncated form reveal that stabilizing dispersion interactions are also critical, as is induction. We also show that the electrostatic effects and their associated catalytic effects can be further enhanced using charged functional groups.
Introduction
N-Heterocyclic carbenes (NHCs) are among the most widely used organocatalysts and ligands for organometallic catalysts in organic synthesis due to their ability to alter both chemo- and stereo-selectivities.1 The lone pairs from adjacent nitrogen atoms can strongly donate their π-electrons toward the 2p-π orbital of the carbene, which greatly stabilises the closed-shell singlet state of NHCs. Therefore, NHCs usually behave as nucleophiles using their fully occupied sp2-σ orbital to mediate C–C or C–N bond formation. For instance, they can readily attack carbonyl moieties to produce Breslow intermediates, which renders the previously electrophilic carbonyl centre nucleophilic (i.e., umpolung).2 Imines can also be activated in a similar manner through aza-Breslow intermediates.3 Moreover, it has been recently reported that NHCs can also engage in radical reactions through single-electron transfer (SET), the opposite of the traditional two-electron mechanism.4
Although NHC catalysis has been extensively studied from both an experimental and theoretical perspective,5,6 the role of electrostatic effects is often overlooked. Recent theoretical and experimental work has shown that such electrostatic effects, whether these are designed local electric fields (D-LEFs) from charged functional groups (CFGs)7 or coordinated metal ions,8 interfacial electric fields (IEFs)9 or external electric fields (EEFs)10 can have significant impacts on the rates, regio- and stereoselectivity of a range of chemical and photochemical processes.11–13 The NHC-catalysed cycle generally involves (de)protonation steps that create charged intermediates, potentially introducing additional charge–dipole interactions to the reaction axis that might contribute to catalysis. Understanding their role, if any, has important implications for optimizing this important reaction.
Recently, Zhang et al. proposed a new theoretical model to demonstrate that NHC·H+ (i.e., the protonated form of NHC) can catalyse decarboxylation, and used hydrogen bonding (HB) to rationalise such a phenomenon (Fig. 1).14 In the preferred transition state (shown in Fig. 1), the NHC·H+ binds preferentially to the more electronegative carbonyl oxygen. Base·H+ (e.g., DABCO·H+) does not exhibit a similar catalytic effect but instead shows a minor deactivation. In both cases, the pre-reaction complexes via HB are not favoured by free energies. These results inspire us to explore further the nature of NHC·H+ catalysed decarboxylation so as to answer the following questions. (1) If HB is the key for catalysis, why does DABCO·H+, which has a stronger HB than NHC·H+, not show any catalytic effect? (2) What are major resonance structures in the reactant and the transition state? (3) Is there an electrostatic component to the catalysis, and how do we take advantage of it?
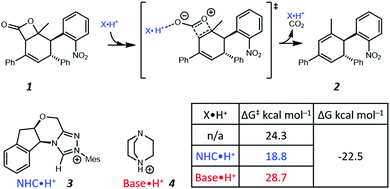 |
| | Fig. 1 Illustration of the NHC·H+ catalysed decarboxylation of 1 proposed by Zhang et al.14 The Gibbs free energy barriers and reaction free energies were calculated at B3LYP-D3/6-311++G(2df,2pd)/SMD(NMP/tBuOH)//B3LYP-D3/6-31G(d,p)/SMD(NMP/tBuOH). | |
In the present work, we use computational chemistry to study the NHC·H+ catalysed decarboxylation so as to address these questions, and provide a better understanding of the role of electrostatics in NHC-catalysed decarboxylation. As a case study, we have selected the model reaction shown in Scheme 1, chosen because steric effects and other dispersion interactions are expected to be relatively minor, thus allowing us to focus better on the interplay between electrostatics and hydrogen bonding. We chose dichloromethane as the solvent because, due to its moderately low polarity, it has been shown in our previous experimental studies of electrostatic catalysis15 to offer a good compromise between maintaining the solubility of charged species while still minimizing solvent screening of electrostatic effects. It has also been used experimentally in NHC catalysed reactions.16 In addition to the NHC·H+ catalyst 3 and DABCO·H+ base 4 studied previously by Zhang et al.,14 we also considered a truncated NHC·H+, 1,3,4-trimethyl-4H-1,2,4-triazol-1-ium (7), to minimise the possible steric interactions between substrate and non-truncated counterparts, NMe3·H+ (8) was considered as a slightly stronger albeit less nucleophilic base than DABCO·H+, and MeOH (9) was included as a neutral HB donor. Finally, we explore whether the inclusion of additional charged functional groups can further improve the catalysis observed.
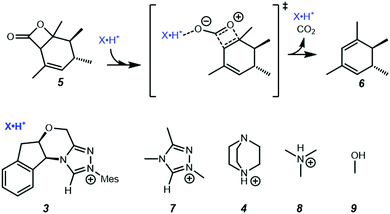 |
| | Scheme 1 Decarboxylation reaction and catalysts studied in the present work. Unless noted otherwise all calculations are performed in dichloromethane at 298 K. | |
Computational details
All geometries and thermal corrections at 298 K were obtained in dichloromethane at M06-2X17/6-31G(d,p)/IEFPCM using the G0918 package, and additional single-point energies in dichloromethane were calculated at M06-2X/6-31+G(d,p)/SMD,19 as this level of theory has previously been shown to accurately predict the electrostatic effects on reaction barriers and enthalpies.7,10,20 Moreover, our recent benchmark study confirms that M06-2X is one of the most accurate functionals for calculating barrier heights and reaction energies in organic systems.21 Transition states were confirmed by IRC calculations, and frequency calculations confirmed that all stationary points had the correct number of imaginary frequencies. The resonance analysis was performed with EzReson,22,23 and energy decomposition was performed at sSAPT0/jun-cc-pVDZ level of theory using PSI4 software.24,25 Figures of molecular structures were generated by Chemcraft.26 The interaction region indicator (IRI) analysis,27 which describes strong and weak interactions simultaneously, were rendered by Multiwfn28 and VMD.29
Results and discussion
Polarity of the transition state
To understand the role of electrostatics in the NHC·H+ catalysed decarboxylation, it is helpful to begin by examining the charge distribution in the reactants and transition state of the uncatalyzed reaction. Fig. 2 compares the contribution of key resonance structures in the reactants and transition state, as calculated using a simplified 5c–4e model based on the O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–O: moiety. The 5c is the three C and one O on the four-membered ring along with the carbonyl O, while the 4e include one π bond of the carbonyl and one lone pair from cyclic O. It is clear that the ionic contributor, in which there is a formal negative charge on the carbonyl oxygen and a formal positive charge on the cyclic oxygen, is significant in the reactant, and becomes substantially more important as the reaction progress. This is why the positively charged NHC·H+ or Base·H+ preferentially binds to the carbonyl, and why this binding preferentially stabilizes the transition state compared with the reactant as reported by Zhang et al.14
C–O: moiety. The 5c is the three C and one O on the four-membered ring along with the carbonyl O, while the 4e include one π bond of the carbonyl and one lone pair from cyclic O. It is clear that the ionic contributor, in which there is a formal negative charge on the carbonyl oxygen and a formal positive charge on the cyclic oxygen, is significant in the reactant, and becomes substantially more important as the reaction progress. This is why the positively charged NHC·H+ or Base·H+ preferentially binds to the carbonyl, and why this binding preferentially stabilizes the transition state compared with the reactant as reported by Zhang et al.14
 |
| | Fig. 2 Resonance analysis based on O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–O: for the reactant and transition state in the uncatalysed reaction showing the contributions of the reactant (I), ionic (II), and remaining configurations. C–O: for the reactant and transition state in the uncatalysed reaction showing the contributions of the reactant (I), ionic (II), and remaining configurations. | |
Electrostatics
Based on the resonance analysis above, stabilization by a positively charged catalyst bound to the carbonyl oxygen would be expected to have an electrostatic component. One of the simplest methods to assess the contribution of electrostatic effects is to replace the catalyst altogether with a point charge, in this case located at the nominal charge centre (i.e., H+) of the NHC·H+ catalyst (Fig. 3). We compared the solution phase single point energies obtained for the transition state when the NHC·H+ is deleted altogether versus its replacement with a positive or negative point charge of one atomic unit (i.e., electric field). Unsurprisingly, the positive charge significantly stabilises the transition state while the negative charge destabilises it, though to a lesser extent due to polarization effects. This can be understood in terms of the charge dipole interaction with the transition state, with the positive charge aligned so as to stabilize the dipole across the leaving CO2 and the negative charge aligned so as to destabilise it. This is clear from the dipole moments (Fig. 4), which are enhanced in the case of the positive charge and diminished with the negative charge. While the magnitude of electrostatic effects is exaggerated for these infinitely localised charges, the trends are clear.
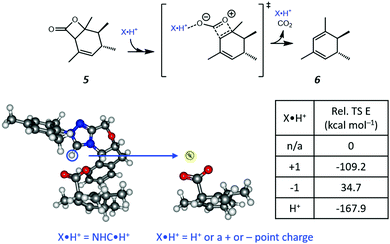 |
| | Fig. 3 The reaction studied in the present work and the model system used to assess electrostatic effects. The H+ position (highlighted in the blue cycle) of the NHC·H+ is replaced by either a positive or negative point charge (i.e., electric field) or an H+ ion in the same position without further optimization. The point charges (and proton) have a magnitude of one atomic unit to mimic the same charge as NHC·H+ and are located exactly where the proton is located in the original NHC·H+ catalyst. The relative energies of the transition states are compared to that obtained without charges or protons. | |
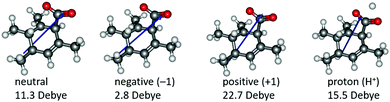 |
| | Fig. 4 Illustration of the calculated dipole moments in Debye (D) for neutral and charged systems. The blue arrows only indicate the direction of the dipole moments rather than the magnitude. | |
To further decouple electrostatic effects from orbital interactions, we also replaced the point charge with a proton in the same position. While the proton's charge is identical, it differs from the positive charge in that it also has vacant orbitals capable of interacting with the substrate. Interestingly, the proton increases the stability of the transition state significantly more than the point charge, indicating that favourable orbital interactions are indeed important. This is also seen with the dipole moments (Fig. 4), where, unlike the positive point charge, the proton does not significantly alter the dipole moment compared with the neutral compound, thus suggesting the electrostatic effects are countered by back bonding. However, it should be emphasised that the proton model represents an extreme case for orbital interaction since all of the proton's orbitals are empty and available to accept the electrons from the oxygen. The orbital interactions are expected to be much weaker in real models.
Effect of HB donation
Since the point charge analysis shows that both electrostatic effects and orbital interactions affect the stability of transition states, we next compared a series of different HB donors to investigate the dominant factor in catalysed decarboxylation (Fig. 5). The decarboxylation of 5 is thermodynamically favoured (ΔG = −10.5 kcal mol−1), and the uncatalysed pathway has a 29.1 kcal mol−1 free energy barrier. In contrast to the previous results reported by Zhang et al.14 with substrate 1 (Fig. 1) NHC·H+ shows a negligible catalytic effect with a 28.7 kcal mol−1 free energy barrier, while DABCO·H+ does lower the barrier by 4.4 kcal mol−1. The truncated NHC·H+ model has a free energy barrier of 30.6 kcal mol−1, suggesting an additional non-electrostatic contribution from the original NHC·H+ molecule. The truncated model of DABCO·H+ (i.e., NMe3·H+) has the same free energy barrier as DABCO·H+ within 0.3 kcal mol−1. Finally, the MeOH affords the highest free energy barrier of 30.8 kcal mol−1.
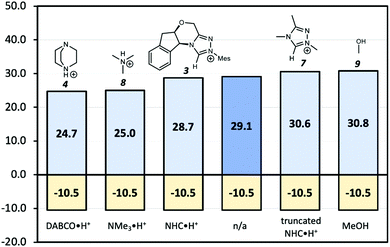 |
| | Fig. 5 Gibbs free energy barriers for the decarboxylation of 5 at 298 K in dichloromethane. The uncatalyzed pathway is compared with that catalysed by the various HB donors shown in Scheme 1. All pre-reaction complexes are not lower in free energies than separated molecules, so they are not included (Table S1, ESI†). The units are in kcal mol−1. | |
To a first approximation, the HB lengths reflect their strengths. The shortest distances are about 1.60 Å for NMe3·H+ and DABCO·H+, followed by 1.84 Å for MeOH and about 2.00 Å for NHC·H+ related donors. Although HBs are present in all systems, not all HB donors show a catalytic effect, suggesting the HB is not the only catalytic driver of decarboxylation. At the same time, both NHC·H+ and DABCO·H+ (and their truncated forms) have a cationic centre, but only DABCO·H+ and its truncated form act as a catalyst. Clearly, a more quantitative analysis of the interactions with the substrate is needed to understand these trends. To this end, an interaction region indicator (IRI) analysis27 was performed (see Fig. 6).
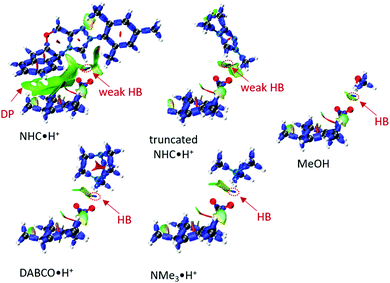 |
| | Fig. 6 The IRI plots of HB donor mediated transition states, where DP stands dispersion, and colour scale bar [−0.04, +0.02] is provided in Fig. S1 (ESI†). The HB lengths are 1.60 Å (DABCO·H+), 1.59 Å (NMe3·H+), 2.00 Å (NHC·H+), 2.09 Å (truncated NHC·H+) and 1.84 Å (MeOH). | |
From Fig. 6, it is clear that all systems possess HBs, and these increase in line with their HB lengths, from the weakest NHC·H+ (in green-blue colour), to MeOH (in blue colour) to DABCO·H+ (in deep blue colour). Although MeOH has a stronger HB than truncated NHC·H+, it does not show a lower free energy barrier, suggesting that charge is more important in this case. NHC·H+ also has additional dispersion interaction due to the aromatic ring (DP region in Fig. 6), which stabilises the transition state more than the truncated NHC·H+. These dispersion or steric interactions may also account for the enhanced catalytic activity of NHC·H+versus DABCO·H+ observed previously for substrate 1, as the substrate in this case substituted with additional aromatic groups.
Energy decomposition analysis
The trends in Fig. 6 reflect a complicated interplay between electrostatics, HB interactions, and dispersion. To further untangle these contributions, we used SAPT to perform an energy decomposition analysis (Table 1). Based on perturbation theory, the electronic interaction energy can be decomposed into various components: (1) classic electrostatic term; (2) exchange-repulsion term; (3) inductive term, and (4) dispersion term.30 Broadly speaking, the barrier height is correlated with the electrostatic and induction components and inversely correlated with the exchange. These in turn largely follow the acidity of the HB hydrogen NMe3·H+ > DABCO·H+ > NHC·H+ > truncated NHC·H+ > MeOH, and are in line with the notion that the barrier height is stabilized substituents that stabilize the δ negative charge on the carbonyl oxygen through a combination of electrostatics, induction, and orbital interactions. In contrast, the dispersion energies are poorly correlated, and fall into a narrow range, except for NHC·H+, which, as seen in Fig. 6, has an additional stabilizing dispersion interaction that is absent from the other catalysts.
Table 1 Decomposition analysis of the interaction energy (gas phase) into electrostatic (Eelst), exchange (Eexch), inductive (Eind) and dispersion (Edis) energies in kcal mol−1
| HB donors |
E
elst
|
E
exch
|
E
ind
|
E
dis
|
E
total
|
|
Correlation with the Gibbs free energy barrier.
|
| NMe3·H+ |
−55.4 |
34.6 |
−20.6 |
−8.1 |
−49.5 |
| DABCO·H+ |
−52.4 |
33.4 |
−19.7 |
−8.4 |
−47.0 |
| NHC·H+ |
−36.3 |
30.3 |
−12.1 |
−19.7 |
−37.8 |
| Truncated NHC·H+ |
−34.5 |
15.5 |
−8.3 |
−6.2 |
−33.5 |
| MeOH |
−13.8 |
13.2 |
−4.6 |
−3.8 |
−9.0 |
|
R
|
0.902 |
−0.912 |
0.981 |
0.133 |
0.827 |
Combination with D-LEFs
Since electrostatics contribute to the catalysis observed, we wondered if the catalysis could be further enhanced with an appropriate electric field. As a case study, we selected –NH2/–NH3+ and –SO3H/–SO3− as charge-neutral pairs to tune electrostatic effects and used –CH2– as a linker to minimise possible resonances with NHC·H+ (Scheme 2). This choice is for a general demonstration of D-LEFs, so the other species like a non-pH sensitive –NMe3+ or –BF3− can also be used when desired, or indeed an external electric field. Two positions were considered for installing CFGs either on the aromatic ring (10–13) or on the ring that contains oxygen (14–17). The aromatic ring is easier to substitute while the latter is closer to the reaction centre, and is thus expected to be more influential.
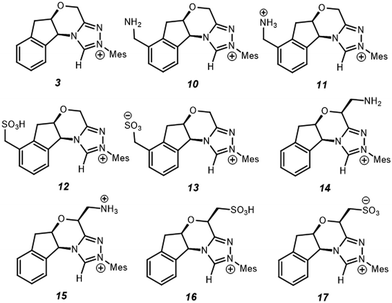 |
| | Scheme 2 Substituted NHC·H+ catalyst studied for exploring D-LEF effects. Unless noted otherwise all calculations are performed at 298 K in dichloromethane. | |
If CFGs are placed on the aromatic ring, a negligible catalytic effect is observed as NHC·H+ (10–13, Fig. 7), and the minor differences are actually due to entropic and thermal contributions. On the other hand, installing a CFG close to the reaction centre confers stronger interactions. Using a positive charged –NH3+ (15), the free energy barrier is 2.9 kcal mol−1 lower than its neutral counterpart (14), and is 1.8 kcal mol−1 lower than the uncatalyzed pathway, inferring an about one-ordered magnitude increase in reaction rates. The result aligns with our understanding that making NHC·H+ more cationic could stabilise the decarboxylation transition state more through electrostatic effects. Interestingly, the neutral –SO3H also gives a comparatively low free energy barrier of 27.9 kcal mol−1, as a result of inductive effects from this strong electron-withdrawing group. This not only further underlies the complex interplay of electrostatic effects with other polar interactions, but also points to another strategy to enhance catalysis in this system.
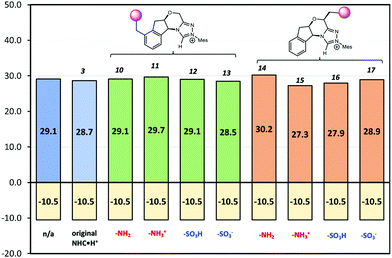 |
| | Fig. 7 The Gibbs free energy barriers and reaction free energies at 298 K for decarboxylation of 5. The uncatalyzed pathway is compared with that catalysed by the original NHC·H+3 and its various modified versions shown in Scheme 2. The units are in kcal mol−1. | |
A major shortcoming of the D-LEF approach is the necessary trade-off between the solubility of charged species (which diminishes in non-polar solvents) and the rapid attenuation of electrostatic effects that occurs with increasing polarity of the solvent. This is seen in Fig. 8, which compares the solution barriers of Fig. 7 with the corresponding gas-phase barriers. In the gas phase, the –NH3+ (11) shows a 4.4 kcal mol−1 lower barrier than the corresponding solvation phase barrier. For both non-charged species (10, 12), the differences of barriers between the two phases are the same within 0.5 kcal mol−1. The negatively charged –SO3− (13) shows a 0.6 kcal mol−1 higher gas-phase barrier. When CFGs are closer to the reaction centre, the –NH3+ (15) has a 16.3 kcal mol−1 gas-phase barrier (Table S2, ESI†), which is 11.0 kcal mol−1 lower than its solvation-phase counterpart. For the neutral –NH2 (14) and –SO3H (16), their gas and solution phase barriers are similar. However, the gas-phase barrier of –SO3− (17) is now 6.1 kcal mol−1 more than the solvation-phase barrier. Therefore, the catalytic effects of the second positively charged centre on NHC·H+ are significant in the gas phase but are largely (but not entirely) screened by dichloromethane. An alternative way to avoid such attenuation, and the need to synthesise alternative catalysts, would be to use external electric fields instead. While at present these have only been implemented experimentally in model scanning tunnelling microscope experiments,10,31–34 molecular modelling suggests that a promising experimental platform for scaling electric field effects is via ordered solvent environments. Specifically, ab initio molecular dynamics35,36 and polarisable molecular dynamics37,38 modelling has shown that when exposed to external fields, solvents such as water,35,36 methanol38 and ionic liquids37,38 become ordered. For ionic liquids at least this ordering generates an experimentally detectable internal electric field that persists when the external stimuli are removed.37 Multi-scale modelling has shown that the internal electric fields generated by this ordering are capable of significant catalysis, even after the external field is removed.38
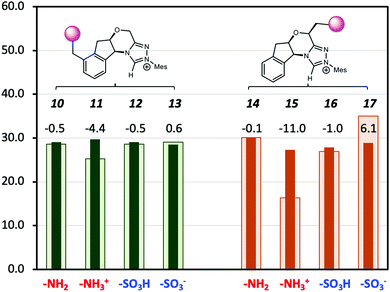 |
| | Fig. 8 The Gibbs free energy barriers at 298 K for decarboxylation of 5 using the various modified NHC·H+ shown in Scheme 2. The geometries and thermal corrections were obtained at M06-2X/6-31G(d,p)/IEFPCM(dichloromethane) with additional single-point calculations with or without dichloromethane at M06-2X/6-31+G(d,p). The darker colour represents the solvation-phase barriers, and the lighter colour represents the gas-phase barriers (in 1 M for comparison), with the data labels representing the difference. The units are in kcal mol−1. | |
Conclusions
In summary, we investigate the nature of NHC·H+ catalysed decarboxylation proposed by Zhang et al.14 Our study demonstrates that while catalysis results from a complicated interplay of interactions, it is electrostatic effects, rather than hydrogen bonding, that dominate. This implies that in an amine-based solvent under acidic conditions, the protonated cation may act as a latent catalyst for decarboxylation. We show that catalysis can be further enhanced by increasing the electrostatic effects with charged functional groups, and electron-withdrawing groups in general, thus providing a design strategy for optimizing catalysis.
Conflicts of interest
The authors declare no conflicts of interest.
Acknowledgements
MLC gratefully acknowledges an Australian Research Council Laureate Fellowship (FL170100041). DW acknowledges financial support from the National Natural Science Foundation of China (No. 21773214), the Training Plan for Young Key Teachers in Colleges and Universities in Henan Province (No. 2020GGJS016), and Natural Science Foundation for Excellent Young Scientist in Henan Province (No. 212300410083).
Notes and references
- M. N. Hopkinson, C. Richter, M. Schedler and F. Glorius, An overview of N-heterocyclic carbenes, Nature, 2014, 510, 485–496 CrossRef CAS PubMed.
- X. Li, J. Xu, S.-J. Li, L.-B. Qu, Z. Li, Y. R. Chi, D. Wei and Y. Lan, Prediction of NHC-catalyzed chemoselective functionalizations of carbonyl compounds: a general mechanistic map, Chem. Sci., 2020, 11, 7214–7225 RSC.
- M. Pareek, Y. Reddi and R. B. Sunoj, Tale of the Breslow intermediate, a central player in N-heterocyclic carbene organocatalysis: Then and now, Chem. Sci., 2021, 12, 7973–7992 RSC.
- L. Dai and S. Ye, Recent advances in N-heterocyclic carbene-catalyzed radical reactions, Chin. Chem. Lett., 2021, 32, 660–667 CrossRef CAS.
- Y. Wang, D. Wei and W. Zhang, Recent advances on computational investigations of N-heterocyclic carbene catalyzed cycloaddition/annulation reactions: Mechanism and origin of selectivities, ChemCatChem, 2018, 10, 338–360 CrossRef CAS.
- X. Chen, H. Wang, Z. Jin and Y. R. Chi, N-Heterocyclic carbene organocatalysis: Activation modes and typical reactive intermediates, Chin. J. Chem., 2020, 38, 1167–1202 CrossRef CAS.
- G. Gryn’ova, D. L. Marshall, S. J. Blanksby and M. L. Coote, Switching radical stability by pH-induced orbital conversion, Nat. Chem., 2013, 5, 474–481 CrossRef PubMed.
- S. J. P. Marlton, B. I. McKinnon, N. S. Hill, M. L. Coote and A. J. Trevitt, Electrostatically tuning the photodissociation of the Irgacure 2959 photoinitiator in the gas phase by cation binding, J. Am. Chem. Soc., 2021, 143, 2331–2339 CrossRef CAS PubMed.
- Y. B. Vogel, C. W. Evans, M. Belotti, L. Xu, I. C. Russell, L.-J. Yu, A. K. K. Fung, N. S. Hill, N. Darwish, V. R. Gonçales, M. L. Coote, K. Swaminathan Iyer and S. Ciampi, The corona of a surface bubble promotes electrochemical reactions, Nat. Commun., 2020, 11, 6323 CrossRef CAS PubMed.
- A. C. Aragonès, N. L. Haworth, N. Darwish, S. Ciampi, N. J. Bloomfield, G. G. Wallace, I. Diez-Perez and M. L. Coote, Electrostatic catalysis of a Diels–Alder reaction, Nature, 2016, 531, 88–91 CrossRef PubMed.
- S. Ciampi, N. Darwish, H. M. Aitken, I. Díez-Pérez and M. L. Coote, Harnessing electrostatic catalysis in single molecule, electrochemical and chemical systems: A rapidly growing experimental tool box, Chem. Soc. Rev., 2018, 47, 5146–5164 RSC.
- T. Stuyver, D. Danovich, J. Joy and S. Shaik, External electric field effects on chemical structure and reactivity, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2020, 10, e1438 CAS.
- S. Shaik, R. Ramanan, D. Danovich and D. Mandal, Structure and reactivity/selectivity control by oriented-external electric fields, Chem. Soc. Rev., 2018, 47, 5125–5145 RSC.
- M. Zhang, Y. Wang, S.-J. Li, X. Wang, Q. Shi, X. Li, L.-B. Qu, D. Wei and Y. Lan, Multiple functional organocatalyst-promoted inert C–C activation: Mechanism and origin of selectivities, ACS Catal., 2021, 11, 3443–3454 CrossRef CAS.
- M. Klinska, L. M. Smith, G. Gryn’ova, M. G. Banwell and M. L. Coote, Experimental demonstration of pH-dependent electrostatic catalysis of radical reactions, Chem. Sci., 2015, 6, 5623–5627 RSC.
- G. Wang, Q. Zhang, C. Wei, Y. Zhang, L. Zhang, J. Huang, D. Wei, Z. Fu and W. Huang, Asymmetric carbene-catalyzed oxidation of functionalized aldimines
as 1,4-dipoles, Angew. Chem., Int. Ed., 2021, 60, 7913–7919 CrossRef CAS PubMed.
- Y. Zhao and D. G. Truhlar, The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other function, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision C.01, Gaussian, Inc., Wallingford, CT, 2010 Search PubMed.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, Universal solvation model based on solute electron density and on a continuum model of the solvent defined by the bulk dielectric constant and atomic surface tensions, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS PubMed.
- V. Doan, B. B. Noble and M. L. Coote, Electrostatic activation of tetrazoles, J. Org. Chem., 2020, 85, 10091–10097 CrossRef CAS PubMed.
- V. K. Prasad, Z. Pei, S. Edelmann, A. Otero-de-la-Roza and G. DiLabio, BH9, a new comprehensive benchmark dataset for barrier heights and reaction energies: Assessment of density functional approximations and basis set incompleteness potentials, ChemRxiv, 2021 DOI:10.33774/chemrxiv-2021-mdjwx.
- Y. Wang, Superposition of waves or densities: Which is the nature of chemical resonance?, J. Comput. Chem., 2021, 42, 412–417 CrossRef CAS PubMed.
- Y. Wang, A reliable and efficient resonance theory based on analysis of DFT wave functions, Phys. Chem. Chem. Phys., 2021, 23, 2331–2348 RSC.
- D. G. A. Smith, L. A. Burns, A. C. Simmonett, R. M. Parrish, M. C. Schieber, R. Galvelis, P. Kraus, H. Kruse, R. Di Remigio, A. Alenaizan, A. M. James, S. Lehtola, J. P. Misiewicz, M. Scheurer, R. A. Shaw, J. B. Schriber, Y. Xie, Z. L. Glick, D. A. Sirianni, J. S. O’Brien, J. M. Waldrop, A. Kumar, E. G. Hohenstein, B. P. Pritchard, B. R. Brooks, H. F. Schaefer, A. Y. Sokolov, K. Patkowski, A. E. DePrince, U. Bozkaya, R. A. King, F. A. Evangelista, J. M. Turney, T. D. Crawford and C. D. Sherrill, PSI4 1.4: Open-source software for high-throughput quantum chemistry, J. Chem. Phys., 2020, 152, 184108 CrossRef CAS PubMed.
- T. M. Parker, L. A. Burns, R. M. Parrish, A. G. Ryno and C. D. Sherrill, Levels of symmetry adapted perturbation theory (SAPT). I. Efficiency and performance for interaction energies, J. Chem. Phys., 2014, 140, 094106 CrossRef PubMed.
- Chemcraft – graphical software for visualization of quantum chemistry computations, https://www.chemcraftprog.com.
- T. Lu and Q. Chen, Interaction region indicator: A simple real space function clearly revealing both chemical bonds and weak interactions, Chemistry – Methods, 2021, 1, 231–239 CrossRef.
- T. Lu and F. Chen, Multiwfn: A multifunctional wavefunction analyzer, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- W. Humphrey, A. Dalke and K. Schulten, VMD: Visual molecular dynamics, J. Mol. Graph., 1996, 14, 33–38 CrossRef CAS PubMed.
- S. Emamian, T. Lu, H. Kruse and H. Emamian, exploring nature and predicting strength of hydrogen bonds: A correlation analysis between atoms-in-molecules descriptors, binding energies, and energy components of symmetry-adapted perturbation theory, J. Comput. Chem., 2019, 40, 2868–2881 CrossRef CAS PubMed.
- X. Huang, C. Tang, J. Li, L.-C. Chen, J. Zheng, P. Zhang, J. Le, R. Li, X. Li, J. Liu, Y. Yang, J. Shi, Z. Chen, M. Bai, H.-L. Zhang, H. Xia, J. Cheng, Z.-Q. Tian and W. Hong, Electric field–induced selective catalysis of single-molecule reaction, Sci. Adv., 2019, 5, eaaw3072 CrossRef CAS PubMed.
- Z.-F. Cai, G. Zhan, L. Daukiya, S. Eyley, W. Thielemans, K. Severin and S. De Feyter, Electric-field-mediated reversible transformation between supramolecular networks and covalent organic frameworks, J. Am. Chem. Soc., 2019, 141, 11404–11408 CrossRef CAS PubMed.
- L. Zhang, E. Laborda, N. Darwish, B. B. Noble, J. H. Tyrell, S. Pluczyk, A. P. Le Brun, G. G. Wallace, J. Gonzalez, M. L. Coote and S. Ciampi, Electrochemical and electrostatic cleavage of alkoxyamines, J. Am. Chem. Soc., 2018, 140, 766–774 CrossRef CAS PubMed.
- Y. Zang, Q. Zou, T. Fu, F. Ng, B. Fowler, J. Yang, H. Li, M. L. Steigerwald, C. Nuckolls and L. Venkataraman, Directing isomerization reactions of cumulenes with electric fields, Nat. Commun., 2019, 10, 4482 CrossRef PubMed.
- G. Cassone, Nuclear quantum effects largely influence molecular dissociation and proton transfer in liquid water under an electric field, J. Phys. Chem. Lett., 2020, 11, 8983–8988 CrossRef CAS PubMed.
- Z. Futera and N. J. English, Influence of external static and alternating electric fields on water from long-time non-equilibrium ab initio molecular dynamics, J. Chem. Phys., 2017, 147, 031102 CrossRef PubMed.
- M. Belotti, X. Lyu, L. Xu, P. Halat, N. Darwish, D. S. Silvester, C. Goh, E. I. Izgorodina, M. L. Coote and S. Ciampi, Experimental evidence of long-lived electric fields of ionic liquid bilayers, J. Am. Chem. Soc., 2021, 143, 17431–17440 CrossRef CAS PubMed.
- L. Xu, E. I. Izgorodina and M. L. Coote, Ordered solvents and ionic liquids can be harnessed for electrostatic catalysis, J. Am. Chem. Soc., 2020, 142, 12826–12833 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Computational details, colour bar, and xyz files. See DOI: 10.1039/d1cp04444c |
|
| This journal is © the Owner Societies 2021 |
Click here to see how this site uses Cookies. View our privacy policy here.  *b and
Michelle L.
Coote
*b and
Michelle L.
Coote
 *a
*a


![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–O: moiety. The 5c is the three C and one O on the four-membered ring along with the carbonyl O, while the 4e include one π bond of the carbonyl and one lone pair from cyclic O. It is clear that the ionic contributor, in which there is a formal negative charge on the carbonyl oxygen and a formal positive charge on the cyclic oxygen, is significant in the reactant, and becomes substantially more important as the reaction progress. This is why the positively charged NHC·H+ or Base·H+ preferentially binds to the carbonyl, and why this binding preferentially stabilizes the transition state compared with the reactant as reported by Zhang et al.14
C–O: moiety. The 5c is the three C and one O on the four-membered ring along with the carbonyl O, while the 4e include one π bond of the carbonyl and one lone pair from cyclic O. It is clear that the ionic contributor, in which there is a formal negative charge on the carbonyl oxygen and a formal positive charge on the cyclic oxygen, is significant in the reactant, and becomes substantially more important as the reaction progress. This is why the positively charged NHC·H+ or Base·H+ preferentially binds to the carbonyl, and why this binding preferentially stabilizes the transition state compared with the reactant as reported by Zhang et al.14

![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–O: for the reactant and transition state in the uncatalysed reaction showing the contributions of the reactant (I), ionic (II), and remaining configurations.
C–O: for the reactant and transition state in the uncatalysed reaction showing the contributions of the reactant (I), ionic (II), and remaining configurations.






