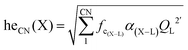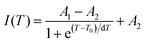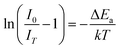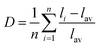Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Luminescence in external dopant-free scandium-phosphorus vanadate solid solution: a spectroscopic and theoretical investigation
Fengwen
Kang
 *ab,
Yongping
Du
cd,
Philippe
Boutinaud
*ab,
Yongping
Du
cd,
Philippe
Boutinaud
 e,
Guohuan
Sun
f,
Xicheng
Wang
e,
Guohuan
Sun
f,
Xicheng
Wang
 g,
Jian
Lu
g,
Jian
Lu
 b and
Sanshui
Xiao
b and
Sanshui
Xiao
 *a
*a
aDTU Fotonik, Department of Photonics Engineering, Technical University of Denmark, Lyngby, Denmark. E-mail: kangfengwen0597@126.com; saxi@fotonik.dtu.dk
bDepartment of Materials Science and Engineering, Department of Mechanical Engineering, City University of Hong Kong (CityU), 83 Tat Chee Avenue, Kowloon, Hong Kong, China
cDepartment of Physics, Technical University of Denmark, Lyngby, Denmark
dDepartment of Applied Physics and Institution of Energy and Microstructure, Nanjing University of Science and Technology, Nanjing 210094, Jiangsu, China
eUniversité Clermont Auvergne, SIGMA Clermont, Institut de Chimie de Clermont-Ferrand, 63000 Clermont-Ferrand, France
fThe State Key Laboratory of Experimental Hematology, SKLEH, Institute of Hematology, Chinese Academy of Medical Sciences, Tianjin 300020, China
gKey Laboratory for Special Function Materials and Structural Design of the Ministry of Education, National and Local Joint Engineering Laboratory for Optical Conversion Materials and Technology, School of Physical Science and Technology, Lanzhou University, Lanzhou 730000, China
First published on 9th September 2020
Abstract
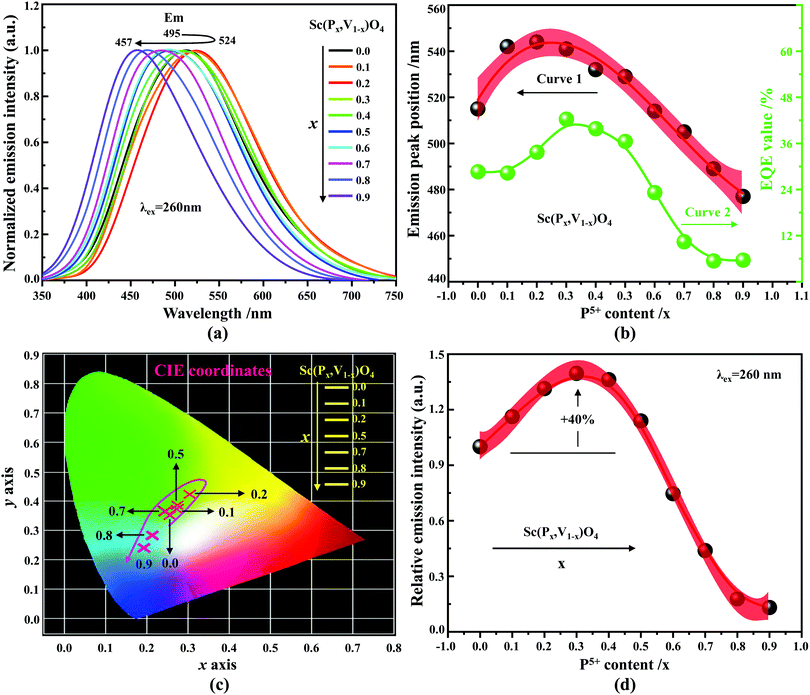
Spectrally tunable inorganic solid solutions discovered in the past few years generally cannot show spectral tuning properties without using either external rare earth (RE) (e.g., Eu2+, Ce3+) and non-RE (e.g., Mn2+, Bi3+) ions, or the coupling arrangement of these RE/non-RE ions as luminescent activator(s). Herein, we report a type of external dopant-free Sc(Px,V1−x)O4 (0.0 ≤ x ≤ 1.0) solid solution that exhibits color tuning, enhanced photoluminescence (PL) intensity, and improved thermally induced PL quenching stability. Our powder X-ray diffraction (XRD) and PL findings show that a gradual substitution of larger V5+ ions with smaller P5+ ions not only leads to the decrease of lattice parameters a(b)c and Sc–O bond lengths and the shrinkage of the cell volume (V), but also causes an initial redshift of the emission position from 495 nm to 524 nm as x increases to 0.2 followed by a subsequent blueshift back to 457 nm for 0.2 < x ≤ 0.9. Meanwhile, an enhancement of ∼40% of room temperature emission intensity at x = 0.3, along with improved quantum efficiency (QE) and thermal PL quenching after adding an appropriate amount of P5+ ions, is observed in the Sc(Px,V1−x)O4 (0.0 ≤ x ≤ 0.9) solid solutions. Through a combined analysis and discussion of the density functional theory (DFT) and dielectric electronegativity calculations as well as the UV-vis diffuse reflectance and temperature-dependent PL spectral measurements, we reveal that the origin of this unusual yet regular spectral tuning and the improved PL properties mostly arises from the interplay of the bandgap energy adjustment, the bond covalency regulation, and the possible presence of a significant amount of oxygen vacancies, together with the closing structural rigidity caused by the lattice microenvironment modification. This work can provide insights into designing and discovering new external dopant-free inorganic solid solutions with color tunability, improved emission intensity and thermally induced PL quenching behavior, and allow gaining better understanding on how the key parameters govern the spectral tunability in virgin (or doped) zircon crystal systems at the same time.
1. Introduction
Due to the merit of the flexible spectral wavelength selection for the device designer (e.g., the phosphor-converted white LED designer), spectrally tunable inorganic solid solutions, formed by the modification of the host isostructural ions that feature the same valence yet different ion radii at the same coordination number (CN), are now receiving growing attention, but almost all of the previously reported solid solutions cannot exhibit their spectral tuning when they lack a rare-earth (RE) and non-RE ion (e.g., Eu2+, Ce3+, Mn2+, Bi3+etc.) as the luminescent center, or the activators coupled by arrangement of these RE and/or non-RE ions.1–7 Besides, some solid solutions, such as (La,Gd)Sr2AlO5:Ce3+,1 Ca1−xLixAl1−xSi1+xN3:Eu2+,2 La2Mg(1−w)ZnwTiO6:Bi3+,Mn4+,4 and (Ca1−xSrx)16Si17N34:Eu2+,6 are found to show unexpected photoluminescence (PL) properties, which include, for instance, the enhanced PL intensity and/or the improved thermally induced PL quenching stability. However, RE- and non-RE-free inorganic solid solutions, which exhibit spectral tuning, enhanced PL intensity, and improved thermal PL stability simultaneously, have still not been reported so far. Note that the luminescent activators mentioned here are those ions that do not belong to any type of cation that constitutes the crystal host itself.LnBO4 (Ln = trivalent lanthanide or Sc3+; B = P5+, V5+, and Nb5+) is a type of important crystal system in the big family of inorganic oxides and possesses advantages of excellent thermal, chemical and mechanical stability, and optical properties. Relying on the Ln and B cations and the coupled arrangement of Ln and B cations, LnBO4 features various crystal systems, including zircon (e.g., ScVO4,8 ScPO4,9 and YVO4,10–12), monazite (e.g., LaPO413), fergusonite (e.g., GdNbO414), and wolframite (e.g., ScNbO415). As a result, diverse LnBO4-related applications, such as laser host materials,16 high-pressure mercury lamps,17 color-television tubes,18 infrared light detectors,19 photocatalysis,20 and ultrasonic generators,21 have been discovered. Among the LnBO4 crystals, zircon-type ScVO4 and ScPO4 crystals are two host materials particularly desirable for single trivalent RE (e.g., Eu3+/Tb3+,22–24 Dy3+,23 Ce3+/Er3+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 23,24) and non-RE (e.g., Bi3+
23,24) and non-RE (e.g., Bi3+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 26–28) dopants, or multiple dopants coupled by these RE and non-RE ions (e.g., Eu3+–Tb3+/Sm3+/Tm3+,22–24 Eu3+–Bi3+
26–28) dopants, or multiple dopants coupled by these RE and non-RE ions (e.g., Eu3+–Tb3+/Sm3+/Tm3+,22–24 Eu3+–Bi3+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 29). Accordingly, a variety of emission colors, such as green from Tb3+,22 red from Eu3+,23 blue from Tm3+,27 and reddish/red from Sm3+
29). Accordingly, a variety of emission colors, such as green from Tb3+,22 red from Eu3+,23 blue from Tm3+,27 and reddish/red from Sm3+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 24 or Bi3+,28 along with tunable colors from a combination of these dopants’ emissions,22,27,30 can be achieved using the ScVO4 and ScPO4 hosts. The crystal structures of ScBO4 (B = V, P), as shown in Fig. 1a, are relatively simple, containing only one type of Sc and B site coordinated respectively by eight and four oxygen atoms, but the Sc–O bonds have two different lengths.26,31–33 Since ScVO4 and ScPO4 are all crystallized in a tetragonal space group of I41/amd and the [ScO8] and [BO4] polyhedral structures share the same oxygen atoms and/or oxygen edges, the formation of the Sc(Px,V1−x)O4 (0 ≤ x ≤ 1) solid solutions becomes, therefore, possible. According to the ICSD files no. 78074 (i.e., for ScVO4) and no. 74483 (i.e., for ScPO4), we show the average V⋯O⋯Sc⋯O⋯V and P⋯O⋯Sc⋯O⋯P bond lengths, from which we can understand well the difference between the two isostructural crystals. Besides, in principle, since the number of Sc ions in the as-expected solid solutions is fixed, a regular change of the crystal lattice cell with the larger V5+ ions (i.e., 0.495 Å at four oxygen coordination numbers (CN)) being gradually replaced by the smaller P5+ (i.e., 0.31 Å at CN = 4)34–36 can therefore be expected further. In this case, when taken into account the emission positions of bulk ScVO4 (i.e., 465 nm,25,33 20.7 × 103 cm−3 (blue-green)32) and ScPO4 (i.e., 430 nm (blue) under a moist atmosphere,32 or ∼210 nm (UV, 5.6–5.9 eV) under dry conditions37,38), varying the V/P ratios in the as-expected Sc(Px,V1−x)O4 solid solutions may lead to spectral tuning. Meanwhile, due to the lattice microenvironment modification that results from the radii matching between the V5+ and P5+ ions, there may exist some unexpected PL properties. Furthermore, several experimental and theoretical studies39–45 have confirmed existence of the oxygen vacancies/defects in the ScVO4 crystals by means of e.g., reduction of a ScVO4 precursor under an H2/N2 flow,39 three-step liquid phase co-precipitation reaction,40 and two-,41 three-42 and four-step43 solid state reactions in air, and the vacancies/defects play a significant role in adjusting the mechanical, optical, and magnetic properties of the ScVO4 crystals.40,42 In this case, the substitution of V5+ ions with P5+ ions would affect the presence of the ScVO4-related vacancies/defects, typically in V-rich intermediate solid solution compounds. In this perspective, we believe that the vacancies/defects are also important in discussing the PL observations that we cannot predict but deserve to be taken into account seriously. Unfortunately, all of the aspects we observed above are still not discussed or noticed in the previous studies, which are also the major motivation of why we carry out this work.
24 or Bi3+,28 along with tunable colors from a combination of these dopants’ emissions,22,27,30 can be achieved using the ScVO4 and ScPO4 hosts. The crystal structures of ScBO4 (B = V, P), as shown in Fig. 1a, are relatively simple, containing only one type of Sc and B site coordinated respectively by eight and four oxygen atoms, but the Sc–O bonds have two different lengths.26,31–33 Since ScVO4 and ScPO4 are all crystallized in a tetragonal space group of I41/amd and the [ScO8] and [BO4] polyhedral structures share the same oxygen atoms and/or oxygen edges, the formation of the Sc(Px,V1−x)O4 (0 ≤ x ≤ 1) solid solutions becomes, therefore, possible. According to the ICSD files no. 78074 (i.e., for ScVO4) and no. 74483 (i.e., for ScPO4), we show the average V⋯O⋯Sc⋯O⋯V and P⋯O⋯Sc⋯O⋯P bond lengths, from which we can understand well the difference between the two isostructural crystals. Besides, in principle, since the number of Sc ions in the as-expected solid solutions is fixed, a regular change of the crystal lattice cell with the larger V5+ ions (i.e., 0.495 Å at four oxygen coordination numbers (CN)) being gradually replaced by the smaller P5+ (i.e., 0.31 Å at CN = 4)34–36 can therefore be expected further. In this case, when taken into account the emission positions of bulk ScVO4 (i.e., 465 nm,25,33 20.7 × 103 cm−3 (blue-green)32) and ScPO4 (i.e., 430 nm (blue) under a moist atmosphere,32 or ∼210 nm (UV, 5.6–5.9 eV) under dry conditions37,38), varying the V/P ratios in the as-expected Sc(Px,V1−x)O4 solid solutions may lead to spectral tuning. Meanwhile, due to the lattice microenvironment modification that results from the radii matching between the V5+ and P5+ ions, there may exist some unexpected PL properties. Furthermore, several experimental and theoretical studies39–45 have confirmed existence of the oxygen vacancies/defects in the ScVO4 crystals by means of e.g., reduction of a ScVO4 precursor under an H2/N2 flow,39 three-step liquid phase co-precipitation reaction,40 and two-,41 three-42 and four-step43 solid state reactions in air, and the vacancies/defects play a significant role in adjusting the mechanical, optical, and magnetic properties of the ScVO4 crystals.40,42 In this case, the substitution of V5+ ions with P5+ ions would affect the presence of the ScVO4-related vacancies/defects, typically in V-rich intermediate solid solution compounds. In this perspective, we believe that the vacancies/defects are also important in discussing the PL observations that we cannot predict but deserve to be taken into account seriously. Unfortunately, all of the aspects we observed above are still not discussed or noticed in the previous studies, which are also the major motivation of why we carry out this work.
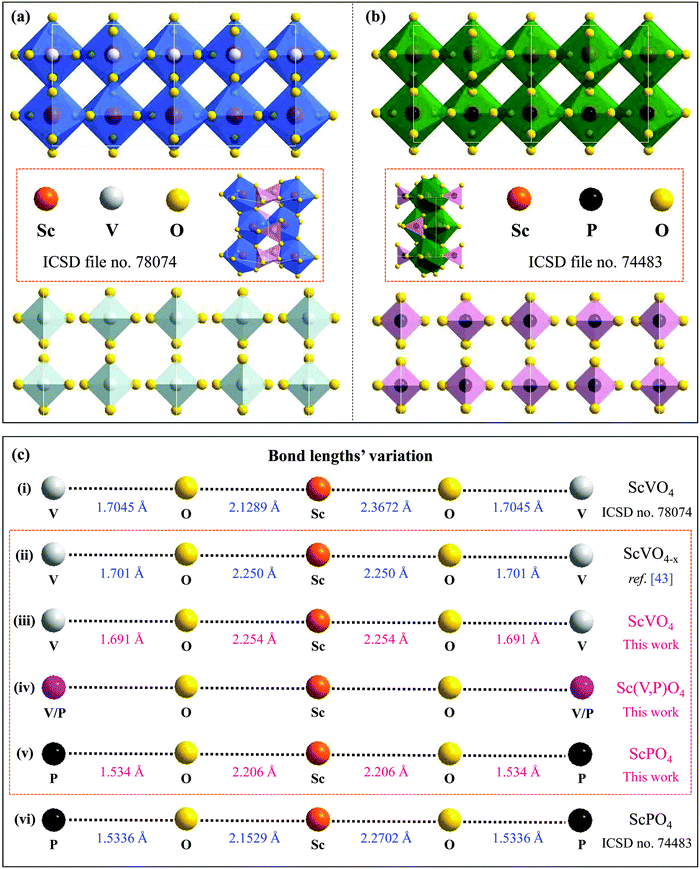 | ||
| Fig. 1 (a and b) Double cell X [−1…+1] of the ScVO4 and ScPO4 isostructural crystals based on the ICSD file no. 78074 and no. 74483, respectively, from which we can clearly see the coordination environments of P5+ and Sc3+ cations and that the [ScO8] and [PO4] polyhedral structures share the same oxygen atoms or the same oxygen edges; (c) The Sc–O and V–O bond lengths of ScPO4 and ScVO4 based on the ICSD file no. 78074 (i) and no. 74483 (vi), as well as the average lengths of Sc–O and V–O bonds achieved from the ScVO4−x crystal (ii),43 and the dependence of the average Sc–O and V/P–O bond length variation on the x value in the as-obtained Sc(Px,V1−x)O4 (0.0 ≤ x ≤ 1) solid solutions (iii–v). Noted that the average interatomic Sc–O and V/P–O distances in (ii), (iii) and (v) were calculated using Vesta software and the atomic positions we used for establishing the model were based on the refined XRD atomic positions. Since the Vesta modeling process does not consider other factors such as the XRD pattern backgrounds, scale factors, and peak shapes, the calculated Sc–O and V/P–O distances are a little shorter than that derived from the refined data, but they are all correct and fine results. | ||
In this work, we have prepared and characterized structurally and spectroscopically external dopant-free scandium-phosphorus vanadate solid solutions, i.e., Sc(Px,V1−x)O4 (0.0 ≤ x ≤ 1.0). We show that the PL properties of ScPxV1−xO4 (0.0 ≤ x ≤ 0.9) are very peculiar since: (1) emission is observed at room temperature, which is not expected in zircon orthovanadates, and (2) the emission position is found to first switch to longer wavelengths as x increases up to 0.3 and then tune back to shorter wavelengths as x increases further. This unusual behavior is investigated in detail based on Rietveld XRD refinement, bandgap energies and environmental factor calculations based respectively upon density functional theory (DFT) and dielectric theory of electronegativity, as well as UV-vis diffuse reflectance and temperature-dependent PL spectral measurements. The origin of this anomaly can allow gaining better insight into the key parameters governing the spectral tunability of virgin (or doped) zircon crystal systems.
2. Experimental details
Based upon the nominal chemical composition of Sc(Px,V1−x)O4 (0.0 ≤ x ≤ 1.0, with an interval x value of 0.1), we ground the raw reagents of Sc2O3 (99.9%), NH4H2PO4 (99.99%), and NH4VO3 (99.95%) in an agate mortar and then fired the mixtures at 1100 °C for 2 h in an alumina tube furnace under air atmosphere. After cooling down to room temperature, the products were ground again in the same agate mortar for the below-mentioned characterization.The powder X-ray diffraction (XRD) patterns were collected from a Rigaku D/max-IIIA X-ray diffractometer using Cu Kα radiation (λ = 1.5405 Å, 1.2° min−1) and a scanning rate of 1.2° min−1 in the 2θ range of 10–90°. To understand better the dependence relationship between the lattice structural variation and the P/V substitution ratio, we analyzed further the raw XRD data by using a FullProf Suite program. The excitation and emission spectra at room and high temperature were recorded on a Hitachi F-7000 spectrophotometer equipped with a 150 W xenon lamp as the excitation source. During the spectral collection, we kept the emission and excitation slits to 2.0 nm and 2.5 nm, respectively. The internal quantum efficiency (IQE) and external quantum efficiency (EQE) values were measured using a home-built PL quantum yield (QY) collection system which used a 266 nm UV laser (Jewel Laser series) as the excitation source and equipped with an integrating sphere connected to an optical spectrometer. The UV-vis diffuse reflectance spectra of the solid solutions were recorded on a Hitachi U-4100 UV-vis-NIR spectrophotometer by using BaSO4 as a reference.
3. Theoretical details
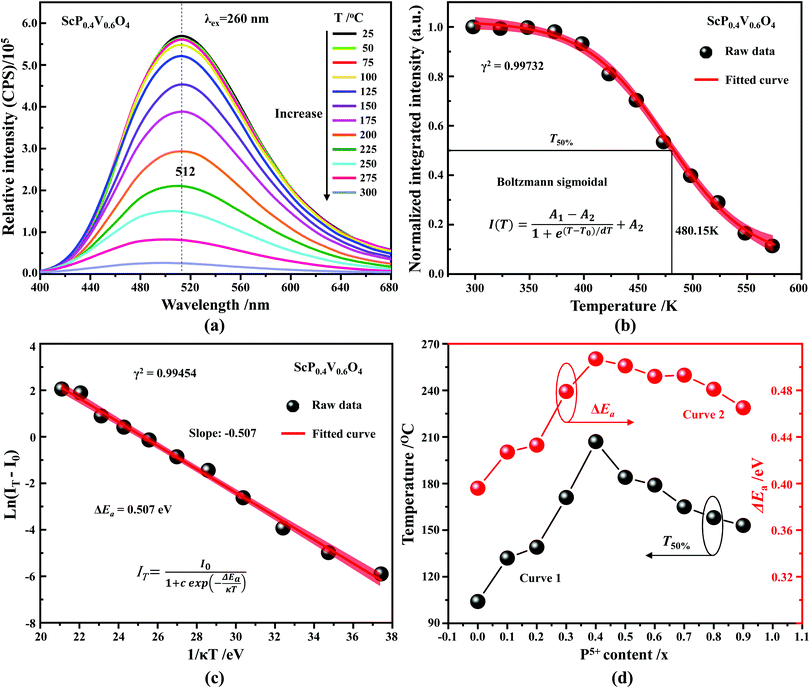
Our first-principle calculations were performed within the framework of DFT using the Vienna ab initio simulation package (VASP).46 A kinetic energy cutoff of 400 eV was used for the plane wave basis set expansion and 2π × 0.1 Å−1k-spacing had been chosen to sample the Brillouin zone. Lattice dynamical properties were calculated with projector-augmented plane-wave (PAW) potentials47 with the generalized gradient approximation (GGA) of Perdew–Burke–Ernzerhof (PBE) parametrization.48 The total energy and forces were converged to smaller than 10−7 eV and 10−2 eV Å−1 during the structural relaxation. To obtain an accurate bandgap, we also used the Heyd–Scuseria–Ernzerhof (HSE)49 screened hybrid functional. We adopted virtual crystal approximation (VCA) to describe the V–P alloying.A convenient manner to obtain information on the degree of covalency of a chemical bond in a crystal lattice is through calculating the environmental factor he(X) experienced by a cation site X of interest. The methodology derived from the dielectric theory of electronegativity50–52 that had been applied successfully to a wide variety of physical problems in the years 60–70 before being extended to phosphors at the end of the 90's53–56 and more recently in ref. 57. Following these models, we have the formula:
4. Results
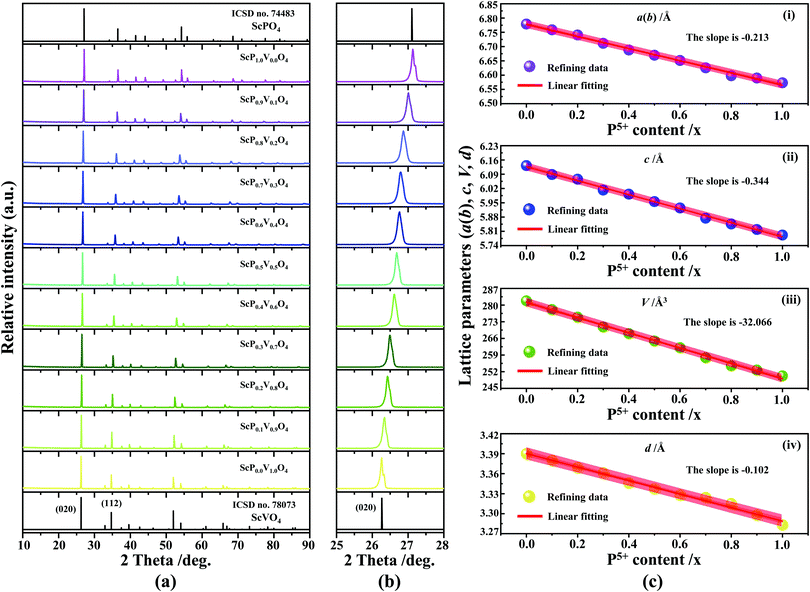
4.1 Analysis of structural phase-purity
The XRD patterns of Sc(Px,V1−x)O4 (0.0 ≤ x ≤ 1.0) (Fig. 2a) confirm the successful formation of continuous solid solutions that are crystallized in the zircon-type structure with a space group of I41/amd. As expected, the substitution of larger V5+ ions with smaller P5+ ions causes the shift of the diffraction position to a higher angle (Fig. 2b), revealing the shrinkage of the crystal lattice cell. The dhkl values corresponding to the plane spacing (020) reflection are compiled in Table 1 and Fig. 2c(i), which are evaluated by the Bragg equation of 2d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) sin
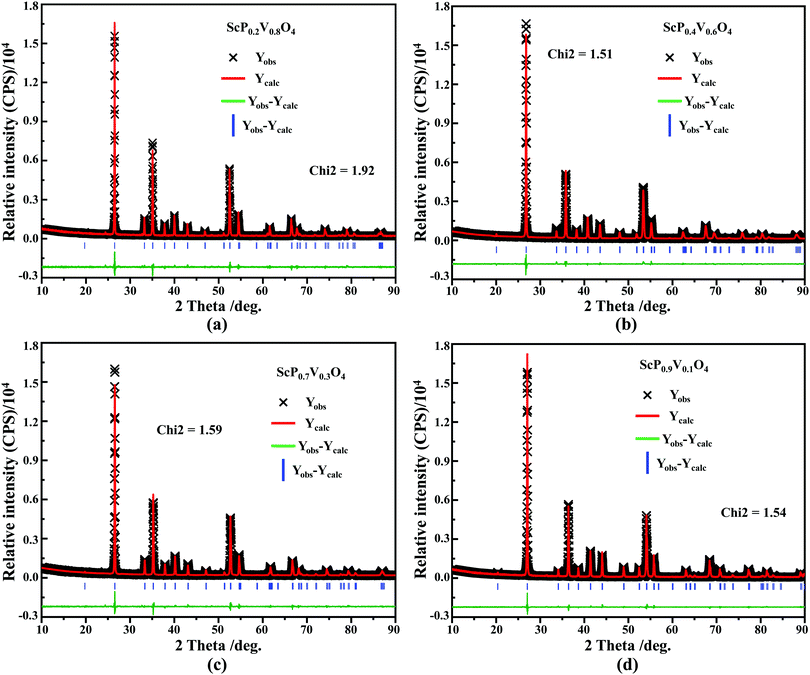
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ = λ (where λ is the X-ray wavelength, and θ is the diffraction angle).25,26 All the raw XRD data are refined further using the Rietveld refining method, and four typical refined XRD patterns are shown in Fig. 3, i.e., the Sc(Px,V1−x)O4 (x = 0.2 (Fig. 3a), 0.4 (Fig. 3b), 0.7 (Fig. 3c), and 0.9 (Fig. 3d)). The refined lattice parameters a(b)c and cell volumes (V) are compiled in Table 1, which, together with the refined finial reliability factors, reveal that our refined results are desirable. The P5+ content dependent lattice parameters a(b)c and V values can be linearly fitted (Fig. 2c(ii–iv)), revealing the regular variation of the crystal structure as the V5+ ions are replaced by the P5+ ions. Based on our refined parameters, we have re-drawn the crystal structure (Fig. 1b). Obviously, it is the same as that of Fig. 1a. Moreover, with Fig. 1c, we can also know how the V⋯O⋯Sc⋯O⋯V, V/P⋯O⋯Sc⋯O⋯V/P and P⋯O⋯Sc⋯O⋯P bond lengths change in the Sc(Px,V1−x)O4 (0.0 ≤ x ≤ 1.0) solid solutions with a substitution of larger V5+ ions with smaller P5+ ions.
θ = λ (where λ is the X-ray wavelength, and θ is the diffraction angle).25,26 All the raw XRD data are refined further using the Rietveld refining method, and four typical refined XRD patterns are shown in Fig. 3, i.e., the Sc(Px,V1−x)O4 (x = 0.2 (Fig. 3a), 0.4 (Fig. 3b), 0.7 (Fig. 3c), and 0.9 (Fig. 3d)). The refined lattice parameters a(b)c and cell volumes (V) are compiled in Table 1, which, together with the refined finial reliability factors, reveal that our refined results are desirable. The P5+ content dependent lattice parameters a(b)c and V values can be linearly fitted (Fig. 2c(ii–iv)), revealing the regular variation of the crystal structure as the V5+ ions are replaced by the P5+ ions. Based on our refined parameters, we have re-drawn the crystal structure (Fig. 1b). Obviously, it is the same as that of Fig. 1a. Moreover, with Fig. 1c, we can also know how the V⋯O⋯Sc⋯O⋯V, V/P⋯O⋯Sc⋯O⋯V/P and P⋯O⋯Sc⋯O⋯P bond lengths change in the Sc(Px,V1−x)O4 (0.0 ≤ x ≤ 1.0) solid solutions with a substitution of larger V5+ ions with smaller P5+ ions.
| X | Rietveld refined XRD parameters | DFT-Optimized a(b) and c values | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a(b)/Å | c/Å | V/Å3 | R p /% | R wp /% | R exp /% | R Bragg /% | R F /% | Chi2 | (020)/° | d hkl /Å | Sc–O/Å | a(b)/Å | c/Å | |
| a R p: profile factor. b R wp: weighted profile. c R exp: factor expected weighted profile factor. d R Bragg: Bragg factor. e R F: crystallographic factor. f —: not given. | ||||||||||||||
| No. 78073 | 6.78041 | 6.13451 | 282.03 | —f | — | — | — | — | — | — | — | — | 6.81615 | 6.14763 |
| 0.0 | 6.77894 | 6.13225 | 281.80 | 19.6 | 13.3 | 11.63 | 3.279 | 2.764 | 1.41 | 26.265 | 3.3901 | 2.3027 | 6.80319 | 6.11607 |
| 0.1 | 6.75879 | 6.08848 | 278.13 | 19.5 | 12.8 | 12.49 | 2.798 | 2.503 | 1.37 | 26.343 | 3.3803 | 2.2932 | 6.79330 | 6.07653 |
| 0.2 | 6.74064 | 6.06569 | 274.95 | 20.9 | 13.1 | 19.73 | 2.833 | 2.691 | 1.92 | 26.430 | 3.3693 | 2.2836 | 6.78678 | 6.05859 |
| 0.3 | 6.71137 | 6.01219 | 270.80 | 20.1 | 14.9 | 13.03 | 2.814 | 2.781 | 1.63 | 26.492 | 3.3616 | 2.2735 | 6.78060 | 6.03465 |
| 0.4 | 6.68809 | 5.99231 | 268.04 | 19.6 | 14.4 | 11.72 | 3.952 | 3.887 | 1.51 | 26.615 | 3.3463 | 2.2635 | 6.76314 | 5.99310 |
| 0.5 | 6.66973 | 5.95567 | 264.94 | 15.4 | 16.2 | 11.80 | 3.234 | 1.973 | 1.79 | 26.685 | 3.3377 | 2.2551 | 6.74104 | 5.94191 |
| 0.6 | 6.65137 | 5.92461 | 262.11 | 17.0 | 14.8 | 10.39 | 3.015 | 2.161 | 1.68 | 26.762 | 3.3283 | 2.2465 | 6.71116 | 5.88822 |
| 0.7 | 6.62547 | 5.87436 | 257.87 | 16.2 | 14.9 | 10.89 | 3.197 | 1.678 | 1.59 | 26.794 | 3.3244 | 2.2356 | 6.66779 | 5.83943 |
| 0.8 | 6.59784 | 5.84598 | 254.48 | 16.7 | 13.6 | 10.87 | 2.917 | 1.459 | 1.57 | 26.869 | 3.3153 | 2.2247 | 6.64385 | 5.81420 |
| 0.9 | 6.58996 | 5.81881 | 252.70 | 13.9 | 12.1 | 11.36 | 1.989 | 1.580 | 1.54 | 27.011 | 3.2982 | 2.2177 | 6.62343 | 5.78482 |
| 1.0 | 6.57320 | 5.79160 | 250.24 | 13.2 | 11.6 | 10.08 | 2.697 | 1.946 | 1.48 | 27.135 | 3.2834 | 2.2106 | 6.58242 | 5.76767 |
| Nno. 74483 | 6.57872 | 5.79632 | 250.86 | — | — | — | — | — | — | — | — | — | 6.62504 | 5.81775 |
4.2 Density functional theory (DFT) calculations and reflectivity spectra
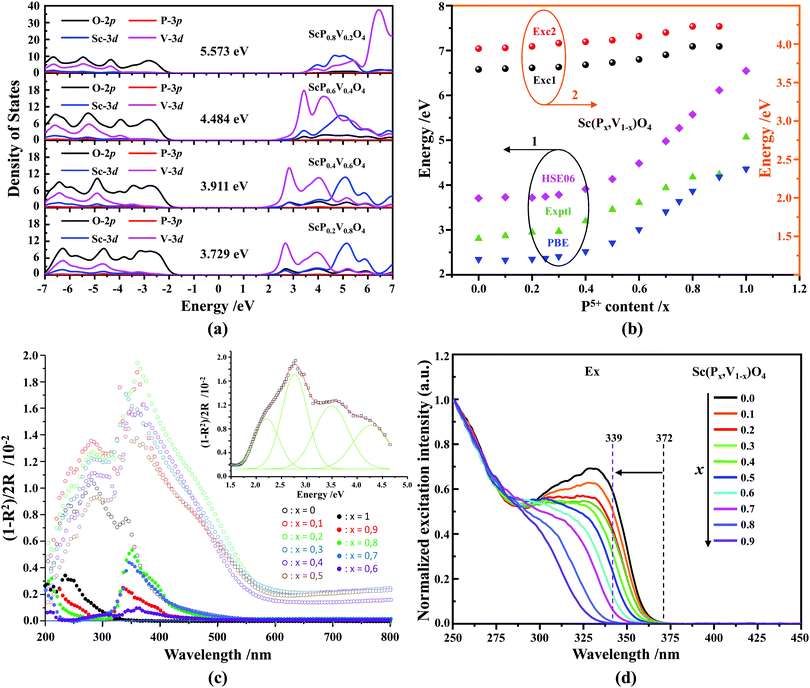
Fig. 4a shows the results of density of state (DOS) calculations for the energy region associated with the valence band (VB) and conduction band (CB) of Sc(Px,V1−x)O4 (x = 0.2, 0.4, 0.6, 0.8) solid solutions. For bulk ScPO4, the top of the VB and the bottom of the CB mainly consist of the O(2p) states with non-bonding character and the Sc(3d) empty states. The incorporation of V atoms results in the formation of antibonding V(3d) states at the bottom of the CB. These V(3d) states are strongly mixed with the Sc(3d) states, and their contributions become readily prominent as the V amount increases. The P(3p) states only weakly contribute to the bottom of the CB and can be neglected. The DFT-optimized parameters a(b)c and cell volumes (V) are listed in Table 1, the tendency of which is consistent with that of the Rietveld refined parameters. The electronic bandgap (Eg) energies of Sc(Px,V1−x)O4 (0.0 ≤ x ≤ 1.0) and the corresponding DOS position maxima for Sc(3d), V(3d), P(3p) and O(2p) states are given in eV in Tables 2 and 3, respectively.| x | Exptl Ega | Calcd Egb | Room temperature | High temperature | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Previous | Here | Previous | Here | Abs0 | Abs1 | Abs2 | R/% | Exc1 | Exc2 | λ em | I emr/% | CIE | IQE/% | EQE/% | T 50%/K | ΔEa | ||
| #, &, and $ denote the electronic bandgap (Eg) values are from ref. 13, 35 and 45, respectively.a Exptl: experimental.b Calcd: calculated.c —: Not given or measured. | ||||||||||||||||||
| —c | — | — | — | PBE | HSE06 | — | — | — | — | — | — | — | — | — | — | — | — | — |
| 0.0 | 2.80& | 2.81 | 2.56# | 2.344 | 3.706 | 3.27 | 3.63 | 4.29 | 12 | 3.67 | 3.94 | 2.50 | 100 | (0.193, 0.240) | 55.1 | 28.6 | 377.15 | 0.39 |
| 0.1 | — | 2.87 | — | 2.329 | 3.729 | 2.89 | 3.46 | 4.16 | 30 | 3.68 | 3.95 | 2.37 | 116.2 | (0.212, 0.283) | 57.3 | 28.3 | 405.15 | 0.43 |
| 0.2 | — | 2.95 | — | 2.348 | 3.721 | 2.73 | 3.42 | 4.33 | 21 | 3.69 | 3.97 | 2.36 | 131.4 | (0.242, 0.365) | 68.1 | 33.7 | 412.15 | 0.43 |
| 0.25 | — | — | 2.87 # | 2.369 | 3.743 | — | — | — | — | — | — | — | — | — | — | — | — | — |
| 0.3 | — | 2.97 | — | 2.407 | 3.785 | 2.70 | 3.51 | 4.42 | 24 | 3.70 | 4.01 | 2.38 | 139.6 | (0.253, 0.353) | 66.7 | 42.3 | 444.15 | 0.48 |
| 0.4 | — | 3.20 | — | 2.520 | 3.911 | 2.89 | 3.46 | 4.33 | 27 | 3.73 | 4.03 | 2.42 | 136.2 | (0.273, 0.373) | 59.9 | 39.8 | 480.15 | 0.51 |
| 0.5 | — | 3.46 | 2.92 # | 2.712 | 4.134 | 2.70 | 3.49 | 4.38 | 19 | 3.76 | 4.05 | 2.43 | 113.9 | (0.277, 0.389) | 50.1 | 36.5 | 457.15 | 0.50 |
| 0.6 | — | 3.61 | — | 3.008 | 4.484 | 2.97 | 3.49 | 4.13 | 18 | 3.80 | 4.1 | 2.51 | 74.6 | (0.297, 0.402) | 38.2 | 23.2 | 452.15 | 0.49 |
| 0.7 | — | 3.94 | — | 3.408 | 4.978 | 3.12 | 3.49 | 4.18 | 35 | 3.86 | 4.15 | 2.55 | 43.9 | (0.303, 0.422) | 35.3 | 10.4 | 438.15 | 0.49 |
| 0.75 | — | — | 3.20# | 3.636 | 5.271 | — | — | — | — | — | — | — | — | — | — | — | — | — |
| 0.8 | — | 4.18 | — | 3.863 | 5.573 | 3.03 | 3.59 | — | — | 3.97 | 4.23 | 2.64 | 17.7 | (0.273, 0.386) | 28.0 | 5.40 | 431.15 | 0.48 |
| 0.9 | — | 4.24 | — | 4.182 | 6.114 | 2.76 | 3.42 | — | — | 3.97 | 4.23 | 2.71 | 13.1 | (0.256, 0.350) | 27.6 | 5.60 | 426.15 | 0.46 |
| 1.0 | 7.2$ | 5.07 | 4.11# | 4.361 | 6.547 | — | — | — | — | — | — | — | — | — | — | — | — | — |
| x | DOS position maxima/eV | |||
|---|---|---|---|---|
| Sc(3d) | V(3d) | P(3p) | O(2p) | |
| 0.0 | 5.16 | 2.67 | — | −3.00 |
| 0.1 | 5.16 | 2.67 | −4.51 | −3.04 |
| 0.2 | 5.14 | 2.67 | −4.59 | −3.13 |
| 0.25 | 5.16 | 2.69 | −4.66 | −3.20 |
| 0.3 | 5.14 | 2.73 | −4.70 | −3.25 |
| 0.4 | 5.07 | 2.85 | −4.87 | −3.43 |
| 0.5 | 5.08 | 3.06 | −5.11 | −3.68 |
| 0.6 | 4.91 | 3.42 | −5.38 | −3.99 |
| 0.7 | 4.85 | 4.91 | −5.39 | −4.22 |
| 0.75 | 4.95 | 5.59 | −5.27 | −4.27 |
| 0.8 | 4.68 | 6.46 | −5.48 | −4.33 |
| 0.9 | 4.77 | 9.50 | −7.22 | −4.25 |
| 1.0 | 4.89 | --- | −7.80 | −3.65 |
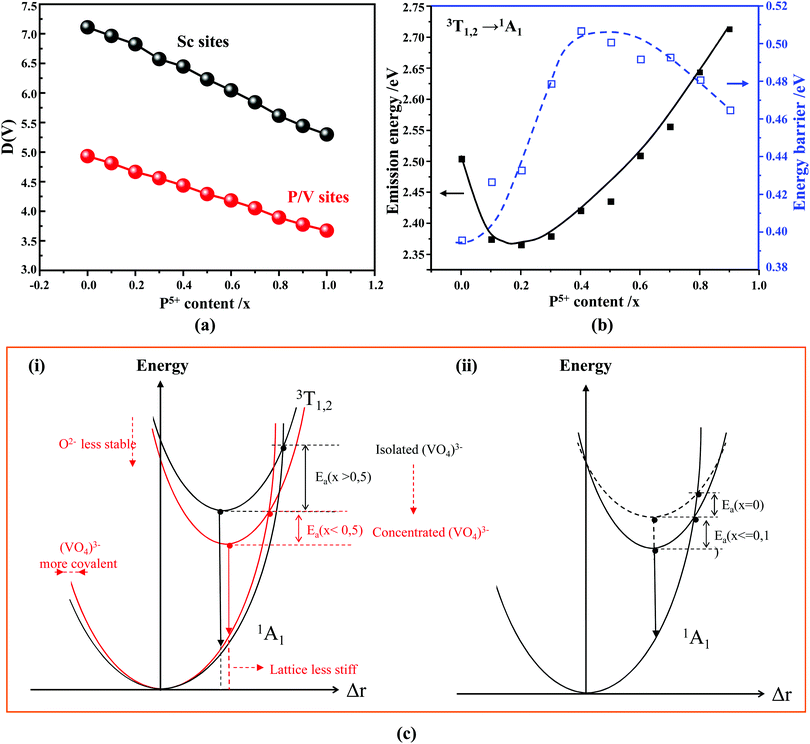
Our first-principles calculations reveal that a gradual substitution of V5+ ions with P5+ ions leads to a gradual increase of Eg energies (Table 2). Typically, the tendency of the Eg energies experiences a relatively flat increase with a P(x) content of less or equal to 0.2. But after that the Eg energy shows a fairly rapid growth as the P(x) content increases further. Although two DFT methods (i.e., PBE, and HSE06) have been adopted to calculate the Eg energies and the Eg values derived from the HSE06 functional (Fig. 4b, curve 2) are larger than those from the PBE functional (Fig. 4b, curve 1), the variation tendency of Eg is on the whole the same. Besides, the VCA simulation matches well the tendency reported in our previous work26 that used supercells to simulate the V–P alloying. To understand better this variation relationship and the differences of Eg values achieved by different DFT calculations, we show in Fig. 4b all the Eg energies.
In addition to the above DFT calculations, we also recorded the UV-vis diffuse reflectance spectra of Sc(Px,V1−x)O4 (0.0 ≤ x ≤ 1.0) at room temperature, and treated them using the Kubelka–Munk method through which the absorption coefficient α is estimated from the reflectance coefficient R using α = (1 − R)2/2R,7,60,61 as shown in Fig. 4c. Obviously, the samples with 0 ≤ x ≤ 0.5 present the strongest absorption in the UV-NUV region, and some of them also exhibit a certain strong absorption in the visible region (e.g., violet-blue), which contributes to color the powders’ body in yellow. In comparison, the samples with x > 0.5 only show reduced absorption in the visible region and thus appear as white body powders.
The reflectivity spectra corresponding to samples with 0 ≤ x ≤ 0.5 can be decomposed into a sum of 4 Gaussian curves, as representatively illustrated in the inset of Fig. 4c for Sc(P0.2,V0.8)O4. The energy positions of the first three absorption bands (i.e., Abs0, Abs1, and Abs2 in order of increasing energy) are listed in Table 2. The fourth component was found in average at 5.22 ± 0.15 eV. In the zircon-type vanadate system, the lower absorbing band Abs0 reveals the presence of defects associated with oxygen vacancies that form in concomitance with vanadium atoms in valence state +4 or +3 located in the V5+ or Y3+ crystal sites.62–64 Following the methodology introduced in ref. 65, we can qualitatively access the defect amounts by calculating the intensity ratio R = Abs0/(Abs0 + Abs1 + Abs2). This was made possible here by integrating the area of the corresponding Gaussian curves obtained after spectral decomposition. The values listed in Table 2 demonstrate the presence of defects in all phosphovanadates, with the amount being smaller in the end member ScVO4 of the solid solution.
Finally, indicative Eg values were determined by plotting the relationship of α(hν)2 = A(hν − Eg) where α, A and hv represent the Kubelka–Munk absorption, the absorption constant and the photon energy, respectively. The experimental Eg data (Table 2, and the curve 3 of Fig. 4b) follow the trends obtained by theoretical calculations, despite the contribution of band Abs0 to the absorption edge.
4.3 Photoluminescence (PL) properties
According to the archival literature studies,66,67 the structurally homogeneous zircon orthovanadates are not expected to show photoluminescence at room temperature. Following ref. 68, the excitation spectrum of the (VO4)3− complex groups in ScVO4 recorded at 77 K contains 3 distinct contributions in the spectral region that we have explored, i.e. Exc1 = 3.49 eV (355 nm), Exc2 = 3.90 eV (318 nm), and Exc3 beyond 5.14 eV (>240 nm), respectively. These excitation signals are due to 3t2 (O2−) → 2e (V5+) and t1 (O2−) → 2e (V5+) electron transitions associated with O2− (2p) → V5+ (3d) CT. The lowest excitation is ascribed to the 1A1 → 1T1 transition; it corresponds to the bandgap of ScVO4 and the excitation signal labelled as Exc1. The emission occurs from the close-lying 3T1,2 triplets and has a charge transfer (CT) character.66,69 It occurs at 483 nm (2.57 eV) in ScVO4 at 77 K.68 Here we observe that the Sc(Px,V1−x)O4 (x < 1) solid solutions glow in the green–blue spectral region when excited by UV light at room temperature. Since the ScPO4 does not glow and following earlier reports dedicated to YVO4,70–72 we ascribe this unusual room temperature emission to the tetrahedral tetroxo (VO4)3− complex groups perturbed by the previously evidenced lattice defects. The excitation spectra collected in correspondence with this emission are shown in Fig. 4d. A band with increasing contribution as x is lowered appears in the near-UV region. We have successfully achieved the spectral decomposition of the low energy part of the excitation spectra shown in Fig. 4d (expressing in energy) into a sum of 3 Gaussian-shaped bands. The third, higher-lying, excitation band is positioned at 5.09 ± 0.04 eV (243 ± 2 nm) and is about 4 times broader (≈1.06 eV) compared to the two other bands. The energy positions corresponding to Exc1 (curve 4) and Exc2 (curve 5) are plotted in Fig. 4b and compiled in Table 2. In the case of ScVO4, the values deviate somehow from the values reported by Boulon,68 which we ascribe to the perturbation (i.e., the local distortion of the (VO4)3− tetrahedral units) by lattice defects. Within the accuracy of the spectral decompositions, Exc1 and Exc2 agree with Abs1 and Abs2, respectively, while Abs3 agrees with Exc3. The agreement with DFT HSE06 calculations is also reasonably good for x ≤ 0.5 and then shows a divergence. Interesting to note is that Exc1 is not the lower-lying absorption in the Sc(Px,V1−x)O4 system.Despite the monotonic variation of the crystal structure and electronic properties of Sc(Px,V1−x)O4 as x increases from 0 to 1, we observe an irregular behavior of the (VO4)3− emission excited at 260 nm (i.e., corresponding to Abs2 or Exc2) that consists of a red shift of the position from 495 nm to 524 nm as x increases to 0.2 followed by a blue-shift back to 457 nm for 0.2 < x ≤ 0.9 (Fig. 5a–c). Concomitantly, we observe a continuous increase of the emission intensity with a maximum in the Sc(P0.3,V0.7)O4 sample and then a rapid decrease of the emitted intensity as x is increased further (Fig. 5d). Moreover, it is shown in Table 2 and Fig. 5b (curve 2) that the variation tendency of EQE values under 266 nm laser excitation basically matches that of the relative emission intensity (Fig. 5d), and it is obvious that the Sc(P0.3,V0.7)O4 sample has a maximum EQE of 42.3%. This PL behavior can be ascribed to the consequence of a complex compromise between the absorption rate at 260 nm (see Fig. 4c) and radiationless losses due to reabsorption by lattice defects contributing to band Abs0 and concentration quenching. In zircon vanadates, the concentration quenching involves the migration of the excitation energy among the isolated vanadate groups followed by radiationless losses of this excitation energy by energy transfer to sinks. As demonstrated by G. Blasse in the solid solution Y(P,V)O4,73 the energy migration and the related emission quenching by the concentration effect start operating for (VO4)3− doping rates of ≈25%, which can be expected to explain the PL intensity variation of the Sc(P,V)O4 in the same manner.
In addition to the room temperature spectra, we also have investigated the temperature-dependent emission spectra of Sc(Px,V1−x)O4 solid solution up to 300 °C, with the aim to collect information on the thermal quenching process and connect these data to the room temperature behaviors. We show the temperature-dependent emission spectra in Fig. 6a for the ScP0.4V0.6O4 sample, which is taken as a representative of the thermal evolution of emission spectra and intensity for all other samples. We also show in Table 2 the temperature T50% at which the emission intensity has lost 50% of its initial room temperature emission intensity in all compounds. The T50% values, as exemplarily depicted by the fitted T50% process of the ScP0.4V0.6O4 sample (Fig. 6b), were obtained by using the integrated emission intensity through the Boltzmann sigmoidal equation:74,75
The temperature-dependent intensity variation of the ScP0.4V0.6O4 sample was reproduced with a reliability above 99% using a single energy barrier model (Fig. 6c):2,3,6,11,60,61,73–76
5. Discussion
As known from the archival literature,77 the energy position of the O–V CT is related to the stabilization of the O2− ions by the electric field created by the nearby cations; the smaller the radius and the higher the charge of these ions, the more stable the O2− ions, the longer the O–V distance, the more ionic the character of the O–V bond, and the more the O–V CT moves to higher energy. Our results clearly demonstrate that this is what happens as x is increased in the Sc(Px,V1−x)O4 solid solutions. We note, however, that the upward shift of the O–V CT is not regular; it is moderate up to x ≈ 0.5 and then accelerates, which is referred to as the bandgap bowing. The lowering of the degree of covalency of the V–O bond on going from ScVO4 to ScPO4 is well confirmed by the regular increase of he(Sc) from 0.95 to 0.97 with a concomitant increase of the bond valence sum (BVS) of Sc from +2.81 to +3.07 that accounts for a reinforcement of the degree of covalency of the Sc–O bond at the expense of that of the V–O bond. In addition to these trends, the progressive increase of the phosphorous amount contributes to enhance the maximum phonon frequency of the crystal lattice (viz. with 914 cm−1 in ScVO478 and up to 1083 cm−1 in ScPO479) and the lattice stiffness around the V atoms as formalized by calculating the lattice distortion D(V) at V sites following the below equation:3,60where li and lav are the distances from V to the ith coordinated O atoms and the average V–O bond lengths, respectively. Values are plotted in Fig. 7a, where the decrease of D(V) values with the increase of P5+ (x) content reveals a closing structural rigidity.
On the above grounds, we further discuss the evolution of the optical behavior of the (VO4)3− groups going from isolated to concentrated systems. As specified earlier and represented in Fig. 7b, the emission intensity maxima of the (VO4)3− groups experiences a redshift on going from ScP0.9V0.1O4 to ScP0.2V0.8O4 followed by a sudden blueshift going from ScP0.1V0.9O4 to ScVO4. Concomitantly, the energy barrier ΔEa associated with the thermal quenching of the emission first increases on going from ScP0.9V0.1O4 to ScP0.6V0.4O4 and then decreases regularly. These variations are due to the subtle consequences of the gradual changes experienced by the crystal lattice across the solid solutions. To conveniently and qualitatively understand these evolutions, we plot a single coordinate configurational diagram based on the potential energy of the (VO4)3− luminescent unit (Fig. 7c(i)). In general, the average distance between the central metal ion and its surrounding anions is taken for this purpose. Within this model, the emission occurs from the thermalized close-lying 3T1,2 excited states to the 1A1 ground state after that internal radiationless relaxation from the absorbing 1T1 state has occurred. Thermal quenching of the emission occurs by cross-over of 3T1,2 to the 1A1 ground state, and it depends critically on the equilibrium distance Δr of the ground and excited states. Thereby, we can understand that the decrease of the lattice stiffness as the vanadate amount is increased releases the constraints experienced by the V–O bond upon optical excitation, increases the Δr, and results in smaller values of ΔEa and of the emission energy (Fig. 7c(i), from a black curve to a red 3T1,2 curve). These effects are reinforced by the downward shift of the excited 1T1 and 3T1,2 states and by the lowering of the bonding force between the V and its nearby O atoms that results in a smaller force constant of the 1A1 ground state potential curve (Fig. 7c(i), red 1A1 curve) on going from ScP0.9V0.1O4 to ScP0.2V0.8O4. The observed blueshift of the 3T1,2 → 1A1 emission in concomitance with the continuous decrease of ΔEa on going from ScP0.9V0.1O4 to ScVO4 is accounted by a lowering of the force constant associated with the 3T1,2 potential curve, as we show in Fig. 7c(ii) (from solid to dotted 3T1,2 curve). We infer that this modification from the V–O bond is related to a smaller amount of oxygen vacancies in ScVO4 as compared to ScP0.9V0.1O4 (see Fig. 4c(i) and Table 2). In this regard, we show in Table 4 the environmental factors and bond valence sums that we have calculated for the end members of the solid solutions, including the data extracted from the archival literature studies and different ICSD files. Clearly, the results show little variability in the case of ScPO4 but are more largely dispersed in ScVO4. We estimate that this variability of BVS(V/P) and he(V/P) values is an indication of the amount of oxygen vacancies contained in the ScVO4 lattice. To support this statement, the crystal structure of the vacancy contained ScVO4 crystals, such as of ScVO3.5+x42 and ScVO4−x,43 has been investigated, where we observe that the presence of oxygen vacancies tends to increase the BVS(V) and correlated he(V) values. Our ScVO4 compound and compound ScVO4-ICSD 164837 exhibit larger BVS(V) and he(V) values of the series and are therefore suspected to contain the largest amount of oxygen vacancies. Furthermore, the BVS(P) and he(P) values of the ScPO4 compound (i.e., a compound with V-free oxygen vacancies) match precisely with the values calculated from other previously investigated ScPO4 compounds. We are currently focusing on this particular point by investigating the ESR signatures of the Sc(Px,V1−x)O4 (0.0 ≤ x ≤ 0.9) solid solutions. This work is not presented here but under progress and will be the subject of a forthcoming paper soon.
| Crystal lattice | Sc–O bond/Å | he(Sc) | BVS(Sc) | V/P–O bond/Å | he(V/P) | BVS(V/P) | Ref. |
|---|---|---|---|---|---|---|---|
| ScVO4 – ICSD 78073 | 2.248 | 0.956 | +2.86 | 1.704 | 3.316 | +5.22 | — |
| ScVO4 – ICSD 164837 | 2.252 | 0.951 | +2.81 | 1.693 | 3.350 | +5.39 | — |
| ScVO4 – ICSD 169173 | 2.248 | 0.956 | +2.86 | 1.709 | 3.307 | +5.16 | — |
| ScVO4 – ICSD 174155 | 2.250 | 0.956 | +2.85 | 1.701 | 3.323 | +5.26 | — |
| ScVO4−x | 2.250 | 0.956 | +2.85 | 1.701 | 3.324 | +5.26 | 43 |
| ScVO4 | 2.254 | 0.953 | +2.81 | 1.691 | 3.354 | +5.41 | This work |
| ScPO4 – ICSD 74483 | 2.211 | 0.967 | +3.04 | 1.534 | 2.666 | +4.84 | — |
| ScPO4 – ICSD 201132 | 2.207 | 0.966 | +3.07 | 1.534 | 2.664 | +4.83 | — |
| ScPO4 – ICSD 275305 | 2.208 | 0.967 | +3.07 | 1.537 | 2.661 | +4.80 | — |
| ScPO4 | 2.206 | 0.967 | +3.07 | 1.534 | 2.666 | +4.84 | This work |
6. Conclusion and perspectives
In summary, we used a conventional high temperature solid-state reaction method to synthesize a type of external dopant-free Sc(Px,V1−x)O4 (0.0 ≤ x ≤ 1) solid solution and reveal that they are all crystallized in the zircon-type structure with a space group of I41/amd as confirmed by the powder XRD patterns and corresponding Rietveld refinement results. In addition, as expected, the XRD positions with the substitution of larger V5+ by smaller P5+ ions follow the Vegard's law nicely, where the shrinkage of the crystal lattice parameters a(b)c, cell volumes (V) and average Sc–O lengths is observed. Our PL findings show that beyond ScPO4, other compounds, i.e., Sc(Px,V1−x)O4 (0.0 ≤ x ≤ 0.9), exhibit that the emission position initially shifts from 495 nm to 524 nm followed by a subsequent blue-shift back to 457 nm as the x is gradually increased from 0.0 to 0.9. Meanwhile, an enhancement of ∼40% of room temperature emission intensity, together with an optimal improved thermally induced PL quenching stability, referenced by the emission intensity of bulk ScVO4, is observed in the intermediate ScP0.3V0.7O4 and ScP0.4V0.6O4 samples, respectively. The DFT calculations reveal the P5+ (x) content dependent electronic band-gap (Eg) energies in the Sc(Px,V1−x)O4 (0.0 ≤ x ≤ 1.0) solid solutions, and the variation tendency of the Eg values matches with those experimentally derived from the diffuse reflectance spectra. Through a combination of the DFT and dielectric electronegativity calculations and corresponding discussions, the underlying reason for the observed color tuning and the improved PL properties is mostly due to the interplay of the electronic bandgap energy adjustment, the bond covalency regulation, the gradual closing structural rigidity caused by the lattice microenvironment modification, and the contribution of lattice defects like oxygen vacancies. Based on the potential energy of the luminescent centre (i.e., (VO4)3− unit) and relevant analysis and discussion, a convenient yet qualitative single-coordinate configurational diagram is constructed further to discuss the observed PL evolutions.Retrospecting this work, it is a little pity that the external dopant-free Sc(Px,V1−x)O4 (0.0 ≤ x ≤ 1) emission-tunable solid solutions do not belong to the class of phosphor materials particularly desirable for phosphor-converted white LEDs because of the following reasons: on one hand, the weakness of their excitation ranges less than the mainstream commercial UV LED chips with emission ranges of 375–410 nm and, on the other hand, their relatively low EQE (λex = 266 nm laser, 5.6–42.3%) values compared to those of RE and/or non-RE doped phosphor materials such as SrxBa2−xSiO4:Eu2+ (λex = 405 nm laser, x = 43–73%, quantum yield (QY) = 88–90%),2 (Y,Lu)VO4:0.02Bi3+ (λex = 330 nm xenon lamp, EQE = 75% for YVO4:Bi3+, and 68% for LuVO4:Bi3+),25 ScVO4:0.01Bi3+ (λex = 330 nm, and 380 nm xenon lamp, EQE = 56%, and 57%, respectively),28 Ca0.97−xSrxSc2O4:0.03Ce3+ (λex = 437 nm xenon lamp, x = 0–1, internal QY (IQY) = 84.8–94.6%),60 K2MgGeO4:0.01Bi3+ (λex = 335 nm xenon lamp, x = 0–1, EQE = 66.6%),61 Y2Mo4O15:0.5%Eu3+ (λex = 465 nm xenon lamp, QY = 85%),75 SrYSi4N7:0.01Eu2+ (λex = 365 nm xenon lamp, QE = ∼41.6%),76 and Sr2.975−xCe0.025BaxAlO4F (λex = 405 nm InGaN LED, QE = ∼100%),80 as well as X2-type Y1.98SiO5:0.01Bi3+,0.01Eu3+ (λex = 360 nm xenon lamp, EQE = 78%).81 However, this situation is reasonable and can be understandable because the Sc(Px,V1−x)O4 solid solutions belong to the family of self-activated phosphors whose luminescence is mainly due to the existence of complex groups and/or defects.82 As a result, in most cases, the self-activated phosphors usually can only show QE values less than 50%, such as those summarized by Dang et al.,83 Huang et al.,84 and Zhou et al.,85 as well as Ba2V2O7 (λex = 360 nm xenon lamp, IQE = 47.5%),86 Ba2V2O7 (IQE = 25.0%),87 Mg3V2O8 (λex = 350 nm xenon lamp, IQE = 6.0%),88 KCa2Mg2V3O12 (λex = 346 nm xenon lamp, IQE = 41.0%),89 although a tiny of them are reported to have high IQE values, such as Rb3YV2O8 (λex = 362 nm xenon lamp, IQE = 71%),83 and Rb3YV2O8 (λex = 362 nm xenon lamp, IQE = 82%),83 and those summarized by Huang et al.,84 and Zhou et al.85 Looking into the IQE and/or EQE values we obtained, it is obvious that some of them, typically for the Sc(P0.3,V0.7)O4 sample, are comparable to and can even be higher than those of many reported self-activated phosphors and some other RE/non-RE doped crystals, such as ScVO4:0.02Bi3+ (λex = 330 nm xenon lamp, EQE = 35%),25 CsPbCl3 (λex = 360 nm xenon lamp, QY = 26.0 ± 0.3%),90 CsxK1−xPbCl3:Eu3+ (λex = 365 nm xenon lamp, EQE = 31.2%),91 and CsPbCl3:Mn2+ (λex = 360 nm xenon lamp, QY = 27%).92 Moreover, the improved thermal stability (T50%) of 480.15 K and/or activation energies (ΔEa) of 0.51 eV for the Sc(P0.4,V0.6)O4 solutions are also higher than or comparable to those of some RE/non-RE doped phosphors, for example, La2MgTiO6:0.005Bi3+ (λex = 350 nm xenon lamp, T50% = ∼175 °C, ΔEa = 0.27 eV),4 La2MgTiO6:0.005Bi3+ (λex = 410 nm xenon lamp, T50% = ∼250 °C, ΔEa = 0.252 eV),6 CaSc2O4:Ce3+ (λex = 437 nm, T50% = ∼225 °C, ΔEa = 0.195 eV),60 K2MgGeO4:Bi3+ (λex = 335 nm xenon lamp, ΔEa = ∼0.397 eV),61 Ca7.92Mg3Al2Si7O28:0.01Eu2+ (λex = 365 nm xenon lamp, ΔEa = 0.2502 eV)74 and Y1.98SiO5:0.01Bi3+,0.01Eu3+ (λex = 360 nm xenon lamp, ΔEa = 0.391 eV),81 and the reported self-activated phosphors like Rb3YV2O8 (λex = 362 nm, T50% = ∼423 K, ΔEa = ∼0.264 eV),83 Ca5Mg4(VO4)6 (T50% = ∼85 °C),84 KCa2Mg2V3O12 (λex = 346 nm, ΔEa = 0.366 eV, T50% = ∼380 K),89 Na1.3Mg1.7V2.7Mo0.3O10 (T50% = ∼115 °C),93 Ca2KZn2(VO4)3 (ΔEa = 0.469 eV, T50% = ∼60 °C),94 CsVO3 (ΔEa = 0.31 eV).95
More importantly, the fundamental aspects this work provided can deepen the understanding of the intrinsic working principle of the PL color tuning, enhanced PL intensity and improved thermal stability appeared in future spectrally tunable inorganic solid solutions. Meanwhile, it can provide some insights into designing and discovering new external dopant-free emission-tunable inorganic solid solutions through manipulating high valence secondary cations (e.g., P5+ and V5+ cations).
Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.Acknowledgements
We acknowledge the funding from the European Union's Seventh Framework Programme and Horizon 2020 Research and Innovation Programme under the Marie Sklodowska-Curie Actions grant agreement no. 609405 (FP7) and 713683 (H2020), Jiangsu Province Science Foundation for Youth (project no. BK20170821), and the National Science Foundation of China for Youth (project no. 11804160).References
- Z. Yu, Z. G. Xia, C. C. Su, R. L. Wang and Q. L. Liu, Effect of Gd/La substitution on the phase structures and luminescence properties of (La,Gd)Sr2AlO5:Ce3+ solid solution phosphors, J. Mater. Chem. C, 2015, 3, 11629–11634 Search PubMed.
- A. D. Kristin, B. Jakoah, W. G. Michael, M. Alexander, P. Ralf, W. Holger, P. D. Steven and S. Ram, Consequences of Optimal Bond Valence on Structural Rigidity and Improved Luminescence Properties in SrxBa2−xSiO4:Eu2+ Orthosilicate Phosphors, Chem. Mater., 2014, 26, 2275–2282 Search PubMed.
- L. Wang, R. J. Xie, Y. Q. Li, X. J. Wang, C. G. Ma, D. Luo, T. Takeda, Y. T. Tsai, R. S. Liu and N. Hirosaki, Ca1−xLixAl1−xSi1+xN3:Eu2+ solid solutions as broadband, color-tunable and thermally robust red phosphors for superior color rendition white light-emitting diodes, Light: Sci. Appl., 2016, 5, e16155 Search PubMed.
- G. C. Xing, Y. X. Feng, M. Pan, Y. Wei, G. G. Li, P. P. Dang, S. S. Liang, M. S. Molokeev, Z. Y. Cheng and J. Lin, Photoluminescence tuning in a novel Bi3+/Mn4+ co-doped La2ATiO6: (A = Mg, Zn) double perovskite structure: phase transition and energy transfer, J. Mater. Chem. C, 2018, 6, 13136–13147 Search PubMed.
- Y. F. Liu, X. Zhang, Z. D. Hao, W. Lu, X. Y. Liu, X. J. Wang and J. H. Zhang, Crystal structure and luminescence properties of (Ca2.94−xLuxCe0.06)(Sc2−yMgy)Si3O12 phosphors for white LEDs with excellent colour rendering and high luminous efficiency, J. Phys. D: Appl. Phys., 2011, 44, 075402 Search PubMed.
- H. Chen, J. Y. Ding, X. Ding, X. C. Wang, Y. X. Cao, Z. Y. Zhao and Y. H. Wang, Synthesis, Crystal Structure, and Luminescence Properties of Tunable Red-Emitting Nitride Solid Solutions (Ca1−xSrx)16Si17N34:Eu2+ for White LEDs, Inorg. Chem., 2017, 56, 10904–10913 Search PubMed.
- B. I. Won, G. Nathan, K. Joshua, B. Stuart, M. Alexander, H. Jerry, F. C. Bradley, P. D. Steve and S. Ram, Efficient and Color-Tunable Oxyfluoride Solid Solution Phosphors for Solid-State White Lighting, Adv. Mater., 2011, 23, 2300–2305 Search PubMed.
- W. Urban, EPR Parameters and Temperature Effects of Gd3+ in ScVO4, Phys. Status Solidi A, 1970, 37, 181–186 Search PubMed.
- F. X. Zhang, J. W. Wang, M. Lang, J. M. Zhang and R. C. Ewing, High-pressure phase transitions of ScPO4 and YPO4, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 184114 Search PubMed.
- M. Yu, J. Lin and J. Fang, Silica Spheres Coated with YVO4:Eu3+ Layers via Sol-Gel Process:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A Simple Method To Obtain Spherical Core-Shell Phosphors, Chem. Mater., 2005, 17, 1783–1791 Search PubMed.
A Simple Method To Obtain Spherical Core-Shell Phosphors, Chem. Mater., 2005, 17, 1783–1791 Search PubMed. - M. Yu, J. Lin, Z. Wang, J. Fu, S. Wang, H. J. Zhang and Y. C. Han, Fabrication, Patterning, and Optical Properties of Nanocrystalline YVO4:A (A = Eu3+, Dy3+, Sm3+, Er3+) Phosphor Films via Sol–Gel Soft Lithography, Chem. Mater., 2002, 14, 2224–2231 Search PubMed.
- M. Yu, J. Lin and S. B. Wang, Effects of x and R3+ on the luminescent properties of Eu3+ in nanocrystalline YVxP1−xO4:Eu3+ and RVO4:Eu3+ thin-film phosphors, Appl. Phys. A., 2005, 80, 353–360 Search PubMed.
- T. S. Michael, L. M. Martha and E. D. M. Peter, Synthesis of monoclinic monazite, LaPO4, by direct precipitation, J. Mater. Chem., 2009, 19, 5720–5722 Search PubMed.
- J. W. Hou, R. Zhou, J. W. Zhang, Z. P. Wang, Z. M. Zhang and Z. J. Ding, Pressure and Temperature Study on the Structural Stability of GdNbO4:Eu3+, J. Phys. Chem. C, 2017, 121, 14787–14794 Search PubMed.
- G. Blasse, G. J. Dirksen and L. H. Brixner, The influence of structural disorder on the luminescence of niobates: scandium niobate (ScNbO4) and magnesium niobate (MgNb2O6), Mater. Chem. Phys., 1986, 14, 485–494 Search PubMed.
- O. Guillot-Noel, B. Viana, B. Bellamy, D. Gourier, G. B. Zogo-Mboulou and S. Jandl, Spectroscopic evidence of inhomogeneous distribution of Nd3+ in YVO4, YPO4 and YAsO4 crystals, Opt. Mater., 2000, 13, 427–437 Search PubMed.
- E. W. Herold, A History of Color Television Displays, Proc. IEEE, 1976, 64, 1331–1338 Search PubMed.
- C. P. Frank and K. L. Albert, YVO4:Eu: a Highly Efficient, Red-Emitting Phosphor for High Pressure Mercury Lamps, Appl. Opt., 1966, 5, 1467–1468 Search PubMed.
- L. C. Meng, L. HØgstedt, P. Tidemand-Lightenberg, C. Pedersen and P. J. Rodrigo, GHz-bandwidth upconversion detector using a unidirectional ring cavity to reduce multilongitudinal mode pump effects, Opt. Mater. Express, 2017, 25, 14783–14794 Search PubMed.
- Y. Shiraishi, S. Takeshita and T. Isobe, Two Photoenergy Conversion Modes of YVO4:Eu3+ Nanoparticles: Photoluminescence and Photocatalytic Activity, J. Phys. Chem. C, 2015, 119, 13502–13508 Search PubMed.
- D. M. Li, P. F. Li, Y. Li, X. X. Wu, G. Y. Fu, Z. X. Liu, X. L. Wang, Q. L. Cui and H. Y. Zhu, High-Pressure Studies of Rubidium Azide by Raman and Infrared Spectroscopies, J. Phys. Chem. C, 2015, 119, 16870–16878 Search PubMed.
- R. Y. Mi, J. Chen, Y. G. Liu, M. H. Fang, L. F. Mei, Z. G. Huang, B. C. Wang and C. L. Zhao, Luminescence and energy transfer of a color tunable phosphor: Tb3+ and Eu3+ co-doped ScPO4, RSC Adv., 2016, 6, 28887–28894 Search PubMed.
- J. A. Dorman, J. H. Choi, G. Kuzmanich and J. P. Chang, High-Quality White Light Using Core-Shell RE3+:LaPO4 (RE = Eu, Tb, Dy, Ce) Phosphors, J. Phys. Chem. C, 2012, 116(23), 12854–12860 Search PubMed.
- H. J. Chang, Y. S. Zhu, J. Xie, H. Y. Li, B. T. Liu, S. L. Xu, X. J. Xie, L. Huang and W. Huang, Surfactant effect on and luminescence tuning of lanthanide-doped ScPO4·2H2O microparticles, J. Mater. Chem. C, 2015, 3, 12385–12389 Search PubMed.
- F. W. Kang, M. Y. Peng, X. B. Yang, G. P. Dong, G. C. Nie, W. J. Liang, S. H. Xu and J. R. Qiu, Broadly tuning Bi3+ emission via crystal field modulation in solid solution compounds (Y,Lu,Sc)VO4:Bi for ultraviolet converted white LEDs, J. Mater. Chem. C, 2014, 2, 6068–6076 Search PubMed.
- F. W. Kang, G. H. Sun, P. Boutnaud, F. Gao, Z. H. Wang, J. Lu, Y. Y. Li and S. S. Xiao, Tuning the Bi3+-photoemission color over the entire visible region by manipulating secondary cations modulation in the ScVxP1−xO4:Bi3+ (0 ≤ x ≤ 1) solid solution, J. Mater. Chem. C, 2019, 7, 9865–9877 Search PubMed.
- D. Y. Shen, Y. F. Zhang, X. M. Zhang, Z. L. Wang, Y. F. Zhang, S. S. Hu and J. Yang, Morphology/phase controllable synthesis of monodisperse ScVO4 microcrystals and tunable multicolor luminescence properties in Sc(La)VO4(PO4):Bi3+,Ln3+ phosphors, CrystEngComm, 2018, 20, 5180–5190 Search PubMed.
- F. W. Kang, X. B. Yang, M. Y. Peng, L. Wondraczek, Z. J. Ma, Q. Y. Zhang and J. R. Qiu, Red Photoluminescence from Bi3+ and the Influence of the Oxygen-Vacancy Perturbation in ScVO4: A Combined Experimental and Theoretical Study, J. Phys. Chem. C, 2014, 118, 7515–7522 Search PubMed.
- F. F. Chi, Y. G. Qin, F. F. Hu, X. T. Wei, Y. H. Chen, C. K. Duan and M. Yin, Efficient red-emitting phosphor ScVO4 doped with Bi3+ and Eu3+ for near-ultraviolet-activated solid-state lighting, J. Mater. Sci., 2017, 52, 11592–11597 Search PubMed.
- H. L. Xu, B. Xu, R. Liu, X. W. Li, S. Q. Zhang, C. Y. Ouyang and S. L. Zhong, Facile microwave synthesis of ScPO4·2H2O flowerlike superstructures: morphology control, electronic structure and multicolor tunable luminescent properties, CrystEngComm, 2017, 19, 5787–5796 Search PubMed.
- W. O. MilliganD, D. F. Mullica, G. W. Beall and L. Boatner, Structural investigations of YPO4, ScPO4, and LuPO4, Inorg. Chim. Acta, 1982, 60, 39–43 Search PubMed.
- G. Blasse and A. Bril, Luminescence of Phosphors Based on Host Lattices ABO4 (A is Sc, In; B is P, V, Nb), J. Chem. Phys., 1969, 50, 2974–2980 Search PubMed.
- F. W. Kang, H. S. Zhang, L. Wondraczek, X. B. Yang, Y. Zhang, D. Y. Lei and M. Y. Peng, Band-Gap Modulation in Single Bi3+-Doped Yttrium-Scandium-Niobium Vanadates for Color Tuning over the Whole Visible Spectrum, Chem. Mater., 2016, 28, 2692–2703 Search PubMed.
- L. H. Ahrens, The use of ionization potentials Part 1. Ionic radii of the elements, Geochim. Cosmochim. Acta, 1952, 2, 155–169 Search PubMed.
- L. Pauling, The Nature of the Chemical Bond, Cornell University Press, Ithaca, 1961 Search PubMed.
- R. D. Shannon, Revised Effective Ionic Radii and Systematic Studies of Interatomic Distances in Halides and Chalcogenides, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751 Search PubMed.
- A. N. Trukhin, K. Shmits, J. L. Jansons and A. B. Lynn, Ultraviolet luminescence of ScPO4, AlPO4 and GaPO4 crystals, J. Phys.: Condens. Matter, 2013, 25, 385502 Search PubMed.
- A. Trukhin and L. A. Boatner, Electronic Structure of ScPO4 Single Crystals: Optical and Photoelectric Properties, Mater. Sci. Forum, 1997, 239–241, 573–576 Search PubMed.
- A. A. José, T. C. María and J. M. L. María, Preparation and topotactical oxidation of ScVO3 with bixbyte structure: a low-temperature route to stabilize the new defect fluorite ScVO3.5 metastable phase, Dalton Trans., 2004, 1294–1297 Search PubMed.
- H. J. Cong, H. J. Zhang, B. Yao, W. T. Yu, X. Zhao, J. Y. Wang and G. C. Zhang, ScVO4: Explorations of Novel Crystalline Inorganic Optical Materials in Rare-Earth Orthovanadate Systems, Cryst. Growth Des., 2010, 10, 4389–4400 Search PubMed.
- A. L. Joey, J. S. Fabian, S. W. Pamela, S. Kalpana, T. Venkataraman and B. Mario, Structure Evolution and Reactivity of the Sc(2−x)VxO3+δ (0 ≤ x ≤ 2.0) System, Inorg. Chem., 2018, 57, 5607–5614 Search PubMed.
- P. S. Shahid, J. L. Rylan, M. D. C. Lachlan and B. Mario, Formation, structure and magnetism of the metastable defect fluorite phases AVO3.5+x (A = In, Sc), J. Solid State Chem., 2007, 180, 3333–3340 Search PubMed.
- P. S. Shahid, W. K. Matthew, M. D. C. Lachlan, K. M. Vladimir, K. Scott and B. Mario, In Situ Powder X-ray Diffraction, Synthesis, and Magnetic Properties of the Defect Zircon Structure ScVO4−x, Inorg. Chem., 2009, 48, 10553–10559 Search PubMed.
- F. W. Kang, Y. Zhang, L. Wondraczek, J. Q. Zhu, X. B. Yang and M. Y. Peng, Processing-dependence and the nature of the blue-shift of Bi3+-related photoemission in ScVO4 at elevated temperatures, J. Mater. Chem. C, 2014, 2, 9850–9857 Search PubMed.
- H. S. Zhang, F. W. Kang, Y. J. Zhao, M. Y. Peng, D. Y. Lei and X. B. Yang, The role of oxygen defects in a bismuth doped ScVO4 matrix: tuning luminescence by hydrogen treatment, J. Mater. Chem. C, 2017, 5, 314–321 Search PubMed.
- G. Kresse and J. Hafner, Ab initio molecular dynamics for liquid metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 Search PubMed.
- G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 Search PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868 Search PubMed.
- A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, Influence of the Exchange Screening Parameter on the Performance of Screened Hybrid Functionals, J. Chem. Phys., 2006, 125, 224106 Search PubMed.
- J. C. Phillips, Dielectric Definition of Electronegativity, Phys. Rev. Lett., 1968, 20, 11–13 Search PubMed.
- J. A. Van Vechten, Quantum Dielectric Theory of Electronegativity in Covalent Systems. I. Electronic Dielectric Constant, Phys. Rev., 1969, 182, 891–905 Search PubMed.
- B. F. Levine, d-Electron Effects on Bond Susceptibilities and Ionicities, Phys. Rev. B: Condens. Matter Mater. Phys., 1973, 7, 2591–2600 Search PubMed.
- J. S. Shi, Z. J. Wu, S. H. Zhou and S. Y. Zhang, Dependence of crystal field splitting of 5d levels on hosts in the halide crystals, Chem. Phys. Lett., 2003, 280, 245–250 Search PubMed.
- J. S. Shi and S. Y. Zhang, Barycenter of Energy of Lanthanide 4fN−15d Configuration in Inorganic Crystals, J. Phys. Chem. B, 2004, 108, 18845–18849 Search PubMed.
- Q. Su, J. Wang and J. S. Shi, Prediction and assignment of site occupation and energy levels for Pb2+ ions in crystal hosts, J. Solid State Chem., 2010, 183, 1174–1779 Search PubMed.
- L. Wang, Q. Su, Q. Liu and J. S. Shi, Investigation and application of quantitative relationship between sp energy levels of Bi3+ ion and host lattice, J. Solid State Chem., 2012, 191, 142–146 Search PubMed.
- M. Amer and P. Boutinaud, The doping sites in Eu2+-doped AIBIIPO4 phosphors and their consequence on the photoluminescence excitation spectra, J. Solid State Chem., 2018, 258, 124–130 Search PubMed.
- K. Momma and F. Izumi, VESTA: a three-dimensional visualization system for electronic and structural analysis, J. Appl. Crystallogr., 2008, 41, 653–658 Search PubMed.
- N. E. Brese and M. O’Keefe, Bond-valence parameters for solids, Acta Crystallogr., 1991, B47, 192–197 Search PubMed.
- J. Yang, J. W. Zhang, Z. Y. Gao, M. X. Tao, P. P. Dang, Y. Wei and G. G. Li, Enhanced photoluminescence and thermal stability in solid solution Ca1−xSrxSc2O4:Ce3+ (x = 0–1) via crystal field regulation and site-preferential occupation, Inorg. Chem. Front., 2019, 6, 2004–2013 Search PubMed.
- H. M. Li, R. Pang, G. Y. Liu, W. Z. Sun, D. Li, L. H. Jiang, S. Zhang, C. Y. Li, J. Feng and H. J. Zhang, Synthesis and Luminescence Properties of Bi3+-Activated K2MgGeO4: A Promising High-Brightness Orange-Emitting Phosphor for WLEDs Conversion, Inorg. Chem., 2018, 57, 12303–12311 Search PubMed.
- T. Katsumata, H. Takashima, T. Michino and Y. Nobe, Non-stoichiometry in yttrium ortho-vanadate, Mater. Res. Bull., 1994, 29, 1247–1254 Search PubMed.
- N. Garces, K. Stevens, G. Foundos and L. Halliburton, Electron paramagnetic resonance and optical absorption study of V4+ centres in YVO4, J. Phys.: Condens. Matter, 2004, 16, 7095–7106 Search PubMed.
- A. L. Joey, M. S. Kevin, Z. S. Arzoo, R. W. Christopher and B. Mario, Order/Disorder and in Situ Oxide Defect Control in the Bixbyite Phase YPrO3+δ (0 ≤ δ < 0.5), Inorg. Chem., 2016, 55, 2381–2389 Search PubMed.
- L. Yang, G. Li, M. Zhao, J. Zheng, X. Guan and L. Li, Preparation and morphology sensitive luminescence properties of Eu3+-doped YVO4: a defect chemistry viewpoint of study, CrystEngComm, 2012, 14, 3227–3235 Search PubMed.
- G. Blasse, The luminescence of closed-shell transition metal complexes. New developments, Struct. Bonding, 1980, 42, 1–41 Search PubMed.
- C. M. Aiube, T. M. Lobo, D. Sousz-Moura, I. B. M. Ferraz, M. E. Osugi, C. K. Grisolia, R. Oliveira and I. T. Weber, Study of YVO4 as a photocatalyst: correlation between synthetic route and ecotoxicity, J. Environ. Chem. Eng., 2018, 6, 2846–2854 Search PubMed.
- G. Boulon, Processus de photoluminescence dans les oxydes et les orthovanadates de terres rares polycristallins, activés par l’ion Bi3+, J. Phys., 1971, 32, 333–347 Search PubMed.
- H. Ronde and G. Blasse, The nature of the electronic transition of the vanadate groups, J. Inorg. Nucl. Chem., 1978, 40, 215–219 Search PubMed.
- L. Yang, G. Li, W. Hu, M. Zhao, L. Sun and J. Zheng, Control over the crystallinity and defect chemistry of YVO4 nanocrystals for optimum photocatalytic property, Eur. J. Inorg. Chem., 2011, 2211–2220 Search PubMed.
- L. Qian, J. Zhu, Z. Chen, Y. Gui, Q. Gong and Y. Yuan, Self-assembled heavy lanthanide orthovanadate architecture with controlled dimensionality and morphology, Chem. – Eur. J., 2009, 15, 1233–1240 Search PubMed.
- Y. Nobe, H. Takashima and T. Katsumata, Decoloration of yttrium orthovanadate laser host crystals by annealing, Opt. Lett., 1994, 19, 1216–1218 Search PubMed.
- G. Blasse, Some considerations and experiments on concentration quenching of characteristic broad-band fluorescence, Philips Res. Rep., 1968, 23, 344 Search PubMed.
- W. Z. Lv, Y. C. Jia, Q. Zhao, M. M. Jiao, B. Q. Shao, W. Lü and H. P. You, Crystal Structure and Luminescence Properties of Ca8Mg3Al2Si7O28:Eu2+ for WLEDs, Adv. Opt. Mater., 2014, 2, 183–188 Search PubMed.
- M. Janulevicius, P. Marmokas, M. Misevicius, J. Grigorjevaite, L. Mikoliunaite, S. Sakirzanovas and A. Katelnikovas, Luminescence and luminescence quenching of highly efficient Y2Mo4O15:Eu3+ phosphors and ceramics, Sci. Rep., 2016, 6, 26098 Search PubMed.
- X. C. Wang, T. Seto, Z. Y. Zhao, Y. Y. Li, Q. S. Qu, H. Li and Y. S. Wang, Preparation of Sr1−xCaxYSi4N7:Eu2+ solid solutions and their luminescence properties, J. Mater. Chem. C, 2014, 2, 4476–4481 Search PubMed.
- G. Blasse and A. Bril, Photoluminescent efficiency of phosphors with electronic transitions in localized centers, J. Electrochem. Soc., 1968, 115, 1067–1075 Search PubMed.
- A. B. Garg, D. Errandonea, P. Rodriguez-Hernandez and A. Munoz, ScVO4 under non-hydrostatic compression: a new metastable polymorph, J. Phys.: Condens. Matter, 2017, 29, 055401 Search PubMed.
- M. Giarola, A. Sanson, A. Rahman, G. Mariotto, M. Bettinelli, A. Speghini and E. Cazzanelli, Virational dynamics of YPO4 and ScPO4 single crystals: an integrated study by polarized Raman spectroscopy and first-principles calculations, Phys. Rev., 2011, 83, 224302 Search PubMed.
- B. I. Won, B. Stuart, H. Jerry, M. Alexander, P. D. Steven and S. Ram, Sr2.975−xBaxCe0.025AlO4F: a Highly Efficient Green-Emitting Oxyfluoride Phosphor for Solid State White Lighting, Chem. Mater., 2010, 22, 2842–2849 Search PubMed.
- F. W. Kang, Y. Zhang and M. Y. Peng, Controlling the Energy Transfer via Multi Luminescent Centers to Achieve White Light/Tunable Emissions in a Single-Phased X2-Type Y2SiO5:Eu3+,Bi3+ Phosphor For Ultraviolet Converted LEDs, Inorg. Chem., 2015, 54, 1462–1473 Search PubMed.
- F. W. Kang, G. H. Sun, P. Boutinaud, H. Y. Wu, F.-X. Ma, J. Lu, J. L. Gan, H. D. Bian, F. Gao and S. S. Xiao, Recent advances and prospects of persistent luminescent materials as inner secondary self-luminous light source for photocatalytic applications, Chem. Eng. J., 2021, 403, 126099 Search PubMed.
- P. P. Dang, D. J. Liu, Y. Wei, G. G. Li, H. Z. Lian, M. M. Shang and J. Lin, Highly Efficient Cyan-Green Emission in Self-Activated Rb3RV2O8 (R = Y, Lu) Vanadate Phosphors for Full-Spectrum White Light-Emitting Diodes (LEDs), Inorg. Chem., 2020, 59, 6026–6038 Search PubMed.
- Y. L. Huang, Y. M. Yu, T. J. Tsuboi and H. J. Seo, Novel yellow-emitting phosphors of Ca5M4(VO4)6 (M = Mg, Zn) with isolated VO4 tetrahedra, Opt. Express, 2012, 20, 4360–4368 Search PubMed.
- J. C. Zhou, F. Huang, J. Xu, H. Chen and Y. S. Wang, Luminescence study of a self-activated and rare earth activated Sr3La(VO4)3 phosphor potentially applicable in W-LEDs, J. Mater. Chem. C, 2015, 3, 3023–3028 Search PubMed.
- R. J. Yu, M. S. Yuan, T. B. Li, Q. Tu and J. Y. Wang, Preparation, structure and luminescence properties of Ba2V2O7 microrods, RSC Adv., 2016, 6, 90711–90717 Search PubMed.
- T. Nakajima, M. Isobe, T. Tsuchiya, Y. Ueda and T. Manabe, Photoluminescence property of vanadates M2V2O7 (M: Ba, Sr and Ca), Opt. Mater., 2010, 32, 1618–1621 Search PubMed.
- T. Nakajima, M. Isobe, T. Tsuchiya, Y. Ueda and T. Manabe, Correlation between Luminescence Quantum Efficiency and Structural Properties of Vanadate Phosphors with Chained, Dimerized, and Isolated VO4 Tetrahedra, J. Phys. Chem. C, 2010, 114, 5160–5167 Search PubMed.
- X. Y. Huang, S. Y. Wang, S. Rtimi and B. Devakumar, KCa2Mg2V3O12: a novel efficient rare-earth-free self-activated yellow-emitting phosphor, J. Photochem. Photobiol., A, 2020, 401, 112765 Search PubMed.
- W. Zheng, P. Huang, Z. L. Gong, D. D. Tu, J. Xu, Q. L. Zou, R. F. Li, W. W. You, J. C. G. Bünzli and X. Y. Chen, Near-infrared-triggered photon upconversion tuning in all-inorganic cesium lead halide perovskite quantum dots, Nat. Commun., 2018, 9, 3462 Search PubMed.
- Y. N. Liu, G. C. Pan, R. Wang, H. Shao, H. Wang, W. Xu, H. N. Cui and H. W. Song, Considerably enhanced exciton emission of CsPbCl3 perovskite quantum dots by the introduction of potassium and lanthanide ions, Nanoscale, 2018, 10, 14067–14072 Search PubMed.
- W. Y. Liu, Q. L. Lin, H. B. Li, K. F. Wu, I. Robel, J. M. Pietryga and V. I. Klimov, Mn2+-Doped Lead Halide Perovskite Nanocrystals with Dual-Color Emission Controlled by Halide Content, J. Am. Chem. Soc., 2016, 138, 14954–14961 Search PubMed.
- L. Q. Mi, Y. L. Huang, L. Cao, Y. Y. Feng and H. J. Seo, Modified optical properties via induced cation disorder in self-activated NaMg2V3O10, Dalton Trans., 2018, 47, 4368–4376 Search PubMed.
- L. K. Bharat, S.-K. Jeon, K. G. Krishna and J. S. Yu, Rare-earth free self-luminescent Ca2KZn2(VO4)3 phosphors for intense white light-emitting diodes, Sci. Rep., 2017, 7, 42348 Search PubMed.
- E. Pavitra, G. S. R. Raju, L. K. Bharat, J. Y. Park, C. H. Kwak, J. W. Chun, Y.-K. Han and Y. S. Huh, Evolution of highly efficient rare-earth free Cs(1−x)RbxVO3 phosphors as a single emitting component for NUV-based white LEDs, J. Mater. Chem. C, 2018, 6, 12746–12757 Search PubMed.
| This journal is © The Royal Society of Chemistry 2020 |