Investigating the adsorption mechanism of glycine in comparison with catechol on cristobalite surface using density functional theory for bio-adhesive materials

Abstract

Using periodic Density Functional Theory (DFT) calculations and DFT-based molecular dynamics simulations, we studied the adhesion mechanism of glycine amino acid and the catechol part of L-dopa on the cristobalite surface. The optimized glycine and catechol molecules are initially placed vertically 3 Å above the cristobalite surface with a vacuum thickness of approximately 40 Å. The catechol adhesion on the cristobalite surface previously studied showed strong binding energy both in dry and wet adsorption. Glycine is the second most abundant amino acid in the mussel adhesive protein, which would have a significant contribution in mussel adhesion. This study of glycine will further enlighten the understanding of marine mussel adhesion. We believe that all the proteins exist in the Mytilus edulis foot protein (mefp) are contributing in this unique and versatile adhesion of marine mussel. We observed that glycine molecules formed four hydrogen bonds with the surface silanols and acted as donors and acceptors. Four hydrogen bond formation is also observed during catechol adhesion on the cristobalite surface. The average binding energy of both molecules on the cristobalite surface lies in the range of hydrogen binding energy. Surface binding energy values of 20.23 and 14.45 kcal mol⁻¹ were obtained for glycine and catechol adsorption, respectively. Including the dispersion energy term further raised the binding energy to 31.29 kcal mol⁻¹ for glycine and 28.58 kcal mol⁻¹ for catechol. The binding energy values suggest that glycine adsorption on the dry cristobalite surface is much stronger as compared to that of catechol.

---

1. Introduction

Interaction between amino acids and mineral surfaces has been the subject of investigation for the last few decades.¹ Almost 60 years ago Bernal proposed^2,3 that mineral surfaces may have played an important catalytic role in the polymerization of amino acids.⁴ It is believed that amino acids may have been trapped by minerals, such as clay or silica, initially forming small biomonomers and ultimately polymerizing into large biomolecules;³ therefore, the fundamental understanding of the adsorption mechanism is a very important step in gaining an insight into the synthesis of small polypeptides and polynucleotides, from which the gradual growth of life has occurred.² Apart from the basic understanding of the origin of life, such interactions find applications in bionanotechnology,⁵ biomedical implants, biosensors, surface modification,¹ development of organic mass spectrometry, and solid-state peptide synthesis.⁶ Many studies have been dedicated to understand the interaction between amino acids and various surfaces:^12–16,29 glycine adsorption on silicon^7,8 and zinc oxide (ZnO),^9,10 co-adsorption of water and glycine on Cu,¹¹ and adsorption of glycine and alanine on montmorillonite³ are a few examples. Catechol adsorption on both α- & β-cristobalite surfaces in dry and wet environments was extensively studied to understand the strong adhesion mechanism of the marine mussel.^15,16 The wet environment we considered in our previous study was realistic, but it was difficult to explore the fundamental mechanism of adhesion due to the large number of water molecules. Furthermore, we modeled the micro-solvated system to understand the fundamental mechanism of catechol adhesion, which made it crystal clear that how catechol adsorbed in the presence of surrounding water.¹⁴

Ab initio molecular dynamics calculations were used by Costa et al.¹² to study the adsorption of micro-solvated glycine on the hydroxylated and hydrophilic cristobalite surface. The results suggested different reactivity of carboxylate and ammonia functions towards the silanol group. Instead of mediating through water molecules, zwitterionic glycine directly binds to the surface through the carboxylate function. On the other hand, the ammonia function of glycine interacts with the silanol group through water.

Glycine adsorbed on the cristobalite surface from aqueous solutions of various concentrations and pHs, characterized by experimental techniques such as middle-IR and UV-Vis-NIR,¹ confirmed the presence of glycine molecules as zwitterions on the surface. Moreover, two different adsorption mechanisms were observed with increasing glycine concentration. At lower concentration, the glycine presumably binds to the surface through its NH₃⁺ moiety, whereas at higher concentration, due to the saturation of specific binding sites, the formation of β-glycine was reported.

Combined NMR spectroscopy and DFT-D calculations on the adsorption of glycine on two representative sites namely vicinal silanols and the silanols nest of cristobalite suggested that the silanols nest is the more favorable site for glycine adsorption due to the increased local hydrogen bond density.¹³ Water co-adsorption is also reported to be favored, specially a water molecule between an SiOH and an ammonium moiety.

Rimola et al.⁵ established an affinity scale for the adsorption of different amino acids on the hydroxylated cristobalite surface using an ab initio method. It was found that the interaction is mainly dictated by both the COOH moiety and the side chain of amino acids and the surface silanol groups. On the basis of calculated adsorption energies, it was concluded that the nonpolar amino acids (including glycine) are least prone to adsorption on the surface, whereas the basic ones are more favorable for adsorption.

In this study, we have investigated the adhesion of glycine and catechol molecules on the cristobalite surface. Cristobalite is an abundantly found mineral that shows stability over a wide range of temperature and pressure. Glycine is the simplest of the 20 amino acids found in nature. Thus, it is reasonable to study the interaction between cristobalite, glycine, and catechol as a simple model. Once the fundamental understanding of the basic adsorption mechanism is reached, we can proceed towards the more complex systems. It is known that the catechol part of L-dopa amino acid is responsible for the strong adhesion of marine mussels and other organisms, even in wet conditions.^14–16 Understanding the adhesion process may, therefore, be helpful for scientists to design biomimetic adhesives, which may be used in a variety of applications, especially in the field of medicine and dentistry.¹⁷

As discussed, the basic aim of this study was to investigate the adsorption mechanism of glycine and catechol on the cristobalite surface. An understanding of the basic mechanism underlying the adsorption of biomolecules is important both from the basic and applied points of view. Moreover, in this study, the surface binding energy, corrected for basis set superposition error (BSSE) and van der Waals interaction, will be calculated for the system under consideration. The structural changes in cristobalite, glycine, and catechol as a result of the adsorption process will also be discussed.

For our calculation, we have chosen the (001) surface of geminal α-cristobalite.¹⁴ It is reasonable to model amorphous cristobalite as hydroxylated cristobalite because both the materials have nearly equal densities and refractive indices.¹⁴ The silanol density of the present cristobalite is 8.1 OH per nm², which is comparable to that of the amorphous cristobalite, which has a value of 5 OH per nm².¹⁶

2. Computational method

In the present work, ab initio molecular dynamics and energy calculations were performed using the SIESTA code,¹⁸ version 3.2. The exchange and correlation functional we have used is the generalized gradient approximation (GGA) by the application of the revised Perdew–Burke–Ernzerhof (RPBE) method.¹⁹ Norm-conserving pseudo potentials of Troullier and Martins²⁰ were used with the standard DZP basis set. Brillouin zone sampling was performed with 3 × 3 × 1 k-points using the Monkhorst–Pack scheme.²¹ Optimization of the system was performed using the conjugate gradient (CG) method²² with variable cell. The system was optimized until the atomic forces were less than (0.04 eV Å⁻¹). We selected a mesh cut-off¹⁸ of 2.72 keV for our atomic orbitals.

The initial configuration for optimization of bulk α-cristobalite was taken from the rectangular unit cell with lattice parameters of 4.97 and 6.93 Å, having P4₁21 symmetry.²³ Initial configuration for the hydroxylated cristobalite surface was constructed as follows. A slab of bulk α-cristobalite with 16 layers along the vertical (z-direction) was taken. When viewed from the top, the slab consisted of 3 × 3 layers in the plane normal to the vertical i.e. the x–y plane. The top cristobalite surface corresponds to cleaving the bulk α-cristobalite along the (001) direction. The dimensions of the simulation box were A = B = 14.7 Å and C = 40 Å; a vacuum gap of 40 Å along the vertical direction was taken to avoid artifacts. Each Si atom on the surface was terminated with two OH groups, resulting in geminal silanols, whereas Si atoms in the bottom layer were terminated with a single hydrogen atom. During the optimization, the bottom Si atoms were kept fixed. The number of atoms in cristobalite was 198, whereas glycine and catechol consisted of 10 and 14 atoms, respectively.

The binding energy was calculated using the relation:

ΔE = −[E^g+s_GS(GS) − E^g_G(G) − E^s_S(S) + δ_BSSE] (1)

We have used a notation system throughout this text in which the term E^Y_X(Z) represents energy of the system Z in the geometry of X using the basis set Y. In eqn (1), E^g+s_GS(GS) represents the energy of a molecule–surface complex, E^g_G(G) is the energy of the molecule (glycine or catechol), and E^s_S(S) denotes the energy of the surface S. Note that in our definition of binding energy, a positive sign refers to an attraction between the surface and the molecule. We have calculated the basis set superposition error using the counterpoise method^24,25 including the deformation using the following equation:

δ_BSSE = [E^g_GS(G) − E^g+s_GS(G)] + [E^s_GS(S) − E^g+s_GS(S)] (2)

In the above equation, molecular and surface geometries are taken from their geometries in the molecule–surface complex. We have calculated E^g_MG(G) using the molecular basis and E^s_MS(S) using the basis of the surface. E^m+s_MS(M) and E^m+s_MS(S) have been calculated using the basis for the molecule–surface complex. Traditional DFT, although accurate in the description of the H-bond, does not include dispersion interaction between the atoms. The dispersion interaction was determined using a method proposed by Grimme.²⁶ The dispersion energy, E^disp_ij between atom i and j is given by

The parameters R_ij, S₆, C^ij₆ and R_r used in the above mentioned equation have specific meanings: R_ij represents the interatomic distance and S₆ is the global scaling factor that depends on the functional used; for PBE, it is equal to 0.75. R_r denotes the sum of the atomic radii and C^ij₆ gives the geometric mean of the dispersive coefficients of atoms i and j, respectively. The values of R_r and C^ij₆ for H, C, O, Si, and N are taken from Grimme. The total dispersion energy is the sum of all E^disp_ij pairs, imposing two-dimensional periodic boundary conditions with negligible interaction between the adjacent images.²⁷

3. Results and discussion

3.1. Catechol, glycine and cristobalite geometries

In Table 1, we have listed the structural parameters of bulk α-cristobalite. Lattice parameters, unit cell volume, the Si–O bond length (d_Si–O), and the bonding angles for the Si–O–Si triples are also listed. The present DFT calculations are consistent with the previous experimental studies.²³

Table 1 Structural parameters of α-cristobalite

Cristobalite (α)	Lattice parameters (Å)	dSi–O (Å)	Unit cell vol. (Å^3)	Si–O–Si (θ°)
a Pluth et al.^23
Present calcn	4.94, 7.03	1.66	171.9	137.3
Experimental^a	4.97, 6.93	1.63	171.2	147

---

Fig. 1 represents the optimized structure of glycine. Atoms in this geometry are labeled and the structural parameters are defined as follows: the bond lengths C₁–H₂, C₁–H₃, C₁–N, C₂–O₁, C₂–O₂, C₂–C₁, O₂–H₁, N–H₄ and N–H₅ are represented by d₁ to d₉, respectively. The bonding angles for O₁–C₂–O₂, O₂–C₂–C₁, O₁–C₂–C₁, H₂–C₁–C₂, C₂–C₁–N, H₂–C₁–N, C₁–N–H₅, H₄–N–H₅, H₁–N–H₄ and C₁–N–H₁ have been represented by θ₁ to θ₁₀, respectively. The top portion of Fig. 1 shows the initial geometry of the glycine, whereas the lower one shows the optimized geometry. Note that one of the hydrogens initially attached to oxygen detaches itself after optimization and binds with the nitrogen atom in the molecule.

Fig. 1 Initial (top) and optimized (bottom) geometry of glycine. The atoms are labelled and bond angles are represented by symbols from θ₁ to θ₁₀.

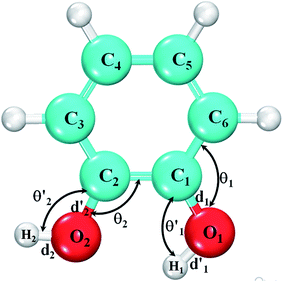
We designed and then optimized the initial geometry of catechol. The optimized catechol is shown in Fig. 2. The angles O₁–C₁–C₆, H₁–O₁–C₁, O₂–C₂–C₁ and H₂–O₂–C₂ are denoted by θ₁, θ′₁, θ₂ and θ′₂, respectively, whereas the bond lengths O₁–C₁, O₁–H₁, O₂–C₂ and O₂–H₂ are labelled as d₁, d′₁, d₂ and d′₂, respectively. We also calculated the dihedral angles ϕ₁ and ϕ₂ for the torsions H₁–O₁–C₁–C₂ and H₂–O₂–C₂–C₁, respectively (not shown in the figure). Data for the structural parameters (bond lengths and angles) of isolated and adsorbed catechol have been presented in Table 2.

Fig. 2 Optimized geometry of catechol. Atoms are labelled in to define various bond lengths and angles. C₁–O₁ and O₁–H₁ bond lengths are represented by d₁ and d′₁, respectively. The symbols d₂ and d′₂ indicates lengths H₂–O₂ and O₂–C₂, respectively. Bond angles θ₁, θ′₁, θ₂ and θ′₂ are also shown.

Table 2 Structural parameters of the isolated and adsorbed catechol

	d1 (Å)	d2 (Å)	d′1 (Å)	d′2 (Å)	θ1 (°)	θ2 (°)	θ′1 (°)	θ′2 (°)	ϕ1 (°)	ϕ2 (°)
a Previous calculation by Gerhards et al.^28b Previous calculation by Mian et al.^15
Isolated	1.35	0.97	0.98	1.38	120.7	113.5	107.1	111.3	−1.3	1.6
Isolated^a	1.35	0.94	0.95	1.36	119.8	115.6	109.6	11.4	0	0
Isolated^b	1.36	0.97	0.98	1.38	120.7	113.4	107.1	111.3	−1.3	1.6
On (001)	1.38	0.98	0.99	1.39	119.0	119.2	110	108.7	−18.9	96.2
On (001)^b	1.38	0.99	0.99	1.40	119.0	119.2	110	108.3	−18.9	96.2

---

3.2. Adsorption geometry of glycine on cristobalite surface

Cristobalite and glycine initial structures were separately optimized. After optimization, glycine was placed at a distance of 3 Å above the cristobalite surface and the combined geometry was optimized again. The adsorption geometry of glycine on the cristobalite surface is shown in Fig. 3. This geometry shows that the glycine molecule forms 4 hydrogen bonds (represented as black dashed lines) with the surface OH groups. It should be noted that the glycine molecule acts both as a donor and acceptor of H to form H-bonds. The hydrogen bond lengths are 1.954, 1.869, 1.710 and 1.539 Å, with an average value of 1.768 Å.

Fig. 3 Optimized adsorption geometry of glycine on α-cristobalite: top view (top) and side view (bottom). Surface silanols are shown as balls and sticks to clearly observe the hydrogen between molecule and surface. Lines represent siloxane bridges attached to the silanols. Hydrogen bonds are represented by black dashed lines.

3.3. Adsorption geometry of catechol on the cristobalite surface

As in the case of glycine, we also placed the optimized geometry of catechol approximately 3 Å above the silica surface. Fig. 4 shows the top and side views of the catechol adsorption geometry. Catechol forms 4 hydrogen bonds with the cristobalite surface, represented by the black dashed lines. The two OH groups of catechol act as donors as well as acceptors of H to form hydrogen bonds. Lengths of these hydrogen bonds are 1.928, 1.742, 1.819 and 1.728 Å, which results in an average value of 1.804 Å.

Fig. 4 Adsorption geometry of catechol on the α-cristobalite surface. Only surface silanols are shown as balls and sticks for visual clarity. Siloxane bridges attached to silanols are represented by lines. Black dashed lines represent hydrogen bonds. Both top view (top) and side view (bottom) are shown in the figure.

3.4. Structural changes in cristobalite, glycine and catechol after adsorption

Table 2 represents the structural parameters (bond lengths and angles) of the isolated catechol and the catechol molecule adsorbed on the cristobalite surface. We have compared our results with the corresponding values of a previous computational study¹⁵ and an experimental study.²⁸ It is clear from the table that our calculation is in close agreement with that of the previous studies.

To qualitatively determine the effect of adsorption on the cristobalite surface, we calculated the bond lengths and angles of surface silanols for isolated cristobalite and in the case of glycine and catechol adsorbed on the surface. Fig. 5 represents the variation in the bond lengths of the surface silanols for three different configurations. In Fig. 6, the bond angle variations of surface silanols (Si–O–H) are shown for three different geometries. The common feature of both the plots shown is that in the case of glycine adsorption, the effect on surface silanols' bond length and bond angle variations is prominent as compared with that of the catechol adsorption on the same surface. Furthermore, the silanols in the vicinity of the adsorbed molecules are affected more as compared to the surface silanols away from the adsorbed molecule area. Note that the trend in both the plots is similar i.e. the silanols' bond lengths and angles are changed almost in similar fashion.

Fig. 5 Variations in the bond lengths of surface silanols after catechol and glycine adsorption.

Fig. 6 Variation in the bond angles of surface silanols after the adsorption of glycine and catechol on cristobalite.

To determine the structural changes in glycine, we calculated bond lengths and angles for isolated and adsorbed glycine. Fig. 7 and 8 show the results. From Fig. 7, it can be concluded that after adsorption, we observe a very slight change in the glycine bond lengths. However, in one particular instance, the bond length has significantly increased. The change in the bond angles of glycine, on the other hand, is more pronounced, as can be seen in Fig. 8.

Fig. 7 Comparison of glycine bond lengths before and after adsorption.

Fig. 8 Variation in glycine bond angles due to adsorption.

3.5. Binding energy and BSSE of glycine and catechol

We calculated the surface binding energy, basis set superposition error (BSSE) using the counterpoise correction method (which includes the deformation of both molecule and surface), and the dispersion energy for glycine and catechol using eqn (1), (2) and (3), respectively. As shown in Table 3, the binding energy for glycine is 20.23 kcal mol⁻¹. We estimated an average binding energy of 5.057 kcal mol⁻¹ for a single hydrogen bond. This value has been calculated as the binding energy divided by the total number of hydrogen bonds and is in the range of the typical binding energy of a hydrogen bond (2.4–6.2 kcal mol⁻¹).²⁹ The corresponding BSSE value is 24.13 kcal mol⁻¹, which is 54.38% of the uncorrected binding energy. Large BSSE's have been previously reported in many investigations.¹⁵ For a glycine adsorption on edingtonite cristobalite, a BSSE larger than the magnitude of the uncorrected binding energy has been reported.³⁰ For water adhesion on cristobalite (β) surface, a BSSE value up to 77% of the uncorrected binding energy has been reported.¹⁵ For the same surface, a BSSE value of up to 75.7% of the uncorrected energy has been found in the case of catechol adsorption.¹⁵

Table 3 Binding energy (ΔE) of glycine and catechol adsorbed on the cristobalite surface (kcal mol⁻¹)

Energy	Glycine	Catechol
a BSSE correction for each binding energy (δBSSE) appears in parentheses.
ΔE	20.23 (24.13)^a	14.45 (22.52)^a
dEM	23.8	0.8341
ΔEvWdisp	31.29	28.58

---

In the present calculations, the binding energy for catechol is 14.45 kcal mol⁻¹. The average binding energy has a value of 3.53, which is in the range of the typical binding energy of a hydrogen bond. BSSE in the case of catechol–cristobalite is 22.52 kcal mol⁻¹, which is 60.91% of the uncorrected binding energy. As reported by Civalleri and Ugliengo,³¹ for the binding energy of NH₃ on cristobalite, the BSSE of a periodic calculation is greater than that for a cluster calculation. In the present study, the large BSSE may be due to the fact that in this periodic calculation amorphous cristobalite has been modeled as a crystalline surface. In the DFT calculation of the adsorption of C₆₀ on the surface using PBE-GGA DFT with DZP as basis, large BSSEs have been found.³² In their calculation, the BSSE sometimes exceeded twice the value of ΔE; however, it was in agreement with the plane wave calculations using the VASP code.³³ In our study, the large BSSE may be due to the limited size of basis. As discussed, the binding energy value of glycine is larger than that of catechol for the cristobalite surface. This suggests that glycine adsorption is stronger as compared to catechol for the given surface.

The present PBE functional accurately describes the H-bond^34,35 but does not consider the dispersion interaction among the atoms. Ugliengo et al., using B3LYP-DFT, found that the dispersion energy term is significant as it reaches up to 16.7 kcal mol⁻¹.^36,37 Using similar techniques, adsorption of water and catechol on the cristobalite (α) and (β) surfaces was investigated by Mian et al.¹⁵ The dispersive energy contribution to the binding energy ranged from 14.13 to 21.03 kcal mol⁻¹; however, the dispersion energy in the case of catechol was more than water, suggesting a strong adhesion for the catechol. In our calculation, the dispersion energy for glycine, using the method of Grimme,²⁶ is 11.06 kcal mol⁻¹. After adding the dispersion energy, the binding energy increased to 31.29 kcal mol⁻¹. In the case of catechol, a dispersion energy of 14.127 was calculated, which augmented the binding energy of catechol to 28.58 kcal mol⁻¹. This value of dispersion energy is close to the previously calculated values of 13.9 and 21.0 kcal mol⁻¹ for catechol on the cristobalite (α) and (β) surfaces, respectively.¹⁵ A similar value of 16.5–16.7 kcal mol⁻¹ has been reported for benzene-diol on cristobalite.³⁶ It has been reported^36,37 that Grimme's method overestimates the binding energies and a slight modification of this method is used to achieve a closer match with the experiment.³⁸ In this modification, instead of the global scaling factor S₆ (in eqn (3)), each atomic radius is separately scaled and more elaborate combination rules are used for R_r and C^ij₆ in eqn (3). In the present study, we have not used these modifications because they were developed for functionals and bases different from the ones we have used. The values of binding energies show that the glycine amino acid binds strongly with cristobalite (α) surface as compared with the catechol molecule. As already discussed, the catechol strongly binds to silica (α and β) surfaces even in the presence of water molecules.¹⁴ Hence, we can tentatively conclude that the glycine should have a larger binding energy than water; however, this needs to be verified. In future, we plan to study the adsorption behavior of glycine in wet environments to verify our assumption.

4. Conclusion

Understanding the adsorption mechanism of amino acids and other organic molecules on the mineral surfaces has been the subject of intensive research for many decades. An insight into the adsorption process is crucial as it can supplement the hypothesis that life has actually originated from the interaction between small molecules and mineral surfaces. Moreover, understanding the basic mechanism can help scientists to design synthetic adhesives with a variety of applications. In this particular study, we investigated the adsorption of glycine and catechol on the surface of α-cristobalite. DFT-based molecular dynamics simulations suggested that both the molecules make 4 hydrogen bonds with the surface. A binding energy of 20.23 kcal mol⁻¹ was calculated for glycine, whereas the binding energy of catechol was 14.45 kcal mol⁻¹. We can, therefore, conclude that glycine binds more strongly with the surface as compared to catechol. Average binding energy for both the molecules lies in the range of typical hydrogen bond binding energy. The dispersion energy term augmented the binding energies to 31.29 and 28.58 kcal mol⁻¹ for glycine and catechol, respectively. We also studied the effect of adsorption on the structural parameters of the molecules as well as the surface.

Acknowledgements

Shabeer Ahmad Mian and co-authors are thankful to the Higher Education Commission of Pakistan for providing funding under the Startup Research Grant Program (SRGP). I also sincerely acknowledge the support from Dr Masroor Hussain, Computer Science Department, for giving an access to the computational cluster resource in GIKI, Topi, Swabi, Pakistan.

References

1. M. Meng, L. Stievano and J. F. Lambert, Langmuir, 2004, 20, 923.
2. A. Rimola, M. Sodupe, S. Tosoni, B. Civalleri and P. Ugliengo, Langmuir, 2006, 22, 6604.
3. S. Kalra, C. K. Pant, H. D. Pathak and M. S. Mehata, Colloids Surf., A, 2003, 212, 50.
4. A. Rimola, S. Tosoni, M. Sodupe and P. Ugliengo, ChemPhysChem, 2006, 7, 163.
5. A. Rimola, M. Sodupe and P. Ugliengo, J. Phys. Chem. C, 2009, 113, 5750.
6. C. Lomenech, G. Bery, D. Costa, L. Stievano and J. F. Lambert, ChemPhysChem, 2005, 6, 1070.
7. A. C. Ferraz and R. Miotto, Braz. J. Phys., 2006, 36, 312.
8. A. Chatterjee, L. Zhang and K. T. Leung, J. Phys. Chem. C, 2012, 116, 10975.
9. S. Irrera, D. Costa and P. Marcus, J. Mol. Struct.: THEOCHEM, 2009, 903, 58.
10. D. Costa, C. M. Pradier, F. Tielens and L. Savio, Surf. Sci. Rep., 2015, 70, 553.
11. M. Sacchi and S. Jenkins, Phys. Chem. Chem. Phys., 2014, 16, 6107.
12. D. Costa, A. Tougerti, F. Tielens, C. Gervais, L. Stievanoa and J. F. Lambert, Phys. Chem. Chem. Phys., 2008, 10, 6368.
13. N. Folliet, C. Gervais, D. Costa, G. Laurent, F. Babonneau, L. Stievanoa, J. F. Lambert and F. Tielens, J. Phys. Chem. C, 2013, 117, 4114.
14. A. M. Shabeer, L. Yang, C. S. Leton, A. Ejaz, M. Ajmal and E. Ganz, Langmuir, 2014, 30, 6914.
15. A. M. Shabeer, C. S. Leton, J. Jang, L. Wang, X. Gao and S. Nagase, J. Phys. Chem. C, 2010, 114, 20800.
16. A. M. Shabeer, X. Gao, S. Nagase and J. Jang, Theor. Chem. Acc., 2011, 130, 339.
17. J. Yu, W. Wei, M. S. Menyol, A. Masic, J. H. Waite and J. N. Israelachvili, Biomacromolecules, 2013, 14, 1077.
18. J. M. Soler, E. Artacho, J. Gale, A. Garcia, J. Junquera, P. Ordejon and D. Sanchez-Portal, J. Phys.: Condens. Matter, 2002, 14, 2745.
19. B. Hammer, L. B. Hansen and J. K. Nørskov, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 7413.
20. N. Troullier and J. L. Martins, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 1993.
21. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188.
22. M. R. Hestenes and E. Stiefel, J. Res. Natl. Bur. Stand., 1952, 49, 436.
23. J. J. Pluth, J. V. Smith and J. J. Faber, J. Appl. Phys., 1985, 57, 1045.
24. S. S. Xantheas, J. Chem. Phys., 1996, 104, 8821.
25. F. B. van Duijneveldt, J. G. C. M. van Duijneveldt-van de Rijdt and J. H. van Lenthe, Chem. Rev., 1994, 94, 1873.
26. S. Grimme, J. Comput. Chem., 2006, 27, 1787.
27. W. Smith, C. W. Yong and P. M. Rodger, Mol. Simul., 2002, 28, 385.
28. M. Gerhards, W. Perl, S. Schumm, U. Henrichs, C. Jacoby and K. Kleinermanns, J. Chem. Phys., 1996, 104, 9362.
29. A. J. Kinloch, J. Mater. Sci., 1980, 15, 2141.
30. A. Rimola, M. Sodupe, S. Tosoni, B. Civalleri and P. Ugliengo, Langmuir, 2006, 22, 6593.
31. B. Civalleri and P. Ugliengo, J. Phys. Chem. B, 2000, 104, 9491.
32. C. Hobbs, L. Kantorovich and J. D. Gale, Surf. Sci., 2005, 591, 55.
33. G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
34. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215.
35. T. van der Wijst, C. F. Guerra, M. Swart and F. M. Bickelhaupt, Chem. Phys. Lett., 2006, 426, 415.
36. A. Rimola, B. Civalleri and P. Uglieno, Phys. Chem. Chem. Phys., 2010, 12, 6357.
37. B. Civalleri, C. M. Zicovich-Wilson, L. Valenzano and P. Ugliengo, CrystEngComm, 2008, 10, 405.
38. P. Jurecka, J. Cerny, P. Hobza and D. Salahub, J. Comput. Chem., 2007, 28, 555.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra20683b

---