Dynamic mechanical properties of multiwall carbon nanotube reinforced ABS composites and their correlation with entanglement density, adhesion, reinforcement and C factor
Jeevan Jyotiab,
Bhanu Pratap Singh*ab,
Abhishek K. Aryaa and
S. R. Dhakatea
aPhysics and Engineering of Carbon, Division of Materials Physics and Engineering, India. E-mail: bps@nplindia.org; bpsingh2k4@yahoo.com; Fax: +91-11-45609310; Tel: +91-11-45608460
bAcademy of Scientific and Innovative Research (AcSIR), CSIR-National Physical Laboratory, New Delhi-11012, India
First published on 18th December 2015
Abstract
The dynamic mechanical properties of multiwalled carbon nanotube (MWCNTs) reinforced acrylonitrile butadiene styrene (ABS) high performance composites, which were prepared using a micro twin screw extruder with a back flow channel that enabled proper dispersion of MWCNTs into the polymer matrix are studied in detail. The dynamic characteristics of the MWCNTs/ABS composites, such as storage, loss modulus and damping factor were significantly affected by the incorporation of MWCNTs. The dynamic mechanical properties of polymers strongly depend on the adhesion of MWCNTs and polymer and entanglement density of the polymer chains in the presence of MWCNTs. Herein, the entanglement density and C-factor of MWCNTs/ABS composites are evaluated using the dynamic mechanical properties results obtained from a dynamic mechanical analyser and correlated with their mechanical properties. The entanglement density of the MWCNTs/ABS composites increased from 4.31 × 104 mol m−3 (pure ABS) to 7.6 × 104 mol m−3 (5 wt% MWCNTs/ABS composites). C-factor measures the effectiveness of the filler on the modulus of the composites, which decreased from 1.086 (1 wt% MWCNTs/ABS composites) to 0.78 (5 wt% MWCNTs/ABS composites), and beyond this loading, the value of C-factor began to increase; this showed that the utilization of 5 wt% MWCNTs in the ABS matrix is sufficient for their effective use. The “b” factor increased from 6.16 (1 wt% MWCNTs/ABS composites) to 7.625 (5 wt% MWCNT/ABS composites) and after that started to decrease. A larger value of “b” strengthens the MWCNTs/ABS matrix interaction. In addition, Cole–Cole analysis was carried out to understand the phase behaviour of the composites.
Introduction
Polymers reinforced with carbon nanotubes (CNTs) have received great attention in the research community in recent years due to the superior mechanical properties of CNTs.1,2 Dynamic mechanical analysis (DMA) is commonly used to evaluate the stiffness and damping properties of a composite's material. Moreover, structural and viscoelastic behaviour studies of polymeric materials are used for their industrial applications. DMA also determines the primary relaxation of composites material, such as glass transition temperature (Tg), degree of entanglement, adhesion factor and non-Arrhenius variation of the relation with the temperature.3–6 Various aspects of the structural properties, such as the Tg of a polymer, influence different properties such as fatigue and impact resistance. Tg serves as a transition point between the glassy and rubbery region. The glassy region (below the Tg) is mainly used to study the structural properties of composite materials.The properties of composite materials highly depend on the type of filler, its dimensions and aspect ratio as well as the filler incorporation technique. There are mainly three types of incorporation techniques: melt mixing,7–9 solvent casting10–14 and in situ polymerization.15–18 For industrial viability, melt mixing is one of the most preferred techniques for the incorporation of fillers in a polymer matrix.
The recent breakthroughs in nanoscale science and engineering have provided new opportunities for the development of high-performance composite materials. CNTs have shown exceptional properties such as high mechanical and electrical properties.19–25 CNT polymer composites have shown a remarkable increase in elastic modulus and strength because of the addition of MWCNTs.26–30
Dynamic mechanical analyses are expressed in terms of storage modulus, loss modulus and damping factor, which depend upon time (temperature). The addition of MWCNTs in a polymeric matrix reduces the mobility of the macromolecular chains of the polymer that surround the MWCNTs.31
In DMA, a sinusoidal force is applied, which measures the response of the input. The behaviour of the material depends on the response of the output signal. In DMA, stress is applied as a function of time (temperature), and the relation with the frequency is given by32
σ(t) = σ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(ωt + δ) sin(ωt + δ)
| (1) |
Using the Hooke's law, the input and response are related by the dynamic modulus
| σ(t) = E*(ω)(t) | (2) |
The dynamic modulus has in phase and out of phase components, which are given by
| E*(ω) = E′(ω) + iE′′(ω) | (3) |
 is in the real phase and characterizes the elastic behaviour of the composites and the out of phase,
is in the real phase and characterizes the elastic behaviour of the composites and the out of phase,  , characterizes the viscous behaviour of the material.33 Viscoelastic behaviour is the combination of both the viscous and elastic modulus of a material. In DMA, a specimen can be tested in different configuration modes such as single cantilever, dual cantilever, three point bending, torsion, and tension.
, characterizes the viscous behaviour of the material.33 Viscoelastic behaviour is the combination of both the viscous and elastic modulus of a material. In DMA, a specimen can be tested in different configuration modes such as single cantilever, dual cantilever, three point bending, torsion, and tension.
Several studies have been reported on the DMA of synthetic fiber reinforced polymer composites.34–36 All these authors have mainly focused on the importance of fiber loading (wt%) in polymers. Etaati et al.37 studied the static and visco-elastic behaviour of short hemp fiber polypropylene composites manufactured using the injection moulding technique. Their results showed that the increase in storage modulus was negligible in the composites reinforced with more than 40 wt% of hemp fibers. Jawaid et al.38 studied the interfacial bonding between oil palm–epoxy composites. The addition of jute fibres to oil palm composites increased the storage modulus, while the damping factor shifts towards the higher temperature region. The Cole–Cole analysis was carried out to understand the phase behaviour of composite samples. The hybrid composite with oil palm![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) jute (1
jute (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4) showed maximum damping behaviour and the highest tensile properties. In another study by Karaduman et al.,39 the magnitudes of peak storage modulus and loss modulus of nonwoven composites improved with an increase in jute fiber content.
4) showed maximum damping behaviour and the highest tensile properties. In another study by Karaduman et al.,39 the magnitudes of peak storage modulus and loss modulus of nonwoven composites improved with an increase in jute fiber content.
Khare et al.40 studied the effect of MWCNTs dispersion in epoxy polymer composites. Their results showed that polymer composites containing a higher dispersion of MWCNTs have a greater Tg as compared to pure epoxy. Babal et al.9 studied the effect of MWCNTs and functionalized CNTs (FCNTs) on polycarbonate (PC) polymer composites. They studied the DMA and mechanical properties of MWCNTs and FCNTs. Their results showed that the Tg value of CNTs composites was lower as compared to pure PC. Kumar et al.41 studied the dynamic mechanical properties of MWCNTs/poly(acrylonitrile styrene-butadiene)/epoxy hybrid composites. The DMA of the blend composite materials gave two different Tg values: one corresponding to an epoxy-rich and other corresponding to an ABS-rich phase, which confirmed the two-phase morphology in the blends. For hybrid composites, MWCNTs localize in the epoxy phase and ABS phase. The improvement in storage modulus by the addition of nanofillers provided better load bearing capacity for the composites. The thermal and dimensional stability of hybrid composites are comparable with that of neat cross-linked epoxy and the blend. Hatui et al.42 studied the storage modulus (E′) and Tg of ABS, which were significantly increased with the addition of modified MWCNTs as compared to unmodified MWCNTs.
DMA of polymer and CNTs polymer composites materials has provided information regarding the Tg and E′ in the previous studies. For the processing of CNT/polymer composites at the industrial scale the entanglement density, adhesion and C factor are very important. The main aim of this study is to investigate the interfacial adhesion, adhesion factor, and reinforcement efficiency factor of the CNT-based ABS polymer composites using DMA. Adhesion behaviour and reinforcement properties are crucial to determine the reinforcement efficiency of CNTs and the structural stability of the polymer composites.
Materials
In this study, ABS granules were used as the polymer matrix. By employing the catalytic chemical vapour deposition technique, MWCNTs were produced by the thermal decomposition of toluene as a carbon source in a long quartz tube heated at a constant temperature under inert atmosphere, and ferrocene was used as the catalyst. Details of the experimental set-up are given elsewhere.43Preparation of MWCNTs/ABS nanocomposites
ABS polymer granules were dried for a minimum of 10 hours by heating at 95 °C in a vacuum oven to remove moisture trapped within the polymer matrix. MWCNTs/ABS nanocomposites containing 0, 1, 3, 5, 7 and 10 wt% of MWCNTs were prepared using a HAAKE Mini Lab II Micro compounder. In the compounder, ABS granules were softened and the proper mixing of the MWCNTs with the help of the co-rotating screw in the extrusion with a speed of 100 rpm and the mixing time of 3 min for each sample was used. The mixed material was transferred to a mold and then pressed by applying a pressure of 670 bars to obtain the desired shape. Nanocomposites were made from different weight percentages of MWCNTs loading in the ABS polymer matrix (1, 3, 5, 7 and 10 wt%) and designated as ABS-1, ABS-3, ABS-5, ABS-7 and ABS-10, respectively. A pure ABS, sample was also prepared under similar conditions and designated as ABS-0. A schematic illustration of whole process is given in Fig. 1. | ||
| Fig. 1 Schematic representation of the mixing of MWCNTs and ABS, interaction of the MWCNTs and ABS and DMA studies with a variation in temperature. | ||
Characterization
Dynamic mechanical analysis of the ABS and MWCNT/ABS nanocomposites were carried out using a dynamic mechanical thermal analyzer (Perkin Elmer DMA 8000 instruments). Rectangular specimens of 15.75 × 5.80 × 3.23 mm3 [length × breadth × thickness] were used for the analysis. These analyses were carried out in the dual bend cantilever mode at the frequency of 1 Hz. For the analysis, samples were heated from room temperature to 180 °C at a heating rate of 2 °C min−1.Morphology
Scanning electron microscopy (SEM) was used to investigate the microstructure of the MWCNTs/ABS nanocomposites. The fractured surfaces of the nanocomposites were studied using SEM (model EVO MA10 ZIESS) after tensile fracture of the samples.Result and discussion
SEM studies were carried out to investigate the surface morphology of the fractured surface and distribution of MWCNTs in ABS. SEM images of ABS-5 and ABS-10 are shown in Fig. 2. The SEM images clearly show the distribution of MWCNTs in the ABS matrix.Dynamic mechanical analysis
DMA is used to study the Tg of polymer and polymer nanocomposites. The storage modulus (E′), signifies the stiffness of polymer composites. Storage modulus curves show three different regions: the high modulus region is the glassy region, where segmental mobility is very limited, then there is a decrease in the value of E′ with an increase in temperature, known as the transition zone and a rubbery region (the flow region).Storage modulus
The storage modulus is proportional to the energy stored per cycle. The variations in the storage modulus as a function of temperature for the ABS and CNT/ABS composites are shown in Fig. 3.As the temperature increased, the value of E′ decreased for all the polymer composites, and this is attributed to the increase in molecular mobility of the polymer chains.44 The value of E′ for ABS-10 was much higher than ABS-0 at the same temperature. This increase in E′ with the addition of MWCNTs is due to the increase in interfacial adhesion.45 The decrease in the modulus around the glass transition temperature was large for the pure polymer. The difference between the E′ values in the glassy and the rubbery state was smaller for the composites with a higher weight% of MWCNTs. The effect of the MWCNTs on the composites, i.e. their effectiveness, can be better represented by the coefficient “C” in eqn (1):46
 | (4) |
A high “C” value indicates the lower effectiveness of the filler. The value obtained from the different wt% of MWCNTs loading in ABS at the frequency of 1 Hz is given in Fig. 4 and Table 1. The lower value of “C” indicated that the effectiveness of the MWCNTs was maximum in ABS-5. For the low wt% of MWCNTs, the distribution of the MWCNTs in the polymer matrix is less efficient, which results in a higher value of “C”.47 Moreover, the degree of entanglement between the polymer matrix and MWCNTs were calculated.
| S. No | MWCNTs/ABS composite | Storage modulus (glassy region) (130 °C) Pa | Storage modulus (rubbery region) (150 °C) Pa | C-factor | Degree of entanglement (at 150 °C) mol m−3 |
|---|---|---|---|---|---|
| 1 | ABS-0 | 4.26 × 109 | 9.1 × 108 | — | 4.31 × 104 |
| 2 | ABS-1 | 4.75 × 109 | 9.34 × 108 | 1.09 | 4.43× 104 |
| 3 | ABS-3 | 5.33 × 109 | 9.86 × 108 | 1.15 | 4.67 × 104 |
| 4 | ABS-5 | 5.928 × 109 | 1.61 × 109 | 0.78 | 7.60 × 104 |
| 5 | ABS-7 | 6.68 × 109 | 1.17 × 109 | 1.22 | 5.54 × 104 |
| 6 | ABS-10 | 7.11 × 109 | 1.26 × 109 | 1.20 | 5.97 × 104 |
Degree of entanglement density
The degree of entanglement of polymer composites can also be measured via dynamic mechanical analysis. To determine the degree of entanglement, the storage modulus value is used in the following equation48
 | (5) |
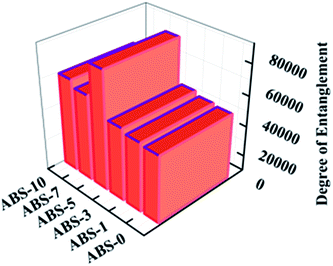 | ||
| Fig. 5 Variation in the degree of entanglement in mol m−3 with wt% of MWCNTs in the ABS matrix at 150 °C. | ||
Reinforcement efficiency factor
The simplest equation used for the calculation of the reinforcement efficiency factor of the composites was introduced by Einstein49| Ec = Em(1 + rVF) | (6) |
Loss modulus
Loss modulus (E′′) measures the maximum heat dissipated per cycle under deformation. Fig. 7 shows the variation of the loss modulus for different wt% of MWCNTs/ABS nanocomposites with temperature. It is clear that the addition of MWCNTs in the polymer matrix caused broadening of the loss modulus peak. This may be attributed to the inhibition of the relaxation process within the composites as a consequence of a higher number of chain segments with the addition of MWCNTs.47 | ||
| Fig. 7 Variation of (a) loss modulus with temperature and (b) magnified plot between 120 and 180 °C for pure ABS and different wt% of MWCNTs/ABS composites. | ||
The value of the loss modulus increased with the increase in wt% of MWCNTs in the ABS polymer. The higher loss modulus value is due to the increase in the value of the internal fraction, which enhances the dissipation energy. The loss modulus curve reached the maximum for the maximum dissipation of mechanical energy. After the maximum peak, height decreased for the higher temperature as a result of the free movement of the polymer chain. A higher wt% of MWCNTs reduces the flexibility of the composite materials by the introduction of constraints on the segmental mobility of the polymeric molecules at the relaxation temperature.47,50,51 There was an apparent shift in the glass transition (Tg) towards the higher temperature as the wt% of MWCNTs (ABS-0 to ABS-5) increased. This is attributed primarily to the segmental immobilization of the matrix chain on the MWCNTs surface.31 A high value of the loss modulus indicates that the system contains more restriction at a high degree of reinforcement.52
Damping parameters (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) δ)
δ)
Damping properties of a material provide the balance between the viscous and elastic phase of polymer composites.53 Fig. 8 shows that the value of tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ for different wt% of MWCNTs/ABS nanocomposites was lower than the ABS-0. As the wt% of MWCNTs increased in the polymer matrix, the tan
δ for different wt% of MWCNTs/ABS nanocomposites was lower than the ABS-0. As the wt% of MWCNTs increased in the polymer matrix, the tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ value decreased.
δ value decreased.
 | ||
Fig. 8 Variation of (a) tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ with temperature (b) magnified image between 145 and 165 °C for pure ABS and different wt% of MWCNTs/ABS composites. δ with temperature (b) magnified image between 145 and 165 °C for pure ABS and different wt% of MWCNTs/ABS composites. | ||
As the temperature increases, the value of damping goes through the maximum in the transition region and then decreases in the rubbery region. Damping factor is low below the Tg because the thermal energy is insufficient to cause the transition and the rotational motion of the segments and the chain segments are in the frozen state.54 Moreover, deformation is the primary mechanism of the elastic and the molecular slips, which results in viscous flow.47 In the rubbery region, the molecular segments are considerably free to move. These motions are also concerned with the cooperative diffusion motion of the molecular chain segments.
Adhesion factor
The adhesion factor (A) is determined from the damping factor of the polymer matrix and polymer composites as the function of the volume fraction of the filler and temperature.55 The damping factor of the polymer composite can be expressed in the term volume fraction and damping factor within the composite system:56
tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δc = øf δc = øf![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) tan tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δf + øi δf + øi![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) tan tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δi + øp δi + øp![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) tan tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δp δp
| (7) |
øf![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) tan tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δf = 0 δf = 0 |
Then, eqn (7) becomes
tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δc = øi δc = øi![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) tan tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δi + øp δi + øp![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) tan tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δp δp
| (8) |
Moreover, we know that øf + øp = 1, thus by substituting eqn (8) and rearranging the equation we get
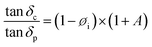 | (9) |
The adhesion factor, ‘A’, can be expressed in terms of the relative damping of the composite and the polymer and the volume fraction of the filler at a given temperature. This assumption would be reasonable only if the development of a transcrystalline layer at the composite interphase could be neglected.
 | (10) |
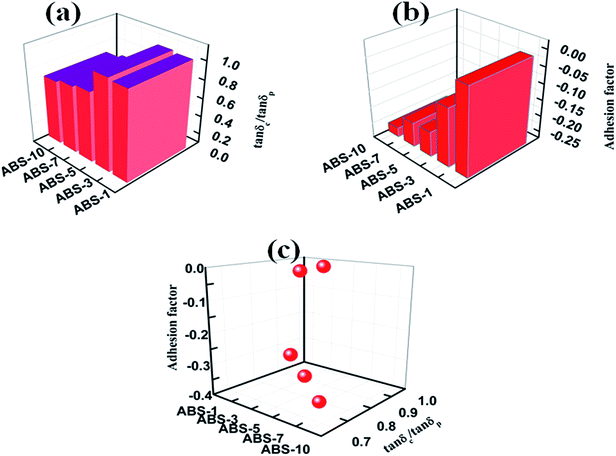
Adhesion factor of different CNTs/ABS composites are shown in Fig. 9. Correa et al.57 also studied the adhesion factor of polymer composites. The higher the degree of interaction between MWCNTs and the matrix, the lower the adhesion factor value.
MWCNTs–ABS matrix interphase adhesion
DMA characterizes the filler matrix interphase in the polymer composites by assuming that the composites dissipation not only attribute to the matrix phase but also depends upon the filler matrix interaction. The interaction between the filler and polymer matrix interface tends to form an immobilized interface. The nanofiller themselves do not contribute to the damping but they depend upon the polymer matrix. The dissipation factor of composites can be calculated from the following relation:58
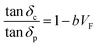 | (11) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δc and tan
δc and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δp are the damping parameter of the composites and polymer matrix, respectively. VF is the volume fraction of the filler and “b” is a parameter that introduces the correct volume fraction of the reinforcement because of the formation of the immobilized interphase layer, which results from the filler–matrix interaction. The value of “b” reaches the maximum value at 5% wt of MWCNTs, as shown in Fig. 10. Subsequently, it starts decreasing due to the MWCNTs–MWCNTs interaction.
δp are the damping parameter of the composites and polymer matrix, respectively. VF is the volume fraction of the filler and “b” is a parameter that introduces the correct volume fraction of the reinforcement because of the formation of the immobilized interphase layer, which results from the filler–matrix interaction. The value of “b” reaches the maximum value at 5% wt of MWCNTs, as shown in Fig. 10. Subsequently, it starts decreasing due to the MWCNTs–MWCNTs interaction.
 | ||
| Fig. 10 Variation of (a) matrix interphase factor b and (b) 3D diagram for damping behaviour and b-factor for different wt% of MWCNTs/ABS composites. | ||
MWCNTs/ABS stiffness calculation
Fig. 11 shows the variation in the ratio of the sample total stiffness with regard to the amount of MWCNTs loading. The stiffness of the composites was enhanced rapidly with MWCNTs loading. The stiffness of the polymer composites depends on the amount of MWCNTs and the length of carbon nanotubes.59–61 | ||
| Fig. 11 (a) Ratio of sample stiffness vs. temperature for different wt% of MWCNTs/ABS composites and (b) at the lower range of the temperature scale (magnified image). | ||
Cole–Cole analysis
Changes in the structural properties due to the addition of MWCNTs in a cross linked polymers matrix can be studied using the Cole–Cole method. The dissipation or loss factor measured during dynamic mechanical measurements is directly analogous to the tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ function, which is relevant to dynamic mechanical testing. The Cole–Cole method is a particular treatment of dielectric relaxation data, which is obtained by plotting E′′ against E′, where each point corresponds to 1 Hz frequency.
δ function, which is relevant to dynamic mechanical testing. The Cole–Cole method is a particular treatment of dielectric relaxation data, which is obtained by plotting E′′ against E′, where each point corresponds to 1 Hz frequency.
The dynamic mechanical properties examined as a function of temperature and frequency are represented on the Cole–Cole complex plane. Fig. 12 shows the Cole–Cole plots of the various composite systems, where the loss modulus is plotted as a function of storage modulus at a frequency of 1 Hz.
The nature of the Cole–Cole plot is reported to be indicative of the nature of the system. Homogeneous polymeric systems are reported to show a semicircle diagram, while two-phase systems show an imperfect semicircle (elliptical path).62,63 On analysing the Cole–Cole plots of the present composite systems, it is seen that the curves show the shape of imperfect semicircles. The shape of the curves thus points towards good adhesion.
The DMA of pure ABS and MWCNTs/ABS composites allowed the investigation of the degree of entanglement, coefficient of the “C” factor and adhesion factor. All these properties showed that 5 wt% of MWCNTs loading is sufficient for a better enhancement of the properties of the ABS matrix. After 5 wt%, MWCNTs–MWCNTs interactions took place.
Conclusion
Dynamic mechanical analysis of pure ABS and MWCNTs/ABS composites were studied. The results showed that the addition of MWCNTs into the ABS matrix increases the value of the storage and loss modulus and decreases the value of the damping factor. The improvement in the storage modulus by the addition of MWCNTs provides a better load bearing capacity for the composite. The glass transition temperature of the composites shifted to the higher region as the wt% of MWCNTs increased. The coefficient of the “C” factor, adhesion factor, reinforcement factor, b factor and degree of entanglement were studied with the incorporation of MWCNT in the ABS matrix by dynamic mechanical analysis. It has been found that the degree of entanglement increases upto 5 wt% MWCNT loading and beyond this loading it decreases. Similarly, the b factor also increased up to 5 wt% loading in ABS and beyond this loading it decreased. The C factor decreased with the increase of MWCNT loading up to 5 wt% loading and then started to increase beyond this loading. The reinforcement factor decreased up to 5 wt% loading and then started to increase beyond this loading. The results from all these factors show that 5 wt% loading of MWCNTs in the ABS matrix is sufficient for better improvement in the properties of MWCNT/ABS composites. DMA can provide significant insight for the design of mechanically strong materials with the incorporation of MWCNTs.Acknowledgements
The authors wish to express their gratitude to DNPL for granting permission to publish the result. Authors are also thankful to Mr K. N. Sood and Mr Jay Tawale for SEM measurement. The studies were carried out under the CSIR-Network project (D-NEED, PSC0109).References
- S. Pande, B. P. Singh and R. B. Mathur, in Polymer Nanotube Nanocomposites: Synthesis, Properties, and Applications, Scrivener Publishing LLC, 2nd edn, 2014, pp. 333–364 Search PubMed.
- R. B. Mathur, S. Pande and B. P. Singh, Polym. Nanotube Nanocompos., 2010, 11, 177 Search PubMed.
- D. Romanzini, A. Lavoratti, H. L. Ornaghi, S. C. Amico and A. J. Zattera, Mater. Des., 2013, 47, 9–15 CrossRef CAS.
- S. N. Cassu and M. I. Felisberti, Quim. Nova, 2005, 28, 255–263 CrossRef.
- H. L. Ornaghi, V. Pistor and A. J. Zattera, J. Non-Cryst. Solids, 2012, 358, 427–432 CrossRef CAS.
- V. Pistor, F. G. Ornaghi, H. L. Ornaghi and A. J. Zattera, Mater. Sci. Eng., A, 2012, 532, 339–345 CrossRef CAS.
- O. M. Istrate, K. R. Paton, U. Khan, A. O'Neill, A. P. Bell and J. N. Coleman, Carbon, 2014, 78, 243–249 CrossRef CAS.
- A. Babal, R. Gupta, B. P. Singh, V. N. Singh, R. B. Mathur and S. R. Dhakate, RSC Adv., 2014, 4, 64649–64658 RSC.
- A. Babal, R. Gupta, B. P. Singh and S. R. Dhakate, RSC Adv., 2015, 5, 43462–43472 RSC.
- T. K. Gupta, B. P. Singh, R. K. Tripathi, S. R. Dhakate, V. N. Singh, O. Panwar and R. B. Mathur, RSC Adv., 2015, 5, 16921–16930 RSC.
- T. K. Gupta, B. P. Singh, V. N. Singh, S. Teotia, A. P. Singh, I. Elizabeth, S. R. Dhakate, S. Dhawan and R. Mathur, J. Mater. Chem. A, 2014, 2, 4256–4263 CAS.
- D. Hanlon, C. Backes, E. Doherty, C. S. Cucinotta, N. C. Berner, C. Boland, K. Lee, P. Lynch, Z. Gholamvand and A. Harvey, arXiv preprint arXiv:1501.01881, 2015.
- J.-M. Thomassin, M. Trifkovic, W. Alkarmo, C. Detrembleur, C. Jérôme and C. Macosko, Macromolecules, 2014, 47, 2149–2155 CrossRef CAS.
- T. K. Gupta, B. P. Singh, S. R. Dhakate, V. N. Singh and R. B. Mathur, J. Mater. Chem. A, 2013, 1, 9138–9149 CAS.
- R. Haggenmueller, H. Gommans, A. Rinzler, J. E. Fischer and K. Winey, Chem. Phys. Lett., 2000, 330, 219–225 CrossRef CAS.
- D. Spasevska, G. Leal, M. Fernández, J. B. Gilev, M. Paulis and R. Tomovska, RSC Adv., 2015, 5, 16414–16421 RSC.
- H. Peng, G. Ma, K. Sun, J. Mu, H. Wang and Z. Lei, J. Mater. Chem. A, 2014, 2, 3303–3307 CAS.
- C. Liao, Q. Wu, T. Su, D. Zhang, Q. Wu and Q. Wang, ACS Appl. Mater. Interfaces, 2014, 6, 1356–1360 CAS.
- S. P. Pawar, D. A. Marathe, K. Pattabhi and S. Bose, J. Mater. Chem. A, 2015, 3, 656–669 CAS.
- B. P. Singh, D. Saket, A. Singh, S. Pati, T. Gupta, V. Singh, S. Dhakate, S. Dhawan, R. Kotnala and R. Mathur, J. Mater. Chem. A, 2015, 3, 13203–13209 CAS.
- H. J. Salavagione, A. M. Díez-Pascual, E. Lázaro, S. Vera and M. A. Gómez-Fatou, J. Mater. Chem. A, 2014, 2, 14289–14328 CAS.
- M. Janani, P. Srikrishnarka, S. V. Nair and A. S. Nair, J. Mater. Chem. A, 2015, 3, 17914–17938 CAS.
- Y. Yao, H. Xiao, P. Wang, P. Su, Z. Shao and Q. Yang, J. Mater. Chem. A, 2014, 2, 11768–11775 CAS.
- S. Teotia, B. P. Singh, I. Elizabeth, V. N. Singh, R. Ravikumar, A. P. Singh, S. Gopukumar, S. Dhawan, A. Srivastava and R. B. Mathur, RSC Adv., 2014, 4, 33168–33174 RSC.
- S. Pande, A. Chaudhary, D. Patel, B. P. Singh and R. B. Mathur, RSC Adv., 2014, 4, 13839–13849 RSC.
- J. Jyoti, S. Basu, B. P. Singh and S. Dhakate, Composites, Part B, 2015, 83, 58–65 CrossRef CAS.
- C. Wei, Appl. Phys. Lett., 2006, 88, 093108 CrossRef.
- B. P. Singh, V. Chaudary, S. Teotia, T. K. Gupta, V. N. Singh, S. R. Dhakate and R. B. Mathur, Adv. Mater. Lett., 2015, 6, 104–113 CAS.
- B. P. Singh, V. Choudhary, P. Saini, S. Pande, V. Singh and R. Mathur, J. Nanopart. Res., 2013, 15, 1–12 Search PubMed.
- B. P. Singh, K. Saini, V. Choudhary, S. Teotia, S. Pande, P. Saini and R. Mathur, J. Nanopart. Res., 2014, 16, 1–11 CrossRef.
- P. Joseph, G. Mathew, K. Joseph, G. Groeninckx and S. Thomas, Composites, Part A, 2003, 34, 275–290 CrossRef.
- W. Goertzen and M. Kessler, Composites, Part B, 2007, 38, 1–9 CrossRef.
- T. Hatakeyama and F. Quinn, Thermal Analysis, 1994 Search PubMed.
- J. Otaigbe, Polym. Eng. Sci., 1991, 31, 104–109 CAS.
- B. Harris, O. Braddell, D. Almond, C. Lefebvre and J. Verbist, J. Mater. Sci., 1993, 28, 3353–3366 CrossRef CAS.
- K. E. Verghese, R. Jensen, J. Lesko and T. Ward, Polymer, 2001, 42, 1633–1645 CrossRef CAS.
- A. Etaati, S. Pather, Z. Fang and H. Wang, Composites, Part B, 2014, 62, 19–28 CrossRef CAS.
- M. Jawaid, H. A. Khalil, A. Hassan, R. Dungani and A. Hadiyane, Composites, Part B, 2013, 45, 619–624 CrossRef CAS.
- Y. Karaduman, M. Sayeed, L. Onal and A. Rawal, Composites, Part B, 2014, 67, 111–118 CrossRef CAS.
- K. S. Khare and R. Khare, J. Phys. Chem. B, 2013, 117, 7444–7454 CrossRef CAS PubMed.
- P. Jyotishkumar, E. Abraham, S. M. George, E. Elias, J. Pionteck, P. Moldenaers and S. Thomas, J. Appl. Polym. Sci., 2013, 127, 3093–3103 CrossRef CAS.
- G. Hatui, G. C. Nayak, C. K. Das and S. B. Yadaw, J. Appl. Polym. Sci., 2013, 129, 57–64 CrossRef CAS.
- R. B. Mathur, S. Chatterjee and B. P. Singh, Compos. Sci. Technol., 2008, 68, 1608–1615 CrossRef CAS.
- J. M. Faulstich de Paiva and E. Frollini, Macromol. Mater. Eng., 2006, 291, 405–417 CrossRef CAS.
- C. Komalan, K. George, P. Kumar, K. Varughese and S. Thomas, eXPRESS Polym. Lett., 2007, 1, 641–653 CrossRef CAS.
- L. A. Pothan, Z. Oommen and S. Thomas, Compos. Sci. Technol., 2003, 63, 283–293 CrossRef CAS.
- N. Hameed, P. Sreekumar, B. Francis, W. Yang and S. Thomas, Composites, Part A, 2007, 38, 2422–2432 CrossRef.
- Z. Oommen, G. Groeninckx and S. Thomas, J. Polym. Sci., Part B: Polym. Phys., 2000, 38, 525–536 CrossRef CAS.
- A. Einstein, Dover, Investigation of the theory of Brownian motion, New-York, 1956 Search PubMed.
- M. A. López-Manchado, J. Biagitti and J. M. Kenny, Polym. Compos., 2002, 23, 779–789 CrossRef.
- S. Mohanty, S. K. Verma and S. K. Nayak, Compos. Sci. Technol., 2006, 66, 538–547 CrossRef CAS.
- J. H. S. A. Júnior, H. L. O. Júnior, S. C. Amico and F. D. R. Amado, Mater. Des., 2012, 42, 111–117 CrossRef.
- H. Gu, Mater. Des., 2009, 30, 2774–2777 CrossRef CAS.
- J. D. Ferry, Viscoelastic properties of polymers, John Wiley & Sons, 1980 Search PubMed.
- L. A. Pothan, S. Thomas and G. Groeninckx, Composites, Part A, 2006, 37, 1260–1269 CrossRef.
- J. Kubat, M. Rigdahl and M. Welander, J. Appl. Polym. Sci., 1990, 39, 1527–1539 CrossRef CAS.
- C. Correa, C. Razzino and E. Hage, J. Thermoplast. Compos. Mater., 2007, 20, 323–339 CrossRef CAS.
- J. Sarasua and J. Pouyet, J. Thermoplast. Compos. Mater., 1998, 11, 2–21 CrossRef CAS.
- K. W. Putz, M. J. Palmeri, R. B. Cohn, R. Andrews and L. C. Brinson, Macromolecules, 2008, 41, 6752–6756 CrossRef CAS.
- L. Schadler, S. Giannaris and P. Ajayan, Appl. Phys. Lett., 1998, 73, 3842–3844 CrossRef CAS.
- J. N. Coleman, U. Khan, W. J. Blau and Y. K. Gun'ko, Carbon, 2006, 44, 1624–1652 CrossRef CAS.
- R. F. Landel and L. E. Nielsen, Mechanical properties of polymers and composites, CRC Press, 1993 Search PubMed.
- R. Chandra, S. Singh and K. Gupta, Compos. Struct., 1999, 46, 41–51 CrossRef.
| This journal is © The Royal Society of Chemistry 2016 |