The Li–S battery: an investigation of redox shuttle and self-discharge behaviour with LiNO3-containing electrolytes†
Matthew J. Lacey*a,
Anurag Yalamanchiliab,
Julia Maibacha,
Carl Tengstedtb,
Kristina Edströma and
Daniel Brandella
aDepartment of Chemistry – Ångström Laboratory, Box 538, Lägerhyddsvägen 1, 751 21 Uppsala, Sweden. E-mail: matthew.lacey@kemi.uu.se
bScania CV AB, SE-151 87 Södertälje, Sweden
First published on 15th December 2015
Abstract
The polysulfide redox shuttle and self-discharge behaviour of lithium–sulfur (Li–S) cells containing the electrolyte additive LiNO3 has been thoroughly explored by a range of electrochemical and surface analysis techniques on simple Li–S (i.e., not specifically optimised to resist self-discharge) and symmetrical Li–Li cells. Despite the relatively effective passivation of the negative electrode by LiNO3, fully charged cells self-discharged a quarter of their capacity within 3 days, although in the short-term cells can be recharged without any noticeable capacity loss. The processes governing the rate and reversibility of self-discharge in these cells have been investigated and explained in terms of the reactions of polysulfides occurring at both electrodes during idle conditions.
1 Introduction
The rechargeable lithium–sulfur (Li–S) battery is currently one of the most actively studied “post-Li-ion” energy storage systems, primarily because of its high energy density: practical energy densities on the cell level in excess of 300 W h kg−1 – higher than the state of the art Li-ion batteries – have been demonstrated in the private sector and energies in the range 400–600 W h kg−1 are widely considered to be practically achievable. Other attractive advantages include the low cost of the active material and good safety, although intrinsic drawbacks of poor conductivity of the active materials and severe issues of parasitic reactions resulting from the solubility of reaction intermediates (polysulfides, often referred to as Li2Sn or simply “PS”) are a barrier to wider practical application.Significant advances have been made in recent years in the development of the positive electrode in this system; these have been covered by numerous recent reviews and it is not necessary to discuss these here.1–4 However, management of the behaviour of dissolved polysulfides remains a topic of considerable interest and importance with a broad range of strategies under consideration.
Polysulfides are readily soluble in most of the commonly investigated electrolyte systems. The unwanted spontaneous reaction of Li2Sn with the reactive Li metal negative electrode is the source of the well-known “polysulfide redox shuttle”, effectively an internal shuttle for electrons carried by multiple polysulfide species.
This problem could logically be tackled by designing the electrolyte to minimise the solubility of Li2Sn species in the electrolyte, as has been variously reported.5–9 However, the solubility and reactivity of these species are important contributors to the overall cell reaction10,11 – so suppression of their solubility likely comes at the cost of decreased energy efficiency and power density. A more common approach is to tolerate the solubility of Li2Sn, at least in the positive electrode environment, and protect the anode by, for example, interlayers,12,13 ion-selective separators,14,15 positive electrodes which may actively adsorb polysulfides,16–18 or additives that aid in the formation of a favourable solid–electrolyte interphase (SEI).19–22
One of the most well-known redox shuttle-suppressing strategies, lithium nitrate, LiNO3, generally used as an electrolyte co-salt or additive, falls into this latter category. It is generally understood that the reduction of nitrate at the anode and a subsequent oxidation of polysulfides aids in the formation of a denser SEI which helps to prevent the reduction of polysulfide at the anode surface.20,22,23
While the use of LiNO3 and many other strategies have been shown to considerably restrain the shuttle effect and improve cycling, and approaches such as polysulfide-impermeable layers or solvents with low polysulfide solubility have been validated by measurements of sulfur content in the electrolyte, it is relatively rare that the electrochemical efficiency of cells is assessed by methods other than measurements of coulombic efficiency from galvanostatic cycling, or other more qualitative measurements. However, a few detailed studies of redox shuttle and self-discharge behaviour have been published.
Mikhaylik and Akridge24 were the first to quantitatively describe the redox shuttle and its relation to capacity and charge efficiency, through a combination of mathematical modelling and experiments covering the effects of charging rate, self-heating and salt concentration. In that work they developed the concept of the “charge-shuttle factor”, a relationship between the effective parasitic current to the applied current, and a shuttle rate constant to quantify the rate of self discharge under rest conditions. More recently, Moy et al.25 quantified the redox shuttle by measuring the steady state current passed through Li–S cells when held under potentiostatic control at pre-determined states-of-charge. The authors demonstrated that the “shuttle current” is highest close to the maximum state-of-charge, where the concentration of the higher order (i.e., longer chain) polysulfides is highest. The shuttle currents for cells containing LiNO3 in the electrolyte were also measured, but were more than an order of magnitude lower compared with the cells without LiNO3, and considered to be almost negligible. Gordin et al.26 quantified self-discharge of cells with different electrolytes by inserting a 2 week rest period between galvanostatic cycles at low rate, measuring the percentage loss of capacity after the rest period, while Hart et al.16 similarly quantified self-discharge for a range of different sulfur host materials by stopping cells mid-cycle for three days and measuring the capacity loss. Very recently, Xu et al.27 quantitatively assessed the effect of self-discharge through using LiNO3 and a Nafion-coated separator.
While LiNO3 (among other strategies) enables cycling of cells at low rate with a reasonable coulombic efficiency, self-discharge over even moderate storage or relaxation periods is still a significant issue and one that is largely unexplored. In fact, as the development of the positive electrode continues to improve and performance is increasingly benchmarked by rate capability, the issue of self-discharge can easily be ignored and claims of control over polysulfide mass transport may not be properly scrutinised.
In this work, we present a detailed overview of the redox shuttle and self-discharge behaviour in electrolytes containing LiNO3, through semi-quantitative measurements of polysulfides in the electrolyte when cells are at idle conditions, changes in the SEI, and electrochemical methods for quantifying self discharge over extended cycling. The aim of this work is to demonstrate the significant effect of self-discharge on a Li–S cell even when an additive considered effective – as LiNO3 is – is used, even without particularly heavy usage of the cell. An improved understanding of the redox shuttle and self-discharge processes as well as the use of appropriate measurements to assess medium- and long-term charge storage is essential to the development of this system for wider practical application.
2 Experimental
2.1 Materials
Carboxymethylcellulose sodium salt (CMC, Leclanché), styrene butadiene rubber (SBR, Targray PSBR-100), 1,2-dimethoxyethane (DME, Novolyte), 1,3-dioxolane (DOL, anhydrous, Aldrich) and sulfur (S8, Aldrich) were used as received. Lithium bis(trifluoromethanesulfonyl)imide (LiTFSI, Novolyte), lithium perchlorate (LiClO4, Aldrich), lithium nitrate (LiNO3, Aldrich) and lithium sulfide (Li2S, Aldrich) were dried at 120 °C under vacuum prior to use. A sample of a high conductivity carbon black with a surface area of 1100 m2 g−1 and a pore volume of 1.74 cm3 g−1 as analysed and used in our earlier studies11,28 was kindly provided by Orion Engineered Carbons GmbH.2.2 Electrode preparation
Positive electrodes were prepared by first mixing sulfur and carbon black in a 58![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 35 ratio and heating to 155 °C in order to melt the sulfur into the pores of the carbon. The resulting composite was then dispersed into water with the binders to give a composition of 58
35 ratio and heating to 155 °C in order to melt the sulfur into the pores of the carbon. The resulting composite was then dispersed into water with the binders to give a composition of 58![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 35
35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 S
7 S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C
C![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) binder, where the binder was a 2
binder, where the binder was a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 mixture of CMC
3 mixture of CMC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SBR. The slurry was mixed by planetary ball-milling for 2 hours and coated onto Al foil to a loading of approximately 1 mgs cm−2. The electrodes were allowed to dry at ambient conditions, cut into circular discs of the desired size (13 mm or 20 mm in diameter), then transferred into an Ar-filled glove box and dried further at 55 °C overnight.
SBR. The slurry was mixed by planetary ball-milling for 2 hours and coated onto Al foil to a loading of approximately 1 mgs cm−2. The electrodes were allowed to dry at ambient conditions, cut into circular discs of the desired size (13 mm or 20 mm in diameter), then transferred into an Ar-filled glove box and dried further at 55 °C overnight.
2.3 Cell preparation
Two different cell preparation techniques were employed in this work. For all standard two-electrode electrochemical measurements on Li–S cells, CR2025 coin cells were assembled comprising a 13 mm diameter cathode, a 17 mm diameter porous polyethylene separator (SOLUPOR, Lydall Performance Materials) and a 16 mm diameter piece of a 125 μm-thick Li foil (Cyprus Foote Mineral) as the anode. The electrolyte for all coin cells was 1 M LiTFSI, 0.25 M LiNO3 in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 DME
1 DME![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DOL, and the electrolyte was fixed at 6 μL mgs−1.
DOL, and the electrolyte was fixed at 6 μL mgs−1.
Four-electrode pouch cells, including a second insulated wire electrode as an in situ probe with common counter and reference electrodes, were prepared as described in our previous work11 with some modifications. Briefly, the cells were constructed with a 20 mm diameter cathode, a 25 mm diameter polyethylene separator on the positive electrode side and a 25 mm diameter glass fibre separator (Whatman GF-A) on the negative electrode side, and a 22 mm diameter piece of 125 μm-thick Li foil as the negative electrode. The probe electrode was a 125 μm diameter PTFE-insulated Pt wire (Advent Research Materials). The electrolyte was the same as previously described for coin cell experiments, although a larger amount of electrolyte was required (35 μL mgs−1) in order to achieve comparable performance.
For analysis of anode surfaces, symmetrical Li‖Li pouch cells were prepared using a 20 mm diameter piece of 125 μm-thick Li foil as the working electrode to be analysed, a 22 mm diameter polyethylene separator and a larger piece of Li foil as the anode. The electrolyte was 80 μL of 1 M LiClO4, 0.25 M LiNO3 in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 DME
1 DME![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DOL, presaturated with polysulfides in order to mimic the electrolyte chemistry of the Li–S cell in the symmetrical setup. Sulfur pre-saturation was achieved by agitating equimolar amounts of S8 and Li2S (giving a nominal stoichiometry of “Li2S9”) in the electrolyte for at least 3 days and filtering off any remaining solid. LiClO4 was chosen as the electrolyte salt to avoid the inclusion of F-containing compounds in the SEI, compounds which are highly susceptible to decomposition under X-ray radiation. The use of LiClO4 also ensures that sulfur compounds incorporated into the SEI can only originate from the dissolved polysulfides.
DOL, presaturated with polysulfides in order to mimic the electrolyte chemistry of the Li–S cell in the symmetrical setup. Sulfur pre-saturation was achieved by agitating equimolar amounts of S8 and Li2S (giving a nominal stoichiometry of “Li2S9”) in the electrolyte for at least 3 days and filtering off any remaining solid. LiClO4 was chosen as the electrolyte salt to avoid the inclusion of F-containing compounds in the SEI, compounds which are highly susceptible to decomposition under X-ray radiation. The use of LiClO4 also ensures that sulfur compounds incorporated into the SEI can only originate from the dissolved polysulfides.
2.4 Electrochemical testing
Electrochemical measurements were made with either MPG2 or VMP2 potentiostats (Bio-Logic). All galvanostatic cycling steps were at a rate of C/10 (167.2 mA g s−1) between the voltage limits of 1.8 V and 2.6 V vs. Li/Li+. Three different test protocols are described in this work:(1) Shuttle current measurement under potentiostatic control: Cells were cycled galvanostatically as described above. Measurements were made on pre-determined cycles (1st, 5th, 10th and every following 10th cycle) by holding the cell potential at 2.38 V on charge for 72 hours.
(2) Shuttle current measurement under OCV conditions (“cycle/wait” test): Cells were cycled galvanostatically as described above. Every third cycle the cell was stopped at 100% charge (2.6 V) and left to relax at OCV for a period between 12 hours and 14 days. Following the rest, cycling was recommenced with the discharge step.
(3) Polysulfide concentration measurements with an in situ probe: Tests were run on the VMP in bipotentiostat mode using two synchronised channels to allow the use of common counter and reference electrodes. The cell was subjected to a single discharge/charge cycle and left to relax under open circuit conditions from 100% charged. Linear sweep voltammograms (LSVs) were then made at the probe electrode between OCV and 2.85 V vs. Li/Li+ at a scan rate of 1 mV s−1 every four hours for 200 hours.
For symmetrical Li‖Li cells, “discharge” and “charge” currents (400 μA cm−2) were calculated based on the area of the 20 mm diameter Li working electrode. The discharge and charge times were 6 hours each for all experiments (i.e., 2.4 mA h cm−2).
2.5 Surface analysis
Cells were disassembled in an Ar-filled glove box. All extracted samples were washed with a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of DME
1 mixture of DME![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DOL.
DOL.
Samples analysed by X-ray photoelectron spectroscopy (XPS) were first transferred to the spectrometer through a sealed transfer system to avoid air exposure. XPS characterisation was performed using a PHI 5500 spectrometer (Physical Electronics) using monochromatic Al K radiation (1468.7 eV). Spectra were recorded with a pass energy of 23.5 eV giving an overall instrumental resolution of 0.6 eV as determined from the broadening of a Ag Fermi edge. All sulfur lines are curve fitted using a doublet peak with a spin–orbit splitting of 1.18 eV and an intensity ratio of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 characteristic for S2p. Spectra were calibrated in binding energy to the hydrocarbon peak at 285 eV. Reference samples of Li2SO4, Li2S, Na2S2O3 and Na2S2O3 were measured to assist with peak assignment (ESI, Fig. S1†).
1 characteristic for S2p. Spectra were calibrated in binding energy to the hydrocarbon peak at 285 eV. Reference samples of Li2SO4, Li2S, Na2S2O3 and Na2S2O3 were measured to assist with peak assignment (ESI, Fig. S1†).
Following XPS measurements the same transfer system was used to return the samples to the glove box to prepare for SEM analysis. Samples were removed from the glove box in sealed vials and then introduced to the microscope (Carl Zeiss SIGMA FE-SEM) via a N2-filled glove bag.
3 Results and discussion
3.1 “Baseline” Li–S cell electrochemistry
For studying the behaviour of “full” Li–S cells, we have used a simple cathode composition similar to that used in our previous work11,28 comprising a porous carbon/sulfur composite with a total sulfur content of 58% in the electrode. The electrolyte volume used, at 6 μL mgs−1 was first determined as the lowest possible amount which could be used with the cathodes without resulting in a serious decrease in cell performance. For comparison purposes, the galvanostatic cycling performance of the benchmark cell used in this work is given in Fig. 1.After an initial drop in capacity over the first few cycles, the cell gives a relatively stable reversible capacity of 800 mA h g−1 over the first 100 cycles. The coulombic efficiency, however, is relatively low, decreasing from ∼95% in the initial cycles to ∼92% over the first 100 cycles. The low coulombic efficiency is expected given that no specific strategies for suppressing the redox shuttle other than the addition of LiNO3 to the electrolyte are used here, and the use of the smallest possible amount of electrolyte ensures that the electrolyte becomes saturated with polysulfides during the charge and discharge process, ensuring the highest possible rate of reaction with the anode surface. Furthermore, the sulfur loading in the cell is relatively low at ∼1 mgs cm−2, which as previously reported26 may in fact contribute further to the rate of self-discharge. The continuous decrease in the coulombic efficiency can be interpreted as a continuous increase in the rate of self-discharge over the cycling period. However, as has been previously discussed,25 the coulombic efficiency does not give any specific information about the rate of self-discharge and can vary considerably depending on sulfur utilisation, charging rate and so on. Nonetheless, this behaviour is typical of cells of this type without a specifically optimised positive electrode and is a reasonable baseline for further investigation.
3.2 Electrolyte–anode interface and SEI formation
The reactions of dissolved polysulfides with Li metal and the surface layer formed on the anode in contact with the electrolyte (without cycling, with cycling, and after a long relaxation time following cycling) was studied with X-ray photoelectron spectroscopy (XPS) using simplified symmetrical (Li‖Li) cells with an electrolyte pre-saturated with polysulfides and a supporting salt not containing S (LiClO4). SEM images for Li metal samples are given in Fig. 2, and XPS spectra for the S2p orbital are given in Fig. 3.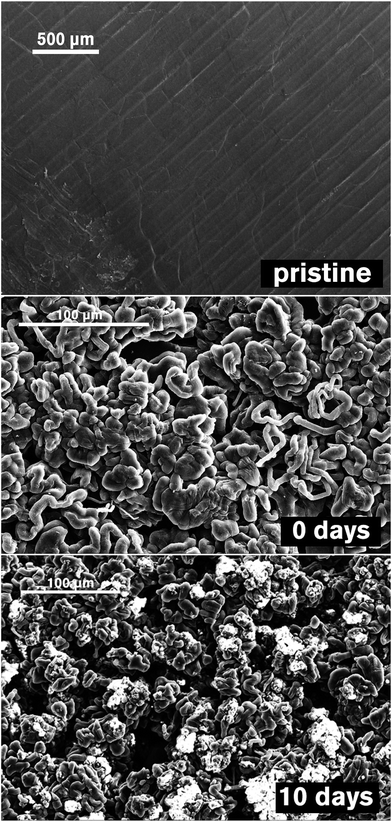 | ||
| Fig. 2 SEM images of Li anodes. (Top) Pristine Li, (middle) after 1 discharge/charge cycle (“charged”), (bottom) after 1 cycle and 10 days rest (“self-discharged”). | ||
As is clear from Fig. 3a, the as-received Li foil is free from any S-containing compounds in the surface layer. Following 12 hours of soaking in the polysulfide-saturated electrolyte, several different S-containing species are present (Fig. 3b). The most prominent emission at 169.2 eV coincides in binding energy with sulfate ([![[S with combining low line]](https://www.rsc.org/images/entities/char_0053_0332.gif) O4]2−, S(+VI)). The peak at 167.2 eV originates from the S(+IV) oxidation state, and likely assignments are sulfite ([
O4]2−, S(+VI)). The peak at 167.2 eV originates from the S(+IV) oxidation state, and likely assignments are sulfite ([![[S with combining low line]](https://www.rsc.org/images/entities/char_0053_0332.gif) O3]2−) or the central S-atom in lithium thiosulfate ([S–
O3]2−) or the central S-atom in lithium thiosulfate ([S–![[S with combining low line]](https://www.rsc.org/images/entities/char_0053_0332.gif) O3]2−). These oxidised sulfur species are an expected result of oxidation reactions following reduction of the LiNO3 additive in the electrolyte, as has been investigated previously.20 Thiosulfate is a likely product of a disproportionation reaction between sulfite and polysulfide. For thiosulfate, a peak for [S–
O3]2−). These oxidised sulfur species are an expected result of oxidation reactions following reduction of the LiNO3 additive in the electrolyte, as has been investigated previously.20 Thiosulfate is a likely product of a disproportionation reaction between sulfite and polysulfide. For thiosulfate, a peak for [S–![[S with combining low line]](https://www.rsc.org/images/entities/char_0053_0332.gif) O3]2− – should be accompanied by a second peak at ∼162 eV for [S–
O3]2− – should be accompanied by a second peak at ∼162 eV for [S–![[S with combining low line]](https://www.rsc.org/images/entities/char_0053_0332.gif) O3]2− in a 1
O3]2− in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio29 (see also the reference spectra in the ESI, Fig. S1†).
1 ratio29 (see also the reference spectra in the ESI, Fig. S1†).
In this case, the peak observed in this binding energy range is smaller in intensity. Terminal atoms (![[S with combining low line]](https://www.rsc.org/images/entities/char_0053_0332.gif) T) of polysulfide species (Li2Sn, e.g., Li2S2 and Li2S4) may furthermore also contribute to the photoelectron intensity in this binding energy range. Therefore, it is most likely that the peak at 167.2 eV is primarily from [SO3]2−. The remaining peak at 164 eV is attributed to the S(0) oxidation state. Since this peak is higher in intensity than the peak at 162 eV (
T) of polysulfide species (Li2Sn, e.g., Li2S2 and Li2S4) may furthermore also contribute to the photoelectron intensity in this binding energy range. Therefore, it is most likely that the peak at 167.2 eV is primarily from [SO3]2−. The remaining peak at 164 eV is attributed to the S(0) oxidation state. Since this peak is higher in intensity than the peak at 162 eV (![[S with combining low line]](https://www.rsc.org/images/entities/char_0053_0332.gif) T), it is plausible that this signal originates from the bridging-S (
T), it is plausible that this signal originates from the bridging-S (![[S with combining low line]](https://www.rsc.org/images/entities/char_0053_0332.gif) B) of metastable Li2Sn where n > 4. However, just as it is difficult to distinguish [S–
B) of metastable Li2Sn where n > 4. However, just as it is difficult to distinguish [S–![[S with combining low line]](https://www.rsc.org/images/entities/char_0053_0332.gif) O3]2− from
O3]2− from ![[S with combining low line]](https://www.rsc.org/images/entities/char_0053_0332.gif) T in Li2Sn, it is difficult to distinguish an
T in Li2Sn, it is difficult to distinguish an ![[S with combining low line]](https://www.rsc.org/images/entities/char_0053_0332.gif) B environment from elemental sulfur (S8). It therefore cannot be currently established if higher order Li2Sn exists in the surface layer or if such compounds have decomposed into S8 and lower order Li2Sn; though not, as evidenced by a lack of a peak at 160 eV, lithium sulfide (Li2S).
B environment from elemental sulfur (S8). It therefore cannot be currently established if higher order Li2Sn exists in the surface layer or if such compounds have decomposed into S8 and lower order Li2Sn; though not, as evidenced by a lack of a peak at 160 eV, lithium sulfide (Li2S).
After a single discharge/charge cycle with immediate extraction from the cell, SEM analysis reveals the expected “mossy” deposition of lithium metal (Fig. 2, middle), and five different sulfur environments can be distinguished in the XPS spectrum (Fig. 3c). Of principal importance is the appearance of an emission from Li2S (S(−II)) at 160 eV. Relative to the “soaked” sample (Fig. 2b), the “charged” sample also shows increased intensity in the peaks at 167 eV ([S–![[S with combining low line]](https://www.rsc.org/images/entities/char_0053_0332.gif) O3]2− or [
O3]2− or [![[S with combining low line]](https://www.rsc.org/images/entities/char_0053_0332.gif) O3]2−) and 162 eV ([
O3]2−) and 162 eV ([![[S with combining low line]](https://www.rsc.org/images/entities/char_0053_0332.gif) –SO3]2− or
–SO3]2− or ![[S with combining low line]](https://www.rsc.org/images/entities/char_0053_0332.gif) T).
T).
After 10 days exposure to the electrolyte following a single discharge/charge cycle (Fig. 3d), the S2p spectrum is dominated by the emission located at 162 eV (![[S with combining low line]](https://www.rsc.org/images/entities/char_0053_0332.gif) T and [
T and [![[S with combining low line]](https://www.rsc.org/images/entities/char_0053_0332.gif) –SO3]2−). Compared to the “soaked” and “charged” samples, the emission of
–SO3]2−). Compared to the “soaked” and “charged” samples, the emission of ![[S with combining low line]](https://www.rsc.org/images/entities/char_0053_0332.gif) B is shifted to lower binding energy by ∼0.7–0.9 eV. This may indicate the presence of an environment such as the
B is shifted to lower binding energy by ∼0.7–0.9 eV. This may indicate the presence of an environment such as the ![[S with combining low line]](https://www.rsc.org/images/entities/char_0053_0332.gif) B-atom in S32− (i.e., [S–
B-atom in S32− (i.e., [S–![[S with combining low line]](https://www.rsc.org/images/entities/char_0053_0332.gif) –S]2−), in which
–S]2−), in which ![[S with combining low line]](https://www.rsc.org/images/entities/char_0053_0332.gif) B is more strongly affected by secondary chemical shifts as compared with longer polysulfides. Crucially, contributions from Li2S and [
B is more strongly affected by secondary chemical shifts as compared with longer polysulfides. Crucially, contributions from Li2S and [![[S with combining low line]](https://www.rsc.org/images/entities/char_0053_0332.gif) O4]2− are almost negligible, indicating a general increase in thickness of the SEI which obscures these compounds, since the probing depth of XPS is only of the order of a few nanometres. This observation is supported further by the appearance of insulating particles on the surface as seen with the SEM (Fig. 2, bottom). Li2S, perhaps surprisingly, appears to be added to the surface layer only in very small quantities while the cell is not in operation. Given the overall intensities of the peaks at 162 eV and 167 eV it is most likely that the major products formed on the anode during a long idle time are short chain polysulfides such as Li2S2 and possibly Li2S3, with additional contributions from oxidised sulfur species such as Li2SO3 and Li2S2O3 formed by reaction of the reduction products of LiNO3.
O4]2− are almost negligible, indicating a general increase in thickness of the SEI which obscures these compounds, since the probing depth of XPS is only of the order of a few nanometres. This observation is supported further by the appearance of insulating particles on the surface as seen with the SEM (Fig. 2, bottom). Li2S, perhaps surprisingly, appears to be added to the surface layer only in very small quantities while the cell is not in operation. Given the overall intensities of the peaks at 162 eV and 167 eV it is most likely that the major products formed on the anode during a long idle time are short chain polysulfides such as Li2S2 and possibly Li2S3, with additional contributions from oxidised sulfur species such as Li2SO3 and Li2S2O3 formed by reaction of the reduction products of LiNO3.
It should be noted here that the substitution of LiTFSI for LiClO4 could be expected to affect the reactions of polysulfides at the negative electrode surface; LiClO4, like LiNO3, is a powerful oxidising agent which may contribute to the passivation of the negative electrode. Indeed, a shuttle-inhibiting effect from the use of LiClO4 has been previously reported by Kim et al.30 However, in that work, while the use of an electrolyte of 1 M LiClO4 offered some improvement in coulombic efficiency compared to 1 M LiTFSI (∼80% compared to ∼70%), an electrolyte containing 0.2 M LiNO3 in addition to LiClO4 showed by far the highest coulombic efficiencies (95–100%; 1 M LiTFSI and 0.2 M LiNO3 was not tested, but our own tests under similar conditions gave similar results). LiNO3 is much less kinetically stable than LiClO4, and this is the most likely reason for its stronger effect in passivating the negative electrode. Consequently, we believe the differences in the reactions of polysulfides at the negative electrode in the presence of LiTFSI or LiClO4 to be minor while a large amount of LiNO3 is present, and that the conclusions we draw from these experiments remain valid for the LiTFSI electrolyte system.
3.3 Changes in electrolyte composition during self-discharge
The processes governing self-discharge can be visualised through the use of an in situ electrochemical probe, as we have previously reported.11 The technique uses a small insulated wire (probe) electrode placed between two separators in an otherwise standard cell setup. The probe electrode and cell positive electrode can be simultaneously controlled or measured using common counter and reference electrodes. At the probe electrode, standard electrochemical techniques can be used to analyse the behaviour of polysulfides dissolved in the electrode, outside of the positive electrode environment.In this work, we used a PTFE-insulated Pt wire cut to expose a 125 μm-diameter Pt surface inside the cell. To allow for incorporation of the probe electrode, a pouch cell format rather than a coin cell was used. For this reason, and because of the need for an extra separator, the cell requires a considerably larger volume of electrolyte (35 μL mgs−1 was found to give approximately the same cell performance when comparing pouch cells with the coin cell baselines). Despite these differences, the reactions occurring in solution are not expected to be significantly different and we consider observations made with this technique to be valid at the very least for qualitative purposes.
To assess the changes in polysulfide concentration in the electrolyte, linear sweep voltammetry (LSV) measurements were made at 4 hour intervals over the course of a long (>200 hour) relaxation period following a single discharge/charge cycle. The results have been summarised in Fig. 4. Each LSV measurement shows either a peak or a plateau in current at around 2.75 V vs. Li/Li+, consistent with the oxidation of all polysulfide species to elemental sulfur. Since the peak or steady-state current in a diffusion-limited voltammetric measurement at a planar electrode is proportional to the concentration of the electrochemically active species, we can take the peak current in this case as an indicator of the concentration. However, it is not possible to ascribe it directly to relative concentrations of polysulfides, because the number of electrons transferred per polysulfide is not constant; that is, if the major polysulfide species in solution are S42− and S62−, then the major electrochemical oxidations to elemental sulfur would be:
 | (1) |
Since, as is known, the ratio of S62− and S42− (among other species) varies during the charge/discharge process, the number of electrons therefore also varies. Nonetheless, consideration of the peak current is still qualitatively useful.
The peak currents from the LSVs in (Fig. 4 left) were extracted and plotted against time alongside the cell OCV (Fig. 4 right). From the charged state, the peak current increases gradually over the first 125 hours indicating a gradual increase in the concentration of polysulfides in the electrolyte. The largest value for the peak current coincides almost exactly with the minimum in the cell OCV (i.e., the clear start of the lower voltage plateau). This is consistent with what is already known about the discharge process; the lower voltage plateau even at low discharge rate generally begins with a peak in the voltage, usually ascribed to an increase in overpotential caused by over-saturation of polysulfides.
The upper plateau is understood in this electrolyte system to correspond to the complete conversion reduction of S8 with S62− as the major product:
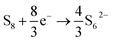 | (2) |
The coincidence of the start of the lower plateau – implying an equilibrium of S62− and S42− in the electrolyte – and the maximum in the peak current suggests that at this point all elemental sulfur formed on the charge has been re-reduced back to soluble forms. This process is driven by the redox shuttle effect as it is generally understood, where lower order polysulfides formed by reaction with the anode can react with elemental sulfur – and not necessarily be oxidised only by electron transfer. Such reactions could be written as, for example:
2Li + 2S62− ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) 2Li+ + 3S42− 2Li+ + 3S42−
| (3) |
4S42− + S8 ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) 4S62− 4S62−
| (4) |
Combination of eqn (3) and (4) gives an overall reaction of:
4Li + S8 ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) 2Li2S4 2Li2S4
| (5) |
After 125 hours, the cell voltage remains roughly constant at close to 2.1 V, and the peak currents as measured by the probe begin to decrease, indicating a decreasing concentration of soluble polysulfides. This could indicate further consumption of polysulfides by the anode, forming further reduced species such as Li2S2 or Li2S3, as indicated previously by XPS. Alternatively, it may be that lower-order polysulfides such as Li2S4 tends either to precipitate as a solid or disproportionate into other solids such as Li2S and S8 elsewhere in the cell.
3.4 Quantifying self-discharge and its effect on cycling performance
Self-discharge can be simply quantified by measuring the capacity of the cell before and after a specified rest time. In this work, we have measured self-discharge for multiple relaxation periods ranging from 12 hours to 2 weeks in duration (hereafter referred to as a “cycle/wait” test for simplicity). Studying a range of relaxation times over an extended period enables the building of a detailed picture of cell stability when the cell is both in and not in continuous operation. The results of this experiment are summarised in Fig. 5.As seen in Fig. 5a, the cell shows an initial capacity in excess of 1000 mA h g−1 which decreases over the first 10 cycles to a relatively stable reversible capacity of about 800 mA h g−1, which is consistent with the reference cell (Fig. 1). The charge efficiency also remains at >90% throughout the experiment also consistent with the reference cell. It is also easily seen from this plot that the capacity loss increases with increasing OCV relaxation time and that the capacity loss does not increase significantly after the first three days. It is therefore immediately apparent that the rate of self-discharge changes depending on the state of charge, as has been previously noted by Moy et al.25 The capacity loss for each rest period was calculated as the difference between the measured discharge capacity and the estimated discharge capacity in the absence of a rest period (extrapolated from the discharge capacity of the cycles immediately before and after). This analysis is shown graphically in Fig. 5b. An alternative plot presenting the cell voltage profiles on the same time axis as the capacity loss is given in the ESI, Fig. S2.† In order to put the rate of self-discharge into context, one can define an “equivalent C-rate”, i.e., the current that would have to pass in an ideally efficient cell to draw the same capacity in the same time. This can be simply calculated from the capacity loss divided by the relaxation time, expressed as a fraction of the theoretical capacity:
 | (6) |
| Rest time | C-Rate equiv. (total rest) | C-Rate equiv. (relative) |
|---|---|---|
| 12 h | C/330 | C/330 (12 h) |
| 24 h | C/280 | C/240 (12 h) |
| 72 h | C/510 | C/890 (48 h) |
| 7 d | C/1200 | C/29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 (4 d) 000 (4 d) |
| 14 d | C/2000 | C/8400 (7 d) |
| 12 h | C/175 | C/175 (12 h) |
| 24 h | C/210 | C/260 (12 h) |
| 72 h | C/440 | C/960 (48 h) |
| 7 d | C/990 | C/18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 (4 d) 000 (4 d) |
| 14 d | C/2000 | — |
From Fig. 5b and Table 1 it is easily seen that self-discharge is fastest during the first three or so days and subsequently slows dramatically. Furthermore, the rate of self-discharge appears to increase as the cell ages, as indicated by the larger capacity losses on cycles 17–32 compared with the first 16 cycles. Over the first 24 hours, the rate of self-discharge is of the order of C/300, approximately 30 times slower than the charging rate. After the first 16 cycles this rate increases to a value of the order of C/200. After the first 72 hours the rate of discharge sharply decreases to a point at which it is too slow to be measured accurately (i.e., changes of only a few mA h g−1 over the course of several days). A maximum capacity loss of approx. 278 mA h g−1 could be considered consistent with the interpretation that the capacity loss comes largely from the reduction of elemental sulfur in the cathode, since the first reduction of sulfur:
 | (7) |
For further comparison, the capacity losses for relaxation times up to three days were analysed according to the model proposed by Mikhaylik and Akridge,24 in which a shuttle constant can be derived according to the equation:
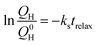 | (8) |
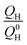 is the remaining fraction of the upper plateau (Q0H in this case was taken to be 278 mA h g−1), trelax is the relaxation time and ks is the shuttle constant, with units of h−1. The shuttle constant can then be determined by the gradient of the line in a plot of
is the remaining fraction of the upper plateau (Q0H in this case was taken to be 278 mA h g−1), trelax is the relaxation time and ks is the shuttle constant, with units of h−1. The shuttle constant can then be determined by the gradient of the line in a plot of  vs. relaxation time, which is given in the ESI, Fig. S3.† From this analysis we arrive at shuttle constants of 0.027 h−1 for the first loop in this experiment (cycles 1–16), and 0.049 h−1 for the second loop (cycles 17–32). These values are somewhat higher than the values of ∼0.014 h−1 as very recently reported for similar electrolyte systems.27
vs. relaxation time, which is given in the ESI, Fig. S3.† From this analysis we arrive at shuttle constants of 0.027 h−1 for the first loop in this experiment (cycles 1–16), and 0.049 h−1 for the second loop (cycles 17–32). These values are somewhat higher than the values of ∼0.014 h−1 as very recently reported for similar electrolyte systems.27
That self-discharge appears to effectively cease after the cells reach the lower voltage plateau, coupled with the observation from XPS that Li2S is not formed to any significant extent on the negative electrode during self-discharge, may suggest that there is an equilibrium of soluble polysulfides with the anode, as in eqn (3), i.e.:
| 2Li + 2S62− ⇌ 2Li+ + 3S42− | (9) |
An important observation is that this self-discharge is very much reversible: even after two weeks and two months of testing the cell is still capable of delivering the same capacity of 800 mA h g−1 as the reference cell. This good reversibility may be a direct result of the slow or even absent conversion of polysulfides to more kinetically inert compounds such as Li2S.
3.5 Redox shuttle measurement under potentiostatic control
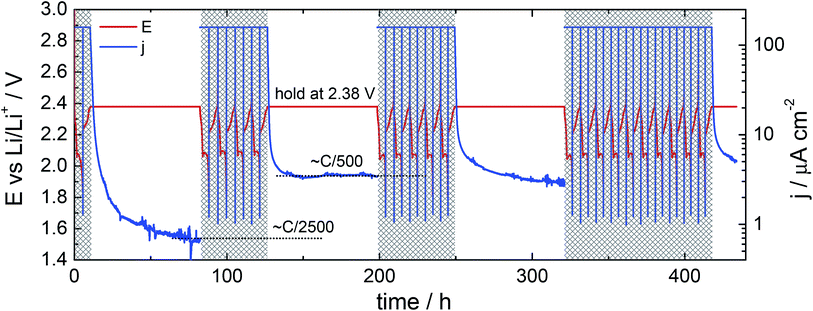
The rate of the redox shuttle itself, as opposed to the rate of capacity loss, can be assessed by measurement of the current passing through a cell under potentiostatic control. This method was previously used by Moy et al.25 to determine the variation in the effective redox shuttle current with the cell state-of-charge. Here, we have investigated the change in the redox shuttle on cycling by holding the cell potential at the arbitrary value of 2.38 V for three days on selected charges. The measurements made at the 1st, 5th and 10th cycles are given in Fig. 6.The current transients show a decay in the current to approximately 0.7 A cm−2 (corresponding approximately to an C-rate equivalent of C/2500) following the first cycle. This steady state current increases to approximately 3 A cm−2 on the fifth cycle, and gradually decreases with continued cycling (transients up to the 60th cycle are given in the ESI, Fig. S4†). Since the rate of the redox shuttle would be expected to be proportional to both the surface area of the anode and the concentration of polysulfides at the surface, it is most likely that the increase in the redox shuttle current from the first to the fifth cycle is the consequence of the increasing surface area of the lithium anode over the first few cycles. The increasing roughness of lithium within a small number of cycles can be seen quite clearly with SEM, as shown in Fig. 7. The decreasing shuttle current over continued cycling could then be a result either of a decreasing concentration of polysulfides, if, for example, decomposition of the electrolyte reduces the solubility, or if an increasingly thick SEI reduces the rate of the reaction between lithium and polysulfides.
 | ||
| Fig. 7 SEM images of Li metal electrodes from symmetrical Li‖Li cells subjected to a number of 6 hour discharge/6 hour charge cycles at a current density of 400 μA cm−2. | ||
It should be noted that the reduction of the shuttle current over cycling as determined by this method conflicts with the “cycle/wait” measurements discussed previously, which showed an increased rate of self-discharge with increased cycling. While the differences (i.e., increases or decreases in the rate of self-discharge) are relatively minor, this nonetheless indicates that self-discharge and lithium anode stability could be significantly influenced by real-life usage, for example charging rate, storage conditions, etc. To the best of our knowledge, such a study has not yet been undertaken, and would be an interesting direction for future work.
4 Conclusions
In this work, we have explored the self-discharge behaviour of simple Li–S cells containing the common electrolyte additive LiNO3, and related this behaviour to the polysulfide redox shuttle phenomenon through a range of electrochemical and surface analysis techniques. LiNO3 is an effective suppressant of the polysulfide redox shuttle – reducing the effective electronic leak by one or two orders of magnitude – and enables the reversible cycling of Li–S cells with coulombic efficiencies in excess of 90% at low cycling rates. However, the redox shuttle is still fast enough to cause cells to self-discharge at a relatively rapid rate, with cells in this work observed to lose more than 25% of their capacity from fully charged in less than three days. This capacity loss is shown to largely come from the reduction of elemental sulfur back to soluble polysulfides, as observed through the use of an in situ electrochemical probe. The changes in anode surface chemistry after self-discharge was investigated with XPS, where a significant increase in the amount of reduced sulfur species was found after long exposure to the electrolyte following cycling.A key observation is the relatively good reversibility of the self-discharge of these cells; that is, cells rested for weeks following a full charge were still able to deliver the same discharge capacities as those which were cycled continuously. This reversibility is attributed primarily to the relative lack of continuous formation of Li2S on the anode during self-discharge, as confirmed by XPS, which in turn is due to the very slow reaction of polysulfides with the anode once the cell voltage has reached equilibrium at the lower voltage plateau of ∼2.15 V.
From a practical perspective, the rapid self-discharge in this system, despite the application of an electrolyte considered to be effective, remains a challenge which merits considerably more attention, especially if the system is expected to challenge existing Li-ion batteries in any consumer application. Furthermore, it is important for future research into redox shuttle suppression strategies that self-discharge be quantified directly, by methods such as, for example, the “cycle/wait”-type measurements as discussed in this work, rather than assessed indirectly from the coulombic efficiency on galvanostatic cycling. This is especially important if cells are tested at relatively fast rates, since self-discharge is increasingly uninfluential the faster cells are continuously cycled.
Acknowledgements
The SEM and XPS analysis included in this work in Sections 3.2 and 3.5 formed part of a Master degree project entitled “Insights into the morphological changes undergone by the anode in the lithium sulphur battery system” by Anurag Yalamanchili under the supervision of Dr Matthew Lacey and Dr Carl Tengstedt in 2014. The full text of the final thesis is available online from Uppsala University at http://www.diva-portal.org/smash/record.jsf?pid=diva2:765276. The authors wish to thank Dr Martin Cadek (Orion Engineered Carbons GmbH) for providing the carbon black used in this work, and the Era Net Transport project “MaLiSu” and Vinnova in Sweden for financial support.References
- A. Manthiram, S.-H. Chung and C. Zu, Adv. Mater., 2015, 27, 1980–2006 CrossRef CAS PubMed.
- A. Manthiram, Y. Fu and Y.-S. Su, Acc. Chem. Res., 2013, 46, 1125–1134 CrossRef CAS PubMed.
- D. Bresser, S. Passerini and B. Scrosati, Chem. Commun., 2013, 49, 10545 RSC.
- M. A. Pope and I. A. Aksay, Adv. Energy Mater., 2015, 1500124 Search PubMed.
- K. Ueno, J. W. Park, A. Yamazaki, T. Mandai, N. Tachikawa, K. Dokko and M. Watanabe, J. Phys. Chem. C, 2013, 117, 20509–20516 CAS.
- M. Cuisinier, P.-E. Cabelguen, B. D. Adams, A. Garsuch, M. Balasubramanian and L. F. Nazar, Energy Environ. Sci., 2014, 7, 2697 CAS.
- J. T. Lee, Y. Zhao, S. Thieme, H. Kim, M. Oschatz, L. Borchardt, A. Magasinski, W.-I. Cho, S. Kaskel and G. Yushin, Adv. Mater., 2013, 25, 4573–4579 CrossRef CAS PubMed.
- E. S. Shin, K. Kim, S. H. Oh and W. Il Cho, Chem. Commun., 2013, 49, 2004–2006 RSC.
- L. Suo, Y.-S. Hu, H. Li, M. Armand and L. Chen, Nat. Commun., 2013, 4, 1481 CrossRef PubMed.
- Y.-C. Lu, Q. He and H. A. Gasteiger, J. Phys. Chem. C, 2014, 118, 5733–5741 CAS.
- M. J. Lacey, K. Edström and D. Brandell, Electrochem. Commun., 2014, 46, 91–93 CrossRef CAS.
- X. Wang, Z. Wang and L. Chen, J. Power Sources, 2013, 242, 65–69 CrossRef CAS.
- Y. S. Su and A. Manthiram, Nat. Commun., 2012, 3, 1166 CrossRef PubMed.
- I. Bauer, S. Thieme, J. Brückner, H. Althues and S. Kaskel, J. Power Sources, 2014, 251, 417–422 CrossRef CAS.
- Z. Jin, K. Xie, X. Hong, Z. Hu and X. Liu, J. Power Sources, 2012, 218, 163–167 CrossRef CAS.
- C. J. Hart, M. Cuisinier, X. Liang, D. Kundu, A. Garsuch and L. F. Nazar, Chem. Commun., 2015, 51, 2308–2311 RSC.
- Q. Pang, D. Kundu, M. Cuisinier and L. F. Nazar, Nat. Commun., 2014, 5, 1–19 Search PubMed.
- J. Song, T. Xu, M. L. Gordin, P. Zhu, D. Lv, Y.-B. Jiang, Y. Chen, Y. Duan and D. Wang, Adv. Funct. Mater., 2013, 24, 1243–1250 CrossRef.
- C. Zu and A. Manthiram, J. Phys. Chem. Lett., 2014, 5, 2522–2527 CrossRef CAS PubMed.
- D. Aurbach, E. Pollak, R. Elazari, G. Salitra, C. S. Kelley and J. Affinito, J. Electrochem. Soc., 2009, 156, A694 CrossRef CAS.
- Z. Lin, Z. Liu, W. Fu, N. J. Dudney and C. Liang, Adv. Funct. Mater., 2013, 23, 1064–1069 CrossRef CAS.
- S. S. Zhang, Electrochim. Acta, 2012, 70, 344–348 CrossRef CAS.
- W. Li, H. Yao, K. Yan, G. Zheng, Z. Liang, Y.-M. Chiang and Y. Cui, Nat. Commun., 2015, 6, 7436 CrossRef CAS PubMed.
- Y. V. Mikhaylik and J. R. Akridge, J. Electrochem. Soc., 2004, 151, A1969–A1976 CrossRef CAS.
- D. Moy, A. Manivannan and S. R. Narayanan, J. Electrochem. Soc., 2014, 162, A1–A7 CrossRef.
- M. L. Gordin, F. Dai, S. Chen, T. Xu, J. Song, D. Tang, N. Azimi, Z. Zhang and D. Wang, ACS Appl. Mater. Interfaces, 2014, 6, 8006–8010 CAS.
- W.-T. Xu, H.-J. Peng, J.-Q. Huang, C.-Z. Zhao, X.-B. Cheng and Q. Zhang, ChemSusChem, 2015, 8, 2892–2901 CrossRef CAS PubMed.
- M. J. Lacey, F. Jeschull, K. Edström and D. Brandell, J. Phys. Chem. C, 2014, 118, 25890–25898 CAS.
- X. Liang, C. Hart, Q. Pang, A. Garsuch, T. Weiss and L. F. Nazar, Nat. Commun., 2015, 6, 5682 CrossRef PubMed.
- H. S. Kim, C.-S. Jeong and Y.-T. Kim, J. Appl. Electrochem., 2011, 42, 75–79 CrossRef.
- M. Cuisinier, P.-E. Cabelguen, S. Evers, G. He, M. Kolbeck, A. Garsuch, T. Bolin, M. Balasubramanian and L. F. Nazar, J. Phys. Chem. Lett., 2013, 4, 3227–3232 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Reference XPS spectra and supporting plots for redox shuttle rate determination. See DOI: 10.1039/c5ra23635e |
| This journal is © The Royal Society of Chemistry 2016 |