Non-contact electrochemical imaging of Young's modulus of single living cells
Rong
Jin†
ac,
Yanyan
Xu†
ab,
Kang
Wang
 a,
Dechen
Jiang
a,
Dechen
Jiang
 *a and
Danjun
Fang
*a and
Danjun
Fang
 *b
*b
aState Key Laboratory of Analytical for Life Science, School of Chemistry and Chemical Engineering, Nanjing University, Nanjing, 210023, China. E-mail: dechenjiang@nju.edu.cn
bSchool of Pharmacy, Nanjing Medical University, Nanjing, 211126, China. E-mail: djf@njmu.edu.cn
cSchool of Chemistry and Chemical Engineering, Southeast University, Nanjing, 211189, China
First published on 19th November 2025
Abstract
A non-contact electrochemical imaging method based on hydrodynamic resistance is developed to image the apparent Young's modulus of living cells. This strategy realizes nanometer cell deformation and high-resolution 3D modulus mapping with minimal disturbance to living cells and further reveals the cytoskeleton-associated modulus distribution in migrating cells.
Young's modulus of single cells is a key parameter for studying cellular mechanics and physiological states, being closely linked to processes such as growth, division, migration and adhesion.1–4 Various techniques, such as atomic force microscopy (AFM), micropipette aspiration (MA), optical tweezers (OTs), and cell magnetic twisting cytometry (MTC), have emerged in the field of Young's modulus research of single cells.5–8 AFM is widely used for its imaging capability,9–11 but requires nN level indentation that depresses the membrane by microns, introducing mechanical distortion during live-cell imaging.5,12,13 To avoid puncture, probes are enlarged and smoothed, reducing spatial resolution to hundreds of nanometres.6 Yet, since the modulus is defined by the stress-to-strain response, applying force without contact poses a major challenge.
Scanning ion conductance microscopy (SICM) is a non-contact electrochemical imaging technique that uses ionic current through a nanocapillary orifice as feedback.14,15 To image rough cell membranes, a hopping mode is employed, in which the capillary retracts above the surface before each approach. The ionic current is highly distance-sensitive, enabling ∼10 nm resolution morphology of living cells16 while preserving activity and near-real structure.17–21 Early attempts to measure the modulus using SICM introduced hydrostatic pressure (0.1–150 kPa) into the capillary,22 applying forces of 1–10 nN, which is comparatively large for live-cell imaging.23,24 Besides, the tip pressure is affected by capillary action (surface tension) and flow dynamics, typically resulting in a lower pressure at the tip. This will affect the calculation accuracy of the pressure applied to the tip, as well as the precise quantification of Young's modulus.
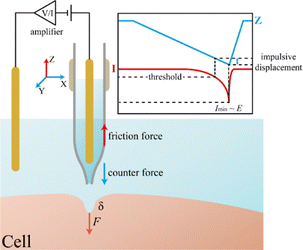
Herein, a novel strategy based on non-contact SICM imaging is developed to achieve the highly spatial measurement of Young's modulus at the cellular membrane, which does not need any additional hydrostatic pressure. It should be noted that the reported values represent the apparent surface modulus, reflecting membrane-level mechanics at nanometer deformation depth, and are referred to as Young's modulus for simplicity. As illustrated in Fig. 1, during the approaching process in the hopping mode, the fast movement of the capillary can induce friction with the surrounding solution. At the same time, the counterforce works on a solution, which has the same strength and opposite direction to the hydrodynamic resistance. When the tip is close enough to the cellular membrane, the hydrodynamic resistance of the solution near the tip will be transmitted to the membrane. The force is so tiny that it can only induce a small deformation of the cellular membrane. Due to the sensitive response of the ionic current to the tip-membrane distance, the membrane deformation could be measured based on the alteration of the current. Consequently, Young's modulus at the cellular membrane is determined without contact with the membrane. The proposed ionic current-based non-contact strategy is expected to have the advantages of high imaging resolution (∼20 nm) and tiny force (fN level) at the cellular membrane, which decreases the interruption on cellular activity and enables high-spatial resolution investigation of the actual modulus distribution at single living cells. Comparative studies between AFM and SICM support this concern. In live-cell imaging, AFM, even in tapping mode, produces both normal and lateral forces that cause loss of fine structures, reduced accuracy of height and volume measurements, and distortion of fragile features such as microvilli or thin cellular extensions during prolonged imaging. In contrast, SICM maintains image fidelity without noticeable morphological changes under similar conditions.24,25
The basic SICM setup for ionic current measurement is shown in Fig. 1, with one electrode in bulk solution and another inside the nanocapillary. A small tip provides high spatial resolution but suffers reduced stability (ion current noise) and lower stress (weaker hydrodynamic resistance, eqn (S1)). To balance resolution and stability, a capillary with 15 nm inner and 20 nm outer diameter was used. By applying a bias across the electrodes, the ionic current was recorded. During the rapid approach to the membrane, hydrodynamic resistance between the nanocapillary and electrolyte arises and can be described by fluid mechanics as:
| f = 8πηvd | (1) |
The relationship between Young's modulus and the minimum ion current (Imin) is presented in eqn (2) (more details in the SI) based on an empirical mathematical model:
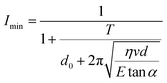 | (2) |
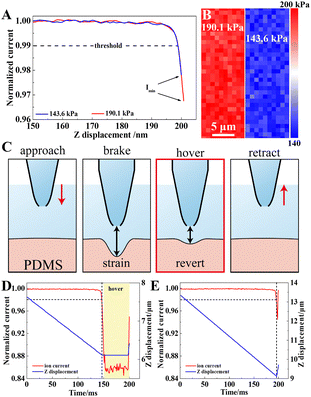
To validate the method, PDMS samples with different moduli were prepared by adjusting the curing agent ratio. Their Shore hardness (HA) values ranged from 140 to 440 kPa. Each sample was positioned below a nanocapillary with 15/20 nm inner/outer diameters (Fig. S6, SI). For relatively hard (182.2 kPa) and soft (139.8 kPa) samples, the initial approach curves were similar, but ionic current differences appeared below 15 nm tip–sample distance (Fig. 2a). This reflects deformation-dependent current changes, distinguishable by Imin. From surface scans (32 × 16 pixels, Fig. 2b), the average moduli were found to be 182.2 ± 10.9 and 139.8 ± 5.7 kPa (n = 512), consistent with the HA results. The other three PDMS samples also followed the theoretical curve (Fig. S7, SI). Variation of viscosity (η) and approach velocity (v) altered the Imin values (Fig. S8, SI), matching theoretical predictions.
To further confirm deformation, a “hovering” step was introduced (Fig. 2c). After impulsive displacement, the capillary remained stationary, eliminating hydrodynamic resistance. The gradual recovery of sample deformation caused a further current decrease, in contrast to direct retraction (Fig. 2d). This effect, seen as a smaller Imin (Fig. 2e), supports the recovery process and confirms that hydrodynamic resistance is transmitted to the sample. Finally, detection sensitivity depends on the threshold and approach velocity. Lower thresholds and faster approach speeds not only enhance sensitivity but also increase noise levels. Thus, optimized conditions of 99% threshold and 20 µm s−1 velocity were chosen for cell imaging. For small-area scans, 96% threshold and 35 µm s−1 velocity were applied to enhance recognition. Accordingly, Young's modulus of the sample could be determined from our established non-contact measurement strategy.
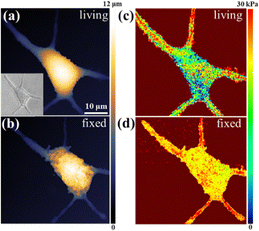
After validating the method with PDMS, we simultaneously imaged the morphology and modulus of a single MCF7 cell. Ionic currents were recorded at two approach distances: at ∼20 nm, no hydrodynamic resistance was transmitted and morphology was obtained (threshold 99%); at 10 nm, hydrodynamic resistance induced membrane deformation, and Imin yielded local modulus values. Bright-field and SICM images confirmed consistent cell morphology (Fig. 3a), and the calculated modulus was 6.27 ± 1.45 kPa (Fig. 3c), close to the AFM results.7,25 Statistical analysis revealed 23% relative standard deviation, indicating heterogeneity. Continuous non-contact scanning preserved cell shape (Fig. S10, SI), with modulus images remaining consistent with morphology. Dynamic pseudopodia extension and contraction confirmed good cellular vitality during the 7-hour imaging process. Additional control experiments involving direct tip–cell contact and membrane disruption confirmed the non-contact nature of the measurement, as evidenced by distinctly different current responses (Fig. S11).
Chemical fixation is widely used to preserve membrane structure, but it induces protein aggregation and forms spherical structures at the plasma membrane.26,27 Previous studies have shown that most cells exhibit an increased modulus after fixation,28–30 although limited spatial resolution has restricted detailed visualization. Here, morphology and modulus images of the same cell after fixation are collected (Fig. 3b and d). The morphology reveals a rougher surface due to protein aggregation, accompanied by a clear modulus increase. Statistical analysis (Fig. S12, SI) shows an average modulus of 16.78 ± 4.77 kPa, nearly three times higher than that of the living cell, while the heterogeneous distribution remains, consistent with literature reports.26
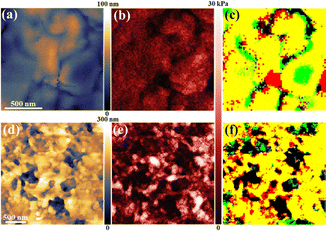
To obtain high-resolution information on the plasma membrane morphology and modulus, a 2.56 × 2.56 µm2 region at the pseudopodia was scanned with 20 nm steps. In the living cell, numerous folds (200–500 nm) were observed (Fig. 4a), likely arising from aggregated protein clusters. The modulus image (Fig. 4b) showed high values at clusters and low values in grooves. Overlapping morphology and modulus maps (Fig. 4c) revealed good correspondence, with a high modulus at folds (yellow), elevated modulus at grooves (green), and low modulus at grooves (red). After fixation, morphology, modulus, and overlap images of the same region (Fig. 4d–f) demonstrated an increased modulus at both folds and grooves, reaching ∼30 kPa at spherical structures.
Further validation was performed on SKOV3 cells, where fixation induced both larger partitioned surface structures (Fig. S13) and a higher modulus than in live cells (Fig. S14). Control experiments with a PDMS array (Fig. S15) showed that a ∼100 nm topographical height difference produced no modulus contrast, confirming the reliability and generality of the method.
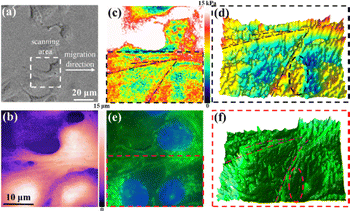
Cell migration is closely linked to dynamic cytoskeletal remodeling,31,32 with cells undergoing continuous stretching and contraction, though many mechanisms remain unclear. High-spatial modulus imaging offers insights into these processes, particularly during membrane deformation. SICM has previously been applied to study migrating platelets using pressure-based methods.33 Here, to validate our modulus imaging approach, a scratch wound-healing assay was used to induce SKOV3 migration (Fig. S16). Within 2 h, cells at the wound edge migrated toward the centre. A representative migrating cell (Fig. 5a) was scanned. SICM topography (Fig. 5b) revealed filaments tilted toward the migration direction, and modulus mapping (Fig. 5c and d) displayed linear high-modulus regions aligned with this trajectory.
As cytoskeletons beneath the plasma membrane sustain cell structure and drive migration, the linear high-modulus regions are likely associated with actin filaments. To verify this, cells were phalloidin-stained. The bright-field image after fixation (Fig. S17, SI) resembled the live-cell morphology (Fig. 5a). Fluorescence images (Fig. 5e and f) showed actin filaments aligned with the migration direction, matching high-modulus regions in Fig. 5c and d. Correlation was highlighted by dashed lines, indicating that cytoskeletons induce an elevated membrane modulus and explain heterogeneity. Some high-modulus regions lacked cytoskeleton signals (circled in Fig. 5f), likely due to protein aggregates or other factors. Overall, the non-contact electrochemical method enables high-resolution modulus cytoskeleton mapping at the plasma membrane.
In summary, we present a high-resolution modulus imaging method that achieves ∼20 nm spatial resolution in live cells while remaining contact-free and nearly nondestructive. The resulting fN level forces induce only nanometre-scale membrane deformation, minimizing perturbation and yielding near-real information on modulus distribution. 3D imaging revealed that fixation-induced modulus increases mainly arise from nanoscale protein aggregates, while strong correlations between high-modulus regions and cytoskeletal extensions provide new insights into the heterogeneous mechanics of the plasma membrane.
Conflicts of interest
There are no conflicts to declare.Data availability
The data supporting this article including additional SEM images, simulation results, continuous scanning results and verification results have been included in the supplementary information (SI). Supplementary information is available. See DOI: https://doi.org/10.1039/d5cc05775b.Notes and references
- G. S. Worthen, B. Schwab 3rd, E. L. Elson and G. P. Downey, Science, 1989, 245, 183–186 CrossRef CAS.
- M. S. Samuel, J. I. Lopez, E. J. McGhee, D. R. Croft, D. Strachan, P. Timpson, J. Munro, E. Schroder, J. Zhou, V. G. Brunton, N. Barker, H. Clevers, O. J. Sansom, K. I. Anderson, V. M. Weaver and M. F. Olson, Cancer Cell, 2011, 19, 776–791 CrossRef CAS PubMed.
- W. Huang, M. Tan, Y. Wang, L. Liu, Y. Pan, J. Li, M. Ouyang, C. Long, X. Qu, H. Liu, C. Liu, J. Wang, L. Deng, Y. Xiang and X. Qin, Theranostics, 2020, 10, 8528–8540 CrossRef CAS PubMed.
- P. Sacco, G. Baj, F. Asaro, E. Marsich and I. Donati, Adv. Funct. Mater., 2020, 30 Search PubMed.
- A. Tajik, Y. Zhang, F. Wei, J. Sun, Q. Jia, W. Zhou, R. Singh, N. Khanna, A. S. Belmont and N. Wang, Nat. Mater., 2016, 15, 1287–1296 CAS.
- P. H. Wu, D. R. Aroush, A. Asnacios, W. C. Chen, M. E. Dokukin, B. L. Doss, P. Durand-Smet, A. Ekpenyong, J. Guck, N. V. Guz, P. A. Janmey, J. S. H. Lee, N. M. Moore, A. Ott, Y. C. Poh, R. Ros, M. Sander, I. Sokolov, J. R. Staunton, N. Wang, G. Whyte and D. Wirtz, Nat. Methods, 2018, 15, 491–498 CrossRef CAS PubMed.
- N. Mandriota, C. Friedsam, J. A. Jones-Molina, K. V. Tatem, D. E. Ingber and O. Sahin, Nat. Mater., 2019, 18, 1071–1077 CrossRef CAS PubMed.
- J. Gieseler, J. R. Gomez-Solano, A. Magazzù, I. Pérez Castillo, L. Pérez García, M. Gironella-Torrent, X. Viader-Godoy, F. Ritort, G. Pesce, A. V. Arzola, K. Volke-Sepúlveda and G. Volpe, Adv. Opt. Photon., 2021, 13 Search PubMed.
- S. E. Cross, Y.-S. Jin, J. Rao and J. K. Gimzewski, Nat. Nanotechnol., 2007, 2, 780–783 CrossRef CAS.
- Y. Ding, G.-K. Xu and G.-F. Wang, Sci. Rep., 2017, 7 Search PubMed.
- M. D. A. Norman, S. A. Ferreira, G. M. Jowett, L. Bozec and E. Gentleman, Nat. Protoc., 2021, 16, 2418–2449 CrossRef CAS.
- J. Seifert, J. Rheinlaender, P. Novak, Y. E. Korchev and T. E. Schäffer, Langmuir, 2015, 31, 6807–6813 CrossRef CAS.
- J. Rheinlaender, N. A. Geisse, R. Proksch and T. E. Schäffer, Langmuir, 2011, 27, 697–704 CrossRef CAS.
- P. K. Hansma, B. Drake, O. Marti, S. A. Gould and C. B. Prater, Science, 1989, 243, 641–643 CrossRef CAS PubMed.
- C. Zhu, K. Huang, N. P. Siepser and L. A. Baker, Chem. Rev., 2021, 121, 11726–11768 CrossRef CAS.
- A. I. Shevchuk, G. I. Frolenkov, D. Sanchez, P. S. James, N. Freedman, M. J. Lab, R. Jones, D. Klenerman and Y. E. Korchev, Angew. Chem., Int. Ed., 2006, 45, 2212–2216 CrossRef CAS.
- P. Novak, C. Li, A. I. Shevchuk, R. Stepanyan, M. Caldwell, S. Hughes, T. G. Smart, J. Gorelik, V. P. Ostanin, M. J. Lab, G. W. Moss, G. I. Frolenkov, D. Klenerman and Y. E. Korchev, Nat. Methods, 2009, 6, 279–281 CrossRef CAS PubMed.
- D. Perry, B. Paulose Nadappuram, D. Momotenko, P. D. Voyias, A. Page, G. Tripathi, B. G. Frenguelli and P. R. Unwin, J. Am. Chem. Soc., 2016, 138, 3152–3160 CrossRef CAS PubMed.
- H. Ida, Y. Takahashi, A. Kumatani, H. Shiku and T. Matsue, Anal. Chem., 2017, 89, 6015–6020 CrossRef CAS PubMed.
- N. Schierbaum, M. Hack, O. Betz and T. E. Schäffer, Anal. Chem., 2018, 90, 5048–5054 CrossRef CAS PubMed.
- Y. Zhang, Y. Takahashi, S. P. Hong, F. Liu, J. Bednarska, P. S. Goff, P. Novak, A. Shevchuk, S. Gopal, I. Barozzi, L. Magnani, H. Sakai, Y. Suguru, T. Fujii, A. Erofeev, P. Gorelkin, A. Majouga, D. J. Weiss, C. Edwards, A. P. Ivanov, D. Klenerman, E. V. Sviderskaya, J. B. Edel and Y. Korchev, Nat. Commun., 2019, 10, 5610 CrossRef CAS.
- D. Sánchez, N. Johnson, C. Li, P. Novak, J. Rheinlaender, Y. Zhang, U. Anand, P. Anand, J. Gorelik, G. I. Frolenkov, C. Benham, M. Lab, V. P. Ostanin, T. E. Schäffer, D. Klenerman and Y. E. Korchev, Biophys. J., 2008, 95, 3017–3027 CrossRef.
- J. Rheinlaender and T. E. Schaffer, Soft Matter, 2013, 9, 3230–3236 RSC.
- P. Swiatlowska, J. L. Sanchez-Alonso, P. T. Wright, P. Novak and J. Gorelik, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 2764–2766 CrossRef CAS PubMed.
- S. Leporatti, D. Vergara, A. Zacheo, V. Vergaro, G. Maruccio, R. Cingolani and R. Rinaldi, Nanotechnology, 2009, 20, 055103 CrossRef PubMed.
- J. H. Hoh and C. A. Schoenenberger, J. Cell Sci., 1994, 107, 1105–1114 CrossRef PubMed.
- T. Ichikawa, D. Wang, K. Miyazawa, K. Miyata, M. Oshima and T. Fukuma, Commun. Biol., 2022, 5, 487 CrossRef CAS.
- E. A. Corbin, F. Kong, C. T. Lim, W. P. King and R. Bashir, Lab Chip, 2015, 15, 839–847 RSC.
- E. A. Hoffman, B. L. Frey, L. M. Smith and D. T. Auble, J. Biol. Chem., 2015, 290, 26404–26411 CrossRef CAS.
- S.-O. Kim, J. Kim, T. Okajima and N.-J. Cho, Nano Convergence, 2017, 4, 5 CrossRef PubMed.
- P. Lappalainen, T. Kotila, A. Jégou and G. Romet-Lemonne, Nat. Rev. Mol. Cell Biol., 2022, 23, 836–852 CrossRef CAS.
- S. Seetharaman and S. Etienne-Manneville, Trends Cell Biol., 2020, 30, 720–735 CrossRef CAS.
- J. Seifert, J. Rheinlaender, H. von Eysmondt and T. E. Schaffer, Nanoscale, 2022, 14, 8192–8199 RSC.
Footnote |
| † Rong Jin and Yanyan Xu made equal contributions to this work. |
| This journal is © The Royal Society of Chemistry 2026 |