Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Combining a daily temperature pattern analysis and a heat-pulse system to estimate sediment depths in sewer systems†
Manuel
Regueiro-Picallo
 *a,
Jeroen
Langeveld
*a,
Jeroen
Langeveld
 b,
Haoyu
Wei
b,
Haoyu
Wei
 c,
Jean-Luc
Bertrand-Krajewski
c,
Jean-Luc
Bertrand-Krajewski
 d and
Jörg
Rieckermann
d and
Jörg
Rieckermann
 e
e
aUniversidade da Coruña, Water and Environmental Engineering Group (GEAMA), Centro de Innovación Tecnolóxica en Edificación e Enxeñaría Civil (CITEEC), 15071 A Coruña, Spain. E-mail: manuel.regueiro1@udc.es
bFaculty of Civil Engineering and Geosciences, TU Delft, 2628 CN Delft, The Netherlands
cUrban Water Engineering, Luleå University of Technology, 971 87 Luleå, Sweden
dUniversity of Lyon, INSA Lyon, DEEP EA 7429, F-69621 Villeurbanne cedex, France
eEawag, Swiss Federal Institute of Aquatic Science and Technology, CH-8600 Dübendorf, Switzerland
First published on 6th February 2024
Abstract
Sediments in urban drainage systems (UDS) significantly impact their operation, so effective strategies are required to reduce their negative effects. Monitoring sediment accumulation provides valuable insights into sediment characteristics, sediment transport dynamics, and system performance. However, the effectiveness of monitoring systems is limited due to cost constraints and installation challenges. This study describes the development and application of a new system based on temperature dynamics to measure sediment depths in sewer systems. The methodology involves the analysis of temperature time series under dry weather flow conditions to identify harmonic patterns between wastewater and sediment-bed temperatures. These patterns are increasingly attenuated by increasing sediment depth. This study combines a system called MONitoring Temperatures in SEdiments (MONTSE), which integrates a dual-probe heat-pulse (DPHP) method to characterize sediment thermal properties, and a surrogate model, which includes temperature pattern analysis, to estimate sediment depths. Likewise, laboratory-scale experiments were performed to validate the temperature monitoring system and the surrogate model performance. The maximum absolute errors in measured sediment depths were less than 22 mm, and the uncertainty of the system was estimated at ±7.3 mm. Groundbreaking measurements of thermal properties of UDS sediments were also reported. Reliable information on sediment depths and properties was provided, so the system could significantly optimize sewer system operation and cleaning strategies.
Water impactSediments pose a major problem for sanitation systems. We present a methodology that combines MONitoring Temperatures in SEdiments (MONTSE), measurements of thermal properties and the development of a surrogate model to estimate sediment depths in sewer pipes. The methodology was laboratory-tested using samples with varying organic matter contents, showing its potential to optimize sediment cleaning strategies of sanitation systems. |
1. Introduction
Sediments pose a major challenge to the performance of urban sewer systems, e.g., to reduce hydraulic capacities, generate unpleasant gases/odours, and intensify pollutant loadings discharged to receiving waterbodies through combined sewer overflows (CSOs).1 Optimal operation and cleaning strategies are crucial to cost-effectively reduce the negative impacts of sediments on the effectiveness of sewer systems. However, established sewer sediment models lead to significant uncertainty in predicting sediment accumulation in sewer systems. These models, such as Ackers2 and May,3 were adapted from riverbed approaches in which non-cohesive mineral particles predominate, and relevant key processes and influential parameters observed in sewers were not considered, such as cohesion, biochemical reactions, and consolidation, among others. Therefore, the models do not satisfactorily simulate sediment depths or the subsequent accumulation, erosion and transport processes in sewer systems.4,5 Poorly predictive sediment models stress the need for an improved technique to monitor sediment accumulation in sewer systems by developing a robust evidence base and establishing a proactive data-driven sewer maintenance regime. Monitoring in-pipe sediment properties and accumulation behaviours could offer valuable insights into sediment transport dynamics and performance. Nevertheless, up-to-date experiences based on monitoring sediment accumulation in sewers were mostly limited by the measuring periods and the number of locations because of both the high cost of equipment (e.g., acoustic profilers) and the challenges of their installation regarding pipe accessibility, equipment limitations, and the potential risks associated with sediment sampling.6–8 Addressing these challenges and obtaining reliable information on sediments is crucial for optimal operation and cleaning strategies, ultimately improving the performance of sewer systems and reducing associated impacts on receiving waters.This study therefore develops a system to estimate sediment depths in sewer pipes by monitoring temperature dynamics. The system is inspired by river streambed transport studies that measure temperature time series to estimate groundwater fluxes and sediment thermal properties.9–13 There are also examples of long-term monitoring of temperatures to quantify the deposition and scour of sediments in riverbeds.14 In addition, it builds on an initial study by Regueiro-Picallo et al.,15 which showed the utility of using heat transfer processes to estimate sediment depths in urban drainage systems (UDS). This new methodology consists of measuring temperature time series that followed harmonic patterns under dry weather flow conditions in both wastewater and the base of the sediment layer. Sediment-bed temperature patterns are amplitude-attenuated and phase-lagged (in relation to sediment depth) in comparison to wastewater temperatures according to the sediment depth. However, there is no comprehensive model that relates sediment depth and harmonic features, i.e., amplitude and phase, to other factors that influence heat transfer processes in pipes, such as sediment thermal properties and boundary heat loss.
Likewise, the thermal properties of UDS sediments should be characterized. These sediments are organic and are often described by their density, particle size distribution, and volatile content.1 The relatively high levels of heterogeneity and elevated volatile content of sewer sediments, which are a function of their source and in-pipe hydraulic conditions,16 negate the use of thermal property data from other compounds, such as soils, sands, and marine sediments, as a surrogate for UDS sediments. In particular, sewer sediments are subject to stratification processes within the sediment layer, resulting in granular and cohesive materials in the lower layer and in organic materials in the upper layer.17,18 On a temporal scale, the interaction between sewer sediments and wastewater favours changes in their properties due to biological processes.19 Both spatial and temporal variability provide further complexities to use reference data, e.g., soil thermal properties.
The thermal properties of UDS sediments could be monitored with a specifically tailored active heat system based on the dual-probe heat-pulse (DPHP) method. This method is commonly used in soil studies to determine thermal properties and to monitor moisture content.20 Active heat systems consist of introducing a heat pulse into the sediment layer from a heating source (first probe) and measuring the heating and subsequent heat recovery with a temperature sensor (second probe). At a laboratory scale, compact DPHP devices were developed to determine thermal properties in soil samples (e.g., Ravazzani).21 Full-scale active heat systems were combined with distributed temperature sensing (DTS) measurements to obtain both in situ soil thermal properties and moisture content values.22–24 However, these devices are not customized to measure the thermal properties of heterogeneous and volatile sediments such as those in UDS.
This study develops a novel system called MONTSE (MONitoring Temperatures in SEdiments) that combines heat pulses and temperature time series measurements, hereafter referred to as active and passive temperature measurements, respectively. The aim of the MONTSE system is to determine sediment thermal properties in situ by using a customized DPHP system and to estimate depths from heat transfer processes in sewer systems. For this purpose, a surrogate model was developed to obtain sediment depths from the active and passive temperature measurements, also including the influence of boundary heat loss. The surrogate model was a simplified solution of the diffusion heat equation, which considered actual wastewater temperature patterns, and multiple ranges of sediment depths, thermal properties and boundary heat losses and, therefore, extended and generalized the model introduced by Regueiro-Picallo et al.15 Finally, a laboratory-scale experimental campaign was then performed with artificial and actual urban drainage sediments to evaluate the performance of the thermal property measurements with the DPHP system and the accuracy of the sediment depth estimations when applying the surrogate model. In addition to sewer sediments, organic samples from other UDS as well as an inorganic sand sample were considered to cover a wide range of thermal properties due to the heterogeneity that could be found in sediment properties. The characterization of thermal properties of various UDS sediments also provided a useful reference for future studies.
The following sections present the experimental setup, including the temperature monitoring system, the DPHP method to determine sediment thermal properties, and the surrogate model to estimate sediment depth. The results are highly promising because the device shows field-ready capabilities and provides sediment depth estimations with an accuracy of ±7.3 mm. This accuracy would be sufficient for most field applications, e.g., to detect substantial sediment layers in sewers or to monitor sediment accumulation in pipes and in other UDS, such as gully pots.
2. Materials
2.1. Description of the laboratory-scale setup
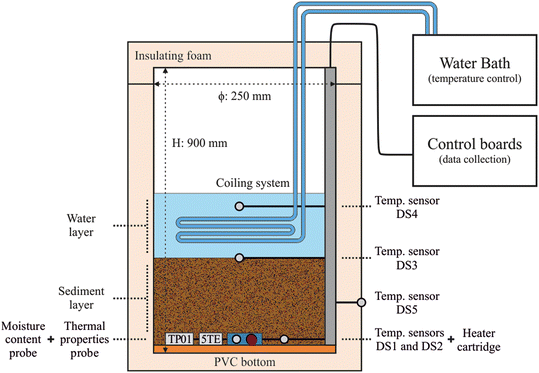
The laboratory-scale setup was built to reproduce sediment-bed heat transfer processes in combined sewer pipes, which are triggered by the wastewater temperature variations (upper boundary) and influenced by the sediment properties, the pipe contour, and the surrounding soil. It consisted of a transparent plexiglass cylinder (900 mm in height by 250 mm in diameter) with rigid PVC lids at the top and bottom, and experiments were performed by placing a sediment layer at the bottom of the cylinder overlaid by a water layer. A water bath circulator (Julabo FN25-ME, Germany) was used to develop a temperature-controlled system that simulated daily temperature variations of combined sewer pipes. For this purpose, water was pumped from the temperature-controlled system into the water layer of the model. A coil system was also built to distribute temperature in the water layer. No flow conditions were considered in the water layer during the experiments, i.e., temperature stratification resulted in the water layer despite the coil system and convection processes at the water–sediment interface were not simulated (see section 3.2.1).The heat transfer between the sediment, the pipe wall and the surrounding soil was considered. The daily temperature of the surrounding soil was assumed to be nearly constant based on field observations.25 Consequently, the cylinder was coated with a foam insulation case and the setup was placed in a temperature-controlled room to ensure nearly constant temperatures outside and controlled heat transfer conditions inside the cylinder. Finally, three measuring tapes were installed on the cylinder wall to visually measure sediment depths as a reference. Fig. 1 shows the experimental design performed in the experimental hall facilities at Eawag (Dübendorf, Switzerland).
2.2. The MONTSE system and supplementary sensors
The MONTSE system consisted of an Arduino MKRZero microcontroller to measure and log temperatures. The prototype included one cartridge heater (Probag, Switzerland) and five DS18B20 temperature sensors (DFRobot, China) (temperature sensor ID: from DS1 to DS5, see Fig. 1). The cartridge heater was designed to be installed in UDS environments to reduce intrusion of the heat pulse probe into the overlying wastewater to prevent clogging. The heating resistor inside the cartridge was 46 mm in length and 4 mm in diameter, and temperature sensors were 45 mm in length and 6 mm in diameter. A technical description of the MONTSE system is provided by Regueiro-Picallo et al.26The cartridge heater and one temperature sensor (DS1) were placed at the bottom of the cylinder as part of the DPHP system to determine sediment thermal properties. The distance between the heater and the temperature sensor was 12.5 mm. Likewise, an additional temperature sensor (DS2) was installed at the bottom of the cylinder, 25.5 mm away from the heater. Furthermore, three temperature sensors were placed in other parts of the setup: the first one was placed at the water–sediment interface (DS3, at varied depths between experiments), the second one was submerged in the water layer (DS4), and the third one was placed outside the cylinder to measure the temperature at the outer contour (DS5).
Moreover, the sediment properties obtained by the DPHP system were compared with that of a commercial TP01 sensor (Hukseflux, The Netherlands). An electrical conductivity 5TE sensor (Decagon Devices, USA) was also included to measure volumetric moisture content. Both supplementary probes were placed at the bottom of the cylinder.
2.3. Sediment samples
Six types of water-saturated sediment samples (S1–S6) were collected for the experimental campaign (see Table 1). The aim was to cover a wide range of sediment thermal properties and, for this purpose, samples with varying volatile contents were selected, including organic sediments from various UDS. As a benchmark, washed sand (S1) was included as a synthetic sediment sample, with a grain size distribution between 0.315 and 0.500 mm. The remaining samples were collected at various locations in the urban drainage system of Zurich: samples S2 and S3 were collected in gully pots (residential and industrial areas), samples S4 and S5 in combined sewer pipes (residential and industrial areas), and sample S6 in a stormwater tank. Their volatile content was measured in triplicate according to the 2540 G standard.27| ID# | Sediment type | Volatile contenta (%) | Volumetric water contentb (%) | Thermal conductivityb (W m−1 °C−1) | Volumetric heat capacityb (MJ m−3 °C−1) |
|---|---|---|---|---|---|
| Key:a Laboratory-based measurements in triplicate.b Sensor-based measurements. | |||||
| S1 | Sand | 0 | 34.4 ± 0.5 | 1.374 ± 0.018 | 2.654 ± 0.027 |
| S2 | Gully pot | 16.7 ± 0.9 | 43.2 ± 3.6 | 0.684 ± 0.042 | 3.446 ± 0.457 |
| S3 | Gully pot | 13.7 ± 1.4 | 35.4 ± 6.4 | 0.662 ± 0.022 | 3.587 ± 0.181 |
| S4 | Stormwater tank | 19.4 ± 1.9 | 39.1 ± 3.0 | 0.641 ± 0.042 | 2.587 ± 0.175 |
| S5 | Sewer pipe | 2.6 ± 0.1 | 40.7 ± 2.6 | 1.074 ± 0.036 | 1.810 ± 0.100 |
| S6 | Sewer pipe | 3.6 ± 0.3 | 35.4 ± 2.2 | 0.915 ± 0.034 | 1.952 ± 0.080 |
2.4. Experimental procedure
Firstly, saturated sediment samples were poured into the cylinder to form a uniform sediment layer without compaction. The depth of the layer was visually measured with measuring tapes attached to the wall of the cylinder. Secondly, a water layer was added on top to allow temperature oscillations to be introduced. For this purpose, actual in-sewer temperature measurements were taken as a reference from the Urban Water Observatory (UWO) (see Fig. 2), operated by the Eawag in the municipality of Fehraltorf, Switzerland.25 Finally, a function was programmed in the water bath circulator to reproduce daily temperature patterns in the laboratory-scale setup.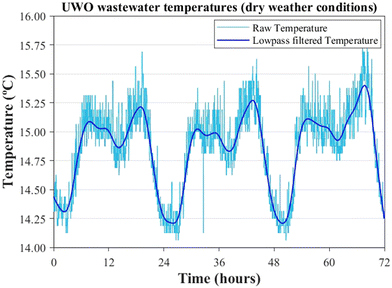 | ||
| Fig. 2 Three-day time series of the wastewater temperatures measured in a combined sewer pipe at the UWO under dry weather conditions. | ||
Experiments were performed by combining passive and active temperature measurements. Passive temperature time series were recorded both at the water–sediment interface (sensor DS3) and at the bottom of the sediment layer (sensor DS2). They were used to determine the attenuation and phase-lag of daily temperature patterns. In addition, temperatures were measured at the outer contour to determine the boundary condition (sensor DS5). Three daily cycles (72 hours) were therefore performed for each experiment, avoiding the influence of the initial conditions on the temperature analysis. Furthermore, the sediment thermal properties were simultaneously measured with the DPHP system by periodically introducing heat pulses into the sediment layer.
The MONTSE system was programmed to measure temperatures and to place heat pulses at the bottom of the sediment layer every 24 hours. Each cycle began with 1-second frequency measurements for 30 seconds to assess initial conditions before the heat pulse started, followed by the activation of the cartridge sensor for 120 seconds. Afterward, the heat pulse stopped, thus cooling the sediments. The measurement frequency was maintained at 1 s−1 during both the sediment heating phase and the subsequent 450 seconds after switching off. Subsequently, temperature measurements continued at a 60 second interval until completing a 24 hour cycle.
3. Methods
Firstly, the heat pulse model used to calculate sediment thermal properties with the DPHP system is described. Secondly, details on the solution of the heat equation are given, including the nondimensional form. This equation is the basis to build a surrogate model that estimates sediment depths from the attenuation and phase-lag features of the temperature time series, the sediment thermal properties and the heat loss at the low boundary. Finally, the application of the surrogate model is described to obtain sediment depths and performance assessment according to the laboratory-scale experiments.3.1. Determining sediment thermal properties with active temperature sensing using a heat pulse model
A DPHP system was developed to determine the thermal properties in UDS sediments. Thermal properties are commonly defined by three parameters: (i) thermal conductivity (kt, W m−1 °C−1), (ii) volumetric heat capacity (Cv, J m−3 °C−1), and 9iii) effective thermal diffusivity (ke, m2 s−1), which represents the ratio of the previous parameters.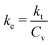 | (1) |
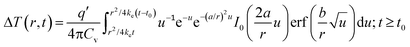 | (2) |
Differentiating eqn (2) with respect to time and setting the result equal to zero gives the following expression from which the thermal diffusivity (ke) can be determined:30
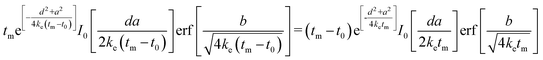 | (3) |
The model for pulsed heating from a finite cylindrical source was selected according to the relationships between the heater dimensions (diameter and length) and the distance to the temperature sensor DS1. Generally, the DPHP systems developed to determine kt and Cv in soil applications use the line source heat pulse model,31 which does not consider the dimensions of the heater.21,23 However, the use of the model for pulsed heating from an infinite line source would lead to high uncertainties in thermal property estimations. According to the uncertainty analysis developed by Kluitenberg et al.,30 neglecting the diameter and length of the heater in the heat pulse model would imply errors of thermal diffusivity measurements of around 3% and 5%, respectively. Furthermore, the model for pulsed heating from a finite cylindrical source assumes an infinite domain, but the DPHP system was stuck to the bottom of the setup. The measurement of the thermal properties using a radial heat-pulse model was assumed to be highly conditioned by the sediment between the heater cartridge and the passive temperature sensor and, consequently, the model could be applied, leading to small errors. Thermal property measurements in the experimental setup and in a wide laboratory beaker were performed to quantify the influence of the low boundary and, subsequently, confirm this assumption (see section 5.1).
The characteristics of the heater, including the heat pulse strength and duration, were measured or provided by the manufacturer (see section 2.2.). In addition, the measurements of the temperature sensor DS1 placed at a distance of d = 12.5 mm from the heater were used to obtain the sediment thermal properties (hereinafter kt and Cv). Finally, the kt and Cv values obtained by the DPHP system were compared with commercial sensor measurements. The absolute errors of kt and Cv were therefore computed to assess and compare the performance of both systems.
3.2. Estimating sediment depths with passive temperature sensing using a heat transfer model
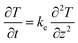 | (4) |
The heat transfer processes of the sediment layer under regular operating conditions in combined sewer pipes (no heat supply) are influenced by the daily oscillations of the wastewater flow at the top boundary, i.e., water–sediment interface, and by the heat energy loss at the low boundary.
A Cauchy-type boundary condition was used to introduce the heat loss into the low boundary:
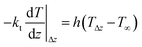 | (5) |
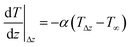 | (6) |
A Cauchy-type boundary condition would also be required to consider the convection processes at the top boundary due to the flow conditions and, consequently, the convective heat transfer coefficient would depend on the pipe flow velocity. Instantaneous heat transfer to the sediment domain was assumed, omitting the hydraulic variables in the model (see the ESI†). Therefore, a Dirichlet-type boundary condition was used to introduce water temperature oscillations into the top boundary:
| Tw = f(t) | (7) |
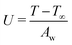 | (8) |
| τ = ωt | (9) |
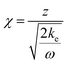 | (10) |
The variables can be differentiated, and the following equations are obtained:
| ∂T = Aw∂U | (11) |
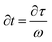 | (12) |
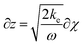 | (13) |
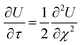 | (14) |
| Uw = g(τ) | (15) |
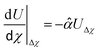 | (16) |
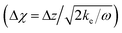 and
and ![[small alpha, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e101.gif)
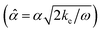 are the nondimensional form of the sediment depth and the leakage coefficient, respectively.
are the nondimensional form of the sediment depth and the leakage coefficient, respectively.
By nondimensionalizing, the heat transfer model could be characterized by two main variables, i.e., Δχ and ![[small alpha, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e101.gif) . Likewise, the model could be rescaled by the sediment thermal diffusivity and the daily fundamental frequency.
. Likewise, the model could be rescaled by the sediment thermal diffusivity and the daily fundamental frequency.
3.3. Surrogate model for the nondimensional 1D diffusion heat equation to estimate sediment depths
A surrogate model was developed to estimate sediment depths by reducing the complexity of heat transfer processes in combined sewer systems to a simple and low computationally expensive solution. The surrogate model for the nondimensional 1D heat transfer equation was built using the harmonic regression analysis of temperature time series. Likewise, harmonic regression methods were applied to relate sediment depths and groundwater fluxes to heat transfer processes in river streambeds10,32 and were recently introduced for sediment depth estimation in UDS.15 Wastewater temperature time series show a sinusoidal daily pattern in combined sewer pipes under dry weather conditions (see Fig. 2), so the fundamental frequency (or first harmonic) of the temperature time series described by its diurnal temperature amplitude (A, in °C) and phase (ϕ, in rad) can be calculated. The methodology consisted of both identifying the fundamental frequency of nondimensional water and sediment-bed temperatures and computing the differences. Consequently, the amplitude ratio (Ar) and the phase difference (Δϕ) were identified as main features of the surrogate model.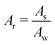 | (17) |
| Δϕ = ϕs − ϕw | (18) |
The surrogate model was built by simulating the nondimensional solution of the 1D heat diffusion equation for multiple scenarios. The UWO's dry weather temperature time series were therefore used as well as various sets of both sediment thermal properties (kt = [0.5, 1.7] W m−1 °C−1, and Cv = [1.5, 3.9] MJ m−3 °C−1) and sediment depths (Δz = [1, 190] mm). These variables were chosen to encompass many measurements within the laboratory-scale setup. Furthermore, the mean of the wastewater temperature time series was used as an approach to the out-of-domain temperature (T∞) for being transformed to the nondimensional form (Uw, eqn (8)). In addition, a range of convective heat transfer coefficients (h) was established to describe the heat loss in the low boundary. h values ranged from perfect insulation conditions (h = 0 W m−2 °C−1) up to h = 12 W m−2 °C−1, exceeding the reference values for PVC pipes.33
As a result, sediment temperature time series were simulated at the bottom of the cylinder and, subsequently, the harmonic features between wastewater and the sediment bed temperature time series were computed. Finally, the surrogate model was developed according to the relationships between the nondimensional parameters ![[small alpha, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e101.gif) and Δχ (section 3.2) and the harmonic features Ar and Δϕ (see Fig. 3, (a) and (b)).
and Δχ (section 3.2) and the harmonic features Ar and Δϕ (see Fig. 3, (a) and (b)).
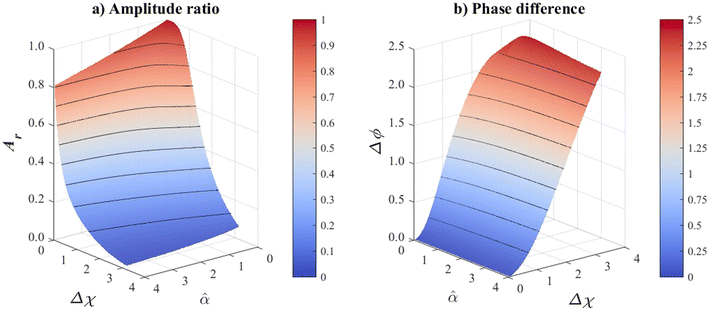 | ||
Fig. 3 Relationships between the nondimensional parameters, ![[small alpha, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e101.gif) and Δχ, of the 1D diffusion heat equation and the harmonic features, (a) amplitude ratio and (b) phase difference. and Δχ, of the 1D diffusion heat equation and the harmonic features, (a) amplitude ratio and (b) phase difference. | ||
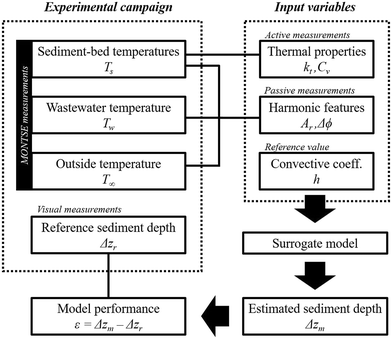
The surrogate model was tested to assess its performance in estimating the known sediment depths of the laboratory-scale experiments. Temperature sensor measurements and one reference value of the convective heat transfer coefficient were therefore required as inputs. Fig. 4 describes the input parameters required to apply the surrogate model and, consequently, to estimate sediment depths. The measurements of the temperature sensor DS1 were used to calculate the sediment thermal properties (kt and Cv, see section 3.1). These properties were determined at least three times for each experiment (1 cycle per day), and the average values were considered as the input parameters of the surrogate model. Likewise, the measurements of the temperature sensors DS2 (sediment bottom) and DS3 (water–sediment interface) were used to perform the FFT frequency analysis of sediment bed and water temperature series, respectively. In addition, the average temperature measured by sensor DS5 outside the model was used to obtain nondimensional temperatures (eqn (8)). The FFT frequency analysis to obtain the fundamental frequency parameters (A and ϕ) was performed without considering the first 24 hours of the experiments to avoid the influence of the initial conditions. The harmonic features resulted from calculating the fundamental frequency differences of the nondimensional water and sediment-bed temperatures (Ar and Δϕ, eqn (17) and (18)). Finally, the nondimensional heat loss at the low boundary (![[small alpha, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e101.gif) , see section 3.2) was computed by considering a convective heat transfer coefficient of h = 1.75 W m−2 °C−1, like the coefficient used by Koju.34 This value was obtained by averaging the best-fitting h values between the simulated and experimental sediment-bed temperature time series (see the ESI†).
, see section 3.2) was computed by considering a convective heat transfer coefficient of h = 1.75 W m−2 °C−1, like the coefficient used by Koju.34 This value was obtained by averaging the best-fitting h values between the simulated and experimental sediment-bed temperature time series (see the ESI†).
Two values of Δχ were obtained by introducing the previous inputs (Ar, Δϕ and ![[small alpha, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e101.gif) ) into the relationships developed for the harmonic features and were transformed into sediment depths
) into the relationships developed for the harmonic features and were transformed into sediment depths 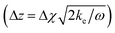 . The average value was established as a final sediment depth estimation of the laboratory-scale experiments (Δzm). The estimated sediment depth was compared with the reference values measured with the measuring tapes attached to the cylinder (Δzr). Finally, the absolute error was also used as a metric to assess the performance of the method (ε = Δzm − Δzr, see Fig. 4).
. The average value was established as a final sediment depth estimation of the laboratory-scale experiments (Δzm). The estimated sediment depth was compared with the reference values measured with the measuring tapes attached to the cylinder (Δzr). Finally, the absolute error was also used as a metric to assess the performance of the method (ε = Δzm − Δzr, see Fig. 4).
3.4. Uncertainty analysis
An uncertainty analysis was performed to assess the accuracy of the sediment depth estimations based on the temperature measurements. The uncertainty propagation of both the input variables and the surrogate model was therefore performed according to the Monte Carlo method. The uncertainty of sensor temperature measurements was calculated considering the manufacturer's specifications and the calibration process. In addition, the uncertainties of the heat pulse characteristics were calculated based on the heater dimensions and the power supplied. The accuracy of the DPHP system was assessed by propagating the previous uncertainties, thus determining sediment thermal properties.The h value was unknown, so a uniform distribution was selected for the h values that best fitted between the simulated and the experimental sediment bed temperature time series. Uncertainties were also assessed for the surrogate model, where the uncertainty associated with UWO temperature measurements was propagated in the 1D diffusion heat equation to obtain the uncertainties of the harmonic features. Likewise, Monte Carlo simulations were performed with one-million iterations to propagate all the uncertainties listed, thus deriving the resulting uncertainty of the sediment depth estimations for each experiment. Finally, error distributions could be calculated by computing the absolute errors of the sediment depth estimations obtained by the Monte Carlo simulations. The uncertainty propagation model is described in detail in the ESI.†
4. Results
4.1. Sediment properties
The physical and thermal properties of the sediment samples analysed in the laboratory-scale setup were determined from laboratory analysis and sensor-based measurements (Table 1). It is worth stressing that this is the first time that thermal properties of organic sediments from UDS are reported. The sediment samples collected in gully pots and sewers were not significantly different between high density and residential areas.Compared with the sediments collected from both the gully pots and the stormwater tank, sewer sediments contained lower volatile content (<5%) and consisted of granular particles. This might be because sediments were collected from a rather steep sewer section, limiting the accumulation of fine particles with greater organic matter content.17,18 The highest volatile content values were obtained in the sample from the stormwater tank, with this assumed to be a function of the sediment collection depth (where the upper part of the sediment layer concentrates a greater percentage of organic material).
The mean values of volumetric water content (VWC) were obtained by averaging the electroconductivity sensor measurements. Sediments were saturated, so their VWC could be used to approximate porosity. Considering the variability of VWC measurements, UDS sediments reported higher standard deviation compared to sand. Likewise, the continuous sensor measurements showed a progressive decrease in VWC values during the tests (e.g., stormwater tank, 46.4–33.5%). Each sediment sample remained at least 12 days in the laboratory model setup (corresponding to four sediment depths, with each being tested for three days), which might have changed sediment properties due to compaction and biological processes. The sand used in the experiments was inert, with a uniform particle distribution of 0.3–0.5 mm, so no compaction process occurred in comparison to UDS sediments. The continuous measurements of the electroconductivity sensor are available in the database of the experimental campaign.26
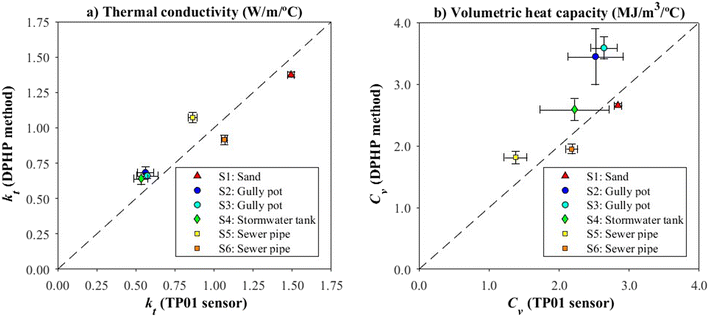
Thermal conductivity (kt) and volumetric heat capacity (Cv) values were obtained by averaging the DPHP system measurements for each sediment type. The thermal properties of the sand matched the values for saturated sandy clays (1.61 W m−1 °C−1 and 2.53 MJ m−3 °C−1).35 A comparison of the thermal properties by sediment types also showed a varied magnitude of differences with, e.g., the variation in mean kt between sand and stormwater tank sediment being twice as large. The kt values decreased as sediment volatile content increased, i.e., sediments with low volatile content showed high kt values, while sediments with high volatile content showed the lowest kt values. Furthermore, Cv values for UDS sediments showed a greater deviation than for sand. The deviation of Cv is related to the compaction processes previously described because its value directly depends on VWC; Cv = VWCρwcw + ρbscs, where the subscripts w and s indicate the water and solid fractions of the saturated sediments, ρ and ρb are the density and bulk density, respectively, and c is the specific heat capacity. Therefore, Cv measurements generally decreased as the consolidation time increased.
4.2. Error analysis of DPHP system measurements
The kt and Cv values determined by the DPHP system were compared with the TP01 sensor (Fig. 5, (a) and (b)). On the one hand, the kt values determined with the DPHP system showed errors of less than 0.21 W m−1 °C−1 with respect to the TP01 sensor measurements. The greatest errors were obtained by sediments with lower volatile content. On the other hand, the Cv values deviated by 0.51 MJ m−3 °C−1 on average between the DPHP system and TP01 sensor measurements. Samples collected in gully pots (S2 and S3) showed the greatest Cv absolute errors between the measurement systems.Considering the deviation of each measurement, both systems presented similar kt standard deviations. Nevertheless, the DPHP system generally showed smaller deviations of Cv measurements than the TP01 sensor. Besides the deviations on Cv measurements due to sediment compaction processes, deviations could be related to measurement accuracy. According to the heat pulse model (eqn (2) and (3)), DPHP measurement accuracy depended on the measured temperature time series, the characteristics of the heat pulse, and the dimensions of the heater. The accuracy of kt and Cv measurements of the DPHP system was calculated to be ±0.04 W m−1 °C−1 and ±0.10 MJ m−3 °C−1, respectively (see further details in the ESI†).
4.3. Sediment depth estimations
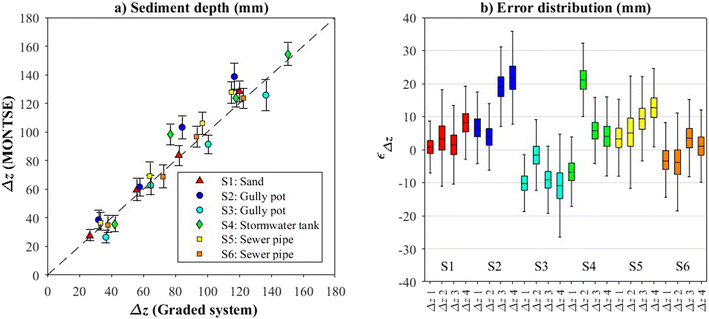
The sediment depths estimated by the surrogate model were compared with the measuring tape observations (Fig. 6, (a) and (b)). The absolute errors of sediment depths were less than 22 mm, and the mean absolute error (MAE) was less than 7.3 mm. The greatest differences were obtained by sediments with high volatile content, i.e., gully pot and stormwater tank samples (S2, S3, and S4). These sediments also showed the greatest deviations in their thermal properties (Fig. 5), which were related to the occurrence of compaction and biological processes during the experiment. Moreover, these processes also affected the direct measurements by using the measuring tapes. According to the measurements taken before and after each experiment, direct measurements were estimated to vary by 2.5 mm for sediments with high volatile content.Likewise, the uncertainty analysis from Monte Carlo simulations showed less variability of estimations for small sediment depths than for large sediment depths. As expected, the greater the sediment depth, the greater the attenuation and phase lag of the temperature series. The uncertainty of the harmonic features therefore increased for large sediment depths. This analysis also showed that estimations performed with the temperature-based system implied non-symmetric distributions for small sediment depths (see further details in the ESI†). As for small sediment depths, the distribution was skewed towards low values. Conversely, great sediment depth estimations followed normal distributions. An overall accuracy of the sediment depth estimation performed with the temperature-based system was computed by considering the coverage interval at a confidence level of 95%. As a safety factor, the average distance between the mean values and the upper boundary of the coverage intervals was therefore considered, thus overestimating the uncertainty of the lower boundary. As a result, the accuracy of the system was of ±7.3 mm.
5. Discussion
The MONTSE system can be used to measure temperatures in UDS, thus providing a new opportunity to monitor sediment depths by analysing heat transfer processes. The results obtained in a laboratory-scale setup showed an accuracy of ±7.3 mm, so it could be potentially used in operational applications. For a better understanding, it is crucial to address two key points: (i) the application of DPHP systems to characterize sediment thermal properties in UDS, and (ii) the field applications and future perspectives of temperature-based systems to estimate sediment depths, focusing on advantages, limitations, alternatives, and potential uses.5.1. Application of DPHP systems in UDS
The DPHP system emerged as part of the MONTSE system, which was devised by solving the heat pulse model of a finite cylindrical source. Subsequently, the DPHP system underwent rigorous testing very close to the base of a laboratory-scale setup. Likewise, heat-pulse methods assume sediment homogeneity in the surroundings of the heat source.20 The potential for basal sediment boundary conditions to affect the measurement of thermal properties was therefore assessed by comparing thermal properties of saturated sand at the base of the model and in a laboratory beaker (see the ESI†). The thermal properties showed similar values (relative error <5%), suggesting that the distance from the heater to the bottom did not significantly affect the measurements of sediment thermal properties.The experimental campaign provided the first references for thermal properties of UDS sediments, which can be used as a benchmark for further studies. The comparison among thermal properties by sediment type suggested that volatile content values appeared to be inversely proportional to thermal conductivities. Acknowledging volatile content as an indicator of pollution level in UDS, this system could therefore be potentially applied in estimating the level of organic substances associated with UDS sediments. On the other hand, the variability of volumetric heat capacity values in UDS sediments was mainly caused by compaction processes. These processes were also observed due to the decrease of the VWC values and to the sediment depth measurements taken with the measuring tapes before and after experiments. Despite these oscillations, the use of the DPHP method to obtain sediment thermal properties was reliable for sediment depth estimations.
The active system offered the advantage of on-site measurements of the sediment thermal properties. For field applications, the frequency of heat pulses should be optimized in the case of battery-operated systems as they consume most of the energy (7.2 W active measurements, and 0.0008 W passive measurements). Therefore, the heating pulse frequency could be decreased to reduce power consumption. Although the measurement system is sensitive to the change of sediment types, no major exchanges in sediment type are expected at a single measurement location, but the potential impacts of sediment compaction and biological processes are inevitable. Alternatively, the same system could be used without the cartridge heater, i.e., using only passive temperature measurements. For these cases, active measurements could be replaced by collecting sediment samples to analyse their thermal properties in the laboratory or by using future benchmark values. This could compromise the accuracy of sediment depth estimations for the sediments with high volatile content, but it is most sufficient for routine applications, for which ATEX issues should also be considered.
The active temperature system was developed to be installed in sewer systems, and two criteria were considered when proposing the heat-pulse system. Firstly, the system must resist damage that sediment transport can cause to the submerged sensors due to the impact of solid particles. Secondly, as the system is submerged in wastewater, clogging and malfunctioning of the sensor must be avoided. For both reasons, the dimensions of the heater were like those of the DS18B20 temperature sensors (45 mm in length and 6 mm in diameter), whose robustness and performance were shown when monitoring campaigns in sewer systems, such as the UWO.25
5.2. Field applications and future perspectives of temperature-based systems to estimate sediment depths
A surrogate model was also developed to estimate sediment depths. The UWO temperature patterns used to develop this model were independent of the experimental campaign measurements, although they were used as a reference for the temperature control system. Therefore, the selected features are valid in other sewer pipes that follow daily temperature patterns.The model covers a range of depths up to 190 mm. However, sediment depths greater than those tested can be found in sewer collectors and interceptors (e.g., 200 to 500 mm).36–39 To estimate large sediment depths, additional sensors should be put in the pipe cross section as the bottom temperature measurements would be strongly attenuated and the system would provide great uncertain estimations in the sediment depth (see Fig. S2, ESI†). For these cases, analytical approaches developed for river streambeds could also be used.9,10,13 The errors in the estimation of organic sediment depths greater than 100 mm with analytical approaches were less than 10 mm.15
The sediment depths estimated with both the MONTSE system and the surrogate model showed an accuracy of ±7.3 mm. This accuracy included variability due to the systematic changes from the compaction processes during the experiments with UDS sediments. The sediment depths were difficult to monitor in field applications. For instance, the sediment depth measurement with measuring tapes and sticks could lead to uncertain values due to both the compaction of leaves in gully pots40 and the sediment organic content in sewer pipes.8 However, from the practical perspective, millimetre levels of accuracy are not required to monitor the accumulation and wash-off of sediment deposits. The same holds for the decision on whether a UDS system needs to be cleaned.
Albeit other techniques, such as acoustic profilers,7 are also effective in estimating sediment depths, their installation is costly and power intensive. In addition, monitoring sediment depths with acoustic profilers, e.g., sonars, requires a minimum wastewater depth of 125 mm.41 A major advantage of the proposed system is that its installation and application is simple since temperature sensors do not require complex electronics. Future versions of the MONTSE system will include exchangeable batteries and data transfer modules, and will integrate the surrogate model into the microcontroller software, leading to edge computing.
The temperature-based system, which was already validated for natural systems,9–14 aims to be transferred to urban drainage systems. In addition to sewer systems, the system is clearly potential to monitor other drainage infrastructures, such as gully pots, pumping stations, and sediment traps as well as to settle devices for primary stormwater treatment. The analysis of heat transfer processes should therefore be adapted according to the geometry or temperature variations in infrastructures, such as the gully pots affected by the temperature gradients caused by runoff. This methodology could also be combined with the use of DTS devices, which are used to detect illicit connections and to characterize infiltration into sewers (e.g., Vosse et al.,42 Panasiuk et al.43), but they could also be adapted to measure longitudinal sediment-bed distributions with suitable installation at the bottom of sewer pipes.
In addition to the operational applications, the system could be used to study sediment accumulation after cleaning UDS. For instance, sewer pipes recently cleaned could show a rapid build-up of organic sediments with high pollution potential, which could be slowly replaced by granular and coarse sediments.18,19 This system could therefore be used to estimate the evolution of pollution potential, and subsequently to develop and validate sediment transport models.
6. Conclusions
The results of this study show that the combination of active and passive temperature measurements can be used to estimate sediment accumulation in sewer pipes with daily temperature patterns under dry weather conditions. The main conclusions are provided below:• The MONTSE monitoring system can robustly measure daily temperature patterns within the water layer and sediments, enabling the analysis of heat transfer processes in sewer systems. This system also integrates active temperature measurements to estimate sediment thermal properties as key parameters in the analysis of heat transfer processes.
• A surrogate model was built based on the nondimensional solution of the 1D diffusion heat transfer equation. This model established a relationship between the harmonic features of water and sediment temperature patterns, sediment depth, thermal properties, and the low-boundary condition. The nondimensional analysis reduced the number of parameters of the model, thus enabling the model to be used under various conditions.
• A laboratory-scale campaign was carried out to evaluate the performance of both the MONTSE system and the surrogate model to estimate sediment depths, resulting in absolute errors of less than 22 mm compared to the measuring tapes. The performance of the DPHP system was also assessed, resulting in kt and Cv measurements in agreement with those of a commercial sensor (MAE: 0.21 W m−1 °C−1 and 0.51 MJ m−3 °C−1, respectively).
• The thermal properties of UDS sediments were lower than those in sands, with values for kt and Cv being approximately twice as small in sediments with high volatile content. Additionally, the thermal conductivity showed an inverse relationship with volatile content as well as the compaction processes increased the variability of the volumetric heat capacity in sediments.
• The accuracy of the sediment depth estimations of the proposed temperature-based system was ±7.3 mm, which is acceptable in the context of decision making in the cleaning and maintenance operations of sewer pipes as well as in sediment transport research.
• This new temperature-based system was designed to be implemented in sewer systems. It also overcomes the challenges associated with traditional systems that monitor sediment accumulation, such as continuous measurements. Additionally, the system has potential for sediment control applications in other UDS, such as gully pots, stormwater treatment systems, and sediment traps, among others. However, fundamental adaptations are required to implement it effectively, including the re-analysis of relevant heat transfer processes and geometries.
Data availability
The dataset for this research is available in these in-text data citation references: Regueiro-Picallo et al. (2023b), with a license Creative Commons Attribution 4.0 International (CC BY-NC 4.0). https://doi.org/10.5281/zenodo.8414446.Author contributions
M. R.-P.: investigation, methodology, formal analysis, data curation, writing – original draft. J. L.: funding acquisition, writing – review & editing. H. W.: writing – review & editing, J.-L. B.-K.: resources, supervision, writing – review & editing. J. R.: conceptualization, resources, supervision, writing – review & editing.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The work developed by M. R.-P. is funded within the postdoctoral fellowship programme from the Xunta de Galicia (Consellería de Cultura, Educación e Universidade, ED481B-2021-082). This work includes the results from a transnational access funded by the EU under the Horizon 2020 INFRAIA program (Co-UDlabs project. GA No. 101008626). The authors are indebted to all members of the Transnational Access HALL-Eawag User Group and the facility provider for their support in the experimental campaign. H. W. acknowledges support from the VINNOVA DRIZZLE – Centre for Stormwater Management (Grant: 2016–05176). Funding for open access charge: Universidade da Coruña/CISUG.References
- R. M. Ashley, J. L. Bertrand-Krajewski, T. Hvitved-Jacobsen and M. Verbanck, Solids in sewers, IWA Publishing, London, UK, 2004, ISBN 1900222914 Search PubMed.
- P. Ackers, Sediment aspects of drainage and outfall design, presented in part at International Symposium on Environmental Hydraulics, ed. Y. K. Cheung , J. H. W. Lee and A. A. Balkema, Rotterdam, Netherlands, 1991, pp. 215–230 Search PubMed.
- R. W. P. May, Sediment transport in pipes and sewers with deposited beds, Report SR 320, HR Wallingford, 1993 Search PubMed.
- R. De Sutter, P. Rushforth, S. Tait, M. Huygens, R. Verhoeven and A. Saul, Validation of existing bed load transport formulas using in-sewer sediment, J. Hydraul. Eng., 2003, 129(4), 325–333, DOI:10.1061/(ASCE)0733-9429(2003)129:4(325).
- I. Seco, A. Schellart, M. Gómez-Valentín and S. Tait, Prediction of organic combined sewer sediment release and transport, J. Hydraul. Eng., 2018, 144(3), 04018003, DOI:10.1061/(ASCE)HY.1943-7900.0001422.
- J. L. Bertrand-Krajewski, F. Clemens-Meyer and M. Lepot, Metrology in urban drainage and stormwater management: Plug and pray, IWA Publishing, London, UK, 2021, ISBN 9781789060119, Open Access available at DOI:10.2166/9781789060119.
- M. Lepot, T. Pouzol, X. Aldea Borruel, D. Suner and J. L. Bertrand-Krajewski, Measurement of sewer sediments with acoustic technology: from laboratory to field experiments, Urban Water J., 2017, 14(4), 369–377, DOI:10.1080/1573062X.2016.1148181.
- J. L. Bertrand-Krajewski, J. P. Bardin and C. Gibello, Long term monitoring of sewer sediment accumulation and flushing experiments in a man-entry sewer, Water Sci. Technol., 2006, 54(6–7), 109–117, DOI:10.2166/wst.2006.619.
- C. H. Luce, D. Tonina, F. Gariglio and R. Applebee, Solutions for the diurnally forced advection-diffusion equation to estimate bulk fluid velocity and diffusivity in streambeds from temperature time series, Water Resour. Res., 2013, 49(1), 488–506, DOI:10.1029/2012WR012380.
- D. Tonina, C. Luce and F. Gariglio, Quantifying streambed deposition and scour from stream and hyporheic water temperature time series, Water Resour. Res., 2014, 50(1), 287–292, DOI:10.1002/2013WR014567.
- E. Sebok, C. Duque, P. Engesgaard and E. Bøgh, Application of Distributed Temperature Sensing for mapping spatial and temporal variability of groundwater discharge and sedimentation processes in soft-bedded streams, Hydrol. Processes, 2015, 29(15), 3408–3422, DOI:10.1002/hyp.10455.
- C. Duque, S. Müller, E. Sebok, K. Haider and P. Engesgaard, Estimating groundwater discharge to surface waters using heat as a tracer in low flux environments: The role of thermal conductivity, Hydrol. Processes, 2016, 30(3), 383–395, DOI:10.1002/hyp.10568.
- R. van Kampen, U. Schneidewind, C. Anibas, A. Bertagnoli, D. Tonina, G. Vandersteen, C. Luce, S. Krause and M. van Berkel, LPMLEn–A Frequency Domain Method to Estimate Vertical Streambed Fluxes and Sediment Thermal Properties in Semi-Infinite and Bounded Domains, Water Resour. Res., 2022, 58(3) DOI:10.1029/2021WR030886.
- E. Sebok, P. Engesgaard and C. Duque, Long-term monitoring of streambed sedimentation and scour in a dynamic stream based on streambed temperature time series, Environ. Monit. Assess., 2017, 189(9), 1–15, DOI:10.1007/s10661-017-6194-x.
- M. Regueiro-Picallo, J. Anta, A. Naves, A. Figueroa and J. Rieckermann, Towards urban drainage sediment accumulation monitoring using temperature sensors, Environ. Sci.: Water Res. Technol., 2023, 9, 3200–3212, 10.1039/D2EW00820C.
- J. Gasperi, M. C. Gromaire, M. Kafi, R. Moilleron and G. Chebbo, Contributions of wastewater, runoff and sewer deposit erosion to wet weather pollutant loads in combined sewer systems, Water Res., 2010, 44(20), 5875–5886, DOI:10.1016/j.watres.2010.07.008.
- R. W. Crabtree, Sediments in sewers, Water Environ. J., 1989, 3(6), 569–578, DOI:10.1111/j.1747-6593.1989.tb01437.x.
- E. Ristenpart, Sediment properties and their changes in a sewer, Water Sci. Technol., 1995, 31(7), 77–83, DOI:10.1016/0273-1223(95)00325-H.
- M. Regueiro-Picallo, J. Suárez, E. Sañudo, J. Puertas and J. Anta, New insights to study the accumulation and erosion processes of fine-grained organic sediments in combined sewer systems from a laboratory scale model, Sci. Total Environ., 2020, 716, 136923, DOI:10.1016/j.scitotenv.2020.136923.
- H. He, M. F. Dyck, R. Horton, T. Ren, K. L. Bristow, J. Lv and B. Si, Development and application of the heat pulse method for soil physical measurements, Rev. Geophys., 2018, 56(4), 567–620, DOI:10.1029/2017RG000584.
- G. Ravazzani, Open hardware portable dual-probe heat-pulse sensor for measuring soil thermal properties and water content, Comput. Electron. Agric., 2017, 133, 9–14, DOI:10.1016/j.compag.2016.12.012.
- J. Benítez-Buelga, C. Sayde, L. Rodríguez-Sinobas and J. S. Selker, Heated fiber optic distributed temperature sensing: A dual-probe heat-pulse approach, Vadose Zone J., 2014, 13(11) DOI:10.2136/vzj2014.02.0014.
- M. Shehata, J. Heitman, J. Ishak and C. Sayde, High-resolution measurement of soil thermal properties and moisture content using a novel heated fiber optics approach, Water Resour. Res., 2020, 56(7), e2019WR025204, DOI:10.1029/2019WR025204.
- N. Simon, O. Bour, N. Lavenant, G. Porel, B. Nauleau, B. Pouladi, L. Longuevergne and A. Crave, Numerical and experimental validation of the applicability of active-DTS experiments to estimate thermal conductivity and groundwater flux in porous media, Water Resour. Res., 2021, 57(1), e2020WR028078, DOI:10.1029/2020WR028078.
- F. Blumensaat, S. Bloem, C. Ebi, A. Disch, C. Förster, M. Rodriguez, M. Maurer and J. Rieckermann, The UWO dataset: Long-term data from a real-life field laboratory to better understand urban hydrology at small spatiotemporal scales, engrxiv, 2023, preprint, DOI:10.31224/3208.
- M. Regueiro-Picallo, J. Rieckermann, C. Ebi, S. Bloem and J. Langeveld, Combining active and passive temperature signals for estimating sediment depths [Data set], Zenodo, 2023 DOI:10.5281/zenodo.8414446.
- APHA, AWWA and WEF, Standard Methods for the Examination of Water and Wastewater, American Public Health Association/American Water Works Association/Water Environment Federation, Washington DC, USA, 20th edn, 1998 Search PubMed.
- H. S. Carslaw and J. C. Jaeger, Conduction of heat in solids, Oxford University Press, Oxford, UK, 2nd edn, 1959 Search PubMed.
- G. J. Kluitenberg, J. M. Ham and K. L. Bristow, Error analysis of the heat pulse method for measuring soil volumetric heat capacity, Soil Sci. Soc. Am. J., 1993, 57(6), 1444–1451, DOI:10.2136/sssaj1993.03615995005700060008x.
- G. J. Kluitenberg, K. L. Bristow and B. S. Das, Error analysis of heat pulse method for measuring soil heat capacity, diffusivity, and conductivity, Soil Sci. Soc. Am. J., 1995, 59(3), 719–726, DOI:10.2136/sssaj1995.03615995005900030013x.
- K. L. Bristow, G. J. Kluitenberg and R. Horton, Measurement of soil thermal properties with a dual-probe heat-pulse technique, Soil Sci. Soc. Am. J., 1994, 58(5), 1288–1294, DOI:10.2136/sssaj1994.03615995005800050002x.
- R. P. Gordon, L. K. Lautz, M. A. Briggs and J. M. McKenzie, Automated calculation of vertical pore-water flux from field temperature time series using the VFLUX method and computer program, J. Hydrol., 2012, 420, 142–158, DOI:10.1016/j.jhydrol.2011.11.053.
- C. Z. Fu, W. R. Si, L. Quan and J. Yang, Numerical study of convection and radiation heat transfer in pipe cable, Math. Probl. Eng., 2018, 2018, 1–12, DOI:10.1155/2018/5475136.
- S. M. Koju, Thermal behaviour of expanded polystyrene based lightweight concrete sandwich panel at various temperatures, Guoli Zhongxing Daxue Ligong Xuebao, 2017, 4, 47–52 Search PubMed.
- I. N. Hamdhan and B. G. Clarke, Determination of thermal conductivity of coarse and fine sand soils, presented in part at World Geothermal Congress, Bali, Indonesia, 2010 Search PubMed.
- D. Laplace, Y. Sanchez, D. Dartus and A. Bachoc, Sediment movement into the combined trunk sewer no. 13 in Marseille, Water Sci. Technol., 1990, 22(10–11), 259–266, DOI:10.2166/wst.1990.0312.
- M. Verbanck, Sewer sediment and its relation with the quality characteristics of combined sewer flows, Water Sci. Technol., 1990, 22(10–11), 247–257, DOI:10.2166/wst.1990.0311.
- E. Ristenpart, R. M. Ashley and M. Uhl, Organic near-bed fluid and particulate transport in combined sewers, Water Sci. Technol., 1995, 31(7), 61–68, DOI:10.1016/0273-1223(95)00323-F.
- C. Oms, M. C. Gromaire and G. Chebbo, In situ observation of the water-sediment interface in combined sewers, using endoscopy, Water Sci. Technol., 2003, 47(4), 11–18, DOI:10.2166/wst.2003.0209.
- M. W. J. Rietveld, F. Clemens-Meyer and J. Langeveld, Monitoring and statistical modelling of the solids accumulation rate in gully pots, Urban Water J., 2020, 17(6), 549–559, DOI:10.1080/1573062X.2020.1800760.
- I. Carnacina, F. Larrarte and N. Leonardi, Acoustic measurement and morphological features of organic sediment deposits in combined sewer networks, Water Res., 2017, 112, 279–290, DOI:10.1016/j.watres.2017.01.050.
- M. Vosse, R. Schilperoort, C. de Haan, J. Nienhuis, M. Tirion and J. Langeveld, Processing of DTS monitoring results: automated detection of illicit connections, Water Pract. Technol., 2013, 8(3–4), 375–381, DOI:10.2166/wpt.2013.037.
- O. Panasiuk, A. Hedström, J. Langeveld, C. de Haan, E. Liefting, R. Schilperoort and M. Viklander, Using distributed temperature sensing (DTS) for locating and characterising infiltration and inflow into foul sewers before, during and after snowmelt period, Water, 2019, 11(8), 1529, DOI:10.3390/w11081529.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ew00825h |
| This journal is © The Royal Society of Chemistry 2024 |