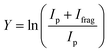Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
IR spectroscopic characterization of [M,C,2H]+ (M = Ru and Rh) products formed by reacting 4d transition metal cations with oxirane: Spectroscopic evidence for multireference character in RhCH2+†
Frank J.
Wensink
 a,
Corry E.
Smink
a,
Brandon C.
Stevenson
b,
Ryan P.
Steele
b,
Joost M.
Bakker
a,
Corry E.
Smink
a,
Brandon C.
Stevenson
b,
Ryan P.
Steele
b,
Joost M.
Bakker
 *a and
P. B.
Armentrout
*a and
P. B.
Armentrout
 *b
*b
aRadboud University, Institute for Molecules and Materials, HFML-FELIX, Toernooiveld 7, 6525 ED Nijmegen, The Netherlands. E-mail: joost.bakker@ru.nl
bDepartment of Chemistry, University of Utah, 315 South 1400 East, Salt Lake City, Utah 84112, USA. E-mail: peter.armentrout@chem.utah.edu
First published on 15th March 2024
Abstract
A combination of infrared multiple-photon dissociation (IRMPD) action spectroscopy and quantum chemical calculations was employed to investigate the [M,C,2H]+ (M = Ru and Rh) species. These ions were formed by reacting laser ablated M+ ions with oxirane (ethylene oxide, c-C2H4O) in a room-temperature ion trap. IRMPD spectra for the Ru species exhibit one major band and two side bands, whereas spectra for the Rh species contain more distinct bands. Comparison with density functional theory (DFT), coupled-cluster (CCSD), and equation-of-motion spin–flip CCSD (EOM-SF-CCSD) calculations allows assignment of the [M,C,2H]+ structures. For the spectrum of [Ru,C,2H]+, a combination of HRuCH+ and RuCH2+ structures reproduces the observed spectrum at all levels of theory. The well-resolved spectrum of [Rh,C,2H]+ could not be assigned unambiguously to any calculated structure using DFT approaches. The EOM-SF-CCSD calculations showed that the ground-state surface has multireference electronic character, and symmetric carbenes in both the 1A1 and 3A2 states are needed to reproduce the observed spectrum.
Introduction
The functionalization of C–H bonds is a longstanding topic in chemistry.1,2 Functionalization reactions start with activation, which is a bottleneck for energy-efficient and selective functionalization processes involving C–H bonds because of their typically high bond energies. As the major component of natural gas and the simplest alkane molecule, methane is the most commonly studied alkane, often with the objective to investigate how to selectively convert methane into liquid fuels like methanol that remain energy rich but are more easily transported. Methane activation catalysis is currently neither specific nor energy efficient enough for direct utilization of methane. Rather, current schemes rely on thermal cracking, followed by synthetic pathways to more valuable chemicals. For more efficient, direct utilization of methane, it is imperative to develop better C–H bond activation catalysts.Rational design of more active and selective catalyst materials requires a detailed understanding of the interaction between potential catalyst materials and substrates. One way to obtain this information for methane is to study its interactions with model systems for the active site.3–5 To obtain the most detailed information, the reaction can be isolated in the gas phase, which removes the perturbing effects of a support or solvent. This approach enables studies to focus on the intrinsic interactions. Once such interactions are understood in detail, support, solvent, and pressure effects can be considered.
Previously, studies have shown that methane is activated at room temperature by the third-row (5d) transition metal (TM) cations, Ta+, W+, Os+, Ir+, and Pt+, leading to dehydrogenation and the formation of [M,C,2H]+ products.6–17 Infrared (IR) spectroscopic characterization of [M,C,2H]+ products showed that [Pt,C,2H]+ has a PtCH2+ carbene structure with C2v symmetry, whereas [Ta,C,2H]+ and [W,C,2H]+ are carbene structures that are distorted by agostic interactions.18–21 In contrast, [Os,C,2H]+ and [Ir,C,2H]+ have a hydrido metal carbyne HMCH+ structure, and for Ir+, experimental evidence was also found for the co-existence of a higher-energy symmetric IrCH2+ carbene structure.18–20,22 The observation of the HIrCH+ structure demonstrated the need for spectroscopic characterization, because the same structure had been discarded earlier on energetic grounds.23
In contrast to third-row TM cations, none of the second-row (4d) TM cations dehydrogenates methane exothermically,15,24–37 although the reaction with Zr+ is only slightly endothermic.38 To understand the underlying reasons why reactions of the lighter TM cations are endothermic, it is of interest to characterize the structures of [M,C,2H]+ products where M is a second-row TM. Because Os+ and Ir+ were shown to be the most reactive ions for methane dehydrogenation and also show the most diversity in their structures,13,16–19,22 the present study focuses on the bonding nature and structures of [M,C,2H]+ with their second-row congeners: the elements of groups 8 and 9, M = Ru and Rh. Earlier studies investigated the M+–CH2 bond strengths for first-row TMs and found that the bond dissociation energy (BDE, D0) decreases with an increase in the promotion energy (required for promoting a metal atom in its ground state to an electron configuration where there is one electron in the valence s orbital that is spin-decoupled from the remaining metal d electrons) of the atomic metal cation.39 It seems likely that a parallel trend is followed for the second-row TMs considered here, although this has not been quantified. The value of D0(Ru+–CH2) has been determined to be 3.57 ± 0.05 eV,37 such that formation of RuCH2+ and H2 from Ru+ and CH4 requires 1.17 ± 0.05 eV given D0(CH2–H2) = 4.743 ± 0.001 eV.40 Analogously, D0(Rh+–CH2) has been determined as 3.69 ± 0.08 eV in guided ion beam experiments41 and as 4.08 ± 0.22 eV by ion–molecule bracketing reactions.42 Thus, formation of RhCH2+ and H2 from Rh+ and CH4 requires an energy of 1.03 ± 0.08 (0.67 ± 0.22) eV.32
Elsewhere, a B3LYP potential energy surface (PES) for the reaction between Ru+ and CH4 identified the first step as physisorption with an exothermicity of 0.78 eV.37 This energy can be used to transfer one hydrogen atom from methane to Ru+, forming H–Ru+–CH3, which still lies 0.18 eV below the energy of the reactants. A further step toward (H2)RuCH2+ requires the crossing of endothermic energy barriers and a spin flip from quartet to doublet. Formation of the doublet-spin (H2)RuCH2+ intermediate is still exothermic by 0.09 eV, but loss of H2 requires over 1 eV, such that the overall dehydrogenation reaction to form RuCH2+ (2A2) + H2 is calculated to be endothermic by 1.08 eV. Energetically more favorable are the formation of the doublet-spin HRuCH+ (+0.97 eV) and quartet-spin RuCH2+ (+0.94 eV) products. Formation of the former has no barriers exceeding the product energy, whereas progress along the quartet-spin surface requires passing over a tight-transition state barrier of 1.03 eV.37
For RhCH2+, multireference – single double configuration interaction – complete active space self-consistent field (MR-SDCI-CASSCF)43 and B3LYP44 calculations have identified a 1A1-state carbene as lowest in energy, followed by a 3A2 state lying 0.20 and 0.19 eV, respectively, higher in energy. (The relative energies of higher-lying states identified in the former study are included in Table S1, ESI†). Again, the only intermediate that can be formed exothermically on the PES of Rh+(3F) + CH4 is the physisorption step;43,44 however, the CASSCF calculations found a barrier of about 0.4 eV for the reverse RhCH2+ + H2 reaction, whereas the later B3LYP calculations found no barrier. The latter result agrees with experiments for both the forward and reverse reactions.32,42
As described above, none of the metal cations we study here react exothermally with methane.26,31,32,37 Therefore, in order to form the [M,C,2H]+ species of interest, we react the corresponding M+ ions with oxirane (ethylene oxide, c-C2H4O). Oxirane readily reacts with many TM cations because of its ring strain and because [M,C,2H]+ formation is accompanied by the stable CH2O neutral product. Thus, extraction of CH2 from oxirane requires much less energy than from methane, D0(CH2–CH2O) = 3.375 ± 0.004 eV, compared to the D0(CH2–H2) = 4.743 ± 0.001 eV already mentioned.40 In contrast to the endothermic reactions with methane, the thermochemistry noted above indicates that formation of MCH2+ + CH2O in the reaction of M+ with oxirane is exothermic by 0.20 ± 0.05 and 0.32 ± 0.08 eV for M = Ru and Rh, respectively. Although it has been shown that laser-ablated Rh+ reacts at thermal energies with oxirane to yield RhCH2+,42 product distributions for the reactions of Ru+ and Rh+ with c-C2H4O have not been published previously.
In the present work, we probe the structures of the [M,C,2H]+ product ions for M = Ru and Rh using a combination of IR multiple photon dissociation (IRMPD) action spectroscopy and DFT or coupled cluster with single and double excitations (CCSD) calculations. IRMPD spectra are recorded using the same Fourier transform ion cyclotron resonance (FTICR) mass spectrometer recently used to show that the reaction of Pt+ with two methane molecules leads to the formation of a Pt+(ethene) complex following two dehydrogenations and C–C coupling.21 In that same work, we demonstrated that the spectrum of [Pt,C,2H]+ recorded with this instrument is consistent with that reported previously,18 where [Pt,C,2H]+ was formed in a molecular beam environment without mass-isolation prior to irradiation. Earlier attempts to record IRMPD spectra of [M,C,2H]+ with M = Ru were unsuccessful in the molecular beam apparatus because the ion intensities were insufficient. Here, we take advantage of the possibility to react TM+ with c-C2H4O over longer times and to mass-isolate the formed [M,C,2H]+ species in order to obtain the desired spectra.
Critically, these small ions also form benchmark systems for the accuracy of quantum chemistry methods. Previously, we found that relatively standard DFT methods proved sufficient to accurately predict the IR fingerprints, both in terms of frequencies and IR intensities that are necessary for assigning the experimental IR spectra of [M,C,2H]+ species with 5d TM elements.18–22 In contrast, in a parallel publication investigating the IR spectra of FeCH2+ and CoCH2+,45 3d congeners of the species currently under investigation, we found that a large variety of DFT methods provide a significant underestimation of the IR absorption intensity for the M–C stretch vibration. We provided computational evidence suggesting that this relates to inaccurate charge separation of these DFT methods. One motivation of the present work is therefore to assess whether DFT treatments of this mode are as poor as they were for 3d elements, or whether they are accurate enough, like for the 5d elements studied earlier. We therefore also employ higher-level single- and multireference methods to interpret the observed spectra. One previous computational study,43 based on CASSCF and MR-SDCI-CASSCF methods, noted only modest multireference contributions to the ground-state wavefunction of RhCH2+. The same analyses were unable to reproduce the experimentally observed Rh+–CH2 binding energy and yielded relative electronic state energies that differ appreciably from the ones computed herein. We find that adequately treating the multireference character, while employing modern core potentials and basis sets, is needed to properly reproduce the observed spectrum of RhCH2+. In the case of [Ru,C,2H]+, multi-reference character does not appear to be relevant, but here contributions from multiple structures and states, whose energies vary with the level of theory, are required to match the experimental spectrum.
Methods
Experimental
Atomic metal (Ru, Rh) cations were produced in a laser vaporization source.46,47 In this source, a solid metal target disk was irradiated by a frequency doubled Nd:YAG laser at 30 Hz in the presence of helium gas injected by a pulsed valve. The helium cooled the metal ions through collisions and guided them toward the end of the source, where the gas mixture adiabatically expanded into vacuum, thereby further cooling the ions. They were then transferred, via a quadrupole mass filter in guidance mode, to a quadrupole ion trap with rectangular electrodes where they were trapped by dissipating the kinetic energy with 5 × 10−4 mbar of argon buffer gas. In the trap, the metal ions reacted with oxirane at a partial pressure of 1 × 10−6 mbar, which was mixed into the argon. After accumulating ions for approximately 400 ms, the voltage on the exit electrode of the ion trap was lowered. This released the ions from the ion trap after which they were guided into the cavity of the Free Electron Laser for IntraCavity Experiments (FELICE). Here, the ions were trapped in one of the cells of the FTICR mass spectrometer integrated within the laser cavity. This FTICR has four cells, with the first (cell 1) located in the laser focus and the fourth 30 cm from the focus, thereby lowering the photon fluence by a factor of 14. After ion capture, all unwanted masses were ejected from the FTICR cell using a combination of radio frequency (rf) excitation pulses (chirped and single-frequency),48 so that only the species of interest were irradiated by IR light produced by FELICE. Resonant absorption of IR photons increased the internal energy of the ions and once the fragmentation threshold was overcome, the ions dissociated, which indicates the presence of a vibrational band at the resonant IR frequency. The IRMPD spectrum was obtained by recording the intensities of precursor (Ip) and fragment (Ifrag) ions present in the FTICR cell after irradiation and is expressed as the fragmentation yield Y:The IR light of FELICE is tunable in the 100–2000 cm−1 spectral range, although for this work only the 300–2000 cm−1 spectral range was used. The spectral bandwidth was near transform limited and, during these measurements, the full-width at half-maximum (FWHM) was approximately 0.7% of the central frequency. FELICE produced micropulses at 1 GHz, and the macropulses lasted between 6–10 μs and were repeated at 5 or 10 Hz. All spectra were recorded using a single macropulse with the ions in FTICR cell 4 (low fluence) unless specifically indicated otherwise. FELICE macropulse energies used ranged from 0.3 J at lower frequencies to 0.5 J at higher frequencies, corresponding to macropulse fluences ranging from 0.9 to 6.6 J cm−2 in FTICR cell 4.
Computational
The DFT calculations were done using the Gaussian 16 software package,49 where all molecular structures, closed- and open-shell, were optimized using the unrestricted B3LYP hybrid functional and the def2-TZVPPD basis set.50–52 This combination was used because the M+–CH2 BDEs calculated for the metals explored here matched the experimental values relatively well: D0(Ru+–CH2) = 3.73 eV (experimental 3.57 ± 0.05 eV) and D0(Rh+–CH2) = 3.60 eV (experimental 3.69 ± 0.08 eV). All electrons were treated explicitly for H and C, whereas an effective core potential (ECP) of 28 electrons (small core) was used for Ru and Rh with the 4s, 4p, 5s, and 4d orbitals treated explicitly by the basis set. To ascertain true minima and for comparison with the experimental spectra, harmonic vibrational frequencies were calculated. All relative energy values provided below include harmonic zero-point vibrational energies. For each vibrational mode, rovibrational envelopes were simulated assuming pure a-, b-, or c-type transitions on the basis of moments obtained from the computations.53 For comparison with experiment, the simulated rotational substructures were shifted to the unscaled, calculated vibrational frequencies and the individual rotational transition intensities multiplied by the vibrational transition intensities. (For these calculations, no scaling factors were used to compare the theoretical spectra with experiment, which is unusual for these types of systems.18–22,54–56 Nevertheless, such scaling factors were not found to improve the agreement between theory and experiment and therefore are not used throughout this work except as noted.) The resulting rovibrational transition lines were subsequently convoluted using a Gaussian line shape function with a FWHM of 0.9% of the central frequency, mimicking the FELICE spectral bandwidth. It should be noted that because all calculated spectra correspond to absorption of a single IR photon, the predicted intensities can differ from the experimental multiple-photon spectra.Additional geometry and frequency calculations were performed at the second-order Möller–Plesset, MP2,57 and coupled-cluster with single and double excitations, CCSD,58 levels using the same def2-TZVPPD basis set. These calculations were followed by single-point calculations with added perturbative triple excitations, i.e., at the CCSD(T)/def2-TZVPPD level of theory.
Because of the large degree of spin contamination initially observed in DFT (and even CCSD) computations of the singlet [Rh,C,2H]+ and doublet [Ru,C,2H]+ species, additional calculations were performed with the equation-of-motion spin–flip59,60 CCSD (EOM-SF-CCSD) level of theory using the cc-pVTZ-PP basis set61 and the ECP28MDF pseudopotential61 on Ru/Rh and the cc-pVTZ basis set62 on C and H. To clarify relative energies, perturbative triples were added via single-point computations with the EOM-SF-CCSD using the perturbative Fock triples correction (fT)63 on optimized structures. The Q-Chem software package was utilized for the MP2, CCSD, and EOM computations, and the 4s and 4p electrons on Ru/Rh and the 1s electrons on C were frozen for the electron-correlation calculations. The ground triplet state was used as the spin–flip reference for [Rh,C,2H]+. For [Ru,C,2H]+, a peculiar symmetry restriction required special treatment: the effectively doubly degenerate ground quartet states of B1 and B2 symmetry led to independent (and also nearly degenerate) manifolds of spin–flip states. Therefore, both quartets were used as spin–flip references, and properties of both manifolds will be presented herein. In the asymmetric HRuCH+ configuration, the lowest 4A′′ state was used as the spin–flip reference. The structures of at least the two lowest-energy electronic states of each spin–flip transition symmetry were first optimized with the analogous cc-pVDZ-PP basis set, using a series of disparate starting structures. Stable structures were then re-optimized with the cc-pVTZ-PP basis, and harmonic zero-point corrections and spectra were computed. Total electronic densities, spin densities, 〈S2〉 values, and Mulliken spin populations and charges were computed with the resulting EOM-SF-CCSD wavefunctions. Constrained potential energy curves along the metal–carbene coordinate were also computed by optimizing the structure of the lowest-energy electronic state at a series of Rh–C(A1)/Ru–C(B1/B2) distances between 1.5 and 2.5 Å. The energies of all other electronic states were computed as vertical single-points from these structures. Here, adequate comparison of the predicted IR spectrum for [Rh,C,2H]+, but not [Ru,C,2H]+, with experiment required the use of frequency scaling factors, which are detailed below.
Results & discussion
Reactions between M+ (M = Ru, Rh) and oxirane resulted in the ionic products MC+, [M,C,2H]+, [M,O,2H]+ for both M, MO+ and [M,2C,2H]+ for M = Ru, and MH+, [M,C,3H]+, [M,C,O]+, and [M,C,O,H]+ for M = Rh. These product mass distributions are shown in Fig. S1 of the ESI.† Relative product intensities are dependent on the metal ion; for example, MO+ is fairly intense for Ru+, whereas it is barely visible for Rh+. A low-intensity RhH+ ion was also observed, but the reaction of ground-state Rh+ with c-C2H4O to form RhH+ + CH3CO (the lowest energy isomer) is endothermic by 0.95 ± 0.04 eV.40,64 It seems possible that this species is formed by reactions with contaminants, by electronically excited Rh+, or by trap loading at excess kinetic energy. Overall, we conclude that these reactions are likely to mainly generate species that can be formed exothermically from ground-state reactants, but some excess excitation energy may be available as well.IR spectroscopy of RuCH2+
Ruthenium has a complex isotopic distribution with natural abundances at 96 (5.5%), 98 (1.9%), 99 (13%), 100 (13%), 101 (17%), 102 (32%), and 104 (19%) amu. Fig. 1(a) shows the experimental IRMPD spectrum of [Ru,C,2H]+. The spectrum was recorded using two FEL settings, indicated by the trace colors, with overlap between 900–1200 cm−1. It is constructed using only the 101Ru and 102Ru isotopes (m/z 115, 116), using RuC+ as the only photofragment observed (m/z 113, 114, Fig. S2a, ESI†), consistent with the dissociation thermochemistry in Table 1. Mass isolation of m/z 115, 116 prior to IR irradiation leaves small amounts of 104RuC+ (m/z 116), 99RuO+ (m/z 115), 100RuO+ (m/z 116), and 98RuOH2+ (m/z 116), all of which can be distinguished at the mass resolution of the FT-ICR. Because these species cannot fragment into mass channels m/z 113, 114, their presence does not affect the spectrum of [Ru,C,2H]+. The spectrum of [Ru,C,2H]+ in Fig. 1(a) shows one dominant band peaking at 637 cm−1. The band extends a bit further into the blue with positions of submaxima at 778 and 987 cm−1, identified from fitting the bands with Gaussian functions.| Species | Fragments | Bond dissociation energy D0 (eV) | |
|---|---|---|---|
| Theorya | Experiment | ||
| a Theoretical values are calculated at the uB3LYP/def2-TZVPPD level of theory ignoring any barriers. b Uses D0(C–H2) = 3.320 ± 0.001 eV.40 c Ref. 37. d Ref. 65. e Ref. 32,41. f Ref. 42. | |||
| RuCH2+ | RuC+ + H2 | 1.15 | 0.72 ± 0.09bcd |
| Ru+ + CH2 | 3.73 | 3.57 ± 0.05c | |
| RhCH2+ | RhC+ + H2 | 1.29 | 2.76 ± 0.20be |
| Rh+ + CH2 | 3.60 | 3.69 ± 0.08,e 4.08 ± 0.22f | |
Fig. 1(b)–(h) shows the simulated IR spectra of different [Ru,C,2H]+ isomers and states calculated at the B3LYP level. Here, the 4B2 ground state (GS) is a symmetric ruthenium carbene geometry. With the convention that the z-axis is the symmetry axis and that the molecule lies in the yz plane, the 4B2 GS has a Ru–C σ bonding molecular orbital (MO) (a1 symmetry, using 4dz2 on Ru, double occupancy), a Ru–C π bond (b1, Ru 4dxz, double), three non-bonding MOs localized on Ru: (a1, 4dx2−y2, single; a2, 4dxy, double; a1, 5s, single), and an antibonding MO combining the Ru 4dyz and CH2 orbitals (b2, single). Thus, the valence MO occupation (excluding the four CH2 bonding electrons) is (1a1)2(1b1)2(2a1)1(1a2)2(3a1)1(1b2)1. These valence molecular orbitals are shown in Fig. S3 of the ESI.†
A second electronic state, 4B1, calculated to lie only 0.001 eV higher in energy, reverses the occupation of the 4dx2−y2 (2a1) and 4dxy (1a2) non-bonding orbitals, explaining the small energy difference between these two states. In another low-lying state (4A2), one electron in the non-bonding 4dxy (1a2) MO is transferred to the antibonding 1b2 MO, leading to decreased stability, 0.15 eV above the GS. Additional carbene structures were located for different spin states. The most stable doublet-spin ruthenium carbene is 2A2, 0.13 eV above the GS with the MO occupation of (1a1)2(1b1)2(2a1)2(1a2)1(3a1)0(1b2)2. Moving an electron between the 4dx2−y2 and 4dxy non-bonding orbitals results in a 2A1 state 0.16 eV above the GS. Energetics and selected orbital configurations of all stable [Ru,C,2H]+ species located computationally are listed in Table S1 of the ESI.†
Interestingly, early generalized valence bond (GVB) calculations of RuCH2+ by Carter and Goddard obtained a very different ordering of these states.66 They found a ground state of 2A2 with a nearly degenerate 2A1 state, followed by the three quartet states (4A2, 4B2, and 4B1) lying about 0.41 eV above the ground state, with a 2B2 state at 0.87 eV (see also Table S1, ESI†). However, they calculate a bond energy (De) at their most advanced level of theory of 2.95 eV and an estimated “exact” value of 3.19 eV, which is well below the experimentally observed values. In their analysis of the bonding of these states, they characterize the bonding in the doublet spin states as covalently bound “metal–methylidenes”, whereas the quartet states are viewed as “metal–carbenes” formed by σ-donor/π-acceptor interactions.
We checked for agostic carbene geometries in the DFT calculations, but these structures converged to symmetric carbenes. More interestingly, we did find a hydrido ruthenium carbyne geometry, HRuCH+, with planar Cs symmetry. This species has a 2A′ electronic state that lies only 0.029 eV above the GS, in agreement with previous theoretical results.37 The 4A′′ hydrido carbyne was found at 1.32 eV above the GS. The lowest-energy dihydrido ruthenium carbide, HHRuC+, is the 2A′ state lying 1.72 eV above the GS. The lowest-energy dihydrogen ruthenium carbide, (H2)RuC+, is the 2A′ state at 0.47 eV above the GS. The lowest-energy sextet species located is a 6A′ state, 1.43 eV higher in energy than the GS. This species exhibits the ruthenium carbene geometry, but both hydrogen atoms are bent slightly out of plane (dihedral angle H–H–Ru–C = 8.8°).
The B3LYP-generated IR spectrum for the 4B2 state of RuCH2+ is dominated by the CH2 rocking and wagging modes, which are calculated at 542 and 739 cm−1, respectively, Fig. 1(b). These vibrations are shifted to 441 and 865 cm−1 for the 4B1 state, where the CH2 rocking-mode intensity is decreased by a factor of seven while that of the CH2 wagging mode is increased by a factor of three. Thus, the spectra of the 4B1 and 4B2 states of RuCH2+ differ appreciably. Interestingly, MP2 calculations enhance the intensity of the Ru–C stretch, but CCSD calculations yield an intensity similar to that obtained by B3LYP. For example, for the 4B2 GS, the frequencies in cm−1 (intensities, km mol−1) for the stretch calculated at the B3LYP/CCSD levels are 655 (1)/660 (9) compared to MP2 at 648 (53). Other RuCH2+ states have similar comparisons. It seems plausible that the experimental spectrum could be reproduced by a superposition of the five low-lying RuCH2+ states (4B2, 4B1, 2A2, 4A2, and 2A1), all of which are accessible according to the B3LYP calculations (Fig. 1) because the reaction of Ru+ with oxirane is exothermic by 0.20 ± 0.05 eV. At the CCSD(T)//CCSD level of theory, these states lie 0.045, 0.044, 0.150, 0.091, and 0.134 eV, respectively (Table S1, ESI†), above the ground-state HRuCH+ species (see next paragraph), such that all five states could be formed exothermically.
Complicating the assignment of the experimental spectrum is the low energy of the HRuCH+ ground state. For the HRuCH+ (2A′) species, B3LYP predicts four modes below 1500 cm−1: an out-of-plane C–H bending mode (743 cm−1, c-type), two in-plane H–M–C–H bending modes (611 and 965 cm−1, both with mixed a- and b-type transition character), and the M–C stretch mode (1058 cm−1, a-type). The M–H and C–H stretch modes are calculated to lie above 2000 cm−1 and are thus out of the scope of our investigation. According to B3LYP theory, only the two low-frequency modes have appreciable intensities, and these transitions fall directly in line with the observed spectrum, Fig. 1(d). For this structure, MP2 calculations again enhance the intensities of these transitions and the other two modes in the experimentally observed window. In contrast, CCSD calculations yield results in good agreement with the relative intensities predicted by B3LYP, with frequencies of 622, 751, 974, and 1036 cm−1, Table 2. Where the B3LYP method puts this HRuCH+ state 0.029 eV above the RuCH2+ (4B2) state, CCSD(T)//CCSD and EOM-SF-CCSD(fT)/EOM-SF-CCSD calculations make it the ground state, lying 0.045 eV and 0.006 eV, respectively, below the 4B2 state. The role of perturbative triples corrections was found to be critical here, as both CCSD and EOM-SF-CCSD predicted the 4B states to be lower in energy without these corrections. The potential energy landscape of the EOM-SF-CCSD computed states is further clarified in Fig. S4 of the ESI.†
| Experiment | Theory B3LYP/CCSD/EOMa | Mode description | |||
|---|---|---|---|---|---|
| Frequency (cm−1) | Strength | Frequency (cm−1) | Intensity (km mol−1) | ||
| a B3LYP and CCSD calculations used the def2-TZVPPD basis set. EOM-SF-CCSD calculations used the cc-pVTZ-PP basis set and ECP28MDF core potential on the metal and cc-pVTZ on the C/H atoms. | |||||
| RuCH2+ (4B2) | 542/534/508 | 27/34/33 | CH2 rock | ||
| 637 | s | 655/660/649 | 1/9/10 | M–C stretch | |
| 778 | s | 739/731/765 | 42/49/62 | CH2 wag | |
| 987 | m | 1313/1343/1336 | 0/0/2 | CH2 scissor | |
| RuCH2+ (4B1) | 441/516/489 | 4/22/23 | CH2 rock | ||
| 637 | s | 651/659/648 | 1/9/10 | M–C stretch | |
| 778 | s | 865/759/781 | 115/64/72 | CH2 wag | |
| 987 | m | 1310/1341/1335 | 0/0/3 | CH2 scissor | |
| RuCH2+ (2A2) | 568/597/388 | 0/1/31 | CH2 rock | ||
| 637 | s | 734/739/745 | 8/0/3 | M–C stretch | |
| 778 | s | 933/924/947 | 59/65/67 | CH2 wag | |
| 987 | m | 1397/1413/1360 | 3/2/0 | CH2 scissor | |
| RuCH2+ (2A1) | 566/593/470 | 0/1/1 | CH2 rock | ||
| 637 | s | 766/749/747 | 8/0/0 | M–C stretch | |
| 778 | s | 946/925/942 | 59/64/69 | CH2 wag | |
| 987 | m | 1401/1415/1413 | 3/2/3 | CH2 scissor | |
| RuCH2+ (4A2) | 703/517/471 | 25/22/1 | CH2 rock | ||
| 637 | s | 667/647/490 | 1/8/30 | M–C stretch | |
| 778 | s | 980/766/689 | 104/58/0 | CH2 wag | |
| 987 | m | 1407/1352/1334 | 4/1/13 | CH2 scissor | |
| HRuCH+ (2A′) | 637 | s | 611/622/633 | 92/97/94 | HMCH ip bend |
| 778 | s | 743/751/718 | 91/94/121 | C–H oop bend | |
| 987 | m | 965/974/1003 | 1/1/3 | HMCH ip bend | |
| 1058/1036/1102 | 5/3/3 | M–C stretch | |||
| RhCH2+ (1A1) | 774 | s | 606/624/600 | 0/1/1 | CH2 rock |
| 904 | s | 793/748/819 | 13/1/28 | M–C stretch | |
| 1029 | s | 964/971/964 | 57/65/83 | CH2 wag | |
| 1269 | m | 1386/1408/1386 | 4/1/19 | CH2 scissor | |
| 1783 | s | Overtone | |||
| RhCH2+ (3A2) | 774 | s | 646/627/657 | 8/21/6 | CH2 rock |
| 904 | s | 674/674/669 | 21/27/28 | M–C stretch | |
| 1029 | s | 942/933/948 | 89/110/125 | CH2 wag | |
| 1269 | m | 1396/1431/1425 | 5/2/2 | CH2 scissor | |
| 1783 | s | Overtone | |||
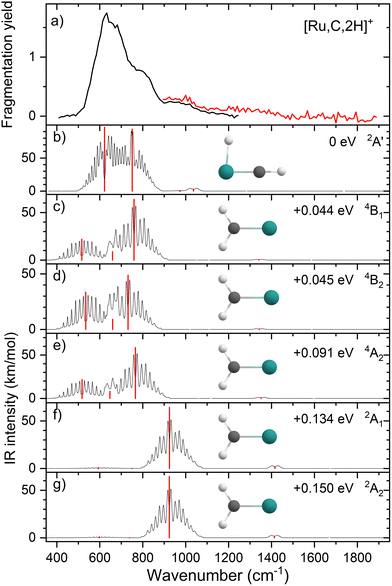
Comparisons of the predicted CCSD and EOM-SF-CCSD spectra for the low-lying states with the experimental spectrum are shown in Fig. 2 and 3, respectively. We conclude that the HRuCH+ species is present and captures the main feature at 637 cm−1, but does not capture the full shape of the 637 and 778 cm−1 structure. CCSD, with the pure vibrational splitting of the bright transitions in the HRuCH+ (2A′) spectrum of 622 and 751 cm−1, can account for both features, but does not provide the peak intensity for the 637 cm−1 band, whereas EOM (633 and 718 cm−1) is not sufficient to capture the peak at 778 cm−1. Moreover, neither method can explain the broad band observed at 987 cm−1.
We, therefore, consider additional contributors to the unique lineshape observed experimentally for RuCH2+. One option is that the 2A1 and 2A2 states account for the 987-cm−1 transition. For the EOM computations, the combination of the spectra for these states with that for HRuCH+ (2A′) would lead to two bands, roughly centered at 700 and 950 cm−1, respectively, but a large drop in the predicted spectral brightness between them (see Fig. S5 in the ESI†). For CCSD results, a more reasonable, continuous band is formed, but the intensity for the 978 cm−1 band is comparable to that near 637 cm−1. Energetically, inclusion of these A states is plausible given the 0.20 ± 0.05 eV experimental exothermicity of the Ru+ + oxirane reaction. A more reasonable solution is to include both 2A1/2A2 states and the 4B1/4B2 states. In both the EOM and CCSD computations, such a combination appears satisfactory to explain the observed spectral substructure, although a minor point of criticism is predicted intensity below 500 cm−1 (originating from the 4B1/4B2 states), in contrast to the experimental spectrum (Fig. S5, ESI†). It seems likely that an enhanced contribution of the ground state HRuCH+ (2A′) would provide an even better reproduction of the experimental bands observed and also suppress the tail to the red of 500 cm−1. A final, unambiguous assignment of this spectrum remains challenging because of the rotational widths and possibility of multiple-photon effects.
IR spectroscopy of RhCH2+
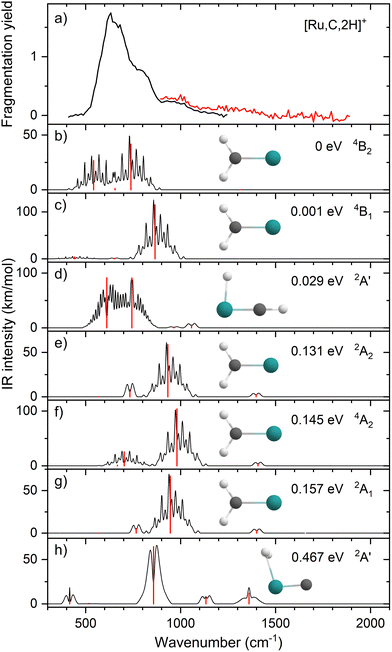
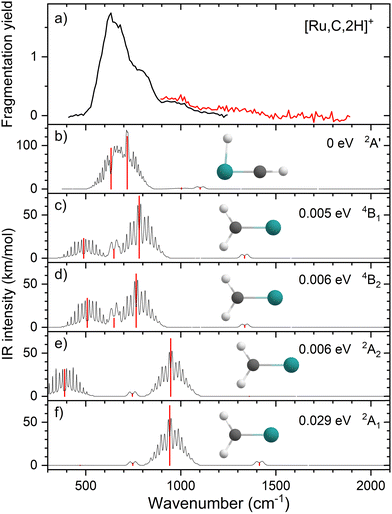
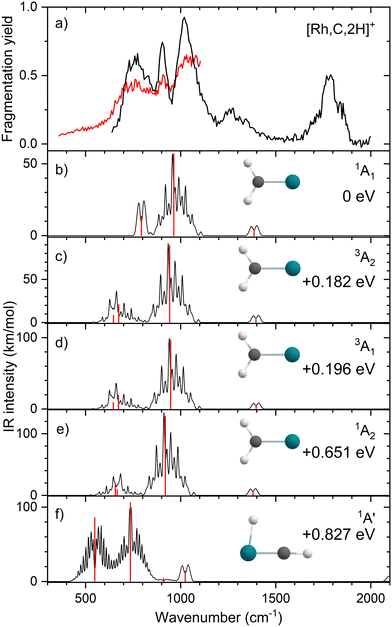
Upon photofragmentation of [Rh,C,2H]+ (m/z 117), RhC+ was the only fragment observed, as shown in Fig. S2b (ES), consistent with the thermochemistry in Table 1. The experimental IRMPD spectrum of [Rh,C,2H]+ is shown in Fig. 4(a). The spectra were recorded in cell 4 (black trace, lowest IR fluence) and cell 1 (red trace, higher IR fluence). In contrast to the more poorly resolved, one-band-dominated spectrum for Ru, we observed five distinct IR bands: a triad of three strong bands at 774, 904, and 1029 cm−1, with a relatively well-resolved satellite band of medium intensity at 1269 cm−1 and a clear, relatively intense band at 1783 cm−1. The five experimental bands for the rhodium species are more than the three bands observed for the ruthenium species, which could potentially indicate the formation of multiple species. Also, the narrow width of the band observed at 904 cm−1 is striking as it is much sharper than the bands observed for the Ru species. The structure observed under the lower fluence conditions (black trace) slightly broadens when using a significantly increased laser fluence (red trace) but remains clearly distinguishable, which is at odds with the Ru species where only drastic broadening was observed at higher fluence. In addition, the rhodium species has experimental bands at much higher frequencies than found for [Ru,C,2H]+.Fig. 4(b)–(f) shows the B3LYP-simulated IR spectra of different [Rh,C,2H]+ isomers and states. The 1A1 ground state has the symmetric rhodium carbene geometry with C2v symmetry and a valence MO occupation of (1a1)2(1b1)2(2a1)2(1a2)2(3a1)0(1b2)2. This configuration is markedly different from the Ru case, as this species has a ground state with multiple unpaired electrons on the metal center, including an electron in the 3a1 (5s-like) orbital. In contrast, the RhCH2+ GS clearly has no unpaired electrons nor any electrons in the 5s orbital. Identification of the true ground state was complicated by finding another 1A1 state that differed from that shown because the 2a1 (4dx2−y2) and 1a2 (4dxy) orbitals were mixed, leading to a lower energy by 0.020 eV. This outcome is an artifact of the B3LYP calculation, as demonstrated by the EOM calculations described below.
The lowest-energy triplet species for [Rh,C,2H]+ according to the B3LYP method is a symmetric carbene with a 3A2 state and lies only 0.18 eV above the GS. This 3A2 state has one electron in the 4dxy (1a2) orbital, two electrons in the 4dx2−y2 (2a1) orbital, and one electron in the 5s (3a1) orbital. A 3A1 state, slightly higher in energy at 0.20 eV above the GS, has two electrons in the 4dxy orbital, one electron in the 4dx2−y2 orbital, and one electron in the 5s orbital. We find two singlet carbene states with 5s occupancy at 0.65 eV (1A2) and 0.66 eV (1A1), Table S1 (ESI†), and the lowest-energy quintet at 1.78 eV above the GS. Hydrido rhodium carbyne structures are found at 0.83 eV (1A′) and 1.53 eV (3A′) above the GS. The lowest-energy dihydrido rhodium carbide (3A′′) lies 3.42 eV above the GS, while the lowest energy dihydrogen rhodium carbide (1A′) is 0.79 eV above the GS. The energetically preferred geometry is thus clearly a symmetric carbene.
The calculated IR spectra of the 1A1 and 3A2 states exhibit moderately intense bands for the Rh–C stretch (a narrow a-type transition, 13 and 21 km mol−1) and strong bands for the out-of-plane CH2 wag (a broad b-type transition, 57 and 89 km mol−1), whereas the in-plane CH2 rock and scissors modes are relatively weak with intensities <10 km mol−1. The two states differ mainly in the frequency of the Rh–C stretch vibration, which is 793 cm−1 for the 1A1 GS and 674 cm−1 for the 3A2 state, Table 2. Both states have similar CH2 wag frequencies of 964 and 942 cm−1, respectively. In comparison to the Ru carbene cation, the Rh–C stretch vibration is calculated to have a significantly higher IR intensity. The three intense bands calculated at 674, 793, and 964/942 cm−1 could conceivably match the three main peaks observed experimentally, but they are systematically shifted to lower frequencies. The band observed at 1269 cm−1 could be associated with the RhCH2+ scissor vibration, but conceivably has components of overtones of the in-plane CH2 rock (606/646 cm−1). Likewise, the band observed at 1783 cm−1 seems likely to be either a combination band or an overtone, as found earlier for a similar system.19 An anharmonic frequency calculation, using the second-order vibrational perturbation theory (VPT2) method67,68 and the same B3LYP/def2-TZVPPD potential energy surface, places the CH2 wagging overtone at 1892 cm−1 with an intensity of 1.3 km mol−1, and the combination band of the CH2 rocking and scissoring modes at 1918 cm−1 with a similar intensity. The strong intensity with which this band is experimentally found is remarkable, but it could be attributed to a higher IRMPD efficiency for higher photon energies.
Fig. 4(f) shows the spectrum calculated for the hydrido carbyne HRhCH+ species, which has a 1A′ ground state. This species is found at fairly high energy, 0.83 eV above RhCH2+ (1A1), which would make its formation unlikely. Further, it exhibits two strong bands at 548 and 736 cm−1 that do not match the experimental spectrum. From a spectroscopic point of view, the possibility that this species has a small population cannot be eliminated, in particular because the predicted low-frequency band could explain the small intensity near 500 cm−1 observed in the high-intensity (red) IR spectrum. However, it is clear that the majority of the spectrum must be associated with low-energy carbene species. This conclusion is even more evident from the more advanced theoretical results found in the next section.
EOM-SF-CCSD results for RhCH2+
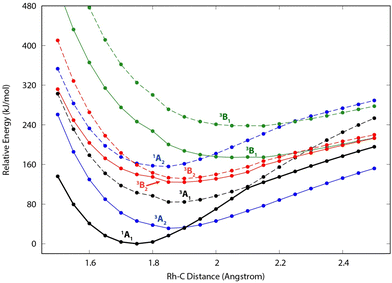
Because of the unusual spectrum for the [Rh,C,2H]+ species and the difficulty in assigning the ground state computed with the B3LYP level of theory, we also explored more advanced EOM-SF-CCSD calculations. The potential energy curves along the Rh–C coordinate, shown in Fig. 5, indicate a manifold of electronic states for the carbene species with many curve crossings (with relative energies at the equilibrium Rh–C distances listed in Table 3). In particular, the 1A1 ground-state potential crosses the 3A2 potential near 1.9 Å, which also nearly coincides with the minimum in the latter state. Furthermore, the ground state also exhibits an avoided crossing with the next-lowest A1 state (3A1) near 2.1 Å. Such interactions are likely to explain why the single-reference calculations encountered substantial difficulties in establishing the structures and electronic state of this species. Even the ground 1A1 state exhibited notable open-shell singlet character in these EOM-SF computations, with Mulliken spin populations (using the EOM-SF-CCSD wavefunctions) of −0.38 and +0.38 on the Rh and CH2 subunits, respectively. This outcome is consistent with the spin density depicted in Fig. S6 of the ESI.† Notably, although previous computational studies of RhCH2+ correctly identified the 1A1 ground state and 3A2 first excited state,43,44 the role of multireference character in the ground state has not been fully appreciated, particularly as the Rh+–CH2 bond is stretched.| Structure | State | E rel (eV) | E rel + ZPE (eV) | 〈S2〉 |
|---|---|---|---|---|
| a Significant remnant spin contamination in EOM-SF-CCSD state. b Species corresponds to a transition state in C2v symmetry. c Finite-difference frequency alternated electronic states; no ZPE correction available. | ||||
| RuCH2+ | 4B1 | 0.000 | 0.000 [0.005] | 4.098 |
| 4B2 | 0.001 | 0.001 [0.006] | 4.101 | |
| 2A2 | 0.010 | 0.012 [0.006] | 0.967 | |
| 2A1 | 0.021 | 0.036 [0.029] | 0.938 | |
| 4A2 | 1.036 | 1.018 [1.013] | 2.835a | |
| HRuCH+ | 2A′ | 0.119 | 0.072 [0.000] | 0.967 |
| RhCH2+ | 1A1 | 0.000 | 0.000 [0.000] | 0.244 |
| RhCH2+ | 3A2 | 0.296 | 0.295 [0.312] | 2.251 |
| (H2)RhC+ (Cs) | 1A1 | 0.795 | 0.636 [0.570] | 0.149 |
| RhCH2+ | 3A1 | 0.833 | 0.833 [0.764] | 1.556a |
| HRhCH+ | 1A′ | 0.947 | 0.895 [0.785] | 0.256 |
| RhCH2+ | 3B2 | 1.271 | 1.242 [1.185] | 1.355a |
| RhCH2+ | 3B2 | 1.358 | 1.355 [1.272] | 1.137b |
| RhCH2+ | 1A2 | 1.594 | 1.598 [1.569] | 0.277 |
| RhCH2+ | 3B1 | 1.761 | —c | 1.546a |
| HRhCH+ | 3A′′ | 2.080 | 2.012 [1.958] | 2.011 |
| RhCH2+ | 3B2 | 2.430 | 2.392 [2.315] | 1.493a |
| (H2)RhC+ (Cs) | 3A′′ | 3.189 | 3.020 [2.878] | 1.144a |
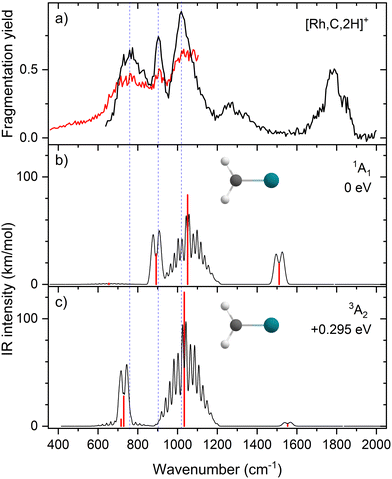
The EOM results identified eleven distinct species (some of which are excited states of a given symmetry): several RhCH2+ carbenes along with (H2)RhC+ (1A1) and HRhCH+ (1A′ and 1,3A′′) structures (Table 3). On the basis of these calculations, the 1A1 and 3A2 carbenes seem to be the likely candidates for formation in the experiments conducted here. The vibrational spectra of these two states are similar to those found at the B3LYP level, although the Rh–C stretch intensity is notably enhanced, particularly in the ground-state singlet, as listed in Table 2. The combination of these two species results in a spectrum that reproduces the three strong bands observed experimentally, as shown in Fig. 6 where the frequencies have been scaled by a factor 1.09, resulting in a blue-shift of about 90 cm−1. (The scaling factor of 1.09 is chosen to best match the experimental spectrum. The comparison to the unshifted spectrum is shown in Fig. S7 of the ESI.†) The spectrum computed for the 3A2 carbene may even rationalize the larger spectral width of the band observed at 774 cm−1 compared to the 904 cm−1 band. This is because the Rh–C stretch for the 1A1 species is isolated whereas the same mode for the 3A2 state, at 668 cm−1, nearly overlaps with the more intense CH2 rocking mode. Cooperative excitation of these bands could lead to the broadening observed, especially in the high-fluence spectrum. The assignment of the additional bands observed experimentally at higher wavenumbers remains inconclusive but seems likely to be the overtones identified above, similar to the overtone band previously found in the spectrum of PtCH2+.18,19
Although a systematic methodology comparison is not the focus of the present study, we note anecdotally that the more recently developed, range-separated hybrid functional ωB97M-V69 was found to exhibit harmonic frequencies and intensities that are notably more closely aligned with the EOM-based spectra (Fig. S8 of the ESI†). This functional may serve as a more accurate, cost-efficient method for future studies of this complex, although the state selectivity of the EOM methods provides considerably more control over the targeted electronic states.
Given the relative success of this alternative functional for [Rh,C,2H]+, the spectra of [Ru,C,2H]+ were also reexamined with ωB97M-V/cc-pVTZ-PP. The density functional encouragingly exhibited harmonic spectra for [Ru,C,2H]+ (Fig. S9 of the ESI†) that were quite similar to those computed by CCSD (Fig. 2). However, the energy of the HRuCH+ 2A′ state was computed to be more than 0.6 eV above the ground 4B2 state, in stark contrast to the results of CCSD(T) and EOM-SF-CCSD(fT) where it is the ground state structure. Simultaneously capturing both the overall energy landscape and the nuanced shape of the potential energy surface near equilibrium evidently remains a daunting challenge for density functional theory for these ionic transition-metal complexes.
DFT performance for prediction of M–C stretch vibrational intensities
Judging from the comparison between the B3LYP-, CCSD-, and EOM-SF-CCSD-calculated spectra for RuCH2+ (Table 2), the drastic underestimation of the IR intensities identified for the FeCH2+ and CoCH2+ species45 remains evident for this system. For the quartet spin carbenes, B3LYP predicts intensities for the Ru–CH2 stretch vibration that are an order of magnitude smaller than the CCSD and EOM-SF-CCSD calculations. Only for the 2A2 state does B3LYP predict an intensity for this stretch that is comparable to the EOM-SF-CCSD result. However, the concluded presence of the HRuCH+ species makes it complex to test this observation on the basis of comparison with experiment. Because the latter species is identified from dominant bands associated with bending modes, which are less sensitive to potential underestimations of charge separation, the RuCH2+ species cannot form a good theoretical benchmark.On the other hand, comparison of the computed spectra for the 1A1 and 3A2 RhCH2+ species suggests that the single-reference B3LYP method does not underperform compared to the CCSD/EOM approaches for frequencies (Table 2). Comparison with experiment would require an anomalous scaling factor for the B3LYP spectra compared with previous work. For IR intensities, the enhanced intensities of the Rh–C stretch found by EOM-SF-CCSD method helped solidify the assignment of the spectra (in particular, the bands at 774 and 904 cm−1). Of course, the vicinity of so many low-lying electronic states clearly complicates finding the experimental ground states.
Group 8 and 9 trends: carbene versus hydrido carbyne structures
In previous work, we have presented the experimental IRMPD spectra of [Os,C,2H]+ and [Ir,C,2H]+.18–20,22 We concluded that the osmium species had the hydrido carbyne HOsCH+ structure, as did the iridium species, which exhibited small amounts of a higher-energy, symmetric carbene, as well. If we put the current assignments for Ru and Rh in perspective with these previous findings, we note that both 5d elements prefer the formation of a hydrido carbyne structure, whereas the 4d Ru forms both this and a carbene species and Rh yields only the carbene. As shown in Table 4, the 5d hydrido carbynes are energetically preferred, but more strongly so for the group 8 Os case. This observation is consistent with the assignment of HOsCH+ (2A′), whereas part of the product for iridium (group 9) is assigned to a carbene structure (0.3 or 0.7 eV higher in energy). This trend appears to hold for 4d elements, where the RuCH2+ (4B2) carbene is competitive with the 2A′ HRuCH+ hydrido carbyne, whereas HRhCH+ (1A′) is significantly higher in energy than RhCH2+ (1A1). Intrinsically, the 5d TMs have stronger bonds to C and H than the 4d TMs, e.g., for group 9, see Fig. 4 in ref. 13. (For group 8, see ref. 16, 37, 70 and 65). Because HMCH+ has four covalent bonds to the metal whereas MCH2+ only has two covalent M–C bonds, the more highly coordinated hydrido carbyne structure becomes more favorable for 5d relative to 4d TMs.| M | B3LYP | CCSD(T)//CCSD |
|---|---|---|
| Ru | 0.03 | −0.005 |
| Rh | 0.80 | 0.76 |
| Os | −0.50 | −0.82 |
| Ir | −0.30 | −0.69 |
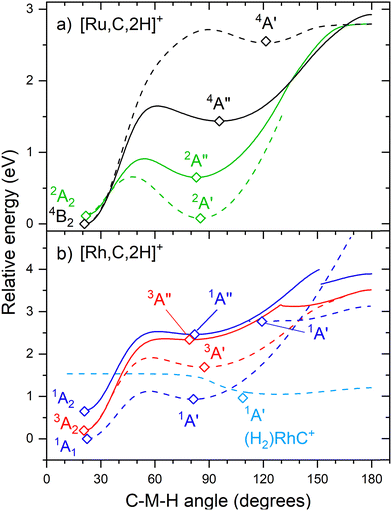
The hydrido carbyne structures for 4d and 5d elements are found on the same or a lower spin surface as that of the lowest-energy carbene structure. To investigate whether we might have missed hydrido carbyne structures, the potential energy surfaces (PESs) connecting the MCH2+ and HMCH+ structures were calculated for M = Ru and Rh (Fig. 7) with B3LYP. PESs were generated by starting from a symmetric carbene structure and systematically increasing the C–M–H angle while the rest of the molecule was allowed to relax. The PES scans were generated for both the A′ and A′′ configurations in dashed and solid lines, respectively. The PESs for Ru and Rh show clear minima and appreciable barriers for H migration from the metal to carbon. Here again, the higher stability of carbyne structures for Ru in comparison to Rh is clearly visible.
Conclusion
Reacting the 4d group 8 and 9 transition metal ions M+ (M = Ru and Rh) with oxirane in a room temperature ion trap led to the formation of [M,C,2H]+. These species were mass-isolated in the FTICR mass spectrometer coupled to the infrared intracavity free-electron laser FELICE, where they were spectroscopically characterized. The IRMPD spectrum of [Ru,C,2H]+ contains one broad band around 700 cm−1, whereas the IRMPD spectrum of [Rh,C,2H]+ is characterized by much sharper, distinct bands. On the basis of B3LYP and CCSD(T)//CCSD energetics, the [Rh,C,2H]+ species is expected to be a carbene, and for [Ru,C,2H]+, a competitive hydrido carbyne structure is also found. Comparison of the experimental IRMPD spectra with the predictions from B3LYP calculations offers moderate agreement. Calculations at the CCSD and EOM-SF-CCSD levels offer a modest improvement, but also show how sensitive an experimental constraint the spectroscopic fingerprint provides for these electronically complex systems. These comparisons suggest the presence of the HRuCH+ species, with contributions from RuCH2+ carbenes. The case of [Rh,C,2H]+ offers a similar complexity. Despite the much more structured experimental IR spectrum, assignment based on either B3LYP or conventional CCSD simulations is difficult. Because population of the energetically close singlet and triplet spin surfaces could significantly influence the behavior of this species and because of moderately strong state mixing within the singlet manifold, EOM-SF-CCSD calculations were performed. These computational results suggest that a combination of the (partially open-shell) 1A1 and 3A2 carbenes can explain the complex structure of the [Rh,C,2H]+ spectrum. Notably, including the multireference character of this species was critical in properly assigning the spectrum, but a modest shift in the calculated harmonic frequencies was still required to match experiment.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work was funded by NWO's Materials for Sustainability program (grant no. 739.017.008). We gratefully acknowledge the Nederlandse Organisatie voor Wetenschappelijk Onderzoek (NWO) for the support of the FELIX Laboratory and for CPU time on the Dutch National Supercomputers Cartesius and Snellius (project number 2021.055). Additional financial support was provided by the National Science Foundation (grant no. CHE-2313553) and by a generous grant of computer time from the Center for High-Performance Computing at the University of Utah. RPS acknowledges funding from the U.S. Department of Energy under Grant DE-SC0019405 and helpful conversations regarding EOM methods with Prof. Anna Krylov.References
- R. H. Crabtree, Organometallic alkane CH activation, J. Organomet. Chem., 2004, 689, 4083–4091 CrossRef CAS.
- K. L. Stone and A. S. Borovik, Lessons from Nature: Unraveling Biological C–H Bond Activation, Curr. Opin. Chem. Biol., 2009, 13, 114–118 CrossRef CAS PubMed.
- D. K. Böhme and H. Schwarz, Gas-Phase Catalysis by Atomic and Cluster Metal Ions: The Ultimate Single-Site Catalysts, Angew. Chem., Int. Ed., 2005, 44, 2336–2354 CrossRef PubMed.
- J. Roithová and D. Schröder, Selective Activation of Alkanes by Gas-Phase Metal Ions, Chem. Rev., 2010, 110, 1170–1211 CrossRef PubMed.
- J. Sauer and H. J. Freund, Models in Catalysis, Catal. Lett., 2015, 145, 109–125 CrossRef CAS.
- S. W. Buckner, T. J. MacMahon, G. D. Byrd and B. S. Freiser, Gas-Phase Reactions of Nb+ and Ta+ with Alkanes and Alkenes. C–H Bond Activation and Ligand-Coupling Mechanisms, Inorg. Chem., 1989, 28, 3511–3518 CrossRef CAS.
- K. K. Irikura and J. L. Beauchamp, Osmium Tetroxide and Its Fragment Ions in the Gas Phase: Reactivity with Hydrocarbons and Small Molecules, J. Am. Chem. Soc., 1989, 111, 75–85 CrossRef CAS.
- K. K. Irikura and J. L. Beauchamp, Electronic Structure Considerations for Methane Activation by Third-row Transition-metal Ions, J. Phys. Chem., 1991, 95, 8344–8351 CrossRef CAS.
- K. K. Irikura and J. L. Beauchamp, Methane Oligomerization in the Gas Phase by Third-Row Transition-Metal Ions, J. Am. Chem. Soc., 1991, 113, 2769–2770 CrossRef CAS.
- U. Achatz, M. Beyer, S. Joos, B. S. Fox, G. Niedner-Schatteburg and V. E. Bondybey, The Platinum Hydrido-Methyl Complex: A Frozen Reaction Intermediate?, J. Phys. Chem. A, 1999, 103, 8200–8206 CrossRef CAS.
- X.-G. Zhang, R. Liyanage and P. B. Armentrout, The Potential Energy Surface for Activation of Methane by Pt+: A Detailed Guided-Ion Beam Study, J. Am. Chem. Soc., 2001, 123, 5563–5575 CrossRef CAS PubMed.
- P. B. Armentrout, S. Shin and R. Liyanage, Guided-Ion Beam and Theoretical Study of the Potential Energy Surface for Activation of Methane by W+, J. Phys. Chem. A, 2006, 110, 1242–1260 CrossRef CAS PubMed.
- F.-X. Li, X.-G. Zhang and P. B. Armentrout, The Most Reactive Third-row Transition Metal: Guided Ion Beam and Theoretical Studies of the Activation of Methane by Ir+, Int. J. Mass Spectrom., 2006, 255–256, 279–300 CrossRef CAS.
- L. G. Parke, C. S. Hinton and P. B. Armentrout, Experimental and Theoretical Studies of the Activation of Methane by Ta+ and the Bond Energies of Ta+–CHx (x = 1–3), J. Phys. Chem. C, 2007, 111, 17773–17787 CrossRef CAS.
- A. Shayesteh, V. V. Lavrov, G. K. Koyanagi and D. K. Böhme, Reactions of Atomic Cations with Methane: Gas Phase Room-Temperature Kinetics and Periodicities in Reactivity, J. Phys. Chem. A, 2009, 113, 5602–5611 CrossRef CAS PubMed.
- P. B. Armentrout, L. Parke, C. Hinton and M. Citir, Activation of Methane by Os+: Guided Ion Beam and Theoretical Studies, ChemPlusChem, 2013, 78, 1157–1173 CrossRef CAS PubMed.
- P. B. Armentrout, Methane Activation by 5d Transition Metals: Energetics, Mechanisms, and Periodic Trends, Chem. – Eur. J., 2017, 23, 10–18 CrossRef CAS PubMed.
- V. J. F. Lapoutre, B. Redlich, A. F. G. van der Meer, J. Oomens, J. M. Bakker, A. Sweeney, A. Mookherjee and P. B. Armentrout, Structures of the Dehydrogenation Products of Methane Activation by 5d Transition Metal Cations, J. Phys. Chem. A, 2013, 117, 4115–4126 CrossRef CAS PubMed.
- C. J. Owen, G. C. Boles, V. Chernyy, J. M. Bakker and P. B. Armentrout, Structures of the Dehydrogenation Products of Methane Activation by 5d Transition Metal Cations Revisited: Deuterium Labeling and Rotational Contours, J. Chem. Phys., 2018, 148, 044307 CrossRef PubMed.
- J. M. Bakker, C. J. Owen, S. W. Nooteboom, O. V. Lushchikova and P. B. Armentrout, Structural characterization of [M,C,2H]+ products formed by reaction of 5d metal cations Pt+ and Ir+ with ethylene oxide and Ta+ with methane using messenger spectroscopy, J. Mol. Spectrosc., 2021, 378, 111472 CrossRef CAS.
- F. J. Wensink, N. Roos, J. M. Bakker and P. B. Armentrout, C–H Bond Activation and C–C Coupling of Methane on a Single Cationic Platinum Center: A Spectroscopic and Theoretical Study, Inorg. Chem., 2022, 61, 11252–11260 CrossRef CAS PubMed.
- P. B. Armentrout, S. Kuijpers, O. V. Lushchikova, R. L. Hightower, G. C. Boles and J. M. Bakker, Spectroscopic Identification of the Carbyne Hydride Structure of the Dehydrogenation Product of Methane Activation by Osmium Cations, J. Am. Soc. Mass Spectrom., 2018, 29, 1781–1791 CrossRef CAS PubMed.
- J. K. Perry, G. Ohanessian and W. A. Goddard, Mechanism and Energetics for Dehydrogenation of Methane by Gaseous Iridium Ions, Organometallics, 1994, 13, 1870–1877 CrossRef CAS.
- L. F. Halle, P. B. Armentrout and J. L. Beauchamp, Formation of Chromium Carbene Ions by Reaction of Electronically Excited Chromium Ions with Methane in the Gas Phase, J. Am. Chem. Soc., 1981, 103, 962–963 CrossRef CAS.
- N. Aristov and P. B. Armentrout, Methane Activation by V+: Electronic and Translational Energy Dependence, J. Phys. Chem., 1987, 91, 6178–6188 CrossRef CAS.
- R. H. Schultz, J. L. Elkind and P. B. Armentrout, Electronic Effects in C-H and C-C Bond Activation: State-specific Reactions of Fe+(6D, 4F) with Methane, Ethane and Propane, J. Am. Chem. Soc., 1988, 110, 411–423 CrossRef CAS.
- L. S. Sunderlin and P. B. Armentrout, Methane Activation by Ti+: Electronic and Translational Energy Dependence, J. Phys. Chem., 1988, 92, 1209–1219 CrossRef CAS.
- R. Georgiadis and P. B. Armentrout, Translational and Electronic Energy Dependence of Chromium Ion Reactions with Methane, J. Phys. Chem., 1988, 92, 7067–7074 CrossRef CAS.
- L. S. Sunderlin and P. B. Armentrout, Periodic Trends in Chemical Reactivity: Reactions of Sc+, Y+, La+, and Lu+ with Methane and Ethane, J. Am. Chem. Soc., 1989, 111, 3845–3855 CrossRef CAS.
- R. Georgiadis and P. B. Armentrout, Translational and Electronic Energy Dependence of the Reaction of Mn+ with Ethane, Int. J. Mass Spectrom. Ion Processes, 1989, 91, 123–133 CrossRef CAS.
- C. L. Haynes, Y.-M. Chen and P. B. Armentrout, The Potential Energy Surface for Activation of Methane by Co+: An Experimental Study, J. Phys. Chem., 1995, 99, 9110–9117 CrossRef CAS.
- Y.-M. Chen and P. B. Armentrout, Activation of Methane by Gas-Phase Rh+, J. Phys. Chem., 1995, 99, 10775–10779 CrossRef CAS.
- Y.-M. Chen, M. R. Sievers and P. B. Armentrout, Activation of CH4, C2H6, C3H8, and c-C3H6 by Gas-phase Pd+ and the Thermochemistry of Pd–ligand Complexes, Int. J. Mass Spectrom. Ion Processes, 1997, 167–168, 195–212 Search PubMed.
- M. R. Sievers, Y.-M. Chen, C. L. Haynes and P. B. Armentrout, Activation of CH4, C2H6, and C3H8 by Gas-Phase Nb+ and the Thermochemistry of Nb–ligand Complexes, Int. J. Mass Spectrom., 2000, 195–196, 149–170 CrossRef.
- F. Liu, X.-G. Zhang and P. B. Armentrout, Activation of CH4 by Gas-phase Ni+ and the Thermochemistry of Ni Ligand Complexes, Phys. Chem. Chem. Phys., 2005, 7, 1054–1064 RSC.
- P. B. Armentrout, Activation of CH4 by Gas-phase Mo+ and the Thermochemistry of Mo–ligand Complexes, J. Phys. Chem. A, 2006, 110, 8327–8338 CrossRef CAS PubMed.
- P. B. Armentrout and Y.-M. Chen, Activation of Methane by Ru+: Experimental and Theoretical Studies of the Thermochemistry and Mechanism, Int. J. Mass Spectrom., 2016, 413, 135–149 CrossRef.
- P. B. Armentrout and M. R. Sievers, Activation of CH4 by Gas-phase Zr+ and the Thermochemistry of Zr ligand Complexes, J. Phys. Chem. A, 2003, 107, 4396–4406 CrossRef CAS.
- P. B. Armentrout, L. S. Sunderlin and E. R. Fisher, Intrinsic Transition Metal–Carbon Double Bond Dissociation Energies: Periodic Trends in M+–CH2 Bond Strengths, Inorg. Chem., 1989, 28, 4436–4437 CrossRef CAS.
- B. Ruscic and D. H. Bross, Active Thermochemical Tables (ATcT) values based on ver. 1.130 of the Thermochemical Network, available at ATcT.anl.gov (accessed 2/12/24).
- Y.-M. Chen and P. B. Armentrout, Activation of C2H6, C3H8, and c-C3H6 by Gas-phase Rh+ and the Thermochemistry of Rh–ligand Complexes, J. Am. Chem. Soc., 1995, 117, 9291–9304 CrossRef CAS.
- D. B. Jacobson and B. S. Freiser, Transition-metal-carbene chemistry. Structure, thermodynamics, and reactivity of rhodium methylidene ion (RhCH2+) in the gas phase, J. Am. Chem. Soc., 1985, 107, 5870–5876 CrossRef CAS.
- D. G. Musaev, N. Koga and K. Morokuma, Ab initio molecular orbital study of the electronic and geometric structure of RhCH2+ and the reaction mechanism: RhCH2+ + H2 → Rh+ + CH4, J. Phys. Chem., 1993, 97, 4064–4075 CrossRef CAS.
- J. Westerberg and M. R. A. Blomberg, Methane Activation by Naked Rh+ Atoms. A Theoretical Study, J. Phys. Chem. A, 1998, 102, 7303–7307 CrossRef CAS.
- F. J. Wensink, C. E. Smink, J. M. Bakker and P. B. Armentrout, IR spectroscopic characterization of 3d transition metal carbene cations, FeCH2+ and CoCH2+: A failure of DFT approaches, Phys. Chem. Chem. Phys., 2024 10.1039/D4CP00026A.
- F. J. Wensink, M. G. Münst, J. Heller, M. Ončák, J. M. Bakker and C. Van Der Linde, IR Multiple Photon Dissociation Spectroscopy of MO2+ (M = V, Nb, Ta), J. Chem. Phys., 2020, 153(17), 171101 CrossRef CAS PubMed.
- C. Berg, T. Schindler, G. Niedner-Schatteburg and V. E. Bondybey, Reactions of Simple Hydrocarbons with Nbn+: Chemisorption and Physisorption on Ionized Niobium Clusters, J. Chem. Phys., 1995, 102, 4870–4884 CrossRef CAS.
- A. G. Marshall, C. L. Hendrickson and G. S. Jackson, Fourier Transform Ion Cyclotron Resonance Mass Spectrometry: A Primer, Mass Spectrom. Rev., 1998, 17, 1–35 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson and H. Nakatsuji, et al., Gaussian 16 Rev. C.01, Wallingford, CT, 2016 Search PubMed.
- A. D. Becke, Density-functional Thermochemistry. III. The Role of Exact Exchange, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy, Phys. Chem. Chem. Phys, 2005, 7, 3297–3305, 10.1039/B508541A.
- W. L. Meerts and M. Schmitt, Application of Genetic Algorithms in Automated Assignments of High-Resolution Spectra, Int. Rev. Phys. Chem., 2006, 25, 353–406 Search PubMed.
- P. B. Armentrout, B. C. Stevenson, F. Yang, F. J. Wensink, O. V. Lushchikova and J. M. Bakker, Infrared Spectroscopy of Gold Carbene Cation (AuCH2+): Covalent or Dative Bonding?, J. Phys. Chem. A, 2019, 123, 8932–8941 CrossRef CAS PubMed.
- O. W. Wheeler, M. Salem, A. Gao, J. M. Bakker and P. B. Armentrout, Sequential Activation of Methane by Ir+: An IRMPD and Theoretical Investigation, Int. J. Mass Spectrom., 2019, 435, 78–92 CrossRef CAS.
- O. W. Wheeler, M. Salem, A. Gao, J. M. Bakker and P. B. Armentrout, Activation of C–H bonds in Pt+ + xCH4 Reactions, Where x = 1–4: Identification of the Platinum Dimethyl Cation, J. Phys. Chem. A, 2016, 120, 6216–6227 CrossRef CAS PubMed.
- C. Möller and M. S. Plesset, Note on an Approximation Treatment for Many-Electron Systems, Phys. Rev., 1934, 46, 618–622 CrossRef.
- R. J. Bartlett, Many-body Perturbation Theory and Coupled Cluster Theory for Electron Correlation in Molecules, Ann. Rev. Phys. Chem., 1981, 32, 359–401 CrossRef CAS.
- A. I. Krylov, Size-consistent wave functions for bond-breaking: the equation-of-motion spin–flip model, Chem. Phys. Lett., 2001, 338, 375–384 CrossRef CAS.
- A. I. Krylov, Spin–Flip Equation-of-Motion Coupled-Cluster Electronic Structure Method for a Description of Excited States, Bond Breaking, Diradicals, and Triradicals, Acc. Chem. Res., 2006, 39, 83–91 CrossRef CAS PubMed.
- K. A. Peterson, D. Figgen, M. Dolg and H. Stoll, Energy-consistent Relativistic Pseudopotentials and Correlation Consistent Basis Sets for the 4d Elements Y–Pd, J. Chem. Phys., 2007, 126, 124101 CrossRef PubMed.
- T. H. Dunning, Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- P. U. Manohar and A. I. Krylov, A noniterative perturbative triples correction for the spin–flipping and spin-conserving equation-of-motion coupled-cluster methods with single and double substitutions, J. Chem. Phys., 2008, 129 Search PubMed.
- Y.-M. Chen, J. L. Elkind and P. B. Armentrout, Reactions of Ru+, Rh+, Pd+, and Ag+ with H2, HD and D2, J. Phys. Chem., 1995, 99, 10438–10445 CrossRef CAS.
- P. B. Armentrout and I. Kretzschmar, Guided Ion Beam and Theoretical Studies of the Reaction of Ru+ with CS2 in the Gas-phase: Thermochemistry of RuC+, RuS+, and RuCS+, Phys. Chem. Chem. Phys., 2010, 12, 4078–4091 RSC.
- E. A. Carter and W. A. Goddard, Bonding in Transition-Metal-Methylene Complexes. 2. (RuCH2)+, a Complex Exhibiting Low-Lying Methylidene-like and Carbene-like States, J. Am. Chem. Soc., 1986, 108, 2180–2191 CrossRef CAS PubMed.
- V. Barone, Anharmonic vibrational properties by a fully automated second-order perturbative approach, J. Chem. Phys., 2005, 122, 014108 CrossRef PubMed.
- V. Barone, Vibrational zero-point energies and thermodynamic functions beyond the harmonic approximation, J. Chem. Phys., 2004, 120, 3059–3065 CrossRef CAS PubMed.
- N. Mardirossian and M. Head-Gordon, Mapping the genome of meta-generalized gradient approximation density functionals: The search for B97M-V, J. Chem. Phys., 2015, 142, 074111 CrossRef PubMed.
- P. B. Armentrout and Y.-M. Chen, Activation of C2H6, C3H8, HC(CH3)3, and c-C3H6 by Gas-Phase Ru+ and the Thermochemistry of Ru–ligand Complexes, J. Am. Soc. Mass Spectrom., 1999, 10, 821–839 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Figures showing the mass spectrum for reaction of Ru+ and Rh+ with oxirane, branching ratios for the photofragmentation of [Ru,C,2H]+ and [Rh,C,2H]+, valence Kohn–Sham orbitals for RuCH2+ (4B2), EOM-SF-CCSD potential energy curves for RuCH2+, spectra of various superpositions of [Ru,C,2H]+ states, spin density of the RhCH2+ (1A1) state, comparison of the experimental spectrum of [Rh,C,2H]+ to the unscaled spectra calculated at the EOM-SSF-CCSD level, a comparison of RhCH2+ spectra calculated at different levels of theory, and ωB97M-V spectra for [Ru,C,2H]+. A table provides details regarding the calculated states of [M,C,2H]+ and a comparison to literature calculations. See DOI: https://doi.org/10.1039/d4cp00012a |
| This journal is © the Owner Societies 2024 |