Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Defect chemistry and ion transport in low-dimensional-networked Li-rich anti-perovskites as solid electrolytes for solid-state batteries†
Ana Carolina
Coutinho Dutra
 a,
George E.
Rudman
a,
George E.
Rudman
 ab,
Karen E.
Johnston
ab,
Karen E.
Johnston
 b and
James A.
Dawson
b and
James A.
Dawson
 *ac
*ac
aChemistry – School of Natural and Environmental Sciences, Newcastle University, Newcastle upon Tyne, NE1 7RU, UK. E-mail: james.dawson@newcastle.ac.uk
bDepartment of Chemistry, Durham University, Durham, DH1 3LE, UK
cCentre for Energy, Newcastle University, Newcastle upon Tyne, NE1 7RU, UK
First published on 20th March 2023
Abstract
Solid-state batteries are attracting significant attention due to their plethora of potential advantages, including energy density gains and safety enhancements. The heart of this technology can be found in its solid electrolytes and thus its progress is intrinsically attached to the discovery and understanding of novel solid electrolyte materials. In recent years, Li-rich anti-perovskites have become promising solid electrolyte candidates as they combine high ionic conductivity, structural versatility and stability against Li metal. Here, the energetics of defect formation, stability, Li-ion transport and fluorine doping in a range of LixOXx−2 (X = Cl or Br; x = 3–6) anti-perovskites with zero- to three-dimensional-networked structures are explored via atomistic simulations. Our calculations show that these materials generally present Li–halide Schottky defect pairs as the dominant native defects. We find that defect formation is generally energetically more favourable in the LixOClx−2 series compared to the equivalent structures in the LixOBrx−2 set. Additionally, our molecular dynamics simulations reveal the strong relationship between Li-ion dynamics and dimensionality in these materials, namely, increasing Li-ion diffusion and decreasing activation energy with reduced dimensionality. Enhanced Li-ion diffusion is observed for the low-dimensional-networked Br-based materials (4.81 × 10−9 and 6.08 × 10−9 cm2 s−1 for Li5OBr3 and Li6OBr4 at 300 K, respectively) compared to their Cl-based counterparts (9.85 × 10−10 and 2.06 × 10−9 cm2 s−1 for Li5OCl3 and Li6OCl4 at 300 K, respectively), illustrating the importance of lattice polarisability in these soft and unstable materials. This is further exemplified by the significant reduction in Li-ion diffusion and increase in activation energies observed in F-doped LixOXx−2.
1. Introduction
Advances in energy storage technologies are fundamental for achieving net-zero emissions as they drive the electrification of transport and the efficient large-scale storage of intermittently generated renewable energy. Current Li-ion batteries, however, are not capable of meeting the performance, safety and cost requirements that future energy storage devices will impose and solely refining existing technologies in an incremental manner will not be sufficient to power future leading-edge applications.1–5Solid-state batteries represent a next-generation technology currently attracting significant interest due to their potential to revolutionise energy storage. Solid-state batteries display an abundance of potential advantages when compared to liquid electrolyte architectures, including reduced costs and improved energy density, voltage, cycle life and safety profiles.5–10 Despite their promising nature, their widespread utilisation is still significantly blocked by various challenges, including lithium dendrite growth, low ionic conductivity, electrochemical stability, interfacial resistance and large-scale solid electrolyte synthesis.5,9–12 Given the central role that solid electrolytes possess in solid-state batteries, the continuous pursuit of understanding and designing novel solid electrolyte materials is vital for the future of this field.
Li-rich anti-perovskites have the typical formula of Li3OX (X = Cl, Br, I or a mixture of halides) and are capturing significant interest as a solid electrolyte family endowed with promising features, including good Li-ion conductivity, stability against Li metal, wide electrochemical windows and low-cost synthesis.13–17 Anti-perovskites also benefit from a remarkably versatile structure that allows for easy structural manipulation, enabling the tailoring of performance, properties and ion transport mechanisms, as well as providing substantial chemical versatility and diversity.18–22
The accurate measurement of the Li-ion conductivities and activation energies in anti-perovskite solid electrolytes has gained fresh prominence in the context of recent findings. While an early study by Zhao and Daemen13 on Li3OCl, Li3OBr and Li3OCl0.5Br0.5 reported Li-ion conductivities of >10−3 S cm−1 at room temperature and activation energies of 0.2–0.3 eV, more recent works have obtained activation energies of ∼0.6 eV and lower conductivities (e.g., 10−6 S cm−1 at room temperature) for bulk Li3OCl and Li3OBr.14,19,23–30 Several reasons for this disparity, including high grain boundary resistance, unintended doping and the presence of moisture (e.g., Li2OHCl), have been proposed.14,18,23,24,26,27,29,31–37
Such discrepancies have highlighted the importance of atomistic modelling studies in accessing fundamental information on the ion transport mechanisms and defect chemistry present in Li-rich anti-perovskites,22–25,29–31,38–50 contributing to unravelling the underlying processes that cause their intriguing behaviour. In particular, significant efforts have been made to determine the dominant defect types in anti-perovskites and how they affect their ionic diffusion.21,43,44,48,51 For example, in a density functional theory (DFT) study of Li3OCl, Li3OBr and Li3OCl0.5Br0.5, Emly et al.43 investigated a three-ion hop mechanism that involved Li interstitial dumbbells that promoted a very low Li-ion migration barrier of ∼0.17 eV for all systems, indicating a concerted Li-ion motion that is seen in several other solid electrolytes.28,49–56 However, the high formation energies of Li interstitials found for these structures suggested that this mechanism was not responsible for the high conductivities found. Mouta et al.44 also found a low enthalpy of 0.13 eV for interstitial migration in Li3OCl via classical atomistic quasi-static calculations. However, their explorations deemed vacancy migration, with a vacancy migration enthalpy of 0.30 eV, to be the pertinent transport mechanism in the system due to the concentration of Li vacancies being six orders of magnitude greater than the one found for Li interstitials. The dominance of vacancy hopping mechanisms from interstitial diffusion was also reported by Dawson et al.23 in a study that explored the defect chemistry of a wide range of Li3−xNaxOCl1−yBry anti-perovskites.
In addition to the well-reported three-dimensional-networked (3DN) anti-perovskites discussed above, low-DN Cl-based anti-perovskites (i.e., 2DN Li4OCl2, 1DN Li5OCl3 and 0DN Li6OCl4) have recently been considered by Lu et al.57 based on advances in low-DN hybrid perovskites for photovoltaic applications.58 Using DFT and ab initio molecular dynamics (AIMD) simulations, the authors found that the Li-ion conductivity increases with decreasing dimensionality due to the decreased ion migration bottlenecks and the softening of the rotation modes of the OLi6 octahedra. The structures of these materials are presented in Fig. 1.
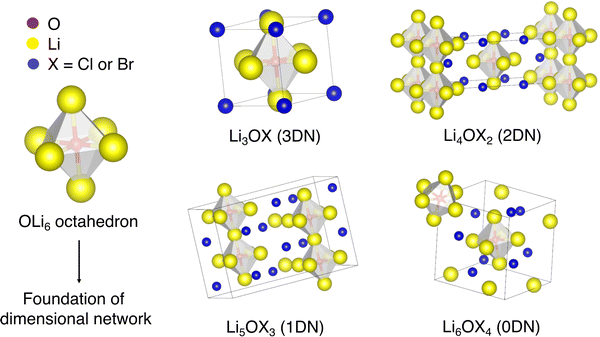 | ||
| Fig. 1 Schematic representation of OLi6 octahedron as the foundation of the cation network and crystal structures of LixOXx−2 (X = Cl or Br; x = 3–6) anti-perovskites. | ||
Although the synthesis of such 1DN and 0DN anti-perovskites has yet to be reported, recent progress in terms of synthesising 2DN Br-based anti-perovskites has been made. Zhu et al.59 were successful in synthesising a mixture of 2DN Li7O2Br3 and 3DN Li3OBr anti-perovskites, which possessed enhanced ionic conductivity (5 × 10−5 S cm−1) compared to Li3OBr alone (10−6 S cm−1), suggesting the possibility of low-DN anti-perovskites displaying higher ionic conductivities than their 3DN counterparts. Wakazaki et al.60 recently synthesised Li4OBr2, a member of the inverse Ruddlesden–Popper family, for the first time by high-pressure synthesis. The authors experimentally measured the activation energy of Li-ion conduction in this system as 0.63 eV and this was further lowered by halide (F and I) substitution and the addition of Li–Br defects. Advances have also been made for the synthesis of 2DN Na-based low-DN anti-perovskites, with Zhu et al.41 reporting the synthesis of Na4OI2 (first reported by Sabrowsky et al.61) via a solid-state reaction.
Despite the considerable body of work focused on anti-perovskites, many of the elementary processes that explain their behaviour are still misunderstood. For low-DN anti-perovskites, the ion transport mechanisms and defect chemistry are yet to be fully explored and understood. Considering the pivotal role that ionic diffusion and structural disorder have on the ion transport behaviour of anti-perovskites, there is a heightened need for studies that investigate these factors in these materials.
In this study, we use classical defect simulations to investigate the energetics of defect formation in the composition range of LixOXx−2 (X = Cl or Br; x = 3–6) anti-perovskites with 3DN to 0DN structures. Additionally, large-scale molecular dynamics (MD) studies for a range of temperatures (200–800 K) are carried to calculate the Li-ion diffusion activation energy of these systems. Our results reveal the strong relationship between defect chemistry, stability, Li-ion dynamics and dimensionality in these materials, namely, increasing Li-ion diffusion and decreasing activation energy and defects formation energy with reduced dimensionality. Our simulations also show the impact different halides have on defect formation, with lower formation energies found for Cl-containing systems. Finally, we also consider the role of fluorine doping in these materials as a potential method of improving their Li-ion conductivity but find that it actually significantly reduces the Li-ion conductivity and increases the activation energy. The results reported here strengthen our current understanding of the chemistry of low-DN anti-perovskites, contributing to the guidance of future experimental decisions and comprehending their potential as solid electrolytes in the urgent quest of finding novel materials that could make energy storage safer, more efficient and, most importantly, more sustainable.
2. Methodology
The procedures followed to perform both the defect and classical MD calculations in this work are based on well-established protocols that have been widely and successfully used to explore defect energetics and ion transport mechanisms in a wide range of battery materials.62–672.1 Structural details
The structural details (e.g., lattice parameters and atomic sites) for the Li3OCl system were obtained from the Materials Project repository,68 while the details for the remaining investigated anti-perovskites were taken from the work by Lu et al.57 The structural details for Li2O, LiCl and LiBr were also needed for the purpose of calculating the partial Schottky defect formation energies and were also obtained from the Materials Project repository. The optimised structures and lattice parameters of all explored 3DN, 2DN, 1DN and 0DN anti-perovskites are attached as CIFs in the ESI.†2.2 Potential model
The Buckingham potential model of Mouta et al.,44 with refinements from Dawson et al.,23 was used herein for all the calculations. This model has previously been used to successfully describe Li-rich anti-perovskites for the exploration of their defect chemistry and ion transport behaviour. The fluorine interactions were taken from Clarke et al.28 The long-range ionic interactions were modelled using Coulombic terms. Formal valence charges were used for all ions. The shell model of Dick and Overhauser69 was used to account for ionic polarisation. This model divides each ion into a core, which is constituted of the nucleus and inner electrons, and a massless shell, which is formed solely by the valence electrons. The core and shell are connected by a harmonic spring of constant k.2.3 Defect formation energy calculations
A wide range of defect types (including full Schottky, alkaLi–halide partial Schottky, Li2O partial Schottky, antisite and lithium, oxygen and halide Frenkel defects) and fluorine doping were investigated in the selected anti-perovskites using the General Utility Lattice Program (GULP)70 with the Mott–Littleton approximation.71 The creation of a defect significantly impacts the atoms surrounding the defect centre as it generates a Coulombic perturbation in the disordered region. Therefore, to account for the lattice relaxation around the defect centre, the Mott–Littleton approximation divides the area around the created defect into two spherical regions. The first region, region I, is closest to the defect centre and includes the defect centre itself and all ions surrounding it. Due to the proximity of region I to the defect centre and thus to the origin of perturbation, the lattice relaxation in this region will be stronger than in any other regions and the relaxation of the ions will be calculated explicitly for region I. The second region, region II, starts at the border of region I and extends to infinity. This region is subdivided into region IIa, closest to the defect centre, and region IIb. The relaxation of ions in region IIa is allowed and is considered as impacted by the central defect, whereas region IIb is treated as continuous and the impact of the defect is considered to only be dielectric. For our calculations, we used radii of 13 and 21 Å for regions I and IIa, respectively.2.4 Molecular dynamics calculations
The LAMMPS code72 was used to perform all MD simulations. An example LAMMPS input file is given in the ESI.† Long MD runs of 10 ns were completed using a time step of 2 fs with supercells of 10 × 10 × 10. Long-range Li-ion diffusion was achieved by randomly removing ∼2% of Li and halide ions from the structures. The constant-temperature, constant-pressure ensemble (NPT) was used in all simulations with a Nosé–Hoover thermostat.73 The MD simulations were run for a temperature range of 500–800 K at intervals of 100 K for all systems and for an additional temperature range of 200–400 K at intervals of 50 K for the 1DN and 0DN systems. Self-diffusion data for the Li ions were acquired from the mean-squared displacement (MSDs) according to:| 〈ri2(t)〉 = 6DLit | (1) |
3. Results and discussion
3.1 Structures, stability and intrinsic defect formation
In the ABX3 perovskite structure, cations occupy the A and B sites while the X site is populated by an anion. Alternatively, in anti-perovskites, the A and B sites are occupied by anions while a cation occupies the X site. As illustrated for Li3OX (X = Cl or Br) in Fig. 1, in the anti-perovskite structure, the O2− anion at the B site is octahedrally coordinated to six X-site Li+ cations and the A-site halide anions are cuboctahedrally coordinated to twelve nearest-neighbour cations.17Structurally, in an ABX3 anti-perovskite (space group Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m), a 3D network for the cation is formed as the cations on the vertices are shared by neighbouring BX6 sets, establishing octahedra that will form a cubic (sub)lattice that represents the foundation of the cation 3D network.57 The connectivity between these octahedra enables the hopping of the cations, which is a process that has been linked to the high ionic conductivities that anti-perovskites display.
m), a 3D network for the cation is formed as the cations on the vertices are shared by neighbouring BX6 sets, establishing octahedra that will form a cubic (sub)lattice that represents the foundation of the cation 3D network.57 The connectivity between these octahedra enables the hopping of the cations, which is a process that has been linked to the high ionic conductivities that anti-perovskites display.
Lu et al.57 recently introduced the concept of low-dimensional-networked (low-DN) anti-perovskites, which are formed when the dimensionality of the interconnected BX6 octahedra is lowered. In the 2DN anti-perovskite (space group I4/mmm), the BX6 octahedra are connected along planes separated by LiX (X = Cl or Br) layers. Analogously, if a 2DN anti-perovskite is further sliced perpendicular to the inorganic sheets, the octahedra remain connected only along one axis, thereby forming a 1DN anti-perovskite (space group Pnam). 0DN (space group R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c) anti-perovskites are derived by the further slicing of a 1DN anti-perovskite to form nonconnected (i.e., isolated) octahedra. Additional details regarding the nomenclature and structures of low-DN perovskites are available in the review of Saidaminov et al.58
c) anti-perovskites are derived by the further slicing of a 1DN anti-perovskite to form nonconnected (i.e., isolated) octahedra. Additional details regarding the nomenclature and structures of low-DN perovskites are available in the review of Saidaminov et al.58
To assess the stability of these materials, we calculated their formation energies with respect to their starting oxides (i.e., Li2O and LiX (X = Cl or Br)). For the Cl-based materials, we obtained values of −0.60, −0.63, −0.44 and −0.08 eV for the 3DN, 2DN, 1DN and 0DN systems, respectively. These energies are in good agreement with the decomposition energies calculated by Lu et al.57 using DFT for the same systems, i.e., 2DN Li4OCl2 is predicted to be the most thermodynamically stable and 0DN Li6OCl4 Li is predicted to be the least thermodynamically stable at 0 K. For the Br-based materials, we obtained values of −0.93, −1.06, −0.85 and −0.64 eV for the 3DN, 2DN, 1DN and 0DN systems, respectively. Our calculations therefore suggest that the Br-based materials are more stable than their Cl-based counterparts. A similar finding was also reported by Lu et al.57 for the 3DN and 0DN materials. These results highlight the clear reduction in stability with reducing dimensionality in these materials.
Different types of intrinsic defects have different characteristics, which can cause them to impact ion transport and conductivity within a material differently. Therefore, the investigation of intrinsic defect energetics can provide a wealth of information, not only regarding the defect chemistry of a system but also its ion transport mechanisms.
Herein, we computed the energetics of intrinsic Schottky, Frenkel and antisite defects in a wide range of LixOXx−2 (X = Cl or Br; x = 3–6) anti-perovskites with 3DN to 0DN structures. All the defect types explored in this study are given below in Kröger–Vink notation for the Cl-based materials (equivalent equations for the Br-based materials can be formulated by simply replacing Cl with Br):
Li Frenkel:
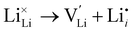 | (2) |
O Frenkel:
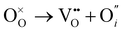 | (3) |
Cl Frenkel:
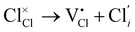 | (4) |
Antisite:
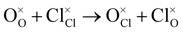 | (5) |
Full Schottky:
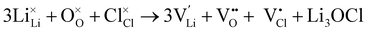 | (6) |
Li2O partial Schottky:
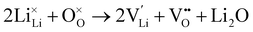 | (7) |
Li–halide partial Schottky:
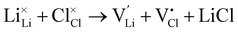 | (8) |
The calculated formation energies for these intrinsic defects in the investigated systems are presented in Fig. 2. These energies are for the lowest energy (most stable) defect configurations obtained in each system. Given that a lower defect formation energy indicates its more energetically favourable formation, the results in Fig. 2 reveal key information related to the concentration of intrinsic defects in the analysed materials and therefore their potential role in Li-ion diffusion.
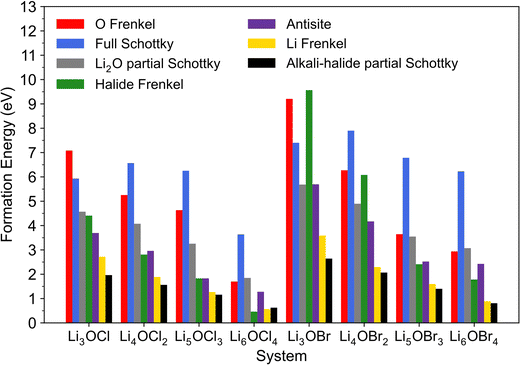 | ||
| Fig. 2 Calculated formation energies for Schottky, Frenkel and antisite defects in LixOXx−2 (X = Cl or Br; x = 3–6) anti-perovskites. | ||
First, the results show that the formation of almost all defects in both the Cl- and Br-based materials explored becomes energetically more favourable when the dimensions are reduced for the 3DN to 0DN materials, with the only exception being the full Schottky defect pairs. This trend is in accordance with previous literature findings for the Cl-based materials.57 The calculations also suggest that the formation of the great majority of defect types is more energetically favourable in Cl-based structures if compared to their equivalent Br-containing systems. This relationship found between defect formation energy and the nature of the halide contained in a system is in agreement with previous simulations results reported for Li3OCl, Li2NaOCl and LiNa2OCl and their Br-containing counterparts.23 This potential for higher defect concentrations in their structures suggest that systems with lower dimensions and with Cl instead of Br as their chosen halide can potentially present enhanced Li-ion transport and conductivity, albeit with a concomitant reduction in stability.
The comparison of the results across the different halide sets also shows that the concentrations of halide Frenkel defects in the 3DN and 2DN Br-containing structures are expected to be significantly lower than those for their counterparts in the Cl set based on the calculated formation energies. Additionally, whereas almost all these systems are predicted to present Li–halide Schottky defect pairs as dominant native defects, which aligns with previous literature reports for Li3OCl,23 Cl interstitials are the predicted dominant type of intrinsic disorder in Li6OCl4. This result suggests that Li6OCl4 may present interstitial diffusion as the main ion transport mechanism and not a Li vacancy hopping mechanism, in contrast to the other anti-perovskites investigated, as well as to what has been predicted for this structure in the literature previously.57 Frenkel-type defects have been reported to be more mobile in anti-perovskites and other important solid electrolytes and present lower migration barriers than other types of defects,43,44,55,74 which could potentially lead to more favourable ion transport mechanisms in systems possessing higher concentrations of Frenkel-type defects. Therefore, these results indicate that Li-ion transport and conductivity could be enhanced in Li6OCl4 compared to the other investigated systems, as also discussed below.
In addition to the intrinsic defects discussed above, we also considered the energetics of doping fluorine into these anti-perovskites as a potential route to increasing their Li-ion conductivity. F− dopant ions can occupy either the halide or oxygen site in anti-perovskites, as illustrated for the Cl-based materials below:
F doping at Cl site:
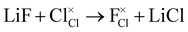 | (9) |
F doping at O site:
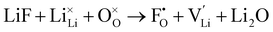 | (10) |
The two possible doping site raises the question of which is more energetically favourable and therefore more likely to be occupied.
Fig. 3 shows the calculated energies for the F doping of LixOXx−2 (X = Cl or Br; x = 3–6) considering both occupation at the halide and oxygen sites. The results indicate that the energies are significantly higher for fluorine doping on the oxygen site, suggesting that the isovalent fluorine doping mechanism (eqn (1)) is the energetically favourable doping mechanism in these systems. This finding was also previously reported for Li3OCl.28 Furthermore, we can see that the 2DN materials have the highest energies associated with fluorine doping on the halide site. For the Cl-based materials, the 0DN configuration provides the lowest energy and hence the most favourable structural motif for fluorine doping. In contrast, for the Br-based systems, the 1DN material provides the most preferential environment for fluorine incorporation.
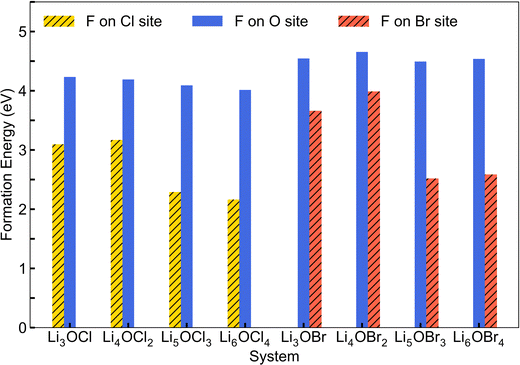 | ||
| Fig. 3 Calculated formation energies for fluorine doping of LixOXx−2 (X = Cl or Br; x = 3–6) anti-perovskites. | ||
It is well known that point defects can interact with one another, especially when they are oppositely charged, to form localised defect clusters that can influence ion transport. Clarke et al.28 recently suggested that high binding energies between F− doped on the O site and 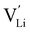 in Li3OCl likely arise due to the small Li–O interatomic spacing (<2 Å). The clustering of F− ions and
in Li3OCl likely arise due to the small Li–O interatomic spacing (<2 Å). The clustering of F− ions and 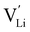 throughout the structure was found to inhibit long-range Li-ion migration. On this basis, we calculated the binding energies (Fig. 4) that arise from the interaction between oppositely charged
throughout the structure was found to inhibit long-range Li-ion migration. On this basis, we calculated the binding energies (Fig. 4) that arise from the interaction between oppositely charged 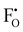 and
and 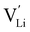 through the aliovalent fluorine doping mechanism (eqn (10)). These energies give insight into potential
through the aliovalent fluorine doping mechanism (eqn (10)). These energies give insight into potential 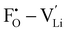 pair formation and therefore long-range Li-ion mobility. Our results show that F doping on the oxygen site results in high binding energies of greater than –0.5 eV in all systems modelled except for Li5OCl3. The magnitude of these binding energies will also substantially reduce the energy required for F doping at the oxygen site. In fact, if we were to combine the formation energies in Fig. 3 for F doping at the oxygen site with the binding energies in Fig. 4, the overall energies for F doping at the halide or oxygen site become similar. This suggests the possibility of F doping at both sites depending on the synthesis conditions employed.
pair formation and therefore long-range Li-ion mobility. Our results show that F doping on the oxygen site results in high binding energies of greater than –0.5 eV in all systems modelled except for Li5OCl3. The magnitude of these binding energies will also substantially reduce the energy required for F doping at the oxygen site. In fact, if we were to combine the formation energies in Fig. 3 for F doping at the oxygen site with the binding energies in Fig. 4, the overall energies for F doping at the halide or oxygen site become similar. This suggests the possibility of F doping at both sites depending on the synthesis conditions employed.
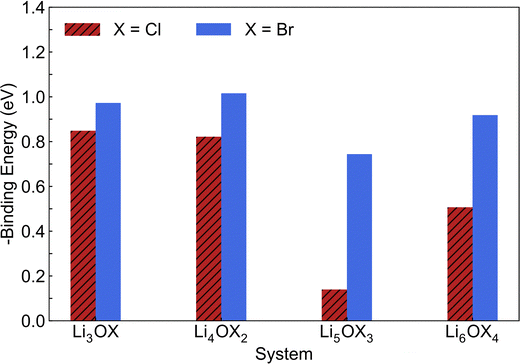 | ||
| Fig. 4 Calculated binding energies for fluorine doping of LixOXx−2 (X = Cl or Br; x = 3–6) anti-perovskites at the oxygen site. | ||
Given the critical role that Li vacancies have in determining the Li-ion conductivity of these materials, such binding energies represent a significant potential hindrance to their performance as solid electrolytes. Furthermore, the binding energies calculated for the Br-based systems are significantly higher than those calculated for the equivalent Cl-based systems. Therefore, these results suggest that F doping in these anti-perovskites may have a detrimental effect on their Li-ion conducting properties but this must be confirmed using MD simulations.
3.2 Li-ion transport
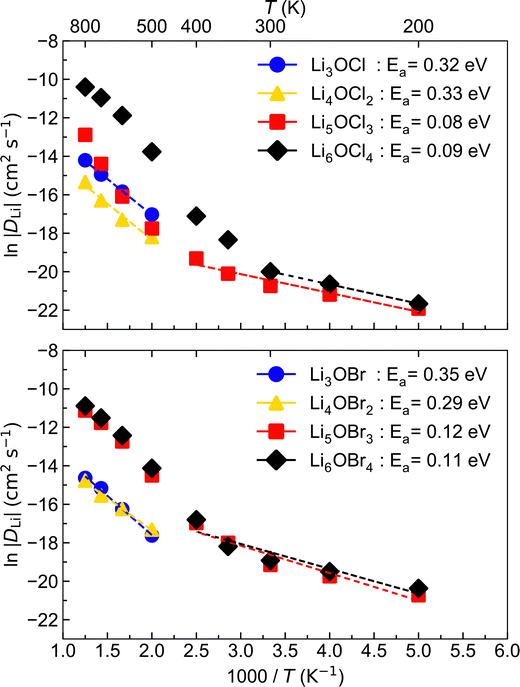
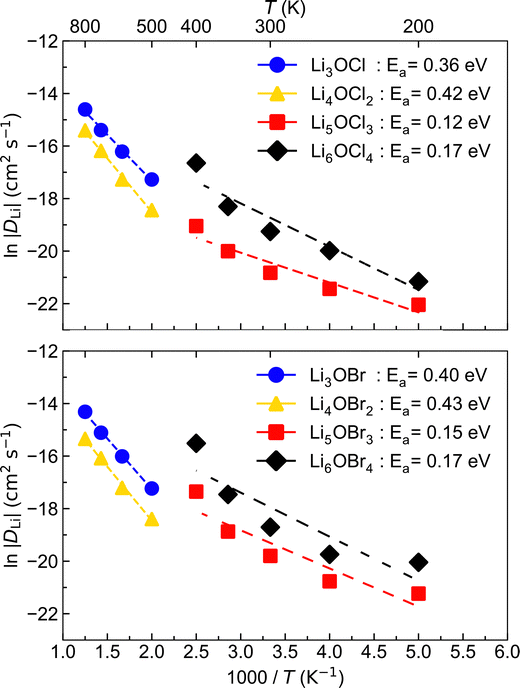
To investigate Li-ion diffusion in these anti-perovskite systems, we conducted MD calculations for all the selected materials with a representative Li–halide Schottky defect concentration of ∼2%. Li–halide Schottky defect pairs were the defect type chosen for the MD calculations as these have been confirmed as the dominant disorder for all systems analysed except for Li6OCl4, as discussed above.The self-diffusion coefficients obtained via MSD plots as a function of time along with their corresponding temperatures were used to produce the Arrhenius plots in Fig. 5, which were used to calculate the activation energies for Li-ion conductivity for all systems. Example MSD plots for the Br-based structures at a representative temperature of 700 K are given in Fig. S1 (ESI†).
The Arrhenius plots in Fig. 5 reveal that the low-dimensional-networked systems (1DN and 0DN) exhibit a strong increase in Li-ion diffusion above ∼300 K, which prevents the data across the whole temperature range for these materials to be described by a single linear fit. To determine the reason for such a significant increase in Li-ion diffusion at relatively modest temperatures for these low-dimensional-networked systems, we computed all their possible radial distribution functions (RDFs) throughout the MD simulations, as shown in Fig. S2 (ESI†) for 300 K.
There is a clear distinction between the structures of the 3DN (Li3OX) and 2DN (Li4OX2) structures compared to the 1DN (Li5OX3) and 0DN (Li6OX4) systems. While the high-dimensional-networked systems show distinct peaks for all elemental combinations across the entire range of interatomic distances (r), the low-dimensional-networked systems present remarkably flat RDFs at >5 Å, indicative of a solid-to-liquid transition, i.e., melting. This discrepancy is further verified by the smooth curves for the integrated RDFs of the 1DN and 0DN materials, which indicate an almost linear increase in coordination number with increasing r. In contrast, for the 3DN and 2DN anti-perovskites, regular plateaus are observed where the coordination number remains unchanged with increasing r, thereby highlighted their highly ordered crystalline structures. The effect of temperature on the RDFs in these materials is illustrated in Fig. 6 for the example of Li–Li at 300 and 600 K. These plots again show the increase in disorder with decreasing dimensionality in the systems. At 600 K, this trend becomes even clearer with the Li–Li RDFs for the 1DN and 0DN material presenting liquid-like behaviour beyond 3 Å.
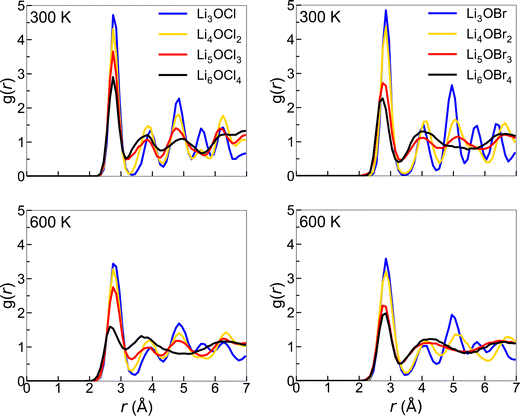 | ||
| Fig. 6 Li–Li RDFs for LixOXx−2 (X = Cl (left) or Br (right); x = 3–6) anti-perovskites at 300 and 600 K. | ||
Although Lu et al.57 reported the melting of Li5OCl3 at 800 K in their smaller scale DFT simulations, this is the first time the melting of these 1DN and 0DN anti-perovskites at temperatures as low as 300 K has been reported. This melting at low temperatures is indicative of instability (and therefore superionic Li-ion conductivity) in the 1DN and 0DN systems, which is reasonable considering the low dimensionality within the structures and the fact that the feasibility of their synthesis is still yet to be confirmed experimentally.
The comparison of the self-diffusion coefficients obtained at 300 K for all systems in Fig. 7 reveals the clear relationship between Li-ion dynamics and dimensionality in these materials, with Li-ion diffusion increasing and the associated activation energy decreasing with reducing dimensionality. The calculated values and observed trends are in excellent agreement with the DFT results of Lu et al.57 for the Cl-based materials, who ascribed their findings to the enlarged bottleneck sizes for Li-ion hopping and the softening of the lattice with reducing dimensionality. The calculated activation energies for Li3OCl (0.32 eV) and Li3OBr (0.35 eV) are also similar to those predicted by Dawson et al.23 (0.29 and 0.31 eV, respectively). It is noteworthy that these calculated values are significantly lower than recently reported experimental results (∼0.6 eV),17 which has been ascribed to the high grain boundary resistance in these materials that is not typically accounted for in atomistic simulations.18
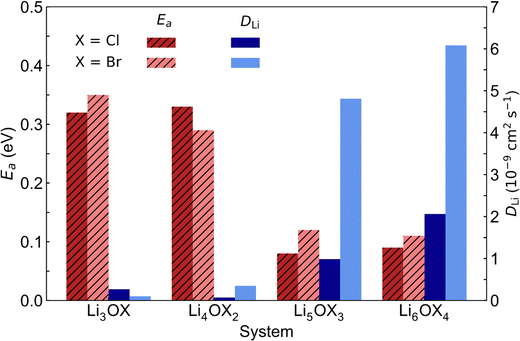 | ||
| Fig. 7 Self-diffusion coefficients (DLi) at 300 K and activation energies (Ea) for Li-ion diffusion in LixOXx−2 (X = Cl or Br; x = 3–6) anti-perovskites. | ||
This work is the first to consider low-dimensional-networked Br-based anti-perovskites. A comparison between the different halide sets reveals the generally greater Li-ion diffusion for the Br-containing systems, with Li6OBr4 showing a very high self-diffusion coefficient of 6.08 × 10−9 cm2 s−1 that is almost three times the value found for Li6OCl4 (2.06 × 10−9 cm2 s−1). The prevalence of increased Li-ion diffusion in Br-containing systems is also seen for the 2DN and 1DN systems, with Li4OBr2 and Li5OBr3 showing self-diffusion coefficients of 3.49 × 10−10 and 4.81 × 10−9 cm2 s−1, respectively, compared to values of 7.07 × 10−11 and 9.85 × 10−10 cm2 s−1 for Li4OCl2 and Li5OCl3, respectively. The results in Fig. 7 show that the activation energies for the 3DN and 2DN systems are very similar for both sets of materials, ranging from 0.29 to 0.35 eV. Similar activation energies were also calculated for the 1DN and 0DN systems for both sets, with values ranging from 0.08 to 0.12 eV.
The only exception to the trend of increasing Li-ion diffusion with decreasing dimensionality is for Li4OCl2, which exhibits a self-diffusion coefficient at 300 K of 7.07 × 10−11 cm2 s−1 and an activation energy of 0.33 eV, values that are lower and higher than the respective values for its 3DN counterpart, Li3OCl (2.68 × 10−10 cm2 s−1 and 0.32 eV, respectively). This behaviour is perhaps expected given that the structure of Li4OCl2 contains LiCl layers that represent barriers for Li-ion hopping, thereby resulting in 2D Li-ion diffusion. This is clearly illustrated by the Li-ion diffusion density plots presented in Fig. 8 for the Cl-based materials at 300 K (the equivalent plots for the Br-based materials are given in Fig. S3, ESI†). As illustrated, while strong isotropic 3D Li-ion diffusion is observed in Li3OCl, Li5OCl3 and Li6OCl4, Li-ion diffusion in Li4OCl2 is primarily restricted to the perovskite layer.
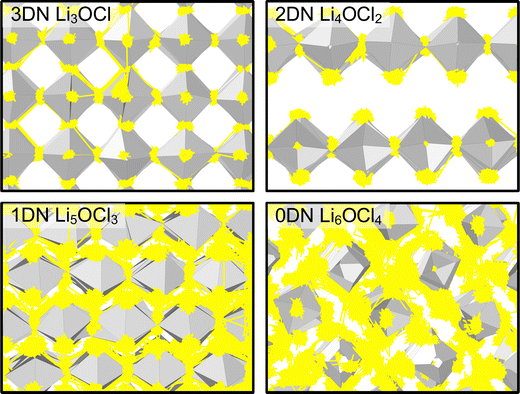 | ||
| Fig. 8 Diffusion density plots of Li ions (yellow) overlaid on OLi6 (grey) octahedra in LixOClx−2 (x = 3–6) anti-perovskites at 300 K. Cl ions have been omitted for clarity. | ||
In contrast, as noted above, 2DN Li4OBr2 does not exhibit the same reduction in Li-ion diffusion and increase in activation energy as 2DN Li4OCl2 despite having the same structure. As shown by Fig. 8 and Fig. S3 (ESI†), this discrepancy is not related to the LiX (X = Cl or Br) layer as both materials primarily exhibit 2D Li-ion diffusion and the fact that the width of the LiBr layer is larger than that of the LiCl layer. This therefore suggests another fundamental reason why the 2D, 1D and 0D Br-based materials exhibit higher Li-ion diffusion than their Cl-based counterparts, as visualised in Fig. 8 and Fig. S3 (ESI†). An obvious explanation could be the increased volume of the Br-based materials; however, it has been shown that the bottlenecks for Li-ion transport in Br-based anti-perovskites are smaller than in Cl-based anti-perovskites, thereby potentially limiting it.52
Another factor to consider is the polarisability of the halide sublattice. It is well known that highly polarisable anion sublattices can have a significant effect on Li-ion conductivity in solid electrolytes by weakening the interaction between the Li ions and surrounding anions.75 Several studies have shown that replacing the harder Cl ions with softer and more polarisable Br ions can result in significantly enhanced Li-ion transport.75–77 Furthermore, the importance of a soft anion sublattice for fast Li-ion transport in hydride-based anti-perovskites has been revealed.20 Given the inherent metastability/instability of the low-dimensional-networked materials in this study, it is likely that the presence of Br further weakens the Li–halide interactions, resulting in superionic Li-ion diffusion. This also raises the question of whether iodine doping in these systems could further enhance their ionic conductivity. As proposed previously for thiophosphate solid electrolytes, tailoring of the halide composition could also be an important strategy for tuning the conductivity and stability of anti-perovskite solid electrolytes.
We also assessed the impact of fluorine doping on Li-ion transport in the LixOXx−2 (X = Cl or Br; x = 3–6) systems. We considered doping at both the halide and oxygen (with Li vacancy charge compensation) sites at concentrations of 2% and 10%. Fig. 9 shows the Arrhenius dependencies for Li-ion diffusion in these anti-perovskite systems for F doping at the more energetically favourable halide sites with concentration of 2%.
 | ||
| Fig. 9 Arrhenius plots of Li-ion diffusion for 2% F doping at the halide sites of LixOXx−2 (X = Cl (left) or Br (right); x = 3–6) anti-perovskites. | ||
Compared to the results for the undoped systems in Fig. 5, F doping causes a significant reduction in Li-ion conductivity for the majority of the systems and temperatures. Furthermore, substantial increases in the activation energy are observed as a result of F doping. These findings strongly suggest that the F doping of these materials has a negative influence on their Li-ion transport performance. As discussed above, this further illustrates the important role of polarisability of the halide sublattice in anti-perovskite Li-ion conductors. The replacement of softer and more polarisable Cl and Br ions with F, as the least polarisable anion, is likely to strengthen the interaction between the Li ions and surrounding anions, resulting in reduced Li-ion conductivity.75 Even larger activation energies were found for fluorine doping at the oxygen sites, as shown in Fig. S4 (ESI†). This is because in addition to the polarisability effect, in this case, the binding between the fluorine dopants and Li vacancies also inhibits long-range Li-ion diffusion, as precited from the defect calculations above.28 Fig. S4 (ESI†) shows that upon increasing the F doping concentration from 2% to 10%, there is generally a concomitant increase in the calculated activation energies. This further confirms the determinantal impact of F doping in these systems.
4. Conclusion
In this work, we have explored the energetics of Schottky, Frenkel and antisite defect formation, stability and Li-ion transport in a wide range of undoped and F-doped LixOXx−2 (X = Cl or Br; x = 3–6) anti-perovskites with 3DN to 0DN structures. We find that defect formation for all systems becomes energetically more favourable as the dimensionality of the system is lowered. Additionally, we predict that the formation of the majority of defect types is more energetically favourable in Cl-containing systems rather than in systems with Br. With the exception of Li6OCl4, where Cl interstitials are the dominant type of intrinsic disorder, our results show that all the investigated systems are predicted to present Li–halide Schottky defect pairs as the dominant native defects. Fluorine doping at the halide sites is shown to be more energetically favourable than at the oxygen sites in these systems.Using MD calculations and structural analysis, we predict the low-temperature melting of the 1DN and 0DN systems at temperatures as low as 300 K, highlighting the clear instability of these systems but potential for superionic Li-ion transport if they can be stabilised. We show that the Li-ion diffusion increases and the activation energy decreases with reducing dimensionality in these anti-perovskite materials. Furthermore, the highest Li-ion diffusion is found for the low-dimensional-networked Br-based materials, indicating that lattice polarisability plays an important role in these soft and unstable materials. The introduction of fluorine is found to be determinantal to Li-ion transport in these anti-perovskites as a result of its poor polarisability compared to Cl and Br and its binding to Li vacancies when doped at the oxygen sites.
Considering the critical importance of solid electrolytes in the development of solid-state batteries and the unique potential of anti-perovskite solid electrolytes, the results presented here can potentially guide future experimental synthesis choices and further advances in energy storage. Nevertheless, the preparation of these materials will have to account for their instability (or metastability), potentially through doping. Alternative synthesis routes may also provide a route their preparation, for example, mechanochemistry. Given the recent advances in the preparation and stabilisation of solid electrolytes, we are hopeful that variations of these materials will be reported in the near future.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
A. C. C. D. and J. A. D. thank the Newcastle University Academic Track (NUAcT) Fellowship Scheme for financial support. J. A. D. gratefully acknowledges the Engineering and Physical Sciences Research Council (EPSRC, EP/V013130/1) for funding. G. E. R. acknowledges support from the EPSRC CDT in Renewable Energy Northeast Universities (ReNU) for funding (EP/S023836/1). Via membership of the UK's HEC Materials Chemistry Consortium, which is funded by the EPSRC (EP/R029431), this work used the ARCHER2 UK National Supercomputing Service. The Rocket High Performance Computing service at Newcastle University was also used.References
- E. C. Evarts, Lithium batteries: to the limits of lithium, Nature, 2015, 526, S93–S95 CrossRef CAS PubMed
.
- K. Turcheniuk, D. Bondarev, V. Singhal and G. Yushin, Ten years left to redesign lithium-ion batteries, Nature, 2018, 559, 467–470 CrossRef CAS PubMed
.
- A. Masias, J. Marcicki and W. A. Paxton, Opportunities and Challenges of Lithium Ion Batteries in Automotive Applications, ACS Energy Lett., 2021, 6, 621–630 CrossRef CAS
.
- N. Nitta, F. Wu, J. T. Lee and G. Yushin, Li-ion battery materials: present and future, Mater. Today, 2015, 18, 252–264 CrossRef CAS
.
- T. Famprikis, P. Canepa, J. A. Dawson, M. S. Islam and C. Masquelier, Fundamentals of inorganic solid-state electrolytes for batteries, Nat. Mater., 2019, 18, 1278–1291 CrossRef CAS PubMed
.
- C. Li, Z. Yu Wang, Z. Jiang He, Y. Jiao Li, J. Mao, K. Hua Dai, C. Yan and J. Chao Zheng, An advance review of solid-state battery: challenges, progress and prospects, Sustainable Mater. Technol., 2021, 29, e00297 CrossRef CAS
.
- J. A. Lewis, J. Tippens, F. J. Q. Cortes and M. T. McDowell, Chemo-Mechanical Challenges in Solid-State Batteries, Trends Chem., 2019, 1, 845–857 CrossRef CAS
.
- J. Janek and W. G. Zeier, A solid future for battery development, Nat. Energy, 2016, 1, 1–4 Search PubMed
.
- Q. Zhao, S. Stalin, C. Z. Zhao and L. A. Archer, Designing solid-state electrolytes for safe, energy-dense batteries, Nat. Rev. Mater., 2020, 5, 229–252 CrossRef CAS
.
- M. Pasta, D. Armstrong, Z. L. Brown, J. Bu, M. R. Castell, P. Chen, A. Cocks, S. A. Corr, E. J. Cussen, E. Darnbrough, V. Deshpande, C. Doerrer, M. S. Dyer, H. El-Shinawi, N. Fleck, P. Grant, G. L. Gregory, C. Grovenor, L. J. Hardwick, J. T. S. Irvine, H. J. Lee, G. Li, E. Liberti, I. McClelland, C. Monroe, P. D. Nellist, P. R. Shearing, E. Shoko, W. Song, D. S. Jolly, C. I. Thomas, S. J. Turrell, M. Vestli, C. K. Williams, Y. Zhou and P. G. Bruce, roadmap on solid-state batteries, J. Phys. Energy, 2020, 2, 032008 CrossRef CAS
.
- K. Kerman, A. Luntz, V. Viswanathan, Y.-M. Chiang and Z. Chen, Review—Practical Challenges Hindering the Development of Solid State Li Ion Batteries, J. Electrochem. Soc., 2017, 164, A1731–A1744 CrossRef CAS
.
- S. Xia, X. Wu, Z. Zhang, Y. Cui and W. Liu, Practical Challenges and Future Perspectives of All-Solid-State Lithium-Metal Batteries, Chem, 2019, 5, 753–785 CAS
.
- Y. Zhao and L. L. Daemen, Superionic conductivity in lithium-rich anti-perovskites, J. Am. Chem. Soc., 2012, 134, 15042–15047 CrossRef CAS PubMed
.
- X. Lü, J. W. Howard, A. Chen, J. Zhu, S. Li, G. Wu, P. Dowden, H. Xu, Y. Zhao and Q. Jia, Antiperovskite Li3OCl superionic conductor films for solid-state Li-ion batteries, Adv. Sci., 2016, 3, 1500359 CrossRef PubMed
.
- H. Fang and P. Jena, Li-rich antiperovskite superionic conductors based on cluster ions, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 11046–11051 CrossRef CAS PubMed
.
- J. A. S. Serejo, J. S. Pereira, R. Mouta and L. G. C. Rego, Sluggish anion transport provides good kinetic stability to the anhydrous anti-perovskite solid electrolyte Li3OCl, Phys. Chem. Chem. Phys., 2021, 23, 6964–6973 RSC
.
- J. A. Dawson, T. Famprikis and K. E. Johnston, Anti-perovskites for solid-state batteries: recent developments, current challenges and future prospects, J. Mater. Chem. A, 2021, 9, 18746–18772 RSC
.
- J. A. Dawson, P. Canepa, T. Famprikis, C. Masquelier and M. S. Islam, Atomic-Scale Influence of Grain Boundaries on Li-Ion Conduction in Solid Electrolytes for All-Solid-State Batteries, J. Am. Chem. Soc., 2018, 140, 362–368 CrossRef CAS PubMed
.
- Y. Li, W. Zhou, S. Xin, S. Li, J. Zhu, L. Xujie, Z. Cui, Q. Jia, J. Zhou, Y. Zhao and J. B. Goodenough, Fluorine-Doped Antiperovskite Electrolyte for All-Solid-State Lithium-Ion Batteries, Angew. Chem., Int. Ed., 2016, 55, 9965–9968 CrossRef CAS PubMed
.
- S. Gao, T. Broux, S. Fujii, C. Tassel, K. Yamamoto, Y. Xiao, I. Oikawa, H. Takamura, H. Ubukata, Y. Watanabe, K. Fujii, M. Yashima, A. Kuwabara, Y. Uchimoto and H. Kageyama, Hydride-based antiperovskites with soft anionic sublattices as fast alkali ionic conductors, Nat. Commun., 2021, 12, 1–10 CrossRef PubMed
.
- K. Kim and D. J. Siegel, Correlating lattice distortions, ion migration barriers, and stability in solid electrolytes, J. Mater. Chem. A, 2019, 7, 3216–3227 RSC
.
- Z. Deng, B. Radhakrishnan and S. P. Ong, Rational composition optimization of the lithium-rich Li3OCl1−xBrx anti-perovskite superionic conductors, Chem. Mater., 2015, 27, 3749–3755 CrossRef CAS
.
- J. A. Dawson, H. Chen and M. Saiful Islam, Composition Screening of Lithium- and Sodium-Rich Anti-Perovskites for Fast-Conducting Solid Electrolytes, J. Phys. Chem. C, 2018, 122, 23978–23984 CrossRef CAS
.
- A. Y. Song, Y. Xiao, K. Turcheniuk, P. Upadhya, A. Ramanujapuram, J. Benson, A. Magasinski, M. Olguin, L. Meda, O. Borodin and G. Yushin, Protons Enhance Conductivities in Lithium Halide Hydroxide/Lithium Oxyhalide Solid Electrolytes by Forming Rotating Hydroxy Groups, Adv. Energy Mater., 2018, 8, 1700971 CrossRef
.
- J. A. Dawson, T. S. Attari, H. Chen, S. P. Emge, K. E. Johnston and M. S. Islam, Elucidating lithium-ion and proton dynamics in anti-perovskite solid electrolytes, Energy Environ. Sci., 2018, 11, 2993–3002 RSC
.
- X. Lü, G. Wu, J. W. Howard, A. Chen, Y. Zhao, L. L. Daemen and Q. Jia, Li-rich anti-perovskite Li3OCl films with enhanced ionic conductivity, Chem. Commun., 2014, 50, 11520–11522 RSC
.
- S. Li, J. Zhu, Y. Wang, J. W. Howard, X. Lü, Y. Li, R. S. Kumar, L. Wang, L. L. Daemen and Y. Zhao, Reaction mechanism studies towards effective fabrication of lithium-rich anti-perovskites Li3OX (X = Cl, Br), Solid State Ionics, 2015, 284, 14–19 CrossRef
.
- M. J. Clarke, J. A. Dawson, T. J. Mays and M. S. Islam, Atomistic insights into the effects of doping and vacancy clustering on Li-ion conduction in the Li3OCl antiperovskite solid electrolyte, ACS Appl. Energy Mater., 2021, 4, 5094–5100 CrossRef CAS
.
- E. Ahiavi, J. A. Dawson, U. Kudu, M. Courty, M. S. Islam, O. Clemens, C. Masquelier and T. Famprikis, Mechanochemical synthesis and ion transport properties of Na3OX (X = Cl, Br, I and BH4) antiperovskite solid electrolytes, J. Power Sources, 2020, 471, 228489 CrossRef CAS
.
- Z. Lu, C. Chen, Z. M. Baiyee, X. Chen, C. Niu and F. Ciucci, Defect chemistry and lithium transport in Li3OCl anti-perovskite superionic conductors, Phys. Chem. Chem. Phys., 2015, 17, 32547–32555 RSC
.
- A. S. Bhalla, R. Guo and R. Roy, The perovskite structure—a review of its role in ceramic science and technology, Mater. Res. Innov., 2000, 4, 3–26 CrossRef CAS
.
- I. Hanghofer, G. J. Redhammer, S. Rohde, I. Hanzu, A. Senyshyn, H. M. R. Wilkening and D. Rettenwander, Untangling the Structure and Dynamics of Lithium-Rich Anti-Perovskites Envisaged as Solid Electrolytes for Batteries, Chem. Mater., 2018, 30, 8134–8144 CrossRef CAS
.
- A. Koedtruad, M. A. Patino, N. Ichikawa, D. Kan and Y. Shimakawa, Crystal structures and ionic conductivity in Li2OHX (X = Cl, Br) antiperovskites, J. Solid State Chem., 2020, 286, 121263 CrossRef CAS
.
- A. Y. Song, K. Turcheniuk, J. Leisen, Y. Xiao, L. Meda, O. Borodin and G. Yushin, Understanding Li-Ion Dynamics in Lithium Hydroxychloride (Li2OHCl) Solid State Electrolyte via Addressing the Role of Protons, Adv. Energy Mater., 2020, 10, 1903480 CrossRef CAS
.
- K. Shen, Y. Wang, J. Zhang, Y. Zong, G. Li, C. Zhao and H. Chen, Revealing the effect of grain boundary segregation on Li ion transport in polycrystalline anti-perovskite Li3ClO: a phase field study, Phys. Chem. Chem. Phys., 2020, 22, 3030–3036 RSC
.
- M. Wu, B. Xu, W. Luo, B. Sun, J. Shi and C. Ouyang, First-principles study on the structural, electronic, and Li-ion mobility properties of anti-perovskite superionic conductor Li3OCl (1 0 0) surface, Appl. Surf. Sci., 2020, 510, 145394 CrossRef CAS
.
- H. J. Lee, B. Darminto, S. Narayanan, M. Diaz-Lopez, A. W. Xiao, Y. Chart, J. H. Lee, J. A. Dawson and M. Pasta, Li-ion conductivity in Li2OHCl1−xBrx solid electrolytes: grains, grain boundaries and interfaces, J. Mater. Chem. A, 2022, 10, 11574–11586 RSC
.
- J. A. Dias, S. H. Santagneli and Y. Messaddeq, Methods for Lithium Ion NASICON Preparation: From Solid-State Synthesis to Highly Conductive Glass-Ceramics, J. Phys. Chem. C, 2020, 124, 26518–26539 CrossRef CAS
.
- H. Fang, S. Wang, J. Liu, Q. Sun and P. Jena, Superhalogen-based lithium superionic conductors, J. Mater. Chem. A, 2017, 5, 13373–13381 RSC
.
- Y. Wang, Q. Wang, Z. Liu, Z. Zhou, S. Li, J. Zhu, R. Zou, Y. Wang, J. Lin and Y. Zhao, Structural manipulation approaches towards enhanced sodium ionic conductivity in Na-rich antiperovskites, J. Power Sources, 2015, 293, 735–740 CrossRef CAS
.
- J. Zhu, Y. Wang, S. Li, J. W. Howard, J. Neuefeind, Y. Ren, H. Wang, C. Liang, W. Yang, R. Zou, C. Jin and Y. Zhao, Sodium Ion Transport Mechanisms in Antiperovskite Electrolytes Na3OBr and Na4OI2: An in Situ Neutron Diffraction Study, Inorg. Chem., 2016, 55, 5993–5998 CrossRef CAS PubMed
.
- H. Nguyen, S. Hy, E. Wu, Z. Deng, M. Samiee, T. Yersak, J. Luo, S. Ping Ong and Y. Shirley Meng, Experimental and Computational Evaluation of a Sodium-Rich Anti-Perovskite for Solid State Electrolytes, J. Electrochem. Soc., 2016, 163, 2165–2171 CrossRef
.
- A. Emly, E. Kioupakis and A. Van Der Ven, Phase stability and transport mechanisms in antiperovskite Li3OCl and Li3OBr superionic conductors, Chem. Mater., 2013, 25, 4663–4670 CrossRef CAS
.
- R. Mouta, M. Á. B. Melo, E. M. Diniz and C. W. A. Paschoal, Concentration of charge carriers, migration, and stability in Li3OCl solid electrolytes, Chem. Mater., 2014, 26, 7137–7144 CrossRef CAS
.
- J. Howard, Z. D. Hood and N. A. W. Holzwarth, Fundamental aspects of the structural and electrolyte properties of Li2OHCl from simulations and experiment, Phys. Rev. Mater., 2017, 1, 075406 CrossRef
.
- Z. Wang, H. Xu, M. Xuan and G. Shao, From anti-perovskite to double anti-perovskite: tuning lattice chemistry to achieve super-fast Li+ transport in cubic solid lithium halogen-chalcogenides, J. Mater. Chem. A, 2017, 6, 73–83 RSC
.
- T. H. Wan, Z. Lu and F. Ciucci, A first principle study of the phase stability, ion transport and substitution strategy for highly ionic conductive sodium antipervoskite as solid electrolyte for sodium ion batteries, J. Power Sources, 2018, 390, 61–70 CrossRef CAS
.
- Y. Zhang, Y. Zhao and C. Chen, Ab initio study of the stabilities of and mechanism of superionic transport in lithium-rich antiperovskites, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 134303 CrossRef
.
- S. Stegmaier, J. Voss, K. Reuter and A. C. Luntz, Li+ Defects in a Solid-State Li Ion Battery: Theoretical Insights with a Li3OCl Electrolyte, Chem. Mater., 2017, 29, 4330–4340 CrossRef CAS
.
- M. H. Chen, A. Emly and A. Van Der Ven, Anharmonicity and phase stability of antiperovskite Li3OCl, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 214306 CrossRef
.
- R. Mouta, E. M. Diniz and C. W. A. Paschoal, Li+ interstitials as the charge carriers in superionic lithium-rich anti-perovskites, J. Mater. Chem. A, 2016, 4, 1586–1590 RSC
.
- S. Zhao, C. Chen, H. Li and W. Zhang, Theoretical insights into the diffusion mechanism of alkali ions in Ruddlesden-Popper antiperovskites, New J. Chem., 2021, 45, 4219–4226 RSC
.
- J. G. Smith and D. J. Siegel, Low-temperature paddlewheel effect in glassy solid electrolytes, Nat. Commun., 2020, 11, 1–11 CrossRef PubMed
.
- X. He, Y. Zhu and Y. Mo, Origin of fast ion diffusion in super-ionic conductors, Nat. Commun., 2017, 8, 1–7 CrossRef PubMed
.
- R. Jalem, Y. Yamamoto, H. Shiiba, M. Nakayama, H. Munakata, T. Kasuga and K. Kanamura, Concerted migration mechanism in the Li ion dynamics of garnet-type Li7La3Zr2O12, Chem. Mater., 2013, 25, 425–430 CrossRef CAS
.
- A. M. Nolan, Y. Zhu, X. He, Q. Bai and Y. Mo, Computation-Accelerated Design of Materials and Interfaces for All-Solid-State Lithium-Ion Batteries, Joule, 2018, 2, 2016–2046 CrossRef CAS
.
- Z. Lu, J. Liu and F. Ciucci, Superionic conduction in low-dimensional-networked anti-perovskites, Energy Storage Mater., 2020, 28, 146–152 CrossRef
.
- M. I. Saidaminov, O. F. Mohammed and O. M. Bakr, Low-Dimensional-Networked Metal Halide Perovskites: The Next Big Thing, ACS Energy Lett., 2017, 2, 889–896 CrossRef CAS
.
- J. Zhu, S. Li, Y. Zhang, J. W. Howard, X. Lü, Y. Li, Y. Wang, R. S. Kumar, L. Wang and Y. Zhao, Enhanced ionic conductivity with Li7O2Br3 phase in Li3OBr anti-perovskite solid electrolyte, Appl. Phys. Lett., 2016, 109, 101904 CrossRef
.
- S. Wakazaki, Q. Liu, R. Jalem, T. Nishikubo, Y. Sakai, N. Matsui, G. Zhao, K. Suzuki, K. Shigematsu, T. Yamamoto, R. Kanno, H. Das, Y. Tateyama and M. Azuma, High-Pressure Synthesis and Lithium-Ion Conduction of Li4OBr2 Derivatives with a Layered Inverse-Perovskite Structure, Chem. Mater., 2021, 33, 9194–9201 CrossRef CAS
.
- H. Sabrowsky, K. Paszkowski, D. Reddig and P. Vogt, Na3OCl und Na3OBr, die ersten Alkalimetallchalkogenidhalogenide Na3OCl and Na3OBr, the First Alkali Metal Chalcogenide Halides, Z. Naturforsch., 1988, 43, 238–239 CrossRef CAS
.
- M. S. Islam and C. A. J. Fisher, Lithium and sodium battery cathode materials: computational insights into voltage, diffusion and nanostructural properties, Chem. Soc. Rev., 2014, 43, 185–204 RSC
.
- F. N. Forrester, J. A. Quirk, T. Famprikis and J. A. Dawson, Disentangling Cation and Anion Dynamics in Li3PS4 Solid Electrolytes, Chem. Mater., 2022, 34, 10561–10571 CrossRef CAS PubMed
.
- S. M. Wood, C. Eames, E. Kendrick and M. S. Islam, Sodium Ion Diffusion and Voltage Trends in Phosphates Na4M3(PO4)2P2O7 (M = Fe, Mn, Co, Ni) for Possible High-Rate Cathodes, J. Phys. Chem. C, 2015, 119, 15935–15941 CrossRef CAS
.
- J. C. Treacher, S. M. Wood, M. S. Islam and E. Kendrick, Na2CoSiO4 as a cathode material for sodium-ion batteries: structure, electrochemistry and diffusion pathways, Phys. Chem. Chem. Phys., 2016, 18, 32744–32752 RSC
.
- Y. Deng, C. Eames, B. Fleutot, R. David, J. N. Chotard, E. Suard, C. Masquelier and M. S. Islam, Enhancing the Lithium Ion Conductivity in Lithium Superionic Conductor (LISICON) Solid Electrolytes through a Mixed Polyanion Effect, ACS Appl. Mater. Interfaces, 2017, 9, 7050–7058 CrossRef CAS PubMed
.
- A. D. Poletayev, J. A. Dawson, M. S. Islam and A. M. Lindenberg, Defect-driven anomalous transport in fast-ion conducting solid electrolytes, Nat. Mater., 2022, 21, 1066–1073 CrossRef CAS PubMed
.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, Commentary: The Materials Project: a materials genome approach to accelerating materials innovation, APL Mater., 2013, 1, 011002 CrossRef
.
- B. G. Dick and A. W. Overhauser, Theory of the Dielectric Constants of Alkali Halide Crystals, Phys. Rev., 1958, 112, 90 CrossRef
.
- J. D. Gale and A. L. Rohl, The General Utility Lattice Program (GULP), 2011, 29, 291–341, DOI:10.1080/0892702031000104887
.
- M. J. Mott and N. F. Littleton, Conduction in Polar Crystals. I. Electrolytic Conduction in Solid Salts, Trans. Faraday Soc., 1938, 34, 485–499 RSC
.
- S. Plimpton, Fast Parallel Algorithms for Short-Range Molecular Dynamics, JCoPh, 1995, 117, 1–19 CAS
.
- D. J. Evans, B. L. Holian, D. J. Evans and B. L. Holian, The Nose–Hoover thermostat, J. Chem. Phys., 1998, 83, 4069 CrossRef
.
- A. G. Squires, J. M. Dean and B. J. Morgan, Aliovalent doping response and impact on ionic conductivity in the antiperovskite solid electrolyte Li3OCl, ChemRxiv, 2021, 1, 1–14 Search PubMed
.
- M. A. Kraft, S. P. Culver, M. Calderon, F. Bo, T. Krauskopf, A. Senyshyn, C. Dietrich, A. Zevalkink, J. Janek and W. G. Zeier, Influence of Lattice Polarizability on the Ionic Conductivity in the Lithium Superionic Argyrodites Li6PS5X (X = Cl, Br, I), J. Am. Chem. Soc., 2017, 139, 10909–10918 CrossRef CAS PubMed
.
- K. Kaup, A. Assoud, J. Liu and L. F. Nazar, Fast Li-Ion Conductivity in Superadamantanoid Lithium Thioborate Halides, Angew. Chem., Int. Ed., 2021, 60, 6975–6980 CrossRef CAS PubMed
.
- I. Hanghofer, B. Gadermaier, H. Martin and R. Wilkening, Fast Rotational Dynamics in Argyrodite-Type Li6PS5X (X: Cl, Br, I) as Seen by 31P Nuclear Magnetic Relaxation-On Cation-Anion Coupled Transport in Thiophosphates, Chem. Mater., 2019, 31, 4591–4597 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ya00075c |
| This journal is © The Royal Society of Chemistry 2023 |