Atomistic simulations of chitosan as a possible carrier system for miRNA transport

Abstract

MicroRNA (miRNA) is considered today as a prospective pharmacological agent for the development of novel high-technological medicines. In order to maintain its active form in the aggressive biological environment, it usually needs protective drug delivery carriers. Chitosan is one of the most promising materials for such carriers, since it bears many useful properties such as mucoadhesion, the ease of modification, low cost and biocompatibility. Here, we present the results of the classical molecular dynamics simulations of polymeric chitosan/miRNA complexes. We show that the degree of protonation and acetylation of chitosan have a clear influence on the formation of the complexes. Whereas the protonation degree affects the total number of RNA chains forming contacts with chitosan, the acetylation degree affects the mutual adsorption configuration and leads to lower adsorption energies for individual chains.

---

1 Introduction

MicroRNAs (miRNAs) are short non-coding oligonucleotides with about 22 bases that play an important regulatory role in the proliferation and differentiation of eukaryotic cells,¹ targeting messenger RNA for cleavage or translational repression. They were found for the first time in mammalian cells more than 20 years ago.² Meanwhile, they present a new promising class of therapeutic activities, which are already employed in the treatment of different types of cancer,^3–11 including carcinoms³ and pancreatic,¹² breast^4,8 and liver cancers.^11,13 Nowadays also synthetic miRNAs have become more and more important.³ As an important application, they are employed in attenuated virus vaccines loaded with an expression cassette encoding a synthetic miRNA, which targets the structural proteins of the virus.^14,15

Independently of the type of treatment, miRNA molecules need a delivery system that protects them against serum endonucleases, avoids immune detection, prevents non-specific interactions with proteins or non-target cells and promotes cell entry.¹⁶ Ideally, the miRNA should be released in the cytosol of target cells to be available for the translation machinery. Therefore, miRNA delivery systems should have a balance between the association outside the cytosol and the dissociation within it.

To date, many strategies have been investigated for RNA carrying systems. Many delivery systems form cationic complexes with miRNA, which can be taken up by the cell by endocytosis.¹⁷ Examples are peptide-based nanoparticles rich in arginine and lysine amino acids^18,19 or lipid-based nanoparticles.^20–22 Despite some problems related to toxicity, degradability and immune stimulation, liposomes are widely used as RNA carriers^20–22 due to a large number of possible modification paths and the good fluidity of lipid bilayers, which enable them to easily cross the cell membrane. As an alternative, also inorganic delivery systems have been tested, due to their small size in combination with non-toxic and immunologically inert properties. These showed a high transfection potency, especially for luciferase mRNA.²¹ Another class of carriers are polymeric nanoparticles (NPs).^23–28 Numerous studies deal with the effect of the composition and topology of the polymers^29,30 on the transfection rate. It has been found that an increasing number of amino groups in cationic polymers lead to an increase of the transfection efficiency.³¹

A very prominent candidate among polysaccharide-based delivery systems is chitosan. Chitosan has unique physicochemical and biological properties, including high biocompatibility, low cost and good mucoadhesion.^32–34 It is a biodegradable cationic polysaccharide formed by deacetylation of chitin and consists of units of D-glucosamine and N-acetyl-D-glucosamine.¹ The number of units in each chain is defined as the degree of polymerization (DP) and the number of N-acetyl-D-glucosamine in the chitosan chain is defined as the fraction of acetylation (FA).^1,35 Due to the presence of an amino group in each D-glucosamine monomer, chitosan can be easily modified to tailor its properties, such as solubility or a certain biological activity.^32,33 The amino group can undergo protonation, acylation or alkylation, can react with aldehydes and ketones, provide a grafting site of the polymer chain, induce the chelation of metals, and drive the formation of quaternary ammonium salts, hydrogen bonds with polar atoms, and other reactions. In addition to the amino group, two hydroxyl groups are present at the C2 and C6 positions of the glucopyranose monomer ring. Owing to these groups, a further number of reactions become possible, such as etherification,^36,37 graft copolymerization,^38,39 and O-acylation.³⁴ Thus, it is possible to modify chitosan to obtain antibacterial, antifungal, and antiviral properties, combined with hypoallergenicity, biological compatibility and biodegradability.³⁴ In particular, the possibility of various chemical modifications makes chitosan a promising candidate for miRNA delivering systems, as the interplay of association and dissociation could be triggerd by a balance between carefully tuned molecular states.¹

The complexity of chitosan's molecular properties, leading to various and difficult to predict conformational states with different coordination and reaction activities, has motivated many mechanistic investigations based on molecular dynamics (MD) methods. During the last decade, MD simulations have been carried out for both RNA^40–42 and chitosan^43–45 molecules. However, studies of the interaction between these molecules and the formation of chitosan/RNA complexes are limited by the lack of reliable force fields that allow a consistent description of the behaviour and interaction of the two molecules together. A reliable chitosan parametrization was developed recently by Naumov et al.⁴⁶ within the modified GROMOS 56ACARBO force field. It was shown that the modified GROMOS 56ACARBO allows for a reliable description of the interactions between chitosan and proteins such as insulin.⁴⁷ However, the force-field parametrization of Naumov et al.⁴⁶ is limited to the description of non-terminal units of N-acetyl-D-glucosamine. In recent studies, Cord-Landwehr et al.⁴⁸ emphasized the influence of the patterns of terminal acetylated units (PA) in chitosan on its specific biological activity. These patterns are formed by use of different types of chitinases and chitosanases. Most experiments are limited to the analysis of the degree of polymerization (DP) and the FA, whereas the analysis of the PA has been rarely performed to date.^35,48

This motivated us to generate a new set of terminal and non-terminal N-acetyl-D-glucosamine residues within the framework of the GLYCAM force field.⁴⁹ After a validation of the new AMBER-based parameter set, we performed simulations of chitosan molecules with different protonation degrees (PDs) in D-glucosamine and different FA, forming complexes with a pharmacologically relevant miRNA fragment. On the basis of the obtained results, we discuss the potential capability of chitosan-based delivery systems at the molecular level.

2 Methods

2.1 Description of the miRNA model

Our study focuses on the hsa-miR-145 miRNA, which has been considered as a potential candidate for anti-metastatic therapies in complex with chitosan as the delivery carrier, because of its role as a regulator of cancer-related genes in human cells.¹ The entire hsa-miR-145 molecule is composed of a single strand of 88 nucleotides folded in a stem-loop structure with some degrees of imperfect pairing in the stem. The biologically relevant unit of hsa-miR-145 is a 22-mer RNA duplex present in the stem part of the molecule, with base sequences of the two strands 3′-GGAUUCCUGGAAAUACUGUUCU-5′ and 5′-GUCCAGUUUUCCCAGGAAUCCC-3′, respectively. An initial 3D model of the duplex, which we will call for brevity miRNA-145 or just miRNA, has been produced by predicting the entire structure of hsa-miR-145 with the SimRNA web server and carving out of the stem the biologically active miRNA-145 portion. The duplex was equilibrated in a water cell using the standard MD protocols presented below. The resulting structure was then used as the basis for simulations in complex with chitosan.

2.2 Description of the chitosan model

Nine new residues were created within the AMBER force field, starting from one terminal residue with a free OH group at C4; one intra-chain (inner) residue that can be repeated n times in a chitosan polymer, and one reducing terminal residue with a free OH group at C1 (see Fig. 1). Each of these three residues can be either protonated, acylated and non-protonated. In the following, these residues will be designated according to the GLYCAM naming rules from the AMBER-based carbohydrate forcefield GLYCAM06.⁴⁹ The C1 terminal residues of acetylated, protonated, and non-modified β-D-glucosamine are called 0YB, 0YnP and 0Yn, respectively. The inner residues are called, accordingly, 4YB, 4YnP and 4Yn. To highlight the reducing character of the C4 glycosidic terminal, the residues are called rYB, rYnP and rYn, respectively (Fig. 1).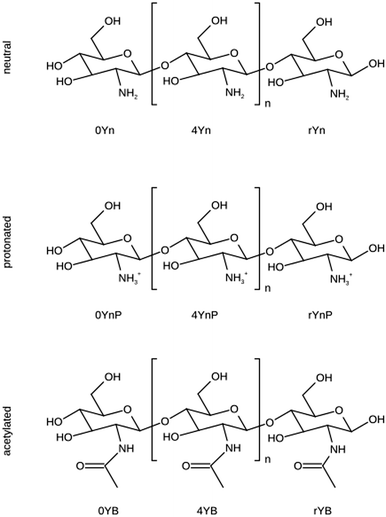

Fig. 1 Schematic view of chitosan residues. D-Glucosamine is represented in its neutral or protonated form. N-Acetyl-D-glucosamine is named the acetylated unit. The naming scheme used is in line with the GLYCAM AMBER-based carbohydrate force field.⁴⁹ In the three-position code, the second (central) position holds a “Y” for the carbohydrate ring species. The first sign describes the unit position in the chain: “0” for the C4 terminal residues, “4” for the central unit in a chain and “r” for the C1 terminal residue. The code in the 3rd position describes the substitution at the C2 positions with the letters “n” for the normal residue mode, “nP” for the protonated version and “B” for the acetylated species.

The geometry of the chitosan residues was optimized using DFT calculations at the b3pw91/6-311G(d,p) level in analogy to the GROMOS-based chitosan force field by Naumov and Ignatov.⁴⁶ In the AMBER-based carbohydrate force field GLYCAM06,⁴⁹ the calculations of RESP charges were performed at the HF/6-31G* level. In our work, we did not average the charges for the conformers to better represent the intermolecular properties, in view of the complexity of the calculations. All the DFT calculations were carried out using the Gaussian03⁵⁰ code. Two terminal residues (protonated and non-modified β-D-glucosamine) are present in GLYCAM06.⁴⁹ This allows us to compare our derived RESP charges with the values of the conventional AMBER force field⁵¹ (Table S1 of the ESI†). Using the reparametrized residues, we computed the potential energy surface of a water molecule interacting with our parametrized residues and the ones in GLYCAM06. The very small difference confirms the very good agreement among the two parametrizations (Fig. S1 of ESI†). The bonding force constants and Lennard Jones parameters for the complete description of the force field could be adopted directly from the GLYCAM06 force field.⁴⁹ In combination with the newly established set of RESP charges and the optimized geometries, prepi files for all nine residues shown in Fig. 1 were created and made available in Fig. S2 (ESI†).

2.3 miRNA–chitosan systems

Chitosan presents variations in the degree of polymerization (DP), the degree of acetylation (DA) and the patterns of acetylation (PA).^35,48 The pH sensitive degree of protonation (PD) is limited by the presence of amino groups in D-glucosamine and thus, indirectly, is influenced by the degree of acetylation. In our work, we have chosen a uniform polymer length (20 monomers), in the region between oligomers (<10 monomers) and polymers (>100 monomers).^35,48 This length is sufficient to allow chitosan molecules to form individual cage networks around the miRNA molecules. The variations of DP and DA should give us insights into the possible variability of chitosan–miRNA interactions.

As stated in the Introduction section, delivery systems for miRNA molecules are cationic substances. Under physiological conditions, nucleic acids are polyanions. Each phosphodiester in the backbone (with pK_a values close to 2⁵²) is negatively charged under physiological conditions, whereas all nucleobases and the ribose sugar are uncharged. The pK_a values of adenine, cytosine, guanine and uracile are 3.6, 3.6,⁵³ 4.2, and 9.2,⁵⁴ respectively. The 2 OH of the ribose sugar has a pK_a value of around 12.^54,55

In contrast, the pK_a values of the amino group in the chitosan residues are in the range of 6.17–6.51, depending on the molecular weight and degree of acetylation.⁵⁶ Thus, under physiological conditions, the protonation state of this group can vary easily, leading to a PD of 0% at pH values of around 8.5 and a PD of 90% at pH values of around 5.55. At a physiological pH of 7.4, the PD is expected to be around 30%. Therefore, in our study of miRNA complexation, we varied the PD of chitosan by keeping the charge of miRNA constant. Namely, we simulated five systems of chitosan/miRNA complexes, in which the PD values of chitosan are 0, 30, 50, 75, and 90%, without acetylation (DA = 0). Additionally, we simulated a sixth system with a PD of 50% and a DA of 20%.

Each system consisted of 18 chains of chitosan with 20 monomer units per chain, surrounding one miRNA duplex (22 nucleotides). The respective topology and coordinate files were created using the AmberTools v.18⁵⁷ and the generated input files were converted to GROMACS inputs via the conversion script acpype.⁵⁸ The same initial geometry was used for all PD systems to reach a high degree of comparability. The simulation cell had dimensions of 15 × 15 × 15 nm³ and was solvated with around 100 000 SPC water molecules.⁵⁹ The net system charge was balanced by adding the necessary amount of Na⁺ or Cl⁻ counterions, depending on the PD of chitosan, resulting in about 310 000 total atoms in each system.

2.4 Calculation protocol

All classical force field simulations were performed using the GROMACS program package v.2018.3.⁶⁰ All systems were equilibrated according to the standard MD protocols. First, the system was minimized until the convergence of the forces below a threshold of 1000 nN mol⁻¹ was reached, with position restraints on the chitosan and miRNA molecules. Afterwards, a minimization of the complete system was performed. A cutoff of 1.5 nm was used for the VdW interactions and the electrostatics. Afterwards, MD simulations in the NVT and NPT ensembles, each lasting 0.15 ns, were performed using the velocity-rescaling thermostat and the Parrinello-Rahman barostat as implemented in GROMACS, gradually increasing the temperature of the system to 300 K and adjusting the pressure to 1 atm. A time step of 2 fs was used for all molecular dynamics simulations, keeping fixed the distances of bonds including hydrogen atoms with the LINCS algorithm. After a careful check that the water solvent reached its equilibrium density, 100 ns production runs were performed for each system. The structural analyses of all miRNA/chitosan complexes were performed on the basis of the production runs only.

2.4.1 Metadynamics simulations. In the Metadynamics (MetaD) simulations, small systems containing only one chain of chitosan or chitin with a length of ten monomers were placed in a box of 5 × 5 × 7 nm³ and solvated with about 5500 SPC water molecules. The systems included neutral, protonated and acetylated chitosan states, and were used to compare two sets of force field parameters: (i) the previous GROMOS-based force field,⁴⁶ and (ii) the AMBER-based parametrization⁴⁹ including our new residues. In the calculations with GROMOS, the fully acetylated system contained 96.6% rather than 100% acetylated residues, because there are no terminal residues for acetylated chitosan in this force field. During the MetaD simulations, Gaussian potential hills with a height of 1.2 Å and a width of 0.03 Å were placed every 1 ps along the chosen one-dimensional collective variable, namely the θ coordinate describing the glycosidic ring puckering. The simulations lasted about 30 ns, which were always enough to achieve convergence the associated free-energy profile. A plot of the convergence of ΔG values computed from the obtained profiles is illustrated in Fig. S3 of the ESI.†

2.4.2 Replica-exchange simulations. In the replica-exchange (RE) simulations, systems containing only one chain of chitin or chitosan with a PD of 50% PD with a length of sixty monomers were placed in a box of 5 × 6 × 30 nm³ and solvated with 27 600 water molecules. The RE simulations were performed with PLUMED v 2.4.3⁶¹ linked to GROMACS v.2018.3,⁶⁰ with 24 replicas in a temperature window from 300 to 500 K and lasted 100 ns each. Tables with the exchange probabilities and round table times (RTT) of chitosan and chitin are listed in Tables S4 and S5 in the ESI.† The exchange-maps of chitosan and chitin are plotted in Fig. S4 and S5 in the ESI.†

2.4.3 Potential of mean force calculations. For selected miRNA/chitosan complexes, the interaction energy was quantified in terms of the potential of mean force (PMF). For this, the selected structures corresponding to representative adsorption modes were cut out of the simulation cell and added into a new box with a maximum size of 10 × 10 × 30 nm³. These systems contained the miRNA molecule and only one chain of chitosan. To compute the PMF, the chitosan chain was positioned at varying distances from the miRNA molecule. The starting distance 0 was the initially identified stable adsorption mode. The distance is increased by intervals of 2 Å up to 17 nm. The forces were averaged over a set of 40–50 frames sampled every 10 ns. The force constant of the spring used to restrain the chitosan molecule at an appropriate distance was 1000 kJ mol⁻¹ nm⁻².

3 Validation of the chitosan model

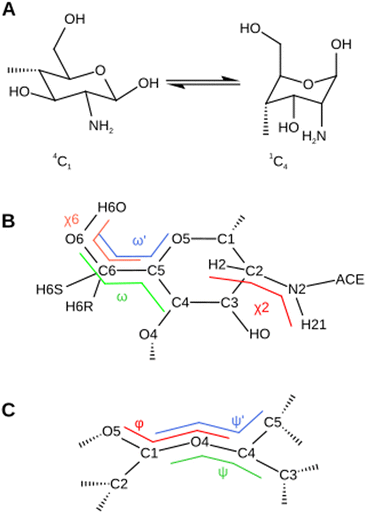
The newly calculated charges, listed in Table S1 of the ESI,† are in very good agreement with the GLYCAM06⁴⁹ parameters. The coefficient of determination R² is 0.96 and 0.98 for the protonated and non-protonated residues, respectively. Three key structural parameters of the chitosan residue (Fig. 2) are investigated with our new parameter set, namely the ring puckering the the pyranose ring (Fig. 2A), the conformation of the exocyclic groups (Fig. 2B) and the conformation of the glycosidic bond (Fig. 2C). All values predicted in the MD simulations are compared either to chitin systems simulated with the conventional GLYCAM06 ff,⁴⁹ to the established GROMOS forcefield for chitosan⁴⁶ or to literature values.

Fig. 2 Schematic illustration of the conformations and torsional angles of chitosan used for the validation of the newly parameterized force field. (A) The transition of the pyranose ring specified as ⁴C₁ → ¹C₄. (B) The position of the exocyclic acetyl group is described by the (χ₂) torsional angle. The (ω), (ω′) and (χ₆) torsional angles describe the gauche/trans conformations and influence the NMR coupling constants. (C) The glycosidic conformation is specified by the torsional angles (ϕ) and (ψ).

3.1 Conformation of the pyranose ring

The conformations of glucopyranose rings are very sensitive to the intramolecular force field parameters. Among the possible conformational transitions, the ⁴C₁ → ¹C₄ transition is the most sensitive. There are no parameters in the here-investigated force fields that directly affect this transition. Thus, the predicted transition energies depend on the whole set of force field parameters and special attention should be paid to evaluate how well the new parameter set influences them. The conformation of the pyranose ring is well described by the three Kremer–Pople spherical coordinates – the meridian angle ϕ, the azimuth angle θ and the radius Q.⁶⁸ The ⁴C₁ → ¹C₄ transition corresponds to a variation of θ within the window [0,180] degrees, respectively (Fig. 2A). In general, the ring puckering energy landscapes differ for different monosaccharides in glycosaminoglycans.^69,70 However, the large majority is stable in the ⁴C₁ conformation with θ = 10°, which is separated from the ¹C₄ conformations by a barrier of about 10 kcal/mol.^69,70 For chitin, the ground state corresponds to a value of θ = 10.1 ± 5.5°.⁷¹ To assess the reliability of our force field in describing the glucopyranose ring puckering, we calculated the free-energy profile along θ for both force fields using MetaD simulations (Section 2.4.1) (Fig. 3A). The ground state of all chitosan residues corresponds to θ = 10° for both force fields, which is in perfect agreement with the experimental data.⁷¹ However, the transition barriers predicted by the AMBER based parameter set vary from 7 to 15 kcal mol⁻¹ depending on the residue. In the GROMOS ff,⁴⁶ the barriers are smaller and never exceed 10 kcal mol⁻¹. Nevertheless, in both cases, the energy barriers are in the range of reported literature values for saccharides^69,70 and predict the residues in chitin⁷¹ and chitosan to assume a ⁴C₁ chair conformation. Thus, the new parameter set gives an appropriate description of the puckering properties of the glucopyranose ring.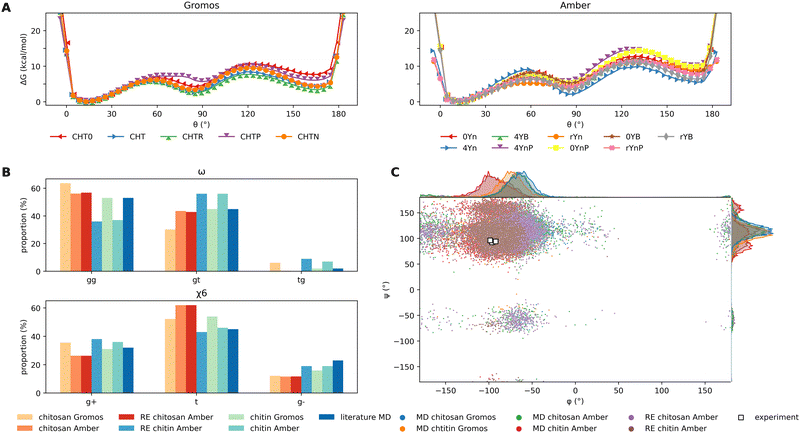

Fig. 3 The newly parametrized residues for chitosan based on the AMBER parametrization scheme are validated for the characteristic glycosidic properties against the GROMOS force field published in Naumov et al.:⁴⁶ (A) the resulting energy barriers for the transition of the pyranose ring ⁴C₁ → ¹C₄ for chitosan and chitin residues are calculated using MetaD simulations for all individual residues with the GROMOS force field⁴⁶ and our new AMBER based parameterization. In the GROMOS force field, the nomenclature is as follows: CHT0 is the C1 terminal chitosan, CHT, CHTR and CHTP are the central neutral, acetylated and protonated chitosan residues and CHTN is the C4 terminal residue. The naming scheme for our parameterization is shown in Fig. 1. Despite the energy barriers being consistently higher for the AMBER parameterization, the same lowest energy conformation at θ = 10° is obtained. (B) The chitin and chitosan rotamers are divided into gauche and trans populations named gg, gt and tg regarding the ω torsional angle and (g+, t and g−) regarding the χ₆ torsional angle. All values are evaluated from the classical simulations of either chitin (CHTR, yellow/red coloring scheme) or chitosan (CHT, cyan/blue coloring scheme) with GROMOS⁴⁶ or our AMBER paramterization. In addition, the conformational sampling is verified by means of replica-exchange (RE) simulations (RE) and compared to literature values.^62–64 (C) The distribution of the glycosidic conformations over the simulation time in both the MD and RE simulations is illustrated by superimposed torsional plots of (ψ) and (ϕ) for the chitin and chitosan chains for the AMBER and GROMOS parameterizations. The corresponding distributions of each angle are plotted at the graph sides in their corresponding color. The respective experimental values are marked as white dots.^65–67

3.2 Conformation of exocyclic groups

The analysis of the conformation of the exocyclic groups, as defined by their corresponding torsional angles, was carried out taking into account the conformer populations obtained in MD simulations of solvated chitin and chitosan systems. From these populations, we also computed NMR coupling constants that could be compared to the experimental results. Since different conformations can be separated by significant energy barriers, the standard MD simulations were supplemented with Hamiltonian RE calculations (Subsection 2.4.2), which ensure better ergodicity and allow for a more accurate prediction of conformation probabilities. The details of the RE simulations are listed in Tables and Fig. S4 and S5 in the ESI.† Two conformations attained by the exocyclic groups are representative of the dynamics and therefore the intermolecular interactions between chitosan molecules. The position of the acetyl group can be quantified by the torsion angle H2A–N2–C2–H2 (χ₂). Another important exocyclic group is the hydroxymethyl group (C6–O6–H6O atoms). The conformation of this group is characterized by the torsional angles C4–C5–C6–O6 (ω), O5–C5–C6–O6 (ω′) and C5–O6–O6–H6O (χ₆) (Fig. 2B). The chitosan and chitin rotamers are therefore divided into two gauche and one trans conformers (g+, g−, and t) depending on the χ₆ angle, and in gg, gt and tg conformers depending on the ω angles, corresponding to the value windows (0°, 120°], (120°, 240°] and (240°, 360°], respectively (Fig. 2B).

As seen in Fig. 3B, the ω and χ₆ populations of the simulations predicted by our AMBER-based parameter set are in good agreement with the populations of the GROMOS simulations and of other MD works in the literature.^62–64 The NMR constants ³J_H2;H21, ³J_H5;H6R and ³J_H5;H6S coupling pairs of hydrogen atoms (Fig. 2B) can be estimated on the basis of equations given by Stenutz et al.⁷⁵ and compared directly with the corresponding experimental values^62,76 (Table 1). The ³J_H5,H6R and ³J_H5,H6S values are in very good agreement with both the experimental data and the results of the GROMOS force field.⁴⁶ In the case of chitin, the ³J_H5,H6S values are slightly overestimated. The values of ³J_H2,H21 for the AMBER-based parameter set are slightly underestimated compared to the GROMOS calculations and experimental data.

Table 1 The ³J_H,H NMR constants HZ are calculated for chitin and chitosan residues using the AMBER based parametrization and the GROMOS force field.⁴⁶ The MD reference values of Mobil et al.⁶² were evaluated from 5 ns MD simulations of N-acetyl-D-glucosamine monomers and the ones of Hansen et al.⁶³ from 50 ns MD simulations

	MD chitosan	MD chitin	MD chitosan	MD chitin	RE chitosan	RE chitin	Ref.; Method
	GROMOS	GROMOS	AMBER	AMBER	AMBER	AMBER
a The values for coli capsular polysaccharide K5 comprise N-acetyl-D-glucosamine (GlcNAc) and glucuronic acid (GlcA) and are identical to N-acetyl-heparosan. b Since our system does not present H2 atoms, the representative positions were calculated from the positions of the C2, C3 and N atoms. c The reported value refers to β-D-glucopyranose and its derivatives.
^3 J ^TH5,H6R	5.25	5.34	5.71	6.45	5.21	6.28	5.57^a; NMR^72
^3 J ^SH5,H6R	4.77	4.97	5.43	6.3	4.72	6.09	5.95^c; NMR^73
							6.0^c; NMR^74
^3 J ^TH5,H6S	1.70	2.27	2.50	3.12	1.70	2.96	1.85^a; NMR^72
^3 J ^SH5,H6S	1.58	2.18	2.42	3.07	1.57	2.91	2.27^c; NMR^73
							2.1^c; NMR^74
^3 J H2,H21	—	9.19^b	—	8.35	—	8.91	9.07; NMR^62
							10.39; MD^62

---

3.3 Glycoside conformation

There are two important angles that characterize the glycosidic bond between two pyranose rings (Fig. 2C), named ϕ (O5–C1–O4–C4) and ψ (C1–O4–C4–C3). Some authors use the angle ψ′ defined by C1–O4–C4–C5 instead.^65,66 As we can see from Fig. 3C, the values of ϕ and ψ predicted by both the AMBER-based and the GROMOS force fields are close to each other and well distributed around the experimental values.^65–67 The results of MD simulations were confirmed by RE simulations with better statistics.

4 Results and discussion

In this section, the results of the simulations of miRNA complexed with chitosan are presented. Besides the influence of protonation/acetylation on the self-association of the chitosan strands, also their influence on the adsorption mode and interaction with miRNA will be discussed.

4.1 Influence of the degree of protonation of chitosan on miRNA complexation.

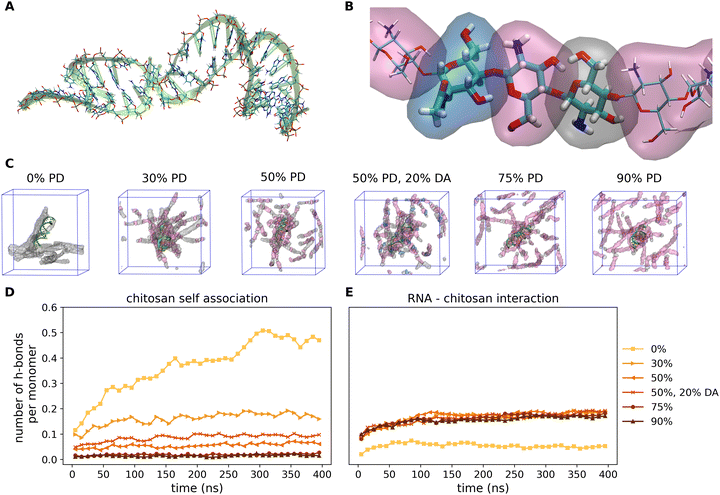
Fig. 4 shows the representative snapshots of the miRNA–chitosan complexes with varying protonation degrees (PDs) of the chitosan chains. With neutral chitosan (PD = 0%), a significant portion of the strands in the image section is seen to be in contact with each other even though the packing around the miRNA appears rather loose. In contrast, with 30% PD, the chitosan strands are clearly more centered around the miRNA molecule. This impression is also maintained in the PD 50% systems. Only the systems with a higher PD show a low density of chitosan strands around miRNA.

Fig. 4 Dependence of the miRNA complexation upon the chitosan protination degree. (A) Schematic snapshots of the equilibrated miRNA structure used in this work. The molecule is presented in a “new ribbon” structure in green and the atomistic details in the conventional naming scheme (carbon (cyan), oxygen (red), nitrogen (blue), phosphor (taupe), and hydrogen (white)). (B) Through the combination of chitosan units in neutral (grey), protonated (magenta), or acetylated (blue isosurface) forms, chains with a total length of 20 monomers with specific degrees of protonation and acetylation (PD and DA) are created. (C) Snapshots of the simulated miRNA–chitosan simulation cells after 400 ns of simulation time for PD equal to 0%, 30%, 50%, 75%, 90% and a 50% PD with 20% DA are illustrated. The miRNA ribbons are green and the chitosan chains are shown in transparent surfaces according to the colouring scheme introduced in (B) (water not shown). (D and E) Number of hydrogen bonds over the simulation time among chitosan chains and between miRNA and chitosan, respectively, depending on the degrees of protonation and acetylation.

This observation can be further quantified. In Fig. 4D and E, the number of hydrogen bonds representative of the self-association of chitosan chains and the chitosan/miRNA complexation are plotted as a function of the simulation time. It is clearly visible that the amount of chitosan self-association decreases continuously with increasing PD. Whereas for the neutral system the value saturates at about 0.5 hydrogen bonds per chitosan monomer unit (meaning that each second monomer is engaged in a hydrogen bond), this value is reduced to 0.15 for a PD of 30%, and is reduced further at higher PD values. However, it is striking that the system with a PD of 50% and a DA of 20% presents more hydrogen bonds (about 0.1 per monomer) that the respective non-acetylated system (about 0.07 per monomer), which indicates that the degree of acetylation can also influence the self-association of the chitosan strands. In contrast, regarding the miRNA–chitosan interactions (Fig. 4E), a very small value of hydrogen bonds forms in the case of neutral chitosan, whereas about 0.15 hydrogen bonds per monomer form at PD values of 30% and a further PD increase does not lead to more bonds. It thus seems that a PD of 30% is already large enough to enable the maximum possible embedding of the miRNA in chitosan.

So far, the number of hydrogen bonds refers to the total number of chitosan monomer units in the simulation cell without a relationship to the identity of the monomers to a specific chitosan chain. In the next step, we focused on individual chitosan chains to determine at which degree of protonation the largest contact area to miRNA is established. The evaluation is performed using the GROMACS evaluation tool “gmx hbond”⁶⁰ with default parameters. The last 100 ns of the total simulation time are used for this evaluation as we are interested in the equilibrium values. Fig. 5A shows the histograms of the percentage of individual chitosan chains (out of a total of 18) presenting a number of H-bonds per monomer in the range of 0.0 to 0.8. For reference, a value of 0.2 indicates that one out of five monomers in a chain is bonded to miRNA. For all protonation degrees, the majority of chitosan chains have less than 0.1 H-bonds per monomer. However, whereas for neutral chitosan only 20% of the chains engage in more than 0.1 bonds, this increases to 50% at PD values of 30% and 50%. Furthermore, for the largest PD values (75% and 90%), one or two chains are able to form 0.7 and 0.8 H-bonds per monomer to miRNA. This indicates that the miRNA is tightly complexed by a small number of chains, in which every five monomers four are bound to it. This leaves little space for the other chain to bind the molecule. This complexation regime is not observed at all for the neutral chitosan system, where the highest complexation degree is 0.5 for only one chain. The systems with PD values of 30 and 50% show the highest amount of chains forming an intermediate number of H-bonds to miRNA. It is noticeable that the acetylated system has a significantly higher proportion of strands with 0.4 H-bonds per monomer than the comparable pure D-glucosamine system at the expense of higher amounts of H-bonds per chain. In summary, the MD simulations suggest that, at very high PD, only a few chains bind to miRNA but all of them with a larger contact area, whereas an intermediate PD results in more chains connected more loosely to the miRNA, balancing the degrees of chitosan self-association and chitosan/miRNA complexation. This rather complex adsorption behaviour motivated us to have a closer look on which functional groups in the chain are actually involved in the mutual miRNA/chitosan interaction, which will be the focus of the next section.

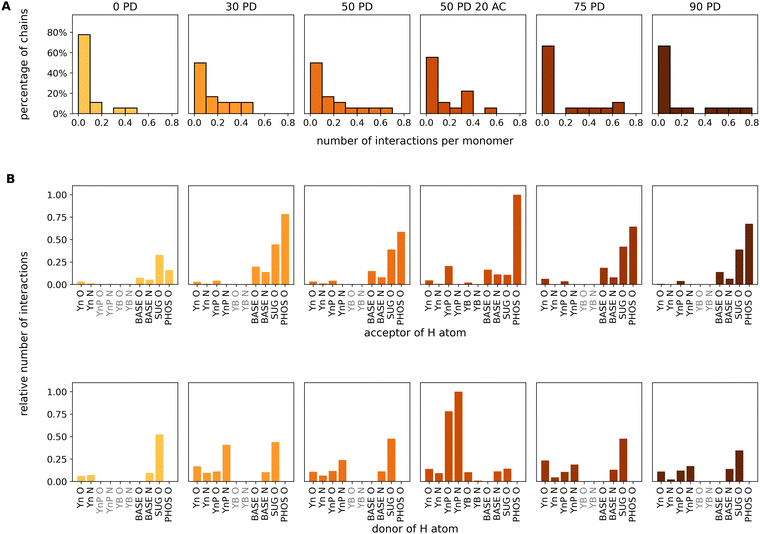Fig. 5 Analysis of intermolecular interactions based on the last 100 ns of the MDs for the miRNA/chitosan complexes with different protonation degrees and one acetylation degree of chitosan. The color code for the PD is analogous to Fig. 4D and E. (A) Percentage distributions of the chitosan chains interacting to miRNA in dependence of the number of hydrogen bonds per chitosan monomer in the corresponding chains. (B) Relative number of interactions for the individual acceptor or donor atoms in intermolecular hydrogen bonds or salt bridges. The chitosan residues (see Fig. 1) are labeled as Yn (neutral), YnP (protonated), and YB (acetylated). PHOS, SUG, and BASE indicate the phosphate group, the ribose and the base of the miRNA. Donor groups form bonds via H atoms bound to either O or N atoms. Acceptor groups carry either O or N atoms involved in H-bonds with a donor. In total, there are seven acceptor groups and eight donor groups in our systems. Residues which are not present in the individual systems are highlighted in gray.

4.2 Analysis of functional groups contributing to miRNA/chitosan contacts.

The analysis of all possible chitosan/miRNA contacts revealed that intermolecular interactions only form via donor–acceptor H-bond pairs. These were analysed using the GROMACS h-bond tool “gmx hbond”,⁶⁰ and the results are presented in Fig. 5B. We have specified all functional groups in the chitosan and nucleic acids either as a donor (holding a hydrogen atom) or an acceptor (with an oxygen or a nitrogen atom). Regarding acceptors, it is quite clear that the phosphate group of miRNA dominates the hydrogen-bond contacts of all systems except for neutral chitosan. However, while all pure D-glucosamine systems also have a significant contribution from other parts of the nucleotides, the role of the acceptor is most pronounced in the acetylated system. Regarding the donor, more variations are revealed. At the miRNA side, hydrogen atoms bound to N atoms of the bases or to O atoms of ribose can act as donors. Except for the neutral system, the dominating donor group is always one of the amino groups in the chitosan chain. Whereas for the 30% PD system the amino group of the protonated monomers dominates, it is more equally distributed between protonated and neutral residues of the other PD values. The hydroxyl groups of the pyranose rings contribute as well. At a PD of 50%, the effect of acetylation is visible as a significant larger number of H-bonds formed by the protonated D-glucosamine residues with respect to the non-acetylated chain. Notably, the relative distributions of different h-bonds are very similar for all protonation degrees, except for the neutral system. Here, the total number of contacts is much smaller, in agreement with the results shown in Fig. 4.

4.3 Modes of miRNA–chitosan interactions

Based on the previous findings, it becomes apparent that there must be different types of interaction configurations within the chitosan/miRNA complexes. We found, in particular, three representative adsorption modes, as shown in Fig. 6A. In type I, the chitosan chain is oriented parallel to the miRNA molecule along the major axis. Approximately 50% of chitosan chains bind to miRNA in this way. In type II, accounting for about 35% of the complexes, the chitosan strand is embedded in the major grove of miRNA. The remaining 15% of binding chitosan chains are located along the minor grove of miRNA (type III). The difference between the types of the adsorption modes I, II, and III can be quantified using the so-called coordination angles of the chitosan–miRNA interaction regions. These are defined as the angle between the tangential direction to the miRNA strand and the vector connecting the most-distant C atoms (i.e. C1 and C4) of adjacent chitosan sugar rings (a chitosan dimer) at the point of mutual interaction. Fig. 6B shows the typical distributions of the coordination angles for the different modes corresponding to the exemplary snapshots in Fig. 6A. In Type I, most of the angles are less than 40°. In type II, most angles exceed 40°. In type III, the angles distribute evenly above and below 40°. Even though these three types are the most representative ones in our simulations, the adsorption configurations of mixed type have been observed as well. All adsorption modes in the systems with varying PD and DA can be visualized in two-dimensional maps constructed in the following way. For each chitosan chain interacting with miRNA, we first compute the distribution of the coordination angles, which contains a certain number of coordination angles below 40° (n_<) and a number of coordination angles above 40° (n_>). This distribution (i.e. this binding chain) is then represented by a dot in a Cartesian map spanned by the n_< and n_> coordinates. All interacting chains in each system (with a given PD) are then added to the map, increasing the diameter of each dot according to the number of hits in the same map point (the number of distributions with same n_<, n_> values). The resulting maps are plotted in Fig. 6C for all studied systems with different PD and DA. Depending on the predominant adsorption modes, the maps present the clusters of dots located either below or above the map diagonal. Clusters in the lower map region correspond to a predominantly type I adsorption mode. Clusters in the upper map region correspond to a predominantly type II adsorption mode. Clusters along the diagonal correspond to a predominantly type III adsorption mode. Whereas all non-acetylated systems mostly present adsorption modes of type I and, in minor amount, of type II, the acetylated system clearly favors an adsorption mode of type III. Finally, we quantified the interaction strength in each of these three modes. For this purpose, the representative structures from Fig. 6A were used as initial configurations for PMF simulations. The resulting free-energy profiles as a function of the distance between the geometric centers of the miRNA and chitosan are plotted in Fig. 6C. While the modes of types I and II are associated by adsorption free energies of about 200 kJ mol⁻¹, the adsorption energy of type III (corresponding to an acetylated chain) is much lower, about 80 kJ mol⁻¹. It may be generally true that acetylation may sterically hinder the adsorption of chitosan according to the modes of types I and especially type II, resulting in type III being the dominating one with a reduced free energy of adsorption. Whether or not acetylation would generally lead to less strong miRNA/chitosan interaction remains an open point, which would be interesting to address in future investigations, especially focusing on the ability of chitosan-based carrier systems to easily release the miRNA in the intracellular environment.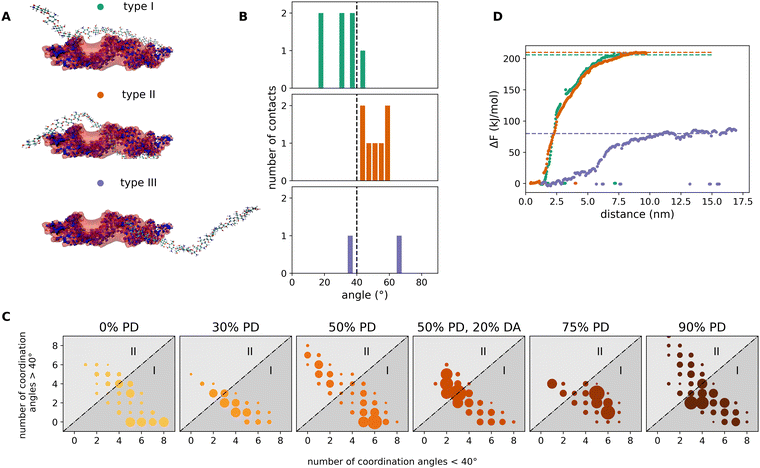

Fig. 6 Analysis of the most representative adsorption modes of chitosan chains on a miRNA molecule. (A) Representative snapshots corresponding to type I, type II and type III modes. In type I, the chitosan chain lies parallel to the miRNA molecule and binds to it via the backbone ribs. In type II, the chitosan chain is embedded in the major grove of the miRNA molecule, wrapping it in a partly helical conformation. In type III, the chitosan chain binds to the minor grove of the miRNA. (B) The three different adsorption modes are defined by the distributions of chitosan/miRNA coordination angles (see text). The angle distributions are calculated for all interacting regions of each adsorbed chitosan chain. The angle distributions mostly below 40° correspond to type I; distributions above 40° to type II and distributions equally split above and below 40° correspond to type III. (C) Adsorption-mode maps based on the number of coordination angles above 40° (abscissa) and the number of coordination angles below 40° (ordinate) in each distribution. Each dot (colored as in Fig. 4) corresponds to an individual chitosan chain. If more than one chain locates in the same map point, the diameter of the dot is increased accordingly. (D) Free-energy adsorption profiles along the distance between the geometrical centers of miRNA and chitosan computed in PMF simulations for the representative miRNA/chitosan complexes shown in (A).

5 Conclusions

In this work, we used atomistic simulations to fundamentally understand chitosan/miRNA interactions, given the promising potential of chitosan as a possible delivery system for miRNA-based drugs. Currently, a variety of biomolecular force fields are available to perform MD simulations of such complex simulation systems. Among them, the AMBER force field is known to reproduce the properties of nucleic acids reasonably well. In particular, the fine-tuning of the AMBER parametrization of RNA oligomers is being currently carried out with the aim of improving the dynamical behaviour of terminal nucleotides.⁷⁷ We have added a set of GLYCAM-based parameters⁷⁸ for terminal and non terminal D-glucosamine and N-acetyl-D-glucosamine residues which consist chitosan and validated them against existing GROMOS parametrization and available experimental results. The new residues have indeed been proven to reproduce the properties of the glycoside chains with high accuracy. When chitosan interacts with miRNA in an aqueous solution, two competing processes take place: the self-association of chitosan and the chitosan/miRNA complexation. We found out that the complexation of miRNA with chitosan is only slightly sensitive to pH (i.e. to the protonation degree of the chitosan monomers), even though the chitosan self-association is significantly reduced. However, the introduction of steric hindrances such as the acetylation of the chitosan monomers promotes a change in the most-dominant adsorption mode of chitosan chains to miRNA. This might also be associated with a reduction of interaction free energy within the complexes, which gives an important clue as to how to keep the complexation reversible after delivery of chitosan/miRNA in the cellular environment. In future experimental works, we would propose to test chitosan candidates as carrier materials with different sized substitute functional groups, to ensure a perfect balance between the protective function during transport and dissolution in the cell at the site of delivery.

Author contributions

The following authors contributed to this work: Alexander Avdoshin: investigation, methodology, validation and visualization, interpretation of the results and writing of the manuscript; Vladimir Naumov: software and methodology; Lucio Colombi Ciacchi: funding acquisition, interpretation of the results and writing of the manuscript; Stanislav Ignatov: funding acquisition, supervision, and writing of the manuscript; Susan Köppen: conceptualization and project management, supervision, interpretation of the results and writing of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We greatfully acknowledge the ZIMMM project ZF4295101AJ6 for providing us the miRNA model structure and the scientists community of the German Research Foundation funded research training group 2247 “Quantum Mechanical Materials Modeling-QM3” for fruitful discussions. The research at the Lobachevsky State University (LSU) was carried out within the framework of the Strategic Academic Leadership Program “Priority 2030”. The student internships between the LSU and the University of Bremen are funded by the German Academic Exchange Service within the “Eastern partnerships” program.

Notes and references

1. B. Santos-Carballal, L. J. Aaldering, M. Ritzefeld, S. Pereira, N. Sewald, B. M. Moerschbacher, M. Götte and F. M. Goycoolea, Sci. Rep., 2015, 5, 13567–13582.
2. B. J. Reinhart, F. J. Slack, M. Basson, A. E. Pasquinelli, J. C. Bettinger, A. E. Rougvie, H. R. Horvitz and G. Ruvkun, Nature, 2000, 403, 901–906.
3. A. Bouchie, Nat. Biotechnol., 2013, 31, 577.
4. C. V. Pecot, R. Rupaimoole, D. Yang, R. Akbani, C. Ivan, C. Lu, S. Wu, H.-D. Han, M. Y. Shah, C. Rodriguez-Aguayo, J. Bottsford-Miller, Y. Liu, S. B. Kim, A. Unruh, V. Gonzalez-Villasana, L. Huang, B. Zand, M. Moreno-Smith, L. S. Mangala, M. Taylor, H. J. Dalton, V. Sehgal, Y. Wen, Y. Kang, K. A. Baggerly, J.-S. Lee, P. T. Ram, M. K. Ravoori, V. Kundra, X. Zhang, R. Ali-Fehmi, A.-M. Gonzalez-Angulo, P. P. Massion, G. A. Calin, G. Lopez-Berestein, W. Zhang and A. K. Sood, Nat. Commun., 2013, 4, 2427–2441.
5. P. Trang, J. F. Wiggins, C. L. Daige, C. Cho, M. Omotola, D. Brown, J. B. Weidhaas, A. G. Bader and F. J. Slack, Mol. Ther., 2011, 19, 1116–1122.
6. A. L. Kasinski and F. J. Slack, Cancer Res., 2012, 72, 5576–5587.
7. M. A. Cortez, D. Valdecanas, X. Zhang, Y. Zhan, V. Bhardwaj, G. A. Calin, R. Komaki, D. K. Giri, C. C. Quini, T. Wolfe, H. J. Peltier, A. G. Bader, J. V. Heymach, R. E. Meyn and J. W. Welsh, Mol. Ther., 2014, 22, 1494–1503.
8. L. Ma, F. Reinhardt, E. Pan, J. Soutschek, B. Bhat, E. G. Marcusson, J. Teruya-Feldstein, G. W. Bell and R. A. Weinberg, Nat. Biotechnol., 2010, 28, 341–347.
9. N. Dimitrova, V. Gocheva, A. Bhutkar, R. Resnick, R. M. Jong, K. M. Miller, J. Bendor and T. Jacks, Cancer Discovery, 2015, 6, 188–201.
10. C. J. Cheng, R. Bahal, I. A. Babar, Z. Pincus, F. Barrera, C. Liu, A. Svoronos, D. T. Braddock, P. M. Glazer, D. M. Engelman, W. M. Saltzman and F. J. Slack, Nature, 2014, 518, 107–110.
11. J.-K. Park, T. Kogure, G. J. Nuovo, J. Jiang, L. He, J. H. Kim, M. A. Phelps, T. L. Papenfuss, C. M. Croce, T. Patel and T. D. Schmittgen, Cancer Res., 2011, 71, 7608–7616.
12. D. Pramanik, N. R. Campbell, C. Karikari, R. Chivukula, O. A. Kent, J. T. Mendell and A. Maitra, Mol. Cancer Ther., 2011, 10, 1470–1480.
13. R. Rupaimoole and F. J. Slack, Nat. Rev. Drug Discovery, 2017, 16, 203–222.
14. J. Li, M. T. Arévalo, D. Diaz-Arévalo, Y. Chen, J.-G. Choi and M. Zeng, J. Controlled Release, 2015, 207, 70–76.
15. S. A. Leon-Icaza, M. Zeng and A. G. Rosas-Taraco, ExRNA, 2019, 1, 1–8.
16. S. L. Ginn, I. E. Alexander, M. L. Edelstein, M. R. Abedi and J. Wixon, J. Gene Med., 2013, 15, 65–77.
17. S. Okay, Ö. Ö. Özcan and M. Karahan, AIMS Biophysics, 2020, 7, 323–338.
18. B. Scheel, R. Teufel, J. Probst, J.-P. Carralot, J. Geginat, M. Radsak, D. Jarrossay, H. Wagner, G. Jung, H.-G. Rammensee, I. Hoerr and S. Pascolo, Eur. J. Immunol., 2005, 35, 1557–1566.
19. T. Schlake, A. Thess, M. Fotin-Mleczek and K.-J. Kallen, RNA Biol., 2012, 9, 1319–1330.
20. K. Muppidi, A. S. Pumerantz, J. Wang and G. Betageri, ISRN Pharm., 2012, 2012, 1–8.
21. F. T. Zohra, E. H. Chowdhury and T. Akaike, Biomaterials, 2009, 30, 4006–4013.
22. R. A. Schwendener, Ther. Adv. Vaccines, 2014, 2, 159–182.
23. J. S. Chahal, T. Fang, A. W. Woodham, O. F. Khan, J. Ling, D. G. Anderson and H. L. Ploegh, Sci. Rep., 2017, 7, 252–261.
24. J. S. Chahal, O. F. Khan, C. L. Cooper, J. S. McPartlan, J. K. Tsosie, L. D. Tilley, S. M. Sidik, S. Lourido, R. Langer, S. Bavari, H. L. Ploegh and D. G. Anderson, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, E4133–E4142.
25. Z. Sharifnia, M. Bandehpour, H. Hamishehkar, N. Mosaffa, B. Kazemi and N. Zarghami, Iran. J. Pharm. Res., 2019, 18, 1659–1675.
26. J. C. Kaczmarek, A. K. Patel, K. J. Kauffman, O. S. Fenton, M. J. Webber, M. W. Heartlein, F. DeRosa and D. G. Anderson, Angew. Chem., Int. Ed., 2016, 55, 13808–13812.
27. A. K. Patel, J. C. Kaczmarek, S. Bose, K. J. Kauffman, F. Mir, M. W. Heartlein, F. DeRosa, R. Langer and D. G. Anderson, Adv. Mater., 2019, 31, 1805116.
28. Y. Liu, Y. Li, D. Keskin and L. Shi, Adv. Healthcare Mater., 2018, 1801359.
29. U. C. Palmiero, J. C. Kaczmarek, O. S. Fenton and D. G. Anderson, Adv. Healthcare Mater., 2018, 7, 1800249.
30. C. Lacroix, A. Humanes, C. Coiffier, D. Gigmes, B. Verrier and T. Trimaille, Pharm. Res., 2020, 37, 30–42.
31. Y. Dong, J. R. Dorkin, W. Wang, P. H. Chang, M. J. Webber, B. C. Tang, J. Yang, I. Abutbul-Ionita, D. Danino, F. DeRosa, M. Heartlein, R. Langer and D. G. Anderson, Nano Lett., 2016, 16, 842–848.
32. J. Zhang, W. Xia, P. Liu, Q. Cheng, T. Tahi, W. Gu and B. Li, Mar. Drugs, 2010, 8, 1962–1987.
33. R. N. Tharanathan and F. S. Kittur, Crit. Rev. Food Sci. Nutr., 2003, 43, 61–87.
34. C. Pillai, W. Paul and C. P. Sharma, Prog. Polym. Sci., 2009, 34, 641–678.
35. J. Wattjes, S. Sreekumar, C. Richter, S. Cord-Landwehr, R. Singh, N. E. El Gueddari and B. M. Moerschbacher, React. Funct. Polym., 2020, 151, 104583.
36. M. A. Krayukhina, N. A. Samoilova and I. A. Yamskov, Russ. Chem. Rev., 2008, 77, 799–813.
37. N. Gorochovceva and R. Makuška, Eur. Polym. J., 2004, 40, 685–691.
38. R. Jayakumar, M. Prabaharan, R. Reis and J. Mano, Carbohydr. Polym., 2005, 62, 142–158.
39. D. W. Jenkins and S. M. Hudson, Chem. Rev., 2001, 101, 3245–3274.
40. G. Paciello, A. Acquaviva, E. Ficarra, M. A. Deriu and E. Macii, J. Mol. Model., 2011, 17, 2895–2906.
41. S. Vangaveti, S. V. Ranganathan and A. A. Chen, Wiley Interdiscip. Rev.: RNA, 2016, 8, e1396.
42. J. Šponer, G. Bussi, M. Krepl, P. Banáš, S. Bottaro, R. A. Cunha, A. Gil-Ley, G. Pinamonti, S. Poblete, P. Jurečka, N. G. Walter and M. Otyepka, Chem. Rev., 2018, 118, 4177–4338.
43. C. H. Borca and C. A. Arango, J. Phys. Chem. B, 2016, 120, 3754–3764.
44. M. T. McDonnell, D. A. Greeley, K. M. Kit and D. J. Keffer, J. Phys. Chem. B, 2016, 120, 8997–9010.
45. J.-W. Shen, J. Li, Z. Zhao, L. Zhang, G. Peng and L. Liang, Sci. Rep., 2017, 7, 5050–5059.
46. V. S. Naumov and S. K. Ignatov, J. Mol. Model., 2017, 23, 244–259.
47. I. Glazova, L. Smirnova, O. Zamyshlyayeva, S. Zaitsev, A. Avdoshin, V. Naumov and S. Ignatov, Supramol. Chem., 2019, 31, 412–423.
48. S. Cord-Landwehr, C. Richter, J. Wattjes, S. Sreekumar, R. Singh, S. Basa, N. E. El Gueddari and B. M. Moerschbacher, React. Funct. Polym., 2020, 151, 104577.
49. K. N. Kirschner, A. B. Yongye, S. M. Tschampel, J. González-Outeiriño, C. R. Daniels, B. L. Foley and R. J. Woods, J. Comput. Chem., 2007, 29, 622–655.
50. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 09, Revision A.02, Gaussian, Inc., Wallingford CT, 2016.
51. T. E. Cheatham III and D. A. Case, Biopolymers, 2013, 99, 969–977.
52. K. G. Devine and S. Jheeta, Life, 2020, 10, 346.
53. National Center for Biotechnology Information. PubChem Database. Adenosine CID = 60961.; Available from.
54. R. M. Izatt, J. J. Christensen and J. H. Rytting, Chem. Rev., 1971, 71, 439–481.
55. I. Velikyan, S. Acharya, A. Trifonova, A. Földesi and J. Chattopadhyaya, J. Am. Chem. Soc., 2001, 123, 2893–2894.
56. Q. Z. Wang, X. G. Chen, N. Liu, S. X. Wang, C. S. Liu, X. H. Meng and C. G. Liu, Carbohydr. Polym., 2006, 65, 194–201.
57. D. A. Case, T. E. Cheatham, T. Darden, H. Gohlke, R. Luo, K. M. Merz, A. Onufriev, C. Simmerling, B. Wang and R. J. Woods, J. Comput. Chem., 2005, 26, 1668–1688.
58. https://parmed.github.io/ParmEd/html/index.html .
59. H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren and J. Hermans, The Jerusalem Symposia on Quantum Chemistry and Biochemistry, Springer, Netherlands, 1981, pp. 331–342.
60. M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1–2, 19–25.
61. M. Bonomi, D. Branduardi, G. Bussi, C. Camilloni, D. Provasi, P. Raiteri, D. Donadio, F. Marinelli, F. Pietrucci, R. A. Broglia and M. Parrinello, Comput. Phys. Commun., 2009, 180, 1961–1972.
62. M. Mobli and A. Almond, Org. Biomol. Chem., 2007, 5, 2243.
63. H. S. Hansen and P. H. Hünenberger, J. Comput. Chem., 2010, 32, 998–1032.
64. W. Plazinski, A. Lonardi and P. H. Hünenberger, J. Comput. Chem., 2015, 37, 354–365.
65. T. Yui, K. Imada, K. Okuyama, Y. Obata, K. Suzuki and K. Ogawa, Macromolecules, 1994, 27, 7601–7605.
66. T. Yui, N. Taki, J. Sugiyama and S. Hayashi, Int. J. Biol. Macromol., 2007, 40, 336–344.
67. K. Okuyama, K. Noguchi, T. Miyazawa, T. Yui and K. Ogawa, Macromolecules, 1997, 30, 5849–5855.
68. Fushinobu S. Cremer-Pople parameter calculator.
69. I. Alibay and R. A. Bryce, J. Chem. Inf. Model., 2019, 59, 4729–4741.
70. O. Guvench, D. Martin and M. Greene, Int. J. Mol. Sci., 2022, 23, 473.
71. B. M. Sattelle and A. Almond, Glycobiology, 2011, 21, 1651–1662.
72. C. D. Blundell, I. S. Roberts, J. K. Sheehan and A. Almond, J. Mol. Microbiol. Biotechnol., 2009, 17, 71–82.
73. M. U. Roslund, P. Tähtinen, M. Niemitz and R. Sjöholm, Carbohydr. Res., 2008, 343, 101–112.
74. Y. Nishida, H. Ohrui and H. Meguro, Tetrahedron Lett., 1984, 25, 1575–1578.
75. R. Stenutz, I. Carmichael, G. Widmalm and A. S. Serianni, J. Org. Chem., 2002, 67, 949–958.
76. M. Tafazzoli and M. Ghiasi, Carbohydr. Res., 2007, 342, 2086–2096.
77. V. Mlýnský, P. Kührová, T. Kühr, M. Otyepka, G. Bussi, P. Banáš and J. Šponer, J. Chem. Theory Comput., 2020, 16, 3936–3946.
78. https://glycam.org/docs/forcefield/glycam-naming-2/ .

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ma00830k

---