Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Predicting and accessing metastable phases†
V.
Kocevski
 *a,
J. A.
Valdez
a,
B. K.
Derby
b,
Y. Q.
Wang
a,
G.
Pilania
*a,
J. A.
Valdez
a,
B. K.
Derby
b,
Y. Q.
Wang
a,
G.
Pilania
 a and
B. P.
Uberuaga
a and
B. P.
Uberuaga
 a
a
aMaterials Science and Technology Division, Los Alamos National Laboratory, Los Alamos, NM 87545, USA. E-mail: kocevski@lanl.gov; vancho.vk@gmail.com
bCenter for Integrated Nanotechnologies, Los Alamos National Laboratory, Los Alamos, NM 87545, USA
First published on 13th January 2023
Abstract
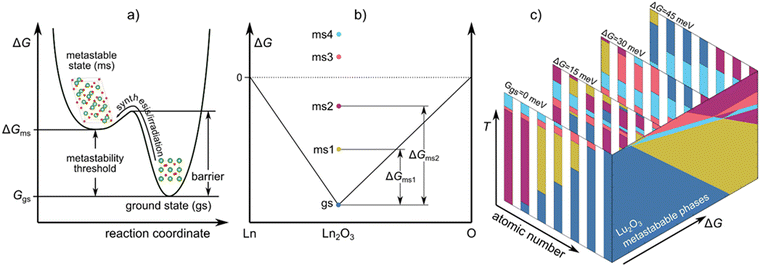
Metastable forms of matter are invaluable to our everyday lives, from advancing technology to understanding biological processes, with their unique properties often offering novel functionality. Despite their importance, synthesizing metastable phases is more art than science, often either serendipitous or trial-and-error. Insight into the amount of stored energy needed to form a metastable phase can aid in their fabrication. Here, we calculate metastable phase diagrams, from which we extract the metastability threshold – the excess energy stored in the metastable phase relative to the ground state. Using lanthanide sesquioxides (Ln2O3) as a case study, we demonstrate how metastable phase diagrams provide new insight into their synthesis and irradiation behavior. We successfully predict the sequence of metastable phases induced by irradiation in Lu2O3, forming three metastable phases with increasing irradiation fluence.
Introduction
Gazing out through our glass windows, satisfying our sweet tooth with chocolate, or enjoying the beauty of diamonds, we encounter metastable forms of matter throughout our everyday lives. Metastable phases make our lives more convenient, but they are also necessary ingredients for all biological systems, as exemplified by the metabolic pathways responsible for cellular-level energy generation via the formation of metastable adenosine triphosphate molecules. A metastable phase or a molecule is a non-equilibrium state of matter, and its formation depends on the accessibility of the configuration under changes in environmental conditions (temperature, pressure, electromagnetic fields, irradiation, etc.), see Fig. 1a.A group of materials having rich polymorphism with various properties shown to form metastable phases are lanthanide sesquioxides (Ln2O3), making them an ideal case study for understanding metastable phase formation. The relative ease with which they transform to different polymorphs enhances their ionic conductivity and amorphization resistance, making them useful for solid oxide fuel cells1 and irradiation resistant materials.2 Ln2O3s are also used as gate oxides,3–5 ultrafast and high-power solid-state lasers,6–9 heterogeneous catalysts,10–12 high performance super-capacitors,13 corrosion resistive coatings,3,14 and in biomedical applications.15–17 Furthermore, their functionality often depends on the formation of metastable phases; for example, the metastable phases have a much higher dielectric constant compared to the ground state phase, which makes them attractive as high-κ gate oxides.5,18,19 To analyze the propensity of Ln2O3 compounds to form metastable phases, we use density functional theory (DFT) to determine the metastability threshold of all relevant phases (see Fig. 1b) and use those to generate metastable phase diagrams (see Fig. 1c). The metastable phase diagrams were ultimately used to understand the formation of metastable phases and predict which metastable phases can form at specific conditions.
As highlighted in Fig. 2a, five polymorphs of Ln2O3 have been reported, termed as A, B, C, H and X, with their stability depending on the temperature and pressure. At room temperature and atmospheric pressure, lanthanides with large ionic radius (La–Nd) preferably adopt a trigonal A phase, while the smaller lanthanides (Pm–Lu) adopt a cubic C phase. At intermediate temperatures (1000–2000 K), lanthanides with intermediate radius (Sm–Ho) adopt a monoclinic B phase. At high temperatures (>2000 K), the Ln2O3 form two disordered phases, the hexagonal H and cubic X phases, with the H phase forming at lower temperatures than the X phase. These structures are highlighted in Fig. 2b–d.
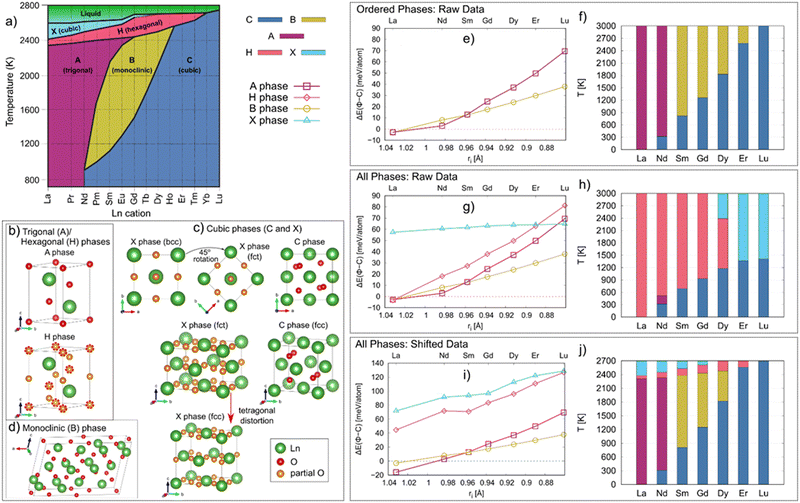 | ||
| Fig. 2 (a) Phase diagram of the Ln2O3 (Ln = La–Lu) oxides [Adapted from ref. 39]. The C, A, H, B and X phase regions are shown in blue, magenta, red, yellow, and light blue, respectively. Structures of Ln2O3 phases: (b) trigonal/hexagonal (A and H), (c) cubic (C and X), and (d) monoclinic (B) phases. The Ln and O atoms are shown in green and red, respectively. The partially occupied O sites are shown in orange. For better comparison between the A and H phases, in the H phase structure the O sites also occupied in the A phase are circled with red dashed lines. Evidently, the H phase contains the same O sites as the A phase; hence, the H phase can be viewed as an oxygen disordered variant of the A phase. The cationic sublattice of the X phase is body center cubic (bcc) which can be turned into body center tetragonal (bct) by a 45° rotation around the c-axis (c). The arrow highlights how a tetragonal distortion along the c-axis would make the X phase cationic sublattice shift from bct to fcc, the same as the cationic sublattice of the C phase (c). (e) Energy of the ordered phases Φ relative to the C phase, ΔE(Φ–C), as a function of the cationic radius (ri), as calculated via DFT. (f) Phase stability regions in Ln2O3 as a function of temperature. (g) Energy of all studied phase (ordered and disordered) relative to the C phase, ΔE(Φ–C), as a function of the cationic radius (ri) as calculated by DFT. (h) Phase stability regions in Ln2O3 as a function of temperature. (i) Adjusted ΔE(Φ–C) for all studied phases (see text for details). (j) Phase stability regions as a function of temperature based on adjusted energies. The data for the C, A, H, B and X phases are shown in blue (dashed line), magenta (squares), red (diamonds), yellow (circles), and light blue (triangles), respectively. | ||
Our current knowledge of the stability of these phases and which are likely to form under non-equilibrium conditions comes from extensive experimental trial and error. One way to predict which metastable phases can form before performing experiments is to use DFT calculations. Over the years, DFT has been demonstrated to be a valuable tool that complements experimental findings, provides a more fundamental understanding of observed phenomena, and predicts novel phases. However, there are limited number of DFT studies focused on the formation of metastable phases and the thermodynamic conditions for their formation.20–25 This work goes beyond the previous studies by focusing on the stability and formability of metastable Ln2O3 polymorphs using various synthesis methods and irradiation, utilizing calculated thermodynamic properties of these structures.
For the purpose of our study, we chose Ln2O3 with Ln = La, Nd, Sm, Gd, Dy, Er, and Lu, lanthanides that display different phase behavior at low and high temperatures, as shown in Fig. 2a, while capturing chemical trends over the entire lanthanide series. This system provides a valuable case study for testing methodology as the phase behavior varies systematically with chemistry, and there is extensive experimental data of phase formation under non-equilibrium conditions to compare against. We compare the calculated and experimental phase stability of the different Ln2O3 phases as a function of chemistry. We then calculate the metastable phase diagrams, from which we extract the metastability threshold of the studied phases – defined to be the amount of stored energy at which that phase becomes competitive with the ground state phase – and correlate it with the experimentally observed metastable phases to rationalize and predict the formation of metastable phases. To test and validate our predictions, we synthesized Lu2O3 pellets, irradiated them to different fluences, and characterized the irradiated structures. Our results highlight how first-principles thermodynamics can be used to assess, interpret, and even predict the metastability of compounds under non-equilibrium conditions, providing new avenues for materials design. Also, our work demonstrates that multiple phase transitions are possible under increasing irradiation fluence, increasing our ability to tune the structure and thus the applicability of materials.
More rigorous approaches would consider the influence of defects on phase stability, the kinetic mechanisms that dictate the rate at which phases transform and the lifetime of metastable phases. However, the prohibitively high computational cost of accounting for all such effects makes such an approach feasible only for a very small set of structures and chemistries. The main goal of this study is to showcase that a simple computational approach can provide an initial, computationally inexpensive screening for the possibility of accessing metastable phases, based on the energy required for their formation.
Methodology
Calculations
DFT calculations were performed using the Vienna Ab initio Simulation Package (VASP).26–29 The electron exchange correlation was modeled using the generalized gradient approximation (GGA) of Perdew, Burke and Ernzernhof parametrization for solids (PBEsol)30 and projector augmented wave (PAW) potentials.31,32 We chose PBEsol because it was the only functional amongst the five functionals we tested (the others are PBE,33 revPBE,34 PW9135 and SCAN36) that correctly reproduced the stability of the A phase of La2O3. For the lanthanides (Ln) we used the PAW potentials from the VASP distribution with formal valence of 3, that is “Ln_3” and La pseudopotentials. We used these PAW potentials because the formal valency of 3 agrees with the valence state (+3) of the cations in the studied Ln2O3 oxides. The unit cells of the different phases were fully relaxed using a cut-off energy of 520 eV for expanding the electronic wave functions. Convergence criteria of 0.001 eV Å−1 and 10−6 eV were adopted for the forces and total energy, respectively, and a γ-centered k-point spacing of <0.025 Å−1 was applied for sampling the Brillouin zone for each structure.To model the partial occupancy of the O site in the disordered phases, H and X, we generated special quasirandom structures (SQS) of their 2 × 2 × 2 supercell of the conventional cells having ½ oxygen using the mcsqs tool.37 Note that the H phase structure of La2O3 reported in ICSD has two different O sites (2a and 4f), and when generating the SQS we considered that both sites are independently occupied. Also, the H phase structure in ICSD has partially occupied cationic sites, but the two sites are spatially very close to each other, separated by only 0.28 Å, and thus, we considered the cations to occupy only one site having average coordinates of the two sites. The relaxed crystallographic parameters of the studied polymorphs for all studied chemistries are given in Table S1 (ESI†).
To evaluate the stability of the different phases at finite temperature, the vibrational contribution to the free energy is required, which can be calculated using the phonon dispersion. The phonon dispersion, in turn, was calculated using the PHONOPY code,38 employing the finite displacement method in a 2 × 2 × 2 supercell of each phase's respective unit cell, except for the A and B phases, for which we used different supercells to obtain positive phonon frequencies (see Fig. S1a and b, ESI†). For the A phase we used a 3 × 3 × 2 supercell, while for the B phase we used a 1 × 4 × 2 supercell. Note that we chose these supercell sizes because the three lattice parameters are much closer to each other compared to a 2 × 2 × 2 supercell. For the B phase we also had to explicitly specify the B phase primitive cell vectors (0.5, 0.5, 0.0) (−0.5, 0.5, 0.0) (0.0, 0.0, 1.0) to obtain positive phonon frequencies (see Fig. S1b, ESI†). The X phase exhibits imaginary phonon frequencies (see Fig. S1c, ESI†), which means that the relaxed structure is dynamically unstable, and a more stable structure with slightly different phonon dispersion exists (possibly related to relaxation of the oxygen associated with short-ranged order). However, the imaginary phonon band is very small, and therefore, removing this band would have a minimal influence on the vibrational entropy of the X phase.
The vibrational contribution to the free energy, Fvib, was calculated using the equation:
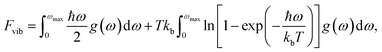 | (1) |
| G(T) = E + Fvib, | (2) |
| G(T) = H + Fvib − TSconf. | (3) |
S conf is calculated using Boltzmann's entropy formula:
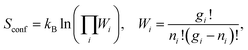 | (4) |
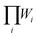 are different. The H phase has two partially occupied oxygen sites with g = 2 and 4, while the X phase has only one partially occupied oxygen site with g = 6. The different degeneracy of the O sites in the H and X phase gives rise to
are different. The H phase has two partially occupied oxygen sites with g = 2 and 4, while the X phase has only one partially occupied oxygen site with g = 6. The different degeneracy of the O sites in the H and X phase gives rise to 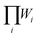 of 12 and 20, respectively. The use of SQS and eqn (4) to describe these disordered compounds inherently assumes that they are randomly disorder. Recent work has shown that these types of materials exhibit short range order in their disordered state.40 However, we have shown that the fully random limit reproduces experimental trends in disordering tendencies41 and so, for convenience, we make that assumption here.
of 12 and 20, respectively. The use of SQS and eqn (4) to describe these disordered compounds inherently assumes that they are randomly disorder. Recent work has shown that these types of materials exhibit short range order in their disordered state.40 However, we have shown that the fully random limit reproduces experimental trends in disordering tendencies41 and so, for convenience, we make that assumption here.
The metastable phase diagrams were built using the approach described by Srinivasan et al.25 First, the metastable Gibbs energy, ΔGms(T), is calculated as:
| ΔGms(T) = Gms(T) − Ggs(T), | (5) |
| 0 ≤ ΔGΦms(T) ≤ ΔG, and ≤ ΔGΦms(T) > ΔGother phasems(T). | (6) |
From eqn (5) and (6), it is evident that for those Ln2O3 with multiple stable phases, the ground state phase will change with increasing temperature. Fig. 3b shows the free energy of the different phases relative to phase C while Fig. 3c shows the free energy of those phases relative to the ground state at temperature T for Sm2O3. Since the C phase is not always the ground state, the relative energies in Fig. 3b can be negative. However, by construction, they are always positive in Fig. 3c. Finally, in Fig. 3d, we present the metastable phase diagram of Sm2O3, in which the stability windows of the different polymorphs of Sm2O3 are shown versus temperature and ΔG – the metastable phase diagrams for all studied Ln2O3 chemistries are reported in Fig. S2 (ESI†). To find what energy is stored in an experimentally observed metastable phase Φ at temperature T, we extract the metastability threshold (ΔGms) from the metastable phase diagrams (see Fig. 1b). See Fig. 3g for more details how the metastability threshold is calculated. Note that the choice for the highest ΔG of 45 meV per atom for representing the metastable phase diagrams is arbitrary, and a better choice for the highest ΔG would be the thermodynamic limit – the energy difference between an amorphous phase and the ground state;22 however, we do not know the thermodynamic limit for these compounds.
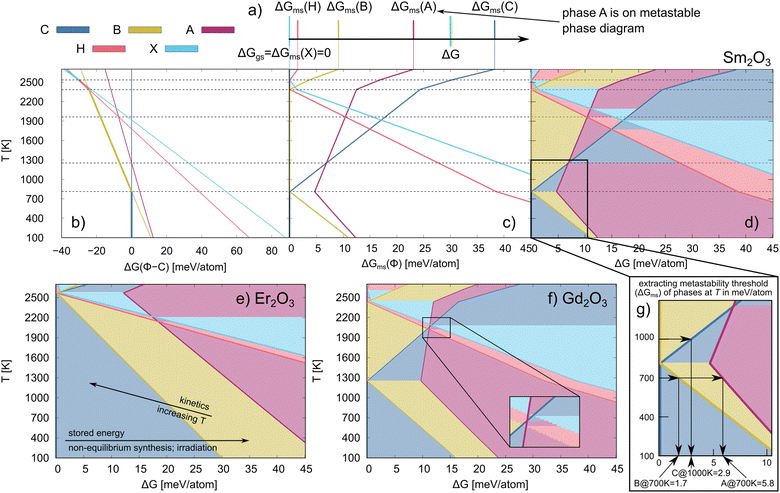 | ||
| Fig. 3 (a) Schematic representation of the approach for identifying metastable phases (see eqn (6)). (b) G(T) of Sm2O3 phases relative the C phase, ΔG (Φ–C) as function of temperature; the thicker lines represent the ground state phases. (c) Metastability threshold of the Sm2O3 phases as a function of temperature, i.e., the free energy of the different polymorphs relative to the ground state phase at temperature T. (d) Sm2O3 metastable phase diagram. The dashed lines connect temperatures at which the ground state changes or there is a change in the metastable phase. Metastable phase diagrams for (e) Er2O3 and (f) Gd2O3. In (e), the lines indicate how different drivers push the system in different directions along the metastable phase diagram. The inset in (f) shows one example where multiple metastable phases intersect. (g) Schematic representation of the method for extracting the metastability threshold (ΔGms) of different phases at given T from a metastability phase diagram. The C, A, H, B and X phases are shown in blue, magenta, red, yellow and light blue, respectively. | ||
The metastable phase diagrams depend on G(T), and hence, having reliable G(T) is very important. From Fig. 2h it is evident that, using G(T) solely based on our DFT calculations, the disordered phases dominate over the ordered phases, which arises from the added configurational entropy of the disordered phases, lowering their G(T). Thus, to obtain better agreement with experiment, we resorted to an additive positive shift to the energies of the disordered phases, so their experimental phase transition temperatures are reproduced. To reproduce the linear trend in ΔE(Φ–C) as function of the cation type seen in Fig. 2g, we also added a negative shift to the energy of the La2O3 A phase. The shifting parameters applied to the enthalpies of each phase are given in Table S2 (ESI†) while the ΔE(Φ–C) resulting from applying those shifts are shown in Fig. 2i. Alternatively, DFT+U can be used, which has been shown to give better agreement with experimental order–disorder transition temperatures of lanthanide-containing pyrochlores;42 however, we would need to find appropriate values of U for each chemistry and polymorph of Ln2O3 studied here because of the different coordination number of the cations in the different phases. That would be a challenging task, raising questions of how to compare energies of systems with different values of U, and in the end, reducing to another set of fitting parameters. We therefore choose the more pragmatic route here.
Experiments
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) space group (C phase) as in the mineral bixbyite.
space group (C phase) as in the mineral bixbyite.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) eV for Lu and O.
eV for Lu and O.
Results
Before detailing the connection between experiments and calculations of metastable phases, we examine the energetics of the ordered and disordered phases, and how well the experimental phase transition temperatures are reproduced by DFT. We then discuss the relation between experimentally observed phases and their metastability threshold. Lastly, we focus on Lu2O3, a perfect model system for the examination of metastable phase formation, the relationship between predicted metastable phases, and the formation of these phases under irradiation.Ordered phases
Of the five phases reported in the experimental phase diagram in Fig. 2a, three – A, B, and C – are ordered, in the sense that each Wykoff position in the crystal structure has an occupancy of one. Of these ordered phases, we found that the C phase is the most stable phase at 0 K for each of the studied Ln2O3 oxides, except for La2O3 for which the A phase is the most stable. Thus, we used the energy of the C phase as a reference to compare the stability of other phases Φ, with Φ = A or B: ΔE(Φ–C) = EΦ − EC. This energy is shown in Fig. 2e. Clearly, ΔE(Φ–C) monotonically decreases with increasing cationic radius, from Lu to La, until eventually the A and B phases become more stable than C for La2O3. The energy difference between the A and B phase also increases with increasing cationic radius, with the A phase being more stable than the B phase for La2O3 and Nd2O3, while the two phases are nearly degenerate in energy for Sm2O3. This agrees with the experimental observation that both La2O3 and Nd2O3 form the A phase at lower temperatures (Fig. 2a). Also, the lower energy of the B phase compared to the A phase for those cations smaller than Sm reinforces the notion that the A phase structure for these cations is the transition state towards the B phase.44The finite temperature stability of the phases shown in Fig. 2f, obtained by calculating their Gibbs energies G(T) (eqn (2)) as detailed in the Methods, are directly comparable with experiments. We correctly find that La2O3 should only form the A phase, while the B phase energy is negligibly higher (ΔE(B–A) < 0.1 meV per atom), suggesting that, in principle, both phases should be able to form. However, the B phase of La2O3 is dynamically unstable, which explains why the B phase has not been reported for La2O3. In the case of Nd2O3, we find that the A phase should form above 320 K, which is close to room temperature (298.15 K) where the A phase has been reported experimentally. Interestingly, initial attempts at the synthesis of Nd2O3 reported the C phase at room temperature,39,45,46 suggesting that the C phase might be stable at lower temperatures, but there are no measurements of a phase transition below room temperature or estimates of C → A transition temperature using thermodynamic modeling. When it comes to the other sesquioxides, we underestimate the C → B transition temperatures of Sm2O3, Gd2O3, and Dy2O3 by approximately 300 K. On the other hand, we reproduce the experimental C → B phase transition temperature for Er2O3, while Lu2O3 is stable in the C phase up to the melt, ∼2800 K. Overall, while there are some quantitative differences between our predictions and the experimental literature, the trends in the phase stability of the ordered phases versus chemistry are well reproduced by our calculations.
Disordered phases
We now turn to the relative stability of the disordered phases, H and X-the phases with partially occupied O sites. Fig. 2g compares their stability relative to the C phase and the other ordered phases. Both the H and X phases have higher energies compared to the other three phases, except for La2O3, for which the energies of the A and H phase are degenerate, and for Lu2O3, for which the X phase has lower energy than both the A and H phases. There is an apparent relationship in the energy differences between the X and C phase, and the A and H phase, with these two energy differences being almost constant along the Ln series. This trend is a reflection of the structural relation between these phases, as shown in Fig. 2b and d. Further, the close structural relationship between the A and H phase gives rise to similar phonon dispersions, with some matching bands (note the purple bands in Fig. S1d, ESI†).To evaluate the phase stability regions versus temperature of the disordered phases, we calculate their G(T), shown in Fig. 2h, using eqn (3). Clearly, and in contrast to experiment, the disordered phases H and X dominate the phase stability region of for all Ln2O3, and are the only phases present in addition to the C phase. The only exception is Nd2O3, where a small stability region for the A phase is identified; however, this stability region is smaller by an order of magnitude compared to experiment. In contrast, and as discussed above, we were able to reproduce the phase stability of the ordered phases. Thus, to obtain better agreement with experiment, we resort to empirically correcting our DFT energies by adding a positive shift to the energies of the disordered phases, as shown in Fig. 2i, so the experimental phase transition temperatures are reproduced (see Fig. 2j); see Methods section for more details. This amounts to an added enthalpic penalty for the disordered phases. Alternatively, the configurational entropy could be modified to include contributions from short-range ordering, known to reduce the magnitude of configuration entropy in disordered phases;47 however, identifying the detailed short-range order of a disordered compound as a function of temperature requires extensive experiments and/or calculations, both of which are outside of the scope of this study. Thus, while multiple factors may account for the discrepancy between the theoretical and experimental G(T) for these disordered phases, we choose to incorporate that difference as a shift in the enthalpy.
Metastable phase diagram
We use the methodology of Srinivasan et al.25 to construct metastable phase diagrams of the Ln2O3 compounds. In this methodology, a Gibbs energy difference (ΔG) determines which phase is considered as metastable (see Methods section); the concept is schematically illustrated in Fig. 3a, and the physics of ΔG is detailed in Methods section. ΔG is a variable that represents the amount of excess energy in the system – the amount of energy above the ground state for which we will determine which metastable phase is present; we refer to the lowest energy at which a given metastable phase is present as the metastability threshold for that phase. Note that this threshold depends on temperature and chemistry. The method for extracting the metastability threshold at synthesis temperature from metastable phase diagrams is schematically represented in Fig. 3g. The metastability threshold can also be viewed as the stored energy that is needed for the metastable phase to be produced. The stored energy can be introduced using different synthesis methods, such as decomposition of salts or other non-equilibrium synthesis (sputtering, filtered cathodic arc, molecular beam epitaxy), or by irradiation.Detailed in Table 1 are experimentally synthesized Ln2O3 metastable phases that have been reported in the literature, including their synthesis method, temperature, and metastability threshold (ΔGms) as determined by our analysis. This metastability threshold can be viewed as the amount of stored energy in the ground state at which the indicated phase becomes energetically competitive. That is, conceptually, if we introduce an excess energy of ΔGms into the ground state phase, the associated metastable phase will be degenerate in energy (assuming it has no stored energy of its own). Via synthesis from salts and hydrothermal synthesis, only those Ln2O3 oxides with cationic radii larger than Gd are reported to form metastable phases. The reason for the anomalous behavior of La2O3 is the high stability of the A phase, which yields a large metastability threshold (>19 eV per atom at 300 K) for the other phases (see Fig. S2a, ESI†), requiring different methodology, such as molecular beam epitaxy with stabilization via strain, to produce the metastable C phase. Layers of metastable C phase of Nd2O3 and B phase of Gd2O3 have also been produced by magnetron sputtering and molecular beam epitaxy. In the case of the smaller cations, introducing a sputtering power56 or negative biased voltage55 helps in producing the B phase of Er2O3, although its metastability threshold is large (see Table 1 and Fig. 1a).
| Oxide | Φ | Synthesis method/radiation | T [K] | Ref. | ΔGms |
|---|---|---|---|---|---|
| Nd2O3 | C | Hydrothermal | 970 | 48 | 6.9 |
| Nd2O3 | B | Hydrothermal | 1205 | 48 | 3.1 |
| Nd2O3 | C | Nitrate solid state | 860, 1080 | 45 and 49 | 6.5, 8.0 |
| Nd2O3 | C | Carbonate decomposition | 790, 820–1020 | 45 and 49 | 5.3–7.4 |
| Nd2O3 | C | Oxalate decomposition | 820, 920–1020 | 45 and 49 | 6.4–7.4 |
| Nd2O3 | C | Hydroxide decomposition | 820–1020 | 45 | 5.3–7.4 |
| Nd2O3 | C | Acetate combustion | 1050 | 45 | 7.7 |
| Sm2O3 | B | Fused nitride decomposition | 700 | 50 | 1.8 |
| Sm2O3 | C | Chloride decomposition | 1170 | 51 | 5.6 |
| Gd2O3 | B | Fused nitride decomposition | 700 | 50 | 7.8 |
| La2O3 | C | Molecular beam epitaxy <2 nm | 1020 | 52 | 27.2 |
| Nd2O3 | C | Molecular beam epitaxy | 950 | 53 | 6.6 |
| Nd2O3 | C | Magnetron sputtering | 420 | 18 | 1.2 |
| Gd2O3 | B | Magnetron sputtering system | 920 | 54 | 4.6 |
| Gd2O3 | B | Molecular beam epitaxy | 520 | 19 | 10.2 |
| Er2O3 | B | Pulsed magnetron sputtering | <620 | 55 | 23.8 |
| Er2O3 | B | Filtered cathode Arc | <770 | 56 | 21.9 |
| Dy2O3 | B | 300 keV Kr++ ions; 5 dpa | 120 | 57 | 22.3 |
| Er2O3 | B | 300 keV Kr++ ions; 17 dpa | 120 | 57 | 29.8 |
| Dy2O3 | H | 300 keV Kr++ ions; 125 dpa | 120 | 58 | 91.1 |
Another way to produce metastable phases with high metastability thresholds at low temperatures is by irradiation. Tang et al. have shown that irradiating the C phase of Dy2O3 and Er2O3 with 300 keV Kr++ ions at 120 K produces the B phase57 and the H phase for Dy2O3,58 with the lowest irradiation dose producing the B and H phases listed in Table 1. The higher irradiation dose required for Er2O3 agrees with the larger metastability threshold of Er2O3 compared to Dy2O3 (see Table 1). Also, the higher irradiation dose used to produce Dy2O3 H phase correlates with the larger metastability threshold of the H phase than the B phase.
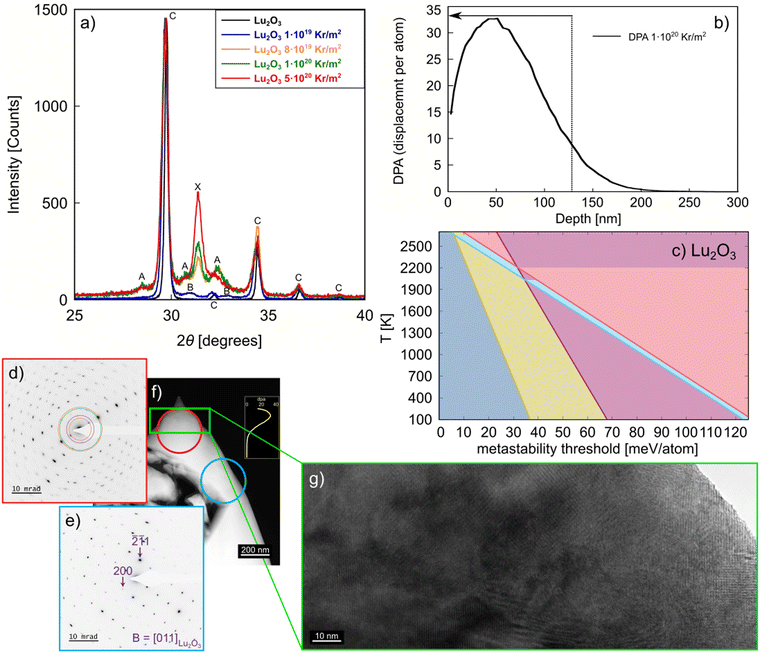
Irradiation of Lu2O3
To validate the computational results presented above, we consider the formation of metastable phases via stored energy introduced by irradiation. Of the studied Ln2O3, Lu2O3 is an excellent compound for further study because of its easy synthesizability to high purity and the high stability of the C phase. Also, our calculations show significant differences between the metastability threshold of the Lu2O3 metastable phases (see Fig. 4c), allowing for distinct separation of metastable phase formation with increasing stored energy, such as that introduced by increasing irradiation fluence. We irradiated Lu2O3 to four different fluences (see Methods section), covering a wide range of stored energy to access multiple metastable phases. As revealed in Fig. 4a, grazing incidence X-ray diffraction analysis of the irradiated Lu2O3 pellets shows that, at the lowest fluence of 1 × 1019 Kr m−2, only the B phase is formed. At 8 × 1019 and 1 × 1020 Kr m−2, a mixture of the A and X phases is observed. Increasing the fluence to 5 × 1020 Kr m−2 produces primarily the X phase. While it has been shown that e.g. MAX phases can also undergo multiple phase transitions under increasing irradiation fluence,59–61 reports of multiple phase transformations under increasing fluence are rare.For additional characterization of the irradiated Lu2O3 pellets we used scanning/transmission electron microscopy (S/TEM) (Fig. 4d) and selected area electron diffraction (SAED) of the irradiated region (Fig. 4e) and the bulk of the pellet (Fig. 4f). The irradiation depth in the Lu2O3 pellet is ∼150 nm, as shown in Fig. 4b. A high-resolution S/TEM image of the irradiated region of the pellet is shown in Fig. 4g. Together, the S/TEM and SAED reveal the existence of multiple phases in the irradiated region of Lu2O3, and the C phase in the unirradiated region of the pellet, indicating that the radiation-induced phase transformation involves a complex post-irradiation microstructure. We note that these results are in contrast with previous experiments, which reported no phase transition in irradiated Lu2O3.57 This sequence of metastable phases – C → B → A + X → X – is very close to the sequence of metastable phases we predict for this system, as highlighted in Fig. 4c.
Discussion
As schematically illustrated in Fig. 1a, a metastable phase occupies a local minimum on the potential energy surface (PES), separated by a barrier from the deepest (global) minimum, i.e., the ground state. This energy barrier between the two minima needs to be overcome to produce the metastable phase, which can be achieved through synthesis, irradiation, or change in pressure. In the case of the metastable phases produced by thermal synthesis there is an apparent limit in the amount of stored energy achievable via these routes, about 8 meV per atom, and only Ln2O3 with Ln = Nd–Gd are within this limit, as shown in Table 1. The Ln2O3 with smaller ions, on the other hand, have metastability thresholds above this limit (>10 meV per atom; see Fig. S2, ESI†), which explains why only their ground state (the C phase) has been synthesized. It is also worth noting that using different salts at the same synthesis temperature can produce different phases,62 and that synthesizability depends on the oxygen partial pressure.54 Not surprisingly, this indicates that the synthesizability of a metastable phase is also dependent on the synthesis pathway, in addition to the metastability threshold, and that knowing the metastability threshold is only part of the story.As illustrated in Fig. 3e, increasing the temperature lowers the metastability threshold, allowing, in principle, for easier production of the metastable phases – less stored energy is needed to access the metastable phases. However, at elevated temperatures the rate of kinetic pathways is also increased, providing easier access to the equilibrium phases – as described in Fig. 1a, the rate of overcoming the barrier from the metastable phase to the ground state is higher at higher temperature. In the case of Nd2O3, both Stecura49 and Glushkova et al.45 show that the dominant phase at higher temperatures is the ground state A phase regardless of the Nd salt used, while Wendlandt showed that Sm and Gd also form their ground state phases at elevated temperatures.51 This indicates that, although the metastability threshold is decreased at higher temperatures, the kinetic hindrance is also removed, and the system can reach the thermodynamically-preferred the ground state phase. Hence, increasing the temperature is not enough to overcome the metastability threshold of those oxides with a higher threshold (Ln2O3 oxides with smaller ions and La2O3), and other non-equilibrium methods need to be applied. The negative biased voltage and sputtering power used in some synthesis approaches add enough energy at lower temperature to overcome the metastability threshold of Er2O3 without influencing the kinetics. As in the case of the other Ln2O3 oxides, increasing the temperature stabilizes the ground state C phase of Er2O3 in both synthesis methods. Metastable phase formation can be promoted by growing the Ln2O3 on a substrate that supports the metastable phase formation via strain or isomorphic structure. This is the case of the metastable C phase of La2O3 which can be stabilized on Si(111) substrates for a thickness up to 2 nm, though increasing the thickness produces the ground state A phase.52 It is also worth noticing that the metastable B phase has not been observed for neither La2O3 nor Lu2O3. In the case of La2O3, we determine that to be because of the dynamical instability of the La2O3 B phase. In contrast, for Lu2O3, there is a significant metastability threshold of the Lu2O3 B phase. To overcome this large metastability threshold, the temperature must be increased, but in this case the melt becomes thermodynamically favorable first. Another way to add energy to the system while maintaining a low temperature to prevent either kinetic recovery or a shift in the thermodynamically preferred state is by irradiation, which we show is a practical way of producing Lu2O3 metastable phases.
Our experiments confirm that irradiation can be used to produce multiple metastable phases that are not on the phase diagram of Lu2O3, essentially moving to the right in our calculated metastable phase diagram shown in Fig. 4c. The observed sequence of phases with increasing irradiation fluence agrees with the increasing metastability threshold of the B, A and X phases, as shown in Fig. 4c. It is also worth noting that the highly metastable X phase that is reported to form when swift heavy ion irradiation is used,44 in which the system is essentially brought down from the melt, can also be produced by gradually introducing stored energy, as done here. Interestingly, the metastable phases resemble a sequence of ground state phases of larger cations than Lu at increased temperatures, basically moving diagonally in the Ln2O3 phase diagram shown in Fig. 2a.
Our observations align with Wigner's stipulation that, with increasing fluence, the defect concentration in a phase increases, and hence, the internal energy of that phase is also increased.63 At the same time, the increased defect concentration will act to lower the nucleation barrier for the kinetics to drive a phase transition64 which, with the increased internal energy, will cause the phase transition to a metastable phase. At this time we cannot identify which defects are responsible for the phase transformations.
As defined in ref. 25 and performed here, this methodology provides information about the energy difference between the global and local minima of phases on the PES. A more complete picture of the PES schematically illustrated in Fig. 1a contains information on the width of the minima (basin of attraction) and the lifetime of the metastable phases (the barriers between them). Further, we have, for the sake of pragmatism, made several assumptions that limit the fidelity of our results. For example, the free energy of a given phase will not only be dictated by the properties of the perfect crystal, but also the equilibrium and non-equilibrium defect content present. In addition, we have not accounted for any kinetic factors that may govern the actual phase-to-phase transformations. Finally, recognizing that the assumption of a random solid solution overestimates the configurational entropy of these materials, we have elected to shift the enthalpy rather than the entropy as a correction to our free energies. In reality, these materials exhibit short-ranged order, meaning that not all configurations are equally likely. However, calculating the temperature and chemistry-dependent configuration entropy would be a daunting task for one chemistry65 and its associated phases, much less the full set of chemistries considered here. That said, and as discussed earlier, the approach used here can explain the relative metastability of the ordered phases; the issue arises when both ordered and disordered phases are compared, for which a more careful treatment of the entropy is required. If we did not calibrate the energetics of the disordered phases against experiment, then we would not have been able to relate the metastability of the disordered phases with experiments without significantly more computational effort.
Thus, accounting for all of these factors21,66 is a very challenging and computational expensive endeavor. We have shown that using a simpler and computationally much less demanding approach is valuable for initial screening in search of functional metastable phases producible by ether synthesis or irradiation. For example, materials that exhibit dynamic regimes and sit at the intersection or in the vicinity of multiple phases on the PES, such as regions of the metastable phase diagrams where various phases co-exist (see inset Fig. 3f), can be more efficient heterogeneous catalysts.67–69 A low metastability threshold indicates a possibly easy phase transition induced by electrical pulse, helping in discovering new materials for phase change memory devices. This approach can also help discover materials that are more radiation tolerant by predicting what phases can form under extreme conditions.’
Conclusions
In summary, we explained the formation of metastable phases, either by synthesis or irradiation, in the Ln2O3 family of compounds using the metastability threshold extracted from metastable phase diagrams. Furthermore, we demonstrate that multiple metastable phases of Lu2O3 can be formed under irradiation, with the phase formation sequence being correlated with their metastability threshold. We also identify a metastability limit (∼8 meV per atom) above which metastable phases cannot be synthesized from decomposition of salts or hydrothermal synthesis. This explains why metastable phases of Ln2O3 with smaller cations (Ln = Tb–Lu) have not been synthesized via these approaches, and why other non-equilibrium synthesis methods or irradiation are required to produce metastable phases of these Ln2O3. These results provide new insight into the metastability of an essential class of compounds, help explain experimental results regarding their synthesis and irradiation behavior, and most importantly guide future experimental studies of these materials.Conflicts of interest
The authors declare that they have no competing interests.Acknowledgements
This work, performed at Los Alamos National Laboratory, was supported by the U. S. Department of Energy, Office of Science, Basic Energy Sciences, Materials Sciences and Engineering Division. Los Alamos National Laboratory is operated by Triad National Security, LLC, for the National Nuclear Security Administration of U. S. Department of Energy (Contract No. 89233218CNA000001). This work was performed, in part, at the Center for Integrated Nanotechnologies, an Office of Science User Facility operated for the U. S. Department of Energy Office of Science. Computational support for this work was provided by LANL's high performance computing clusters. This research also used resources of the National Energy Research Scientific Computing Center (NERSC), a U. S. Department of Energy Office of Science User Facility located at Lawrence Berkeley National Laboratory, operated under Contract No. DE-AC02-05CH11231 using NERSC award BES-ERCAP-0016919.References
- Q. Wang, et al., Applications and recent advances of rare earth in solid oxide fuel cells, J. Rare Earths, 2021, 40, 1668, DOI:10.1016/j.jre.2021.09.003.
- K. E. Sickafus, et al., Radiation induced amorphization resistance in A2O3–BO2 oxides, Nucl. Instrum. Methods Phys. Res., Sect. B, 2002, 191, 549–558 CrossRef CAS.
- G.-Y. Adachi and N. Imanaka, The Binary Rare Earth Oxides, Chem. Rev., 1998, 98, 1479–1514 CrossRef CAS PubMed.
- H. J. Osten, J. P. Liu and H. J. Müssig, Band gap and band discontinuities at crystalline Pr2O3/Si(001) heterojunctions, Appl. Phys. Lett., 2002, 80, 297–299 CrossRef CAS.
- K. H. Goh, A. S. M. A. Haseeb and Y. H. Wong, Lanthanide rare earth oxide thin film as an alternative gate oxide, Mater. Sci. Semicond. Process., 2017, 68, 302–315 CrossRef CAS.
- U. Griebner, et al., Passively mode-locked Yb:Lu2O3 laser, Opt. Express, 2004, 12, 3125–3130 CrossRef CAS PubMed.
- C. J. Saraceno, et al., SESAMs for high-power femtosecond modelocking: power scaling of an Yb:LuScO3 thin disk laser to 23 W and 235 fs, Opt. Express, 2011, 19, 20288–20300 CrossRef CAS PubMed.
- L. Hao, et al., Spectroscopy and laser performance of Nd:Lu2O3 crystal, Opt. Express, 2011, 19, 17774–17779 CrossRef CAS PubMed.
- F. Druon, et al., and Yb:Y2O3 crystals grown by an original flux method, Opt. Lett., 2013, 38, 4146–4149 CrossRef CAS PubMed.
- H. X. Dai, C. F. Ng and C. T. Au, Raman spectroscopic and EPR investigations of oxygen species on SrCl2-promoted Ln2O3 (Ln = Sm and Nd) catalysts for ethane-selective oxidation to ethene, Appl. Catal., A, 2000, 202, 1–15 CrossRef CAS.
- B. M. E. Russbueldt and W. F. Hoelderich, New rare earth oxide catalysts for the transesterification of triglycerides with methanol resulting in biodiesel and pure glycerol, J. Catal., 2010, 271, 290–304 CrossRef CAS.
- Z. Taherian, et al., A comparative study of ZrO2, Y2O3 and Sm2O3 promoted Ni/SBA-15 catalysts for evaluation of CO2/methane reforming performance, Int. J. Hydrogen Energy, 2017, 42, 16408–16420 CrossRef CAS.
- M. Majumder, et al., Impact of rare-earth metal oxide (Eu2O3) on the electrochemical properties of a polypyrrole/CuO polymeric composite for supercapacitor applications, RSC Adv., 2017, 7, 20037–20048 RSC.
- V. S. Saji, Review of rare-earth-based conversion coatings for magnesium and its alloys, J. Mater. Res. Technol., 2019, 8, 5012–5035 CrossRef CAS.
- L. Zhou, et al., Size-tunable synthesis of lanthanide-doped Gd2O3 nanoparticles and their applications for optical and magnetic resonance imaging, J. Mater. Chem., 2012, 22, 966–974 RSC.
- J. Yin, et al., Hollow-structured upconverting sesquioxide targeted nanoprobes for magnetic resonance and fluorescence combined imaging, RSC Adv., 2016, 6, 72836–72844 RSC.
- V. Muthulakshmi, M. Balaji and M. Sundrarajan, Biomedical applications of ionic liquid mediated samarium oxide nanoparticles by Andrographis paniculata leaves extract, Mater. Chem. Phys., 2020, 242, 122483 CrossRef CAS.
- M. Shao, et al., Effect of deposition temperature on structure and properties of Nd2O3 thin films prepared by magnetron sputtering, Vacuum, 2019, 169, 108936 CrossRef CAS.
- P. Gribisch and A. Fissel, Tuning of structural and dielectric properties of Gd2O3 grown on Si(001), J. Appl. Phys., 2020, 128, 055108 CrossRef CAS.
- W. Sun, et al., The thermodynamic scale of inorganic crystalline metastability, Sci. Adv., 2016, 2, e1600225 CrossRef PubMed.
- V. Stevanović, Sampling Polymorphs of Ionic Solids using Random Superlattices, Phys. Rev. Lett., 2016, 116, 075503 CrossRef PubMed.
- M. Aykol, et al., Thermodynamic limit for synthesis of metastable inorganic materials, Sci. Adv., 2018, 4, eaaq0148 CrossRef PubMed.
- A. Anelli, et al., Generalized convex hull construction for materials discovery, Phys. Rev. Mater., 2018, 2, 103804 CrossRef CAS.
- J.-H. Pöhls, M. Heyberger and A. Mar, Comparison of computational and experimental inorganic crystal structures, J. Solid State Chem., 2020, 290, 121557 CrossRef.
- S. Srinivasan, R. Batra, D. Luo, T. Loeffler, S. Manna, H. Chan, L. Yang, W. Yang, J. Wen, P. Datancet and S. K. R. S. Sankaranarayanan, Machine learning the metastable phase diagram of covalently bonded carbon, Nat. Commun., 2022, 13, 3251 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Ab initio molecular dynamics for liquid metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Ab initio molecular-dynamics simulation of the liquid-metal–amorphous-semiconductor transition in germanium, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmüller, Efficient iterative schemes forab initiototal-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- G. I. Csonka, et al., Assessing the performance of recent density functionals for bulk solids, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 155107 CrossRef.
- P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- Y. Zhang and W. Yang, Comment on “Generalized Gradient Approximation Made Simple”, Phys. Rev. Lett., 1998, 80, 890 CrossRef CAS.
- J. P. Perdew, et al., Atoms, molecules, solids, and surfaces: Applications of the generalized gradient approximation for exchange and correlation, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671–6687 CrossRef CAS PubMed.
- J. Sun, A. Ruzsinszky and J. P. Perdew, Strongly Constrained and Appropriately Normed Semilocal Density Functional, Phys. Rev. Lett., 2015, 115, 036402 CrossRef PubMed.
- A. van de Walle, et al., Efficient stochastic generation of special quasirandom structures, Calphad, 2013, 42, 13–18 CrossRef CAS.
- A. Togo and I. Tanaka, First principles phonon calculations in materials science, Scr. Mater., 2015, 108, 1–5 CrossRef CAS.
- M. Foex and J. Traverse, Investigations about crystalline transformation in rare earths sesquioxides at high temperatures, Rev. Int. Hautes Temp. Refract., 1966, 3, 429–453 CAS.
- J. Shamblin, et al., Probing disorder in isometric pyrochlore and related complex oxides, Nat. Mater., 2016, 15, 507–511 CrossRef CAS PubMed.
- G. Pilania, et al., Using Machine Learning To Identify Factors That Govern Amorphization of Irradiated Pyrochlores, Chem. Mater., 2017, 29, 2574–2583 CrossRef CAS.
- P. M. Kowalski, Formation enthalpy of Ln2B2O7-type (B = Ti,Sn,Hf,Zr) compounds, Scr. Mater., 2020, 189, 7–10 CrossRef CAS.
- J. F. Ziegler, M. D. Ziegler and J. P. Biersack, SRIM – The stopping and range of ions in matter, Nucl. Instrum. Methods Phys. Res., Sect. B, 2010, 268, 1818–1823 CrossRef CAS.
- C. L. Tracy, et al., Phase transformations in Ln2O3 materials irradiated with swift heavy ions, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 174101 CrossRef.
- V. B. Glushkova and A. G. Boganov, Polymorphism of rare-earth sesquioxides, Bull. Acad. Sci. USSR, Div. Chem. Sci., 1965, 14, 1101–1107 CrossRef.
- I. Warshaw and R. Roy, Polymorphism of the rare earth sesquioxides, J. Phys. Chem., 1961, 65, 2048–2051 CrossRef CAS.
- A. D. Pelton and Y.-B. Kang, Modeling short-range ordering in solutions, Int. J. Mater. Res., 2007, 98, 907–917 CrossRef CAS.
- M. W. Shafer and R. Roy, Rare-Earth Polymorphism and Phase Equilibria in Rare-Earth Oxide-Water Systems, J. Am. Ceram. Soc., 1959, 42, 563–570 CrossRef CAS.
- S. Stecura, Crystallographic Modifications and Phase Transformation Rates of Five Rare-earth Sesquioxides: Lanthanum Oxide, Neodymium Oxide, Samarium Oxide, Europium Oxide, and Gadolinium Oxide, US Department of the Interior, Bureau of Mines, 1965, resreport.
- G. Brauer and A. Siegert, Beiträge zur Polymorphie der Sesquioxide der Seltenen Erden. II. Über die Abscheidung von Seltenerdoxiden aus Nitratschmelzen, Z. Anorg. Allg. Chem., 1969, 371, 263–273 CrossRef CAS.
- W. W. Wendlandt, The thermal decomposition of the heavier rare earth metal chloride hydrates, J. Inorg. Nucl. Chem., 1959, 9, 136–139 CrossRef CAS.
- A. Proessdorf, et al., Epitaxial polymorphism of La2O3 on Si(111) studied by in situ x-ray diffraction, Appl. Phys. Lett., 2014, 105, 021601 CrossRef.
- J. Wang, T. Liu and Z. Wang, Crystalline Nanoscale M2O3 (M = Gd, Nd) (M = Gd, Nd) Thin Films Grown by Molecular Beam Epitaxy on Si(111), Mater. Trans., 2009, 50, 2115–2117 CrossRef CAS.
- Y.-L. Li, et al., Effect of the oxygen concentration on the properties of Gd2O3 thin films, J. Cryst. Growth, 2004, 265, 548–552 CrossRef CAS.
- X. Li, et al., Crystallization behavior and mechanical properties of erbium oxide coatings fabricated by pulsed magnetron sputtering, Thin Solid Films, 2012, 520, 2316–2320 CrossRef CAS.
- C. Adelhelm, et al., Influence of deposition temperature and bias voltage on the crystalline phase of Er2O3 thin films deposited by filtered cathodic arc, J. Nucl. Mater., 2011, 417, 798–801 CrossRef CAS.
- M. Tang, et al., Ion-irradiation-induced phase transformation in rare earth sesquioxides (Dy2O3,Er2O3,Lu2O3), J. Appl. Phys., 2006, 99, 063514 CrossRef.
- M. Tang, et al., Heavy ion irradiation effects in the rare-earth sesquioxide Dy2O3, Nucl. Instrum. Methods Phys. Res., Sect. B, 2006, 250, 142–147 CrossRef CAS.
- C. Wang, et al., Role of the X and n factors in ion-irradiation induced phase transformations of Mn+1AXn phases, Acta Mater., 2018, 144, 432–446 CrossRef CAS.
- C. Wang, et al., Disorder in Mn+1AXn phases at the atomic scale, Nat. Commun., 2019, 10, 622 CrossRef CAS PubMed.
- C. Wang, C. L. Tracy and R. C. Ewing, Radiation effects in Mn+1AXn phases, Appl. Phys. Rev., 2020, 7, 041311 CAS.
- L. Eyring, The Binary Lanthanide Oxides: Synthesis and Identification, in Synthesis of Lanthanide and Actinide Compounds, ed. G. Meyer and L. R. Morss, Dordrecht, Springer, Netherlands, 1991, pp. 187–224 Search PubMed.
- E. P. Wigner, Theoretical Physics in the Metallurgical Laboratory of Chicago, J. Appl. Phys., 1946, 17, 857–863 CrossRef.
- X. Zhang, et al., Defect-characterized phase transition kinetics, Appl. Phys. Rev., 2022, 9, 041311 CAS.
- A. van de Walle and G. Ceder, The effect of lattice vibrations on substitutional alloy thermodynamics, Rev. Mod. Phys., 2002, 74, 11–45 CrossRef CAS.
- D. Turnbull and J. C. Fisher, Rate of Nucleation in Condensed Systems, J. Chem. Phys., 1949, 17, 71–73 CrossRef CAS.
- K. Reuter, D. Frenkel and M. Scheffler, The Steady State of Heterogeneous Catalysis, Studied by First-Principles Statistical Mechanics, Phys. Rev. Lett., 2004, 93, 116105 CrossRef PubMed.
- G. Pilania, P.-X. Gao and R. Ramprasad, Establishing the LaMnO3 Surface Phase Diagram in an Oxygen Environment: An ab Initio Kinetic Monte Carlo Simulation Study, J. Phys. Chem. C, 2012, 116, 26349–26357 CrossRef CAS.
- G. Cao, et al., Artificial intelligence for high-throughput discovery of topological insulators: The example of alloyed tetradymites, Phys. Rev. Mater., 2020, 4, 034204 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Phonon dispersions of studied polymorphs. Table containing the crystallographic parameters of the different polymorphs for all studied chemistries. Table containing the parameters used for shifting the total energies. Metastable phase diagrams of the studied chemistries. See DOI: https://doi.org/10.1039/d2ma00995a |
| This journal is © The Royal Society of Chemistry 2023 |