Investigating the Eley–Rideal recombination of hydrogen atoms on Cu (111) via a high-dimensional neural network potential energy surface
Lingjun
Zhu†
a,
Ce
Hu†
a,
Jialu
Chen
 b and
Bin
Jiang
b and
Bin
Jiang
 *a
*a
aSchool of Chemistry and Materials Science, Department of Chemical Physics, Key Laboratory of Surface and Interface Chemistry and Energy Catalysis of Anhui Higher Education Institutes, University of Science and Technology of China, Hefei, Anhui 230026, China. E-mail: bjiangch@ustc.edu.cn
bDepartment of Physics, City University of Hong Kong, Hong Kong, SAR, People's Republic of China
First published on 19th January 2023
Abstract
As a prototypical system for studying the Eley–Rideal (ER) mechanism at the gas–surface interface, the reaction between incident H/D atoms and pre-covered D/H atoms on Cu (111) has attracted much experimental and theoretical interest. Detailed final state-resolved experimental data have been available for about thirty-years, leading to the discovery of many interesting dynamical features. However, previous theoretical models have suffered from reduced-dimensional approximations and/or omitting energy transfer to surface phonons and electrons, or the high cost of on-the-fly ab initio molecular dynamics, preventing quantitative comparisons with experimental data. Herein, we report the first high-dimensional neural network potential (NNP) for this ER reaction based on first-principles calculations including all molecular and surface degrees of freedom. Thanks to the high efficiency of this NNP, we are able to perform extensive quasi-classical molecular dynamics simulations with the inclusion of the excitation of low-lying electron–hole pairs (EHPs), which generally yield good agreement with various experimental results. More importantly, the isotopic and/or EHP effects in total reaction cross-sections and distributions of the product energy, scattering angle, and individual ro-vibrational states have been more clearly shown and discussed. This study sheds valuable light on this important ER prototype and opens a new avenue for further investigations of ER reactions using various initial conditions, surface temperatures, and coverages in the future.
I Introductions
Surface reactions are of both fundamental and practical importance in many interfacial processes, such as interstellar/atmospheric chemistry,1 heterogeneous catalysis,2 and crystal growth.3 A majority of surface reactions follow the well-known Langmuir–Hinshelwood (LH) mechanism,4 in which reactions take place between adsorbates located in adjacent sites that are completely thermalized with the surface. On the other hand, reactions can also occur between a gaseous projectile and an adsorbed species on the surface, following the so-called Eley–Rideal (ER) mechanism.5 In more detail, the gaseous species may directly react with the adsorbate by a single collision (often referred to as the direct ER mechanism) or first convert to a highly diffusible “hot” precursor on the surface as a result of strong gas–surface interaction and then react with the adsorbate by multiple bounces way before accommodating to the surface (often referred to as the hot-atom (HA) mechanism6). Such ER/HA reactions differ from the LH ones in nature so that the corresponding product energies and momenta are often non-thermally distributed, where dynamics play a significant role.The dynamical features of various ER/HA processes have been investigated by a large body of experiments.7–19 For example, Kuipers et al.8 showed that a hyperthermal N(C2H4)3N molecule directly scattered from hydrogen-covered Pt (111) can be protonated, leaving with a kinetic energy strongly dependent on the incident energy thereof. Rettner9 found that the angular distribution of the HD is asymmetrical with respect to the surface normal and displays a dependence on the incidence energy when H(D) atoms collide with D(H) + Cu (111). ER/HA reactions could also lead to a high internal energy distribution in products as a result of a larger exothermicity than LH reactions, for example, the vibrational state distribution of HCl peaks at its first excited state in the reaction of the incident H atom with pre-adsorbed Cl–Au (111).7,10,14 More recently, Zaharia et al.19 observed the ER mechanism between two heavy species, namely the gaseous nitrogen atom and the O atom adsorbed on Ru (0001). Quan et al.20 further revealed the vibrational effect in an ER reaction involving a polyatomic projectile, where the vibrational excitation of the incident CO2 molecule can remarkably promote its association with pre-covered H atoms on Cu surfaces.
Among these examples, the ER reaction between gaseous and pre-covered hydrogen atoms on Cu (111) serves as one of the simplest representatives and is thus of great experimental and theoretical interests.9,11–13,21–26 Experimentally, Rettner and Auerbach13 measured the total abstraction cross-section for this reaction of ∼5.2 ± 1.3 Å2 per atom, which is almost independent of the isotopic substitution and the coverage. The resulting molecular hydrogen products were found with high translational, vibrational, and rotational excitations, resulting from the large exothermicity. In addition, a strong isotope effect appeared in the angular and vibrational state distributions.13 On the theoretical side, earlier dynamical calculations on the ER/HA recombination of H2 largely relied on potential energy surfaces (PESs) parameterized with empirical functions. For example, low-dimensional quantum dynamical models with empirical PESs of the London–Eyring–Polanyi–Sato (LEPS) function were first applied by Kratzer and Brenig21 and later extended by Jackson and Persson22 within a flat-surface approximation. Dai and Light23 considered the corrugation of the rigid surface in a four-dimensional quantum model on a LEPS PES. With a modified LEPS PES and an embedded atom method-based expression accounting for surface degrees of freedom (DOFs),25 Vurdu et al.24,25 performed extensive quasi-classical trajectory (QCT) calculations on this ER reaction on a realistic Cu (111) surface at different surface temperatures.
In recent years, dynamical calculations have been more frequently carried out with first-principles determined PESs, for instance, for studying the ER reactions of H with H + W (110) or W (100) and N with N + Ag (111).27–33 However, surface DOFs have been neglected in these PESs, although the energy transfer to surface phonons and/or electron–hole pairs (EHPs) was in several cases described by approximate models. To deal with such high-dimensional problems, the ab initio molecular dynamics (AIMD) method, in which energies and forces are computed on-the-fly by density functional theory (DFT), has been employed for studying the ER, HA, or hyperthermal H atom collisional processes.34–38 Based on AIMD simulations associated with an electronic friction (EF) theory39,40 within the local density friction approximation (LDFA)41 (referred to as the AIMDEF42 method hereafter), Zhou et al.37 discussed the respective effect of surface phonon and low-lying EHP excitations during the ER reaction between impinging H atoms and Cl atoms adsorbed on Au (111). But their impact on the reactivity and final state distributions was found to be limited. However, Alducin and coworkers found that in the ER recombination of H2 on tungsten surfaces, HA abstraction cross-sections are drastically reduced at low incident energies and low coverage due to energy loss to EHPs, while the effect on the ER reactivity is negligible.30,31,33 Using the same method, some of us38 identified the importance of including the EHP effects in quantitatively reproducing the measured reaction cross-sections and product translational energy distributions for D(H) + H(D)/Cu (111) ER reactions. Nevertheless, limited by the high computational cost, only a few hundreds of AIMD trajectories were typically affordable, rendering noticeable statistical errors in dynamics results. Moreover, some minor probability channels, e.g. individual rotational states of the product, cannot be well captured by AIMD.
Recent advances in atomistic neural network (AtNN)-based approaches have shown great promise in constructing high-dimensional PESs with surface DOFs for studying the gas–surface dynamics from first principles at affordable costs.43,44 Such PESs, once well-trained, will allow efficient calculation of a larger number of trajectories at the same level of accuracy as AIMD with merely about ten to hundred thousandth of cost. There have been successful applications of AtNN to molecular adsorption and desorption on metal surfaces.45–49 One example relevant to the present system is a universal PES for describing H2 dissociation on multiple copper surfaces, which accurately reproduced measured dissociative sticking probabilities for H2 dissociation on multiple copper surfaces under different conditions.50 However, the PES for an ER reaction needs to cover a larger configuration space where the two reactive species are well separated (one in the gas phase and the other on the surface) and the highly energetic gaseous atom may penetrate into the surface.
In this work, we report the first high-dimensional AtNN PES for the titled ER reaction, taking advantage of numerous data points generated by previous AIMD(EF) simulations.38 Additionally, the electron density of the metal surface is also fitted to an AtNN representation as a function of spatial position, allowing us to simulate the effects of EHP excitation by the EF model within LDFA. QCT(EF) calculations on this new PES not only well reproduce the AIMD(EF) results with much better statistics but also predict the rotational state distributions of each vibrational state. A majority of experimental data are well reproduced and the remaining discrepancies between theory and experiments are discussed.
II Computational details
A. Density functional theory calculations
Total energies and forces of data points were calculated using the Vienna Ab initio Simulation Package (VASP)51,52 in terms of plane-wave DFT at the generalized gradient approximation (GGA) level, using an optPBE-vdW53 functional, which describes the dissociative chemisorption of H2 on Cu (111) with chemical accuracy.50,54 Since the impinging H atom is a radical, spin-polarization was imposed in all calculations. The H-covered Cu (111) surface was modeled with two hydrogen atoms pre-adsorbed on a slab with a 2 × 2 supercell of four copper layers (top three layers are relaxed), labeled as 2H(a)/Cu (111), corresponding to the coverage of 0.5 ML in experiments.12,55 The projector augmented wave (PAW) method was applied to describe the electron-core interaction.56 The kinetic energy in the plane wave basis set was truncated at 350 eV. The Brillouin zone was sampled via a 5 × 5 × 1 Monkhorst–Pack k-point mesh.57 A vacuum region of 15 Å was created between periodic slabs and the dipole correction in the Z direction was imposed to avoid the interaction between the vertically repeated images.AIMD(EF) simulations have been performed in our previous work using this setup.38 To model experimental conditions as much as possible, the incident H or D atom was initiated at 5.0 Å above the surface with a mean incident energy of 0.07 eV and an incidence angle of 10.0° about the surface normal. The surface configurations were sampled at the temperature of 100 K. Three hundred trajectories were propagated in each of four conditions with a time step of 1 fs and a maximum simulation time of 1 ps, namely incident H(D) atom hitting on the pre-covered D*(H*) atoms (referred as H-on-D (D-on-H) hereafter, respectively), with or without electron friction. A total of 728![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 015 data points were generated with both energies and forces available for the fitting.
015 data points were generated with both energies and forces available for the fitting.
B. Embedded atom neural network potential energy surface
The H(g) + 2H(a)/Cu (111) PES was constructed by our recently proposed embedded atom neural network (EANN) approach,46 in which the total energy of the system is regarded as the sum of atomic energies by a local approximation. Each atomic energy is the output of an atomic neural network (ANN) mapping from the electron density of this atom embedded in the environment consisting of surrounding atoms,58 expressed as,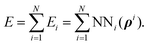 | (1) |
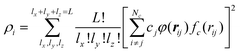 | (2) |
| φ(rij) = xlxylyzlz exp(−α|r − rm|2) | (3) |
A total of 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 851 points were selected from 1200 AIMD(EF) trajectories reported in ref. 38 based on a generalized Euclidian distance criterion for the bond distance (1 Å) and for the atomic force (0.3 meV Å−1), respectively. Such criteria effectively filter out similar structures in these trajectories.46 Nine tenths of data points were used for training and the rest for validation. The hyperparameters of GTO are as follows: L = 0, 1, and 2; rc = 6.2 Å; α = 0.8 Å−2; and rm = 0.0, 0.5, 1.0, 1.5, 2.0, 2.5, 3.0, 3.5, 4.0, 4.5, 5.0, 5.5, and 6.0 Å, resulting in 39 EAD features. Each ANN consists of two hidden layers with 40 and 60 neurons in each layer.
851 points were selected from 1200 AIMD(EF) trajectories reported in ref. 38 based on a generalized Euclidian distance criterion for the bond distance (1 Å) and for the atomic force (0.3 meV Å−1), respectively. Such criteria effectively filter out similar structures in these trajectories.46 Nine tenths of data points were used for training and the rest for validation. The hyperparameters of GTO are as follows: L = 0, 1, and 2; rc = 6.2 Å; α = 0.8 Å−2; and rm = 0.0, 0.5, 1.0, 1.5, 2.0, 2.5, 3.0, 3.5, 4.0, 4.5, 5.0, 5.5, and 6.0 Å, resulting in 39 EAD features. Each ANN consists of two hidden layers with 40 and 60 neurons in each layer.
C. Quasi-classical trajectory calculations
In this work, molecular dynamics calculations were performed using a heavily modified in-house version of the VENUS code,67 in which the quasi-classical quantization of the ER product was implemented. Such calculations based on the analytical EANN PES distinct from previous on-the-fly AIMD simulations by VASP and are marked as QCT for clarification, despite that, both essentially use the same treatment for initial conditions and product analysis. Following the previous AIMD work,38 the incident H(D) atom was launched from 5.0 Å above the surface with a mean incident energy (Ein = 0.07 eV), which was sampled to satisfy the experimental distribution68 given by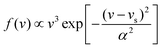 , where vs is the stream velocity and α characterizes the width of the velocity distribution. The incident angle (θin) was taken as 10° relative to the surface normal, and the incident azimuthal angle and the impact position in the unit cell were randomly sampled. The two hydrogen atoms were placed at two favorable fcc sites. Note that the three top layers of the metal surface including the pre-adsorbed H(D) were allowed to relax. The initial velocities and configurations of surface and pre-adsorbed atoms were taken from molecular dynamics trajectories sampled according to the Andersen thermostat69 with a target surface temperature Ts = 100 K. No thermostat was imposed when simulating the collisional process.
, where vs is the stream velocity and α characterizes the width of the velocity distribution. The incident angle (θin) was taken as 10° relative to the surface normal, and the incident azimuthal angle and the impact position in the unit cell were randomly sampled. The two hydrogen atoms were placed at two favorable fcc sites. Note that the three top layers of the metal surface including the pre-adsorbed H(D) were allowed to relax. The initial velocities and configurations of surface and pre-adsorbed atoms were taken from molecular dynamics trajectories sampled according to the Andersen thermostat69 with a target surface temperature Ts = 100 K. No thermostat was imposed when simulating the collisional process.
In order to take the nonadiabatic energy dissipation channel into account, the EF model based on LDFA41 was employed. In this LDFA-based EF model, an electronic friction force is introduced as the feedback of fast electrons to the slow nuclear motion, resulting in a generalized Langevin equation,41
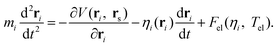 | (4) |
The friction coefficient of H(D) for a given electron density has been tabulated elsewhere.70 Since the upper three metal layers are movable, the surface motion would change the electron density.71 To capture this, we constructed another EANN model to approximate the relationship between embedded electron density and the position of the embedded atom above the mobile surface, i.e., electron density surface (EDS), as has been recently done for NO on Au (111)72 and H2O on Pt (110)-(1 × 2).64 In this respect, the EDS formally amounts to the PES of a pseudo atom adsorbed on this surface. Specifically, six hundred distinct Cu (111) surface configurations were selected from AIMD trajectories of the clean surface at Ts = 100 K, and the corresponding electron densities in the three-dimensional space were saved for each configuration. The hyperparameters of the EANN EDS include L = 0, 1, and 2; rc = 4.1 Å; α = 0.99 Å−2; rm = 0.00, 0.45, 0.90, 1.35, 1.80, 2.25, 2.70, 3.15, 3.60, 4.05 Å; and 50/50 neurons in the first/second hidden layer. As the electron density varies mildly with the atomic position, this EANN EDS reproduced the DFT calculated electron densities (ranging from 0.0198 e Å−3 to 1.88 e Å−3) very well, with an extremely low root-mean-square-error (RMSE) of 3.66 × 10−5 e Å−3.
In dynamics calculations, each trajectory was propagated with a time step of 0.05 fs via the velocity Verlet algorithm and the longest propagation time was 1 ps. A trajectory was regarded as reactive if one of the absorbed D(H) atoms is abstracted by the impinging H(D) atom or the other absorbed atom to form a molecule desorbing away from the surface up to 5.0 Å above the top layer. The reaction can take place either via a so-called HA mechanism,6 in which the impinging atom does not collide with the adsorbate directly, or a direct ER mechanism, in which the product is generated by a single bounce between the impinging atom and the adsorbate. The HA mechanism was identified in the following cases: (a) the incident atom reaches 1.2 Å above the surface with a distance larger than 2.0 Å to any pre-adsorbates and thus becomes a hot adatom; (b) the distance between this hot adatom and the pre-adsorbate stretches back and forth for more than once before forming a molecule. A non-reactive trajectory was regarded as scattering if the incident atom is directly reflected to the vacuum, whereas it is considered to be sticking if the incident atom remains staying on the surface after 1 ps. The Einstein–Brillouin–Keller (EBK) method73 was performed to determine the vibrational action number (v) of the formed molecule semi-classically, via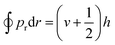 , where pr is the relative momentum along the molecular bond. In addition, rotational quantum numbers were calculated by the rotational angular momentum of diatomic molecules. Finally, the vibrational and rotational distributions of the product were determined using the histogram binning method. This quasi-classical treatment allows the analysis of the final state distribution of the ER products for comparison with experiments.
, where pr is the relative momentum along the molecular bond. In addition, rotational quantum numbers were calculated by the rotational angular momentum of diatomic molecules. Finally, the vibrational and rotational distributions of the product were determined using the histogram binning method. This quasi-classical treatment allows the analysis of the final state distribution of the ER products for comparison with experiments.
We note that the high efficiency of the EANN PES enables much faster QCT simulations than on-the-fly AIMD simulations. The average wall-time for running a QCT trajectory is ∼0.056 s per step per CPU core, compared with ∼625 s per step per core for an AIMD trajectory with the same Intel Xeon Gold 6132 CPU, exhibiting an acceleration of roughly five orders of magnitude. To obtain statistically converged results, a total of 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 trajectories were propagated in each condition, i.e., incident H(D) atom hitting on the pre-adsorbed D(H) atoms [labeled as H-on-D (D-on-H) hereafter], without or with electron friction, corresponding to QCT and QCTEF results, respectively.
000 trajectories were propagated in each condition, i.e., incident H(D) atom hitting on the pre-adsorbed D(H) atoms [labeled as H-on-D (D-on-H) hereafter], without or with electron friction, corresponding to QCT and QCTEF results, respectively.
III Results and discussion
A. Potential energy surface
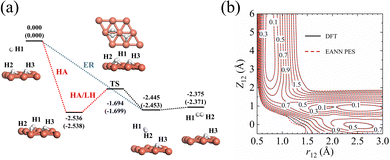
The accuracy of the EANN PES of the H(g) + 2H(a)/Cu (111) system has been quantified in several aspects. First, the overall RMSEs are 6.5/8.1 meV in energy per (2 × 2) cell and 16.6/17.0 meV Å−1 in atomic force for the training/test set, respectively. Second, stationary points calculated via our EANN PES are compared with the corresponding DFT results as shown in Fig. 1 and Table 1. The PES predictions on the static structures and energies of the adsorption state and the transition state (TS) for H2 recombinative desorption (or H2 dissociation) are all in good agreement with DFT values, with errors as small as 8 meV in energy, 0.01 Å in bond length, and 0.05° in angle. Specifically, the incident hydrogen atom can adsorb at the neighboring unoccupied fcc site of pre-covered H adatoms with an adsorption energy of 2.536 eV on the PES vs. 2.538 eV by DFT. The direct ER reaction channel is barrierless with a large exothermicity (2.375 eV), which agrees well with the DFT (2.371 eV) and experimentally estimated value (∼2.3 eV).13 Alternatively, an incident hydrogen atom can be accelerated by the adsorption well to become a translationally hot atom, which can extract a pre-adsorbed H atom before being fully thermalized with the substrate. This so-called HA mechanism and the thermal LH process share the same barrier of 0.842 eV for associative desorption and 0.681 eV for dissociative chemisorption. This predicted barrier height of dissociative chemisorption compares well with 0.672 eV using the same optPBE-vdW functional50 and higher than 0.636 eV using the SRP-48 functional reported previously.74 Note that a well depth of 82 meV for the physisorbed H2 on Cu (111) due to the vdW effect is also captured by the EANN PES (70 meV). But the optPBE-vdW functional seems to somewhat overestimate the well depth compared to the experimental values (29.5 meV,75 22.2 meV76).| Configuration | r 12 (Å) | Z 12 (Å) | θ 12 (°) | Z 3 (Å) | E (eV) |
|---|---|---|---|---|---|
| H(g) + 2H(a) | — | — | — | 0.91 (0.92) | 0.000 (0.000) |
| H(a) + 2H(a) | 2.62 (2.62) | 0.88 (0.87) | 90.0 (90.0) | 0.88 (0.87) | −2.536 (−2.538) |
| TS | 1.06 (1.05) | 1.17 (1.17) | 86.3 (86.3) | 0.95 (0.95) | −1.694 (−1.699) |
| H2(a) + H(a) | 0.75 (0.75) | 3.93 (3.92) | 66.6 (66.7) | 0.96 (0.97) | −2.445 (−2.453) |
| H2(g) + H(a) | 0.75 (0.75) | — | — | 0.96 (0.96) | −2.375 (−2.371) |
In addition, Fig. 1b shows the two-dimensional cut of the PES as a function of the height of the H1–H2 centroid above the surface (Z12) and the bond length of H1–H2 (r12), representing the dissociative adsorption of H2 on Cu (111). The EANN PES reproduces quite well these evenly distributed grid points directly calculated by DFT (not included in the training data). Note that there is a shallow well at r12 ∼ 2.5 Å and Z12 ∼ 0 Å, corresponding to one of hydrogen atoms penetrating into the surface. On the other hand, Fig. 2 clearly shows the ER channel by a two-dimensional energy contour plot with respect to the height of H1 and H2 above the surface with the H1–H2 centroid fixed at the fcc site. A representative ER trajectory is projected onto this contour plot to illustrate how the ER reaction takes place. Following this trajectory, the incident hydrogen (H1) gradually approaches the surface and abstracts the adsorbed hydrogen (H2) to form the H2 molecule, which escapes from the surface with large exothermicity.
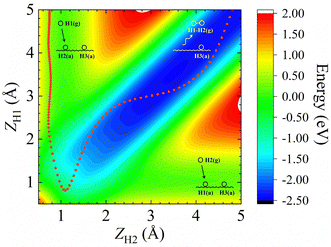 | ||
| Fig. 2 Two-dimensional energy contour plot for showing the ER and exchange channels (corresponding structures illustrated by insets) as a function of ZH1 (distance between the surface and H1) and ZH2 (distance between the surface and H2). A representative ER trajectory is projected onto this contour plot by red dots. The energy zero is the same as that shown in Fig. 1. | ||
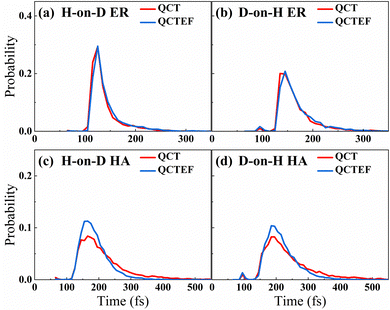
B. Abstraction reaction cross sections
Table 2 compares the calculated probabilities of different events and abstraction reaction cross sections from QCT(EF) and AIMD(EF),38 as well as experimental data whenever available. Because it was difficult to distinguish the direct ER and indirect HA mechanisms through experiments, the measured product flux included signals of both channels. Consistent with experimental13 and AIMD(EF)38 results, the overall abstraction reaction is quite efficient regardless of the incident isotope, in which the HA mechanism is always dominant. Interestingly, this channel is more significantly affected by the low-lying electronic excitation than the direct ER channel because the hot hydrogen atom in the former channel could stay nearby or even penetrate into the surface and more strongly interact with the metallic electrons for sufficient time. This is supported by the simulation time distributions for reactive trajectories shown in Fig. 3, where HA trajectories generally occur longer than the direct ER ones. One can see that energy dissipation to EHPs reduces the reaction time for trajectories undergoing the HA mechanism more obviously than that for those undergoing the direct ER mechanism. One would expect a more significant EHP effect for a lower coverage of pre-adsorbed H atoms, as the impinging H atom can travel more easily and for a longer time close to the surface before the abstraction. This is consistent with the finding of Alducin and coworkers for the abstraction reaction of H(g) and H-covered W surfaces.30,31,33 Energy loss to EHPs described by the EF model reduces the kinetic energy of the hot atom and thus its reactivity. For a similar reason, the formation probability of the H2/D2 products between pre-adsorbed atoms via the secondary HA mechanism,77 which is a minor channel undetected in experiment, is also significantly lowered due to the energy dissipation to EHPs. Quantitatively, for the direct ER channel and H atom scattering event in both H-on-D and D-on-H cases, QCT results agree very well with the AIMD ones. However, QCT calculations yield slightly higher sticking probabilities and lower abstraction probabilities via the HA mechanism than those of AIMD,38 whereas QCTEF results do the opposite. The smaller time-step and more ergodic sampling of surface configurations imposed in QCT(QCTEF) calculations than AIMD(EF) ones may cause the numerical differences. Anyhow, the abstraction reaction cross sections obtained by QCTEF are lower than QCT ones by ∼1/4 and in excellent agreement with the experimental values with much better statistics than AIMDEF ones, confirming the quantitative role of low-lying EHPs in the overall process.| Outcome | H-on-D | D-on-H | Expt. | ||
|---|---|---|---|---|---|
| QCT (AIMD) | QCTEF (AIMDEF) | QCT (AIMD) | QCTEF (AIMDEF) | ||
| a Direct Eley–Rideal mechanism. b Hot-atom mechanism. c Secondary hot-atom recombination between pre-adsorbed atoms. | |||||
| Scattering | 0.003 ± 0.000 (0.00) | 0.001 ± 0.000 (0.00) | 0.001 ± 0.000 (0.00) | 0.000 (0.00) | 0.02–0.10 |
| HD (ER)a | 0.103 ± 0.001 (0.11 ± 0.02) | 0.105 ± 0.001 (0.11 ± 0.02) | 0.141 ± 0.002 (0.13 ± 0.02) | 0.148 ± 0.002 (0.15 ± 0.02) | 0.47 ± 0.12 |
| HD (HA)b | 0.481 ± 0.002 (0.54 ± 0.03) | 0.353 ± 0.002 (0.33 ± 0.03) | 0.413 ± 0.002 (0.49 ± 0.03) | 0.313 ± 0.002 (0.29 ± 0.03) | |
| H2/D2c | 0.031 ± 0.001 (0.04 ± 0.01) | 0.009 ± 0.000 (0.01 ± 0.01) | 0.068 ± 0.001 (0.08 ± 0.02) | 0.025 ± 0.001 (0.01 ± 0.01) | |
| Sticking | 0.382 ± 0.002 (0.32 ± 0.03) | 0.532 ± 0.002 (0.55 ± 0.03) | 0.377 ± 0.002 (0.30 ± 0.03) | 0.514 ± 0.002 (0.55 ± 0.03) | |
| Abstraction reaction cross section (Å2) | |||||
| HD (ER + HA) | 6.683 ± 0.026 (7.43 ± 0.32) | 5.241 ± 0.026 (5.05 ± 0.33) | 6.346 ± 0.026 (7.12 ± 0.31) | 5.275 ± 0.026 (5.01 ± 0.33) | 5.2 ± 1.3 |
C. Product state distributions
Compared with the overall probability of each channel presented above, final state and angular distributions of the ER/HA products are more challenging for AIMD simulations, as one requires a sufficient number of trajectories to reduce statistical errors of individual states. Indeed, previous AIMD(EF) results in this aspect contain significant error bars,38 while this is not a problem at all using the highly efficient EANN PES. In Fig. 4a and b, we compare the theoretical and experimental vibrational state distributions of the HD products from the overall ER/HA reaction in both H-on-D and D-on-H cases. Note that statistical errors are negligibly small for QCT(EF) results and thus not shown for making the plot less crowded. While QCT(EF) results coincide well with AIMD(EF) ones, they all predict colder vibrational state distribution than that of the experiment,13 regardless of the isotopic effect or the EHP effect. The calculated vibrational state distributions decrease monotonically from v = 0 to v = 4, while the experimental ones peak at v = 1 or even higher.13 The mean vibrational energies of 0.59(0.54) eV and 0.62(0.57) eV for H-on-D and D-on-H via QCT(QCTEF) simulations are compared with 0.60 ± 0.05 and 0.68 ± 0.05 eV of experimental values (Table 3). However, note that the experimental values do not include the zero-point energy (∼0.23 eV for HD) so that the theory virtually underestimates the product vibrational energy significantly.13 This underestimation of vibrational excitation was observed in previous QCT studies,25,77–80 which may be attributed to the artificial leakage of vibrational energy to other DOFs, since previous low-dimensional quantum dynamical results on the rigid surface appeared to behave more analogously to experimental distributions with respect to this quantity.23,26 Unfortunately, full-dimensional quantum dynamics calculations for the ER reaction involving surface DOFs remain infeasible and necessitate further development.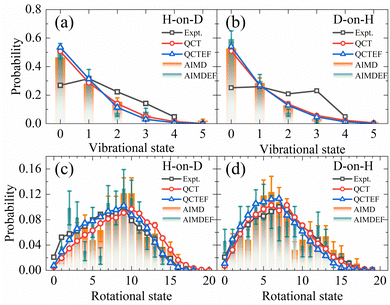 | ||
| Fig. 4 Comparison of vibrational state (a and b) and overall rotational state (c and d) distributions for HD products in the H-on-D and D-on-H reactions (see text) from QCT(EF) and AIMD(EF) calculations. The experimental data of vibrational state and rotational state are taken from ref. 13 at Ein = 0.07 eV and θin = 10°. | ||
Fig. 4c and d compare the overall rotational state distributions of HD corresponding to sums over all vibrational states. The overall shapes of the AIMD(EF)38 distributions are well reproduced by QCT(EF) results, but the latter are free of artificial oscillations owing to the negligible statistical errors. Moreover, QCT(EF) distributions show more clearly the peak positions and the subtle effect due to EHP excitations, which marginally shifts the distribution to the lower-J end. In the H-on-D case, in particular, this nonadiabatic effect results in better agreement with the experimental distribution. In general, QCT(EF) calculations confirm the experimental observation that the rotational state distribution of D-on-H is slightly colder than that of H-on-D.13 The calculated mean rotational energies for H-on-D and D-on-H by QCT(EF) are 0.45(0.37) and 0.34(0.30) eV, respectively, in good agreement with the experimental values of 0.37 ± 0.05 and 0.35 ± 0.05 eV (Table 3).13
In Fig. 5a and b, the translational energy distributions of HD in QCT(EF) and AIMD(EF)38 simulations are compared. Thanks to much smaller statistical errors, the QCT(EF) results eliminate these oscillating structures in the distributions and provide more convincing evidence for a broader translational energy distribution for D-on-H than for H-on-D, an isotopic effect mistily observed in previous AIMD(EF) results.38 The inclusion of electronic friction shifts the QCT distribution notably to the low energy end for H-on-D, while more weakly for D-on-H. It is likely that the more significant energy loss due to EHPs for the incident H atom than D atom plays a role, because the former has a higher speed at a given incidence energy and will feel stronger frictional force. This seems a possible origin of the isotopic effect here. The mean translational energies for H-on-D and D-on-H predicted by QCT(QCTEF) are 1.00(0.90) and 1.10(1.05) eV, respectively. They agree well with the experimental trend and values12 of 0.85 ± 0.20 and 1.10 ± 0.20 eV in the two cases, even though the latter were measured under a different initial condition with Ein = 0.33 eV and θin = 60°.12
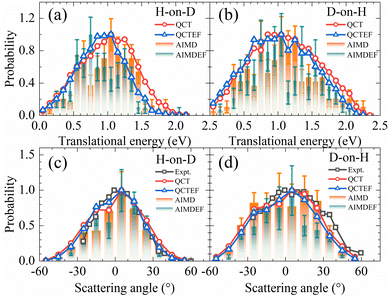 | ||
| Fig. 5 Comparison of translational energy (a and b) and scattering angle (c and d) distributions for HD products in H-on-D and D-on-H reactions from QCT(EF) and AIMD(EF) calculations. In each distribution, the maximum population is scaled to be one. The experimental translational energy distributions are taken from ref. 12 at Ein = 0.33 eV and θin = 60°. The experimental scattering angle distributions are taken from ref. 9 at Ein = 0.07 eV and θin = 70° and it was stated there that the angular distribution is relatively insensitive to the incidence energy and angle. | ||
Scattering angle distributions of HD products obtained from QCT(EF), AIMD(EF)38 are compared with the available experimental data shown in Fig. 5c and d.9 The QCT(EF) calculations well reproduce the slightly asymmetrical angular distributions and mistily predict that the distribution for D-on-H is ∼1.5 times broader than that for H-on-D, as observed in the experiment. QCT and QCTEF results are very close to each other in both cases, implying that EHP excitations have a minor effect on the angular distribution. Although AIMD and AIMDEF results also qualitatively agree with experiments, their discrepancy (especially in the D-on-H case) seems more apparent due to the poor statistics. The asymmetry in angular distributions is consistent with the fact that the ER or HA reaction occurs prior to the parallel momentum accommodation. As assumed by Kratzer and Brenig21 and confirmed in our previous work,38 the difference between H-on-D and D-on-H comes from the fact that the parallel momentum for D is 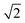 times as large as that for H, giving rise to a ∼1.5 times broader angular distribution for D-on-H.
times as large as that for H, giving rise to a ∼1.5 times broader angular distribution for D-on-H.
The present QCT(EF) calculations allow us to analyze the rotational excitation of each individual vibrational state, which was difficult to extract from a limited number of AIMD trajectories. In Fig. 6a and b, the calculated and measured mean rotational energies of each vibrational state13 for H-on-D and D-on-H are compared. In general, it is clear from Fig. 6 that the degree of rotational excitation decreases with increasing vibrational energy, indicating an anti-correlation between vibrational and rotational excitation. Our calculations properly capture the different decreasing behaviors of the mean rotational energy with an increasing vibrational excitation in both H-on-D and D-on-H cases. Specifically, for H-on-D, the degree of rotational excitation decays almost linearly with increasing vibrational energy in the experiment,13 which is reproduced by our QCT(EF) results despite a smaller decreasing rate. For D-on-H, the QCT(EF) results qualitatively capture the level-off behavior of the mean rotational energy from v = 1 and v = 2, but significantly underestimate the decreasing slope for lower and higher v. In any cases, the energy loss to EHPs systematically reduces the mean rotational energies of all vibrational state, but barely alters the decreasing rate.
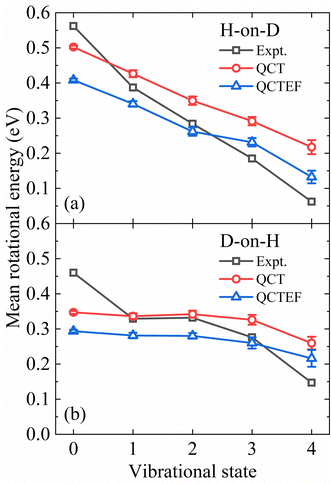 | ||
| Fig. 6 Comparison of the mean rotational energy as a function of vibrational state for the H-on-D (a) and D-on-H (b) collisions obtained from QCT(EF) and experiments. The experimental data are taken from ref. 13 at Ein = 0.07 eV and θin = 10°. | ||
In addition, the calculated and experimental distributions of internal energy (vibrational energy plus rotational energy) of each vibrational state are compared in Fig. 7. Note that the population of each individual ro-vibrational state is rather small, especially for v > 1, so that the statistical error bars are no longer negligible. The overall agreement with experiments13 is reasonably good. Including the energy dissipation to EHPs described by the EF model generally lowers the rotational excitation and improves the agreement between the theory and experiment. Especially, in the H-on-D case, the QCTEF distribution shows a gradually higher peak position and narrower width, with the increasing vibrational energy, in general accord with the experiment. On the other hand, the D-on-H rotational distributions have more low-J populations for lower v and more high-J populations for higher v, compared with H-on-D. QCTEF results reasonably capture this general experimental trend, but somewhat underestimate the rotational excitation for v = 0, while these overestimate for v ≥ 2. This behavior may be related to the narrower angular distribution for H-on-D than that for D-on-H, implying that the collision geometry in the former case is probably more focused to the surface normal.81 It is interesting to remind that the overall rotational state distribution is slightly colder for D-on-H than for H-on-D, as shown in Fig. 4, which is actually dominated by the v = 0 and v = 1 components.
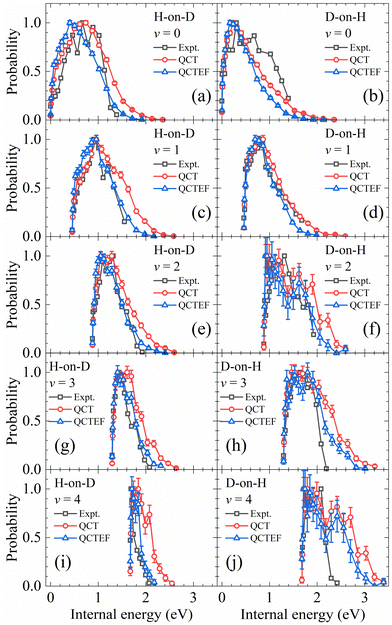 | ||
| Fig. 7 Comparison of internal energy distributions of the HD products in different vibrational states of the H-on-D (a, c, e, g and i) and D-on-H (b, d, f, h and j) reactions obtained from QCT(EF) and experimental data. The experimental data are taken from ref. 13 at Ein = 0.07 eV and θin = 10°. In each distribution, the maximum population is scaled to be one. | ||
IV Conclusions
In summary, we report the first high-dimensional NN PES with surface DOFs included for describing the abstraction reaction between H(g)/D(g) and pre-covered D(a)/H(a) on Cu (111) via the direct ER and HA mechanisms, which is fitted to over ten thousands DFT data points extracted from previous AIMD simulations. Based on this efficient PES and an EF model accounting for the EHP effect, extensive QCT(EF) calculations yield total abstraction reaction cross-sections and product state distributions with much better statistics than previous AIMD results. This helps us elucidate more clearly the EHP and isotopic effects in the ER dynamics. Interestingly, the energy dissipation to EHPs has a notable effect on the total reaction cross-section, rotational state and translational energy distributions for H-on-D, while it has a marginal effect on other quantities. This leads to an isotopic effect in the rotational state and translational energy distributions. On the other hand, the isotropic effect in the angular distribution appears irrelevant to the electronic excitation, which instead comes from the fact that the parallel momentum for the incident D atom is larger than that for the H atom. Overall, the theory–experiment agreement is good, except that the theory predicts too cold vibrational excitation, probably due to the neglect of quantum effects. Further quantum studies, possibly combined with some reduced-dimensional approximations,23,82 are desirable. It is worth noting that an even colder vibrational state distribution with a 90% (83%) of H2(D2) population at the vibrationally ground state was observed in the experiments of atomic hydrogen recombination on the copper polycrystalline film at 293–303 K.83 This means that the vibrational state distribution may be dependent on experimental conditions and the sample status. With some additional training data of a larger supercell and of a varying number of adsorbates sampled at different surface temperatures, the NN PES can be improved to describe more surface status and allow us to study, for example, the coverage- and temperature-dependent ER and HA reaction dynamics. Work along this direction is in progress in our group. Future investigations in this benchmark ER reaction based on this PES are expected to reveal the influence of the incidence conditions, coverage and surface temperature.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by the National Natural Science Foundation of China (Grant No. 22073089). Numerical calculations have been performed on the Supercomputing Center of USTC, Hefei Advanced Computing Center, and Beijing PARATERA Tech CO., Ltd.References
- Y. Yao, P. Shushkov, T. F. Miller and K. P. Giapis, Nat. Commun., 2019, 10, 2294 CrossRef PubMed.
- G. A. Somorjai and Y. Li, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 917–924 CrossRef CAS PubMed.
- Z. Qiu, P. Li, Z. Li and J. Yang, Acc. Chem. Res., 2018, 51, 728–735 CrossRef CAS PubMed.
- C. T. Rettner and M. N. R. Ashfold, Dynamics of Gas-Surface Interaction, The Royal Society of Chemistry, London, 1991 Search PubMed.
- D. D. Eley and E. K. Rideal, Nature, 1940, 146, 401–402 CrossRef CAS.
- J. Harris and B. Kasemo, Surf. Sci., 1981, 105, L281–L287 CAS.
- K. R. Lykke and B. D. Kay, SPIE, 1990, 1208, 18–29 CrossRef CAS.
- E. W. Kuipers, A. Vardi, A. Danon and A. Amirav, Phys. Rev. Lett., 1991, 66, 116–119 CrossRef CAS PubMed.
- C. T. Rettner, Phys. Rev. Lett., 1992, 69, 383–386 CrossRef CAS PubMed.
- C. T. Rettner and D. J. Auerbach, Science, 1994, 263, 365–367 CrossRef CAS PubMed.
- C. T. Rettner and D. J. Auerbach, Phys. Rev. Lett., 1995, 74, 4551–4554 CrossRef CAS PubMed.
- C. T. Rettner and D. J. Auerbach, Surf. Sci., 1996, 602–608 CrossRef CAS.
- C. T. Rettner and D. J. Auerbach, J. Chem. Phys., 1996, 104, 2732–2739 CrossRef CAS.
- C. T. Rettner, J. Chem. Phys., 1994, 101, 1529–1546 CrossRef CAS.
- T. Kammler, J. Lee and J. Küppers, J. Chem. Phys., 1997, 106, 7362–7371 CrossRef CAS.
- S. Wehner and J. Küppers, J. Chem. Phys., 1998, 108, 3353–3359 CrossRef CAS.
- J.-Y. Kim and J. Lee, Phys. Rev. Lett., 1999, 82, 1325–1328 CrossRef CAS.
- F. Khanom, A. Aoki, F. Rahman and A. Namiki, Surf. Sci., 2003, 536, 191–205 CrossRef CAS.
- T. Zaharia, A. W. Kleyn and M. A. Gleeson, Phys. Rev. Lett., 2014, 113, 053201 CrossRef CAS PubMed.
- J. Quan, F. Muttaqien, T. Kondo, T. Kozarashi, T. Mogi, T. Imabayashi, Y. Hamamoto, K. Inagaki, I. Hamada, Y. Morikawa and J. Nakamura, Nat. Chem., 2019, 11, 722–729 CrossRef CAS PubMed.
- P. Kratzer and W. Brenig, Surf. Sci., 1991, 254, 275–280 CrossRef CAS.
- M. Persson and B. Jackson, J. Chem. Phys., 1995, 102, 1078–1093 CrossRef CAS.
- J. Dai and J. C. Light, J. Chem. Phys., 1999, 110, 6511–6518 CrossRef CAS.
- C. D. Vurdu, S. Özçelik and Z. B. Güvenç, Surf. Sci., 2007, 601, 3745–3749 CrossRef CAS.
- C. D. Vurdu and Z. B. Güvenç, J. Chem. Phys., 2011, 134, 164306 CrossRef PubMed.
- C. Kalyanaraman, D. Lemoine and B. Jackson, Phys. Chem. Chem. Phys., 1999, 1, 1351–1358 RSC.
- M. Blanco-Rey, E. Díaz, G. A. Bocan, R. Díez Muiño, M. Alducin and J. I. Juaristi, J. Phys. Chem. Lett., 2013, 4, 3704–3709 CrossRef CAS.
- O. Galparsoro, R. Pétuya, J. I. Juaristi, C. Crespos, M. Alducin and P. Larrégaray, J. Phys. Chem. C, 2015, 119, 15434–15442 CrossRef CAS.
- R. Pétuya, M. A. Nosir, C. Crespos, R. D. Muiño and P. Larrégaray, J. Phys. Chem. C, 2015, 119, 15325–15332 CrossRef.
- O. Galparsoro, R. Petuya, F. Busnengo, J. I. Juaristi, C. Crespos, M. Alducin and P. Larregaray, Phys. Chem. Chem. Phys., 2016, 18, 31378–31383 RSC.
- O. Galparsoro, H. F. Busnengo, J. I. Juaristi, C. Crespos, M. Alducin and P. Larregaray, J. Chem. Phys., 2017, 147, 121103 CrossRef PubMed.
- O. Galparsoro, J. I. Juaristi, C. Crespos, M. Alducin and P. Larrégaray, J. Phys. Chem. C, 2017, 121, 19849–19858 CrossRef CAS.
- O. Galparsoro, H. F. Busnengo, A. E. Martinez, J. I. Juaristi, M. Alducin and P. Larregaray, Phys. Chem. Chem. Phys., 2018, 20, 21334–21344 RSC.
- A. Groß, Phys. Rev. Lett., 2009, 103, 246101 CrossRef PubMed.
- M. Pavanello, D. J. Auerbach, A. M. Wodtke, M. Blanco-Rey, M. Alducin and G.-J. Kroes, J. Phys. Chem. Lett., 2013, 4, 3735–3740 CrossRef CAS.
- G.-J. Kroes, M. Pavanello, M. Blanco-Rey, M. Alducin and D. J. Auerbach, J. Chem. Phys., 2014, 141, 054705 CrossRef PubMed.
- L. Zhou, X. Zhou, M. Alducin, L. Zhang, B. Jiang and H. Guo, J. Chem. Phys., 2018, 148, 014702 CrossRef PubMed.
- J. Chen, X. Zhou and B. Jiang, J. Chem. Phys., 2019, 150, 061101 CrossRef PubMed.
- B. Hellsing and M. Persson, Phys. Scr., 1984, 29, 360–371 CrossRef CAS.
- M. Head-Gordon and J. C. Tully, J. Chem. Phys., 1995, 103, 10137–10145 CrossRef CAS.
- J. I. Juaristi, M. Alducin, R. Díez Muiño, H. F. Busnengo and A. Salin, Phys. Rev. Lett., 2008, 100, 116102 CrossRef CAS PubMed.
- P. Saalfrank, J. I. Juaristi, M. Alducin, M. Blanco-Rey and R. Díez Muiño, J. Chem. Phys., 2014, 141, 234702 CrossRef PubMed.
- B. Jiang, J. Li and H. Guo, J. Phys. Chem. Lett., 2020, 11, 5120–5131 CrossRef CAS PubMed.
- X. Zhou, Y. Zhang, R. Yin, C. Hu and B. Jiang, Chin. J. Chem., 2021, 39(10), 2917–2930 CrossRef CAS.
- B. Kolb, X. Luo, X. Zhou, B. Jiang and H. Guo, J. Phys. Chem. Lett., 2017, 8, 666–672 CrossRef CAS PubMed.
- Y. Zhang, C. Hu and B. Jiang, J. Phys. Chem. Lett., 2019, 10, 4962–4967 CrossRef CAS PubMed.
- X. Zhou, Y. Zhang, H. Guo and B. Jiang, Phys. Chem. Chem. Phys., 2021, 23, 4376–4385 RSC.
- K. Shakouri, J. Behler, J. Meyer and G.-J. Kroes, J. Phys. Chem. Lett., 2017, 8, 2131–2136 CrossRef CAS PubMed.
- N. Gerrits, K. Shakouri, J. Behler and G.-J. Kroes, J. Phys. Chem. Lett., 2019, 10, 1763–1768 CrossRef CAS PubMed.
- L. Zhu, Y. Zhang, L. Zhang, X. Zhou and B. Jiang, Phys. Chem. Chem. Phys., 2020, 22, 13958–13964 RSC.
- G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- G. Kresse and J. Furthmuller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- J. Klimeš, D. R. Bowler and A. Michaelides, J. Phys.: Condens. Matter, 2010, 22, 022201 CrossRef PubMed.
- M. Wijzenbroek, D. M. Klein, B. Smits, M. F. Somers and G.-J. Kroes, J. Phys. Chem. A, 2015, 119, 12146–12158 CrossRef CAS PubMed.
- G. Anger, A. Winkler and K. D. Rendulic, Surf. Sci., 1989, 220, 1 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- Y. Zhang, X. Zhou and B. Jiang, J. Phys. Chem. Lett., 2019, 10, 1185–1191 CrossRef CAS PubMed.
- J. Behler, J. Chem. Phys., 2011, 134, 074106 CrossRef PubMed.
- Y. Zhang, J. Xia and B. Jiang, Phys. Rev. Lett., 2021, 127, 156002 CrossRef CAS PubMed.
- J. Xia, Y. Zhang and B. Jiang, Chin. J. Chem. Phys., 2021, 34, 695–703 CrossRef CAS.
- Y. Zhang, J. Xia and B. Jiang, J. Chem. Phys., 2022, 156, 114801 CrossRef CAS PubMed.
- Y. Zhang, C. Hu and B. Jiang, Phys. Chem. Chem. Phys., 2021, 23, 1815–1821 RSC.
- C. Hu, Y. Zhang and B. Jiang, J. Phys. Chem. C, 2020, 124, 23190–23199 CrossRef CAS.
- A. Serrano Jiménez, A. Sánchez Muzas, Y. Zhang, J. Ovcar, B. Jiang, I. Lončarić, J. Juaristi and M. Alducin, J. Chem. Theory Comput., 2021, 17, 4648–4659 CrossRef PubMed.
- Y. Zhang, R. J. Maurer and B. Jiang, J. Phys. Chem. C, 2020, 124, 186–195 CrossRef CAS.
- X. Hu, W. L. Hase and T. Pirraglia, J. Comput. Chem., 1991, 12, 1014–1024 CrossRef CAS.
- C. T. Rettner, L. A. DeLouise and D. J. Auerbach, J. Chem. Phys., 1986, 85, 1131–1149 CrossRef CAS.
- H. C. Andersen, J. Chem. Phys., 1980, 72, 2384–2393 CrossRef CAS.
- M. J. Puska and R. M. Nieminen, Phys. Rev. B: Condens. Matter Mater. Phys., 1983, 27, 6121–6128 CrossRef CAS.
- D. Novko, M. Blanco-Rey, J. I. Juaristi and M. Alducin, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 201411 CrossRef.
- R. Yin, Y. Zhang and B. Jiang, J. Phys. Chem. Lett., 2019, 10, 5969–5974 CrossRef CAS PubMed.
- G. H. Peslherbe, H. Wang and W. L. Hase, Adv. Chem. Phys., 1999, 105, 171–201 CAS.
- C. Díaz, E. Pijper, R. A. Olsen, H. F. Busnengo, D. J. Auerbach and G.-J. Kroes, Science, 2009, 326, 832–834 CrossRef PubMed.
- S. Andersson and M. Persson, Phys. Rev. Lett., 1993, 70, 202–205 CrossRef CAS PubMed.
- U. Harten, J. P. Toennies and C. Wöll, J. Chem. Phys., 1986, 85, 2249–2258 CrossRef CAS.
- D. V. Shalashilin, B. Jackson and M. Persson, Faraday Discuss., 1998, 110, 287–300 RSC.
- B. Jackson and M. Persson, J. Chem. Phys., 1992, 96, 2378–2386 CrossRef CAS.
- S. Caratzoulas, B. Jackson and M. Persson, J. Chem. Phys., 1997, 107, 6420 CrossRef CAS.
- D. V. Shalashilin, B. Jackson and M. Persson, J. Chem. Phys., 1999, 110, 11038–11046 CrossRef CAS.
- C. T. Rettner, H. A. Michelsen and D. J. Auerbach, J. Chem. Phys., 1995, 102, 4625–4641 CrossRef CAS.
- L. Zhang, L. Zhu and B. Jiang, Chin. J. Chem. Phys., 2022, 35, 143–152 CrossRef CAS.
- S. Markelj and I. Čadež, J. Chem. Phys., 2011, 134, 124707 CrossRef PubMed.
Footnote |
| † These authors contributed equally. |
| This journal is © the Owner Societies 2023 |