Growth mechanism of metal halide perovskite single crystals in solution
Mingquan
Liao
a,
Mengling
Xia
*a,
Yinsheng
Xu
 a,
Ping
Lu
a and
Guangda
Niu
a,
Ping
Lu
a and
Guangda
Niu
 *b
*b
aSchool of Materials Science and Engineering & State Key Laboratory of Silicate Materials for Architectures, Wuhan University of Technology, Wuhan 430070, China. E-mail: xiamengling@whut.edu.cn
bWuhan National Laboratory for Optoelectronics (WNLO), Huazhong University of Science and Technology (HUST), Wuhan 430074, China. E-mail: guangda_niu@hust.edu.cn
First published on 20th June 2023
Abstract
Metal halide perovskite (MHP) single crystals (SCs) have been demonstrated to have significant potential in photodetectors and photovoltaic devices due to their exceptional optoelectronic properties. The most promising approach for large-scale fabrication of high-quality MHP SCs is the synthesis of MHP SCs in solution. To explain the mechanism and guide the crystal growth process, the classical nucleation-growth theory was established. However, it mainly focuses on zone melting systems and does not account for the interaction between perovskite and solvent. In this review, we specifically focus on the difference in the growth mechanism between MHP SCs in solution and traditional SCs synthesized by the melting method, which includes a discussion of the dissolution, nucleation, and growth processes. We then summarize recent advances in the preparation of MHP SCs based on the special growth mechanism of the perovskite system. The purpose of this review is to provide comprehensive information to offer targeted theoretical guidance as well as unified understanding for the preparation of high-quality MHP SCs in solution.
1. Introduction
Metal halide perovskite (MHP) single crystals (SCs) have shown dramatic achievements in photodetectors and photovoltaic devices over recent years.1–4 The unique antibonding orbital and remarkable defect tolerance characteristic of perovskites prompt low trap-state densities (107–109 cm−3) and long carrier lifetimes (102–104 ns), which are comparable with the photovoltaic-quality silicon.5–8 As the core component of an optoelectronic device, the inherent trait of MHP SCs rules the optoelectronic performance of the device. For example, the crystal structure and dimensions of MHP SCs directly determine the carrier mobility, while the bulk and surface defects determine the carrier lifetime, which directly affects the magnitude of the photocurrent in photodetectors.9–12Despite the great application potential, fabrication of MHP SCs is still at the groping stage compared with the traditional SCs, such as LuYSiO5:Ce (LYSO), Bi4Ge3O12 (BGO), Y3Al5O12 (YAG), etc. Currently, there are various techniques available for fabricating MHP crystals, including melting–cooling growth, chemical vapor deposition (CVD), and solution-based approaches. Among these methods, the melting and cooling method is based on the principle of subjecting the raw material to a predetermined temperature gradient within a furnace. After melting in the heating zone, the raw material undergoes crystallization as it traverses the gradient zone and reaches the cooling zone. While the melting and cooling method facilitates the growth of large-sized crystals, it is primarily utilized for the preparation of all-inorganic MHP crystals.13–15 As for the CVD method, the raw material is vaporized at elevated temperatures and subsequently deposited onto a substrate. By precisely adjusting the parameters such as temperature, pressure, and reaction time, the deposition of perovskite onto the substrate can be accurately controlled. However, it is usually applied for the preparation of the perovskite polycrystalline film.16,17 In recent years, the solution-based approach has gained increasing popularity due to its inherent advantages of cost-effectiveness and ease of operation. Considering the various compositions and structures of metal halide perovskites, especially the organic–inorganic hybrid ones, the solution synthesis of MHP SCs has great potential for large-scale production.18–22 At present, MHP SCs are prepared with various derivative solution-based methods, which is essentially the oversaturation driving by temperature (e.g. inverse temperature crystallization (ITC)23,24), precursor concentration (e.g. solvent evaporation method25,26) or solvent polarity (e.g. antisolvent vapor-assisted crystallization (AVC)27,28). By providing cost-effective and efficient approaches, these methods can facilitate the production of high-quality MHP SCs and potentially accelerate the commercialization of perovskite devices.
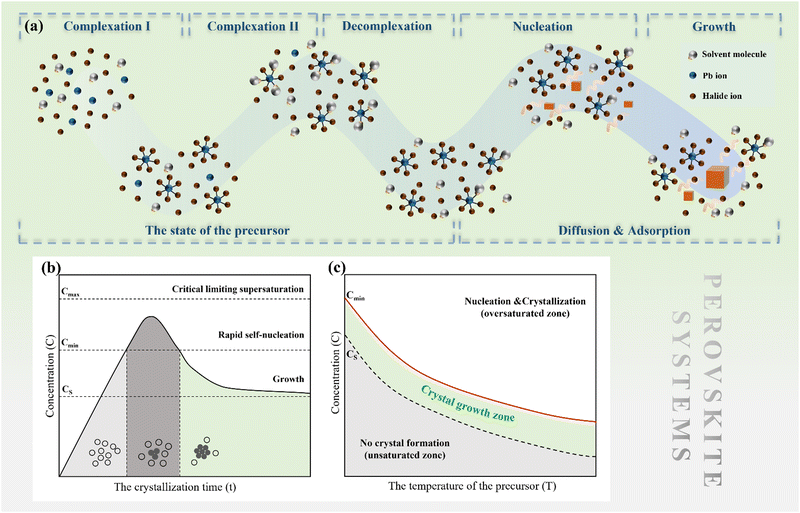
In order to guide the crystal growth process, classical theories and models have been established earlier, which mainly focus on zone melting systems without the involvement of solvent.29,30 Later, LaMer's theories put forward the supplementary understanding of general nucleation and growth towards solution concentration, taking the role of solvents into consideration.31,32 However, the interaction between perovskite and solvent, such as the complexation and decomplexation processes between metal ions and polar solvents, has not been taken into account. The complexation between solute and solvent affects the dissolution process, while decomplexation affects the subsequent nucleation rate and quantity. Therefore, in our opinion, dissolution, nucleation and growth, associated with the interaction between perovskite and solvent, are three key factors toward precise control over reproducibility and crystal quality of MHP SCs.
Growth of MHP SCs in solution has achieved great progress including exploring new categories, unfolding new mechanisms, and developing new technologies. Although several review articles have summarized the preparation principles and methods of MHP SCs, they mainly focus on the nucleation and growth mechanisms, the same as classical theories and models, without summarizing the unique growth theories for MHP systems, including the interaction between solvents and solutes.33–36 In this review, we mainly describe the difference of growth mechanism between MHP SCs and traditional SCs by the melting method, and provide additional elucidation on precursor solution complexation. We hope that this review could offer comprehensive information aiming a targeted theoretical guidance as well as a unified understanding for the preparation of high-quality MHP SCs in solution.
2. Principles of nucleation and growth
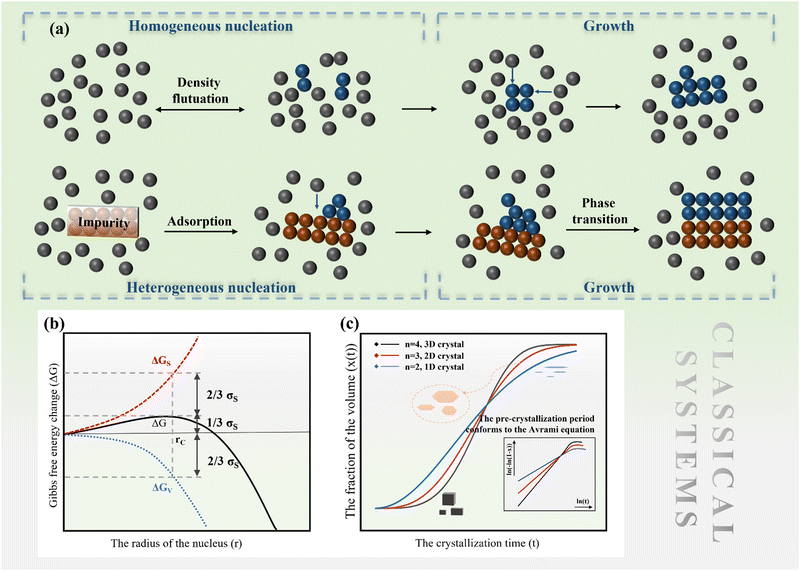
2.1 Classical nucleation and growth
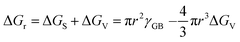 | (1) |
The nucleation barrier is reduced for the heterogeneous nucleation compared to homogeneous nucleation due to the reduced surface energy required. Heterogeneous nucleation forms at the interfaces of different phases. In particular, the nucleation sites emerge at the boundary between the liquid and another substrate, as shown in Fig. 1a. In this scenario, the formulation of interfacial enthalpy is altered, taking into account the interface energies of the liquid–solid (LS), liquid–core (LC), and core–solid (CS) interfaces. Assuming that the shape of the crystal nucleus is a partial sphere with a radius r, the area of the liquid–crystal nucleus interface is ALC, and the contact angle between the liquid and solid interface is θ, the enthalpy of the system forming the new phase can be expressed as:37
ΔGh = VΔGV + γLCALC − πr2γLS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ θ | (2) |
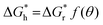 can be obtained, where f(θ) is a coefficient that is solely related to the contact angle. This relationship reveals that as the contact angle decreases, the value of f(θ) also decreases, which results in a lower nucleation barrier. In other words, when the atomic arrangement of the nucleus and nucleator are similar, better wettability leads to more favorable nucleation. These findings underscore the crucial role that the interface plays in nucleation, and the importance of considering it when investigating liquid–solid phase transitions.
can be obtained, where f(θ) is a coefficient that is solely related to the contact angle. This relationship reveals that as the contact angle decreases, the value of f(θ) also decreases, which results in a lower nucleation barrier. In other words, when the atomic arrangement of the nucleus and nucleator are similar, better wettability leads to more favorable nucleation. These findings underscore the crucial role that the interface plays in nucleation, and the importance of considering it when investigating liquid–solid phase transitions.
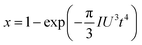 | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(t) as the horizontal coordinate can be obtained, as shown in the inset of Fig. 1c. The slope of the curve corresponds to n, which remains constant in the early and middle growth stages, indicating that the JMA equation is a good fit for describing the crystal growth process. After the solute is depleted completely, the curve deviates significantly, suggesting that the JMA equation no longer provides an accurate description of the crystallization process.
ln(t) as the horizontal coordinate can be obtained, as shown in the inset of Fig. 1c. The slope of the curve corresponds to n, which remains constant in the early and middle growth stages, indicating that the JMA equation is a good fit for describing the crystal growth process. After the solute is depleted completely, the curve deviates significantly, suggesting that the JMA equation no longer provides an accurate description of the crystallization process.
2.2 Perovskite nucleation and growth
The nucleation rate is determined by the concentration of critical nuclei in the parent phase per unit volume and the diffusion rate of atom to the nuclei. The widely accepted Arrhenius-type equation can well describe the formation rate of crystal nuclei (the number of crystal nuclei formed in unit volume of metastable solution within unit time).45 The nucleation rate J can be expressed as:
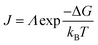 | (4) |
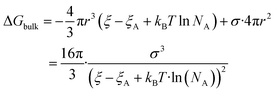 | (5) |
The nucleation barrier can be characterized by the binding energy ξ of the precursor molecule in the cluster, the energy ξA of the precursor molecule, the mole fraction NA of isolated A molecule, the surface energy σ of the cluster (based on a sphere model), and the nuclear radius r. To enhance the accuracy of this expression for the nucleation barrier, Wang et al. provided a more comprehensive description of the nucleation barrier for the MHP SCs system, expressed as:40
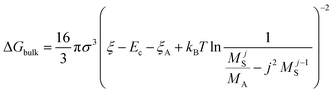 | (6) |
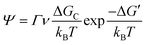 | (7) |
An effective method for controlling the concentration of perovskite precursor involves the use of a room-temperature liquid diffusion separation-induced crystallization (LDSC) technique. This approach employs silicone oil to separate the solvent from the perovskite precursor, allowing for a balance between the accumulation and consumption of the precursor during the nucleation and growth stages. The LDSC method has proven to be highly successful in producing high-quality perovskite single crystals, thereby providing further evidence that maintaining the solution concentration within the metastable region (between CS and Cmin) enables stable growth of single crystals.52 This technique offers significant potential for the growth of large, high-quality perovskite single crystals for use in optoelectronic applications.
3. Understanding the formation process of MHP SCs
It is highlighted that perovskite solution systems involve dissolution, which represents a significant departure from classical systems. The dissolution and growth processes involve complexation and decomplexation, which require careful consideration. Moreover, in classical theory, it is well-known that the interface plays a crucial role in crystal growth. The objective of this chapter is to explore the effects of these factors on nucleation and growth in perovskite solution systems, with the ultimate goal of providing a comprehensive understanding of the MHP SC growth mechanism.3.1 A specific description of the precursor state
As discussed earlier, perovskite solution systems comprise of solute and solvent in various forms, where Pb2+ acts as a Lewis acid coordinated with a Lewis base. As shown in Fig. 3a, with the increase in MAI concentration in PbI2 solution, the layered structure of PbI2 is further broken down to form various lead-iodine complexes,53 which results in a series of changes in solution color with different species.54 The addition of excess MAI can fill the empty coordination around Pb2+ and inhibit the formation of defective structures and the increase in colloid size (Fig. 3b).55 As a result, the MAI-rich perovskite solution system can form an octahedral structure with high symmetry.56 The choice of solvent also influences the crystal conversion, and the solvation ability of the solvent can be quantified using the Dn value.57 Solvents with high Dn have a stronger binding with Pb2+ and thus higher stability of intermediates, making it difficult to separate Pb2+ from the coordinated solvent and affecting the crystallization kinetics of the perovskite solution system.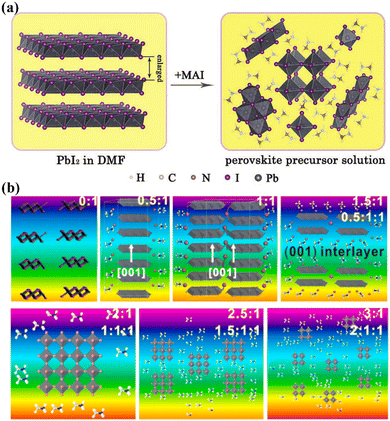 | ||
| Fig. 3 (a) Schematic of the evolution of lead-iodine complexes after MAI addition.53 Copyright 2019, Wiley-VCH Verlag. (b) Types of lead iodine complexes that may occur in precursors with different MAI/PbI2 mole ratios.55 Copyright 2015, American Chemical Society. | ||
Short-term and long-term stability of precursors is critical in perovskite solution systems.58–60 On the one hand, aging of the precursor affects the crystallinity of the MHP SCs. It has been reported that with the increase of aging resistance time of precursor solution, the colloid clusters in solution can maintain a larger volume for a long time.61 Large colloidal clusters serve as nucleation sites, promoting crystal growth and improving the crystallinity of perovskite crystals.61 On the other hand, organic solvents in the system can hydrolyze over time, leading to the destruction of the perovskite crystal structure. For instance, DMF hydrolyzed dimethylammonium ion (DMA+) can replace MA+ ions in the perovskite lattice.62 Moreover, I− in the precursor solution is easily oxidized to I2, leading to an increase in the vacant coordination number of Pb2+ and an increase in defects in the generated perovskite.63,64 Therefore, it is evident that the precursor state is closely linked to the crystallization kinetics of perovskite crystals. By adjusting the solution components or external conditions, the perovskite solution system can remain in the appropriate stage for single crystal growth for an extended period, enabling the regulation of single crystal growth.
3.2 Control of complexation release crystallization
During the nucleation and growth of MHP SCs through the solution method, the process of decomplexation is also involved in addition to atomic diffusion and accumulation. Complexation and decomplexation has been widely used to slow down the crystallization rate of perovskite and control the crystallization quality.65,66 In the case of MAPbI3 SCs synthesized through ITC, organic solvent molecules bind to the octahedral lead iodine coordination. This leads to the formation of (MA+)(PbI3−)2DMSO2, wherein the organic solvent occupation regulates the nucleation and growth of perovskite crystals. As depicted in Fig. 4a and b, when PbI2, MAI, and DMSO are mixed, an intermediate complex (INT-7) is initially formed. As the temperature increases to 100 °C, the organic complex gradually dissociates from the lead iodine octahedron, which helps to control nucleation.39 By regulating the nucleation and growth of perovskite in this way, the size and dimensions of the crystals can be further adjusted.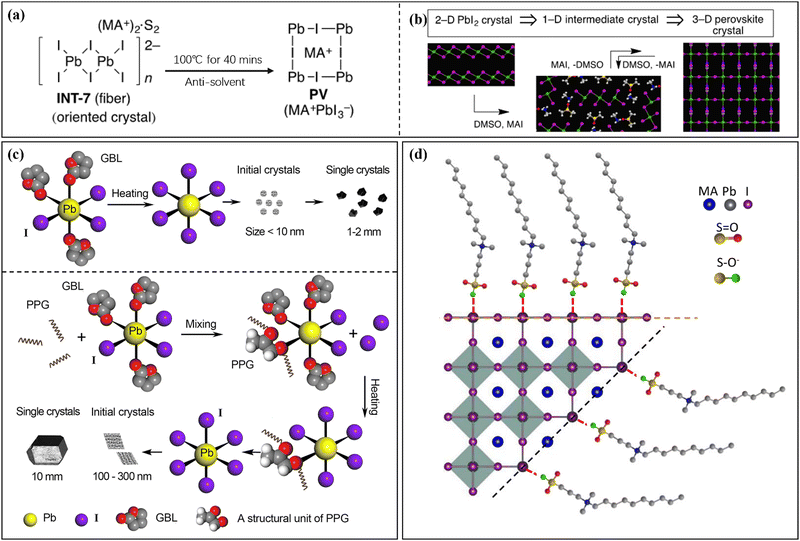 | ||
| Fig. 4 Complex transformation of the MAPbI3 perovskite single crystal (a) after adding organic solvent (DMSO).39 Copyright 2015, American Chemical Society. (b) Schematic diagram of the crystal structure during the transformation process.39 Copyright 2015, American Chemical Society. (c) Schematic diagram of crystallization mechanism after adding additive (PGG).66 Copyright 2021, Springer Nature. (d) DPSI absorption differences on crystal planes with different Pb2+ densities.65 Copyright 2021, Springer Nature. | ||
After gaining an understanding of how organic solvents impact perovskite crystal nucleation and growth, some researchers have proposed using organic macromolecules in the precursor solution of perovskite to control nucleation and crystal growth. Initially, this method involved adding supplementary additives to adjust the active layer performance of perovskite solar cells.67–71 In recent studies, this strategy has also been implemented for the production of large-sized MHP SCs.65,66,72 Typically, organic macromolecules or polymers with specific functional groups are employed to regulate the nucleation and growth of MHP SCs. Examples of such functional groups include the carbon–oxygen bond in polyether (ester)-based molecules and the fluorine ion group,68 as well as the carbon–nitrogen bond in polymethyl methacrylate-acrylamide and 2-cyanoacrylate.69,70 These additives are broadly categorized into three groups based on their functional groups: S-donors, O-donors, and N-donors, with varying coordination capabilities. The coordination strength of the donors with Pb2+ follows the order: S-donor > O-donor > N-donor. Due to the unique coordination properties of these ionic groups, coordination complexes such as (MA+)2(Pb3I82−)DMSO2 can be formed.39 Furthermore, the presence of certain groups and carbon chain length characteristics in the additive contributes to the hydrophobicity and stability of the active layer in perovskite solar cells.73–75 As shown in Fig. 4c, the conventional solvent (e.g. GBL) can form Pb-solvent complexes at room temperature, while polypropylene glycol (PPG) that contains oxygen groups can coordinate with Pb2+.66 At low temperature, the solution primarily exists in a complex form, and as the temperature increases, dissociation between the groups of this complex occurs, leading to improved ion diffusion efficiency in the precursor solution. This efficient transfer of ions to the growth interface layer enables the solution to quickly and stably reach a saturated state, which is the fundamental principle behind polymer-assisted controlling nucleation. The dissociation under higher temperature conditions also serves as the driving force for crystal nucleation. Furthermore, studies have demonstrated that crystal faces with different Pb2+ densities grow at different rates, with crystal faces exhibiting lower Pb2+ density growing faster but being more prone to disappearing (Fig. 4d).65 This steric hindrance effect of the polymer impedes the diffusion of ions to the perovskite surface, leading to varying crystal face growth rates. Understanding these mechanisms will aid in the selection of macromolecules and provide more possibilities for preparing large-sized SCs.
3.3 Interfacial extra tensile elastic stress induced crystallization
Solute deposition during crystal growth is a necessary process for the formation of crystal nuclei. The assembly of solute molecules or atoms is a complex process that involves interfacial dynamics.76,77 Crystal growth is essentially a transport process that involves mass, heat, and momentum. A solute boundary layer is assumed to exist on the surface of the crystal, with an ideal fluid outside this boundary layer. Mass and heat transport outside the boundary layer are mainly governed by convection outside the boundary layer, while inside the layer, convection and diffusion play a more significant role due to the presence of large concentration and temperature gradients. This theory provides a basis for understanding the interface's role in the growth of MHP SCs. Differs from the liquid–solid interface in classical theory system, the surface tension generated by the solution–air interface plays a critical role in MHP SCs nucleation and growth.46,78–80 As depicted in Fig. 5a and b, surface molecules experience strain owing to the presence of surface tension. Consequently, crystals suspended at the solution surface exhibit faster growth rates at the edges, resulting in a length-to-diameter ratio exceeding unity. The solvated surface molecules exist in a strained state with low energy. Crystal nuclei continue to grow on the surface of the solution until they reach a size at which surface tension no longer supports their buoyancy. Combined with eqn (5), the nucleation barrier of the solution–air interface layer can be expressed as:46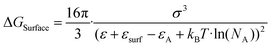 | (8) |
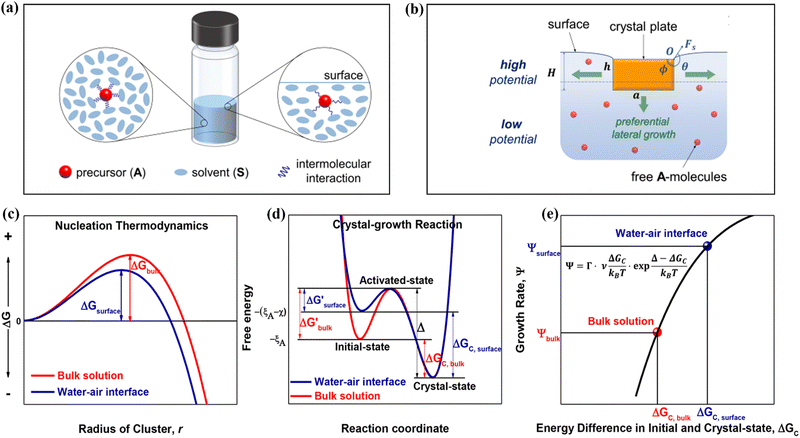 | ||
| Fig. 5 (a) Schematic diagram of changes in molecular interaction energy in bulk solution (left) and surface layer (right).46 Copyright 2017, American Chemical Society. (b) Schematic of the growth of a crystal in a floating state.46 Copyright 2017, American Chemical Society. (c) Nucleation barrier at different interfaces.40 Copyright 2018, American Chemical Society. (d) Initial state free energy, excited state free energy and crystalline free energy at different interfaces.40 Copyright 2018, American Chemical Society. (e) Crystal growth rates corresponding to nucleation barriers at different interfaces.40 Copyright 2018, American Chemical Society. | ||
Conclusions
MHP SCs have garnered significant attention as a new generation of photoelectric materials due to their exceptional properties. The solution method is a cost-effective and efficient approach for obtaining MHP SCs, and this review delves into the nucleation and growth mechanism, exploring the commonalities and differences between classical systems and perovskite solution systems. Unique aspects of perovskite solution systems, such as intermolecular complexation and decomplexation of precursor molecules, have a profound influence on nucleation and growth. The size of the colloid clusters is reflected in the deposition rate of the solute. The addition of large molecules containing specific groups can effectively modulate the ratio of the diffusion rate to deposition rate, optimizing the system for ideal crystal growth. By manipulating the components or external factors in the perovskite solution system, the system can be maintained in a suitable non-nucleated state for an extended period, facilitating the growth of large-sized single crystals. Nevertheless, there are still many aspects that need additional work, including but not limited to:(1) Establishing comprehensive growth model of MHP SCs
The investigation of the growth mechanisms of MHP is still in its nascent stage compared to the traditional oxide single crystals. Although the LaMer's diagram has been employed to elucidate the nucleation and growth processes, the interaction between perovskite and solvent remains inadequately illustrated. Besides, molecular dynamics, phase-field, and thermal field simulations have been sufficiently applied in investigating the growth mechanisms of conventional crystals, such as SiC and NaCl. ANSYS Fluent, focusing on the sedimentary growth of the vapor phase, has been used to calculate heat and mass transfer during the growth process of MHP. However, there remains a dearth of studies on the theoretical simulations within perovskite solution systems, particularly in the realm of theoretical simulations pertaining to nucleation and growth processes. To provide a more comprehensive understanding of the growth mechanism in MHP, the development of a thorough theoretical model is urgently required.
(2) Real-time monitoring of the growth process of MHP SCs
Conventional real-time monitoring methods predominantly concentrate on crystal size and visual characteristics. However, when investigating the mechanism of MHP SCs, elucidating the nucleation and growth processes within the perovskite solution system, encompassing the underlying pathways of crystal formation and the structure of colloidal clusters, poses significant challenges for direct confirmation. Consequently, the advancement of a technique capable of real-time monitoring of solute diffusion and deposition processes has potential to expedite the progress in MHP SC development.
(3) Exploring new solvent and additives for the growth of MHP SCs
The conventional solution-based method presents challenges in achieving the growth of large-sized MHP SCs, and the process itself is time-consuming, significantly restricting the potential applications of MHP SCs. Moreover, even slight temperature fluctuations within the solution can result in undesirable outcomes, such as nucleation disorders and crystal defects. To address this issue, various passivation strategies have been proposed, as outlined in Section 3.2. However, the currently employed additives still fail to effectively control the crystal growth process. Therefore, there is an urgent demand for exploring more suitable new solvent and functional additives to facilitate the production of large-sized MHP SCs with minimal defects.
(4) Post-processing of MHP SCs
MHP SCs exhibit the absence of grain boundaries (GBs), which effectively mitigates non-radiative recombination at interfaces. While the elimination of GBs can diminish bulk phase defects in MHP SCs, the presence of surface defects, such as dangling bonds and dislocations, can significantly affect the optical and electrical properties of the MHP SCs. Furthermore, the residual organic solvents tend to accumulate on the crystal surface and can strongly interact with water molecules in humid environments, resulting in poor surface morphology. Consequently, effective post-treatment processes are of utmost importance to mitigate the impact of surface defects. Post-treatment has been a very important research direction in commercial single crystal, such as monocrystalline silicon and cadmium zinc telluride, but it has not been paid attention to in MHP SCs. Notably, the polishing method, including chemical polishing and mechanical polishing, and the selection of suitable polishing agents represent critical steps warranting meticulous attention in the post-treatment process.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge the financial support of the National Natural Science Foundation of China (62275206, U2241236, 61905082, 61975156) and State Key Laboratory of Silicate Materials for Architectures (Wuhan University of Technology) (SYSJJ2021-01).References
- L. Lei, Q. Dong, K. Gundogdu and F. So, Adv. Funct. Mater., 2021, 31, 2010144 CrossRef CAS.
- J. A. Steele, W. Pan, C. Martin, M. Keshavarz, E. Debroye, H. Yuan, S. Banerjee, E. Fron, D. Jonckheere, C. W. Kim, W. Baekelant, G. Niu, J. Tang, J. Vanacken, M. Van der Auweraer, J. Hofkens and M. B. J. Roeffaers, Adv. Mater., 2018, 30, 1804450 CrossRef PubMed.
- J. Jiang, M. Xiong, K. Fan, C. Bao, D. Xin, Z. Pan, L. Fei, H. Huang, L. Zhou, K. Yao, X. Zheng, L. Shen and F. Gao, Nat. Photonics, 2022, 16, 575–581 CrossRef CAS.
- D. Corzo, T. Wang, M. Gedda, E. Yengel, J. I. Khan, R. Li, M. R. Niazi, Z. Huang, T. Kim, D. Baran, D. Sun, F. Laquai, T. D. Anthopoulos and A. Amassian, Adv. Mater., 2022, 34, 2109862 CrossRef CAS PubMed.
- G. W. Kim and A. Petrozza, Adv. Energy Mater., 2020, 10, 6 Search PubMed.
- H. Tan, F. Che, M. Wei, Y. Zhao, M. I. Saidaminov, P. Todorović, D. Broberg, G. Walters, F. Tan, T. Zhuang, B. Sun, Z. Liang, H. Yuan, E. Fron, J. Kim, Z. Yang, O. Voznyy, M. Asta and E. H. Sargent, Nat. Commun., 2018, 9, 3100 CrossRef PubMed.
- I. du Fosse, J. T. Mulder, G. Almeida, A. G. M. Spruit, I. Infante, F. C. Grozema and A. J. Houtepen, J. Am. Chem. Soc., 2022, 144, 11059–11063 CrossRef CAS PubMed.
- W. Chu, Q. Zheng, O. V. Prezhdo, J. Zhao and W. A. Saidi, Sci. Adv., 2020, 6, eaaw7453 CrossRef CAS PubMed.
- J. Siekmann, S. Ravishankar and T. Kirchartz, ACS Energy Lett., 2021, 6, 3244–3251 CrossRef CAS.
- E. Aydin, M. De Bastiani and S. De Wolf, Adv. Mater., 2019, 31, 20 CrossRef PubMed.
- L. K. Ono, S. Z. Liu and Y. B. Qi, Angew. Chem., Int. Ed., 2020, 59, 6676–6698 CrossRef CAS PubMed.
- C. W. Li, Z. N. Song, D. W. Zhao, C. X. Xiao, B. Subedi, N. Shrestha, M. M. Junda, C. L. Wang, C. S. Jiang, M. Al-Jassim, R. J. Ellingson, N. J. Podraza, K. Zhu and Y. F. Yan, Adv. Energy Mater., 2019, 9, 9 Search PubMed.
- Y. Cai, S. Yan, X. Du, T. Lin, Y.-J. Lin, L. Qiu and W. Wang, Adv. Funct. Mater., 2023, 33, 2211191 CrossRef CAS.
- V. B. Mykhaylyk, M. Rudko, H. Kraus, V. Kapustianyk, V. Kolomiets, N. Vitoratou, Y. Chornodolskyy, A. S. Voloshinovskii and L. Vasylechko, J. Mater. Chem. C, 2023, 11, 656–665 RSC.
- Q. Sun, B. Xiao, L. Ji, D. Zhao, J. Liu, W. Zhang, M. Zhu, W. Jie, B.-B. Zhang and Y. Xu, J. Energy Chem., 2022, 66, 459–465 CrossRef CAS.
- P. Luo, S. Zhou, W. Xia, J. Cheng, C. Xu and Y. Lu, Adv. Mater. Interfaces, 2017, 4, 1600970 CrossRef.
- Y. Zhou, K. Fernando, J. Wan, F. Liu, S. Shrestha, J. Tisdale, C. J. Sheehan, A. C. Jones, S. Tretiak, H. Tsai, H. Huang and W. Nie, Adv. Funct. Mater., 2021, 31, 2101058 CrossRef CAS.
- R. Quintero-Bermudez, A. Gold-Parker, A. H. Proppe, R. Munir, Z. Yang, S. O. Kelley, A. Amassian, M. F. Toney and E. H. Sargent, Nat. Mater., 2018, 17, 900–907 CrossRef CAS PubMed.
- Y. Lei, Y. Chen, R. Zhang, Y. Li, Q. Yan, S. Lee, Y. Yu, H. Tsai, W. Choi, K. Wang, Y. Luo, Y. Gu, X. Zheng, C. Wang, C. Wang, H. Hu, Y. Li, B. Qi, M. Lin, Z. Zhang, S. A. Dayeh, M. Pharr, D. P. Fenning, Y.-H. Lo, J. Luo, K. Yang, J. Yoo, W. Nie and S. Xu, Nature, 2020, 583, 790–795 CrossRef CAS PubMed.
- W. Li, H. Li, J. Song, C. Guo, H. Zhang, H. Wei and B. Yang, Sci. Bull., 2021, 66, 2199–2206 CrossRef CAS PubMed.
- L. Zhao, Y. Zhou, Z. Shi, Z. Ni, M. Wang, Y. Liu and J. Huang, Nat. Photonics, 2023, 17, 315–323 CrossRef CAS.
- D. Ju, Y. Dang, Z. Zhu, H. Liu, C.-C. Chueh, X. Li, L. Wang, X. Hu, A. K. Y. Jen and X. Tao, Chem. Mater., 2018, 30, 1556–1565 CrossRef CAS.
- R. K. Battula, G. Veerappan, P. Bhyrappa, C. Sudakar and E. Ramasamy, Surf. Interfaces, 2023, 36, 7 Search PubMed.
- Z. H. Chen, Q. Zhang, M. L. Zhu, X. Y. Wang, Q. X. Wang, A. T. S. Wee, K. P. Loh, G. Eda and Q. H. Xu, Adv. Funct. Mater., 2020, 30, 8 Search PubMed.
- Y. C. Liu, Y. X. Zhang, Z. Yang, J. S. Feng, Z. Xu, Q. X. Li, M. X. Hu, H. C. Ye, X. Zhang, M. Liu, K. Zhao and S. Z. Liu, Mater. Today, 2019, 22, 67–75 CrossRef CAS.
- Y. X. Zhang, Y. C. Liu, Z. Xu, H. C. Ye, Q. X. Li, M. X. Hu, Z. Yang and S. Z. Liu, J. Mater. Chem. C, 2019, 7, 1584–1591 RSC.
- D. Shi, V. Adinolfi, R. Comin, M. J. Yuan, E. Alarousu, A. Buin, Y. Chen, S. Hoogland, A. Rothenberger, K. Katsiev, Y. Losovyj, X. Zhang, P. A. Dowben, O. F. Mohammed, E. H. Sargent and O. M. Bakr, Science, 2015, 347, 519–522 CrossRef CAS PubMed.
- D. Shi, V. Adinolfi, R. Comin, M. Yuan, E. Alarousu, A. Buin, Y. Chen, S. Hoogland, A. Rothenberger, K. Katsiev, Y. Losovyj, X. Zhang, P. A. Dowben, O. F. Mohammed, E. H. Sargent and O. M. Bakr, Science, 2015, 347, 519–522 CrossRef CAS PubMed.
- A. Kanak, O. Kopach, L. Kanak, I. Levchuk, M. Isaiev, C. J. Brabec, P. Fochuk and Y. Khalavka, Cryst. Growth Des., 2022, 22, 4115–4121 CrossRef CAS.
- B. Wang, C. Y. Zhang, W. L. Zheng, Q. G. Zhang, Q. Wan, L. Kong and L. Li, Chem. Commun., 2020, 56, 11291–11294 RSC.
- V. K. LaMer, Ind. Eng. Chem., 1952, 44, 1270–1277 CrossRef CAS.
- V. K. LaMer and R. H. Dinegar, J. Am. Chem. Soc., 1950, 72, 4847–4854 CrossRef CAS.
- Y. Cho, H. R. Jung and W. Jo, Nanoscale, 2022, 14, 9248–9277 RSC.
- Y. Wu, J. Feng, Z. Yang, Y. Liu and S. Liu, Adv. Sci., 2023, 10, 2205536 CrossRef CAS PubMed.
- J. X. Hao and X. Xiao, Front. Chem., 2022, 9, 11 Search PubMed.
- L. Chouhan, S. Ghimire, C. Subrahmanyam, T. Miyasaka and V. Biju, Chem. Soc. Rev., 2020, 49, 2869–2885 RSC.
- F. L. Binsbergen, J. Polym. Sci., Part C: Polym. Symp., 1977, 59, 11–29 CAS.
- M. Avrami, J. Chem. Phys., 1940, 8, 212–224 CrossRef CAS.
- Y. L. Guo, K. Shoyama, W. Sato, Y. Matsuo, K. Inoue, K. Harano, C. Liu, H. Tanaka and E. Nakamura, J. Am. Chem. Soc., 2015, 137, 15907–15914 CrossRef CAS PubMed.
- K. Wang, C. C. Wu, D. Yang, Y. Y. Jiang and S. Priya, ACS Nano, 2018, 12, 4919–4929 CrossRef CAS PubMed.
- M. Jung, S. G. Ji, G. Kim and S. I. Seok, Chem. Soc. Rev., 2019, 48, 2011–2038 RSC.
- P. Barua and I. Hwang, Materials, 2023, 16, 2110 CrossRef CAS PubMed.
- P. K. Nayak, D. T. Moore, B. Wenger, S. Nayak, A. A. Haghighirad, A. Fineberg, N. K. Noel, O. G. Reid, G. Rumbles, P. Kukura, K. A. Vincent and H. J. Snaith, Nat. Commun., 2016, 7, 13303 CrossRef CAS PubMed.
- J. Chen, D. J. Morrow, Y. Fu, W. Zheng, Y. Zhao, L. Dang, M. J. Stolt, D. D. Kohler, X. Wang, K. J. Czech, M. P. Hautzinger, S. Shen, L. Guo, A. Pan, J. C. Wright and S. Jin, J. Am. Chem. Soc., 2017, 139, 13525–13532 CrossRef CAS PubMed.
- J. Frenkel, J. Chem. Phys., 1939, 7, 538–547 CrossRef.
- A. A. Zhumekenov, V. M. Burlakov, M. I. Saidaminov, A. Alofi, M. A. Hague, B. Turedi, B. Davaasuren, I. Dursun, N. Cho, A. M. El-Zohry, M. De Bastiani, A. Giugni, B. Torre, E. Di Fabrizio, O. F. Mohammed, A. Rothenberger, T. Wu, A. Goriely and O. M. Bakr, ACS Energy Lett., 2017, 2, 1782–1788 CrossRef CAS.
- S. Matt, Z. Kun, H. Christopher, H. A. Robert, M. Mischa, H. Andrew, B. R. William, C. Zhengdong, M. Thomas and P. M. Chaikin, J. Phys.: Condens. Matter, 2003, 15, S11 CrossRef.
- M. R. Singh and D. Ramkrishna, Chem. Eng. Sci., 2014, 107, 102–113 CrossRef CAS.
- D. Chakraborty and G. N. Patey, Chem. Phys. Lett., 2013, 587, 25–29 CrossRef CAS.
- M. J. Yang, T. Y. Zhang, P. Schulz, Z. Li, G. Li, D. H. Kim, N. J. Guo, J. J. Berry, K. Zhu and Y. X. Zhao, Nat. Commun., 2016, 7, 9 Search PubMed.
- Z. Yao, W. Wang, H. Shen, Y. Zhang, Q. Luo, X. Yin, X. Dai, J. Li and H. Lin, Sci. Technol. Adv. Mater., 2017, 18, 253–262 CrossRef CAS PubMed.
- F. Yao, J. L. Peng, R. M. Li, W. J. Li, P. B. Gui, B. R. Li, C. Liu, C. Tao, Q. Q. Lin and G. J. Fang, Nat. Commun., 2020, 11, 9 CrossRef PubMed.
- B. Li, D. Binks, G. Cao and J. Tian, Small, 2019, 15, 1903613 CrossRef CAS PubMed.
- C. M. Raghavan, T. P. Chen, S. S. Li, W. L. Chen, C. Y. Lo, Y. M. Liao, G. Haider, C. C. Lin, C. C. Chen, R. Sankar, Y. M. Chan, F. C. Chou and C. W. Chen, Nano Lett., 2018, 18, 3221–3228 CrossRef CAS PubMed.
- K. Y. Yan, M. Z. Long, T. K. Zhang, Z. H. Wei, H. N. Chen, S. H. Yang and J. B. Xu, J. Am. Chem. Soc., 2015, 137, 4460–4468 CrossRef CAS PubMed.
- Z. Q. Xu, Z. H. Liu, N. X. Li, G. Tang, G. H. J. Zheng, C. Zhu, Y. H. Chen, L. G. Wang, Y. Huang, L. Li, N. Zhou, J. W. Hong, Q. Chen and H. P. Zhou, Adv. Mater., 2019, 31, 9 Search PubMed.
- J. C. Hamill, J. Schwartz and Y. L. Loo, ACS Energy Lett., 2018, 3, 92–97 CrossRef CAS.
- F. Fei, L. Gu, Y. Xu, K. Du, X. Zhou, X. Dong, X. Chen, N. Yuan, S. Wang and J. Ding, ACS Appl. Mater. Interfaces, 2022, 14, 52960–52970 CrossRef CAS PubMed.
- F. Luan, H. Li, S. Gong, X. Chen, C. Shou, Z. Wu, H. Xie and S. Yang, Nanotechnology, 2023, 34, 055402 CrossRef PubMed.
- D. P. Nenon, J. A. Christians, L. M. Wheeler, J. L. Blackburn, E. M. Sanehira, B. Dou, M. L. Olsen, K. Zhu, J. J. Berry and J. M. Luther, Energy Environ. Sci., 2016, 9, 2072–2082 RSC.
- D. P. McMeekin, Z. P. Wang, W. Rehman, F. Pulvirenti, J. B. Patel, N. K. Noel, M. B. Johnston, S. R. Marder, L. M. Herz and H. J. Snaith, Adv. Mater., 2017, 29, 8 CrossRef PubMed.
- B. J. Dou, L. M. Wheeler, J. A. Christians, D. T. Moore, S. P. Harvey, J. J. Berry, F. S. Barnes, S. E. Shaheen and M. van Hest, ACS Energy Lett., 2018, 3, 979–985 CrossRef CAS.
- W. Zhang, S. Pathak, N. Sakai, T. Stergiopoulos, P. K. Nayak, N. K. Noel, A. A. Haghighirad, V. M. Burlakov, D. W. deQuilettes, A. Sadhanala, W. Z. Li, L. D. Wang, D. S. Ginger, R. H. Friend and H. J. Snaith, Nat. Commun., 2015, 6, 9 Search PubMed.
- D. Meggiolaro, S. G. Motti, E. Mosconi, A. J. Barker, J. Ball, C. A. R. Perini, F. Deschler, A. Petrozza and F. De Angelis, Energy Environ. Sci., 2018, 11, 702–713 RSC.
- Y. Liu, X. P. Zheng, Y. J. Fang, Y. Zhou, Z. Y. Ni, X. Xiao, S. S. Chen and J. S. Huang, Nat. Commun., 2021, 12, 8 CrossRef PubMed.
- L. Ma, Z. G. Yan, X. Y. Zhou, Y. Q. Pi, Y. P. Du, J. Huang, K. W. Wang, K. Wu, C. Q. Zhuang and X. D. Han, Nat. Commun., 2021, 12, 10 CrossRef PubMed.
- W. M. Gu, K. J. Jiang, Y. Zhang, G. H. Yu, C. Y. Gao, X. H. Fan and L. M. Yang, Chem. Eng. J., 2022, 430, 7 Search PubMed.
- M. Luo, X. P. Zong, W. H. Zhang, M. N. Hua, Z. Sun, M. Liang and S. Xue, ACS Appl. Mater. Interfaces, 2022, 14, 31285–31295 CrossRef CAS PubMed.
- B. Q. Zhang, C. Chen, X. Z. Wang, X. F. Du, D. C. Liu, X. H. Sun, Z. P. Li, L. Z. Hao, C. Y. Gao, Y. M. Li, Z. P. Shao, X. Wang, G. L. Cui and S. P. Pang, Angew. Chem., Int. Ed., 2023, 62, 6 Search PubMed.
- X. D. Li, W. X. Zhang, W. J. Zhang, H. Q. Wang and J. F. Fang, Nano Energy, 2019, 58, 825–833 CrossRef CAS.
- Y. H. Ma, Y. H. Cheng, X. W. Xu, M. L. Li, C. J. Zhang, S. H. Cheung, Z. X. Zeng, D. Shen, Y. M. Xie, K. L. Chiu, F. Lin, S. K. So, C. S. Lee and S. W. Tsang, Adv. Funct. Mater., 2021, 31, 9 Search PubMed.
- Y. Q. Zhu, Y. X. Liu, B. W. Jin, Y. Shi, Z. X. Wu, J. G. Cao, H. J. Li and C. C. Wu, Macromol. Mater. Eng., 2022, 307, 9 CrossRef.
- W. Jiang, J. Ren, H. Li, D. Liu, L. Yang, Y. Xiong and Y. Zhao, Small Methods, 2023, 7, 2201636 CrossRef CAS PubMed.
- C. Park, H. Ko, D. H. Sin, K. C. Song and K. Cho, Adv. Funct. Mater., 2017, 27, 1703546 CrossRef.
- S. J. Khanam, N. Parikh, S. Satapathi, A. Kalam, M. Banavoth and P. Yadav, ACS Appl. Energy Mater., 2022, 5, 14732–14738 CrossRef CAS.
- M. Wang, X. B. Yin, P. G. Vekilov, R. W. Peng and N. B. Ming, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1999, 60, 1901–1905 CrossRef CAS PubMed.
- E. Vlieg, J. Cryst. Growth, 2022, 597, 126850 CrossRef CAS.
- H. Du, K. Wang, L. Zhao, C. Xue, M. Zhang, W. Wen, G. Xing and J. Wu, ACS Appl. Mater. Interfaces, 2020, 12, 2662–2670 CrossRef CAS PubMed.
- Y. Liu, H. Ye, Y. Zhang, K. Zhao, Z. Yang, Y. Yuan, H. Wu, G. Zhao, Z. Yang, J. Tang, Z. Xu and S. Liu, Matter, 2019, 1, 465–480 CrossRef.
- E. Hong, Z. Li, T. Yan and X. Fang, Nano Lett., 2022, 22, 8662–8669 CrossRef CAS PubMed.
- Y. Liu, Q. Dong, Y. Fang, Y. Lin, Y. Deng and J. Huang, Adv. Funct. Mater., 2019, 29, 1807707 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2023 |