A zero-field single-molecule magnet with luminescence thermometry capabilities containing soft donors†
Riccardo
Marin‡
 *a,
Diogo Alves
Gálico‡
*a,
Diogo Alves
Gálico‡
 b,
Rezeda
Gayfullina
b,
Rezeda
Gayfullina
 c,
Jani O.
Moilanen
c,
Jani O.
Moilanen
 c,
Luís D.
Carlos
c,
Luís D.
Carlos
 d,
Daniel
Jaque
d,
Daniel
Jaque
 ae and
Muralee
Murugesu
ae and
Muralee
Murugesu
 *b
*b
aNanomaterials for Bioimaging Group (nanoBIG), Departamento de Física de Materiales, Facultad de Ciencias, Universidad Autónoma de Madrid, C/Francisco Tomás y Valiente 7, Madrid, 28049, Spain. E-mail: riccardo.marin@uam.es
bDepartment of Chemistry and Biomolecular Sciences, University of Ottawa, Ottawa, Ontario K1N 6N5, Canada. E-mail: m.murugesu@uottawa.ca
cDepartment of Chemistry, Nanoscience Centre, University of Jyväskylä, P.O. Box 35, FI-40014, Finland
dPhantom-g, CICECO – Aveiro Institute of Materials, Department of Physics, Universidade de Aveiro, 3810-193, Aveiro, Portugal
eNanomaterials for Bioimaging Group (nanoBIG), Instituto Ramón y Cajal de Investigación Sanitaria, Hospital Ramón y Cajal, Ctra. De Colmenar Viejo, Km. 9100, 28034, Madrid, Spain
First published on 23rd June 2022
Abstract
Simultaneous fine-tune of magnetic and optical properties in lanthanide single-molecule magnets (SMMs) is a daunting task. Even more so when additional functionalities, like luminescence thermometry, are sought after. Herein, we explore the use of a ligand with both soft and hard donor atoms (thiobenzoate, tba−) as a strategy to prepare a multifunctional optomagnetic lanthanide complex. The proposed mononuclear Dy3+ complex acts as a zero-field SMM, whose energy barrier to magnetization reversal was confirmed from the analysis of the photoluminescence spectrum. Moreover, the temperature dependence of the emission spectral profile was harnessed to build a thermometric approach working below 12 K – where the complex behaves as an SMM. In search for general trends informing the preparation of similar multifunctional SMMs, we modelled the electronic properties of a series of complexes where the sulfur atom of tba− is replaced for other chalcogens (O, Se, Te). These calculations show that careful choice of ligands with soft donor atoms can boost both magnetic and thermometric performances, paving the way for the rational design of novel multifunctional lanthanide complexes.
Introduction
In the fast-paced digital era, information is created and exchanged at an unprecedented rate, thus requiring increasingly efficient physical storage units. In addition, electronic devices are undergoing extreme miniaturization and the first case of “quantum supremacy” – i.e., a quantum processor outperforming a classical computer – was recently reported.1 In the frame of this digital revolution, single-molecule magnets (SMMs) are prime candidates for becoming building blocks of the next-generation of electronic devices. Lanthanide (Ln3+) complexes are the cream of the crop of this family of compounds,2–4 with working temperatures recently reaching the boiling point of liquid nitrogen, bringing these species one step closer to real-world applications.5To ensure the proper functioning of an SMM, its temperature should be controlled and maintained below a specific threshold. To that end, we reported the first examples of Ln3+-SMMs whose photoluminescence (PL) can be harnessed to monitor their thermal state.6–11 However, the preparation of Ln3+-complexes simultaneously performing well as SMMs and luminescent thermometers is no easy task, and it requires judicious choice of the ligand framework, metal, and coordination geometry.8,12 In this context, ligands containing soft donors like heavy chalcogens (E = S, Se, Te) hold promise. This is because the large radial extension of their valence orbitals affects the ligand field around the metal centre. Ln–E bonds have also lower associated vibrational energies compared to Ln–O bonds. Not only this promotes high barrier to magnetization reversal (Ueff),13,14 but also supports efficient Ln3+ PL.15 Yet, these ligands are underexplored compared to N- and O-containing ligands.
Moving from these considerations, we propose the first example of soft-donor-containing SMM acting as luminescent thermometer in the form of a novel thiobenzoate (tba−)-based Dy3+ complex: [Dy(tba)3phen]·CH2Cl2 (1; phen = 1,10-phenanthroline). This complex brings together the stable Ln–O interaction along with the property-modulating features imparted by Ln–S bonds. Analysis of the photoluminescence (PL) spectrum allowed interpreting the magnetic relaxation mechanism of this zero-field SMM, while the temperature-dependent spectral variations were harnessed to develop a luminescence thermometric approach. Stimulated by these results, we deepened our exploration of soft-donor-containing ligands for tuning optical and magnetic features in complexes with the use of ab initio and density functional theory calculations. Modelling of a series of Dy3+ complexes generated from 1 replacing tba− for benzoate, selenobenzoate, and tellurobenzoate show trends of optical and magnetic properties that highlight how soft donor atoms can be valuable allies in pursuit of luminescent SMMs with thermometric capabilities.
Results and discussion
Structural characterization
[Dy(tba)3phen]·CH2Cl2 (1) was synthesized by adding an aqueous solution of Dy(NO3)3·5H2O to a solution of potassium thiobenzoate (Ktba) and phen in water (Ktba![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) phen = 3
phen = 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1). The precipitated yellow powder was recrystallized from dichloromethane (DCM), yielding transparent pale yellow crystals with needle-like morphology. Details about the experimental procedure are given in the ESI.† Complex 1 crystallizes in the monoclinic P21/c space group, with one DCM crystallization molecule for every complex molecule in the structure (Fig. 1, Fig. S1 and Table S1, ESI†).
1). The precipitated yellow powder was recrystallized from dichloromethane (DCM), yielding transparent pale yellow crystals with needle-like morphology. Details about the experimental procedure are given in the ESI.† Complex 1 crystallizes in the monoclinic P21/c space group, with one DCM crystallization molecule for every complex molecule in the structure (Fig. 1, Fig. S1 and Table S1, ESI†).
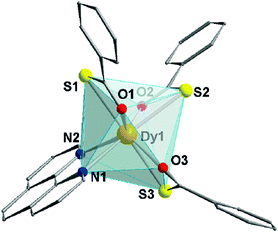 | ||
| Fig. 1 Partially labelled molecular structure of (1). Hydrogen atoms are omitted for clarity. Colour code: Dy – orange; O – red; S – yellow; N – blue. | ||
These DCM molecules evaporate from the lattice when the crystals are exposed to the atmosphere for a prolonged time, resulting in loss of crystallinity. The octa-coordinated Dy3+ ion adopts a distorted triangular dodecahedron configuration (D2d maximum symmetry – see Table S2, ESI†) observed in other mononuclear and dinuclear Dy3+ SMMs.16,17 The coordination environment of Dy3+ is composed of three oxygen and three sulphur atoms belonging to the tba− ligands, along with two phen nitrogen atoms. The Dy⋯O distances range between 2.34 and 2.37 Å, while Dy⋯S bonds are longer (2.80–2.84 Å). These values are in line with other lanthanide coordination compounds based on tba−.18,19 Inspection of the packing (Fig. S2, ESI†) reveals a 3D arrangement of the complexes governed by π–π stacking (Fig. S3, ESI†) both in the face-to-face and edge-to-face configurations – centroid-to-centroid distances of 3.76 and 4.78 Å, respectively (see ESI† for more details). Within the crystal, the shortest intermolecular Dy⋯Dy distance is 7.20 Å (Fig. S3, ESI†).
We should point out that in Ln3+-complexes Ln–E bonds are less common than Ln–O ones, owing to the weaker interaction between Ln3+ (hard acid) and E (soft donor). Among E-containing ligands, carbamates, xanthates, and diphenyl chalcogenides are the most studied ones.20–23 Thiobenzoate has instead been poorly investigated, with only two reported Ln3+-tba complexes to date.18,19 Yet, as observed in 1, this ligand can promote both magnetic and PL properties in Ln3+-complexes, since it provides simultaneously strong and stable Ln–O interaction along with property modulation imparted by Ln–S bonds.
Magnetic characterization
To investigate the magnetic properties of 1, the dc (direct current) magnetic susceptibility was first measured between 300–1.8 K under an applied field of 1000 Oe (Fig. S5A, ESI†). The χT product exhibited a gradual decrease from 14.15 to 12.41 cm3 K mol−1 upon cooling from 300 to 1.8 K. Its value at room temperature is in good agreement with the theoretical value for a single Dy3+ ion (S = 5/2, L = 5, 6H15/2g = 4/3, C = 14.17 cm3 K mol−1). The decrease at low temperature can arise from a combination of thermal depopulation of Stark sublevels, significant magnetic anisotropy, and small yet non-negligible antiferromagnetic intermolecular interactions between Dy3+ centres.12 The presence of magnetic anisotropy was confirmed by the field-dependent magnetization observed in the magnetization (M vs. H) and reduced magnetization (M vs. HT−1) plots, which reaches a maximum value of 5.70 MμB at 1.9 K and 7 T (Fig. S5b, ESI†). Therein, the non superimposition of the isofield lines indicates the presence of non negligible magnetic anisotropy (Fig. S5c, ESI†).The SMM properties of 1 were studied via ac (alternating current) susceptibility measurements in the 0.1–1500 Hz range with an oscillating field Hac = 3.78 Oe. Below 12 K, frequency-dependent susceptibility was observed (Fig. 2a) indicative of slow relaxation of the magnetization intrinsic to the molecule. In the absence of an external field (Hdc = 0 Oe), a frequency-dependent signal was observed with a strong contribution of quantum tunnelling of magnetization (QTM) at low temperature. QTM within the ground KD is not fully suppressed despite the good axiality of the g-tensor of the ground KD (gx = gy = 0.001 and gz = 19.832; vide infra). This observation is supported by the calculated transition magnetic moment matrix elements between the spin–orbit states in the ground multiplet of 6H15/2 (vide infra). To probe the mechanisms responsible for the spin-reversal, the relaxation times (τ) of the individual peaks were extracted from the χ′′ data using the generalized Debye model (Tables S3–S5, ESI†).24 Considering the most common relaxation mechanisms – Orbach, Raman, and QTM – and the temperature regimes at which they operate, the τ−1vs. T dataset (Fig. 2c and Fig. S6a, ESI†) was fit to the following equation:
| τ−1 = τ0−1exp[−Ueff/KbT] + CTn + B1/(1 + B2H2) | (1) |
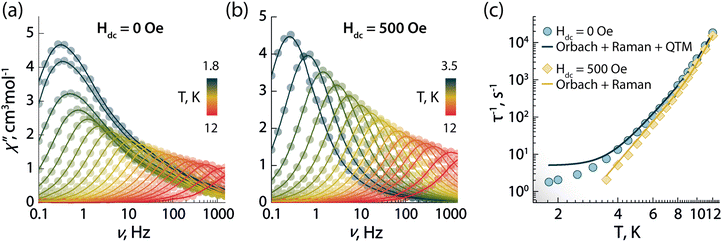 | ||
| Fig. 2 Frequency dependence of the out-of-phase (χ′′) magnetic susceptibility as a function of temperature obtained in absence of an external dc magnetic field (a) and under an applied static field of 500 Oe (b). (c) Temperature dependence of the magnetic relaxation times (τ) in absence (blue circles) and in the presence of a 500 Oe applied field (yellow diamonds). Solid lines in (c) are the best fit to the experimental data using eqn (1). | ||
To determine the optimal applied dc field that minimizes QTM at low temperature, field-dependent relaxation dynamics were investigated at 5 K (Fig. S7, ESI†). Frequency-dependent signals in the out-of-phase χ′′ susceptibility were observed between 0 and 5000 Oe. The field-dependent τ values were obtained fitting the χ′′ susceptibility to the generalized Debye model, and the resulting τ−1vs. T dataset was fit with the following equation (which includes the field-dependent direct, Raman, and QTM mechanisms):
| τ−1 = AH4 + CTn + B1/(1 + B2H2) | (2) |
Optical properties and luminescence thermometry
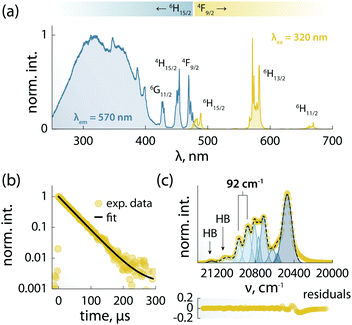
The combination of ligands and Dy3+ in 1 yields also augmented the optical properties. The emission spectrum is dominated by the typical Ln3+ narrow emission lines (Fig. 3a). The excitation spectrum – recorded while monitoring the Dy3+ emission at 570 nm – shows both sharp and broadband features (Fig. 3a), ascribed respectively to the 4f–4f Ln3+ transitions and the organic ligands. The appearance of this latter contribution is indicative of ligand-sensitized emission. In this process, the ligands absorb the excitation photons and transfer the optical energy to the coordinated metal centre, which then relaxes radiatively to its ground state (i.e., emits photons). Upon fitting with a single exponential function the decay curve obtained monitoring the Dy3+:4F9/2 → 6H13/2 transition (Fig. 3b), a characteristic decay time of 40 μs was found for the Dy3+ emitting state (4F9/2). This value is almost 3 times larger than the lifetime of the luminescent Dy3+-SMM with thermometric capabilities we recently reported,6 and similar to the value observed in a dimetallic ZnDy SMM.4The 4F9/2 → 6H15/2 transition was deconvoluted (Fig. 3c) to garner information regarding the mj levels of the ground state (6H15/2), obtaining an energy separation of 92 cm−1 between the first two mj levels. This value is in agreement with the calculated energy separation of 107 cm−1 (vide infra), and larger than or on par with the values reported for other optomagnetic Dy3+ complexes.4,6,25 Moreover, it is close to the energy barriers observed in ac magnetic studies (95.1 and 96.1 cm−1, without and with applied field, respectively), and hence indicates that the Orbach magnetic relaxation process occurs through the first excited mj level.
The PL of the systems shows also sensitivity towards temperature changes, and can thus be employed for thermal monitoring purposes.12 To study the thermometric performance of 1, we recorded PL spectra between 10 and 50 K (Fig. 4a). This range encompasses the high end of the temperature window wherein 1 acts as SMM – i.e., <12 K. As expected, variations in the relative intensities of the Stark components of the 4F9/2 → 6H13/2 manifold were observed.
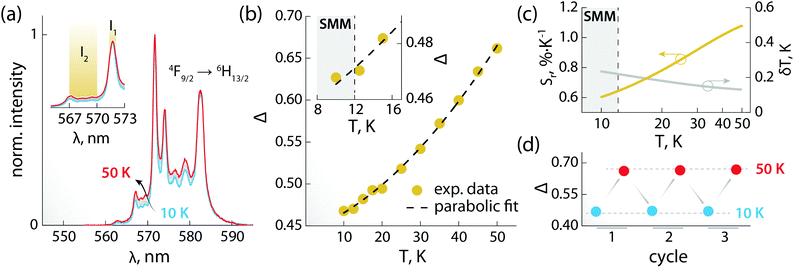 | ||
| Fig. 4 Luminescence thermometry performance of 1. (a) PL spectra recorded in the 10–50 K range under 320 nm excitation. In the inset, a zoom-in of the 565–573 nm range is shown, along with the integration ranges I1 and I2 (yellow) used for calculating the areas used to obtain the thermometric parameter (Δ). (b) Calibration curve obtained using the thermometric parameter Δ = I2/I1 (yellow circles) and its fit to a parabolic function (dashed black line). In the inset, a zoom-in of the 8–17 K range is shown. The range wherein 1 behaves as SMM is indicated as a grey rectangle. (c) Relative thermal sensitivity and associated uncertainty calculated from the data in (b) and the mathematical treatment detailed in the ESI.† A logarithmic scale is used for the abscissa to better visualize the low-temperature range. (d) Results of three cycles of measurements performed at 10 and 50 K to determine the repeatability of the thermometric approach. | ||
The ratio between the intensity integrated over conveniently selected ranges (I1 and I2, as indicated in the inset of Fig. 4a) was chosen as thermometric parameter (Δ = I2/I1, Fig. 4b). The Δ vs. T dataset was fit to a parabolic function (Table S8, ESI†) that, along with its first derivative, was used to determine the relative thermal sensitivity according to the following equation:26,27
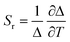 | (3) |
Theoretical modelling of the chalcogen atom effects
Stimulated by the experimental results, we decided to model the effect of hard (O) and soft (S, Se, and Te) donor atoms on the magnetic and optical properties of the reported optomagnetic complex (Tables S10–S24, ESI†). Specifically, we were interested in the general trends that could serve as a predictive tool to fine-tune simultaneously the magnetic, optical, and thermometric performance of a Ln3+-SMM. With this goal in mind, density functional theory (DFT) and CASSCF/RASSI calculations were performed on systems 1O, 1S, 1Se, and 1Te, containing benzoate (ba−), thiobenzoate (tba−), selenobenzoate (sba−), and tellurobenzoate (teba−), respectively (Fig. 5). The results show that in 1O, the stabilization and axiality of the ground Kramers doublet (KD; Table S13, ESI†) are lost. Hence, a low Ueff (32 cm−1) and significant QTM within the ground KD are observed. However, the microscopic magnetic properties and energy spectrum of the 6H15/2 ground multiplet drastically change in 1S, 1Se, and 1Te compared to 1O. The height of the energy spectrum is increased (Fig. S8, ESI†), the ground KD is more stabilized, the axiality of the lowest KDs is improved (as evinced from the calculated g-tensors (Fig. 6a) and crystal field parameters), the main magnetic axes of the lowest KDs are more collinear (Fig. S9, ESI†), and the calculated qualitative energy barriers are higher (Fig. 6b and Tables S13–S16, ESI†). Overall, among 1S, 1Se, and 1Te, the latter has the best parameters by a slight margin: a result of the elongation and decrease in the ionic nature of Ln–E bonds when descending the chalcogen group.§ This is shown by the optimized geometries and calculated electron densities (ρ(r)), Laplacians (∇2ρ(r)), delocalization indices (DI), and effective atomic charges obtained from the quantum theory of atoms in molecules analysis (Table S23, ESI†). Since the longer radical extensions of the valence orbitals of heavier chalcogens weaken the equatorial crystal ligand field around Dy3+, O and N atoms of the carbonyl groups and phen ligand, respectively, start to dominate the axial crystal ligand field of Dy3+ ion in 1S, 1Se, and 1Te. The weakening of the equatorial ligand field around the Dy3+ ion has been proven to improve the axiality and SMM properties of Dy3+-based SMMs in tandem.5,32 This is best illustrated by investigating the calculated crystal-field parameters (Bqk) and visualizing the main magnetic axis of Dy3+ ion in the studied systems. For all other systems, except for 1O, the axial crystal-field parameter B02 dominates the crystal ligand field because its value is order of magnitude larger than the values of any other crystal-field parameters, whereas for 1O the non-axial crystal-field parameters are of the same magnitude or even larger than the axial crystal-field parameters for all values of k (Tables S17–S21, ESI†). Moreover, the visualization of the main magnetic axis of the first three KDs of Dy3+ ion reveals that they are almost collinear in all other system expect in 1O because of the stronger axiality observed in the heavier chalcogen systems (Fig. S9, ESI†). These findings are in line with previous studies on Ln3+-based SMMs containing soft donor atoms from the chalcogen groups.14,33 | ||
| Fig. 5 Benzoate, thiobenzoate, selenobenzoate, and tellurobenzoate ligands, along with the corresponding complexes derived from 1. | ||
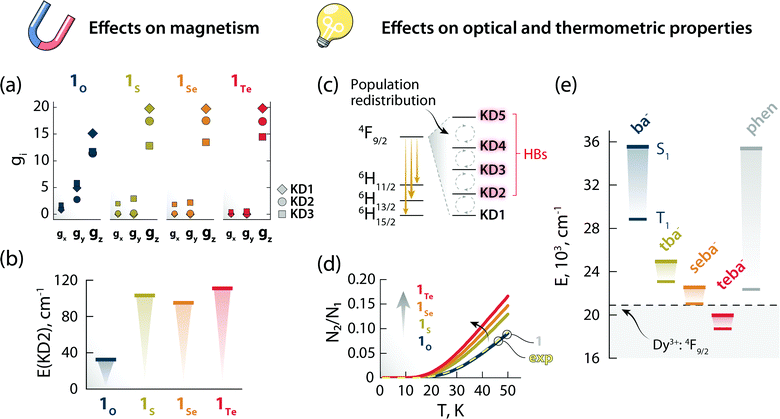 | ||
| Fig. 6 The effects of changing the chalcogen atom in the benzoate ligand on the magnetic and optical properties. Components of the g-tensor (gx, gy, gz) of the first three KDs (a) and energy of KD2 (b) for the Dy3+:6H15/2 ground multiplet of 1O, 1S, 1Se, and 1Te. Scheme depicting the temperature-induced electron population redistribution between the KDs (i.e., mj levels) of the Dy3+:4F9/2 excited state (c). Ratio between the electron population of KD2 and KD1 as obtained from the Boltzmann model for 1O, 1S, 1Se, and 1Te (d). The results of the same calculations for 1 (solid gray line, beneath 1O) and considering the position of the 4F9/2 components obtained from the deconvolution (Fig. S11, ESI†) of the 6H15/2 → 4F9/2 transition in the excitation spectrum (exp, dashed yellow line) are also reported. The overlap between the curves 1 and 1O is a serendipitous result stemming from the similar energy difference between the first two 4F9/2mj levels obtained for these two systems. Energy of the first singlet (S1) and triplet (T1) excited states of the different ligands calculated by the CAM-B3LYP exchange-correlation functional (e). The position of the Dy3+:4F9/2 excited state is also indicated with a dashed black line (centroid of the 4F9/2 manifold obtained from the deconvolution of the 6H15/2 → 4F9/2 transition in the excitation spectrum – Fig. S10, ESI†). | ||
The nature of chalcogen atom influences the optical properties of the complex and its expected luminescence thermometry performance too. In this study, we have harnessed the spectral changes arising from temperature-induced population redistribution between the mj levels (i.e., KDs) to define a ratiometric thermometric approach (Fig. 4). Specifically, the integrated intensity I2 mainly contains contributions from hot bands (HBs), i.e., transitions from the Dy3+:4F9/2 excited mj levels to the Dy3+:6H13/2 state (Fig. 6c). I1 has its major contribution stemming from the lowest Dy3+:4F9/2mj level. The population of each level (Ni) as a function of temperature can be modelled with a system of equations based on the Boltzmann function (see ESI† for details). Since the intensity ratio is proportional to the electron population, and considering the low temperature range investigated, the ratio between the electron population of the first excited level and ground level (N2/N1) can thus approximate the intensity ratio Δ = I2/I1 used for the thermometric approach. This assumption is corroborated by the overlap between the N2/N1-vs.-temperature curves (Fig. 6d) for 1 and using the energy values extracted from the deconvolution of the 6H15/2 → 4F9/2 transition in the excitation spectrum (Fig. S11, ESI†). Because of the effect that different chalcogen atoms have on the Dy3+:4F9/2mj levels separation (Tables S13–S16, ESI†), the N2/N1 curve becomes steeper and has an earlier onset following the order 1Te > 1Se > 1S > 1O (Fig. 6d). These observations indicate that a thermometric approach based on the fine structure of the 4F9/2 → 6H13/2 manifold is more sensitive and can extend to lower temperatures using heavier chalcogens.
Thus, it appears that moving downwards along the chalcogen group can be a viable strategy to simultaneously boost the magnetic properties and luminescence thermometry performance of luminescent Ln3+-SMMs. However, there is an additional piece of the puzzle to consider: the lower energy of the first excited singlet (S1) and triplet (T1) states of heavy-chalcogen-containing ligands. Indeed, the calculated energies of these states decrease in the following the order: 1O > 1S > 1Se > 1Te. It is therefore possible that the S1 or T1 or both states of the chalcogen ligand fall too close or even below the emitting Dy3+:4F9/2 state. In that case, lack of sensitization or efficient quenching of the lanthanide PL due to back energy transfer to the ligand would occur.
It should be pointed out that the observations based on the modelled Dy3+ ground state (6H15/2) are reliable, as confirmed by the good match between the mj levels retrieved from the ab initio calculations and the deconvolution of the 4F9/2 → 6H15/2 transition (Fig. S10, ESI†). However, modelling of the excited states is generally less accurate, and the absolute energy values of spin–orbit states are accompanied by a large error (Fig. S11, ESI†). This discrepancy also applies to the simulated thermometric performance of the complexes (Fig. 6d). For this reason, particularly for the optical properties of the complexes, we analysed relative trends instead of absolute values. From these trends, a positive effect seems to be played by the introduction of soft chalcogen donors in the Dy3+ coordination sphere both in terms of magnetism and mj-level-based luminescence thermometry. Yet, the lowering of the ligand states’ energy could frustrate these beneficial effects, up to a complete quenching of Dy3+ emission.
Conclusions
In conclusion, we reported the first thiobenzoate-based Ln3+-SMM in the form of a mononuclear Dy3+ complex. Slow relaxation of the magnetization under no applied field was observed up to 12 K. The mechanisms involved in this process were interpreted combining analysis of magnetic data, photoluminescence spectrum, and theoretical calculations. A ratiometric luminescence thermometry approach was established harnessing the thermal dependence of Dy3+ emission, with a relative thermal sensitivity between 0.6 and 1.1%·K−1 and temperature uncertainty well below 1 K across the 10–50 K temperature range. We subsequently used this complex as a model system to investigate how the introduction of different chalcogen donors (O, S, Se, Te) in the metal coordination sphere impact on the magnetic, optical, and luminescence thermometry performance. The trends obtained from ab initio calculations indicate that softer chalcogen donors can simultaneously boost the SMM performance and the sensitivity of thermometric approaches based on variations of the Stark levels’ intensity. On the other hand, lowering of the energy states of the chalcogen-bearing ligand could result in an unfavourable energy scheme, and hence ultimately loss of appreciable Dy3+ emission.Overall, this novel optomagnetic complex is a remarkable example of how the use of ligands that combine the features of soft (S, Se, and Te) and hard (O) donors (i.e., electronic cloud modulation and strong/weak interaction with the metal centre) is a promising strategy for the preparation of Ln3+-SMMs with tailored optical properties. Moreover, the general considerations obtained from modelling of the family of complexes used herein as case study are envisaged to support the design of novel multifunctional Ln3+-complexes based on soft-donor-bearing ligands that combine magnetic, optical, and luminescence thermometry properties.
Author contributions
R. M. – conceptualization, data curation, formal analysis, funding acquisition, investigation, methodology, visualization, writing original draft. D. A. G. – formal analysis, investigation, methodology, writing original draft. R. G. – formal analysis, methodology, writing original draft. J. O. M. – formal analysis, funding acquisition, supervision, methodology, writing original draft. L. D. C. – supervision, writing – review & editing. D. J. – supervision, writing – review & editing. M. M. – supervision, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
R. M. acknowledges the support of the European Commission through the European Union's Horizon 2020 research and innovation program under the Marie Skłodowska-Curie Grant agreement 797945 (LANTERNS). This work was supported by Ministerio de Ciencia e Innovación de España (PID2019-106211RB-I00) and developed within the scope of the project CICECO-Aveiro Institute of Materials, UIDB/50011/2020, financed by Portuguese funds through FCT/MEC and co-financed by FEDER under the PT2020 Partnership Agreement. We thank the University of Ottawa, the CFI, and the NSERC for financial support of this work. J. O. M. and R. G. acknowledge Academy of Finland (project numbers 315829, 320015, and 345484) for funding. CSC-IT Centre for Science in Finland, the Finnish Grid and Cloud Infrastructure (persistent identifier urn:nbn:fi:research-infras-2016072533) and Prof. H. M. Tuononen (University of Jyväskylä) are acknowledged for providing computational resources for the project. We are greatly indebted to Dr Josefina Perles Hernáez from the Interdepartmental Investigation Service (SIDI) of the Universidad Autónoma de Madrid for performing the X-ray diffraction experiment and solving the crystal structure of the complex investigated.References
- F. Arute, K. Arya, R. Babbush, D. Bacon, J. C. Bardin, R. Barends, R. Biswas, S. Boixo, F. Brandao, D. A. Buell, B. Burkett, Y. Chen, Z. Chen, B. Chiaro, R. Collins, W. Courtney, A. Dunsworth, E. Farhi, B. Foxen, A. Fowler, C. Gidney, M. Giustina, R. Graff, K. Guerin, S. Habegger, M. P. Harrigan, M. J. Hartmann, A. Ho, M. Hoffmann, T. Huang, T. S. Humble, S. V. Isakov, E. Jeffrey, Z. Jiang, D. Kafri, K. Kechedzhi, J. Kelly, P. V. Klimov, S. Knysh, A. Korotkov, F. Kostritsa, D. Landhuis, M. Lindmark, E. Lucero, D. Lyakh, S. Mandra, J. R. McClean, M. McEwen, A. Megrant, X. Mi, K. Michielsen, M. Mohseni, J. Mutus, O. Naaman, M. Neeley, C. Neill, M. Y. Niu, E. Ostby, A. Petukhov, J. C. Platt, C. Quintana, E. G. Rieffel, P. Roushan, N. C. Rubin, D. Sank, K. J. Satzinger, V. Smelyanskiy, K. J. Sung, M. D. Trevithick, A. Vainsencher, B. Villalonga, T. White, Z. J. Yao, P. Yeh, A. Zalcman, H. Neven and J. M. Martinis, Nature, 2019, 574, 505–510 CrossRef CAS.
- D. N. Woodruff, R. E. Winpenny and R. A. Layfield, Chem. Rev., 2013, 113, 5110–5148 CrossRef CAS PubMed.
- J. Long, Y. Guari, R. A. S. Ferreira, L. D. Carlos and J. Larionova, Coord. Chem. Rev., 2018, 363, 57–70 CrossRef CAS.
- J. Long, J. Rouquette, J. M. Thibaud, R. A. Ferreira, L. D. Carlos, B. Donnadieu, V. Vieru, L. F. Chibotaru, L. Konczewicz, J. Haines, Y. Guari and J. Larionova, Angew. Chem., Int. Ed., 2015, 54, 2236–2240 CrossRef CAS PubMed.
- F. S. Guo, B. M. Day, Y. C. Chen, M. L. Tong, A. Mansikkamaki and R. A. Layfield, Science, 2018, 362, 1400–1403 CrossRef CAS PubMed.
- D. Errulat, R. Marin, D. A. Galico, K. L. M. Harriman, A. Pialat, B. Gabidullin, F. Iikawa, O. D. D. Couto Jr., J. O. Moilanen, E. Hemmer, F. A. Sigoli and M. Murugesu, ACS Cent. Sci., 2019, 5, 1187–1198 CrossRef CAS PubMed.
- G. Brunet, R. Marin, M. J. Monk, U. Resch-Genger, D. A. Galico, F. A. Sigoli, E. A. Suturina, E. Hemmer and M. Murugesu, Chem. Sci., 2019, 10, 6799–6808 RSC.
- D. A. Galico, R. Marin, G. Brunet, D. Errulat, E. Hemmer, F. A. Sigoli, J. O. Moilanen and M. Murugesu, Chem. – Eur. J., 2019, 25, 14625–14637 CrossRef CAS PubMed.
- M. Fondo, J. Corredoira-Vázquez, A. M. García-Deibe, J. Sanmartín-Matalobos, M. Amoza, A. M. P. Botas, R. A. S. Ferreira, L. D. Carlos and E. Colacio, Inorg. Chem. Front., 2020, 7, 3019–3029 RSC.
- R. A. S. Ferreira, E. Mamontova, A. M. P. Botas, M. Shestakov, J. Vanacken, V. Moshchalkov, Y. Guari, L. F. Chibotaru, D. Luneau, P. S. André, J. Larionova, J. Long and L. D. Carlos, Adv. Opt. Mater., 2021, 9, 2101495 CrossRef CAS.
- A. N. Carneiro Neto, E. Mamontova, A. M. P. Botas, C. D. S. Brites, R. A. S. Ferreira, J. Rouquette, Y. Guari, J. Larionova, J. Long and L. D. Carlos, Adv. Opt. Mater., 2021, 10, 2101870 CrossRef.
- R. Marin, G. Brunet and M. Murugesu, Angew. Chem., Int. Ed., 2021, 60, 1728–1746 CrossRef CAS PubMed.
- F. Tuna, C. A. Smith, M. Bodensteiner, L. Ungur, L. F. Chibotaru, E. J. McInnes, R. E. Winpenny, D. Collison and R. A. Layfield, Angew. Chem., Int. Ed., 2012, 51, 6976–6980 CrossRef CAS PubMed.
- A. B. Canaj, S. Dey, O. Cespedes, C. Wilson, G. Rajaraman and M. Murrie, Chem. Commun., 2020, 56, 1533–1536 RSC.
- G. A. Kumar, R. E. Riman and J. G. Brennan, Coord. Chem. Rev., 2014, 273-274, 111–124 CrossRef CAS.
- J. Xi, X. Ma, P. Cen, Y. Wu, Y. Q. Zhang, Y. Guo, J. Yang, L. Chen and X. Liu, Dalton Trans., 2021, 50, 2102–2111 RSC.
- W. Huang, Z. Zheng and D. Wu, Inorg. Chem. Commun., 2017, 84, 40–44 CrossRef CAS.
- L. Tian and J. J. Vittal, Cryst. Growth Des., 2006, 6, 822–824 CrossRef CAS.
- T. Kanda, M. Ibi, K.-I. Mochizuki and S. Kato, Chem. Lett., 1998, 957–958 CrossRef CAS.
- M. D. Regulacio, M. H. Pablico, J. A. Vasquez, P. N. Myers, S. Gentry, M. Prushan, S. W. Tam-Chang and S. L. Stoll, Inorg. Chem., 2008, 47, 1512–1523 CrossRef CAS PubMed.
- S.-S. Liu, J.-M. Zhao, S. Deng, J. Xiong, M.-F. Yang, J.-X. Li, S.-J. Lin, Y.-Q. Zhang and B.-W. Wang, Inorg. Chem. Commun., 2018, 95, 82–85 CrossRef CAS.
- D. Brown and D. G. Holah, Chem. Commun., 1968, 1545–1546 RSC.
- J. H. Melman and T. J. Emge, Chem. Commun., 1997, 2269–2270 RSC.
- S. M. J. Aubin, Z. Sun, L. Pardi, J. Krzystek, K. Folting, L.-C. Brunel, A. L. Rheingold, G. Christou and D. N. Hendrickson, Inorg. Chem., 1999, 38, 5329–5340 CrossRef CAS.
- Y. Xin, J. Wang, M. Zychowicz, J. J. Zakrzewski, K. Nakabayashi, B. Sieklucka, S. Chorazy and S. I. Ohkoshi, J. Am. Chem. Soc., 2019, 141, 18211–18220 CrossRef CAS.
- S. A. Wade, S. F. Collins and G. W. Baxter, J. Appl. Phys., 2003, 94, 4743–4756 CrossRef CAS.
- C. D. S. Brites, A. Millán and L. D. Carlos, in Handbook on the Physics and Chemistry of Rare Earths, ed., J.-C. G. Bünzli, V. K. Pecharsky, Elsevier Science, B. V. Amsterdam, 2016, vol. 49, pp. 339–427 Search PubMed.
- A. Skripka, A. Morinvil, M. Matulionyte, T. Cheng and F. Vetrone, Nanoscale, 2019, 11, 11322–11330 RSC.
- L. Li, Y. Zhu, X. Zhou, C. D. S. Brites, D. Ananias, Z. Lin, F. A. A. Paz, J. Rocha, W. Huang and L. D. Carlos, Adv. Funct. Mater., 2016, 26, 8677–8684 CrossRef CAS.
- G. Bao, K. L. Wong, D. Jin and P. A. Tanner, Light: Sci. Appl., 2018, 7, 96 CrossRef.
- J. Wang, J. J. Zakrzewski, M. Zychowicz, V. Vieru, L. F. Chibotaru, K. Nakabayashi, S. Chorazy and S. I. Ohkoshi, Chem. Sci., 2020, 12, 730–741 RSC.
- H. S. Wang, K. Zhang, J. Wang, Z. B. Hu, Z. Zhang, Y. Song and Y. Q. Zhang, Inorg. Chem., 2021, 60, 9941–9955 CrossRef CAS PubMed.
- K. R. Vignesh, D. I. Alexandropoulos, B. S. Dolinar and K. R. Dunbar, Dalton Trans., 2019, 48, 2872–2876 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available: Experimental details, structural and chemical characterization, additional magnetic data, mathematical treatment of luminescence thermometry, computational details and simulation of the thermometric performance. CCDC 2167973. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d2tc01661c |
| ‡ These authors contributed equally to this work. |
| § Due to the core-like nature of the 4f orbitals, it is expected that the lanthanides interact with the coordinating ligands through an electrostatic interaction rather than form a covalent bond. However, recent publications have shown that there can be a non-negligible covalent contribution to the bonding in the lanthanide complexes (Aravena et al., Inorg. Chem., 2016, 55, 4457-4469; Briganti et al., Chem. Sci., 2019, 10, 7233-7245; Panetti et al., Nat. Commun., 2021, 12, 1731). For the investigated systems, the AIM analyses support that the electrostatic interactions dominates the interaction between the coordinating ligands and Dy3+ ion, but this does not automatically rule out the plausible covalent contribution. Indeed, the values of ∇2ρ(r) and DI for Ln–E bonds simultaneously decrease and increase, respectively, when descending the group 16. The results indicate that the covalent contribution of Ln–E bond gradually increases, when going from O to Te, albeit its ionic nature. |
| This journal is © The Royal Society of Chemistry 2022 |