Open Access Article
Open Access ArticleThe resistive nature of decomposing interfaces of solid electrolytes with alkali metal electrodes†
Juefan
Wang
a,
Abhishek A.
Panchal
a,
Gopalakrishnan
Sai Gautam
 b and
Pieremanuele
Canepa
b and
Pieremanuele
Canepa
 *ac
*ac
aDepartment of Materials Science and Engineering, National University of Singapore, 9 Engineering Drive 1, Singapore 117575, Singapore
bDepartment of Materials Engineering, Indian Institute of Science, Bangalore 560012, India
cChemical and Biomolecular Engineering, National University of Singapore, 4 Engineering Drive 4, Singapore 117585. E-mail: pcanepa@nus.edu.sg
First published on 7th June 2022
Abstract
A crucial ingredient in lithium (Li) and sodium (Na)-ion batteries (LIBs and NIBs) is the electrolyte. The use of Li metal (Na metal) as the anode in liquid electrolyte LIBs (NIBs) is constrained by several issues including thermal runaway, flammability, electrolyte leakage, and limited chemical stability. Considerable effort has been devoted toward the development of solid electrolytes (SEs) and all-solid-state batteries, which are presumed to mitigate some of the issues of Li metal (Na metal) in contact with flammable liquid electrolytes. However, most SEs, such as Li3PS4, Li6PS5Cl and Na3PS4 readily decompose against the highly reducing Li-metal and Na-metal anodes. Using first-principles calculations we elucidate the stability of more than 20 solid‖solid interfaces formed between the decomposition products of Li3PS4, Li6PS5Cl (and Na3PS4) against the Li-metal (Na-metal) electrode. We suggest that the work of adhesion needed to form a heterogenous interface is an important descriptor to quantify the stability of interfaces. Subsequently, we clarify the atomistic origins of the resistance to Li-ion transport at interfaces of the Li-metal anode and selected decomposition products (Li3P, Li2S and LiCl) of SEs, via a high-fidelity machine learning potential. Utilising an machine learning potential enables nano-second-long molecular dynamics simulations on ‘large’ interface models (here with 8320 atoms), but with similar accuracy to first-principles approaches. Our simulations demonstrate that the interfaces formed between Li metal and argyrodite (e.g., Li6PS5Cl) decomposition products are resistive to Li-ion transport. The implications of this study are important since binary compounds are commonly found in the vicinity of the Li(Na) metal anode upon chemical and/or electrochemical decomposition of ternary and quaternary SEs.
1 Introduction
Rechargeable lithium-ion batteries (LIBs) keep gaining importance for the development of next-generation energy storage devices and electric vehicles because of their outstanding gravimetric and volumetric energy densities.1–5 Lithium metal batteries (LMBs) utilizing Li-metal anodes—that can achieve unprecedented energy densities theoretically, as compared to LIBs—have become one of the central topics of current research in rechargeable batteries.4–6 The primary challenge in constructing practical LMBs is stabilizing the Li-metal‖electrolyte interface, with scientific studies mostly focused on identifying electrolyte formulations with limited reactivity and/or suitable additives.1,5,7 Stabilizing the metal‖electrolyte interface is also a bottleneck in developing Na-metal batteries (NMBs).4,5,8–10Solid electrolytes (SEs) are critical components in the development of LMBs and solid-state LIBs.11–18 Besides acting as separators between electrodes, SEs are also expected to alleviate some of the safety issues between Li-metal anodes and liquid electrolytes.4,5,19 Nevertheless, numerous reports have demonstrated high electrochemical instabilities of SEs when in contact with the Li-metal anode (and other electrode materials).4 For example, sulfur-containing SEs are unstable against Li metal, resulting in the formation of undesired decomposition products, which may resist Li-ion transport and/or facilitate electron transport.12–15,20–22 Thus, the stabilization of interfaces formed between Li metal (or other alkali-metal electrodes) and SEs remains a significant bottleneck in designing practical solid-state batteries.
Electrolyte decomposition occurs at small length scales away from the exteriors of the cell packs that constitute a battery. Therefore, the characterization of decomposition products in fully assembled and operating devices requires dedicated custom-made and expensive tools.13,14,23,24 A number of reports have analyzed the compositions, structures, and formation mechanisms of the decomposing products of SEs against metal electrodes (metal electrode‖SE).12–15,20–22 For example, X-ray photoemission spectroscopy (XPS) experiments by Wenzel et al.14 reported that Li6PS5X (with X = Cl, Br and I), upon contact with Li metal, forms Li2S, LiX, and Li3P. As a result, the decomposition products of metal electrode‖SE interfaces are expected to be multiphased and highly heterogeneous, which complicates the description of ionic transport across interfaces. Furthermore, the structures and properties of the metal electrode‖SE interfaces are expected to be markedly different from the bulk materials. A detailed study of the interfacial properties, particularly ionic transport is needed for the advancement of solid-state batteries.
Another aspect of solid-state batteries relates to the mechanical stability (i.e., adhesion) of the solid‖solid interfaces that are chemically or electrochemically formed. The loss of contact due to the lack of adhesion between Li metal and SEs appears as a major cause driving the buildup of interfacial impedance in solid-state devices.4,5,25 To evaluate the mechanical stabilities of the interfaces, Lepley and Holzwarth26 have performed accurate first-principles calculations of several Li-metal‖SE interfaces (such as, Li‖Li2O, Li‖Li2S, Li‖Li3PO4 and Li‖Li3PS4) and found that all interfaces were stable except Li‖Li3PS4. Other studies have investigated the effects of the stability of heterogeneous interfaces on the Li-ion transport properties.27–29
Yang and Qi27 have proposed that an interface with good adhesion, i.e. a “lithiophilic interface” can result in a faster critical stripping current density, which is crucial to prevent dendrite growth. Recently, Seymour and Aguadero28 have shown that Li (or Na)-ion transport across alkali-metal‖SE interfaces correlates directly with interfacial adhesion. Yang et al.29 have employed classical molecular dynamics (MD) to study the process of Li plating and stripping on solid Li2O, showing that a coherent interface with strong interfacial adhesion and fast Li-ion diffusion can prevent pore formation at the interface. Here, we perform a systematic investigation including a larger data set of solid‖solid interfaces, particularly focusing on the correlation between the atomistic structure of interfaces and ionic transport, which is presently lacking.
We address the interfacial stability and Li-ion mobility of multiple interfaces formed between the Li-metal electrode and decomposition products of topical SEs, such as, Li3PS4,15,26,30,31 argyrodite-Li6PS5Cl14 and LiPON, with general formula LixPOyNz.23,24,32 We also analyze the Na‖Na2S and Na‖Na3P interfaces, which form upon the decomposition of Na3PS4 against Na metal.13 We perform large-scale MD simulations of selected interfaces, (i.e., Li‖Li3P, Li‖Li2S and Li‖LiCl) based on high-fidelity machine learning potentials (MLPs) trained on accurate first-principles data, which carry the accuracy of ab initio molecular dynamics (AIMD) while giving access to appreciably larger time and length scale simulations.
We reveal that the mechanical stabilities of the Li (or Na)-metal‖SE interfaces are primarily governed by the atomistic structures of the interfaces, which in turn are dependent on the surface orientations and/or terminations of the decomposition products. Furthermore, we show that the interfaces formed between Li metal and decomposition products of the argyrodite Li6PS5Cl SE (i.e., Li3P, Li2S and LiCl) are resistive to Li-ion transport, explaining the observed impedance buildup. Our results provide insights into engineering solid‖solid interfaces with better interfacial stability and improved ionic transport.
2 Construction of interfaces of decomposition products and metal anodes
We discuss the procedure to build heterogeneous interfaces between an alkali metal (Li or Na) with one of their binary compounds (e.g., Li3P), formed as a result of SE decomposition. In constructing the heterogeneous interfaces between the alkali metal (e.g., Li or Na) and the binary compounds, we identify stable stoichiometric surfaces (following Tasker's criteria33) with low surface energies, γ, of both materials, which are paired into an interface (see Table S1 of the ESI†). To describe γ, we have used the slab model in eqn (1).34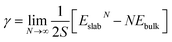 | (1) |
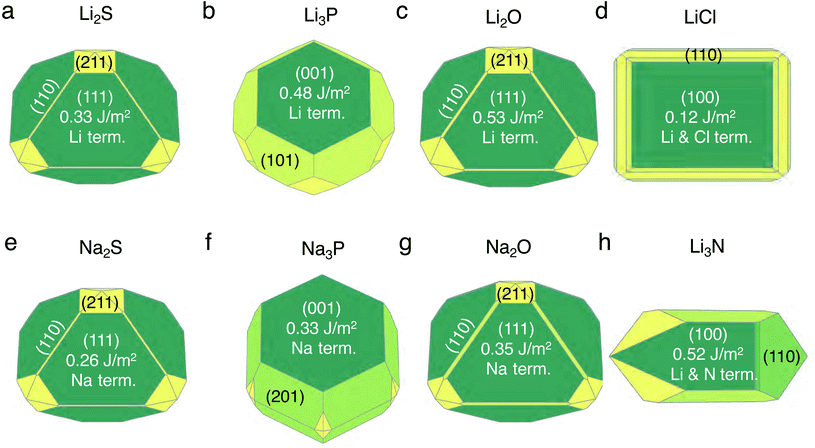
The set of stable surfaces in Li (or Na)-metal and binary compounds are considered, and their corresponding γ values are displayed in the Wulff shapes shown in Fig. 1.35,36 The values of γ, not shown in Fig. 1, are included in Tables S2 and S3 of the ESI.† The (100) surface of Li metal has the lowest surface energy of ∼0.46 J m−2, while for Na metal, the (100) and (110) surfaces have similar γ values, ∼0.22 J m−2 and ∼0.21 J m−2. In Li2S, Li2O, Na2S, and Na2O, the (111) facet dominates the Wulff shape, while for Li3P, LiCl, Li3N, and Na3P, the {001}-type surfaces have the lowest γ values (Fig. 1). Our calculated surface energies, ∼0.33 J m−2 for the (111) surface and ∼0.51 J m−2 for the (110) surface of Li2S, as well as ∼0.53 J m−2 for the (111) surface of Li2O are consistent with the values reported in previous literature studies.37,38 Li3N and LiCl exhibit stable facets that are terminated with both Li and anion species, while other compounds have stable facets exposing a Li (or Na) layer.
The surfaces shown Fig. 1 are subsequently paired to form heterogeneous interfaces. Different metrics serve to quantify the effect of mechanical strain and/or the chemical bond formation/destruction at the interface.39,40 The interface formation energy (Ef calculated using eqn (2)) is the energy difference between the interface model and bulk structures of A and B, and includes both mechanical (i.e., elastic strain) and chemical components.34
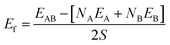 | (2) |
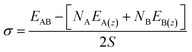 | (3) |
The work of adhesion, Wadhesion (of eqn (4)) is the work done to part two adherent surfaces to an infinite distance, and quantifies the mechanical stability of an interface.
| Wadhesion = γA + γB − σ | (4) |
| Wadhesion = γA + γB − Ef | (5) |
For the creation of interface models, we use the algorithm by Taylor et al.,43 which samples the configurational space to find interface models that minimize the lattice mismatch between two materials. While pairing surfaces, we used the in-plane lattice constants of the binary compounds (e.g., Li3P) and applied a lattice mismatch-induced strain to the metal surface, since the bulk moduli of binary compounds are typically greater than the alkali metals (i.e., Li and Na).11,44 The constructed interface models are symmetric; for example, Li2S‖Li-metal consists of two identical interfaces that forms a Li2S‖Li-metal‖Li2S system, as displayed in panel c in Fig. 2. The slab thickness of binary compounds is typically ∼10 Å, which is sufficient to distinguish the interface features from their bulk-like properties. However, thicker slabs are required for Li (∼12 Å) and Na (∼14 Å) to distinguish the interface regions from the bulk region.26
3 Stability of interfaces of decomposition products and metal electrodes
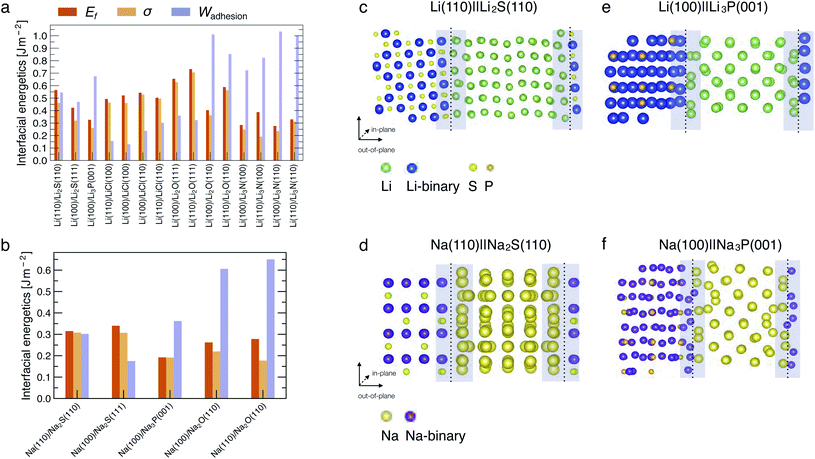
Fig. 2a and b show the computed interfacial energetics, Ef, σ, and Wadhesion (as defined in eqn (4)), for a number of interfaces considered. An illustration of the interface models for Li(110)‖Li2S(110), Na(110)‖Na2S(110), Li(100)‖Li3P(001) and Na(100)‖Na3P(001) is shown in Fig. 2c–f, where the interfacial regions are indicated by the shaded areas. Representations of other interfaces are shown in Fig. S1–S5 of the ESI.† In the Li cases considered, we find the most stable interfaces are those formed with Li3N, displaying Wadhesion in the range of 0.8–1.0 J m−2, and σ ∼ 0.25 J m−2 (Fig. 2a). In contrast, the least stable interfaces are Li‖LiCl, which exhibit a low Wadhesion and high σ. In Na-based systems, the most and least stable interfaces are Na(110)‖Na2O(110) and Na(100)‖Na3P(001), respectively. Note that results of Wadhesion from eqn (5) (including strain contributions) in Fig. S7 and S8† appear similar in magnitude (and sign) to those obtained using eqn (4) (excluding strain) in Fig. 2. Therefore, we will refer to Wadhesion of eqn (4) and Fig. 2 throughout the remainder of the manuscript.Previous computational and experimental studies have suggested that Li‖Li2S, Li‖Li3P and Li‖LiCl interfaces are expected to form when argyrodite-Li6PS5Cl SE reacts with Li metal.14,15 A comparison of the Wadhesion (Fig. 2a) of these interfaces indicates that Li‖LiCl ≪ Li‖Li2S < Li‖Li3P. Li(100)‖Li3P(001) is expected to dominate the overall interface of Li metal and Li6PS5Cl, if similar quantities of Li2S and Li3P are produced upon decomposition. In the case of Li3PS4, predicted values of Wadhesion (Fig. 2a) suggest the coexistence of both Li‖Li2S and Li‖Li3P interfaces, consistent with prior literature studies.15,45,46 For LiPON, Wadhesion follows the order Li‖Li3P ≪ Li‖Li2O ≈ Li‖Li3N, implying that the Li-metal anode will mostly interface with Li2O and Li3N, also consistent with previous investigations.15,23,24,32,47
In most cases considered, the interfacial region (shaded regions in Fig. 2c and d) exhibits substantial atomic rearrangements upon full relaxation, with the exceptions being Li(110)‖Li3N(110) (Fig. S3†) and Li(110)‖LiCl(100) (Fig. S2†). A qualitative analysis of the interface models suggests that there is always a pronounced atomic reconstruction on the metal side of the interface as compared to that of the binary compound for all Li (and Na) interfaces. This is another confirmation that both Li and Na metals are softer than their binary compounds.44 Li (or Na) atoms originating from the metal side of the interfacial region form stabilising bonds with anion species from the compound side, with bond lengths that are similar to the bulk binary structures (see Table S5†).
In general, interfaces with a lattice mismatch smaller than a few percent can be considered as epitaxial, and the re-organization of atoms at the interface remains minimal compared to others with a significant lattice mismatch (≥5%). In some cases, we find large lattice mismatches when interfaces are formed between the dominant facets of binary compounds with the (100) or (110) surfaces of the metals (Li or Na). For example, the Li2S(111) facet displays a lattice mismatch of ∼14.2% with the Li(100) surface (Table S3†), indicating that such an interface may not occur practically. The lattice mismatch between Li2S(110) and Li(110) facets is lower (∼5.1%) and consequently exhibits a higher Wadhesion than Li2S(111)‖Li(100). The Li2S‖Li interface is likely to exhibit significant structural re-arrangement since the Li2S(110) facet does not occupy a significant portion of the Wulff volume of Li2S, and consequently results in a Li2S‖Li interface that is susceptible to delamination in real devices.
We also find that the surface terminations of binary compounds are crucial to determine the interfacial stability. For example, the Li(110)‖Li2O(111) interface has a small lattice mismatch of ∼1.73% (Table S3†). However, its fully relaxed geometry exhibits larger lattice distortion of the interfacial region as compared to other Li‖Li2O based interfaces (see Fig. S4†). This interfacial instability comes from the fact that the Li2O(111) surface is terminated with only Li atoms—this excess number of Li atoms and lack of anions near the interface region affects the chemical stabilization of the interface due to the lack of bond formation between Li (from the metal side of the interface) and O.
In Na systems, the Na(110)‖Na2S(110), Na(100)‖Na2S(111), and Na(100)‖Na3P(001) show reconstructions in the interfacial region similar to their Li analogues (Fig. 2c and S1c, d†). Additionally, we find the computed values of Wadhesion (and σ) to be lower (less positive) than their corresponding Li analogues (see Fig. 2a and b). Despite the low values of Wadhesion (<0.35 J m−2), both Na‖Na2S and Na‖Na3P may still occur at the Na-metal electrode. The Na‖Na2O interface has a significantly larger Wadhesion (∼0.65 J m−2) than Na‖Na3P (∼0.35 J m−2) and Na‖Na2S interfaces (∼0.30 J m−2).
4 Lithium transport at heterogeneous interfaces
To quantify ionic transport through heterogeneous interfaces, we have used the tracer diffusivity, D* of eqn (6) and (7). While we quantify only Li-ion transport across heterogeneous interfaces, similar qualitative trends might hold for Na-ion transport as well.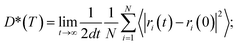 | (6) |
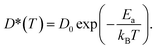 | (7) |
The calculated D* as a function of temperature for bulk binary compounds Li2S, Li3P and LiCl, with and without Li+ vacancies (Vac) are shown in Fig. 3. We have not included the case of LiCl without vacancies where we could only probe a limited number of diffusion events, which are insufficient to estimate accurate Li-ion diffusivities. The assessment of Li-ion transport in the bulk structures of Li2S, Li3P and LiCl is crucial to compare the transport across heterogeneous interfaces. Notably, our calculated Ea is in reasonable agreement with the experimental results (see Table S7†). For example, the calculated Ea in LiCl with Vac, (∼399 ± 5 meV), is qualitatively similar to the existing experimental value (∼510 meV).49 The computed Ea of Li3P with Vac (∼155 ± 7 meV) is in better agreement with the experiment value (∼180 meV)50 as compared to pristine Li3P (∼1061 ± 53 meV). On the other hand, the calculated Ea in pristine-Li2S (∼1573 ± 104 meV) is closer to the experimental value (∼1.5 eV at T > 800 K)51 than the calculated Ea in Li2S with Vac (∼313 ± 2 meV). Unsurprisingly, the introduction of Vac lowers the activation energies of both Li2S and Li3P as shown in Fig. 3. The calculated Ea of Li3P (with Vac) is lower than that of Li2S (with Vac), which is in agreement with previous studies showing superior Li-ion conductivity of Li3P over Li2S.52
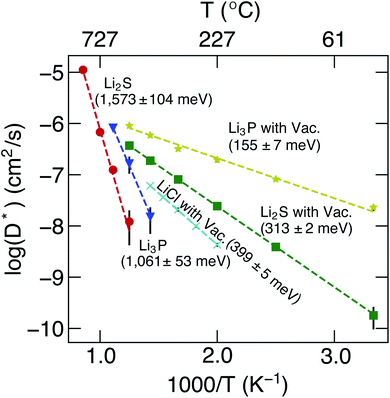 | ||
| Fig. 3 Arrhenius plots of Li+D* (in cm2 s−1) of bulk binary compounds from MTP-MD simulations. The activation energies, calculated from eqn (7), and the related error bars are provided as text annotations. Vac. stands for structures with a Li vacancy. | ||
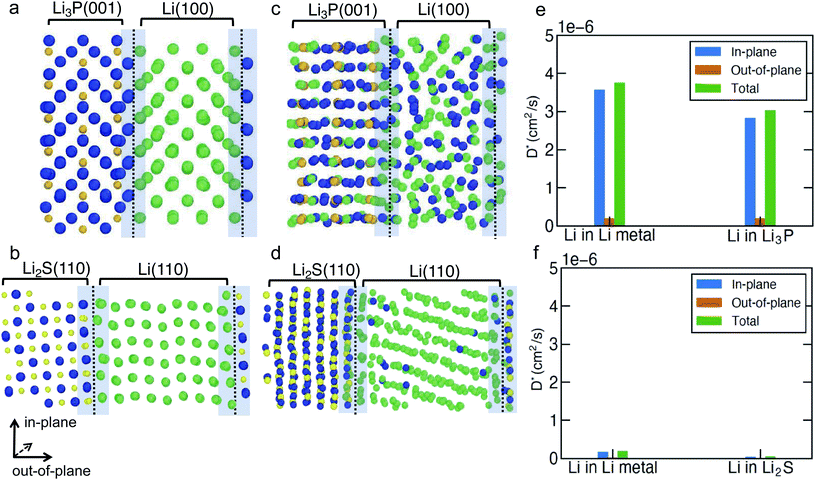
To investigate the Li-ion transport across the argyrodite-Li6PS5Cl‖Li-metal interface (i.e., the interfaces formed by the decomposition products of argyrodite with Li metal), we performed MTP-MD simulations on three interface models, namely, Li(110)‖Li2S(110), Li(100)‖Li3P(001) and Li(110)‖LiCl(100). The choice of these specific interfaces is motivated by their highest Wadhesion values (Fig. 2a) compared to other possible configurations using Li metal and the same binary compound. Although Li(110)‖LiCl(110) has the highest Wadhesion, we have chosen Li(110)‖LiCl(100) as the representative model because of its lower computational cost for AIMD simulations. We randomly introduced a number of Li+ vacancies (∼1.1%) into the interface region to calculate D*, since it is likely that heterogeneous interfaces will comprise highly defective materials, especially due to the in situ formed decomposition products. To distinguish Li+ belonging either to Li metal or binary compounds, we have labeled Li+ in Li metal as Li+ (metal) (green spheres in Fig. 4 and S9†), and Li+ in binary compounds as Li+ (binary) (dark blue spheres), respectively. Furthermore, the direction of Li-ion transport with respect to the interfacial plane, i.e., in-plane or out-of-plane, helps to qualify the nature of Li transport. Indeed, only Li ions diffusing out-of-plane will contribute to effective ion-transport across the interface. The predicted Li+-D* in both Li metal and binary compounds are summarized in Table S8.† The mean square displacement (MSD) plots used to derive Li+-D* are shown in Fig. S11–S13.†
In Fig. 4a–d and S9a, b,† we show the snapshots of different interfaces at 400 K during the MTP-MD simulations. In the following paragraphs, bulk is intended as the portion of the interface model which mimics the bulk structure. Initially, all interfaces exhibit modest atomic rearrangements near the interface region (violet shaded area). After ∼5 ns, significant Li+ displacement in both the metal and binary bulk along with Li+ exchange (i.e., there is a significant amount of Li+ (metal) diffusing into Li3P bulk and vice versa) can be clearly observed in Li(100)‖Li3P(001). This can be understood by the high values of Li+-D* (Fig. 4e) in both the in-plane (within bulk systems, 3.03 × 10−6 to 3.76 × 10−6 cm2 s−1) and out-of-plane (across the bulk systems, 1.93 × 10−7 to 1.99 × 10−7 cm2 s−1) directions in the Li(100)‖Li3P(001) system.
In contrast, in Li(110)‖Li2S(110) and Li(110)‖LiCl(100), we observe limited diffusion events and sparse exchange of Li ions during the MTP-MDs, which in turn is quantified by the low in-plane (4.86 × 10−8 to 1.89 × 10−7 cm2 s−1) and even lower out-of-plane (6.43 × 10−9 to 2.21 × 10−8 cm2 s−1) diffusivities in both systems. We find that for all interfaces, the out-of-plane components of both Li+ (metal) and Li+ (binary) are much smaller than their respective in-plane components, which indicate that the Li+ diffusion across the interface remains limited.
5 Discussion
A systematic study of the structures, interfacial energetics, and ionic transport properties of solid/solid interfaces is paramount for the development of solid-state batteries. Here, we have used a combination of accurate DFT calculations to explore the stability of interfaces arising from the decomposition of SEs with highly reducing alkali-metals, i.e., Li and Na. Upon identifying the thermodynamically stable heterogeneous interfaces, we trained MTPs based on accurate AIMD simulations, and in turn used such MTPs to run long duration (>10 ns) simulations to elucidate the Li-ion transport properties across specific interfaces.Although the morphology of real electrode‖SE interfaces can be far more complex than the interface models used here, our detailed atomistic models provide insights into the microscopic structure and mechanical stability of buried interfaces between SEs and alkali-metals. Still, one major limitation of our analysis is the finite number of interface models considered (20 in this study). Clearly, it is impossible to survey the whole configurational space of interfaces (potentially thousands11,16,34), and alternative strategies should be sought.
This study demonstrates that both surface orientations together with the surface terminations of binary compounds can largely affect the atomistic structures of interfaces (see Sec. 3), which in turn determine the interfacial lattice coherence, the thermodynamic stability of interfaces and the mechanical stability of such interfaces in LMBs and solid-state batteries. Several studies have revealed the crucial role played by surface terminations of SEs in determining the interfacial stability.11,53,54 For example, using first-principles calculations, Tateyama et al.53 reported that the low-energy Li7La3Zr2O12 (LLZO) surfaces lead to the chemical instability of the LLZO‖Li-metal interface.
Our analysis also suggests that Wadhesion (of eqn (4))—measuring the energy cost to separate two materials of a heterogeneous interface—is an important descriptor to evaluate the mechanical stability of interfaces.
In particular, Wadhesion should be large enough to avoid interface delamination.55 Yang et al. demonstrated that for common Li-metal‖SE interfaces, a Wadhesion > 0.7 J m−2 was required to prevent the formation of interfacial voids with the application of an external pressure of 20–30 MPa.29 Recently, Seymour and Aguadero28 have developed a “bond breaking” approach and derived that if Wadhesion > 2γ (where γ is the surface energy of Li or Na metal), the formation of interfacial voids with potential loss of contact during Li (or Na) stripping could be avoided. Our data suggest that among the Li-based interfaces (Table S4†), only the Li(100)‖Li2O(110), Li(100)‖Li3N(110) and Li(110)‖Li3N(110) interfaces satisfy this criterion. For interfaces with Na metal, only the two Na‖Na2O interfaces have a Wadhesion larger than twice the surface energy of Na(110) (or Na(100)).
The mechanisms of LiPON passivation of Li metal has been a matter of debate.23,24,32 Recent studies by Hood et al.23 have indicated that Li3N and Li2O are distributed uniformly on the surface of Li metal, while Li3P was not in direct contact with Li metal. In contrast, the study led by the Meng research group had suggested that only Li3N, Li2O and Li3PO4 could be present in the interfacial region formed between Li-metal and LiPON.24 Our results show that Li‖Li2O and Li‖Li3N interfaces have better interfacial stabilities than Li‖Li3P, which agree well with the experimental scenario that both Li2O and Li3N can be in direct contact with Li metal, while Li3P can only exist in the sub-interfacial layer.23
It has been established that argyrodite SEs are prone to decomposition against Li metal,14,52 with evidence of formation of Li2S, Li3P and LiX (with X = Cl, Br or I) at the potential of Li metal (i.e., 0 volts vs. Li/Li+). Among the interfaces formed between Li metal and the decomposition products of argyrodite Li6PS5Cl as SE, i.e. Li‖Li2S, Li‖Li3P and Li‖LiCl, Li‖Li3P has the largest value of Wadhesion (Fig. 2), suggesting that Li3P is more likely to form a stable interface with Li metal as compared to the other binary compounds. On one hand, the appreciable electronic conductivity of Li3P could lead to continuous reactions with Li metal and growth of the decomposing interphases.56 On the other hand, we have not considered the interfacial stability between binary compounds and Li6PS5Cl. Because these interfaces may not be mechanically stable, loss of contact between the SE and its decomposition products may also contribute to increased impedance.14,22 Indeed, it has been shown that the change in particle size of Li2S upon lithiation leads to loss of contact of the Li6PS5Cl‖Li2S interface and increases resistance.25
The Li+ conductivity (or diffusivity) determined in experiments largely depends on the sample quality, its crystallinity and experimental conditions. In particular, the presence of defects, grain boundaries, and lattice disorder all affect Li+ transport significantly.57,58 Therefore, here we have restricted our study to the crystalline structures (both decomposing products and interfaces), a situation where the MTP approach has been proven to be adequate to predict ionic transport properties.52,59,60 However, one major limitation of the current implementation of MTP is its lack of transferability from training within the binary bulk systems to being directly used in heterogeneous interfaces, requiring significant retraining of MTP with new training sets for each distinct interface. Therefore, a complete retraining of the MTP for each interface combination considered in this work is highly resource intensive, which pushes a comprehensive examination of Li (and Na) transport across all interfaces out of the scope of our work.
Assume that Li6PS5Cl reacts entirely with Li metal (at 0 volts vs. Li/Li+) according to eqn (8):14,15,52
| Li6PS5Cl + 8Li → 5Li2S + Li3P + LiCl | (8) |
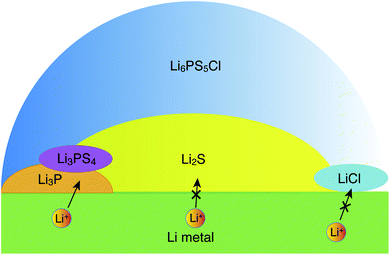 | ||
| Fig. 5 Schematic illustration of a possible structure of the interface between Li metal and argyrodite-Li6PS5Cl, as inferred from the interfacial energetics and Li-ion transport simulations. | ||
Our data suggest a lower stability of the LiCl‖Li-metal interface as compared to Li3P and Li2S, which indicates that LiCl may be in direct contact with Li metal over a negligible interfacial area. It appears that LiCl may not be directly involved in interfacial Li-transport. At voltages larger than 0.0 volts vs. Li/Li+ other decomposition products have been reported and observed, with the most prominent being Li3PS4,15,20,22 which may form in the sub-interfacial layers of the SE. Since Li2S is in molar excess over Li3P and LiCl, the Li-ion percolation in the proximity of the metal electrode‖SE interfaces will be largely limited by the lower ionic conductivity of Li2S.14 Furthermore, our explicit study on interfaces confirmed that only Li metal‖Li3P displays facile Li-ion transport (Fig. 4c) as signified by the black arrows in Fig. 5, while the interfaces of Li metal with Li2S and LiCl are resistive to Li-ion transport (Fig. 4 and S9†). Therefore, our qualitative results suggest that the decomposing interfaces are resistive to Li-ion transport as compared to the unreacted argyrodite SE.14 Note that the interfaces formed among different decomposition products (e.g., Li3P‖Li2S) or the decomposition products with a solid electrolyte (e.g., Li6PS5Cl) are also of crucial importance to Li-ion transport. Therefore, explicit studies of these interfaces using high-fidelity machine learned potentials are certainly needed.
6 Conclusion
Chalcogen-containing SEs show among the highest room temperature ionic conductivities (∼10−2 S cm−1), but their practical applications in LMBs are limited by the decomposing interfaces when in contact with Li metal. Similar constraints bottleneck the implementation of SEs in NIBs as well. Therefore, it is vital to understand the interfacial properties of these decomposing interfaces, either experimentally or theoretically. In this work, we have systematically evaluated the thermodynamic stability (of Li- and Na-systems) and Li-ion transport properties of multiple decomposing interfaces, by employing first-principles calculations and large-scale MD simulations based on MLPs. Our results reveal that the interfacial stability of decomposition products with alkali-metals is largely affected by the surface properties of the decomposition products. In general, we have observed that the interfaces formed between alkali-metal with argyrodite-Li6PS5Cl are resistive to Li-ion transport. Finally, our high-fidelity MLPs, trained explicitly for interfaces, shed light on the complicated interfacial transport properties, which will aid in the study and optimization of SEs in the future.7 Methods
7.1 First-principles calculations
DFT was used to approximate the energy contributions introduced in Sec. 2. The wavefunctions were described using plane-waves for the valence electrons together with projected augmented wave potentials for the core electrons as implemented in the Vienna Ab initio Simulation Package (VASP).61–63 The exchange–correlation contributions were treated within the generalized gradient approximation (GGA) as parameterized by Perdew, Burke, and Ernzerhof (PBE).64 The valence electron configurations for each element were as follows: Li: s1p0, N: s2p3, O: s2p4, Na: s1p0, P: s2p3, S: s2p4 and Cl: s2p5. The parameters we used for geometry optimization, surface energy and interfacial energetics calculations of the binary compounds and the constructed interfaces follow the MITRelaxSet, as in pymatgen.65 We used a plane wave energy cutoff of 520 eV and a k-point mesh generated using a k-point density of 25 Å−1. The total energy of each structure was converged to 10−5 eV per cell, and the geometry optimizations were stopped when the change in the total energy between two subsequent ionic steps was smaller than 10−4 eV.AIMD simulations were performed with the VASP to generate the initial training sets for the MTP-MD (see Sec. 7.2). A plane-wave energy cutoff of 400 eV and a Γ-only k-mesh were used. The canonical ensemble (NVT) was achieved using a Nosé–Hoover thermostat and a time step of 2 fs.66,67 Since previous studies have reported59,68 that the training set for MTP-MD should cover the whole configurational space and contain sufficient data so as to rarely invoke DFT calculations, we performed AIMD calculations at 1000 K for 14–20 ps (preceded by a temperature ramping of 2 ps), which resulted in training sets containing 7000–10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 configurations. The supercell sizes used for binary compound pristine structures were 4 × 4 × 4 for Li metal (128 atoms), 2 × 2 × 2 for Li2S (96 atoms), 3 × 3 × 3 for Li3P (216 atoms) and 3 × 3 × 3 for LiCl (216 atoms). We also studied vacancy-mediated diffusion by creating Li+ vacancies inside the Li metal and binary compounds.
000 configurations. The supercell sizes used for binary compound pristine structures were 4 × 4 × 4 for Li metal (128 atoms), 2 × 2 × 2 for Li2S (96 atoms), 3 × 3 × 3 for Li3P (216 atoms) and 3 × 3 × 3 for LiCl (216 atoms). We also studied vacancy-mediated diffusion by creating Li+ vacancies inside the Li metal and binary compounds.
Li+ vacancies were introduced by removing Li atoms and compensating for them with a uniform (jellium) charge background. Also, we created specific supercells that enabled a Li+ vacancy concentration of ∼0.8% for all compounds, which can arise at a synthesis temperature of 1200 K with a defect formation energy of 0.5 eV. Specifically, we used supercells of 4 × 4 × 4 with one Li+ vacancy for Li metal (127 atoms), 2 × 2 × 4 with one Li+ vacancy for Li2S (191 atoms), 3 × 3 × 3 with one Li+ vacancy for Li3P (215 atoms) and 3 × 3 × 3 with one Li+ vacancy for LiCl (215 atoms). To study Li+ transport across Li-metal‖decomposition product interfaces, we have created Li+ vacancies randomly in the interface region (shaded regions in Fig. 2 and 4), with a vacancy concentration of ∼1.1%. The interfaces that we chose were Li(110)‖Li2S(110) (520 atoms), Li(100)‖Li3P(001) (406 atoms) and Li(110)‖LiCl(100) (439 atoms).
7.2 Moment-tensor potential molecular dynamics
MTPs for the bulk and interfaces investigated in this study were trained using the machine learning of interatomic potentials (MLIP) package.69 In the training of the MTP potentials, several parameters need to be carefully selected to balance computational cost vs. accuracy of the trained potentials. During training, we have extensively tested the effects of weights on reproducing the ab initio total energies, forces and stresses, as well as the cutoff radius (Rcut) and the maximum level of basis functions (levmax) on the accuracy of energy and forces of trained MTP potentials. We concluded that a ratio of weights of 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 for energies, forces, and stresses, respectively, was appropriate to achieve good accuracy. Also, we found that a levmax of 10 and a Rcut of 5 Å, provided a tolerable level of fitting and validation errors in energies (<10 meV per atom) and forces (<30 meV Å−1), as documented in Table S6.†
1 for energies, forces, and stresses, respectively, was appropriate to achieve good accuracy. Also, we found that a levmax of 10 and a Rcut of 5 Å, provided a tolerable level of fitting and validation errors in energies (<10 meV per atom) and forces (<30 meV Å−1), as documented in Table S6.†
Since our MTPs were trained at high temperatures (∼1000 K), we further validated the transferability of the potentials to lower temperatures (i.e., 300–500 K). Specifically, we constructed validation sets by performing AIMD at 300 K/500 K for 4 ps (∼2000 snapshots for each temperature). The fitting and validation errors on the total energies in both binary compounds and interface models were always <10 meV, while the errors on forces were within ∼30 meV Å−1.
Upon training, MTP-MD simulations were performed using LAMMPS,70 where the MD simulations were performed in the temperature range of 300–1000 K at intervals of 100 K. A Nosé–Hoover thermostat was used to simulate the canonical ensemble (NVT).66,67 Long MD simulations were carried out for at least 10 ns with a short time step of 1 fs, preceded by a temperature ramping for 100 ps and an equilibration period of 1 ns to reach each target temperature. We also benchmarked our MTP D* data with AIMD results (see Table S9†). Specifically, we find that our MTP-MD calculated D* at 900 K and 800 K are in reasonable agreement with AIMD calculations at the same temperatures, signifying the high fidelity of our MTP-MD simulations. The trained moment tensor potentials for both binary compounds and interface models are publicly available in the repository https://github.com/caneparesearch/MTP-Li_interface_binaries.git.
7.3 Error analysis of lithium ion diffusivity
To attain a better estimate of the computed Li-ion diffusivity and activation energy, we have considered the statistical variance of tracer diffusivity, D*(T) and performed a weighted linear least squares regression, following He et al. methodology.71 In our Arrhenius plot, the weight of each point is determined by using the reciprocal of the variance of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D*(T). The variance of log
D*(T). The variance of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D*(T) is calculated based on the propagation of uncertainty using eqn (9):
D*(T) is calculated based on the propagation of uncertainty using eqn (9):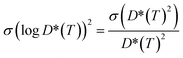 | (9) |
7.4 Validation of interfacial models
To verify the accuracy of our methodology in predicting interfacial properties, we have calculated interfacial energetics using two additional “constrained” optimization methods, namely, (i) “Fix-binary”: the middle layers of the decomposition product was fixed to mimic the bulk in-plane lattice constants of the binary compound, and, (ii) “Fix-metal”: middle layers of Li(Na) metal are fixed. The default method used throughout the work is when we do not constrain the middle layers of either binary compounds or the metal, referred to as “Fully-relaxed”. To test these scenarios, we chose Na(110)‖Na2O(110) for Na-based and Li(100)‖Li3P(001) for Li-based interfaces, respectively. The calculated Ef, with and without constrained optimization, are shown in Fig. S6.† Notably, Ef calculated using constrained optimization is ∼0.02 J m−2 and ∼0.1 J m−2 higher than that of Fully-relaxed for Li(100)‖Li3P(001), and Na(110)‖Na2O(110), respectively.Another typically used approach for calculating interfacial energy σ excluding the strain effect is to compute interface formation energy at varied slab thicknesses of Li (or Na) metal, and σ is obtained by taking the y-intercept of the extrapolated value of Ef.26 To test this approach, we have taken Li(100)‖Li3P(001) and Li(110)‖Li2S interfaces which are used later to investigate Li-ion transport. We fixed the in-plane lattice constants of the interfaces to that of the binary compounds, while varying the number of Li-metal slabs. We find that in both cases, the variations of Ef with different formula units of Li-metal slab (denoted as nLi) are not significant (see Fig. S10†). This indicates that the strain energy is not very sensitive to the system size. Using both approaches, the Li(100)‖Li3P(001) interface appears consistently more stable than the Li(110)‖Li2S interface.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
J. W., A. A. P. and P. C. acknowledge funding from the National Research Foundation under its NRF Fellowship NRFF12-2020-0012. The computational work was performed on resources of the National Supercomputing Centre, Singapore (https://www.nscc.sg).Notes and references
- J. B. Goodenough and Y. Kim, Chem. Mater., 2010, 22, 587–603 CrossRef CAS.
- W. Xu, J. Wang, F. Ding, X. Chen, E. Nasybulin, Y. Zhang and J.-G. Zhang, Energy Environ. Sci., 2014, 7, 513–537 RSC.
- D. Lin, Y. Liu and Y. Cui, Nat. Nanotechnol., 2017, 12, 194–206 CrossRef CAS PubMed.
- T. Krauskopf, F. H. Richter, W. G. Zeier and J. Janek, Chem. Rev., 2020, 120, 7745–7794 CrossRef CAS PubMed.
- X.-B. Cheng, R. Zhang, C.-Z. Zhao and Q. Zhang, Chem. Rev., 2017, 117, 10403–10473 CrossRef CAS PubMed.
- C. Fang, B. Lu, G. Pawar, M. Zhang, D. Cheng, S. Chen, M. Ceja, J.-M. Doux, H. Musrock, M. Cai, B. Liaw and Y. S. Meng, Nat. Energy, 2021, 6, 987–994 CrossRef CAS.
- K. Xu, Chem. Rev., 2004, 104, 4303–4418 CrossRef CAS PubMed.
- N. Yabuuchi, K. Kubota, M. Dahbi and S. Komaba, Chem. Rev., 2014, 114, 11636–11682 CrossRef CAS PubMed.
- P. K. Nayak, L. Yang, W. Brehm and P. Adelhelm, Angew. Chem., Int. Ed., 2018, 57, 102–120 CrossRef CAS PubMed.
- C. Delmas, Adv. Energy Mater., 2018, 8, 1703137 CrossRef.
- J. Haruyama, K. Sodeyama, L. Han, K. Takada and Y. Tateyama, Chem. Mater., 2014, 26, 4248–4255 CrossRef CAS.
- H. Tang, Z. Deng, Z. Lin, Z. Wang, I.-H. Chu, C. Chen, Z. Zhu, C. Zheng and S. P. Ong, Chem. Mater., 2018, 30, 163–173 CrossRef CAS.
- E. A. Wu, C. S. Kompella, Z. Zhu, J. Z. Lee, S. C. Lee, I.-H. Chu, H. Nguyen, S. P. Ong, A. Banerjee and Y. S. Meng, ACS Appl. Mater. Interfaces, 2018, 10, 10076–10086 CrossRef CAS PubMed.
- S. Wenzel, S. J. Sedlmaier, C. Dietrich, W. G. Zeier and J. Janek, Solid State Ionics, 2018, 318, 102–112 CrossRef CAS.
- W. D. Richards, L. J. Miara, Y. Wang, J. C. Kim and G. Ceder, Chem. Mater., 2016, 28, 266–273 CrossRef CAS.
- B. Gao, R. Jalem and Y. Tateyama, ACS Appl. Mater. Interfaces, 2021, 13, 11765–11773 CrossRef CAS PubMed.
- T. Famprikis, P. Canepa, J. A. Dawson, M. S. Islam and C. Masquelier, Nat. Mater., 2019, 18, 1278–1291 CrossRef CAS PubMed.
- T. Famprikis, Ö. U. Kudu, J. A. Dawson, P. Canepa, F. Fauth, E. Suard, M. Zbiri, D. Dambournet, O. J. Borkiewicz, H. Bouyanfif, S. P. Emge, S. Cretu, J.-N. Chotard, C. P. Grey, W. G. Zeier, M. S. Islam and C. Masquelier, J. Am. Chem. Soc., 2020, 142, 18422–18436 CrossRef CAS PubMed.
- L. Baggetto, R. A. H. Niessen, F. Roozeboom and P. H. L. Notten, Adv. Funct. Mater., 2008, 18, 1057–1066 CrossRef CAS.
- Y. Zhu, X. He and Y. Mo, J. Mater. Chem. A, 2016, 4, 3253–3266 RSC.
- V. Lacivita, Y. Wang, S.-H. Bo and G. Ceder, J. Mater. Chem. A, 2019, 7, 8144–8155 RSC.
- T. K. Schwietert, V. A. Arszelewska, C. Wang, C. Yu, A. Vasileiadis, N. J. J. de Klerk, J. Hageman, T. Hupfer, I. Kerkamm, Y. Xu, E. van der Maas, E. M. Kelder, S. Ganapathy and M. Wagemaker, Nat. Mater., 2020, 19, 428–435 CrossRef CAS PubMed.
- Z. D. Hood, X. Chen, R. L. Sacci, X. Liu, G. M. Veith, Y. Mo, J. Niu, N. J. Dudney and M. Chi, Nano Lett., 2021, 21, 151–157 CrossRef CAS PubMed.
- D. Cheng, T. A. Wynn, X. Wang, S. Wang, M. Zhang, R. Shimizu, S. Bai, H. Nguyen, C. Fang, M.-c. Kim, W. Li, B. Lu, S. J. Kim and Y. S. Meng, Joule, 2020, 4, 2484–2500 CrossRef CAS.
- C. Yu, S. Ganapathy, N. J. J. de Klerk, I. Roslon, E. R. H. van Eck, A. P. M. Kentgens and M. Wagemaker, J. Am. Chem. Soc., 2016, 138, 11192–11201 CrossRef CAS PubMed.
- N. D. Lepley and N. A. W. Holzwarth, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 214201 CrossRef.
- C.-T. Yang and Y. Qi, Chem. Mater., 2021, 33, 2814–2823 CrossRef CAS.
- I. D. Seymour and A. Aguadero, J. Mater. Chem. A, 2021, 9, 19901–19913 RSC.
- M. Yang, Y. Liu, A. M. Nolan and Y. Mo, Adv. Mater., 2021, 33, 2008081 CrossRef CAS PubMed.
- F. Mizuno, A. Hayashi, K. Tadanaga and M. Tatsumisago, Adv. Mater., 2005, 17, 918–921 CrossRef CAS.
- T. Hakari, M. Nagao, A. Hayashi and M. Tatsumisago, J. Power Sources, 2015, 293, 721–725 CrossRef CAS.
- A. Schwöbel, R. Hausbrand and W. Jaegermann, Solid State Ionics, 2015, 273, 51–54 CrossRef.
- P. W. Tasker, J. Phys. C: Solid State Phys., 1979, 12, 4977–4984 CrossRef CAS.
- K. T. Butler, G. Sai Gautam and P. Canepa, npj Comput. Mater., 2019, 5, 19 CrossRef.
- T. Einstein, Handbook of Crystal Growth, Elsevier, 2015, pp. 215–264 Search PubMed.
- R. Tran, Z. Xu, B. Radhakrishnan, D. Winston, W. Sun, K. A. Persson and S. P. Ong, Sci. Data, 2016, 3, 160080 CrossRef CAS PubMed.
- Y.-X. Chen and P. Kaghazchi, Nanoscale, 2014, 6, 13391–13395 RSC.
- W. C. Mackrodt, J. Chem. Soc., Faraday Trans. 2, 1989, 85, 541 RSC.
- Z. Liu, Y. Qi, Y. X. Lin, L. Chen, P. Lu and L. Q. Chen, J. Electrochem. Soc., 2016, 163, A592–A598 CrossRef CAS.
- A. Hashibon, C. Elsasser and M. Ruhle, Acta Mater., 2005, 53, 5323–5332 CrossRef CAS.
- R. Benedek, D. N. Seidman and C. Woodward, J. Phys.: Condens. Matter, 2002, 14, 2877–2900 CrossRef CAS.
- A.-L. Dalverny, J.-S. Filhol and M.-L. Doublet, J. Mater. Chem., 2011, 21, 10134 RSC.
- N. T. Taylor, F. H. Davies, I. E. M. Rudkin, C. J. Price, T. H. Chan and S. P. Hepplestone, Comput. Phys. Commun., 2020, 257, 107515 CrossRef CAS.
- Z. Deng, Z. Wang, I.-H. Chu, J. Luo and S. P. Ong, J. Electrochem. Soc., 2016, 163, A67–A74 CrossRef CAS.
- A. Kato, H. Kowada, M. Deguchi, C. Hotehama, A. Hayashi and M. Tatsumisago, Solid State Ionics, 2018, 322, 1–4 CrossRef CAS.
- Y. Xiao, Y. Wang, S.-H. Bo, J. C. Kim, L. J. Miara and G. Ceder, Nat. Rev. Mater., 2020, 5, 105–126 CrossRef CAS.
- J. Bates, Solid State Ionics, 1992, 53–56, 647–654 CrossRef CAS.
- A. V. Shapeev, Multiscale Model. Simul., 2016, 14, 1153–1173 CrossRef.
- R. Court-Castagnet, Solid State Ionics, 1993, 61, 327–334 CrossRef CAS.
- G. Nazri, Solid State Ionics, 1989, 34, 97–102 CrossRef CAS.
- F. Altorfer, W. Bührer, I. Anderson, O. Schärpf, H. Bill, P. Carron and H. Smith, Phys. B, 1992, 180–181, 795–797 CrossRef CAS.
- C. Wang, K. Aoyagi, M. Aykol and T. Mueller, ACS Appl. Mater. Interfaces, 2020, 12, 55510–55519 CrossRef CAS PubMed.
- B. Gao, R. Jalem and Y. Tateyama, ACS Appl. Mater. Interfaces, 2020, 12, 16350–16358 CrossRef CAS PubMed.
- H.-K. Tian, R. Jalem, B. Gao, Y. Yamamoto, S. Muto, M. Sakakura, Y. Iriyama and Y. Tateyama, ACS Appl. Mater. Interfaces, 2020, 12, 54752–54762 CrossRef CAS PubMed.
- A. Wang, S. Kadam, H. Li, S. Shi and Y. Qi, npj Comput. Mater., 2018, 4, 15 CrossRef.
- P. Gorai, T. Famprikis, B. Singh, V. Stevanović and P. Canepa, Chem. Mater., 2021, 33, 7484–7498 CrossRef CAS.
- V. Lacivita, N. Artrith and G. Ceder, Chem. Mater., 2018, 30, 7077–7090 CrossRef CAS.
- E. Sebti, H. A. Evans, H. Chen, P. M. Richardson, K. M. White, R. Giovine, K. P. Koirala, Y. Xu, E. Gonzalez-Correa, C. Wang, C. M. Brown, A. K. Cheetham, P. Canepa and R. J. Clément, J. Am. Chem. Soc., 2022, 144, 5795–5811 CrossRef CAS PubMed.
- C. Wang, K. Aoyagi, P. Wisesa and T. Mueller, Chem. Mater., 2020, 32, 3741–3752 CrossRef CAS.
- J. Qi, S. Banerjee, Y. Zuo, C. Chen, Z. Zhu, M. Holekevi Chandrappa, X. Li and S. Ong, Mater. Today Phys., 2021, 21, 100463 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, Comput. Mater. Sci., 2013, 68, 314–319 CrossRef CAS.
- S. Nosé, J. Chem. Phys., 1984, 81, 511–519 CrossRef.
- W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695–1697 CrossRef PubMed.
- I. Novoselov, A. Yanilkin, A. Shapeev and E. Podryabinkin, Comput. Mater. Sci., 2019, 164, 46–56 CrossRef CAS.
- E. V. Podryabinkin and A. V. Shapeev, Comput. Mater. Sci., 2017, 140, 171–180 CrossRef CAS.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- X. He, Y. Zhu, A. Epstein and Y. Mo, npj Comput. Mater., 2018, 4, 18 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2ta02202h |
| This journal is © The Royal Society of Chemistry 2022 |