Reversible assembly of nanoparticles: theory, strategies and computational simulations

Abstract

The significant advances in synthesis and functionalization have enabled the preparation of high-quality nanoparticles that have found a plethora of successful applications. The unique physicochemical properties of nanoparticles can be manipulated through the control of size, shape, composition, and surface chemistry, but their technological application possibilities can be further expanded by exploiting the properties that emerge from their assembly. The ability to control the assembly of nanoparticles not only is required for many real technological applications, but allows the combination of the intrinsic properties of nanoparticles and opens the way to the exploitation of their complex interplay, giving access to collective properties. Significant advances and knowledge gained over the past few decades on nanoparticle assembly have made it possible to implement a growing number of strategies for reversible assembly of nanoparticles. In addition to being of interest for basic studies, such advances further broaden the range of applications and the possibility of developing innovative devices using nanoparticles. This review focuses on the reversible assembly of nanoparticles and includes the theoretical aspects related to the concept of reversibility, an up-to-date assessment of the experimental approaches applied to this field and the advanced computational schemes that offer key insights into the assembly mechanisms. We aim to provide readers with a comprehensive guide to address the challenges in assembling reversible nanoparticles and promote their applications.

---

Denis Gentili

Denis Gentili is a researcher at the Institute for the Study of Nanostructured Materials (ISMN) of the Italian National Research Council (CNR) since 2018. He graduated with honors in Industrial Chemistry from the University of Bologna (Italy) in 2006 and received his PhD in Chemical Sciences at the same University in 2010. His current research interests encompass chemistry, materials science and biology, with a focus on the design, synthesis, and characterization of nanostructured functional systems that address the need to develop innovative technologies, as well as the rational engineering of nanomaterials to study and understanding their interactions with biological systems.

Guido Ori

Guido Ori is a CNRS researcher at the Institut de Physique et de Chimie des Matériaux de Strasbourg since 2014. He holds an MSc in Industrial Chemistry (2006, Univ. of Bologna) and a PhD in computational materials science from the Univ. of Modena and Reggio Emilia (2010). He deepened his expertise on hybrid interfaces at the CNRS-MIT joint laboratory “MultiScale Materials Science for Energy and Environment” in 2012–2014. He has a recognized expertise in combining different computational approaches and current topics of research span over FPMD modelling of complex materials and MLP for amorphous materials for energy and electronic applications.

---

1. Introduction

Nanoparticles (NPs) are extensively studied in different scientific fields because their multifaceted exceptional physicochemical properties can be manipulated through the control of size, shape, composition, and surface chemistry, making them suitable for a wide range of applications.^1–5 The significant advances in synthesis and functionalization have enabled the preparation of high-quality NPs that have found successful application in electronics as well as in nanomedicine and will have an increasing impact on our daily life, as recently demonstrated by the key role played by lipid NPs in the development of mRNA-based vaccines against COVID-19.^6–13

The technological application possibilities of NPs are further expanded by exploiting the properties that emerge from their assembly. Collective interactions of individual NPs resulting from their close proximity within the assembled structures lead to the emergence of otherwise inaccessible properties. For instance, the assembly of metal NPs shows unique optical, electronic, and magnetic properties that can be engineered for many technological uses.^14–20 Therefore, the ability to control the assembly of NPs not only is required for many real technological applications, but allows the combination of the intrinsic properties of NPs and opens the way to the exploitation of their complex interplay, giving full access to collective properties. In light of this, the assembly of NPs has been extensively addressed, both from the viewpoints of laboratory work and computational simulations. Many strategies have been reported to control the assembly of NPs through the manipulation of intermolecular interactions which occur between the designed molecules (or ligands) used to functionalize their surface or by the interaction of the external field and the NP core.^21–36 In addition, the considerable progress and knowledge gained in recent decades on nanoparticle assembly have enabled the implementation of an increasing number of strategies for reversible nanoparticle assembly, i.e., processes in which both assembly and disassembly are controlled. In addition to being of interest for fundamental studies, these developments further broaden the range of applications and the possibility of developing innovative devices using nanoparticles.

In this review, we focused on recent advances in experimental and computational developments in reversible nanoparticle assembly with a section on theoretical aspects, providing the reader with in-depth integrated guidance for future research studies and applications of NPs assemblies (see Scheme 1). The first section presents the theoretical formalisms proposed behind the assembly of NPs in terms of thermodynamics and kinetics metrics, with a dedicated focus on the role of reversibility. Starting with a brief presentation of the applicability and limits of the Derjaguin, Landau, Verwey, Overbeek (DLVO) theory developed for colloidal dispersions, we then cover the additional contributions proposed in subsequent theoretical extensions for improving the description of the interactions between NPs. Then, a dedicated section is devoted to a thorough description of the experimental strategies that have been proposed to achieve the reversible and controlled assembly of NPs. Interest in guiding the assembly of NPs into tailored extended structures has greatly fueled the development of strategies that allow control and manipulation of the interactions between them by a broad range of external stimuli. The most relevant examples for controlling assembly of NPs are reviewed and classified based on the biochemical, chemical or physical stimulus used to activate the assembly process and we then highlight the relevant applications proposed and envisioned. The following section describes the different computational methods that can be used and applied to gain an insightful understanding of the diverse variety of chemico-physical interactions at play during the reversible assembly of NPs. In particular, this review covers from density functional theory-based methods (DFT), targeting individual interactions involved between particles, to molecular dynamical simulations (classical and first-principles) and machine learning schemes aiming to untangle mechanisms involved in the whole assembly process. Finally, we summarize the decisive points for employing a cooperative approach in terms of theory, simulation and experimental workloads and, from a perspective viewpoint, we outline current challenges and potential areas where reversible assembly could play a pivotal role.

Scheme 1 A schematic representation of the theoretical, computational and laboratory strategies and their breakdown that are the focus of the present review.

2. Theory

The propensity for reversible assembly of nanoparticles in solution relies on thermodynamics and kinetics metrics.^37,38 In terms of thermodynamics, the interactions are governed by the total pair potential (V_tot) that is the result of a multitude of attractive and repulsive interparticle forces. When the pair potential is dominated by repulsive interactions, the NPs are stable in solution, while they are unstable and aggregate if attractive ones prevail. The interparticle interactions are due to core–core interactions as well as to ligand–ligand and ligand–solvent interactions and, therefore, their extent depends on the chemical and physical properties of both the NPs (core and surface ligands) and the medium and the combination of these will concur to the overall stability of NPs and their propensity for assembly.

The most widely applied theoretical models, which are extensions of the Derjaguin, Landau, Verwey, Overbeek (DLVO) theory developed to predict the stability of colloidal suspensions, estimate the V_tot between a pair of NPs as a function of their separating distance (r) through the sum of all relevant interparticle interaction contributions:^39–42

V_tot(r) = V_vdW(r) + V_ele(r) + V_hp(r) + V_ster(r) + V_dip(r), (1)

V_vdW and V_ele correspond to the van der Waals (vdW) and electrostatic potentials, while V_hp, V_ster and V_dip stand for the hydrophobic, steric and dipolar potentials. Table 1 summarizes and these interactions.

Table 1 Main attractive and repulsive interactions between NPs

Interaction	Type	x/DLVO^a	Origin
a DLVO: original; xDLVO: extended DLVO. b For like-charged NPs.
van der Waals	Attractive	DLVO	Interactions of electrons in particles and their dipolar and dielectric properties
Electrostatic	Repulsive^b	DLVO	Surface charges
Hydrophobic	Attractive	xDLVO	Decrease in solubility of the shell that protects the NP surface
Dipolar and charge-dipole	Attractive	xDLVO	Dipole moment, exchange interactions, dielectric properties of the medium, NP surface magnetization and effective NP surface charge
Steric	Repulsive	xDLVO	Exclusion of solvent molecules within the ligand interaction region, and deformation and compression of ligands

---

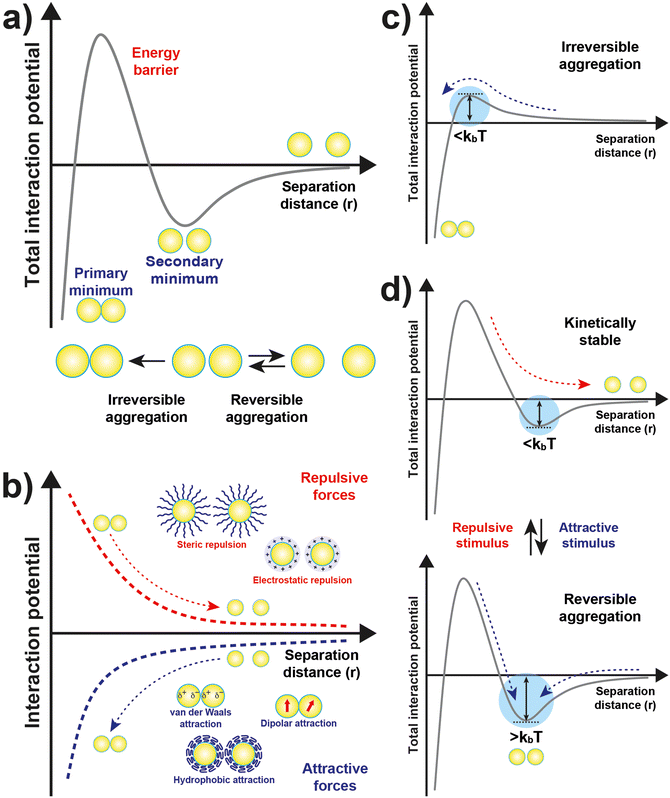
The original DLVO determines the stability of colloids by taking into account only van der Waals (V_vdW) and electrostatic (V_ele) interaction energies. The van der Waals force originates from interactions of electrons in particles and their dipolar and dielectric properties and, between similar particles in a medium, is always attractive. The electrostatic force between two interacting particles arises from the charging processes occurring on their surface in a liquid, such as by ionization or dissociation of surface groups and adsorption or binding of ions, and the following attraction of counter-charged ions from the bulk solution with the formation of electric double layer (EDL). The resulting electrostatic interaction is repulsive for similar particles (i.e., like-charged particles), thus favoring the stability of NPs in solution, or attractive between oppositely charged particles.^41,43,44 While electrostatic repulsion favors the stability of similar NPs in solution, electrostatic attraction of oppositely charged NPs have been exploited to promote their self-assembly into superstructure.^45–48 Although the classical DLVO theory provides a fundamental framework for rationalizing the stability of colloidal systems, the integration of the other contributions, besides the vdW and electrostatic forces, has been proposed in later extensions (xDLVO) to improve the description of nanoparticle surface characteristics and, consequently, the ability to predict the stability of nanoparticle systems. In particular, the integration of additional parameters is necessary because, while the long-range interaction forces occurring between NPs that are 50 nm in diameter or larger are accurately described,^49–52 DLVO theory fails to explain the interactions between NPs approaching closer a few nanometers in a liquid medium.⁵³ DLVO theory typically fails at distances approaching a few nanometers due to the intricate interaction coupling at play at such scale in addition to completely overlooking some very crucial effects (polarizability, NP size, dipolar among others).⁵³ The relevant contributions to the total interaction potential strongly depend on the system tested and, frequently, on top of V_vdW and V_ele, more than one additional contribution must be taken into account to accurately describe the interparticle interactions. Furthermore, the nonadditivity of all major classes of interactions at play between particles at the nanoscale also represents an entirely overlooked factor by the original DLVO.⁵³ Several alternative theories have been proposed over the years to overcome the omissions of the original DLVO theory (see the last section of the Theory section). As shown in eqn (1), the proposition of extensions of DLVO theory, which account for factors in addition to the vdW and electrostatic forces, allows precious insights into the overall comprehension and description of NP properties, medium properties and the interaction between them. As schematically shown in Fig. 1a, by superimposing the individual intermolecular and surface forces, an energy–distance curve is obtained that describes the behavior of the total interaction potential between the NPs as a function of their separation distance. The total pair potential results from the combination of all the attractive and repulsive forces that take place between NPs in a liquid, and while the former promote the aggregation of NPs, the latter favor the formation of stable dispersions in solution (Fig. 1b).

Fig. 1 Schematic representation of: (a) the total interaction potential between particles showing primary, secondary minimum and energy barrier; (b) attractive and repulsive forces and their contribution to the interaction potential; (c) irreversible aggregation in the primary minimum; and (d) reversible aggregation in the secondary minimum. The depth of the secondary minimum is qualitatively highlighted with a light blue circle with respect to the thermal energy (expressed as k_bT with k_b as the Boltzmann constant and T the temperature).

The total potential curve shows a primary minimum at short interparticle distances and a positive potential barrier at intermediate distances. However, there is also the possibility that a shallow secondary minimum is created at greater interparticle distances (Fig. 1a). The primary minimum is a rather deep potential well created at a short interparticle distance since the short-range nature of the van der Waals attraction force, which shows an inverse power law dependence on the distance, prevails over the repulsive forces. When NPs reach the primary minimum, their surfaces come into intimate contact and irreversible aggregation occurs. The well-defined maximum in the potential curve separates the primary and secondary minimum and indicates the barrier that needs to be overcome by the NPs for the interparticle interactions to become irreversibly attractive. Following the Brownian diffusion, which represents a ubiquitous source of kinetic energy and is related to the system's thermal energy, NPs must physically collide and their thermal energy (k_bT) must overcome the potential energy barrier to experience inelastic collision and form irreversible aggregates (Fig. 1c). Therefore, although the state of thermodynamic equilibrium may be with the particles in contact in the deep primary minimum, the higher the barrier due to repulsive interactions, the less NPs will be prone to aggregate irreversibly, but they will either remain stable in the solution or aggregate in the weaker secondary minimum. In particular, when the thermal energy is sufficient to drive the particles out of the secondary minimum, the NPs will be totally dispersed in the solution and the system is referred to as being kinetically stable (Fig. 1d, top). On the other hand, NPs aggregate when the depth of the secondary minimum prevails over the thermal energy, but the interparticle adhesion is much weaker than the primary minimum because the depth of the potential well is considerably shallower (Fig. 1d, bottom). It follows that, unlike in the primary minimum, nanoparticles in the secondary minimum are weakly connected without close contact and thus tend to form reversible aggregates.^{29,38,41,54–59} Starting from a stable NP/medium system (not-aggregated), in which long-range repulsive NP interactions exceed attractive short-range potentials (Fig. 1d, top), the aggregation process can be initiate by an external stimulus (named attractive stimulus in Fig. 1d) that leads to an increase of the depth of the secondary potential well since, in this way, NP assemblies stable enough not to be broken by thermal motion can be formed. On the other hand, NP assemblies can be disassembled by decreasing the depth of the secondary potential well through a different external stimulus (named repulsive stimulus in Fig. 1d) or by removing the stimulus that led to the assembly. However, it should keep in mind that stimuli do not act only on the secondary minimum, but also on the primary one and on the potential energy barrier. For example, nanoparticles stabilized by electrostatic repulsion can be aggregate in the secondary minimum by increasing salt concentration (i.e., increasing the ionic strength) and disassembled upon salt dilution. However, the increase of ionic strength also decreases the potential energy barrier, thus also favoring irreversible aggregation. Similarly, an excessive increase in kinetic energy could also favor the irreversible aggregation in the primary minimum.^55,60–64 For the above reasons, a good control of the chemical and physical properties of the system (NPs and medium) and, in turn, of the competing colloidal interactions, as well as a fine control of the external triggers and thermal particle motion is essential to avoid irreversible aggregation of NPs and, instead, achieve a reproducible reversible aggregation. Although the overall interaction potential between two NPs is usually intended as a sum of contributions of the individual interactions, as mentioned above, we have to point out that this assumption is not precisely accurate for NPs in a dispersion due to the coupled behavior of the NP and the medium.⁵³ Thus, xDLVO theories often describes only qualitatively the NPs stability, agglomeration tendency and assembly ability witnessed in experiments. The predictive power of xDLVO theories relies on properly assessing the type and number of the individual interaction potentials to be considered. Therefore, the accuracy of the chosen input parameters of the different xDLVO components is of paramount importance. Overall, xDLVO theories provide a simplified platform to analyze the individual contributions from each interaction.^23,41,65 As outlined in the following sections, robust efforts have been made in recent years to refine the assessment of the different interactions in play, enabling a clear improvement in the prediction of NP stability. In the following sections, we will illustrate and discuss recent developments and improvements that have been proposed for the individual interaction contributions for systems made of interacting NPs. A particular viewpoint is dedicated to aspects linked to the reversibility of NPs assembly. Regarding the general mathematical formulations proposed to describe the individual interaction contribution, the reader is encouraged to refer to the thorough reviews already available in the literature.^{38,41,54,66–68}

2.1. van der Waals interaction

The contribution of van der Waals interaction between two objects is usually split into a product of a size-dependent term and a size- and morphology-independent constant, known as the Hamaker (or Lifshitz) constant, that depends on the dielectric properties of the materials. However, for the case of nanoparticle systems, a not-negligible dependence of Hamaker constant to the size has been reported⁶⁹ and has been taken into consideration in a recent extension of the DLVO.⁷⁰ In particular, the Hamaker constant increases with decreasing NP diameter and, for instance, 13 nm citrate-stabilized AuNPs show a Hamaker constant 50% larger than that of bulk gold. However, the extent of size dependence of the Hamaker constant tends to decrease with increasing the NP diameter up to reach the bulk value. The effect of a size-dependent Hamaker constant is that larger attractive interactions between smaller NPs persist at longer separation distances with respect to those between NPs with radii greater than 50 nm.⁷⁰ Although the deviations in the attractive potential due to the size-dependent Hamaker constant may appear modest, it is essential to apprehend that the attractive potential decays slowly to zero at large separation distances. In contrast, the other contributions to the total interaction potential decay to zero at shorter separation distances. Thus, even a modest change in V_vdW can considerably affect nanoparticle stability because of the interplay between the different contributions at relatively long separation distances.⁷⁰

2.2. Electrostatic interaction

The electrostatic interaction potential (V_ele) between two NPs results from the long-range electrostatic forces that are established as a result of the EDL formation when particles are dispersed in a solvent. The overlap between EDLs of like-charged NPs leads to a repulsive electrostatic force that helps prevent their aggregation. As mentioned before, the interplay between electrostatic repulsion and attractive van der Waals forces forms the basis of the classical DLVO theory of colloid science. V_ele depends on Debye length and surface potential. The Debye length describes the thickness of the EDL and can be calculated as function of the ionic strength and dielectric constant of the solvent. The increase in ionic strength leads to a compression of the EDL ion cloud extension around the particle and thus a decrease of electrostatic interaction.⁴¹ The surface potential is estimated using the zeta potential, but this approximation is reasonable only for ionic strengths of the solution sufficiently high that the Debye length is small in relation to the separation distance. Therefore, the V_ele is significantly underestimated in low ionic strength conditions, i.e. the most common for solution containing nanoparticle. Wijenayaka et al. proposed to overcome the underestimation of surface potential by solving the Poisson–Boltzmann equation for the distribution of point charges that decay as a function of the radial distance from the charged nanoparticle surface.⁷⁰ In another example concerning the anisotropic self-assembly of charged AuNPs into chains, Zhang et al. improved the capability of the DLVO theory by assessing the electrostatic repulsion potential between NPs chain side by side and at either end of a NP chain. Based on this modified xDLVO model, the electrostatic interaction between elongated objects can be correlated with the NP surface charge density, NP radii and the number of NPs composing the NP chains. Within this formalism, the self-assembly of NPs in chains is promoted when the end chain potential is relatively weaker than side potential, thus strongly inhibiting the attachment of the NPs into the sides of newly formed NP chains. The final number of NPs per chain is controlled by the surface charge density, which can be tailored by external stimuli such as the ionic strength of the surrounding aqueous environment.⁷¹

Since the electrostatic interaction is strongly influenced by the presence of charged ligands on NP surface, the gradual replacement of these ligands with uncharged ones allows the modulation of their repulsive contribution. The increasing replacement of citrate ions onto AuNP surface with an uncharged oligo(ethylene glycol)alkanethiol ligand (MUHEG, Fig. 2a) leads to a decrease of the V_ele (Fig. 2b, solid lines). On the other hand, the electrostatic repulsion decreases to a considerably minor extent when citrate is replaced with a similar ligand (MUHEG–COOH, Fig. 2a) terminated with a negatively charged functional group (Fig. 2b, dashed lines).⁷² As discussed in the Section 3, this strategy can be exploited to modulate both the electrostatic and steric repulsions (see Steric repulsions forces section) between the NPs and, consequently, their assembly.

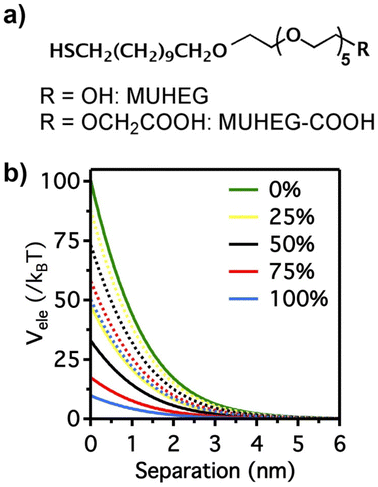Fig. 2 (a) Molecular structures of MUHEG and MUHEG–COOH. (b) Electrostatic potential as a function of AuNPs separation distance for AuNPs with increasing replacement of citrate ions (from 0 to 100%) with MUHEG (solid lines) and MUHEG–COOH (dashed lines). Figure adapted from ref. 72 (copyright 2017, Wiley-VCH).

2.3. Hydrophobic interaction

Hydrophobic interactions are grounded on the alteration of the structure of water molecules around interfaces and solutes and, for this reason, they have a critical role in various biological processes. It is recognized that hydrophobic interactions play a key role in nanomedicine applications since they directly influence the stability and bio-distribution of nanoobjects and because they affect the nanoobject's mode of action in a given environment.⁷³ The hydrophobic interactions result from a decrease in solubility of the shell that protects the NP surface, which can be accomplished either by the addition of a non-solvent or by temperature variation (see Sections 3.3 and 3.8). The hydrophobic interaction contribution (V_hp) to the total interaction potential between nanoparticles can be accounted considering three parameters: (i) the interfacial energy of the NP organic ligand protective layer in a specific solvent composition; (ii) the hydrophobic decay length parameter; and (iii) the hydrophobic–hydrophilic term (f) that describes the degree of hydrophobicity in the system (f = 1 for zero hydrophobicity and f = 0 when the system shows maximum hydrophobicity).⁷⁴

For example, Sánchez-Iglesias et al. proposed a theoretical description for the assembly process, triggered by the addition of water, of polystyrene (PS)-stabilized AuNPs dispersed in THF.⁷⁴ As shown in Fig. 3, in good solvent for PS chains (i.e. THF) the hydrophobicity is zero (f = 1) and the steric repulsion due to the polymer chains overcomes the attractive van der Waals interactions, resulting in a potential barrier that prevents the assembly of NPs. Following the addition of non-solvent (i.e. water) in the system, the polymer chains compress and attract each other and minimize the interaction to solvent molecules, leading to an increase of attractive hydrophobic interactions (f < 1). The potential barrier decreases with increasing the amount of non-solvent as the total pair potential is increasingly dominated by the attractive hydrophobic interactions, which are the main driving force behind nanoparticle assembly.

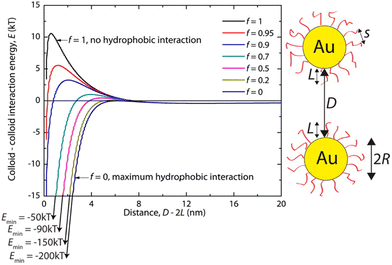Fig. 3 Effect of hydrophobic interactions on the total interaction potential of nanoparticle pair for different solvent compositions (f = 1 for pure good solvent, f < 1 for mixture of good and non-solvent). Reprinted with permission from ref. 74 (copyright 2012, American Chemical Society).

2.4. Dipolar and charge-dipole attractive forces

Among others, dipolar and charge-dipole attractive forces (V_dip) have also been considered one of the possible driving contributions of the total potential for promoting NPs assembly. V_dip of citrate-stabilized AuNPs arises from surface defects and nonuniform ligand capping that, yet, is usually negligibly small. However, the surface functionalization of AuNPs with alkanethiol-based ligands can dramatically enhance the dipole moment by introducing Au–S bonds (of the order of several k_bT).⁷¹ In certain cases, such short-range attractive forces may overcome the electrostatic repulsion, thus leading to the coupling of neighboring particles. For instance, Gentili et al. reported that successful progressive replacement of the electrostatic and steric repulsions between the AuNPs, due to the citrate ions adsorbed onto their surface, with dipolar interactions and enhanced steric repulsions by controlled ligand exchange with a hydroxyl-terminated oligo(ethylene glycol)alkanethiol promotes the formation of chain-like assemblies.⁷² Because of the anisotropic character of the dipolar interaction, the coupling of AuNPs is anisotropic. V_dip forces typically depend on the NPs separation distance, dipole moment, exchange interactions, dielectric properties of the medium and the effective surface charge of the NPs.^75–78

Regarding the magnetic properties (dipolar and exchange interactions and surface magnetization), their role on the stability and assembly of very small NPs can still be an issue.²³ At this scale, the surface magnetization becomes critical and depends on the magnetic order and thickness of the layer. Grzybowski et al. proposed the assessment of the dipole–dipole interaction of two separate magnetic NPs with fluctuating moments on the basis of the dipole moment of the individual NPs, the separation distance and vacuum permittivity can reach values of the order of 10k_bT for 15 nm iron oxide NPs at room temperature. In the case of static moments, the dipolar energy scales linearly with particle volume and the magnetic interaction becomes directional and the free energy is minimized when the particle moments are aligned.⁴⁴ Hence, magnetic nanoparticles tend to form chains or rings in suspension, and this tendency is strongly enhanced in the presence of a field.

2.5. Steric repulsions forces

Steric repulsion potential (V_ste) represents a further relevant contribution to the total potential deriving from the ligand–ligand and ligand–solvent interactions. The type and magnitude of steric forces at play between ligand-protected NPs are determined by the chemical nature of both the ligand and the solvent and, in the case of mixed ligands, the composition of the protecting shell. According to several works, the contribution of steric repulsions can be described by combining the osmotic and elastic interaction potentials.^70,72,79 The osmotic contribution comes into play when the interdigitation and overlap of the organic ligand layers protecting two approaching NPs lead to the exclusion of solvent molecules within the ligand interaction region, producing an increase of the local osmotic pressure and, consequently, the increase of repulsion between the NPs. Therefore, the osmotic contribution depends on the solvent properties, the ligand's volume fraction and the ordering degree of the ligand coverage. On the other hand, when NP pairs approach also lead to the deformation and compression of their ligands, providing an elastic contribution to the steric repulsions. Fig. 4a and b shows the evaluation of the role of theoretical ligand thickness (0.4, 0.8, and 2.0 nm) on the osmotic and elastic interactions potential as a function of the edge-to-edge separation distance between NPs. Both the osmotic and the elastic contributions vary as a function of the separation distance of the NPs and the thickness of the ligands that protect them, but the osmotic potential is both greater and decays more slowly with increasing the separation distance compared to the elastic one.⁷⁰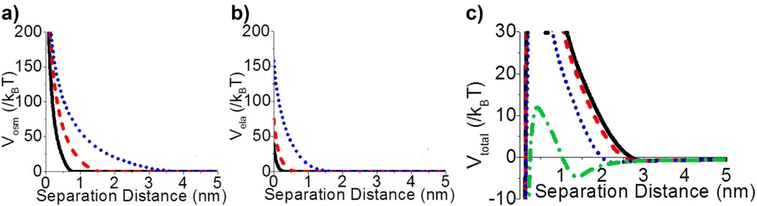

Fig. 4 Effect of ligand thickness at t = 0.4 (solid black line), 0.8 (red dashed line), and 2.0 (blue dotted line) nm on the (a) osmotic (V_osm) and (b) elastic (V_ela) interaction potentials as a function of edge-to-edge separation distances between two NPs. (c) Effect of ligand tilt angle, 0 (solid black line), 20 (red dashed line), 40 (blue dotted line), and 60° (green dashed and dotted line), on the total potential of a NPs pair functionalized. Adapted with permission from ref. 70 (copyright 2015, American Chemical Society).

It is worth note that, for NPs coated with well-ordered self-assembled monolayers (SAMs), ligand thickness depends on both the molecular length and the tilt angle of the surface-bound molecules relative to the surface normal. Most SAMs form with a significant tilt relative to the surface normal, meaning that the ligand length is, by itself, a poor approximation for the monolayer thickness. For example, ∼30° tilt angles are commonly reported for alkanethiol monolayers. However, the tilt angle is often neglected in many xDLVO calculations. The short-range height of the repulsive barrier between the first and second minimum of the total potential results particularly sensitive to the SAM thickness and the tilt angle of a monolayer often determines not only the barrier height but also it affects the separation distance at which this repulsive contribution decays to zero, thereby allowing for the possibility of a shallow attractive basin where steric repulsions decay to zero. Fig. 4c shows the evaluation of the total potential between a pair of NPs functionalized with a 1.5 nm ligand oriented on the surface at 0°, 20°, 40°, and 60° tilt angles. For tilt angles less than ∼40°, no secondary minimum is observed, and the NPs would need to overcome large (>30/k_bT) energy barriers for aggregation to occur. In contrast, however, NPs with a tilt angle of 60° show a secondary minimum where the NPs can be transiently trapped before overcoming the barrier that is ∼19/k_bT. Aggregation, therefore, can be kinetically hindered if the repulsive barrier is of sufficiently large amplitude.⁷⁰ Similar to what was discussed above for the electrostatic repulsion, the steric contribution to the repulsion between NPs is strongly affected by the nature and the composition of the protecting shell on their surface. As shown in Fig. 5, the V_ste of citrate-coated AuNPs drastically increases upon exchange of citrate molecules with oligo(ethylene glycol)alkanethiol ligands, such as MUHEG (solid lines) or MUHEG–COOH (dashed lines) (see Fig. 2a for molecular structures). Noteworthy, the increase of steric potential strongly correlates with the extent of ligand substitution.⁷²

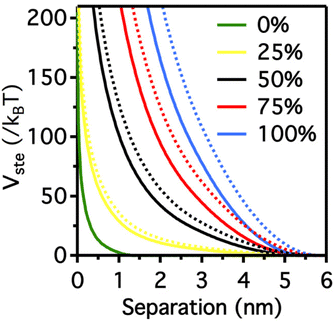Fig. 5 Potential as a function of AuNPs separation distance for AuNPs with increasing replacement of citrate ions (from 0 to 100%) with MUHEG (solid lines) and MUHEG–COOH (dashed lines). Figure adapted from ref. 72 (copyright 2017, Wiley-VCH).

2.6. Alternative theories beyond (x)DLVO

Although applying classical DLVO theory to interacting NPs can be improved by extending the original theoretical formulation with additional empirical parameters, it still fails over some fundamental aspects. This failure can be ascribed to the omissions of factors that required further or alternative theoretical developments to be properly described, such as: statistical thermodynamics approach,⁸⁰ fluctuations of surface polarization charge distribution,⁸¹ solvation shell reorganization,⁸² NP shape,⁸³ ion-specific effects⁸⁴ and multiscale collective effects become essential for accurate accounting of NP interactions.⁵³ Indeed, it becomes impossible to neatly decompose the potential of mean force (PMF) for the interaction of two NPs into separate additive contributions from these interactions, as performed in (x)DLVO, due to the coupled structural dynamics of neighbouring NPs and surrounding media. An alternative approach explored in the literature has been to work pursuing the assessment of the PMF between interacting NPs through atomistic simulations.^85–88 These simulations compute the actual PMF as a function of particle–particle distance directly by calculating all of the interatomic forces without using any smoothed models or superposition of assumed additive forces.

3. Strategies for reversible assembly of nanoparticles

The assembly of nanoparticles has been extensively addressed and many strategies have been reported.^{14,21,27–31,89} However, reversible assembly of NPs remains challenging due to their tendency to aggregate irreversibly. The assembly process of NPs is driven by intermolecular interactions, such as hydrogen bonding interaction, host–guest interaction, metal–ligand interaction, hydrophobic interactions and electrostatic forces, which occur between the designed molecules (or ligands) used to functionalize their surface or, as in the case of magnetically polarizable NPs, by the interaction of the external field and the NP core. Therefore, in general, the response of the NPs to an external stimulus, with the exception of the magnetic field, is not due to the NP core properties, but arises from the chemical/physical properties of the ligands exposed on their surface. The modulation of these interactions by means of physical or chemical stimuli, or by a combination of them, enables to control the assembly and disassembly processes of NPs. However, the assembly and disassembly processes of the same system can be triggered using different stimulus. For this reason and for the sake of simplicity, in this section we review the main strategies to achieve reversible assembly of NPs classified into categories based on the biochemical, chemical or physical stimulus used to activate the assembly process, except for a few examples. Scheme 2 summarizes the main strategies and in the following sections each approach is described and discussed considering the most relevant examples and applications.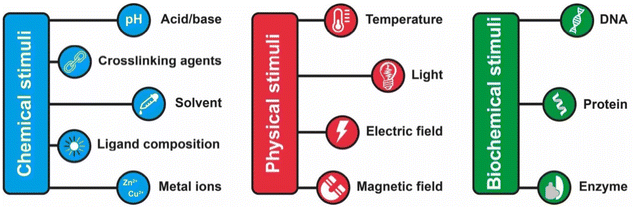

Scheme 2 Summary of the main chemical, physical and biochemicals stimuli employed to trigger the reversible assembly of nanoparticles.

As summarized in Table 2, almost all of the reviewed examples involve AuNPs because they are employed in the vast majority of reversible assembly studies but, in our opinion, this review may be also useful for the controlled assembly of other nanomaterials, such as polyoxometalates, silica nanoparticles and quantum dots,^90–92 as well as for newly emerging 2D materials^93–95 and biomaterials.⁹⁶

Table 2 Experimental strategies employed for reversible assembly of nanoparticles

Stimulus	Driving force	Particle type	Ref.
Biomolecular interactions	DNA base pairing	AuNPs, AuNRs, AgNCs	97–108
	Artificial protein pairing	AuNPs	109
	Streptavidin–biotin binding	AuNPs	110
	Lectin–carbohydrate binding	AuNPs	111
	Enzymatic activity	AuNPs, Fe3O4 NPs	112 and 113
pH	Modulation of the electrostatic forces	AuNPs, AgNPs, AuNRs, CdTe NPs, Fe3O4 NPs	114–126
	Conformational transitions of ligands	AuNPs, AuNRs	127–130
	Electrostatic or hydrogen bonding interactions of zwitterionic ligands	AuNPs, AgNPs	131–135
Solvent	Hydrophobic interactions	AuNPs, AuNRs, Janus Au-organosilica NPs	74 and 136–140
Metal ions	Chelation of metal ions	AuNPs, AuNRs	141–146
Crosslinking agents	Thiol–gold bonding	AuNPs	147 and 148
	Molecular recognition	AuNPs	149–152
Ligand shell composition	Modulation of electrostatic, steric and dipolar interactions	AuNPs	72
Light	Photoisomerization	AuNPs, Fe3O4 NPs	153–166
	Photodimerization	AuNPs	167 and 168
Temperature	Hydrophilic–hydrophobic phase transition of polymers	AuNPs, AuNRs, AgNPs, Fe3O4 NPs, Ag–Fe3O4 dimers	169–178
	Hydrophilic–hydrophobic phase transition of biopolymers	AuNPs, AuNRs	179–182
	Modulation of electrostatic repulsions	AuNPs	183
	Molecular recognition	AuNPs	184
Electric and magnetic fields	Electric field	Core–shell Au–Ag NPs, AgNPs, AuNPs	185–189
	Magnetic field	Fe3O4 NPs	190–194

---

3.1. Biomolecular recognition (interactions)

One of the most exploited strategies to program the assembly of NPs involves the use of biological macromolecules and relies on their inherent recognition properties. Among all, biospecific recognition of complementary DNA base pairing has been exploited to develop different strategies to drive and control assembly of NPs. The first example was reported by Mirkin et al. in 1996, who reported the rational and reversible assembly of two batches of AuNPs into macroscopic aggregates through their surface functionalization with non-complementary DNA oligonucleotides capped with thiol groups.⁹⁷ The addition of an oligonucleotide duplex containing sticky ends that are complementary to the two grafted sequences induces self-assemble of NPs into aggregates. Increasing the temperature above the dissociation temperature (T_m, melting temperature) of the DNA-duplex, the assembly process can be reversed and, thereby, can be modulated cyclically through changes of the temperature above and below the melting temperature of the hybridized DNA.^97–99 A similar approach has been reported for the reversible assembly of gold nanorods,¹⁰⁰ which are anisotropic nanoparticles widely studied for biological and medical applications,^195–197 silver nanocubes¹⁰¹ and gold nanoparticle clusters¹⁰² but, in these last two cases, nanocubes and clusters were conjugated with two complementary sequences, therefore assembly was carried out without the addition of a linking DNA duplex. It is worth noting that the exceptional understanding of the use of programmable interactions between oligonucleotides allowed Mirkin and collaborators to deduce a set of rules to control the self-assembly of superlattice nanoparticles.¹⁹⁸

As reported by Niemeyer et al., reversible assembly of DNA-conjugated AuNPs can be also accomplished using two complementary “fueling” oligonucleotides comprised of three stretches. As shown in Fig. 6, the first oligonucleotide (F_a) induces aggregation of NPs using two stretches complementary to the two batches of DNA-modified AuNPs (1 and 2). The subsequent addition of the second oligonucleotide (F_d) promotes the redispersion of the nanoparticles, as it is fully complementary to and hybridizes with the first oligonucleotide, exploiting the third, dangling-end, stretch which is not involved in the duplex DNA that interconnects the nanoparticles. The reversible switching of the nanoparticle aggregation can be therefore triggered by subsequent alternating addition of the two fueling oligomers.¹⁰³

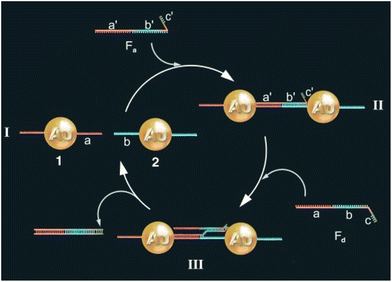Fig. 6 Schematic drawing of the reversible aggregation of DNA-modified AuNPs utilizing fueling oligonucleotides F_a and F_d. Figure adapted from ref. 103 (copyright 2004, Wiley-VCH).

Moreover, Sturla et al. more recently reported that similar results can be achieved using two complementary oligonucleotides without the need for third dangling-end stretch, but they highlight that only a perfectly complementary oligonucleotides can reverse the assembly of the nanoparticles, as a single base mismatch already compromises the disassembly process.¹⁰⁴ Also, protons can be used to trigger and control assembly/disassembly of DNA-functionalized AuNPs exploiting the pH-dependent formation of triple-helix DNA¹⁰⁵ or of intra-molecular DNA quadruplex (i-motif).¹⁰⁶ As the aggregation of AuNPs is accompanied by a color change, from red-to-pinkish/purple, the assembly of DNA-functionalized AuNPs by hybridization can be easily exploited to develop systems for selective colorimetric detection of polynucleotides.¹⁰⁷ In addition, since the use of AuNPs excludes photobleaching and cytotoxicity problems, their reversible assembly mediated by DNA hybridization has also proved useful for in vitro detection. Irudayaraj et al. exploited the reversible assembly of DNA-functionalized AuNPs to form a network of NP assemblies (<150 nm) onto cell surface for the specific detection of biomarkers by means of SERS mapping and hyperspectral SPR imaging. The strategy is based on pointer NPs, which are AuNPs functionalized with an antibody (anti-CD44 or anti-CD24) and a single stranded DNA (ssDNA), and enhancer NPs that are AuNPs functionalized with a ssDNA complementary to those used for pointer NPs functionalization and a Raman labels (4-mercaptopyridine or 4,6-dimethyl-2-pyrimidinethiol). As shown in Fig. 7a, the two pointer NPs bind to the respective marker (CD44 or CD24) on the cell surface and the subsequent addition of the two types of enhancer NPs leads to the formation of aggregates around the respective pointer NPs by DNA hybridization (Fig. 7b, i–iii). In this way, the formation of aggregates, which can be disassembled by raising the temperature (Fig. 7b, iv), prevents the nanoparticle uptake by cells and a Raman label is specifically paired to a biological marker (CD44 or CD24) which, therefore, can be selectively probed by SERS.¹⁰⁸

Fig. 7 (a) Schematic of the cell marker detection strategy. After targeting a cell surface receptor by a pointer particle, network forming nanoparticles are added to form the network structure. (b) Back scattering SEM images show the growth of network structures due to DNA hybridization. The temperature-dependent nature of network formation and its reversibility is illustrated. Each image shows the network structure after a hybridization time of (i) 5 min (inset: 3 min, scale bar = 100 nm), (ii) 20 min, (iii) 40 min, and (iv) after a temperature step above the hybridization melting point (45 °C). Reprinted with permission from ref. 108 (copyright 2011, American Chemical Society).

As we discuss below, other biological macromolecules have been exploited to address the reversible assembly of NPs, but we have to point out that their use has been considerably less than those of the DNA. For example, similar to the above-discussed examples that exploit DNA base pairing, artificial protein pairs with high mutual binding affinity have been employed to functionalize AuNPs and drive their assembly. The extent of aggregation can be controlled by changing the protein-particle stoichiometry and the aggregates are reversibly disassembled by addition of free protein, but it is not reported if the assembly/disassembly process can be repeated more than once.¹⁰⁹

Pérez-Luna et al. reported the reversibility of aggregation of biotinylated AuNPs, exploiting the high affinity of biotin with streptavidin. AuNPs were passivated with a carboxylic-terminated alkane thiol and, subsequently, functionalized with a ligand containing biotin and ethylene glycol groups to prevent nonspecific interactions that can adversely affect the reversibility of the assembly process, through a covalent coupling. The biotin content on the surface of the nanoparticles was adjusted by using a second ligand without biotin groups. The aggregation of biotinylated gold nanoparticles was driven by addition of streptavidin, while reversal of aggregation was accomplished by the addition of soluble biotin that, however, it was checked only after 80 days.¹¹⁰ Using a similar approach, Kataoka et al. exploited the carbohydrate-binding properties of lectin to control the assembly of lactose-immobilized AuNPs, which have been achieved through the functionalization of NPs with heterobifunctional poly(ethylene glycol) derivative containing both thiol and acetal groups. In particular, when exposed to a bivalent lectin that specifically recognizing the β-D-galactose residue, lactose-conjugated AuNPs exhibit selective aggregation whose extent is proportional to lectin concentration, allowing the system to be used to quantify the concentration of lectin. The aggregation process can be reversed by adding an excess of competitive ligand, i.e. galactose, and the dissociated NPs can be recovered by centrifugation and undergo a new aggregation by re-addition of lectin. This reversible process was confirmed to be repeatable through several cycles. Noteworthy, the passivation of the nanoparticle surface with heterobifunctional poly(ethylene glycol) derivatives allows the immobilization of biomolecules on the NP surface and, at the same time, improves the stability of nanoparticles.¹¹¹

A very interesting approach to control the assembly/disassembly of magnetic NPs, proposed by Bhatia et al., exploits not only the biomolecular recognition, but is also based on the biochemical activity of two antagonistic enzymes (tyrosine kinase/phosphatase).¹¹² As schematically shown in Fig. 8, magnetic NPs are modified with suitable peptides to become “substrates” that can be phosphorylated by a tyrosine kinase and, subsequently, dephosphorylated by a phosphatase. Meanwhile, a second batch of magnetic NPs are modified with peptides containing domains (Sh2) that recognize and bind the phosphorylated substrates. As a result, the phosphorylation of magnetic NPs by Abl tyrosine kinase in presence of ATP induces their assembly with the Sh2-functionalized NPs, while the subsequent dephosphorylation by addition of YOP phosphatase leads to disassembly. The assembly/disassembly processes of NPs can be assessed by monitoring changing of both hydrodynamic diameter and T₂ relaxation in MRI and allow indirect visualization of the activity of two specific and antagonistic enzymes.

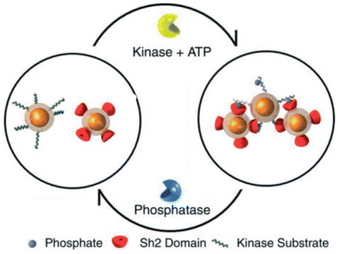Fig. 8 Schematic representation of reversible assembly of magnetic NPs based on the biochemical activity of two antagonistic enzymes. Figure adapted from ref. 112 (copyright 2007, Wiley-VCH).

Very recently, Klajn et al. have reported the reversible assembly of positively charged NPs exploiting the enzymes activity in combination with the ability of triply or more charged anions to induce the aggregation of charged NPs, as opposed to mono- or dianions. AuNPs functionalized with (11-mercaptoundecyl)-N,N,N-trimethylammonium bromide are assembled by the addition of deprotonated adenosine triphosphate (ATP; i.e. an anion with multiple charge), however the presence of a phosphatase enzyme leads to the ATP hydrolysis into adenosine monophosphate (AMP) and HPO₄²⁻, which are anions incapable of inducing NP aggregation and, therefore, the disassembly of NPs follows. As the assembly of NPs induced by ATP is faster than ATP hydrolysis, the assembly/disassembly process can be repeated for more than 20 cycles by injecting fresh ATP. However, while the assembly rate remains almost the same, the disassembly process becomes slower during the cycles due to lowering of the enzyme activity.¹¹³

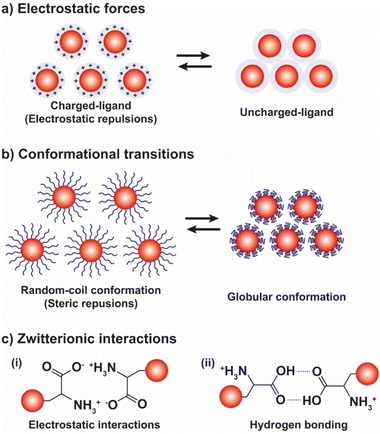
3.2. pH

The pH-controlled assembly of NPs exploits the protonation/deprotonation of functional groups exposed on the outer shell of the NPs and the arising attractive or repulsive interparticle forces, such as hydrogen bonding, electrostatic or hydrophobic interactions. Several pH-driven strategies have been proposed and the most common are schematically reported in the Fig. 9.

Fig. 9 Schematic illustration of the most exploited pH-driven strategies to control the assembly of NPs. pH variation induces reversible assembly of NPs through the (a) modulation of the electrostatic forces, (b) conformational transitions of ligands, and (c) the electrostatic (i) or hydrogen bonding (ii) interactions of zwitterionic ligands.

The most common pH-driven strategy to induce the assembly of NPs relies on the neutralization of the interparticle electrostatic repulsions through the protonation or deprotonation of functional groups such as carboxylate and amine groups (Fig. 9a). Upon neutralization of the functional groups, the electrostatic repulsion is significantly lowered and the assembly of NPs is driven by the predominance of attractive forces, such as van der Waals attraction and often by the establishment of intermolecular interactions between NP ligands (i.e., hydrogen bonding). For example, NPs passivated with carboxylic-terminated ligands can be assembled at low pH values, because of carboxylic acid groups form intermolecular H-bonds, and disassembled increasing the pH as to promote electrostatic repulsions by deprotonation and formation of negatively charged carboxylate anions.¹¹⁴ However, Grzybowski et al. highlighted that using “short” ionizable ligands, such as 2-fluoro-4-mercaptophenol, for the functionalization of NPs can lead to bistability and hysteresis during aggregation, i.e., NPs can exist in either dispersed or aggregated states at the same value of pH.¹¹⁵ On the other hand, the co-existence of a small ionizable ligand, such as 4-mercaptobenzonic acid (4-MBA), and oleylamine on AuNPs allows their reversible assembly into nanovesicles as a function of protonation/deprotonation of the 4-MBA.¹¹⁶ In addition, oscillatory aggregation of NPs can be observed when they are functionalized with ionizable ligands, such as 2-fluoro para-mercaptophenol and 12-mercaptododecanoic acid, and integrated with pH oscillator systems whose pH range includes the pK_a of the SAMs covering the NPs.^117,118 It should be noted that in the case of 2-fluoro-4-mercaptophenol, the authors argue that the assembly is driven by the dominance of van der Waals attractions upon protonation of the ligands.

In the studies reviewed up to here, the protonation/deprotonation of ligands has been achieved by adding acidic or basic solutions, however this can be also performed by addition of gases. Lu et al. reported that aggregation and redispersion of the magnetic NPs functionalized with 1,8-diaminooctane can be repeatedly induced by bubbling nitrogen and carbon dioxide sequentially, as they provoke the deprotonation and protonation of the amine groups, respectively.¹¹⁹

The protonation/deprotonation of ionizable ligands can be also used to control the assembly of NPs at the interface between two immiscible liquids by changing the pH. AuNPs and CdTe NPs functionalized with 3-mercaptopropionic acid (3-MPA) or 4-MBA assemble at the liquid–liquid interface (LLI) between water and heptane when the ligands are protonated and the NPs are uncharged (i.e., the pH solution is below the pK_a of the ligands). The increase of the pH above the pK_a of 3-MPA and 4-MBA leads to the deprotonation of the carboxylic acid groups and to the dispersion of the resulting negatively charged NPs in the aqueous phase. However, the reversibility of the interfacial assembly, for more than one cycle, has been experimentally demonstrated only for AuNPs coated with 4-MBA and NP size smaller than 10 nm, but also in this case further cycling of the pH leads to the coalescence of NPs.¹²⁰ Similarly, Turek et al. reported that the assembly of 12-mercaptododecanoic acid (MDDA)-functionalized AuNPs at the water/1,2-dichloroethane interface, at first achieved by salt addition and centrifugation, can be completely reversed once by changing the pH in the aqueous phase.¹²¹ Better results, in terms of reversibility of pH-driven assembly at the LLI, could be achieved through the functionalization of NPs with ion-pair complexes, in agreement with what was reported for assembly at the toluene–water interface of AuNPs functionalized with mercaptohexadecanoic acid and tetrapentylammonium chloride.¹²²

All the above-mentioned examples exploit the neutralization of ionizable functional groups introduced on the NP surface through the grafting with “small” organic ligands, but polymers can also be used successfully. For example, AuNPs capped with poly(4-vinylpyridine) (P4VP), which is as a water-soluble polymer, are monodispersed at low pH (∼3) due to the repulsive forces arising from the protonation of the pyridyl groups of P4VP while, at higher pH values, the P4VP chains collapse and the AuNPs aggregate.¹²³ Similarly, AgNPs coated with poly(acrylic acid) (PAA) can be assemble and disassemble through pH variation,¹²⁴ as well as, Janus magnetic NPs, which expose PAA and polystyrene sodium sulfonate (PSSNa) or polydimethylaminoethyl methacrylate (PDMAEMA) on their surface, form assemblies when the pH is lowered below the pK_a of the PAA as protonation of acid groups occurs. The formation of assemblies is reversible and their size can be controlled by changing the molecular weight of the grafted polymer.¹²⁵ In addition, the same research group reported that temperature-driven assembly of the Janus NPs can be achieved using a temperature-responsive polymer, such as poly(N-isopropyl acrylamide), instead of PSSNa or PDMAEMA, however, the Janus NPs lose their ability to reversibly aggregate to changes in pH because, according to the authors, the PNIPAM did not provide sufficient steric stabilization at low pH.¹⁹⁹

Contrary to the above described concepts, Wang et al. reported that the functionalization of gold nanorods (AuNRs) with 3-mercaptopropionic acid (MPA) or 11-mercaptoundecanoic acid (MUA) induce their assembly at pH values at which MPA and MUA are negatively charged.¹²⁶ However, in this case, albeit the thiol groups of the ligands bind to the surface of AuNRs and the carboxyl groups are exposed and can assist the assembly process, the cationic bilayer on the surface of AuNRs made of cetyltrimethylammonium bromide (CTAB) is not completely displaced by the functionalization with MPA and MUA. Therefore, the pH-dependent assembly/disassembly must be rationalized considering the presence of both ligands.

As shown in Fig. 9b, beside the interparticle electrostatic forces, the functionalization of NPs with suitable polymers, whose protonation/deprotonation induces chain conformational transitions, enables to control the aggregation processes by exploiting their hydrophobic interactions in aqueous environments. For example, AuNPs functionalized with poly-L-lysine (PLL) undergo assembly by increasing the pH because the deprotonation of the lysine residues results in the conversion of the dominant conformations of PLL, i.e., random coil and β-turn structures, into α-helix and β-sheet structures.¹²⁷ On the contrary, when AuNPs are functionalized with disulfide modified poly(L-glutamic acid) (PGA) their assembly occurs at low pH values, because of the protonation of the carboxylic acid groups leads to a secondary structure of the PGA dominated by α-helical structures. The increase of pH causes the deprotonation of the acid groups and, in turn, PGA becomes progressively negatively charged and undergoes the helix–coil transition, favoring the disassembly of AuNPs.¹²⁸ Exploiting the pH-dependent conformation change of the same polypeptide, Gupta et al. also reported the reversible end-to-end assembly of AuNRs through selective functionalization of their ends with the polypeptide chains.¹²⁹

Similar to what was discussed above, gases can also be employed to induce the conformational transition in polymer chains, for example polymers containing tertiary-amine side groups, such as poly(N,N-diethylaminoethyl methacrylate) (PDEAEMA), can switch from hydrophobic to hydrophilic upon reaction with carbon dioxide in water and vice versa by adding nitrogen. Consequently, AuNPs functionalized with thiol-terminated PDEAEMA can be dispersed or phase-separated in water by purging CO₂ and N₂, respectively. Note that this system was employed as a catalyst in the reduction of 4-nitrophenol into 4-aminophenol and its reversible phase separation and re-dispersion upon gas purging has been proven useful for the easy recovery and reuse of the NPs, without compromising their catalytic activity.¹³⁰

The reversible pH-depend assembly of NPs can be also pursued through the surface functionalization of NPs with zwitterionic ligands, such as amino acids and oligopeptides (see Fig. 9c). However, in this case, at least two different mechanisms of assembly are possible: (i) via electrostatic interactions between zwitterionic forms; and, (ii) the assembly by hydrogen bonding. As we discuss below, examples of both mechanisms are reported in literature, but a general rule cannot be easily deduced, rather the specific nature of the ligand seems to play a crucial role. For example, functionalization of AuNPs with homocysteine, which is a thiol-containing amino acid found in plasma, leads to their assembly at the pH range 5–7 through head-to-head electrostatic interaction of the zwitterionic forms, while the disassembly take places when the pH is increased up to ∼11, following the deprotonation of the amine groups, and accelerated by raising the temperature of the solution.¹³¹ On the other hand, the same research group reported that the hydrogen bonding of the carboxylic acid groups is mainly responsible for the assembly of AuNPs functionalized with the tripeptide glutathione.¹³² Peptides have been also exploited to control the assembly of silver NPs (AgNPs).¹³³ Similarly, the functionalization of gold and silver NPs with DL-penicillamine (PEN) or its amine protected counterpart, N-acetyl-DL-penicillamine (NAP), leads to their assembly by hydrogen bonding. In particular, as explained by the authors, the decrease of pH leads to the assembly of NPs following the protonation of the carboxylic groups and the consequent decrease in their stability by electrostatic interactions and the advent of hydrogen bonding interactions. Electrostatic repulsions are restored by increasing the pH, thus promoting the disaggregation process.¹³⁴

In all the above-mentioned strategies, the pH-induced assembly of NPs is achieved in a single specific pH range as well as for the disassembly. However, using zwitterionic ligands, assembly/disassembly of NPs should theoretically be possible at two different pH ranges, but the different intermolecular forces at play drastically limit the switchability. Very recently, He et al. reported that the functionalization of AuNPs with a thiolated derivative of guanidiniocarbonyl pyrrole carboxylate zwitterion (GCPZ, 1, Fig. 10a), which is a self-complementary molecule able to form extremely stable head-to-tail dimers by H-bond enforced ion pairing, enables their dual pH-induced reversible self-assembly in DMSO/water mixtures. As shown in Fig. 10b, increasing the pH of the mixture (from left to right), the thiolate GCPZ ligand form moves through the sequence protonated–zwitterionic–deprotonated. While intermolecular repulsive forces prevail for the protonated and deprotonated GCPZ forms, in the zwitterionic form the ionic hydrogen bond between the GCPZ groups and the hydrophobic effect favor their supramolecular pairing, as a results AuNPs assemble at neutral pH and disassemble by addition of base or acid. However, the authors showed that the dual pH-induced reversible self-assembly depends strongly on both the water content of the solvent mixtures and the GCPZ ligand density that was varied through co-functionalization with ligand 2 (Fig. 10a).¹³⁵

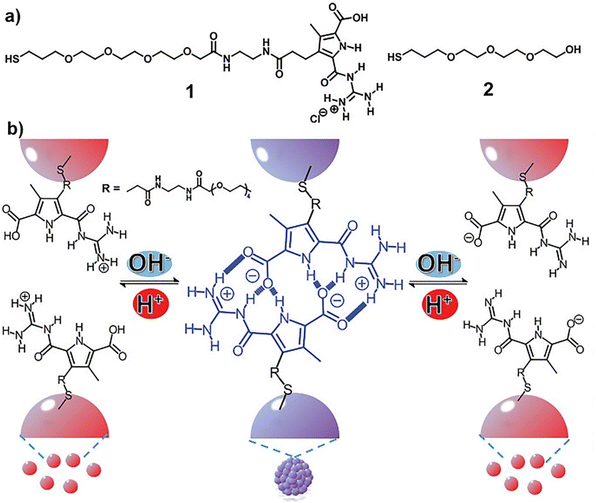Fig. 10 (a) Molecular structures of ligand 1 and 2. (b) Schematic representation of the dual pH-induced reversible self-assembly of AuNPs functionalized with 1. Figure adapted from ref. 135 (copyright 2020, Wiley-VCH).

Similarly, Liz-Marzán et al. exploited the “U-shaped” pH-solubility profile of a protein, i.e. bovine serum albumin (BSA), to control the assembly of AuNPs through changes in solution pH. AuNPs modified with BSA showed a pH-dependent behavior similar to pure BSA. At pH values below and above the isoelectric point (pI) of BSA, the AuNPs are respectively positively or negatively charged and, therefore, do not aggregate due to electrostatic stabilization. At pH = pI, the surface of AuNPs is not charged and, therefore, the lack of electrostatic repulsions leads to their aggregation. The pH-induced aggregation of the AuNPs coated with BSA is reversible and can be repeated multiple times, but, in the acidic pH range, the disaggregation is incomplete.²⁰⁰

3.3. Solvent

Similar to what happen for crystallization/precipitation of chemical compounds dissolved in a good solvent, i.e. a solvent in which they are highly soluble, by addition of a bad solvent, i.e. a solvent in which the desired compound is insoluble, the assembly of NPs can be induced through the addition of a bad solvent (or non-solvent) to NPs dispersed in a good solvent. The solubility of NPs is ruled by the nature of the ligands grafted onto their surface and, therefore, a fine tuning of their surface functionalization allows the controlled and reversible assembly through the addition of a non-solvent, as well as a control over the geometry and complexity of the assemblies. For example, as reported by Liz-Marzán et al., the addition of water (bad solvent) to a AuNPs stabilized with thiolated polystyrene and dispersed in tetrahydrofuran (THF) leads to form spherical aggregates consisting of nanoparticles with the same diameter (see Fig. 11a)⁷⁴ or two different diameters.¹³⁶ As revealed by UV-vis-NIR spectra and TEM images (Fig. 11b), PS-coated AuNPs in THF (1) are assembled into spherical aggregates upon addition of water (2) and the growth of NP assemblies can be controlled by adding a polymeric surfactant able to encapsulate them in micelle. Subsequent addition of THF leads to gradual disintegration of the assemblies (3), and complete disassembly is achieved after water removal (4). The assemblies and the distances between the particles increase as the length of the polymer chains increases, regardless of the diameter of the nanoparticles, while the volume fraction of metallic gold in the aggregates increases with increasing NP diameter and decreasing polymer chain length (Fig. 11c).⁷⁴ Noteworthy, highly reproducible shifts of the LSPR can be achieved through the confinement of AuNPs in permeable silica shells, thereby fixing the number of particles participating in the assembly process.¹³⁷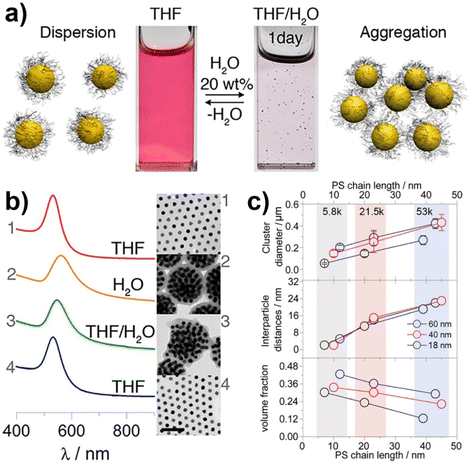

Fig. 11 (a) Schematic representation of nonsolvent-induced reversible assembly of PS-coated gold nanoparticles in THF and the consequent change of color solution. (b) UV-vis-NIR spectra and TEM images of PS-coated AuNPs in different mixture: (1) stable colloid solution in THF; (2) self-assembly, thermal treatment, and transfer into water maximize the redshift of the plasmon band; (3) gradual disassembly of the clusters by addition of good solvent; (4) recovery of the initial plasmon band position and colloidal stability of the building blocks in THF. (c) Average aggregate diameter (top), interparticle distance (middle) and nanoparticles volume fraction (bottom) as a function of length of the PS chains for 18, 40, and 60 nm gold nanoparticles. Figure adapted from ref. 74 (copyright 2012, American Chemical Society).

Using a different good solvent, i.e. dimethyl formamide (DMF), Kumacheva et al. reported that the addition of water to AuNPs coated with PS induces the assembly in linear chains or spherical aggregates or both as a function of the length of the polymer chains and amount of non-solvent. The disaggregation process can be achieved through the reduction of water below a critical concentration that depends on the molecular weight of the PS grafted on the NP surface but, while globular aggregates directly disassembly in individual NPs, the disaggregation of NP chains achieved with PS of high molecular weight (∼20 kDa) occurs via an intermediate globular state.¹³⁸

The addition of a non-solvent can be also employed to trigger the assembly of amphiphilic NPs at the liquid–liquid interface of a biphasic system. Duan et al. reported that the amphiphilic AuNPs obtained by the coating with polyethylene glycol and polymethyl methacrylate (PMMA), which confer solubility in water and in chloroform, respectively, can be assembled at the chloroform–water interface through the addition of hexane. Noteworthy, using a polymer having ionizable basic residues instead of PMMA, such as poly(2-(diethylamino)ethyl methacrylate), the assembly/disassembly process of NPs can be triggered by the pH variation.¹³⁹

Examples discussed so far exploit the NP surface functionalization with polymers and the addition of a solvent in which the NPs are insoluble to induce their assembly. A completely different approach to achieve the reversible assembly of NPs in dimers and trimers exploits the use of the Janus nanostructure to induce the directional assembly of NPs in combination with the different strength of interaction between the same ligand and the two materials composing the Janus nanoparticles. In particular, Janus gold-organosilica NPs can be assembled in dimers or trimers upon adding ethanol solution because of the selective removal of the ligand, i.e. CTAB molecules, bonded to the gold core, as organosilica possesses a stronger interaction with CTAB than gold. However, CTAB molecules on the gold surface are not completely removed, thus enabling the reversible disassembly of dimers and trimers by ultrasonication in CTAB aqueous solution. The ratio between dimers and trimers can be modulate by tuning the steric hindrance of the Janus NPs, i.e. through the ratio between the size of AuNPs and the size of organosilica.¹⁴⁰

3.4. Metal ions

The interest towards the assembly of NPs induced by the chelation of metal ions stems from the desire to develop simple techniques for the detection of small concentrations of aqueous heavy metal ions, rather than from the need to control the assembly process itself.¹⁴¹ Therefore, while there are many examples of detection of metal ions based on assembly of NPs, few research articles address the reversible assembly of NPs triggered by the chelation of metal ions. In particular, the reported studies exploit the chelating properties of carboxylate groups. For example, Mandal et al. were able to assemble peptide-functionalized AuNPs by chelation between carboxylate groups, which are exposed on the surface of NPs, and metal ions, such as Pb²⁺, Cd²⁺, Cu²⁺ and Zn²⁺ but, upon the addition of a competitive chelating agent, such as EDTA, the assembly process was completely reversed.¹⁴² Using a similar approach, Wang et al. exploited the carboxylic acid groups of poly(acrylic acid) to induce the assembly of poly(acrylic acid)-1-dodecanethiol-stabilized AuNPs.¹⁴³ More recently, Pillai et al. reported that a balance between the attractive and repulsive forces is needed to obtain the controlled aggregation of NPs induced by the chelation of metal ions.¹⁴⁴ As a proof of concept, the authors studied the assembly behavior of AuNPs functionalized with mixed self-assembled monolayer of 11-mercaptoundecanoic acid (MUA) and (N,N,N-trimethyl(11-mercaptoundecyl)ammonium chloride (TMA)). As schematically shown in Fig. 12a, the interparticle attractive forces due to the chelation of metal ions by the carboxylic acid groups of the MUA molecules lead to uncontrolled and irreversible aggregation of NPs. The regulation of interparticle forces through the balance between the attractive forces with the electrostatic repulsive ones, which are provided by the positively charged quaternary ammonium groups of the TMA molecules (Fig. 12b), allow the authors to achieve a controlled and reversible aggregation of AuNPs. However, in contrast to the previous examples, the disaggregation of NPs is not complete after the addition of EDTA, but the addition of sodium hydroxide is required. The use of mixed surface ligands has been recently exploited also by Su et al. to control the assembly of AuNPs by the addition of metal ions. In this study, the surface of AuNPs is protected by a mixture of tannic acid and sodium citrate. While the former ligand favors the assembly of NPs through metal–phenolic bonding following the addition of ferric ions, the latter limits assembly process by providing electrostatic repulsion. The disassembly of AuNPs, also in this case, is achieved by adding EDTA which is a stronger chelation ligand for ferric ions.¹⁴⁵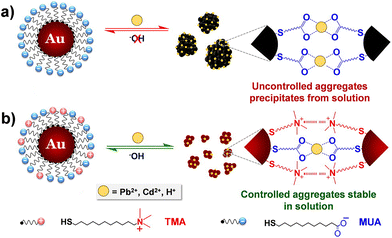

Fig. 12 Schematic representation of the concept of regulating interparticle forces to achieve controlled aggregation in charged NPs. (a) Homogeneously charged AuNPs functionalized with MUA and (b) heterogeneously charged AuNPs functionalized with a mixture of MUA and TMA. Reprinted with permission from ref. 144 (copyright 2016, American Chemical Society).

In the above-described cases, metal ions and competitive chelating agents are employed to induce assembly and disassembly of NPs respectively, but a reverse approach is also possible. For example, electrostatic interaction between EDTA and cetyltrimethylammonium bromide (CTAB) bilayer adsorbed on the surface of gold nanorods (AuNRs) has been exploited to induce their assembly. Noteworthy, while low concentration of EDTA induces the formation of end-to-end assemblies of AuNRs, higher concentrations of EDTA lead to sheet-like AuNRs structures. Upon addition of metal ions, EDTA detaches from the AuNRs and forms stronger complexes with metal ions, resulting in disassembly. Assembly and disassembly processes can be reversed for three times, before the irreversible aggregation of the AuNRs.¹⁴⁶

3.5. Crosslinking agents

Crosslinking agents are molecules with two (or more) functional groups able to either directly or indirectly interact with the surface of NPs. The direct approach, in which the crosslinking molecules simultaneously bind the “naked” surface of two NPs, has been poorly investigated to develop reversible aggregation processes of NPs and very few examples have been reported. Guarise et al. reported the reversible aggregation of AuNPs by using a blend of cleavable-dithiol and colloid-stabilizing thiol. Citrate-capped AuNPs were passivated using a blend of monothiol, which ensures stability, and a dithiol that contains carboxylate ester functions and promotes the aggregation of NPs. The addition of a cleaving agent, such as hydrazine, cleaves the ester bonds of dithiol leading to the disaggregation of NPs, however, further addition of dithiol causes the formation of the assemblies again.¹⁴⁷ Therefore, the reversibility of this strategy is based on alternation of the cleavage of a covalent bond and the introduction of fresh dithiol. Differently, Law et al. reported that AuNPs cross-linked by hexa(ethylene glycol) dithiol can be disassembled, in presence of citrate ions, by a brief treatment with ozone. The oxidizing action of ozone converts thiol groups, which are strongly bound to the gold surface, into sulfonates that are weakly bound and easily exchanged with free citrate ions in solution, favoring the NP redispersion. Similarly to the previous example, the reversibility of this process was achieve by consecutively adding dithiol and ozone.¹⁴⁸

By contrast to the above examples, the use of crosslinking agents that indirectly interact with the surface of NPs to control their assembly process is based on the modulation of noncovalent interactions. This strategy has been widely exploited using supramolecular systems. For examples, Jiang et al. proposed to exploit host–guest inclusion complexation between cyclodextrins and ditopic guests to control the self-assembly and disassembly of AuNPs. The β-cyclodextrin modified AuNPs aggregate together upon addition of a guest compound designed, thanks to the double-azobenzene structure, to act as bridge to link the NPs. The degree of the particle aggregation is proportional to the concentration of the guest compound and, above all, aggregates can be dissociated into discrete NPs by addition of α-cyclodextrin, which acts as competitive host by capturing the guest molecules from the cavity of the β-cyclodextrins on the particle surface. The aggregation/disaggregation process of β-cyclodextrin modified AuNPs can cyclically repeated by sequential addition of guest compound, re-addition of competitive host and subsequent recovery by centrifugation.¹⁴⁹ In another study, aggregation of AuNPs has been achieved through the charge transfer interaction between pyrenyl groups immobilized on their surface and a crosslinking agent containing two terminal dinitrophenyl groups. However, in this case, the disaggregation process was obtained by heating, thus exploiting temperature-dependent stability of the involved noncovalent interactions.¹⁵⁰

The above-mentioned studies exemplified that supramolecular systems can be suitably used to control the assembly/disassembly process of NPs, however, as proposed by Stoddart, Grzybowski et al., the formation of supramolecular host–guest complexes along with the design of molecular templates, which act as crosslinking agents, can be exploited to assemble NPs in precise predetermined spatial arrangements.¹⁵¹ The reversible assembly of AuNPs into homodimers, trimers, and tetramers has been reported exploiting the reversible formation of a pseudorotaxane,²⁰¹i.e. supramolecular entities consisting of linear guests threaded through and bound to macrocyclic hosts, between the cyclobis(paraquat-p-phenylene) (CBPQT⁴⁺) tetracationic cyclophane and the diethylene glycol-disubstituted tetrathiafulvalene (TTF-DEG). When the electrochemically active recognition unit, i.e. TTF, of the latter is in its neutral state, the TTF-DEG is threaded through the CBPQT⁴⁺ macrocyclic to form a 1 : 1 complex (pseudorotaxane) via noncovalent bonding interactions. However, the chemical or electrochemical oxidation of TTF unit generates the dicationic TTF²⁺ species that triggers the dethreading of the complex because of the arising coulombic repulsion with the tetracationic CBPQT⁴⁺ ring. These threading and dethreading events can be repeated numerous times through the oxidation/reduction of the TTF/TTF²⁺ unit by addition of chemical oxidants and reductants or electrochemically. The authors have synthesized CBPQT⁴⁺-based derivatives (1–3 in Fig. 13a), containing 2, 3 or 4 CBPQT⁴⁺ units, that act as molecular templates, while AuNPs were functionalized with a mixed monolayer of dithiolane derivatives 4 and 5 (Fig. 13a), the latter of which contains the TTF unit. As shown in Fig. 13b, AuNPs are assembled into dimers, trimers and tetramers when combined with the templates 1–3, which act as crosslinking agents through the formation of pseudorotaxanes between their CBPQT⁴⁺ units and the TTF units exposed on the NP surface. Noteworthy, the use of mixed monolayer of 4 and 5, to “dilute” the TTF units on the NP surface, allows the authors to prevent the formation of network-like NP aggregates. The assembly process can be reversed through the oxidation of the TTF units and, according to the reversibility of the pseudorotaxane formation, the authors claim that assembly process is fully reversible. Interestingly, the authors also demonstrated that this strategy can be extended to the reversible capture of gold and silver NPs with CBPQT⁴⁺-decorated polymers.¹⁵²

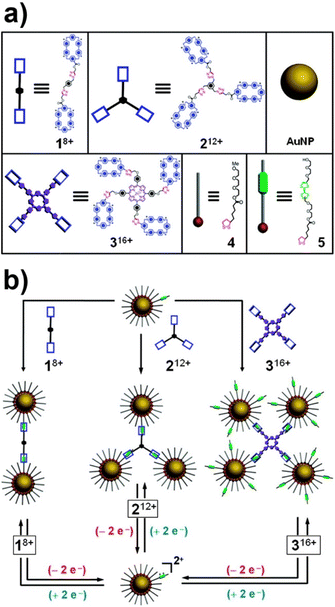Fig. 13 (a) Structural formulas of the CBPQT⁴⁺ dimer 1⁸⁺, trimer 2¹²⁺, tetramer 3¹⁶⁺, and the dithiolane-functionalized triethylene glycol 4 and TTF-DEG 5 (green station = TTF). (b) Schematic representation of the reversible assembly of AuNPs in homodimers, trimers and tetramers exploiting the reversible formation of pseudorotaxanes. Adapted with permission from ref. 151 (copyright 2009, American Chemical Society).

3.6. Ligand shell composition

Beside the chemical nature of the ligands that protect the NP surface, as discussed in the Theory section, the composition of the protecting shell in NPs coated with a mixture of ligands competes to determine both the type and the extent of interparticle interactions. It follows that the modulation of the ligand shell composition can be exploited to control both attractive and repulsive interactions between NPs. For example, Gentili et al. demonstrated that the electrostatic, steric and dipolar interactions of citrate-coated AuNPs can be modulated by controlled ligand exchange with a hydroxyl-terminated oligo(ethylene glycol)alkanethiol (MUHEG, see Fig. 2a for molecular structure) and exploited to achieve reversible assembly.⁷² As shown in Fig. 14a, citrate-coated AuNPs are stabilized by the prevalence of electrostatic repulsion. The weakly associates citrate ions to the AuNP surface can be gradual replaced with MUHEG molecules by exploiting the ability of thiol containing molecules to bind strongly to the gold surfaces. The replacement of citrate ions with MUHEG molecules leads to a decrease of electrostatic repulsion and an increase of steric repulsion and dipolar attractive interaction. However, for a percentage of MUHEG molecules on the NP surface less than 50–55% of that required for complete capping, the attractive interactions exceed the repulsive ones, resulting in the assembly of AuNPs (Fig. 14b). The extent of assembly is strictly correlated to the MUHEG coverage, but following further increases in ligand percentage the repulsive forces return to prevail over attractive interactions (Fig. 14a) leading to a gradual decrease in the volume of NP assemblies up to reach the complete disassembly with a coverage of 100% (Fig. 14c). As schematically shown in Fig. 14a and b, this process can be reversed through the addition of citrate-coated AuNPs because, exploiting the process of interparticle ligand exchange, a decrease of MUHEG coverage on the NPs surface is obtained. Noteworthy, the authors demonstrated that the AuNPs can be assembled and disassembled cyclically 6 times with alternating MUHEG coverage between 50 and 100%. Therefore, the modulation of interparticle interactions is driven by the extent of ligand substitution and allows the reversible assembly of nanoparticles. On the contrary, the gradual replacement of citrate ions with MUHEG molecules on the surface of silver NPs does not lead to their assembly but, by exploiting the ability of MUHEG to form protein resistant self-assembled monolayers, can be used to modulate the ability of NPs to adsorb proteins and, in turn, their biological activity.^202–204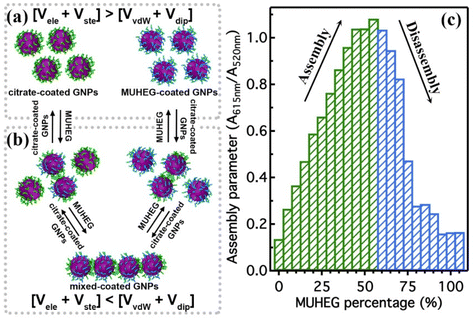

Fig. 14 (a) Schematic illustration of stable dispersions of AuNPs coated with 100% citrate or MUHEG, on the basis of the prevailing role of electrostatic and steric repulsions. (b) Schematic illustration of the citrate-to-MUHEG exchange process and the ligand-driven chain-like AuNPs assembly, promoted by the overcoming roles of vdW and dipolar attractive interactions. (c) AuNPs assembly parameter as a function of MUHEG coverage (the assembly parameter is defined as the ratio between the absorbance value at 615 and 520 nm). Figure adapted from ref. 72 (copyright 2017, Wiley-VCH).

3.7. Light

Among all stimulus to control the assembly process of nanoparticles, light is one of the most attractive because it is noninvasive and can be applied remotely and easily modulated, as also recently highlighted by Klajn and coworkers.²⁰⁵ Although optical trapping²⁰⁶ and thermophoresis^207,208 have been exploited to control the assembly of NPs, this strategy is mainly based on the functionalization of NPs with ligands containing photoresponsive groups that can be reversibly photoisomerized, between a conformation that favors assembly and one that favors the disassembly of nanoparticles (Fig. 15a and b), or photodimerized (Fig. 15c).

Fig. 15 Photoisomerization of (a) azobenzene and (b) spiropyran, and (c) photodimerization of coumarin.

Azobenzene is one of the most commonly used light-responsive functional groups as it undergoes a reversible conformation change from the planar trans to the folded cis isomer under ultraviolet light illumination radiation and reverts to the trans conformation under visible light radiation (Fig. 15a). For example, Grzybowski et al. reported the light-controlled reversible self-assembly of AuNPs through their surface functionalization with azobenzene dithiol ligands in methanol/toluene mixtures. Low-intensity UV irradiation causes trans–cis isomerization of dithiol molecules bound onto the surfaces of NPs and leads to their assembly into three-dimensional crystals. The authors argue that the assembly is mediated by dipole–dipole interactions that are established between particles since photoisomerization to cis conformation induces molecular dipoles on the azobenzene units. The micrometer-sized crystals are stable only under continuous UV-irradiation and can be disassembled by either thermally or upon exposure to visible light. However, to obtain a reversible assembly of NP, the number of azobenzene dithiol ligands adsorbed for NP and the methanol content must be precisely controlled, otherwise irreversible crystals are obtained.¹⁵³ The same research group has exploited the dynamic, light-controlled assembly/disassembly of AuNPs mediated by azobenzene thiol ligands, instead of dithiol ligands, both to develop nanoparticle-based inks for the fabrication of self-erasable and rewritable materials¹⁵⁴ and to control the catalytic activity of gold nanoparticles.¹⁵⁵ Exploiting the same light-induced attractive electric dipole interactions, Shibu et al. reported the reversible assembly of thiolated azobenzene-stapled Au₂₅ nanoclusters¹⁵⁶ and Klajn et al. were able to control the self-aggregation of magnetic nanoparticles (Fe₃O₄) capped with azobenzene-catechol ligands,¹⁵⁷ as well as their assembly onto hydrophilic silica NPs.¹⁵⁸ Noteworthy, this strategy was also used to achieve reversible formation of nanoflasks, i.e. the interstitial spaces between aggregated NPs, that provide confined environments in which polar molecules can be trapped and can undergo chemical reactions with increased rates and with stereoselectivities significantly different from those in bulk solution. Moreover, enantioenrichment of racemic mixtures has been obtained by exploiting the trapping selectivity of enantioselective nanoflasks achieved through the co-functionalization of the nanoparticles with a mixture of a photoresponsive ligand and a non-photoresponsive chiral thiol.¹⁵⁹

In sharp contrast to what was observed in the systems described above, Samorì et al. reported that AuNPs coated with azo-biphenyl thiol ligands are well dispersed when ligands are in their cis form, but they aggregate following the ligand photoisomerization to the trans conformation. However, in this case the used azobenzene-based ligand contains also two phenyl rings that enhance intermolecular p–p stacking interactions and, in turn, favor the interparticle interdigitation of ligands in trans conformation, thereby promoting aggregation and precipitation of the NPs.¹⁶⁰

Beside azobenzene, spiropyrans are light-responsive organic molecules that have been exploited to control the assembly of NPs because they can be isomerized between nonpolar, non-planar and closed spiropyran (SC) form, and the zwitterionic, planar and open merocyanine (MC) form by UV or visible-light irradiation (Fig. 15b). As the MC form can readily bind metal ions, AuNPs modified with spiropyran-terminated alkanethiols aggregate quickly and completely after UV light irradiation followed by the addition of Cu²⁺ ions because of the formation of coordination bond between the metal ions and the MC units on different NPs. The irradiation with visible light leads to the photoisomerization to the SP form and, in turn, to the release of chelated metal ions, resulting in the disassembly of AuNPs.¹⁶¹ Taking advantage of the concomitant color change, from red to purple, of the solution following the aggregation of the AuNPs, the same authors have applied this system to construct logic gates. As shown in Fig. 16a, an AND logic gate can be developed using UV light irradiation and the addition of Cu²⁺ ions as inputs, and the color change of solutions containing spiropyran-AuNPs as the output. The output is in state “0”, that is the solution is red, when at least one input is absent (input state = 0). While, in presence of both inputs (input state = 1), the AuNPs aggregate and the solution turns purple, resulting in an output in state “1” (Fig. 16d). The status of the output can be easily “read” either with the naked eye or by UV-vis spectroscopy (Fig. 16b and c). The AuNP-based AND logic gate can be reset to the initial conditions by photoconversion of MC to SP form by exposure to visible light and moreover, as reported by the authors, the same system can be implement to develop also different logic gates.¹⁶¹

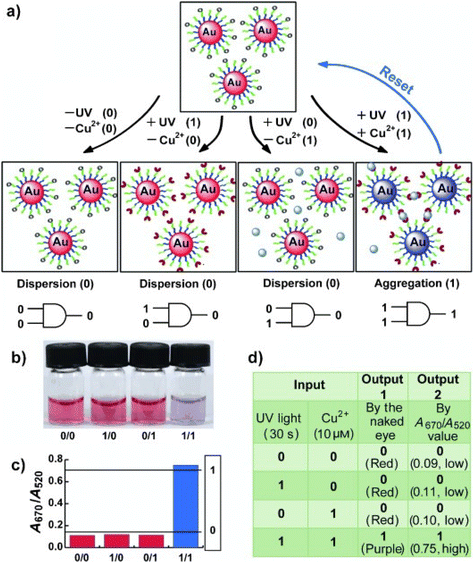Fig. 16 (a) Schematic representation of the spiropyran-AuNP-based resettable AND logic gate. (b) Photograph of AuNP solutions and (c) their corresponding UV-vis absorption. (d) A truth table of the AND logic gate. Figure adapted from ref. 161 (copyright 2011, Wiley-VCH).

Beside the ion-mediated assembly, the MC form has a large dipole moment due to its charge-separated state that leads to attractive intermolecular interactions without requiring the addition of metal ions. As shown in Fig. 17, Shiraishi et al. reported that UV-induced isomerization of SP to the highly polar MC isomer can be exploited to induce assembly of AuNPs modified with a thiol-terminated spiropyran dye. The resulting aggregates, whose size can be controlled with irradiation time, are stable and disassemble only by irradiation with visible light.¹⁶² However, the stability of aggregates strongly depends on the structure of the thiolated spiropyrans, in fact, using a ligand in which the spiropyran moiety is separated from the NP surface by a long alkyl linker, the disassembly process is rapidly accomplished removing the UV stimulus.¹⁶³ Note that the functionalization of NPs with photoresponsive groups and control of their assembly by irradiation can be also accomplished using photoresponsive polymers such as polymethacrylate and polymethylmethacrylate containing spiropyran units.^164,165

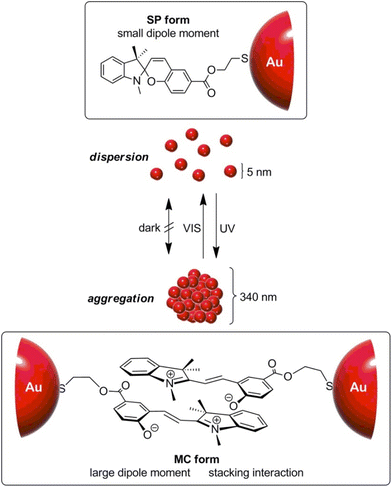Fig. 17 Schematic representation of the light-triggered reversible aggregation/dispersion of AuNPs modified with a spiropyran dye. Reprinted with permission from ref. 162 (copyright 2014, American Chemical Society).

Interestingly, Klajn et al. proposed a completely different and fascinating approach which exploits the ability of spiropyrans to modulate the solution pH with light to develop photoswitchable medium for the light-controlled assembly of non-photoresponsive, pH-responsive NPs. 11-Mercaptoundecanoic acid (MUA)-functionalized AuNPs in methanol are stable at low pH values and aggregate when the pH is increased, because of the strong interparticle interactions resulting from deprotonation of the ligands and, as shown on Fig. 18, following the addition of light-switchable molecules capable of releasing and capturing protons (spiropyran), the acidity of the medium can be modulated reversibly with visible light and thus control their assembly. The use of blue light minimizes the photodegradation, resulting in an excellent reversibility of NP assembly even after performing 100 disassembly–assembly cycles.¹⁶⁶ It is noteworthy that by trapping in a poly(ethylene glycol) (PEG) gel, the authors exploited the reversible color change associated with the assembly/disassembly process of NPs to create self-permanent images, i.e., patterns are created by irradiation of the gel through a shadow mask and disappear spontaneously when the light source is removed.¹⁶⁶

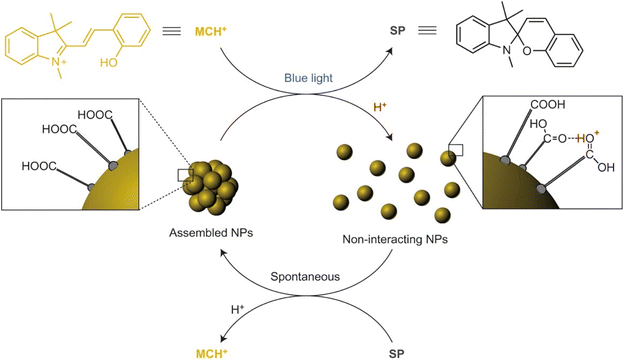Fig. 18 Schematic representation of light-controlled self-assembly of MUA-functionalized AuNPs in methanol that contains spiropyran molecules. Reprinted by permission from ref. 166 (copyright 2015, Nature Publishing Group).

So far, we have discussed the assembly strategies based on photoisomerization processes, however light-induced self-assembly of NPs can be promoted also through the interparticle photodimerization of ligands. As shown in Fig. 19, coumarin-functionalized AuNPs can be reversibly assembled inducing the interparticle photodimerization or the photocleavage of the coumarin groups exposed on their surface.¹⁶⁷ The extent of aggregation is not directly correlated to the number of coumarin molecules per nanoparticles, because further increase, compared to the optimal number of 11, favors the intraparticle photodimerization and leads to a drastic decrease of assembly. Noteworthy, while the assembly process requires light irradiation at 365 nm for 72 h, the disassembly takes place after 1 h exposure to 254 nm light, but oxidation of thiol groups when subjected to 254 nm UV light irradiation limits the reversibility to four assembly–disassembly cycles. However, as recently reported, this drawback can be overcome through the use of polymers instead of thiol-based small molecules to decorate the surface of AuNPs with coumarin units.¹⁶⁸

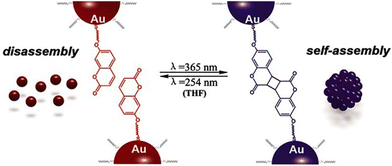Fig. 19 Schematic representation of the light-induced reversible assembly of AuNPs mediated by the photodimerization of coumarin groups. Figure adapted from ref. 167 (copyright 2015, Wiley-VCH).

3.8. Temperature

Temperature offers a simple and effective trigger to control the assembly of NPs, however, as in the case of triggering by light, the introduction of a thermosensitive moiety is usually needed. For example, Li et al. developed thermosensitive AuNPs through the anchoring of a temperature-responsive polymer, i.e. poly(N-isopropylacrylamide) (PNIPAM), on their surface.¹⁶⁹ In particular, PNIPAM in aqueous solution undergoes a coil-to-globule transition when temperature is increased above its lower critical solution temperature (LCST, ∼32 °C) due to the change of polymer chains from hydrophilic to hydrophobic behavior, resulting in a clear-opaque transition of the solution. When temperature of PNIPAM-coated AuNPs is increased above the LCST, the nanoparticle surface switches from hydrophilic to hydrophobic because of intrachain collapse of PNIPAM, leading to the aggregation of AuNPs in water and the formation of an opaque suspension which does not precipitate (Fig. 20). The transparent-to-opaque transition of thermosensitive AuNPs is sharp and reversible following heat–cool cycles between 35 and 25 °C.¹⁶⁹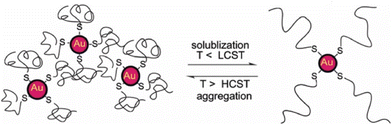

Fig. 20 Schematic illustration of reversible assembly of PNIPAM functionalized AuNPs following the temperature-dependent coil-to-globule transition of PNIPAM. Reprinted with permission from ref. 169 (copyright 2004, American Chemical Society).

Similar to what we have discussed in the section dedicated to the solvent induced strategies, the selective functionalization of AuNRs ends with thiol-terminated PNIPAM allows their end-to-end assembly by heating the solution above LCST. However, in this case, the assembly process can be also photothermally-driven by exploiting the ability of AuNRs of absorb light and release energy as heat through non-radiative energy transfer when they are irradiated at the wavelength close to the longitudinal plasmon band.¹⁷⁰ Similarly, reversible assembly of heterodimers, composed of silver (Ag) and magnetite (Fe₃O₄) nanoparticles,¹⁷¹ and AuNPs¹⁷² capped with PNIPAM was achieved by exploiting the plasmonic photothermal effect of silver and gold NPs, respectively. The aggregation temperature of linear thermosensitive polymer exhibits little dependence on the structural parameters, such as molecular weight, therefore the transition temperatures can only be modulated in a narrow temperature range. However, this limit can be overcome using hyperbranched thermosensitive polymers, which showed a stronger dependence of phase transition on their molecular weight,¹⁷³ or using copolymers containing thermoresponsive and hydrophilic units, as their LCST can be controlled through the proportion of hydrophilic units.^174,175 Moreover, the transition temperature of thermoresponsive polymers can be also affected by the nanoparticle size, in fact, the decrease of the aggregation temperature of AuNPs coated with a statistical polymer constituted by ethylene oxide and propylene oxide groups was observed with increasing their size because, according to the authors, the decrease of surface curvature leads to a compression of the polymer chains and, in turn, a decrease of their hydration.¹⁷⁵ The same group reported that the addition of a free copolymer, which possesses the same chemical composition as the polymer grafted on AuNPs, allows them to control the extent of aggregation through the copolymer-particle ratio, but at temperatures above both the temperature of aggregation and at the critical micellization temperature of the copolymer.¹⁷⁶ Similar to AuNPs, Davis et al. reported the thermally driven aggregation of PNIPAM-coated magnetic nanoparticles. In this case, the copolymerization of PNIPAM with a dye-containing acrylate monomer allows monitoring of the temperature-dependent aggregation of the NPs through their fluorescence properties, as the aggregation of nanoparticle above the LCST of the polymer leads to concomitant dye aggregation and fluorescence quenching. Moreover, the temperature-induced aggregation of magnetite nanoparticles leads to an enhancement of NMR relaxometric behavior, i.e. shortening of T₂ relaxation times, above the LCST transition temperature of PNIPAM.¹⁷⁷ It is worth noting that, when temperature-responsive NPs are prepared through the ligand exchange with temperature-responsive polymers, the electrostatic repulsions due to the residual pristine ligands on the surface of NPs, such as citrate ions on AuNPs, can prevent their assembly ever at temperatures above the LCST and the presence of salt in solution becomes crucial.¹⁷⁸

Similar to what happen with polymers, biopolymers exhibit a reversible hydrophilic–hydrophobic phase transition in response to temperature variation, which can be exploited to develop strategies for the reversible assembly of NPs in aqueous solution. Elastin-like polypeptides (ELPs) are thermally responsive biopolymer characterized by the sequence Val–Pro–Gly–Xaa–Gly (where Val = valine, Pro = proline, Gly = glycine, and Xaa = any amino acid except proline) that, when heated, undergo a transition from hydrophilic to hydrophobic conformation following the formation of hydrogen bonds between the valine residues. Nath and Chilkoti reported the reversible assembly of AuNPs through their surface functionalization with mercaptoundecanoic acid and subsequent adsorption of ELP. Upon raising the temperature, the adsorbed ELP undergoes an intramolecular hydrophilic–hydrophobic transition, resulting in aggregation of NPs that can be reversed by cooling. Noteworthy, the authors reported that AuNPs with adsorbed ELPs show greater reversibility than AuNPs with covalently immobilized ELPs.¹⁷⁹ Interestingly, the ability of nanoparticles, such as AuNRs, to convert energy from light to heat energy due to surface plasmon resonance activity, along with the temperature-responsive properties of ELPs can be exploited to generate optically responsive nanoparticle¹⁸⁰ and, moreover, Kaplan et al. reported that addition of functional peptide modules, such as silk-like polypeptides, to ELPs has a stabilizing effects on the regulation of aggregate size and pattern.¹⁸¹ The preparation of polypeptides involves genetically encoded recombinant methods and can be nontrivial, however, van Hest et al. reported that also AuNPs capped with a single repeat unit of thiol-functionalized VPGVG peptide show thermoresponsive properties. In this case, because of the end-group of the VPGVG ligand bears a free carboxylic acid, the transition temperature can be modulated by varying the pH of the solutions. In fact, in neutral solutions the carboxylic acid moieties are deprotonated and the AuNPs functionalized with the VPGVG peptide show no thermal response, while lowering the pH they are gradually protonated and the nanoparticle surface becomes more hydrophobic, enabling their temperature-dependent assembly.¹⁸²

The above-mentioned strategies are based on the reversible hydrophilic–hydrophobic phase transition of the ligands grafted onto the NPs. By varying the temperature, ligands change their conformation and, in turn, the surface of nanoparticles undergoes a hydrophilic–hydrophobic phase transition, favoring or disfavoring the assembly. However, Yin et al. reported that NPs can also be reversibly assembled by exploiting the temperature dependence of electrostatic repulsions at play between nanoparticles stabilized by a charged protective shell. The decrease in temperature leads to a decrease in the magnitude of zeta potential of negatively charged AuNPs (i.e. bis(p-sulfonatophenyl)phenylphosphine dihydrate dipotassium salt protected AuNPs) and, thereby, their assembly. The zeta potential can be restored by increasing the temperature, thus reversing the assembly process. Because this strategy relies on the modulation of electrostatic repulsions, salt concentration (i.e., ionic strength) plays an important role in governing assembly behavior. The assembly/disassembly process can be performed in solution, but in presence of agarose, which forms a hydrogel network that helps to maintaining the stability of AuNP assemblies against precipitation, has been successfully repeated for 9 times.¹⁸³

Exploiting the temperature dependence of interparticle interactions, Macfarlane et al. reported the reversible assembly of AuNPs coated with polystyrene chains that terminate in molecular recognition units with complementary hydrogen-bonding motifs, i.e. diaminopyridine (DAP) and thymine (Thy). Upon mixing, the complementary NPs rapidly assemble and precipitate from solution but, after heating, can be completely redispersed. This process can be repeated without any alteration of the assembly behavior through multiple heating and cooling cycles and, interestingly, the disassembly temperature can be controlled by varying both particle diameter and polymer length.¹⁸⁴

3.9. Electric and magnetic fields

The electric field, although a noninvasive stimulus that can be easily modulated, has been little explored as a means to control the process of NP assembly. As discussed below, the electric field has primarily been exploited to reversibly assemble NPs at the liquid–liquid interface, however Orme et al. reported that it can also be used at the liquid–solid interface. In their work, the authors show that aggregation and superlattice formation of AgNPs capped with 1-dodecanethiol can be driven by applying a voltage between two parallel single-sided gold coated p-type silicon wafer electrodes.¹⁸⁵ Above a threshold field strength, charged NPs migrate toward the oppositely charged electrode and then accumulate near the electrode, creating a concentration gradient that decays from the electrode surface to bulk solution. In neat toluene solution, AgNPs form highly ordered colloidal crystals on the cathode (see SEM images in Fig. 21) whose lattice constants and degree of preferential orientation can be controlled by tuning the electric field strength, but by adding tetraoctylammonium bromide (TOAB) the charge of AgNPs is reversed and, therefore, the colloidal crystals are formed on the anode. Turning off the electric field terminates the AgNPs flow toward the electrode, which decreases the nanocrystal concentration and dissolves the superlattices.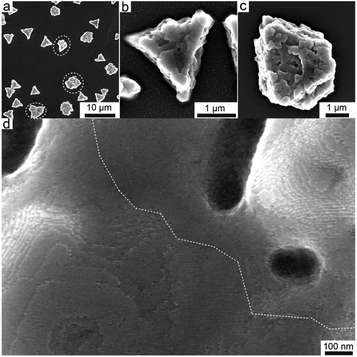

Fig. 21 (a) SEM image of AgNPs superlattices formed on the cathode at 400 V cm⁻¹, showing faceted colloidal crystals. SEM images of AgNPs colloidal crystals with (b) triangular prism and (c) truncated triangular prism shapes. (d) High-resolution SEM image showing the preferential orientation of superlattices and a grain boundary highlighted with white dashed lines. Reprinted with permission from ref. 185 (copyright 2017, American Chemical Society).

The reversibly assembly of charged NPs by controlling the electric field can occur at the liquid–liquid interface between immiscible electrolyte solutions, similar to what we have discussed in the section dedicated to the solvent induced strategies. As schematically reported in Fig. 22, in an electrochemical cell, negatively charged NPs dispersed in water can be pushed and assembled at the liquid–liquid interface through the negative polarization of the aqueous phase relative to the organic phase and, as the electrostatic repulsion prevents the irreversible aggregation, disassembled changing the polarity of the applied potential. For example, gold and silver NPs, and core–shell gold–silver NPs have been reversibly assembled at the interface between water and 1,2-dichloroethane or 1,2-dichlorobenzene by controlling the Galvani potential difference applied between the two liquid phases.^186–188 The assembly of metal NPs at the liquid–liquid interface leads to the formation of reflective films that find application as surface enhanced Raman scattering (SERS) substrates^188,209 and, taking advantage from the interparticle coupling of the surface plasmon resonance, as liquid mirrors.²¹⁰ Montelongo et al. recently reported an electrically switchable liquid mirror-window based on voltage-controlled self-assembly/disassembly of negative-charge functionalized AuNPs at the interface between two immiscible electrolyte solutions, i.e. at the interface between water and 1,2-dichloroethane containing NaCl and tetrabutylammonium tetraphenylborate, respectively.¹⁸⁹ The interparticle distances at the liquid–liquid interface (LLI) is controlled by varying the potential drop across the interface, thus allowing to modulate the density of the NPs at the interface and, in turn, the reflectivity of the NP array.

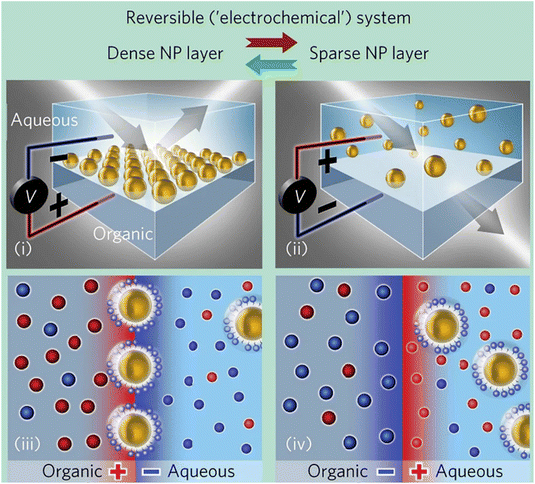Fig. 22 Schematic representation of the assembly (left) and disassembly (right) processes at the LLI of negatively charged NPs as a function of the polarity of the applied potential drop across the interface. Reprinted by permission from ref. 189 (copyright 2017, Nature Publishing Group).

Magnetic forces provide an effective and selective stimulus for the manipulation of NPs that can be initiated instantly and easily modulated and, unlike the others, their effect is due to the direct, or indirect, interactions of the magnetic field with the NPs regardless to the ligands on their surface. A key strength of magnetic field-assembly is the reversibility of the interactions, which leads to a rapid return to the disordered state when the field is removed.^54,56,211 Magnetic field has been successful applied to the manipulation and assembly of magnetic and non-magnetic colloidal particles, also taking advantage of ferrofluids,^212–214 as well as the assembly of soft materials, such as cyclodextrin vesicles (CDV), by incorporating magnetic NPs,²¹⁵ and to the magnetic separation. In particular, Colvin et al. reported that the magnetic separation of magnetite (Fe₃O₄) NPs from a solution can be accomplished at very low magnetic field gradients thanks to their aggregation, which is due to the high field gradients at the NP surfaces.¹⁹⁰ This aggregation is reversible for NPs whose size is below the critical value at which superparamagnetic behavior emerges, but, on the other hand, the decrease of the NP size requires an increase of the field to ensure the complete separation. Moreover, this size dependence of magnetic separation permits to separate different populations of Fe₃O₄ NPs by the application of different magnetic fields. The high efficiency of recovery of superparamagnetic NPs by magnetic separation can be exploited for the arsenic removal from water,¹⁹⁰ as well as for the immobilization, recovery and reuse of organic and inorganic catalysts.^216–218 Noteworthy, catalysts recovered by magnetic decantation proved to be reusable for several cycles while retaining high activity and selectivity profiles.^216–219

Beside the magnetic separation, magnetic fields can be used to guide and control the assembly of superparamagnetic NPs to develop responsive photonic nanostructures.²²⁰ Yin et al. reported that clusters of Fe₃O₄ NPs, which are composed of superparamagnetic crystallites, can be assembled to form colloidal photonic crystals whose interparticle distance can be tuned by varying the strength of magnetic field to manipulate the distance between the magnet and the sample. Consequently, as shown in Fig. 23, the maximum of the reflection spectra of the colloidal photonic crystals moves reversibly across the entire visible spectral region in response to the applied magnetic field.^191,192 Noteworthy, using ferrofluids, magnetic fields as the external stimulus can also be employed to assemble nonmagnetic NPs into photonic crystals.¹⁹³

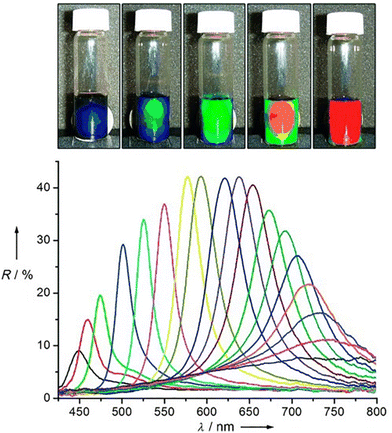Fig. 23 (Top) Photographs of colloidal crystals formed in response to an external magnetic field; the magnet–sample distance decreases gradually from right to left. (Bottom) Dependence of the reflection spectra at normal incidence of the colloidal crystals on the distance of the sample from the magnet. Diffraction peaks blue-shift (from right to left) as the distance decreases from 3.7 to 2.0 cm with step size of 0.1 cm. The average diameter of the clusters of Fe₃O₄ in this sample is 120 nm. Figure adapted from ref. 191 (copyright 2007, Wiley-VCH).

Interestingly, the integration of magnetic NPs with biomolecules can provide an effective means to increase the complexity of achievable NP assemblies through the control of external magnetic field. For example, Sim et al. have entrapped magnetic NPs into a chaperonin GroEL mutant, which bears merocyanine (MC) units at its apical domains, and the resulting inclusion complexes were assembled into 1D nanotubes, exploiting the formation of coordination bond between the MC units and Mg²⁺. These nanotubes can be magnetically assembled laterally to form bundles then disassemble when the applied magnetic field is turned off.¹⁹⁴

4. Computational simulations

Self-assembly of nanoparticles is governed by many competing interactions. However, relatively little is known about the time-dependent mechanisms and energetics involved through which these interactions enable and guide the nanoparticle (reversible) self-assembly process. As we have outlined in a previous section, different theoretical formalisms tentatively try to describe the whole process of NPs self-assembly by breaking down the role of the individual contribution to the total interaction potential that is at play. However, despite the importance of this flourishing field and the wealth of experimental and theoretical studies dedicated to NP assembly, a detailed comprehension of all the forces at play is yet to be thoroughly achieved.

In this regard, in the last decades several advances have been made in computational modelling to help and complement the theoretical prediction as well as our comprehension over the structural and energetics involved in the assembly of objects (colloidal or nanoparticles) with the aim to describe the mechanisms observed in experiments (Fig. 24).³² Computer simulations offer a unique approach to identify and separate individual contributions to the NPs self-assembly process.

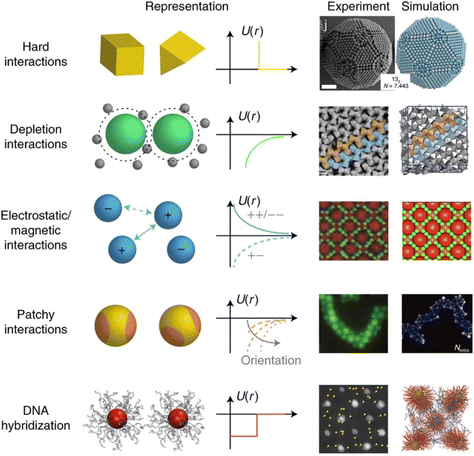Fig. 24 A selection of interactions, recently reviewed, involved between objects (colloids and NPs), with representative cases of the resulting self-assembly mechanisms observed in experiments and predicted in computational modelling. From top to bottom, the examples are hard interactions, depletion interactions, electrostatic interactions, hydrophobic patchy interactions and interactions based on DNA hybridization. Reprinted by permission from ref. 32 (copyright 2021, Nature Publishing Group).

As summarized in Scheme 3 and Table 3, the following section will cover the application of different computational modelling schemes that address different time and size scales (Fig. 25a) based on a different degree of accuracy and applicability (Fig. 25b) for nanoparticle-based systems.^33,221

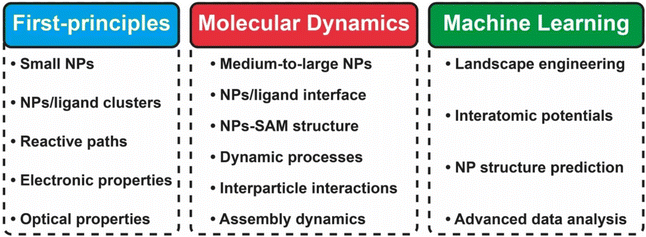Scheme 3 Summary and breakdown of the possible targets that can addressed by the different computational schemes considered in the present review.

Fig. 25 A bird's-eye view of computational methods applied to materials science and nanoparticles-based system. (a) System size vs. time scales and relevant simulation methods from molecules to self-assembled nanostructures. Reprinted by permission from ref. 221 (copyright 2021, Nature Publishing Group). (b) Computational methods based on different levels of theory provide different accuracies. Reprinted by permission from ref. 33 (copyright 2021, Nature Publishing Group). Acronym definitions: QC, quantum-chemical; DFT, density functional theory; MM, molecular mechanics; MD, molecular dynamics and CG, coarse-grained.

Table 3 Computational methods employed to study the structure, dynamics, energetics and properties of the whole NPs assembly process or relevant mechanisms that interest sub-parts of it

Computational method	Object of the study	Property/approach	Particle type	Ref.
a Polyoxometalates.
DFT, FPMD	Ligand/NP interaction and organization	Vibrational, noncovalent forces, binding energy, reactive paths, electronic and magnetic	Au NPs, Co NPs, Fe NPs	222–229
	NPs welding process	Density profiles, dynamics	Au NPs, Ag2S NPs	230
	Ligand thermal stability	Dynamic stability	Au NPs	231–233
cMD, CGMD	NPs self-assembly process	Dynamics, geometry, interaction energy profiles, PMF	Au NPs, Ag NPs	234–239
	NPs self-assembly process, ligand SAM organization	Molecular environment, hydrophobic interactions, SOAP, interparticle spacing, PMF	Au NPs Au NCs, Au NRs, PbS NPs, Cd NPs	113 and 240–249
	NPs agglomeration and packing, NPs/ligand interaction, solvent effects	Molecular interaction, dynamics, PMF	Au NPs	250–253
	NPs/ligand interaction, NPs/protein interaction	Molecular interaction, dynamics, PMF	Au NPs	248 and 254–256
QM/MM	NPs/ligand interaction, ligand surface orientation, surface reactivity, surface catalysis, NPs/protein interaction, self-assembly process, ligand conformational analysis	Electronic structure, HDO reaction path, dynamic stability, ligand adsorption free energies, surface ligands patterning, electrostatic interactions, nanoaggregates stability, PMF	Pd NPs, Au NPs, TiO2 NPs, POM^a NPs	257–268
ML	NPs shapes, phase diagram	MLP, NN, GAP, SOAP, polynomial kernels	AuNPs, CuNPs	249 and 269–272
	NPs self-assembly, particles aggreagation	Landscape engineering	Generic NPs	273–276
	Data analytics for NPs	Pattern recognition	Generic NPs	277
	NPs assembly	Phase transition dynamics	Generic NPs, generic NRs	278

---

We will cover both studies that tentatively target the assessment of the singular factor and interaction between particles as well as the dynamical mechanisms involved in the whole self-assembly process.

The first section will review the application of, mostly, density functional theory (DFT) and first-principles-based computational modelling where the electronic-ground-state total energy of a system is expressed as a functional of the ground-state charge density. We also consider here the application of the so-called first-principles (or ab initio) molecular dynamics (FPMD) scheme where DFT is combined with MD in order to follow the temporal evolution of atoms dynamics at the ground-state level of electronic structure. In the second part, atomistic simulations based whether on classical molecular dynamics (MD) or coarse-grained modelling, that allow to reach size and time scales beyond DFT and FPMD, will be reviewed. A few examples where hybrid quantum-mechanics (QM)/molecular-mechanics (MM) method (referenced as QM/MM) method is applied to the study of NPs, NPs/ligand, NPs assembly are also presented.

In the last part, we will cover how machine learning-based approaches (ML) can help the study of NPs-based systems and their assembly process. In particular, a great focus will be given to the use of ML in the development of hybrid machine learning/molecular mechanics (ML/MM) methods that will help to approach substantially larger systems and longer time scales than currently accessible with state-of-the-art methods.

4.1. First-principles methods

Nowadays, various aspects related to the chemistry and physics of ligand-protected nanoparticles and their assembly are studied using quantum mechanical methods. Most quantum mechanical studies on nanoclusters and nanoparticles employ density functional theory (DFT) and first-principles molecular dynamics (FPMD),^279–281 while few works reported in this review have also been performed with so-called time-dependent DFT, as an extension of ground-state DFT method that allows for calculations of excited state properties as well. In addition to these techniques, enhanced sampling methods (such as metadynamics^282,283 and blue moon schemes²⁸⁴) are also usually employed to improve the sampling efficiency of FPMD simulations and explore the free energy landscape of reactive paths. Within the FPMD scheme, dynamical simulations using quantum-mechanical forces are however limited to rather short time scales, on the order of 100 ps. In this time scale, breaking and forming of chemical bonds, as well as structural transformation of small nanoparticles can be targeted. Within DFT, exchange correlation functionals that utilize the local density approximation (LDA) or the generalized gradient approximation (GGA) are the most common, even though the use of meta-GGA, hybrid and novel functionals formulations is growing. Although highly computationally expensive, nowadays ligand-protected NP made of a few hundred atoms can be modelled by these techniques. However, most of the works on this topic have been mainly dedicated to precise relevant interactions and the energetics involved within a sub-space of the whole assembly process, such as structural and conformational optimization of an individual ligand molecule or in a simplified model of a SAM and NP–ligand interactions. Although the majority of these first-principles studies do not focus entirely on the NPs assembly or its reversibility aspects, they offer crucial insights into the accurate assessment of the interactions at play between the individual components of the objects (for instance, NP–ligand, ligand–ligand or molecular clusters) involved in the context of NP assembly. Furthermore, this quantum-mechanical information is often directly used to build upon the empirical or semiempirical potentials employed in larger-scale computational methods such as atomistic or coarse-grained molecular dynamics (nowadays, the methods mostly used to study NPs (reversible) assembly). Typically, FPMD cover size scale up to few NP nm² (in terms of NP surface area) and tens/hundreds of picoseconds time scales. Employing DFT and FPMD can be assessed the role of several relevant factors, such as NP surface-ligand binding energy, ligand conformation/geometry, ligand monolayer thickness, ligand orientation and surface packing density. Many different DFT methodological schemes have been tested in this context. Early applications of DFT in this scenario were aimed at the proper computation and description of the chemical interaction at play between an organic ligand and the surface of the whole nanoobject (nanocluster). Extensive benchmarks of exchange–correlation functionals on real X-ray resolved ligand-protected nanoclusters have been reported by Muniz-Miranda and coworkers.²²² This work represents one of the first application of DFT-based calculations to untangle the role of ligand–nanocluster interactions on the structural and optical properties of the whole nanoobject. Time-dependent DFT has been used to compare calculations with experimental data on optical gaps of two undecagold and one Au₂₄⁺-based nanoclusters stabilized by thiol and phosphine ligands. It has been observed that GGA functionals employing PBE-like correlation²⁸⁵ coupled with a proper pseudopotential and basis set provide accurate results for both the structure and optical gap of gold nanoclusters, at a reasonable computational cost. Good geometries have been also obtained using some global hybrid and range-separated hybrid (e.g., HSE06 ²⁸⁶) functionals making use of PBE-like correlation, even though they yield optical gaps overestimating the experimental findings up to 0.5 eV. It has been found that the organic ligands lead to an energy increase of the eigenstates of the metal cores, but do not alter significantly the energy separation between the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) states, nor the optical gaps. This means that the simplified models employed are indeed suitable choices to perform a wider number of tests, and also suggests that the low energy region of the electronic spectrum is probably only slightly affected by the organic coating. This work presented the first step towards full DFT simulations of structural, optoelectronic, and spectroscopic properties of realistic organic–noble metal nanoparticles of technological interest. More recently, Muniz-Miranda et al. targeted, with a similar approach, the adsorption of xanthine, a nucleobase presents in human tissue and fluids that is involved in important metabolic processes, on citrate-reduced gold NPs together with a set of experimental analysis (absorption, SERS and XPS). It was found that the citrate anions stabilize the colloidal suspensions by strongly binding the gold NP. However, these anions do not impair the adsorption of xanthine on positively-charged active sites present on the metal surface. These authors reported that the addition of chloride ions to the Au/xanthine colloid induces the aggregation of the gold NP, whose plasmonic band is shifted to the near infrared region where there is the exciting laser line of the FT-Raman instrument. In this case, the TDDFT calculations were instrumental to the correct assignment and interpretation of the observed SERS bands.²²³

Nonappa et al., by employing DFT calculations studied capsid-like colloidal self-assembled materials based on NPs as driven by ligand-driven hydrogen bonding. In this case DFT calculations were instrumental to untangle the mechanism of reversible supra-colloidal hydrogen bond-driven self-assembly of cobalt nano-particles. In particular, the role of hydrogen bonding in capsid formation, binding energy, diffusion barrier for ligand rearrangements, and magnetic moments of a model spherical cluster was interpreted based on DFT calculations, which finally suggested a facile ligand rearrangement around NP surface.²²⁴

The geometry of the organic ligands on colloidal NPs is central for understanding the self-assembly behavior and many properties of NP-based matters. Zhang et al. have shown that NPs capped with 3-mercaptopropionic acid (MPA) serve as a convenient model to elucidate the effect of surface ligand geometry on collective noncovalent forces at play in highly concentrated NPs. Contrary to expectations, MPA was found to form surface layers with different thicknesses varying from monolayer to multilayers depending on the ratio of isopropanol to the as-made NP dispersions in the purification. In this case, DFT simulations and solution-state nuclear magnetic resonance (NMR) uncovered that the monolayer includes strongly coordinated ligands and adsorbed ligands interacting with the NP surface non-covalently. Increased density of the non-covalently attached ligands results in a multilayered ligand shell. These observations enabled a better understanding of the complexity of water-soluble NP dispersions and collective non-covalent forces of supramolecular NPs.²²⁵

To explore structural interaction at the interface between gold surfaces and a hydroxyl-terminated alkanethiol, Roy et al. have employed a combined computational and experimental approach. DFT and FPMD calculations were carried out on the thiol–gold interface using both the PBE and a van der Waals density functionals. FPMD simulations revealed that the interface consists of four different distinguished phases, each with different ligand orientations. The computed molecular parameters including tilt angles and the thickness of SAMs agreed with the XPS and ellipsometry results. The stability of the different phases was found to be primarily governed by hydrogen bonding arising from the terminal hydroxyl groups (Fig. 26). This work demonstrated that the combination of DFT/FPMD simulations with XPS and ellipsometry experimental data is a viable way to assess the role of the organization and orientation of organic ligands on the interaction at the interface between gold surfaces.²²⁶

Fig. 26 (a) Snapshots of different orientations obtained from a 16 ps FPMD simulation of hydroxyl-terminated alkanethiol over a gold surface (top view). The red dotted line represents the hydrogen bonding between two adjacent –OH groups of the ligand. For clarity, the hydrogen atoms are not shown with the exception of hydrogens of –OH functional group. (b) DFT computed FPMD averaged density of states of the valence band and experimental XPS spectra at two different X-ray energies. Reproduced from ref. 226 (copyright 2019, Royal Society of Chemistry).

Huang et al., by means of FPMD simulations, report a welding phenomenon occurred directly between as-synthesized dispersions of single-component Au and chalcogenide NPs, leading to asymmetric formation Au–chalcogenide hybrid NPs (HNPs).²³⁰ The welding of dissimilar NPs in dispersion was found to be mainly driven by the ligand desorption-induced conformal contact between NPs and the diffusion of Au into chalcogenide NPs. The welding process can occur between NPs with distinct shapes or different capping agents or in different solvent media.²³⁰ A two-step assembly-welding mechanism was proposed for this process, based on FPMD simulation and in situ electron spin resonance measurements. The understanding of NP welding in dispersion may lead to the development of unconventional synthetic tools to promote NPs assembly through oriented or non-oriented attachment with the possibility to fabricate hybrid nanostructures for diverse applications.²³⁰

As mentioned before, nanoclusters, stabilized and functionalized by organic ligands, are nanomaterials with potential applications in plasmonics, nano-electronics, bio-imaging, nanocatalysis, and as therapeutic agents or drug carriers in nanomedicine. The organic ligand layer has an important role in modifying the physico-chemical properties of the clusters and in defining the interactions between the clusters and the environment. While this role is well recognized from plenty of experimental studies, there is very little theoretical information on dynamical processes within the layer itself. Häkkinen et al. have performed extensive MD simulations, with forces calculated from the DFT, to investigate thermal stability and dynamics of the ligand layer of the meta-mercaptobenzoic acid (m-MBA) protected Au₆₈ and Au₁₄₄ nanoclusters, which are the first two gold nanoclusters structurally solved to atomic precision by electron microscopy.^231,232

Häkkinen et al. visualize and analyze dynamics of three distinct non-covalent interactions, viz., ligand–ligand hydrogen bonding, metal–ligand O=C–OH⋯Au interaction, and metal–ligand Ph(π)⋯Au interaction. They discuss their relevance for defining, at the same time, the dynamic stability and reactivity of the cluster. These interactions promote the possibility of ligand addition reactions for bio-functionalization or allow the protected cluster to act as a catalyst where active sites are dynamically accessible inside the ligand layer.²³³

Covalent binding of carboxylic acids to metal NPs can induce biocompatibility, whilst also preventing the formation of surface oxides which reduce the magnetic properties of cobalt. Understanding the origin of the acid–metal interaction is key, yet probably the most experimentally challenging step, for the rational design of such entities. Özdamar et al., by means of FPMD and enhanced sampling techniques such as Blue Moon (BM) scheme, unveiled the role of the nature of the initial transition metal (Co, Fe) stearates precursors and their interaction with the local environment during the first stages of formation of NPs. These authors have shown that the presence of water and the nature of the molecular precursor have a direct effect on the physical and chemical properties of metallic NPs and deeply influence their composition and morphology.^227,228 With a similar approach, the same authors showed how FPMD is found instrumental in quantitatively assessing the strength of the chemical interactions (e.g. H-bonding) that can be at play when simple or complex carboxylic-based ligands interact with metal or metal hydroxides surfaces.^228,287 Farkaš et al. employed FPMD metadynamics simulations to establish a 57-atom Co cluster that is the smallest model able to reproduce the adsorption behaviour of carboxylic acids, and to obtain the structure and the free energy landscape for its interaction with valeric acid. The simulations have shown that a bridging bidentate binding mode has a stronger affinity and energetically higher transition barriers compared to monodentate binding (Fig. 27). A chelate interaction mode of two carboxyl oxygen atoms can be formed as an intermediate. These results clarify the organic–inorganic interactions in the cobalt–acid system, providing a basis for the rational design of biocompatible metallic NPs.²²⁹

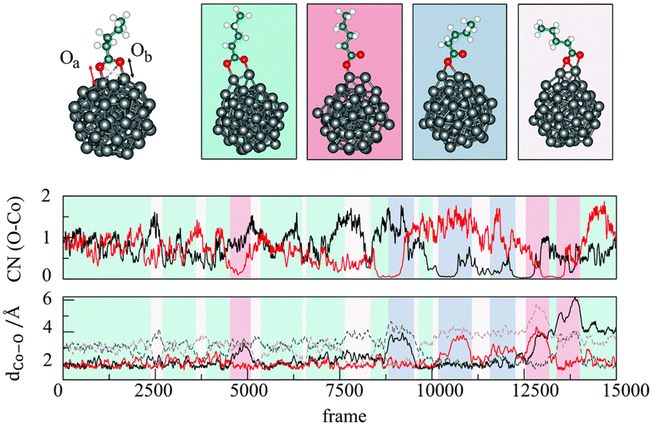Fig. 27 Representative structures sampled during metadynamics simulations (top). Changes in the coordination numbers CN (middle), and Co–O bond distances dCo–O (bottom) throughout the metadynamics trajectory. Reproduced from ref. 229 (copyright 2020, Royal Society of Chemistry).

4.2. Classical and coarse-grained molecular dynamics

Atomistic modelling techniques such as classical and coarse grain molecular dynamics (cMD and CGMD, respectively) are principally used to target the whole self-assembly process or relevant mechanisms that interest a sub-part. These methods are based on following the motion of a collection of particles and molecules (from thousands to millions of atoms systems) through time and space by numerically integrating Newton's equations of motions (cMD: nm² (in terms of NP surface area) and nanoseconds; CGMD: nm² and sub-μm², microseconds). In order to progress the simulation in time, the potential energy for the entire system is expressed as the sum of a series of intra- and inter-actions between its components (atoms, molecules and particles).^288–290 Different forms and types of potentials are selected to describe the interactions between the various components with different degrees of approximations as a function of the complexity to properly assess the chemical interaction involved. Among others, the role of the following factors has been targeted by cMD and CGMD simulations up to now: the role of organic linkers, NPs shape, solvation forces, counter ions and NPs localization, surface packing density, particle size and ligand shell structure/textures and the role of solvent-mediated effective interactions.

cMD and CGMD represent two of the most exploited simulation techniques employed to model processes relevant to NPs assembly. Typically, the former MD scheme is based on the representation of the whole system down to the atomic-scale to the individual atoms forming the NP and the surrounding local environment such as organic ligands and solvents molecules, while in the latter MD scheme often beads identify groups of atoms to simplify the molecular features at the cost of losing atomic-scale details but gaining in computational performance in terms of larger size or time scales to be accessible. The work of Lin et al. can be taken as an archetypical example of the capability and potential of MD simulations in this context. Through MD simulations in combination with in situ liquid cell transmission electron microscopy (TEM), Lin et al. disentangled the stepwise self-assembly of surfactant-coated and hydrated GNPs into linear chains or branched networks (Fig. 28a and b). This work allowed assessing the role of organic linker molecules, such as ethylenediammonium, in facilitating NP binding by promoting hydrogen bonds with surfactant molecules of neighbouring NPs. The observed spacing between bound neighbouring NPs, ∼15 Å, matches the combined length of two surfactants and one linker molecule. MD simulations revealed that for lower concentrations of linkers, NPs with charged surfactants cannot be fully neutralized by strongly binding divalent linkers, so that NPs carry higher effective charges and tend to form chains, due to poor screening. The highly polar NP surfaces polarize and partly immobilize nearby water molecules, which promotes NPs binding (Fig. 28c and d).²³⁴

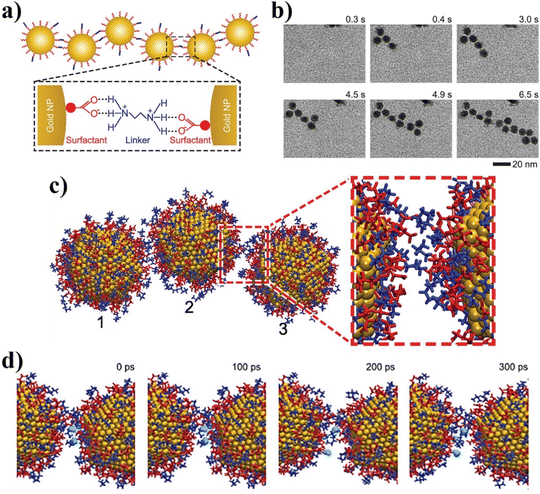Fig. 28 (a) Schematic of a gold NP chain assembly. Linker (ethylenediammonium) connects the surfactant (citrate) molecules of the adjacent gold NPs by forming hydrogen bonds between –NH₃⁺ of ethylenediammonium and –COO– of citrate. (b) Time series of in situ TEM images shows the growth dynamics of a gold NP chain. (c) Attachment of NP (3) to a pair of NPs (1 and 2) along 10 ns by means of classical MD simulation, when NP (3) is initially placed (center-to-center distance) at 6.2 nm from NP with only ethylenediammonium linkers as counterions. (d) Time MD dynamics of three selected water molecules (shown in cyan) between two NPs separated by ∼1 nm. During 300 ps long simulations, selected water molecules stay within 1 nm from each other. Adapted with permission from ref. 234 (copyright 2016, American Chemical Society).

Tan et al., by employing MD simulations combined with in situ TEM imaging, reported that the forces governing the self-assembly of hydrophobic NPs change with the NP shapes. By comparing how gold nanospheres, nanocubes, nanorods, and nanobipyramids assemble, it is revealed that the strength of the hydrophobic interactions depends on the overlap of the hydrophobic regions of the interacting NP surfaces determined by the nanoparticle shapes. This work revealed that, in contrast to spherical NP, where vdW forces play a crucial role, hydrophobic interactions can be more relevant for nanocubes with flat side faces, where these interactions promoted an oriented attachment between the nanocubes.²⁴⁰ Welch et al. employed steered MD simulations combined with in situ liquid cell TEM and imaging to demonstrate that the experimentally observed preference for end-to-end attachment of nanorods is a result of weaker solvation forces occurring at rod ends. MD reveals that when the side of a nanorod approaches another rod, a perturbation in the surface-bound water at the nanorod surface creates significant energy barriers to the attachment. Additionally, rod morphology (i.e., facet shape) effects can explain the majority of the side attachment effects that are observed experimentally.²³⁵ Bera et al. have shown that the transport of NPs in a biphasic system (water/organic solvent) is accompanied by counter ions condensation onto the portion of the charged NPs exposed to the organic phase, which shields the NP charge from the low permittivity phase (Fig. 29). MD simulations show that NPs form a nearly close-packed 2D array on the organic side of the interface, the spacing of which can be tuned by varying the voltage. The tunability occurs because the voltage alters the interfacial distribution of supporting electrolytes, which mediate the interactions between NPs. The MD simulations also reveal that the sharing of condensed counter ions contributes to the coupling between neighbouring NPs.²³⁶ Self-assembly of nanocrystals into functional materials requires precise control over NP interactions in solution that are dominated by organic ligands that densely cover the surface of nanocrystals. Bian et al., by combining CGMD simulations with a set of experimental techniques, recently demonstrated that small charged molecules can effectively induce attractive interactions between oppositely charged NPs in water.¹¹³ With such an approach, transient NPs assemblies can be generated using positively charged NPs and multiply charged anions. In this work, CGMD allowed to model the anion-mediated self-assembly of positively charged NPs on a large scale. In particular, CGMD simulations of two TMA-coated Au NPs neutralized by different anions (Cl⁻, HPO₄²⁻ or citrate) showed that only citrates had the ability to bring the particles to assemble together during the CGMD runs timescale, despite the fact that all anions exhibited a strong affinity to the NPs. By combining the CGMD findings with machine learning (ML-SOAP), Bian et al. have been able to study the variability of the arrangement of citrates in the NPs assemblies. The analysis, based on the use of SOAP descriptors, of the molecular environment that surrounded each citrate in the CGMD model, allowed the classification of different citrates based on differences in the local environment: (i) citrates located at the interface between the two NPs, (ii) citrates that interact with a single NP and (iii) an intermediate state between the first two. The movement and reshuffling of citrates between the three clusters during the CGMD revealed the dynamics between these states. These results demonstrated the internal dynamics of the system, in which the citrates at the interface between two bound NPs are less dynamic (but not completely static) than those bound to the surface of a single NP. These results support the hypothesis that the facile diffusion of oligoanions between charged NPs might facilitate the controlled transformation of the initial, mostly amorphous, aggregates into regular, crystalline assemblies.¹¹³ Furthermore, recent experiments have demonstrated that small truncated-octahedral nanocrystals can self-assemble into a range of superstructures with different translational and orientational order of nanocrystals. In this context, Fan et al. employed MD simulations to study the self-assembly of these nanocrystals over a broad range of ligand lengths and solvent conditions with the aim to bring light on the origin of this structural diversity. The proposed model, which is based on a coarse-grained MD description of ligands and solvent effects, reproduces the experimentally observed superstructures, including recently observed superlattices with partial and short-ranged orientational alignment of nanocrystals. It is shown that small differences in nanoparticle shape, ligand length and coverage, and solvent conditions can lead to markedly different self-assembled superstructures due to subtle changes in the free energetics of ligand interactions.²³⁷

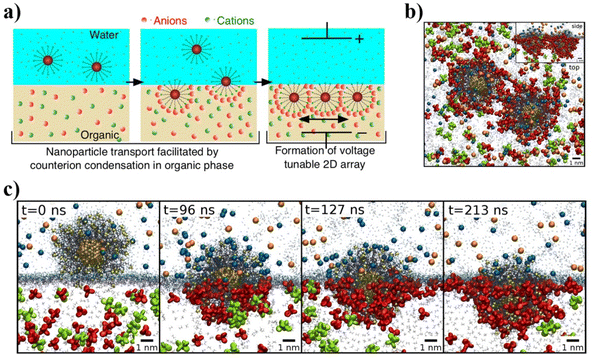Fig. 29 (a) Cartoon of Au NPs transport facilitated by counterion condensation in an organic phase and formation of voltage tunable 2D array assembly. (b) Two NPs in the simulation cell forming a stable assembly pair at t = 68 ns. (c) Time sequence snapshots taken from a 213 ns MD simulation that shows the submersion of a NP from an aqueous (top) to an organic (bottom) electrolyte phase accompanied by the exchange of loosely bound Cl⁻ ions (blue) in the aqueous phase for condensed organic TPFB⁻ ions (red) in the organic phase. Adapted with permission from ref. 236 (copyright 2014, American Chemical Society).

The localized deformation of molecular monolayers constrained between the spherical surfaces of Au NPs can be studied by MD simulations. Copie et al. found that shorter ligands can be more densely packed on the surface, but do not interdigitate upon compression. They respond to the applied force by bending and twisting, thus changing their conformation while remaining disjointed. On the other hand, longer ligands attain lower surface densities and can interpenetrate when the NPs are compressed against each other. Such molecules remain rather straight and benefit from the increased overlap, to maximize the adhesion by dispersion forces. The mechanical properties (Young's and shear moduli) of the dense nanostructure, composed of a triangular arrangement of identical MUDA-decorated Au NPs, are found to be smaller than estimates indirectly deduced by atomic-force experiments but quite close to previous computer simulations of molecular monolayers on flat surfaces and of bulk nanoparticle assemblies.²⁴¹ Nowadays, classical MD is routinely applied to assess the structure, conformational organization and bonding of monolayer-protected NPs functionalized with novel synthetic organic ligands. cMD simulations can be particularly beneficial to complement experimental data based on XPS and ellipsometry measurements about the thickness of a SAM protecting NPs. cMD simulations can also give access to further details such as the localization of specific functional groups with respect to the NPs surface as well as the degree of extension of the H-bonding network promoted by ligand-bearing amide groups.²⁴² Kister et al. found that the agglomeration of apolar particles is dominated by either the core or the ligand shell depending on the particle size and materials. In this case, MD simulations, are used to characterize the interaction between hexadecanethiol passivated gold NPs in decane solvent. For smaller particles, the agglomeration temperature and interparticle spacing are found to be determined by ordering of the ligand shell into bundles of aligned ligands that attract one another and interlock. In contrast, the agglomeration of larger particles is driven by vdW attraction between the gold cores, which eventually becomes strong enough to compress the ligand shell. Their results provide a microscopic description of the forces that determine the colloidal stability of apolar nanoparticles and explain why classical colloid theory fails.²⁵⁰ Waltmann et al. have reported a detailed analysis of the interaction between two nanocrystals capped with ligands consisting of hydrocarbon chains. They found that the bonding of two nanocrystals is characterized by ligand textures in the form of vortices (Fig. 30). These results are generalized to nanocrystals of different types (differing core and ligand sizes) where the structure of the vortices depends on the softness asymmetry. They provide rigorous calculations for the binding free energy, show that these energies are independent of the chemical composition of the cores, and derive analytical formulas for the equilibrium separation. Overall, these results show that the structure of the ligands completely determines the bonding of nanocrystals, fully supporting the predictions of the recently proposed orbifold topological model.²⁵¹

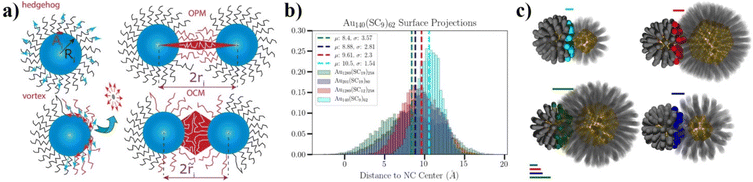Fig. 30 (a) NCs as soft skyrmions: hedgehog and vortex, with the different parameters identified to screen a variety of optimal packing model (OPM) and overlap cone model (OCM) models. (b) Histograms defining the interaction plane for the Au₁₄₀(SC₉)₆₂ NC interacting with Au₁₄₀(SC₉)₆₂ (cyan), Au₁₂₈₉(SC₁₂)₂₅₈ (red), Au₂₀₁(SC₁₉)₈₀ (blue), and Au₁₂₈₉(SC₁₉)₂₅₈ (green). The location and roughness of the interaction plane are realized in the surface histograms as the mean and standard deviation, respectively. (c) The softness symmetry decreases from the top left to bottom left cases, circling clockwise. Adapted with permission from ref. 251 (copyright 2014, American Chemical Society).

Yadav et al. found that the extent to which solvent-mediated effective interactions between NPs can be predicted based on structure and associated thermodynamic estimators for bulk solvents and for solvation of single and pairs of NPs. They report on the possibilities of using structural estimators of various thermodynamic quantities to analyse the complex interplay of ligand fluctuations and solvent quality in self-assembly as well as to design solvation environments.²⁵² Landman et al. reported on the simulations of assemblies made of crystalline gold nanoclusters of variable sizes, passivated by monolayers of alkyl-thiol molecules. They proposed an analytic optimal packing model that correlates several structural characteristics of three-dimensional super lattice assemblies in a unified manner. The model successfully organizes and systematizes a large amount of experimental and simulation data, and it predicts the phase-boundary between different super lattice structural motifs that evolve as a function of the ratio between the chain-length of the extended passivating molecules and the radius of the underlying gold nanocluster. The entropic contribution to the formation free energy of the super lattice assembly is found to be large and of similar magnitude as the potential energy component of the free energy. The major contribution to the cohesive potential energy of the super lattice is shown to originate from van der Waals interactions between molecules that passivate neighboring nanoclusters.²⁵³

Cooper et al. examine how changes in the ligand surface coverage and facet dimensions affect the ordering of ligands, the arrangement of nearby solvent molecules, and the interaction between ligand monolayers on different particles. Depending on the facet dimensions and surface coverage, they observe three distinct ordered states that differ in how the ligands are packed together, and which affect the thickness of the ligand shell and the structure of the ligand–solvent interface. The temperature dependence of the order–disorder transition also broadens and shifts to lower temperature in a nonlinear manner as the nanoscale is approached from above. They found that ligands on nanoscale facets can behave very similarly to those on macroscopic surfaces in solution, and that some facet dimensions affect the ligand alignment more strongly than others. As the ligands become ordered, the interaction between opposing monolayers becomes attractive, even well below full surface coverage. The strength of attraction per unit surface area is strongly affected by ligand coverage, but only weakly by facet width. Conversely, they found that bringing two monolayers together just above the order–disorder transition temperature can induce ordering and attraction.²⁴³

Based on large-scale MD simulations, Liu et al. calculated interparticle spacing in alkylthiol-stabilized gold supracrystals as a function of the NP size, ligand length and external pressure. The repulsive many-body interactions in the supracrystals are also quantified by comparing the interparticle spacing with that between two individual NPs at equilibrium. Their results are consistent with available experiments, and are expected to help precise control of interparticle spacing in supracrystal devices.²⁴⁴

The thermodynamic driving forces for these structures are not fully understood and conflicting theories have been proposed. In this paper, Fan et al. systematically study the thermodynamic stability of fcc and bcc superlattices as a function of ligand length, core size, and ligand coverage with a coarse-grained molecular model. Their simulations reveal that bcc superlattices are stabilized via two fundamentally different mechanisms, depending on ligand length. For shorter ligands, the bcc superlattice has lower potential energy than fcc, due to additional interactions between ligands on next-nearest neighbours in the superlattice. For longer ligands, the bcc superlattice is stabilized due to a larger configurational entropy of ligands.²⁴⁵

Patra et al. combine CGMD simulations and small angle X-ray scattering experiments to demonstrate that coverage density of capping ligands (i.e., number of ligands per unit area of a nanoparticle's surface), strongly influences the structure, elasticity, and high-pressure behavior of nanoparticle superlattices (NPSLs) using face-centered cubic PbS-NPSLs as a representative example. They demonstrate that ligand coverage density dictates (a) the extent of diffusion of ligands over NP surfaces, (b) spatial distribution of the ligands in the interstitial spaces between neighboring NPs, and (c) the fraction of ligands that interdigitate across different nanoparticles. They find that below a critical coverage density (1.8 nm⁻² for 7 nm PbS NPs capped with oleic acid), NPSLs collapse to form disordered aggregates via sintering, even under ambient conditions. Above the threshold ligand coverage density, NPSLs surprisingly preserve their crystalline order even under high applied pressures (∼40–55 GPa), and show a completely reversible pressure behavior. This opens the possibility of reversibly manipulating lattice spacing of NPSLs, and in turn, finely tuning their collective electronic, optical, thermo-mechanical, and magnetic properties.²⁴⁶ Waltmann et al. reported a detailed analysis of the interaction between two nanocrystals capped with ligands consisting of hydrocarbon chains by united atom MD simulations. They analyzed large cores (up to 10 nm in diameter) and ligands with unsaturated carbon bonds (oleic acid) and investigated the accuracy of the computed potential of mean force by comparing different force fields. They also analyze the vortices that determine the bonding, including the case of asymmetric nanocrystals, and discuss effects related to the intrinsic anisotropy of the core. Overall these results found are in fair agreement with the predictions of the recently proposed orbifold topological model.²⁴⁷ Yang et al. showed by employing cMD and CGMD simulations that stabilizer-free polydispersed inorganic nanoparticles can spontaneously organize into porous nanoshells. The association of water-soluble CdS NPs into self-limited spherical capsules results from scale-modified electrostatic, dispersion and other colloidal forces. They cannot be accurately described by the (original) DLVO theory, whereas MD simulations with combined atomistic and coarse-grained description of NPs reveal the emergence of nanoshells and some of their stabilization mechanisms (Fig. 31). Morphology of the simulated assemblies formed under different conditions matched nearly perfectly the transmission electron microscopy tomography data. This study bridged the gap between biological and inorganic self-assembling nanosystems and conceptualized the comprehension of the stabilization mechanisms for a wide range of inorganic and biological NPs.²⁴⁸

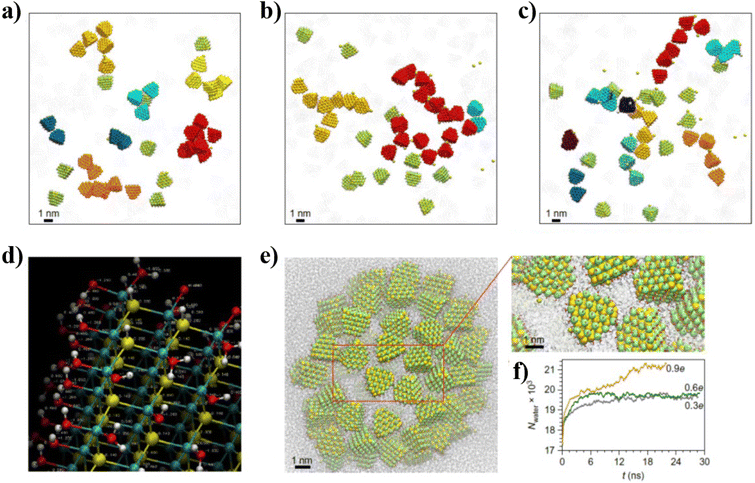Fig. 31 (a–c) Snapshots taken after ∼65 ns simulations of assemblies from NPs that carry different surface charges: q = 0.3e (a), 0.9e (b) and 1.34e (c). Yellow-green units represent individual NPs. Other colours denote assembled NP particles with different degrees of connectivity. Sodium counterions are shown as yellow spheres. Note the extended assemblies from multiple connected particles (red, orange and yellow). (d) Atomic charges on the NP surfaces and in the cores were calculated with ab initio methods using small atomic clusters. (e) Snapshot after ∼22 ns equilibration for pre-assembled NPs that carry q = 0.9e. Inset shows an enlarged view of the highlighted region; note the atomistic description of both the surface and media. (f) Plots for the number of water molecules inside the nanoshells with q = 0.3e, 0.6e and 0.9e. Stabilization of the cavity size for q = 0.3e and 0.6e is indicative of stabilization of the shell in a (local) thermodynamic minimum. Reprinted by permission from ref. 248 (copyright 2016, Nature Publishing Group).

MD and CGMD are nowadays considered as the MD schemes of choice for the modeling of ligand-protected NPs in an environment (solvent or other) and its interactions with other systems (other NPs or other (macro)chemical systems). As an example, Tavanti et al. employed CGMD to model the role of NP size and ligand-shell composition (mono or mixed) on the interaction with amyloid-β fibrils. Amyloids-β (Aβ) fibrils are involved in several neurodegenerative diseases.²⁵⁴ Tavanti et al. reported that small gold NP bind with the external side of amyloid-β fibrils that is involved in the fibrillation process.²⁵⁵ The binding affinity, studied for both kinds of fibrils as a function of the monolayer composition and the nanoparticle diameter, is found to be modulated by hydrophobic interactions and ligand monolayer conformation. In this case, CGMD has been instrumental in finding that monolayer-protected nanoparticles can be considered good candidates to prevent fibril aggregation and secondary nucleation or to deliver drugs to specific fibril regions (Fig. 32).

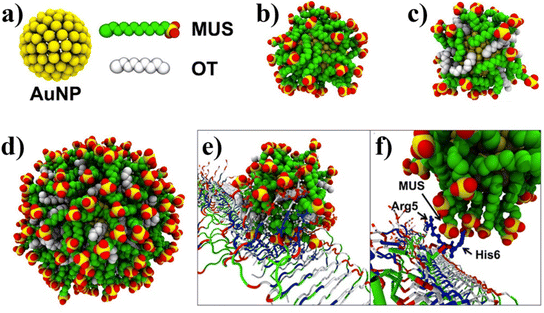Fig. 32 (a) Representation of a bare 2 nm AuNP and of its hydrophilic 11-mercapto-1-undecanesulfonate (MUS) and hydrophobic 1-octanethiol (OT) ligands. 2 nm-diameter AuNPs are covered with (b) all MUS and (c) 70% MUS–30% OT, respectively. (d) A 5 nm-diameter 70% MUS–30% OT AuNP. (e) A snapshot of the simulation of the 70/30 AuNP bound to the beta-1 region of the Aβ(1–40) protofibril grabbed by 5 tails. (f) Are shown an arginine (R5) and a histidine (H6) grabbing the head of a MUS ligand in the early steps of the binding of all the MUS AuNP with the Aβ(1–40) fibril. MUS ligands are colored green with the heads colored yellow (sulfur) and red (oxygen), while OT ligands are colored white. Protofibrils are colored according to amino acid hydrophobicity and charge (hydrophobic in white, hydrophilic in green, positively charged in blue, and negatively charged in red). Adapted with permission from ref. 254 (copyright 2020, American Chemical Society).

Tavanti et al., by means of replica exchange solute tempering molecular dynamics simulations (REST-MD), also reported how the chemistry of gold NPs surface can be tuned in order to have a specific binding interactions with amyloid fibrils, obtaining effective tools to control the aggregation.²⁵⁶ In this work, the authors how electrostatic interactions drive the absorption of amyloid-β monomers onto citrates-capped gold NPs (Fig. 33a–c). Importantly, upon binding, amyloid monomers show a reduced propensity in forming β-sheets secondary structures that are characteristics of mature amyloid fibrils.

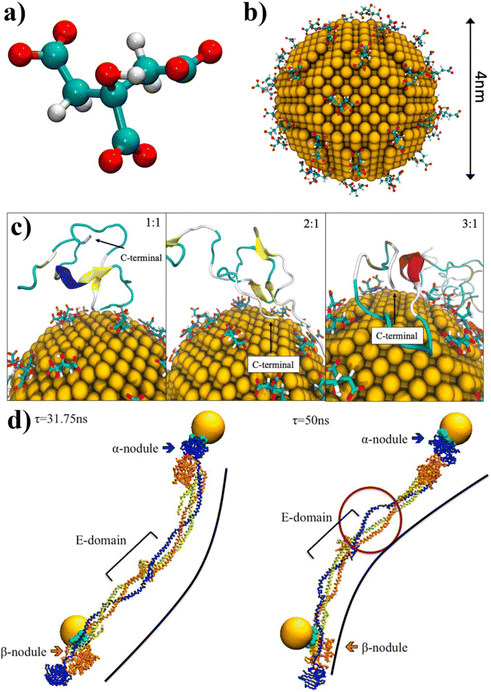Fig. 33 (a) The citrate molecule represented in ball-and-stick, and (b) a 4 nm diameter AuNP covered by citrates. (c) Representative snapshots of the adsorption of amyloid monomers onto citrate-capped AuNP at the three different ratios, respectively. Proteins are represented in cartoons colored accordingly to their secondary structures highlighting the C-terminal region. Reproduced from ref. 256. (d) Snapshots of fibrinogen, at CGMD level, bound to two citrate-coated AuNPs taken at two different time-steps (31.75 and 50 ns) during the dynamics simulation. Green beads represent amino acids in contact with AuNPs. Black line shows the bending of fibrinogen along its principal axis. In part left, the purple circle shows the partial unfolding of the α-helix bundle near the central nodule. Adapted with permission from ref. 255 (copyright 2015, American Chemical Society).

CGMD was also employed by Tavanti et al. to model citrate-coated AuNPs in interaction with insulin and fibrinogen, two of the most abundant proteins in the plasma. This work represents the potential of CGMD in modeling NPs coated or with (macro)molecular systems more complex than simple organic ligands. In particular, 5 nm citrate-stabilized AuNPs are coated by a single layer protein corona consisting of 20 insulins and 3 fibrinogens. The binding site for insulin was found to be specific and independent from the number of insulins considered in the computational simulations, whereas fibrinogen presents different binding modes, as a function of protein concentration and composition. Moreover, fibrinogen was found to be able to accommodate two citrate-coated AuNPs in independent binding sites localized at the ending nodes (Fig. 33d). A competitive process for AuNP binding was observed when insulins and fibrinogens are contemporaneously present in the simulations. The overall protein secondary structure was maintained upon binding to a single citrate-coated AuNP, but small changes in helix and sheet percentages were observed for both proteins. A partial unfolding of the α-helix bundle was found for fibrinogen bound to two AuNPs.

Coropceanu et al., by employing CGMD simulations based on a minimal model that takes into account the induced charges on the NP surface, investigated the role of dielectric mismatch between the metallic nanocrystals (NCs) and the surrounding medium on the reversibility of NCs binding. In this case, CGMD simulations revealed that the interactions of NCs with high and low dielectric constant with multivalent ions resulted in reversible and sticky NC binding, respectively (Fig. 34). This computational study was combined with the application of a modified version of DLVO theory that took into account steric repulsion mediated by the ligands at very short interparticle separation, in addition to the original attractive interaction due to dispersion forces and a repulsive term due to electrostatic repulsion. A clear focus has been given to the computed repulsive component of the interparticle potential at varying the dielectric contrast between NCs and the surrounding medium. This repulsive interaction has been found to increase with NCs with high polarizability (Fig. 34).²³⁸ Zhao et al. employed atomistic molecular dynamics simulations to better understand the mechanism underlying the trapping and release polar guest molecules between trans- and cis-azobenzene-functionalized nanoparticles. cis-Coated NPs were found to spontaneously assembled, in agreement with the experimental observations, confining several polar molecules which interacted with the NPs azobenzene-based ligands nitrogen atoms by hydrogen bonding. In contrast, trans-decorated NPs remained separated and had no appreciable affinity to polar molecules. This study revealed how ultraviolet and visible light irradiation can be used to reversibly create and destroy confined environments, where polar guest molecules can be trapped, in-between assembling colloidal nanocrystals functionalized with light-responsive ligands. This dynamic and reversible mechanism is intended to be very useful for studying chemical reactivities in confined environments and for synthesizing molecules that are otherwise hard to achieve in bulk solution.¹⁵⁹ As the latest MD contribution to this section, we like to highlight a quite captivating work performed by Santos et al., where coarse-grained MD was used in order to better comprehend how to control nanoparticle assembly via systems-level control of molecular multivalency. In this work, polymer-coated nanoparticle material where supramolecular bonding and nanoscale structure are simulated in conjunction to dictate the thermodynamics of their multivalent interactions, resulted in emergent bundling of supramolecular binding groups that would not be expected on the basis of the molecular structures alone. Additionally, Santos et al. showed that these emergent phenomena can controllably alter the superlattice symmetry by using the mesoscale particle arrangement to alter the thermodynamics of the supramolecular bonding behavior. The ability to rationally program molecular multivalency via a systems-level approach therefore provides a major step forward in the assembly of complex artificial structures, with implications for future designs of both nanoparticle-based materials and their (reversible) assembly process.²³⁹

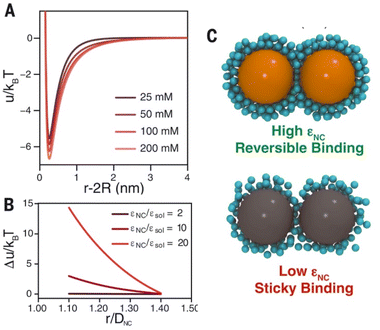Fig. 34 (A) Estimated pair potential for 4.5 nm Au NCs in the presence of different concentrations of 1 : 3 electrolyte by using a modified DLVO theory. (B) Computed repulsive component of the interparticle potential at varying dielectric contrast ε_NC/ε_sol, where ε_sol is solvent dielectric constant. The repulsive interaction increases for NCs with high polarizability. (C) MD-inspired models difference in interactions of NCs with high (ε_NC = 200) and low (ε_NC = 10) dielectric constant, with multivalent ions resulting in reversible and sticky NC binding, respectively. Figure adapted from ref. 238 (copyright 2022, American Association for the Advancement of Science).

In the last part of this section, we would like to mention the so-called hybrid quantum-mechanics (QM)/molecular-mechanics (MM) method (referenced as QM/MM),²⁵⁷ which has been widely used in computational molecular biology,^257–259 quantum chemistry^260–262 and in recent years in nanotechnology and nanoparticles-based systems.^263–267 QM/MM simulations are popular tools for the simulation of extended (i.e. millions of atoms) atomistic systems, in which the atoms in a core region of interest are treated with at quantum-mechanics level and the surrounding atoms are treated with an empirical potential.²⁵⁷ As a recent archetypical example of application of QM/MM method to study ligand-protected metal NPs, Mark et al. used such approach to untangle the complex interplay between NPs surface chemistry, ligand grafting density, ligand dynamics, NPs curvature, and interaction with environment for systems of remarkable application interest in heterogeneous catalysis, biomass upgrading, and protein adsorption.^266,267 It is without doubt that in the near future such approach will be applied directly to the modelling of NPs assembly, offering a direct look into the NPs assembly (ir)reversibility dynamics and mechanism together with the added-value of having access to the electronic structure of local regions.

4.3. Machine learning-based approaches

Machine learning (ML) holds a wide-ranging variety of algorithms and modelling tools used for many data processing tasks, which has entered most scientific disciplines in recent years. This translated into the rise of the use of ML to accelerate computational schemes aimed at understanding material phenomena. ML has been used to predict parameters, generate configurations in material simulations, design many-body (classical/coarse-grain) potentials, and classify materials properties. In a selective and non-exhaustive way, this section reviews the recent research on the interface between machine learning and the physical sciences with particular attention to works focused on NPs, NPs assembly and relevant factors related to this topic.³²

One growing field where ML schemes have been important is related to ML application to accelerate MD and FPMD simulations. Botu et al. employed kernel ridge regression to accelerate MD method for nuclei-electron systems by learning the selection of possible configurations in MD simulations, which enabled bypassing explicit simulations for several steps.²⁹¹ More recently, ML has been used to predict specific outcomes (the dissociation timescale of compounds) of first-principles MD simulations by bypassing the time evolution of the particle trajectories.²⁹² Recently, convolutional neural network-based ML “emulators” have been introduced to predict output functions (e.g., power spectrum) of simulations gaining up to two billion times acceleration.²⁹³ However, the field of application of ML that is receiving a tremendous boost in recent years is the so-called class of machine-learned potentials (MLPs). MLPs constitute a promising approach to solve computationally challenging problems in materials sciences (Fig. 35) that were previously neither accessible by classical force fields nor by computationally demanding DFT and FPMD methods.²⁹⁴

Fig. 35 System size/time scales vs. accuracy/applicability plot for dynamical approaches where machine learning potentials stands out as potential solution to the trade-off between cost and accuracy of conventional atomistic simulations. Reprinted by permission from ref. 294 (copyright 2021, Nature Publishing Group). Acronym definitions: QC, quantum-chemical; DFT, density functional theory; MM, molecular mechanics; MD, molecular dynamics, CG, coarse-grained; ML, machine learning.

Behler and Parrinello lead the way to the systematic development of MLPs,^295,296 while the fitting of force field parameters using ab initio data dates back to earlier work.^297–299 More recent breakthroughs in developing highly accurate MLPs for organic molecules and disordered or crystalline materials demonstrate that MLPs have the ability to boost materials modelling and design to an unprecedented level of prediction.^{221,300–305} In the last decade, the application of ML schemes, as a subset of the broader field of ‘artificial intelligence’ (AI), into materials science enabled a new degree of realism in NPs-based materials science. By ‘learning’ electronic-structure data (based on DFT and FPMD datasets), MLPs give access to fast simulations that still retain a first-principles accuracy. Yet, while ML data-driven research has a long history in biology or chemistry, it only rose to prominence recently in the field of NPs for assessing the role of shape and surface composition on their assembly.

Generally, a MLP fitting framework combines three components (Fig. 36a–e): a database of reference structures and associated quantum-mechanical data; the representation of atomic environments using suitable mathematical descriptors; and finally, the regression or “learning” task itself.^269,306,307

Fig. 36 (a) General overview of how MLP can be obtained: assembling a database of representative structural models, computing energies and forces using a reference quantum-mechanical method, expressing the atomic structure in “machine-readable” form using descriptors, and finally regressing (“learning”) the potential-energy surface. (b) Different types of descriptors for atomic environments, as commonly used in ML potentials. (c) The basic idea behind the SOAP representation, in which the neighbour density of a given atom is expressed through Gaussian functions centered on atoms. (d) Sketch of a neural-network architecture for fitting interatomic potential models. The atomic environment is represented by input functions, and the result is an atomic energy. (e) Schematic of kernel methods to interpolate atomic properties by comparing an environment (red) with N entries in the reference database (green). (f) Schematic of a hierarchical approach, starting with an empirical baseline (e.g., the exchange repulsion between atoms that come very close to one another), to which “machine-learned” terms are then gradually added. Figure adapted from ref. 269 (copyright 2019, Wiley-VCH).

The usefulness of MLPs has now been firmly established, with a rapidly evolving body of literature in the field, combining new methodology with practical research questions. The quality of any MLP model hinges on the quality of its input data. The choice of reference data is critical because MLP are nonparametric: they lack a physically justified functional form, and thus they have enormous variational freedom that the input data must constrain.²⁶⁹ A range of approaches has been developed for the construction of reference databases. The intended purpose of the potential primarily guides the choice of the approach: hand-built databases, iterative and active learning, automatic training/testing set selection and general-purpose databases represent just a selection of the possible choices. In terms of representation of the local environment, suitable mathematical descriptors need to be chosen with a high degree of completeness, while remaining smooth and continuous with respect to the movement of atoms. Commonly used examples are distances and angles between atoms or the many-body SOAP representation with a polynomial kernel.^306,308 Concerning the fitting operation itself, hierarchical MLP models are nowadays receiving particular attention as a viable way to overcome one of the typical issues of MLP development: typical cut-off radii of MLP enclose the first few coordination shells, but not more. This short-sight is primarily due since there are at least two distinct energy and length scales in potential-energy surfaces: the attractive regime of interatomic bond formation on the length scale of Angstrom and energy scale of electron volts and the repulsive regime between nuclei on the length scale of tenths of Angstroms and energy scale of tens of electron volts and higher. On top of this lies the challenge of properly describing the long-range dispersions forces whenever necessary. The interest and use of new mathematical representations of local environments (such as SOAP) is continuously growing even beyond the use in MLP. For instance, Gardin et al. after building on unsupervised clustering of SOAP data obtained from equilibrium MD simulations, compared a variety of soft supramolecular assemblies via a robust SOAP metric. This work highlighted the usefulness of such a tool, providing a data-driven “defectometer” to classify different types of supramolecular particles and assemblies based on the structural dynamics (continuously forming-and-repairing) of the ordered/disordered local molecular environments that statistically emerge within them.²⁴⁹

A further issue linked to current MLP is that they deal with inorganic/metallic materials or molecules-but not typically together. This hints at their direct application to the study of NP-based systems and the study of the assembly process of ligand-protected NPs. While there are connections between the two worlds (inorganic/metallic NPs-based materials and ligands), a truly unified ML potential framework that would simultaneously treat a wide range of inorganic/metallic solids and organic molecules is not currently available. One of the challenges is linked to the localized (delocalized) nature of electrons in molecules (periodic solids), respectively, and how this manifest in the different physical models and simplifications that can be made for them. Deringer et al. proposed to incorporate high-level quantum-chemistry methods inputs into fitting frameworks for materials that could powerfully aid the construction of MLP: by adding corrections on top of the (DFT-fitted) long- and short-range parts, thereby contributing to the final step of the hierarchical approach outlined here (top of the pyramid in Fig. 36f).²⁶⁹

A successful case of use of ML potentials is its application to the reproduction of NPs shapes in good agreement with DFT calculations.²⁷⁰ MLP combined to Monte Carlo simulations scheme allowed the reproduction of the formation of “onion-like” structure of the NP as the simulation progress.²⁷⁰ This approach can be applied to both gas-phase NPs as well as in a solvent environment (Fig. 37). Recently, a few exhaustive works reviewing the present state of machine-learning-driven alloy research have dedicated a great focus over the simulation through MLPs of alloy NPs and phase diagrams of particular interest for a large window of applications.^271,272

Fig. 37 Monte Carlo simulations on Au/Cu NPs, driven by an NN potential. (a) Exemplary snapshots are shown that illustrate how the “onion”-like structure gradually emerges. (b) Same for an Au/Cu nanoparticle where the ML potential includes four species, adding also H and O and, therefore, a description of explicit water molecules around the particle. Snapshots have been taken from the ESI of ref. 270. Figure adapted from ref. 269 (copyright 2019, Wiley-VCH).

Future work may now deal with more complex entities, such as ligands coming from a chemical synthesis route and designed for bringing tailored functionalities at NPs surface or promoting specific interactions with the surrounding environment.

As the last aspect related to MLP, we would like to underline that MLP represent intriguing candidates for the MM calculator in hybrid QM/MM methods. MLP potentials provide several natural advantages when employed in such a scheme, potentially offering newer, simpler QM/MM frameworks while also avoiding the need for extensive training sets to produce the MLP itself. The drawbacks of employing MLP in QM/MM schemes (so-called hybrid QM/MLP) are primarily based on the added complexity to the algorithm of training and re-training ML models.²⁶⁸

In the following will be listed other areas of application of ML approaches that are of interest for the study of NPs-base systems and their assembly mechanisms. The first one is represented by work of Long and co-authors that proposed a novel data-driven inverse design platform for self-assembling materials, named “landscape engineering”.^273,274 The first work of Long et al., inspired by the original works of Glotzer,^275,276 presented a new approach to infer systematically self-assembly pathways by nonlinear ML of molecular simulation trajectories. This approach to assembly pathway inference aimed at overcoming the previous short-sights not able to reveal the full microscopic mechanistic details of the process. The great strength of this approach was that it recovers thermodynamic assembly pathways independently of system dynamics by capturing the thermodynamically and kinetically meaningful assembly pathways within a single unified framework. In a more recent work, Long et al. proposed a landscape engineering approach where the essence is shaping the self-assembly free energy landscape to favour target aggregates’ formation by rationally manipulating building block properties (Fig. 38). The approach integrates nonlinear manifold learning with hybrid Monte Carlo techniques to efficiently recover self-assembly landscapes, which we subsequently optimize using the covariance matrix adaptation evolutionary strategy. Long et al. demonstrated the effectiveness of this technique in the design of anisotropic patchy particles to form hollow polyhedral capsids. In the case of icosahedral capsids, the approach discovers a building block possessing a 76% improvement in the assembly rate over an initial expert-designed building block. In the case of octahedral clusters, the proposed platform produces a building block with a 60% yield despite being challenged with a poor initial building block design incapable of forming stable octahedra.

Fig. 38 Self-assembly free energy landscapes for different colloidal architectures and generations in the optimization process (for the (a) icosahedron and (b) octahedron cases). The fittest candidate in the generation is projected in two collective variables furnished by the diffusion maps (Ψ₂, Ψ₃), furnished by the diffusion map. The arbitrary zero of the free energy (βF) in each system is specified by asserting that the monomer has βF = 0 (F to denote the Helmholtz free energy and β = 1/(k_bT)). In each case it is illustrated the locations in the low-dimensional embeddings corresponding to the monomer, octahedral target aggregate, icosahedral aggregate, and dimer chains. Reproduced from ref. 274 (copyright 2018, Royal Society of Chemistry).

Another field of application of ML-based schemes is their employment in data analytics with multivariate sensors based on monolayer-protected metal nanoparticles for multivariable gas and vapor sensors. In this area, multivariate statistical and machine learning methodologies are expanding their applicability not only for pattern recognition, but also for quantitative analysis of responses of multivariable sensors.²⁷⁷

Yao et al. reported the use of a customized analysis framework based on a machine learning reveals nanoparticle (assembly) dynamics from liquid phase TEM videos. This approach allowed to gain a quantitative extraction of physical and chemical parameters from the liquid-phase TEM videos. This approach paved the way to the fundamental understanding of various reaction and phase transition dynamics at nanometer resolution. In this work, a neural network-based scheme is combined to a workflow for generating simulated TEM images as the training data with well-defined ground truth. This approach targeted three typical systems of colloidal NPs, with a focus on their diffusion and interaction, reaction kinetics, and assembly dynamics, all resolved in real-time and real-space by liquid-phase TEM. A diversity of properties for differently shaped anisotropic nanoparticles are mapped, including the anisotropic interaction landscape of nanoprisms, curvature-dependent and staged etching profiles of nanorods, and an unexpected kinetic law of first-order chaining assembly of concave nanocubes. These systems representing properties at the nanoscale are otherwise experimentally inaccessible. Compared to the prevalent image segmentation methods, this approach showed a superior capability to predict nanoparticles’ position and shape boundary from a highly noisy and fluctuating background. This approach is expected to push the potential of liquid-phase TEM to its full quantitative level and to shed insights, in a high-throughput and statistically significant fashion, on the nanoscale (assembly) dynamics of synthetic and biological nanomaterials as well as ligand-protected nanoparticles.²⁷⁸

5. Conclusions and outlook

The goal of fully exploiting the properties of NPs has driven the development of strategies for their controlled and reversible assembly. A variety of strategies are already available in the scientific literature that represent valuable tools for designing nanoparticle systems that are applicable in many areas of science and technology. However, theoretical aspects related to the concept of reversibility integrated with advanced computational schemes can offer key insights into the mechanisms of nanoparticle assembly and provide the basis for improving existing strategies and developing new ones.

In this review, we have focused our efforts to bring together state-of-the-art theoretical, experimental, and computational knowledge on reversible nanoparticle assembly. From the theoretical viewpoint, extensions of the original DLVO theory developed for colloidal dispersions have been proposed for improving the qualitative description of the interactions between NPs, but further insights are required to move towards a more quantitative description of the total interaction potential between NPs and, in turn, to more reliably infer the mechanism driving their reversible assembly. Experimental strategies to control assembly are, except for those that exploit the magnetic field, based on the intermolecular interactions that occur between the ligand layers that protect the NP surface. Therefore, they have been implemented through the introduction on their outer shell of chemical moieties that, following a specific chemical, physical or biological stimulus, allow the modulation of these interactions. Assembly strategies can be arbitrarily divided on the basis of the stimulus used to trigger the assembly which, in several cases, does not coincide with that used to promote the disassembly process. Many efforts have been made to develop different strategies to drive and control assembly of NPs; the most exploited stimuli are light, temperature, specific recognition of DNA bases, and chemical stimuli, such as pH change, ligand and solvent composition. The rich variety of strategies discussed in this review already provides a toolbox for the implementation of NPs-based systems, which exploit reversible assembly, for specific applications. However, not infrequently, details about the repeatability of the assembly/disassembly process are not reported and it is therefore difficult to understand both the limitations and reliability of these systems and, consequently, their potential applicability. So far, the most numerous applications of the reversible assembly of NPs are directed to the detection of biological markers and inorganic species. Examples have also been reported where reversible assembly is exploited to control catalytic activity and develop technologically relevant applications, such as logic gates, liquid mirrors and self-erasable and rewritable materials. However, a wide range of applications, from functional devices to nanomedicine, can be envisioned for NP assemblies whose interparticle separation can be dynamically controlled, but more efforts are needed to develop reproducible and reliable systems. In this direction, computational simulations can be used and applied to gain an insightful understanding of the diverse variety of chemico-physical interactions at play during the (reversible) assembly of NPs. DFT and first-principles-based methods represent valuable tools to target individual interactions involved at the ligand/particle interface and keep track of the electronic structure of sub-systems or “small” ligand–NP systems and their temporal dynamical evolution at finite conditions. While classical and coarse-grained MD simulations allow targeting the whole self-assembly process or relevant mechanisms that interest sub-parts of it. Finally, the use of machine learning potentials, QM/ML schemes and data-driven engineering can allow going beyond the time and size limits of the DFT/FPMD methods keeping quantum mechanics accuracy and expanding the applicability of rational manipulation of NPs and their assembly towards their use for novel applications. However, to date, the majority of work has been based on the focus of sub-components of the NPs/ligands system or individual aspects of the assembly process and, therefore, a major computational challenge is the lack of metrics to characterize and monitor the crucial aspects of reversibility of the whole assembly process. As computers’ speed and capability increase, atomic simulations of NPs interactions and their assembly become increasingly practical. And so, the direct determination of the potential mean force by atomistic simulation will allow circumventing the account of individual forces and therefore resolves the nonadditivity problem that is still largely affecting the true predictive power of current theories applied to these matters.

Overall, the examples discussed make us confident that reversible assembly has great potential to be further exploited as a key strategy for future applications of NPs-based systems. In our opinion, a synergistic combination of theory and computational simulation with experimental strategies will help deepen our understanding of the mechanisms involved in the reversible assembly of NPs. In particular, this joint effort will pave the way to the rational design of NPs down to an unprecedented degree of control and address future challenges, such as the development of multicomponent reversible assemblies, asymmetric/chiral reversible assemblies, and functional reversible assemblies for specific applications.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

D. G. acknowledges support from the CNR via Progetti di Ricerca@CNR (NOENDCAT). G. O. acknowledges the HPC computing facilities of GENCI (grant DARI no. A0120807670) and of the University of Strasbourg (funded by the Equipex Équip@Meso project and the CPER Alsacalcul/Big Data) for computational allocation resources.

References

1. L. Cheng, C. Wang, L. Feng, K. Yang and Z. Liu, Chem. Rev., 2014, 114, 10869–10939.
2. W. J. Stark, P. R. Stoessel, W. Wohlleben and A. Hafner, Chem. Soc. Rev., 2015, 44, 5793–5805.
3. C. Burda, X. B. Chen, R. Narayanan and M. A. El-Sayed, Chem. Rev., 2005, 105, 1025–1102.
4. Z. He, Z. Zhang and S. Bi, Mater. Res. Express, 2020, 7, 012004.
5. M. Gu, Q. Zhang and S. Lamon, Nat. Rev. Mater., 2016, 1, 16070.
6. J. Hühn, C. Carrillo-Carrion, M. G. Soliman, C. Pfeiffer, D. Valdeperez, A. Masood, I. Chakraborty, L. Zhu, M. Gallego, Z. Yue, M. Carril, N. Feliu, A. Escudero, A. M. Alkilany, B. Pelaz, P. del Pino and W. J. Parak, Chem. Mater., 2016, 29, 399–461.
7. T. W. Kim, Y. Yang, F. Li and W. L. Kwan, NPG Asia Mater., 2012, 4, e18.
8. E. Stratakis and E. Kymakis, Mater. Today, 2013, 16, 133–146.
9. C. Clavero, Nat. Photonics, 2014, 8, 95–103.
10. A.-H. Lu, E. L. Salabas and F. Schüth, Angew. Chem., Int. Ed., 2007, 46, 1222–1244.
11. E. Boisselier and D. Astruc, Chem. Soc. Rev., 2009, 38, 1759.
12. X. Hou, T. Zaks, R. Langer and Y. Dong, Nat. Rev. Mater., 2021, 1–17.
13. Y. Eygeris, M. Gupta, J. Kim and G. Sahay, Acc. Chem. Res., 2022, 55, 2–12.
14. Z. Nie, A. Petukhova and E. Kumacheva, Nat. Nanotechnol., 2010, 5, 15–25.
15. K. J. Stebe, E. Lewandowski and M. Ghosh, Science, 2009, 325, 159–159.
16. K. Thorkelsson, P. Bai and T. Xu, Nano Today, 2015, 10, 48–66.
17. Y. Liu, J.-J. Yin and Z. Nie, Nano Res., 2014, 7, 1719–1730.
18. S. A. Majetich, T. Wen and R. A. Booth, ACS Nano, 2011, 5, 6081–6084.
19. M. C. Daniel and D. Astruc, Chem. Rev., 2004, 104, 293–346.
20. M. S. Lee, D. W. Yee, M. Ye and R. J. Macfarlane, J. Am. Chem. Soc., 2022, 144, 3330–3346.
21. J. M. Romo-Herrera, R. A. Alvarez-Puebla and L. M. Liz-Marzan, Nanoscale, 2011, 3, 1304–1315.
22. H. Zhang, Y. Liu, D. Yao and B. Yang, Chem. Soc. Rev., 2012, 41, 6066–6088.
23. J. K. Stolarczyk, A. Deak and D. F. Brougham, Adv. Mater., 2016, 28, 5400–5424.
24. L. Chen, B. Su and L. Jiang, Chem. Soc. Rev., 2019, 48, 8–21.
25. C. Yi, Y. Yang, B. Liu, J. He and Z. Nie, Chem. Soc. Rev., 2020, 49, 465–508.
26. Z. Lu and Y. Yin, Chem. Soc. Rev., 2012, 41, 6874–6887.
27. M. Grzelczak, J. Vermant, E. M. Furst and L. M. Liz-Marzán, ACS Nano, 2010, 4, 3591–3605.
28. L. Cademartiri and K. J. M. Bishop, Nat. Mater., 2014, 14, 2.
29. N. Vogel, M. Retsch, C.-A. Fustin, A. del Campo and U. Jonas, Chem. Rev., 2015, 115, 6265–6311.
30. S. Y. Zhang, M. D. Regulacio and M. Y. Han, Chem. Soc. Rev., 2014, 43, 2301–2323.
31. K. Liu, N. Zhao and E. Kumacheva, Chem. Soc. Rev., 2011, 40, 656–671.
32. M. Dijkstra and E. Luijten, Nat. Mater., 2021, 20, 762–773.
33. S. G. Louie, Y.-H. Chan, F. H. da Jornada, Z. Li and D. Y. Qiu, Nat. Mater., 2021, 20, 728–735.
34. A. Rao, S. Roy, V. Jain and P. P. Pillai, ACS Appl. Mater. Interfaces, 2022 DOI:10.1021/acsami.2c05378.
35. T. Hueckel, G. M. Hocky and S. Sacanna, Nat. Rev. Mater., 2021, 6, 1053–1069.
36. R. J. Macfarlane, Nano Lett., 2021, 21, 7432–7434.
37. H. T. Phan and A. J. Haes, J. Phys. Chem. C, 2019, 123, 16495–16507.
38. E. M. Hotze, T. Phenrat and G. V. Lowry, J. Environ. Qual., 2010, 39, 1909–1924.
39. B. Deraguin and L. Landau, Acta Physicochim. URSS, 1941, 14, 633–662.
40. E. Verwey and J. T. G. Overbeek, Theory of the stability of lyophobic colloids, Elsevier, Amsterdam, 1948.
41. J. N. Israelachvili, Intermolecular and Surface Forces, Elsevier Science, 2015.
42. B. W. Ninham, Adv. Colloid Interface Sci., 1999, 83, 1–17.
43. D. G. Capco and Y. Chen, Nanomaterial: Impacts on Cell Biology and Medicine, Springer, Netherlands, 2014.
44. K. J. Bishop, C. E. Wilmer, S. Soh and B. A. Grzybowski, Small, 2009, 5, 1600–1630.
45. A. M. Kalsin, B. Kowalczyk, S. K. Smoukov, R. Klajn and B. A. Grzybowski, J. Am. Chem. Soc., 2006, 128, 15046–15047.
46. A. M. Kalsin, M. Fialkowski, M. Paszewski, S. K. Smoukov, K. J. M. Bishop and B. A. Grzybowski, Science, 2006, 312, 420–424.
47. H. Nakanishi, A. Deak, G. Hollo and I. Lagzi, Angew. Chem., Int. Ed., 2018, 57, 16062–16066.
48. A. Rao, G. S. Kumar, S. Roy, A. T. Rajesh, G. Devatha and P. P. Pillai, ACS Appl. Nano Mater., 2019, 2, 5625–5633.
49. N. I. Lebovka, in Polyelectrolyte Complexes in the Dispersed and Solid State I: Principles and Theory, ed. M. Müller, Springer Berlin Heidelberg, Berlin, Heidelberg, 2014, pp. 57–96.
50. W. A. Ducker, T. J. Senden and R. M. Pashley, Nature, 1991, 353, 239–241.
51. S. L. Eichmann, S. G. Anekal and M. A. Bevan, Langmuir, 2008, 24, 714–721.
52. L. Tong, V. D. Miljković, P. Johansson and M. Käll, Nano Lett., 2011, 11, 4505–4508.
53. C. A. S. Batista, R. G. Larson and N. A. Kotov, Science, 2015, 350, 1242477.
54. J. Faraudo, J. S. Andreu and J. Camacho, Soft Matter, 2013, 9, 6654–6664.
55. M. W. Hahn and C. R. O'Melia, Environ. Sci. Technol., 2004, 38, 210–220.
56. J. Faraudo and J. Camacho, Colloid Polym. Sci., 2009, 288, 207–215.
57. N. Tufenkji and M. Elimelech, Langmuir, 2005, 21, 841–852.
58. M. Elimelech and C. R. O'Melia, Langmuir, 1990, 6, 1153–1163.
59. C. Shen, B. Li, Y. Huang and Y. Jin, Environ. Sci. Technol., 2007, 41, 6976–6982.
60. H. Minami, T. Inoue and R. Shimozawa, Langmuir, 1996, 12, 3574–3579.
61. M. W. Hahn, D. Abadzic and C. R. O'Melia, Environ. Sci. Technol., 2004, 38, 5915–5924.
62. G. Odriozola, R. Leone, A. Schmitt, J. Callejas-Fernández, R. Martínez-García and R. Hidalgo-Álvarez, J. Chem. Phys., 2004, 121, 5468–5481.
63. M. Cortada, J. A. Anta and J. A. Molina-Bolívar, J. Phys. Chem. B, 2007, 111, 1110–1118.
64. N. Kovalchuk, V. Starov, P. Langston and N. Hilal, Colloid J., 2009, 71, 503–513.
65. C. Rodrıguez-Abreu, Nanocolloids, 2016, ch. 1.
66. X. Li, X. Liu and X. Liu, Chem. Soc. Rev., 2021, 50, 2074–2101.
67. M. A. Boles, M. Engel and D. V. Talapin, Chem. Rev., 2016, 116, 11220–11289.
68. E. Piacenza, A. Presentato and R. J. Turner, Crit. Rev. Biotechnol., 2018, 38, 1137–1156.
69. A. O. Pinchuk, J. Phys. Chem. C, 2012, 116, 20099–20102.
70. L. A. Wijenayaka, M. R. Ivanov, C. M. Cheatum and A. J. Haes, J. Phys. Chem. C, 2015, 119, 10064–10075.
71. H. Zhang and D. Wang, Angew. Chem., Int. Ed., 2008, 47, 3984–3987.
72. D. Gentili, G. Ori, L. Ortolani, V. Morandi and M. Cavallini, ChemNanoMat, 2017, 3, 874–878.
73. A. Valsesia, C. Desmet, I. Ojea-Jiménez, A. Oddo, R. Capomaccio, F. Rossi and P. Colpo, Commun. Chem., 2018, 1, 53.
74. A. Sánchez-Iglesias, M. Grzelczak, T. Altantzis, B. Goris, J. Pérez-Juste, S. Bals, G. Van Tendeloo, S. H. Donaldson, B. F. Chmelka, J. N. Israelachvili and L. M. Liz-Marzán, ACS Nano, 2012, 6, 11059–11065.
75. Y. Lalatonne, J. Richardi and M. P. Pileni, Nat. Mater., 2004, 3, 121–125.
76. A. Kostopoulou, K. Brintakis, M. Vasilakaki, K. N. Trohidou, A. P. Douvalis, A. Lascialfari, L. Manna and A. Lappas, Nanoscale, 2014, 6, 3764–3776.
77. G. L. Nealon, B. Donnio, R. Greget, J.-P. Kappler, E. Terazzi and J.-L. Gallani, Nanoscale, 2012, 4, 5244–5258.
78. R. Gréget, G. L. Nealon, B. Vileno, P. Turek, C. Mény, F. Ott, A. Derory, E. Voirin, E. Rivière, A. Rogalev, F. Wilhelm, L. Joly, W. Knafo, G. Ballon, E. Terazzi, J.-P. Kappler, B. Donnio and J.-L. Gallani, ChemPhysChem, 2012, 13, 3092–3097.
79. W. Xi, H. T. Phan and A. J. Haes, Anal. Bioanal. Chem., 2018, 410, 6113–6123.
80. I. T. Koponen, Phys. A, 2009, 388, 2659–2665.
81. K. Barros and E. Luijten, Phys. Rev. Lett., 2014, 113, 017801.
82. D. F. Parsons, M. Bostrom, T. J. Maceina, A. Salis and B. W. Ninham, Langmuir, 2010, 26, 3323–3328.
83. B. Bozorgui, D. Meng, S. K. Kumar, C. Chakravarty and A. Cacciuto, Nano Lett., 2013, 13, 2732–2737.
84. M. Bostrom, D. R. Williams and B. W. Ninham, Phys. Rev. Lett., 2001, 87, 168103.
85. A. Widmer-Cooper and P. Geissler, Nano Lett., 2014, 14, 57–65.
86. G. I. Guerrero-García, P. González-Mozuelos and M. Olvera de la Cruz, ACS Nano, 2013, 7, 9714–9723.
87. S. Franco-Ulloa, G. Tatulli, S. L. Bore, M. Moglianetti, P. P. Pompa, M. Cascella and M. De Vivo, Nat. Commun., 2020, 11, 5422.
88. J. Xia, M. Lee, P. J. Santos, N. Horst, R. J. Macfarlane, H. Guo and A. Travesset, Soft Matter, 2022, 18, 2176–2192.
89. M. Grzelczak, L. M. Liz-Marzan and R. Klajn, Chem. Soc. Rev., 2019, 48, 1342–1361.
90. D.-L. Long, R. Tsunashima and L. Cronin, Angew. Chem., Int. Ed., 2010, 49, 1736–1758.
91. E. Marino, T. E. Kodger, J. B. ten Hove, A. H. Velders and P. Schall, Sol. Energy Mater. Sol. Cells, 2016, 158, 154–159.
92. S. Mohammed, I. Kuzmenko and G. Gadikota, Nanoscale, 2021, 14, 127–139.
93. J. Zha, Z. Yuan, Z. Zhou, Y. Li, J. Zhao, Z. Zeng, L. Zhen, H. Tai, C. Tan and H. Zhang, Small Struct., 2021, 2, 2100067.
94. Z. Lai, Y. Chen, C. Tan, X. Zhang and H. Zhang, Chem, 2016, 1, 59–77.
95. C. Tan, X. Qi, Z. Liu, F. Zhao, H. Li, X. Huang, L. Shi, B. Zheng, X. Zhang, L. Xie, Z. Tang, W. Huang and H. Zhang, J. Am. Chem. Soc., 2015, 137, 1565–1571.
96. J. B. Addison, W. S. Weber, Q. Mou, N. N. Ashton, R. J. Stewart, G. P. Holland and J. L. Yarger, Biomacromolecules, 2014, 15, 1269–1275.
97. C. A. Mirkin, R. L. Letsinger, R. C. Mucic and J. J. Storhoff, Nature, 1996, 382, 607–609.
98. J. J. Storhoff, A. A. Lazarides, R. C. Mucic, C. A. Mirkin, R. L. Letsinger and G. C. Schatz, J. Am. Chem. Soc., 2000, 122, 4640–4650.
99. R. C. Jin, G. S. Wu, Z. Li, C. A. Mirkin and G. C. Schatz, J. Am. Chem. Soc., 2003, 125, 1643–1654.
100. Z. Li, Z. Zhu, W. Liu, Y. Zhou, B. Han, Y. Gao and Z. Tang, J. Am. Chem. Soc., 2012, 134, 3322–3325.
101. H.-G. Park, J. H. Joo, H.-G. Kim and J.-S. Lee, J. Phys. Chem. C, 2012, 116, 2278–2284.
102. J.-Y. Kim and J.-S. Lee, Nano Lett., 2009, 9, 4564–4569.
103. P. Hazarika, B. Ceyhan and C. M. Niemeyer, Angew. Chem., Int. Ed., 2004, 43, 6469–6471.
104. I. A. Trantakis, S. Bolisetty, R. Mezzenga and S. J. Sturla, Langmuir, 2013, 29, 10824–10830.
105. Y. H. Jung, K. B. Lee, Y. G. Kim and I. S. Choi, Angew. Chem., Int. Ed., 2006, 45, 5960–5963.
106. J. Sharma, R. Chhabra, H. Yan and Y. Liu, Chem. Commun., 2007, 477–479.
107. R. Elghanian, J. J. Storhoff, R. C. Mucic, R. L. Letsinger and C. A. Mirkin, Science, 1997, 277, 1078.
108. K. Lee, V. P. Drachev and J. Irudayaraj, ACS Nano, 2011, 5, 2109–2117.
109. K. L. Gurunatha, A. C. Fournier, A. Urvoas, M. Valerio-Lepiniec, V. Marchi, P. Minard and E. Dujardin, ACS Nano, 2016, 10, 3176–3185.
110. K. Aslan, C. C. Luhrs and V. H. Pérez-Luna, J. Phys. Chem. B, 2004, 108, 15631–15639.
111. H. Otsuka, Y. Akiyama, Y. Nagasaki and K. Kataoka, J. Am. Chem. Soc., 2001, 123, 8226–8230.
112. G. von Maltzahn, D. H. Min, Y. Zhang, J. H. Park, T. J. Harris, M. Sailor and S. N. Bhatia, Adv. Mater., 2007, 19, 3579–3583.
113. T. Bian, A. Gardin, J. Gemen, L. Houben, C. Perego, B. Lee, N. Elad, Z. Chu, G. M. Pavan and R. Klajn, Nat. Chem., 2021, 13, 940–949.
114. S. Si and T. K. Mandal, Langmuir, 2007, 23, 190–195.
115. D. Wang, B. Kowalczyk, I. Lagzi and B. A. Grzybowski, J. Phys. Chem. Lett., 2010, 1, 1459–1462.
116. C. Fan, T. Bian, L. Shang, R. Shi, L. Z. Wu, C. H. Tung and T. Zhang, Nanoscale, 2016, 8, 3923–3925.
117. I. Lagzi, B. Kowalczyk, D. W. Wang and B. A. Grzybowski, Angew. Chem., Int. Ed., 2010, 49, 8616–8619.
118. H. Nabika, T. Oikawa, K. Iwasaki, K. Murakoshi and K. Unoura, J. Phys. Chem. C, 2012, 116, 6153–6158.
119. S. Chen, C. X. Guo, Q. Zhao and X. Lu, Chem. – Eur. J., 2014, 20, 14057–14062.
120. F. Reincke, W. K. Kegel, H. Zhang, M. Nolte, D. Wang, D. Vanmaekelbergh and H. Möhwald, Phys. Chem. Chem. Phys., 2006, 8, 3828–3835.
121. V. A. Turek, M. P. Cecchini, J. Paget, A. R. Kucernak, A. A. Kornyshev and J. B. Edel, ACS Nano, 2012, 6, 7789–7799.
122. M. Luo, G. K. Olivier and J. Frechette, Soft Matter, 2012, 8, 11923–11932.
123. D. Li, Q. He, Y. Cui and J. Li, Chem. Mater., 2007, 19, 412–417.
124. L. Liu, Z. Gao, B. Jiang, Y. Bai, W. Wang and Y. Yin, Nano Lett., 2018, 18, 5312–5318.
125. M. Lattuada and T. A. Hatton, J. Am. Chem. Soc., 2007, 129, 12878–12889.
126. Z. Sun, W. Ni, Z. Yang, X. Kou, L. Li and J. Wang, Small, 2008, 4, 1287–1292.
127. Y. Guo, Y. Ma, L. Xu, J. Li and W. Yang, J. Phys. Chem. C, 2007, 111, 9172–9176.
128. J.-Y. Shim and V. K. Gupta, J. Colloid Interface Sci., 2007, 316, 977–983.
129. D. A. Walker and V. K. Gupta, Nanotechnology, 2008, 19, 435603.
130. J. Zhang, D. Han, H. Zhang, M. Chaker, Y. Zhao and D. Ma, Chem. Commun., 2012, 48, 11510–11512.
131. I. I. S. Lim, W. Ip, E. Crew, P. N. Njoki, D. Mott, C.-J. Zhong, Y. Pan and S. Zhou, Langmuir, 2007, 23, 826–833.
132. I. I. S. Lim, D. Mott, W. Ip, P. N. Njoki, Y. Pan, S. Zhou and C.-J. Zhong, Langmuir, 2008, 24, 8857–8863.
133. P. Graf, A. Mantion, A. Foelske, A. Shkilnyy, A. Masic, A. F. Thunemann and A. Taubert, Chemistry, 2009, 15, 5831–5844.
134. P. Taladriz-Blanco, N. J. Buurma, L. Rodriguez-Lorenzo, J. Perez-Juste, L. M. Liz-Marzan and P. Herves, J. Mater. Chem., 2011, 21, 16880–16887.
135. H. He, J. E. Ostwaldt, C. Hirschhauser, C. Schmuck and J. Niemeyer, Small, 2020, 16, e2001044.
136. M. Grzelczak, A. Sánchez-Iglesias and L. M. Liz-Marzán, Soft Matter, 2013, 9, 9094–9098.
137. A. Sanchez-Iglesias, N. Claes, D. M. Solis, J. M. Taboada, S. Bals, L. M. Liz-Marzan and M. Grzelczak, Angew. Chem., Int. Ed., 2018, 57, 3183–3186.
138. R. M. Choueiri, A. Klinkova, H. Therien-Aubin, M. Rubinstein and E. Kumacheva, J. Am. Chem. Soc., 2013, 135, 10262–10265.
139. L. Cheng, A. Liu, S. Peng and H. Duan, ACS Nano, 2010, 4, 6098–6104.
140. H. Hu, F. Ji, Y. Xu, J. Yu, Q. Liu, L. Chen, Q. Chen, P. Wen, Y. Lifshitz, Y. Wang, Q. Zhang and S. T. Lee, ACS Nano, 2016, 10, 7323–7330.
141. Y. Kim, R. C. Johnson and J. T. Hupp, Nano Lett., 2001, 1, 165–167.
142. S. Si, M. Raula, T. K. Paira and T. K. Mandal, ChemPhysChem, 2008, 9, 1578–1584.
143. L. Zhu, D. H. Xue and Z. X. Wang, Langmuir, 2008, 24, 11385–11389.
144. A. Rao, S. Roy, M. Unnikrishnan, S. S. Bhosale, G. Devatha and P. P. Pillai, Chem. Mater., 2016, 28, 2348–2355.
145. J. Su, X. Huang and M. Yang, Eur. J. Inorg. Chem., 2020, 2020, 4477–4482.
146. T. S. Sreeprasad and T. Pradeep, Langmuir, 2011, 27, 3381–3390.
147. C. Guarise, L. Pasquato and P. Scrimin, Langmuir, 2005, 21, 5537–5541.
148. Z. Luan, T. Salk, A. Abelson, S. Jean and M. Law, J. Phys. Chem. C, 2019, 123, 23643–23654.
149. Z. Liu and M. Jiang, J. Mater. Chem., 2007, 17, 4249–4254.
150. K. Naka, H. Itoh and Y. Chujo, Langmuir, 2003, 19, 5496–5501.
151. M. A. Olson, A. Coskun, R. Klajn, L. Fang, S. K. Dey, K. P. Browne, B. A. Grzybowski and J. F. Stoddart, Nano Lett., 2009, 9, 3185–3190.
152. R. Klajn, M. A. Olson, P. J. Wesson, L. Fang, A. Coskun, A. Trabolsi, S. Soh, J. F. Stoddart and B. A. Grzybowski, Nat. Chem., 2009, 1, 733–738.
153. R. Klajn, K. J. M. Bishop and B. A. Grzybowski, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 10305.
154. R. Klajn, P. J. Wesson, K. J. M. Bishop and B. A. Grzybowski, Angew. Chem., Int. Ed., 2009, 48, 7035–7039.
155. Y. Wei, S. Han, J. Kim, S. Soh and B. A. Grzybowski, J. Am. Chem. Soc., 2010, 132, 11018–11020.
156. J. V. Rival, Nonappa and E. S. Shibu, ACS Appl. Mater. Interfaces, 2020, 12, 14569–14577.
157. S. Das, P. Ranjan, P. S. Maiti, G. Singh, G. Leitus and R. Klajn, Adv. Mater., 2013, 25, 422–426.
158. O. Chovnik, R. Balgley, J. R. Goldman and R. Klajn, J. Am. Chem. Soc., 2012, 134, 19564–19567.
159. H. Zhao, S. Sen, T. Udayabhaskararao, M. Sawczyk, K. Kucanda, D. Manna, P. K. Kundu, J. W. Lee, P. Kral and R. Klajn, Nat. Nanotechnol., 2016, 11, 82–88.
160. C. Raimondo, F. Reinders, U. Soydaner, M. Mayor and P. Samorì, Chem. Commun., 2010, 46, 1147–1149.
161. D. Liu, W. Chen, K. Sun, K. Deng, W. Zhang, Z. Wang and X. Jiang, Angew. Chem., Int. Ed., 2011, 50, 4103–4107.
162. Y. Shiraishi, E. Shirakawa, K. Tanaka, H. Sakamoto, S. Ichikawa and T. Hirai, ACS Appl. Mater. Interfaces, 2014, 6, 7554–7562.
163. P. K. Kundu, S. Das, J. Ahrens and R. Klajn, Nanoscale, 2016, 8, 19280–19286.
164. L. Zhang, L. Dai, Y. Rong, Z. Liu, D. Tong, Y. Huang and T. Chen, Langmuir, 2015, 31, 1164–1171.
165. N. S. Bell and M. Piech, Langmuir, 2006, 22, 1420–1427.
166. P. K. Kundu, D. Samanta, R. Leizrowice, B. Margulis, H. Zhao, M. Boerner, T. Udayabhaskararao, D. Manna and R. Klajn, Nat. Chem., 2015, 7, 646–652.
167. H. He, M. Feng, Q. Chen, X. Zhang and H. Zhan, Angew. Chem., Int. Ed., 2016, 55, 936–940.
168. Y. Chen, Z. Wang, Y. He, Y. J. Yoon, J. Jung, G. Zhang and Z. Lin, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, E1391–E1400.
169. M.-Q. Zhu, L.-Q. Wang, G. J. Exarhos and A. D. Q. Li, J. Am. Chem. Soc., 2004, 126, 2656–2657.
170. D. Fava, M. a. Winnik and E. Kumacheva, Chem. Commun., 2009, 2571–2573.
171. H. Han, J. Y. Lee and X. Lu, Chem. Commun., 2013, 49, 6122–6124.
172. T. Ding, V. K. Valev, A. R. Salmon, C. J. Forman, S. K. Smoukov, O. A. Scherman, D. Frenkel and J. J. Baumberg, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 5503–5507.
173. Y. Shen, M. Kuang, Z. Shen, J. Nieberle, H. Duan and H. Frey, Angew. Chem., Int. Ed., 2008, 47, 2227–2230.
174. K. L. Hamner and M. M. Maye, Langmuir, 2013, 29, 15217–15223.
175. C. Durand-Gasselin, M. Capelot, N. Sanson and N. Lequeux, Langmuir, 2010, 26, 12321–12329.
176. C. Durand-Gasselin, N. Sanson and N. Lequeux, Langmuir, 2011, 27, 12329–12335.
177. S. Balasubramaniam, N. Pothayee, Y. Lin, M. House, R. C. Woodward, T. G. St. Pierre, R. M. Davis and J. S. Riffle, Chem. Mater., 2011, 23, 3348–3356.
178. Z. Zhang, S. Maji, A. B. d. F. Antunes, R. De Rycke, Q. Zhang, R. Hoogenboom and B. G. De Geest, Chem. Mater., 2013, 25, 4297–4303.
179. N. Nath and A. Chilkoti, J. Am. Chem. Soc., 2001, 123, 8197–8202.
180. H.-C. Huang, P. Koria, S. M. Parker, L. Selby, Z. Megeed and K. Rege, Langmuir, 2008, 24, 14139–14144.
181. Y. Lin, X. Xia, M. Wang, Q. Wang, B. An, H. Tao, Q. Xu, F. Omenetto and D. L. Kaplan, Langmuir, 2014, 30, 4406–4414.
182. V. Lemieux, P. H. H. M. Adams and J. C. M. van Hest, Chem. Commun., 2010, 46, 3071–3073.
183. Y. D. Liu, X. G. Han, L. He and Y. D. Yin, Angew. Chem., Int. Ed., 2012, 51, 6373–6377.
184. J. Zhang, P. J. Santos, P. A. Gabrys, S. Lee, C. Liu and R. J. Macfarlane, J. Am. Chem. Soc., 2016, 138, 16228–16231.
185. Y. Yu, D. Yu and C. A. Orme, Nano Lett., 2017, 17, 3862–3869.
186. B. Su, J.-P. Abid, D. J. Fermín, H. H. Girault, H. Hoffmannová, P. Krtil and Z. Samec, J. Am. Chem. Soc., 2004, 126, 915–919.
187. J.-P. Abid, M. Abid, C. Bauer, H. H. Girault and P.-F. Brevet, J. Phys. Chem. C, 2007, 111, 8849–8855.
188. S. G. Booth, D. P. Cowcher, R. Goodacre and R. A. Dryfe, Chem. Commun., 2014, 50, 4482–4484.
189. Y. Montelongo, D. Sikdar, Y. Ma, A. J. S. McIntosh, L. Velleman, A. R. Kucernak, J. B. Edel and A. A. Kornyshev, Nat. Mater., 2017, 16, 1127–1135.
190. C. T. Yavuz, J. T. Mayo, W. W. Yu, A. Prakash, J. C. Falkner, S. Yean, L. Cong, H. J. Shipley, A. Kan, M. Tomson, D. Natelson and V. L. Colvin, Science, 2006, 314, 964.
191. J. Ge, Y. Hu and Y. Yin, Angew. Chem., Int. Ed., 2007, 46, 7428–7431.
192. J. Ge, Y. Hu, T. Zhang, T. Huynh and Y. Yin, Langmuir, 2008, 24, 3671–3680.
193. L. He, Y. Hu, H. Kim, J. Ge, S. Kwon and Y. Yin, Nano Lett., 2010, 10, 4708–4714.
194. S. Sim, D. Miyajima, T. Niwa, H. Taguchi and T. Aida, J. Am. Chem. Soc., 2015, 137, 4658–4661.
195. C. J. Murphy, A. M. Gole, J. W. Stone, P. N. Sisco, A. M. Alkilany, E. C. Goldsmith and S. C. Baxter, Acc. Chem. Res., 2008, 41, 1721–1730.
196. P. K. Jain, X. Huang, I. H. El-Sayed and M. a. El-Sayed, Acc. Chem. Res., 2008, 41, 1578–1586.
197. D. Gentili, G. Ori and M. C. Franchini, Chem. Commun., 2009, 5874–5876.
198. R. J. Macfarlane, B. Lee, M. R. Jones, N. Harris, G. C. Schatz and C. A. Mirkin, Science, 2011, 334, 204–208.
199. T. Isojima, M. Lattuada, J. B. Vander Sande and T. A. Hatton, ACS Nano, 2008, 2, 1799–1806.
200. M. S. Strozyk, M. Chanana, I. Pastoriza-Santos, J. Pérez-Juste and L. M. Liz-Marzán, Adv. Funct. Mater., 2012, 22, 1436–1444.
201. P. L. Anelli, P. R. Ashton, N. Spencer, A. M. Z. Slawin, J. F. Stoddart and D. J. Williams, Angew. Chem., Int. Ed. Engl., 1991, 30, 1036–1039.
202. M. Barbalinardo, J. Bertacchini, L. Bergamini, M. S. Magaro, L. Ortolani, A. Sanson, C. Palumbo, M. Cavallini and D. Gentili, Nanoscale, 2021, 13, 14119–14129.
203. M. Barbalinardo, F. Caicci, M. Cavallini and D. Gentili, Small, 2018, 14, 1801219.
204. F. Decataldo, M. Barbalinardo, D. Gentili, M. Tessarolo, M. Calienni, M. Cavallini and B. Fraboni, Adv. Biosyst., 2020, 4, 1900204.
205. T. Bian, Z. Chu and R. Klajn, Adv. Mater., 2020, 32, 1905866.
206. H. Yoshikawa, T. Matsui and H. Masuhara, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 70, 061406.
207. L. Lin, X. Peng, M. Wang, L. Scarabelli, Z. Mao, L. M. Liz-Marzan, M. F. Becker and Y. Zheng, ACS Nano, 2016, 10, 9659–9668.
208. C.-Y. Kang, J.-J. Li, L.-A. Wu, C.-C. Wu and Y.-F. Chen, Part. Part. Syst. Charact., 2018, 35, 1700405.
209. M. P. Konrad, A. P. Doherty and S. E. J. Bell, Anal. Chem., 2013, 85, 6783–6789.
210. P.-P. Fang, S. Chen, H. Deng, M. D. Scanlon, F. Gumy, H. J. Lee, D. Momotenko, V. Amstutz, F. Cortés-Salazar, C. M. Pereira, Z. Yang and H. H. Girault, ACS Nano, 2013, 7, 9241–9248.
211. A. Kotnala and Y. Zheng, Part. Part. Syst. Charact., 2019, 36, 1900152.
212. B. Gates and Y. Xia, Adv. Mater., 2001, 13, 1605–1608.
213. R. M. Erb, H. S. Son, B. Samanta, V. M. Rotello and B. B. Yellen, Nature, 2009, 457, 999–1002.
214. A. F. Demirörs, P. P. Pillai, B. Kowalczyk and B. A. Grzybowski, Nature, 2013, 503, 99–103.
215. J. H. Schenkel, A. Samanta and B. J. Ravoo, Adv. Mater., 2014, 26, 1076–1080.
216. O. Gleeson, R. Tekoriute, Y. K. Gun'ko and S. J. Connon, Chem. – Eur. J., 2009, 15, 5669–5673.
217. P. Riente, J. Yadav and M. A. Pericàs, Org. Lett., 2012, 14, 3668–3671.
218. C. Ó. Dálaigh, S. a. Corr, Y. Gun’ko and S. J. Connon, Angew. Chem., Int. Ed., 2007, 46, 4329–4332.
219. D. Guin, B. Baruwati and S. V. Manorama, Org. Lett., 2007, 9, 1419–1421.
220. L. He, M. Wang, J. Ge and Y. Yin, Acc. Chem. Res., 2012, 45, 1431–1440.
221. S. Malola and H. Häkkinen, Nat. Commun., 2021, 12, 2197.
222. F. Muniz-Miranda, M. C. Menziani and A. Pedone, J. Phys. Chem. C, 2014, 118, 7532–7544.
223. S. Caporali, F. Muniz-Miranda, A. Pedone and M. Muniz-Miranda, Sensors, 2019, 19, 2700.
224. Nonappa, J. S. Haataja, J. V. I. Timonen, S. Malola, P. Engelhardt, N. Houbenov, M. Lahtinen, H. Häkkinen and O. Ikkala, Angew. Chem., Int. Ed., 2017, 56, 6473–6477.
225. J. Zhang, F. Tian, M. Zhang, T. Li, X. Kong, Y. Zhou and N. A. Kotov, Nanoscale Horiz., 2019, 4, 1416–1424.
226. J. K. Roy, E. S. Vasquez, H. P. Pinto, S. Kumari, K. B. Walters and J. Leszczynski, Phys. Chem. Chem. Phys., 2019, 21, 23320–23328.
227. B. Özdamar, A. Bouzid, G. Ori, C. Massobrio and M. Boero, J. Chem. Theory Comput., 2018, 14, 225–235.
228. G. Cotin, C. Kiefer, F. Perton, M. Boero, B. Özdamar, A. Bouzid, G. Ori, C. Massobrio, D. Begin, B. Pichon, D. Mertz and S. Begin-Colin, ACS Appl. Nano Mater., 2018, 1, 4306–4316.
229. B. Farkaš, U. Terranova and N. H. de Leeuw, Phys. Chem. Chem. Phys., 2020, 22, 985–996.
230. Z. Huang, Z.-J. Zhao, Q. Zhang, L. Han, X. Jiang, C. Li, M. T. P. Cardenas, P. Huang, J.-J. Yin, J. Luo, J. Gong and Z. Nie, Nat. Commun., 2019, 10, 219.
231. M. Azubel, J. Koivisto, S. Malola, D. Bushnell, L. Hura Greg, L. Koh Ai, H. Tsunoyama, T. Tsukuda, M. Pettersson, H. Häkkinen and D. Kornberg Roger, Science, 2014, 345, 909–912.
232. M. Azubel, A. L. Koh, K. Koyasu, T. Tsukuda and R. D. Kornberg, ACS Nano, 2017, 11, 11866–11871.
233. N. Mammen, S. Malola, K. Honkala and H. Häkkinen, Nanoscale, 2020, 12, 23859–23868.
234. G. Lin, S. W. Chee, S. Raj, P. Král and U. Mirsaidov, ACS Nano, 2016, 10, 7443–7450.
235. D. A. Welch, T. J. Woehl, C. Park, R. Faller, J. E. Evans and N. D. Browning, ACS Nano, 2016, 10, 181–187.
236. M. K. Bera, H. Chan, D. F. Moyano, H. Yu, S. Tatur, D. Amoanu, W. Bu, V. M. Rotello, M. Meron, P. Král, B. Lin and M. L. Schlossman, Nano Lett., 2014, 14, 6816–6822.
237. Z. Fan and M. Grünwald, J. Am. Chem. Soc., 2019, 141, 1980–1988.
238. I. Coropceanu, E. M. Janke, J. Portner, D. Haubold, T. D. Nguyen, A. Das, C. P. N. Tanner, J. K. Utterback, S. W. Teitelbaum, M. H. Hudson, N. A. Sarma, A. M. Hinkle, C. J. Tassone, A. Eychmüller, D. T. Limmer, M. Olvera de la Cruz, N. S. Ginsberg and D. V. Talapin, Science, 2022, 375, 1422–1426.
239. P. J. Santos, Z. Cao, J. Zhang, A. Alexander-Katz and R. J. Macfarlane, J. Am. Chem. Soc., 2019, 141, 14624–14632.
240. S. F. Tan, S. Raj, G. Bisht, H. V. Annadata, C. A. Nijhuis, P. Král and U. Mirsaidov, Adv. Mater., 2018, 30, 1707077.
241. G. Copie, M. Biaye, H. Diesinger, T. Melin, C. Krzeminski and F. Cleri, Langmuir, 2017, 33, 2677–2687.
242. G. Ori, D. Gentili, M. Cavallini, M. C. Franchini, M. Zapparoli, M. Montorsi and C. Siligardi, Nanotechnology, 2012, 23, 055605.
243. A. Widmer-Cooper and P. L. Geissler, ACS Nano, 2016, 10, 1877–1887.
244. X. P. Liu, Y. Ni and L. H. He, Nanotechnology, 2016, 27, 135707.
245. Z. Fan and M. Gruenwald, ChemRxiv, 2019,  DOI:10.26434/chemrxiv.9178037.v1.
246. S. Maity, D. Bain and A. Patra, Nanoscale, 2019, 11, 22685–22723.
247. C. Waltmann, N. Horst and A. Travesset, J. Chem. Phys., 2018, 149, 034109.
248. M. Yang, H. Chan, G. Zhao, J. H. Bahng, P. Zhang, P. Král and N. A. Kotov, Nat. Chem., 2017, 9, 287–294.
249. A. Gardin, C. Perego, G. Doni and G. M. Pavan, Commun. Chem., 2022, 5 DOI:10.1038/s42004-022-00699-z.
250. T. Kister, D. Monego, P. Mulvaney, A. Widmer-Cooper and T. Kraus, ACS Nano, 2018, 12, 5969–5977.
251. C. Waltmann, N. Horst and A. Travesset, ACS Nano, 2017, 11, 11273–11282.
252. H. O. S. Yadav, G. Shrivastav, M. Agarwal and C. Chakravarty, J. Chem. Phys., 2016, 144, 244901.
253. U. Landman and W. D. Luedtke, Faraday Discuss., 2004, 125, 1–22.
254. F. Tavanti, A. Pedone, M. C. Menziani and A. Alexander-Katz, ACS Chem. Neurosci., 2020, 11, 3153–3160.
255. F. Tavanti, A. Pedone and M. C. Menziani, J. Phys. Chem. C, 2015, 119, 22172–22180.
256. F. Tavanti, A. Pedone and M. C. Menziani, Int. J. Mol. Sci., 2021, 22, 26.
257. A. Warshel and M. Levitt, J. Mol. Biol., 1976, 103, 227–249.
258. H. M. Senn and W. Thiel, Angew. Chem., Int. Ed., 2009, 48, 1198–1229.
259. F. L. Gervasio, M. Boero and M. Parrinello, Angew. Chem., Int. Ed., 2006, 45, 5606–5609.
260. M. J. Field, P. A. Bash and M. Karplus, J. Comput. Chem., 1990, 11, 700–733.
261. M. Böckmann, N. L. Doltsinis and D. Marx, J. Phys. Chem. A, 2010, 114, 745–754.
262. I. Tavernelli, B. F. E. Curchod and U. Rothlisberger, Chem. Phys., 2011, 391, 101–109.
263. G. Li, E. M. Sproviero, R. C. Snoeberger III, N. Iguchi, J. D. Blakemore, R. H. Crabtree, G. W. Brudvig and V. S. Batista, Energy Environ. Sci., 2009, 2, 230–238.
264. G. Izzet, B. Abécassis, D. Brouri, M. Piot, B. Matt, S. A. Serapian, C. Bo and A. Proust, J. Am. Chem. Soc., 2016, 138, 5093–5099.
265. D. Liang, J. Hong, D. Fang, J. W. Bennett, S. E. Mason, R. J. Hamers and Q. Cui, Phys. Chem. Chem. Phys., 2018, 20, 3349–3362.
266. L. O. Mark, C. Zhu, J. W. Medlin and H. Heinz, ACS Catal., 2020, 10, 5462–5474.
267. S. E. Hoff, D. Di Silvio, R. F. Ziolo, S. E. Moya and H. Heinz, ACS Nano, 2022, 16, 8766–8783.
268. Y.-J. Zhang, A. Khorshidi, G. Kastlunger and A. A. Peterson, J. Chem. Phys., 2018, 148, 241740.
269. V. L. Deringer, M. A. Caro and G. Csányi, Adv. Mater., 2019, 31, 1902765.
270. N. Artrith and A. M. Kolpak, Nano Lett., 2014, 14, 2670–2676.
271. G. L. W. Hart, T. Mueller, C. Toher and S. Curtarolo, Nat. Rev. Mater., 2021, 6, 730–755.
272. C. W. Rosenbrock, K. Gubaev, A. V. Shapeev, L. B. Pártay, N. Bernstein, G. Csányi and G. L. W. Hart, npj Comput. Mater., 2021, 7, 24.
273. A. W. Long and A. L. Ferguson, J. Phys. Chem. B, 2014, 118, 4228–4244.
274. A. W. Long and A. L. Ferguson, Mol. Syst. Des. Eng., 2018, 3, 49–65.
275. Z. Zhang and S. C. Glotzer, Nano Lett., 2004, 4, 1407–1413.
276. C. Glotzer Sharon, Science, 2004, 306, 419–420.
277. R. A. Potyrailo, Chem. Soc. Rev., 2017, 46, 5311–5346.
278. L. Yao, Z. Ou, B. Luo, C. Xu and Q. Chen, ACS Cent. Sci., 2020, 6, 1421–1430.
279. M. Born and R. Oppenheimer, Ann. Phys., 1927, 389, 457–484.
280. R. Car and M. Parrinello, Phys. Rev. Lett., 1985, 55, 2471–2474.
281. D. Marx and J. Hutter, Ab initio molecular dynamics: basic theory and advanced methods, Cambridge University Press, 2009.
282. M. Iannuzzi, A. Laio and M. Parrinello, Phys. Rev. Lett., 2003, 90, 238302.
283. A. Laio and M. Parrinello, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 12562–12566.
284. M. Sprik and G. Ciccotti, J. Chem. Phys., 1998, 109, 7737–7744.
285. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
286. J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215.
287. Q. Evrard, Z. Chaker, M. Roger, C. M. Sevrain, E. Delahaye, M. Gallart, P. Gilliot, C. Leuvrey, J.-M. Rueff, P. Rabu, C. Massobrio, M. Boero, A. Pautrat, P.-A. Jaffrès, G. Ori and G. Rogez, Adv. Funct. Mater., 2017, 27, 1703576.
288. M. P. Allen, M. P. Allen, D. J. Tildesley, D. J. Tildesley and T. ALLEN, Computer Simulation of Liquids, Clarendon Press, 1989.
289. M. Levitt and A. Warshel, Nature, 1975, 253, 694–698.
290. M. Levitt, Angew. Chem., Int. Ed., 2014, 53, 10006–10018.
291. V. Botu and R. Ramprasad, Int. J. Quantum Chem., 2015, 115, 1074–1083.
292. F. Häse, I. F. Galván, A. Aspuru-Guzik, R. Lindh and M. Vacher, Chem. Sci., 2019, 10, 2298–2307.
293. M. Kasim, D. Watson-Parris, L. Deaconu, S. Oliver, P. Hatfield, D. Froula, G. Gregori, M. Jarvis, S. Khatiwala and J. Korenaga, arXiv, 2020,  DOI:10.48550/arXiv.2001.08055.
294. P. Friederich, F. Häse, J. Proppe and A. Aspuru-Guzik, Nat. Mater., 2021, 20, 750–761.
295. J. Behler and M. Parrinello, Phys. Rev. Lett., 2007, 98, 146401.
296. J. Behler, Phys. Chem. Chem. Phys., 2011, 13, 17930–17955.
297. S. Izvekov, M. Parrinello, C. J. Burnham and G. A. Voth, J. Chem. Phys., 2004, 120, 10896–10913.
298. T. B. Blank, S. D. Brown, A. W. Calhoun and D. J. Doren, J. Chem. Phys., 1995, 103, 4129–4137.
299. F. Ercolessi and J. B. Adams, MRS Proc., 1992, 291, 31–36.
300. J. Behler, J. Phys.: Condens. Matter, 2014, 26, 183001.
301. V. L. Deringer, D. M. Proserpio, G. Csányi and C. J. Pickard, Faraday Discuss., 2018, 211, 45–59.
302. S. Chmiela, A. Tkatchenko, H. E. Sauceda, I. Poltavsky, K. T. Schütt and K.-R. Müller, Sci. Adv., 2017, 3, e1603015.
303. A. P. Bartók, M. C. Payne, R. Kondor and G. Csányi, Phys. Rev. Lett., 2010, 104, 136403.
304. L. Zhang, J. Han, H. Wang, R. Car and W. E, Phys. Rev. Lett., 2018, 120, 143001.
305. J. Schmidt, M. R. G. Marques, S. Botti and M. A. L. Marques, npj Comput. Mater., 2019, 5, 83.
306. V. L. Deringer, A. P. Bartók, N. Bernstein, D. M. Wilkins, M. Ceriotti and G. Csányi, Chem. Rev., 2021, 121, 10073–10141.
307. F. Musil, A. Grisafi, A. P. Bartók, C. Ortner, G. Csányi and M. Ceriotti, Chem. Rev., 2021, 121, 9759–9815.
308. A. P. Bartók, R. Kondor and G. Csányi, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 184115.

---