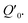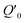Open Access Article
Open Access ArticleSpiers Memorial Lecture: From optical to THz control of materials
Steven L.
Johnson
 ab
ab
aInstitute for Quantum Electronics, ETH Zürich, Auguste-Piccard-Hof 1, 8093 Zürich, Switzerland. E-mail: johnson@phys.ethz.ch; Fax: +41 44 633 10 54; Tel: +41 44 633 76 31
bSwissFEL, Paul Scherrer Institute, Forschungsstrasse 111, 5232 Villigen PSI, Switzerland
First published on 7th June 2022
Abstract
Advances over the past decade have presented new avenues to achieve control over material properties using intense pulses of electromagnetic radiation, with frequencies ranging from optical (approximately 1 PHz, or 1015 Hz) down to below 1 THz (1012 Hz). Some of these new developments have arisen from new experimental methods to drive and observe transient material properties, while others have emerged from new computational techniques that have made nonequilibrium dynamics more tractable to our understanding. One common issue with most attempts to realize control using electromagnetic pulses is the dissipation of energy, which in many cases poses a limit due to uncontrolled heating and has led to strong interest in using lower frequency and/or highly specific excitations to minimize this effect. Emergent developments in experimental tools using shaped X-ray pulses may in the future offer new possibilities for material control, provided that the issue of heat dissipation can be resolved for higher frequency light.
1 Introduction
The idea of using intense pulses of light to control the outcome of chemical reactions has been a subject of active interest for some time, and in fact has been a prominent subject of several past Faraday Discussions (FD 113 and FD 153). Here, the core idea is that for at least some kinds of chemical processes, it is possible to use appropriately tailored electromagnetic radiation to influence the outcome in some way, which usually relies on the persistent coherence of excited electronic states in the molecules involved. While this work on chemical processes has yielded important new insights and potential applications,1–3 the rapid energy redistribution and decoherence of electronic states observed in most molecular systems has presented challenges.4In view of this, it might seem problematic to extend the idea of light-driven control to solid-state materials, where the size of the system becomes much larger than the small molecules that have been most amenable to coherent control in chemistry. While this might be true in many cases, in materials where there is already in equilibrium strong competition between incompatible ordering mechanisms, a tiny nudge toward one direction can produce outsized effects. One example of such a competition is between superconductivity and charge or spin order in many unconventional superconductors, which in equilibrium results in complex phase diagrams.5,6 Another is the related phenomenon of charge density waves, which results also in solid–solid phase transitions from a competition between vibrational and electronic energies.7 In other cases, emergent many-body effects can lead to surprisingly long coherence times that can in principle be exploited for control.8 Electronic coherence may not even be necessary for some control concepts, as long-lived vibrational coherences can also be manipulated by appropriately shaped light.9
Recent methodological advances over the last few decades have now made possible the first explorations of these possibilities. One important development is the advent of intense sources of short-pulse radiation in the THz and mid-infrared ranges.10,11 There are several reasons why this is useful for the control of materials. For insulators and semiconductors, excitation at low frequencies can be used to drive specific dipole-active excitations without the delivery of a significant amount of energy density to delocalized electronic states. If the driven excitations couple in some way to a change in order, this may be used to change this order with minimal uncontrolled heating of the material. In materials where several different excitations couple to the desired material control parameter, it may be more efficient and less damaging to drive the excitation with the lowest energy. In yet other materials, such as Mott insulators, sufficiently high electric fields can drive a phase transition; high intensity quasi-single-cycle THz-frequency pulses may offer a way to achieve this on sub-picosecond timescales.12 In superconductors, nonlinear interactions in the THz frequency range make it in principle possible to excite the Higgs mode, an oscillation of the amplitude of the superconducting order parameter.13
Another important enabling technology is the development of experimental methods to study transient material properties on femtosecond and picosecond time scales. Both electron and X-ray diffraction have now been successfully extended to achieve femtosecond time resolution in pump–probe experiments, offering the possibility to observe directly transient structural changes on atomic length scales.14–19 In parallel to this, angle-resolved photoemission (ARPES) is also now an established tool for the direct measurement of electronic structure.20–22 Taken together, these methods are a unique tool for observing and understanding the interactions of the lattice, charge and spin degrees of freedom in materials, which is essential for the development and validation of light-driven control mechanisms.
In parallel to this experimental work, there have also been significant advances in theoretical concepts and computational tools for understanding the potential for material control with light. For molecular solids, new methods to approximate the rates of intersystem crossing have been developed and applied.23,24 The phenomenon of nucleation and growth of a new phase in a molecular crystal was also successfully modeled using coupling between localized electronic excitations and vibrational modes, both showing the importance of vibrational coupling in molecular crystals and providing an indication of how to treat such phenomena more generally.25 In strongly correlated systems, an important new tool is the extension of dynamical mean field theory to nonequilibrium cases, which has allowed for fundamental study of nonequilibrium phenomena in quantum materials.26 On a more applied level, there have also been several developments in applying density functional theory to the study of several phenomena that have been observed experimentally, including ionic Raman scattering (also called nonlinear phononics)27 and interactions between spins and time-dependent polarizations that arise from particular coherent vibrational motions.28
Here, I give a brief overview of selected aspects of light-driven material control research, with an emphasis on topics discussed in papers in this Faraday Discussion. As an organizing principle, I separate potential control schemes by the initial mechanism of light–matter coupling. First, I discuss control via the driving of electronic transitions, which has to date been the most experimentally studied mechanism for material control. Then, I discuss possibilities for control using the direct excitation of vibrations with light, made possible with intense radiation at lower frequencies in the mid-infrared and THz ranges. Next are analogous studies where magnetic or hybrid magnetic-vibrational excitations are driven. Lastly, I talk about some other control schemes where the electric field of an intense laser pulse initiates some change to a material that is not included in the previously discussed categories. In all cases, I indicate some of the key factors relevant to current and future work in the area.
2 Control using electronic transitions
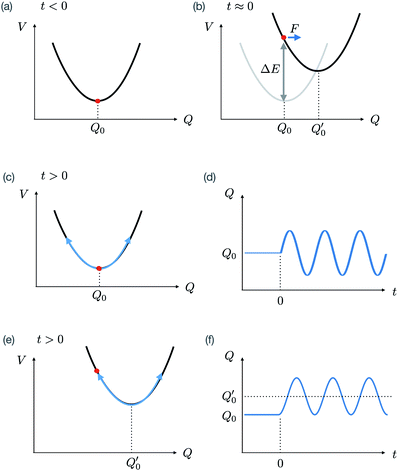
One of the most actively investigated mechanisms for material control is the direct excitation of electric-dipole active electronic transitions. These transitions can have very high cross sections and are often accessible at near-optical wavelengths, and so are a relatively easy way to deliver a considerable amount of energy density into a material. Depending on the interactions of either the initial or final electronic state with other excitations in the material, this initial electronic excitation can then lead to other changes to the material. An understanding of the interactions of the excited electronic transition with the full array of other electronic and vibrational excitations are often needed to predict how the material can respond.A very general phenomenon and a prominent example of this is the generation of coherent vibrational excitations via electron–phonon coupling, often called “coherent phonons” in the literature when discussing crystalline materials.29 Coherent phonon generation is often described as having two “mechanisms”: impulsive stimulated Raman scattering30 or displacive excitation.31 This is not strictly accurate, since in both cases the microscopic mechanisms are very similar, but the resulting dynamics manifest in different forms.32 In general, a particular electronic state transition can drive coherent oscillations of a vibrational mode if the state change causes a shift of the local minimum of the potential energy along the vibrational mode coordinate.
Fig. 1 presents a simplified view of how coherent phonons are generated in both the impulsive and displacive limits. For a light pulse with a duration much shorter than the vibrational period, the lifetime of the electronic states populated by the light interaction relative to the period of the vibration changes the form of the dynamics. If the lifetime is very short compared to the light pulse duration, the potential energy shift occurs only during the light pulse interaction. This results in an effective force along the vibrational mode coordinate that is impulsive in nature, leading to coherent oscillations with a sine-like phase around the initial equilibrium structure. This is the limit that corresponds to impulsive stimulated Raman scattering. If instead the electronic state (or in some cases, collections of excited states) that causes the potential energy shift has a long lifetime compared to the period of vibration, the resulting effective force is step-like. This leads to coherent oscillations about the shifted potential energy minimum with a cosine-like phase. This limit is called displacive excitation. In a more general case (where the state lifetime is neither very short nor very long compared to the vibrational period), the phase of the oscillation is somewhere in between. It is also possible to drive similar dynamics in the variance of the vibrational coordinate by exciting electronic states that change the frequency of vibrational modes, a phenomenon sometimes called phonon squeezing due to similarities with light squeezing in quantum optics.33–35 Tracking such dynamics using diffuse X-ray scattering is in fact a newly developed method to determine electron–phonon coupling and phonon dispersion in strongly photoexcited materials, a method called Fourier transform inelastic X-ray scattering.36
A class of systems where these dynamics play a key role is molecular spin-crossover materials,37 which serves as one key example of light-driven material control. The spin-crossover phenomenon refers to a change in the spin state of a 3d-transition metal ion component by changing the temperature, pressure or photoexcitation. The typical photoexcitation pathway, depicted in Fig. 2, involves an initial excitation into a manifold of so-called MLCT (metal-to-ligand change transfer) states which, as the name suggests, involves a shift of charge density from the ion to a nearby ligand. This MLCT manifold then relaxes to a high-spin state. Due to the rapidity of these decay processes, the local structure of the metal–ligand complex does not coincide with a local minimum of the interatomic potential energy surface in the excited high-spin electronic state. This results in an elongation of the metal–ligand bond distance, which ends up effectively trapping the ion in a metastable configuration.38 In crystalline materials, the structural component of the transition results in cooperative structural transformations over multiple length and time scales, which are possible to resolve using a variety of methods, including time-resolved microscopy, diffraction and spectroscopy.39 Note also that typically a large fraction of the energy initially deposited by the excitation is dissipated during the relaxation process, resulting in an increase in the effective temperature of the metastable state relative to the initial low-spin state, which also has an influence on the structure.
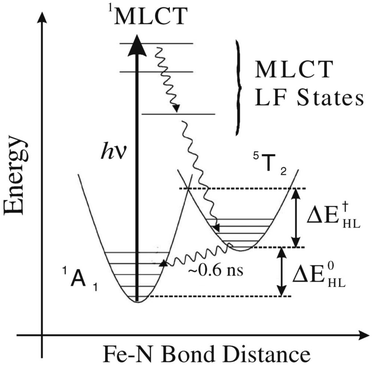 | ||
| Fig. 2 Configuration-coordinate diagram for photoexcited Fe(bpy)3, one example of a spin-crossover molecule. The transition to a high-spin electronic state of the Fe ion occurs via a higher energy MLCT state that is directly excited by the absorption of a visible or UV photon. Reprinted with permission from ref. 40 [Gawelda et al., Phys. Rev. Lett., 2007, 98, 054401]. Copyright 2007 by the American Physical Society. | ||
Control has also been explored in materials with more delocalized electronic states. In semiconductors, excitation can result in the formation, destruction or modulation of excitons (bound pairs of electrons and holes) that can be tracked using ultrafast spectroscopy.41–43 As with the molecular solids, electron–phonon coupling often strongly affects the dynamics.44 In some low-dimensional metals, another manifestation of electron–phonon coupling is the formation of charge density waves (CDWs), a periodic modulation of the charge and an associated lattice distortion that results in the formation of a gap in the electronic density of states at the Fermi energy. Photon-driven electronic excitation across the CDW band gap shifts this balance, leading to displacive excitation of the amplitude mode of the distortion or, at higher excitation levels, a transient phase change to an unmodulated “melted” state observable by optical spectroscopy and X-ray diffraction.45–49 Electronic excitation has also been used to drive other kinds of structural symmetry changes in various materials.50,51
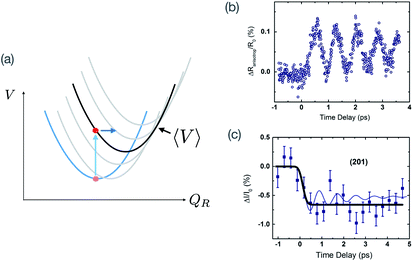
Another new development in this arena is the interest in Higgs mode spectroscopy of superconductors, recently stimulated due to the ability to generate intense THz pulses suitable for nonlinear interactions at low frequencies.13 The Higgs mode in superconductors refers to an oscillation of the amplitude of the complex-valued superconducting order parameter. The name of the mode is derived from a mathematical analogy to the Higgs mechanism in particle physics. The Higgs mode carries no charge moments, and so usually does not couple to light in any linear-response regime. It is also a very low energy excitation that exists in the THz frequency regime. It can be shown that the Higgs mode can in some circumstances contribute to an enhancement of third-harmonic generation for THz frequency pulses when the THz frequency is half of the superconducting pair energy gap, and experimental evidence for such an enhancement has been observed in both BCS and cuprate superconductors.89–91 An alternative method that has been proposed to excite and observe the Higgs mode is to use pump–probe THz methods to very suddenly disrupt (“quench”) the pairing interactions by using a THz pulse to inject quasiparticles near the superconducting gap, leading to a change of the free energy as a function of the amplitude of the condensate. This can then launch coherent oscillations of the Higgs mode that can be observed as a modulation of the reflectance of a probe (see Fig. 3). Such an experiment was performed by Matsunaga et al., which indeed observed coherent oscillations at the Higgs mode frequency in a BCS superconductor.88
It is also possible to strongly control magnetic order in materials using electronic excitation. One of the earliest and still much discussed phenomena is ultrafast demagnetization, reported first by Beaurepaire et al.52 Intense electronic excitation of several different ferromagnetic transition metals and alloys results in a rapid drop of the magnetization density on a time scale of tens of femtoseconds.53,54 The precise mechanism in all observed cases is still under debate but appears to be a combination of rapid spin transport55 and spin-flip scattering with phonons56 that occurs during the extremely high transient electron temperatures caused by laser heating of the conduction electrons. Ultrafast X-ray scattering measurements have demonstrated that a significant fraction of the angular momentum of the spins in laser excited iron is transferred to the lattice in the form of transverse strain launched from the surface.57
A related phenomenon observed in some metallic ferrimagnetic systems with a magnetic compensation point is all-optical switching of the net magnetization.58,59 In these materials, it is possible to understand the switching dynamics as primarily driven by changes in the transient temperature of the metal that occur in response to short pulse excitation. This was first observed in the FeGdCo alloy,60 an amorphous alloy where the Gd and FeCo spins are antiferromagnetically coupled. At room temperature, the magnetic moment contributed by the Gd is smaller and the alloy has a net magnetization along the direction of the FeCo. The sudden heating of the electrons by light-pulse excitation causes a faster and larger demagnetization of the Fe component, resulting in a transient net magnetization aligned to the Gd component. During the slow cooling of the system, angular momentum conservation within the spin system then leads to a reversal of the total ferrimagnetic order relative to the initial configuration.
It is also possible to excite coherent spin dynamics in magnetically ordered systems in a manner analogous to the excitation of coherent vibrational dynamics. This has been of particular interest recently in antiferromagnetic systems, which have attracted interest for their potential for fast dynamics not limited by angular momentum conservation.61,62 One example is offered by the orthoferrites, where electronic excitation can launch spin dynamics by inducing a sudden transient change to the magnetic anisotropy that determines the orientation of the sublattice magnetisations.63 In a semi-classical treatment, the Lagrangian for antiferromagnetic dynamics contains a term mathematically analogous to the kinetic energy of a massive particle in a simple harmonic oscillator, and thus shows inertial motion that can be exploited to achieve actual switching of the magnetic order in response to the impulsive excitation of coherent magnetic dynamics.64
The manipulation of magnetic anisotropy is another means to control materials with a non-zero net magnetic moment, as has been demonstrated by exciting d–d transitions in insulating ferrimagnetic garnets, where the dissipation of energy into general heating is very low compared to similar switching in metallic systems.66 This can also be extended to very low frequencies. The orthoferrite TmFeO3 is an antiferromagnet with a small ferromagnetic spin canting.67 By strong near-field enhancement of an electromagnetic pulse in the THz frequency range, Schlauderer et al. were able to demonstrate coherent switching of the ferromagnetic orientation via excitation of the local electronic states of the Tm3+ ions (see Fig. 3).65 The idea that such low energy excitations can be effectively exploited to achieve ferromagnetic switching is highly promising, since this appears to approach a minimal dissipation limit for such control schemes.
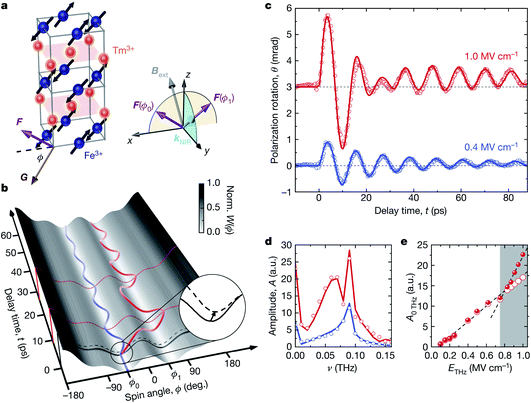 | ||
| Fig. 3 THz-driven switching in the canted antiferromagnet TmFeO3. (a) The structure of TmFeO3, showing the sublattice spin orientations and the direction of the net magnetic moment. (b) A sketch of the magnetic potential energy and spin dynamics for low (blue) and high (red) field excitations. (c) Measured dynamics of the Faraday rotation angle, an experimental measure of the spin angle orientation. (d) Amplitude of the Fourier transform of the data in panel c. (e) Simulated behavior of the long-lived offset in the Faraday rotation as a function of the excitation level for two alignments of the near-infrared probe (red circles and red spheres). The difference at high fields is a consequence of the metastable transfer of spins over the potential energy barrier. Reprinted with permission from Nature65 [Schlauderer et al., Temporal and spectral fingerprints of ultrafast all-coherent spin switching]. Copyright 2019 Springer Nature. | ||
3 Control by vibrational excitations
For material control where a structural coordinate is either an order parameter or strongly coupled to an order parameter, the direct excitation of vibrations with electromagnetic fields can offer an attractive alternative. If the order parameter itself happens to couple directly to the electromagnetic radiation, it may be possible to very directly drive some metastable change. An example of this would be soft-mode structural ferroelectrics, with typical soft mode frequencies in the THz frequency range. Time-resolved X-ray diffraction experiments have been applied to directly measure such dynamics.68,69 Appropriately shaped and timed THz pulses have been predicted as a means to drive domain reversal.70 In SrTiO3, there is evidence that very high transient THz fields can drive the structure to a metastable ferroelectric state, possibly via a soft mode excitation, which has been inferred from time-resolved measurements of second harmonic generation.71In other materials, it may not be possible to directly affect the order parameter with electromagnetic radiation, but it is nevertheless coupled nonlinearly to particular vibrational modes that it is possible to drive directly, usually at frequencies raging from 1–40 THz. This is broadly known as nonlinear phononics, which has been extensively reviewed elsewhere.73 Analogously to electron–phonon driven mechanisms for coherent phonon generation, it is also possible to drive coherent vibrational modes by exciting high frequency vibrational modes with appropriate symmetry.72,74 To illustrate the basic idea, assume that the interatomic potential energy can be written as a function of two coupled normal mode coordinates as
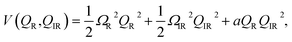 | (1) |
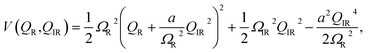 | (2) |
 | ||
| Fig. 4 Displacive excitation of coherent phonons using vibrational excitation and nonlinear vibrational coupling. (a) Potential energy as a function of a Raman-active phonon mode with coordinate QR for different fixed values of a driven infrared coordinate QIR. The blue curve shows the QIR = 0 potential energy relation, while the grey curves are fixed non-zero values of QIR with shifted minima due to QRQIR2 coupling. (b) Measured anisotropic reflectivity changes in La0.7Sr0.3MnO3 due to coherent excitation of an Eg mode via driving of a high-frequency Eu mode. (c) Corresponding changes in X-ray diffraction from the (201) lattice planes, demonstrating unambiguously the displacement of the Eg mode coordinate. Panels (b) and (c) are reprinted from ref. 72 [Först et al., Displacive lattice excitation through nonlinear phononics viewed by femtosecond X-ray diffraction, Solid State Commun., 2013, 169, 24]. Copyright 2013, with permission from Elsevier. | ||
A variety of material phase transitions using nonlinear phononics have been reported. One early example is the driving of an insulator–metal transition in a manganite by vibrational excitation, which was interpreted as a nonlinear phononics phenomenon.76 A later example of a similar phase transition was explained instead by a more direct nonlinear coupling between an excited mode and the electronic band gap.77 It is also possible to destroy electronic and magnetic ordering using vibrational excitation, in a manner qualitatively similar to electronic excitation.78–80 Nonlinear phononics is also a promising mechanism to explain experiments on cuprates where the resonant excitation of selected vibrational modes has been shown to enhance spectroscopic signatures of superconductivity.81 Similar excitations have been shown to enhance superconducting transport in other materials as well, although it is not at present clear whether nonlinear phononics or some other mechanism leads to the enhancement of the superconducting order in general.82,83
Much of the interest in using the excitation of vibrational modes to control materials is connected to the idea that such a mechanism can lead to more selective deposition of energy into the system, minimizing possibly undesirable heating that inevitably leads to a state of higher entropy. Typical experiments nevertheless require very high intensities for the stimulating pump pulse, which can also drive nonlinear optical processes that compete with the excitation of the vibrational mode and can lead to undesirable nonspecific excitations.84 It is probably still necessary in most cases to carefully select materials that are amenable to such control by seeking situations where strongly competing orders already exist in equilibrium and can be rebalanced via specific structural distortions.
4 Driving magnetic and hybrid vibrational–magnetic excitations
It is also possible to use the magnetic field component of pulsed radiation to drive magnetic excitations via magnetic dipole interactions, although due to the relative weakness of the magnetic Zeeman interaction, this usually leads to fairly weak perturbations compared to other control methods. The use of broadband single-cycle THz pulses to drive and control the amplitude of coherent antiferromagnetic spin excitations has been demonstrated in NiO.85 In this work, Kampfrath et al. estimate that peak magnetic fields of more than 10 T are needed to drive dynamics out of the linear regime, which would imply peak electric fields on the order of 3 GV m−1, where many gapped materials experience strong nonlinear electronic interactions from effects like Zener tunneling that lead to massive Joule heating from field-generated carriers.86 It might therefore be quite challenging to exploit Zeeman interactions for magnetization control into new metastable configurations for general magnetic systems.An alternative is to drive hybrid excitations of spin and vibration, where the vibrational component confers an electric dipole moment that can more strongly couple to the light. These are called electromagnon modes and appear in several materials, including some multiferroics. One example is TbMnO3, where Mochizuki et al. predicted that intense THz pulses with peak field strengths on the order of 1 GV m−1 can lead to persistent switching of the antiferromagnetic order. Ultrafast magnetic X-ray scattering measurements of similar THz-induced motion validated the basic idea that such pulses can drive large amplitude coherent electromagnons in this material (see Fig. 5), and suggested that even more moderate peak fields of 200 MV m−1 could lead to spin reorientations to new metastable configurations.87 While fields this high might also lead to transient temperature increases via Joule heating, the fields are considerably lower than those that would be needed for similar effects from Zeeman coupling.
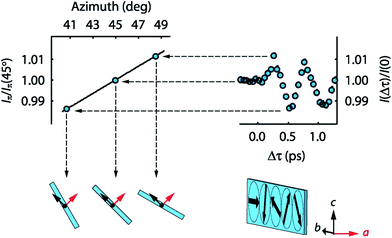 | ||
| Fig. 5 Direct measurement of coherent rotations of the cycloidal spin order in TbMnO3, driven by THz excitation of an electromagnon excitation. The left side shows the dependence of the diffracted X-ray intensity from a magnetic order peak as a function of the angle of the spin cycloid plane. On the right is shown example data of the time-dependence of the diffracted magnetic intensity, showing the coherent oscillations of the magnetic order. This figure is reproduced from Kubacka et al.87 with permission from the American Association for the Advancement of Science. | ||
5 Electric-field-driven control
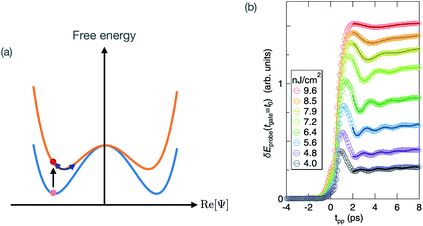 | ||
| Fig. 6 Quench-driving of the Higgs mode in a superconductor. (a) The Landau–Ginzburg free energy in a superconductor as a function of the real part of the condensate wavefunction Ψ. The blue curve shows the initial free energy, which is suddenly changed to the orange curve by quasiparticle injection from a THz-pulse. This displacively excites coherent oscillations of the Higgs mode. (b) Experimental data showing changes in the electric field of a THz probe pulse at the Higgs mode frequency in superconducting NbN. Panel (b) is reprinted with permission from ref. 88 [Matsunaga et al., Phys. Rev. Lett., 2013, 111, 057002]. Copyright 2013 by the American Physical Society. | ||
The advent of extremely short, sub-femtosecond pulses generated by high-harmonics of ultrafast lasers98 or free-electron lasers99 has also offered new opportunities for studying field driven phenomena in materials at near-optical frequencies.100,101 Experiments in this regime are highly challenging, but offer a potential opportunity to study and even guide pure charge dynamics on nanometer length scales.
On the other extreme end of the frequency spectrum, there are some methods of material control where quasi-static electric fields have been shown to drive material transformations. There has recently been interest in exploring the time scale of these transformations, which is now possible using quasi-half-cycle THz radiation.102 In several materials, including Mott insulators, fast changes in conductivity in response to intense THz pulses have been observed.12,103,104 The mechanisms for these changes are not in all cases well understood, but one plausible idea is that the intense electric field causes the excitation of electrons across the Mott gap by a phenomenon analogous to Zener tunneling in semiconductor junctions,105 followed by avalanche ionization and Joule heating from the subsequent acceleration of carriers in the THz electric field.12 This causes a highly inhomogeneous heating along thin fibrous regions of the material aligned to the electric field of the THz pulse. The expansion of the heated fiber and the compression of the surrounding material may lead to the metastable metallization of portions of the material.
6 Conclusions
In this introductory overview for this Faraday Discussion, I have tried to give a unified framework for the diverse methods currently being pursued for material control. One common theme in many aspects of this research is the role of the thermalization of the energy deposited from light–matter interaction. Sometimes, this thermalization process is desirable, for example when the goal is to drive the material into a higher entropy state. This is the case for the melting of charge density waves or ultrafast demagnetization. This photoinduced state is not necessarily identical to a state obtained by a conventional increase of the temperature, since some thermally driven changes, such as lattice expansion, can take much longer than the thermalization of other degrees of freedom. The exact path to thermalization might also result in the trapping of the system in a metastable configuration.In many cases, however, the thermal redistribution of energy can lead to undesired effects. Thus, a recent trend is to try to achieve material control via highly specific excitations that are maximally coupled to the desired dynamics, and minimally coupled to dissipative excitations that lead to thermalization. This has led to strong interest in using THz and mid-infrared light sources, since these are the frequencies where in gapped materials it is possible to drive infrared active collective excitations of vibrations, spins or local electronic transitions without exciting delocalized electronic states that rapidly dissipate. This has generated some spectacular successes, but the ultimate potential of this concept is yet to be determined. In particular, it is not yet clear how generally such control can be applied without requiring such high intensities that strong nonlinear field driven effects compete with the targeted linear or low-order nonlinear interactions.
The applications of new seeded femtosecond and even sub-femtosecond X-rays from free electron lasers are still mostly only conceptual, but may offer unique new opportunities in material understanding and control. One such opportunity is the ability to drive and observe purely electronic dynamics on attosecond time scales, which has already begun to be explored using existing sources. Another potential application to materials would exploit the short wavelength of such radiation, which is comparable to interatomic distances. The short wavelength, combined with high intensities and transform limited pulses, makes possible the manipulation of short-wavelength excitations in materials, spanning the Brillouin zone of crystals. Of course, with intense X-rays, parasitic heating is an even bigger issue than for optical pulses, since the inevitable ionization of core levels leads inexorably to a cascade of electronic and other excitations. It may therefore be necessary for such control concepts to focus predominantly on very fast time scales, before thermalization from those cascading excitations takes hold. It is nevertheless an interesting new frontier to explore.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The author acknowledges financial support from project grant 200020_192337 of the Swiss National Science Foundation.Notes and references
- D. Goswami, Phys. Rep., 2003, 374, 385–481 CrossRef CAS.
- M. Shapiro and P. Brumer, Rep. Prog. Phys., 2003, 66, 859 CrossRef CAS.
- Y. Silberberg, Annu. Rev. Phys. Chem., 2009, 60, 277–292 CrossRef CAS PubMed.
- W. S. Warren, H. Rabitz and M. Dahleh, Science, 1993, 259, 1581–1589 CrossRef CAS PubMed.
- J. Chang, E. Blackburn, A. T. Holmes, N. B. Christensen, J. Larsen, J. Mesot, R. Liang, D. A. Bonn, W. N. Hardy, A. Watenphul, M. v. Zimmermann, E. M. Forgan and S. M. Hayden, Nat. Phys., 2012, 8, 871–876 Search PubMed.
- P. Dai, Rev. Mod. Phys., 2015, 87, 855–896 CrossRef CAS.
- G. Grüner, Density Waves in Solids, Westview Press, 2009 Search PubMed.
- A. Streltsov, G. Adesso and M. B. Plenio, Rev. Mod. Phys., 2017, 89, 041003 CrossRef.
- S. L. Johnson, in X-Ray Free Electron Lasers: Applications in Materials, Chemistry and Biology, RSC Energy and Environment Series, 2017, pp. 284–300 Search PubMed.
- M. Knorr, J. Raab, M. Tauer, P. Merkl, D. Peller, E. Wittmann, E. Riedle, C. Lange and R. Huber, Opt. Lett., 2017, 42, 4367 CrossRef CAS PubMed.
- N. Stojanovic and M. Drescher, J. Phys. B: At., Mol. Opt. Phys., 2013, 46, 192001 CrossRef.
- F. Giorgianni, J. Sakai and S. Lupi, Nat. Commun., 2019, 10, 1159 CrossRef PubMed.
- R. Shimano and N. Tsuji, Annu. Rev. Condens. Matter Phys., 2019, 11, 1–22 Search PubMed.
- G. Sciaini and R. J. D. Miller, Rep. Prog. Phys., 2011, 74, 096101 CrossRef.
- S. Lahme, C. Kealhofer, F. Krausz and P. Baum, Struct. Dyn., 2014, 1, 034303 CrossRef CAS PubMed.
- P. Zhu, Y. Zhu, Y. Hidaka, L. Wu, J. Cao, H. Berger, J. Geck, R. Kraus, S. Pjerov, Y. Shen, R. I. Tobey, J. P. Hill and X. J. Wang, New J. Phys., 2015, 17, 063004 CrossRef.
- R. J. D. Miller, Science, 2014, 343, 1108–1116 CrossRef CAS PubMed.
- R. Schoenlein, T. Elsaesser, K. Holldack, Z. Huang, H. Kapteyn, M. Murnane and M. Woerner, Philos. Trans. R. Soc. London, Ser. A, 2019, 377, 20180384 CrossRef CAS PubMed.
- A. M. Lindenberg, S. L. Johnson and D. A. Reis, in Annual Review of Materials Research, Annual Review of Materials Research, 2017, vol. 47, pp. 1–25 Search PubMed.
- E. J. Sie, T. Rohwer, C. Lee and N. Gedik, Nat. Commun., 2019, 10, 3535 CrossRef PubMed.
- Y. Ishida, T. Togashi, K. Yamamoto, M. Tanaka, T. Kiss, T. Otsu, Y. Kobayashi and S. Shin, Rev. Sci. Instrum., 2014, 85, 123904 CrossRef CAS PubMed.
- E. Carpene, E. Mancini, C. Dallera, G. Ghiringhelli, C. Manzoni, G. Cerullo and S. D. Silvestri, Rev. Sci. Instrum., 2009, 80, 055101 CrossRef CAS PubMed.
- C. M. Marian, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 187–203 CAS.
- C. M. Marian, Annu. Rev.Phys. Chem., 2021, 72, 617–640 CrossRef CAS PubMed.
- K. Ishida and K. Nasu, Phys. Rev. Lett., 2008, 100, 116403 CrossRef PubMed.
- H. Aoki, N. Tsuji, M. Eckstein, M. Kollar, T. Oka and P. Werner, Rev. Mod. Phys., 2014, 86, 779–837 CrossRef.
- A. Subedi, A. Cavalleri and A. Georges, Phys. Rev. B, 2014, 89, 220301 CrossRef.
- D. M. Juraschek, M. Fechner, A. V. Balatsky and N. A. Spaldin, Phys. Rev. Mater., 2017, 1, 014401 CrossRef.
- R. Merlin, Solid State Commun., 1997, 102, 207–220 CrossRef.
- Y.-X. Yan, E. B. Gamble and K. A. Nelson, J. Chem. Phys., 1985, 83, 5391 CrossRef CAS.
- H. J. Zeiger, J. Vidal, T. K. Cheng, E. P. Ippen, G. Dresselhaus and M. S. Dresselhaus, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 768–778 CrossRef PubMed.
- T. Stevens, J. Kuhl and R. Merlin, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 144304 CrossRef.
- G. A. Garrett, A. G. Rojo, A. K. Sood, J. F. Whitaker and R. Merlin, Science, 1997, 275, 1638–1640 CrossRef CAS PubMed.
- X. Hu and F. Nori, Phys. Rev. Lett., 1996, 76, 2294 CrossRef CAS PubMed.
- S. Johnson, P. Beaud, E. Vorobeva, C. Milne, E. Murray, S. Fahy and G. Ingold, Phys. Rev. Lett., 2009, 102, 175503 CrossRef CAS PubMed.
- M. Trigo, M. Fuchs, J. Chen, M. P. Jiang, M. Cammarata, S. Fahy, D. M. Fritz, K. Gaffney, S. Ghimire, A. Higginbotham, S. L. Johnson, M. E. Kozina, J. Larsson, H. Lemke, A. M. Lindenberg, G. Ndabashimiye, F. Quirin, K. Sokolowski-Tinten, C. Uher, G. Wang, J. S. Wark, D. Zhu and D. A. Reis, Nat. Phys., 2013, 9, 790–794 Search PubMed.
- Spin-crossover Materials: Properties and Applications, ed. M. A. Halcrow, John Wiley & Sons, Ltd, Chichester, UK, 2013 Search PubMed.
- S. Decurtins, P. Gutlich, K. M. Hasselbach, A. Hauser and H. Spiering, Inorg. Chem., 1985, 24, 2174–2178 CrossRef CAS.
- E. Collet and P. Guionneau, C. R. Chim., 2018, 21, 1133–1151 CrossRef CAS.
- W. Gawelda, V.-T. Pham, M. Benfatto, Y. Zaushitsyn, M. Kaiser, D. Grolimund, S. L. Johnson, R. Abela, A. Hauser, C. Bressler and M. Chergui, Phys. Rev. Lett., 2007, 98, 057401 CrossRef PubMed.
- C. Trovatello, F. Katsch, N. J. Borys, M. Selig, K. Yao, R. Borrego-Varillas, F. Scotognella, I. Kriegel, A. Yan, A. Zettl, P. J. Schuck, A. Knorr, G. Cerullo and S. D. Conte, Nat. Commun., 2020, 11, 5277 CrossRef CAS PubMed.
- P. Merkl, F. Mooshammer, P. Steinleitner, A. Girnghuber, K.-Q. Lin, P. Nagler, J. Holler, C. Schüller, J. M. Lupton, T. Korn, S. Ovesen, S. Brem, E. Malic and R. Huber, Nat. Mater., 2019, 18, 691–696 CrossRef CAS PubMed.
- H. M. Bretscher, P. Andrich, P. Telang, A. Singh, L. Harnagea, A. K. Sood and A. Rao, Nat. Commun., 2021, 12, 1699 CrossRef CAS PubMed.
- G. Antonius and S. G. Louie, Phys. Rev. B, 2022, 105, 085111 CrossRef CAS.
- A. Tomeljak, H. SCHAFER, D. Städter, M. Beyer, K. Biljaković and J. Demsar, Phys. Rev. Lett., 2009, 102, 066404 CrossRef CAS PubMed.
- E. Möhr-Vorobeva, S. L. Johnson, P. Beaud, U. Staub, R. D. Souza, C. Milne, G. Ingold, J. Demsar, H. Schaefer and A. Titov, Phys. Rev. Lett., 2011, 107, 036403 CrossRef PubMed.
- T. Huber, S. O. Mariager, A. Ferrer, H. Schaefer, J. A. Johnson, S. Gruebel, A. Luebcke, L. Huber, T. Kubacka, C. Dornes, C. Laulhe, S. Ravy, G. Ingold, P. Beaud, J. Demsar and S. L. Johnson, Phys. Rev. Lett., 2014, 113, 026401 CrossRef CAS PubMed.
- R. Yusupov, T. Mertelj, V. V. Kabanov, S. Brazovskii, P. Kusar, J.-H. Chu, I. R. Fisher and D. Mihailovic, Nat. Phys., 2010, 6, 681–684 Search PubMed.
- M. Trigo, P. Giraldo-Gallo, M. E. Kozina, T. Henighan, M. P. Jiang, H. Liu, J. N. Clark, M. Chollet, J. M. Glownia, D. Zhu, T. Katayama, D. Leuenberger, P. S. Kirchmann, I. R. Fisher, Z. X. Shen and D. A. Reis, Phys. Rev. B, 2019, 99, 104111 CrossRef CAS.
- E. J. Sie, C. M. Nyby, C. D. Pemmaraju, S. J. Park, X. Shen, J. Yang, M. C. Hoffmann, B. K. Ofori-Okai, R. Li, A. H. Reid, S. Weathersby, E. Mannebach, N. Finney, D. Rhodes, D. Chenet, A. Antony, L. Balicas, J. Hone, T. P. Devereaux, T. F. Heinz, X. Wang and A. M. Lindenberg, Nature, 2019, 565, 61–66 CrossRef CAS PubMed.
- P. Zalden, F. Quirin, M. Schumacher, J. Siegel, S. Wei, A. Koc, M. Nicoul, M. Trigo, P. Andreasson, H. Enquist, M. J. Shu, T. Pardini, M. Chollet, D. Zhu, H. Lemke, I. Ronneberger, J. Larsson, A. M. Lindenberg, H. E. Fischer, S. Hau-Riege, D. A. Reis, R. Mazzarello, M. Wuttig and K. Sokolowski-Tinten, Science, 2019, 364, 1062–1067 CrossRef CAS PubMed.
- E. Beaurepaire, J.-C. Merle, A. Daunois and J.-Y. Bigot, Phys. Rev. Lett., 1996, 76, 4250–4253 CrossRef CAS PubMed.
- E. Carpene, E. Mancini, C. Dallera, M. Brenna, E. Puppin and S. D. Silvestri, Phys. Rev. B, 2008, 78, 174422 CrossRef.
- M. Fähnle, Am. J. Mod. Phys., 2018, 7, 68 CrossRef.
- M. Battiato, K. Carva and P. M. Oppeneer, Phys. Rev. Lett., 2010, 105, 027203 CrossRef CAS PubMed.
- G. P. Zhang and W. Hübner, Phys. Rev. Lett., 2000, 85, 3025–3028 CrossRef CAS PubMed.
- C. Dornes, Y. Acremann, M. Savoini, M. Kubli, M. J. Neugebauer, E. Abreu, L. Huber, G. Lantz, C. A. F. Vaz, H. Lemke, E. M. Bothschafter, M. Porer, V. Esposito, L. Rettig, M. Buzzi, A. Alberca, Y. W. Windsor, P. Beaud, U. Staub, D. Zhu, S. Song, J. M. Glownia and S. L. Johnson, Nature, 2019, 565, 209–212 CrossRef CAS PubMed.
- A. V. Kimel and M. Li, Nat. Rev. Mater., 2019, 4, 189–200 CrossRef.
- C. Banerjee, N. Teichert, K. E. Siewierska, Z. Gercsi, G. Y. P. Atcheson, P. Stamenov, K. Rode, J. M. D. Coey and J. Besbas, Nat. Commun., 2020, 11, 4444 CrossRef CAS PubMed.
- C. D. Stanciu, F. Hansteen, A. V. Kimel, A. Kirilyuk, A. Tsukamoto, A. Itoh and T. Rasing, Phys. Rev. Lett., 2007, 99, 047601 CrossRef CAS PubMed.
- B. A. Ivanov, J. Exp. Theor. Phys., 2020, 131, 95–112 CrossRef.
- D. Bossini, M. Pancaldi, L. Soumah, M. Basini, F. Mertens, M. Cinchetti, T. Satoh, O. Gomonay and S. Bonetti, Phys. Rev. Lett., 2021, 127, 077202 CrossRef CAS PubMed.
- A. V. Kimel, A. Kirilyuk, A. Tsvetkov, R. V. Pisarev and T. Rasing, Nature, 1967, 429, 850–853 CrossRef PubMed.
- A. V. Kimel, B. A. Ivanov, R. V. Pisarev, P. A. Usachev, A. Kirilyuk and T. Rasing, Nat. Phys., 2009, 5, 727–731 Search PubMed.
- S. Schlauderer, C. Lange, S. Baierl, T. Ebnet, C. P. Schmid, D. C. Valovcin, A. K. Zvezdin, A. V. Kimel, R. V. Mikhaylovskiy and R. Huber, Nature, 2019, 569, 383–387 CrossRef CAS PubMed.
- A. Stupakiewicz, K. Szerenos, M. D. Davydova, K. A. Zvezdin, A. K. Zvezdin, A. Kirilyuk and A. V. Kimel, Nat. Commun., 2019, 10, 612 CrossRef CAS PubMed.
- J. A. Leake, G. Shirane and J. P. Remeika, Solid State Commun., 1968, 6, 15–17 CrossRef CAS.
- M. Kozina, M. Fechner, P. Marsik, T. v. Driel, J. M. Glownia, C. Bernhard, M. Radovic, D. Zhu, S. Bonetti, U. Staub and M. C. Hoffmann, Nat. Phys., 2019, 15, 387–392 Search PubMed.
- S. Grübel, PhD thesis, ETH Zurich, 2016.
- T. Qi, Y.-H. Shin, K.-L. Yeh, K. A. Nelson and A. M. Rappe, Phys. Rev. Lett., 2009, 102, 247603 CrossRef PubMed.
- X. Li, T. Qiu, J. Zhang, E. Baldini, J. Lu, A. M. Rappe and K. A. Nelson, Science, 2019, 364, 1079–1082 CrossRef CAS PubMed.
- M. Först, R. Mankowsky, H. Bromberger, D. M. Fritz, H. Lemke, D. Zhu, M. Chollet, Y. Tomioka, Y. Tokura, R. Merlin, J. P. Hill, S. L. Johnson and A. Cavalleri, Solid State Commun., 2013, 169, 24–27 CrossRef.
- R. Mankowsky, M. Först and A. Cavalleri, Rep. Prog. Phys., 2016, 79, 064503 CrossRef PubMed.
- M. Foerst, C. Manzoni, S. Kaiser, Y. Tomioka, Y. Tokura, R. Merlin and A. Cavalleri, Nat. Phys., 2011, 7, 854–856 Search PubMed.
- R. Mankowsky, A. v. Hoegen, M. Först and A. Cavalleri, Phys. Rev. Lett., 2017, 118, 197601 CrossRef CAS PubMed.
- M. Rini, R. Tobey, N. Dean, J. Itatani, Y. Tomioka, Y. Tokura, R. W. Schoenlein and A. Cavalleri, Nature, 2007, 449, 72–74 CrossRef CAS PubMed.
- V. Esposito, L. Rettig, E. M. Bothschafter, Y. Deng, C. Dornes, L. Huber, T. Huber, G. Ingold, Y. Inubushi, T. Katayama, T. Kawaguchi, H. Lemke, K. Ogawa, S. Owada, M. Radovic, M. Ramakrishnan, Z. Ristic, V. Scagnoli, Y. Tanaka, T. Togashi, K. Tono, I. Usov, Y. W. Windsor, M. Yabashi, S. L. Johnson, P. Beaud and U. Staub, Struct. Dyn., 2018, 5, 064501 CrossRef PubMed.
- R. I. Tobey, D. Prabhakaran, A. T. Boothroyd and A. Cavalleri, Phys. Rev. Lett., 2008, 101, 197404 CrossRef CAS PubMed.
- T. Ogasawara, T. Kimura, T. Ishikawa, M. Kuwata-Gonokami and Y. Tokura, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 4 CrossRef.
- M. Först, R. I. Tobey, S. Wall, H. Bromberger, V. Khanna, A. L. Cavalieri, Y.-D. Chuang, W. S. Lee, R. Moore, W. F. Schlotter, J. J. Turner, O. Krupin, M. Trigo, H. Zheng, J. F. Mitchell, S. S. Dhesi, J. P. Hill and A. Cavalleri, Phys. Rev. B, 2011, 84, 241104 CrossRef.
- R. Mankowsky, A. Subedi, M. Först, S. O. Mariager, M. Chollet, H. T. Lemke, J. S. Robinson, J. M. Glownia, M. P. Minitti, A. Frano, M. Fechner, N. A. Spaldin, T. Loew, B. Keimer, A. Georges and A. Cavalleri, Nature, 2014, 516, 71–73 CrossRef CAS PubMed.
- M. Mitrano, A. Cantaluppi, D. Nicoletti, S. Kaiser, A. Perucchi, S. Lupi, P. D. Pietro, D. Pontiroli, M. Riccò, S. R. Clark, D. Jaksch and A. Cavalleri, Nature, 2016, 530, 461–464 CrossRef CAS PubMed.
- D. Fausti, R. I. Tobey, N. Dean, S. Kaiser, A. Dienst, M. C. Hoffmann, S. Pyon, T. Takayama, H. Takagi and A. Cavalleri, Science, 2011, 331, 189–191 CrossRef CAS PubMed.
- M. J. Neugebauer, D. M. Juraschek, M. Savoini, P. Engeler, L. Boie, E. Abreu, N. A. Spaldin and S. L. Johnson, Phys. Rev. Res., 2021, 3, 013126 CrossRef CAS.
- T. Kampfrath, A. Sell, G. Klatt, A. Pashkin, S. Mährlein, T. Dekorsy, M. Wolf, M. Fiebig, A. Leitenstorfer and R. Huber, Nat. Photonics, 2011, 5, 31–34 CrossRef CAS.
- Y. Sanari, T. Tachizaki, Y. Saito, K. Makino, P. Fons, A. V. Kolobov, J. Tominaga, K. Tanaka, Y. Kanemitsu, M. Hase and H. Hirori, Phys. Rev. Lett., 2018, 121, 165702 CrossRef CAS PubMed.
- T. Kubacka, J. A. Johnson, M. C. Hoffmann, C. Vicario, S. d. Jong, P. Beaud, S. Grübel, S. W. Huang, L. Huber, L. Patthey, Y. D. Chuang, J. J. Turner, G. L. Dakovski, W. S. Lee, M. P. Minitti, W. Schlotter, R. G. Moore, C. P. Hauri, S. M. Koohpayeh, V. Scagnoli, G. Ingold, S. L. Johnson and U. Staub, Science, 2014, 343, 1333–1336 CrossRef CAS PubMed.
- R. Matsunaga, Y. I. Hamada, K. Makise, Y. Uzawa, H. Terai, Z. Wang and R. Shimano, Phys. Rev. Lett., 2013, 111, 057002 CrossRef PubMed.
- R. Matsunaga, N. Tsuji, H. Fujita, A. Sugioka, K. Makise, Y. Uzawa, H. Terai, Z. Wang, H. Aoki and R. Shimano, Science, 2014, 345, 1145–1149 CrossRef CAS PubMed.
- K. Katsumi, N. Tsuji, Y. I. Hamada, R. Matsunaga, J. Schneeloch, R. D. Zhong, G. D. Gu, H. Aoki, Y. Gallais and R. Shimano, Phys. Rev. Lett., 2018, 120, 117001 CrossRef CAS PubMed.
- H. Chu, M.-J. Kim, K. Katsumi, S. Kovalev, R. D. Dawson, L. Schwarz, N. Yoshikawa, G. Kim, D. Putzky, Z. Z. Li, H. Raffy, S. Germanskiy, J.-C. Deinert, N. Awari, I. Ilyakov, B. Green, M. Chen, M. Bawatna, G. Cristiani, G. Logvenov, Y. Gallais, A. V. Boris, B. Keimer, A. P. Schnyder, D. Manske, M. Gensch, Z. Wang, R. Shimano and S. Kaiser, Nat. Commun., 2020, 11, 1793 CrossRef CAS PubMed.
- T. Oka and S. Kitamura, Annu. Rev. Condens. Matter Phys., 2019, 10, 387–408 CrossRef.
- T. Ishikawa, Y. Sagae, Y. Naitoh, Y. Kawakami, H. Itoh, K. Yamamoto, K. Yakushi, H. Kishida, T. Sasaki, S. Ishihara, Y. Tanaka, K. Yonemitsu and S. Iwai, Nat. Commun., 2014, 5, 5528 CrossRef CAS PubMed.
- Y. H. Wang, H. Steinberg, P. Jarillo-Herrero and N. Gedik, Science, 2013, 342, 453–457 CrossRef CAS PubMed.
- R. Moessner and S. L. Sondhi, Nat. Phys., 2017, 13, 424–428 Search PubMed.
- K. Viebahn, J. Minguzzi, K. Sandholzer, A.-S. Walter, M. Sajnani, F. Görg and T. Esslinger, Phys. Rev. X, 2021, 11, 011057 Search PubMed.
- O. R. Diermann and M. Holthaus, Sci. Rep., 2019, 9, 17614 Search PubMed.
- A. Baltuška, T. Udem, M. Uiberacker, M. Hentschel, E. Goulielmakis, C. Gohle, R. Holzwarth, V. S. Yakovlev, A. Scrinzi, T. W. Hänsch and F. Krausz, Nature, 2003, 421, 611–615 CrossRef PubMed.
- J. Duris, S. Li, T. Driver, E. G. Champenois, J. P. MacArthur, A. A. Lutman, Z. Zhang, P. Rosenberger, J. W. Aldrich, R. Coffee, G. Coslovich, F.-J. Decker, J. M. Glownia, G. Hartmann, W. Helml, A. Kamalov, J. Knurr, J. Krzywinski, M.-F. Lin, J. P. Marangos, M. Nantel, A. Natan, J. T. O'Neal, N. Shivaram, P. Walter, A. L. Wang, J. J. Welch, T. J. A. Wolf, J. Z. Xu, M. F. Kling, P. H. Bucksbaum, A. Zholents, Z. Huang, J. P. Cryan and A. Marinelli, Nat. Photonics, 2020, 14, 30–36 CrossRef CAS.
- S. Ghimire, Nat. Photonics, 2022, 16, 7–9 CrossRef CAS.
- M. F. Ciappina, J. A. Pérez-Hernández, A. S. Landsman, W. Okell, S. Zherebtsov, B. Förg, J. Schötz, J. L. Seiffert, T. Fennel, T. Shaaran, T. Zimmermann, A. Chacón, R. Guichard, A. Zaïr, J. W. G. Tisch, J. P. Marangos, T. Witting, A. Braun, S. A. Maier, L. Roso, M. Krüger, P. Hommelhoff, M. F. Kling, F. Krausz and M. Lewenstein, arXiv, 2016, 80, 054401 Search PubMed.
- M. Zhang, R. A. McKinnon, G. Viola, B. Yang, D. Zhang, M. J. Reece, I. Abrahams and H. Yan, ACS Photonics, 2021, 8, 147–151 CrossRef CAS.
- P. Zalden, M. J. Shu, F. Chen, X. Wu, Y. Zhu, H. Wen, S. Johnston, Z.-X. Shen, P. Landreman, M. Brongersma, S. W. Fong, H.-S. P. Wong, M.-J. Sher, P. Jost, M. Kaes, M. Salinga, A. v. Hoegen, M. Wuttig and A. M. Lindenberg, Phys. Rev. Lett., 2016, 117, 067601 CrossRef PubMed.
- E. Abreu, D. Babich, E. Janod, S. Houver, B. Corraze, L. Cario and S. Johnson, 2019 44th International Conference on Infrared, Millimeter, and Terahertz Waves (IRMMW-THz), 2019, pp. 1–2 Search PubMed.
- T. Oka, R. Arita and H. Aoki, Phys. Rev. Lett., 2003, 91, 066406 CrossRef PubMed.
| This journal is © The Royal Society of Chemistry 2022 |