Non-adiabatic dynamics in collisions of sodium and chlorine atoms and their ions
Martina
Šimsová née Zámečníková
 a,
Magnus
Gustafsson
a,
Magnus
Gustafsson
 a and
Pavel
Soldán
a and
Pavel
Soldán
 *b
*b
aDepartment of Engineering Sciences and Mathematics, Division of Materials Science, Applied Physics, Luleå University of Technology, 971 87 Luleå, Sweden
bFaculty of Mathematics and Physics, Charles University, Ke Karlovu 3, 121 16 Prague 2, Prague, Czech Republic. E-mail: pavel.soldan@mff.cuni.cz
First published on 12th October 2022
Abstract
Collisions of sodium and chlorine atoms and of their ions are studied within the diabatic two-state picture at energies below and above the ionic threshold with focus on the processes of radiative association, chemiionisation, and mutual neutralisation. The radiative-association cross sections as functions of collision energy are calculated up to 4.6 eV in the case of neutral atoms and up to 3.12 eV in the case of ions. The non-radiative charge-exchange cross sections as functions of collision energy are calculated up to 12 eV for chemiionisation and up to 10.52 eV for mutual neutralisation. The corresponding radiative-association rate coefficients are then determined up to 5300 K for the radiative association of neutral atoms and non-radiative charge-exchange and up to 3615 K for the radiative association of ions. Contribution of many Fano–Feshbach-type resonances is included to the rate coefficient of neutral-atom radiative association. The chemiionisation rate coefficients were calculated from 1000 K to 5300 K. The process of mutual neutralisation exhibits the largest cross sections and also the largest rate coefficients with values around 10−9 cm3 s−1 at all calculated temperatures, 120–5300 K.
1 Introduction
The alkali-metal halides are prototype systems for studies of non-adiabatic dynamics. They were the subject of many theoretical and experimental studies mainly focusing on non-radiative charge transfer, i.e. on the chemiionisation and mutual neutralisation.1–9 Recently, Gustafsson10 and Šimsová-Zámečníková et al.11 showed that the non-adiabatic dynamics has a profound effect on the radiative association of sodium atoms (Na) with chlorine atoms (Cl), where the differences in the calculated cross section, and consequently also in the calculated rate coefficient, were in orders of magnitude.This fully quantum dynamical study is devoted solely to the collisions between the sodium and chlorine atoms (or their ions) and has stemmed from astrophysical motivation. Being the first molecular bearer of a sodium atom detected in space,12,13 the gas-phase NaCl molecules have been observed in various space environments. These observations are usually associated with stars in their final evolution stage (carbon-rich or oxygen-rich stars), where NaCl molecules briefly exist in the inner layers of expanding circumstellar shells12,14–18 before being eventually condensed onto dust grains. Recently, however, the gas-phase NaCl was also detected above the protostellar oxygen-rich disk around a massive accreting young star,19 which was its first observation not related to evolved stars. Charge transfer and radiative association can play significant roles in the interstellar medium and related environments; the corresponding temperature-dependent rate coefficients are part of the input data for various interstellar-environment models.
Key information about a quantum system is contained in its wavefunctions. Thus, the goal of fully quantum dynamical calculations is to determine these wavefunctions as accurately as possible. When molecular systems exhibit non-adiabatic couplings between electronic states, then these need to be taken into account, which leads to sets of coupled Schrödinger equations. And when the non-adiabatic effects are strong, the wavefunctions obtained by solving these coupled equations differ significantly from the wavefunctions calculated just from uncoupled Born–Oppenheimer curves/surfaces, affecting thus the calculated quantities even for seemingly ‘uncoupled’ problems, such as determining the cross sections for radiative association. On the other hand, the quantum dynamics formulation of non-radiative charge transfer is only possible as a ‘coupled’ problem.
We have decided to revisit the charge transfer between Na and Cl (or Na+ and Cl−) and radiative association of Na and Cl making use of the state-of-the-art ab initio results of Giese and York,20 which provided data for the two-state formulation in both the adiabatic and diabatic representations. The purpose of this study is thus twofold: first, to determine the cross sections for radiative associations
| 1Σ+[Na(2S) + Cl(2P)] → NaCl(1Σ+) + ħω, | (1) |
| 1Σ+[Na+(1S) + Cl−(1S)] → NaCl(1Σ+) + ħω, | (2) |
| A1Π[Na(2S) + Cl(2P)] → NaCl(X1Σ+) + ħω | (3) |
| 1Σ+[Na(2S) + Cl(2P)] → 1Σ+[Na+(1S) + Cl−(1S)], | (4) |
| 1Σ+[Na+(1S) + Cl−(1S)] → 1Σ+[Na(2S) + Cl(2P)]. | (5) |
Within the adiabatic picture NaCl exhibits a long-range avoided crossing between the lowest two 1Σ+ adiabatic molecular states, where the ionic and covalent configurations are interchanged. Then the covalent configuration dissociates to Na(2S) + Cl(2P) and the ionic configuration dissociates to energetically higher Na+(1S) + Cl−(1S) by 1.4845 eV. Consequently, the corresponding off-diagonal coupling element has a sharp peak in the vicinity of the avoided crossing. Within the diabatic picture, mostly used for dynamical calculations, the ionic state crosses the covalent state and the corresponding coupling element is non-zero.
2 Methods
2.1 Non-adiabatic dynamics
The theory for the non-adiabatic dynamics employed here was described in detail by Gustafsson10 and Šimsová-Zámečníková et al.11 and is based on the work of Tchang-Brillet et al.21 and Cooper et al.9In this approach, the Schrödinger equation for continuum states has the form of two coupled differential equations
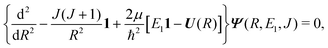 | (6) |
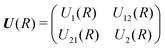 | (7) |
The Schrödinger eqn (6) is solved with the asymptotic boundary conditions
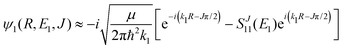 | (8) |
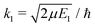 and SJ11(E1) is a scattering matrix (S-matrix) element. The boundary condition for the second component varies depending on which process is studied and will be thus specified later.
and SJ11(E1) is a scattering matrix (S-matrix) element. The boundary condition for the second component varies depending on which process is studied and will be thus specified later.
The coupled Schrödinger equations (6) are solved making use of the close coupling code COUPLE written by Mies, Julienne and Sando (F. H. Mies et al. 1993, priv. comm.).
2.2 Chemiionisation and mutual neutralisation
Chemiionisation and mutual neutralisation are non-radiative continuum–continuum processes. For their treatment we adopted the approach of Cooper et al.9 The spin–orbit splitting of the chlorine 2P atomic state22,23 (0.10939764 eV) is taken into account by the corresponding distance-independent splitting of the diabatic interaction energies U1(R) distinguishing thus the dissociation limits Na(2S) + Cl(2P3/2) and Na(2S) + Cl(2P1/2).The initial and final continuum states for the chemiionisation are supported by U1(R) and U2(R), respectively, and vice versa for the mutual neutralisation. Let us denote ΔE = U2(R → ∞) − U1(R → ∞) = 1.4845 eV the energy difference between the ionic and neutral dissociation limits. Apparently, the chemiionisation can occur only when E1 > ΔE because for E1 < ΔE the ionic dissociation channel is closed. It is reasonable to introduce the collision energy E2 for the reverse process, i.e. for the mutual neutralisation, relative to the ionic dissociation limit Na+(1S) + Cl−(1S). Then E1 and E2 are related by
| E2 = E1 − ΔE. | (9) |
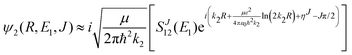 | (10) |
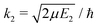 , ηJ is the Coulomb phase shift, and SJ12(E1) is the S-matrix element.24
, ηJ is the Coulomb phase shift, and SJ12(E1) is the S-matrix element.24
The chemiionisation cross section at initial energy E1 is given by
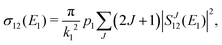 | (11) |
The cross section for the mutual neutralisation can be expressed as
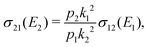 | (12) |
2.3 Radiative association
Radiative association is a transition process from a continuum state to a lower lying bound state while emitting a photon. The radiative association cross sections25 can be expressed as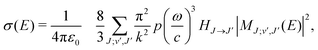 | (13) |
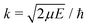 , ω is the angular frequency of an emitted photon, c is the speed of light,
, ω is the angular frequency of an emitted photon, c is the speed of light, 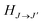 are the Hönl–London factors, and
are the Hönl–London factors, and 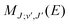 is the dipole-moment matrix element between the wavefunction of the initial continuum state and the wavefunction of the final bound state. Because in this case we do not distinguish between the spin–orbit states of Cl, the statistical weights are p = 1/12 for process (1), p = 1 for process (2), and p = 1/6 for process (3).
is the dipole-moment matrix element between the wavefunction of the initial continuum state and the wavefunction of the final bound state. Because in this case we do not distinguish between the spin–orbit states of Cl, the statistical weights are p = 1/12 for process (1), p = 1 for process (2), and p = 1/6 for process (3).
For process (1), E = E1, k = k1 and
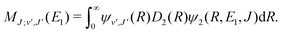 | (14) |
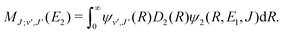 | (15) |
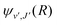 supported by U2(R). The Schrödinger eqn (6) is solved with the asymptotic boundary conditions (8) and ψ2(R → ∞,E1,J) → 0 for E1 < ΔE, while for E1 > ΔE it is solved with the asymptotic boundary condition (10). Target bound states
supported by U2(R). The Schrödinger eqn (6) is solved with the asymptotic boundary conditions (8) and ψ2(R → ∞,E1,J) → 0 for E1 < ΔE, while for E1 > ΔE it is solved with the asymptotic boundary condition (10). Target bound states 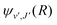 are obtained by standard single-channel calculation with boundary condition
are obtained by standard single-channel calculation with boundary condition 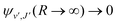 . For both the processes the only non-zero Hönl–London factors are HJ→J+1 = J + 1 and HJ→J−1 = J.
. For both the processes the only non-zero Hönl–London factors are HJ→J+1 = J + 1 and HJ→J−1 = J.
For process (3), E = E1, k = k1 and
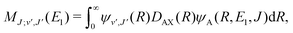 | (16) |
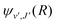 supported by the X1Σ+ potential. The only non-zero Hönl–London factors for this process are HJ→J+1 = J/2, HJ→J = (2J + 1)/2, and HJ→J−1 = (J + 1)/2.
supported by the X1Σ+ potential. The only non-zero Hönl–London factors for this process are HJ→J+1 = J/2, HJ→J = (2J + 1)/2, and HJ→J−1 = (J + 1)/2.
2.4 Thermal rate coefficients
Rate coefficients, which are of interest in reaction networks, can be expressed at temperature T as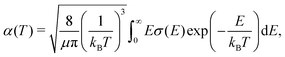 | (17) |
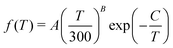 | (18) |
In the case of radiative association, one is often interested in the total rate coefficient for formation of a molecule, given specific reactants. That can be obtained as a sum of eqn (17) over individual processes in the corresponding collision channel.
2.5 Ab initio data
The ab initio data are taken from Giese and York20 and Zeiri and Balint-Kurti.27 The extrapolated data20 were used here for the non-adiabatic dynamics calculations.
extrapolated data20 were used here for the non-adiabatic dynamics calculations.
Diabatic potential energy curves of the two lowest 1Σ+ electronic states are illustrated in top-left panel of Fig. 1 together with the corresponding diabatic coupling element. The dipole-moment function D2(R) needed for processes (1) and (2) is illustrated in the bottom-left panel of Fig. 1. Born–Oppenheimer potential energy curves of the X1Σ+ and A1Π electronic states are illustrated in the top-right panel of Fig. 1. The transition dipole-moment function for process (3) is depicted in the bottom-right panel.
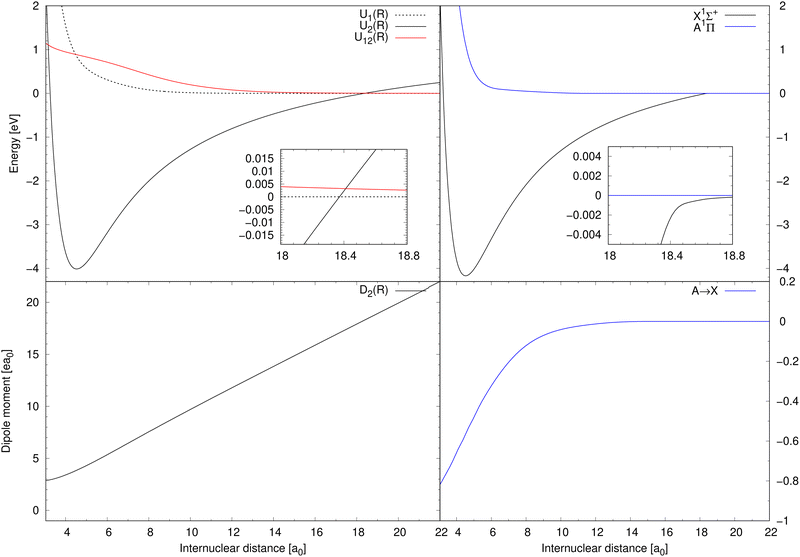 | ||
| Fig. 1 Top-left: The potential energy curves of two lowest 1Σ+ diabatic electronic states of NaCl and the diabatic coupling between them.20 Bottom-left: The dipole-moment function for the diabatic ionic state.20 Top-right: The Born–Oppenheimer potential energy curves for the A1Π and X1Σ+ states.20,27 Bottom-right: The transition dipole-moment function for the A1Π → X1Σ+ transitions.27 | ||
3 Results and discussion
3.1 Chemiionisation and mutual neutralisation
The chemiionisation and mutual neutralisation cross sections have been calculated with distinguished spin–orbit states of Cl(2P), 2P1/2 and 2P3/2.The cross sections for mutual neutralisation are illustrated in the top-right panel of Fig. 2. The cross section values are larger for the target continuum Na(2S) + Cl(2P3/2) states by around one order of magnitude than the Na(2S) + Cl(2P1/2) cross sections. Both the cross sections exhibit sharp decrease with increasing collision energy.
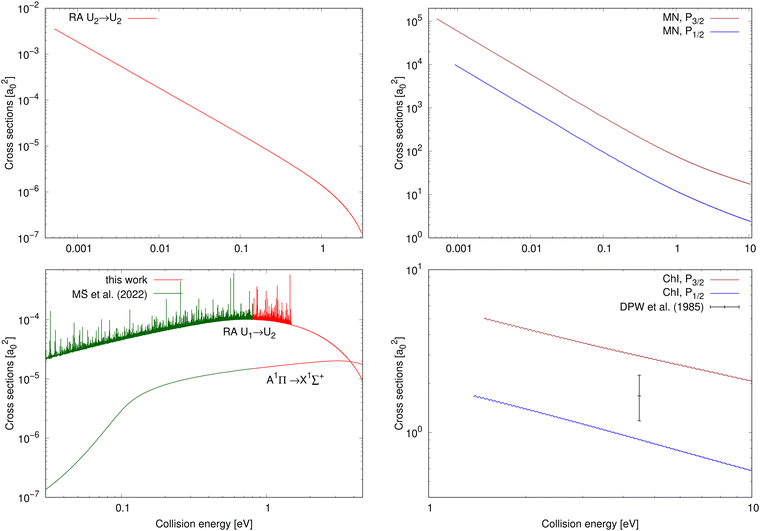 | ||
| Fig. 2 Top row: Cross sections for processes starting in the ionic continuum (collision energy E = E2); left: radiative-association cross sections of process (2); right: mutual-neutralisation cross sections for both the target continuum Na(2S) + Cl(2P3/2) and Na(2S) + Cl(2P1/2) states. Bottom row: Cross sections for processes starting in the neutral continuum (collision energy E = E1); left: radiative-association cross sections for processes (1) and (3) (the cross-section values up to E1 = 0.8 eV for processes (1) and (3) are taken from Šimsová-Zámecníková et al.11); right: chemiionisation cross sections for both the initial continuum Na(2S) + Cl(2P3/2) and Na(2S) + Cl(2P1/2) states. The only measured cross-section value for chemiionisation is taken from Wang et al.8 | ||
The cross sections for chemiionisation are illustrated in the bottom-right panel of Fig. 2. Both the chemiionisation cross sections slowly decrease with increasing collision energy. The chemiionisation for the initial Na(2S) + Cl(2P3/2) states has larger values than for the initial Na(2S) + Cl(2P1/2) states: at collision energy 1.485 eV the difference is 3.37 a02 and at 10.52 eV the difference is 1.36 a02.
The mutual-neutralisation cross sections are larger than the chemiionisation cross sections, and both of them show curly character. This curly character can be seen also in other mutual-neutralisation studies.28,29 Mutual neutralisation typically has considerably larger values at lower energies than chemiionisation. Both of them decrease with increasing energy and tend to approach each other at larger energies.7
The rate coefficients for chemiionisation and mutual neutralisation are illustrated in Fig. 3. The chemiionisation rate coefficients were calculated from 1000 K to 5300 K, while the mutual-neutralisation rate coefficients were calculated from 120 K to 5300 K. The chemiionisation rate coefficients are zero at low temperatures as the channel stays closed up to 1.4845 eV. For both the processes, the rate-coefficient values are larger when starting in the continuum of the P3/2 state. The mutual-neutralisation rate coefficient slowly decreases with increasing temperature, while the chemiionisation rate coefficient increases with increasing temperature.
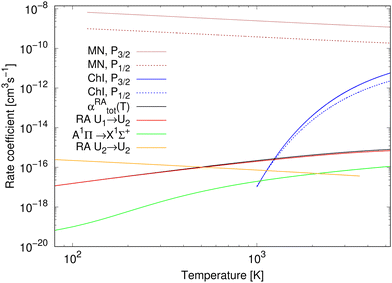 | ||
| Fig. 3 Rate coefficients for studied processes: for mutual neutralisation (MN), chemiionisation (ChI), and radiative association (RA). αRAtot is a total rate coefficient for formation of NaCl by radiative association of neutral atoms (by summing over processes (1) and (3)). The results for radiative association of the neutral atoms up to 750 K are taken from Šimsová-Zámecníková et al.11 | ||
Wang et al.8 measured one absolute value of the chemiionisation cross section from the initial continuum Na(2S) + Cl(2P3/2) state at E1 = 4.4845 eV and obtained σexp(E1) = 1.68+0.57−0.50a02 (see bottom-right panel of Fig. 2), which is lower by 44% than our calculated value σcalc(E1) = 3.00 a02. Simple scaling of the diabatic coupling element aU12(R) lead to the reproduction of the experimental value for a = 0.75. Because we could not find any more experimental chemiionisation data, we have not tried any more-sophisticated methods of morphing the diabatic-potential matrix elements.
The rate coefficients for the chemiionisation and mutual neutralisation with distinguished isotopes Cl(2P3/2) and Cl(2P1/2) were fitted to the Kooij function, eqn (18). The fitting parameters are summarised in Table 1. The maximum relative error was kept below 0.0007.
| Process | T [K] | A [cm3 s−1] | B | C [K] |
|---|---|---|---|---|
| x(−y) ≡ x × 10−y. | ||||
| ChI, P3/2 | 1000–2700 | 4.7834(−10) | −0.417878 | 17170.3 |
| 2700–5300 | 3.7720(−10) | −0.343242 | 16969.5 | |
| ChI, P1/2 | 1000–2700 | 1.4816(−10) | −0.414646 | 15904.3 |
| 2700–5300 | 1.1935(−10) | −0.346528 | 15722.6 | |
| MN, P3/2 | 120–580 | 4.3751(−9) | −0.483320 | 3.90020 |
| 580–1800 | 4.0955(−9) | −0.444913 | −20.3502 | |
| 1800–4400 | 3.3525(−9) | −0.373901 | −153.752 | |
| 4400–5300 | 2.7182(−9) | −0.315094 | −383.860 | |
| MN, P1/2 | 120–580 | 6.8053(−10) | −0.482807 | 8.97396 |
| 580–1700 | 6.3639(−10) | −0.443277 | −15.4042 | |
| 1700–4300 | 5.2931(−10) | −0.376769 | −134.333 | |
| 4300–5300 | 4.3955(−10) | −0.324248 | −334.240 | |
| RA Na + Cl | 750–1400 | 9.9314(−17) | 0.818813 | 199.659 |
| 1400–2400 | 1.8595(−16) | 0.572579 | 548.561 | |
| 2400–4000 | 4.4857(−16) | 0.287147 | 1240.66 | |
| 4000–5300 | 1.0285(−15) | 0.053504 | 2141.74 | |
| RA Na++Cl− | 80–500 | 1.3512(−16) | −0.507243 | 6.56034 |
| 500–1600 | 1.4171(−16) | −0.537171 | 23.2164 | |
| 1600–3615 | 1.7526(−16) | −0.615503 | 155.222 | |
3.2 Radiative association
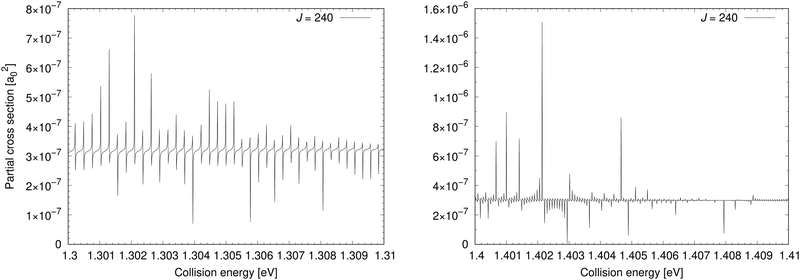
The cross section for process (1) is illustrated in the bottom-left panel of Fig. 2, where the cross section is shown from 0.03 eV to 4.6 eV (up to 0.8 eV, the cross section is taken from ref. 11). With increasing collision energy, resonances occur on the cross-section function more frequently until they cease around the threshold 1.4845 eV where the ionic channel opens. The background contribution begins to decrease around 0.7 eV (at E1 = 4.6 eV the cross section is 9.37 × 10−6a02). Because of huge number of overlapping resonances, it is not possible to use the approach, where the background and resonance contributions are calculated separately,30,31 thus it is difficult to see where precisely the background contribution reaches maximum.Fig. 4 shows a partial cross section for J = 240 at collision energies E1 between 1.3 eV and 1.31 eV in the left panel and 1.4 eV and 1.41 eV in the right panel. This partial wave is one of the most contributing at these collision energies. The number of resonances per energy unit increases with increasing energy. The resonances have clearly asymmetrical shapes with the dips being the evidence of destructive interference, thus they are of the Fano–Feshbach type.32,33
The cross section of process (2) as a function of collision energy E = E2 is illustrated in the top-left panel of Fig. 2. At the beginning of the energy scale, the cross section is roughly equal to 3.5 × 10−3a02. The cross section decreases with increasing energy over the entire energy range. At low collision energies, the cross-section values are larger than for the two studied radiative-association processes in the collisions of the neutral atoms.
The cross-section values for process (3) are illustrated for collision energy E = E1 from 0.03 eV to 4.6 eV in the bottom-left panel of Fig. 2. The continuum of the A1Π state does not support any orbiting resonances. Its background contribution increases with increasing collision energy up to around E1 = 3.1 eV, after which its values begin to decrease. Around E1 = 3.79 eV, the cross-section values start to be larger than the non-adiabatically calculated cross sections for the 1Σ+ → 1Σ+ process (1) in collisions of the neutral atoms.
The total rate coefficient and the individual radiative-association rate coefficients for the colliding neutral atoms were calculated from 750 K to 5300 K and are illustrated in Fig. 3. For completeness, the results from 80 K to 750 K, taken from Šimsová-Zámečníková et al.,11 are also shown in the figure. The values of individual rate coefficients increase with increasing temperature. Naturally, the total rate coefficient has the same character. The 1Σ+ → 1Σ+ process dominates the formation of NaCl and contributes to the total rate coefficient the most. The A1Π → X1Σ+ process's contribution is negligible at low temperatures up to around 200 K.
The rate coefficient for radiative association of the ions is also illustrated in Fig. 3. It was calculated for temperatures from 80 K to 3615 K, for which it decreases. Up to around 500 K, the values are larger than those of the total rate coefficient for radiative association of the neutral atoms.
The total rate coefficient for radiative association of Na(2S) + Cl(2P) and rate coefficient for radiative association of Na+(1S) + Cl−(1S) are fitted to the Kooij function, eqn (18). Table 1 summarises the fitting parameters. Similarly as for chemiionisation and mutual neutralisation, the maximum relative error was kept below 0.0007.
At all studied temperatures, the rate coefficient for the mutual neutralisation has larger values than the rate coefficient for the radiative association for ions. This means that the most of ions ‘prefer’ the non-radiative charge exchange to radiative association at these temperatures.
4 Conclusions
In this work we have studied how the non-adiabatic coupling between the ionic and atomic states of Na and Cl in the 1Σ+ symmetry affects various collisional processes at energies below and above the ionic threshold. Below the threshold, which is 1.4845 eV above the asymptotic energy of the neutral atoms, the NaCl formation through radiative association can take place. Besides radiative association within the 1Σ+ symmetry, i.e. according to eqn (1), also uncoupled two-channel radiative association from neutral atoms approaching in the A1Π electronic state, eqn (3), is accounted for. The latter is the only process in this work that is not affected by the non-adiabatic coupling. We have obtained thermal rate coefficients up to a temperature of 5300 K, and over this temperature interval reaction (3) has a non-discernible effect on the total rate coefficient. Thus non-adiabatic dynamics completely dominates all the processes that we have studied in this work.Above the ionic threshold there are other possible reactions, besides the radiative association. First, the collisions of neutral atoms may result in ionic products, which is the process of chemiionisation. The chemiionisation cross sections are zero up to threshold collision energy, E1 = 1.4845 eV, making the reaction rather slow compared to the radiative association up to a temperature of about 1000 K. The rate coefficients increase fast, however, due to the large cross sections above the threshold. An experimental value8 of the cross section for the chemiionisation at one single energy is smaller than our computed value by 44%, and the experimental error bars are not large enough to account for this discrepancy. Secondly, colliding ionic species can undergo mutual neutralisation. This process also has a rather large cross section, and it is the fastest reaction of those studied in this work over the entire temperature interval, from 120 K to 5300 K. Similarly to Cooper et al.9 we have determined spin–orbit (Cl(2P1/2) vs. Cl(2P3/2)) resolved cross sections and rate coefficients for the chemiionisation and mutual neutralisation, but dynamical spin–orbit couplings are not included in the scattering calculations. Thirdly, colliding ions may form molecules through radiative association. This process has similar cross section to the radiative association with colliding neutral atoms at low energies, but it decreases with increasing energy. The radiative association from colliding ions is faster than that from colliding neutrals only at temperatures below about 500 K. It should be noted that the two latter processes are relevant only if the interstellar environment of interest has significant concentrations of Na+ and Cl−.
We have encountered one numerical challenge in this work, which deserves to be mentioned. The interaction between the ionic fragments, which is Coulomb attraction, is very long range. As a consequence, when the energy approaches the threshold from below, the outer classical turning point of the closed channel rapidly approaches large distances. This makes the convergence of the calculations challenging since the coupled Schrödinger equation has to be integrated past the classical turning point.
Resonances affect the cross sections only in one of all the processes we have studied, which is the radiative-association reaction (1). Those resonances are of the Fano–Feshbach type and interfere with each other. Thus they are not straightforward to parametrise for the use of a Breit–Wigner style formula, which is otherwise typically used for evaluation of resonant rate coefficients.34 Fortunately, in our work the resonances are not so sharp, but may be resolved on a reasonably dense energy grid, making the evaluation of thermal rate coefficients possible.
The thermal rate coefficients for the various processes we have studied here should be relevant for modelling of chemistry in interstellar environments.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The support of Kempestiftelserna (project no. SMK-2045) is greatly appreciated by MŠ and MG. MŠ is also grateful to the Royal Swedish Academy of Sciences (KVA from Kungl. Vetenskapsakademien in Swedish) for the support (project no. AST2020-0010). The computations and data handling were enabled by resources provided by the Swedish National Infrastructure for Computing (SNIC), partially funded by the Swedish Research Council through grant agreement no. SNIC 2021/5-341 and SNIC 2022/5-324. MG and MŠ thank Åke Sandgren at SNIC for his assistance with overcoming technical difficulties with running the code, which was made possible through application support provided by SNIC. Computational resources were supplied by the project “e-Infrastruktura CZ” (e-INFRA CZ LM2018140) supported by the Ministry of Education, Youth and Sports of the Czech Republic.References
- E. S. Rittner, J. Chem. Phys., 1951, 19, 1030–1035 Search PubMed.
- J. J. Ewing, R. Milstein and R. S. Berry, J. Chem. Phys., 1971, 54, 1752–1760 CrossRef.
- R. Grice and D. R. Herschbach, Mol. Phys., 1974, 27, 159–175 CrossRef.
- R. D. Levine and M. B. Faist, J. Chem. Phys., 1976, 64, 2953–2970 CrossRef.
- D. Arora, J. E. Turner and P. G. Khubchandani, Phys. Rev. A: At., Mol., Opt. Phys., 1976, 14, 2089–2094 CrossRef.
- R. E. Olson, Combust. Flame, 1977, 30, 243–249 CrossRef.
- S. Bienstock and A. Dalgarno, J. Chem. Phys., 1983, 78, 224–228 CrossRef CAS.
- D. P. Wang, S. Y. Tang and R. H. Neynaber, J. Phys. B: At. Mol. Phys., 1985, 18, L513–L518 CrossRef CAS.
- D. L. Cooper, S. Bienstock and A. Dalgarno, J. Chem. Phys., 1987, 86, 3845–3851 CrossRef CAS.
- M. Gustafsson, J. Chem. Phys., 2020, 153, 114305 CrossRef CAS PubMed.
- M. Šimsová-Zámečníková, P. Soldán and M. Gustafsson, Astron. Astrophys., 2022, 664, A5 CrossRef.
- J. Cernicharo and M. Guélin, Astron. Astrophys., 1987, 183, L10–L12 CAS.
- J. Cernicharo, C. Kahane, M. Guélin and J. Gomez-Gonzales, Astron. Astrophys., 1988, 189, L1–L2 CAS.
- M. Agúndez, J. P. Fonfría, J. Cernicharo, C. Kahane, F. Daniel and M. Guélin, Astron. Astrophys., 2012, 543, A48 CrossRef.
- J. L. Highberger, K. J. Thomson, P. A. Young, D. Arnett and L. M. Ziurys, Astrophys. J., 2003, 593, 393–401 CrossRef CAS.
- L. M. Ziurys, S. N. Milam, A. J. Apponi and N. J. Woolf, Nature, 2007, 447, 1094–1097 CrossRef CAS PubMed.
- S. N. Milam, A. J. Apponi, N. J. Woolf and L. M. Ziurys, Astrophys. J., 2007, 668, L131–L134 CrossRef CAS.
- C. Sánchez Contreras, J. Alcolea, V. Bujarrabal and A. Castro-Carrizo, Astron. Astrophys., 2018, 618, A164 CrossRef PubMed.
- A. Ginsburg, B. McGuire, R. Plambeck, J. Bally, C. Goddi and M. Wright, Astrophys. J., 2019, 872, 54 CrossRef CAS.
- T. J. Giese and D. M. York, J. Chem. Phys., 2004, 120, 7939–7948 CrossRef CAS.
- W.-U. L. Tchang-Brillet, P. S. Julienne, J. Robbe, C. Letzelter and F. Rostas, J. Chem. Phys., 1992, 96, 6735–6745 CrossRef CAS.
- A. Kramida, Y. Ralchenko, J. Reader and NIST ASD Team, NIST Atomic Spectra Database (ver. 5.9), [Online]. Available: https://physics.nist.gov/asd [2022, Sep 22]. National Institute of Standards and Technology, Gaithersburg, MD, 2021.
- L. J. Radziemski and V. Kaufman, J. Opt. Soc. Am., 1969, 59, 424–443 CrossRef CAS.
- A. R. Barnett, D. H. Feng, J. W. Steed and L. J. B. Goldfarb, Comput. Phys. Commun., 1974, 8, 377–395 CrossRef.
- B. Zygelman and A. Dalgarno, Astrophys. J., 1990, 365, 239–240 CrossRef CAS.
- J. F. Babb and A. Dalgarno, Phys. Rev. A: At., Mol., Opt. Phys., 1995, 51, 3021–3026 CrossRef CAS PubMed.
- Y. Zeiri and G. G. Balint-Kurti, J. Chem. Phys., 1983, 99, 1–24 CAS.
- Å. Larson, S. M. Nkambule and A. E. Orel, Phys. Rev. A, 2016, 94, 022709 CrossRef.
- Å. Larson, J. Hörnquist, P. Hedvall and A. E. Orel, J. Chem. Phys., 2019, 151, 214305 CrossRef PubMed.
- L. Augustovičová, V. Špirko, W. P. Kraemer and P. Soldán, Chem. Phys. Lett., 2012, 531, 59–63 CrossRef.
- M. Zámečníková, W. P. Kraemer and P. Soldán, Astrophys. J., 2018, 867, 157 CrossRef.
- H. Feshbach, Ann. Phys., 1958, 5, 357–390 Search PubMed.
- U. Fano, Phys. Rev., 1963, 131, 259–268 CrossRef.
- R. A. Bain and J. N. Bardsley, J. Phys. B: At. Mol. Phys., 1972, 5, 277–285 CrossRef.
| This journal is © the Owner Societies 2022 |