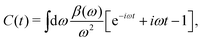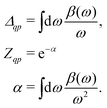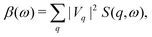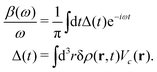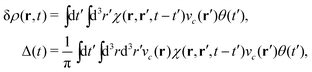DOI:
10.1039/D2CP01167K
(Perspective)
Phys. Chem. Chem. Phys., 2022,
24, 13461-13473
Ab initio calculation of X-ray and related core-level spectroscopies: Green's function approaches
Received
10th March 2022
, Accepted 13th May 2022
First published on 26th May 2022
Abstract
X-Ray and related spectroscopies are powerful probes of atomic, vibrational, and electronic structure. In order to unlock the full potential of such experimental techniques, accurate and efficient theoretical and computational approaches are essential. Here we review the status of a variety of first-principles and nearly first principles techniques for X-ray spectroscopies such as X-ray absorption, X-ray emission, and X-ray photoemission, with a focus on Green's function based methods. In particular, we describe the current state of multiple scattering Green's function techniques available in the FEFF10 code and cumulant Green's function techniques for including the effects of many-body electronic excitations. Illustrative examples are shown for a variety of materials and compared with other theoretical and experimental results.
1 Introduction
X-ray absorption and related spectroscopies have proven to be important experimental techniques for probing atomic, electronic, vibrational, and magnetic structure in a wide variety of materials and applications. Among these are energy materials,1 chemical, geological and biological systems,2 surface science and magnetism.3 In addition, the advent of femto-second and free-electron lasers has added the capability to probe time and temperature at extreme scales.4,5 For example, chemical reactions can be probed in real-time,4 and high intensity pumps can used to create short lived warm-dense states of matter.6
In order to interpret the results of these experiments, advanced theories and computational approaches are essential. There have been tremendous advances in the theory and calculation of X-ray spectra, both from formal developments, as well as computational algorithms that take advantage of the ever-increasing computational power. Most of these approaches can be classified as either ab initio or model Hamiltonian based. Currently there are a wide variety of ab initio approaches, such as density functional theory (DFT),7–9 time-dependent density functional theory,10–12 many-body perturbation theory as in the solution of the Bethe–Salpeter equation (BSE) with or without the GW approximation,13–15 and quantum chemistry methods such as configuration interaction (CI) and restricted-active space self-consistent field (RASSCF).16–18 Of the model Hamiltonian based approaches, the most widely used are atomic multiplet and charge transfer multiplet models,19 for which advanced methods exist for ab initio calculations of the parameters involved,20,21 and solutions based on dynamical mean field theory (DMFT) are also available.22,23
In this article, we review a number of recent advances in the theory and calculations of X-ray spectra, with a focus on Green's function techniques and especially the real-space multiple scattering approach (RSMS) used in the FEFF codes.24–26 This review covers a variety of recent advances implemented in the FEFF codes, including quasiparticle self-energy effects,27ab initio treatments of vibrational disorder through Debye–Waller factors,28 and the description of systems at finite-temperature and out of equilibrium.29 In particular, we discuss the application of the cumulant expansion for the one-electron Green's function,30–33 which has been shown to yield accurate many-body satellite structure in X-ray spectra.33–37 Finally, we describe the Python-based workflow framework dubbed Corvus, which facilitates advanced calculations that require multiple auxiliary scientific software packages.
In the remainder of this article Section 2 contains a brief overview of the basic theory of X-ray spectra, focusing on X-ray absorption spectra (XAS); Section 3 discusses the real-space multiple scattering (RSMS) theory of XAS; Section 4, advances in treating many-body satellites within the cumulant approach; and Section 5 the workflow framework Corvus and some applications. Finally, Section 6 contains a summary and concluding remarks. Throughout this article, we use atomic units ℏ = e = m = 1, c = 1/α = 137.037, unless explicitly stated.
2 X-Ray absorption and related spectroscopies
Experimentally, XAS measures the probability that photons of a particular energy ω are absorbed by a sample. As the energy is increased, jumps called “edges” are observed in the absorption spectrum, roughly at the binding energy of core electrons in the system. These are related to the fact that these core electrons are not allowed to participate in the absorption process until the photons have enough energy (roughly the binding energy) to promote them to unoccupied states of the system. These edges have a nomenclature denoting the quantum state of the associated core-level, i.e., K = 1s, L1 = 2s, L2,L3 = 2p1/2,2p3/2, etc. Above each edge, there exist oscillations called fine structure, due to quantum interference between the outgoing photoelectron and that backscattered from neighboring atoms. Due to different considerations in calculation and analysis, the absorption near the edge up to about 50 eV above the edge is termed X-ray absorption near edge structure (XANES), while above that, the term extended X-ray absorption fine structure (EXAFS) is used. In this section we briefly review the basic theory of XAS and discuss the connection to theories of related spectroscopies, such as X-ray emission spectroscopy (XES), electron energy loss spectroscopy (EELS) and non-resonant inelastic X-ray scattering (NRIXS).
2.1 XAS, EELS, NRIXS
The basic theory of X-ray absorption is usually expressed in terms of a Fermi's golden rule,38| | 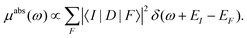 | (1) |
Here |I〉 and EI are the many-body ground state wavefunction and energy, |F〉 and EF are an excited state wavefunction and its associated energy, and D is the many-body transition operator, which characterizes the interaction of the many-body electronic system with the probe (usually X-rays or electrons). The energy of the X-ray (or that lost by the probe) is given by ω, and the δ function enforces energy conservation. While this expression is formally exact within 2nd order perturbation theory for weak probes, and useful for the purpose of discussion, the many-body nature of molecular or solid state systems where the number of electrons varies from of order 102 to 1023, makes calculations based on the golden rule impossible. Thus one must reduce the problem to a smaller number of degrees of freedom. One way to do this is to approximate the spectrum using an effective one-electron Hamiltonian, such as the Kohn–Sham Hamiltonian of DFT, or a quasi-particle approach where the many-body effects are included in terms of an exchange-correlation potential or a dynamic self-energy. Then the many-body spectrum μabs(ω) can be written in terms of a convolution of a quasiparticle spectrum and a many-body spectral function A(ω,ω′),27,34,39| | 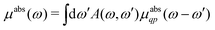 | (2) |
| | 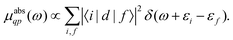 | (3) |
Here the one-particle states |i〉, |f〉 are quasiparticle occupied and unoccupied states, respectively, with εi, εf their quasiparticle energies. For the case of core-level spectroscopy, we are interested in transitions from a particular deep core-level |c〉, so that the contribution from that core level to the quasiparticle spectrum reduces to| | 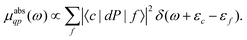 | (4) |
In this case the final states |f〉 are calculated in the presence of a screened core-hole potential, i.e., within the final state rule, while P is a projection operator onto the unoccupied levels of the ground state, which enforces orthogonality and accounts for the Mahan edge-singularity effects.40,41 For simplicity we set P = 1 in the following and only include states f above the Fermi level εF. The transition operator depends on the type of spectroscopy, i.e.,
d = ![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) ·r; XAS/XES, ·r; XAS/XES, |
where ![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) is the polarization of the X-rays, and q is the momentum transferred to the system by the probe. For XAS, XES, and EELS, the transitions are, to a good approximation, dipole limited, and thus the dipole approximation is used as shown above for these spectroscopies. However, for NRIXS, the transition operator is given by the exponential form shown, and is only dipole limited at very small momentum transfer. The transition operator, along with the symmetry of the core-state, determines the local symmetries of the final states that can be probed, with the orbital angular momentum of the possible final states determined within the dipole and quadrupole approximations as follows,
is the polarization of the X-rays, and q is the momentum transferred to the system by the probe. For XAS, XES, and EELS, the transitions are, to a good approximation, dipole limited, and thus the dipole approximation is used as shown above for these spectroscopies. However, for NRIXS, the transition operator is given by the exponential form shown, and is only dipole limited at very small momentum transfer. The transition operator, along with the symmetry of the core-state, determines the local symmetries of the final states that can be probed, with the orbital angular momentum of the possible final states determined within the dipole and quadrupole approximations as follows,
| | | Δl = 0, ±2; quadrupole. | (6) |
Thus XAS and EELS probe unoccupied states of angular momentum l = lc ± 1, while NRIXS can access higher multipole excitations by probing larger momentum transfer.
While the Fermi golden rule approach to spectra is useful for discussions and has been implemented in a variety of codes it is usually computationally difficult to obtain reasonable spectra at high energy (e.g., tens to hundreds of eV) relative to the X-ray edge. The reason is that with such sum-over-states approaches one must first calculate all of the unoccupied eigenstates and their eigenenergies, both for excitations to bound states, as well as the continuum. Here we take a different approach, and formulate the problem in terms of the effective one-electron Green's function, G(E),
| | | μabsqp(ω) ∝ Im[〈c|d†G(ω + εc)d|c〉]θ(ω + εc − εF), | (7) |
where
εF is the Fermi energy, and the function
θ(
ω +
εc) is the unit step function ensuring that transitions are from the occupied core-level to unoccupied states of the system. The one-electron Green's function is given by
| | 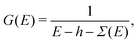 | (8) |
where
h is the single particle Hamiltonian, which includes the kinetic energy term, the potential from the nuclei, and the mean-field Hartree approximation to the interaction.
Σ(
E) is the quasiparticle self-energy operator, which takes dynamic exchange and correlation into account. In this formulation the sum over unoccupied states |
f〉 is implicit in the definition of the Green's function, as can be seen by expanding
G(
E) in the eigenstates of the system, and thus there is no need to solve for these eigenstates explicitly. Instead, the Green's function is found directly by solving an energy dependent differential equation, for which the solution is written in terms of the real-space multiple scattering basis.
3 Real-space multiple-scattering Green's function theory of XAS
This approach is also referred to as real-space Green's function (RSGF) theory. Within multiple scattering theory, the potential V(r) due to the atomic nuclei and the mean-field Kohn–Sham potential are expressed as a sum of single-site muffin-tin (MT) potentials, centered about one of the atoms in the system, and zero outside a sphere of radius RMT, and a constant interstitial potential Vinter between the sites,| | 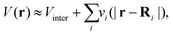 | (9) |
| | | vi(|r − Ri|) = [Vi(|r − Ri|) − Vinter]θ(RMT − |r − Ri|). | (10) |
Here Vi(|r − Ri|) is the total DFT potential, spherically averaged about the ith site center. The choice of interstitial potential and muffin-tin radii is not unique, and can be set by the user within the FEFF codes. By default, the muffin-tins are overlapping, which has been found to correct for some of the errors due to the neglect of non-spherical potentials. Details of the prescription for finding the default muffin-tin radii and interstitial potential can be found elsewhere.24 Since the core-level is localized at the central (absorbing) site, we are interested only in the portion of the Green's function with both spatial arguments within the central cell i corresponding to the absorbing atom,| | 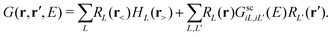 | (11) |
Here the scattering states are defined as RL(r) = ilRl(r)YL(![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) ) following the conventions in ref. 42 where Rl and Hl are the regular and irregular solutions of the single site radial Dirac equation for site i, and YL(
) following the conventions in ref. 42 where Rl and Hl are the regular and irregular solutions of the single site radial Dirac equation for site i, and YL(![[r with combining circumflex]](https://www.rsc.org/images/entities/char_0072_0302.gif) ) are the spherical harmonic functions where L denotes the combined orbital angular momentum l and magnetic m quantum numbers (or their relativistic counterparts). In general, the Green's function can be written in terms of an expansion in orders of the single site scattering potentials vi about the free particle Green's function G0(r,r′,E). However, it is more convenient to sum all consecutive scatterings from a given site by defining the single site scattering matrices ti = vi + viG0ti. The scattering Green's function in the above equation is then given by,
) are the spherical harmonic functions where L denotes the combined orbital angular momentum l and magnetic m quantum numbers (or their relativistic counterparts). In general, the Green's function can be written in terms of an expansion in orders of the single site scattering potentials vi about the free particle Green's function G0(r,r′,E). However, it is more convenient to sum all consecutive scatterings from a given site by defining the single site scattering matrices ti = vi + viG0ti. The scattering Green's function in the above equation is then given by,| | 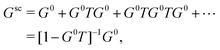 | (12) |
where the free particle Green's function G0 and the scattering matrix T are now matrices in a site and angular momentum basis {i, L}. In the above, the scattering matrix is site and angular momentum diagonal, i.e., 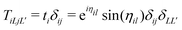 , where ηil is the phase shift of the ith site potential, and δij is the Kronecker δ, which is one if i = j and zero otherwise. With this representation of the Green's function, the quasiparticle spectrum is given by,
, where ηil is the phase shift of the ith site potential, and δij is the Kronecker δ, which is one if i = j and zero otherwise. With this representation of the Green's function, the quasiparticle spectrum is given by,| | 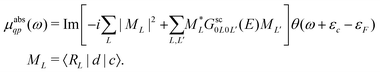 | (13) |
At energies high above an X-ray absorption edge, the scattering Green's function can be approximated via a multiple-scattering path expansion, as in the series expansion of eqn (12), with the aid of the Rehr-Albers separable approximation.42 In addition, the path-expansion yields an EXAFS equation similar in form to that of Sayers et al.43 but now builds in curved wave corrections to the effective scattering amplitudes feff(k), from which the FEFF codes are named. The path expansion in the FEFF codes converges rapidly, typically with 10–100 paths, and has been used extensively to provide theoretical standards for EXAFS analysis.44,45 At low energies, near an absorption edge where inelastic mean-free paths are long, multiple scattering can be substantial leading to poor convergence of the path-expansion. In that case, the full multiple-scattering (FMS) approach is necessary, which can be calculated using the matrix inverse in eqn (12).
In many cases, the spectral function in eqn (2), can be approximated by a Lorentzian with width Γc, corresponding to the inverse core-hole lifetime. For efficiency, and to avoid numerical instability associated with calculations of the Green's function on the real energy axis, we perform the convolution on a contour in the complex energy plane, starting from εF, proceeding up the imaginary axis to εF + iΓc, then to ∞ +iΓc.
In addition to the spectrum, we must be able to calculate the relaxed ground state electron density self-consistently, since the electron density is required for the mean-field muffin-tin potentials. Within the Green's function approach, the density is given by,
| | 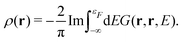 | (14) |
In addition, one must find the Fermi energy, which is determined by enforcing charge neutrality,
| | 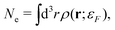 | (15) |
where
Ne is the number of electrons in the system. In practice, relaxation of the core-electrons is neglected, so that the lower bound of the integral in
eqn (14) is given by the core-valence separation energy
Ecv ≈
EFermi − 40 eV.
With these definitions, one can calculate a variety of spectra beyond XAS, including XES, EELS,46 and NRIXS,47 but also others such as Compton,48 and resonant inelastic X-ray scattering (RIXS).49 See ref. 42 for additional details.
3.1 Many-pole model self-energy
Due to the relaxation of the valence electrons when a particle-hole excitation occurs, peaks in the experimental spectrum are shifted and broadened (due to finite lifetime) relative to those of the single particle theory. The energy dependent shift and Lorentzian width are related to the quasiparticle self-energy, which is usually calculated within the GW approximation50 as Σ(E) ≈ iGW, where G is the one-electron Green's function, W = ε−1(ω)v is the dynamically screened Coulomb interaction, and ε(ω) is the dielectric function of the material. It is now standard in calculations of XAS to approximate this self-energy by using a plasmon pole approximation for the dielectric function ε(q, ω).51 In this case the loss function −Im[ε−1(q,ω)] is given by a single δ function, which allows for an analytic calculation of the quasiparticle lifetime. While this approximation works surprisingly well for high photoelectron energy, it can break down near the edge. In order to improve the approximation while retaining the efficiency of a pole model, one can use a many-pole approximation to the loss function,27| | 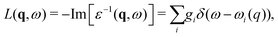 | (16) |
where the strengths gi, and energies ωi(0) are constrained by matching the model to moments of a calculation of the zero momentum transfer loss function, as seen in Fig. 1. The dispersion of these poles is assumed to be that of the electron gas.
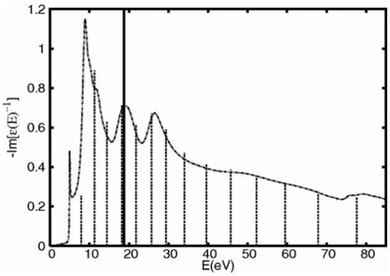 |
| | Fig. 1 Calculated loss function (dot-dash) compared to the single pole model (solid impulse) and many-pole model (short dashes). Reprinted figure with permission from [J. Kas, A. P. Sorini, M. P. Prange, L. W. Cambell, J. A. Soinine and J. J. Rehr, Phys. Rev. B, 2007, 76, 195116], Copyright (2022) by the American Physical Society. | |
The zero momentum-transfer loss function can be calculated using a variety of methods, including an efficient real-space multiple scattering approach, which sums eqn (13) over all edges in the system,52,53 or more accurate approaches such as those based on the Bethe–Salpeter equation.13 In addition, it has been shown that an embedded atomic approximation to the zero frequency loss function can be used with very little loss of accuracy for the quasiparticle self-energy, as shown in Fig. 2.
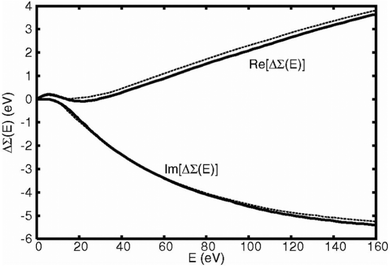 |
| | Fig. 2 Real and imaginary parts of the quasiparticle shift calculated with the many-pole model fit to a full calculation of loss function (dashes) compared to results from a fit to an efficient atomic calculation of the loss function (solid). Reprinted figure with permission from [J. Kas, A. P. Sorini, M. P. Prange, L. W. Cambell, J. A. Soi and J. J. Rehr, Phys. Rev. B, 2007, 76, 195116], Copyright (2022) by the American Physical Society. | |
The many-pole self-energy yields improved agreement with experiment for near-edge XAS and EELS spectra compared to ground state calculations, as shown in Fig. 3 which shows calculated and experimental results of the O K-edge of SnO2. In addition, quantitative improvement is observed in the analysis of extended X-ray absorption fine structure (EXAFS).54
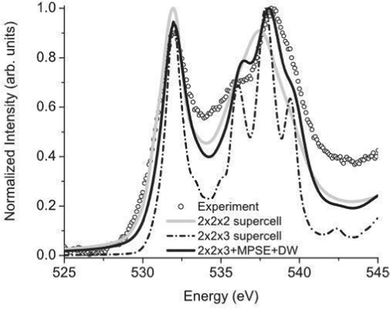 |
| | Fig. 3 Many-pole self-energy (MPSE) applied to calculations of the O K-edge spectrum of SnO2. Reprinted figure with permission from [M. S. Moreno, J. J. Kas, C. Ma, F. Wang, J. J. Rehr and M. Malac, Phys. Rev. B, 2017, 95, 245206], Copyright (2022) by the American Physical Society. | |
3.2
Ab initio Debye–Waller factors
In addition to the broadening of the spectrum due to interaction of the photoelectron with the valence electrons, there is broadening and damping due to vibrational disorder, which is highly temperature dependent. In particular eqn (13) gives the absorption for a fixed set of nuclear coordinates, ignoring the effects of vibrational disorder, which tend to damp the fine-structure at high energies. In this section we show how the Green's function approach can also be used to address these vibrational damping effects using ab initio force constants. The effect on the spectrum can be characterized by path-dependent EXAFS Debye–Waller factors exp(−2k2σR2(T)), where k is the EXAFS wave number, and σR2(T) = 〈[(uR − u0)·![[R with combining circumflex]](https://www.rsc.org/images/entities/b_char_0052_0302.gif) ]2〉 is the mean-square relative displacement (MSRD).55 These factors damp the spectrum at high energy, with the effect increasing with temperature, with σR2 ≈ kBT/κ where κ is an effective spring constant. The need for path dependent Debye–Waller factors creates a major difficulty for the analysis of EXAFS due to the large number of free parameters involved, especially for disordered or molecular systems, where a simple model such as the correlated Debye model is inapplicable. In such cases it is advantageous to obtain the Debye–Waller factors through ab initio approaches. A number of theoretical methods have been used to this end, based, e.g., on DFT,56–58 or molecular dynamics.59 Here we provide details of the approach of ref. 56 which is implemented within the FEFF10 code.
]2〉 is the mean-square relative displacement (MSRD).55 These factors damp the spectrum at high energy, with the effect increasing with temperature, with σR2 ≈ kBT/κ where κ is an effective spring constant. The need for path dependent Debye–Waller factors creates a major difficulty for the analysis of EXAFS due to the large number of free parameters involved, especially for disordered or molecular systems, where a simple model such as the correlated Debye model is inapplicable. In such cases it is advantageous to obtain the Debye–Waller factors through ab initio approaches. A number of theoretical methods have been used to this end, based, e.g., on DFT,56–58 or molecular dynamics.59 Here we provide details of the approach of ref. 56 which is implemented within the FEFF10 code.
The temperature dependence of the MSRD is given by the Debye integral
| | 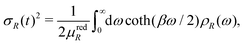 | (17) |
where
β = 1/
kBT,
μredR is the reduced mass associated with the path
R, and
ρR(
ω) is the path-projected vibrational density of states (VDOS). Thus the difficulty in calculating the MSRD lies in calculations of the projected VDOS. Simple correlated Debye or Einstein models of the VDOS can be used in some cases, although their application is limited to systems with high symmetry.
57,60 Alternatively, the VDOS can be related to the lattice dynamical Green's function,
| | 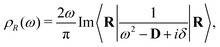 | (18) |
where
D is the lattice dynamical matrix given by second derivatives of the internal energy of the system with respect to atomic displacements, and
|R〉 is a unit vector projecting onto the path in question. The dynamical matrix can be obtained through standard approaches within DFT, after which the matrix inverse is performed
via an efficient Lanczos algorithm.
61 Beyond efficiency, the Lanczos algorithm is also useful since it can stabilize the calculation, and provides a simple many-pole model of the VDOS. In particular, the first iteration gives a single pole model, similar to the correlated Einstein model, where the pole matches the first moment of the VDOS. High accuracy can be achieved efficiently with ∼6 iterations.
56Fig. 4 shows the resulting pole model for the total VDOS of Cu compared to experimental results.
56
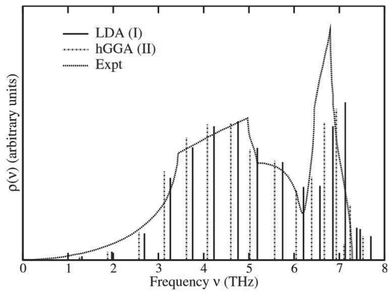 |
| | Fig. 4 Lanczos pole model of the total VDOS of Cu calculated using two different exchange correlation potentials (LDA and hGGA) compared with experimental results. Reprinted figure with permission from [F. D. Vila, J. J. Rehr, H. H. Rossner and H. J. Krappe, Phys. Rev. B, 2007, 76, 014301], Copyright (2022) by the American Physical Society. | |
This approach has been used to predict EXAFS Debye–Waller factors for simple metals, semiconductors, and even more complex systems with negative thermal expansion such as zirconium-tungstate ZrW2O8, as shown in Fig. 5.
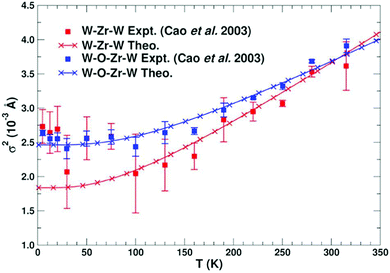 |
| | Fig. 5 Calculated MSRD of various paths in ZrW2O8 compared with experimental results. Reprinted figure with permission from [F. D. Vila, J. W. Spencer, J. J. Kas, J. J. Rehr and F. Bridges, Front. Chem., 2018, 6, 1]. | |
In addition to the EXAFS MSRD, other quantities related to vibrational disorder can be obtained. For example, the mean-squared displacements u2(T) associated with diffraction experiments can be calculated via an integral similar to that of eqn (17). Other EXAFS cumulants have a simple relationship to the MSRD, which allows calculations of the Debye–Waller factors beyond the harmonic approximation. Thermal expansion coefficients can also be found via minimization of the Helmholtz free energy, or through calculation of the Grüneisen parameters.56
3.3 Time-resolved and finite-temperature XAS
Recent interest and advances in the time resolution of pump-probe experiments has led to X-ray absorption probes of systems out of equilibrium and at very high electronic temperatures, up to the warm-dense-matter regime.6,62–65 In order to simulate XAS at finite temperatures, both the temperature dependence of the lattice and that of the electronic system must be treated. While the previous section discussed an approach for treating the lattice temperature, here we provide details about our RSMS treatment of finite electronic temperature in X-ray spectra. Other finite temperature multiple-scattering theories have been developed previously.66,67 More recent developments have shown that predictions of high temperature spectra are possible with multiple-scattering approaches.68,69 Three extensions of the theory must be implemented in order to treat finite electronic temperatures.29 First, Fermi–Dirac statistics must be taken into account both in the formula for the quasiparticle XAS, and in the definition of the self-consistent density. Second, the self-consistent density should be calculated using a finite-temperature exchange-correlation potential.70 Third, the quasiparticle self-energy used in the calculation of the spectrum should be calculated at finite temperature. The first of these three effects is the most important well below the Fermi temperature kTF = εF, and this is our focus below. However, at higher temperature, i.e., the warm-dense matter regime where T is of order TF the temperature dependence of the exchange correlation potential and self-energy can become important. This effect can be calculated within FEFF using the finite temperature exchange correlation potential of ref. 70. Temperature dependent self-energies have also been developed using the finite temperature GW approximation,71 or the finite temperature generalization of the static Coulomb-hole screened-exchange (COHSEX) approximation.72
The form of the quasiparticle XAS at finite temperature is similar to that of zero temperature XAS, i.e., from eqn (13), except that the unit step function ensuring contributions only from excitations to the unoccupied states is replaced by a Fermi function, thereby taking Fermi–Dirac statistics into account.
| | 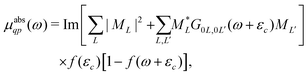 | (19) |
| | 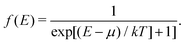 | (20) |
In order to account for the finite lifetime of the hole, the quasiparticle spectrum is convolved with a Lorentzian as in the zero temperature case. Again, for efficiency, the integral is performed in the complex plane, although at finite temperature, the contour is taken from
Ecv to
Ecv +
iγ, then to ∞ +
iγ, where the size of the imaginary part
γ is chosen to ensure that the Green's function is sufficiently smooth (
γ ≈ 4 eV). In addition,
γ is set halfway between two Matsubara poles, as seen in
Fig. 6. Thus the Green's function must also be calculated at any Matsubara poles enclosed by the contour and the residues must be subtracted from the result of the contour integral.
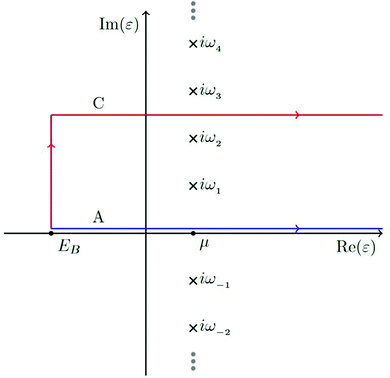 |
| | Fig. 6 The contour labeled C is used for integration of the Green's function defining the core-lifetime broadened XAS as well as the electron density. Reprinted figure with permission from [T. S. Tan, J. Kas and J. Rehr, Phys. Rev. B, 2021, 104, 035144], Copyright (2022) by the American Physical Society. | |
The integral defining the density is modified in a similar manner, replacing the upper bound restricting the integral to occupied states in eqn (14) with a Fermi function,
| | 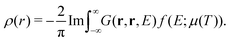 | (21) |
Again, this integral is calculated on a contour going from
Ecv to
Ecv +
iγ and up the real axis to ∞ +
iγ, and subtracting the residues at the Matsubara poles,
i.e.,
| | 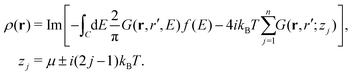 | (22) |
In addition, temperature dependence of the chemical potential
μ(
T) is defined implicitly by enforcing charge neutrality,
| | 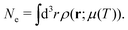 | (23) |
The inclusion of Fermi–Dirac statistics in the definition of the spectrum and density modify the calculated XAS in several ways. At finite temperature, the Fermi function broadens to a width ∼
kBT. This causes the chemical potential, and thus the X-ray edge, to shift at finite temperatures. At low temperature, this shift is proportional to the logarithmic derivative of the density of states at the Fermi energy
D (
εF), in accordance with a Sommerfeld expansion
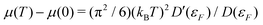
. This approximation is often valid to moderate temperatures
T <
TF. Another effect of the broadening of the Fermi function is that excitation of states below the chemical potential is allowed. This effect, known as continuum lowering can be especially prominent in L-edges of the late 3d transition metals, where a high concentration of density of d-states lies right below the Fermi energy. This effect is shown for Cu in
Fig. 7, which shows the L-edge XAS of Cu calculated at various electronic temperatures.
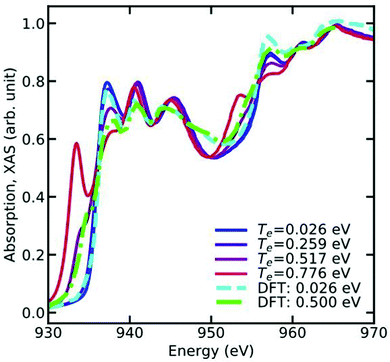 |
| | Fig. 7 L-Edge XAS of Cu metal at various electronic temperatures. Note the sharp peak appearing below the X-ray edge as function of increasing electronic temperature, which occurs due to the broadening of the Fermi function. Reprinted figure with permission from [T. S. Tan, J. Kas and J. Rehr, Phys. Rev. B, 2021, 104, 035144], Copyright (2022) by the American Physical Society. | |
For systems out of equilibrium, the lattice and electronic temperatures generally have different values, and the coupling between the lattice and the electrons can be approximated using a two-temperature model. Generally, the effect of lattice vibrations is to damp the spectrum, with increased damping at higher energy, as well as higher temperatures. These effects can be calculated as detailed in the previous section for energies well above the edge. Near the edge, symmetry breaking can cause forbidden transitions to appear in the spectrum, which cannot be predicted by the use of Debye–Waller factors. An alternative approach is to use either molecular dynamics, which is applicable at high temperatures in the classical limit, or to populate the phonon modes using Monte-Carlo approaches. The XAS is then averaged over many configurations of the atomic positions.
4 Cumulant Green's function treatment of many-body satellites
Many-body electronic effects in X-ray spectra are also apparent in some other ways, beyond the energy dependent shift and broadening associated with quasiparticles. In particular, the sudden appearance of the core-hole and photoelectron can cause additional electronic excitations such as plasmon, particle-hole, and charge transfer excitations. These inelastic losses show up as extra satellite peaks in X-ray spectra, shifted from the main quasiparticle peak by the energy of the many-body excitation. Such satellites show up in all spectra to varying extents, but are especially prominent in X-ray photoemission spectra (XPS), which are directly related to the one-electron spectral function. Effective single particle (or quasiparticle) theories predict only a single peak for each core-level, while multiple peaks are present in experiment. Formally, these many-body excitations can be treated via an energy dependent self-energy as seen in eqn (8). However, standard approaches for calculating the self-energy, e.g., based on many-body perturbation theory, such as the GW approximation of Hedin73 fail to describe the many-body satellites.74 In particular, the GW approximation fails to describe the multiple plasmon satellites observed in the XPS of nearly free-electron metals,30,31,35,74 and even semiconductors,36 producing only a single satellite at an energy ∼1.5 times that of the first satellite seen in experiment. In contrast, the cumulant expansion correctly describes these multiple plasmon satellites at the correct energy corresponding to the plasmon energy in the loss function, as shown in Fig. 8.31,33,35–37,75
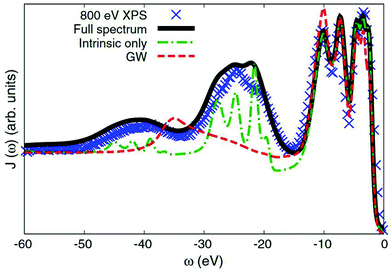 |
| | Fig. 8 Valence XPS of Si calculated with the cumulant approach (green dot-dash) compared to that of the GW approximation (red dash), and experimental results (blue crosses). Theory including an approximate treatment of extrinsic effects is also shown (black solid). Reprinted figure with permission from [M. Guzzo, G. Lani, F. Sottile, P. Romaniello, M. Gatti, J. J. Kas, J. J. Rehr, M. Silly, F. Sirotti and L. Reining, Phys. Rev. Lett., 2011, 107, 166401], Copyright (2022) by the American Physical Society. | |
The cumulant Green's function is given by an exponential in real-time,
where
g0c = −
ie
−iεctθ(−
t) is the single-particle core-level Green's function, and
C(
t) is the cumulant, which builds in dynamic correlation. For core-levels, the XPS spectrum is approximately given by the spectral function which is the Fourier transform of the core-electron Green's function,
Ac(
ω) = −(1/π)ImFT[
gc(
t)]. To facilitate the analysis, it is useful to express the cumulant in Landau form,
| | 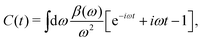 | (25) |
where
β(
ω) describes a quasi-boson excitation spectrum. The first term in the above expression yields the satellites, while the second and third terms are associated with the complex quasiparticle shift
Δqp and renormalization factor
Zqp,
i.e.,
| | 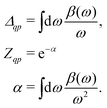 | (26) |
The behavior of the excitation spectrum
β(
ω) was first derived by Langreth
30 for an electron gas, but is more generally valid within the linear response approximation. Formally
β(
ω) is related to the dynamic structure factor,
| | 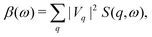 | (27) |
where
Vq is the core-hole potential.
4.1 Real-time cumulant
The above expression for the cumulant can be generalized to real-space and real-time, and is related to the time dependent density fluctuations caused by a core-hole potential turned on at time t = 0,76| | 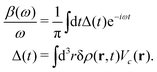 | (28) |
To make the connection with the Langreth form in eqn (27), note that the induced density can be expressed in terms of the response function χ and the external potential, which in this case is the core-hole potential,| | 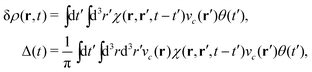 | (29) |
which is just the space and time Fourier transform of eqn (27). This form has been implemented within the real-time TDDFT version of the SIESTA code,77 and has been used to describe charge tranfer excitations in transition metal oxides, as shown in Fig. 9. The real-space, real-time approach described above yields an analysis of the excited states through the induced density fluctuations. In particular, the Fourier transform to frequency gives a real-space picture of the excitation density. For example, Fig. 10 clearly shows ligand to metal electron transfer in the excitation density, which is shown at the calculated charge transfer energy of 14.8 eV in rutile, corresponding to the main-peak satellite splitting seen in Fig. 9.
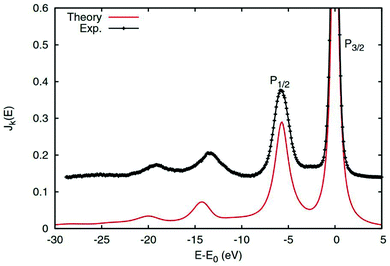 |
| | Fig. 9 2p core-level XPS of rutile TiO2 calculated with the real-time cumulant approach (red solid) compared to experimental results (black). The main quasiparticle peaks are labeled P1/2 and P3/2, while the charge transfer satellites appear at ∼14 eV lower energy. Reprinted figure with permission from [J. J. Kas, F. D. Vila, J. J. Rehr and S. A. Chambers, Phys. Rev. B, 2015, 91, 121112], Copyright (2022) by the American Physical Society. | |
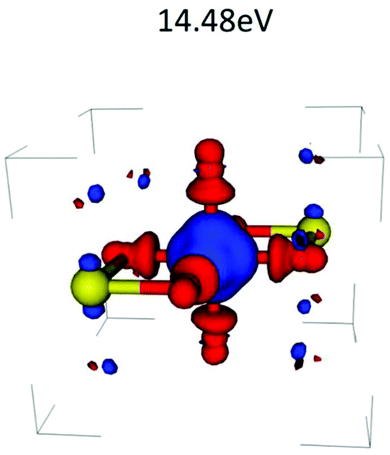 |
| | Fig. 10 Excitation density δρ(r, ω), i.e., taken at a frequency ω = 14.8 (eV) corresponding to the charge transfer energy. Reprinted figure with permission from [J. C. Woicik, C. Weiland, C. Jaye, D. A. Fischer, A. K. Rumaiz, E. L. Shirley, J. J. Kas and J. J. Rehr, Phys. Rev. B, 2020, 101, 245119], Copyright (2022) by the American Physical Society. | |
4.2 Extrinsic and interference terms, and the particle-hole cumulant for XAS
In addition to the interaction between the core-hole and the valence excitations, i.e., intrinsic losses, the photoelectron also interacts with the valence electrons and creates extrinsic excitations, and there is interference between them.78,79 The cumulant form for XPS is still valid when extrinsic and interference terms are considered, although the excitation spectrum β(ω) seen in the Landau form of eqn (25) must be replaced with the combined excitation spectrum created by the appearance of the particle-hole system,34i.e., γ(ω) = βint(ω) + βext(ω) +βinf(ω), where int/ext/inf denote intrinsic, extrinsic, and interference terms. Thus the cumulant can also be separated into intrinsic, extrinsic and interference terms. Since the contribution from the extrinsic and interference terms has roughly the same shape as the intrinsic spectrum, these effects can be modeled by an energy dependent amplitude factor R(ω) = αtot(ω)/αint,35,37,80 which can be calculated within an electron gas model.78 Since intrinsic excitations dominate at low excitation energy, the factor is approximately linear, i.e., R(ω) ≈ 1 + aω. Calculations of the extrinsic to intrinsic ratio show that the extrinsic weight dominates for plasmonic excitations of free-electron metals, although it is not expected to contribute substantially for more localized excitations such as charge-transfer.75,81 Finally, the particle-hole cumulant can be applied to XAS and EELS through the convolution seen in eqn (2). At low energies near the edge it has been found that extrinsic and interference terms largely cancel, and the intrinsic spectral function alone is a reasonable approximation, as shown in Fig. 11.34,82,83
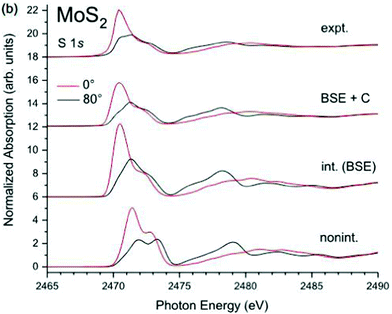 |
| | Fig. 11 K-Edge XAS of MoS2 calculated within the non-interacting approximation (bottom), BSE (second curves), and BSE + cumulant (third curves), compared to experiment (top). The angle of polarization is shown by the colors. Reprinted figure with permission from [J. C. Woicik, C. Weiland, A. K. Rumaiz, M. T. Brumbach, J. M. Ablett, E. L. Shirley, J. J. Kas and J. J. Rehr, Phys. Rev. B, 2020, 101, 245105], Copyright (2022) by the American Physical Society. | |
4.3 Multiplet + cumulant approach
The approach detailed above works quite well for systems with small to medium correlation strength, where only small satellites appear. For highly correlated systems, such as the 2p XPS and XAS spectra of some of the transition metal oxides, methods based on ligand field multiplet models, as well as dynamical mean field theory have been highly successful,19,20,22 although they are not fully ab initio. An alternative approach is to calculate the atomic multiplet spectrum, including the effects of the ligands on the d-state splittings but not allowing charge transfer, and then to include charge transfer (as well as other longer range excitations such as plasmons) through a convolution with the cumulant spectral function,84i.e.,| | | A2p(ω) = Aloc2p(ω) × AC2p(ω). | (30) |
Here Aloc2p is the spectral function arising from the local Hamiltonian, while AC2p is the cumulant spectral function, which builds in long-range interactions such as charge-transfer and plasmons. This approach was inspired by a similar convolution formula developed to include plasmon excitations in DMFT.85 The cumulant spectral function is then calculated in real-time as detailed above, while the local spectral function is calculated via exact diagonalization within the 2p–3d subsystem.86 In order to avoid double counting, the spherical Coulomb interaction terms are neglected in the local Hamiltonian since they only contribute an overall shift, and the cumulant is calculated using the density response to a spherical core-hole. The parameters of the local Hamiltonian are given by the crystal field strength and the Slater–Condon parameters. For calculations of core-level XPS, only a rough estimate is required for the crystal field strength, which we estimate via the eg, t2g splitting. The Slater–Condon parameters are sensitive to the covalency of the transition metal bonds, which we take into account using an extension of the FEFF10 code, i.e., by calculating self-consistent Dirac-Fock radial functions. This method gives very similar results to the ab initio Slater–Condon parameters found using a Wannier state basis.20Fig. 12 shows the calculated 2p XPS spectrum of hematite Fe2O3 compared to the multiplet-only spectral function, and experimental results. Note the reduction of the spin-orbit- and multiplet-split main peaks at ∼0 and 12 eV relative to the multiplet-only spectrum. This reduction occurs due to the weight transferred to the shake-up satellites seen at 9 eV lower energies through the convolution with the cumulant spectral function.
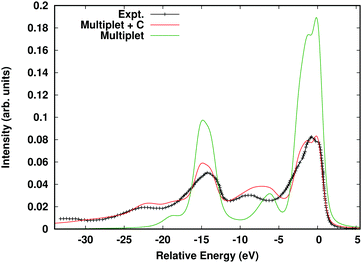 |
| | Fig. 12 Fe 2p XPS of α Fe2O3 calculated within the multiple + C approach (red) compared to the multiplet-only spectrum (green), and experimental results (black crosses). Reprinted figure with permission from [J. J. Kas, J. J. Rehr and T. P. Devereaux, Ab initio multiplet plus cumulant approach for correlation effects in X-ray photoelectron spectroscopy, 2021, https://arxiv.org/abs/2107.10409]. | |
5 The Corvus workflow framework
Many of the advanced approaches detailed in the previous sections require either multiple calculations with the FEFF10 code, or additional calculations carried out with external software packages. For example, resonant inelastic X-ray scattering (RIXS) can be calculated with FEFF10 by itself, but requires several separate runs, and an external script to handle output to input conversion. Similarly, the ab initio Debye–Waller factors and the many-body spectral function convolution both require input from external codes. In order to simplify these advanced workflows and facilitate non-expert use, we have developed a Python-based workflow framework Corvus, which focuses on calculations of spectroscopy.26,87 Corvus does this by managing all input and output translation, as well as the execution of various codes, required for a given workflow. Users are thus only required to learn one simplified input structure, with input parameters focused on physical properties that define the problem at hand in a simplified input file. Other parameters are included implicitly by default. For example, to include the many-body satellites for the M-edge XAS of CeO2, a user only needs to provide the target property (in this case named mbxanes), the X-ray edge and absorbing atom, and the crystal structure in the form of a crystallographic information file (CIF), as shown in Fig. 13. Corvus then (i) creates all required input files; (ii) creates the workflow, and then runs the workflow which consists of (iii) a real-time SIESTA77 calculation of the cumulant spectral function; (iv) a FEFF10 calculation of the XAS, and finally, (v) a convolution of the XAS with the spectral function. The results of this workflow are shown in Fig. 14 and compared to the quasiparticle spectrum, as well as experimental EELS data.88 The Corvus software currently has interfaces to a variety of software, including FEFF10, ABINIT,89 and NWCHEM.90 Corvus is capable of running a variety of workflows, such as optimized structures + XAS, RIXS, ab initio Debye–Waller factors, and a recent development which allows full-spectrum optical constants from UV to X-ray energies,53 and interfaces with the Materials Project Database.91
 |
| | Fig. 13 Corvus input for a calculation of the M-edge XANES of CeO2 including the many-body convolution with the cumulant spectral function. | |
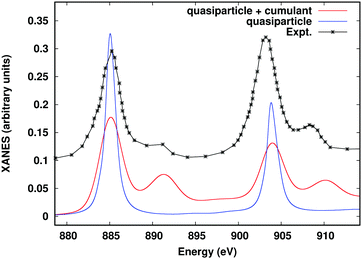 |
| | Fig. 14 Ce M-edge XANES of CeO2 including the many-body convolution with the cumulant spectral function compared to the quasiparticle spectrum and experiment.88 | |
6 Summary and conclusions
In this review we have summarized a number of recent developments in the theory and computation of core-level X-ray spectra, focusing on the advanced methods available within the real-space multiple scattering (RSMS) code FEFF10. The RSMS theory of X-ray absorption and related spectra is briefly described, and attention is given to improved ab initio treatments of the quasiparticle self-energy, e.g., using a many-pole model. This model improves upon the conventional plasmon pole model by representing the dielectric function as a set of poles rather than a single δ function. The model also treats the energy dependent broadening seen in the experimental spectra, and can improve the quantitative analysis of the EXAFS. Interactions with phonons are treated using ab initio calculations of the EXAFS Debye–Waller factors. This approach is based on DFT calculations of the dynamical matrix and an efficient Lanczos representation of the lattice dynamical Green's function. These effects are especially important for the EXAFS analysis of complex systems, where it is difficult to manage the large number of fitting parameters. The approach also includes corrections for finite temperatures beyond the harmonic approximation, since simple relationships allow calculations of the EXAFS third cumulant for example. Finite electronic temperature effects are incorporated through extensions which include Fermi–Dirac statistics in the spectrum as well as in the self-consistent calculation of density and chemical potential. This allows for calculations of XAS over a broad range of temperatures up to the warm dense matter regime. Coupling these effects with molecular dynamics or ab initio Debye–Waller factors allows simulation of systems out of equilibrium, as in ultra-fast pump-probe experiments. At very high electronic temperatures, the Fermi function broadens, and excitations to previously occupied states are now allowed, while the edge shifts due to the temperature dependence of the chemical potential. Many-body satellites in XPS and XAS, due to multi-electron excitations can also be treated, via a convolution of the quasiparticle spectrum with a many-body spectral function. The spectral function is calculated within the cumulant approximation for the one-electron Green's function. The cumulant is related to the density induced when a core-hole appears, and is calculated via real-time TDDFT. These advanced calculations are managed by the Python workflow engine Corvus, which allows users to focus on the physics of the problem at hand rather than the details of the underlying algorithms or the input and output translations necessary for complex workflows requiring multiple scientific software packages. Many extensions of this method are possible. For example, for near-edge spectra full-potential corrections to the RSMS theory and an improved treatment of excitonic effects, as in the Bethe–Salpeter equation are desirable.
Author contributions
All authors contributed to Conceptualization, Methodology, Software, Validation, Writing and Editing, with major contributions by J. J. Kas.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work was supported primarily by DOE Grant DE-FG02-97ER45623 (JJK, JJR and TST), with code developments carried out at the Theory Institute for Materials and Energy Spectroscopies (TIMES) at SLAC, funded by the U.S. DOE, Office of Basic Energy Sciences, Division of Materials Sciences and Engineering under contract DE-AC02-76SF00515, and with computer support from the NERSC, a DOE Office of Science User Facility, under contract no. DE-AC02-05CH11231.
References
- X. Liu and T.-C. Weng, MRS Bull., 2016, 41, 466–472 CrossRef CAS.
- G. George, B. Hedman and K. Hodgson, Nat. Struct. Mol. Biol., 1998, 5, 645–647 CrossRef CAS PubMed.
- H. Wende, Rep. Prog. Phys., 2004, 67, 2105–2181 CrossRef CAS.
- C. Bressler and M. Chergui, Chem. Rev., 2004, 104, 1781–1812 CrossRef CAS PubMed.
- B. D. Patterson and R. Abela, Phys. Chem. Chem. Phys., 2010, 12, 5647–5652 RSC.
- B. Mahieu, N. Jourdain, K. T. Phuoc, F. Dorchies, J. P. Goddet, A. Lifschitz, P. Renaudin and L. Lecherbourg, Nat. Commun., 2018, 9, 3276 CrossRef CAS PubMed.
- M. Taillefumier, D. Cabaret, A.-M. Flank and F. Mauri, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 195107 CrossRef.
-
K. Hermann, L. Pettersson, M. Casida, C. Daul, A. Goursot, A. Koester, E. Proynov, A. St-Amant, D. Salahub and V. Carravetta, et al., StoBe-deMon Code, 2001 Search PubMed.
- D. Prendergast and G. Galli, Phys. Rev. Lett., 2006, 96, 215502 CrossRef PubMed.
- J. J. Rehr and A. L. Ankudinov, Int. J. Quantum Chem., 2003, 95, 487–492 CrossRef CAS.
- K. Lopata, B. E. Van Kuiken, M. Khalil and N. Govind, J. Chem. Theory Comput., 2012, 8, 3284–3292 CrossRef CAS PubMed.
- C. Pemmaraju, Comput. Condens. Matter, 2019, 18, e00348 CrossRef.
- J. Vinson, E. L. Shirley, J. J. Rehr and J. J. Kas, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 115106 CrossRef PubMed.
- C. Vorwerk, C. Cocchi and C. Draxl, Phys. Rev. B, 2017, 95, 155121 CrossRef.
- Y. Liang, J. Vinson, S. Pemmaraju, W. S. Drisdell, E. L. Shirley and D. Prendergast, Phys. Rev. Lett., 2017, 118, 096402 CrossRef PubMed.
- M. Roemelt, D. Maganas, S. DeBeer and F. Neese, J. Chem. Phys., 2013, 138, 204101 CrossRef PubMed.
- I. Josefsson, K. Kunnus, S. Schreck, A. Föhlisch, F. de Groot, P. Wernet and M. Odelius, J. Phys. Chem. Lett., 2012, 3, 3565–3570 CrossRef CAS PubMed.
- B. Helmich-Paris, Int. J. Quantum Chem., 2021, 121, e26559 CrossRef CAS.
-
F. de Groot and A. Kotani, Core Level Spectroscopy of Solids, CRC Press, 2008 Search PubMed.
- M. W. Haverkort, M. Zwierzycki and O. K. Andersen, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 165113 CrossRef.
- H. Ikeno, F. de Groot, E. Stavitski and I. Tanaka, J. Phys.: Condens. Matter, 2009, 21, 104208 CrossRef PubMed.
- M. Ghiasi, A. Hariki, M. Winder, J. Kuneš, A. Regoutz, T.-L. Lee, Y. Hu, J.-P. Rueff and F. M.-F. de Groot, Phys. Rev. B, 2019, 100, 075146 CrossRef CAS.
- O. S. Šipr, J. Minár, A. Scherz, H. Wende and H. Ebert, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 115102 CrossRef.
- J. J. Rehr and R. C. Albers, Rev. Mod. Phys., 2000, 72, 621–654 CrossRef CAS.
- J. J. Rehr, J. J. Kas, F. D. Vila, M. P. Prange and K. Jorissen, Phys. Chem. Chem. Phys., 2010, 12, 5503–5513 RSC.
- J. J. Kas, F. D. Vila, C. D. Pemmaraju, T. S. Tan and J. J. Rehr, J. Synchrotron Radiat., 2021, 28, 1801–1810 CrossRef CAS PubMed.
- J. Kas, A. P. Sorini, M. P. Prange, L. W. Cambell, J. A. Soinine and J. J. Rehr, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 195116 CrossRef.
- F. D. Vila, J. J. Rehr, H. H. Rossner and H. J. Krappe, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 014301 CrossRef.
- T. S. Tan, J. Kas and J. Rehr, Phys. Rev. B, 2021, 104, 035144 CrossRef CAS.
- D. Langreth, Phys. Rev. B: Solid State, 1970, 1, 471 CrossRef.
- F. Aryasetiawan, L. Hedin and K. Karlsson, Phys. Rev. Lett., 1996, 77, 2268 CrossRef CAS PubMed.
- O. Gunnarsson, V. Meden and K. Schönhammer, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 10462–10473 CrossRef CAS PubMed.
- J. Lischner, D. Vigil-Fowler and S. G. Louie, Phys. Rev. Lett., 2013, 110, 146801 CrossRef PubMed.
- J. J. Kas, J. J. Rehr and J. B. Curtis, Phys. Rev. B, 2016, 94, 035156 CrossRef.
- J. Zhou, J. Kas, L. Sponza, I. Reshetnyak, M. Guzzo, C. Giorgetti, M. Gatti, F. Sottile, J. Rehr and L. Reining, J. Chem. Phys., 2015, 143, 184109 CrossRef PubMed.
- M. Guzzo, G. Lani, F. Sottile, P. Romaniello, M. Gatti, J. J. Kas, J. J. Rehr, M. Silly, F. Sirotti and L. Reining, Phys. Rev. Lett., 2011, 107, 166401 CrossRef PubMed.
- J. S. Zhou, L. Reining, A. Nicolaou, A. Bendounan, K. Ruotsalainen, M. Vanzini, J. Kas, J. Rehr, M. Muntwiler and V. N. Strocov,
et al.
, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 28596–28602 CrossRef CAS PubMed.
-
J. J. Sakurai, Advanced Quantum Mechanics, Addison-Wesley Publishing Co., 1967 Search PubMed.
- L. Campbell, L. Hedin, J. J. Rehr and W. Bardyszewski, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 064107 CrossRef.
- G. D. Mahan, Phys. Rev., 1967, 163, 612–617 CrossRef CAS.
- P. Nozières and C. T. de Dominicis, Phys. Rev., 1969, 178, 1097–1107 CrossRef.
- J. J. Rehr and R. C. Albers, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 8139 CrossRef PubMed.
-
D. E. Sayers, F. W. Lytle and E. A. Stern, in Advances in X-Ray Analysis, ed. B. L. Henke, J. B. Newkirk and G. R. Mallett, Plenum, New York, 1970, vol. 1070, p. 248 Search PubMed.
- M. Newville, J. Synchrotron Radiat., 2001, 8, 322–324 CrossRef CAS PubMed.
- B. Ravel and M. Newville, J. Synchrotron Radiat., 2005, 12, 537–541 CrossRef CAS PubMed.
- K. Jorissen, J. J. Rehr and J. Verbeeck, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 155108 CrossRef.
- H. Sternemann, J. A. Soininen, C. Sternemann, K. Hämäläinen and M. Tolan, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 075118 CrossRef.
- B. A. Mattern, G. T. Seidler, J. J. Kas, J. I. Pacold and J. J. Rehr, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 115135 CrossRef.
- J. J. Kas, J. J. Rehr, J. A. Soininen and P. Glatzel, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 235114 CrossRef.
- L. Hedin and S. Lundqvist, Solid State Phys., 1969, 54, 1–218 Search PubMed.
- J. Mustre de Leon, J. J. Rehr, S. I. Zabinsky and R. C. Albers, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 4146–4156 CrossRef CAS PubMed.
- M. P. Prange, J. J. Rehr, G. Rivas, J. J. Kas and J. W. Lawson, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 155110 CrossRef.
- J. Kas, F. Vila, C. Pemmaraju, M. Prange, K. Persson, R. Yang and J. Rehr, Comput. Mater. Sci., 2022, 201, 110904 CrossRef.
- M. Newville, J. J. Kas and J. J. Rehr, J. Phys.: Conf. Ser., 2009, 190, 012023 CrossRef.
-
E. D. Crozier, J. J. Rehr and R. Ingalls, in X-Ray Absorption: Principles, Applications, Techniques of EXAFS, SEXAFS, and XANES, ed. D. C. Koningsberger and R. Prins, Wiley, New York, 1988, p. 375 Search PubMed.
- F. D. Vila, J. J. Rehr, H. H. Rossner and H. J. Krappe, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 014301 CrossRef.
- N. Dimakis and G. Bunker, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 2467–2475 CrossRef CAS.
- D. Strauch, P. Pavone, N. Nerb, K. Karch, W. Windl, G. Dalba and P. Fornasini, Phys. B, 1996, 219–220, 436–438 CrossRef.
- F. D. Vila, V. E. Lindahl and J. J. Rehr, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 024303 CrossRef.
- A. V. Poiarkova and J. J. Rehr, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 948–957 CrossRef CAS.
-
P. Deuflhard and A. Hohmann, Numerical Analysis, de Gruyter, Berlin, 1995 Search PubMed.
- J.-W. Lee, G. Kang, M. Kim, M. Kim, S. H. Park, S. Kwon, S. Yang and B. I. Cho, J. Synchrotron Radiat., 2020, 27, 953–958 CrossRef CAS PubMed.
- B. I. Cho, K. Engelhorn, A. A. Correa, T. Ogitsu, C. P. Weber, H. J. Lee, J. Feng, P. A. Ni, Y. Ping, A. J. Nelson, D. Prendergast, R. W. Lee, R. W. Falcone and P. A. Heimann, Phys. Rev. Lett., 2011, 106, 167601 CrossRef CAS PubMed.
- R. Torchio, F. Occelli, O. Mathon, A. Sollier, E. Lescoute, L. Videau, T. Vinci, A. Benuzzi-Mounaix, J. Headspith, W. Helsby, S. Bland, D. Eakins, D. Chapman, S. Pascarelli and P. Loubeyre, Sci. Rep., 2016, 6, 26402 CrossRef CAS PubMed.
- G. Kang and B. I. Cho, Curr. Appl. Phys., 2021, 30, 58–68 CrossRef.
- D. M.-C. Nicholson, G. M. Stocks, Y. Wang, W. A. Shelton, Z. Szotek and W. M. Temmerman, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 14686–14689 CrossRef CAS PubMed.
- R. Zeller, J. Phys.: Condens. Matter, 2005, 17, 5367–5379 CrossRef CAS.
- C. E. Starrett, Phys. Rev. E, 2018, 97, 053205 CrossRef CAS PubMed.
- M. Laraia, C. Hansen, N. Shaffer, D. Saumon, D. Kilcrease and C. Starrett, High Energy Density Phys., 2021, 40, 100940 CrossRef CAS.
- V. V. Karasiev, L. Calderín and S. B. Trickey, Phys. Rev. E, 2016, 93, 063207 CrossRef PubMed.
- J. J. Kas and J. J. Rehr, Phys. Rev. Lett., 2017, 119, 176403 CrossRef CAS PubMed.
- T. S. Tan, J. J. Kas and J. J. Rehr, Phys. Rev. B, 2018, 98, 115125 CrossRef CAS.
- L. Hedin, Phys. Rev., 1965, 139, A796–A823 CrossRef.
- L. Hedin, J. Phys.: Condens. Matter, 1999, 11, R489 CrossRef CAS.
- F. Caruso, H. Lambert and F. Giustino, Phys. Rev. Lett., 2015, 114, 146404 CrossRef PubMed.
- J. J. Kas, F. D. Vila, J. J. Rehr and S. A. Chambers, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 121112 CrossRef.
- Y. Takimoto, F. D. Vila and J. J. Rehr, J. Chem. Phys., 2007, 127, 154114 CrossRef CAS PubMed.
- L. Hedin, J. Michiels and J. Inglesfield, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 15565 CrossRef CAS.
- W. Bardyszewski and L. Hedin, Phys. Scr., 1985, 32, 439 CrossRef CAS.
- J. J. Rehr and J. J. Kas, J. Vac. Sci. Technol., A, 2021, 39, 060401 CrossRef CAS.
- J. D. Lee, O. Gunnarsson and L. Hedin, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 8034 CrossRef CAS.
- J. C. Woicik, C. Weiland, A. K. Rumaiz, M. T. Brumbach, J. M. Ablett, E. L. Shirley, J. J. Kas and J. J. Rehr, Phys. Rev. B, 2020, 101, 245105 CrossRef CAS PubMed.
- J. C. Woicik, C. Weiland, C. Jaye, D. A. Fischer, A. K. Rumaiz, E. L. Shirley, J. J. Kas and J. J. Rehr, Phys. Rev. B, 2020, 101, 245119 CrossRef CAS PubMed.
-
J. J. Kas, J. J. Rehr and T. P. Devereaux, Ab initio multiplet plus cumulant approach for correlation effects in X-ray photoelectron spectroscopy, 2021, https://arxiv.org/abs/2107.10409, Accepted to Phys. Rev. Lett Search PubMed.
- M. Casula, A. Rubtsov and S. Biermann, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 035115 CrossRef.
- T. P. Devereaux, B. Moritz, C. Jia, J. J. Kas and J. J. Rehr, Comput. Mater. Sci., 2021, 200, 110814 CrossRef CAS.
- S. M. Story, F. D. Vila, J. J. Kas, K. B. Raniga, C. D. Pemmaraju and J. J. Rehr, J. Synchrotron Radiat., 2019, 26, 1694–1704 CrossRef CAS PubMed.
- K. Song, H. Schmid, V. Srot, E. Gilardi, G. Gregori, K. Du, J. Maier and P. A. van Aken, APL Mater., 2014, 2, 032104 CrossRef.
- X. Gonze, F. Jollet, F. Abreu Araujo, D. Adams, B. Amadon, T. Applencourt, C. Audouze, J.-M. Beuken, J. Bieder, A. Bokhanchuk, E. Bousquet, F. Bruneval, D. Caliste, M. Côté, F. Dahm, F. Da Pieve, M. Delaveau, M. Di Gennaro, B. Dorado, C. Espejo, G. Geneste, L. Genovese, A. Gerossier, M. Giantomassi, Y. Gillet, D. Hamann, L. He, G. Jomard, J. Laflamme Janssen, S. Le Roux, A. Levitt, A. Lherbier, F. Liu, I. Lukaević, A. Martin, C. Martins, M. Oliveira, S. Poncé, Y. Pouillon, T. Rangel, G.-M. Rignanese, A. Romero, B. Rousseau, O. Rubel, A. Shukri, M. Stankovski, M. Torrent, M. Van Setten, B. Van Troeye, M. Verstraete, D. Waroquiers, J. Wiktor, B. Xu, A. Zhou and J. Zwanziger, Comput. Phys. Commun., 2016, 205, 106–131 CrossRef CAS.
- M. Valiev, E. Bylaska, N. Govind, K. Kowalski, T. Straatsma, H. Van Dam, D. Wang, J. Nieplocha, E. Apra, T. Windus and W. de Jong, Comput. Phys. Commun., 2010, 181, 1477–1489 CrossRef CAS.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. Persson, APL Mater., 2013, 1, 011002 CrossRef.
|
| This journal is © the Owner Societies 2022 |
 *,
Fernando D.
Vila
*,
Fernando D.
Vila
 ,
Tun S.
Tan
and
John J.
Rehr
,
Tun S.
Tan
and
John J.
Rehr

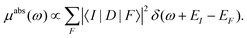
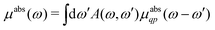
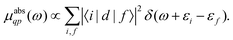
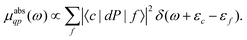
![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) ·r; XAS/XES,
·r; XAS/XES,![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) is the polarization of the X-rays, and q is the momentum transferred to the system by the probe. For XAS, XES, and EELS, the transitions are, to a good approximation, dipole limited, and thus the dipole approximation is used as shown above for these spectroscopies. However, for NRIXS, the transition operator is given by the exponential form shown, and is only dipole limited at very small momentum transfer. The transition operator, along with the symmetry of the core-state, determines the local symmetries of the final states that can be probed, with the orbital angular momentum of the possible final states determined within the dipole and quadrupole approximations as follows,
is the polarization of the X-rays, and q is the momentum transferred to the system by the probe. For XAS, XES, and EELS, the transitions are, to a good approximation, dipole limited, and thus the dipole approximation is used as shown above for these spectroscopies. However, for NRIXS, the transition operator is given by the exponential form shown, and is only dipole limited at very small momentum transfer. The transition operator, along with the symmetry of the core-state, determines the local symmetries of the final states that can be probed, with the orbital angular momentum of the possible final states determined within the dipole and quadrupole approximations as follows,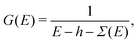
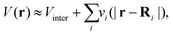
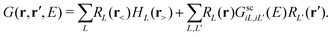
![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) ) following the conventions in ref. 42 where Rl and Hl are the regular and irregular solutions of the single site radial Dirac equation for site i, and YL(
) following the conventions in ref. 42 where Rl and Hl are the regular and irregular solutions of the single site radial Dirac equation for site i, and YL(![[r with combining circumflex]](https://www.rsc.org/images/entities/char_0072_0302.gif) ) are the spherical harmonic functions where L denotes the combined orbital angular momentum l and magnetic m quantum numbers (or their relativistic counterparts). In general, the Green's function can be written in terms of an expansion in orders of the single site scattering potentials vi about the free particle Green's function G0(r,r′,E). However, it is more convenient to sum all consecutive scatterings from a given site by defining the single site scattering matrices ti = vi + viG0ti. The scattering Green's function in the above equation is then given by,
) are the spherical harmonic functions where L denotes the combined orbital angular momentum l and magnetic m quantum numbers (or their relativistic counterparts). In general, the Green's function can be written in terms of an expansion in orders of the single site scattering potentials vi about the free particle Green's function G0(r,r′,E). However, it is more convenient to sum all consecutive scatterings from a given site by defining the single site scattering matrices ti = vi + viG0ti. The scattering Green's function in the above equation is then given by,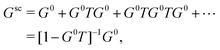
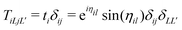 , where ηil is the phase shift of the ith site potential, and δij is the Kronecker δ, which is one if i = j and zero otherwise. With this representation of the Green's function, the quasiparticle spectrum is given by,
, where ηil is the phase shift of the ith site potential, and δij is the Kronecker δ, which is one if i = j and zero otherwise. With this representation of the Green's function, the quasiparticle spectrum is given by,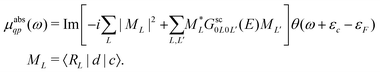
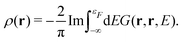
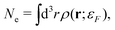
![[R with combining circumflex]](https://www.rsc.org/images/entities/b_char_0052_0302.gif) ]2〉 is the mean-square relative displacement (MSRD).55 These factors damp the spectrum at high energy, with the effect increasing with temperature, with σR2 ≈ kBT/κ where κ is an effective spring constant. The need for path dependent Debye–Waller factors creates a major difficulty for the analysis of EXAFS due to the large number of free parameters involved, especially for disordered or molecular systems, where a simple model such as the correlated Debye model is inapplicable. In such cases it is advantageous to obtain the Debye–Waller factors through ab initio approaches. A number of theoretical methods have been used to this end, based, e.g., on DFT,56–58 or molecular dynamics.59 Here we provide details of the approach of ref. 56 which is implemented within the FEFF10 code.
]2〉 is the mean-square relative displacement (MSRD).55 These factors damp the spectrum at high energy, with the effect increasing with temperature, with σR2 ≈ kBT/κ where κ is an effective spring constant. The need for path dependent Debye–Waller factors creates a major difficulty for the analysis of EXAFS due to the large number of free parameters involved, especially for disordered or molecular systems, where a simple model such as the correlated Debye model is inapplicable. In such cases it is advantageous to obtain the Debye–Waller factors through ab initio approaches. A number of theoretical methods have been used to this end, based, e.g., on DFT,56–58 or molecular dynamics.59 Here we provide details of the approach of ref. 56 which is implemented within the FEFF10 code.
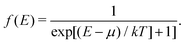
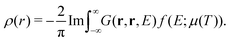
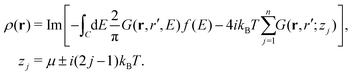
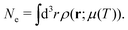
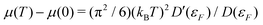 . This approximation is often valid to moderate temperatures T < TF. Another effect of the broadening of the Fermi function is that excitation of states below the chemical potential is allowed. This effect, known as continuum lowering can be especially prominent in L-edges of the late 3d transition metals, where a high concentration of density of d-states lies right below the Fermi energy. This effect is shown for Cu in Fig. 7, which shows the L-edge XAS of Cu calculated at various electronic temperatures.
. This approximation is often valid to moderate temperatures T < TF. Another effect of the broadening of the Fermi function is that excitation of states below the chemical potential is allowed. This effect, known as continuum lowering can be especially prominent in L-edges of the late 3d transition metals, where a high concentration of density of d-states lies right below the Fermi energy. This effect is shown for Cu in Fig. 7, which shows the L-edge XAS of Cu calculated at various electronic temperatures.