 Open Access Article
Open Access ArticleComputational approaches for XANES, VtC-XES, and RIXS using linear-response time-dependent density functional theory based methods
Daniel R.
Nascimento
*a and
Niranjan
Govind
 *b
*b
aDepartment of Chemistry, The University of Memphis, Memphis, TN 38152, USA. E-mail: daniel.nascimento@memphis.edu
bPhysical and Computational Sciences Directorate, Pacific Northwest National Laboratory, Richland, Washington 99352, USA. E-mail: niri.govind@pnnl.gov
First published on 10th June 2022
Abstract
The emergence of state-of-the-art X-ray light sources has paved the way for novel spectroscopies that take advantage of their atomic specificity to shed light on fundamental physical, chemical, and biological processes both in the static and time domains. The success of these experiments hinges on the ability to interpret and predict core-level spectra, which has opened avenues for theory to play a key role. Over the last two decades, linear-response time-dependent density functional theory (LR-TDDFT), despite various theoretical challenges, has become a computationally attractive and versatile framework to study excited-state spectra including X-ray spectroscopies. In this context, we focus our discussion on LR-TDDFT approaches for the computation of X-ray Near-Edge Structure (XANES), Valence-to-Core X-ray Emission (VtC-XES), and Resonant Inelastic X-ray Scattering (RIXS) spectroscopies in molecular systems with an emphasis on Gaussian basis set implementations. We illustrate these approaches with applications and provide a brief outlook of possible new directions.
1 Introduction
X-ray spectroscopies are quickly becoming essential experimental techniques for the chemical characterization of molecules and materials. Their main advantage results from the localized nature of the orbitals from which electrons are excited, which leads to spectral features that are atom-specific and highly sensitive to their chemical environment.1–4 Thus, the spectral features involving electronic transitions in the X-ray region contain valuable structural information.Recent advances in light-source technologies5 have resulted in immense improvements in the temporal and energy resolution that can be obtained from X-ray spectroscopies, broadening its domain of applicability. In addition, the development of laboratory-based X-ray spectroscopies6 has added to this growing trend. These advances have also resulted in an increased demand for inexpensive computational approaches that can aid in the interpretation of complex spectroscopic features and help the design of new experiments.
Single-photon X-ray spectroscopies (X-ray absorption and emission) can be modeled with a wide range of quantum chemical techniques ranging from simplistic single-reference wavefunction-based approaches to elaborate multi-reference methods. In recent years, considerable progress has been made in the development of highly-accurate methods to model X-ray spectroscopies.7 Calculations based on the algebraic diagrammatic construction,8–10 equation-of-motion11–15 and linear-response16,17 coupled-cluster, and multiconfigurational self-consistent-field theories18,19 can now be routinely performed on small molecules. Nonetheless, the most popular approaches to model X-ray spectroscopies are those based on density functional theory (DFT).
The popularity of DFT-based methods stems from their ability to provide sufficiently accurate results for a broad range (both in complexity and size) of chemical systems at a significantly lower computational cost and broad applicability when compared to more accurate wavefunction-based methods. In this regard, LR-TDDFT,20 in particular, has proven to be a powerful and versatile technique in the treatment of excited states.
In this paper, we give a short perspective from the point of view of our experiences in the development and application of Gaussian basis set based LR-TDDFT methods for X-ray spectroscopies in the NWChem computational chemistry program.21,22 To this end, we focus our discussion on the computation of X-ray Near-Edge Structure (XANES), Valence-to-Core X-ray Emission (VtC-XES), and Resonant Inelastic X-ray Scattering (RIXS) spectroscopies in molecular systems within the LR-TDDFT framework. We have also tried to provide an exhaustive reference list for the interested reader covering the topics discussed.
2 X-ray absorption near-edge structure
X-ray absorption edges are labelled according to the core orbitals from where the electrons are excited. XAS K-, L-, and M-edge spectra originate from photo-excitations of electrons in n = 1, n = 2, and n = 3 orbitals, respectively, where n represents the principal quantum number. In addition, spin–orbit coupling splits the degenerate orbitals with angular momentum l into l ± 1/2 manifolds. These splittings give rise to unique features that also need to be considered in the calculations.The near edge region of the XAS is typically referred to as the near edge X-ray absorption fine structure (NEXAFS) or the X-ray absorption near edge structure (XANES). This region of the spectrum is composed of excitations from the relevant core orbitals to the bound electronic states close to the ionization potential. An illustration of the XANES process for a hypothetical octahedral transition metal complex at the K-edge is shown in the left panel of Fig. 1.
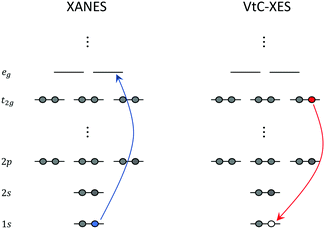 | ||
| Fig. 1 Schematic representation of XANES and VtC-XES at the K-edge of a hypothetical octahedral transition metal complex. | ||
XANES carries important information about the chemical state of the atom (for example, oxidation state, coordination, bonding, etc.). On the other hand, the extended X-ray absorption fine structure (EXAFS) region, is composed of excitations to energies sufficient to cause ejection of a photoelectron, with subsequent scattering off nearby atoms. EXAFS yields structural information about neighboring atoms (for example, identity, distances, coordination/solvent shells, etc.).
From a theoretical standpoint, XANES and EXAFS are usually treated distinctly. In EXAFS, the spectral oscillations arise from modulation of X-ray absorption due to scattering of the photoelectron from nearby atoms. The essential physical quantities in EXAFS are the scattering amplitude and phase shifts, from which the spectrum is typically computed using a damped spherical photoelectron wavefunction approximation. These quantities can now be routinely computed using Green's function formalisms with localized (“muffin tin”) potentials and have been very successful in modeling EXAFS spectra. Since a detailed discussion of EXAFS is beyond the scope of this paper, we refer the interested reader to comprehensive reviews on the subject.23–25
The XANES region, on the other hand, requires an accurate electronic structure treatment of the absorbing atom and neighboring atoms bonded to it. Since core electrons move at significant fractions of the speed of light, relativistic effects have to be considered in the electronic structure descriptions. Over the years many ab initio methods have been developed to compute XANES at different levels of computational complexity.26,27 These include methods based on density functional theory (DFT),28 linear response (LR) and real-time (RT) time-dependent density functional theory (TDDFT),29–45 Bethe–Salpeter equation (BSE),46–48 algebraic-diagramatic construction (ADC),49–51 linear-response density cumulant theory,52 coupled-cluster theory using both the complex polarization propagator53,54 and equation-of-motion55–58 frameworks, restricted active space (RAS) multiconfigurational methods,59–62 and multireference coupled cluster methods.63
Over the past two decades, LR-TDDFT has become a computationally attractive approach for studying excited-state spectra, within the space of single excitations, in a wide range of molecular systems. Excitation energies in LR-TDDFT are obtained as solutions to the non-Hermitian eigenvalue equation or Casida matrix equations,64,65
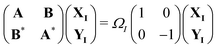 | (1) |
| Aia,jb = (εa − εi)δijδab + (ia|jb) − cx(ij|ab) + fxcia,jb | (2) |
| Bia,jb = (ia|bj) − cx(ib|aj) + fxcia,bj. | (3) |
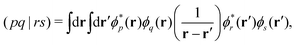 | (4) |
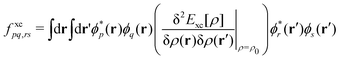 | (5) |
Within the Tamm–Dancoff approximation (TDA), the above matrix equation reduces to the Hermitian equation,67
| AXI = ΩIXI | (6) |
So far we have implicitly assumed the computation of K-edge XANES, which is preferred for studying light elements due to the larger core-hole lifetimes. It is also simpler to compute and interpret. On the other hand, the L-edge is preferred for transition metals and heavier elements. For instance, in transition metal complexes, the 2p → nd transitions are dipole allowed, making the L-edge XANES sensitive to partially occupied d orbitals and the bonding environment. However, computations of the L-edge XANES are more complicated due spin–orbit (SO) splitting associated with the 2p orbitals leading to the L2,3 XANES. The SO splitting requires at least a scalar relativistic approach with perturbative spin–orbit effects82 or more rigorously, relativistic two-component (2c)36,39 or four-component (4c)40,41,44 LR-TDDFT treatments, where the scalar and SO effects are treated variationally, to be able to assign the spectral features at the L- and M-edges XANES accurately.
A key point in the simulation of X-ray spectroscopies is the computation of oscillator strengths, where it is important to go beyond the dipole approximation to capture the spectral features observed in experiment. Transition metal K-edge XANES is dominated by intense electric dipole allowed 1s → np transitions. However, the spectra also contain weak transitions lying at lower energies that are electric quadrupole allowed transitions to unoccupied valence d orbitals.83,84 Including the electric quadrupolar contribution brings in an arbitrary dependence on the molecular origin. A widely used approach for remedying this problem is to shift the origin to the coordinates of the absorbing atom. However, this protocol fails when there are symmetry-equivalent or several absorbing centers (for example, in multivalent transition metal clusters). Another important requirement is the Thomas–Reiche–Kuhn (TRK) sum rule, which states that the integrated oscillator strength equals the number of electrons in the system.85 The TRK sum rule is satisfied only if the oscillator strengths are treated to infinite order. Any finite order treatment of the oscillator strengths does not guarantee this.86,87 This suggests a more careful treatment is required. Jacob and co-workers have reported a detailed analysis and importance of the higher-order contributions to the oscillator strength.88 More advanced treatments of going beyond the dipole approximation have since been developed and reported by List and co-workers.89–91
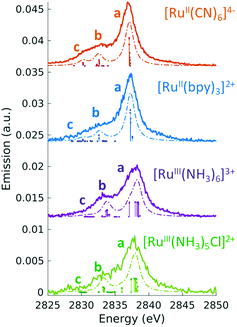
LR-TDDFT/TDA is sufficiently predictive and has been applied to a broad range of systems to compute K-edge, L-edge, and M-edge XANES29–45,84,92–103 as well as transient X-ray absorption spectroscopy.104–109 In Fig. 2 and 3 we show the experimental and computed K-edge XANES and L3-edge XANES of model Fe and Ru complexes in different oxidation states. Despite this broad applicability, we emphasize that care must be taken especially in terms of the exchange–correlation functional and basis set choices, which have to be carefully assessed when performing XANES calculations. We refer the reader to recent papers by Besley43 and Jensen and co-workers110 for a discussion of these topics.
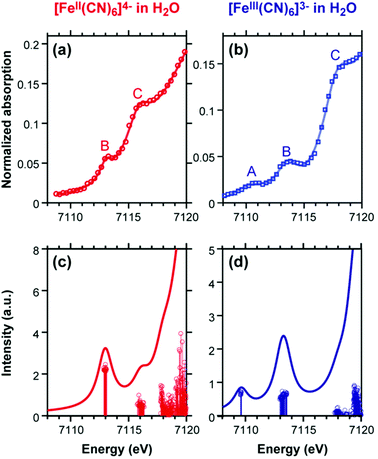 | ||
| Fig. 2 Experimental (top) and simulated (bottom) Fe K-edge XANES spectra of [FeII(CN)6]4− and [FeIII(CN)6]3− simulated results have been blue-shifted by 143.0 eV to match the experiment. The A and B features in the two complexes are quadrupolar transitions from the Fe 1s → 3d orbitals. Reproduced with permission from ref. 84. Copyright 2018 American Chemical Society. | ||
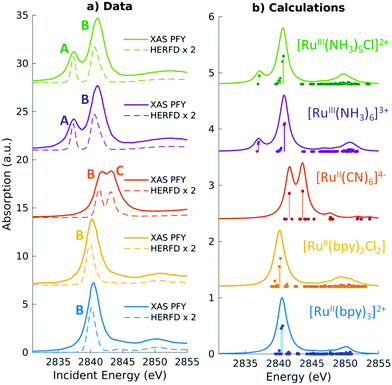 | ||
| Fig. 3 Experimental and simulated Ru L3 edge XANES spectra of a series of Ru(II) and Ru(III) complexes with low-spin d6 and d5 configurations, respectively. The features in the two complexes correspond to dipolar transitions from the Ru 2p → 4d orbitals. A shift of 2.3 eV has been applied to the calculated spectra to match experiment. Reproduced with permission from ref. 102. Copyright 2021 Royal Society of Chemistry. | ||
3 Valence-to-core X-ray emission spectroscopy
Over the last several years, there has been a growing interest in X-ray emission spectroscopy (XES), and especially valence-to-core (VtC) XES,4,111 which can be viewed as a complement to XANES. VtC-XES has emerged as a powerful technique for the structural characterization of transition metal complexes. Understanding the local chemical environment and electronic structure of these complexes is essential to the development of novel catalysts and materials that can be leveraged in photochemical energy conversion.In a VtC-XES process, a core-hole is created via X-ray photoionization or radioactive electron capture decay112 followed by the emission of a photon as electrons in higher occupied core or valence orbitals re-populate the core-hole. The resulting VtC-XES lines, which lie in the high-energy tail of the X-ray emission spectrum, thus represent the electronic transitions from valence orbitals into the empty core orbital. An illustration of the VtC-XES process for a hypothetical octahedral transition metal complex at the K-edge (where a core-hole is created in the metal 1s orbital) is shown in the right panel of Fig. 1. Since the dipole selection rule forbids transitions between the metal d and 1s orbitals, the weak signals that emerge from VtC-XES result from the mixing of the metal d and ligand s and p orbitals. These orbitals play a dominant role in the chemical bonding between the metal centers and ligands. Thus, VtC-XES can provide valuable information about the nature of metal–ligand bonding.
VtC-XES features are traditionally grouped into two categories: Kβ′′ and Kβ2,5 as shown in Fig. 4. The Kβ′′ peaks, weak and appearing at lower energy, correspond to transitions involving the ligand s orbitals, while the Kβ2,5 dominant feature is assigned to transitions involving ligand p orbitals.113 Thus, the splitting between the Kβ′′ and Kβ2,5 peaks is associated with the difference in binding energies between the ligand s and p orbitals. Bergmann et al. showed that the strength of the Kβ′′ peak depends exponentially on the metal–ligand distance,114 and thus, provide important information for ligand characterization. The intensities of VtC-XES features can also be used to analyze the composition of valence orbitals.115–117
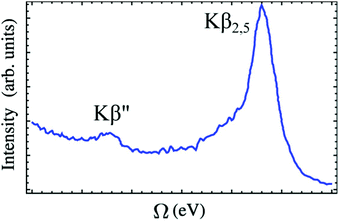 | ||
| Fig. 4 A typical VtC X-ray emission spectrum showing Kβ′′ and Kβ2,5 features (experimental spectrum of [CrIII(NH3)6]3+ adapted from ref. 118). The baseline of the spectrum is not horizontal because the exponential tail of the strong Kβ mainline has not been subtracted. Reproduced with permission from ref. 119. Copyright 2015 American Chemical Society. | ||
Over the last few years, several studies employing an independent-particle density functional theory (DFT) approach to model VtC-XES have emerged.115–118,120–125 In this approach, core-hole and valence-ionized states are simply represented as single Slater determinants of ground-state Kohn–Sham orbitals, where emission energies are given by the difference in valence (v) and core (c) orbital energies,
| ΔE = εv − εc | (7) |
f ∝ |〈ϕc|![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) |ϕv〉|2. |ϕv〉|2. | (8) |
As an alternative, the initial core hole state can be modeled within a core-hole approximation120,126–136 and used as the reference for a LR-TDDFT calculation. Emission energies and transition moments are thus obtained from the solutions of the LR-TDDFT equations.135,136 This procedure corrects for many-body and multichannel effects as it introduces orbital relaxation in the final valence-ionized states. This approach has been successfully explored by Govind and co-workers84,102,136–139 and recently in machine learning models to chemically classify sulphorganic140 and organophosphorus compounds.
In this LR-TDDFT based protocol, a neutral ground state calculation is first performed, a full core-hole (FCH) ionized state is then obtained self-consistently where the 1s core orbital of the emitting center is swapped with a virtual orbital, then a LR-TDDFT141,142 calculation employing the TDA143 is performed with the FCH ionized state as reference. The maximum overlap constraint method is employed to prevent core hole collapse during the FCH calculation.144–146 This approach is well-suited to describe emission processes with multideterminant character as seen in the spectra of the [MnII(H2O)6]2+ complex (shown in Fig. 5). In Fig. 5, the B, C and D features consist of transitions from linear combinations of oxygen 2p orbitals to the Mn 1s core hole, and the A feature is composed of transitions involving the oxygen 2s orbitals. The experimental spectrum shows a strong broad peak and some weak features in the low energy region. The asymmetric shape of the strong peak indicates the existence of adjacent weak shoulders at both low and high energies in the region around the main peak. The simulated spectrum clearly captures these weak features (B and D features in Fig. 5) in good agreement with experiment.136 In Fig. 6, the computed 4d → 2p VtC-XES spectra of a series of Ru(II) and Ru(III) complexes using the same method are shown and compared with experiment.102
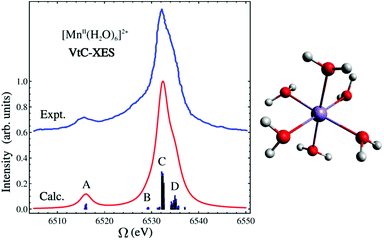 | ||
| Fig. 5 Experimental and simulated VtC-XES spectra of [MnII(H2O)6]2+. Simulated results have been red-shifted by 30.4 eV to match experiment.120 The molecular structure is shown on the right. Color code: O (red), Mn (purple), H (white). Reproduced with permission from ref. 119. Copyright 2015 American Chemical Society. | ||
 | ||
| Fig. 6 Experimental (solid lines) and simulated (dashed lines) 4d → 2p VtC-XES spectra of a series of Ru(II) and Ru(III) complexes with low-spin d6 and d5 configurations, respectively. A global shift of 96.3 eV is applied to the calculated spectra. Reproduced with permission from ref. 102. Copyright 2021 Royal Society of Chemistry. | ||
4 Resonant inelastic X-ray spectroscopy
Resonant inelastic X-ray scattering (RIXS)147–149 is a scattering process involving two-photons. The system is initially excited at a given X-ray absorption region accompanied by the emission of a photon of lower energy. The RIXS process results in a final excited state that cannot be accessed directly from the ground state via a one-photon process. Hence, RIXS maps carry important information about the electronic structure of the system that is not readily available from one-photon spectroscopies due to selection rule restrictions. A schematic representation of the RIXS process for a prototypical octahedral transition metal complex is shown in Fig. 7. Fig. 7 illustrates a scenario where the goal is to determine the crystal field splitting, 10 Dq, for a low-spin d6 octahedral complex. A direct t2g → eg transition is forbidden via single-photon absorption but accessible via a 3p4d RIXS process. In 3p4d RIXS, an electron is resonantly excited from the 3p orbitals in the metal center into the empty 4d orbitals (of eg symmetry in the illustration above) accompanied by the re-population of the 3p orbitals with one of the t2g electrons, resulting in the t52ge1g excited state.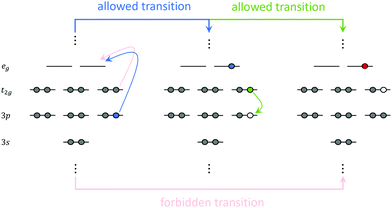 | ||
| Fig. 7 Schematic representation of the RIXS process for a hypothetical octahedral transition metal complex. | ||
RIXS has been employed in the study of molecular systems in the condensed phase since its inception almost three decades ago,150 nonetheless, application of RIXS in the study of molecules in the gas or solution phase only became a reality in recent years.84,151–159 One of the factors that restricts the applicability of RIXS in the study of gas or solution-phase molecular systems is the need for high-intensity light sources, as the concentration of absorbing atomic centers in solution is relatively low. This is not necessarily the case in condensed phases, where the abundance of absorbing atomic centers means that core-excited states can be easily accessed without the need of high-intensity light sources.160 With current advances in light-source technologies and the introduction of the Linac Coherent Light Source II (LCLS-II) and European X-Ray Free-Electron Laser (European XFEL), RIXS is quickly becoming an important technique in the study of molecular systems. As RIXS experiments are rapidly becoming routine, there is an increasing demand for inexpensive electronic structure methods that are sufficiently accurate to aid in the interpretation and prediction of complicated spectral features.
In recent years, several theoretical approaches aimed at the description of RIXS spectra for molecules have been proposed. Accurate methodologies based on the damped response and equation-of-motion coupled-cluster,161–164 algebraic diagrammatic construction,165 multiconfigurational self-consistent field,166 and configuration interaction167 theories, can now be applied to small molecules with remarkable accuracy. However, wavefunction-based methods, despite their high-accuracy and black-box nature, remain too expensive to be routinely applied to large molecular systems with 100 or more electrons. Thus, simpler approaches based on density functional theory (DFT), are valuable alternatives to study large molecules, as they are significantly cheaper than wavefunction-based methods and are able to provide sufficiently accurate descriptions of spectroscopic properties.168
RIXS maps can be simulated by employing the Kramers–Heisenberg (KH) equation within the electric dipole approximation,
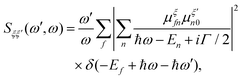 | (9) |
The simplest way to simulate RIXS in the context of DFT calculations is to employ the independent-particle approximation as outlined in Section 3. For 3p4d RIXS (as illustrated in Fig. 7), excitation energies are simply taken as orbital energy differences, and transition moments are calculated with respect to Kohn–Sham orbitals. Such an approach is too crude as it neglects any kind of relaxation effects in the excited states, and thus, have very limited use. A viable alternative where relaxation effects is introduced in the intermediate states (but either neglected or only partially included in the emission step) has been employed by Besley and co-workers in the RIXS study of several organic molecules.169–171 In their scheme, core-excited states are calculated using a regular LR-TDDFT computation yielding accurate values for E0n and μn0 whereas Efn and μfn are either determined via the independent-particle approximation, or by performing another LR-TDDFT computation with the core-excited determinant as a reference. Both of these schemes yield surprisingly accurate RIXS spectra when compared with high-level second-order algebraic diagrammatic [ADC(2)-x] calculations (as illustrated in Fig. 8) or experiment.169 Although the schemes employed by Beasley and co-workers can be successfully employed for small organic molecules, it can become problematic as the level of correlation of the final excited states become significant, or when many intermediate excited states participate in the RIXS process. Under these circumstances, the independent-particle model for the emission process is insufficient, and the choice of a single intermediate excited state reference becomes ambiguous and a manifold of intermediate and final states must be considered.
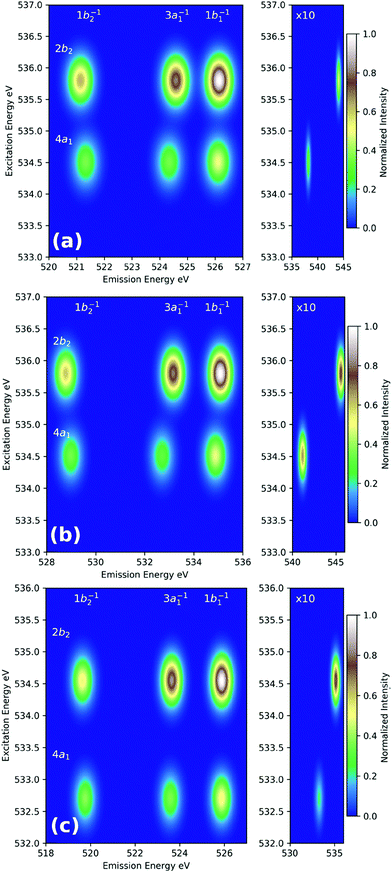 | ||
| Fig. 8 Simulated RIXS maps of gas-phase water calculated with the (a) LR-TDDFT absorption/Kohn–Sham DFT emission, (b) LR-TDDFT absorption/emission, and (c) ADC(2)-x schemes for the equilibrium water structure. Adapted with permission from ref. 170. Copyright 2018 American Chemical Society. | ||
A consistent treatment of relaxation in both intermediate and final states can be achieved via a quadratic-response (QR) TDDFT treatment. In the QR-TDDFT framework, excited-state transition densities have the form
| δnQRIJ = δn(1)0Iδn(1)0J + δn(2)IJ, | (10) |
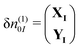 | (11) |
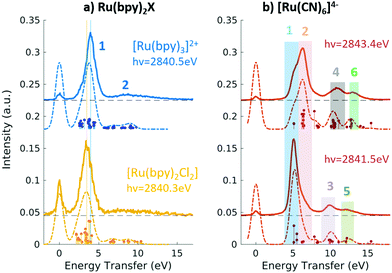 | ||
Fig. 9 Experimental (solid lines) and theoretical (dashed lines) 2p4d RIXS spectra of (a) [RuII(bpy)3]2+ (top) and [RuII(bpy)2Cl2] (bottom) measured with incident X-ray energy resonant with the 2p → eg transition as a function of energy transfer. (b) [RuII(CN)6]4− measured with incident X-ray energy resonant with the 2p → eg transition (bottom) and resonant with the 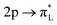 transition (top). Reproduced with permission from ref. 159. Copyright 2021 Royal Society of Chemistry. transition (top). Reproduced with permission from ref. 159. Copyright 2021 Royal Society of Chemistry. | ||
Alternatively, one can completely neglect the second-order relaxation correction and build excited-state transition densities directly from the first-order amplitudes obtained from a LR-TDDFT calculation. In this approach, two orthogonal sets of excited states (intermediate and final) are computed within a restricted subspace, and transition dipole moments are calculated as
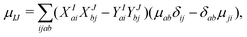 | (12) |
In the context of light–matter interactions, Sheng and co-workers demonstrated that the (spin-conserving) PWF-TDDFT framework may be used to simulate excited-state absorption spectra with errors in the order of 0.07 eV with a suitable choice of exchange–correlation functional.181 Vaz da Cruz and co-workers showed that PWF-TDDFT can also be applied in the simulation of RIXS spectra of organic molecules at the K-edge of light elements.182 In a more recent study, Nascimento and co-workers successfully employed the PWF-TDDFT approach to simulate 2p4d RIXS of representative ruthenium complexes,183 followed by a joint theoretical and experimental investigation to understand and characterize the ground and excited valence states of Ru complexes159 (as illustrated in Fig. 9). Fig. 9 shows the experimental and theoretical spectra of [RuII(bpy)3]2+, [RuII(bpy)2Cl2] and [RuII(CN)6]4− under different conditions. The calculated spectra is in excellent agreement with experiment and is able to reproduce all experimental features with relative transfer energies predicted to within 0.6 eV of accuracy.
5 Summary and outlook
With the rapid growth of experimental X-ray spectroscopy studies, there is a simultaneous need for predictive and computationally cost-effective theoretical approaches. Spectroscopy simulations are key to disentangling spectral features and for a detailed understanding of the observed signals. Great strides have been made in the development of ab initio wavefunction-based methods for the simulation of X-ray spectroscopies over the last few years. Nevertheless, low-order DFT-based methods, like LR/RT-TDDFT, are still very useful. Their ability to provide sufficient accuracy for a broad range of large chemical systems in realistic environments at a significantly lower computational cost makes these low cost methods very appealing. In this brief review, we have highlighted the utility of LR-TDDFT based approaches to tackle XANES, VtC-XES, and RIXS to analyse and interpret experimental data. However, TDDFT is not a panacea and many open questions remain and new theoretical developments are needed.184,185 As we have emphasized earlier, care must be taken especially in terms of the exchange–correlation functional and basis set choices, which have to be carefully assessed when performing excited-state computations in general including core-level spectra. Other areas of development include simulations of non-linear X-ray spectroscopic signals,186 transient spectroscopies187 including dynamics, real-time domain simulations, and TDDFT coupled to strong fields.42 Additionally, developments in applied mathematics are also needed for efficient solvers for large systems.Author contributions
D. R. N. and N. G. jointly wrote the article.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, Chemical Sciences, Geosciences and Biosciences Division under Award No. KC-030105172685 (D. R. N., N. G.). D. R. N. acknowledges support from the University of Memphis. This research benefited from computational resources provided by EMSL, a DOE Office of Science User Facility sponsored by the Office of Biological and Environmental Research and located at PNNL. PNNL is operated by Battelle Memorial Institute for the United States Department of Energy under DOE Contract No. DE-AC05-76RL1830. This research also used resources of the National Energy Research Scientific Computing Center (NERSC), a U.S. Department of Energy Office of Science User Facility operated under Contract No. DE-AC02-05CH11231.Notes and references
- F. De Groot, Chem. Rev., 2001, 101, 1779–1808 CrossRef CAS PubMed.
- J. Stöhr, NEXAFS Spectroscopy, Springer-Verlag, 2003 Search PubMed.
- F. De Groot and A. Kotani, Core Level Spectroscopy of Solids, CRC Press, 2008 Search PubMed.
- M. Bauer, Phys. Chem. Chem. Phys., 2014, 16, 13827–13837 RSC.
- R. Schoenlein, T. Elsaesser, K. Holldack, Z. Huang, H. Kapteyn, M. Murnane and M. Woerner, Philos. Trans. R. Soc., A, 2019, 377, 20180384 CrossRef CAS.
- G. Seidler, D. Mortensen, A. Remesnik, J. Pacold, N. Ball, N. Barry, M. Styczinski and O. Hoidn, Rev. Sci. Instrum., 2014, 85, 113906 CrossRef CAS PubMed.
- F. M. de Groot, H. Elnaggar, F. Frati, R.-P. Wang, M. U. Delgado-Jaime, M. van Veenendaal, J. Fernandez-Rodriguez, M. W. Haverkort, R. J. Green and G. van der Laan, et al. , J. Electron Spectrosc. Relat. Phenom., 2021, 249, 147061 CrossRef CAS.
- A. Trofimov, T. Moskovskaya, E. Gromov, N. Vitkovskaya and J. Schirmer, J. Struct. Chem., 2000, 41, 483–494 CrossRef CAS.
- J. Wenzel, M. Wormit and A. Dreuw, J. Comput. Chem., 2014, 35, 1900–1915 CrossRef CAS PubMed.
- J. Wenzel, M. Wormit and A. Dreuw, J. Chem. Theory Comput., 2014, 10, 4583–4598 CrossRef CAS PubMed.
- B. Peng, P. J. Lestrange, J. J. Goings, M. Caricato and X. Li, J. Chem. Theory Comput., 2015, 11, 4146–4153 CrossRef CAS.
- D. R. Nascimento and A. E. DePrince III, J. Phys. Chem. Lett., 2017, 8, 2951–2957 CrossRef CAS PubMed.
- M. L. Vidal, X. Feng, E. Epifanovsky, A. I. Krylov and S. Coriani, J. Chem. Theory Comput., 2019, 15, 3117–3133 CrossRef CAS PubMed.
- M. L. Vidal, A. I. Krylov and S. Coriani, Phys. Chem. Chem. Phys., 2020, 22, 2693–2703 RSC.
- M. L. Vidal, P. Pokhilko, A. I. Krylov and S. Coriani, J. Phys. Chem. Lett., 2020, 11, 8314–8321 CrossRef CAS.
- S. Coriani and H. Koch, J. Chem. Phys., 2015, 143, 181103 CrossRef.
- R. Faber and S. Coriani, J. Chem. Theory Comput., 2018, 15, 520–528 CrossRef PubMed.
- R. V. Pinjari, M. G. Delcey, M. Guo, M. Odelius and M. Lundberg, J. Chem. Phys., 2014, 141, 124116 CrossRef PubMed.
- B. Helmich-Paris, Int. J. Quantum Chem., 2021, 121, e26559 CrossRef CAS.
- C. A. Ullrich, Time-Dependent Density-Functional Theory: Concepts and Applications, Oxford University Press, 2011 Search PubMed.
- M. Valiev, E. J. Bylaska, N. Govind, K. Kowalski, T. P. Straatsma, H. J. Van Dam, D. Wang, J. Nieplocha, E. Apra, T. L. Windus and W. A. De Jong, Comput. Phys. Commun., 2010, 181, 1477–1489 CrossRef CAS.
- E. Apra, E. J. Bylaska, W. A. De Jong, N. Govind, K. Kowalski, T. P. Straatsma, M. Valiev, H. J. van Dam, Y. Alexeev and J. Anchell, et al. , J. Chem. Phys., 2020, 152, 184102 CrossRef CAS PubMed.
- J. J. Rehr and R. C. Albers, Rev. Mod. Phys., 2000, 72, 621–654 CrossRef CAS.
- J. J. Rehr, J. J. Kas, M. P. Prange, A. P. Sorini, Y. Takimoto and F. Vila, C. R. Phys., 2009, 10, 548–559 CrossRef CAS.
- J. J. Rehr, J. J. Kas, F. D. Vila, M. P. Prange and K. Jorissen, Phys. Chem. Chem. Phys., 2010, 12, 5503–5513 RSC.
- P. Norman and A. Dreuw, Chem. Rev., 2018, 118, 7208–7248 CrossRef CAS PubMed.
- J. M. Kasper, T. F. Stetina, A. J. Jenkins and X. Li, Chem. Phys. Rev., 2020, 1, 011304 CrossRef.
- N. A. Besley, Acc. Chem. Res., 2020, 53, 1306–1315 CrossRef CAS PubMed.
- M. Stener, G. Fronzoni and M. de Simone, Chem. Phys. Lett., 2003, 373, 115–123 CrossRef CAS.
- K. Ray, S. DeBeer George, E. I. Solomon, K. Wieghardt and F. Neese, Chem. – Eur. J., 2007, 13, 2783–2797, DOI:10.1002/chem.200601425.
- N. A. Besley and F. A. Asmuruf, Phys. Chem. Chem. Phys., 2010, 12, 12024–12039 RSC.
- W. Liang, S. A. Fischer, M. J. Frisch and X. Li, J. Chem. Theory Comput., 2011, 7, 3540–3547 CrossRef CAS.
- K. Lopata, B. E. Van Kuiken, M. Khalil and N. Govind, J. Chem. Theory Comput., 2012, 8, 3284–3292 CrossRef CAS.
- B. Peng, P. J. Lestrange, J. J. Goings, M. Caricato and X. Li, J. Chem. Theory Comput., 2015, 11, 4146–4153 CrossRef CAS PubMed.
- R. Van Beeumen, D. B. Williams-Young, J. M. Kasper, C. Yang, E. G. Ng and X. Li, J. Chem. Theory Comput., 2017, 13, 4950–4961 CrossRef CAS PubMed.
- G. Fronzoni, M. Stener, P. Decleva, M. D. Simone, M. Coreno, P. Franceschi, C. Furlani and K. Prince, J. Phys. Chem. A, 2009, 113, 2914–2925 CrossRef CAS PubMed.
- M. Kadek, L. Konecny, B. Gao, M. Repisky and K. Ruud, Phys. Chem. Chem. Phys., 2015, 17, 22566–22570 RSC.
- M. Repisky, L. Konecny, M. Kadek, S. Komorovsky, O. L. Malkin, V. G. Malkin and K. Ruud, J. Chem. Theory Comput., 2015, 11, 980–991 CrossRef CAS.
- T. F. Stetina, J. M. Kasper and X. Li, J. Chem. Phys., 2019, 150, 234103 CrossRef PubMed.
- C. South, A. Shee, D. Mukherjee, A. K. Wilson and T. Saue, Phys. Chem. Chem. Phys., 2016, 18, 21010–21023 RSC.
- T. Fransson, D. Burdakova and P. Norman, Phys. Chem. Chem. Phys., 2016, 18, 13591–13603 RSC.
- X. Li, N. Govind, C. Isborn, A. E. DePrince and K. Lopata, Chem. Rev., 2020, 120, 9951–9993 CrossRef CAS PubMed.
- N. A. Besley, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 11, e1527 CAS.
- L. Konecny, J. Vicha, S. Komorovsky, K. Ruud and M. Repisky, Inorg. Chem., 2021, 61, 830–846 CrossRef PubMed.
- A. Bussy and J. Hutter, Phys. Chem. Chem. Phys., 2021, 23, 4736–4746 RSC.
- G. Onida, L. Reining and A. Rubio, Rev. Mod. Phys., 2002, 74, 601 CrossRef CAS.
- J. Vinson, J. Rehr, J. Kas and E. Shirley, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 115106 CrossRef PubMed.
- Y. Yao, D. Golze, P. Rinke, V. Blum and Y. Kanai, J. Chem. Theory Comput., 2022, 18, 1569–1583, DOI:10.1021/acs.jctc.1c01180.
- J. Wenzel, M. Wormit and A. Dreuw, J. Comput. Chem., 2014, 35, 1900–1915, DOI:10.1002/jcc.23703.
- J. Wenzel, M. Wormit and A. Dreuw, J. Chem. Theory Comput., 2014, 10, 4583–4598 CrossRef CAS PubMed.
- J. Wenzel, A. Holzer, M. Wormit and A. Dreuw, J. Chem. Phys., 2015, 142, 214104 CrossRef PubMed.
- R. Peng, A. V. Copan and A. Y. Sokolov, J. Phys. Chem. A, 2019, 123, 1840–1850 CrossRef CAS PubMed.
- S. Coriani, O. Christiansen, T. Fransson and P. Norman, Phys. Rev. A, 2012, 85, 022507 CrossRef.
- T. Fransson, S. Coriani, O. Christiansen and P. Norman, J. Chem. Phys., 2013, 138, 124311 CrossRef PubMed.
- D. R. Nascimento and A. E. DePrince III, J. Phys. Chem. Lett., 2017, 8, 2951–2957 CrossRef CAS.
- J. Liu, D. Matthews, S. Coriani and L. Cheng, J. Chem. Theory Comput., 2019, 15, 1642–1651 CrossRef CAS PubMed.
- Y. C. Park, A. Perera and R. J. Bartlett, J. Chem. Phys., 2021, 155, 094103 CrossRef CAS PubMed.
- D. A. Matthews, Mol. Phys., 2020, 118, e1771448 CrossRef.
- I. Josefsson, K. Kunnus, S. Schreck, A. Föhlisch, F. de Groot, P. Wernet and M. Odelius, J. Phys. Chem. Lett., 2012, 3, 3565–3570 CrossRef CAS PubMed.
- R. V. Pinjari, M. G. Delcey, M. Guo, M. Odelius and M. Lundberg, J. Chem. Phys., 2014, 141, 124116 CrossRef PubMed.
- M. Roemelt and F. Neese, J. Phys. Chem. A, 2013, 117, 3069–3083 CrossRef CAS PubMed.
- M. Roemelt, D. Maganas, S. DeBeer and F. Neese, J. Chem. Phys., 2013, 138, 204101 CrossRef PubMed.
- J. Brabec, K. Bhaskaran-Nair, N. Govind, J. Pittner and K. Kowalski, J. Chem. Phys., 2012, 137, 171101 CrossRef PubMed.
- M. E. Casida, Time-Dependent Density-functional Response Theory for Molecules, World Scientific, 1995, pp. 155–193 Search PubMed.
- C. A. Ullrich, Time-Dependent Density-Functional Theory: Concepts and Applications, OUP, Oxford, 2011 Search PubMed.
- N. T. Maitra, F. Zhang, R. J. Cave and K. Burke, J. Chem. Phys., 2004, 120, 5932–5937 CrossRef CAS PubMed.
- S. Hirata and M. Head-Gordon, Chem. Phys. Lett., 1999, 314, 291–299 CrossRef CAS.
- E. R. Davidson, J. Comput. Phys., 1975, 17, 87–94 CrossRef.
- J. Brabec, L. Lin, M. Shao, N. Govind, C. Yang, Y. Saad and E. G. Ng, J. Chem. Theory Comput., 2015, 11, 5197–5208 CrossRef CAS PubMed.
- F. Furche, B. T. Krull, B. D. Nguyen and J. Kwon, J. Chem. Phys., 2016, 144, 174105 CrossRef PubMed.
- E. Vecharynski, J. Brabec, M. Shao, N. Govind and C. Yang, Comput. Phys. Commun., 2017, 221, 42–52 CrossRef CAS.
- C. Huang, W. Liu, Y. Xiao and M. R. Hoffmann, J. Comput. Chem., 2017, 38, 2481–2499 CrossRef CAS PubMed.
- J. M. Kasper, D. B. Williams-Young, E. Vecharynski, C. Yang and X. Li, J. Chem. Theory Comput., 2018, 14, 2034–2041 CrossRef CAS PubMed.
- C. Huang and W. Liu, J. Comput. Chem., 2019, 40, 1023–1037 CrossRef CAS PubMed.
- S. Komorovsky, P. J. Cherry and M. Repisky, J. Chem. Phys., 2019, 151, 184111 CrossRef PubMed.
- S. Tretiak, C. M. Isborn, A. M. Niklasson and M. Challacombe, J. Chem. Phys., 2009, 130, 054111 CrossRef PubMed.
- L. S. Cederbaum, W. Domcke and J. Schirmer, Phys. Rev. A: At., Mol., Opt. Phys., 1980, 22, 206 CrossRef CAS.
- M. F. Herbst and T. Fransson, J. Chem. Phys., 2020, 153, 054114 CrossRef CAS PubMed.
- T. Tsuchimochi, M. Kobayashi, A. Nakata, Y. Imamura and H. Nakai, J. Comput. Chem., 2008, 29, 2311–2316 CrossRef CAS PubMed.
- U. Ekström and P. Norman, Phys. Rev. A: At., Mol., Opt. Phys., 2006, 74, 042722 CrossRef.
- U. Ekström, P. Norman, V. Carravetta and H. Ågren, Phys. Rev. Lett., 2006, 97, 143001 CrossRef PubMed.
- M. Roemelt, D. Maganas, S. DeBeer and F. Neese, J. Chem. Phys., 2013, 138, 204101 CrossRef PubMed.
- S. D. George, T. Petrenko and F. Neese, Inorg. Chim. Acta, 2008, 361, 965–972 CrossRef.
- M. Ross, A. Andersen, Z. W. Fox, Y. Zhang, K. Hong, J.-H. Lee, A. Cordones, A. M. March, G. Doumy, S. H. Southworth, M. A. Marcus, R. W. Schoenlein, S. Mukamel, N. Govind and M. Khalil, J. Phys. Chem. B, 2018, 122, 5075–5086 CrossRef CAS PubMed.
- H. A. Albrecht and E. E. Salpeter, Quantum Mechanics for One-and Two-electron Atoms, Springer, 1957 Search PubMed.
- P. J. Lestrange, F. Egidi and X. Li, J. Chem. Phys., 2015, 143, 234103 CrossRef PubMed.
- L. Zheng, N. F. Polizzi, A. R. Dave, A. Migliore and D. N. Beratan, J. Phys. Chem. A, 2016, 120, 1933–1943 CrossRef CAS PubMed.
- S. Bernadotte, A. J. Atkins and C. R. Jacob, J. Chem. Phys., 2012, 137, 204106 CrossRef PubMed.
- N. H. List, J. Kauczor, T. Saue, H. J. A. Jensen and P. Norman, J. Chem. Phys., 2015, 142, 244111 CrossRef PubMed.
- N. H. List, T. Saue and P. Norman, Mol. Phys., 2017, 115, 63–74 CrossRef CAS.
- N. H. List, T. R. L. Melin, M. van Horn and T. Saue, J. Chem. Phys., 2020, 152, 184110 CrossRef CAS PubMed.
- B. E. Van Kuiken, M. Valiev, S. L. Daifuku, C. Bannan, M. L. Strader, H. Cho, N. Huse, R. W. Schoenlein, N. Govind and M. Khalil, J. Phys. Chem. A, 2013, 117, 4444–4454 CrossRef CAS PubMed.
- A. Vjunov, J. L. Fulton, T. Huthwelker, S. Pin, D. Mei, G. K. Schenter, N. Govind, D. M. Camaioni, J. Z. Hu and J. A. Lercher, J. Am. Chem. Soc., 2014, 136, 8296–8306 CrossRef CAS PubMed.
- J. L. Fulton, N. Govind, T. Huthwelker, E. J. Bylaska, A. Vjunov, S. Pin and T. D. Smurthwaite, J. Phys. Chem. B, 2015, 119, 8380–8388 CrossRef CAS PubMed.
- N. Govind and W. A. D. Jong, Thom H. Dunning, Jr., Springer, 2015, pp. 247–253 Search PubMed.
- M. Vijayakumar, N. Govind, E. Walter, S. D. Burton, A. Shukla, A. Devaraj, J. Xiao, J. Liu, C. Wang and A. Karim, et al. , Phys. Chem. Chem. Phys., 2014, 16, 10923–10932 RSC.
- K. Henzler, E. O. Fetisov, M. Galib, M. D. Baer, B. A. Legg, C. Borca, J. M. Xto, S. Pin, J. L. Fulton and G. K. Schenter, et al. , Sci. Adv., 2018, 4, eaao6283 CrossRef PubMed.
- M. Galib, G. Schenter, C. Mundy, N. Govind and J. Fulton, J. Chem. Phys., 2018, 149, 124503 CrossRef CAS PubMed.
- A. Andersen, N. N. Rajput, K. S. Han, H. Pan, N. Govind, K. A. Persson, K. T. Mueller and V. Murugesan, Chem. Mater., 2019, 31, 2308–2319 CrossRef CAS.
- A. Vjunov, M. Wang, N. Govind, T. Huthwelker, H. Shi, D. Mei, J. L. Fulton and J. A. Lercher, Chem. Mater., 2017, 29, 9030–9042 CrossRef CAS.
- V. Murugesan, J. S. Cho, N. Govind, A. Andersen, M. J. Olszta, K. S. Han, G. Li, H. Lee, D. M. Reed and V. L. Sprenkle, et al. , ACS Appl. Energy Mater., 2019, 2, 1832–1843 CrossRef CAS.
- E. Biasin, D. R. Nascimento, B. I. Poulter, B. Abraham, K. Kunnus, A. T. Garcia-Esparza, S. H. Nowak, T. Kroll, R. W. Schoenlein, R. Alonso-Mori, M. Khalil, N. Govind and D. Sokaras, Chem. Sci., 2021, 3713–3725, 10.1039/D0SC06227H.
- D. Boglaienko, A. Andersen, S. M. Heald, T. Varga, D. R. Mortensen, S. Tetef, G. T. Seidler, N. Govind and T. G. Levitskaia, J. Alloys Compd., 2022, 897, 162629 CrossRef CAS.
- A. M. March, G. Doumy, A. Andersen, A. Al Haddad, Y. Kumagai, M.-F. Tu, J. Bang, C. Bostedt, J. Uhlig and D. R. Nascimento, et al. , J. Chem. Phys., 2019, 151, 144306 CrossRef PubMed.
- D. R. Nascimento, Y. Zhang, U. Bergmann and N. Govind, J. Phys. Chem. Lett., 2020, 11, 556–561 CrossRef CAS PubMed.
- A. S. Folorunso, A. Bruner, F. Mauger, K. A. Hamer, S. Hernandez, R. R. Jones, L. F. DiMauro, M. B. Gaarde, K. J. Schafer and K. Lopata, Phys. Rev. Lett., 2021, 126, 133002 CrossRef CAS PubMed.
- C. E. Liekhus-Schmaltz, P. J. Ho, R. B. Weakly, A. Aquila, R. W. Schoenlein, M. Khalil and N. Govind, J. Chem. Phys., 2021, 154, 214107 CrossRef CAS PubMed.
- C. M. Loe, C. Liekhus-Schmaltz, N. Govind and M. Khalil, J. Phys. Chem. Lett., 2021, 12, 9840–9847 CrossRef CAS PubMed.
- C. Liekhus-Schmaltz, Z. W. Fox, A. Andersen, K. S. Kjaer, R. Alonso-Mori, E. Biasin, J. Carlstad, M. Chollet, J. D. Gaynor and J. M. Glownia, et al. , J. Phys. Chem. Lett., 2022, 13, 378–386 CrossRef CAS PubMed.
- M. A. Ambroise and F. Jensen, J. Chem. Theory Comput., 2018, 15, 325–337 CrossRef PubMed.
- E. Gallo and P. Glatzel, Adv. Mater., 2014, 26, 7730–7746 CrossRef CAS PubMed.
- P. Glatzel and U. Bergmann, Coord. Chem. Rev., 2005, 249, 65–95 CrossRef CAS.
- P. E. Best, J. Chem. Phys., 1966, 44, 3248–3253 CrossRef CAS.
- U. Bergmann, C. R. Horne, T. J. Collins, J. Workman and S. P. Cramer, Chem. Phys. Lett., 1999, 302, 119–124 CrossRef CAS.
- N. Lee, T. Petrenko, U. Bergmann, F. Neese and S. DeBeer, J. Am. Chem. Soc., 2010, 132, 9715–9727 CrossRef CAS PubMed.
- M. A. Beckwith, M. Roemelt, M.-N. Collomb, C. DuBoc, T.-C. Weng, U. Bergmann, P. Glatzel, F. Neese and S. DeBeer, Inorg. Chem., 2011, 50, 8397–8409 CrossRef CAS PubMed.
- K. M. Lancaster, K. D. Finkelstein and S. DeBeer, Inorg. Chem., 2011, 50, 6767–6774 CrossRef CAS PubMed.
- S. N. MacMillan, R. C. Walroth, D. M. Perry, T. J. Morsing and K. M. Lancaster, Inorg. Chem., 2015, 54, 205–214 CrossRef CAS PubMed.
- Y. Zhang, S. Mukamel, M. Khalil and N. Govind, J. Chem. Theory Comput., 2015, 11, 5804–5809 CrossRef CAS PubMed.
- G. Smolentsev, A. V. Soldatov, J. Messinger, K. Merz, T. Weyhermüller, U. Bergmann, Y. Pushkar, J. Yano, V. K. Yachandra and P. Glatzel, J. Am. Chem. Soc., 2009, 131, 13161–13167 CrossRef CAS PubMed.
- J. C. Swarbrick, Y. Kvashnin, K. Schulte, K. Seenivasan, C. Lamberti and P. Glatzel, Inorg. Chem., 2010, 49, 8323–8332 CrossRef CAS PubMed.
- E. R. Hall, C. J. Pollock, J. Bendix, T. J. Collins, P. Glatzel and S. DeBeer, J. Am. Chem. Soc., 2014, 136, 10076–10084 CrossRef CAS PubMed.
- A. M. March, T. A. Assefa, C. Bressler, G. Doumy, A. Galler, W. Gawelda, E. P. Kanter, Z. Németh, M. Pápai, S. H. Southworth, L. Young and G. Vankó, J. Phys. Chem. C, 2015, 119, 14571–14578 CrossRef CAS PubMed.
- M. Qureshi, S. H. Nowak, L. I. Vogt, J. J. Cotelesage, N. V. Dolgova, S. Sharifi, T. Kroll, D. Nordlund, R. Alonso-Mori and T.-C. Weng, et al. , Phys. Chem. Chem. Phys., 2021, 23, 4500–4508 RSC.
- N. Levin, S. Peredkov, T. Weyhermüller, O. Rüdiger, N. B. Pereira, D. Grötzsch, A. Kalinko and S. DeBeer, Inorg. Chem., 2020, 59, 8272–8283 CrossRef CAS PubMed.
- P. Noziéres and C. T. de Dominicis, Phys. Rev., 1969, 178, 1097–1107 CrossRef.
- W. H. E. Schwarz and R. J. Buenker, Chem. Phys., 1976, 13, 153–160 CrossRef CAS.
- Y. Zhang, W. Hua, K. Bennett and S. Mukamel, Density-Functional Methods for Excited States, Springer Science + Business Media, 2015, vol. 368, pp. 273–345 Search PubMed.
- W. J. Hunt and W. A. Goddard, Chem. Phys. Lett., 1969, 3, 414–418 CrossRef CAS.
- H. Ågren, V. Carravetta, O. Vahtras and L. G. Pettersson, Chem. Phys. Lett., 1994, 222, 75–81 CrossRef.
- H. Åren, V. Carravetta, O. Vahtras and L. G. M. Pettersson, Theor. Chem. Acc., 1997, 97, 14–40 Search PubMed.
- M. Stener, A. Lisini and P. Decleva, Chem. Phys., 1995, 191, 141–154 CrossRef CAS.
- L. Triguero, L. G. M. Pettersson and H. Ågren, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 8097–8110 CrossRef CAS.
- D. Prendergast and G. Galli, Phys. Rev. Lett., 2006, 96, 215502 CrossRef PubMed.
- J. D. Wadey and N. A. Besley, J. Chem. Theory Comput., 2014, 10, 4557–4564 CrossRef CAS PubMed.
- Y. Zhang, S. Mukamel, M. Khalil and N. Govind, J. Chem. Theory Comput., 2015, 11, 5804–5809 CrossRef CAS PubMed.
- D. Mortensen, G. Seidler, J. J. Kas, N. Govind, C. P. Schwartz, S. Pemmaraju and D. G. Prendergast, Phys. Rev. B, 2017, 96, 125136 CrossRef.
- E. P. Jahrman, W. M. Holden, N. Govind, J. J. Kas, J. Rana, L. F. Piper, C. Siu, M. S. Whittingham, T. T. Fister and G. T. Seidler, J. Mater. Chem. A, 2020, 8, 16332–16344 RSC.
- W. Holden, E. Jahrman, N. Govind and G. Seidler, J. Phys. Chem. A, 2020, 124, 5415–5434 CrossRef CAS PubMed.
- S. Tetef, N. Govind and G. T. Seidler, Phys. Chem. Chem. Phys., 2021, 23, 23586–23601 RSC.
- M. E. Casida, Recent Advances in Density Functional Methods (Part I), World Scientific, 1995, ch. 5, vol. 1, pp. 155–192 Search PubMed.
- R. E. Stratmann, G. E. Scuseria and M. J. Frisch, J. Chem. Phys., 1998, 109, 8218–8224 CrossRef CAS.
- S. Hirata and M. Head-Gordon, Chem. Phys. Lett., 1999, 302, 375–382 CrossRef CAS.
- P. G. Lykos and H. N. Schmeising, J. Chem. Phys., 1961, 35, 288–293 CrossRef CAS.
- H. F. King, R. E. Stanton, H. Kim, R. E. Wyatt and R. G. Parr, J. Chem. Phys., 1967, 47, 1936–1941 CrossRef CAS.
- A. T. B. Gilbert, N. A. Besley and P. M. W. Gill, J. Phys. Chem. A, 2008, 112, 13164–13171 CrossRef CAS PubMed.
- F. Gel'mukhanov and H. Ågren, Phys. Rep., 1999, 312, 87–330 CrossRef.
- F. de Groot, Chem. Rev., 2001, 101, 1779–1808 CrossRef CAS PubMed.
- L. J. P. Ament, M. van Veenendaal, T. P. Devereaux, J. P. Hill and J. van den Brink, Rev. Mod. Phys., 2011, 83, 705–767 CrossRef CAS.
- E. D. Isaacs and P. Platzman, Phys. Today, 1996, 49, 40–45 CrossRef CAS.
- F. Hennies, A. Pietzsch, M. Berglund, A. Föhlisch, T. Schmitt, V. Strocov, H. O. Karlsson, J. Andersson and J.-E. Rubensson, Phys. Rev. Lett., 2010, 104, 193002 CrossRef PubMed.
- J. Nordgren and J.-E. Rubensson, J. Electron Spectrosc., 2013, 188, 3–9 CrossRef CAS.
- K. Kunnus, I. Josefsson, S. Schreck, W. Quevedo, P. S. Miedema, S. Techert, F. M. F. de Groot, M. Odelius, P. Wernet and A. Föhlisch, J. Phys. Chem. B, 2013, 117, 16512–16521 CrossRef CAS PubMed.
- A. Pietzsch, F. Hennies, P. S. Miedema, B. Kennedy, J. Schlappa, T. Schmitt, V. N. Strocov and A. Föhlisch, Phys. Rev. Lett., 2015, 114, 088302 CrossRef CAS PubMed.
- S. Eckert, J. Norell, P. S. Miedema, M. Beye, M. Fondell, W. Quevedo, B. Kennedy, M. Hantschmann, A. Pietzsch, B. E. Van Kuiken, M. Ross, M. P. Minitti, S. P. Moeller, W. F. Schlotter, M. Khalil, M. Odelius and A. Föhlisch, Angew. Chem., Int. Ed., 2017, 56, 6088–6092 CrossRef CAS PubMed.
- A. W. Hahn, B. E. Van Kuiken, V. G. Chilkuri, N. Levin, E. Bill, T. Weyhermüller, A. Nicolaou, J. Miyawaki, Y. Harada and S. DeBeer, Inorg. Chem., 2018, 57, 9515–9530 CrossRef CAS PubMed.
- R. H. Temperton, S. T. Skowron, K. Handrup, A. J. Gibson, A. Nicolaou, N. Jaouen, E. Besley and J. N. OShea, J. Chem. Phys., 2019, 151, 074701 CrossRef PubMed.
- A. Fouda, L. C. Seitz, D. Hauschild, M. Blum, W. Yang, C. Heske, L. Weinhardt and N. A. Besley, J. Phys. Chem. Lett., 2020, 11, 7476–7482 CrossRef CAS PubMed.
- E. Biasin, D. R. Nascimento, B. I. Poulter, B. Abraham, K. Kunnus, A. T. Garcia-Esparza, S. H. Nowak, T. Kroll, R. W. Schoenlein and R. Alonso-Mori, et al. , Chem. Sci., 2021, 12, 3713–3725 RSC.
- A. Kotani and S. Shin, Rev. Mod. Phys., 2001, 73, 203–246 CrossRef CAS.
- R. Faber and S. Coriani, J. Chem. Theory Comput., 2019, 15, 520–528 CrossRef CAS PubMed.
- R. Faber and S. Coriani, Phys. Chem. Chem. Phys., 2020, 22, 2642–2647 RSC.
- K. D. Nanda, M. L. Vidal, R. Faber, S. Coriani and A. I. Krylov, Phys. Chem. Chem. Phys., 2020, 22, 2629–2641 RSC.
- K. D. Nanda and A. I. Krylov, J. Chem. Phys., 2020, 152, 244118 CrossRef PubMed.
- D. R. Rehn, A. Dreuw and P. Norman, J. Chem. Theory Comput., 2017, 13, 5552–5559 CrossRef CAS PubMed.
- I. Josefsson, K. Kunnus, S. Schreck, A. Föhlisch, F. de Groot, P. Wernet and M. Odelius, J. Phys. Chem. Lett., 2012, 3, 3565–3570 CrossRef CAS PubMed.
- D. Maganas, S. DeBeer and F. Neese, Inorg. Chem., 2017, 56, 11819–11836 CrossRef CAS PubMed.
- N. Ferré, M. Filatov, M. Huix-Rotllant and C. Adamo, Density-functional methods for excited states, Springer, 2016 Search PubMed.
- M. W. D. Hanson-Heine, M. W. George and N. A. Besley, J. Chem. Phys., 2017, 146, 094106 CrossRef.
- A. E. A. Fouda, G. I. Purnell and N. A. Besley, J. Chem. Theory Comput., 2018, 14, 2586–2595 CrossRef CAS PubMed.
- N. A. Besley, Acc. Chem. Res., 2020, 53, 1306–1315 CrossRef CAS PubMed.
- E. Dalgaard, Phys. Rev. A: At., Mol., Opt. Phys., 1982, 26, 42–52 CrossRef CAS.
- S. M. Parker, S. Roy and F. Furche, J. Chem. Phys., 2016, 145, 134105 CrossRef PubMed.
- S. M. Parker, D. Rappoport and F. Furche, J. Chem. Theory Comput., 2018, 14, 807–819 CrossRef CAS PubMed.
- D. N. Bowman, J. C. Asher, S. A. Fischer, C. J. Cramer and N. Govind, Phys. Chem. Chem. Phys., 2017, 19, 27452–27462 RSC.
- E. C. Alguire, Q. Ou and J. E. Subotnik, J. Phys. Chem. B, 2015, 119, 7140–7149 CrossRef CAS PubMed.
- X. Zhang and J. M. Herbert, J. Chem. Phys., 2014, 141, 064104 CrossRef PubMed.
- Q. Ou, G. D. Bellchambers, F. Furche and J. E. Subotnik, J. Chem. Phys., 2015, 142, 064114 CrossRef PubMed.
- Q. Ou, E. C. Alguire and J. E. Subotnik, J. Phys. Chem. B, 2015, 119, 7150–7161 CrossRef CAS PubMed.
- X. Zhang and J. M. Herbert, J. Chem. Phys., 2015, 142, 064109 CrossRef PubMed.
- X. Sheng, H. Zhu, K. Yin, J. Chen, J. Wang, C. Wang, J. Shao and F. Chen, J. Phys. Chem. C, 2020, 124, 4693–4700 CrossRef CAS.
- V. V. da Cruz, S. Eckert and A. Föhlisch, Phys. Chem. Chem. Phys., 2021, 23, 1835–1848, 10.1039/D0CP04726K.
- D. R. Nascimento, E. Biasin, B. I. Poulter, M. Khalil, D. Sokaras and N. Govind, J. Chem. Theory Comput., 2021, 17, 3031–3038 CrossRef CAS PubMed.
- N. T. Maitra, J. Chem. Phys., 2016, 144, 220901 CrossRef PubMed.
- J. M. Herbert, 2022, arXiv preprint arXiv:2204.10135.
- Y. Zhang, W. Hua, K. Bennett and S. Mukamel, Density-Functional Methods for Excited States, 2014, pp. 273–345 Search PubMed.
- F. Segatta, M. Russo, D. R. Nascimento, D. Presti, F. Rigodanza, A. Nenov, A. Bonvicini, A. Arcioni, S. Mukamel and M. Maiuri, et al. , J. Chem. Theory Comput., 2021, 17, 7134–7145 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2022 |
