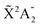Vibrationally resolved photoelectron angular distributions of ammonia
Celso M.
González-Collado
 *a,
Etienne
Plésiat
b,
Piero
Decleva
*a,
Etienne
Plésiat
b,
Piero
Decleva
 c,
Alicia
Palacios
c,
Alicia
Palacios
 ad and
Fernando
Martín
ad and
Fernando
Martín
 *abe
*abe
aDepartamento de Química, Módulo 13, Universidad Autónoma de Madrid, 28049 Madrid, Spain. E-mail: celso.gonzalez@uam.es; fernando.martin@uam.es
bInstituto Madrileño de Estudios Avanzados en Nanociencia (IMDEA-Nanociencia), Cantoblanco, 28049 Madrid, Spain
cDipartimento di Scienze Chimiche e Farmaceutiche, Università degli Studi di Trieste and CNR-IOM, 34127 Trieste, Italy
dInstitute of Advanced Research in Chemical Sciences (IAdChem), Universidad Autónoma de Madrid, 28049 Madrid, Spain
eCondensed Matter Physics Center (IFIMAC), Universidad Autónoma de Madrid, 28049 Madrid, Spain
First published on 7th March 2022
Abstract
We present a theoretical study of vibrationally resolved photoelectron angular distributions for ammonia in both laboratory and molecular frames, in the photon energy range up to 70 eV, where only valence and inner-valence ionization is possible. We focus on the band resulting from ionization of the 3a1 HOMO orbital leading to NH3+ in the electronic ground state, 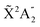 , for which the dominant vibrational progression corresponds to the activation of the umbrella inversion mode. We show that, at room temperature, the photoelectron angular distributions for randomly oriented molecules or molecules whose principal C3 symmetry axis is aligned along the light polarization direction are perfectly symmetric with respect to the plane that contains the intermediate D3h conformation connecting the pyramidal structures associated with the double-well potential of the umbrella inversion mode. These distributions exhibit symmetric, nearly perfect two-lobe shapes in the whole range of investigated photon energies. In contrast, for molecules where the initial vibrational state is localized in one of the two wells, a situation that can experimentally be achieved by introducing an external electric field, the molecular-frame photoelectron angular distributions (MFPADs) are in general asymmetric, but the degree of asymmetry of the two lobes dramatically changes and oscillates with photoelectron energy. We also show that, at ultracold temperatures, where all aligned molecules initially lie in the delocalized ground vibrational state, the photoelectron angular distributions are perfectly symmetric, but the two-lobe shape is only observed when the final vibrational state of the resulting NH3+ cation has even parity. When the latter vibrational state has odd parity, the angular distributions are much more involved and, at photoelectron energies of ∼10 eV, they directly reflect the bi-pyramidal geometry of the molecule in its ground vibrational state. These results suggest that, in order to obtain structural information from MFPADs in ammonia and likely in other molecules containing a similar double-well potential, one could preferably work at ultracold temperatures, which is not the case for most molecules.
, for which the dominant vibrational progression corresponds to the activation of the umbrella inversion mode. We show that, at room temperature, the photoelectron angular distributions for randomly oriented molecules or molecules whose principal C3 symmetry axis is aligned along the light polarization direction are perfectly symmetric with respect to the plane that contains the intermediate D3h conformation connecting the pyramidal structures associated with the double-well potential of the umbrella inversion mode. These distributions exhibit symmetric, nearly perfect two-lobe shapes in the whole range of investigated photon energies. In contrast, for molecules where the initial vibrational state is localized in one of the two wells, a situation that can experimentally be achieved by introducing an external electric field, the molecular-frame photoelectron angular distributions (MFPADs) are in general asymmetric, but the degree of asymmetry of the two lobes dramatically changes and oscillates with photoelectron energy. We also show that, at ultracold temperatures, where all aligned molecules initially lie in the delocalized ground vibrational state, the photoelectron angular distributions are perfectly symmetric, but the two-lobe shape is only observed when the final vibrational state of the resulting NH3+ cation has even parity. When the latter vibrational state has odd parity, the angular distributions are much more involved and, at photoelectron energies of ∼10 eV, they directly reflect the bi-pyramidal geometry of the molecule in its ground vibrational state. These results suggest that, in order to obtain structural information from MFPADs in ammonia and likely in other molecules containing a similar double-well potential, one could preferably work at ultracold temperatures, which is not the case for most molecules.
1 Introduction
Photoelectron spectra can reveal, under certain conditions, the geometry of ionized molecules in the gas phase. Indeed, in their way out, the ejected electrons are scattered by the molecular potential and thus carry information on the position of the atomic centers, which is finally imprinted in the measured spectra. In this context, photoionization studies using synchrotron radiation have been proven to be very helpful.1–16 For example, ratios of vibrationally resolved spectra arising from K-shell and inner-valence shell photoionization of small molecules exhibit pronounced oscillations, from which the bond lengths of the molecule and its corresponding cation can be determined with reasonable accuracy.9–14 The method works better at high photoelectron energies, where the wavelength of the escaping electron is comparable to the bond distances and, therefore, simple diffraction models can be used to fit the spectra and extract the distances between different atomic centers.1–10,15,16 Though experimentally more involved, this structural information can also be retrieved from photoelectron angular distributions, ideally in the molecular frame, since such distributions provide direct information on the way the electron escapes in different directions.Molecular-frame photoelectron angular distributions (MFPADs) can reflect details of the molecular potential that are usually hidden in measurements performed in the laboratory frame, in which information related to molecular orientation may be lost. To record MFPADs, the molecule must have a well-defined orientation with respect to the polarization of the incoming radiation. This can be achieved in two different ways: (i) by orienting the molecule with an external field, e.g., a laser pulse or a static electric field,17–20 or (ii) by detecting photoelectrons in coincidence with positively charged fragments resulting from the breakup of the remaining cation.21 However, not every molecule can be oriented by an external electric field (e.g., molecules with no permanent dipole moment) or a laser (because of their low polarizability), and not every experimental set-up yields enough statistics after dissociative ionization to realize coincidence measurements. In one way or another, MFPADs have been determined for a large number of molecular systems22–31 and, in some cases, they have been successfully used to get structural information.23–25,32–34 For example, polarization-averaged MFPADs resulting from K-shell ionization of the CH4 molecule24,25 show that the electrons are mainly ejected along the bond directions, thus providing a direct imaging of the molecular geometry. The same has been predicted to occur in K-shell ionization of other molecules.35,36 Very recent theoretical work37 has also proposed that MFPADs, when resolved in time, can reveal structural changes in real time that might be difficult to visualize by using more traditional time-resolved spectroscopic techniques.
In this work, we present a theoretical study of vibrationally resolved photoelectron angular distributions for ammonia, NH3, in both laboratory and molecular frames, in the photon energy range up to 70 eV, where only valence and inner-valence ionization is possible. Ammonia is particularly interesting from the structural point of view due to its well known umbrella inversion mode. This vibrational mode is associated with a symmetric double-well potential in the ground state of the molecule, with minima representing two identical pyramidal configurations of C3v symmetry, corresponding to the nitrogen atom being above or below the plane defined by the three hydrogen atoms. The two wells are connected through a transition state of D3h symmetry, i.e., with a planar geometry. The height of this barrier is 0.25 eV (2020 cm−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 38,39), which is much larger than the thermal energy at room temperature, and the tunneling time between the two wells in the lowest vibrational state is about ≃40 ps. Consequently, in a purely stationary picture and in the absence of any external interaction, the vibrational wave functions for this umbrella mode are delocalized over the two potential wells and are symmetric and antisymmetric with respect to the umbrella mode coordinate, with an energy separation between the corresponding (two lowest) vibrational levels of only ≃0.1 meV (0.793 cm−1
38,39), which is much larger than the thermal energy at room temperature, and the tunneling time between the two wells in the lowest vibrational state is about ≃40 ps. Consequently, in a purely stationary picture and in the absence of any external interaction, the vibrational wave functions for this umbrella mode are delocalized over the two potential wells and are symmetric and antisymmetric with respect to the umbrella mode coordinate, with an energy separation between the corresponding (two lowest) vibrational levels of only ≃0.1 meV (0.793 cm−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40–42). This unusual feature in a molecule as simple as ammonia has raised significant interest in the scientific community43–47 and has generated a debate about the physical meaning of localized vs. delocalized initial vibrational states of NH3 in different experimental scenarios.48,49
40–42). This unusual feature in a molecule as simple as ammonia has raised significant interest in the scientific community43–47 and has generated a debate about the physical meaning of localized vs. delocalized initial vibrational states of NH3 in different experimental scenarios.48,49
Photoionization of NH3 has been studied through the years by using different experimental techniques,50–57 as He I excitation,50,53 X-rays,51 and synchrotron radiation.52 Synchrotron radiation experiments by Edvardsson et al.53 carried out in the binding energy range E = 10–27 eV showed the appearance of three bands in the photoelectron spectrum. Among them, only the band centered at E ≃ 11 eV presents an extended and well-resolved vibrational progression due to the activation of the umbrella inversion mode.53,58,59 This band is associated to ionization of the 3a1 HOMO orbital (with an ionization potential of 10.85 eV51), leading to NH3+ in the electronic ground state, 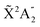 . We focus the present study on the vibrationally resolved photoelectron angular distributions associated with this band for two extreme cases that could be realized under different experimental conditions: perfectly localized and perfectly delocalized initial vibrational states with respect to the umbrella mode coordinate. We employ linearly polarized light along the C3 symmetry axis of the molecule for which the angle-integrated cross sections are larger, as we have checked. We demonstrate that, at room temperature, the photoelectron angular distributions for randomly oriented and aligned molecules are symmetric with respect to the plane containing the D3h transition state and slowly change with photoelectron energy and within the vibrational progression. In contrast, when the molecules are oriented by an external field, the MFPADs are in general asymmetric, which is the result of the breakup of the original molecular symmetry, and the degree of asymmetry rapidly changes and oscillates with photoelectron energy. At ultracold temperatures, the photoelectron angular distributions for aligned molecules are symmetric and, when the final vibrational state of the resulting NH3+ cation has odd parity, they reflect the bi-pyramidal geometry of the molecule in its ground, symmetrically delocalized vibrational state.
. We focus the present study on the vibrationally resolved photoelectron angular distributions associated with this band for two extreme cases that could be realized under different experimental conditions: perfectly localized and perfectly delocalized initial vibrational states with respect to the umbrella mode coordinate. We employ linearly polarized light along the C3 symmetry axis of the molecule for which the angle-integrated cross sections are larger, as we have checked. We demonstrate that, at room temperature, the photoelectron angular distributions for randomly oriented and aligned molecules are symmetric with respect to the plane containing the D3h transition state and slowly change with photoelectron energy and within the vibrational progression. In contrast, when the molecules are oriented by an external field, the MFPADs are in general asymmetric, which is the result of the breakup of the original molecular symmetry, and the degree of asymmetry rapidly changes and oscillates with photoelectron energy. At ultracold temperatures, the photoelectron angular distributions for aligned molecules are symmetric and, when the final vibrational state of the resulting NH3+ cation has odd parity, they reflect the bi-pyramidal geometry of the molecule in its ground, symmetrically delocalized vibrational state.
It is important to stress that, to evaluate angle-integrated photoelectron spectra, one can usually rely on the fixed-nuclei approximation. Obviously, this assumption is no longer valid to obtain vibrationally resolved cross sections, since one also has to account for the nuclear motion in the potential created by the electrons. This makes calculations significantly more expensive, hence applications are scarcer, because the electronic structure must be determined for many molecular geometries, including the equilibrium one used in the fixed-nuclei approximation.
The paper is organized as follows. In Section 2, we describe the theoretical details of our calculations, explaining our model for the umbrella mode to compute the vibrational structure, and the key expressions to compute the energy- and angle-differential photoionization cross sections for ammonia. In Section 3, we first show the total cross sections and β asymmetry parameters that can be compared with existing experimental data. We then present and discuss in detail the phototoelectron angular distributions for room and ultracold temperatures, and different scenarios for the molecular orientation: randomly, aligned and oriented molecules. Conclusions are given in Section 4.
2 Theory
2.1 Vibrational motion
Since the main vibrational progression of the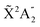 band corresponds to excitation of the umbrella mode, we will focus only on this mode. Umbrella motion mostly depends on two degrees of freedom, namely the inversion coordinate z (the signed distance from the N atom to the xy plane spanned by the three H atoms) and the angle γ between the N–H bonds and the xy plane. However, as shown by density functional theory (DFT) calculations performed by Aquino et al.,60 in the geometries undergoing the umbrella motion, the distance between adjacent hydrogen atoms, dHH, and the fraction dHH/dNH, where dNH is the bond distance, follow a nearly perfect linear relation, given by
band corresponds to excitation of the umbrella mode, we will focus only on this mode. Umbrella motion mostly depends on two degrees of freedom, namely the inversion coordinate z (the signed distance from the N atom to the xy plane spanned by the three H atoms) and the angle γ between the N–H bonds and the xy plane. However, as shown by density functional theory (DFT) calculations performed by Aquino et al.,60 in the geometries undergoing the umbrella motion, the distance between adjacent hydrogen atoms, dHH, and the fraction dHH/dNH, where dNH is the bond distance, follow a nearly perfect linear relation, given by 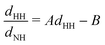 , where A = 0.6221 a.u. and B = 0.3153, with a regression coefficient of R2 = 0.9998. Therefore, the umbrella mode can be simplified as:
, where A = 0.6221 a.u. and B = 0.3153, with a regression coefficient of R2 = 0.9998. Therefore, the umbrella mode can be simplified as: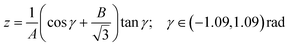 | (1) |
The potential energy curves of umbrella mode were then calculated for the electronic ground states of both NH3 and NH3+, using geometries implicitly given by eqn (1) as a function of z, and they are shown in Fig. 1 (left). In this figure, we also plot the lowest vibrational states for the neutral molecule and the cation, whose eigenenergies and eigenfuctions have been calculated by solving the one-dimensional time-independent Schrödinger equation (TISE) (see ref. 61):
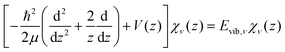 | (2) |
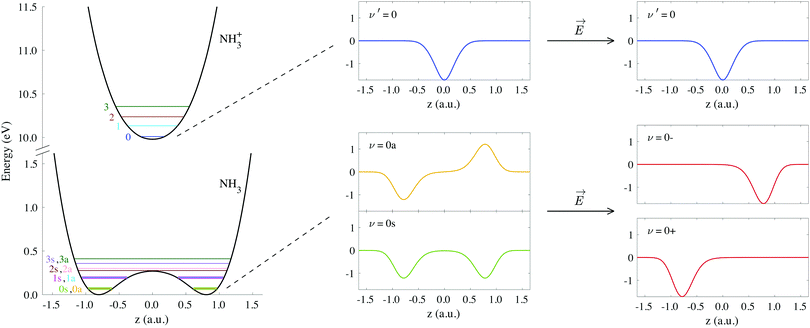 | ||
| Fig. 1 Potential curves corresponding to the umbrella mode of vibration for both the neutral NH3 and the cation NH3+ in their electronic ground states. Horizontal lines on these curves indicate the energies of the first vibrational wave functions. We also include the explicit form of the wave functions labeled as ν′ = 0, ν = 0s and ν = 0a, as well as the coherent superpositions of the last two, ν = 0− and ν = 0+ (see eqn (3)). | ||
As a consequence of the double-well potential of neutral ammonia's ground state (with two minima at the equilibrium geometries), the corresponding vibrational levels are grouped in quasi-degenerate pairs of symmetric and antisymmetric wave functions.41 The small energy gap in a given pair results from tunneling splitting, and thus increases with the vibrational quantum number. The two states of lowest energy are commonly labeled as 0s (symmetric) and 0a (antisymmetric) and describe the molecule being equally probable in both equilibrium geometries, delocalized over the two minima (see Fig. 1). The lowest value for the tunneling splitting is thus associated to the lowest levels with an energy difference of ≃0.1 meV (≃40 ps). These are thus the only and equally populated states at room temperature in the Boltzman's distribution, but cannot be distinguished in standard photoelectron spectroscopy due to energy resolution. The only technique than can achieve such a resolution is the threshold method known as ZEKE,63–65 which precludes the measurement of angular information.54,57 At room temperature, thus, the initial condition is defined by the incoherent mixture of the 0s and 0a states. Following Bolzmann's distribution, the lowest 0s state can only be significantly isolated from 0a for a sample's temperature below 0.5 K.
When the molecules are oriented by the presence of a weak external field, the initial state will be approximately described by the coherent superposition of 0a and 0s states:
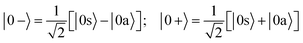 | (3) |
2.2 Differential cross section
We evaluate the vibrationally resolved differential cross sections in the molecular frame (MF), centered in the N atom. The z axis is placed along the molecule's C3 axis, which is also the direction of the molecule's dipole moment, and the x axis follows the azimuthal direction along one of the N–H bonds. The electronic structure for the bound and continuum electronic states are computed using the static exchange DFT method described in detailed in previous works,66–69 incorporating a one-dimensional description of the vibrational structure16,70,71 within the Born–Oppenheimer approximation. In the following, we briefly describe the most relevant methodological aspects for the present study. All expressions use atomic units, unless otherwise indicated.The wave function of the final electronic continuum state with momentum ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) is expressed in terms of a N-centered partial wave expansion:
is expressed in terms of a N-centered partial wave expansion:
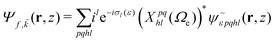 | (4) |
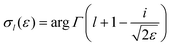 | (5) |
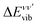 :
: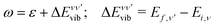 | (6) |
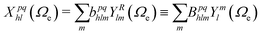 | (7) |
The vibrationally resolved photoionization amplitudes are then evaluated to first order of perturbation theory within the Born–Oppenheimer and dipole approximations. In the length gauge, they can be expressed as:
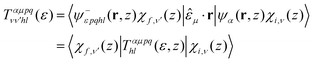 | (8) |
![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) μ denotes the electric field's polarization vector. The dipole matrix elements Tαμpqhl(ε, z) for each partial wave are thus evaluated as a function of the photoelectron energy and the inversion coordinate z. In the multicenter B-spline static-exchange DFT method,67,68,72,73 bound and continuum electronic states are written as Slater determinants of Kohn–Sham orbitals. For the present study, we perform a standard LCAO-DFT calculation (LCAO stands for linear combination of atomic orbitals) for the ground state of the molecule by using the program ADF (Amsterdam Density Functional),74 with a double zeta plus polarization basis set centered on each atom and a LB94 functional to describe exchange and correlation effects. The resulting ground state density is then used to build the Hamiltonian matrix in a new basis set of B-spline functions and real spherical harmonics. The Kohn–Sham orbitals are then written as an expansion over several centres: the centre of the molecule and the positions occupied by the nuclei (the N atom and the three equivalent hydrogens, in the present case). The orbitals associated with continuum states are obtained by block inverse iteration of the Kohn–Sham Hamiltonian on a previously defined energy grid.
μ denotes the electric field's polarization vector. The dipole matrix elements Tαμpqhl(ε, z) for each partial wave are thus evaluated as a function of the photoelectron energy and the inversion coordinate z. In the multicenter B-spline static-exchange DFT method,67,68,72,73 bound and continuum electronic states are written as Slater determinants of Kohn–Sham orbitals. For the present study, we perform a standard LCAO-DFT calculation (LCAO stands for linear combination of atomic orbitals) for the ground state of the molecule by using the program ADF (Amsterdam Density Functional),74 with a double zeta plus polarization basis set centered on each atom and a LB94 functional to describe exchange and correlation effects. The resulting ground state density is then used to build the Hamiltonian matrix in a new basis set of B-spline functions and real spherical harmonics. The Kohn–Sham orbitals are then written as an expansion over several centres: the centre of the molecule and the positions occupied by the nuclei (the N atom and the three equivalent hydrogens, in the present case). The orbitals associated with continuum states are obtained by block inverse iteration of the Kohn–Sham Hamiltonian on a previously defined energy grid.
Using expression (8), one can then evaluate the vibrationally resolved MFPADs, for an electron emission within the solid angle dΩe, and from a molecule with fixed orientation in space dΩM:
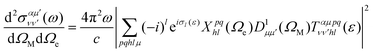 | (9) |
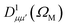 is a Wigner rotation matrix and μ′ denotes the electric field's polarization in the laboratory frame (LF): 0 for linear polarization along the z axis of the LF (that is what we will consider in this paper) and ±1 for circular polarization (right or left-handed). Put in simple terms, the MFPAD represents the probability distribution of the photoelectron being ejected in a certain direction with respect to the polarization direction for a given molecular orientation. As eqn (4), (7) and (9) show, they include contributions from different spherical harmonics (with different l's and m's) in the N-centered partial wave expansion of the final continuum state.
is a Wigner rotation matrix and μ′ denotes the electric field's polarization in the laboratory frame (LF): 0 for linear polarization along the z axis of the LF (that is what we will consider in this paper) and ±1 for circular polarization (right or left-handed). Put in simple terms, the MFPAD represents the probability distribution of the photoelectron being ejected in a certain direction with respect to the polarization direction for a given molecular orientation. As eqn (4), (7) and (9) show, they include contributions from different spherical harmonics (with different l's and m's) in the N-centered partial wave expansion of the final continuum state.
For randomly oriented molecules, one has to transform eqn (9) into the LF and then average over the solid angle dΩM. The resulting vibrationally resolved differential cross section only depends on the polar angle 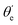 between the photoelectron emission direction and the z axis in the LF, so there is symmetry over the azimuthal angle
between the photoelectron emission direction and the z axis in the LF, so there is symmetry over the azimuthal angle 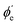 . Also, assuming μ′ = 0, this dependence on
. Also, assuming μ′ = 0, this dependence on 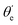 can be expressed in terms of the Legendre polynomial
can be expressed in terms of the Legendre polynomial 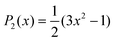 , in the following way:
, in the following way:
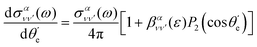 | (10) |
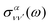 is the vibrationally resolved integrated cross section, given by
is the vibrationally resolved integrated cross section, given by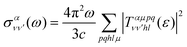 | (11) |
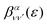 is the so-called beta asymmetry parameter, which can be expressed as (see ref. 61, 75 and 76 for details):
is the so-called beta asymmetry parameter, which can be expressed as (see ref. 61, 75 and 76 for details):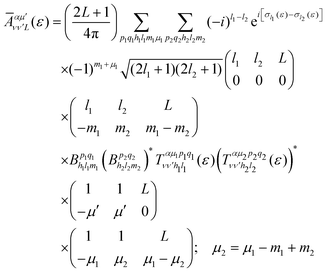 | (12) |
The total photoionization cross section is given by the sum over the final vibrational states ν′ (integral for dissociative states):
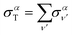 | (13) |
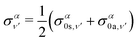 | (14) |
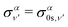 | (15) |
Similarly, the angle-differential cross section given by eqn (10), can be summed (integrated) over the final vibrational states to define a β parameter given by:
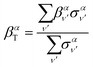 | (16) |
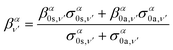 | (17) |
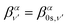 | (18) |
Finally, it is also useful to define the relative intensity of each vibrational transition, for a given initial state, as the quotient between the vibrationally resolved and the total cross sections:
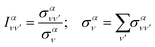 | (19) |
In the following, we first present the total cross sections, as well as the vibrationally resolved photoelectron spectra, and compare with existing experimental data. We then present a systematic analysis on the photoelectron angular distributions at different temperatures and molecular orientations.
3 Results and discussion
3.1 Comparison with experimental results
We first obtain the total photoionization cross section (eqn (13) and (14)), i.e., integrated over vibrational states, and compare it with the available experimental data from Brion et al.78 and Banna et al.79 This comparison is shown in Fig. 2a and we obtain a reasonable agreement. We also include the theoretical results obtained within the fixed nuclei approximation by Stener et al., employing the same static exchange Kohn–Sham DFT method as in the present work (labeled as KS) and the more advanced linear-response time-dependent DFT (TDDFT) methodology that partly accounts for interchannel couplings. As expected for a smooth molecular potential and in the absence of highly excited states resonances, the total cross sections for one-photon absorption are fairly well described already in the fixed nuclei approximation.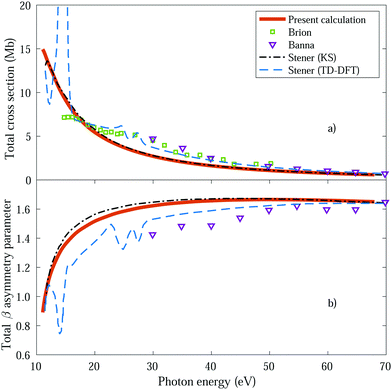 | ||
| Fig. 2 Total cross section (panel a) and total β asymmetry parameter (panel b), obtained for ammonia's valence shell and compared with experimental data from Brion et al.78 and Banna et al.,79 as well as with theoretical data from Stener et al.66 | ||
We further extract and compare the β parameter (eqn (16) and (17)), for which, again, the fixed nuclei approximation yields very similar results, as it is shown in Fig. 2b. We observe a deviation from the experimental results, which are only available for the larger photon energies (above 30 eV), although still present a reasonable agreement.
We then calculate the vibrationally resolved photoelectron spectra (eqn (19)) for a photon energy of 21.22 eV to compare with the available vibrationally resolved experimental data by Edvardsson et al.53 It corresponds to the vibrational progression of the 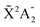 cationic state, depicted in Fig. 3a, after ionization from the 3a1 HOMO orbital. As shown in Fig. 3a, we obtain a very good agreement with the experimental photoelectron spectrum. Our theoretical data yields almost exactly the intensities for every peak, but for a slight deviation at lower energies. We obtain an energy for the lowest transition (0–0) of 9.94 eV, in a reasonable agreement with the experimental value (10.07 eV);53 and an energy spacing between consecutive absorption lines which also closely follows the experimental one. In panels b and c of Fig. 3, we also show the ionization probabilities associated to antisymmetric (0a) and symmetric (0s) initial states. The assignment of each peak in the vibrational progression also agrees with previous works,52,80–82 with the maximum intensity being associated to the 0–7 transition, dominated by the antisymmetric initial state.
cationic state, depicted in Fig. 3a, after ionization from the 3a1 HOMO orbital. As shown in Fig. 3a, we obtain a very good agreement with the experimental photoelectron spectrum. Our theoretical data yields almost exactly the intensities for every peak, but for a slight deviation at lower energies. We obtain an energy for the lowest transition (0–0) of 9.94 eV, in a reasonable agreement with the experimental value (10.07 eV);53 and an energy spacing between consecutive absorption lines which also closely follows the experimental one. In panels b and c of Fig. 3, we also show the ionization probabilities associated to antisymmetric (0a) and symmetric (0s) initial states. The assignment of each peak in the vibrational progression also agrees with previous works,52,80–82 with the maximum intensity being associated to the 0–7 transition, dominated by the antisymmetric initial state.
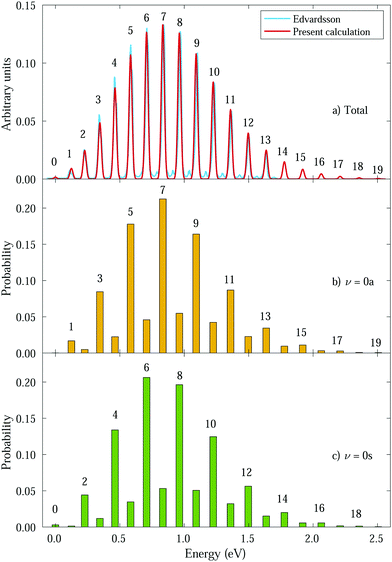 | ||
| Fig. 3 Photoelectron spectra from ammonia's valence shell for different initial vibrational states. Intensities were calculated for a photon energy ω = 21.22 eV.53 Horizontal axes represent the binding energy relative to the 0–0 peak and the numbers above the peaks correspond to ν′. Panel a shows the total spectrum (average of 0s and 0a intensities) compared to the experimental one from Edvardsson et al.53 Our calculated peaks were convoluted with gaussians (red curve) for comparison purposes. Panels b and c show the transition probabilities from 0a and 0s initial states, respectively, with ν′ indicated for favored transitions. | ||
As can be expected, the photoelectron spectrum for ammonia's outer band could already be predicted, to a given extent, by the Frank–Condon (F–C) overlaps, which, in this particular case, give almost the same relative peak intensities as those presented in Fig. 3a, where the variation of the transition dipole moment with the nuclear degrees of freedom is properly accounted for (eqn (8)). However, while the total photoelectron spectra can be predicted overall by the F–C overlaps, it fails to reproduce the separate contributions from the 0s and 0a states. The F–C approximation only allows for transitions between vibrational states with the same parity, i.e., from 0s to symmetric states (ν′ even) and from 0a to antisymmetric states (ν′ odd), and predicts zero intensities for all other transitions. However, these transitions between vibrational states with different parity are not forbidden, they are just less probable and have smaller intensities due to the smaller couplings. As a result, for every vibrational line, both the 0s and 0a states contribute (see Fig. 3b and c). We will then refer to F–C allowed transitions as “favored” ones (with no parity change) and F–C forbidden transitions as “non-favored” ones (with parity change).
In the following, we discuss the angle- and energy-differential (vibrational and electronic) photoionization cross sections for two different temperature regimes: room temperature, for which there are the same amount of molecules in the 0s and 0a initial states, and temperatures below 0.5 K (ultracold regime), for which there are molecules only in the 0s state. In each regime, we obtain the angular distributions that would be observed for aligned, oriented and randomly oriented molecules. For aligned molecules, the dipole moment is set in a given direction, specifically, along the C3 axis, and it can have a positive or negative value. For the oriented molecules, the sign of the dipole moment is also fixed. Alignment can be experimentally achieved, for instance, with non-ionizing laser pulses. But molecular orientation further requires an external field, usually a weak static electric field,18–20 which, for ammonia, would break the symmetry of the molecular potential with respect to the planar configuration in the inversion coordinate z, leading to a localization of the wave function in one of the wells.
3.2 Molecules at room temperature
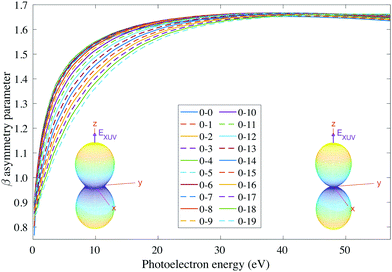
The thermal energy at room temperature is orders of magnitude larger than the energy gap between the v = 0s and 0a states (0.1 meV), but significantly smaller than the energy difference between the 0s and 1s (or 0a and 1a) vibrational states (∼125 meV). Consequently, the initial vibrational distribution at room temperature is given by the incoherent mixture of the 0s and 0a ground states. It should be noted that the photoelectron spectra and total photoionization cross sections shown in Fig. 3a and 2a are identical whether we consider the incoherent mixture or the coherent superposition of states 0s and 0a as an initial condition. However, as it is expected, these different scenarios lead to quite different photoelectron angular distributions.We first explore the scenario of randomly oriented molecules at room temperature. The vibrationally resolved photoelectron spectrum for a given photon energy (21.22 eV) was already shown in Fig. 3a. However, the variation of this signal with photon energy is captured in Fig. 4. In Fig. 4, we plot the photoionization cross section for each final vibrational state of the cation (labeled from 0 to 19) as a function of the photon energy (eqn (11) and (14)). For the sake of clarity, we use dashed lines for the vibrational cross sections where the dominant contribution comes from the antisymmetric state (0a) and full lines for those dominated by the symmetric one (0s), although as explained above and depicted in panels b and c in Fig. 3, both contribute. For every photon energy, the 0–7 transition presents the largest signal, as was also predicted by the F–C overlap.
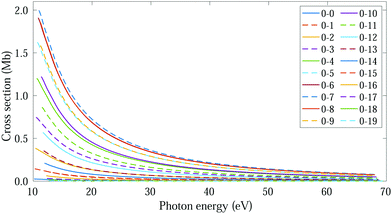 | ||
| Fig. 4 Vibrationally resolved cross sections for measurements at room temperature and ammonia's valence shell. | ||
We then examine the angle- and energy-dependent cross sections, given by eqn (10), i.e., we incoherently add the contribution from the initial 0s and 0a states, respectively. The angular distribution is determined by the β asymmetry parameter given by eqn (12) and (17). As we can see in Fig. 5, all β parameters present a similar qualitative behavior, therefore, also similar to the vibrationally-integrated β value shown in Fig. 2b. One can see, however, a gradual variation of β with respect to the final state along the vibrational progression. This dependence on ν′ is specially noticeable in the energy range ε = 5–15 eV, with no particular difference between even and odd final states. For a better visualization of the physical meaning of the β parameter variation, we also plotted as insets in Fig. 5, the corresponding angular distributions for a given vibrational state (ν′ = 15) at two different photoelectron energies (2 and 50 eV). We can see that they are almost identical, except for a slight variation with an increased probability of photoelectron emission along the plane given by the planar structure of the molecule for the lowest photoelectron energy.
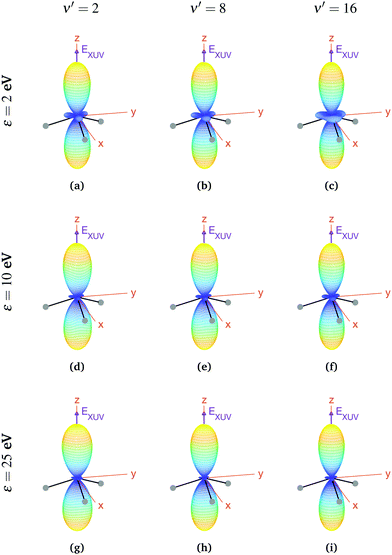
We now explore photoionization of aligned molecules at room temperature, for which the total MFPADs are given by the incoherent sum of the MFPADs (eqn (9)) corresponding to 0s and 0a. These MFPADs are plotted in Fig. 6 for different final vibrational states of the  band and different photoelectron energies. We have chosen one of the lowest (ν′ = 1) and one of the highest (ν′ = 15) vibrational states with a non-negligible ionization probability (see Fig. 3), and the one with the largest F–C overlap (ν′ = 7).
band and different photoelectron energies. We have chosen one of the lowest (ν′ = 1) and one of the highest (ν′ = 15) vibrational states with a non-negligible ionization probability (see Fig. 3), and the one with the largest F–C overlap (ν′ = 7).
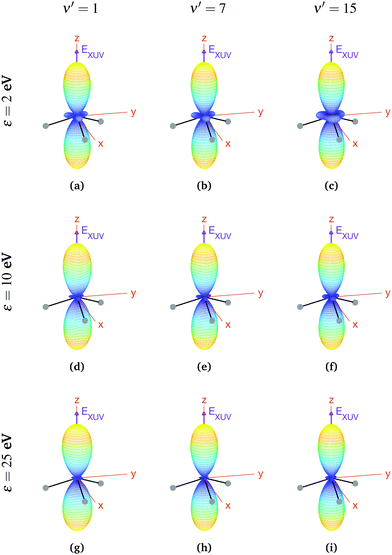 | ||
| Fig. 6 Vibrationally resolved MFPADs for aligned molecules at room temperature, ammonia's valence shell and an ionizing pulse linearly polarized in the z axis of the MF. All MFPADs are renormalized, the real scale can be seen approximately in Fig. 4. | ||
In every subplot of Fig. 6, the polarization direction of the ionizing laser pulse (EXUV) is indicated by a violet arrow, together with the molecular frame axes. We also depict the three hydrogen atoms in one of its equilibrium geometries (although notice that there is the same probability of finding them on both sides of the xy plane, because of the delocalized nature of the initial state). Note that the LF axes are the same as the MF ones as a consequence of the laser orientation we have chosen.
As we can see, all MFPADs in Fig. 6 present two symmetrical lobes in the ±z directions, following the polarization direction of the laser pulse. These lobes are symmetric with respect to the xy plane, which is what one could expect as it reflects the fact that the probability for photoelectron emission is the same in +z and −z directions as a consequence of the symmetry of 0s and 0a states. These lobes are, however, significantly “thinner” than those obtained in the case of randomly oriented molecules (see Fig. 5), i.e., there is a larger probability closer to the light polarization axis. One of the main observations to be retrieved from Fig. 6 is the tiny variation of these MFPADs with respect to the final state of the cation, slightly more visible for the lowest photoelectron energies (upper row in the figure). Although, not shown here, we did not find any significant difference between even and odd final states either. The variation with the photoelectron energy is also hardly visible (apart from, obviously, the absolute value of the MFPADs, which decreases with photoelectron energy), except for the three small lobes located at z = 0 that follow the azimuthal angles of the N–H bonds, which have a decreasing probability as the electron energy increases. This trend is also followed at larger photoelectron energies (ε > 25 eV), although not shown here.
In the case of oriented molecules, the initial state is described by a wave function well localized in one of the wells with respect to the inversion coordinate z, i.e., the initial state is a coherent superposition of 0s and 0a, i.e., 0− or 0+ (see eqn (3)). As discussed above, orientation can be achieved by applying a weak static electric field, which effectively breaks the quasi-degeneracy of 0s and 0a states. It thus leads to new eigenstates (0− and 0+), with an energy difference83 that, depending on the strength of the applied field, can be larger than the thermal energy, so that the molecules will be confined in one side of the vibrational potential. The vibrational wave functions for these localized 0− and 0+ states are shown in Fig. 1. It is important to remark that, in the presence of the electric field, the molecules will always remain in the same 0− or 0+ state as long as the field-induced splitting is larger than the field-free tunneling splitting of the state. Assuming that all the molecules are oriented, for example, with their dipole moment fixed in the −z direction, we calculate the MFPADs using eqn (9) and taking 0+ as the initial vibrational state (the outcome would be the same taking the 0− state, but with the MFPADs inverted with respect to the xy plane). The MFPADs for oriented molecules at room temperature are shown in Fig. 7, again for different final states and photoelectron energies. As in the previous figures, every subplot shows the polarization direction of the ionizing field (EXUV), the axes of the MF and the molecule's orientation in the equilibrium geometry, although in this case, it actually corresponds to the geometry given by the potential's well where it is localized. As we can see in Fig. 7, there are some important differences with respect to the previous cases, randomly oriented or aligned molecules. The obvious one is that, by fixing the orientation of the molecule, one breaks the symmetry with respect to the xy plane. Now the two principal lobes are no longer the specular image of each other. In fact, they can be remarkably asymmetric for specific final vibrational states. This asymmetry is mostly due to the differences in the electronic potential along the two oposite directions.
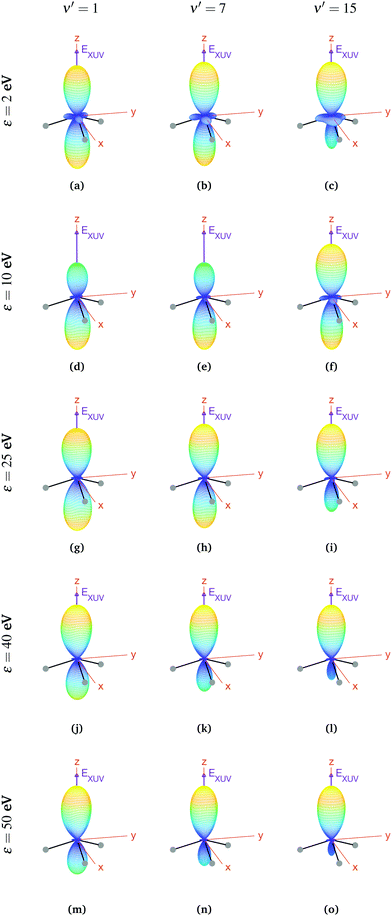 | ||
| Fig. 7 Vibrationally resolved MFPADs for oriented molecules (in 0+ initial state) at room temperature, ammonia's valence shell and an ionizing pulse linearly polarized in the z axis of the MF. All MFPADs are renormalized, the real scale can be seen approximately in Fig. 4. | ||
In a first inspection of Fig. 7, we can see that, for the higher photoelectron energies (ε > 25 eV), there is a general trend where the larger the photoelectron energy the larger the asymmetry of the photoelectron emission with respect to the plane perpendicular to the light polarization. More interestingly, one can observe that, at these photoelectron energies, the higher the final vibrational state the more asymmetric the photoelectron emission. However, at lower photoelectron energies, these trends are not so clear. For instance, for the lowest final vibrational level plotted in the figure, ν′ = 1, we observe that, for the lowest photoelectron energy, the two lobes are quite similar. However, as the electron energy increases up to ε = 10 eV, the top lobe decreases, before increasing again at higher energies, ε = 25 eV. The bottom lobe, however, remains equally probable for every electron energy and only decreases at higher energies, ε = 40 eV. In contrast, for the highest vibrational state, ν′ = 15, the top lobe dominates at the lower energies, ε = 2 eV, then both lobes become similar as the energy increases up to ε = 10 eV (although the top one is still thicker), and finally the bottom lobe starts decreasing from ε = 25 eV, although it does it faster than for ν′ = 1 and it practically disappears for ε = 50 eV. This indicates that the electron emission is more favorable in the direction opposite to the position of the H atoms, at least for the higher energies.
3.3 Molecules at ultracold temperatures
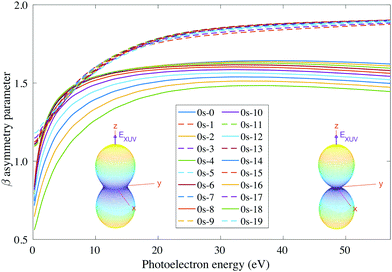
In this regime (<0.5 K), there are only molecules in the 0s initial state, so the photoelectron spectrum corresponds to the one presented in Fig. 3c, where there is a remarkable different signal for the favored (even) and non-favored (odd) transitions. This strong variation is also imprinted in the integrated cross sections, calculated with eqn (11), as they present larger maximum values for the even final states (see Fig. 8).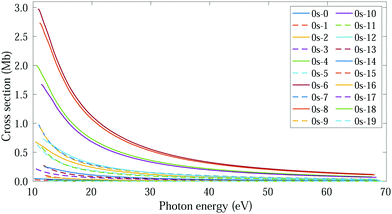 | ||
| Fig. 8 Vibrationally resolved cross sections for measurements in the ultracold regime (0s initial state) and ammonia's valence shell. | ||
For consistency, we will again perform a systematic study for randomly oriented, aligned and oriented molecules. First of all, for randomly oriented molecules, the β parameter (calculated with eqn (12) only for 0s) is quite different depending on the parity of the final vibrational state. As we can see in Fig. 9, there are two different branches: the top one corresponding to odd final vibrational states (non-favored transitions) and the bottom one corresponding to even final vibrational states (favored transitions). There is also a gradual variation of β with ν′ in the bottom branch for all studied energies, while in the top one β is practically the same for all odd values of ν′.
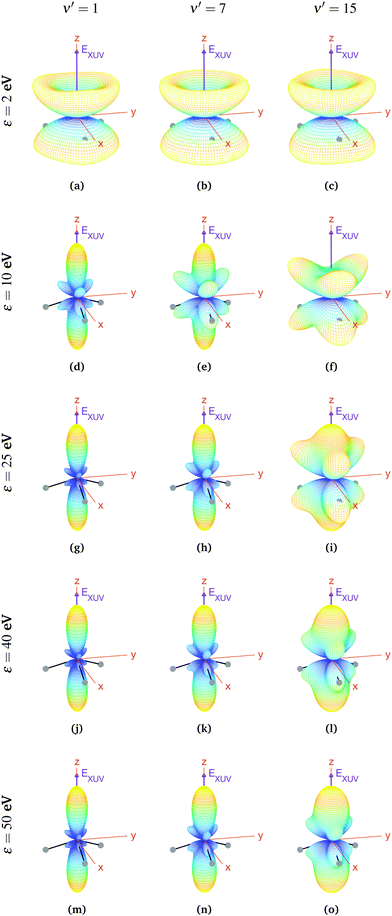
For aligned molecules at ultracold temperature, we can calculate the MFPADs using eqn (9) only for 0s. We present them for different photoelectron energies and final states in Fig. 10 (for ν′ even) and 11 (for ν′ odd). We have chosen the same final states as before (odd) and the ones immediately above (even). Also, in every panel of Fig. 10 and 11, we have indicated the polarization direction of the ionizing laser pulse (EXUV), as well as the axes of the MF and the molecule's orientation in one of its equilibrium geometries (although there is the same probability of finding it in both of them because it is delocalized over the two). As we can see, the MFPADs are symmetric with respect to the xy plane for all final states, again as a consequence of the symmetry of the 0s state. But, in contrast with the room temperature case (Fig. 6), in the ultracold regime there is a large difference between even and odd final states, i.e., between favored and non-favored transitions. For instance, the MFPADs for even final states are very similar to those obtained at room temperature for all final states (both even and odd), but the MFPADs for odd final states are really different. This is because, when we take the incoherent sum of 0s and 0a, favored transitions always weight much more than non-favored ones. This fact can be also seen in Fig. 3b and c, although in MFPADs the differences are much more apparent. Also, the shapes of all the MFPADs for favored transitions are almost the same, both for transitions from 0s to even states and from 0a to odd states. The MFPADs for favored transitions is what we mostly see at room temperature, but when only the 0s initial state is populated, we can also see the MFPADs for non-favored transitions (which by the way would be almost identical to the transitions from 0a to even states).
The favored even transitions shown in Fig. 10 are very similar to those already discussed for aligned molecules at room temperature (Fig. 6). We focus now on the non-favored transitions presented in Fig. 11. As we can see in that figure, for ε = 2 eV the probability of the photoelectron being ejected in the z direction is almost zero, in contrast with all the MFPADs discussed till now, and the corresponding angular distribution has a shape similar to that of a diabolo. This shape changes with the energy. As the latter increases up to ε = 10 eV, six prominent lobes whose azimuthal angles coincide with the positions of the H atoms emerge (three above and the other three below the xy plane). These lobes clearly reflect the bi-pyramidal geometry of the ammonia molecule associated with the two wells of the vibrational potential. At higher energies, two additional lobes develop symmetrically in the ±z directions, finally overcoming the former six lobes at around ε = 50 eV. One can also see a significant change over the final odd states of the vibrational progression. For example, if we look at the MFPADs for ν′ = 15, the already discussed change with the energy occurs much more slowly than for ν′ = 1, and also the main lobes in the ±z directions remain always thicker.
Finally, if one was able to orientate the ammonia molecules at ultracold temperatures with a weak external field that induces a Stark shift larger than the tunneling splitting in the absence of that field, the lowest vibrational state will be localized in one of the wells of the light-induced potential, which will be close to the 0− or the 0+ states given in eqn (3) depending on the field direction. Therefore, the resulting MFPADs would be identical to those already discussed for the case of oriented molecules at room temperature.
4 Summary and conclusions
We have applied the static-exchange DFT method to evaluate vibrationally resolved photoelectron angular distributions resulting from ionization of the 3a1 HOMO orbital of ammonia in both laboratory and molecular frames, in the photon energy range up to 70 eV. We have considered the two extreme cases corresponding to perfectly delocalized and perfectly localized initial vibrational states in the umbrella mode, and molecules whose C3 symmetry axis is parallel to the light polarization direction. The calculated angle-integrated cross sections and β asymmetry parameters (without vibrational resolution), as well as the angle-integrated vibrationally resolved photoelectron spectrum, are in good agreement with the experimental results available in the literature, showing the appropriateness of the theoretical approach. More importantly, we have found that, at room temperature, the vibrationally-resolved MFPADs for NH3 molecules aligned along the polarization direction, for which there are no experimental results reported in the literature, are perfectly symmetric with respect to the plane containing the planar D3h transition state, exhibiting symmetric, nearly perfect two-lobe shapes in the whole range of investigated photoelectron energies. In contrast, the MFPADs for oriented molecules, i.e., for molecules where the N vertex of all pyramidal structures point to the same direction, are in general asymmetric and the degree of asymmetry changes with photoelectron energy. Finally, we have also predicted that, at ultracold temperatures, where all aligned molecules initially lie in the ground vibrational state, which is perfectly symmetric for the umbrella mode, the MFPADs are symmetric again, but the two-lobe shape should only be observed when the final vibrational state of the resulting NH3+ cation has even parity. When the final vibrational state has odd parity, the MFPADs are much more involved and at photoelectron energies of ∼10 eV they directly reflect the bi-pyramidal geometry of the molecule in its ground vibrational state. These results suggest that, in order to obtain structural information from MFPADs in ammonia and likely in other molecules containing a similar double-well potential, one could preferably work at very low temperatures, which is not the case for most molecules studied so far.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
Calculations were performed at the Mare Nostrum Supercomputer of the Spanish Supercomputing Network (BSC-RES) and the Centro de Computación Científica de la Universidad Autónoma de Madrid (CCC-UAM). Work supported by the European COST Action AttoChem CA18222, the Spanish Ministry of Science and Innovation MICIN through the projects PDI2019-105458RB-I00, the “Severo Ochoa” Programme for Centres of Excellence in R&D (SEV-2016-0686) and the “María de Maeztu” Programme for Units of Excellence in R&D (CEX2018-000805-M), and the Comunidad de Madrid project FULMATEN (Y2018/NMT-5028).References
- M. Patanen, K. Kooser, L. Argenti, D. Ayuso, M. Kimura, S. Mondal, E. Plésiat, A. Palacios, K. Sakai and O. Travnikova, et al. , J. Phys. B: At., Mol. Opt. Phys., 2014, 47, 124032 CrossRef.
- A. Hitchcock and C. Brion, J. Electron Spectrosc. Relat. Phenom., 1978, 14, 417–441 CrossRef CAS.
- B. Yang, J. Kirz and T. Sham, Phys. Rev. A: At., Mol., Opt. Phys., 1987, 36, 4298 CrossRef CAS PubMed.
- J. Stöhr and K. Bauchspiess, Phys. Rev. Lett., 1991, 67, 3376 CrossRef PubMed.
- A. Landers, T. Weber, I. Ali, A. Cassimi, M. Hattass, O. Jagutzki, A. Nauert, T. Osipov, A. Staudte and M. Prior, et al. , Phys. Rev. Lett., 2001, 87, 013002 CrossRef CAS PubMed.
- B. Zimmermann, D. Rolles, B. Langer, R. Hentges, M. Braune, S. Cvejanovic, O. Geßner, F. Heiser, S. Korica and T. Lischke, et al. , Nat. Phys., 2008, 4, 649–655 Search PubMed.
- R. K. Kushawaha, M. Patanen, R. Guillemin, L. Journel, C. Miron, M. Simon, M. N. Piancastelli, C. Skates and P. Decleva, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 15201–15206 CrossRef CAS PubMed.
- A. Hitchcock and D. Mancini, J. Electron Spectrosc. Relat. Phenom., 1994, 67, 1–12 CrossRef CAS.
- S. Canton, E. Plésiat, J. Bozek, B. Rude, P. Decleva and F. Martin, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 7302–7306 CrossRef CAS.
- X. Liu, N. Cherepkov, S. Semenov, V. Kimberg, F. Gel'mukhanov, G. Prümper, T. Lischke, T. Tanaka, M. Hoshino and H. Tanaka, et al. , J. Phys. B: At., Mol. Opt. Phys., 2006, 39, 4801 CrossRef CAS.
- L. Argenti, T. D. Thomas, E. Plésiat, X. Liu, C. Miron, T. Lischke, G. Prümper, K. Sakai, T. Ouchi and R. Püttner, et al. , New J. Phys., 2012, 14, 033012 CrossRef.
- E. Plésiat, L. Argenti, E. Kukk, C. Miron, K. Ueda, P. Decleva and F. Martín, Phys. Rev. A: At., Mol., Opt. Phys., 2012, 85, 023409 CrossRef.
- S. Nandi, E. Plésiat, M. Patanen, C. Miron, J. D. Bozek, F. Martín, D. Toffoli and P. Decleva, Phys. Chem. Chem. Phys., 2016, 18, 3214–3222 RSC.
- S. Engin, J. González-Vázquez, G. G. Maliyar, A. R. Milosavljević, T. Ono, S. Nandi, D. Iablonskyi, K. Kooser, J. D. Bozek and P. Decleva, et al. , Struct. Dyn., 2019, 6, 054101 CrossRef PubMed.
- K. Amini and J. Biegert, in Advances In Atomic, Molecular, and Optical Physics, ed. L. F. Dimauro, H. Perrin and S. F. Yelin, Academic Press, 2020, vol. 69, pp. 163–231 Search PubMed.
- D. Ayuso, M. Kimura, K. Kooser, M. Patanen, E. Plésiat, L. Argenti, S. Mondal, O. Travnikova, K. Sakai, A. Palacios, E. Kukk, P. Decleva, K. Ueda, F. Martín and C. Miron, J. Phys. Chem. A, 2015, 119, 5971–5978 CrossRef CAS PubMed.
- J. J. Larsen, K. Hald, N. Bjerre, H. Stapelfeldt and T. Seideman, Phys. Rev. Lett., 2000, 85, 2470 CrossRef CAS PubMed.
- L. Holmegaard, J. L. Hansen, L. Kalhøj, S. L. Kragh, H. Stapelfeldt, F. Filsinger, J. Küpper, G. Meijer, D. Dimitrovski and M. Abu-Samha, et al. , Nat. Phys., 2010, 6, 428–432 Search PubMed.
- L. Holmegaard, J. H. Nielsen, I. Nevo, H. Stapelfeldt, F. Filsinger, J. Küpper and G. Meijer, Phys. Rev. Lett., 2009, 102, 023001 CrossRef PubMed.
- H. Stapelfeldt and T. Seideman, Rev. Mod. Phys., 2003, 75, 543 CrossRef CAS.
- R. Dörner, V. Mergel, O. Jagutzki, L. Spielberger, J. Ullrich, R. Moshammer and H. Schmidt-Böcking, Phys. Rep., 2000, 330, 95–192 CrossRef.
- J.-i. Adachi, K. Hosaka, S. Furuya, K. Soejima, M. Takahashi, A. Yagishita, S. Semenov and N. Cherepkov, Phys. Rev. Lett., 2003, 91, 163001 CrossRef CAS PubMed.
- J.-i. Adachi, M. Kazama, T. Teramoto, N. Miyauchi, T. Mizuno, M. Yamazaki, T. Fujikawa and A. Yagishita, J. Phys. B: At., Mol. Opt. Phys., 2012, 45, 194007 CrossRef.
- J. B. Williams, C. Trevisan, M. Schöffler, T. Jahnke, I. Bocharova, H. Kim, B. Ulrich, R. Wallauer, F. Sturm and T. Rescigno, et al. , Phys. Rev. Lett., 2012, 108, 233002 CrossRef CAS PubMed.
- J. Williams, C. Trevisan, M. Schöffler, T. Jahnke, I. Bocharova, H. Kim, B. Ulrich, R. Wallauer, F. Sturm and T. Rescigno, et al. , J. Phys. B: At., Mol. Opt. Phys., 2012, 45, 194003 CrossRef.
- P. Billaud, M. Geleoc, Y. Picard, K. Veyrinas, J.-F. Hergott, S. Marggi Poullain, P. Breger, T. Ruchon, M. Roulliay, F. Delmotte, F. Lepetit, A. Huetz, B. Carre and D. Dowek, J. Phys. B: At., Mol. Opt. Phys., 2012, 45, 194013 CrossRef.
- H. Köppe, A. Kilcoyne, J. Feldhaus and A. Bradshaw, J. Electron Spectrosc. Relat. Phenom., 1995, 75, 97–108 CrossRef.
- B. Kempgens, A. Kivimäki, M. Neeb, H. Köppe, A. M. Bradshaw and J. Feldhaus, J. Phys. B: At., Mol. Opt. Phys., 1996, 29, 5389 CrossRef CAS.
- S. Semenov, N. Cherepkov, A. De Fanis, Y. Tamenori, M. Kitajima, H. Tanaka and K. Ueda, Phys. Rev. A: At., Mol., Opt. Phys., 2004, 70, 052504 CrossRef.
- S. Semenov, N. Cherepkov, T. Jahnke and R. Dörner, J. Phys. B: At., Mol. Opt. Phys., 2004, 37, 1331 CrossRef CAS.
- R. Holmes and G. Marr, J. Phys. B: At. Mol. Phys., 1980, 13, 945 CrossRef CAS.
- M. Kazama, H. Shinotsuka, T. Fujikawa, M. Stener, P. Decleva, J.-I. Adachi, T. Mizuno and A. Yagishita, J. Electron Spectrosc. Relat. Phenom., 2012, 185, 535–545 CrossRef CAS.
- H. Fukuzawa, R. Lucchese, X.-J. Liu, K. Sakai, H. Iwayama, K. Nagaya, K. Kreidi, M. Schöffler, J. Harries, Y. Tamenori, Y. Morishita, I. Suzuki, N. Saito and K. Ueda, J. Chem. Phys., 2019, 150, 174306 CrossRef PubMed.
- M. Gregory, P. Hockett, A. Stolow and V. Makhija, J. Phys. B: At., Mol. Opt. Phys., 2021, 54, 145601 CrossRef CAS.
- C. Trevisan, C. McCurdy and T. Rescigno, J. Phys. B: At., Mol. Opt. Phys., 2012, 45, 194002 CrossRef.
- E. Plésiat, P. Decleva and F. Martín, Phys. Rev. A: At., Mol., Opt. Phys., 2013, 88, 063409 CrossRef.
- F. Ota, S. Abe, K. Hatada, K. Ueda, S. Daz-Tendero and F. Martín, Phys. Chem. Chem. Phys., 2021, 23, 20174–20182 RSC.
- J. Swalen and J. A. Ibers, J. Chem. Phys., 1962, 36, 1914–1918 CrossRef.
- S. A. Henck, M. A. Mason, W.-B. Yan, K. K. Lehmann and S. L. Coy, J. Chem. Phys., 1995, 102, 4783–4792 CrossRef CAS.
- D. Papoušek, J. Mol. Struct., 1983, 100, 179–198 CrossRef.
- A. Douglas and J. Hollas, Can. J. Phys., 1961, 39, 479–501 CrossRef CAS.
- D. M. Dennison and J. Hardy, Phys. Rev., 1932, 39, 938 CrossRef CAS.
- J. Förster and A. Saenz, ChemPhysChem, 2013, 14, 1438–1444 CrossRef PubMed.
- J. Förster, E. Plésiat, A. Magana and A. Saenz, Phys. Rev. A, 2016, 94, 043405 CrossRef.
- I. S. Ulusoy and M. Nest, J. Am. Chem. Soc., 2011, 133, 20230–20236 CrossRef CAS PubMed.
- F. Bouakline and J. C. Tremblay, Phys. Chem. Chem. Phys., 2020, 22, 15401–15412 RSC.
- F. Bouakline and P. Saalfrank, J. Chem. Phys., 2021, 154, 234305 CrossRef CAS PubMed.
- F. Bouakline, Phys. Chem. Chem. Phys., 2021, 23, 20509–20523 RSC.
- C.-D. Yang and S.-Y. Han, Int. J. Mol. Sci., 2021, 22, 8282 CrossRef CAS PubMed.
- J. Rabalais, L. Karlsson, L. Werme, T. Bergmark and K. Siegbahn, Chem. Phys., 1973, 58, 3370–3372 CAS.
- M. Banna and D. Shirley, J. Chem. Phys., 1975, 63, 4759–4766 CrossRef CAS.
- R. Locht, K. Hottmann, G. Hagenow, W. Denzer and H. Baumgartel, Chem. Phys. Lett., 1992, 190, 124–129 CrossRef CAS.
- D. Edvardsson, P. Baltzer, L. Karlsson, B. Wannberg, D. Holland, D. Shaw and E. Rennie, J. Phys. B: At., Mol. Opt. Phys., 1999, 32, 2583 CrossRef CAS.
- P. Hockett, M. Staniforth, K. Reid and D. Townsend, Phys. Rev. Lett., 2009, 102, 253002 CrossRef PubMed.
- P. Hockett, M. Staniforth and K. L. Reid, J. Phys. Chem. A, 2010, 114, 11330–11336 CrossRef CAS PubMed.
- P. Hockett, M. Staniforth and K. L. Reid, Mol. Phys., 2010, 108, 1045–1054 CrossRef CAS.
- D. Townsend and K. Reid, J. Chem. Phys., 2000, 112, 9783–9790 CrossRef CAS.
- A. Viel, W. Eisfeld, S. Neumann, W. Domcke and U. Manthe, J. Chem. Phys., 2006, 124, 214306 CrossRef PubMed.
- P. Limão-Vieira, N. Jones, S. Hoffmann, D. Duflot, M. Mendes, A. I. Lozano, F. Ferreira da Silva, G. Garcia, M. Hoshino and T. Tanaka, J. Chem. Phys., 2019, 151, 184302 CrossRef PubMed.
- N. Aquino, G. Campoy and H. Yee-Madeira, Chem. Phys. Lett., 1998, 296, 111–116 CrossRef CAS.
- E. Plésiat, P. Decleva and F. Martín, J. Phys. B: At., Mol. Opt. Phys., 2012, 45, 194008 CrossRef.
- B. Friedrich and D. Herschbach, J. Chem. Phys., 1999, 111, 6157–6160 CrossRef CAS.
- R. Seiler, U. Hollenstein, T. Softley and F. Merkt, J. Chem. Phys., 2003, 118, 10024–10033 CrossRef CAS.
- W. Habenicht, G. Reiser and K. Muller-Dethlefs, Chem. Phys., 1991, 95, 4809–4820 CAS.
- G. Reiser, W. Habenicht and K. Muller-Dethlefs, J. Chem. Phys., 1993, 98, 8462–8468 CrossRef CAS.
- M. Stener, G. Fronzoni, D. Toffoli and P. Decleva, Chem. Phys., 2002, 282, 337–351 CrossRef CAS.
- M. Stener, P. Decleva, I. Cacelli, R. Moccia and R. Montuoro, Chem. Phys., 2001, 272, 15–25 CrossRef CAS.
- M. Stener and P. Decleva, J. Chem. Phys., 2000, 112, 10871–10879 CrossRef CAS.
- A. Palacios and F. Martín, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2020, 10, e1430 CAS.
- D. Ayuso, A. Palacios, P. Decleva and F. Martín, J. Electron Spectrosc. Relat. Phenom., 2014, 195, 320–326 CrossRef CAS.
- E. Plésiat, M. Lara-Astiaso, P. Decleva, A. Palacios and F. Martín, Chem. – Eur. J., 2018, 24, 12061–12070 CrossRef PubMed.
- M. Stener, G. Alti and P. Decleva, Theor. Chim. Acta, 1999, 101, 247–256 CrossRef CAS.
- M. Stener, G. Fronzoni and P. Decleva, Chem. Phys. Lett., 2002, 351, 469–474 CrossRef CAS.
- G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967 CrossRef CAS.
- N. Chandra, Chem. Phys., 1986, 108, 301–315 CrossRef CAS.
- N. Chandra, J. Phys. B: At. Mol. Phys., 1999, 20, 3405 CrossRef.
- H. T. Johansson and C. Forssén, SIAM J. Sci. Comput., 2016, 38, A376–A384 CrossRef.
- C. Brion, A. Hamnett, G. Wight and M. Van der Wiel, J. Electron Spectrosc. Relat. Phenom., 1977, 12, 323–334 CrossRef CAS.
- M. S. Banna, H. Kossmann and V. Schmidt, Chem. Phys., 1987, 114, 157–163 CrossRef CAS.
- H. Ågren, I. Reineck, H. Veenhuizen, R. Maripuu, R. Arneberg and L. Karlsson, Mol. Phys., 1982, 45, 477–492 CrossRef.
- W. Domcke, L. Cederbaum, H. Köppel and W. Von Niessen, Mol. Phys., 1977, 34, 1759–1770 CrossRef CAS.
- A. Peluso, R. Borrelli and A. Capobianco, J. Phys. Chem. A, 2009, 113, 14831–14837 CrossRef CAS PubMed.
- B. Bertsche and A. Osterwalder, Phys. Rev. A: At., Mol., Opt. Phys., 2010, 82, 033418 CrossRef.
| This journal is © the Owner Societies 2022 |