 Open Access Article
Open Access ArticleLaMer's 1950 model of particle formation: a review and critical analysis of its classical nucleation and fluctuation theory basis, of competing models and mechanisms for phase-changes and particle formation, and then of its application to silver halide, semiconductor, metal, and metal-oxide nanoparticles†
Christopher B.
Whitehead
 a,
Saim
Özkar
a,
Saim
Özkar
 b and
Richard G.
Finke
b and
Richard G.
Finke
 *a
*a
aDepartment of Chemistry, Colorado State University, Fort Collins, CO 80523, USA. E-mail: Richard.Finke@colostate.edu
bDepartment of Chemistry, Middle East Technical University, 06800 Ankara, Turkey
First published on 23rd December 2020
Abstract
A review is presented of the pioneering 1950 model (V. K. LaMer, R. H. Dinegar, Theory, Production and Mechanism of Formation of Monodispersed Hydrosols, J. Am. Chem. Soc., 1950, 72, 4847–4854) of how monodisperse particles might possibly be formed. The review begins with a look at the basis of the 1950 model in fluctuation and classical nucleation theories. Presented next are the competing phase-change models and then also chemical mechanisms for particle formation available since the 1950 paper, including a little-cited nucleation mechanism that LaMer insightfully wrote in 1952. This review then takes a critical look at the 164 (∼8%) of the 192 total (∼10%) out of the 1953 papers (as of March 2019) that cite the 1950 model while also providing at least some discussion, analysis, or additional data bearing on the 1950 model postulating “effectively infinite nucleation” and “diffusion-controlled growth”. (The other 28 papers out of the 192 total papers describe Sn sol formation were covered in an earlier, Part I review that is cited.) Those 164 papers are broken down into five tables provided in the Supporting Information and are then covered in separate sections in the main text: first 13 papers on silver halide nanoparticles (Table S1) where the single best evidence in support of the 1950 model has been thought to exist; 26 papers on semiconductor nanoparticles (Table S2); then 69 papers on transition-metal nanoparticle formation (Table S3); 39 papers on oxide-based nanoparticles (Table S4); and 17 papers presenting alternative models or mechanisms in comparison to the 1950 model (Table S5). The review focuses on answering the critical question of: do the concepts of “burst/instantaneous nucleation” and “diffusion-controlled growth” have sound, compelling experimental support in the 70 years since the model first appeared and in the 164 papers examined more closely that do more than just cite the 1950 model? A Conclusions section listing sixteen bullet points is provided, as is a final section entitled “A Look Towards the Future” that discusses evolving areas and suggested emphasis points for facilitating future research in particle formation kinetics, mechanism and associated particle syntheses.
1. Introduction
Seventy years ago, LaMer and co-workers postulated a model1 for particle formation consisting of nucleation with an effectively infinite rate and then diffusion-controlled growth, a classic paper that has yielded over 1953 citations as of the time this review was constructed. As described in Fig. 1 on page 4847 of the 1950 paper, “The rate of nucleation, as judged by the reproducibility of the timing and the concentration of sulfur at which the system becomes heterogeneous, is so exceedingly sensitive to an increase in the concentration of dissolved sulfur that the rate becomes effectively infinite”.1 Hence the words used since then in many of the aforementioned total citations of the 1950 model of nucleation as “instantaneous” or “burst” are an accurate citation of the model in at least its most widely cited, schematic/qualitative form that is Fig. 1 of the classic 1950 paper.1 The significance of “instantaneous or burst” nucleation and continuing allure of the 1950 model seems clear: it at least previously (vide infra) was the only way to explain the formation of (near) “monodisperse” particles, the word monodisperse appearing in the title of the famous 1950 paper, “Theory, Production and Mechanism of Formation of Monodispersed Hydrosols”.1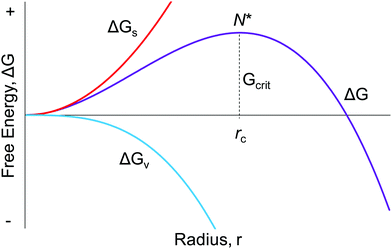 | ||
| Fig. 1 The classic, widely cited, free energy diagram of CNT9 in which ΔG for the particle formation is plotted against the radius, r, of the assumed spherical particle. Important variables in CNT are: ΔGs, the free energy of the particle's surface; ΔGv, the free energy of the bulk crystal; rc, the critical radius which is the minimum size required for the particle to form without being re-dissolved; and Gcrit, the maximum free energy of the particle that is the definition of the “critical radius”, N*. | ||
1.1. The Part I review
Recently, in our Part I review2 we provided 13 sections in a first attempt to begin to look critically and comprehensively at the extensive literature citing the 1950 model. More specifically, in our Part I review we started the effort needed to address the important question of what experimental evidence for that 1950 model has accumulated in 70 years and via 1953 papers citing the classic 1950 paper.1 Those 13 sections in our Part I review are: (i) the chemical origins of the 1950 model; (ii) the original sulfur hydrosol formation system; (iii) the often-cited schematic/qualitative, and then associated words-only descriptions of the 1950 model; (iv) the nine assumptions underlying the little employed quantitative mathematical model and associated equation in the 1950 paper; (v) the question of “Is LaMer's model actually a ‘growth model’”?; (vi) the actual quantitative equation in the 1950 paper—plus the question of when has it been used in the last 70 years to fit particle formation kinetics data?; (vii) the disconnect between the 1950 quantitative model and associated differential equation vs. any testing against experimental kinetics data; (viii) a look at the kinetics data for, and the current understanding of, the mechanism of sulfur sol formation; (ix) the 1926, first kinetics data for sulfur sol formation; (x) light scattering data for sulfur sol formation on which the 1950 model was originally founded; (xi) fitting of the 1926 kinetics data for sulfur sol formation by a minimalistic 2-step mechanism;3 (xii) the interesting effect of microfiltration and the removal of dust on the size distribution of sulfur sols; and then (xiii) a summary and conclusions section.2 Reading the Part I review prior to reading the present Part II review is recommended in order to fully understand what follows. That said, every attempt has been made to make the following, Part II review as self-contained as possible.1.2. The contents of the present, Part II review
What was not done in the Part I review,2 and hence is a focus of the present Part II review of the 1950 model, is to critically examine the remaining ∼8% of the 1953 citations (164 papers) that do more than merely cite the 1950 model (i.e., and which go beyond the 28 papers on Sn sol formation that gave rise to the 1950 model and are covered in our Part I review2). Any associated, relevant literature needed to understand and place in context those 164 papers is also presented. In particular, the present Part II review also looks at key theories that underlie the 1950 mathematical model and that were not presented in the Part I review, notably classical nucleation theory (CNT) and the related topic of fluctuation theory. Also examined are the other models and chemical mechanisms since 1950 available for interpreting particle formation and other phase-change kinetics and related data.Specifically then and to start, the relevant background materials are presented of (i) CNT and fluctuation theory, vide infra, (ii) LaMer's 1952 paper4 on nucleation in phase transitions, including his little-cited experimental investigations of BaSO4 formation, and (iii) Turkevich's groundbreaking 1951 and 1953 papers5,6 on the synthesis of gold colloids. The overarching goal of this Part II review is to collect and critically examine the experimental evidence gathered in the last 70 years that provides support for (or against) “instantaneous/burst” nucleation followed by “diffusion controlled” growth.
Our own interest in the experimental evidence for the 1950 model began in 19947 when we observed the reproducible formation of near-monodisperse (≤15% polydispersity) Ir(0)n nanoparticle formation.7 Those particles were remarkable at the time in that they disproved several myths: that one could not have a “colloid” outside of water solvent; that one could not have reproducible formation of a “colloidal”; and that no “colloid” could be isolated and bottled (i.e., that all “colloids” had a “critical colloid concentration” past which they could not be concentrated without aggregation).7 But even more intriguing to us was how could any such particle having anything like n = 300 to 900 Ir(0) atoms as in our Ir(0)n systems, and therefore mechanisms that had to have at least 300–900 steps (and likely several 1000s of steps), ever possible yield reproducible, near-monodisperse, particles? What is the mechanism(s) for such a complex, multistep particle formation process?
A search of the literature at the time (pre-1994)7 led to the 1950 model1 and its thermodynamically based, burst-nucleation and diffusion-controlled growth hypothesis for particle formation. Yet there were hints in the literature even then that the “burst nucleation” model might not be generally applicable, or perhaps not even correct. E. Matijević noted in his 1993 review describing his pioneering work on the “Preparation and Properties of Uniform Size Colloids” that “…the recognition of the limitations of the 1950 model came through a number of experimental findings that contradicted it.”8 In 1994 we noted for our Ir(0)n nanoparticle formation system that the nucleation and growth steps were “…much smoother and more continuous than the popular and often cited ‘burst’ nucleation phenomenon from a supersaturated solution associated with LaMer's mechanism.”7 Our 1994 paper7 contained a preliminary version of the disproof-based, deliberately minimalistic, pseudo-elementary 2-step mechanism for particle formation that we published in full form in 1997 composed of kinetically “continuous nucleation” plus “autocatalytic surface growth”.3 In that work we noted, at the time and in our opinion, that “LaMer's pioneering work” may have been “inappropriately cited”, a comment intended to note that any such incorrect citations were not 1950s author's fault but, instead, “a phenomenon which really only points to the dearth of new, broadly applicable and kinetically verified alternative mechanisms in the intervening nearly 50 years.”3
In the ensuing 23 years we continued to read the many papers citing the creative and pioneering 1950 work.1 The more we read, the more we became increasingly puzzled by continued, wide citation of the 1950 model despite the lack of experimental evidence, that at least we could find, in support of a particle formation model involving true instantaneous/burst nucleation followed by diffusion-controlled growth. Relevant here is this word version of the 1950 model often being cited as if it were compellingly documented, disproof-based, scientific fact. Several years back we decided it was finally time to put in the effort required to examine critically the 1953 available references we found (as of March 2019) that cited the classic 1950 paper. That exhaustive literature search revealed that it was especially important to focus on 164 papers we identified that did more than just cite the 1950 model in passing.
Hence, the present Part II review is the long-overdue, needed review and analysis of those 164 papers accomplished via an extensive (74 pages of) ESI,† 5 tables with individual assessments and summaries for each paper, and then the main text and discussion which follows. The attached 5 tables and ESI† are intended as an introductory resource that readers can refer to and use as desired. Moreover, the reader that wants to be driven to their own, independent conclusions about the 1950 model and where particle formation mechanisms and science stand can review those five tables carefully—indeed, we urge this self-study of the ESI† several times in the presentation and discussion that follows.
Our goal of this Part II review is not to support any specific model or mechanism, nor any of those listed in Tables 1 and 2 for instance, vide infra, especially since several of the mechanistic models are from our own work. Instead, our goal via our Part I and Part II reviews is to provide the community with the first comprehensive look at the burst nucleation and diffusion-controlled growth model with an emphasis on the experimental evidence testing it over the intervening 70 year period. We start by a short review of classical nucleation theory that underlies the 1950 model, and the related topic of fluctuation theory.
| Year | Person | Model | Resultant equation |
|---|---|---|---|
| 1939 | Avrami42–44 | Mathematical; semi-empirical | ln(1 − α) = −(kt)n |
| Equivalently, α(t) = 1 − exp{−[kt]n} | |||
| (Then Kolmogorov (1937), Johnson and Mehl (1939) (“KJMA”),45,46 Erofe’ev (1946)47) | |||
| [α = extent (fraction) of reaction; k = a rate parameter; n = the “Avrami exponent”] | |||
| 1950 | LaMer1 | Stat. mech; CNT (for Sn sol formation) |
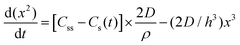
|
| [x = nucleus radius; ss = supersaturation; D = diffusion coefficient; ρ = (bulk) Sn density; h = sphere radius] | |||
| Word version: burst nucleation from supersaturated solution, then diffusion-controlled growth | |||
| 2017 | Martin (M-KJMA)49 | Mathematical; semi-empirical | α(t) = 1 − exp{−[kA(t − t0]n} |
[M stands for “Modified”; kA = rate parameter; n = Avrami exponent; kA is postulated to be composed of 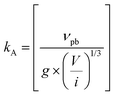 where νvp = velocity of the phase boundary; g = geometric factor; ac = anisotropy correction; n′ = anisotropy corrected dimensionality exponent; V = volume] where νvp = velocity of the phase boundary; g = geometric factor; ac = anisotropy correction; n′ = anisotropy corrected dimensionality exponent; V = volume] |
|||
| Year | Person(s) | Mechanism (A, B, and C formalism) | Mechanism (in words), and comments |
|---|---|---|---|
| 1952 | V. K. LaMer4 | mA1 ⇌ Bm | Stepwise bimolecular addition leading to “burst nucleation” (NB: “diffusion-controlled growth”1 was not included4 as part of the scheme provided) |
| Bm + A1 ⇌ Bm+1 | |||
| B(i−1) + A1 ⇌ Bi | |||
| [A1 = “kinetically independent unit of phase A′′, Bi = “embryo of phase B containing i units”, and “m is usually 2, whereas i in the case of water vapor condensation is about 80—i.e., this reaction is of the 80th order”]4 | |||
| 1953 | Turkevich,5,6 Stevenson, Hillier | No pseudo-elementary step mechanism was provided in ref. 5 or 6 | Turkevich's “organizer” hypothesis: nucleating agents form a chemical complex, organize macromolecularly, then undergo a molecular rearrangement to produce the metal nucleus, |
| 1997 | Finke, Watzky3 |

|
Slow, kinetically continuous nucleation followed by typically fast, explosive autocatalytic surface growth. Important to note is that higher order  nucleations are covered by (i.e., can be hidden in) the pseudo-elementary first step, as the subsequent discovery of second-order and termolecular nucleations demonstrates.17,26,27 nucleations are covered by (i.e., can be hidden in) the pseudo-elementary first step, as the subsequent discovery of second-order and termolecular nucleations demonstrates.17,26,27 |
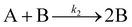
|
|||
| [A = metal precursor, B = growing, metal(0) particle] | |||
| 2004 | Hornstein, et al.55 |

|
Evidence for bimolecular agglomeration as a 3rd step added to the 1997 2-step mechanism |
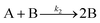
|
|||
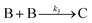
|
|||
| 2005 | Besson, Finney, et al.56–58 |

|
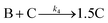
Evidence for a 4th step of autocatalytic agglomeration where the smaller particles, B, and larger particles, C, agglomerate with a separate, k4, rate constant |
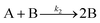
|
|||
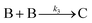
|
|||
|
|||
| [A = metal precursor, B = small particles, C = larger particles] | |||
| 2005 | Drew, Katsoulakis, Tsapatsis59 |

|
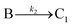
A proposed mechanism for crystal growth by aggregation of meta-stable nanoparticle precursors, one used with Population-Balance Modeling. Three alternative mechanisms were tested; shown is the author's preferred Mechanism II. |
|
|||
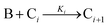
|
|||
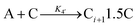
|
|||
| [A = primary colloidal particles; B = growing crystal; C1 = nucleated primary particles] | |||
| 2014 | Kent, Mondloch, et al.60 |

|
Evidence for a new 4th step of secondary autocatalytic growth where larger particles, C, growth with a separate, 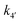 ’, rate constant. ’, rate constant. |
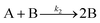
|
|||
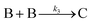
|
|||

|
|||
| [A = metal precursor, B = smaller particles, C = larger particles] | |||
| 2017 | Karim, et al.63 | A + L ⇌ A·L | Proposed four step mechanism, including two ligand binding equilibria steps, for the formation of metal nanoparticles, the first A·L step having additional precedent.26,27 |

|
|||
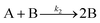
|
|||
| B·L ⇌ B + L | |||
| [A = metal precursor, B = growing particle, A·L = precursor with ligand, B·L = growing particle with ligand; bh ligand steps have associated Keq equilibrium constants] | |||
| 2019 | Handwerk, Shipman, Whitehead, Özkar, et al.61,62 |

|
A new, 3-step mechanism, discovered by disproof-based mechanism-enabled population-balance modeling, in which the 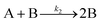 pseudo-elementary step of the 1997 2-step mechanism is expanded into two growth steps (or, alternatively, and as actually discovered61,62 the 2nd and 3rd steps of the 2014 4th mechanism are combined into a single, new 2nd step). Eleven alternative mechanisms were disproved. Quantitative fitting of particle-size distributions (PSDs) was demonstrated, including the PSD shape. pseudo-elementary step of the 1997 2-step mechanism is expanded into two growth steps (or, alternatively, and as actually discovered61,62 the 2nd and 3rd steps of the 2014 4th mechanism are combined into a single, new 2nd step). Eleven alternative mechanisms were disproved. Quantitative fitting of particle-size distributions (PSDs) was demonstrated, including the PSD shape. |
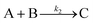
|
|||

|
|||
| [A = metal precursor, B = smaller particles, C = larger particles] | |||
1.3. Classical nucleation theory: a concise look at an often misapplied theory that underlies the 1950 model
Classical nucleation theory (CNT) was developed in an attempt to explain the phenomenon of nucleation,9–13 a theory that continues to be the most popular model for nucleation even today.14,15 The widespread application of CNT continues across many types of systems in nature despite the now well-demonstrated inapplicability of CNT to strong-bonding (also called “strongly associating”) systems16,17 and to cases involving high levels of supersaturation where CNT was never claimed to work, vide infra. It is now abundantly clear that CNT is misapplied if used beyond weakly bonding (“weakly associating”) systems, an example of a weakly bonding system being hydrocarbon (RH) aggregation in the gas phase where CNT has some of its best success as discussed more in a moment. Relevant here is that applying classic theories far beyond their original, intended applications and beyond the limits of their assumptions is a documented, more general problem in chemical science as described in a highly recommended paper by B. Peters.18 Additionally, the dominant effect of surface ligands on nanoparticles that will be apparent throughout the review, plus the fact that CNT lacks any provision for handling ligands (is “ligand-blind”), means that CNT cannot possibly handle nucleation in most modern systems that include binding ligands, except conceivably by accident.The mathematical foundation for CNT was developed in the late 19th century by Gibbs,19 with the now approaching 100 years-old theory being constructed in the early 20th century by Farkas,20 Volmer,21,22 Becker and Döring,23 Frenkel,24 and Zeldovich.25 Critical to understanding CNT and where it should or should not be applied is to realize that CNT is a thermodynamic-based theory—a hypothesis—for nucleation that we now know is more generally a kinetically controlled process.2,3,5,6,10–14,16,17,26,27 In the thermodynamically based CNT, the free energy change of the particle formation is defined/assumed to be the sum of the free energy changes of the phase transformation and formation of the surface, Fig. 1. Additional assumptions employed in CNT that are most relevant to this review include, but are not limited to:16 (i) the so-called capillary approximation, whereby the molecular arrangement of the droplet (a, huge, oversized “nucleus”, from this macroscopic, top-down approach) is assumed to be identical to that of the bulk, macroscopic material,2 a crude approximation/assumption that is perhaps never true; (ii) that the surface energy is independent of temperature; and (iii) that surface growth is assumed to occur one monomer at a time with collisions between two or more particles being neglected (i.e., agglomeration not being allowed). Hence, (iv) the assumed underlying mechanism for particle formation is reversible monomer addition,16,28 A + A ⇌ A2, A2 + A ⇌ A3,…An−1 + A ⇌ An as detailed in Reiss’ highly recommended review of CNT.28 Additionally, CNT assumes (v) that “the stationary distribution of subcritical solute cluster distribution is established instantaneously (italics added) after the onset of supersaturation”16 (see also Fig. 2 in Reiss’ 1986 paper for a schematic showing a proposed effectively infinite nucleation rate28). That is, CNT posits instantaneous/burst nucleation, even though it is the time dependence and kinetics of nucleation that one needs to measure along with other important factors such as the composition and structure of the nuclei and the number of nuclei vs. time. In CNT (vi) the nucleation rate is actually assumed to be independent of time, which implies a chemically and mechanistically implausible, zero-order process—rather than the ostensibly nth order implied by the reversible associations shown for the postulated overall nA ⇌ An in (iv) above.
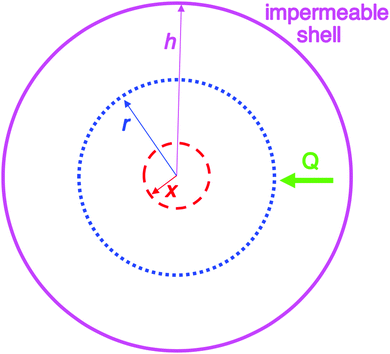 | ||
| Fig. 2 Schematic illustration of the 1950 model consisting of a spherical volume with radius h (solid pink circle), having a concentric spherical nucleus with radius x (red dashed circle). In this model, radial growth occurs on the surface of the concentric spherical nucleus upon arrival of diffusing sulfur. Q is the flux of diffusing sulfur through any concentric spherical shell with radius r (blue dotted circle) within the sphere of impermeable shell (pink solid circle). Reproduced with permission from ref. 2. Copyright 2019 American Chemical Society. | ||
The CNT expression used to describe the free energy of the particle in terms of the particle radius is then given as eqn (1) with its competing, negative and positive terms:29
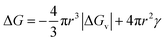 | (1) |
Eqn (1) assumes a spherical nucleus because a sphere minimizes the surface area of the nucleus. Here, r is the radius of the particle, ΔGv is the difference of free energy per volume between the old bulk phase and the new bulk phase, and γ is the free energy of the surface per unit area.
An often-overlooked aspect of the putative “critical nucleus” of CNT as defined in Fig. 1 is that the critical nucleus is a theoretical concept, not something one expects to be able to observe experimentally. The “critical nucleus” as described by CNT is the most unstable transient at the top of the combined ΔG curve according to CNT. As noted by Professor H. Reiss already back in 1986 (on p. 127 of his paper28) “the nuclei themselves are never observed; only the entities which develop from them can be interrogated”.28 Restated, papers professing to have observed the “Critical Nucleus” of CNT are, in all probability, actually seeing what has been called, instead and in modern particle-formation language, the first observable cluster (FOC)17—that is, the FOC detected by the inherent, limiting sensitivity of whatever physical method is being employed.
What is experimentally measurable is the kinetics of nucleation, including the reaction order, n, in the precursor concentration (i.e., [A]n) of the nucleation step,3,17,26,27 that reaction order nominally giving one the nuclearity (An) of the what has recently been defined as the kinetically effective nucleus (KEN).17 Such an experimental measurement of the nucleation reaction order also looks to be one version of the so-called “Nucleation Theorem”; see p. 1963, 1970 and ref. 132, 133 and 139 provided in ref. 12. Of considerable interest and importance here is the mounting evidence that, in at least strongly-bonded systems, the KEN may more generally be of low nuclearity, perhaps often just 2–3 (i.e., A2–3), and hence much smaller experimentally than the critical nucleus, An, of CNT where n ≫ 2–3 has at least historically been implied.
Hence, the pen-and-paper theory—really the hypothesis; the mathematical model—we know as CNT is what was possible at the time.19–25 It is based on the thermodynamic approach possible at the time. An approach to the kinetics of nucleation would have had to account for the transition state, a challenging job even today with all of our modern computational prowess and powerful physical methods. CNT works best for vapor phase, single component, weakly associating systems at relatively low levels of supersaturation such as the gas-phase aggregation of hydrocarbons30,31—that, therefore, can have the facile nA ⇌ An assembly, disassembly kinetics required by the thermodynamic basis of CNT. CNT therefore looks to work best for “weakly-bonded” or “weakly associating” systems that are also not far beyond supersaturation. CNT was never claimed to be valid at large supersaturations19–25 such as one can easily run into for strong-bonded, low solubility systems such as zero-valent metals as one example. Hence, CNT was never intended for—and therefore should not be applied to—“strong-bonded” nucleating systems such as transition-metal nanoclusters to pick a specific example.
For the case of Ir(0)n nanoparticles as just one example, each new Ir–Ir bond is worth an estimated ∼26 kcal mol−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3,17 and “Ir(0)” metal is generally listed as “insoluble”32 so that one cannot speak of its level of “supersaturation”. Hence, the reversible aggregation of monomers, nA ⇌ An, for such a relatively strong bonding system is not plausible thermodynamically because every M–M bond made is worth ∼26 kcal mol−1 corresponding to an associated ΔHvaporization of 159 kcal mol−1 in at least (bulk) Ir(0)n.3,17 The presence of excess ligands, L, and when the M–L vs. M–M bond energies are comparable, could change the situation and could lead to thermodynamic reversibility in some of the nucleation step(s), at least in principle.
3,17 and “Ir(0)” metal is generally listed as “insoluble”32 so that one cannot speak of its level of “supersaturation”. Hence, the reversible aggregation of monomers, nA ⇌ An, for such a relatively strong bonding system is not plausible thermodynamically because every M–M bond made is worth ∼26 kcal mol−1 corresponding to an associated ΔHvaporization of 159 kcal mol−1 in at least (bulk) Ir(0)n.3,17 The presence of excess ligands, L, and when the M–L vs. M–M bond energies are comparable, could change the situation and could lead to thermodynamic reversibility in some of the nucleation step(s), at least in principle.
However, more to the point, Ir(0) is not involved in the nucleation step in the example of a {(1,5-COD)Ir·POM}8− precursor (= A) reduced under H2 to yield isolable near-monodisperse nanoparticles, {Ir(0)n·(POM)x}−9x (where POM9− is a custom-made, polyoxometalate stabilizing ligand). There the kinetically effective nucleus composition has been determined via classical kinetics dependence on [A] and other experiments to be {IrI3H2x·POM}6−.26 Hence, the stronger metal-hydride, M–H–M, bond is involved,17,26,27 for reference a single Ir–H bond energy is on the order of ∼75 kcal mol−1.17 In this system the evidence is strong that nucleation does not involve a reversible, nA ⇌ An system but, instead, involves a low nuclearity17,26,27 KEN with a n = 3.26 This is a good example of where classical experimental kinetics, but now of nucleation, are both necessary and powerful, kinetics generally giving one the composition of the transition state of the rate-determining step in all but a few special cases.
Additional evidence for the inapplicability of CNT to M(0)n systems comes from studies of nucleation to form Li(0)n or Na(0)n particles12 that are also no longer composed of individual, M(0) atoms as is the case for assembled (RH)n subunits. CNT fails badly for these covalent, strong-bonded, M(0)n systems too, as opposed to clusters of individual hydrocarbons, (RH)n, inert gases (e.g., (Ar)n), and water (H2O)n or alcohols (ROH)n, where CNT has proven to be applicable.12 Even there for simple (MeOH)n or ostensibly even simpler (Ar)n for example, the CNT-computed nucleation rates can differ from experimental measurements by 106 to 1011–13, respectively,12,33 although nucleation rate measurements can be problematic even for the simplest systems. Even for the best systems, agreement within ±101–2 is considered a success, with errors of 106–10 between CNT calculated and experimental nucleation rates not uncommon.12,16,34,35
Noteworthy here is that a Sn sol on which the 1950 model is based, and its relatively strong S–S bonds, is not a system where CNT should have been applied2 one can now say—while also acknowledging our additional 70 years of knowledge in fairness to those early researchers and as discussed more in our Part I review.2 Moreover, in terms of realizing where CNT should or should not be applied, it helps to realize that CNT is a macroscopic to microscopic (but not atomic), “top-down” theory—again, really just a hypothesis expressed as one possible mathematical model—brought down to the size of a still large “droplet” via the capillary approximation. CNT theorists likely had no idea at the time if they would need to treat 1000s of atoms, or <10 or (as it now appears) ≤3 atoms17,26,27 in the “critical nucleus” of at least some strong bonding systems, borrowing CNT language for a moment. Even for H2O, the best current computations suggest there are no more than 10–50 water molecules in the, therefore, (H2O)∼10–50 “critical cluster”.36,37 Those DFT studies also bear on the “strong” vs. “weak” bonded classifications of nucleating species noted above: increasing the ΔHbinding in (H2O)n by ∼0.5 kcal mol−1 leads to a ∼1010 increase in the nucleating rate.37 DFT computational studies provide further evidence on the failings of several of the approximations made in CNT.36,37
Meriting mention here is a 2015, 557-page Faraday Discussions by multiple experts presenting their work and understanding of mostly crystal nucleation, entitled “Nucleation—A Transition State to the Directed Assembly of Materials”.11 CNT of homogeneous solutions or gels is used repeatedly to try to explain data presented at that meeting. Yet, the Concluding Remarks section38 states that “classical nucleation theory does not adequately explain the crystal nucleation process”. Also valuable is a 2016 review of nucleation in the journal Crystal Growth and Design13 noting, overall, that non-classical pathways are gradually replacing CNT as the explanation for nucleation in crystal formation.13 Examples of non-classical nucleation pathways are those involving prenucleation clusters (PNCs), a topic we will return to later while seeing that Turkevich made important suggestions even back in 1951 about what we now call PNCs.
What is needed to move our understanding of nucleation forward is not more attempts to tweak the approaching 100-years old theory/mathematical model that we know as CNT. Instead, we hypothesize that needed, first, are better, faster, more precise ways to experimentally monitor nucleation kinetics and mechanism(s) in real time for a variety of systems across nature. Even in atmospheric chemistry where nucleation is heavily researched, the minimum size nucleus presently observable is ∼1.5–3.0 nm, so ∼0.5–2.0 nm above what some find as a ∼1.0 nm (H2O)∼4 “critical cluster” size.12 Second, new, better theories that treat the kinetics problem we know as nucleation will be needed. We refer the interested reader to B. Garrett and co-workers computational efforts and scholarly, well-referenced, insightful papers.36,37
In short, the evidence strongly suggests that CNT should not be applied to any strongly bonding systems where the identity of the associating units are lost and where high supersaturations look to be involved, such as sulfur (Sn) as in the original 1950 model1 or metal (Mn) nanoparticles,2 as two examples. LaMer notes in his 1950 paper1 that his model was developed “in conjunction with modern theories of phase transitions”,1 that is, in conjunction with CNT.22–24 The 1950 model assumes that CNT is correct (as one might expect for the times, CNT being reported 24 years prior21–25 to the 1950 paper1) and starts with nuclei of radius x from which growth is then postulated to start, as illustrated in Fig. 2. An underappreciated point here is that the 1950 model does not address nucleation directly. Instead, the 1950 model assumes a hypothetical form of nucleation—specifically instantaneous/burst nucleation—so that the mathematics of the growth model could be developed. As oddly as it sounds, the (assumed) “burst nucleation” model is actually not a physically or experimentally based nucleation model. Instead, it is really just a mathematical model of growth as documented in our Part I review.2 The irony here is that many of the citations of 1950's model cite it for its “instantaneous or burst nucleation” feature, that is, cite it if for an assumption in the model: the assumed, “word-only” postulate about nucleation. Those citations are often trying to explain how a relatively narrow particle-size distribution can or has been formed—claiming near-monodisperse particle formation is due to the—again assumed—initial burst of particles that, in the burst-nucleation postulate, would lead to the complete separation of nucleation and growth in time. But, that “instantaneous/burst nucleation” postulate ultimately leads back to CNT that, as detailed in this section, is ultimately a false foundation for a large fraction of the ca. 1761 (∼90%) out of the total citations2 of the 1950 paper.1
Finally, it is useful to mention here that within CNT, the formation of the critical nucleus was historically believed to be possible and thus occur according to fluctuation theory. Fluctuation theory is described in the literature as “the process…governed by the probability of the occurrence of the least probable of these fluctuations, that is, the critical fluctuation, which, in terms of the more familiar nucleation theory, is known as the critical nucleus.”39 Under CNT, the general “rate equation” is given10 as eqn (2),
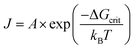 | (2) |
One final point here is the CNT-based “rate” of nucleation does not change with progress of the reaction, but instead is a constant once it commences—thereby implied to be a chemically and mechanistically implausible zero-order process as already noted. Literature reviews on CNT confirm this with the statement that the “the rate of nucleation, J, is defined as the rate of growth of the critical nucleus”41 (italics have been added). What this somewhat confusing statement is implying is that evidence for the putative critical nucleus itself is not possible, only its growth is observable. Again, this is just what H. Reiss noted in his aforementioned statement that “the nuclei themselves are never observed”,28 at least when one is speaking of the “critical nucleus” as defined by CNT.
1.4. The 1950 mathematical model en route to the first explanation in the literature of how monodisperse particles might possibly be formed
An examination of the 1950 model leads to Fig. 2 that helps illustrate that mathematical model.2Instantaneous nucleation as assumed by CNT/fluctuation theory is expressed in the instantaneous formation of nuclei with radius of size x as shown in Fig. 2. Growth is postulated to occur on the surface of each nuclei at the same rate, resulting in monodisperse particles. A full list of the assumptions used to establish the 1950 model can be found in our Part I review.2 The important insight is ref. 2 “…the LaMer model is a growth model, one that says nothing about nucleation past making the assumption of ‘instantaneous/burst’ nucleation as was necessary at the time for developing the growth model.”2 The key point is that “Having all of the nuclei there instantaneously in uniform size x then allowed a mathematical model for growth in this first, creative attempt to try to understand how ‘monodisperse’ particles could possibly be formed.”2
1.5. Phase change or particle-formation models available in the literature since 1939
In order to understand and put into historical perspective what follows, it is necessary to be aware of the mathematical models (and then the experimentally based chemical mechanisms, Section 1.6, vide infra) that have appeared in the literature to try to account for phase change kinetics data—or, in the case of the 1950 model, for particle-formation “phase-change” kinetics data.The Avrami42–44 and later KJMA45,46 and Erofe’ev (A–E)47 are early mathematical/semi-empirical models in the literature from 1939 to 1946 striving to account for often sigmoidal-shaped phase-change kinetics throughout nature, the Avrami model used originally to analyze the crystallization of fat.42–44 There are at least ≥12 variants of the original Avrami model as workers strived to refine the model and deal with issues and problems inherent to these non-mechanistic models (see Table S1 in the ESI† elsewhere that tabulates and provides references to solid-state kinetics models48). Such a proliferation of derivative models with additional parameters, often striving to provide physical meaning and sense to the model, are a hallmark feature of models in trouble from the outset.
Most recently in 2017, a modified-KJMA (M-KJMA)49 was proposed to “ensure rate constants are intrinsic to the sample and reaction conditions, not the specific technique of measurement.”49 The assumptions behind and issues with these models are discussed elsewhere50,51 and need not be rehashed here, save to emphasize four key points:50,51 (i) all the models in Table 1 assume instantaneous/burst nucleation no matter if they are postulated to occur instantaneously at t = 0 or for example at some later, predetermined time, t = t0 (known as “sporadic” as opposed to “instantaneous” nucleation in the Avrami-model literature42–47,49); (ii) hence these mathematical models say nothing about nucleation; instead, are really growth models post some presumed, undetailed nucleation events of unknown kinetics and unknown molecularity; (iii) the Avrami exponent, n, is a convolution of the dimension in space that the growth takes place in plus a parameter related to the assumed time dependence of the nucleation function.42–47,49 Hence and unfortunately, the Avrami exponent parameter, n, has been destined to failure despite >80 years of literature trying to deconvolute and interpret nucleation and growth convoluted from the start into the single Avrami parameter, n. Additionally, (iv) the one k in the Avrami model is not a rate constant, as it is not defined by a balanced equation as rate constants must be. Instead it is a composite rate parameter that is a convolution of a linear diffusional growth (kg) and some assumed, for example zero-order kinetics, linear nucleation rate parameter (J). As a result, deconvolution of anything resembling actual nucleation from growth using the Avrami and related equations continues to be hopelessly confused despite years of literature trying to clarify things and make these models physically valid. For example, how can one possibly talk rationally and kinetically about the two processes of nucleation and growth when you have only one rate parameter, k? You can’t, at least not directly—nor easily nor clearly.
The reader wishing to learn more and make up their own mind about whether or not to use these models for their phase changes including particle formation is referred to other discussions, including a recent Comment,52 then a Response,51 that debates if the M-KJMA equation vs. the 1997 2-step mechanism3 discussed in the next section as ways to analyze initially particle-formation reactions. A related, valuable paper from Prof. G. Lente and R. Szabó shows53 that a stochastic kinetics approach to the 1997 2-step mechanism in the next section aligns well with the deterministic kinetics approach that originally discovered that 2-step mechanism,3 all as Kurtz’ theorem54 connecting stochastic and deterministic kinetics requires.
1.6. A brief summary of particle-formation mechanisms available since 1952
Table 2 is a summary in historical order of particle-formation mechanisms that at least we are aware of that have been generalized to an “A, B, C…” species form,55–63 as kineticists strive to do in the hope that their chemical mechanisms can be seen in more general form and, ideally, therefore applied more broadly. We have also included Turkevich's word-only organizer mechanism because it can be seen as an early version of the Prenucleation Cluster concept idea, vide infra. Reviews covering other, important contributions to particle formations,14 as well as to related topics of protein particle formation (aggregation),64 are available to the interested reader (please also see the many references provided in these reviews to the excellent work of the many authors cited14,64) in addition to the references covered in Table 2.Entry 1 in Table 2 is of considerable historical interest because it cites the 19524 chemical mechanism LaMer was considering for how one chemically might get to the postulated “burst nucleation”. LaMer based his proposed mechanism, as one would expect for the time in 1952, on the assumption of thermodynamic control of, therefore, reversible reactions where he envisioned that “…the embryos of the type Bi are continually forming and disappearing by the reverse processes of dissociation”. Interesting is that he says that for the initial mA1 × Bm process “m is usually 2”,4 but then that for the proposed, reversible step B(i−1) + A1 ⇌ Bi, “i in the case of water vapor condensation is about 80—i.e., this reaction is of the 80th order”.4 The ‘rate’, J, of this process according to eqn (2) and the energetics according to Fig. 1, vide supra, were never reconciled with this proposed, exorbitant 80th reaction order, kinetics with little precedent to this day according to our knowledge or according to a search of the literature.65
Of further interest is that LaMer reported in that same 1952 paper4 an interesting log–log plot of the log [Ba2+][SO42−] ionic mean molality vs. the log (lag time) to the appearance of turbidity, reproduced below as Fig. 3.
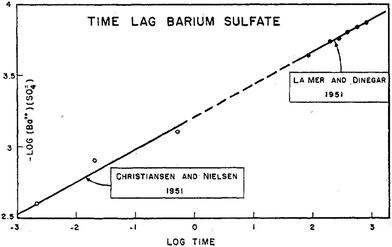 | ||
Fig. 3 Reproduction of Fig. 5 from ref. 4. The log of ionic mean molality for [Ba2+][SO42−] is plotted against the log (lag time) data from both Christiansen and Nielsen's 1951 study66 and LaMer and Dinegar's slightly later, also 1951 study.67 Here the lag time is the time until the turbidity first became observable (by eye in Christiansen and Nielsen's study66 and by a Tyndall beam in LaMer and Dinegar's study.67 BaSO4 particles were visible by eye once the condensation point was reached and large particles precipitated and fell to the bottom of the reaction flask. The y = m(x) + b line fits −log[Ba2+][SO42−] = 0.22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) t + b, that is, −4.5·log[Ba2+][SO42−] = log([Ba2+][SO42−])−4.5 = log t + b, that is, −4.5·log[Ba2+][SO42−] = log([Ba2+][SO42−])−4.5 = log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) t + 4.5·b. This in turn corresponds to the plot for an integrated rate law for a n(BaSO4) → (BaSO4)n rate law, where the math shows that n − 1 = 4.5, so n = 4.5 + 1 = 5.5 (≈6, upon rounding up), consistent with LaMer's report of a net ∼6th order reaction.67 Reproduced with permission from ref. 4. Copyright 1952 American Chemical Society. t + 4.5·b. This in turn corresponds to the plot for an integrated rate law for a n(BaSO4) → (BaSO4)n rate law, where the math shows that n − 1 = 4.5, so n = 4.5 + 1 = 5.5 (≈6, upon rounding up), consistent with LaMer's report of a net ∼6th order reaction.67 Reproduced with permission from ref. 4. Copyright 1952 American Chemical Society. | ||
Based on the data in Fig. 3, LaMer proposed a mechanism4 consisting of 3 Ba2+ reacting with 3SO42− (as his explanation for the overall ∼6th order reaction to observable precipitate) where “all of the preceding steps are assumed in a quasi-equilibrium state.”4 Interestingly and again as one would expect for the time, LaMer thought that he had observed the critical nucleus of CNT. Hence, he interpreted the overall reaction as being 7th (not 6th) order, as the critical nucleus would then need to add one more ion (Ba2+ or SO42−) to be consistent with the postulated, CNT-based rate-determining step. LaMer insightfully concluded his paper with “This new attack on the size of the nucleus merits further refinement and extension to new systems”,4 a statement true today given that definitive studies of the kinetics and mechanisms of nucleation are often still lacking.
Of course, we now can hypothesize that these early researchers were actually observing what we would now call the first observable clusters17 (really particles) from “burst (autocatalytic) growth”—not burst nucleation. Those particles had to be at least ∼100 microns to be seen by the naked eye,68 so something on the order of (BaSO4)n where n ∼ 6 × 1015, one can estimate.69 These would then be large particles way beyond the nucleation stage—the result of (burst) autocatalytic growth. Even a Tyndall beam, the best light scattering technique at the time, could only observe particles of ∼0.2 microns (∼200 nm) diameter, hence n ∼ 4 × 107, still relatively large particles almost surely way past the nucleation stage. Additionally, we also know from mathematical analysis of the first, second, and third (“jerk”) derivatives of sigmoidal curves70 that the tinduction time is a function of three variables: the nucleation rate constant, the growth rate constant, and the starting monomer concentration (e.g., k1, k2, and [A]0 in the case of the 2-step mechanism in Table 270).
Fascinating here as well is Turnbull's 1953 publication71 where he thoroughly evaluates the claims of LaMer's 1952 paper and questions the assumption that 1/tinduction is proportional to homogeneous nucleation. In fact, Turnbull convincingly demonstrates that nucleation in the (BaSO4)n precipitation system is heterogeneous,71 almost surely due to dust contamination and its kinetic effects—heterogeneous nucleation being the way around anything approaching something like a putative “80th order reaction”, one can say in reference back to LaMer's comment about water nucleation. Turnbull also points out that growth is not limited “by diffusion, but by a process occurring at the crystal-solution interface.”71 Turnbull observed sigmoidal growth curves in his studies, curves fit using an Avrami-type equation.48,51 We now know that those sigmoidal curves will, therefore,48 also be well-fit by a chemical equivalent48 of the Avrami mathematical and semi-empirical equation, specifically by the 2-step mechanism back in Table 2 corresponding to slow, continuous nucleation and autocatalytic surface growth.3,48
Hence, as early as 1951, others5,6,71 in the literature were aware of (i) the limitations of classical nucleation theory, (ii) the issues associated with only using turbidity measurements, (iii) the omnipresence of dust effects and heterogeneous nucleation, all while they were also (iv) collecting experimental evidence against the 1950 model of burst nucleation and diffusion-controlled growth. Most importantly, (v) both LaMer and Turnbull had experimental evidence disproving a fluctuation/CNT theory type of high-order nucleation for the (BaSO4)n precipitation system, and Turnbull had strong evidence for heterogeneous nucleation and non-diffusion-controlled growth.
If follows that these early studies of the kinetics of (BaSO4)n precipitation are actually still of considerable current interest and, hence, merit careful reanalysis. If we discard CNT for interpreting these 1950's results on the belief that (BaSO4)n is a strong-bonding system, vide supra, then the straightforward, simplest interpretation of these early chemical kinetics is that they indicate a rate law third-order in BaSO4. That is, a rate law α[BaSO4]3 is implied, in turn suggesting a rate-determining step for the observation of observable precipitate of just 3BaSO4 → (BaSO4)3. Of considerable interest here is that an analogous, low molecularity kinetically effective nucleus (KEN)17 of just 2–3 has now been documented kinetically for several strong-bonding nucleating systems in nature.17,26,27 While it is not at all clear that the net 3rd order, [BaSO4]3 kinetics correspond to a KEN = 3 in that system—because considerable growth has had to occur before any “nucleus” becomes visible as a much larger particle (pretty much exactly as Turnbull insightfully cautioned66)—a deeper, modern look at the (BaSO4)n system, Turnbull's 1953 study and Fig. 3 above are warranted.
The important historical example of (BaSO4)n precipitation also documents that LaMer was aware of the need for chemical kinetics and mechanistic investigations, that he too knew about heterogeneous versus homogeneous nucleation,4 and that he did provide a possible chemical mechanistic alternative in 1952. Hence, researchers could have—and should have—not ignored but instead compared and contrasted the (BaSO4)n mechanistic model to the 1950 mathematical model and its postulate of burst nucleation and diffusion-controlled growth. While with 70 years of hindsight one can say it is unfortunate that the above BaSO4 investigations and the proposed 1952 chemical mechanism in Table 2, entry 1, were not part of the classic 1950 paper.1 However, as we noted in our Part I review2 “LaMer and his co-workers labored in a pioneering and creative way, both theoretically and experimentally” and “that they labored in much different times, where physical methods were limited, modern computation power did not exist, and classical nucleation theory was a relatively new, exciting, and probably seductive theory that likely seemed compelling at the time.”2
After additional study, in 1953 Turkevich sought to explain the nucleation of Au(0)n sols by postulating his own “Organizer” pathway, whereby he postulated “the nucleating agents gradually build up a chemical complex between themselves and gold ions, organizing the latter into a macromolecule (precursor of the nucleus). When the size of the macromolecular inorganic–organic polymer is sufficiently great, it will undergo a molecular rearrangement to produce the metal nucleus and oxidation products of the organizer.”6 Turkevich postulated his “Organizer mechanism” for nucleation because of what he felt were unrealistic components of fluctuation theory, where, as he described it, “…the fundamental difficulty in building up a nucleus is the accumulation of a sufficiently large local concentration of atoms whose size is greater than just demanded by the stability of the particle.”6 Turkevich reasoned that such a build-up is unrealistic statistically because, he argued, that his gold sol nuclei “are about 30 Å diameter and this would involve a fluctuation of the order of a million of gold atoms.”5 Hence, Turkevich proposed his “Organizer” model what he felt is as a more realistic alternative en route to assembling the atoms or molecules needed for nucleation. Anyone who has read Turkevich's work will likely be impressed with his efforts and before-their-time insights.
In modern-day terms, we can recognize Turkevich's creative “Organizer” hypothesis as analogous to—and really the first instance of—the currently popular concept of “prenucleation clusters”, namely the assembly of reaction precursors into large macrostructures with longer-range order that are on-path, kinetically viable nuclei able to undergo facile growth.72 The concept of prenucleation clusters has been increasingly applied in the literature to the following systems: H2SO4,73 CaCO3,72,74 homogeneous crystallizations,75 Na2S2O3,76 heterogeneous protein crystallization,77 glass-type transitions in the solid-state,78–80 and most recently Au(0)n nanoparticles.81 The allure of the prenucleation cluster concept so noted, one critical issue with prenucleation clusters is if the observed clusters are kinetically on, vs. off, path to the final product. The observable clusters may sometimes, and perhaps often, be too stable off-path clusters or clusters trapped in off-path kinetic bottlenecks. Noteworthy here is that that the famous mechanistic chemist and kineticist Professor Jack Halpern82 among others83,84 have emphasized that no measurement made under steady-state conditions can tell if a given “intermediate” is on- versus off-path. Pre- and/or post-steady-state kinetics measurements are required to differentiate those challenging-to-distinguish, two limiting kinetics interpretations.82–84 Nevertheless, at present the concept of prenucleation clusters remains an intriguing and exciting alternative hypothesis to CNT for many literature systems, a concept that merits additional attention and more extensive study by direct methods monitoring the kinetics of the observable clusters, including pre- and post-steady state kinetics measurements.
The limitations of the 2-step (and 3-, and two 4-step) mechanistic models in Table 2 merit emphasis and have been published many times.48,60,89 Those limitations are required reading for anyone using these deliberately minimal mechanistic models. Those limitations ultimately derive from the too-simple and average-property results from the minimalistic model (e.g., size-averaged nucleation, k1, and average autocatalytic growth, k2, rate constants, as well as inability of at least the 2-step mechanism to describe anything beyond the average particle size90). The general species “B” and “C” are in some sense ill-defined as only smaller and larger particles, something that hides the underlying elementary steps such as monomer addition A + Bj → Bj, although this is taken care of in the population-balance modeling in the next section. As already briefly noted, a paper showing that the 2-step model appears to be the minimum chemical mechanism underlying Avrami-based equations has also been described.48 That said, use of the 2-step model is by no means accepted among at least one member of the solid-state kinetics community52 (see also ref. 51, 53 and 54) where the Avrami-based semi-empirical models back in Table 1 have historically dominated.
In at least the initial example,61,62 the ME-PBM was also able to contribute to the “inverse problem” of yielding a better idea of the “cause”—the mechanism—from observation of the “effects”, namely the PSD.61,62 Indeed, that is how the new 3-step mechanism in Table 2 was discovered, via disproving 11 alternative mechanisms and their ME-PBMs en route to the new 3-step mechanism.61,62
Very excitingly, the new 3-step mechanism that was discovered can account for near-monodisperse particle formation by the paradigm-shifting finding that the smaller particles, B, grow faster and thereby catch up with the slower growing, larger particle C, that is, k2 > k3 in the 2019 paper that is the last entry in Table 2. There is, in turn, no need for the postulate of “burst/instantaneous” nucleation in order to obtain (near) “monodisperse” PSDs. Hence, it would appear that the “smaller grow faster than larger particles” finding is the missing link needed for a paradigm shift away from 1950 postulate of instantaneous/burst nucleation. The ME-PBM's MATLAB code is posted on GitHub, hence freely available61,62 for others to use to test and their own particle formation systems and postulated mechanisms. The ability to predict PSDs for a known mechanism and input rate constants and concentration parameters is a notable “first” of the ME-PBM methodology,61,62 something that is it hoped will drive rational syntheses of narrower and narrower particle-size distributions.
A 2005 paper by Tsapatsis and co-workers59 and listed in Table 2 merits mention before ending this section. There, even though they were able to rule out only two other mechanisms, and did not fit any PSD data, that work is still a very valuable early precursor to ME-PBM.59 A paper that qualifies as ME-PBM in the polymer literature and from Waymouth's laboratories92 at Stanford also is recommended to anyone interested in applying ME-PBM to their own system. These and other related, recommended literature are discussed in the publications reporting ME-PBM.61,62
2. Survey and selection of literature citing the 1950 model
It is important that we present how we found and then sorted through the references that cite the 1950 model. That “Experimental” section is as follows: a Web of Science search was performed to start and revealed that Professor Victor LaMer's original 1950 J. Am. Chem. Soc. paper1 has garnered 1953 citations (multiple literature searches were done over a multi-year period, with our final search being done and adding just a few more papers in March 2019). We then inspected all those papers with the goal of sorting them into two groups: those that provide just a reference to the 1950 model or just a “words-only” claim about the applicability of the 1950 model vs. those that provide new data plus those that just provide any depth of discussion or analysis at all (i.e., vs. just a citation of the 1950 model). This sorting was accomplished by reading first the abstract, then checking the details in the paper, and eventually then a at least cursory reading of the entire paper.The inspection of those 1953 papers resulted in 192 papers (again as of our March 2019 cut-off time) that provide at least a discussion if not additional data bearing on the applicability of the 1950 model to the system at hand. The remaining 1761 papers (∼90%) provide in our opinion little if any depth of discussion on the applicability of the 1950 model to the system at hand. Instead, ∼90% of the total papers we found just cite the 1950 model.
Next, the ∼10% (192 papers) located, that do provide at least some discussion of or data related to the applicability (or not) of the 1950 model (to the specific system in a given paper), were examined critically. Those papers are tabulated thematically with comments in a series of six summary tables: 28 papers on classic sulfur sol formation (covered in our Part I review, Table S1, ESI therein2); 13 papers on silver halide nanoparticles (the present Part II review, Table S1, ESI†); 26 papers on semiconductor nanoparticles (Table S2, ESI†); 69 papers on transition-metal nanoparticle formation (Table S3, ESI†); 39 papers on oxide-based nanoparticles (Table S4, ESI†); and 17 papers presenting alternative models or mechanisms compared to the 1950 model (Table S5, ESI†), for a total of 164 papers examined in detail herein (plus 28 papers in our Part I review,2 accounting for the total of 192 papers).
We wish to emphasize that the reader wanting to reach their own at least preliminary conclusions is strongly urged to stop at this stage and read and study the 5 tables and 74 pages of ESI† before proceeding further. This is not a trivial point given that the senior author of the present review is responsible for 4 of the 11 total models or mechanisms in Tables 1 and 2 that compete with LaMer's 1950 model. That fact places him and his group in either a position of some arguably unavoidably bias or perhaps a position of some authority to write the present review—and practically speaking probably a bit of both. Many times we have thought that it would have been much better if the 1997 2-step mechanism back in Table 2 had been discovered back in 1926 or a bit thereafter rather than in 1997.3 If it had been, then as argued in our Part I review2 “…the discovery of particle formation mechanisms would have been considerably accelerated…” because an experimental alternative to the LaMer theoretical model would have been available for competing consideration for the last 70, and not just the last 23 years. A much earlier discovery of the 2-step mechanism by others would have also removed us from constantly being in an apparent if not real conflict-of-interest position vs. the 1950 model just because we discovered the first minimum mechanism3 that serves as an alternative to the 1950 model.
In what follows, we present a critical analysis—and to the best of our abilities an impartial, attempted unbiased analysis—of those additional 164 papers that cite or otherwise invoke the 1950 model. We also present the other, relevant literature required to understand or place in context those papers or our analysis. This Part II review along with our Part I contribution2 constitute the first comprehensive review of the 1950 model and its voluminous literature since the model's 1950 inception.1 The key, overarching question we aim to answer in what follows is whether or not there is compelling experimental evidence for “instantaneous nucleation” or “diffusion-controlled” growth in any of the 164 papers culled from the total literature citing the 1950 model. We start with (AgX)n, and then move on to semiconductor nanoparticles such as (CdS)n, (CdSe)n, or (InP)n, because these systems are where the literature suggested that the 1950 model had the best experimental support.
3. Formation of silver halide nanoparticles
Nanoparticles of silver halides are of considerable interest because of their potential applications in many fields including photocatalysis,93 biosensing,94 and treating infections caused by microbacteria.95 Performance of silver halide nanoparticles in these applications depends on the particle size and size-distribution, as well as the morphology and composition in the case of ternary silver halides. Hence, the synthesis of (AgX)n nanoparticles requires an understanding the nanoparticle formation process in order to control nanoparticle size and size-distributions.Table S1 of the ESI† gives a summary review of thirteen selected papers reporting efforts to unravel the formation mechanism of silver halide nanoparticles. In what follows, key papers from Table S1 (ESI†) are discussed as their evidence and results bear on either the support or disproof of the 1950 model for the specific case of silver halide nanoparticles.
3.1. Early work on the formation of monodisperse silver halide particles
An early 1947 study96 reports the preparation of monodisperse silver sols by combining solutions of Ag+ ions and Cl− ions. The transmittance (turbidity) of silver chloride sols was studied, and a first-order decay in the transmittance was observed in this early silver halide system.Fifteen years later, a 1961 paper by Ottewill and Woodbridge97 reported the preparation of silver bromide and silver iodide sols in water. Electron microscopy and higher order Tyndall spectra (HOTS) were used to examine the particle size and degree of dispersity. The formation of silver bromide sol from the decomposition of the complex ion, AgBr32−, was followed by monitoring the optical density, Fig. 4.97 The authors contend that their data are “in agreement with LaMer's hypothesis.”97 However, the optical density versus time plot in one of the two curves in Fig. 4 has a small but detectable induction period that is hard to explain in terms of “burst nucleation”. More kinetics early in the reaction are needed to understand the induction period and mechanism in this 1961 system that is still of interest. Controlling the dust content in this system should be one of the first orders of business.
 | ||
| Fig. 4 (Fig. 7 in ref. 97.) Decomposition of the AgBr32− complex, by the addition of distilled water (open circles) or 10−9 M silver nitrate solution (filled circles), to form (AgBr)n. Reproduced with permission from ref. 97. Copyright 1961 Elsevier. | ||
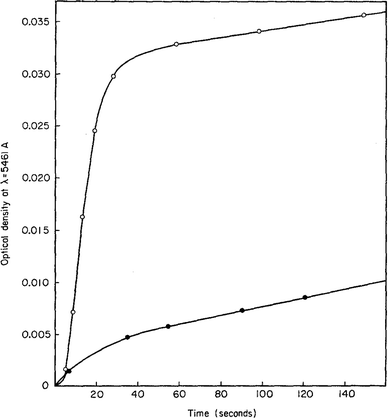
In 1968, Insley and Parfitt98 reported the preparation of monodisperse (AgCl)n sols from the hydrolysis of allyl chloride in aqueous silver nitrate solution, monitored by conductance measurements, electron microscopy and electrophoresis. Shown in Fig. 5 are the conductivity measurements, Fig. 5a,98 and the “critical ion product” (defined by the authors as Kss = [Ag+][Cl−]), for the precipitation of silver chloride from the equilibrium solution) from the fraction of the precipitated silver chloride vs. time data combined with the final size data, Fig. 5b.
 | ||
| Fig. 5 (Reproduced with permission from Fig. 1 and 2 in ref. 98.) (a) (left) Change in conductance with time during the precipitation of silver chloride from the hydrolysis of allyl chloride in aqueous silver nitrate solution. Extrapolation of the initial hydrolysis curve is shown as a broken line. Initial concentrations: silver nitrate 1.0 × 10−5 M, allylchloride 5.7 × 10−4 M. (b) (right) The “critical ion product” extracted from W1/3versus time over the initial growth period, where W is “the ratio of the mass of silver chloride actually precipitated at any time to that required to reduce the ion product to the equilibrium solubility product (1.77 × 10−10).”98 Reproduced with permission from ref. 98. Copyright 1968 Royal Society of Chemistry. | ||
In Fig. 5a, the conductance versus time plot shows an initial linear increase in conductivity due to release of hydrochloric acid from the slow Cl− abstraction and hydrolysis reaction of allyl chloride assisted by Ag+. The subsequent slow deviation from the linear conductivity was attributed to the solution having become saturated with respect to AgCl precipitation. No dramatic change that could be attributed to “burst” nucleation is observed. In Fig. 5b, an extrapolation back to zero of the fraction-precipitated versus time plot gives a non-zero time-axis intercept, suggesting an induction period is present. The authors concluded that their results are inconsistent with the 1950 model because the critical ion product changes quickly in the zero-point-of-charge region.98 In short, this 1968 study provides evidence against the burst nucleation model in the classic (AgCl)n formation system and under the specific conditions examined.
3.2. Formation of colloidal silver halide in an open system: Sugimoto's classic system and efforts
Sugimoto and co-workers99,100 developed a nucleation model for the formation of sparingly soluble, near monodisperse colloidal silver halide particles in an open system, in which the source of the monomer is introduced at a constant feeding rate (i.e., constant supply rate), Q. In one experimental system carefully examined by Sugimoto and co-workers,100 AgNO3 and KBr were separately introduced via “double jet” apparatus with two mixing tubes into a pH 5.0 and 2 wt% gelatin solution (the latter to inhibit coagulation of AgBr particles) all with efficient, impeller mixing (see a schematic of the apparatus that is Fig. 2 in ref. 99). Samples were withdrawn at predetermined times followed by quenching at liquid N2 temperatures (or, as a control, adding a dye to arrest the growth or any dissolution of the particles); both procedures gave equivalent results in the subsequent TEM visualization experiments in this again well-designed, carefully executed study.100 The final number of particles was used to infer the total number of “stable nuclei”, n∞+,100 defined by the authors as the nuclei that can grow (versus, putatively, dissolve).100Fig. 6a shows that the number of nuclei determined this way depends on the feeding rate of precursor as one might expect, while Fig. 6b shows that the particle number is a function of both temperature and time—contradicting the burst-nucleation model's assumptions2 of a constant number of particles vs. time post burst nucleation.1Fig. 6c shows the average radius vs. time of the growing particles (termed “nuclei” by the authors100). Relevant here is the minimum particle size observable by the microscopy employed was about 6 nm, which we estimate corresponds to a (AgBr)n of n ≈ 2350—that is, a size presumably almost surely beyond any actual nuclei. Hence, more consistent is the alternative hypothesis that instead of “nuclei” the authors are actually monitoring the first observable cluster (FOC)17 discernable by their particular microscopy technique.
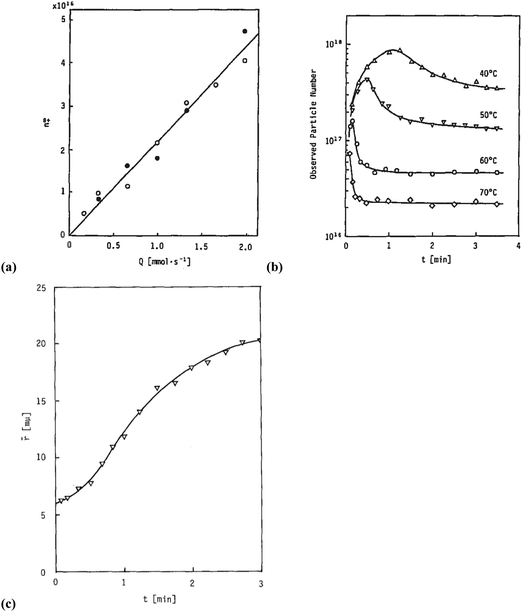 | ||
Fig. 6 (Fig. 9, 11 and 15 in ref. 100.) (a) The final number of observed particles (n∞+) as a function of Q, “the molal feed rate of the monomer source into the system”,100 at 70 °C and pBr 3.0 in the (AgBr)n formation open system. The closed circles represent a repeat set of experiments at the same Q values. (b) The number of the observed particles (n∞+) as a function of time at different temperature (Q = 10−3 mol s−1 and pBr 3.0). (c) The change of the mean radius, ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) , of “nuclei” (in the author's100 nomenclature; really the growing particle) as a function of time in the early stage of precipitations at 50 °C. Observed lines are arbitrary and do not represent any fitting function. Reproduced with permission from ref. 100. Copyright 1992 Academic Press, Inc. , of “nuclei” (in the author's100 nomenclature; really the growing particle) as a function of time in the early stage of precipitations at 50 °C. Observed lines are arbitrary and do not represent any fitting function. Reproduced with permission from ref. 100. Copyright 1992 Academic Press, Inc. | ||
Contrasting this n value, stopped-flow kinetic measurements by Tanaka and Iwasaki (cited by Sugimoto in ref. 100 on p. 223) lead to much smaller (AgBr)n with n values of just 3 to 10 as the implied nuclei. An educated guess is that the Tanaka and Iwasaki study is an early, perhaps seminal example of subsequent, but still rare, measurements of kinetically effective nuclei (KEN)17,26 of perhaps up to ≤10 in this strong-bonding system. Additional studies reproducing and further analyzing this classic (AgBr)n system, combined with an appropriate mechanism or other model, would be most welcome and should in our opinion be a priority of the community interested in nucleation, growth and any subsequent agglomeration.
3.3. Sugimoto's model: underlying key features and assumptions
Anyone wanting to understand Sugimoto's important experiments and resultant model will need to read the original papers99–102 carefully while striving to understand the model's key features, the assumptions behind the model, and where the Sugimoto model is similar to or different from the 1950 model or classical nucleation theory. Additionally, one needs to strive to understand where the mathematical equations given and the words used to describe the model jibe or seem disconnected, and the other interesting questions raised by the model, vide infra. Highly recommended additional reading is Chu, Owen, and Peters’ concise derivation and analysis of the Sugimoto model,103 an important contribution that we will return to in a moment. The Sugimoto work merits careful examination as it makes the claim that the “LaMer diagram…has actually been demonstrated by experiment”.101 Hence, the classic, well designed and executed Sugimoto experiments are more generally believed to be one of the best pieces of evidence in support of the 1950 model.The basic equation of the Sugimoto model is eqn (3) below taken from his 2007 paper,99 an equation that breaks up the supply of solute (QVm) into its use to generate stable nuclei 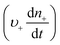 or to grow those “stable” (i.e., growable) nuclei (
or to grow those “stable” (i.e., growable) nuclei (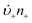 ):99
):99
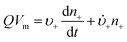 | (3) |
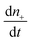 is the rate of change of those stable nuclei, and
is the rate of change of those stable nuclei, and 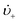 is the “mean volume growth rate of the stable nuclei”. Sugimoto's verbal description of his model from his 1992 paper in ref. 100 (with our explanatory comments provided in (parentheses)): “The theory is based on a nucleation model as origins of (i.e., as giving rise to) the product particles (that) are produced through a kind of Ostwald ripening from stationary unstable nuclei that are in a quasi-steady state of balance between the generation of their embryos by instantaneous reaction of the introduced reactants and either dissolution or growth”.100 Note the proposed “instantaneous reaction” to generate the n+ nuclei embryos. This language will conflict with the diagram in Fig. 7 and the notion of nucleation occurring in some, albeit undefined, time period around tm in Fig. 7, in term causing confusion about if nucleation in the Sugimoto model is instantaneous or not.
is the “mean volume growth rate of the stable nuclei”. Sugimoto's verbal description of his model from his 1992 paper in ref. 100 (with our explanatory comments provided in (parentheses)): “The theory is based on a nucleation model as origins of (i.e., as giving rise to) the product particles (that) are produced through a kind of Ostwald ripening from stationary unstable nuclei that are in a quasi-steady state of balance between the generation of their embryos by instantaneous reaction of the introduced reactants and either dissolution or growth”.100 Note the proposed “instantaneous reaction” to generate the n+ nuclei embryos. This language will conflict with the diagram in Fig. 7 and the notion of nucleation occurring in some, albeit undefined, time period around tm in Fig. 7, in term causing confusion about if nucleation in the Sugimoto model is instantaneous or not.
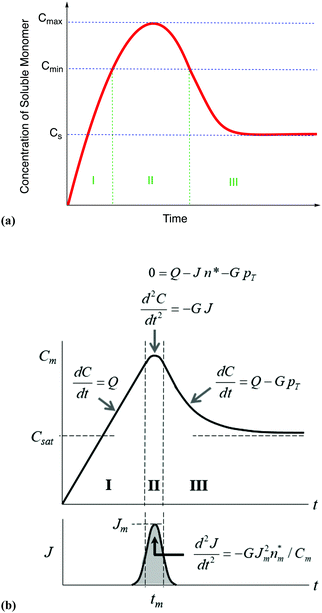 | ||
| Fig. 7 (a) A schematic illustration of the 1950 hypothesis in picture form for the formation of colloidal particles, 1 originally for soluble monomer, S, in the case of sulfur sol formation, (S)n. (a) Is representative of what one finds in the literature, including what we have presented elsewhere,2 although LaMer's actual diagram2 in the original 1950 paper has a more linear initial rise. The hypothetical curve in (a) shows qualitatively the variation of soluble monomer concentration versus time during the whole formation process. Cs is the saturation concentration (of the soluble monomer), Cmin is the hypothetical minimum supersaturation for the nucleation, and Cmax is the hypothetical limiting supersaturation, postulated stage I: formation of soluble monomer in solution. Postulated stage II: nucleation from the solution when the concentration of soluble monomer is higher than the critical supersaturation level Cmin—as typically presented, albeit not shown as truly postulated “effectively infinite rate, burst nucleation”.1 Postulated stage III: growth by diffusion when the supersaturation concentration is lower than Cmin, but higher than Cs. It is critical to note that, in the intervening nearly 70 years, and despite the widespread reproduction and quoting of this figure, no such experimental time dependence of soluble sulfur monomer has ever been published, at least that we have been able to find from an exhaustive literature search. Reproduced with permission, including the figure caption, from ref. 2. Copyright 2019 American Chemical Society. (b) The more quantitative version of the classic 1950 figure1 from B. Peters et al., that they describe by “each stage of a LaMer burst nucleation process is described by different equations that relate the solution concentration C, the nucleation rate J, the number of nuclei pT, the growth rate G, and the nucleus size n*.”103 (b) Also more faithfully reproduces the initial linear rise given in LaMer's classic figure (Fig. 1 in the 1950 paper.1) Reproduced with permission from ref. 103. Copyright 2017 American Chemical Society. | ||
The paper by Chu, Owen, and Peters provides an insightful rederivation and reanalysis of Sugimoto's model.103 Their rederivation starts as Sugimoto does with a pair of differential equations, eqn (4) and (5), that govern the concentration of solutes, C(t), and populations of nuclei, pT(t) respectively (the somewhat different symbols and nomenclature (i.e., vs. that used by Sugimoto) is retained below):
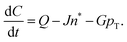 | (4) |
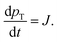 | (5) |
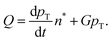 | (6) |
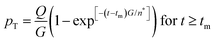 | (7) |
From their treatment Peters et al. draw a LaMer-type diagram, Fig. 7b.
Professor Peters et al. then go on to make several important points: (i) eqn (6) “is true at and only at t = tm”, where tm corresponds to the time of the maximum supersaration, Csat, in the LaMer diagram, Fig. 7, vide infra (as that is the only place where the assumption of dC/dt = 0 used to derive eqn (3) and (6) is true; see their Fig. 1 reproduced as Fig. 7b that differs slightly from Fig. 7a in that Fig. 7b tails asymptotically towards zero at longer times103). Peters et al. also note (ii) Sugimoto assumes, however, that his eqn (3) (and hence eqn (6)) remain valid for all t ≥ tm; (iii) eqn (3) (and hence eqn (6)) are better viewed not as a differential equation, but as a condition on the solution of the coupled eqn (4) and (5); and (iv) that the initial condition invoked by Sugimoto of pT(tm) = 0 is incompatible with any nucleation expression that depends monotonically on supersaturation, real nucleation beginning before tm. B. Peters et al. also note that (v) the assumptions in the Sugimoto model of size- and concentration-independent growth are not physically correct, and they note that the Sugimoto model cannot account for narrow particle-size distributions (PSDs) because the sudden onset of nuclei then exponential decaying rate predicted by eqn (6) makes the predicted PSD “increase exponentially” up to an unrealistic maximum size of G(t − tm). The Sugimoto model's many, non-realistic physical assumptions alone make questionable the (still creative) model's value, not unlike how the 9 assumptions underlying the original, 1950 burst-nucleation model make it inherently somewhat confusing and questionable2 from the beginning.
Reading the words Sugimoto uses to describe his model reveals the insidious disconnect that comes with physical models of dynamic chemical processes that are not described by balanced chemical reactions—the identical type of disconnect present with the burst-nucleation model2 as discussed in detail in our Part I review and supported there by multiple citations of the relevant literature.2 Indeed, it takes some study, and the very helpful Peters et al. treatment cited above, to come to the following realizations about the model: (a) the original n+ nuclei simply appear, in an ill-defined time window around tm (i.e., no details are given as to how the n+ nuclei form, just that they are formed by some unknown pathway and mechanism approaching instantaneously). The model is, then, (b) a burst-nucleation model to form what are termed “stable” nuclei, n+ (i.e., defined as nuclei that are able to grow). For Ag+ and Br− one might write this as: (n − 1)(Ag+ + Br−) → (AgBr)n−1 (they just show up, from supersaturated solution99,102,104 at an approaching infinite rate as the titles of two of Sugimoto's key papers confirm via the term “Spontaneous Nucleation…”.101,102) In this sense, then, an important point is that (c) the model is not really a “Theory of Nucleation…” as the title of his 1992 paper claims,100 no more than the 1950 model is a nucleation model. Both assume burst nucleation, even if one allows it to happen in some unspecified short time period centered around tm in Sugimoto's model. Hence, both the Sugimoto and 1950 models are actually growth models.
Additionally in the Sugimoto model, in what is described only in words as an Ostwald ripening type of step,99–102 (i) unstable (AgBr)n−1 can “dissolve” (e.g., by losing one or more AgBr), but also (ii) grow to a “stable” nuclei, that we write as (AgBr)n−1 + AgBr → (AgBr)n, so that growth occurs by postulate only from “stable” nuclei of size (AgBr)n or larger, as CNT would have it. Nucleation and growth compete with one another for the precursor feed, Q, in the model and as eqn (3) teaches, what Sugimoto describes as “growth-limited nucleation”.101 Growth-limited nucleation will, however, always be present when nucleation and growth compete for a common precursor or other reagent, that is, are parallel reactions and, hence, compete kinetically for precursor. Hence and although “growth-limited nucleation” is not really a new or novel concept, an important part of Sugimoto's model is that it postulates nucleation and growth as parallel reactions (and not serial processes52 as comes out of some models claiming instantaneous nucleation52 but, interestingly and analogously are also really just growth models51 that have mathematically built in an assumed burst nucleation51).
The bottom line is that Sugimoto's model is really a growth model, one that has to date not been convincingly used for quantitative fitting of particle formation kinetics nor particle-size distribution data as is needed to give the growth model a compelling experimental test.
3.4. Sugimoto's model for silver halide particle formation in a biphasic, closed systems
The Sugimoto model100 for the formation of silver halides sols in open systems was modified for biphasic, closed systems.101,102 The first of two papers101 on AgX formation in closed systems reports the experimental examination of (AgCl)n formation in a Teflon-lined container with the following reagents99,101 (see p. 111 of ref. 99): 1.8 × 10−2 M (EtO)2SO2 (that is described as sparingly soluble in water101), 7.0 × 10−3 M KOH, 2.0 × 10−4 M AgNO3, 2.0 × 10−3 M KCl, and 2.0 wt% gelatin. The implied series of reactions in this complex colloidal (AgCl)n formation system is not specified in a clear, equation form, but those reactions are necessary to understand the system and associated model. The reactions involved are presumably something reasonably close to what we have written below in an attempt to more clearly present and better understand this classic system:| (EtO)2SO2 + H2O → (EtO)S(O2)O−H+ + EtOH (slow hydrolysis and H+ formation) | (8) |
| Ag+–gelatin− + H+ ⇌ Ag+ + gelatin−H+ (H+ assisted release of Ag+) | (9) |
| n(Ag+ + Cl−) + gelatin− → (AgCl)n·gelatin− (fast, multi-step formation of gelatin-stabilized (AgCl)n colloid) | (10) |
The gradual release of Ag+ ion in this complex system was carefully monitored using a Ag2S-coated Ag electrode that, in turn, allowed comparison of the observed Ag+ to that expected at equilibrium with AgCl according to the solubility product Ksp = [Ag+][Cl−]. However, a critical point here is that the actual Ksp used in the calculations is never given in the paper—despite the critical need for an independently determined Ksp under the specific conditions of this complex system in order to place the studies on a firm foundation. (For reference, Ksp(AgBr) = 7.7 × 10−13 and Ksp(AgCl) = 1.8 × 10−10 at 25 °C in pure water.105,106) Hence and unfortunately, the calculated maximum supersaturation ratio, Sm, as given and used in the given in the paper (and in Sugimoto's nomenclature) Sm = [Ag+]m[Cl−]0/Ksp (where Sm = ca. 3.5, Tables 2, 3 and Fig. 12 therein101) were not independently verified, may not be accurate, and hence remain as not-yet-reliable estimates (including the supersaturation ratio values, S, defined by Sugimoto and used in Fig. 8).
| T (°C) | k 1, min−1 | k 2, (“particles per volume”)−1 min−1 | R 2 | Chi. sq. |
|---|---|---|---|---|
| 15.4 | — | — | — | — |
| 30.0 | (8.0 ± 1.9) × 10−4 | (1.59 ± 0.08) × 101 | 0.99698 | 1.35 × 10−3 |
| 39.0 | (7.0 ± 3.9) × 10−4 | (3.84 ± 0.27) × 101 | 0.99516 | 2.92 × 10−3 |
| 49.5 | (2.0 ± 0.7) × 10−3 | (6.68 ± 0.39) × 101 | 0.99704 | 2.54 × 10−3 |
 | ||
| Fig. 8 (Fig. 9 from ref. 101.) The calculated supersaturation ratio, S, defined by Sugimoto and co-workers as S = [Ag+]([Cl−]0 − P)/Ksp and shown on the left-most y axis where P (shown on the right-most y-axis) is “the molar concentration of precipitated AgCl” and “in the growth stage” (as stated on p. 191 in ref. 101). The [Ag+] vs. time curve used as input into the S equation to generate this Fig. 8 is given as Fig. 9 in ref. 101. Reproduced with permission from ref. 101. Copyright 2000 Elsevier. | ||
In what appears to be a widely cited, hence apparently generally believed, qualitative claim in the 2000 paper,101 the claim is made that the “LaMer diagram…has actually been demonstrated by experiment”.101 That is, the authors claim that their Fig. 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 101 (reproduced as Fig. 8) supports and reproduces the famous, widely cited diagram in the 1950 paper.1 If so, then Sugimoto's 1992 paper would be a landmark paper in supporting at least the qualitative picture and the often cited 1950 diagram from the 1950 paper.1
101 (reproduced as Fig. 8) supports and reproduces the famous, widely cited diagram in the 1950 paper.1 If so, then Sugimoto's 1992 paper would be a landmark paper in supporting at least the qualitative picture and the often cited 1950 diagram from the 1950 paper.1
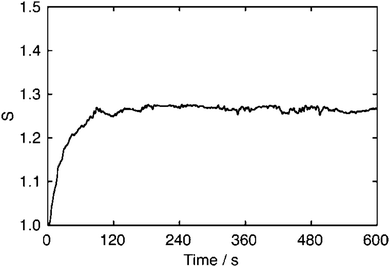 | ||
| Fig. 9 (Fig. 1 from ref. 107.) Time evolution curve of the supersaturation, S, relative to saturation as determined from the Ksp for continuous feeding the reactant solutions of silver nitrate and potassium bromide to a seed solution of dispersed octahedral AgBr particles in pBr 2.0 at 50 °C. The supply rate of solute per particle was Q/nr = 2.56 × 10−12 mol s−1 m−1, where the mean radius of seed particles is r = 0.12 μm and n is the number of seed particles. Reproduced with permission from ref. 107. Copyright 2005 American Chemical Society. | ||
Fig. 8 shows two experimentally determined phenomena: (i) the variation in the supersaturation ratio vs. time, S = [Ag+]([Cl−]0 − P)/Ksp, as defined by Sugimoto (with a reminder of the caveat noted above, namely that the Ksp value used was not independently verified under Sugimoto's reaction conditions and apparatus), and Fig. 8 also shows (ii) P, the molar amount of AgCl precipitated out of solution vs. time expressed as a molar concentration. The results are interesting and a credit to Sugimoto and co-worker's experimental efforts, no matter what the best interpretation of the data turns out to be, as discussed next.
An examination of Fig. 8 reveals that a number of questions need to be addressed before Fig. 8 could be considered a compelling experimental recreation of the classic 1950 diagram and associated hypothesis about particle formation. (i) First, the y-axis in Sugimoto's Fig. 8 above is not just “monomer concentration” as in the 1950 model and classic figure (i.e., for this case soluble, [Ag+][Cl−]), but S, the supersaturation ratio, so a ratio of concentrations; (ii) second, inspection of Fig. 8 in the 2000 paper101 reveals that at ca. 40 minutes (AgCl)n nanoparticles with a mean diameter of 3.3 nm, and hence n ≈ 440, have formed. This large n value means that not just nucleation, but also considerable growth, has occurred by the 40 minute maximum in the supersaturation ratio, S, in Fig. 8. Indeed, Sugimoto defines the P used in his [Ag+]([Cl−]0 – P) term in his S = [Ag+]([Cl−]0 − P)/Ksp equation as P being determined “in the growth stage”. This would seem to strongly imply that the nucleation event(s) that the 1950 pictorial model strives to illustrate are likely mostly over before the experimental data near the y-maximum in Fig. 8 were collected—in turn suggesting the two are for fundamentally different net processes and not comparable. (iii) Third, it is hard to tell if the [Ag+]([Cl−]0 − P) quantity measured can give one the required concentrations, [Ag+][Cl−], because some of the reactions have slow kinetics (eqn (8) and perhaps (9)) including gelatin as a reagent—they might be providing the desired values, but it is hard to be sure; there is also the fact (iv) that the first part of the 1950 diagram's curve in Fig. 7a is concave, while the corresponding part in Fig. 8 is convex. A positive is (vi) that the critical placement of where the Csat line goes on an experimental curve (i.e., Csat in Fig. 7b, or equivalently Cs in Fig. 7a) is something that Sugimoto does achieve—his S = 1.0 value is that line and if one uses the S ratio.
The above important details so noted, the main problem at present with the claim that the “LaMer diagram…has actually been demonstrated by experiment”101 is (v) that Fig. 8 may well be more consistent with other, non-LaMer models and mechanisms that show spikes in growth—note that no alternative explanations for Fig. 8 were proposed or explored. Later in Section 7.1 we will see that continuous nucleation and size-dependent growth can generate spiked concentration curves that (a) have some of the features of Sugimoto's intriguing Fig. 8, but are known to be (b) spiked growth curves—as Sugimoto's probably also is. Additionally, the peak maximum in the Ag+ (and calculated concomitant start of the AgCl precipitation) in Fig. 8 may have more to do with the silver halide precipitation process, m(AgCl)n·gelatin− → (AgCl)n·m (ppt) + m gelatin−, which precedent says might be treatable kinetically as a bimolecularly nucleated, autocatalytic agglomeration process,55–58 an alternative hypothesis meriting experimental testing. The released gelatin− species could then bind previously freely diffusing Ag+, causing that value to drop past its maximum as seen in Fig. 8.
More experimentation is needed to yield unequivocal conclusions regarding Sugimoto's interesting, valuable AgCl precipitation system, specifically: (i) a repeat of the experimental work, including the results reproduced in Fig. 8; (ii) determination of the applicable Ksp under the reaction conditions and then calculation of the true supersaturation with realistic error estimates, all with (iii) keen attention to Turnbull's work71 showing that variable, apparent supersaturation values are a problem due to heterogeneous nucleation probably in turn due to room dust, so that kinetics effects are creeping into one's attempts to measure reliable supersaturation values.71 Additionally, it will be critical to then (iv) test any and all possible models and mechanisms that might be able to fit quantitatively the resultant data analogous to Fig. 8. That needed research will likely give the researchers repeating Sugimoto's original 2000 work a keener appreciation for the cleverness and skills in the design and execution of that classic work.101
A second paper by Sugimoto102 examines the formation of (AgBr)n colloidal nanoparticles using the same experimental system as in eqn (4)–(6) above for AgCl formation, but now with KBr so that the Ag+ ions gradually released from the Ag+ –gelatin− complex are captured by Br− to yield colloidal (AgBr)n, at least initially. The reported Ksp = 1.77 × 10−10, 2.73 × 10−10, 4.13 × 10−10, and 6.15 × 10−10 mol2 L−2 at 25, 30, 35, and 40 °C, respectively, are used along with the electrochemically measured Ag+ to provide curves for the supersaturation ratio, S, as a function of time in Fig. 15 of the 2000 paper102 that are closely analogous in shape and features to, but not exactly identical to, Fig. 8, but now with a still-spiked maximum at 40, 25, 15, and 10 minutes, respectively, which is again when the AgX (X = Br) first is detected. The diameter of the (AgBr)n nanoparticles present at that time is 1.97 nm, so that an average value of an again relatively large n = 83 is present for the (AgBr)n when the Ag+ peaks and the AgBr precipitation is treated as beginning. The final particle size is smaller by a factor of 1/6, an effect attributed by the authors to the lower solubility of AgBr.
Once again, meriting future investigation here are efforts at (i) repeating this also classic work from Sugimoto's laboratories, (ii) verifying the Ksp employed, and (iii) finding mechanisms or other models that can quantitatively fit the sigmoidal-shaped vs. time kinetics curves observed. Attention to the presence of dust and heterogeneous nucleation are two other issues that will need attention.
3.5. Shiba and Okawa's study of silver bromide precipitation
A 2005 paper by Shiba and Okawa107 reports a relationship between the supersaturation level, S, and the supply rate of solute for a related AgBr precipitation system. The authors measure S as a function of time for the continuous feeding of the reactant solutions of silver nitrate and potassium bromide to a seeded solution of octahedral (AgBr)n particles, Fig. 9. The supersaturation in Fig. 9 slowly increases continuously to a steady-state value over nearly 100 minutes, with no appearance of any type of “burst” decrease, for example, as arguably expected given that (AgBr)n seeds were provided.Overall, the AgX formation systems presented above provide a number of interesting results and are of fundamental value given that Ag+ can be monitored to low levels electrochemically and because values for the Ksp of AgX are known in water. The pioneering Sugimoto and related systems merit further investigation and attempts to first reproduce the S vs. time curves and then quantitatively explain the resultant, reproducible curves with modern mechanisms or other models besides just the 1950 model.
3.6. Formation of ternary silver halide nanocubes with mixed chloride and bromide ions
A 2015 paper108 reports the synthesis of photonic crystals of ternary silver chlorobromide (AgClxBr1−x, 0 < x < 1) with a highly uniform size, morphology, and crystallinity through the injection of Ag+ ions into an ethylene glycol solution of Cl− and Br− ions containing poly(vinylpyrrolidone) for particle stabilization. The authors report that the size of the nanocubes is tunable by varying a number of parameters: (i) the molar ratio of Cl− to Br− ions; (ii) the injection rate of Ag+ ions; and (iii) the reaction temperature. Significantly, the formation of colloidal AgClxBr1−x nanocubes was monitored in real-time using in situ high-energy synchrotron X-ray diffraction. The results show that a fast injection rate of Ag+ ions is critical for the formation of highly pure face-centered cubic crystalline AgClxBr1−x nanocubes, Fig. 10.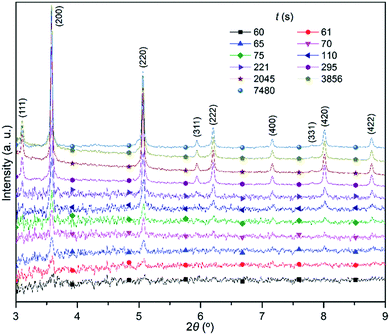 | ||
| Fig. 10 (Fig. 3 from ref. 108). XRD patterns taken from the reaction mixture containing KBr and NaCl with a molar ratio [KBr]/([NaCl] + [KBr]) = 4/8 used for the synthesis of AgClxBr1−x nanocubes (SEM image in Fig. 1 from ref. 108). Different patterns were recorded at different times normalized against time when the AgNO3 solution was injected into the reaction mixture. Injected into the 12 mL ethylene glycol solution of 0.35 mmol NaCl and 0.70 mmol KBr plus 2.5 g polyvinylpyrolidone (PVP) was a 1.0 mL ethylene glycol solution of AgNO3 (0.34 M) at an injection rate of 1 mL min−1 with the assistance of a syringe pump. The X-ray wavelength was 0.1771 Å. Reproduced with permission from ref. 108. Copyright 2015 Royal Society of Chemistry. | ||
The authors claim the applicability of the 1950 model to their system and its resultant data, and interpret their data as overall supporting “two sequential nucleation/growth processes…” leading to a “bimodal size distribution” of AgClxBr1−x nanocubes.108 However, the authors did not consider a continuous nucleation model that (i) can explain the induction period and sigmoidal kinetic data one can estimate from the XRD patterns in Fig. 10 (Fig. 3 in that paper108) at a lower injection rate of 0.2 mL min−1 (Fig. S2 and S3, ESI† in that paper108); and (ii) that continuous nucleation is an arguably more natural explanation for the bimodal distribution for the nanocubes centered at 80 and 300 nm (Fig. 1a and Fig. S6a, ESI† in that paper108)—that is, two competing continuous nucleations rather than two burst nucleations of different compositions at difference times.
Hence, this AgClxBr1−x nanocubes system is another system where additional study and especially more kinetics and their mechanistic analysis would be welcome and might lead to definitive results about the underlying mechanism.
3.7. Further silver halide studies and overall conclusions
Table S1 in the EDI summarizes the studies discussed above as well as additional studies of AgX systems for the interested reader, including studies of reverse micellar systems.109,110 The most critical conclusions from the sum of studies of the AgX systems are that (i) these systems tend if anything to refute, rather than support, the concept of burst nucleation; (ii) Fig. 8, reproduced from Sugimoto's work,101 is a classic system that merits reinvestigation; (iii) Sugimoto's mathematical model has a number of non-realistic physical assumptions that anyone using that model needs to be aware of and take into account; and importantly (iv) there is no compelling support for burst nucleation that at least we could find in any of the silver halide particle-formation studies examined.4. Formation of semiconductor nanoparticles
In the last three decades, semiconductor quantum dots have been the focus of a great deal of interest for optical and imaging applications111,112 and for solar energy harvesting,113,114 among other applications.115 Once again, understanding the mechanism of formation of, now, semiconductor nanocrystals is critical en route to reproducible, optimized syntheses of the highest-quality size and size-dispersion controlled semiconductor quantum dots. Because surface ligands are critical to semiconductor nanocrystals, we review first ligand-stabilized semiconductor quantum dots. Table S2 of the ESI† provides a detailed analysis of 26 papers that the reader especially interested in the next section, or in forming their own initial opinion about what follows, is urged to study before proceeding to the next section.4.1. Formation of semiconductor nanoparticles stabilized by surface ligands
In the formation of semiconductor nanoparticles, the final particle size has been shown to be strongly dependent on the electron-donating, ligating ability of the stabilizing surface ligands.115 Few nanomaterial surfaces are bare, and ligands as well as solvents can adsorb, coordinate, and bond to nanomaterial surfaces.116 These “surface ligands” can, in turn, play important roles in nanoparticle synthesis to modulate nucleation, growth and agglomeration reaction kinetics and associated pathways. Surface ligands can regulate the accessibility and reactivity of the nanoparticle surface,117–119 for example by passivating otherwise coordinatively unsaturated surface atoms and stabilizing the resultant ligated nanoparticles while inhibiting flocculation. Stabilizing ligands are likely often critical to determining the size and size-distribution of the final nanoparticles.120One of the main conclusions in the scholarly 2016 review of the works on indium phosphide nanoparticles by Cossairt,121 post a critical analysis of the semiconductor nanoparticle formation literature, is that the 1950 model is inapplicable to the formation of indium phosphide nanoparticles. The primary evidence for this conclusion is that the stabilizing ligands present on the surface of nanoparticles determines the size of the ultimate particles rather than the diffusion of monomeric species in solution, as the 1950 model postulates.1,121 Indeed, recent experiments by Cossairt and co-workers122 describe the formation of (InP)n quantum dots starting with a magic-sized nanocluster In37P20(O2CCH2Ph)51, which is shown to be a competent single-source precursor for the formation of (InP)n nanocrystals.
In a study of colloidal indium phosphide by Peng and co-workers,123 the accessibility of active sites on the surface of InP and other III–V quantum dots is hypothesized to be the key for breaking the entanglement between nucleation and growth in this system. First, the authors found that the ligands around each nanocrystal are necessary to ensure their colloidal stability by studying the growth of nanoparticles on the pre-synthesized, small seeds of (InP)n quantum dots. Seeds of (InP)n nanocrystals were prepared by injecting a solution of (Me3Si)3P and octylamine in octadecene to a solution of indium(III) acetate and myristic acid in octadecene at 185 °C and then stirring the reaction mixture at 178 °C until the growth of InP nanocrystals to the desired size resulted. The reaction was monitored by UV-vis absorption along with TEM images taken after the reaction to determine the particle size distribution. Starting with the (InP)m seeds, the use of “surface-activation reagents” such as acetylacetone or acetic acid with additional starting materials (indium alkanoates and (Me3Si)3P) yielded surface growth of the (InP)m seed particles. The authors define a “surface-activation reagent” as a reactant that loosens the ligand shell, which the authors believe allows for the “complete separation of nucleation from growth”.123 In the absence of surface-activation reagents, small particles were obtained implying the presence of new nucleation in addition to growth from the seed particles. Furthermore, surface-activation growth on seed particles was shown to be more broadly applicable to (InAs)n and III–V based core/shell quantum dots.123 The authors provide a schematic model, Fig. 11, whereby nanocrystal ligands124 can permit colloidal stability yet allow just growth under “surface activation” conditions.
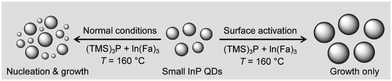 | ||
| Fig. 11 (Fig. 1a in ref. 123). Two proposed reaction pathways for the growth of (InP)n quantum dots (QD) starting with the amine-based pre-synthesized seeds of InP QDs plus In(III) alkanoate, In(Fa)3 (Fa = fatty acid carboxylate anion), and tris(trimethylsilyl)phosphine, (TMS)3P, in the absence (left) or presence (right) of the surface-activation reagent acetylacetone. Reproduced with permission from ref. 123. Copyright 2017 Springer. | ||
Overall, the demonstration of surface ligand participation in the (InP)n system123 is strong evidence indicating that nucleation is chemical-reaction-rate based and, hence, not “burst” in this (InP)n system.123
Two very recent papers on (InP)n nanocrystal quantum dot (QD) formation (i.e., recent enough that they are not included in Table S2 in the ESI†) interpret their data in terms of continuous nucleation.125,126 Owen's system is a well-defined system with 31P and UV-vis (413 nm) handles that merits a detailed kinetics and mechanistic study, although the slow, possibly rate-determining nature of the early precursor conversion step(s) may hinder insights into the desired nucleation, growth and any agglomeration steps present.125 Bawendi's paper cleverly compares continuous, interrupted, and variable rate injections of precursor as a way to yield larger particles with low (albeit unspecified) size dispersity.126 Continuous nucleation3 and the “smaller grow faster than larger”61,62 are used to rationalize the results, although independent evidence for these concepts in the (InP)n system was not provided,126 not unexpectedly as the work is focused on synthesis. A “persistent intermediate” is observed that is believed to be on the reaction pathway, although as discussed earlier pre- and post-steady state kinetics will be needed to support or refute this claim while distinguishing from off-path species. In short, these interesting systems are advancing our knowledge of (InP)n particle synthesis so that kinetics and mechanistic studies, leading to additional insights into the detailed, underlying mechanisms, would be welcome for these important systems.
Peng and co-workers also report127 the synthesis of near-monodisperse zinc blende (CdSe)n nanocrystals, coated with cadmium carboxylate ligands, starting with cadmium stearate and a selenium suspension in octadecene. Given that carboxylates are negatively charged, these seeds have excess Cd2+ ions on their surface and react with Se precursor in the presence of amine to form amine-terminated nanocrystals127 as illustrated schematically in Fig. 12. Addition of Cd(O2CR)2, as shown in Fig. 12, gets one back to a species with surface Cd2+ ions so that the cyclic growth with added Se and amine can be repeated. The mean diameter of the resultant (CdSe)n nanocrystals is found to increase linearly with the number of cycles as shown in Fig. 1e of that paper.127
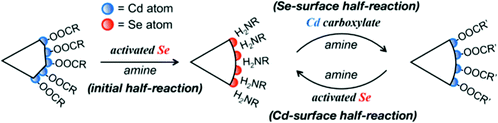 | ||
| Fig. 12 (Fig. 1a in ref. 127) Scheme illustrating growth starting on CdSe quantum dots (QD) seeds via synthesis cycles that start with cadmium stearate and a selenium suspension in octadecene plus fatty amine for selenium activation. The initial half-reaction with the amine-activated selenium yielding amine-terminated nanocrystals. The second half-reaction adds cadmium carboxylate to yield the carboxylate terminated nanocrystals. Additional cycles yield additional growth. Reproduced with permission from ref. 127. Copyright 2018 American Chemical Society. | ||
The two papers by Peng and co-workers123,127 discussed above demonstrate the role of surface ligands in the formation as well as in the stabilization of semiconductor quantum dots. A similar ligand effect has also been observed in the case of coinage metal chalcogenide nanocrystals obtained from N-heterocyclic carbene (NHC) synthons,128 in which the size of metal chalcogenide particles depends on the electron donating ability of the NHC ligands on the surface of nanoparticles.
In contrast to a 2014 paper129 claiming the synthesis of bare (CdS)n nanocrystals from the thermal decomposition of cadmium(II) stearate and sulfur at 260 °C, Owen and co-workers130 reported the formation of cadmium sulfide nanocrystals with tetradecanoate surface termination from the heating of Cd(S2PPh2)2 and cadmium tetradecanoate (≥4 equiv.) to 240 °C with the complete conversion of Cd(S2PPh2)2 to the nanoclusters, as shown in eqn (11). Interestingly, the final average size of (CdS)n nanocrystals (∼3.5 nm by TEM) is insensitive to the reaction conditions, including to the total concentration of the precursors and the initial cadmium to sulfur ratio, an observation that points towards the effect of carboxylate ligand-stabilization of the nanoparticles. That said, a goal for additional studies should be to determine the exact composition of the CdaSb(O2CR)c nanocrystals under the various different conditions.
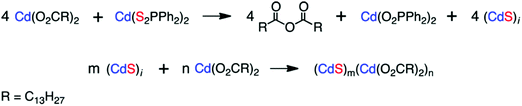 | (11) |
The nanoparticle formation reaction was monitored by 31P NMR, UV-vis, and FT-IR spectroscopies. Fig. 13 shows the formation of (CdS)n nanocrystals versus time, with the caveat that the temperature ramp complicates the early-time kinetics (especially the first 5 minutes) so that, for example, an unequivocal determination of whether or not an induction period is present was not possible. Owen and co-workers were able to determine that “nucleation has a first order dependence on total precursor concentration”.130 Additional work on the early-time kinetics of this interesting, well-defined system, ideally under isothermal kinetics conditions if possible, would be a welcome addition to the literature.
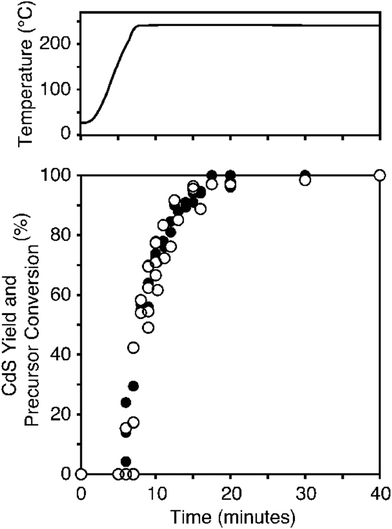 | ||
| Fig. 13 (Fig. 7 of ref. 130). Kinetics data showing both precursor conversion (filled circles) and nanocrystal formation (empty circles), determined by 31P NMR and UV-vis absorption spectroscopies, respectively. The data points, and thus two reaction rates, correspond closely with one another. The top panel shows the temperature ramp during a typical reaction. Reproduced with permission from ref. 130. Copyright 2012 American Chemical Society. | ||
4.2. Formation of semiconductor nanoparticles by the “Heating-Up” method
A 2012 paper by Kim and Jang131 reports the synthesis of (CdSe)n nanocrystals with tunable morphology and optical properties via a microwave-assisted polyol process. The CdSe nucleation and growth kinetics along with the choice of precursor (CdCl2 or CdO) and solvent (ethylene glycol or glycerol) determine the resulting nanocrystal size and shape. XRD and TEM were used to characterize the (CdSe)n nanocrystals. However, no kinetics data monitoring the time dependence on either particle size or precursor/product concentration were reported. The authors interpret the anisotropic growth of the (CdSe)n nanocrystals using the 1950 model in a qualitative discussion and using two different curves (Fig. 8c of that paper131), one with a short time-span in the nucleation stage for the low solubility CdO precursor and one with a long time-span in the nucleation stage for CdCl2, which is highly soluble in ethylene glycol. Despite their citation of the 1950 model, the authors do not have definitive, quantitative evidence to support any mechanism underlying the formation of (CdSe)n nanocrystals under their reaction conditions. Direct, short-time-resolved kinetics studies of semiconductor nanoparticle formation by ideally multiple in operando physical methods are needed and should lead to better understanding of the mechanism(s) of formation of such as (CdSe)n semiconductor nanoparticles.In this regard, a state-of-the-art 2015 in situ SAXS and WAXS study is noteworthy in both what it achieves, as well as what remains to be done to elucidate additional kinetics and mechanistic insight.132 The precursors in eqn (12) were studied by the heating-up method, starting at 150 °C and heating to 240 °C at 1 °C per minute. The balanced reaction was not given, and the source of electrons to reduce the Se to Se2− are not known, but the reaction as far as one can write it is shown in eqn (12):
 | (12) |
The most important results in the study are that direct, in situ SAXS and WAXS reveals an initial lamellar phase, melting to a micellar pre-nucleation phase, then the first-observable clusters (FOCs17) of size ≥1 nm and hence size133 (CdSe)x, x ≥ 10, at 218 °C, plus subsequent growth by an unknown mechanism. The study was also able to rule out diffusion-controlled growth by showing that the observed growth phase is 108 slower than diffusion control. The reduction of Se to Se2− is identified as the slow step of the reaction, as one might expect and consistent with other studies cited in the paper. The authors rationalize their work in terms of CNT and the 1950 model, stating that “Overall, a LaMer-type mechanism is observed”, a statement inconsistent with their own disproof of diffusion-controlled growth that is an integral part of the 1950 model. Hence, still needed to uncover the true underlying mechanism are: (i) establishment of the balanced reaction and especially the source of the reductant for the Se to Se2− reduction that looks to be the rate-determining step, (ii) development of either a faster reductant that, then, may not obscure the desired nucleation and growth kinetics, or development of a way to study the reaction isothermally while starting at a higher temperature close to 218 °C, and then (iii) kinetics and a rate law under those isothermal conditions in order to identify the true underlying mechanism.
4.3. Formation of semiconductor nanoparticles by the hot-injection method
A 2013 paper by Mukai and co-workers134 reports the synthesis of colloidal (PbS)n quantum dots by hot-injection of an oleylamine and sulfur solution into a suspension of PbCl2 in oleylamine at 70 or 80 °C. The resulting (PbS)n nanocrystals are unfortunately not well characterized. Additionally, the existence of potential surface ligands was not investigated. This system is similar to the (CdSe)n nanocluster system described in Section 4.1, where oleylamine surface ligands are present. Hence, it is likely the surface of the PbS nanocrystals are amine-passivated, a point that merits additional study.The authors claim that the nucleation and growth of the (PbS)n nanocrystals occur by the 1950 model, but this claim is presented without any kinetics data to support or refute this claim. The authors claim the length (time period) of the nucleation period is dependent on the degree of supersaturation, but, again any type of quantitative analysis as a function of any true, measured supersaturation is missing. In short, the true mechanism underlying (PbS)n nanoparticle formation remains to be established, ideally after first establishing the average (PbaScAminec)n composition of the particles and then ideally by in operando monitoring of the kinetics of particle formation by ≥2 direct physical methods.
4.4. Additional papers on the formation of semiconductor nanoparticles and the 1950 model
Detailed summaries of the 26 papers citing the 1950 model and reporting the formation of semiconductor nanoparticles can be found in Table S2 in the ESI.† In addition to the papers discussed above and added140,141 to this section, additional papers on the following systems are provided in Table S2 (ESI†): lead sulfide,135 cadmium sulfide,136–138 cadmium selenide,139,140 indium phosphide,141 zinc sulfide,142 silver sulfide,143 fullerene nanowires,144 hot-injection,145,146 and continuous microwave-assisted gas–liquid segmented flow.147The bottom line is that direct, compelling evidence for burst nucleation and diffusion-controlled growth in semiconductor nanoparticle formation is missing, a surprising insight given the level of at least apparent acceptance of the 1950 model in the area. Additional, detailed kinetics and mechanistic studies are needed probing especially the nucleation step(s), but also the growth step(s), of semiconductor particle formation systems. Several systems ripe for such studies were identified.
5. Formation of metal nanoparticles
The literature of metal nanoparticle formation is vast from investigations over at least three decades. A search of nanoparticle formation in Web of Science reports 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 citations since 1990 and 9200 in just the past 5 years up to January 2019. (A search of “metal nanoparticle formation” yields 4050 hits, while a search of “gold nanoparticle formation” gives 4100 hits and, as an example, “silver nanoparticle formation” yields 2700 hits. Hence, the search term “metal nanoparticle formation” alone does not pick up all different metals.) Due to the sheer volume of research conducted on transition- and other metal-nanoparticle formation, this section will be focused on selected, especially highly investigated metals (gold, iridium, platinum, silver, and palladium) that have contributed significantly to the development of physical models or mechanisms for nucleation and growth, with of course an eye to those that cite or bear on the 1950 particle formation model. A full list of 69 references to metal nanoparticle formation related to the 1950 model can be found in Table S3 in the ESI,† covering the specific metals: gold,148–153 iridium,3,17 platinum,154,155 silver,156–158 palladium,159–161 and indium.162 Once again we strongly recommend prereading and studying the entries in Table S3 (ESI†) before proceeding, as the data and evidence summarized there will allow the reader to make up their own opinions before reading the next section. That said, the following section is the one where the PI and his students have the greatest amount of published expertise.
700 citations since 1990 and 9200 in just the past 5 years up to January 2019. (A search of “metal nanoparticle formation” yields 4050 hits, while a search of “gold nanoparticle formation” gives 4100 hits and, as an example, “silver nanoparticle formation” yields 2700 hits. Hence, the search term “metal nanoparticle formation” alone does not pick up all different metals.) Due to the sheer volume of research conducted on transition- and other metal-nanoparticle formation, this section will be focused on selected, especially highly investigated metals (gold, iridium, platinum, silver, and palladium) that have contributed significantly to the development of physical models or mechanisms for nucleation and growth, with of course an eye to those that cite or bear on the 1950 particle formation model. A full list of 69 references to metal nanoparticle formation related to the 1950 model can be found in Table S3 in the ESI,† covering the specific metals: gold,148–153 iridium,3,17 platinum,154,155 silver,156–158 palladium,159–161 and indium.162 Once again we strongly recommend prereading and studying the entries in Table S3 (ESI†) before proceeding, as the data and evidence summarized there will allow the reader to make up their own opinions before reading the next section. That said, the following section is the one where the PI and his students have the greatest amount of published expertise.
5.1. Formation of gold colloids via the Turkevich method
The formation of homogenous gold systems dates to 1857 with Faraday's research on gold colloids.163 As mentioned back in Section 1.6.1, the best-known early research on gold nanoparticles is Turkevich's 1951 classic citrate reduction-based synthesis of gold nanoparticles/gold sols,5 influential work that was often ahead of its time in the understanding and insights it provides. In recent years, several other groups have performed additional notable investigations of gold nanoparticle formation using a variety of techniques: pH variation,164 UV-Visible spectroscopy,165–168 and X-ray based techniques.169–172Fig. 14 shows the concentration of trivalent gold ions as a function of time during the gold sol formation from a sodium citrate and chloroaurate mixture. The data indicate a sigmoidal consumption curve as the gold is reduced (see Fig. S1 in the ESI† for the original data). This sigmoidal kinetics curve is characteristic of slow, continuous3 (not “burst”1) nucleation and autocatalytic (not “diffusion-controlled”1) growth. Indeed, the fit of the kinetics data in Fig. 14 to a simple 2-step mechanism3 consisting of slow continuous nucleation and non-diffusion-limited, autocatalytic surface growth demonstrates definitively that neither burst nucleation nor diffusion-controlled growth are part of Turkevich's classic system. The autocatalytic growth rate constant from the curve-fit in Fig. 14, k2 = 0.19 ± 0.01 M−1 min−1, is roughly ∼1012 times slower than diffusion controlled and if one uses ∼1012 M−1 min−1 for a diffusion-controlled reaction of a small molecule or small nanoparticle nucleus. Diffusion control for larger particles will of course be smaller than ∼1012 M−1 min−1, but not more than an order of magnitude or two, so that k2 = 0.19 ± 0.01 M−1 min−1 is still at least ∼1010 times slower than diffusion control in this specific system.
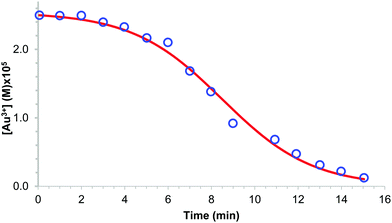 | ||
| Fig. 14 Plot of Au(III) ion concentration versus time during the gold–sol formation from a sodium citrate and chloroaurate mixture measured by withdrawing aliquot portions at prechosen times, placing them into a concentrated potassium iodide solution to quench the reaction, titrating the I2 formed iodine with an excess of standard thiosulfate solution, and then titrating the remaining thiosulfate with a standard iodine solution. The blue circles represents the experimental data obtained by digitizing the scanned plot in Fig. 11 on page 65 of the 1951 paper,5 an original plot reproduced as Fig. S1 of the ESI† accompanying this paper for the convenience of the reader. The red solid curve shows the fit of data to a 2-step mechanism3 of A → B (rate constant, k1) and then autocatalytic surface-growth, A + B → 2B (rate constant k2), yielding the rate constants for continuous nucleation of k1 = (7.9 ± 1.6) × 10−3 min−1 and for chemical-reaction-controlled, autocatalytic surface growth of k2 = 0.19 ± 0.01 M−1 min−1, with R2 = 0.9923 and reduced Chi-Sqr = 6.78 × 10−3, and where A is the Au(III) starting material, and B is by definition3 the average, growing Au(0)n particle. The choice of the 2-step mechanism to fit the kinetics is because doing so allows a ready demonstration that nucleation is not burst nor is growth diffusion controlled while using a normal, easily understood, classical kinetics treatment of the data that yields well-defined rate constants for the balanced-equation-defined continuous nucleation and autocatalytic surface-growth steps. | ||
In 1951 Turkevich provided the particle number versus time, and then particle number versus temperature, data reproduced in Fig. 15,5 data that are the first, compelling, classic evidence disproving the 1950 model as it might be applied to his Au(0)n formation system. Those data show the particle numbers versus time are (i) not instantaneous, (ii) not constant, nor (iii) temperature independent. Turkevich also noted5 that fluctuation theory (as underlies the burst-nucleation model, as discussed back in Section 1.3) could not explain “the marked temperature dependence of nucleation from the fluctuation point of view”.5,173,174 More specifically, Turkevich argued his “investigation indicates that the nuclei are ∼30 Å diameter and this would involve a fluctuation of the order of a million of gold atoms.”5 Turkevich reached these numbers because his largest final Au(0)n particle size was 240 Å (i.e., 24.0 nm) and hence ca. half a million gold atoms, Au∼428![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000. Turkevich was making the point that this early theory implied statistical fluctuations of apparently nearly all those millions of atoms in order to hypothetically yield putatively instantaneously formed nuclei, all ca. Au∼840 in size, something his comment indicates that he considered an extremely improbable event. For the record, Turkevich's observed “nucleus” size5 of ∼3 nm equals ∼840 Au atoms, Au∼840 (what we would now say was actually the first observable cluster (FOC)17 by the methods available at the time). The kinetically effective nucleus in the Turkevich Au(0)n system is still not known to our knowledge, but an educated17,26,27 guess is that the KEN is likely much smaller than Au∼840, and perhaps something closer to Au2–3.
000. Turkevich was making the point that this early theory implied statistical fluctuations of apparently nearly all those millions of atoms in order to hypothetically yield putatively instantaneously formed nuclei, all ca. Au∼840 in size, something his comment indicates that he considered an extremely improbable event. For the record, Turkevich's observed “nucleus” size5 of ∼3 nm equals ∼840 Au atoms, Au∼840 (what we would now say was actually the first observable cluster (FOC)17 by the methods available at the time). The kinetically effective nucleus in the Turkevich Au(0)n system is still not known to our knowledge, but an educated17,26,27 guess is that the KEN is likely much smaller than Au∼840, and perhaps something closer to Au2–3.
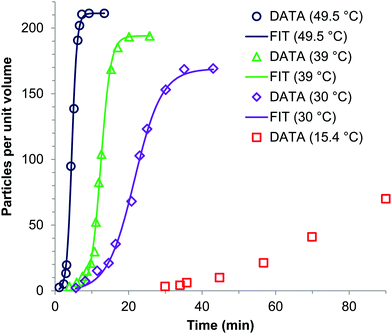 | ||
| Fig. 15 Plots of the number of gold(0) nanoparticles per unit volume versus time during the gold sol formation from a mixture of sodium citrate and chloroaurate at various temperatures (red squares at 15.4 °C, purple diamonds at 30.0 °C, green triangles at 39.0 °C, and dark blue circles at 49.5 °C).5 The data were obtained via nephelometry. The solid curves show the fits of data to a 2-step mechanism3 yielding the rate constants given in Table 1. (The data at 15.4 °C cannot fit because the final, maximum number of particles is missing.) The shortening of the induction period of each curve as temperature increases—that is, the increase in the nucleation rate constant k1, as shown in Table 2, is prima facie evidence for the dependence of nucleation on temperature—an experimental fact inconsistent with the assumption of temperature independence in the 1950 model (see the Part I review2 for details of the 9 approximations/assumptions underlying the burst-nucleation model). Fig. S2 in the ESI† presents the original data for the convenience of the reader. | ||
The resultant rate constants k1 and k2, as a function of temperature, from the fits in Fig. 15 are summarized in Table 3. As Fig. 15 shows (see also Fig. S2 in the ESI† for the original data), the induction period shortens, and the autocatalytic growth portion of the curve steepens, as the temperature of the reaction mixture increases—just as one expects for a two-step process that separates, at least somewhat, nucleation from growth and for temperature-dependent nucleation, k1, and autocatalytic surface growth, k2, rate constants.
A crude activation parameter plot for just the 3 data points in Table 3 over that limited temperature range yields the approximate activation parameters ΔH‡ = 8.9 ± 2.1 kcal mol−1 and ΔS‡ = 3.4 ± 6.5 e.u. (see Fig. S3 in the ESI† for the activation parameter plot; note also the somewhat unusual standard state for the ΔS‡ of (“particles per volume”)−1 min−1).5 The above kinetics data and analysis demonstrates that Turkevich's kinetics data for the formation of his colloidal Au(0)n particles are inconsistent with the “burst nucleation” and “diffusion-controlled growth” model. We have already cited Turkevich's 1953 “Organizer” mechanism6 and noted that Turkevich deserves credit for an early version of what now is the popular concept of prenucleation clusters or gels.72–77,81,175–178
Not surprisingly given the fits already presented in Fig. 15, it is possible to fit additional data from Turkevich's classic work5 with the 2-step mechanism,3Fig. 16 and 17. The resultant fits support the general concepts of slow continuous nucleation, and autocatalytic surface growth3 for the Au(0)n/citrate system (Fig. 18).
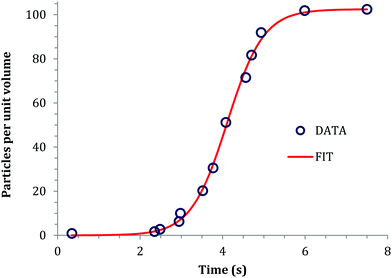 | ||
| Fig. 16 Plot reproduced from Turkevich's 1951 paper5 of the number of gold(0) nanoparticles per unit volume versus time during gold sol formation from a mixture of sodium citrate and tetrachloroauric acid by addition of hydroxylamine. Circles represents the experimental points measured using a nephelometer. The solid curve shows the fit of data to the 2-step mechanism3 of slow, continuous nucleation, A → B, followed by autocatalytic surface growth, A + B → 2B yielding the rate constants k1 = (1.9 ± 0.6) × 10−4 s−1 and k2 = (2.28 ± 0.09) × 10−2 (particles per unit volume)−1 s−1, R2 = 0.99774 and reduced Chi-Sqr = 3.58 × 10−4. Fig. S4 in ESI† presents the original data.5 | ||
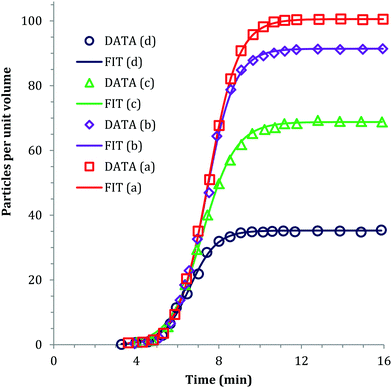 | ||
| Fig. 17 Plot reproduced from Turkevich's 1951 paper5 of the number of gold(0) nanoparticles per unit volume versus time during the gold sol formation from a mixture of sodium citrate and tetrachloroauric acid (a, red squares) nanoparticles obtained after complete development without adding hydroxylamine, and (b–d, purple diamonds, green triangles, dark blue circles) nanoparticles developed until addition of hydroxylamine at 6, 7, and 8 minutes. The solid curves show fits to a 2-step mechanism3 yielding the rate constants given in Table 4. See Fig. S5 in ESI† for the original data.5 | ||
 | ||
| Fig. 18 (Fig. 3 from ref. 6.) The particles per unit volume versus time in minutes for the formation of colloidal gold from tetrachloroauric acid, HAuCl4 and sodium acetonedicarboxylate, Na2[OC(CH2COO)2]. This curve provides direct evidence that new particles continue to appear over the first several minutes of the reaction. Reproduced with permission from ref. 6. Copyright 1953 American Chemical Society. | ||
| Data | Addition time of hydroxylamine | k 1, min−1 | k 2, (particles per volume)−1 min−1 | R 2 | Chi. sq. |
|---|---|---|---|---|---|
| (a) | No addition | (4.6 ± 0.6) × 10−5 | 1.38 ± 0.02 | 0.99972 | 5.02 × 10−5 |
| (b) | 6 min | (3.7 ± 0.9) × 10−5 | 1.58 ± 0.04 | 0.99899 | 1.42 × 10−4 |
| (c) | 7 min | (1.5 ± 0.3) × 10−4 | 1.83 ± 0.05 | 0.99887 | 8.37 × 10−5 |
| (d) | 8 min | (6.0 ± 2.1) × 10−5 | 4.21 ± 0.17 | 0.99763 | 4.71 × 10−5 |
In Fig. 17, Turkevich once again monitored the number of particles versus time, but now while using sodium acetonedicarboxylate as the reductant, the oxidized species of sodium citrate.6 The number of particles per unit volume is not instantaneous, and also increases with time, additional disproof of burst nucleation in his classic Au(0)n nanoparticle formation system.
In short, Turkevich's classic 1951 and subsequent papers, plus the fits of the kinetics to a 2-step mechanism provided herein for the first time, disprove compellingly the burst-nucleation and diffusion-controlled model as applied to Turkevich's classic Au(0)n formation system. It is surprising that Turkevich's 1951 experimental evidence did little to dampen the enthusiasm for the burst nucleation theory in the intervening ∼70 years.
Meriting mention at this point is a scholarly paper by Balashev and co-workers151 that compares the kinetics of Au(0)n formation by five methods: UV-visible (plasmon resonance, including a proper analysis of the plasmon resonance), SEM, DLS, TEM, and AFM, the latter thereby introducing AFM to the toolbox of ways to monitor nanoparticle formation kinetics.151 Important conclusions from this notable work (which used the 2-step mechanism3 to analyze the observed kinetics) include (see Table 1 in their paper151) (i) that both UV-visible and AFM gave the same values of nucleation, k1, and autocatalytic growth, k2, rate constants within experimental error of both methods, but (ii) that TEM and DLS gave k1 values differing by ∼0.16 fold and k2 differing by ∼2.1 fold, while (iii) SEM failed for Au(0)n nanoparticles < 20 nm. Useful in terms of the context of the present review and the curve-fits shown in Fig. 15–17 is their conclusions that “…our findings support strongly…that Turkevich's ‘organizer’ word-only mechanism is really the FW 2-step mechanism and therefore should be replaced by the FW 2-step mechanism”.151 Our added comment here is that while the 2-step mechanism can and does fit Turkevich's kinetics data, that in no way takes away anything from Turkevich's early studies and scholarly, formative contributions to gold nanoparticle chemistry and nanoparticle science more generally.5 And, the prenucleation cluster72–77,81,175–178 notion contained in Turkevich's 1953 Organizer mechanism6 precedes by 67 years what is currently a hot topic72–77,81,175–178 in nanoparticle formation science. Additionally, there is other, more detailed work on the mechanism(s) of Au(0)n nanoparticle formation, for example those in the next section due to Polte's group. The main point of the fittings above to the 2-step minimum mechanism is to test if “instantaneous nucleation” has any support in such Au(0)n nanoparticle formation systems. It does not.
5.2. Direct observation of gold particle formation via synchrotron X-ray radiation techniques
In the last decade, the use of synchrotron X-ray sources has become a preferred way to directly observe the process of metal nanoparticle formation. The use of SAXS,179,180 WAXS,181 and XAFS182,183 provides exceptional detail on particle size, metal oxidation state, number of nearest neighbors, and the identity of those nearest neighbors, all in real-time. In our own, collaborative work on SAXS of Ir nanoparticle formation, an important control experiment reveals that even a small Ir4 (isolable, fully characterized, and hence authentic) cluster184,185 Ir4H4(1,5-COD)4 is readily detectable by synchrotron-based SAXS (A. Karim, C. B. Whitehead, R. G. Finke, collaborative unpublished results). That control alone strongly supports the thesis that synchrotron-based SAXS179,180 holds considerable promise for adding to our insights about especially nucleation, but also growth and agglomeration, of nanoparticles.Polte and co-workers have reported several noteworthy, in-depth studies of Turkevich's classical citrate reduction of tetrachloroauric acid, measured by tandem in situ XANES and SAXS (along with some UV-vis), resulting in time-resolved, direct observation of gold particle formation.169–171 As seen in Fig. 19, the number of particles and hence nucleation is, once again, not instantaneous.169 Additionally, the number of particles decreases implying particle coalescence/agglomeration occurs later in the reaction and under the conditions employed. Polte et al.170 have also reported that the number of particles increases at the beginning of the reaction (observable due to the excellent time-resolution within the first seconds of the reaction, Fig. 5b therein), thereby again disproving “burst” nucleation in at least the specific gold particle formation system studied.
 | ||
| Fig. 19 (Fig. 3d from ref. 169.) The number of particles versus time (in minutes; represented by triangles) showing an initial increase followed by a dramatic decrease, at 75 °C and for 0.375 mM auric acid plus 2.5 mM sodium citrate and as measured by SAXS and XANES. The squares represent the radius (in nanometers) versus time (in minutes) measured in tandem with the number of particles. Reproduced with permission from ref. 169. Copyright 2010 American Chemical Society. | ||
Polte's valuable studies169,170 provide not only direct, synchrotron-radiation-based, additional disproof of the burst nucleation and diffusion-controlled growth model for Au(0)n nanoparticle formation, they also reveal the need for increased time resolution during the first 5 minutes of the reaction so as to better capture nucleation.186 These workers claim, however, that the necessary models to describe quantitatively the formation and growth of particles do not exist. Actually, disproof-based, deliberately minimalistic mechanistic models do in fact exist3,17,26,27,55–58,60–62 as described back in Table 2, mechanisms that can be applied quantitatively (i.e., as used in Fig. 15–17), including mechanisms that can quantitatively describe aggregation and coalescence.55–58 Indeed, it has already been noted that there are now 5 classes and 96 distinct pseudo-elementary step mechanisms that one can use to try to fit quantitatively one's particle formation kinetics data. The Ir(0)n system that gave rise to a number of those mechanisms is examined next, but only briefly, because it is our own work and because multiple full papers describing the systems and the kinetics and mechanistic evidence are available to the interested reader.3,17,26,27,55–58,60–62
5.3. Iridium nanoparticles and the origin of the 2-, 3- and two 4-step mechanisms
Iridium(0)n nanoparticles prepared from an atomically precisely defined precursor {(1,5-COD)IrI·POM}8−, and hence stabilized by a novel [P2W15Nb3O62]9− polyoxometalate (POM) “Gold Standard” stabilizer,187 led to the 2-step mechanism for particle formation, nominally: A → B, then A + B → 2B, where A really is A = A·L (L = ligand) = the {(1,5-COD)IrI·POM}8− precursor or precatalyst, and B = the growing Ir(0)n(POM9−)m prototype system.3 The balanced-equation defined k1 and k2 rate constants, and even more importantly the balanced-equation, mechanistically defined words to describe the process accurately, slow, continuous nucleation, followed by autocatalytic surface growth, are important aspects of the 2-step mechanism—the first alternative in nearly 50 years3 to the 1950 burst-nucleation model.1 Available to the interested reader is a discussion of what turned out to be the five special features27 of the prototype {(1,5-COD)IrI·POM}8− precursor and Ir(0)n(POM9−)m nanoparticle product system and the strengths, but also the weaknesses,48,60,89 of the deliberately minimalistic, Ockham's razor obeying, disproof-based 2-step mechanism. A 3- and two 4-step mechanisms are also available that are extensions of the 2-step mechanism that include bimolecular agglomeration (B + B → C),55,188 autocatalytic agglomeration (B + C → 1.5C),56–58,188 and secondary autocatalytic surface-growth (A + C → 1.5C).60–62Already mentioned in connection with mechanism-enabled population balance modeling (ME-PBM)61,62 is the discovery of a new, 3-step minimalistic mechanism that is a simple, but key, one-step extension of the classic 2-step minimum mechanism in which the A + B → 2B growth step is broken up into two size-dependent growth step. That new 3-step mechanism that was discovered via ME-PBM is the pseudo-elementary step mechanism of A → B (rate constant k1), A + B → C (rate constant k2), and A + C → 1.5C (rate constant k3). The fact that the new 3-step mechanism can account for relatively narrow PSDs, via the finding that k2 > k3 so that the smaller particles, B, grow faster than larger particles, C,61,62 explains how one can have slow, continuous nucleation3 yet still obtain narrow PSDs. Note that despite the general, somewhat ill-defined nature (i.e., outside of the atomistic ME-PBM) of the “smaller” and “larger” particles B and C respectively, the 3-step pseudo-elementary step model was sufficient to (a) discover the critical k2 > k3, “smaller react faster than larger” finding and concept for getting to near-monodisperse PSDs despite continuous nucleation; and (b) to permit MATLAB code to be written that allows a quantitative fitting of the PSDs with extraction of the rate constants from PSD data. The new 3-step in turn obviates the need to postulate “instantaneous/burst” nucleation1 in order to obtain narrow PSD from self-assembly reactions starting from continuous nucleation3 followed by thousands of chemical steps.61,62
5.4. Use of synchrotron X-ray radiation techniques to monitor the formation of platinum, silver, and palladium nanoparticles in separate studies
Several researchers have conducted kinetics studies of Pt, Pd, or Ag nanoparticle formation using either small-angle X-ray scattering (SAXS) or X-ray absorption fine structure (XAFS), while also mentioning the 1950 model in their papers. A list of such studies is given as Table S3 of the ESI.† Next, we describe three such illustrative studies on platinum, silver, and palladium nanoparticles.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) as a particle stabilizer. In situ monitoring at the Pt L3-edge and acquisitions were performed at 10–20 second intervals. Fig. 20 displays (a) the absorbance versus time, (b) the normalized absorbance versus time, (c) plots of [Pt4+]t/[Pt4+]0 and [Pt2+]t/[Pt2+]500versus time, and (d) [Pt2+]t/[Pt2+]500 and [(Pt0)m]t/[(Pt0)m]6000versus time.
000) as a particle stabilizer. In situ monitoring at the Pt L3-edge and acquisitions were performed at 10–20 second intervals. Fig. 20 displays (a) the absorbance versus time, (b) the normalized absorbance versus time, (c) plots of [Pt4+]t/[Pt4+]0 and [Pt2+]t/[Pt2+]500versus time, and (d) [Pt2+]t/[Pt2+]500 and [(Pt0)m]t/[(Pt0)m]6000versus time.
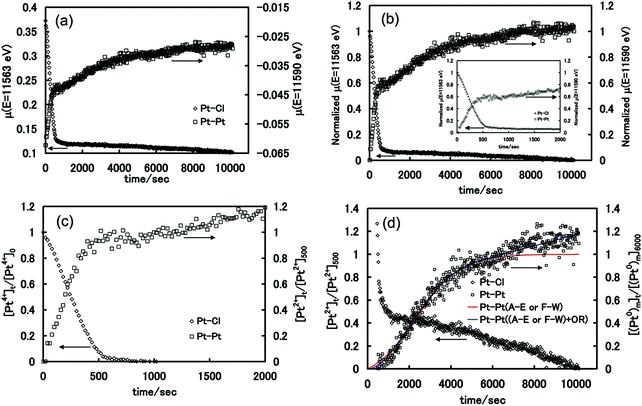 | ||
Fig. 20 (Fig. 4a–d from ref. 189.) (a) Time evolution of the absorbance coefficient, μ(E), intensity at the intrinsic peak energy (11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 563 and 11 563 and 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 590 eV) for the colloidal dispersions of Pt nanoparticles ([Pt] = 24.4 mM). (b) Time evolution of the normalized μ(E) as a function of the reduction time (t). The inset displays the corresponding enlarged plots during the first 2000 s. (c) Plots of [Pt4+]t/[Pt4+]0 and [Pt2+]t/[Pt2+]500 as a function of the reduction time on the basis of the temporal change of the normalized μ(E = 11 590 eV) for the colloidal dispersions of Pt nanoparticles ([Pt] = 24.4 mM). (b) Time evolution of the normalized μ(E) as a function of the reduction time (t). The inset displays the corresponding enlarged plots during the first 2000 s. (c) Plots of [Pt4+]t/[Pt4+]0 and [Pt2+]t/[Pt2+]500 as a function of the reduction time on the basis of the temporal change of the normalized μ(E = 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 563 eV) and μ(E = 11 563 eV) and μ(E = 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 590 eV). (d) Plots of [Pt2+]t/[Pt2+]500 and [(Pt0)m]t/[(Pt0)m]6000 as a function of the reduction time. Curve fitting to the experimental data was carried out on the basis of the Avrami–Erofe’ev (A–E) or Finke–Watzky (FW) 2-step model (red curve) for the solid-state kinetics or for the solution-phase reaction kinetics, and the A–E or FW model plus Ostwald ripening (OR) (blue curve). Reproduced with permission from ref. 189. Copyright 2012 American Chemical Society. 590 eV). (d) Plots of [Pt2+]t/[Pt2+]500 and [(Pt0)m]t/[(Pt0)m]6000 as a function of the reduction time. Curve fitting to the experimental data was carried out on the basis of the Avrami–Erofe’ev (A–E) or Finke–Watzky (FW) 2-step model (red curve) for the solid-state kinetics or for the solution-phase reaction kinetics, and the A–E or FW model plus Ostwald ripening (OR) (blue curve). Reproduced with permission from ref. 189. Copyright 2012 American Chemical Society. | ||
As seen in Fig. 20, Harada and Kamigaito directly monitored both the loss of platinum precursor and the formation of platinum nanoparticles by QXAFS.189 They observe an induction period at the beginning of irradiation followed by autocatalytic growth period. During the latter half of the growth period, the growth appears to be linear, which Harada assigns to be Ostwald ripening. The data were fit using differential equations from two nucleation and growth models: the Avrami–Erofe’ev (A–E) semi-empirical model42–44 and the 2-step mechanism.3 Both the A–E model and the 2-step mechanism fit the kinetics data (i.e., up to the point where linear growth is seen that is attributed by the authors to Ostwald Ripening). The equivalent fits by the A–E and 2-step models are not surprising considering the 2-step mechanism has been shown to be the minimal chemical mechanism underlying the semi-empirical Avrami equation.48 Use of the 2-step mechanism does, however, allow physically meaningful rate constants for nucleation and autocatalytic growth to be obtained rather than the Avrami exponent, n, and k parameters,48 the interpretation of which remains controversial.48,51 The fits by the A–E and 2-step models in turn implies that the burst nucleation model cannot account for the QXAFS data acquired by Harada and Kamigaito.
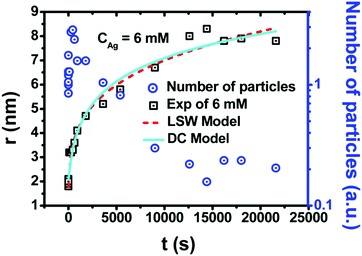 | ||
| Fig. 21 (Fig. 6 from ref. 190.) Particle number (a.u.) and particle size (nanometer) are plotted versus reaction time (seconds) at 6 mM AgNO3. The size vs. time data and the particle number vs. time data are represented, respectively, by black squares and blue circles. The size versus time data were fit with two different growth models. The dashed red line is the LSW (Lifshitz, Slyozov, and Wagner) Model proposing a mean-field theory of Ostwald ripening, and the solid, light blue line is the DC (Diffusion-Coalescence) Model of growth, discussed below. Reproduced with permission from ref. 190. Copyright 2014 American Chemical Society. | ||
During the first seconds of the reaction, Yan and co-workers observed a rapid increase in the number of silver particles due to the use of the strong reductant, NaBH4. Yan and co-workers note that “the nucleation begins at the very early stage, but it probably lasts in the whole formation process”190 while also commenting on the inability of the 1950 model to explain their kinetics data. The observed decrease in the number of particles is prima facie evidence for some type of coalescence/agglomerative process.
However, this study uses a diffusion-coalescence growth model, proposed on the basis of the assumption that Brownian motion drives the Ag particles to diffuse in the suspension and collide with each other to coalesce together (Ag + Ag → Ag2, Agm + Agn → Agm+n,…) and associated eqn (13) to fit the particle size vs. time data, Fig. 21, vide supra,
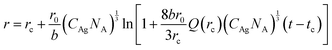 | (13) |
A very recent, important account by Bigioni and his co-workers158 covers the synthesis of silver molecular nanoparticles in some detail noting the importance of coordinating ligands and thermodynamic stability of Ag44 nanoparticles. The M4Ag44(p-MBA)30 nanoclusters are prepared from the sodium borohydride reduction of Ag(I)–p-MBA precursor (p-MBA: p-mercaptobenzoic acid) in the presence of alkali metal cation (M+) at pH = 9 in ethanol–water solution.191 The authors hypothesize the time of nucleation does not affect the size of the nanoparticle product, based on the results obtained from a test of separating nucleation events by arbitrarily long periods of time, and then evaluating the effect on the product size distribution.158 This test was performed by preparing a reaction mixture, splitting it into two parts, reducing only one of the two parts to obtain the Ag44 product, and then mixing the two parts back together such that the second part of the reaction mixture could be reduced in the presence of the Ag44 product (which had nucleated an arbitrary time earlier). Normally, one would have expected the Ag44 nanoparticles added to the reaction mixture to have acted as seeds and grown as the reducing agent was added, at least in the absence of very strong-binding ligands. The authors clearly demonstrated this was not the case; instead, the product is identical to that of the standard preparation as seen in Fig. 3 of their paper.191 The interesting, discrete Ag44 system merits additional mechanistic study and ME-PBModeling.61,62
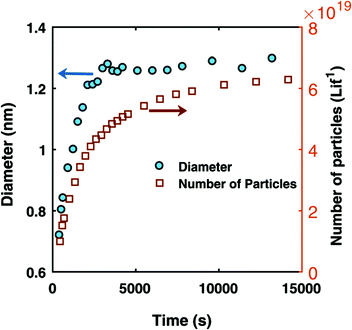 | ||
Fig. 22 (Fig. 1b from ref. 63.) The number of particles per liter of solution and the average particle size (nanometer) are plotted versus reaction time (seconds) obtained via in situ SAXS measurement for the formation of {Pd(0)n(POct3)a(OAc)b}b− nanoparticles starting with 10 mM Pd(OAc)2 plus 2 equivalents of trioctylphosphine per mole of Pd in 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 toluene: hexanol mixture at 100 °C. Reproduced with permission from ref. 63. Copyright 2017 The Royal Society of Chemistry. 50 toluene: hexanol mixture at 100 °C. Reproduced with permission from ref. 63. Copyright 2017 The Royal Society of Chemistry. | ||
While the evidence refuting the 1950 model for the formation of {Pd(0)n(POct3)a(OAc)b}b− nanoparticles is an important and definitive part of the noteworthy study by A. Karim and co-workers,63 the most important part of that work is that (i) it supports and extends significantly the addition to the 2-step mechanism of a A·L ⇌ A + L prior equilibrium first documented in 1997 in ref. 3 and then in more detail in 2017 in ref. 26 and then in 2019 in ref. 27, and very importantly (ii) it is the first compelling evidence for the addition of the B·L ⇌ B + L equilibrium to the 2-step mechanism. In short, the classic 2-step mechanism is thereby expanded to a 4-step, prior- and post-equilibria mechanism of nominally: A·L ⇌ A + L, A → B, B·L ⇌ B + L, and then A + B → 2B.
Harada and co-workers196 reported the formation of palladium (and rhodium) nanoparticles from photoreduction of metal chloride precursors in aqueous ethanol solution in the presence of polyvinylpyrrolidone (PVP) polymer stabilizer, which was followed by UV-vis, TEM, and in situ XAFS. Kinetics data are shown to fit to the 2-step mechanism for the formation of metal nanoparticles.196 A recent study on the palladium nanoparticle formation from the photoreduction of [PdCl4]2− precursor using the same methodology has also been reported and reaches similar conclusions.197
In short, considerable, direct, compelling evidence against—but no evidence for—the burst-nucleation model exists from studies of the formation of Au, Ir, Pt, Ag, and Pd nanoparticles. An important, likely much more general finding that has come out of the metal(0) nanoparticle formation studies described is the extension of the 2-step mechanism3 to the 4-pseudo-elementary-step mechanism that includes ligand effects63,198 of A·L ⇌ A + L, A → B, B·L ⇌ B + L, and then A + B → 2B.
6. A closer look at other systems employing the 1950 model: the formation of oxide nanoparticles
The 1950 model has also been used to try and understand the controlled growth of near-monodisperse silica spheres of micrometer size. Table S4 of the ESI† provides a summary list of 39 silica, titania, iron oxide, and other element-oxide nanoparticle formation papers that have considered the applicability or inapplicability of the 1950 model to the formation of oxide nanoparticles as those papers strove to explain their observed, sometimes record-narrow particle size-distributions. As before, prereading and prestudy of Table S4 (ESI†) is recommended prior to proceeding with the next section.6.1. Stöber process for the formation of silica nanospheres
A classic system describing the formation of “monodisperse” (i.e., actually not monodisperse, but very narrow size dispersion) particles was reported by Stöber, Fink and Bohn in 1968.199 The method, known as the “Stöber Process”, involves the hydrolysis of a dilute solution of tetraethoxysilane (TEOS) at high pH in alcohol solvent to form spherical silica particles of almost identical size with diameters that vary from 0.01–0.5 μm (10–500 nm) depending on pH and concentration of precursor used. Since the formative study by Stöber and his co-workers in 1968,199 the synthesis of colloidal spherical silica nanoparticles has relied extensively on ammonia-catalyzed hydrolysis of TEOS, and subsequent condensation of the resulting silanols, with the resulting silica particles readily tuned in size from 10 to 500 nm simply by altering the ammonia concentration.200 The 1968 paper by Stöber, Fink and Bohn is one of the most cited publications in the field (at present >10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 080 citations according to SCI, June 2019). There is accordingly an enormous, important literature of the Stöber Process. Only those papers that specifically mention the 1950 model are covered in what follows. The reader interested in further insights into the intriguing and important Stöber Process should consult that original literature for all of its additional insights.
080 citations according to SCI, June 2019). There is accordingly an enormous, important literature of the Stöber Process. Only those papers that specifically mention the 1950 model are covered in what follows. The reader interested in further insights into the intriguing and important Stöber Process should consult that original literature for all of its additional insights.
What is clear, however, is that despite a great deal of effort in the last decades, the formation mechanism of Stöber silica particles is still not well understood. Two growth models exist at present, the monomer-addition model201 and an aggregation-only model,202 both of which assume burst nucleation—that is, neither model gives any type of adequate, experimentally based accounting of the critical, initial nucleation event(s). Additionally, both models fail to explain the huge, controllable variation in size and particle-size distribution of the resultant silica particles as a function of the ammonia concentration. Only the aggregative model has been claimed to be able to account for very narrow particle-size distributions, as discussed in the next section that addresses Zukoski's important Aggregative Growth Model.
The basic reactions occurring in the Stöber Process are generally agreed to be:203
 | (14) |
 | (15) |
 | (16) |
Note that equations analogous to (15) and (16) can also be written for the higher Si-containing silanols that are expected to be present.
Notable upfront is a 1993 paper8 by Matijević that reviewed the preparation of “monodisperse” particles of simple or mixed composition and different shapes such as spheres, cubes, rods and ellipsoids. Matijević surprised the community at the time by remarking that “the recognition of the limitations of the 1950 model came through a number of experimental findings that contradicted it”8 so that “LaMer's approach is applicable in a limited number of cases”.8 Additionally, Matijević noted that “it has been proven in several cases for nucleation to be an ongoing process, yet still ‘monodispersed’ colloids were generated.”8 Matijević then discusses a number of alternative pathways for the formation of colloidal particles that are summarized in Table S4 of the ESI.†
 | ||
| Fig. 23 (Fig. 3 and 4 from ref. 204.) (a) 13C NMR peaks of the carbon bonded to oxygen and belonging either to an ethoxy group of TEOS molecule (60.8 ppm), or to a hydrolyzed ethanol molecule (58.8 ppm), as a function of time. The time difference between each scan is 28.8 min, [TEOS] = 0.167 M, [NH3] = 0.668 M, and [H2O] = 1.80 M in propanol solution. (b) Logarithm of the integrated intensity of the ethoxy carbon 13C NMR signal versus time. Reproduced with permission from ref. 204. Copyright 1992 Elsevier. | ||
In the 2017 study203 the concentration of TEOS was determined by ammonium molybdate spectrophotometric measurement throughout in the course of the Stöber process reaction starting with various ammonia concentrations. Conductivity of the reaction medium was also measured to reflect the concentration of anionic silanol intermediates, which exist in deprotonated, anionic and hence conducting form at pH > 9. An important finding is that unhydrolyzed TEOS molecules remain in the reaction medium until the end of process. Additionally, silanol species that are potential intermediates were identified by mass spectrometry, results which support similar findings of putative intermediates in silica particle formation detected by trimethylsilylation and then GC determination of the products.205 From the evaluation of TEOS concentration and conductivity versus time data, depending on the ammonia concentration, rate constants of TEOS hydrolysis were calculated and those of the subsequent condensation were derived by using the steady-state and equilibrium approximations.203 Based on the rate constants, the authors concluded that hydrolysis of one ethoxy group of TEOS molecule to form monovalent anionic silanol, Si(OEt)3(O−)1, is the rate-limiting step for TEOS hydrolysis. Hence, TEOS serves as the precursor undergoing direct hydrolysis (eqn (14)), as well as being able to react with silanol intermediates (eqn (15)) leading to particle growth. These discrete, continuous kinetic events are clearly completely different than a burst nucleation and diffusion-controlled type of process. Moreover, there is excellent agreement among four different studies on the rate law (and its temperature dependence) of rate-determining Si(OEt)4 hydrolysis (as detailed on p. 199, Fig. 9 in Giesche's classic paper205). That evidence indicates that Si(OEt)4 hydrolysis to Si–OH containing species is kinetically continuous. However, it remains to be established if nucleation is continuous or not and what mechanism(s) and concepts are required to explain the strikingly narrow particle-size distributions seen in the Stöber process. Zukoski's aggregative growth model is one idea that has promise, as discussed next.
Zukoski and co-workers then build a number density, population-balance model to try to explain the formation of near-monodisperse silica particles by (a) assuming an average nucleation rate “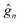 . ”202,206 of formation of particles of size r1 where206gn(t) = gs[e−k1t − e−k2t] corresponding to the A → B → C reaction sequence (and the form of gs given on p. 353 elsewhere206)—hence, continuous and not burst nucleation, plus (b) aggregative growth. Importantly, they find their model can (c) explain the narrow size-distribution as a result of aggregation (i.e., and not because of a “burst nucleation”) in which the “primary particles aggregate with larger particles more rapidly than they do with themselves”.202 The aggregative growth mechanism is further supported by the results of a cryoelectron microscope study211,212 revealing that the large final Stöber particles are not a single, dense particle but, instead, are actually compos of smaller, primary particles in loose, aggregated/polymeric structures209,212 as seen in Fig. S6 and S7 of the ESI.†
. ”202,206 of formation of particles of size r1 where206gn(t) = gs[e−k1t − e−k2t] corresponding to the A → B → C reaction sequence (and the form of gs given on p. 353 elsewhere206)—hence, continuous and not burst nucleation, plus (b) aggregative growth. Importantly, they find their model can (c) explain the narrow size-distribution as a result of aggregation (i.e., and not because of a “burst nucleation”) in which the “primary particles aggregate with larger particles more rapidly than they do with themselves”.202 The aggregative growth mechanism is further supported by the results of a cryoelectron microscope study211,212 revealing that the large final Stöber particles are not a single, dense particle but, instead, are actually compos of smaller, primary particles in loose, aggregated/polymeric structures209,212 as seen in Fig. S6 and S7 of the ESI.†
However and unfortunately, the Zukoski aggregation model provides no explanation for the formation of uniform primary particles that then aggregate. A confusing statement in Zukoski's paper, that would make it appear as if burst nucleation is still believed and part of their model, is their statement on p. 33 in the 1991 paper202 that their aggregation model “…is simply an extension of the 1950 model to the case where the nuclei may be colloidally unstable”. Hence, an issue that remains with the Zukoski aggregation model is how the uniform particles that then aggregate are formed in the first place.
Worth mentioning here is that precedent has existed since 200556–58 that the pseudo-elementary steps of B + B → C (rate constant k3)55–58 then B + C → 1.5C (rate constant k4)56–58 can quantitatively describe the kinetics of a number of aggregating systems,56–58,188,213–217 basically a sequence of bimolecular nucleation of aggregation (B + B → C) followed by smaller-larger size-focusing aggregation (B + C → 1.5C) that has often been found to be faster, k4 ≫ k3.56–58,188,213–217 Hence, further efforts are once again needed to understand what is a historically very important particle-formation system: namely how massive, nearly uniform size silica particles are formed.
However, the ostensibly zero-order kinetics for the hydrolysis of TEOS is inconsistent with the literature that invariably finds first-order [TEOS]1 hydrolysis kinetics204,205 (as for example shown in Fig. 10b elsewhere204). Furthermore, the 29Si NMR spectra taken from the solution after 0.5 and 3 h of the reaction are reported to show no signal for soluble silica species such as either silicate monomer or oligomers—negative evidence that is not usable without a demonstrated detection limit for those species. Note that the 29Si NMR spectra were taken of the aqueous phase of the emulsion system with [Si] > 1 M conditions;218 and that silicon species in ≥1 mM are expected to be readily detectable by 29Si NMR. (The presence of detectable initial oligomers from “burst nucleation” is expected if the 1950 model is correct, so the 29Si NMR spectroscopy would appear to be inconsistent with any model postulating burst nucleation.) Solid state 29Si MAS NMR spectrum of silica nanospheres after evaporation of solvent (Fig. 10 of that paper218) shows the existence of ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) Si–O− or
Si–O− or ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) Si–OH moieties in nanospheres, which are assumed to react with silicate monomers or oligomers when supplied at the interface of emulsion.
Si–OH moieties in nanospheres, which are assumed to react with silicate monomers or oligomers when supplied at the interface of emulsion.
In short, the evidence for a constant number density of silica particles is equivocal, and (negative) evidence exists against any type of burst-formation of particles—the key point being that positive evidence will be required in order to support the author's claim of the 1950 model being applicable to their system. Moreover, the authors did not compellingly rule out Zukoski's competing mechanism of continuous nucleation followed by aggregative growth. Hence, the Okubo et al. system218 is another interesting system that merits further, clarifying examination.
6.2. Iron-oxide nanoparticles obtained by thermal decomposition of precursor
The continuous-precursor-feeding synthesis was used by Huber et al.220 for the preparation of crystalline magnetite (Fe3O4) nanoparticles of sub-nanometer size of low size dispersity, between 9.3 ± 0.7 nm and 34.5 ± 1.6 nm. The Fe(III) oleate precursor was prepared from the reaction of Fe(acac)3 and excess oleic acid (solvent) at 320 °C and used without isolation or purification. The Fe(III) oleate in oleic acid plus 3.0 equiv. acetylacetone per mole of iron was diluted in 1-octadecene and then dripped a constant rate of 3 mL h−1 using a syringe pump into the reaction flask containing docosane and oleic acid and then heated to 350 °C. The precise balanced stoichiometry of the reaction was not established but is of interest, as that experimental stoichiometry is the necessary first step en route to understanding the underlying mechanism of formation of magnetite nanoparticles with such a narrow size distribution. Recall that as detailed elsewhere,2 a balanced reaction stoichiometry is a necessary first step of any reliable mechanism determination because the steps of the proposed mechanism must add up to (and thus serve as a check on) the observed, balanced reaction stoichiometry. Otherwise, one is proposing a mechanism for some reaction other rather than the one under study!
The diameter of magnetite nanoparticles versus time data, obtained by SAXS measurements and redisplayed in Fig. 24, was obtained as part of the reported studies.220 The authors attempted to interpret the growth of the nanoparticles by using a (words only, vide infra) combination of the burst-nucleation model and the FW 2-step mechanism—which at the outset makes no sense, given that the two are at the opposite ends of the spectrum of the kinetics of particle formation (“instantaneous/burst nucleation” and “diffusion-controlled growth”1 being the basis for the 1950 model while the 2-step mechanism involves “slow, continuous nucleation”3 and slower than diffusion controlled, “chemical reaction-controlled autocatalytic surface growth”3). Unfortunately, the authors did not fit their data with either model and, instead, used an empirical power function unconnected to either model/mechanism, all while ignoring the first 50 minutes of data (Fig. 24) in the fitting, the time during which significant nucleation is expected to occur.220
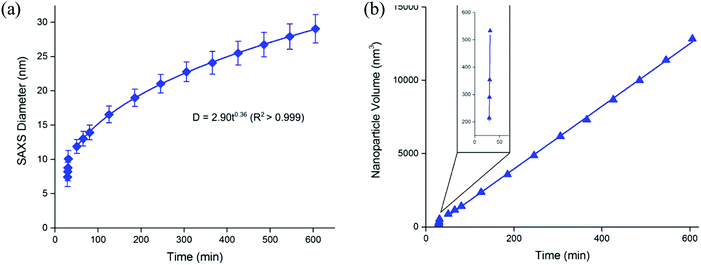 | ||
| Fig. 24 (Fig. 3 in ref. 220.) (a) Plot of diameter versus time calculated from SAXS measurements of the aliquots of magnetite nanoparticles during the decomposition of iron(III) oleate at 350 °C in docosane solution plus oleic acid and 3.0 equiv. acetylacetone at a feeding rate of 3 mL h−1. (b) Plot of nanoparticle volume against reaction time with a close-up of the first four aliquots measured shown in the inset. Reproduced with permission from ref. 220. Copyright 2015 American Chemical Society. | ||
The authors attempted to rationalize their results using a word-only, blended “LaMer plus FW-2-step” model they called the “Extended LaMer mechanism”, illustrated in Fig. 25.220 An examination of Fig. 25 reveals that it superimposes the experimentally determined iron(III) concentration present in solution220 (left-most y axis) with a cartoon presentation of the hypothetical soluble (1950-model-type) monomer concentration1 on the right-most y axis.
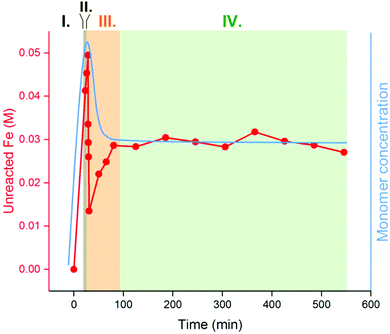 | ||
| Fig. 25 (Fig. 5 in ref. 220.) Experimental data of the unreacted iron precursor (red) are overlaid by a cartoon schematic representing an “extended LaMer” approach to nanoparticle synthesis (blue). The presumed four stages of the postulated “Extended LaMer mechanism” are shaded to identify their believed and hence imposed, approximate boundaries. Reproduced with permission from ref. 220. Copyright 2015 American Chemical Society. | ||
The problem with Fig. 25 is that the concentration of iron(III) oleate present in solution cannot be the same as (and therefore is misleading to co-plot along with) the concentration of the hypothetical soluble monomer of magnetite, (Fe3O4)n, whatever that may be.222 It at least appears that the authors have made the intellectual mistake of trying to “prove a mechanism” while actually constructing a single model that is an ill-advised combination of two physically opposite models. What is needed instead is proper scientific method of attempting to disprove the models,223,224 so that any that cannot be disproved at present remain as possibilities for further, future testing. The failure to try to quantitatively fit the data by either model, while instead using a “words-only” approach, is another classic mistake in the attempted application of physical models as detailed elsewhere.2 Additionally, a chemical reaction mechanism requires balanced chemical reactions that define the rate constants, the associated differential equation, and also quite importantly defines the precise words one can use to describe the proposed, stepwise processes, none of which are present as part of this work.220
Returning to Fig. 25, this figure has little to do with a LaMer-type model, as the four I–IV “phases” labeled in Fig. 25 in an attempt to support a LaMer-type model are, instead, very likely just (I) the initial rise in the precursor expected from injecting it; (II) nucleation and likely autocatalytic growth, perhaps following the 2-step mechanism3 as noted by the authors;220 (III) a dip below steady-state for reasons that are unclear at present (perhaps due to smaller particles reacting faster than larger ones?61,62); and (IV) then steady-state in the continuous injection system. Most telling in this work is how misleading it is to stick with one's initial hypothesis (anchor bias), in this case the hypothetical “Extended LaMer mechanism”, and then perform confirmation bias from one's anchor bias starting point by gathering only the data consistent with one's single, starting hypothesis. Application instead of Chamberlin's223 and Platt's224 superior scientific method emphasizing225 disproof of multiple alternative hypotheses—especially attempting to disprove one's own original, pet hypothesis—is once again what was needed here. As Platt notes “for exploring the unknown, there is no faster method”224 than the attempted disproof of multiple, alternative hypotheses.
Nevertheless, the clever use of the open, continuous injection of precursor system is noteworthy,220 even if not new in studies that mention the 1950 model99–101,104,220,226,227 (e.g., Sugimoto's 1992 report on the formation of colloidal silver bromide in an open system where two solutions of silver nitrate and potassium bromide were simultaneously and continuously introduced into an aqueous solution of inert gelatin at a controlled rate,100 a study we covered back in Section 3.2). The attention to a reproducible formation of the iron oleate precursor, and to a reproducible synthesis, are other valuable parts of this study220 that merit further examination and attempts to quantitatively understand the underlying mechanism and advantages/disadvantages of the open, continuous precursor-injection system(s). Any more detailed look at this system should also endeavor to understand the “question of what causes the batch-to-batch variation in particle sizes” identified by the authors via their careful experimental work (see p. 60603).220 Possible explanations meriting attempted disproof include (a) higher kinetic order (i.e., concentration) effects on nucleation,17,26,27 (b) Epstein's important work on the large effects of imperfect mixing on reactions involving autocatalytic steps,228 and (c) the effects of dust (see Section 10).
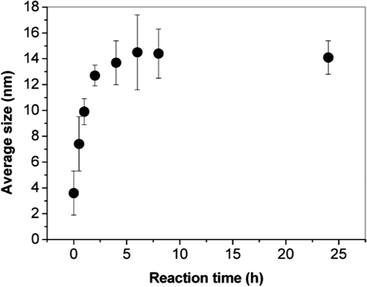 | ||
| Fig. 26 (Fig. 1a in ref. 229.) Average diameter of iron-oxide nanoparticles as function reflux time. The nanoparticles are formed from the decomposition of iron(II) stearate in the presence of 2 equivalents of oleic acid (stabilizer) and refluxing in octyl ether (solvent, b.p. 287 °C). Reproduced with permission from ref. 229. Copyright 2014 American Chemical Society. | ||
The authors conducted in-depth characterization of the resultant nanoparticles, including extensive magnetism studies, that are noteworthy. However, the particle formation was attributed to the 1950 model using a words-only, qualitative explanation229 of how the synthetic parameters are claimed to influence their reaction via the 1950 model. Presently, no data support, or definitively refute, the 1950 model for this iron-oxide system. What is needed to move this system to a better understood level is the complete, balanced reaction stoichiometry and then kinetics and mechanism-based differential equations to describe the pseudo-elementary steps that lead to iron-oxide formation.
A 2008 account by Kwon and Hyeon232 reports the formation of iron-oxide nanocrystals from thermal decomposition of Fe(CO)5 with oleic acid again in dioctyl ether. The authors claim that the nanoparticle formation occurs in three steps consistent with the 1950 model: accumulation of iron(III) oleate monomer, burst nucleation, and size focusing. However, their kinetics data for the extent of the thermal decomposition reaction and concomitant formation of iron-oxide nanocrystals (Fig. 15 of ref. 232) show an induction period in an overall sigmoidal curve, inconsistent with putative “burst nucleation”, but suggestive instead of continuous nucleation. Hence, the evidence in this 2008 study also argues for the inapplicability of the burst-nucleation model to the formation of iron-oxide nanoparticles.
In short, there is no compelling evidence for, and suggestive evidence against, the burst-nucleation model's applicability to iron-oxide particles as well as to silica particles. Some evidence that these systems actually involved continuous nucleation is apparent, arguing that more detailed kinetics and mechanistic investigations are needed in order to be able to write down the true particle-formation mechanism for these metal-oxide systems.
6.3. Formation of other metal-oxide nanoparticles
Thirty-nine other papers on metal oxide nanoparticles that cite the 1950 model have been analyzed as summarized in Table S4 in the ESI† for the interested reader. In addition to the papers that have been discussed (vide supra), the following are included in Table S4 (ESI†): cobalt oxide,233 copper oxide,234,235 zirconia,236 silica and titania,104,237–243 iron oxide,244–249 indium oxide,250 and a mathematical model.251 In all of these reports save three exceptions,233,237,238 the 1950 model is used to rationalize the observations, albeit in a “words-only” fashion. Hence, in each of these cases, additional studies are needed before a better understanding of their particle formation mechanism(s) can be claimed.7. A reminder about the 1950 model's quantitative equations—and the disconnect versus the words-only “burst-nucleation” and diffusion-controlled growth qualitative model
Noteworthy is that none of the studies examined to this point, nor any others2 of the nearly two-thousand papers citing the 1950 paper,1 successfully use the 1950 paper's quantitative radius2 (x2) equation to fit their data, eqn (17). Nor has any paper or study citing the burst-nucleation model used the “special case” as it is called in the 1950 paper,1eqn (18), to fit their data. Noteworthy here is that eqn (17) is the equation LaMer used to fit his smoothly increasing, downwardly concave (S)n sol radius vs. time data in Fig. 7 of his 1950 paper1—data that does not show any “burst” process.1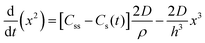 | (17) |
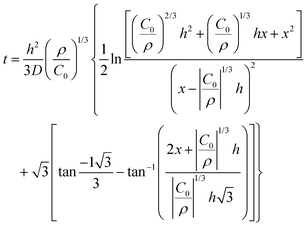 | (18) |
7.1. Recent demonstration of a “burst-nucleation-like plot”—that actually stems from continuous nucleation and size-dependent growth
Of interest here is that the new 3-step mechanism discovered recently via mechanism-enabled population-balance modeling (ME-PBM), for the Ir(0)n nanoparticle formation,61,62 yields a nucleation plot for the formation of the experimentally established Ir3 nuclei that looks a lot like it might support a “burst-nucleation-type” mechanism. See especially the top middle plot of the nucleation rate vs. time in Fig. 27 below. Most researchers looking at that nucleation rate vs. time plot would probably believe that it supports the classic 1950 model and associated, highly cited qualitative figure back in Fig. 7a.However, the top middle plot of the nucleation rate comes (as do the other plots in Fig. 27) from the ME-PBM with the 3-step mechanism of kinetically continuous nucleation3 (specifically experimentally determined continuous “alternative termolecular” nucleation26) that can be summarized in a minimalistic way by the pseudo-elementary step of A → B (rate constant k1)17,26,27 and then the size-dependent growth steps of A + B → C (rate constant k2), and A + C → 1.5C (rate constant k3),61,62 the last mechanistic model back in Table 2. The rates for both nucleation and growth appear to spike and be “burst-like”, yet these rates are actually the result of kinetically continuous nucleation. The full details are available elsewhere for the interested reader.62
 | ||
| Fig. 27 Numerically calculated number of particles (M), nucleation rate (M h−1), and growth rate (M h−1) for the 3-step mechanism with the experimentally established nucleation mechanism (“alternative termolecular nucleation”26,61,62) used to construct the mechanism-enabled population balance model. Both unscaled (top) and scaled (bottom) versions of the results from the ME-PBM are shown. The number of particles increases monotonically demonstrating the continuous nucleation of particles. The nucleation rate spikes, and appears “burst-like”, but actually involves kinetically continuous nucleation. The burst feature is actually due to burst-like autocatalytic growth, as shown in the bottom-left figure. The spike periods of nucleation and growth where the two rates are both relatively very high overlap for approximately one fifth of the measured time. Reproduced with permission from ref. 62. Copyright 2020 American Chemical Society. | ||
The perhaps obvious take-home message is that a curve that qualitative looks like “burst nucleation” may actually really be due to burst-like autocatalytic growth, a feature that will deceive the unwary researcher not using a proper, disproof-based scientific method.223,224 Researchers not also using quantitative equations from either mechanisms or other models to try to fit the kinetics and information-rich PSD61,62 data also have a strong chance of being deceived into claiming they have observed “burst nucleation” as assumed in the 1950 mathematical model.
8. Alternative literature models/mechanisms that cite the 1950 model
The following topics are summarized in seventeen entries in Table S5 in the ESI† for the interested reader: kinetics of precipitation from supersaturated solid solutions,252 oriented attachment at crystallographically specific surfaces,253–255 inverting the nucleation and growth processes,256,257 aggregative growth processes,258–265 another three stage mechanism,251 rethermalization and irreversible diffusional growth,266 mechanisms of diffusional nucleation of nanocrystals and their self-assembly into uniform colloids,267 a classical model and a different two-step model for nucleation of crystals from solution,16 nucleation and growth of nanoparticles in the atmosphere,12 dispersive kinetics,268 nanoscale-modified LaMer model,269 Burst–Schiffrin methods and associated population-balance modeling,270 and the FW 2-step mechanism extended to a photomechanical 9-methylanthracene crystal system.271 We refer the interested reader to those studies and Table S5 (ESI†).9. Conclusions
This second, Part II review has covered the Classical Nucleation and Fluctuation Theory basis for the 1950 model and the models and main pseudo-elementary step, disproof-based mechanisms for phase changes and particle formation in the literature since the 1950 paper by LaMer. Specifically, the papers in the literature up to March 2019 were presented that cite the burst-nucleation model while also providing data for silver halide, semiconductor, metal, and metal-oxide particle formation systems. Those studies contain a wealth of data from often cleverly designed and many times expertly executed studies, more recently using powerful synchrotron-based XAFS and SAXS methods. The primary conclusions one can draw are the following, while emphasizing that we and the community have the advantage of ca. 70 years of additional knowledge, advanced experimental and computational methods and hence associated hindsight in reaching the following conclusions compared to the information and tools that were available in 1950.• Classical nucleation theory that underlies the original burst-nucleation model1 was designed for weakly interacting systems where the identity of the associating unit is retained, such as hydrocarbon association in the gas phase, and where supersaturation is not greatly exceeded. CNT has proved inapplicable to strong bonding systems far beyond supersaturation such as arguably all of the systems and papers examined in this review and the tables in the ESI.†
• No study other than the original 1950 paper1 fits experimental particle radius versus time data with the 1950 paper's equation, eqn (17)vide supra. Noteworthy is that the Fig. 7 data in the 1950 paper that is fit with eqn (17) does not contain a burst nucleation feature. One attempted fit by others using eqn (17) for a (S)n formation system failed272 as discussed in our Part I review.2
• Clear, convincing, definitive experimental evidence for either “instantaneous/burst” nucleation or “diffusion-controlled” growth is not apparent in any of the nearly two-thousand papers examined that cite the 1950 model to date, at least so far as we have been able to discern. Even for the previously believed “best examples” of (AgX)n formation or hot-injection methods for making semi-conductor nanoparticles, compelling kinetics evidence for anything approaching “instantaneous” or burst nucleation seems to be lacking. Our apologies in advance to the Community if we have somehow overlooked a key paper or papers containing definitive evidence as we scoured through the voluminous literature citing the 1950 model.
• A number of studies conclude that their evidence disproves “instantaneous/burst” nucleation in those different, specific systems. Several of those specific systems and studies were mentioned in the main text.3,5,6,17,26,27,48,51,60–63,71,121,122,130,132,159,164,170,188,189,206,233,237,238,260,261,271 All of those studies, and others273–275 that disprove the model, can be found in the tables provided as ESI† and are labeled as providing evidence disproving the 1950 model for their system.
• The 32 independent papers cited just above, when combined with the lack of evidence uncovered from a comprehensive look at the papers citing the 1950 model, provides strong, seemingly compelling evidence against the 1950 mathematical model as well as the often-cited, words only version of the model in the 1950 paper. The reader who has taken time to study the 74 pages and 5 tables in the ESI† can compare this statement to their own conclusions. Note here that we do not mean to imply that words-only models are not useful in science—indeed, qualitative word-only statements are the most powerful in science, but they often come out of, or at least are strongly and best supported by, quantitative data. But for the words-only version of LaMer's 1950 model, one can now state with some confidence that words-only version has not proved useful—and has also proved difficult to try to disprove, thereby hindering scientific advance. Additional discussion of and references to words-only vs. mathematical vs. mechanistic models in science is contained in our Part I review (e.g., see Section 2.6 there2) as well as elsewhere51 for the interested reader.
• Numerous studies that claim their system undergoes “instantaneous/burst” nucleation actually contain data that in our opinion disproves that claim.99,107,108,147,165,169,220,256
• At least at present the widely cited and often reproduced “LaMer figure” (Fig. 1 in the 1950 paper,1Fig. 1a in Part I of this series,2 and reproduced herein as Fig. 7a, vide supra) remains to be experimentally verified and, hence, constructed from actual, quantitative experimental data rather than its status currently as an interesting artistic drawing.
• The valuable Sugimoto et al. study of (AgX)n formation and its associated Fig. 8 merits additional studies, plus efforts to understand mechanistically the spike in the [Ag+] supersaturation ratio seen in Fig. 8 of that classic study—is that spike really a spike in growth rather than nucleation, is one key question that needs to be addressed.
• At present and based on the available literature, one if forced to conclude that the creative 1950 model has little experimental support even after 70 years and despite many claims to the contrary.
• One cannot escape contemplating what would have expedited moving the science and our understanding of nucleation and growth beyond the 1950 model at a faster pace? Some thoughts are summarized in a footnote for the interested reader,276 including an excellent, recent ACS Catalysis editorial entitled “The Burden of Disproof”225 and thoughts about a better consideration and understanding of the different types of models in science.277–279
• Table 2 summarized the main pseudo-elementary step, disproof-based mechanisms for phase changes and particle formation that have appeared in the literature since the 1950 paper and that are in more general “A, B, and C…” species form. Those mechanistic models are available for fitting and initial interpretation of often sigmoidal-shaped particle formation and other phase-change kinetics data, as well as for mechanistically enabling population balance models.
• The available evidence across the systems studied and reviewed herein, and hence a primary working hypothesis going forward to test and to try to disprove, is that nucleation may well more often be continuous3 kinetically.
• A very important point is that kinetically continuous nucleation, even when slower than explosive, exponential, autocatalytic growth as may often be the case, can yield a “burst” of nucleation and can show some separation of nucleation and growth in time, as demonstrated in Fig. 27. What is most often probably observable and hence observed is not burst nucleation, but instead burst growth to first observable clusters17 according to the sensitivity of whatever physical method is being employed. A separate publication is available expanding on the idea of “burst nucleation vs. burst growth”280 while also addressing a few additional issues about the 1950 diagram revealed during the construction of the present review.
• Another important point is the finding that a 3-step mechanism, that is a 1-step upgrade of the 2-step mechanism that can allow smaller particles to grow faster than larger particles, can give rise to narrow PSDs despite continuous nucleation.
• However, the remarkable fact that narrow dispersions of particles are known to result even after tens of thousands (to millions) of assembled atoms or structural units in cases such as silica particles—that, therefore, must have an equivalently large number of elementary steps in their actual, atomistic mechanistic steps—indicates that novel, to-be-discovered mechanistic insights remain hidden in such massive self-assembly systems.
• The need for additional in operando experimental measurements able to time resolve especially nucleation but also growth (as well as any agglomeration), ideally by multiple, complementary physical methods, is apparent and a conclusion reached at the end of several different sections in the review. Fortunately, XAFS, SAXS, in situ microscopy and other advanced physical method studies of multiple systems by a variety of expert investigators are currently ongoing and available to the community.
10. A look towards the future
The future for a better understanding of particle and crystal formation across nature is actually bright in our view. First, a large number of talented researchers using the most powerful physical methods such as SAXS, XAFS, environmental EM, and other method are investigating a variety of nucleating, growing and often agglomerating systems across nature, often in situ or in operando. A number of models and mechanistic efforts were cited in the main text and are noted in the tables in the ESI† that are disproof based and merit additional, careful and deeper investigation along with further attempted disproof anywhere their application might make sense. Disproof-based, deliberately minimalistic 2-, 3-, and two 4-step models that include two types of aggregation/agglomeration are available for fitting kinetics data involving nucleation, growth, and agglomeration processes—with the caveat that attention needs to be paid to the well-advertised limitations of those deliberately minimalistic, Ockham's razor-obeying mechanistic models.48,60,89 Detailed, molecular-level insights into nucleation for strongly bonded systems17 are beginning to appear,17,26,27 and the involvement of dust and prevalence of heterogeneous nucleation5,281–298 are becoming re-appreciated—noteworthy here is that the effects of dust on water vapor nucleation have been known since seminal studies the late 1800s.281–286 The concept of prenucleation clusters is gaining experimental support and hence momentum72–76,175–178—modern ideas that connect back to Turkevich's original “Organizer” concept. Ligand effects are obviously very prevalent in particle formation (e.g., in the studies of semi-conductor particle formation, Table S2 of the ESI†), and just now being added to minimalistic mechanisms in both the nucleation step from an A·L precursor (A·L ⇌ A + L)26,27,63 and subsequent, pseudo-elementary3 steps, notably ligand (L)-binding to the nanoparticle product (B + L ⇌ B·L), as demonstrated in A. Karim's insightful studies of Pdn nanoparticle formation that involve both A·L and B·L species.63,192 Considerable more effort to document, understand, and exploit ligand effects, and to elucidate their underlying mechanistic basis, seem well warranted if not wise. The combination of the precursor26,27,63 A·L and product B·L equilibria,63 with the 2-,3-, and two 4-step minimum mechanisms now available,3,17,55–58,60,187,188 along with minimal unimolecular3 and precedented unimolecular (but in a bimetallic precursor),27 second-order,17 and ter-molecular (specifically “alternative termolecular”26) nucleation, one can write out 5 subclasses of mechanisms containing 96 reasonable, distinct mechanisms to try out for one's particle formation (and any subsequent agglomeration) system.61,62 The anticipated result is the desired synthetic control over especially particle size, particle-size dispersity, and surface ligands that a mechanism-based understanding promises to give. Computational studies continue to become more and more relevant and of increasing reliability.36,37 One can also examine other models/theories for particle growth as alternative hypotheses for the system at hand and to contrast a mechanism-based approach if desired, Table 1, vide supra. Analysis and insights from other areas where nucleation and growth are involved and actively studied such as protein aggregation are available for study.64Promising and potentially very powerful is the advent of mechanism-enabled population balance modeling (ME-PBM) as a tool for predicting particle-size distributions (PSDs) from a given mechanism, as well as for use in the “inverse problem” of extracting the kinetics data buried within the convoluted-information-rich PSD to inform and refine the particle formation mechanism.61,62 One now can and should test one's proposed particle formation mechanism with the powerful tool of ME-PBM.61,62 Especially important is the paradigm-shifting finding from that ME-PBM that narrow size distributions do not require undemonstrated “instantaneous/burst nucleation”. Instead, narrow PSDs can result from continuous nucleation because smaller particles can grow faster than larger ones, thereby catching up with the larger particles en route to narrow PSDs.61,62 Zukoski's PBM work on aggregating systems emphasizing that “primary particles aggregate with larger particles more rapidly than they do with themselves”202 is important, noteworthy, early work that is likely to have broader impact. Polte's scholarly review186 discusses the “Influence of coalescence kinetics on particle size” and emphasizes the somewhat different concepts of an increased “probability of coalescence between particles of similar size” as well as an aggregation probability of smaller and larger particles that “decreases with increasing (particle) size caused by the increasing aggregation barrier”. We can expect important, paradigm-shifting achievements in the coming years based on the concepts of size-differentiated growth as well as size-dependent aggregation and then even size-dependent agglomeration of those larger aggregates. These advances promise to displace perhaps completely the need for “instantaneous/burst nucleation” as a concept behind the formation of many if not most narrow particle-size dispersions. In short, even if the 70+ year era of dominance of the 1950 model is now due to close, the future for greater, mechanism-based, approaching molecular understanding of particle formation nucleation, growth, and agglomeration processes seems very bright indeed. It is hoped that the present review will help expedite the needed progress, research and associated new and exciting discoveries!
Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
Professor Samy El-Shall at Virginia Common Wealth University is thanked for sharing his expertise30,31 and helpful insights regarding classical nucleation theory. An anonymous, critical referee is thanked for their effort, insights, and valuable suggestions. A second, energetic, detailed referee is also thanked for their extensive, thoughtful and critical comments that helped improve the final manuscript. This work was supported at Colorado State University revised by the U.S. Department of Energy (DOE), Office of Science, Office of Basic Energy Sciences, Division of Chemical Sciences, Geosciences & Biosciences, Catalysis Program, via DOE grant SE-FG402-02ER15453.References
- V. K. LaMer and R. H. Dinegar, Theory, Production and Mechanism of Formation of Monodispersed Hydrosols, J. Am. Chem. Soc., 1950, 72, 4847–4854 CrossRef CAS . The number of citations given refers to a March 2019 Web of Science literature search.
- C. B. Whitehead, S. Özkar and R. G. Finke, LaMer's 1950 Model for Particle Formation of Instantaneous Nucleation and Diffusion-Controlled Growth: A Historical Look at the Model's Origins, Assumptions, Equations, and Underlying Sulfur Sol Formation Kinetics Data, Chem. Mater., 2019, 31, 7116–7132 CrossRef CAS.
- M. A. Watzky and R. G. Finke, Transition Metal Nanocluster Formation Kinetic and Mechanistic Studies. A New Mechanism When Hydrogen Is the Reductant: Slow, Continuous Nucleation and Fast Autocatalytic Surface Growth, J. Am. Chem. Soc., 1997, 43, 10382–10400 CrossRef . Please also see references cited therein.
- V. K. La Mer, Nucleation in Phase Transitions, Ind. Eng. Chem., 1952, 44, 1270–1277 CrossRef CAS.
- J. Turkevich, P. C. Stevenson and J. Hillier, A Study of the Nucleation and Growth Processes in the Synthesis of Colloidal Gold, Discuss. Faraday Soc., 1951, 11, 55–75 RSC.
- J. Turkevich, P. C. Stevenson and J. Hillier, The Formation of Colloid Gold, J. Phys. Chem., 1953, 57, 670–673 CrossRef CAS.
- Y. Lin and R. G. Finke, Novel Polyoxoanion-and Bu4N+-Stabilized, Isolable, and Redissolvable, 20–30 Å Ir∼300–900 Nanoclusters: The Kinetically Controlled Synthesis, Characterization, and Mechanism of Formation of Organic Solvent-Soluble, Reproducible Size, and Reproducible Catalytic Activity Metal Nanoclusters, J. Am. Chem. Soc., 1994, 116, 8335–8353 CrossRef CAS.
- E. Matijevic, Preparation and Properties of Uniform Size Colloids, Chem. Mater., 1993, 5, 412–426 CrossRef CAS.
- D. Kashchiev, Nucleation: Basic Theory with Applications, Butterworth Heinemann, Oxford, 2000 Search PubMed.
- D. W. Oxtoby, Homogeneous Nucleation: Theory and Experiment, J. Phys.: Condens. Matter, 1992, 4, 7627–7650 CrossRef.
- Nucleation—A Transition State to the Directed Assembly of Materials, Faraday Discuss., 2015, 179, 9–488 RSC.
- R. Zhang, A. Khalizov, L. Wang, L. Hu and W. Xu, Nucleation and Growth of Nanoparticles in the Atmosphere, Chem. Rev., 2012, 112, 1957–2011 CrossRef CAS . Please also see references cited therein.
- S. Karthika, T. K. Radhakrishnan and P. Kalaichelvi, A Review of Classical and Nonclassical Nucleation Theories, Cryst. Growth Des., 2016, 16, 6663–6681 CrossRef CAS.
- E. E. Finney and R. G. Finke, Nanocluster Nucleation and Growth Kinetic and Mechanistic Studies: A Review Emphasizing Transition-Metal Nanoclusters, J. Colloid Interface Sci., 2008, 317–374 Search PubMed.
- N. T. K. Thanh, N. Maclean and S. Mahiddine, Mechanisms of Nucleation and Growth of Nanoparticles in Solution, Chem. Rev., 2014, 114, 7610–7630 CrossRef CAS . This review is, in our opinion, superficial, often uncritical, and misses key literature. Five specific reasons supporting this opinion, and hence why this 2014 review should be viewed and used only with considerable caution in our opinion, are provided in the Supporting Information available with a prior paper27.
- D. Erdemir, A. Y. Lee and A. S. Myerson, Nucleation of Crystals from Solution: Classical and Two-Step Models, Acc. Chem. Res., 2009, 42, 621–629 CrossRef CAS.
- W. W. Laxson and R. G. Finke, Nucleation is Second Order: An Apparent Kinetically Effective Nucleus of Two for Ir(0)n Nanoparticle Formation from [(1,5-COD)IrI·P2W15Nb3O62]8− Plus Hydrogen, J. Am. Chem. Soc., 2014, 136, 17601–17615 CrossRef CAS . Please also see references cited therein.
- B. Peters, Common Features of Extraordinary Rate Theories, J. Phys. Chem. B, 2015, 119, 6349–6356 CrossRef CAS.
- J. W. Gibbs, On the Equilibrium of Heterogeneous Substances, New Haven Trans. Conn. Acad. Arts Sci., 1874, III, 343–523 Search PubMed.
- L. Farkas, The velocity of nucleus formation in supersaturated vapors, Z. Phys. Chem., 1927, 125, 236–242 CAS.
- M. Volmer and A. Z. Weber, Keimbildung in übersättigten Gebilden, Z. Phys. Chem., 1926, 119, 277–301 CAS.
- M. Volmer, Kinetik der Phasenbildung, Verlag von Theodor Steinkopff, Leipzig, 1939 Search PubMed.
- R. Becker and W. Döring, Kinetische Behandlung der Keimbildung in übersättigten Dampfen, Ann. Phys., 1935, 24, 719–752 CrossRef CAS.
- J. Frenkel, Kinetic Theory of Liquids, Oxford University Press, New York, 1946, ch. VII Search PubMed.
- J. B. Zeldovich, On the Theory of New Phase Formation: Cavitation, Acta Physicochim. URSS, 1943, 18, 1 Search PubMed.
- S. Özkar and R. G. Finke, Nanoparticle Nucleation is Termolecular and Involves Hydrogen: Evidence for a Kinetically Effective Nucleus of Three, {Ir3H2x·P2W15Nb3O62)6−, in Ir(0)n Nanopaticle Formation From [(1,5-COD)IrI·P2W15Nb3O62]8− Plus Hydrogen, J. Am. Chem. Soc., 2017, 139, 5444–5457 CrossRef . See also references cited therein.
- C. B. Whitehead and R. G. Finke, Nucleation Kinetics and Molecular Mechanism in Transition-Metal Nanoparticle Formation: The Intriguing, Informative Case of a Bimetallic Precursor, {[(1,5-COD)IrI·HPO4]2}2−, Chem. Mater., 2019, 31, 2848–2862 CrossRef CAS.
- H. Reiss, Comments on Clusters in Beams, Spectroscopy and Transitions, NATO ASI Series, 1986, 184, 115–133 CAS . See for example p. 118 regarding “the nucleus forms by a series of highly reversible additions of molecules”, and the monomer-addition eqn (4) on p. 120.
- D. Oxtoby, Nucleation of First-Order Transitions, Acc. Chem. Res., 1998, 31, 91–97 CrossRef CAS.
- M. Rusyniak, V. Abdelsayed, J. Campbell and M. S. El-Shall, Vapor Phase Homogeneous Nucleation of Higher Alkanes: Dodecane, Hexadecane, and Octadecane. 1. Critical Supersaturation and Nucleation Rate Measurements, J. Phys. Chem. B, 2001, 105, 11866–11872 CrossRef CAS.
- M. Rusyniak and M. S. El-Shall, Vapor Phase Homogeneous Nucleation of Higher Alkanes: Dodecane, Hexadecane, and Octadecane. 2. Corresponding States and Scaling Law Analysis, J. Phys. Chem. B, 2001, 105, 11873–11879 CrossRef CAS.
- Iridium(0) metal is known to be insoluble, or at best sparingly soluble. It is reported in the CRC handbook that it is only partially soluble in aqua regia, CRC Handbook of Chemistry and Physics, ed. W. M. Haynes, CRC Press, Boca Raton, FL, 95th edn, 2014 Search PubMed.
- H. Laksmono, S. Tanimura and B. E. Wyslouzil, Methanol nucleation in a supersonic nozzle, J. Chem. Phys., 2011, 135, 074305 CrossRef.
- N. M. Dixit and C. F. Zukoski, Nucleation Rates and Induction Times During Colloidal Crystallization: Links Between Models and Experiments, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66, 051602 CrossRef.
- S. D. Lubetkin, Why Is It Much Easier to Nucleate Gas Bubbles than Theory Predicts?, Langmuir, 2003, 19, 2575–2587 CrossRef CAS.
- S. M. Kathmann, G. K. Schenter, B. C. Garrett, B. Chen and J. I. Siepmann, Thermodynamics and Kinetics of Nanoclusters Controlling Gas-to-Particle Nucleation, J. Phys. Chem. C, 2009, 113, 10354–10370 CrossRef CAS . See also the ref. 16 and 25–37 therein concerning DFT studies that strive to go beyond classical nucleation theory.
- S. M. Kathmann, G. K. Schenter and B. C. Garrett, Understanding the Sensitivity of Nucleation Kinetics, J. Chen. Phys., 2002, 116, 5046–5057 CrossRef CAS.
- A. S. Myerson, Concluding remarks, Faraday Discuss., 2015, 179, 543–547 RSC.
- S. Karthika, T. K. Radhakrishnan and P. Kalaichelvi, A Review of Classical and Nonclassical Nucleation Theories, Cryst. Growth Des., 2016, 16, 6663–6681 CrossRef CAS.
- P. R. ten Wolde and D. Frenkel, Enhancement of Protein Crystal Nucleation by Critical Density Fluctuations, Science, 1997, 277, 1975–1978 CrossRef CAS.
- R. Zhang, A. Khalizov, L. Wang, M. Hu and W. Xu, Nucleation and Growth of Nanoparticles in the Atmosphere, Chem. Rev., 2012, 112, 1957–2011 CrossRef CAS.
- M. Avrami, Kinetics of Phase Change. I. General Theory, J. Chem. Phys., 1939, 7, 1103–1112 CrossRef CAS.
- M. Avrami, Kinetics of Phase Change. II. Transformation-Time Relations for Random Distribution of Nuclei, J. Chem. Phys., 1940, 8, 212–224 CrossRef CAS.
- M. Avrami, Kinetics of Phase Change. III. Granulation, Phase Change, and Microstructure, J. Chem. Phys., 1941, 9, 177–184 CrossRef CAS.
- A. N. Kolmogorov, On the Statistical Theory of Metal Crystallization, Bull. Acad. Sci. USSR, Phys. Ser., 1937, 3, 355–360 Search PubMed.
- W. A. Johnson and R. F. Mehl, Reaction Kinetics in Processes of Nucleation and Growth, Trans. AIME, 1939, 135, 416–458 Search PubMed.
- B. V. Erofe’ev, A Generalized Equation of Chemical Kinetics and its Application in Reactions Involving Solids, Dokl. Akad. Sci. USSR, 1946, 52, 511–514 Search PubMed.
- E. E. Finney and R. G. Finke, Is There a Minimal Chemical Mechanism Underlying Classical Avrami-Erofe’ev Treatments of Phase Transformation Kinetic Data?, Chem. Mater., 2009, 21, 4692–4705 CrossRef CAS . See also the ESI† accompanying this 2009 paper for a section and references on “A more detailed look at the A–E model” that contains an introduction to A-E, KJMA and related equations and their approximations and assumptions.
- B. G. Hillis, B. P. Losey, J. Weng, N. Ghaleb, F. Hou and J. D. Martin, From Rate Measurements to Mechanistic Data for Condensed Matter Reactions: A Case Study Using the Crystallization of [Zn(OH2)6][ZnCl4], Crystals, 2017, 7, 11 CrossRef.
- M. Fanfoni and M. Tomellini, The Johnson–Mehl–Avrami–Kolmogorov model: A brief review, Nuovo Cimento D, 1998, 20, 1171–1182 CrossRef.
- R. G. Finke, M. A. Watzky and C. B. Whitehead, Response to: “Particle Size is a Primary Determinant for Sigmoidal Kinetics of Nanoparticle Formation: A “Disproof” of the Finke-Watzky (F-W) Nanoparticle Nucleation and Growth Mechanism”, Chem. Mater., 2020, 32, 3657–3672 CrossRef CAS.
- J. D. Martin, Comment: Particle Size is a Primary Determinant for Sigmoidal Kinetics of Nanoparticle Formation: A “Disproof” of the Finke-Watzky (F-W) Nanoparticle Nucleation and Growth Mechanism, Chem. Mater., 2020, 32, 3651–3656 CrossRef CAS.
- R. Szabó and G. Lente, A Comparison of the Stochastic and Deterministic Approaches in a Nucleation-Growth Type Model of Nanoparticle Formation, Chem. Mater., 2020 Search PubMed , submitted.
- T. G. Kurtz, The Relationship Between Stochastic and Deterministic Models for Chemical Reactions, J. Chem. Phys., 1972, 57, 2976–2978 CrossRef CAS.
- B. J. Hornstein and R. G. Finke, Transition-Metal Nanocluster Kinetic and Mechanistic Studies Emphasizing Nanocluster Agglomeration: Demonstration of a Kinetic Method That Allows Monitoring All Three Phases of Nanocluster Formation and Aging, Chem. Mater., 2004, 16, 139–150 CrossRef CAS . (See also the addition/correction: Chem. Mater., 2004, 16, 3972).
- C. Besson, E. E. Finney and R. G. Finke, A Mechanism for Transition-Metal Nanoparticle Self-Assembly, J. Am. Chem. Soc., 2005, 127, 8179–8184 CrossRef CAS.
- C. Besson, E. E. Finney and R. G. Finke, Nanocluster Nucleation, Growth and Then Agglomeration Kinetic and Mechanistic Studies: A More General, Four-Step Mechanism Involving Double Autocatalysis, Chem. Mater., 2005, 17, 4925–4938 CrossRef CAS.
- E. E. Finney and R. G. Finke, The Four-Step, Double-Autocatalytic Mechanism for Transition-Metal Nanocluster Nucleation, Growth and Then Agglomeration: Metal, Ligand, Concentration, Temperature, and Solvent Dependency Studies, Chem. Mater., 2008, 20, 1956–1970 CrossRef CAS.
- T. O. Drews, M. A. Katsoulakis and M. Tsapatsis, Mathematical Model for Crystal Growth by Aggregation of Precursor Metastable Nanoparticles, J. Phys. Chem. B, 2005, 109, 23879–23887 CrossRef CAS . Note that the authors preferred their more complex, 4-step Mechanism II (that has a typo in the second step; it should be B → C1, and not the repetitive B + Ci → Ci+1).
- P. D. Kent, J. E. Mondloch and R. G. Finke, A Four-Step Mechanism for the Formation of Supported-Nanoparticle Heterogeneous Catalysts in Contact with Solution: The Conversion of Ir(1,5-COD)Cl/γ-Al2O3 to Ir(0)∼170/γ-Al2O3, J. Am. Chem. Soc., 2014, 136, 1930–1941 CrossRef CAS.
- D. R. Handwerk, P. D. Shipman, C. B. Whitehead, S. Özkar and R. G. Finke, Mechanism-Enabled Population Balance Modeling of Particle Formation en Route to Particle Average Size and Size Distribution Understanding and Control, J. Am. Chem. Soc., 2019, 141, 15827–15839 CrossRef CAS.
- D. R. Handwerk, P. D. Shipman, C. B. Whitehead, S. Özkar and R. G. Finke, Particle Size Distributions via Mechanism-Enabled Population Balance Modeling, J. Phys. Chem. C, 2020, 14, 4852–4880 CrossRef.
- S. Mozaffari, W. Li, C. Thompson, S. Ivanov, S. Seifert, B. Lee, L. Kovarik and A. M. Karim, Colloidal nanoparticle size control: experimental and kinetic modeling investigation of the ligand–metal binding role in controlling the nucleation and growth kinetics, Nanoscale, 2017, 9, 13772–13785 RSC.
- A. M. Morris, M. A. Watzky and R. G. Finke, Protein aggregation kinetics, mechanism, and curve-fitting: a review of the literature, Biochim. Biophys. Acta, Proteins Proteomics, 1794, 2009, 375–397 Search PubMed . Please also see the references therein.
- K.-J. Kim, C.-H. Lee and J.-H. Shin, Characteristics of Cu(II) Precipitation by the Liquid Phase Reaction with Sulfide, Hwahak Konghak, 1991, 29, 639–645 CAS . A thorough search of the literature revealed little precedent for nucleation reaction orders greater than 1st or 2nd order. The Kim, at al. article listed is one of the highest claimed reaction orders we could find, a CuS system with a claimed 5th-order nucleation.
- J. A. Christiansen and A. E. Neilsen, On the Kinetics of Formation of Precipitates of Sparingly Soluble Salts, Acta Chem. Scand., 1951, 5, 673–674 CrossRef CAS.
- V. K. La Mer and R. H. Dinegar, The Limiting Degrees of Supersaturation of the Sparingly Soluble Sulfates, J. Am. Chem. Soc., 1951, 73, 380–385 CrossRef CAS.
- In the 1950s, the state-of-the-art technique to collect particle size data was using turbidity/light scattering techniques that had a particle radius limit of detection of 100 nm.1,2 Particles with a radius of 100 nm contain ca. 107−8 atoms! The limit of detection is approximately 103 orders of magnitude better than what the naked eye is able to see. Meanwhile, modern microscopic and synchrotron techniques are able to observe particle formation at the 0.5–1.0 nm scale—an improvement of 102 orders of magnitude in the ensuing 70 years, and an improvement necessary to directly observe the nucleation process that can involve as little as 2–3 primary element atoms.3,17,27.
- The estimate was achieved as follows: the number of BaSO4 units in a nearly spherical particle of 100 micron size, is n = (N0ρ(4/3)π(D/2)3)/W, where n = number of BaSO4 units, N0 = 6.022 × 1023 mol−1, ρ = room-temperature density of BaSO4 (4.49 g cm−3; CRC Handbook of Chemistry and Physics, 77th edn; Lide, D. R., Frederikse, H. P. R., Eds.; CRC Press: Boca Raton, FL, 1996), D = diameter of BaSO4 particles, and W = formula weight of BaSO4 (233.38 g mol−1). From this one calculates n = (6.022 × 1023 mol−1) (4.49 g cm−3)(4/3)π((100/2) × 10−4 cm)3/(233.38 g mol−1), that is, n = 6.0 × 1015.
- L. Bentea, M. A. Watzky and R. G. Finke, Sigmoidal Nucleation and Growth Curves Across Nature Fit by the Finke-Watzky Model of Slow Continuous Nucleation and Autocatalytic Growth: Explicit Formulas for the Lag and Growth Times Plus Other Key Insights, J. Phys. Chem. C, 2017, 121, 5302–5312 CrossRef CAS.
- D. Turnbull, The kinetics of precipitation of barium sulfate from aqueous solution, Acta Metall., 1953, 1, 684–691 CrossRef CAS.
- D. Gebauer, A. Völkel and H. Cölfen, Stable Prenucleation Calcium Carbonate Clusters, Science, 2008, 322, 1819–1822 CrossRef CAS.
- F. L. Eisele and D. R. Hanson, First Measurement of Prenucleation Molecular Clusters, J. Phys. Chem. A, 2000, 104, 830–836 CrossRef CAS.
- E. M. Pouget, P. H. H. Bomans, J. A. C. M. Goos, P. M. Frederik, G. de With and N. A. J. M. Sommerdijk, The Initial Stages of Template-Controlled CaCO3 Formation Revealed by Cryo-TEM, Science, 2009, 323, 1455–1458 CrossRef CAS.
- D. Gebauer, M. Kellermeir, J. D. Gale, L. Bergström and H. Cölfen, Pre-nucleation clusters as solute precursors in crystallization, Chem. Soc. Rev., 2014, 43, 2348–2371 RSC.
- J. Reichenbach and K. Wynne, Frustration vs. Prenucleation: Understanding the Surprising Stability of Supersaturated Sodium Thiosulfate Solutions, J. Phys. Chem. C, 2018, 122, 7590–7596 CrossRef CAS.
- S. Fermani, C. Vettraino, I. Bonacini, M. Marcaccio, G. Falini, J. A. Gavira and J. M. Garcia Ruiz, Heterogeneous Crystallization of Proteins: Is it a Prenucleation Clusters Mediated Process?, Gryst. Gorwth Des., 2013, 13, 3110–3115 CrossRef CAS.
- F. Hou and J. D. Martin, Isotope Effects Reveal the Template Influence on the Crystal Growth of a Metal-Halide Network, J. Phys. Chem. C, 2019, 123, 7475–7485 CrossRef CAS.
- F. Hou, J. D. Martin, E. D. Dill, J. C. W. Folmer and A. A. Josey, Transition Zone Theory of Crystal Growth and Viscosity, Chem. Mater., 2015, 27, 3526–3532 CrossRef CAS.
- J. D. Martin and F. Hou, Transition zone theory of glass transition, J. Non-Cryst. Solids, 2018, 491, 24–33 CrossRef CAS.
- R. K. Ramamoorthy, E. Yildirim, E. Barba, P. Roblin, J. A. Vargas, L.-M. Lacroix, I. Rodriguez-Ruiz, P. Decorse, V. Petkiv, S. Teycheném and G. Viau, The Role of Pre-Nucleation Clusters in the Crystallization of Gold Nanoparticles, Nanoscale, 2020, 12, 16173–16188 RSC.
- J. Halpern, Some aspects of chemical dynamics in solution, J. Chem. Ed., 1968, 45, 372–380 CrossRef CAS.
- G. Dulz and N. Sutin, The effect of chloride ions on the kinetics of the oxidation of chromium(II) by iron(III), J. Am. Chem. Soc., 1964, 86, 829–832 CrossRef CAS.
- H. Freund, An Introduction to the Study of Enzymes, Wiley, New York, 1965, ch. 2. Note that presteady-state kinetics studies of enzymes are well known Search PubMed.
- S. E. Smith, J. M. Sasaki, R. G. Bergman, J. E. Mondloch and R. G. Finke, Platinum-Catalyzed Phenyl and Methyl Group Transfer from Tin to Iridium: Evidence for an Autocatalytic Reaction Pathway with an Unusual Preference for Methyl Transfer, J. Am. Chem. Soc., 2008, 130, 1839–1841 CrossRef CAS.
- J. E. Mondloch, Q. Wang, A. I. Frenkel and R. G. Finke, Development Plus Kinetic and Mechanistic Studies of a Prototype Supported-Nanoparticle Heterogeneous Catalyst Formation System in Contact with Solution: Ir(1,5-COD)Cl/γ-Al2O3 and Its Reduction by H2 to Ir(0)n/γ-Al2O3, J. Am. Chem. Soc., 2010, 132, 9701–9714 CrossRef CAS.
- A. M. Morris, M. A. Watzky, J. N. Agar and R. G. Finke, Fitting neurological protein aggregation kinetic data via a 2-step, minimal/”Ockham's razor” model: the Finke-Watzky mechanism of nucleation followed by autocatalytic surface growth, Biochem., 2008, 47, 2413–2427 CrossRef CAS.
- N. A. Oladoja, A critical review of the applicability of Avrami fractional kinetic equation in adsorption-based water treatment studies, Desalin. Water Treat., 2015, 57, 15813–15825 CrossRef.
- S. Özkar and R. G. Finke, Silver Nanoparticles Synthesized by Microwave Heating: A Kinetic and Mechanistic Re-Analysis and Re-Interpretation, J. Phys. Chem. C, 2017, 121, 27643–27654 CrossRef.
- M. A. Watzky, E. E. Finney and R. G. Finke, Transition-Metal Nanocluster Size vs Formation Time and the Catalytically Effective Nucleus Number: A Mechanism-Based Treatment, J. Am. Chem. Soc., 2008, 130, 11959–11969 CrossRef CAS.
- S. R. K. Perala and S. Kumar, On the Two-Step Mechanism for Synthesis of Transition-metal Nanoparticles, Langmuir, 2014, 30, 12703–12711 CrossRef CAS.
- H. A. Brown, S. Xiong, G. A. Medvedev, Y. A. Chang, M. M. Abu-Omar, J. M. Caruthers and R. M. Waymouth, Zwitterionic Ring-Opening Polymerization: Models for Kinetics of Cyclic Poly(caprolactone) Synthesis, Macromolecules, 2014, 47, 2955–2963 CrossRef CAS . Noteworthy in this paper are: (i) the similar approach of a disproof-based, minimalistic mechanism to start; (ii) the slow initiation, fast propagation polymerization system; (iii) the monomer addition steps in the mechanism; and (iv) the finding that such a system can lead to a relatively narrow size distribution—all features closely paralleling those in the present, nanoparticle ME-PBM study. Two major differences, however, are: (iv) the underlying mechanism is fundamentally different than any in the present nanoparticle study), and (v) a Monte Carlo, stochastic simulation had to be used due to the high polymer MWs and, hence, many monomer addition steps (vs the full ODE approach possible for our nanoparticle formation reaction and its order of magnitude fewer number of steps). Nevertheless, this excellent work is an example that fits our definition of ME-PBM, albeit now in polymer chemistry, something that expands the scope and impact of the concept of Mechanism-Enabled PBModeling. We thank Prof. Waymouth for stimulating discussion of the PBMs of polymer vs particle formation systems.
- C. An, S. Wang, Y. Sun, Q. Zhang, J. Zhang, C. Wang and J. Fang, Plasmonic silver incorporated silver halides for efficient photocatalysis, J. Mater. Chem. A, 2016, 4, 4336–4352 RSC.
- G.-L. Wang, X.-F. Xu, L. Qiu, Y.-M. Dong, Z.-J. Li and C. Zhang, Dual Responsive Enzyme Mimicking Activity of AgX (X = Cl, Br, I) Nanoparticles and Its Application for Cancer Cell Detection, ACS Appl. Mater. Interfaces, 2014, 6, 6434–6442 CrossRef CAS.
- N. Durán, G. Nakazato and A. B. Seabra, Antimicrobial activity of biogenic silver nanoparticles, and silver chloride nanoparticles: an overview and comments, Appl. Microbiol. Biotechnol., 2016, 100, 6555–6570 CrossRef.
- R. Ginell, A. M. Ginell and P. E. Spoerri, Association phenomena. I. The growth of particles of silver chloride and the higher-order Tyndall effect, J. Colloid Sci., 1947, 2, 521–525 CrossRef CAS.
- R. H. Ottewill and R. F. Woodbridge, The preparation of monodisperse silver bromide and silver iodide sols, J. Colloid Sci., 1961, 16, 581–594 CrossRef CAS.
- M. J. Insley and G. D. Parfitt, Precipitation of Silver Chloride from Homogeneous Solution. Part 1. – Particle Size and Shape Characteristics, Trans. Faraday Soc., 1968, 64, 1945–1954 RSC.
- T. Sugimoto, Underlying mechanisms in size control of uniform nanoparticles, J. Colloid Interface Sci., 2007, 309, 106–118 CrossRef CAS.
- T. Sugimoto, The Theory of the Nucleation of Monodisperse Particles in Open Systems and Its Application to AgBr Systems, J. Colloid Interface Sci., 1992, 150, 208–225 CrossRef CAS.
- T. Sugimoto, F. Shiba, T. Sekiguchi and H. Itoh, Spontaneous nucleation of monodisperse silver halide particles from homogeneous gelatin solution I: silver chloride, Colloids Surf., A, 2000, 164, 183–203 CrossRef CAS.
- T. Sugimoto and F. Shiba, Spontaneous nucleation of monodisperse silver halide particles from homogeneous gelatin solution II: silver bromide, Colloids Surf., A, 2000, 164, 205–215 CrossRef CAS.
- D. B. Chu, J. S. Owen and B. Peters, Nucleation and Growth Kinetics from LaMer Burst Data, J. Phys. Chem. A, 2017, 121, 7511–7517 CrossRef CAS.
- S. Zhao, D. Xu, H. Ma, Z. Sun and J. Guan, Controllable preparation and formation mechanism of monodispersed silica particles with binary sizes, J. Colloid Interface Sci., 2012, 388, 40–46 CrossRef CAS.
- Z. Li and Y. Sun, Silver chlorobromide nanoparticles with highly pure phases: synthesis and characterization, J. Mater. Chem. A, 2013, 1, 6786–6793 RSC.
- H. M. Trimble, Solubilities of Salts in Ethylene Glycol and in Its Mixtures with Water, Ind. Eng. Chem., 1931, 23, 165–167 CrossRef CAS.
- F. Shiba and Y. Okawa, Relationship between Supersaturation Ratio and Supply Rate of Solute in the Growth Process of Monodisperse Colloidal Particles and Application to AgBr Systems, J. Phys. Chem. B, 2005, 109, 21664–21668 CrossRef CAS.
- Z. Li, J. S. Okasinski, D. J. Gosztola, Y. Ren and Y. Sun, Silver chlorobromide nanocubes with significantly improved uniformity: synthesis and assembly into photonic crystals, J. Mater. Chem. C, 2015, 3, 58–65 RSC.
- H. Sato, T. Hirai and I. Komasawa, Mechanism of Formation of Silver Halide Particles in Reverse Micellar Systems, J. Chem. Eng. Jpn., 1996, 29, 501–507 CrossRef CAS.
- K. Kimijima and T. Sugimoto, Growth Mechanism of AgCl Nanoparticles in a Reverse Micelle System, J. Phys. Chem. B, 2004, 108, 3735–3738 CrossRef CAS.
- G. Ma, Background-Free In vivo Time Domain Optical Molecular Imaging Using Colloidal Quantum Dots, ACS Appl. Mater. Interfaces, 2013, 5, 2835–2844 CrossRef CAS.
- Y. E. Panfil, M. Oded and U. Banin, Colloidal Quantum Nanostructures: Emerging Materials for Display Applications, Angew. Chem., Int. Ed., 2018, 57, 4274–4295 CrossRef CAS.
- K. Das and S. Baruah, Quantum dots for solar energy harvesting, Curr. Sci., 2018, 115, 659–668 CrossRef CAS.
- S. Kundu and A. Patra, Nanoscale Strategies for Light Harvesting, Chem. Rev., 2017, 117, 712–757 CrossRef CAS.
- L. Jing, S. V. Kershaw, Y. Li, X. Huang, Y. Li, A. L. Rogach and M. Gao, Aqueous Based Semiconductor Nanocrystals, Chem. Rev., 2016, 116, 10623–10730 CrossRef CAS.
- L. S. Ott and R. G. Finke, Nanocluster Formation and Stabilization Fundamental Studies: Investigating “Solvent-Only” Stabilization En Route to Discovering Stabilization by the Traditionally Weakly Coordinating Anion BF4− Plus High Dielectric Constant Solvents, Inorg. Chem., 2006, 45, 8382–8393 CrossRef.
- M. N. O'Brien, M. R. Jones and C. A. Mirkin, The nature and implications of uniformity in the hierarchical organization of nanomaterials, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 11717–11725 CrossRef.
- Q. Dai, Y. Zhang, Y. Wang, B. Zou, W. W. Yu and M. Z. Hu, Ligand Effects on Synthesis and Post-Synthetic Stability of PbSe Nanocrystals, J. Phys. Chem. C, 2010, 114, 16160–16167 CrossRef CAS.
- P. Reiss, M. Carrière, C. Lincheneau, L. Vaure and S. Tamang, Synthesis of Semiconductor Nanocrystals, Focusing on Nontoxic and Earth-Abundant Materials, Chem. Rev., 2016, 116, 10731–10819 CrossRef CAS.
- J. D. Aiken III and R. G. Finke, A review of modern transition-metal nanoclusters: their synthesis, characterization, and applications in catalysis, J. Mol. Catal. A: Chem., 1999, 145, 1–44 CrossRef.
- B. M. Cossairt, Shining Light on Indium Phosphide Quantum Dots: Understanding the Interplay among Precursor Conversion, Nucleation, and Growth, Chem. Mater., 2016, 28, 7181–7189 CrossRef CAS.
- M. R. Friedfeld, D. A. Johnson and B. M. Cossairt, Conversion of InP Clusters to Quantum Dots, Inorg. Chem., 2019, 58, 803–810 CrossRef CAS.
- Y. Li, C. Pu and X. Peng, Surface activation of colloidal indium phosphide nanocrystals, Nano Res., 2017, 10, 941–958 CrossRef CAS.
- N. Pradhan, D. Reifsnyder, R. Xie, J. Aldana and X. Peng, Surface Ligand Dynamics in Growth of Nanocrystals, J. Am. Chem. Soc., 2007, 129, 9500–9509 CrossRef CAS.
- B. M. McMurtry, K. Qian, J. T. Teglasi, A. K. Swarnakar, J. DeRoo and J. S. Owen, Continuous Nucleation and Size Dependent Growth Kinetics of Indium Phosphide Nanocrystals, Chem. Mater., 2020, 32, 4358–4368 CrossRef CAS.
- O. B. Achorn, D. Franke and M. G. Bawendi, Seedless Continuous Injection Synthesis of Indium Phosphide Quantum Dots as a Route to Large Size and Low Dispersity, Chem. Mater., 2020, 32, 6532–6539 CrossRef CAS.
- R. Lai, C. Pu and X. Peng, On-Surface Reactions in the Growth of High-Quality CdSe Nanocrystals in Nonpolar Solutions, J. Am. Chem. Soc., 2018, 140, 9174–9183 CrossRef CAS.
- H. Lu and R. L. Brutchey, Tunable Room-Temperature Synthesis of Coinage Metal Chalcogenide Nanocrystals from N-Heterocyclic Carbene Synthons, Chem. Mater., 2017, 29, 1396–1403 CrossRef CAS.
- B. Li, X. Zhang, L. Li, M. Li, J. Xu and Y. Hong, White luminescence from CdS nanocrystals under the blue light excitation, J. Solid State Chem., 2014, 214, 108–111 CrossRef CAS.
- M. P. Hendricks, B. M. Cossairt and J. S. Owen, The Importance of Nanocrystal Precursor Conversion Kinetics: Mechanism of the Reaction between Cadmium Carboxylate and Cadmium Bis(diphenyldithiophosphinate), ACS Nano, 2012, 6, 10054–10062 CrossRef CAS.
- H.-B. Kim and D.-J. Jang, Precursor-dependent shape variation of wurtzite CdSe crystals in a microwave-assisted polyol process, CrystEngComm, 2012, 14, 6946–6951 RSC.
- B. Abécassis, C. Bouet, C. Garnero, D. Constantin, N. Lequeux, S. Ithurria, B. Dubertret, B. R. Pauw and D. Pontoni, Real-Time in Situ Probing of High-Temperature Quantum Dots Solution Synthesis, Nano Lett., 2015, 15, 2620–2626 CrossRef.
- Using the same equation from ref. 69, we were able to approximate the number of CdSe to be ca. 10 by using a density of 5.81 g cm−3 and a molecular weight of 191.385 g mol−1.
- S. Nakashima, K. Kikushima and K. Mukai, Infrared emitting property and spherical symmetry of colloidal PbS quantum dots, J. Cryst. Growth, 2013, 378, 537–541 CrossRef CAS.
- W.-T. Wu, H. Liu, C. Dong, W.-J. Zheng, L.-L. Han, L. Li, S.-Z. Qiao, J. Yang and X.-W. Du, Gain High-Quality Colloidal Quantum Dots Directly from Natural Minerals, Langmuir, 2015, 31, 2251–2255 CrossRef CAS.
- R. Xie, Z. Li and X. Peng, Nucleation Kinetics vs Chemical Kinetics in the Initial Formation of Semiconductor Nanocrystals, J. Am. Chem. Soc., 2009, 131, 15457–15466 CrossRef CAS.
- S. Libert, V. Gorshkov, D. V. Goia, E. Matijević and V. Privman, Model of Controlled Synthesis of Uniform Colloid Particles: Cadmium Sulfide, Langmuir, 2003, 19, 10679–10683 CrossRef CAS.
- R. Garcia Rodriguez, M. P. Hendricks, B. M. Cossairt, H. Liu and J. S. Owen, Conversion Reactions of Cadmium Chalcogenide Nanocrystal Precursors, Chem. Mater., 2013, 25, 1233–1249 CrossRef CAS.
- L. Qu, W. Yu and X. Peng, In Situ Observation of the Nucleation and Growth of CdSe Nanocrystals, Nano Lett., 2004, 4, 465–469 CrossRef CAS.
- J. S. Owen, E. M. Chan, H. Liu and A. P. Alivisatos, Precursor Conversion Kinetics and the Nucleation of Cadmium Selenide Nanocrystals, J. Am. Chem. Soc., 2010, 132, 18206–18213 CrossRef CAS.
- S. Tamang, C. Lincheneau, Y. Hermans, S. Jeong and P. Reiss, Chemistry of InP Nanocrystal Syntheses, Chem. Mater., 2016, 28, 2491–2506 CrossRef CAS.
- A. Eshuis and C. A. J. Koning, The mechanism of particle formation during homogeneous precipitation of zinc sulfide, Colloid Polym. Sci., 1994, 272, 1240–1244 CrossRef CAS.
- H. Liu, W. Hu, F. Ye, Y. Ding and J. Yang, Growth mechanism of Ag2S nanocrystals in a nonpolar organic solvent, RSC Adv., 2013, 3, 616–622 RSC.
- X. Zhao, T. Liu, Y. Cui, X. Hou, Z. Liu, X. Dai, J. Kong, W. Shi and T. J. S. Dennis, Antisolvent-assisted controllable growth of fullerene single crystal microwires for organic field effect transistors and photodetectors, Nanoscale, 2018, 10, 8170–8179 RSC.
- S. G. Kwon and T. Hyeon, Formation Mechanisms of Uniform Nanocrystals via Hot-Injection and Heat-Up Methods, Small, 2011, 7, 2685–2702 CrossRef CAS.
- P. L. Saldanha, V. Lesnyak and L. Manna, Large scale syntheses of colloidal nanomaterials, Nano Today, 2017, 12, 46–63 CrossRef CAS.
- K.-J. Kim, R. P. Oleksak, E. B. Hostetler, D. A. Peterson, P. Chandran, D. M. Schut, B. K. Paul, G. S. Herman and C.-H. Chang, Continuous Microwave-Assisted Gas–Liquid Segmented Flow Reactor for Controlled Nucleation and Growth of Nanocrystals, Cryst. Growth Des., 2014, 14, 5349–5355 CrossRef CAS.
- H. Xia, Y. Xiahou, P. Zhang, W. Ding and D. Wang, Revitalizing the Frens Method To Synthesize Uniform, Quasi-Spherical Gold Nanoparticles with Deliberately Regulated Sizes from 2 to 330 nm, Langmuir, 2016, 32, 5870–5880 CrossRef CAS.
- J. Turkevich, Colloidal gold. Part I, Gold Bull., 1985, 18, 86–91 CrossRef CAS.
- M. K. Chow and C. F. Zukoski, Gold Sol Formation Mechanisms: Role of Colloidal Stability, J. Colloid Interface Sci., 1994, 165, 97–109 CrossRef CAS.
- P. Georgiev, A. Bojinova, B. Kostova, D. Momekova, T. Bjornholm and K. Balashev, Implementing atomic force microscopy (AFM) for studying kinetics of gold nanoparticle's growth, Colloids Surf., A, 2013, 434, 154–163 CrossRef CAS.
- M. Wuithschick, A. Birnbaum, S. Witte, M. Sztucki, U. Vainio, N. Pinna, K. Rademann, F. Emmerling, R. Kraehnert and J. Polte, Turkevich in New Robes: Key Questions Answered for the Most Common Gold Nanoparticle Synthesis, ACS Nano, 2015, 9, 7052–7071 CrossRef CAS.
- M. Harada and S. Kizaki, Formation Mechanism of Gold Nanoparticles Synthesized by Photoreduction in Aqueous Ethanol Solution of Polymers Using In Situ Quick Scanning X-ray Absorption Fine Structure and Small-Angle X-ray Scattering, Cryst. Growth Des., 2016, 16, 1200–1212 CrossRef CAS.
- J. Zhang, H. Li, Q. Kuang and Z. Xie, Toward Rationally Designing Surface Structures of Micro- and Nanocrystallites: Role of Supersaturation, Acc. Chem. Res., 2018, 51, 2880–2887 CrossRef CAS.
- X. Yin, M. Shi, J. Wu, Y.-T. Pan, D. L. Gray, J. A. Bertke and H. Yang, Quantitative Analysis of Different Formation Modes of Platinum Nanocrystals Controlled by Ligand Chemistry, Nano Lett., 2017, 17, 6146–6150 CrossRef CAS.
- V. N. Richards, N. P. Rath and W. E. Buhro, Pathway from a Molecular Precursor to Silver Nanoparticles: The Prominent Role of Aggregative Growth, Chem. Mater., 2010, 22, 3556–3567 CrossRef CAS.
- G. Dzido, P. Markowski, A. Malachowska-Jutsz, K. Prusik and A. B. Jarzebski, Rapid continuous microwave-assisted synthesis of silver nanoparticles to achieve very high productivity and full yield: from mechanistic study to optimal fabrication strategy, J. Nanopart. Res., 2015, 17, 1–15 CrossRef CAS.
- B. Bhattarai, Y. Zaker, A. Atnagulov, B. Yoon, U. Landman and T. P. Bigioni, Chemistry and Structure of Silver Molecular Nanoparticles, Acc. Chem. Res., 2018, 51, 3104–3113 CrossRef CAS.
- T.-H. Yang, H.-C. Peng, S. Zhou, C.-T. Lee, S. Bao, Y.-H. Lee, J.-M. Wu and Y. Xia, Toward a Quantitative Understanding of the Reduction Pathways of a Salt Precursor in the Synthesis of Metal Nanocrystals, Nano Lett., 2017, 17, 334–340 CrossRef CAS.
- L. Wu, H. Lian, J. J. Willis, E. D. Goodman, I. S. McKay, J. Qin, C. J. Tassone and M. Cargnello, Tuning Precursor Reactivity toward Nanometer-Size Control in Palladium Nanoparticles Studied by in Situ Small Angle X-ray Scattering, Chem. Mater., 2018, 30, 1127–1135 CrossRef CAS.
- J. Wu, H. Qian, L. Lu, J. Fan, Y. Guo and W. Fang, Influence of Reduction Kinetics on the Preparation of Well-Defined Cubic Palladium Nanocrystals, Inorg. Chem., 2018, 57, 8128–8136 CrossRef CAS.
- M. A. Meshgi, M. Kriechbaum, S. Biswas, J. D. Holmes and C. Marschner, Synthesis of indium nanoparticles at ambient temperature; simultaneous phase transfer and ripening, J. Nanopart. Res., 2016, 18, 363–372 CrossRef.
- M. Faraday, The Bakerian Lecture: Experimental Relations of Gold (and Other Metals) to Light, Philos. Trans. R. Soc. London, 1857, 147, 145–181 CrossRef.
- X. Ji, X. Song, J. Li, Y. Bai, W. Yang and X. Peng, Size Control of Gold Nanocrystals in Citrate Reduction: The Third Role of Citrate, J. Am. Chem. Soc., 2007, 129, 13939–13948 CrossRef CAS.
- J. Wang, H. F. M. Boelens, M. B. Thathagar and G. Rothenberg, In Situ Spectroscopic Analysis of Nanocluster Formation, ChemPhysChem, 2004, 5, 93–98 CrossRef CAS.
- B.-K. Pong, H. I. Elim, J.-X. Chong, W. Ji, B. L. Trout and J.-Y. Lee, New Insights on the Nanoparticle Growth Mechanism in the Citrate Reduction of Gold(III) Salt: Formation of the Au Nanowire Intermediate and Its Nonlinear Optical Properties, J. Phys. Chem. C, 2007, 111, 6281–6287 CrossRef CAS.
- Y. Shiraishi, H. Tanaka, H. Sakamoto, N. Hayashi, Y. Kofuji, S. Ichikawa and T. Hirai, Synthesis of Au Nanoparticles with Benzoic Acid as Reductant and Surface Stabilizer Promoted Solely by UV Light, Langmuir, 2017, 33, 13797–13804 CrossRef CAS.
- S. A. Lindley, J. K. Cooper, M. D. Rojas-Andrade, V. Fung, C. J. Leahy, S. Chen and J. Z. Zhang, Highly Tunable Hollow Gold Nanospheres: Gaining Size Control and Uniform Galvanic Exchange of Sacrificial Cobalt Boride Scaffolds, ACS Appl. Mater. Interfaces, 2018, 10, 12992–13001 CrossRef CAS.
- J. Polte, T. T. Ahner, F. Delissen, S. Sokolov, F. Emmerling, A. F. Thunemann and R. Kraehnert, Mechanism of Gold Nanoparticle Formation in the Classical Citrate Synthesis Method Derived from Coupled In Situ XANES and SAXS Evaluation, J. Am. Chem. Soc., 2010, 132, 1296–1301 CrossRef CAS.
- J. Polte, R. Erler, A. F. Thünemann, S. Sokolov, T. T. Ahner, K. Rademann, F. Emmerling and R. Kraehnert, Nucleation and Growth of Gold Nanoparticles Studied via in situ Small Angle X-ray Scattering at Millisecond Time Resolution, ACS Nano, 2010, 4, 1076–1082 CrossRef CAS.
- J. Polte, M. Herder, R. Erler, S. Rolf, A. Fischer, C. Würth, A. F. Thünemann, R. Kraehnert and F. Emmerling, Mechanistic insights into seeded growth processes of gold nanoparticles, Nanoscale, 2010, 2, 2463–2469 RSC.
- T. Yao, Z. Sun, Y. Li, Z. Pan, H. Wei, Y. Xie, M. Nomura, Y. Niwa, W. Yan, Z. Wu, Y. Jiang, Q. Liu and S. Wei, Insights into Initial Kinetic Nucleation of Gold Nanocrystals, J. Am. Chem. Soc., 2010, 132, 7696–7701 CrossRef CAS.
- J. Keizer, A theory of spontaneous fluctuations in macroscopic systems, J. Chem. Phys., 1975, 63, 398–403 CrossRef CAS.
- I. N. Levine, Physical Chemistry, McGraw-Hill, New York City, NY, 6th edn, 2009, pp. 101–103 Search PubMed.
- Z. Zhou, G. J. Bedwell, R. Li, S. Palchoudhury, P. E. Prevelige and A. Gupta, Pathways for Gold Nucleation and Growth over Protein Cages, Langmuir, 2017, 33, 5925–5931 CrossRef CAS.
- D. Zahn, Thermodynamics and Kinetics of Prenucleation Clusters, Classical and Non-Classical Nucleation, ChemPhysChem, 2015, 16, 2069–2075 CrossRef CAS.
- S. J. Khan, C. M. Sorensen and A. Chakrabarti, Computer Simulations of Nucleation of Nanoparticle Superclusters from Solution, Langmuir, 2012, 28, 5570–5579 CrossRef CAS.
- M. Kellermeier, R. Rosenberg, A. Moise, U. Anders, M. Przybylski and H. Cölfen, Amino acids form prenucleation clusters: ESI-MS as a fast detection method in comparison to analytical ultracentrifugation, Faraday Discuss., 2012, 159, 23–45 RSC.
- T. Li, A. J. Senesi and B. Lee, Small Angle X-ray Scattering for Nanoparticle Research, Chem. Rev., 2016, 116, 11128–11180 CrossRef CAS.
- B. Ingham, X-ray Scattering Characterisation of Nanoparticles, Crystallogr. Rev., 2015, 21, 229–303 CrossRef.
- X. Chen, J. Schröder, S. Hauschild, S. Rosenfeldt, M. Dulle and S. Förster, Simultaneous SAXS/WAXS/UV–Vis Study of the Nucleation and Growth of Nanoparticles: A Test of Classical Nucleation Theory, Langmuir, 2015, 31, 11678–11691 CrossRef CAS.
- A. I. Frenkel, Applications of extended X-ray absorption fine-structure spectroscopy to studies of bimetallic nanoparticle catalysts, Chem. Soc. Rev., 2012, 41, 8163–8178 RSC.
- D. Koziej, Revealing Complexity of Nanoparticle Synthesis in Solution by in Situ Hard X-ray Spectroscopy—Today and Beyond, Chem. Mater., 2016, 28, 2478–2490 CrossRef CAS.
- K.-H. Yih, I. K. Hamdemir, J. M. Mondloch, E. Bayram, S. Özkar, R. Vasic, A. I. Frenkel, O. Anderson and R. G. Finke, Synthesis and Characterization of [(1,5-Cyclooctadiene)Ir(μ-H)]4: A Multipurpose, Tetrametallic, Coordinatively Unsaturated Ir4-Based Precatalyst and Synthon, Inorg. Chem., 2012, 51, 3186–3193 CrossRef CAS.
- W. W. Laxson, S. Özkar, S. Folkman and R. G. Finke, The Story of a Mechanism-Based Solution to an Irreproducible Synthesis Resulting in an Unexpected Closed-System Requirement for the LiBEt3H-Based Reduction: the Case of the Novel Subnanometer Cluster, [Ir(1,5-COD)(μ-H)]4, and the Resulting Improved, Independently Repeatable, Reliable Synthesis, Inorg. Chim. Acta, 2015, 432, 250–257 CrossRef CAS.
- J. Polte, Fundamental growth principles of colloidal metal nanoparticles – a new perspective, CrystEngComm, 2015, 17, 6809–6830 RSC.
- L. Starkey-Ott and R. G. Finke, Transition-Metal Nanocluster Stabilization for Catalysis: A Critical Review of Ranking Methods and Putative Stabilizers, Coord. Chem. Rev., 2007, 251, 1075–1100 CrossRef.
- E. E. Finney and R. G. Finke, Catalyst Sintering Kinetic Data: Is There a Minimal Chemical Mechanism Underlying Kinetics Previously Fit by Empirical Power-Law Expressions—and if So, What Are Its Implications?, Ind. Eng. Chem. Res., 2017, 56, 10271–10286 CrossRef CAS.
- M. Harada and Y. Kamigaito, Nucleation and Aggregative Growth Process of Platinum Nanoparticles Studied by in Situ Quick XAFS Spectroscopy, Langmuir, 2012, 28, 2415–2428 CrossRef CAS.
- S. Yan, Z. Wu, H. Yu, Y. Gong, Y. Tan, R. Du, W. Chen, X. Xing, G. Mo, Z. Chen, Q. Cai and D. Sun, Time-Resolved Small-Angle X-ray Scattering Study on the Growth Behavior of Silver Nanoparticles, J. Phys. Chem. C, 2014, 118, 11454–11463 CrossRef CAS.
- A. Desireddy, B. E. Conn, J. Guo, B. Yoon, R. N. Barnett, B. M. Monahan, K. Kirschbaum, W. P. Griffith, R. L. Whetten, U. Landman and T. P. Bigioni, Ultrastable Silver Nanoparticles, Nature, 2013, 501, 399–402 CrossRef CAS.
- A. M. Karim, N. Al Hasan, S. Ivanov, S. Siefert, R. T. Kelly, N. G. Hallfors, A. Benavidez, L. Kovarik, A. Jenkins, R. E. Winans and A. K. Datye, Synthesis of 1 nm Pd Nanoparticles in a Microfluidic Reactor: Insights from in Situ X-ray Absorption Fine Structure Spectroscopy and Small-Angle X-ray Scattering, J. Phys. Chem. C, 2015, 119, 13257–13267 CrossRef.
- M. Harada, N. Tamura and M. Takenaka, Nucleation and Growth of Metal Nanoparticles during Photoreduction Using In Situ Time-Resolved SAXS Analysis, J. Phys. Chem. C, 2011, 115, 14081–14092 CrossRef CAS.
- P. Abellan, L. R. Parent, N. Al Hasan, C. Park, I. Arslan, A. M. Karim, J. E. Evans and N. D. Browning, Gaining Control over Radiolytic Synthesis of Uniform Sub-3-nanometer Palladium Nanoparticles: Use of Aromatic Liquids in the Electron Microscope, Langmuir, 2016, 32, 1468–1477 CrossRef CAS.
- N. Ortiz and S. E. Skrabalak, Manipulating Local Ligand Environments for the Controlled Nucleation of Metal Nanoparticles and their Assembly into Nanodendrites, Angew. Chem., Int. Ed., 2012, 51, 11757–11761 CrossRef CAS.
- M. Harada and Y. Inada, In Situ Time-Resolved XAFS Studies of Metal Particle Formation by Photoreduction in Polymer Solutions, Langmuir, 2009, 25, 6049–6061 CrossRef CAS.
- M. Saeki, D. Matsumura, T. Yomogida, T. Taguchi, T. Tsuji, H. Saitoh and H. Ohba, In Situ Time-Resolved XAFS Studies on Laser-Induced Particle Formation of Palladium Metal in an Aqueous/EtOH Solution, J. Phys. Chem. C, 2019, 123, 817–824 CrossRef CAS.
- S. Özkar and R. G. Finke, Nanoparticle Formation Kinetics and Mechanistic Studies Important to Mechanism-Based Particle-Size Control: Evidence for Ligand-Based Slowing of the Autocatalytic Surface Growth Step Plus Postulated Mechanisms, J. Phys. Chem. C, 2019, 123, 14047–14057 CrossRef.
- W. Stöber, A. Fink and E. Bohn, Controlled Growth of Monodisperse Silica Spheres in the Micron Size Range, J. Colloid Interface Sci., 1968, 26, 62–69 CrossRef.
- K. D. Hartlen, A. P. T. Athanasopoulos and V. Kitaev, Facile Preparation of Highly Monodisperse Small Silica Spheres (15 to >200 nm) Suitable for Colloidal Templating and Formation of Ordered Arrays, Langmuir, 2008, 24, 1714–1720 CrossRef CAS.
- T. Matsoukas and E. Gulari, Self-sharpening Distributions Revisited Polydispersity in Growth by Monomer Addition, J. Colloid Interface Sci., 1991, 145, 557–562 CrossRef CAS.
- G. H. Bogush and C. F. Zukoski, Uniform Silica Particle Precipitation: An Aggregative Growth Model, J. Colloid Interface Sci., 1991, 142, 19–34 CrossRef CAS.
- Y. Han, Z. Lu, Z. Teng, J. Liang, Z. Guo, D. Wang, M.-Y. Han and W. Yang, Unraveling the Growth Mechanism of Silica Particles in the Stöber Method: In Situ Seeded Growth Model, Langmuir, 2017, 33, 5879–5890 CrossRef CAS.
- A. van Blaaderen, J. van Geest and A. Vrij, Monodisperse Colloidal Silica Spheres from Tetraalkoxysilanes: Particle Formation and Growth Mechanism, J. Colloid Interface Sci., 1992, 154, 481–501 CrossRef CAS.
- H. Giesche, Synthesis of Monodispersed Silica Powders I. Particle Properties and Reaction Kinetics, J. Eur. Ceram. Soc., 1994, 14, 189–204 CrossRef CAS.
- J.-L. Look, G. H. Bogush and C. F. Zukoski, Colloidal Interactions during the Precipitation of Uniform Submicrometre Particles, Faraday Discuss. Chem. Soc., 1990, 90, 345–357 RSC.
- C. F. Zukoski, M. K. Chow, G. H. Bogush and J.-L. Look, Precipitation of Uniform Particles: The Role of Aggregation, Mater. Res. Soc. Symp. Proc., 1990, 180, 131–140 CrossRef CAS.
- C. F. Zukoski, J.-L. Look and G. H. Bogush, Formation of Uniform Precipitates from Alkoxides, Adv. Chem. Ser., 1994, 234, 451–465 CrossRef CAS.
- P. Calvert, And they all look just the same, Nature, 1994, 367, 119–120 CrossRef.
- G. H. Bogush and C. F. Zukoski, Studies of the Kinetics of the Precipitation of Uniform Silica Particles through the Hydrolysis and Condensation of Silicon Alkoxides, J. Colloid Interface Sci., 1991, 142, 1–18 CrossRef CAS.
- J. K. Bailey and M. L. Mecartney, Mechanism of Silica and Titania Colloidal Particle Formation from Metal Alkoxide, Mater. Res. Soc. Symp. Proc., 1990, 180, 153–158 CrossRef CAS.
- J. K. Bailey and M. L. Mecartney, Formation of colloidal silica particles from alkoxides, Colloid Surf., 1992, 63, 151–161 CrossRef CAS.
- L. S. Ott and R. G. Finke, Transition-Metal Nanocluster Stabilization vs Agglomeration Fundamental Studies: A Quantitative Measurement of the Two Rate Constants for Agglomeration and Their Informative Temperature Dependence, Chem. Mater., 2008, 20, 2592–2601 CrossRef CAS.
- S. Shields, W. E. Buhro, E. E. Finney and R. G. Finke, Gold Nanocluster Agglomeration Kinetic Studies: Evidence for Parallel Bimolecular Plus Autocatalytic Agglomeration Pathways as a Mechanistic Alternative to an Avrami-Based Analysis, Chem. Mater., 2012, 24, 1718–1725 CrossRef.
- E. Bayram, J. Lu, C. Aydin, N. D. Browning, S. Özkar, E. E. Finney, B. C. Gates and R. G. Finke, Agglomerative Sintering of an Atomically Dispersed Ir1/Zeolite Y Catalyst: Compelling Evidence Against Ostwald Ripening But for Bimolecular and Autocatalytic Agglomeration Catalyst Sintering Steps, ACS Catal., 2015, 5, 3514–3527 CrossRef CAS.
- S. Özkar and R. G. Finke, Palladium(0) Nanoparticle Formation, Stabilization, and Mechanistic Studies: Pd(acac)2 as a Preferred Precursor, [Bu4N]2HPO4 Stabilizer, Plus the Stoichiometry, Kinetics, and Minimal, 4-Step Mechanism of the Palladium Nanoparticle Formation and Subsequent Agglomeration Reactions, Langmuir, 2016, 32, 3699–3716 CrossRef.
- S. Özkar and R. G. Finke, A Classic, Azo-Dye Agglomeration System: Evidence for Slow, Continuous Nucleation, Autocatalytic Agglomerative Growth, Plus the Effects of Dust-Removal by Microfiltration on the Kinetics, J. Phys. Chem. A, 2017, 121, 7071–7078 CrossRef.
- T. Yokoi, J. Wakabayashi, Y. Otsuka, W. Fan, M. Iwama, R. Watanabe, K. Aramaki, A. Shimojima, T. Tatsumi and T. Okubo, Mechanism of Formation of Uniform-Sized Silica Nanospheres Catalyzed by Basic Amino Acids, Chem. Mater., 2009, 21, 3719–3729 CrossRef CAS.
- C. C. M. C. Carcouët, M. W. P. van de Put, B. Mezari, P. C. M. M. Magusin, J. Laven, P. H. H. Bomans, H. Friedrich, A. C. C. Esteves, N. A. J. M. Sommerdijk, R. A. T. M. van Benthem and G. de With, Nucleation and Growth of Monodisperse Silica Nanoparticles, Nano Lett., 2014, 14, 1433–1438 CrossRef.
- E. C. Vreeland, J. Watt, G. B. Schober, B. G. Hance, M. J. Austin, A. D. Price, B. D. Fellows, T. C. Monson, N. S. Hudak, L. Maldonado-Camargo, A. C. Bohorquez, C. Rinaldi and D. L. Huber, Enhanced Nanoparticle Size Control by Extending LaMer's Mechanism, Chem. Mater., 2015, 27, 6059–6066 CrossRef CAS.
- E. Matijević and P. Scheiner, Ferric Hydrous Oxide Sols: III. Preparation of Uniform Particles by Hydrolysis of Fe(III)-Chloride, -Nitrate, and -Perchlorate Solutions, J. Colloid Interface Sci., 1978, 63, 509–524 CrossRef.
- CRC Handbook of Chemistry and Physics, ed. D. R. Lide, CRC Press, Boca Raton, FL, 89th edn, 2008 Search PubMed.
- T. C. Chamberlin, Studies for Students. The Method of Multiple Working Hypotheses, J. Geol., 1897, 5, 837–848 CrossRef.
- J. R. Platt, Strong Inference, Science, 1964, 146, 347–353 CrossRef CAS . Platt and Chamberlin's method is of course a general method of thinking that has broad application far beyond just scientific endeavors.
- S. L. Scott, The Burden of Disproof, ACS Catal., 2019, 9, 4706–4708 CrossRef CAS.
- T. Wen, X. Zhang, D. Zhang, C. Zhang, Q. Wen, H. Zhang and Z. Zhong, Simulation of Batch Nanoparticle Growth by the Generalized Diffusional Model, J. Phys. Chem. C, 2018, 122, 27070–27081 CrossRef CAS.
- S. Famiani, A. P. LaGrow, M. O. Besenhard, S. Maenosono and N. T. K. Thanh, Synthesis of Fine-Tuning Highly Magnetic Fe@FexOy Nanoparticles through Continuous Injection and a Study of Magnetic Hyperthermia, Chem. Mater., 2018, 30, 8897–8904 CrossRef CAS.
- I. R. Epstein, The consequences of imperfect mixing in autocatalytic chemical and biological systems, Nature, 1995, 374, 321–327 CrossRef CAS.
- W. Baaziz, B. P. Pichon, S. Fleutot, Y. Liu, C. Lefevre, J.-M. Greneche, M. Toumi, T. Mhiri and S. Begin-Colin, Magnetic Iron Oxide Nanoparticles: Reproducible Tuning of the Size and Nanosized-Dependent Composition, Defects, and Spin Canting, J. Phys. Chem. C, 2014, 118, 3795–3810 CrossRef CAS.
- C. M. McGilvery, A. E. Goode, M. S. P. Shaffer and D. W. McComb, Contamination of holey/lacey carbon films in STEM, Micron, 2012, 43, 450–455 CrossRef CAS.
- S. Horiuchi, T. Hanada, M. Ebisawa, Y. Matsuda, M. Kobayashi and A. Takahara, Contamination-Free Transmission Electron Microscopy for High-Resolution Carbon Elemental Mapping of Polymers, ACS Nano, 2009, 3, 1297–1304 CrossRef CAS.
- S. G. Kwon and T. Hyeon, Colloidal Chemical Synthesis and Formation Kinetics of Uniformly Sized Nanocrystals of Metals, Oxides, and Chalcogenides, Acc. Chem. Res., 2008, 41, 1696–1709 CrossRef CAS.
- T. He, D. R. Chen, X. L. Jiao, Y. Wang and Y. Duan, Solubility-Controlled Synthesis of High-Quality Co3O4 Nanocrystals, Chem. Mater., 2005, 17, 4023–4030 CrossRef CAS.
- S. Yang and Q. Liu, Formation mechanism of apex-truncated octahedral Cu2O microcrystal, CrystEngComm, 2016, 18, 8229–8236 RSC.
- S. Arshadi, J. Moghaddam and M. Eskandarian, LaMer diagram approach to study the nucleation and growth of Cu2O nanoparticles using supersaturation theory. Korean, J. Chem. Eng., 2014, 31, 2020–2026 CAS.
- P. Stolzenburg and G. Garnweitner, Experimental and numerical insights into the formation of zirconia nanoparticles: a population balance model for the nonaqueous synthesis, React. Chem. Eng., 2017, 2, 337–348 RSC.
- J. K. Beattie, Monodisperse colloids of transition metal and lanthanide compounds, Pure Appl. Chem., 1989, 61, 937–941 Search PubMed.
- T. Okubo, K. Kobayashi, A. Kuno and A. Tsuchida, Kinetic study of the formation reaction of colloidal silica spheres by transmitted-light-intensity and dynamic light-scattering measurements, Colloid Polym. Sci., 1999, 277, 483–487 CrossRef CAS.
- J. Ng, S. Xu, X. Zhang, H. Y. Yang and D. D. Sun, Hybridized Nanowires and Cubes: A Novel Architecture of a Heterojunctioned TiO2/SrTiO3 Thin Film for Efficient Water Splitting, Adv. Funct. Mater., 2010, 20, 4287–4294 CrossRef CAS.
- H. Mehranpour, M. Askari, M. Sasani Ghamsari and H. Farzalibeik, Study on the Phase Transformation Kinetics of Sol–Gel Drived TiO2 Nanoparticles, J. Nanomater., 2010, 2010, 626978 Search PubMed.
- Y. Huang and J. E. Pemberton, Synthesis of uniform, spherical sub-100 nm silica particles using a conceptual modification of the classic LaMer model, Colloids Surf., A, 2010, 360, 175–183 CrossRef CAS.
- C. Wang, H. Shpaisman, A. D. Hollingsworth and D. G. Grier, Celebrating Soft Matter's 10th Anniversary: Monitoring colloidal growth with holographic microscopy, Soft Matter, 2015, 11, 1062–1066 RSC.
- L. Luo, Y. Liang, E. S. Erichsen and R. Anwander, Monodisperse mesoporous silica nanoparticles of distinct topology, J. Colloid Interface Sci., 2017, 495, 84–93 CrossRef CAS.
- J. K. Bailey, C. J. Brinker and M. L. Mecartney, Growth Mechanisms of Iron Oxide Particles of Differing Morphologies from the Forced Hydrolysis of Ferric Chloride Solutions, J. Colloid Interface Sci., 1993, 157, 1–13 CrossRef CAS.
- S. G. Kwon, Y. Piao, J. Park, S. Angappane, Y. Jo, N.-M. Hwang, J.-G. Park and T. Hyeon, Kinetics of Monodisperse Iron Oxide Nanocrystal Formation by “Heating-Up” Process, J. Am. Chem. Soc., 2007, 129, 12571–12584 CrossRef CAS.
- M. Drofenik, M. Kristl, A. Žnidaršič, D. Hanžel and D. Lisjak, Hydrothermal Synthesis of Ba-Hexaferrite Nanoparticles, J. Am. Ceram. Soc., 2007, 90, 2057–2061 CrossRef CAS.
- A. Lassenberger, T. A. Grunewald, P. D. J. van Oostrum, R. Rennhofer, H. Amenitsch, R. Zirbs, H. C. Lichteneggar and E. Reimhult, Monodisperse Iron Oxide Nanoparticles by Thermal Decomposition: Elucidating Particle Formation by Second-Resolved in Situ Small-Angle X-ray Scattering, Chem. Mater., 2017, 29, 4511–4522 CrossRef CAS.
- H. S. Dehsari, R. A. Harris, A. H. Ribeiro, W. Tremel and A. Asadi, Optimizing the Binding Energy of the Surfactant to Iron Oxide Yields Truly Monodisperse Nanoparticles, Langmuir, 2018, 34, 6582–6590 CrossRef.
- S. Belaïd, D. Stanicki, L. Van der Elst, R. N. Muller and S. Laurent, Influence of experimental parameters on iron oxide nanoparticle properties synthesized by thermal decomposition: size and nuclear magnetic resonance studies, Nanotechnology, 2018, 29(165603), 1–12 Search PubMed.
- A. W. Jansons and J. E. Hutchison, Continuous Growth of Metal Oxide Nanocrystals: Enhanced Control of Nanocrystal Size and Radial Dopant Distribution, ACS Nano, 2016, 10, 6942–6951 CrossRef CAS.
- T. O. Drews, M. A. Katsoulakis and M. Tsapatsis, A Mathematical Model for Crystal Growth by Aggregation of Precursor Metastable Nanoparticles, J. Phys. Chem. B, 2005, 109, 23879–23887 CrossRef CAS.
- I. M. Lifshitz and V. V. Slyozov, The kinetics of precipitation from supersaturated solid solutions, J. Phys. Chem. Solids, 1961, 19, 35–50 CrossRef.
- R. L. Penn and J. F. Banfield, Imperfect Oriented Attachment: Dislocation Generation in Defect-Free Nanocrystals, Science, 1998, 281, 969–971 CrossRef CAS.
- R. L. Penn and J. F. Banfield, Morphology development and crystal growth in nanocrystalline aggregates under hydrothermal conditions: Insights from titania, Geochim. Cosmochim. Acta, 1999, 63, 1549–1557 CrossRef CAS.
- R. L. Penn, Kinetics of Oriented Aggregation, J. Phys. Chem. B, 2004, 108, 12707–12712 CrossRef CAS.
- S. Auer and D. Frenkel, Prediction of absolute crystal-nucleation rate in hard-sphere colloids, Nature, 2001, 409, 1020–1023 CrossRef CAS.
- D. Pan, Q. Wang and L. An, Controlled synthesis of monodisperse nanocrystals by a two-phase approach without the separation of nucleation and growth processes, J. Mater. Chem., 2009, 19, 1063–1073 RSC.
- V. Privman, D. V. Goia, J. Park and E. Matijević, Mechanism of Formation of Monodispersed Colloids by Aggregation of Nanosize Precursors, J. Colloid Interface Sci., 1999, 213, 36–45 CrossRef CAS.
- T. Sugimoto, Formation of Monodispersed Nano- and Micro-Particles Controlled in Size, Shape, and Internal Structure, Chem. Eng. Technol., 2003, 26, 313–321 CrossRef CAS.
- D. L. Van Hyning, W. G. Klemperer and C. F. Zukoski, Silver Nanoparticle Formation: Predictions and Verification of the Aggregative Growth Model, Langmuir, 2001, 17, 3128–3135 CrossRef CAS.
- E. Matijević and D. Goia, Formation Mechanisms of Uniform Colloid Particles, Croat. Chem. Acta, 2007, 80, 485–491 Search PubMed.
- T. O. Drews and M. Tsapatsis, Model of the evolution of nanoparticles to crystals via an aggregative growth mechanism, Microporous Mesoporous Mater., 2007, 101, 97–107 CrossRef CAS.
- S. Kumar, T. M. Davis, H. Ramanan, R. L. Penn and M. Tsapatsis, Aggregative Growth of Silicalite-1, J. Phys. Chem. B, 2007, 111, 3398–3403 CrossRef CAS.
- F. Wang, V. N. Richards, S. P. Shields and W. E. Buhro, Kinetics and Mechanisms of Aggregative Nanocrystal Growth, Chem. Mater., 2014, 26, 5–21 CrossRef CAS.
- V. N. Richards, S. P. Shields and W. E. Buhro, Nucleation Control in the Aggregative Growth of Bismuth Nanocrystals, Chem. Mater., 2011, 23, 137–144 CrossRef CAS.
- D. T. Robb and V. Privman, Model of Nanocrystal Formation in Solution by Burst Nucleation and Diffusional Growth, Langmuir, 2008, 24, 26–35 CrossRef CAS.
- V. Privman, Mechanisms of Diffusional Nucleation of Nanocrystals and Their Self-Assembly into Uniform Colloids, Ann. N. Y. Acad. Sci., 2009, 1161, 508–525 CrossRef CAS.
- P. J. Skrdla, Use of Dispersive Kinetic Models for Nucleation and Denucleation to Predict Steady-State Nanoparticle Size Distributions and the Role of Ostwald Ripening, J. Phys. Chem. C, 2012, 116, 214–225 CrossRef CAS.
- S. St. John, Z. Nan, N. Hu, D. W. Schaefer and A. P. Angelopoulos, A nanoscale-modified LaMer model for particle synthesis from inorganic tin-platinum complexes, J. Mater. Chem. A, 2013, 1, 8903–8916 RSC.
- S. R. K. Perala and S. Kumar, On the Mechanism of Metal Nanoparticle Synthesis in the Brust–Schiffrin Method, Langmuir, 2013, 29, 9863–9873 CrossRef CAS.
- F. Tong, M. P. Hanson and C. J. Bardeen, Analysis of reaction kinetics in the photomechanical molecular crystal 9-methylanthracene using an extended Finke-Watzky model, Phys. Chem. Chem. Phys., 2016, 18, 31936–31945 RSC.
- A. B. Levit and R. L. Rowell, Time Dependence of the Size Distribution, Number Concentration and Surface Area in La Mer Sulfur Sols, J. Colloid Interface Sci., 1975, 50, 162–169 CrossRef CAS.
- C. F. Zukoski, J.-L. Look and G. H. Bogush, Formation of Uniform Precipitates from Alkoxides. In The Colloid Chemistry of Silica, in Advances in Chemistry, ed. H. E. Bergna, American Chemical Society, Washington, DC, 1994, pp. 451–465 Search PubMed.
- A. P. LaGrow, B. Ingham, M. F. Toney and R. D. Tilley, Effect of Surfactant Concentration and Aggregation on the Growth Kinetics of Nickel Nanoparticles, J. Phys. Chem. C, 2013, 117, 16709–16718 CrossRef CAS.
- A. P. Sergievskaya, V. V. Tatarchuk, E. V. Makotchenko and I. V. Mironov, Formation of gold nanoparticles during the reduction of HAuBr4 in reverse micelles of oxyethylated surfactant: Influence of gold precursor on the growth kinetics and properties of the particles, J. Mater. Res., 2015, 30, 1925–1933 CrossRef CAS.
- The first thing apparent in analyzing the literature in the tables in the ESI† is (i) a failure to use consistently a proper scientific method of the disproof224,225 of multiple alternative hypotheses223—with too many papers that don't disprove anything, but instead wind up with their (often explicitly unstated) hypothesis as their conclusion. This is not science; it is confirmation bias that in turn inhibits unbiased thinking and reliable science. Second, (ii) there is a pattern apparent in the tables in the ESI† of accepting and supporting theories/models/mechanisms based on their popularity. As stated in an excellent, recent ACS Catalysis editorial entitled “The Burden of Disproof”,225 “the validity of a mechanistic (or any scientific) hypothesis is not established by the strength of a consensus (i.e., what fraction of researchers believe it to be true at any given time).” Awareness of even just Turkevich's groundbreaking 1951 paper5 gives one serious pause about blindly accepting and applying the burst-nucleation and diffusion-controlled growth 1950 model in the absence of strongly supportive evidence. It is upon us as modern researchers to decide if any scientific model is appropriate to our system or is simply being “inappropriately cited”, a broader problem of “The classic theories work(ing) poorly or not at all when applied beyond the validity of their assumptions” as B. Peters has insightfully noted.18 Third, as mentioned in the main text (iii) a better consideration and understanding of the different types of models in science,277,278,279 including the strengths and weaknesses of those different types of models, would have helped expedite the understanding of particle formation in our opinion.
- A. Gelfert, How to Do Science with Models: A Philosophical Primer, Springer, 2016 Search PubMed.
- E. E. Finney and R. G. Finke, Fitting and Interpreting Transition-Metal Nanocluster Formation and Other Sigmoidal Kinetic Data: A More Thorough Testing of Dispersive Kinetics vs Chemical-Mechanism-Based Equations and Treatments for 4-Step Type Kinetic Data, Chem. Mater., 2009, 21, 4468–4479 CrossRef CAS . See the discussion and references in the ESI† on different types of models in science.
- F. Hou, J. D. Martin, E. D. Dill, J. C. W. Folmer and A. A. Josey, Transition Zone Theory of Crystal Growth and Viscosity, Chem. Mater., 2015, 27, 3526–3532 CrossRef CAS.
- C. B. Whitehead, M. A. Watzky and R. G. Finke, “Burst Nucleation” vs. Autocatalytic, “Burst” Growth in Near-Monodisperse Particle-Formation Reactions, J. Phys. Chem. C, 2020, 124, 24543–24554 CrossRef CAS.
- P. Coulier, J. Note sur une nouvelle propriete de l’air, J, J. de Pharmacie et de Chimie, Paris, Ser., 1875, 4, 165–173 Search PubMed.
- J. Aitken, On the dust, fog, and clouds, Proc. Roy. Soc., 1882, 11, 14–18 Search PubMed.
- J. Aitken, On the numbers of dust particles in the atmosphere in certain places in Great Britain and on the continent, with remarks on the relation between the amount of dust and meteorological phenomena, Trans. R. Soc. Edinburgh: Earth Sci., 1889, 35, 1–19 CrossRef.
- J. Aitken, On improvements in the apparatus for counting the dust particles in the atmosphere, Proc. Roy. Soc., 1890, 16, 135–172 Search PubMed.
- J. Aitken, On a simple pocket dust-counter, Proc. Roy. Soc., 1892, 18, 39–52 Search PubMed.
- C. T. R. Wilson, Condensation of water vapour in the presence of dust-free air and other gases, Philos. Trans. R. Soc. London, 1897, 189, 265–307 CrossRef.
- M. Kerker, E. Daby, G. L. Cohen, J. P. Kratohvil and E. Matijevic, Particle size distribution in LaMer sulfur sols, J. Phys. Chem., 1963, 67, 2105–2111 CrossRef CAS.
- A. J. Petro, Particle size distribution in monodisperse sulfur hydrosols, J. Phys. Chem., 1960, 64, 1508–1511 CrossRef CAS.
- R. Strey, P. E. Wagner and Y. Viisanen, The Problem of Measuring Homogeneous Nucleation Rates and the Molecular Contents of Nuclei: Progress in the Form of Nucleation Pulse Measurements, J. Phys. Chem., 1994, 98, 7748–7758 CrossRef CAS.
- K. R. Spurny, Atmospheric Condensation Nuclei P. J. Coulier 1875 and J. Aitken 1880 (Historical Review), Aerosol Sci. Technol., 2000, 32, 243–248 CrossRef CAS.
- S. A. Seifert, S. Von Essen, K. Jacobitz, R. Crouch and C. P. Lintner, Organic dust toxic syndrome: a review, J. Toxicol., Clin. Toxicol., 2003, 41, 185–193 CrossRef CAS.
- J. A. Poole and D. J. Romberger, Immunological and inflammatory responses to organic dust in agriculture, Curr. Opin. Allergy Clin. Immunol., 2012, 12, 126–132 CrossRef CAS.
- S. A. Kulkarni, S. S. Kadam, H. Meekes, A. L. Stankiewicz and J. H. ter Horst, Crystal nucleation kinetics from induction times and metastable zone widths, Cryst. Growth Des., 2013, 13, 2435–2440 CrossRef CAS.
- L. Granasy, F. Podmaniczky, G. I. Toth, G. Tegze and T. Pusztai, Heterogeneous nucleation of/on nanoparticles: a density functional study using the phase-field crystal model, Chem. Soc. Rev., 2014, 43, 2159–2173 RSC.
- G. Kulkarni, C. Sanders, K. Zhang, X. Liu and C. Zhao, Ice nucleation of bare and sulfuric acid-coated mineral dust particles and implication for cloud properties, J. Geophys. Res.: Atmos., 2014, 119, 9993–10011 CAS.
- S. Özkar and R. G. Finke, Dust Effects on Nucleation Kinetics and Nanoparticle Product Size Distributions: Illustrative Case Study of a Prototype Ir(0)n Transition-Metal Nanoparticle Formation System, Langmuir, 2017, 33, 6550–6562 CrossRef . See also references therein to the early literature of dust in nucleating systems.
- J. Pelley, Tracing the chemistry of household dust. C&EN 2017, February 13, pp. 18–21.
- D. R. Handwerk, P. D. Shipman, S. Özkar and R. G. Finke, Dust Effects on Ir(0)n Nanoparticle Formation Nucleation and Growth Kinetics and Particle Size-Distributions: Analysis by and Insights from Mechanism-Enabled Population Balance Modeling, Langmuir, 2020, 36, 1496–1506 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Fig. S1–S7 and Table S1, summary of literature on the formation of silver halide nanoparticles relating to the 1950 model; Table S2, summary of literature on the formation of semiconductor nanoparticles relating to the 1950 model; Table S3, summary of transition-metal nanoparticles literature relating to the 1950 model; Table S4, summary of the literature on oxide-based nanoparticles relating to the 1950 model; Table S5, summary of other, alternative models or mechanisms for nanoparticle formation that cite or impact the 1950 model. See DOI: 10.1039/d0ma00439a |
| This journal is © The Royal Society of Chemistry 2021 |



