Origin of rate enhancement and asynchronicity in iminium catalyzed Diels–Alder reactions

Abstract

The Diels–Alder reactions between cyclopentadiene and various α,β-unsaturated aldehyde, imine, and iminium dienophiles were quantum chemically studied using a combined density functional theory and coupled-cluster theory approach. Simple iminium catalysts accelerate the Diels–Alder reactions by lowering the reaction barrier up to 20 kcal mol⁻¹ compared to the parent aldehyde and imine reactions. Our detailed activation strain and Kohn–Sham molecular orbital analyses reveal that the iminium catalysts enhance the reactivity by reducing the steric (Pauli) repulsion between the diene and dienophile, which originates from both a more asynchronous reaction mode and a more significant polarization of the π-system away from the incoming diene compared to aldehyde and imine analogs. Notably, we establish that the driving force behind the asynchronicity of the herein studied Diels–Alder reactions is the relief of destabilizing steric (Pauli) repulsion and not the orbital interaction between the terminal carbon of the dienophile and the diene, which is the widely accepted rationale.

---

1. Introduction

Iminium catalysis constitutes an important branch of organocatalysis typically leading to the enantioselective β-functionalization of α,β-unsaturated aldehydes.¹ This process is mediated by either chiral primary or secondary amine catalysts which, via condensation with the carbonyl compound, produce a transient iminium intermediate,² which facilitates the conjugate addition to the β-carbon atom. The Knoevenagel condensation mediated by primary or secondary amines is nowadays accepted as the earliest recorded example of an iminium-catalyzed transformation.^3,4 Since then, an impressive number of different iminium-catalyzed chemical reactions, most of them affording high enantioselectivities, have been reported.^1b,5,6 For this reason, it is not surprising that this type of organocatalysis has been thoroughly applied to the synthesis of complex natural products and pharmaceuticals.⁷

The seminal report by MacMillan and co-workers in 2000 on enantioselective Diels–Alder cycloaddition reactions using iminium catalysts established the basics behind this type of organocatalysis.⁸ In analogy with Lewis acids, the term “LUMO-lowering catalysis” was coined by the authors to describe the driving force behind iminium catalysis. In the authors' own words: “…the reversible formation of iminium ions from α,β-unsaturated aldehydes and amines might emulate the equilibrium dynamics and π-orbital electronics that are inherent to Lewis acid catalysis”. Strikingly and in sharp contrast to the widely accepted rationale, we very recently demonstrated, using state-of-the-art quantum chemical calculations, that orbital interactions are not the origin of Lewis acid (LA) catalysis in Diels–Alder cycloaddition reactions.⁹ We found that although Lewis acids indeed stabilize the π-LUMO of the dienophile and, therefore, enhance the corresponding HOMO_diene–LUMO_dienophile interaction,¹⁰ they simultaneously weaken the inverse LUMO_diene–HOMO_dienophile interaction to the same extent. As a result, the total orbital interactions in both LA-catalyzed and uncatalyzed reactions are nearly identical and therefore, not responsible for the acceleration of LA-mediated reactions. Instead, the significant reduction of steric (Pauli) repulsion between the occupied orbitals of the dienophile and the diene becomes the actual driving force behind the LA-catalysis. This unprecedented electronic mechanism, which is also operative in dihalogen-catalyzed aza-Michael addition reactions^11a and related Lewis acid catalyzed (aromatic) Diels–Alder reactions,^11b–d contradicts the widely accepted “LUMO-lowering catalysis” as the mechanism behind the iminium catalysis.

For this reason, herein we shall investigate the ultimate factors governing the iminium-catalysis and check the generality of our “Pauli repulsion-lowering catalysis” in this important reaction. In addition, the reasons behind the catalysis induced by the asynchronicity shall be thoroughly investigated. To this end, we have selected the Diels–Alder cycloaddition reactions involving cyclopentadiene (CP) and various α,β-unsaturated aldehyde (O and O–AlCl₃), imine (NMe and MeN–AlCl₃), and iminium (N(C₄H₈)⁺, N(C₄H₈O)⁺, and NMe₂⁺) dienophiles (Scheme 1) analogous to the processes initially described by MacMillan and co-workers.^8,12

Scheme 1 The Diels–Alder reactions between cyclopentadiene (CP) and various α,β-unsaturated aldehyde (O and O–AlCl₃), imine (NMe and MeN–AlCl₃), and iminium (N(C₄H₈)⁺, N(C₄H₈O)⁺, and NMe₂⁺) dienophiles that were computationally analyzed. N(C₄H₈)⁺ and N(C₄H₈O)⁺ stand for the iminium ions derived from pyrrolidine and morpholine, respectively.

2. Results and discussion

Table 1 summarizes the electronic reaction barriers (ΔE^‡), reaction energies (ΔE_rxn), and HOMO_CP–LUMO_dienophile orbital energy gaps (Δε_H–L) of the Diels–Alder (DA) reaction between cyclopentadiene (CP) and various α,β-unsaturated aldehyde (O and O–AlCl₃), imine (NMe and MeN–AlCl₃), and iminium (N(C₄H₈)⁺, N(C₄H₈O)⁺, and NMe₂⁺) dienophiles. In all the cases, the cycloaddition reaction occurs in a concerted manner through the corresponding transition state TS (see Fig. S1 in the ESI†), after prior formation of an initial reactant complex RC which lies −3 to −10 kcal mol⁻¹ below the separate reactants (the formation of this species becomes endergonic when thermal free energy corrections at 298.15 K are included, see Gibbs free energies in Table S1†).

Table 1 Electronic reactant complex energies (ΔE_RC), reaction barriers (ΔE^‡), reaction energies (ΔE_rxn) (in kcal mol⁻¹), and HOMO_CP–LUMO_dienophile energy gaps (Δε_H–L) (in eV) computed for the Diels–Alder reactions between cyclopentadiene (CP) and various α,β-unsaturated aldehyde, imine, and iminium dienophiles^a,b

X		ΔERC	ΔE^‡	ΔE^‡^c	ΔErxn	ΔεH–L
a All energies were computed at M06-2X/def2-TZVP and were referenced to the isolated reactants. b See ESI Table S1 for Gibbs free reaction barriers and energies. c Computed at DLPNO-CCSD(T)/def2-QZVPP//M06-2X/def2-TZVP. d N(C4H8)^+ and N(C4H8O)^+ stand for the iminium ions derived from pyrrolidine and morpholine, respectively.
O	endo	−3.6	15.2	14.3	−20.3	−6.67
	exo	−2.9	15.8	14.8	−20.1
O–AlCl3	endo	−7.3	1.9	3.2	−22.6	−4.58
	exo	−5.8	2.4	3.3	−22.0
NMe	endo	−3.1	18.6	17.1	−19.3	−7.37
	exo	−2.4	19.1	17.6	−18.9
MeN–AlCl3	endo	−5.1	10.9	10.5	−20.7	−5.52
	exo	−4.5	10.4	10.4	−21.8
N(C4H8)^+	endo	−9.1	−0.3	0.7	−23.6	−1.59
	exo	−8.2	−0.1	1.1	−22.7
N(C4H8O)^+	endo	−9.3	−1.4	−0.1	−24.1	−1.51
	exo	−8.4	−0.1	1.1	−22.7
NMe2^+	endo	−9.7	−2.0	−0.6	−24.1	−1.38
	exo	−8.7	−1.8	−0.4	−23.0

---

Three distinct trends can be observed. In the first place, for a given substrate, the endo DA reaction proceeds with a 0.5–1.5 kcal mol⁻¹ lower reaction barrier than the exo DA reaction in line with our previous theoretical studies and experimentally observed product ratios.^12,13 There is, however, one exception, namely, the Diels–Alder reaction between CP and MeN–AlCl₃. For this reaction, the exo pathway has a slightly lower barrier than the endo pathway. Secondly, both the uncatalyzed and LA-catalyzed DA reactions involving an α,β-unsaturated imine as the dienophile have comparatively higher reaction barriers, 18.6 and 10.9 kcal mol⁻¹, for NMe and MeN–AlCl₃, respectively (endo approach), than the corresponding aldehyde analogs, 15.2 and 1.9 kcal mol⁻¹, for O and O–AlCl₃, respectively. Thirdly, introducing an iminium catalyst significantly accelerates the DA reaction by lowering the reaction barrier from 18.6 kcal mol⁻¹ for NMe to −2.0 kcal mol⁻¹ for NMe₂⁺. This acceleration is even higher than that caused by the strong Lewis acid catalyst AlCl₃. Similar values were found for the iminium dienophiles derived from pyrrolidine and morpholine: N(C₄H₈)⁺ and N(C₄H₈O)⁺, respectively. Furthermore, there is a good linear correlation (R² = 0.91) between the reaction barrier (ΔE^‡) and the HOMO_CP–LUMO_dienophile orbital energy gap (Δε_H–L, see Fig. S2 in the ESI†). Thus, one might, indeed, suspect that lower and more favorable reaction barriers directly arise due to a more stabilizing orbital interaction as a result of priorly reported lowering of the LUMO_dienophile.¹⁰ This result seemingly confirms that this commonly accepted textbook explanation could be the decisive factor behind the computed reactivity trends. We will show next that, similar to the situation for Lewis-acid catalysis,⁹ this is not the case in iminium-ion catalysis either.

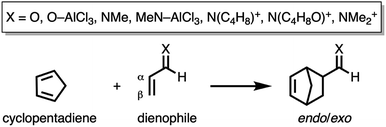
First, we aim to gain quantitative insight into the physical factors leading to the computed difference in reactivity between the uncatalyzed endo Diels–Alder reactions involving the parent α,β-unsaturated aldehyde and imine dienophiles by applying the activation strain model (ASM) of reactivity.¹⁴ This model, which is also known as the distortion/interaction model,^14d involves decomposing the electronic energy (ΔE) into two distinct energy terms, namely, the strain energy (ΔE_strain) that results from the deformation of the individual reactants and the interaction energy (ΔE_int) between the deformed reactants along the reaction coordinate, defined, in this case, by the shorter newly forming C_CP⋯C_β bond between CP and the dienophile. This critical reaction coordinate undergoes a well-defined change throughout the reaction and has successfully been used in the past for the analysis of similar reactions.^9,15,16Fig. 1a shows the activation strain diagrams (ASDs) from the reactants to the transition states (see Fig. S5† for the complete reaction profiles) for the Diels–Alder reactions between CP and the dienophiles O and NMe. The enhanced reactivity for the reaction of O originates from both a less destabilizing strain energy and a more stabilizing interaction energy (rather similar ASDs were obtained using the BP86-D3 and B3LYP-D3 functionals, therefore supporting the selected computational methodology for the present study, see Fig. S6–S9 in the ESI†).

Fig. 1 (a) Activation strain analyses and (b) energy decomposition analyses of the Diels–Alder reactions between the CP and O and NMe going from the reactants to the transition states, where the energy values are projected onto the shorter newly forming C_CP⋯C_β bond between CP and the dienophile, computed at ZORA-M06-2X/TZ2P//M06-2X/def2-TZVP.

By inspecting and comparing the DA reaction modes of O and NMe, we can ascribe their differences in ΔE_strain to the higher degree of asynchronicity of O (O: Δr^TS_C⋯C = 0.19 Å; and NMe: Δr^TS_C⋯C = 0.14 Å, where Δr^TS_C⋯C is the difference between the newly forming C⋯C bond lengths in the TS), which leads to a lower degree of deformation of the reactants since the C_CP⋯C_β bond forms ahead of the C_CP⋯C_α bond (see Fig. S1† for transition state structures).¹⁷ Later on, we analyze and explain the origin of, and differences between, the degrees of asynchronicity of the herein studied Diels–Alder reactions. In addition to the strain, the important role of the interaction energy in the observed reactivity trend prompted the analysis of the different contributors to the interaction energy using the canonical energy decomposition analysis (EDA).¹⁸ Our canonical EDA decomposed the ΔE_int between the reactants into three physically meaningful energy terms: classical electrostatic interaction (ΔV_elstat), steric (Pauli) repulsion (ΔE_Pauli) which, in general, arises from the two-center four-electron repulsion between the closed-shell orbitals of both reactants, and stabilizing orbital interactions (ΔE_oi) that account, among others, for HOMO–LUMO interactions. The corresponding energy decomposition analysis (EDA) results for the Diels–Alder reactions of O and NMe are presented in Fig. 1b. The differences in ΔE_int between O and NMe can solely be assigned to the Pauli repulsion. The electrostatic and orbital interactions are, on the other hand, similar or even more stabilizing for NMe compared to O, despite the more favorable HOMO_CP–LUMO_dienophile gap (Δε_H–L, see Table 1) computed for the latter system.

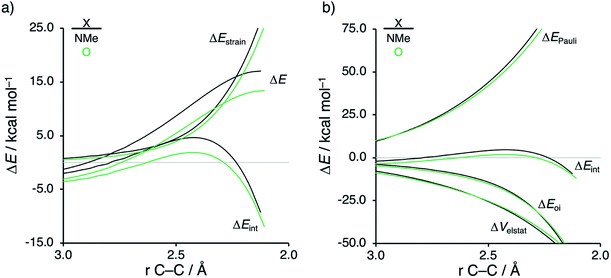
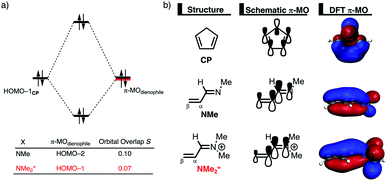
The origin of the less destabilizing Pauli repulsion for the Diels–Alder reaction involving O was investigated by performing a Kohn–Sham molecular orbital (KS-MO) analysis.^18b,19 The occupied molecular orbitals of CP, as well as, O and NMe were quantified at consistent geometries with a C_CP⋯C_β bond length between CP and the dienophile of 2.125 Å (Fig. 2a). Performing this analysis at a consistent point along the reaction coordinate (near all transition structures), rather than the transition state alone, ensures that the results are not skewed by the position of the transition state.^14,20 The most important occupied π-MO of the dienophile involved in the two-center four-electron interaction are the HOMO−2 and HOMO−3 of NMe and O, respectively, where all 2p_π AOs are in-phase. The contributing occupied orbital of CP is HOMO−1, where all 2p_π AOs located on both reacting C=C double bonds are in-phase. The orbital overlap between the HOMO−1_CP and the occupied π-MO of the dienophile is larger (S = 0.10) and, therefore, more destabilizing for NMe and smaller and less destabilizing for O (S = 0.07). The difference in the electronegativity of the heteroatoms is the reason behind the decreased occupied–occupied orbital overlap. The oxygen of O is more electronegative than the nitrogen of NMe and, therefore, polarizes more π-electron density away from the terminal carbon of the C=C double bond of the dienophile, which is directly involved in the Diels–Alder reaction.

Fig. 2 (a) Molecular orbital diagram and the most significant occupied orbital overlaps of the Diels–Alder reactions between CP and dienophiles NMe and O and (b) key occupied orbitals (isovalue = 0.03 au^−3/2) computed at consistent geometries with a C_CP⋯C_β bond length between CP and the dienophile of 2.125 Å at ZORA-M06-2X/TZ2P//M06-2X/def2-TZVP.

Inspection of the spatial distribution of the occupied π-MO of the dienophile (Fig. 2b) reveals that the HOMO−3 of O is polarized towards the oxygen, which results in a small orbital amplitude on the reactive C=C bond, while in the case of NMe this polarizing effect is minimal. Thus, it can be concluded that a large difference in electronegativity induces a significant reduction of the electron density at the reactive C=C double bond of the dienophile which results in a lower 〈HOMO−1_CP|HOMO−3_O〉 overlap and ultimately, in a less destabilizing Pauli repulsion and a lower reaction barrier. We have, as priorly discussed, observed this exact phenomenon in our analysis of Lewis acid-catalyzed Diels–Alder and aza-Michael addition reactions.^9,11 This demonstrates that the applicability of the concept of catalysis through reduced steric (Pauli) repulsion, caused by polarizing the filled π-orbitals on the C=C double bond away from the incoming reactant, is general and not limited only to Lewis acid-catalyzed organic reactions.

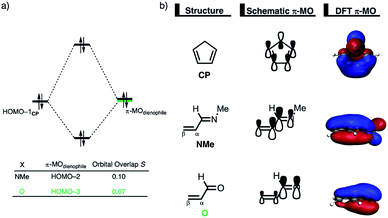
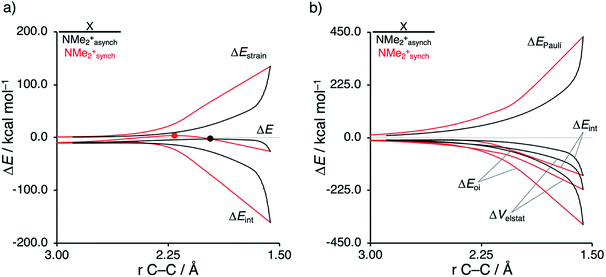
Next, we want to understand the driving mechanism behind iminium-catalyzed Diels–Alder reactions, i.e., why does the Diels–Alder reaction with α,β-unsaturated iminium dienophiles have markedly lower reaction barriers than their imine analogs. Fig. 3 shows the activation strain diagram (ASD) from the reactants to the transition states for the Diels–Alder reactions between CP and the dienophiles NMe and NMe₂⁺.^14e The accelerated reactivity of the iminium catalyst (NMe₂⁺) originates from both a less destabilizing strain energy, as well as a much more stabilizing interaction energy (Fig. 3a). Diels–Alder reactions with more commonly employed iminium catalysts, i.e., pyrrolidine (N(C₄H₈)⁺) and morpholine (N(C₄H₈O)⁺), exhibit identical reactivity trends to NMe₂⁺ and are provided in the ESI (see Fig. S10†).

Fig. 3 (a) Activation strain analyses and (b) energy decomposition analyses of the Diels–Alder reactions between the CP and NMe and NMe₂⁺ going from the reactants to the transition states, where the energy values are projected onto the shorter newly forming C_CP⋯C_β bond between CP and the dienophile, computed at ZORA-M06-2X/TZ2P//M06-2X/def2-TZVP.

The difference in strain energy can again be explained by looking at the degree of asynchronicity, which is the largest for the iminium dienophile (NMe: Δr^TS_C⋯C = 0.14 Å, S_y = 0.93; NMe₂⁺: Δr^TS_C⋯C = 0.86 Å, and S_y = 0.77, where Δr^TS_C⋯C is the difference in newly forming C⋯C bond lengths in the TS and S_y stands for the computed synchronicity¹⁶). The higher degree of asynchronicity of NMe₂⁺ leads to a lower degree of deformation of the reactants since the C_β⋯C_CP bond forms before the C_α⋯C_CP bond. Note that, in the product, the strain energies of both NMe and NMe₂⁺ are identical because both new C⋯C bonds are now completely formed and the reactants, therefore, are deformed to the same degree (see Fig. S10† for the complete reaction profiles). To understand why NMe₂⁺ goes with a more stabilizing interaction energy compared to NMe, we applied the energy decomposition analysis (EDA) (Fig. 3b). In contrast to the commonly accepted view that iminium catalysts enhance the orbital interactions of the Diels–Alder reactions,^8,10 we find that the difference in ΔE_Pauli curves exclusively determines the more stabilizing ΔE_int for NMe₂⁺ and, thus, contributes to the lowering of the reaction barrier. In contrast, the ΔV_elstat and ΔE_oi terms, on the other hand, are, in the transition state region, more stabilizing for the uncatalyzed Diels–Alder reaction with NMe, even though the NMe₂⁺ system benefits from a much more favorable HOMO_CP–LUMO_dienophile energy gap (see Table 1).

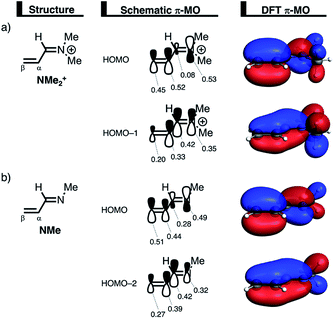
The less destabilizing Pauli repulsion for the reaction involving NMe₂⁺ originates from a reduced occupied–occupied orbital overlap with incoming CP. The most important occupied π-MO of the dienophile participating in the two-center four-electron interaction are the HOMO−2 and HOMO−1 of NMe and NMe₂⁺, respectively, where all 2p_π AOs are in-phase. Furthermore, the contributing occupied orbital of CP is HOMO−1, where all 2p_π AOs located on both reacting C=C double bonds are in-phase. The HOMO–HOMO overlap lowers from 0.10 for NMe to 0.07 for NMe₂⁺, which is in line with the trend in Pauli repulsion (Fig. 4a). The difference in the orbital overlap between NMe and NMe₂⁺ is a direct consequence of their difference in asynchronicity. For a more asynchronous reaction (NMe₂⁺), the reactants have almost exclusively orbital overlap on the β-carbon side of the dienophile, and, therefore, less destabilizing Pauli repulsion and a lower reaction barrier. Besides being more asynchronous, the HOMO−2 of NMe₂⁺ has lower orbital amplitude on the β-carbon compared to NMe, which, in turn, also leads to the computed lower occupied–occupied orbital overlap (Fig. 4b).

Fig. 4 Molecular orbital diagrams of the key orbital interactions of the Diels–Alder reactions between CP and NMe and NMe₂⁺: (a) most significant occupied orbital overlaps and (b) 3D plots of the involved occupied orbitals (isovalue = 0.03 au^−3/2). All data were computed at consistent geometries with a C_CP⋯C_β bond length between CP and the dienophile of 2.125 Å at ZORA-M06-2X/TZ2P//M06-2X/def2-TZVP.

As described above, asynchronicity is a key factor in these reactions. Indeed, a very good linear relationship (correlation coefficient R² of 0.96) was found when plotting the computed activation barriers versus the corresponding difference in newly forming C⋯C bond lengths in the TS, Δr^TS_C⋯C (see Fig. S11 in the ESI†). The origin of the asynchronicity of the Diels–Alder reactions that significantly contributes to the intrinsic catalytic effect of iminium catalysis (by allowing for less reactant deformation and strain; vide supra), deserves further analysis. To this end, we compared the actual concerted asynchronous Diels–Alder reaction to the analogous process which is artificially constrained to be concerted synchronous. In Fig. 5, we solely focus on the activation strain diagrams (ASDs) of the asynchronous and synchronous NMe₂⁺ DA reaction for which the effects are the largest. The ASDs of NMe and the more realistic iminium N(C₄H₈O)⁺ possess the same, albeit with less pronounced features (see Fig. S12 and S13†). The synchronous DA reaction proceeds with a higher barrier compared to its asynchronous counterpart (ΔΔE^‡ = 5.7 kcal mol⁻¹), even though the synchronous DA reaction has surprisingly more stabilizing interaction energy. The strain energy is initially the largest for the synchronous DA reaction because both newly forming C⋯C bonds between CP and NMe₂⁺ are formed simultaneously, causing all involved carbon atoms to pyrimidalize at the same time (i.e., more deformation and thus more strain). However, on the product side (right side of ASD), the strain energies of both the asynchronous and synchronous DA reactions are identical, because, in both cases, the reactants end up in identical products and are, thus, deformed to the same extent.

Fig. 5 (a) Activation strain analyses and (b) energy decomposition analyses of the asynchronous (black) and constrained synchronous (red) Diels–Alder reactions between CP and NMe₂⁺ going from the reactants to the product, where the transition states are indicated with a dot and the energy values are projected onto the shorter newly forming C_CP⋯C_β bond between CP and NMe₂⁺, computed at ZORA-M06-2X/TZ2P//M06-2X/def2-TZVP for NMe₂⁺_asynch and ZORA-M06-2X/TZ2P for NMe₂⁺_synch.

Next, we turn to the EDA to get a more detailed insight into the counterintuitive finding that the interaction energy is more stabilizing for the synchronous DA reaction. In contrast with the current view that the asynchronicity originates from enhanced orbital interactions,²¹ we found that the significantly larger Pauli repulsion for the synchronous DA reaction compared to the asynchronous DA reaction constitutes the actual driving force behind the asynchronous reaction mode. In order to relieve the highly destabilizing Pauli repulsion originating from a larger occupied–occupied orbital overlap (see Fig. S14†) of the synchronous DA reaction, the reaction mode becomes asynchronous despite this resulting in a loss of the stabilizing orbital and electrostatic interactions. The delicate interplay between this reduction of unfavorable Pauli repulsion and loss of favorable orbital and electrostatic interactions determines the degree of asynchronicity. Thus, Diels–Alder reactions only become asynchronous when the gain in stability, as a response to the reduced Pauli repulsion, is large enough to compensate for the significant loss of stabilizing interactions, that is, when the catalyst induces sufficient asymmetry in the occupied π-MOs of the dienophile. We do, as previously reported in the literature,²⁰ find a larger 2p_z-coefficient on the β-carbon of the NMe₂⁺ LUMO than on the α-carbon (Fig. S15†). But, this does not lead to more stabilizing orbital interactions for the asynchronous DA reaction, because the orbital overlap of both the normal electron demand, 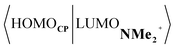, and inverse electron demand, 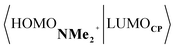, is, along the entire reaction coordinate, larger for, and therefore also favorable for, the synchronous compared to the asynchronous reaction mode (see Fig. S16†).

We can trace the larger orbital overlap and, consequently, stronger Pauli repulsion for the synchronous DA reaction back to the orbital amplitude of the key occupied orbitals, HOMO and HOMO−1, of NMe₂⁺ on the α- and β-carbon atoms (Fig. 6a). The larger MO-coefficient of the 2p_z atomic orbital on the α-carbon of the dienophile leads to a larger orbital overlap and, therefore, more Pauli repulsion with the filled orbitals of CP than the β-carbon, which has a smaller MO-coefficient and, as a consequence, less orbital overlap and Pauli repulsion with CP. To reduce the larger Pauli repulsion originating from the α-carbon of NMe₂⁺ and CP, the newly forming C_α⋯C_CP bond must be elongated to a larger extent than the analogous bond formed between C_β⋯C_CP, making the DA reaction asynchronous.

Fig. 6 Key occupied π-MOs (isovalue = 0.03 au^−3/2) computed at the equilibrium structures of (a) NMe₂⁺ and (b) NMe, where the MO-coefficients of the carbon and nitrogen 2p_z atomic orbitals, contributing to the occupied orbitals, are shown in the schematic π-MOs.

In addition, we want to understand why the DA reaction involving NMe₂⁺ is significantly more asynchronous than NMe (NMe₂⁺: Δr^TS_C⋯C = 0.86 Å; NMe: Δr^TS_C⋯C = 0.14 Å). In order to understand this difference, we need to compare the MO-coefficients on the α- and β-carbon of the key HOMOs of NMe₂⁺ and NMe, Fig. 6a and b, respectively. As priorly discussed, both key occupied orbitals of NMe₂⁺ have a larger MO-coefficient on the α-than on the β-carbon and, thus, both work in favor of an asynchronous reaction mode. The MO-coefficients of the key HOMOs of NMe, on the other hand, do not both point towards the observed asynchronous reaction. As expected, the MO-coefficient of the α-carbon of HOMO−2 is larger than that of the β-carbon, driving the reaction to the observed asynchronous reaction mode. This effect, however, gets partly, but not completely, countered by the MO-coefficients of the HOMO of NMe, which has a larger orbital amplitude on the β-carbon than on the α-carbon, resulting in a DA reaction which has a smaller degree of asynchronicity than NMe₂⁺.

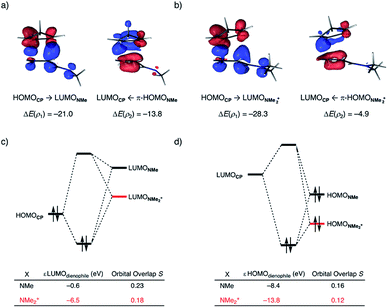
At last, we address why the current rationale behind iminium-catalyzed Diels–Alder reactions is misleading, and thus, why the orbital interactions for NMe₂⁺ are less stabilizing than for NMe even though the former system exhibits a smaller HOMO_CP–LUMO_dienophile energy gap by applying the natural orbitals for chemical valence (NOCV) extension of the EDA.²² This method confirms that although the normal electron demand (NED) interaction, between HOMO_CP–LUMO_dienophile, is enhanced in the NMe₂⁺ reaction (ΔΔE(ρ₁) = −7.3 kcal mol⁻¹), the inverse electron demand (IED) interaction, between the LUMO_CP and HOMO_dienophile, is significantly weakened in the NMe₂⁺ system (ΔΔE(ρ₂) = 8.9 kcal mol⁻¹). As a result, the total orbital interactions are less stabilizing in the catalyzed reaction (Fig. 7a and b). The mechanism behind these EDA-NOCV results is found in the following. In line with the original rationale behind iminium-catalyzed DA reactions,^8,10 the iminium catalyst stabilizes the LUMO_dienophile from −0.6 eV for NMe to −6.4 eV for NMe₂⁺, leading to a smaller 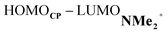energy gap compared to that of the NMe analog (Fig. 7c). This effect surpasses the unfavorable reduction of orbital overlap, which finds its origin in the priorly discussed increased asynchronicity, and, therefore, enhances the NED interaction. The iminium catalyst, however, stabilizes all NMe₂⁺ orbitals, thus also the HOMO_dienophile from −8.4 eV for NMe to −13.8 eV NMe₂⁺, which, in turn, results in a larger 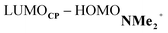gap and, together with a less favorable orbital overlap, weakens the IED interaction (Fig. 7d). The weakening of the IED interaction effectively overrules the more stabilizing NED interaction and, for this reason, the total orbital interactions of NMe₂⁺ are less stabilizing than for NMe.

Fig. 7 NOCV deformation densities Δρ (isovalue = 0.0015 au) and associated energies ΔE(ρ) (in kcal mol⁻¹) for the normal electron demand (NED), HOMO_CP–LUMO_dienophile, and inverse electron demand (IED), LUMO_dienophile–HOMO_CP, where the color flow is red → blue, for (a) NMe, (b) NMe₂⁺; the Kohn–Sham molecular orbital analysis for (c) NED, and (d) IED. All data were computed at consistent geometries with a C_CP⋯C_β bond length between CP and the dienophile of 2.125 Å at ZORA-M06-2X/TZ2P//M06-2X/def2-TZVP.

3. Conclusions

Our computational study, based on the activation strain model and canonical energy decomposition analysis, reveals that iminium groups (NMe₂⁺) efficiently catalyze the Diels–Alder reaction between cyclopentadiene (CP) and α,β-unsaturated dienophiles by accelerating the reaction by up to 15 orders of magnitude compared to the uncatalyzed reactions. Furthermore, we found that the uncatalyzed reactions involving α,β-unsaturated aldehyde dienophiles (O) proceed with a consistently lower reaction barrier than the imine (NMe) analogs.

Strikingly, the enhanced reactivity of the iminium-catalyzed Diels–Alder reactions is exclusively caused by a markedly diminished two-center four-electron steric (Pauli) repulsion between the π-systems of CP and NMe₂⁺ and not from enhanced orbital interactions as a response to the lowering of the LUMO_dienophile. In fact, the net orbital interactions in the iminium reaction are even less stabilizing because of a weakening of the IED HOMO_dienophile–LUMO_diene interaction. This finding contradicts the widely accepted LUMO-lowering catalysis as the actual electronic mechanism behind this mode of catalysis.

Most importantly, the present study establishes for the first time and in a quantitative manner the causal relationship between, on the one hand, synchronicity and reactivity in Diels–Alder cycloaddition reactions and, on the other hand, the Pauli repulsive occupied–occupied orbital overlap between the reactants and the way it depends on the shape of the occupied π-MO of the dienophile.

The reason for the Pauli repulsion lowering-catalysis is that the occupied π-orbitals of the dienophile have a larger orbital amplitude on the α-compared to the β-carbon, resulting in less occupied–occupied orbital overlap between CP and the β-carbon than the α-carbon of the dienophile. This asymmetry introduces a bias towards forming the C_CP⋯C_β bond ahead of the C_CP⋯C_α bond and results in a highly asynchronous reaction. This circumstance has two stabilizing and thus barrier-lowering consequences: (i) reduced Pauli repulsive occupied–occupied overlap and thus a more stabilizing interaction between reactants in the TS at the expense of a less significant loss in bonding HOMO–LUMO overlap and thus stabilizing orbital interaction; and (ii) less pressure on the reactants to deform and thus a less destabilizing activation strain in the TS.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the Netherlands Organization for Scientific Research (NWO), Dutch Astrochemistry Network (DAN), and the Spanish MINECO (CTQ2016-78205-P, CTQ2016-81797-REDC and PID2019-106184GB-I00).

Notes and references

1. (a) D. W. C. MacMillan and A. J. B. Watson, in Science of Synthesis, ed. B. List, Thieme, Stuttgart, Germany, 2012; (b) A. Erkkilä, I. Majander and P. M. Pihko, Chem. Rev., 2007, 107, 5416.
2. This species has been isolated and fully characterized in different reactions using amine salt catalysts or under acid-free conditions. See, for example: (a) C. Sparr, W. B. Schweizer, H. M. Senn and R. Gilmour, Angew. Chem., Int. Ed., 2009, 48, 3065; (b) C. Sparr and R. Gilmour, Angew. Chem., Int. Ed., 2011, 50, 8391; (c) M. C. Holland, J. B. Metternich, C. Daniliuc, W. B. Schweizer and R. Gilmour, Chem.–Eur. J., 2015, 21, 10031; (d) N. Lokesh, A. Seegerer, J. Hioe and R. M. Gschwind, J. Am. Chem. Soc., 2018, 140, 1855.
3. (a) E. Knoevenagel, Chem. Ber., 1894, 27, 2345; (b) E. Knoevenagel, Chem. Ber., 1898, 31, 2596.
4. For a review on the Knoevenagel reaction, see: L. F. Tietze and U. Beifuss, in Comprehensive Organic Synthesis, ed. B. M. Trost and I. Fleming, Pergamon, Oxford, UK, 1991, vol. 2, p. 341.
5. For leading reviews: (a) G. Lelais and D. W. MacMillan, Aldrichimica Acta, 2006, 39, 79; (b) S. Bertelsen and K. A. Jørgensen, Chem. Soc. Rev., 2009, 38, 2178; (c) L. Klier, F. Tur, P. H. Pouldsen and K. A. Jørgensen, Chem. Soc. Rev., 2017, 46, 1080.
6. See, for instance: (a) N. J. Green, A. L. Lawrence, G. Bojase, A. C. Willis, M. N. Paddon-Row and M. S. Sherburn, Angew. Chem., Int. Ed., 2013, 52, 8333; (b) N. J. Green, C. A. Connolly, K. P. W. Rietdijk, G. S. Nichol, F. Duarte and A. L. Lawrence, Angew. Chem., Int. Ed., 2018, 57, 6198.
7. For a recent review, see: Z. Wang, Molecules, 2019, 24, 3412 , and references therein.
8. K. A. Ahrendt, C. J. Borths and D. W. C. MacMillan, J. Am. Chem. Soc., 2000, 122, 4243.
9. P. Vermeeren, T. A. Hamlin, I. Fernández and F. M. Bickelhaupt, Angew. Chem., Int. Ed., 2020, 59, 6201.
10. (a) I. Fleming, Frontier Orbitals and Organic Chemical Reactions, Wiley, New York, 197, New edition: I. Fleming, Molecular Orbitals and Organic Chemical Reactions, Wiley, New Jersey, 2009; (b) K. N. Houk, Acc. Chem. Res., 1975, 8, 361; (c) M. J. R. Dewar, Molecular Orbital Theory for Organic Chemists, Prentice-Hall, Englewood Cliffs, New Jersey, 1975; (d) W. T. Borden, Modern Molecular Orbital Theory for Organic Chemists, Prentice-Hall, Englewood Cliffs, New Jersey, 1975.
11. (a) T. A. Hamlin, I. Fernández and F. M. Bickelhaupt, Angew. Chem., Int. Ed., 2019, 58, 8922; (b) P. Vermeeren, F. Brinkhuis, T. A. Hamlin and F. M. Bickelhaupt, Chem.–Asian J., 2020, 15, 1167; (c) K. Sakata and H. Fujimoto, J. Org. Chem., 2013, 78, 3095; (d) K. Sakata and H. Fujimoto, ChemistryOpen, 2020, 9, 662.
12. A. B. Northup and D. W. C. MacMillan, J. Am. Chem. Soc., 2002, 124, 2458.
13. I. Fernández and F. M. Bickelhaupt, J. Comput. Chem., 2014, 35, 371.
14. (a) W.-J. van Zeist and F. M. Bickelhaupt, Org. Biomol. Chem., 2010, 8, 3118; (b) I. Fernández and F. M. Bickelhaupt, Chem. Soc. Rev., 2014, 43, 4953; (c) L. P. Wolters and F. M. Bickelhaupt, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2015, 5, 324; (d) F. M. Bickelhaupt and K. N. Houk, Angew. Chem., Int. Ed., 2017, 56, 10070 . For a step-by-step protocol, see also: ; (e) P. Vermeeren, S. C. C. van der Lubbe, C. Fonseca Guerra, F. M. Bickelhaupt and T. A. Hamlin, Nat. Protoc., 2020, 15, 649.
15. See, for instance: (a) Y. García-Rodeja and I. Fernández, Chem.–Eur. J., 2017, 23, 6634; (b) Y. García-Rodeja and I. Fernández, Chem.–Eur. J., 2019, 25, 9771; (c) I. Fernández, Chem. Sci., 2020, 11, 3769 and references therein.
16. Similar ASM-EDA plots are obtained when projecting the IRC onto the C_α⋯C_β stretch of the dienophile. See Fig. S3 and S4 in the ESI.†.
17. The computed synchronicity, S_y, is consistent with this finding (S_y = 0.91 and 0.93 for O and NMe reactions, respectively). For a definition of S_y, see: (a) B. Lecea, A. Arrieta, G. Roa, J. M. Ugalde and F. P. Cossío, J. Am. Chem. Soc., 1994, 116, 12314; (b) I. Fernández, M. A. Sierra and F. P. Cossío, J. Org. Chem., 2008, 73, 2083 , and references therein.
18. (a) F. M. Bickelhaupt and E. J. Baerends, in Reviews in Computational Chemistry, ed. K. B. Lipkowitz and D. B. Boyd, Wiley, Hoboken, 2000, pp. 1–86; (b) R. van Meer, O. V. Gritsenko and E. J. Baerends, J. Chem. Theory Comput., 2014, 10, 4432; (c) L. Zhao, M. von Hopffgarten, D. M. Andrada and G. Frenking, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1345.
19. T. A. Albright, J. K. Burdett and W. H. Wangbo, Orbital Interactions in Chemistry, Wiley, New York, 2013.
20. T. A. Hamlin, D. Svatunek, S. Yu, L. Ridder, I. Infante, L. Visscher and F. M. Bickelhaupt, Eur. J. Org. Chem., 2019, 378.
21. (a) R. J. Loncharich, F. K. Brown and K. N. Houk, J. Org. Chem., 1989, 54, 1129; (b) D. M. Birney and K. N. Houk, J. Am. Chem. Soc., 1990, 112, 4127; (c) B. R. Beno, K. N. Houk and D. A. Singleton, J. Am. Chem. Soc., 1996, 118, 9984; (d) A. M. Sarotti, Org. Biomol. Chem., 2014, 12, 187.
22. M. P. Mitoraj, A. Michalak and T. A. Ziegler, J. Chem. Theory Comput., 2009, 5, 962.

---

Footnote

† Electronic supplementary information (ESI) available: Fig. S1–S16, Tables S1 and S2, computational details and Cartesian coordinates. See DOI: 10.1039/d0sc02901g

---