DOI:
10.1039/D0RA08316J
(Paper)
RSC Adv., 2020,
10, 44824-44833
Alkaline all iron redox flow battery with a polyethylene/poly(styrene-co-divinylbenzene) interpolymer cation-exchange membrane†
Received
29th September 2020
, Accepted 13th November 2020
First published on 18th December 2020
Abstract
This work describes the suitability of a polyethylene styrene–DVB based interpolymer cation exchange membrane for use in a highly alkaline redox flow battery (RFB) with a [Fe(TEA)OH]2−/[Fe(TEA)OH]− and Fe(CN)63−/Fe(CN)64− redox couple. The alkaline stability of the membrane for 1440 h was evaluated in 5 N NaOH containing a 200 mM Fe(CN)63−/Fe(CN)64− redox couple. It was assessed according to the changes in the electrochemical and physicochemical properties. The performance of the membrane was evaluated over 40 charge–discharge cycles at a current density of 5 mA cm−2 current in a designed RFB cell. The obtained average coulombic efficiency (CE) was 92%, energy efficiency (EE) was 75%, voltage efficiency (VE) was 82% and volumetric efficiency was 34%. Under identical experimental conditions, the values of CE, EE, and VE for Nafion®-112 were 99%, 75%, and 76%, respectively. These results indicate the suitability of the polyethylene styrene–DVB based interpolymer cation exchange membrane for use in an alkaline RFB.
Introduction
Ion-exchange membranes are an integral part of many electrochemical processes and devices such as diffusion dialysis, electrodialysis, bipolar membrane electrodialysis, reverse electrodialysis, fuel cells and redox flow batteries (RFBs),1 where performance primarily depends on the electrochemical and physicochemical properties of the ion exchange membrane.2 However, the basic polymer backbone and nature of the functional groups define the electrochemical and physicochemical properties. Often cation-exchange membranes are prone to the hydrolytic degradation of sulfonic acid. In contrast, anion exchange membranes are prone to functional group degradation by β-hydrogen Hofmann eliminations and/or direct nucleophilic substitution at α-carbons.3–6 A number of attempts have made over the last decade to explore different synthetic pathways to develop chemically, thermally and mechanically stable new polymer systems to be used in different electrochemical energy storage and conversion devices.7–9 The most widely evaluated systems are thermoplastic engineering materials such as polyether sulfone,10 polyphenylene oxide,11 polyether ether ketones,12 and polybenzimidazole.13 Except for polybenzimidazole, most thermoplastic engineering materials have an arylene ether bond, which is not chemically stable under alkaline conditions at elevated temperature due to attack from strongly nucleophilic hydroxide ions/radicals.14–17 Hence long-term alkaline stability of a membrane is always a concern in device applications such as an alkaline RFB or fuel cell. Although there are reports on the enhancement of the alkaline stability of membranes without ether linkages like polyphenylene and poly(arylene piperidinium),3,18,19 their synthesis procedure and use of highly corrosive acids such as triflic acid hinder further development.
Polyethylene, a commodity polymer, has excellent chemical and mechanical stability.20 Its functionalization has been neatly explained in the literature.21 The first report by de Korosy and Shorr in a patent application22 described the modification of polyethylene with a gaseous mixture of chlorine and sulfur dioxide for sulfonic acid functionalization. Later, its suitability in a methanol fuel cell was evaluated by measuring the ionic conductivity and methanol permeability.23 Ion exchange membranes produced via the copolymerization of polyethylene with styrene-divinyl benzene followed by sulfonation and amination is an exciting approach demonstrated for the first time by the group of Trochimczuk.24,25 Their applications in electrodialytic separation and purification technologies have been demonstrated.2,26,27 A polyethylene-based alkali-stable ion exchange membrane with phosphonium and metallocene functionality and solvent processable ion-exchange membrane made using a second generation Grubbs catalyst have been reported.28–30 A membrane based on an analogue of polyethylene has also been reported with the ring-opening metathesis polymerization of a functional cyclooctene31 as well as a Ziegler–Natta type catalyst.16 However, these approaches have a monotonic synthetic approach. Herein, we demonstrate a robust method of preparing a cation exchange membrane via the copolymerization of styrene–DVB in the presence of polyethylene followed by sulfonation with chlorosulfonic acid and its alkaline stability along with its RFB application by assessing in detail the electrochemical and physicochemical properties.
RFBs have evolved as a suitable option for small- to large-scale energy storage. Redox active species, electrodes and an ion exchange membrane are critical units of a RFB. Halogens, inorganic active materials with a metal of interest such as vanadium, iron, nickel, chromium, cerium, and32,33 zinc, and organic redox species based on quinones, viologen, phenazine, tempo and metallocenes34 have been employed as redox active species in flow battery systems. Carbon-based materials such as carbon felt/paper/cloth or carbon fibres35 and graphite felt or modified graphite felt36 with a high surface area are used as electrode materials. Ion exchange membranes are a crucial part of any RFB,37 in which they act as a separator between the electrolytes and maintain the charge neutrality in the system via the transport of specific ions, i.e. either cations or anions, through it. High ion conductivity and good physiochemical stability in a rigorous chemical environment are the basic requirements for an ion exchange membrane. The excellent chemical stability of the synthesized interpolymer cation exchange membrane in a highly corrosive and oxidative environment encouraged us to use it as a separator in an alkaline all iron RFB.
Experimental section
Materials
Polyethylene (HDPE and LLDPE) granules were procured from Reliance Industries Pvt. Ltd India. Styrene, divinylbenzene (DVB), and benzoyl peroxide were obtained from Tokyo Chemical Industry (India) Pvt. Ltd. Chlorosulfonic acid, toluene, xylene, and 1,2-dichloroethane were supplied by Finar Limited. Potassium ferrocyanide extrapure AR, 99%, and ferrous sulphate heptahydrate extrapure AR, 99.5%, were purchased from Sisco Research Laboratories Pvt. Ltd. Potassium ferricyanide and triethanolamine were obtained from SD Fine Chem Limited. Iron(III) chloride reagent grade, 97%, was acquired from Sigma-Aldrich. Sodium hydroxide flakes were purchased from Qualikems Fine Chem Pvt. Ltd. Nafion®-112 perfluorinated membrane was purchased from Sigma Aldrich.
Synthesis of interpolymer cation exchange membrane (ICEM)
The synthesis of the cation exchange membrane was carried out by dissolving polyethylene (HDPE and LLDPE) granules in xylene followed by the addition of styrene–DVB and polymerization using benzoyl peroxide as a radical initiator. In brief, 3.12 kg of HDPE and 0.78 kg of LLDPE were dissolved in 1.25 L of xylene at 150 °C. After obtaining a homogeneous solution, 2.5 L of toluene was added while maintaining the temperature. This was followed by the slow addition of a mixture of styrene (2.0 L), DVB (1.5 mL) and benzoyl peroxide (20 g) in 500 mL of toluene. The addition was completed in 2 h. The mixture was stirred for a further 2 h by maintaining the temperature and was then cooled to afford the polymer. After thorough washing, an 85% yield of the polymer was obtained. The film was made via blow film extrusion and sulfonated in 10% chlorosulfonic acid in dichloroethane for 4 h. After washing with water the film was stored in saline for further characterization.
Preparation of electrolyte solutions
The anolyte and catholyte solutions were prepared by dissolving known amounts of K3[Fe(CN)6]/K4[Fe(CN)6] and a triethanolamine complex of iron in a 5 M NaOH solution. Specifically, the anolyte solution was a mixture of 200 mM K3[Fe(CN)6]/K4[Fe(CN)6] in 5 M NaOH solution. The mole ratio of ferricyanide and ferrocyanide was kept equal. The catholyte solution was an iron-triethanolamine redox pair (i.e., [Fe(TEA)OH]−/[Fe(TEA)(OH)]2−). It was prepared by dissolving 2.60 g of anhydrous ferric chloride and 4.44 g of ferrous sulfate in 20 mL of degassed distilled water in a round-bottom flask. To this solution, 20 mL of triethanolamine was added dropwise. 20 mL of 20 M NaOH was prepared separately in a beaker and was cooled to room temperature. This NaOH solution was added slowly to ferric chloride and a triethanolamine solution mixture with constant stirring to obtain a clear solution with no suspended solid particles. The concentration of NaOH in solution was adjusted to 5 M by diluting the resulting solution with (20 mL) deionized water.
Characterization
The attenuated total reflectance Fourier-transform infrared (ATR-FTIR) spectra of the membranes were recorded with an Agilent Technologies Cary 600 series spectrometer. The spectra were recorded in the range of 4000–400 cm−1. The water content in terms of water concentration in the membrane phase was calculated using the following equation:2| | |
Cm = (Wwet − Wdry)/ρm/Wwetρw
| (1) |
where ρm is the density of the wet membrane, ρw is the density of water, Wwet is the wet weight and Wdry is the dry weight of the membrane.
Ion exchange capacity
The ion exchange capacity of the membrane was measured by titrimetric analysis (acid–base titration). A membrane sample (2 cm × 2 cm) was immersed in 1 M HCl for 12 h at room temperature to protonate the membrane. Then, the membrane was washed with deionized water and dipped in a 1 M NaCl solution for 12 h and titrated against 0.01 M NaOH (standardized using oxalic acid) using phenolphthalein indicator. The dry weight of the membrane was recorded after it was placed in oven at 80 °C for 4 h. The ion exchange capacity (IEC) was determined according to the following equation:| |
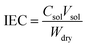 | (2) |
where Csol is the concentration of the NaOH consumed, Vsol is the volume of NaOH consumed and Wdry is the weight of the membrane in the dry state. From the IEC, fixed-ion concentration (Xm) in units of (moles of sites)/(unit volume of wet membrane) was measured using eqn (3) (ref. 2) and number of water molecules (λ) per counter ions using eqn (4):38| |
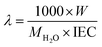 | (4) |
where W is the water content measured gravimetrically by measuring the wet and dry weights of the membrane using the relationship W = Wwet − Wdry/Wdry; where MH2O is the molecular mass of the water (18.015 g mol−1); τ is the membrane void porosity (volume of free water within the membrane per unit volume of wet membrane) obtained using the relationship τ = ΔV/1 + ΔV; where ΔV is the change in the volume of the membrane upon the absorption of water (ΔV) obtained from the relationship ΔV = (Wwet − Wdry)ρd/ρwWdry, where ρd is the density of the dry membrane.
Chemical stability of the membrane was evaluated by means of the change in weight after its immersion in alkaline solution. A membrane sample of known weight was immersed in a 5 M NaOH solution containing the 200 mM K3[Fe(CN)6]/K4[Fe(CN)6] complex. The weight of the membrane was recorded every 24 h after gently wiping off the surface solution. The procedure was continued for 1440 h. The stability of the membrane was determined according to the change in the weight of the membrane with respect to time.
Membrane conductivity
The membrane conductivity was calculated by measuring the impedance. A BT-112 conductivity cell (Scribner Associates, Inc.) and CHI 700E potentiostat/galvanostat were used to measure the impedance. The impedance was recorded in potentiostat mode with an amplitude of 5 mV over a frequency range of 1 Hz to 0.1 MHz. From the impedance, the conductivity (σ) was calculated using the following equation:| |
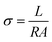 | (5) |
where σ is conductivity (S cm−1), L is the distance between the electrodes used to measure the potential (cm), R (Ω) is the measured impedance of the membrane, and A is the surface area of the membrane. The thickness of the membrane was measured using a screw gauge.
Transport number
The transport number was determined using membrane potential method. In a two-compartment cell, the compartments were separated by a circular membrane sample with an effective area of 8.54 cm2. One compartment was filled with 0.1 M NaCl and the other with 0.01 M NaCl. The solutions in both compartments were continuously circulated using a peristaltic pump. The membrane potential developed across the membrane was measured with the help of a digital voltammeter using saturated calomel electrodes. The solutions were repeatedly renewed until reproducible values were obtained. The transport number was estimated using eqn (6):| |
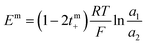 | (6) |
where a1 and a2 are the activities of electrolyte solutions contacting through the membrane and Em is the potential difference between the two solutions of NaCl. The permselectivity of the membrane (Ps) was estimated using the following equation:where the tmi is the counter-ion transport number through the membrane and ti is the counter-ion transport number in the solution phase.
Cell construction and charging–discharging analysis
The all iron RFB was constructed by sandwiching a membrane (thickness 200 μm, area 8 cm × 8 cm) between two pyrolytic graphite electrodes having serpentine flow channels. To make the ‘zero gap’ cell assembly, a carbon paper of thickness 0.1 mm was placed between the membrane and graphite electrode. Connection to the graphite plates was made with a brass plate current collector. In order to avoid the electrolyte contacting the brass plates, inlet and outlets were provided from the graphite plates. They were assembled between two PVC plates. The assembled cell was checked for electrolyte leakage before performing the experiments. The active area of the membrane was 16 cm2. The charge–discharge cycles were recorded chronopotentiometrically using a CHI 700E potentiostat/galvanostat. The volume of the anolyte and catholyte compartment was 14 mL each. A Phenovo DC 12 V peristaltic miniature dosing metering pump was used to maintain an electrolyte flow rate of 10 mL min−1. Furthermore, all experiments were carried out at room temperature with no active temperature control. The coulombic, energy and voltage efficiencies were calculated as reported previously.39
Results and discussion
ICEM was prepared via the copolymerization of styrene–DVB in the presence of polyethylene using benzoyl peroxide initiator and characterized to evaluate its utility in a highly alkaline RFB. A schematic of the preparation is shown in Fig. 1. Because of the polyethylene matrix, the membrane had excellent chemical stability. It was evaluated by immersing the membrane in a highly alkaline and oxidative environment. That is, we kept the membrane (ICEM-A) for 1440 h in 5 M NaOH containing 200 mM K3[Fe(CN)6]/K4[Fe(CN)6] redox couple and recorded changes in its physico- and electrochemical properties. Fig. 2a shows the ATR-FTIR spectra of the membrane before and after chemical stability evaluation in NaOH solution. The presence of strong vibration bands at 1030 and 1096 cm−1 are related to sulfonic acid and were assigned to O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S
S![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching. The C–H aliphatic and aromatic vibration bands were observed at 2800–2900 cm−1 and 3000–3100 cm−1, respectively, for polyethylene and the benzene ring. After 1440 h of 5 M NaOH treatment, there was no change in the peaks or the presence of additional peaks due to the alkaline and oxidative degradation of the polymer backbone, indicating the excellent stability of the membrane. This was supported by gravimetrically recording the change in weight of the membrane (Fig. 2b). The change in weight was measured every day and plotted as the percentage weight loss vs. time. From the figure it is clear that up to 400 h there is no weight loss. After 400 h and up to 1440 h, ∼3% weight loss was observed. This may be due to partial functional group degradation or leaching of low molecular weight physically entangled sulfonated polymer matrix. This functionality degradation results in a change in the physiochemical and electrical properties of the membrane. Fig. 2c shows the change in the measured IEC and water content of the membrane before and after chemical treatment. This was insignificant, suggesting its excellent alkaline stability. Before chemical treatment, the membrane had 2.14 meq g−1 IEC and 26.6% water content, while after treatment it had 1.96 meq g−1 IEC and 17.88% water content, i.e. ∼0.2 meq g−1 change in the IEC and ∼8.72% change in the water content. The water content in terms of water concentration in the membrane, Cm, was found to be 0.38 mol dm−3 before chemical treatment, and after chemical treatment it was 0.25 mol dm−3. The membrane porosity (τ), i.e. volume of free water within the membrane per unit volume of wet membrane, was calculated and found be 0.15 units for ICEM, which is 0.05 units more than ICEM-A. The fixed ion concentration is the measure of (moles of sites)/(unit volume of wet membrane) that gives a clear understanding of the deterioration of a membrane's physicochemical and electrochemical properties. The calculated fixed ion concentration for ICEM and ICEM-A was 0.89 and 0.80 mol dm−3 respectively, suggesting slow deterioration of the membrane properties after 1440 h in the highly alkaline oxidative environment. The ionic conductivity of the membranes was calculated by impedance measurements and is presented in Fig. 2c. The corresponding impedance spectra and simulated circuit diagram are presented in Fig. 2d. The impedance is made up of solution resistance (Rs), membrane resistance (Rm) and capacitance (C) between the electrolyte and electrode surface. From the measured impedance, the calculated conductivity of the membrane was 7.26 mS cm−1. After 1440 h of alkali treatment, the value of conductivity was 4.77 mS cm−1.
O stretching. The C–H aliphatic and aromatic vibration bands were observed at 2800–2900 cm−1 and 3000–3100 cm−1, respectively, for polyethylene and the benzene ring. After 1440 h of 5 M NaOH treatment, there was no change in the peaks or the presence of additional peaks due to the alkaline and oxidative degradation of the polymer backbone, indicating the excellent stability of the membrane. This was supported by gravimetrically recording the change in weight of the membrane (Fig. 2b). The change in weight was measured every day and plotted as the percentage weight loss vs. time. From the figure it is clear that up to 400 h there is no weight loss. After 400 h and up to 1440 h, ∼3% weight loss was observed. This may be due to partial functional group degradation or leaching of low molecular weight physically entangled sulfonated polymer matrix. This functionality degradation results in a change in the physiochemical and electrical properties of the membrane. Fig. 2c shows the change in the measured IEC and water content of the membrane before and after chemical treatment. This was insignificant, suggesting its excellent alkaline stability. Before chemical treatment, the membrane had 2.14 meq g−1 IEC and 26.6% water content, while after treatment it had 1.96 meq g−1 IEC and 17.88% water content, i.e. ∼0.2 meq g−1 change in the IEC and ∼8.72% change in the water content. The water content in terms of water concentration in the membrane, Cm, was found to be 0.38 mol dm−3 before chemical treatment, and after chemical treatment it was 0.25 mol dm−3. The membrane porosity (τ), i.e. volume of free water within the membrane per unit volume of wet membrane, was calculated and found be 0.15 units for ICEM, which is 0.05 units more than ICEM-A. The fixed ion concentration is the measure of (moles of sites)/(unit volume of wet membrane) that gives a clear understanding of the deterioration of a membrane's physicochemical and electrochemical properties. The calculated fixed ion concentration for ICEM and ICEM-A was 0.89 and 0.80 mol dm−3 respectively, suggesting slow deterioration of the membrane properties after 1440 h in the highly alkaline oxidative environment. The ionic conductivity of the membranes was calculated by impedance measurements and is presented in Fig. 2c. The corresponding impedance spectra and simulated circuit diagram are presented in Fig. 2d. The impedance is made up of solution resistance (Rs), membrane resistance (Rm) and capacitance (C) between the electrolyte and electrode surface. From the measured impedance, the calculated conductivity of the membrane was 7.26 mS cm−1. After 1440 h of alkali treatment, the value of conductivity was 4.77 mS cm−1.
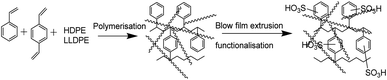 |
| | Fig. 1 Schematic of the preparation of the cation exchange membrane. | |
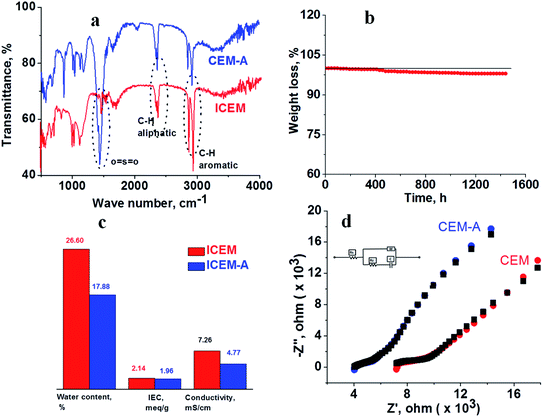 |
| | Fig. 2 Electrochemical and physicochemical characterization of the ICEM before and after 1440 h immersion in 5 M NaOH. (a) ATR spectra of the membranes. (b) Change in weight loss of the membrane recorded every day. (c) IEC, water content and conductivity of the membranes. (d) Impedance spectra along with simulation (black) and circuit diagram. | |
The transport number of the membrane is the fraction of the total current carried by counter ions in the membrane phase, which explains its selectivity and electrochemical performance. It was measured using eqn (6) and the results are presented in Table 1. The obtained values were 0.92 for ICEM and 0.90 for ICEM-A. From the transport number values, the permselectivity of the membrane was calculated using eqn (7) and the calculated permselectivity values were 0.80 and 0.75 for ICEM and ICEM-A, respectively. The transport number and permselectivity values of ICEM and ICEM-A showed no significant difference, suggesting good retention of electrochemical properties, even in a rigorous chemical environment. The number of water molecules absorbed by the membrane per counter ion is the hydration number (λ), calculated using eqn (4). The obtained values were 9.4 and 6.2 for ICEM and ICEM-A, respectively. The slightly lower value for ICEM-A was due to low water content and IEC. The diffusion coefficient of the sodium ion in ICEM and ICEM-A was calculated using the Nernst–Einstein equation:40
| |
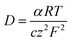 | (8) |
where
F is the Faraday constant,
z the ion charge,
T is the absolute temperature,
R is the gas constant,
α is the measured ion conductivity,
c is the concentration of sodium ions in the membrane and was calculated using the following equation:
c = (0.001 ×
ρdIEC)/(1 + 0.01
Wv).
Table 1 Electrochemical and physicochemical parameters of the interpolymer ion-exchange membrane before (ICEM) and after (ICEM-A) 1440 h in a highly alkaline oxidative environmenta
| |
Cm (mol dm−3) |
τ |
χm (mol dm−3) |
tm |
Pm |
λ |
D × 10−6 (cm2 s−1) |
D/D0 |
| Abbreviations: Cm is the water content in terms of water concentration in the membrane phase (mol dm−3), τ is the membrane porosity, χm is the fixed ion concentration (mol dm−3), Pm is the permselectivity of the membrane, λ is the hydration number, D is the diffusion coefficient of sodium ions in membrane phase (cm2 s−1), D/D0 is the normalized diffusion coefficient. |
| ICEM |
0.38 |
0.15 |
0.89 |
0.92 |
0.80 |
9.4 |
1.81 |
0.14 |
| ICEM-A |
0.25 |
0.10 |
0.80 |
0.90 |
0.75 |
6.2 |
1.29 |
0.10 |
Diffusion coefficient value of ICEM was 1.8 × 10−6 and that of ICEM-A was 1.29 × 10−6. The decrease in the diffusion coefficient of sodium in ICEM-A can be due to partial degradation of functional groups in the membrane in the highly alkaline and oxidative environment. The normalized diffusion coefficient (D/D0) is the ratio of diffusion coefficient of counter ion in the membrane (D) to diffusion coefficient of counter ion in dilute solution (D0). D0 was obtained using the following equation:
where
z is the ion charge,
T is the absolute temperature,
KB is the Boltzmann constant and
μ is the ion mobility in dilute solution. The dilute solution mobility of sodium ions is 50.1 × 10
−5 cm
2 V
−1 s
−1.
41
The normalized diffusion coefficient (D/D0) was used to compare the ionic conductivity of the membrane before and after chemical treatment. There was only a difference of 0.04 in the D/D0 ratio values for ICEM and ICEM-A, indicating similar ionic conductance of the membrane even after chemical treatment. D/D0 values were found to be directly proportional to the hydration number, as reported in the literature.40 ICEM with a hydration number of 9.4 exhibited a D/D0 ratio of 0.14 and ICEM-A with hydration number of 6.2 had D/D0 ratio of 0.10, indicating similar ionic conductance of the membrane even after chemical treatment and slight deterioration of functional groups (i.e. lower IEC and water content). All calculated electrochemical and physicochemical parameters are presented in Table 1.
Flow battery studies
The flow battery consisted of 200 mM [Fe(TEA)OH]2− in 2 M TEA and 5 M NaOH solution as catholyte and 200 mM Fe(CN)63−/Fe(CN)64− in 5 M NaOH solution as an anolyte. Cyclic voltammograms were recorded independently using GC as a working electrode, Pt wire as a counter electrode and Ag/AgCl as a reference electrode. Fig. 3a shows the recorded voltammogram at a scan rate of 50 mV with the corresponding redox reaction. The standard redox potential of [Fe(TEA)OH]2− is −0.86 V versus SHE while the standard redox potential of Fe(CN)63−/Fe(CN)64− is +0.36 V versus SHE. This corresponds to a 1.22 V formal potential difference between the two redox couples. However, in Fig. 3a, the voltammogram shows the formal redox potentials of [Fe(TEA)OH]2−/[Fe(TEA)OH]− and Fe(CN)63−/Fe(CN)64− redox couples are −0.98 V and +0.54 V, respectively. This corresponds to a 1.52 V potential difference between the two redox couples. It is higher than the standard redox potential reported versus SHE. The high potential difference is due to the high ionic strength of the solution. It is reported42 that for the Fe(CN)63−/Fe(CN)64− redox pair the standard redox potential of 0.36 V versus SHE can reach 0.44 V versus SHE in a 0.5 M salt solution.
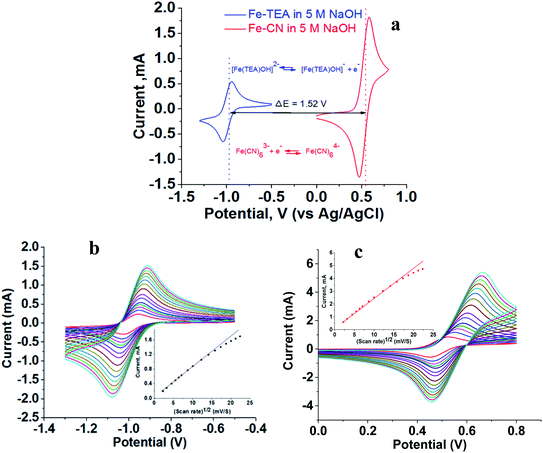 |
| | Fig. 3 Cyclic voltammograms recorded with 200 mM redox couple in 5 M NaOH electrolyte, glassy carbon as working electrode, Pt wire as counter electrode and Ag/AgCl as reference electrode. (a) Voltammogram showing half-cell potential and redox reaction; scan rate, 50 mV s−1. (b) Voltammogram at different scan rates for [Fe(TEA)OH]2−/[Fe(TEA)OH]− redox couple; scan rate, 50–500 mV. (c) Voltammogram at different scan rates for Fe(CN)63−/Fe(CN)64− redox couple; scan rate, 50–500 mV. Insets of (b) and (c) show peak current versus square root of scan rate. | |
Fig. 3b and c show the cyclic voltammograms of the [Fe(TEA)OH]2−/[Fe(TEA)OH]− and Fe(CN)63−/Fe(CN)64− redox couples at different scan rate. From the voltammograms, a single-electron redox behaviour is evident. At a low scan rate, the difference between the anodic and cathodic peak, i.e. (ΔEp), is ∼60 mV. This peak to peak potential difference increases with increase in scan rate due to the ohmic resistance. At a scan rate of 500 mV, the obtained peak to peak potential difference was ∼167 and ∼206 mV, respectively, for [Fe(TEA)OH]2−/[Fe(TEA)OH]− and Fe(CN)63−/Fe(CN)64− redox couple. It is a reversible system with semi-infinite diffusion mode predicted from the Randles–Sevcik model using eqn (10):43,44
| |
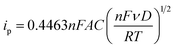 | (10) |
where
ip is the anodic peak current,
n is the number of electrons appearing in the half-reaction for the redox couple,
F is the Faraday constant (96
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
485 C mol
−1),
A is the electrode area (cm
2),
ν is the scan rate at which the potential is swept (V s
−1),
D is the analyte's diffusion coefficient (cm
2 s
−1),
R is the universal gas constant (8.314 J mol
−1 K
−1), and
T is the absolute temperature (K). At 25 °C, the Randles–Sevcik
eqn (10) can be reduced to the following equation:
| | |
ip = (2.687 × 105)n3/2ν1/2AD1/2C
| (11) |
This equation predicts that in the solution phase, when voltammograms are taken at different scan rates, the peak current is proportional to the square root of the scan rate. As predicted by the Randles–Sevcik model, the insets in Fig. 3b and c show plots of anodic peak current versus the square root of scan rate yielding a straight line, suggesting electron transport by diffusion control phenomena. From the slope of the straight line the diffusion coefficient was calculated using eqn (12):
| | |
Slope = (2.687 × 105 C Mol−1 V−1/2)n3/2AD1/2C
| (12) |
The obtained diffusion coefficient was 2.7 × 10−9 and 1.73 × 10−8 for [Fe(TEA)OH]2−/[Fe(TEA)OH]− and Fe(CN)63−/Fe(CN)64− redox couples, respectively. These values are lower than known literature values45,46 due to the presence of high ionic strength. The reported diffusion coefficient for [Fe(TEA)OH]2−/[Fe(TEA)OH]− redox couple was 1.63 × 10−6 in 1 M NaOH solution,44 whereas in 3 M NaOH solution its value was 7.2 × 10−7.46 For Fe(CN)63−/Fe(CN)64−, a thoroughly explored redox couple, the diffusion coefficient was 8.6 × 10−6.46 The standard rate constant of [Fe(TEA)OH]2−/[Fe(TEA)OH]− and Fe(CN)63−/Fe(CN)64− redox couples was calculated from the variation of peak to peak difference (ΔEp) with scan rate (ν) by the Nicolson method,45,47 from which it is possible to determine the redox kinetic potential (Ψ) and hence k0, the electron transfer rate constant, using eqn (13):
| |
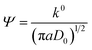 | (13) |
where
a =
nFν/
RT and
D0 is the diffusion coefficient.
The calculated k0 values for the [Fe(TEA)OH]2−/[Fe(TEA)OH]− and Fe(CN)63−/Fe(CN)64− redox couples were 3.1 × 10−3 and 4.6 × 10−3, respectively, at a scan rate of 50 mV. These values are one order of magnitude lower than that of an earlier report46 due to the high ionic concentration of the electrolyte used.
The RFB was assembled as described in the Experimental section and tested for charge–discharge behaviour at different current densities (Fig. 4) and constant flow rate of 10 mL min−1. From Fig. 4 it is clear that the charge–discharge voltage window (0.4–1.8 V) of the cell is high, indicating the successful formation of a battery with good energy density. The energy density of the battery depends upon the concentration of redox active species in the electrolyte solution and cell voltage. The volumetric energy density of the cell was found to be 4.07 W h L−1; it was less as compared to a typical vanadium RFB which has a volumetric energy density of about 20–33 W h L−1.48 This was due to limited solubility of redox active iron complexes in the electrolyte solutions. Fig. 4 shows the initial 10 cycles of charge–discharge curves at current densities of 5, 7.5, 10 and 15 mA cm−2. In all experiments, the time required for the first charge is high due to dissolved oxygen reduction, but with consecutive charging it became constant. The average calculated coulombic efficiency (CE) was 92%, 92%, 94% and 98%; energy efficiency (EE) was 75%, 72%, 65% and 69%; voltage efficiency (VE) was 82%, 78%, 72% and 70% for 5, 7.5, 10 and 15 mA cm−2 current densities respectively. With an increase in current density, there was an increase in CE. The maximum CE was 98% at 15 mA cm−2. This is due to the low crossover of the redox species. Generally, the CE is affected by crossover of redox active species, side reactions, electrode corrosion as well as membrane thickness.49 VE is affected by the ohmic resistance of the membrane and ionic conductivity of the electrolyte. The obtained VE is 70% at a current density of 15 mA cm−2. Fig. 5 shows the overlapping of a single charge/discharge cycle for ICEM at different current densities as well as overlapping of single charge/discharge cycle for ICEM and Nafion®-112 at 5 mA cm−2 current density. Nafion®-112 has the following physiochemical properties: thickness, 0.002 inch; IEC, 0.91 meq g−1; water uptake, 16.30%; and conductivity, 8.7 × 10−2 S cm−1. It had average calculated CE of 99%; volumetric capacity of 27%; EE of 75%; and VE of 76% at 5 mA cm−2 current density. These values are comparable with those of the ICEM and literature values.38,44,45 The literature reported values of CE were 80–90% and VE was 80%45 for all iron RFB. Compared to vanadium RFB50 and organic RFB,51 the admittedly low CE of the all iron RFB is due to low solubility of [Fe(TEA)OH]2−/[Fe(TEA)OH]− redox couple.
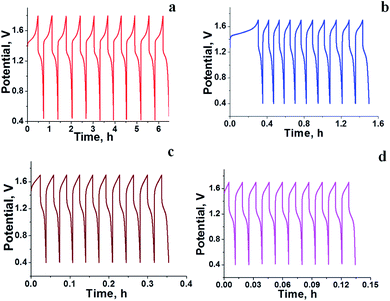 |
| | Fig. 4 Initial 20 charge–discharge cycling curves for all iron RFB at different current densities; (a) 5 mA cm−2, (b) 7.5 mA cm−2, (c) 10 mA cm−2, (d) 15 mA cm−2. | |
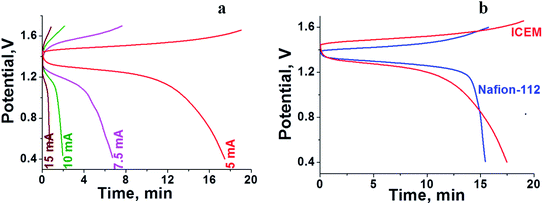 |
| | Fig. 5 (a) Overlapping of single charge/discharge cycle recorded at different current densities. (b) Overlapping of single charge/discharge cycle for Nafion®-112 and ICEM at 5 mA cm−2 current density. | |
Fig. 6 shows the cycling stability of the ICEM at 5 mA cm−2 current density along with CE, VE, EE and volumetric efficiency. The figure also shows the conductivity and images of membrane fouling after 40 charge/discharge cycles (Fig. 6C and D). From Fig. 6, it is clear that the battery was stable for 40 cycles with 92% CE and 75% EE (Fig. 6B). The calculated volumetric efficiency was 34%. These data indicate the usability of the membrane in an alkaline RFB. The obtained CE, EE and volumetric efficiency were slightly lower than those of Nafion® in identical experimental conditions, indicating the necessity of improvement in electrochemical properties of the ICEM.
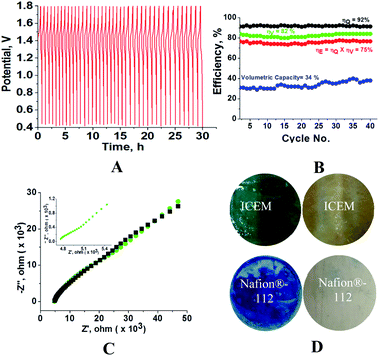 |
| | Fig. 6 Charge–discharge cycles of all iron RFB. (A) 40 charge–discharge cycles at 5 mA cm−2. (B) Corresponding CE, EE, VE and volumetric efficiencies. (C) Impedance spectra (green) with simulation (black) after 40 charge–discharge cycles of the membrane. (D) Photographs of the ICEM and Nafion®-112 membranes before and after cycling. | |
Previous reports of iron species-containing electrolytes used for flow batteries with their efficiency values are summarized in the bar graph in Fig. 7. Except for our present work, most of the reports mentioned in the figure have used commercial available membranes as a separator for their flow battery systems. It is evident from Fig. 7 that the efficiency values of the ICEM are comparable with the literature values. The high chemical stability of ICEM in the rigorous environment makes it a desirable candidate as a separator in an alkaline RFB. In comparison with the literature values,38,44,45 the lower CE, VE, EE and volumetric efficiency are due to an increase in the ohmic resistance of the cell by high ionic strength, slow deterioration of functional groups and may be due to the fouling of the membrane by redox active [Fe(TEA)OH]2−/[Fe(TEA)OH]− complex. The deterioration of redox active species was observed by recording the cyclic voltammogram in the presence of anolyte, catholyte and mixture of anolyte and catholyte. Fig. 8 shows the cyclic voltammograms of [Fe(TEA)OH]2−/[Fe(TEA)OH]− complex, Fe(CN)63−/Fe(CN)64− complex, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of [Fe(TEA)OH]2−/[Fe(TEA)OH]− and Fe(CN)63−/Fe(CN)64− and in the presence of TEA with Fe(CN)63−/Fe(CN)64− complex. As shown in Fig. 8A, the voltammogram of Fe(CN)63−/Fe(CN)64− complex shows oxygen evolution potential of ∼1.5 V. The voltammogram of [Fe(TEA)OH]2−/[Fe(TEA)OH]− complex shows the hydrogen evolution potential of approximately −1.2 V. The potential window of battery cycling was 1.8 to 0.4 V. This clearly reveals that hydrogen evolution is the dominating phenomenon in the deterioration of the battery performance. However, crossover of the redox active species is also equally contributing for performance deterioration and this was confirmed by recording the voltammogram of the 1
1 mixture of [Fe(TEA)OH]2−/[Fe(TEA)OH]− and Fe(CN)63−/Fe(CN)64− and in the presence of TEA with Fe(CN)63−/Fe(CN)64− complex. As shown in Fig. 8A, the voltammogram of Fe(CN)63−/Fe(CN)64− complex shows oxygen evolution potential of ∼1.5 V. The voltammogram of [Fe(TEA)OH]2−/[Fe(TEA)OH]− complex shows the hydrogen evolution potential of approximately −1.2 V. The potential window of battery cycling was 1.8 to 0.4 V. This clearly reveals that hydrogen evolution is the dominating phenomenon in the deterioration of the battery performance. However, crossover of the redox active species is also equally contributing for performance deterioration and this was confirmed by recording the voltammogram of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of [Fe(TEA)OH]2−/[Fe(TEA)OH]− and Fe(CN)63−/Fe(CN)64− complex. The absence of complete reduction peak of Fe(CN)63−/Fe(CN)64− redox couple clearly indicates that crossover of either [Fe(TEA)OH]2−/[Fe(TEA)OH]− or neat TEA has a significant effect on capacity fading. Fig. 8B shows results for the addition of consecutive amounts of 100 μL of [Fe(TEA)OH]2−/[Fe(TEA)OH]− complex in 10 mL solution of Fe(CN)63−/Fe(CN)64−. The successive increase in the oxidative current with suppressing reductive current clearly indicates that crossover of [Fe(TEA)OH]2−/[Fe(TEA)OH]− or neat TEA has a tremendous effect on CE. This can be explained by the following equations:
1 mixture of [Fe(TEA)OH]2−/[Fe(TEA)OH]− and Fe(CN)63−/Fe(CN)64− complex. The absence of complete reduction peak of Fe(CN)63−/Fe(CN)64− redox couple clearly indicates that crossover of either [Fe(TEA)OH]2−/[Fe(TEA)OH]− or neat TEA has a significant effect on capacity fading. Fig. 8B shows results for the addition of consecutive amounts of 100 μL of [Fe(TEA)OH]2−/[Fe(TEA)OH]− complex in 10 mL solution of Fe(CN)63−/Fe(CN)64−. The successive increase in the oxidative current with suppressing reductive current clearly indicates that crossover of [Fe(TEA)OH]2−/[Fe(TEA)OH]− or neat TEA has a tremendous effect on CE. This can be explained by the following equations:
| | |
3Fe(NC)63− + 4[Fe(TEA)OH]2− → Fe4[Fe(CN)6]3 + 4TEA + 4OH−
| (14) |
| | |
Fe(NC)63− + TEA → Fe(NC)64− + oxid TEA
| (15) |
where Fe(CN)
63− is converted to Fe(CN)
64− with the decomposition of [Fe(TEA)OH]
2−/[Fe(TEA)OH]
− complex. It results in the formation of Prussian blue (Fe
4[Fe(CN)
6]
3) on the membrane surface (presence of blue coloration on the membrane surface is a clear indication (
Fig. 6D)). TEA further reacts with Fe(CN)
63− with the formation of Fe(CN)
64− and electrochemical inactive oxidized TEA compounds. Hence, we did not observe the reduction peak in cyclic voltammograms.
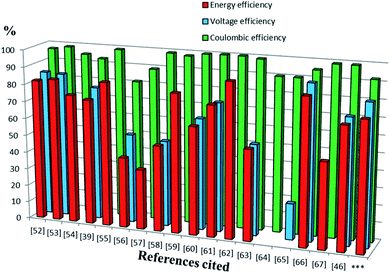 |
| | Fig. 7 The bars represent the CE, EE and VE of redox flow battery systems containing iron in their electrolyte system reported in the literature. Sequence of references followed by electrolyte system with concentration of active redox species, cell voltage (V) and volumetric capacity (Ah L−1) are as follows.52 1.5 M Fe3+/Fe2+/1.5 M V3+/V2+ (1.02 V, 18 A h L−1),53 0.1 M Fc1N112-TFSI/Fe(acac)3 (1.34 V, 2.47 A h L−1),54 Fe3O4/Fe/0.2 M Fe(CN)63−/Fe(CN)64− (1.2 V, 0.00065 A h L−1),39 0.2 M [Fe(TEOA)OH]−/[Fe(TEOA)(OH)]2−/0.2 M Fe(CN)63−/Fe(CN)64− (1.34 V, 4 A h L−1),55 0.5 M 2,6-DHAQ dipotassium salt/0.4 M K4Fe(CN)6 (1.20 V),56 0.1 M FeSO4 + 0.5 M NaCl/0.1 M Fe(acac)3,57 1.5 M Fe2+/Fe3+/1.8 M Cu+/Cu0 (0.25 V),58 0.5 M alloxazine-COOH/0.4 M Fe(CN)64− (1.3 V, 24 A h L−1),59 0.3 M 2,7-AQDS/0.1 M Fe(CN)64− (0.76 V, 17.8 A h L−1),60 0.5 M ACA/0.4 M Fe(CN)64− + 40 mM Fe(CN)63− (1.13 V),61 0.5 M (NH4)4[Fe(CN)6]/0.5 M (SPr)2V (0.82 V, 10 A h L−1),62 0.1 M bislawsone/0.2 M K4Fe(CN)6/0.02 M K3Fe(CN)6 (1.05 V),63 0.1 M Cr(acac)3/0.1 M Fe(acac) (1.2 V, 0.67 A h L−1),64 0.01 M Co(phen)3/0.01 M Fe(phen)3 (2.1 V, 0.10 A h L−1),65 0.2 M [Co(bpy)3]Tf2/0.2 M [Fe(bpy)3]Tf2 (2.0 V),66 0.1 M FeCp2PF6/0.1 M CoCp2 (1.7 V, 2.5 A h L−1),67 0.20 M K4Fe(CN)6, 0.08 M K3Fe(CN)6/0.1 M 2,6-DBEAQ (1.05 V),46 0.5 M Co(II)-mTEA/0.25 M Fe(III)-TEA + 0.5 M Fe(II)-TEA (0.93 V) and ***this work. | |
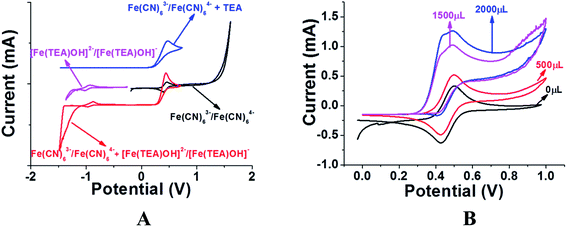 |
| | Fig. 8 (A) Cyclic voltammograms of Fe(CN)63−/Fe(CN)64− (black) and [Fe(TEA)OH]2−/[Fe(TEA)OH]− complex (purple) in wide potential window to show the oxygen and hydrogen evolution potential. The voltammogram of a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of Fe(CN)63−/Fe(CN)64− and Fe(TEA)OH]2−/[Fe(TEA)OH]− complex (red) shows the suppression of reduction current of Fe(CN)63−/Fe(CN)64− and reduction in hydrogen evolution potential. The voltammogram of TEA in Fe(CN)63−/Fe(CN)64− electrolyte (blue) shows the crossover of TEA can also equally suppress the reduction of Fe(CN)63−/Fe(CN)64−. (B) Cyclic voltammograms of Fe(CN)63−/Fe(CN)64− with successive addition of 500 (red), 1500 (purple) and 2000 (blue) microliters of Fe(TEA)OH]2−/[Fe(TEA)OH]− complex. All voltammograms were recorded at 10 mV s−1 scan rate with glassy carbon as working electrode, Ag/AgCl as reference electrode and Pt wire as counter electrode. 1 mixture of Fe(CN)63−/Fe(CN)64− and Fe(TEA)OH]2−/[Fe(TEA)OH]− complex (red) shows the suppression of reduction current of Fe(CN)63−/Fe(CN)64− and reduction in hydrogen evolution potential. The voltammogram of TEA in Fe(CN)63−/Fe(CN)64− electrolyte (blue) shows the crossover of TEA can also equally suppress the reduction of Fe(CN)63−/Fe(CN)64−. (B) Cyclic voltammograms of Fe(CN)63−/Fe(CN)64− with successive addition of 500 (red), 1500 (purple) and 2000 (blue) microliters of Fe(TEA)OH]2−/[Fe(TEA)OH]− complex. All voltammograms were recorded at 10 mV s−1 scan rate with glassy carbon as working electrode, Ag/AgCl as reference electrode and Pt wire as counter electrode. | |
The fouling of the membrane by Prussian blue was observed by washing the membrane with distilled water after completion of experiments (Fig. 6D). The fouling was also observed on the Nafion®-112 membrane (Fig. 6D). The fouling reduced the membrane conductivity. Calculated conductivity for ICEM from impedance spectra (Fig. 6C) was 0.18 mS, which is lower than the 7.26 mS of the membrane before cycling. However with optimized ionic concentration and redox couple, the polyethylene-styrene–DVB based cation exchange membrane will be an excellent candidate for use in highly alkaline RFB applications.
Conclusions
In summary, a highly alkaline RFB was assembled with indigenously developed RFB cell and polyethylene styrene–DVB based ICEM with [Fe(TEA)OH]2−/[Fe(TEA)OH]− and Fe(CN)63−/Fe(CN)64− redox couple. The evaluated 1440 h alkaline stability of the membrane, measured IEC, water content and impedance indicate its suitability as an alternative membrane to Nafion®-112. The membrane exhibited an average calculated CE of 98%; EE of 69%; and VE of 70% at 15 mA cm−2 current density. The obtained volumetric efficiency was 34%. These values are comparable with those of Nafion, indicating the suitability of the ICEM in an alkaline RFB.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
RKN is grateful for the financial support (grant number EMR/2016/00l977) from Science and Engineering Research Board (SERB), DST India and grant no. DST/TMD/MES/2K18/194(G) from Technology Mission Division Energy and Water, DST India. Director CSIR-CSMCRI is acknowledged for continuous support and encouragement. NKS thanks and acknowledges Manipal University, Jaipur for granting permission to work at CSIR-CSMCRI. Instrumentation facilities provided by Analytical Discipline & Centralized Instrument Facility, CSIR-CSMCRI, Bhavnagar, are gratefully acknowledged. CSIR-CSMCRI manuscript number 14/2020.
References
- J. Ran, L. Wu, Y. He, Z. Yang, Y. Wang, C. Jiang, L. Ge, E. Bakangura and T. Xu, J. Membr. Sci., 2017, 522, 267–291 Search PubMed.
- R. K. Nagarale, G. S. Gohil and V. K. Shahi, Adv. Colloid Interface Sci., 2006, 119, 97–130 Search PubMed.
- J. S. Olsson, T. H. Pham and P. Jannasch, Adv. Funct. Mater., 2018, 28, 1702758 Search PubMed.
- D. Mohanty and C. Bae, J. Mater. Chem. A, 2014, 2, 17314–17320 Search PubMed.
- S. Chempath, B. R. Einsla, L. R. Pratt, C. S. Macomber, J. M. Boncella, J. A. Rau and B. S. Pivovar, J. Phys. Chem. C, 2008, 112, 3179–3182 Search PubMed.
- J. B. Edson, C. S. Macomber, B. S. Pivovar and J. M. Boncella, J. Membr. Sci., 2012, 399, 49–54 Search PubMed.
- M. A. Hickner, A. M. Herring and E. B. Coughlin, J. Polym. Sci., Part B: Polym. Phys., 2013, 52, 347 Search PubMed.
- A. Kraytsberg and Y. Ein-Eli, Energy Fuels, 2014, 28, 7303–7330 Search PubMed.
- L. Gubler, Curr. Opin. Electrochem., 2019, 18, 31–36 Search PubMed.
- W. L. Harrison, M. A. Hickner, Y. S. Kim and J. E. McGrath, Fuel Cells, 2005, 5, 201–212 Search PubMed.
- P. Jannasch and E. A. Weiber, Macromol. Chem. Phys., 2016, 217, 1108–1118 Search PubMed.
- X. Yan, G. He, X. Wu and J. Benziger, J. Membr. Sci., 2013, 429, 13–22 Search PubMed.
- H. Kim, S. J. An, J. Kim, J. K. Moon, S. Y. Cho, Y. C. Eun, H. Yoon, Y. Park, H. Kweon and E. Shin, Macromol. Rapid Commun., 2004, 25, 1410–1413 Search PubMed.
- Y. K. Choe, C. Fujimoto, K. S. Lee, L. T. Dalton, K. Ayers, N. J. Henson and Y. S. Kim, Chem. Mater., 2014, 26, 5675–5682 Search PubMed.
- A. G. Wright, T. Weissbach and S. Holdcroft, Angew. Chem., Int. Ed., 2016, 55, 4818–4821 Search PubMed.
- L. Zhu, X. Peng, S. Shang, M. T. Kwasny, T. J. Zimudzi, X. Yu, N. Saikia, J. Pan, Z. Liu, G. N. Tew, W. E. Mustain, M. Yandrasits and M. A. Hickner, Adv. Funct. Mater., 2019, 29, 1902059 Search PubMed.
- C. G. Arges and V. Ramani, Proc. Natl. Acad. Sci. U. S. A., 2013, 110(7), 2490–2495 Search PubMed.
- J. Miyake, R. Taki, T. Mochizuki, R. Shimizu, R. Akiyama, M. Uchida and K. Miyatake, Sci. Adv., 2017, 3(10), eaao0476 Search PubMed.
- M. Adamski, T. J. G. Skalski, B. Britton, T. J. Peckham, L. Metzler and S. Holdcroft, Angew. Chem., Int. Ed., 2017, 56, 9058–9061 Search PubMed.
- H. F. Enderle, Encyclopedia of Materials: Science and Technology, 2nd edn, 2001, pp. 7172–7180 Search PubMed.
- T. C. M. Chung, Macromolecules, 2013, 46, 6671–6698 Search PubMed.
- F. D. Korosy and J. Shorr, US Pat. 3.388.080, 1968 Search PubMed.
- V. Tricoli and N. Carretta, Electrochem. Commun., 2002, 4, 272–276 Search PubMed.
- W. Rożek-Galina and W. Trochimczuk, J. Membr. Sci., 1985, 22, 47–59 Search PubMed.
- G. Poiniak and W. Trochimczuk, Angew. Makromol. Chem., 1980, 92, 155–168 Search PubMed.
- B. G. Shah, V. K. Shahi, S. K. Thampy, R. Rangarajan and P. K. Ghosh, Desalination, 2005, 172, 257–265 Search PubMed.
- R. K. Nagarale, G. S. Gohil, V. K. Shahi, G. S. Trivedi and R. Rangarajan, J. Colloid Interface Sci., 2004, 277, 162–171 Search PubMed.
- K. J. T. Noonan, K. M. Hugar, H. A. Kostalik, E. B. Lobkovsky, H. D. Abruna and G. W. Coates, J. Am. Chem. Soc., 2012, 134, 18161–18164 Search PubMed.
- T. Zhu, D. S. Xu, M. A. Rahman, E. Dogdibegovic, P. Yang, P. Pageni, M. P. Kabir, X. Zhou and C. Tang, Angew. Chem., Int. Ed., 2018, 57, 2388–2392 Search PubMed.
- H. A. Kostalik, T. J. Clark, N. J. Robertson, P. F. Mutolo, J. M. Longo, H. D. Abruna and G. W. Coates, Macromolecules, 2010, 43, 7147–7150 Search PubMed.
- W. You, E. Padgett, S. N. MacMillan, D. A. Muller and G. W. Coates, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 9729–9734 Search PubMed.
- B. Fang, S. Iwasa, Y. Wei, T. Arai and M. Kumagai, Electrochim. Acta, 2002, 47, 3971–3976 Search PubMed.
- B. Fang, S. Iwasa, Y. Wei, T. Arai and M. Kumagai, J. Appl. Electrochem., 2003, 33, 197–203 Search PubMed.
- X. Zhan, X. Lu, D. M. Reed, V. L. Sprenkle and G. Li, MRS Commun., 2020, 1–15 Search PubMed.
- Y. Wei, B. Fang, T. Arai and M. Kumagai, J. Appl. Electrochem., 2005, 35, 561–566 Search PubMed.
- Q. Deng, P. Huang, W. Zhou, Q. Ma, N. Zhou, H. Xie, W. Ling, C. Zhou, Y. Yin, X. Wu, X. Lu and Y. Guo, Adv. Energy Mater., 2017, 1–7, 1700461 Search PubMed.
- X. Wu, J. Hu, J. Liu, Q. Zhou, W. Zhou, H. Li and Y. Wu, Pure Appl. Chem., 2014, 86(5), 633–649 Search PubMed.
- M. T. Kwasny, L. Zhu, M. A. Hickner and G. N. Tew, J. Am. Chem. Soc., 2018, 140(25), 7961–7969 Search PubMed.
- N. Arroyo-Curras, J. W. Hall, J. E. Dick, R. A. Jones and A. J. Bard, J. Electrochem. Soc., 2015, 162(3), 378–383 Search PubMed.
- A. M. A. Mahmoud, A. M. M. Elsaghier, K. Otsuji and K. Miyatake, Macromolecules, 2017, 50, 4256–4266 Search PubMed.
- D. Voet and J. G. Voet, Biochemistry, 4th edn, John Wiley & Sons, 2011, p. 45 Search PubMed.
- I. M. Kolthoff and W. J. Tomsicek, J. Phys. Chem., 1934, 39, 945–954 Search PubMed.
- V. Gau, S. C. Ma, H. Wang, J. Tsukuda, J. Kibler and D. A. Haake, Methods, 2005, 37(1), 73–83 Search PubMed.
- R. K. Nagarale, J. M. Lee and W. Shin, Electrochim. Acta, 2009, 54, 6508–6514 Search PubMed.
- Y. H. Wen, H. M. Zhang, P. Qian, H. T. Zhou, P. Zhao, B. L. Yi and Y. S. Yang, Electrochim. Acta, 2006, 51, 3769–3775 Search PubMed.
- K. Gong, F. Xu, J. B. Grunewald, X. Ma, Y. Zhao, S. Gu and Y. Yan, ACS Energy Lett., 2016, 1, 89–93 Search PubMed.
- R. S. Nicholson, Anal. Chem., 1965, 37, 1351–1355 Search PubMed.
- K. Lourenssen, J. Williams, F. Ahmadpour, R. Clemmer and S. Tasnim, J. Energy Storage, 2019, 25(1–16), 100844 Search PubMed.
- J. Luo, B. Hu, M. Hu, Y. Zhao and T. Leo Liu, ACS Energy Lett., 2019, 4, 2220–2240 Search PubMed.
- J. Xi, Z. Wu, X. Qiu and L. Chen, J. Power Sources, 2007, 166, 531–536 Search PubMed.
- B. Hu, C. DeBruler, Z. Rhodes and T. Leo Liu, J. Am. Chem. Soc., 2017, 139, 1207–1214 Search PubMed.
- Biennial International Conference EESAT 2011, Electrical Energy Storage Applications and Technologies, San Diego Marriott Marquis & Marina Hotel, San Diego, California, USA, October 16–19, 2011 Search PubMed.
- Y. Zhen, C. Zhang, J. Yuan, Y. Zhao and Y. Li, J. Power Sources, 2020, 445, 227331 Search PubMed.
- L. Wei, M. C. Wu, T. S. Zhao, Y. K. Zeng and Y. X. Ren, Appl. Energy, 2018, 215, 98–105 Search PubMed.
- K. Lin, Q. Chen, M. R. Gerhardt, L. Tong, S. Bok Kim, L. Eisenach, A. W. Valle, D. Hardee, R. G. Gordon, M. J. Aziz and M. P. Marshak, Science, 2015, 349, 1529–1531 Search PubMed.
- M. O. Bamgbopa, Y. Shao-Horn, R. Hashaikeh and S. Almheiri, Electrochim. Acta, 2018, 267, 41–50 Search PubMed.
- D. M. Kabtamu, G. Lin, Y. Chang, H. Chen, H. Huang, N. Hsu, Y. Chou, H. Weib and C. Wang, RSC Adv., 2018, 8, 8537–8543 Search PubMed.
- C. Chu, B. W. Kwon, W. Lee and Y. Kwon, Korean J. Chem. Eng., 2019, 36(10), 1732–1739 Search PubMed.
- W. Lee, A. Permatasaria and Y. Kwon, J. Mater. Chem. C, 2020, 8, 5727–5731 Search PubMed.
- K. Lin, R. Gómez-Bombarelli, E. S. Beh, L. Tong, Q. Chen, A. Valle, A. Aspuru-Guzik, M. J. Aziz and R. G. Gordon, Nat. Energy, 2016, 102, 1–8 Search PubMed.
- J. Luo, B. Hu, C. Debruler, Y. Bi, Y. Zhao, B. Yuan, M. Hu, W. Wu and T. L. Liu, Joule, 2019, 3, 149–163 Search PubMed.
- L. Tong, M. Goulet, D. P. Tabor, E. F. Kerr, D. De Porcellinis, E. M. Fell, A. Aspuru-Guzik, R. G. Gordon and M. J. Aziz, ACS Energy Lett., 2019, 4, 1880–1887 Search PubMed.
- M. O. Bamgbopa, Y. Shao-Hornb and S. Almheiri, J. Mater. Chem. A, 2017, 5, 13457–13467 Search PubMed.
- X. Xing, Y. Zhao and Y. Li, J. Power Sources, 2015, 293, 778–783 Search PubMed.
- L. Medab, F. Oldanib, G. Tozzolab, S. Caramoria, E. Benazzia, V. Cristinoa and C. A. Bignozzia, Solid State Ionics, 2018, 317, 142–148 Search PubMed.
- Y. Ding, Y. Zhao, Y. Li, J. B. Goodenough and G. Yu, Energy Environ. Sci., 2016, 1–7 Search PubMed.
- D. G. Kwabi, K. Lin, Y. Ji, E. F. Kerr, M. Goulet, D. D. Porcellinis, D. P. Tabor, D. A. Pollack, A. Aspuru-Guzik, R. G. Gordon and M. J. Azizl, Joule, 2018, 2, 1894–1906 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra08316j |
|
| This journal is © The Royal Society of Chemistry 2020 |
 Open Access Article
Open Access Article *ab
*ab
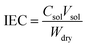
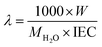
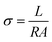
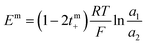
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S
S![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching. The C–H aliphatic and aromatic vibration bands were observed at 2800–2900 cm−1 and 3000–3100 cm−1, respectively, for polyethylene and the benzene ring. After 1440 h of 5 M NaOH treatment, there was no change in the peaks or the presence of additional peaks due to the alkaline and oxidative degradation of the polymer backbone, indicating the excellent stability of the membrane. This was supported by gravimetrically recording the change in weight of the membrane (Fig. 2b). The change in weight was measured every day and plotted as the percentage weight loss vs. time. From the figure it is clear that up to 400 h there is no weight loss. After 400 h and up to 1440 h, ∼3% weight loss was observed. This may be due to partial functional group degradation or leaching of low molecular weight physically entangled sulfonated polymer matrix. This functionality degradation results in a change in the physiochemical and electrical properties of the membrane. Fig. 2c shows the change in the measured IEC and water content of the membrane before and after chemical treatment. This was insignificant, suggesting its excellent alkaline stability. Before chemical treatment, the membrane had 2.14 meq g−1 IEC and 26.6% water content, while after treatment it had 1.96 meq g−1 IEC and 17.88% water content, i.e. ∼0.2 meq g−1 change in the IEC and ∼8.72% change in the water content. The water content in terms of water concentration in the membrane, Cm, was found to be 0.38 mol dm−3 before chemical treatment, and after chemical treatment it was 0.25 mol dm−3. The membrane porosity (τ), i.e. volume of free water within the membrane per unit volume of wet membrane, was calculated and found be 0.15 units for ICEM, which is 0.05 units more than ICEM-A. The fixed ion concentration is the measure of (moles of sites)/(unit volume of wet membrane) that gives a clear understanding of the deterioration of a membrane's physicochemical and electrochemical properties. The calculated fixed ion concentration for ICEM and ICEM-A was 0.89 and 0.80 mol dm−3 respectively, suggesting slow deterioration of the membrane properties after 1440 h in the highly alkaline oxidative environment. The ionic conductivity of the membranes was calculated by impedance measurements and is presented in Fig. 2c. The corresponding impedance spectra and simulated circuit diagram are presented in Fig. 2d. The impedance is made up of solution resistance (Rs), membrane resistance (Rm) and capacitance (C) between the electrolyte and electrode surface. From the measured impedance, the calculated conductivity of the membrane was 7.26 mS cm−1. After 1440 h of alkali treatment, the value of conductivity was 4.77 mS cm−1.
O stretching. The C–H aliphatic and aromatic vibration bands were observed at 2800–2900 cm−1 and 3000–3100 cm−1, respectively, for polyethylene and the benzene ring. After 1440 h of 5 M NaOH treatment, there was no change in the peaks or the presence of additional peaks due to the alkaline and oxidative degradation of the polymer backbone, indicating the excellent stability of the membrane. This was supported by gravimetrically recording the change in weight of the membrane (Fig. 2b). The change in weight was measured every day and plotted as the percentage weight loss vs. time. From the figure it is clear that up to 400 h there is no weight loss. After 400 h and up to 1440 h, ∼3% weight loss was observed. This may be due to partial functional group degradation or leaching of low molecular weight physically entangled sulfonated polymer matrix. This functionality degradation results in a change in the physiochemical and electrical properties of the membrane. Fig. 2c shows the change in the measured IEC and water content of the membrane before and after chemical treatment. This was insignificant, suggesting its excellent alkaline stability. Before chemical treatment, the membrane had 2.14 meq g−1 IEC and 26.6% water content, while after treatment it had 1.96 meq g−1 IEC and 17.88% water content, i.e. ∼0.2 meq g−1 change in the IEC and ∼8.72% change in the water content. The water content in terms of water concentration in the membrane, Cm, was found to be 0.38 mol dm−3 before chemical treatment, and after chemical treatment it was 0.25 mol dm−3. The membrane porosity (τ), i.e. volume of free water within the membrane per unit volume of wet membrane, was calculated and found be 0.15 units for ICEM, which is 0.05 units more than ICEM-A. The fixed ion concentration is the measure of (moles of sites)/(unit volume of wet membrane) that gives a clear understanding of the deterioration of a membrane's physicochemical and electrochemical properties. The calculated fixed ion concentration for ICEM and ICEM-A was 0.89 and 0.80 mol dm−3 respectively, suggesting slow deterioration of the membrane properties after 1440 h in the highly alkaline oxidative environment. The ionic conductivity of the membranes was calculated by impedance measurements and is presented in Fig. 2c. The corresponding impedance spectra and simulated circuit diagram are presented in Fig. 2d. The impedance is made up of solution resistance (Rs), membrane resistance (Rm) and capacitance (C) between the electrolyte and electrode surface. From the measured impedance, the calculated conductivity of the membrane was 7.26 mS cm−1. After 1440 h of alkali treatment, the value of conductivity was 4.77 mS cm−1.
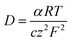
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 485 C mol−1), A is the electrode area (cm2), ν is the scan rate at which the potential is swept (V s−1), D is the analyte's diffusion coefficient (cm2 s−1), R is the universal gas constant (8.314 J mol−1 K−1), and T is the absolute temperature (K). At 25 °C, the Randles–Sevcik eqn (10) can be reduced to the following equation:
485 C mol−1), A is the electrode area (cm2), ν is the scan rate at which the potential is swept (V s−1), D is the analyte's diffusion coefficient (cm2 s−1), R is the universal gas constant (8.314 J mol−1 K−1), and T is the absolute temperature (K). At 25 °C, the Randles–Sevcik eqn (10) can be reduced to the following equation: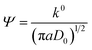

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of [Fe(TEA)OH]2−/[Fe(TEA)OH]− and Fe(CN)63−/Fe(CN)64− and in the presence of TEA with Fe(CN)63−/Fe(CN)64− complex. As shown in Fig. 8A, the voltammogram of Fe(CN)63−/Fe(CN)64− complex shows oxygen evolution potential of ∼1.5 V. The voltammogram of [Fe(TEA)OH]2−/[Fe(TEA)OH]− complex shows the hydrogen evolution potential of approximately −1.2 V. The potential window of battery cycling was 1.8 to 0.4 V. This clearly reveals that hydrogen evolution is the dominating phenomenon in the deterioration of the battery performance. However, crossover of the redox active species is also equally contributing for performance deterioration and this was confirmed by recording the voltammogram of the 1
1 mixture of [Fe(TEA)OH]2−/[Fe(TEA)OH]− and Fe(CN)63−/Fe(CN)64− and in the presence of TEA with Fe(CN)63−/Fe(CN)64− complex. As shown in Fig. 8A, the voltammogram of Fe(CN)63−/Fe(CN)64− complex shows oxygen evolution potential of ∼1.5 V. The voltammogram of [Fe(TEA)OH]2−/[Fe(TEA)OH]− complex shows the hydrogen evolution potential of approximately −1.2 V. The potential window of battery cycling was 1.8 to 0.4 V. This clearly reveals that hydrogen evolution is the dominating phenomenon in the deterioration of the battery performance. However, crossover of the redox active species is also equally contributing for performance deterioration and this was confirmed by recording the voltammogram of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of [Fe(TEA)OH]2−/[Fe(TEA)OH]− and Fe(CN)63−/Fe(CN)64− complex. The absence of complete reduction peak of Fe(CN)63−/Fe(CN)64− redox couple clearly indicates that crossover of either [Fe(TEA)OH]2−/[Fe(TEA)OH]− or neat TEA has a significant effect on capacity fading. Fig. 8B shows results for the addition of consecutive amounts of 100 μL of [Fe(TEA)OH]2−/[Fe(TEA)OH]− complex in 10 mL solution of Fe(CN)63−/Fe(CN)64−. The successive increase in the oxidative current with suppressing reductive current clearly indicates that crossover of [Fe(TEA)OH]2−/[Fe(TEA)OH]− or neat TEA has a tremendous effect on CE. This can be explained by the following equations:
1 mixture of [Fe(TEA)OH]2−/[Fe(TEA)OH]− and Fe(CN)63−/Fe(CN)64− complex. The absence of complete reduction peak of Fe(CN)63−/Fe(CN)64− redox couple clearly indicates that crossover of either [Fe(TEA)OH]2−/[Fe(TEA)OH]− or neat TEA has a significant effect on capacity fading. Fig. 8B shows results for the addition of consecutive amounts of 100 μL of [Fe(TEA)OH]2−/[Fe(TEA)OH]− complex in 10 mL solution of Fe(CN)63−/Fe(CN)64−. The successive increase in the oxidative current with suppressing reductive current clearly indicates that crossover of [Fe(TEA)OH]2−/[Fe(TEA)OH]− or neat TEA has a tremendous effect on CE. This can be explained by the following equations:






