Open Access Article
Open Access ArticleUnraveling the single-atom electrocatalytic activity of transition metal-doped phosphorene†
Akhil S.
Nair
 a,
Rajeev
Ahuja
a,
Rajeev
Ahuja
 bc and
Biswarup
Pathak
bc and
Biswarup
Pathak
 *a
*a
aDiscipline of Chemistry, Indian Institute of Technology Indore, M. P., India
bCondensed Matter Theory Group, Department of Physics and Astronomy, Uppsala University, Box 516, SS-75120 Uppsala, Sweden
cApplied Materials Theory Group, Department of Materials and Engineering, Royal Institute of Technology, (KTH), S-10044 Stockholm, Sweden. E-mail: biswarup@iiti.ac.in
First published on 21st April 2020
Abstract
The development of single-atom catalysts (SACs) for chemical reactions of vital importance in the renewable energy sector has emerged as an urgent priority. In this perspective, transition metal-based SACs with monolayer phosphorous (phosphorene) as the supporting material are scrutinized for their electrocatalytic activity towards the oxygen reduction reaction (ORR), oxygen evolution reaction (OER), and hydrogen evolution reaction (HER) from first-principle calculations. The detailed screening study has confirmed a breaking of the scaling relationship between the ORR/OER intermediates, resulting in various activity trends across the transition metal series. Groups 9 and 10 transition metal-based SACs are identified as potential catalyst candidates with the platinum single atom offering bifunctional activity for OER and HER with diminished overpotentials. Ambient condition stability analysis of SACs confirmed a different extent of interaction towards oxygen and water compared to pristine phosphorene, suggesting room for improving the stability of phosphorene via chemical functionalization.
1. Introduction
Endeavors to curb catalyst loading without dwindling the activity has been a far-reaching goal in the area of heterogeneous catalysis.1–3 Attempts towards the realization of this goal, along with the development of nanotechnology, have explored catalysts of different dimensions such as nanoclusters, nanowires, and 2D sheets. The most recent decades have witnessed the emergence of single-atom catalysts (SACs), whereby the atomically dispersed metals catalyzed the reactions and became quintessential examples for the green chemistry concept of “atom economy”.4,5 A vast number of categories of SACs have been explored so far by varying the supports, such as metal oxides, two-dimensional nanosheets, clusters, and metal organic frameworks.6–9 Apart from the stabilization effects of single atoms anchored on the supports, SACs offer extraordinary catalytic properties owing to their compelling electronic, structural and chemical properties that arise from the synergistic interaction between the support and metal atom. For example, Zhang and coworkers demonstrated that Pt atoms uniformly dispersed over an iron oxide (Pt1/FeOx) support exhibited CO oxidation activity higher than their nanoparticle counterpart.10 This revolutionary study was followed by the discovery of a number of M/NOx (M = Ir, Pt, Au; N = Ti, Fe, Ce) SACs identified as potential catalysts for the water–gas shift reaction.11–13 In order to address the expeditious energy crisis confronted by the modern world, the development of efficient electrocatalysts for the reactions of energy storage (such as the oxygen reduction reaction (ORR), CO2 reduction reaction (COR), oxygen evolution reaction (OER) and hydrogen evolution reaction (HER)) is an area of utmost research interest. Since the primary catalysts used at an industrial level for these reactions are noble expensive metals, such as Pt, Pd, Ir and Rh, the evolution of SACs has set off enormous attempts to reduce catalyst loading by retaining/improving the activity of the one-atom based catalysts. So far, the combined experimental and theoretical studies have unraveled a number of transition metal-based SACs with pristine and vacant graphene-type materials and nanoparticles.14–17 Continuous research is being carried out to disclose novel SACs with optimal metal-support combinations for excellent activity.18–20Few-layer bulk phosphorus, particularly monolayer phosphorene has been proposed as a material of immense interest owing to the exquisite properties, such as its unique anisotropic electronic and transport properties, high mobility, turn off ratio and tunable direct band gap.21–23 These properties have enabled phosphorene to be employed for a diverse set of applications, such as gas sensing, transport devices and optoelectronics.24–26 The major obstacle in the practical utilization of phosphorene is its instability at ambient conditions, the origin of which has been attempted to be understood at an atomic scale.27,28 However, recent studies have been able to synthesize air-stable few-layer black phosphorous (BP) by layer-by-layer thinning of the bulk black phosphorous and by pulsed laser exfoliation.29,30 Such air-stable phosphorene nanosheets have also been identified with a preferred catalytic activity towards electrochemical reactions. In a pioneering study by Zhang and co-workers, few-layer BP nanosheets were identified as potential catalysts for OER, while retaining structural stability over 1000 potential cycles.31 The linear relation between the reduction in the thickness of the BP nanosheets and the electrocatalytic activity suggested by the authors recommended the plausibility of monolayer phosphorene as an efficient electrocatalyst. However, Xue et al. showed through a theoretical study that the enhanced catalytic activity for ORR or OER could be derived from phosphorene only by inducing modifications, such as vacancies and hetero-atom doping.32 Therefore, the selective functionalization of phosphorene draws considerable attention as it can deliver significant electrocatalytic activity by tuning the interaction with reactive intermediates, as well as enhancing the stability by modifying the electronic structure.
Motivated by the aforementioned ideas, we attempted to investigate the activity of transition metal-doped phosphorene SACs (TM–Ph) towards major electrocatalytic reactions, such as ORR, OER and HER based on first-principles calculations. The final transition metals from the 3d (Fe, Co, Ni, Cu), 4d (Ru, Rh, Pd, Ag) and 5d (Os, Ir, Pt, Au) series were considered owing to their catalytic applications for various processes at the bulk level. The structural, electronic and thermodynamic aspects of the catalytic activity were systematically studied and an activity screening among the considered catalyst species was carried out. The origin behind the activity trends observed was scrutinized to derive suitable activity descriptors and related parameters. The active candidates were further analyzed for their stability under ambient conditions by an atomistic approach. The results are expected to provide useful thumbnails for future efforts in enabling phosphorene as an efficient support for SACs.
2. Computational model and details
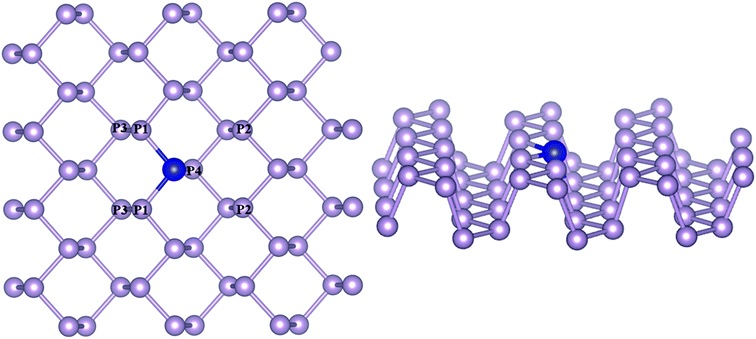
The density functional theory (DFT) calculations were carried out using VASP (Vienna Ab Initio Software Package).33 Gradient corrected approximation using Perdew–Burke–Ernzerhof (GGA–PBE) exchange-correlation functional was employed with the projected augmented wave method (PAW) to describe the periodic boundary conditions.34,35 The study by Hashmi and Chan reported on the exactness between the magnetic ground state prediction between DFT-GGA and DFT-U for the 3d TM–Ph systems.36 Hence, we have avoided considering the Hubbard calculation in our study. A kinetic-energy cutoff of 470 eV with a K-point grid of 5 × 5 × 1 for the Brillouin zone sampling was used for the energy calculations, and 15 × 15 × 1 was used for the electronic structure calculations. The dispersion interactions were accounted for by using the DFT-D3 method.37 All calculations were spin polarized and without any symmetry constraints. An implicit solvation model implemented in VaspSol was used to simulate the electrolyte conditions.38 Crystal orbital Hamilton population (COHP) analysis was carried out using the Lobster program.39A 4 × 4 × 1 supercell with 48 atoms was used to model phosphorene with the transition metals substitutionally doped by replacing one phosphorous atom at the bridge site, constituting an atomic doping percentage of 2.708% (Fig. 1). The doped TM atoms were observed to possess variable geometric features across the series, which are given in Table S1.† While the bond lengths of TMs with P atoms (TM–P1/P4) along the zigzag direction remained close to the pristine values (2.17–2.47 Å), the average TM–P bond length along the armchair directions (TM–P2) differed considerably across the TM series (2.5–3.6 Å), with a closeness observed for the same group metals. The incorporation of TMs was found to be associated with a diminished buckling as compared to pristine phosphorene, which was determined from the interplanar distance (P1–P3) between the outer and basal planes. Of all the TM–Phs considered, only the Fe and Ni-doped systems were magnetic with a total magnetic moment of 1 μB.
3. Results and discussion
The energetics of the phosphorene monovacancy formation, the prerequisite factor for TM doping was analyzed by calculating the formation energy as follows:| FE = EPh-Vac − EPh − EP | (1) |
| EBE = ETM–Ph-Vac − EPh-Vac − ETM | (2) |
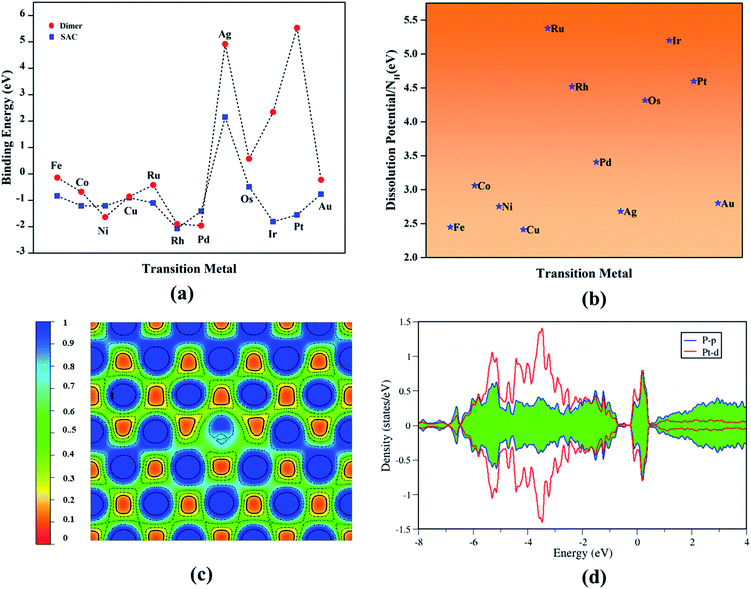
All TM–Ph based systems except Ag–Ph have been found to bind strongly, and hence possess the required thermodynamic stability to be useful as catalyst materials. The structural integrity and tolerance towards electrochemical conditions are crucial parameters in determining the long-term activity of electrocatalysts, and hence to be addressed in detail. Within this consideration, the relative binding energy of TM-dimer on phosphorene was determined to analyze the plausibility of aggregation of the doped TMs under a TM-rich condition (Fig. 2a: red panel), and compared with a single-atom binding scenario. All TM-dimers were found to be weakly binding compared to the single TM atom, except for Ni, Pd undergoing dissociation, suggesting a reduced tendency towards aggregation for the SACs. Furthermore, the sustainability of the TM–Ph SACs under electrochemical conditions was scrutinized by the dissolution potential of TMs calculated from replacing the TM atoms with protons, followed by the work of Singh et al.41 as the free energy of the reaction:
| TM–Ph + nH+ → nH–Ph + TMn+ | (3) |
3.1 Oxygen reduction and evolution reaction
Owing to the similarity between the reaction intermediates involved, we attempted to first study the ORR characteristics of the TM–Ph SACs and utilize the relevant aspects to describe the OER activity trends. The adsorption configuration of the ORR intermediates is given in Fig. 3a–e. ORR was initiated by O2 adsorption, the details of which are given in Table S3.† The absence of local minima with O2 physisorbed on the TM atoms ensured favorable binding to the single atom center, rather than the P atoms where the physisorbed O2 configuration was observed, which is discussed in a later section. A characteristic linear adsorption mode was observed for all TM–Ph SACs with an average vibrational frequency of 1100–1300 cm−1, except for Pd–Ph adsorbing in a di-sigma mode. The O2 binding was highly localized at the metal centers in TM–Phs with a lesser O2 binding strength compared to the P atoms of the pristine phosphorene, among which the highest interaction was evidenced for Fe–Ph with a binding energy of −1.77 eV. The corresponding projected density of states (PDOS) analysis (Fig. S2†) of Fe–Ph showed a strong hybridization between the p states of O2 and the d-states of iron, retaining a magnetic moment of 3 μB. This indicated an additive coupling between Fe and the triplet O2 magnetic moments. The localization of O2 binding on the transition metal atoms was further confirmed by the relatively higher P–O* bond lengths (>3 Å) compared to the TM–O* bond length (<2.5 Å), as shown in Fig. S3.† Top site O* adsorption occurs on the TM centers with an exception for the end series metals, such as Ni, Cu, Pd, Ag and Au, where a bridge type adsorption with P2 atoms occurs. OH*, OOH* and H* adsorptions also occurred in the top mode across all the SACs, which follows their typical adsorption configurations over the (111) facets of the transition metal surfaces. The local adsorption-induced structural changes quantified in terms of the deviation of the TM–P bond lengths in Fig. S4† confirmed the structural deviations within a 0.1 Å change, except for Cu- and Au-based SACs, for which relatively large bond length variations were present. For Ni and Pd, a strong H* binding caused the TM to translate towards the lower layer of TM–Ph, and hence led to a distortion of the system. Therefore, these (Ni and Pd) SACs were not considered for studying the HER activity.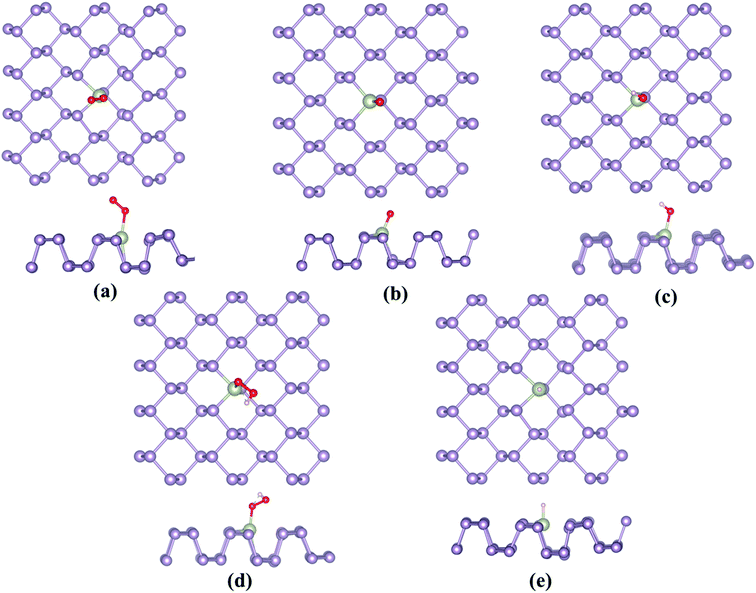 | ||
| Fig. 3 Most stable adsorption configurations of the ORR/OER/HER intermediates, (a) O2, (b) O*, (c) OH*, (d) OOH* and (e) H*. | ||
Since ORR/OER is a multistep reaction with intermediates O*, OH* and OOH* involved, it is preferable to search for an activity descriptor especially based on one intermediate so that a parametric space for the catalytic activity can be simplified in the number of degrees of freedom and a general trend can be expected. Having this as the objective, we investigated the scaling relationship between the adsorption free energies of the intermediates, which were attributed to the fundamental origin for the diminished experimental onset potential for ORR (Fig. 4). The adsorption free energies were calculated with reference to the water from the following equations:
| ΔGO* = GO* − G* − [GH2O − GH2] | (4) |
| ΔGOH* = GOH* − G* − [GH2O − 1/2GH2] | (5) |
| ΔGOOH* = GOOH* − G* − [2GH2O − 3/2GH2] | (6) |
 | ||
| Fig. 4 Scaling relationship of the ORR/OER intermediates, (a) ΔGO*vs. ΔGOH*, (b) ΔGOOH*vs. ΔGOH*, (c) ΔGO*vs. ΔGOOH*. | ||
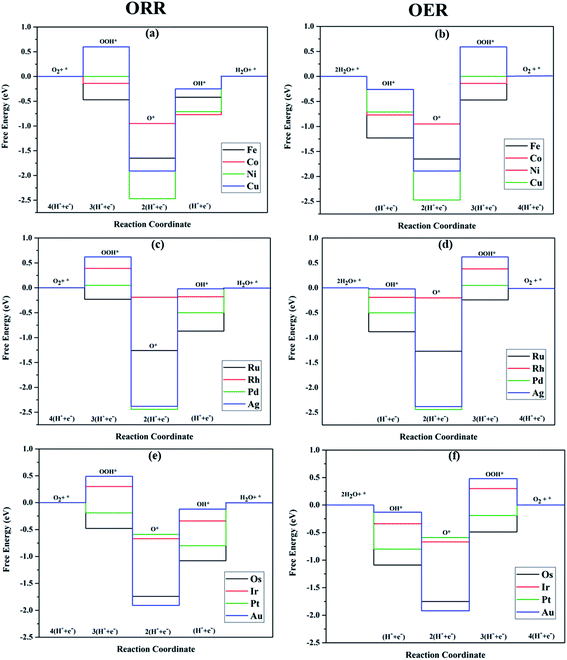
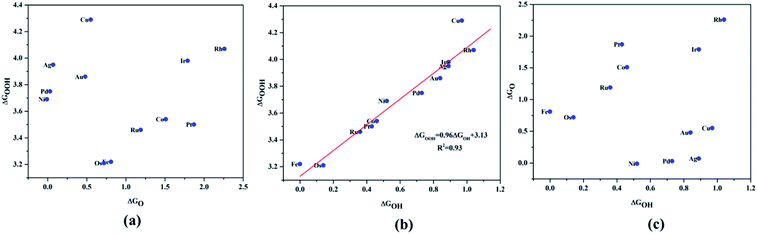
A surprising observation was the consistency in the linear scaling of ΔGOOH = 0.96ΔGOH + 3.13 with a large determination coefficient between OH* and OOH*, as seen for the transition metal surfaces. Conversely, there was almost negligible scaling found for OH* vs. O* and OOH* vs. O*. This suggested a breaking of the scaling relationships across the TM–Ph series, which was a sufficient reason for the catalytic trends. The involvement of nearby phosphorous atoms in bonding with the O atoms could be expected to provide a difference in the binding of ORR intermediates by the SACs and hence gives rise to the nonlinear scaling relationships, while the similar mode of adsorption (top site) sustained the relationship between OH* and OOH*. This observation immediately denied the possibility of considering the O* binding energy as an activity descriptor, which had been considered in many studies. To identify the chemical origin of breaking the scaling relationships, we carried out a projected crystal Hamilton population analysis (pCOHP) for all intermediates, which was recently verified to be an important activity descriptor for computational screening studies (Fig. 5).42 The bonding and antibonding populations were represented on the right and left sides of the plot, respectively. The depicted O* pCOHP involved an average of the TM–O and P–O bonding for the Ni, Cu, Pd, Ag, and Au based SACs as the O* occupied a bridging position in these systems. The observed discrepancies in the adsorption free energy, and hence the scaling relationship, could be ascribed to the relatively higher variation in the spread of the bonding and antibonding populations for the TM–O* binding as compared to the TM–OH* binding. Another noteworthy aspect arising from the pCOHP analysis was that all TM–Ph catalysts possessed a slightly higher population for the TM–O* bonding energy levels than the antibonding energy levels at the valence band. This indicated an optimum bonding scenario that reduced the possibility of strong O* binding-caused catalytic site poisoning, a major drawback of the conventional transition metal-based catalysts. Furthermore, a plot of the integrated COHP (ICOHP) up to the Fermi level against the Mulliken's charge transfer43 revealed a higher order linearity between the charge transferred to OH* compared to O* (Fig. S5†). O* binding is associated with a larger charge span of 0.4–1.2|e|, which is still far from the valence satisfying criteria of 2e−. Conversely, OH* binding features a lower charge fluctuation (0.85–1.06|e|), which is consistent with the valency requirement of 1e−. This difference in the strengths of the covalent character has been previously observed for OH* and OOH* in MN4 complexes by Calle-Vallejo et al.,44 causing a breaking of the scaling relationships in vacuum and is retained under implicit solvent consideration. Since our study involved an implicit solvation consideration, the differences in the covalence of the ORR intermediates emerged as a parameter of interest for the activity enhancement by tuning the metal center. The free energy diagrams for ORR (Fig. 6) constructed at the equilibrium potential of 1.23 V indicated that there was a non-uniform trend in the energetics of ORR over different TM–Ph SACs.
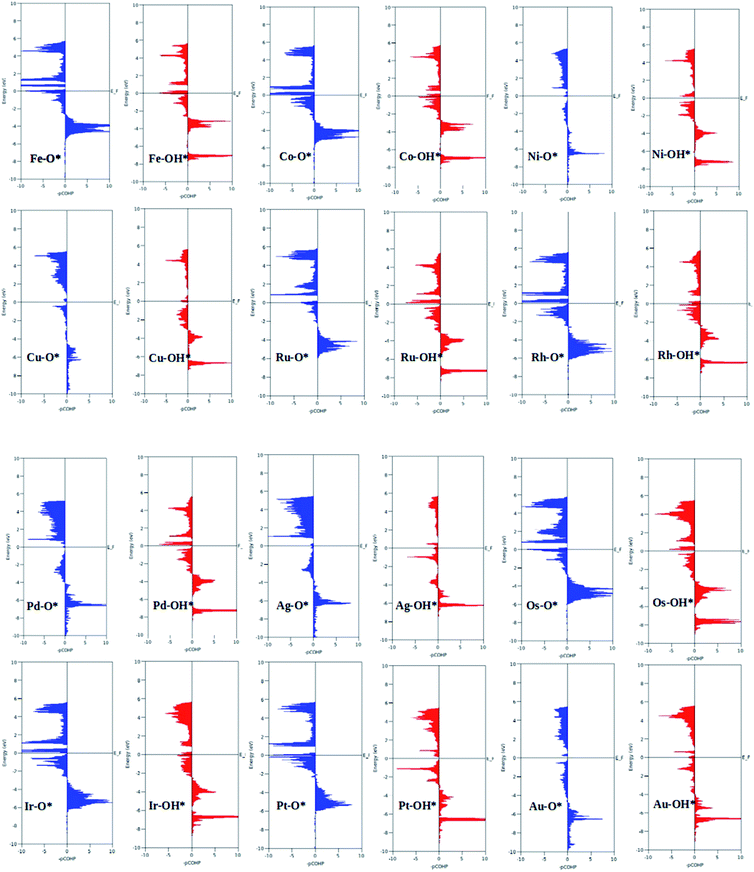 | ||
| Fig. 5 Projected crystal Hamilton population analysis of the O* and OH* intermediates adsorbed on TM–Ph SACS. | ||
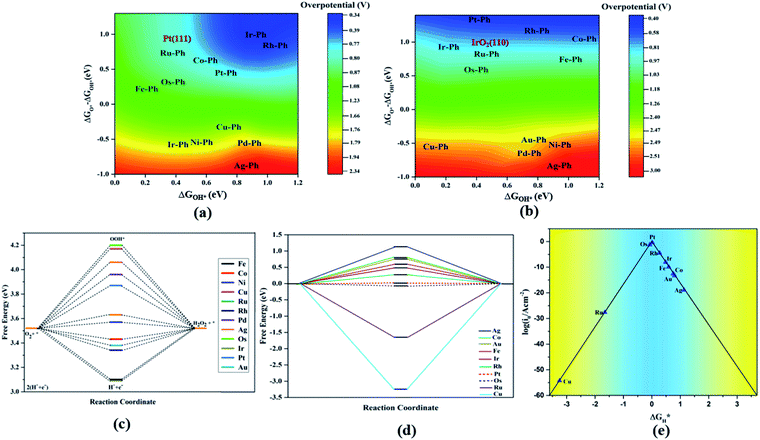
The TM–Phs with 3d series elements Fe, Ni and Cu, along with the end-lying Pd, Ag and Au of the 4d and 5d series featured OH* formation as the rate-determining step. On the contrary, Co, Ru, Os, Ir and Pt-based TM–Phs possessed H2O formation as the rate-limiting step. Rh–Ph emerged as the only system with OOH* formation as the rate-limiting step. Therefore, it was found that the stability of OH* on the catalyst surface can be considered a crucial parameter in determining the catalytic trends among the SACs. From the free energy screening, Ir–Ph was the best ORR catalyst with an overpotential of 0.34 V calculated using the computational hydrogen electrode model (CHE) proposed by Nørskov et al.,45 which was followed by Rh and Co with overpotentials of 0.39 and 0.77 V, respectively. It is interesting that Ir–Ph manifested an almost constant (although non-zero) ΔG (0.30, 0.37, 0.33 and 0.34 eV) for all four protonation steps of ORR, which is an adequate feature of an ideal catalyst. The lowest overpotential value of 0.34 eV reinforced the scaling relationship–driven activity trend by its excellent resemblance with the minimum thermodynamic overpotential of 0.33 V derived from the linear scaling between OH and OOH [(1.23 − (−4.92 + 3.12)/2) V = 0.33 V]. The obtained overpotentials for the active TM–Ph catalysts (Ir–Ph: 0.34 V and Rh–Ph: 0.39 V) were less than the well-known ORR catalyst periodic Pt(111) surface with a value of 0.45 V (ref. 45) (given in Fig. 7a), confirming that these TM–Ph catalysts greatly improved the ORR activity along with a considerable minimization of metal loading. Compared to ORR, the OER activity followed a different trend across the SACs with a uniform rate-determining step of OOH* formation. The highest activity was observed for Pt–Ph for which a free energy change of 0.40 eV was required for the OOH* formation from O*, which was followed by Rh–Ph with a corresponding value of 0.58 eV. The highest activity of Pt–Ph can be attributed to the ΔGO* value of 1.87 eV lying closest to the mean value of ΔGOH* and ΔGOOH*. This is an essential criterion for an efficient catalyst for which either the conversion from O* to OOH* or OH* to O* can be the rate-determining step.46 The dominance of the single Pt atom over Ir or Ru, for which the oxide counterparts are well-known OER catalysts for their high activity, is noteworthy. For example, the well-known OER catalyst periodic IrO2 (110) surface featured an overpotential of 0.51 V (ref. 46) (given in Fig. 7b), which could be outperformed by Pt–Ph SAC with a diminished overpotential by 0.11 V.
For both ORR and OER, high fluxionality was observed between the free energy of the elementary reaction steps across the SACs with a notable uniformity in the end-lying metal center in the TM series (Cu, Ag, Au) exhibiting the lowest activity. This can be ascribed to their high d electrons causing a strong binding towards the intermediates, introducing an energetically uphill trend in the corresponding reactions. This can be also understood from the alignment of these TM–Ph SACs in the strong charge-transferring category during the TM–O* interaction from the Mulliken's charge analysis in Fig. S5(a).† Activity contour plots of the TM–Ph SACs for the ORR and OER are represented in Fig. 7a and b with ΔGOH* and ΔGO* − ΔGOH* as the reference parameters, as the identified scaling between OOH* and OH* reduces the dependency of the ORR/OER activity from four ΔG values into two. From the volcano plots, it is evident that the Ir–Ph, Rh–Ph, Pt–Ph and Os–Ph SACs occupied the highest activity regions and could be considered as potential catalysts. It is also noteworthy that the less stable Ag–Ph and Pd–Ph SACs featured less electrocatalytic activity, as identified from the activity volcano plot.
To elucidate the thickness dependence on the electrocatalytic activity of TM–Ph-based SACs, we calculated the activity of Ir–Ph and Pt–Ph for ORR and HER, respectively, up to a thickness (Fig. S6 and Table S4†) of 3 monolayers (3 MLs). Both systems showed a decrease in the activity with higher overpotentials for 2 ML and 3 ML thicknesses than the 1 ML counterparts, suggesting an inverse relation between the ORR activity vs. thickness. However, the HER activity underwent a comparatively lower (by 1 V) and irregular variation with thickness.
A competitive pathway for the 4e− ORR with H2O formation is the 2e− reduction resulting in H2O2 formation. Simultaneously, the electrochemical synthesis of H2O2 is an important area of industrial importance.47–49 Owing to the similarity in intermediates, we investigated the 2e− oxygen reduction activity of TM–Ph SACS by a free energy analysis with the OOH* formation and H2O2 formation as the two elementary steps. Fig. 7c represents the free energy diagram at the equilibrium potential of 0.7 V of the 2e− reduction. The ORR/OER-active TM–Ph SACs did not show prominent activity towards the 2e− reduction, which diminished the plausibility for the competitive 2e−vs. 4e− reduction pathways. Instead, the 3d series-based TM–Ph SACs (such as Ni–Ph and Co–Ph) emerged as active catalysts with a curtailed energy requisite of 0.05 and 0.09 eV that led to limiting potentials of 0.65 and 0.61 V, respectively. This uncovered a catalytic activity that is equivalent to the performance of the state-of-the-art 2e− reduction catalyst PtHg4.50 There is variation in the activity-determining reaction from the OOH* formation to OOH* protonation along the TM–Ph series that occurred due to the weak and strong binding of OOH* to the metal center, respectively.
3.2 Hydrogen evolution reaction
Apart from the oxygen reduction/evolution reactions, we further investigated the hydrogen evolution activity of the TM–Ph SACs. Many of the recently developed SACs have offered prevalent catalytic activity towards HER. Since Ni–Ph and Pd–Ph have been identified to be structurally unstable during H* adsorption, we avoided them for the HER activity study. Since ΔGH* is the only activity descriptor involved, we considered a Heyrovsky mechanism for our study subjected to the fact that the protons were adsorbed into the catalytic center from the solution and later desorbed as H2*.51 From the HER free energy diagram given in Fig. 7d, it was obvious that H* formation was the rate-determining step for the majority of the SACs, whereas the RDS for Cu and Ru was the combination of the adsorbed H* with protons to form H2. Here, Pt–Ph was the best SAC because it almost achieved the ideal efficiency with ΔGH* = 0.01 eV. This was followed by Os–Ph with an overpotential of 0.07 V. A volcano plot of the exchange current density (a parameter which can be measured experimentally) versus the Gibbs free energy of adsorption is represented in Fig. 7e, where the current density was calculated by the following method proposed by Norskov et al.:52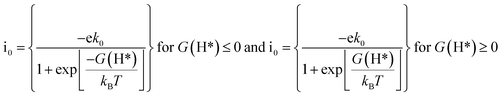 | (7) |
3.3 Ambient condition stability of SACs
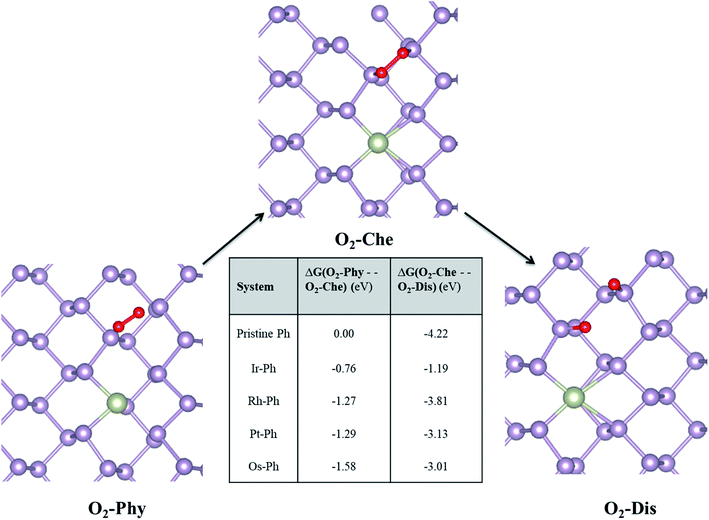
Phosphorene is known to have stability issues under ambient conditions that are caused primarily by its interaction with light, atmospheric oxygen and water/moisture. As many of the TM–Ph SACs are characterized by their exceptional electrocatalytic activity, we attempted to investigate their ambient condition stability via studying the chemical degradation of pristine phosphorene from first-principle calculations. The ambient condition stability investigations were carried out for the most active catalysts (Ir–Ph, Rh–Ph, Pt–Ph, Os–Ph) for all electrocatalytic reactions, considering pristine phosphorene as the frame of reference. To begin with, we carried out ab initio molecular dynamics (AIMD) simulations of these SACs at 300 K with a time step of 2 fs for a time period of 10 ps. The fairly smooth free energy fluctuation during the trajectory evolution (Fig. S7†) confirmed the thermodynamic stability of these SACs. This was followed by a detailed investigation of the chemical interactions of SACs with its surroundings.The mechanism of the O2-induced degradation has been studied in detail by Ziletti et al., which is mediated by the breakage of the structural integrity of the phosphorene monolayer via the dangling oxygen atoms bound to P atoms.53 We extended the three different reported O2 interaction modes on phosphorene to the selected Ir–Ph, Pt–Ph, Rh–Ph and Os–Ph SACs, which are: (i) physisorbed O2 (O2–Phy), (ii) O2 chemisorbed in a bridge fashion (O2-Che), and (iii) dissociated O2 resulting in the formation of two P–O dangling bonds (O2-Dis) on the non-TM region of the TM–Ph systems. The structural details of the three different adsorption modes are given in Table S5.† Deviations in the magnetic moments from 2 μB, as observed for pristine phosphorene, in some of the TM–Ph SACs suggest different interactions in the physisorption mode. The average binding energies of the dangling O atoms for all TM–Ph SACs (except Pt–Ph) are lower than that of pristine phosphorene, implying two less stable (P–O*) configurations for the respective SACs and a diminished affinity towards oxidation. Furthermore, we investigated the free energy change associated with the transfer of the O2 interaction via the discussed three modes (results are represented in Fig. 8). Although there is a thermodynamic plausibility for the movement of O2 from the physisorbed to chemisorbed state, there is less exothermicity associated with the O2 dissociation for the SACs in comparison to the scenario of pristine phosphorene, especially for the highest ORR-active candidate Ir–Ph with the least exothermicity observed. This observation is supported by the low O* binding energy, which can be attributed to the relatively large occupation of the antibonding energy levels. These antibonding energy levels occur under the valence band region for the lowest binding Ir–Ph SAC, as determined from the pCOHP analysis of P–O interaction against pristine phosphorene (Fig. S8†). Transition metal states close to the Fermi level were previously revealed from the density of states analysis. These states can be expected to reduce the pure p orbital character for the P atoms belonging to the immediate ridges, resulting in less interaction with the dissociated O* atoms. These results introduce a future platform where the ambient condition stability can be tuned via chemical modification strategies by varying the composition, doping percentage and synergistic methods with protective measures as well.
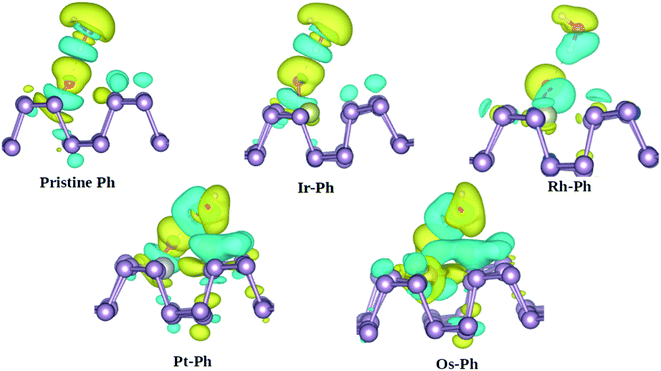
Another important degradation pathway for phosphorene is via the interaction with H2O. Previous reports showed that although phosphorene displays fairly strong hydrophobicity towards H2O, the oxygen-bonded phosphorene is vulnerable to water-catalyzed oxidation.54,55 Herein, we analyzed the interaction of water with the O*-bonded TM–Ph systems, using pristine phosphorene as the reference system. The charge density difference analysis of the H2O interaction with O* bonded to the P atoms of the TM–Ph systems is represented in Fig. 9.
From Fig. 9, it can be understood that although Ir–Ph showed a similar hydrogen bonding interaction to that of pristine phosphorene, Rh–Ph showed less interaction with the charges mainly located within water and the O* species only. The interactions of both Pt–Ph and Os–Ph with H2O involved contributions from the TM atoms as well, and spread over a larger number of P atoms across the upper plane of phosphorene. This indicates that, except for Ir–Ph, all TM–Ph systems exhibited a different extent of interaction with H2O. Rh–Ph exhibited a diminished charge transfer, which suggests the plausibility of controlling the H2O affinity of oxidized phosphorene via chemical modification.
4. Conclusion
We systematically carried out a study of the catalytic activity of transition metal-doped single atom catalysts (TM–Ph SACs) towards important catalytic reactions, such as ORR, OER and HER. The stability analysis via binding energy, dissolution potential and electronic structure analysis confirmed that all TM–Ph SACs (except Ag–Ph) exhibited excellent stability in withstanding the electrochemical conditions. We also observed a breaking of the scaling relationship between the O* and OH* free energy of adsorption, which arises from the differences in the covalent characters attained by the respective species across the SAC series. The free energy analysis suggest that Ir–Ph:Rh–Ph, Pt–Ph:Os–Ph and Pt–Ph:Co–Ph are the most active catalyst systems towards ORR, OER and HER, respectively. The 3d series based SACs, Ni–Ph and Co–Ph, were also found to be active catalysts for 2e− ORR. The ambient condition stability analysis focused on the interactions of TM–Ph SACs with O2 and H2O, suggesting that these interactions can be tuned by incorporating TM atoms into pristine phosphorene. Alternative strategies based on this observation may be developed in the future.Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
The authors acknowledge computing resources from the Swedish National Infrastructure for Computing (SNIC) at NSC and HPC2N. We thank IIT Indore for providing the lab/computational facilities and SPARC (SPARC/2018-2019/P116/S), DSTS SERB (CRG/2018/001131), Swedish Research Council (VR/2019-05317) for funding. A. S. N. thanks the Ministry of Human Resources and Development, India for a research fellowship.References
- L. Liu and A. Corma, Chem. Rev., 2018, 118, 4981–5079 CrossRef CAS PubMed.
- Y. Du, H. Sheng, D. Astruc and M. Zhu, Chem. Rev., 2020, 120, 526–622 CrossRef CAS PubMed.
- I. E. Stephens, A. S. Bondarenko, U. Grønbjerg, J. Rossmeisl and I. Chorkendor, Energy Environ. Sci., 2012, 5, 6744–6762 RSC.
- X.-F. Yang, A. Wang, B. Qiao, J. Li, J. Liu and T. Zhang, Acc. Chem. Res., 2013, 46, 1740–1748 CrossRef CAS PubMed.
- H. Zhang, G. Liu, L. Shi and J. Ye, Adv. Energy Mater., 2018, 8, 1701343 CrossRef.
- A. Wang, J. Li and T. Zhang, Nat. Rev. Chem., 2018, 2, 65–81 CrossRef CAS.
- W. Liu, L. Zhang, W. Yan, X. Liu, X. Yang, S. Miao, W. Wang, A. Wang and T. Zhang, Chem. Sci., 2016, 7, 5758–5764 RSC.
- P. Xie, T. Pu, A. Nie, S. Hwang, S. C. Purdy, W. Yu, D. Su, J. T. Miller and C. Wang, ACS Catal., 2018, 8, 4044–4048 CrossRef CAS.
- T. Sun, L. Xu, D. Wang and Y. Li, Nano Res., 2019, 1–14 Search PubMed.
- J. Lin, A. Wang, B. Qiao, X. Liu, X. Yang, X. Wang, J. Liang, J. Li, J. Liu and T. Zhang, J. Am. Chem. Soc., 2013, 135, 15314–15317 CrossRef CAS PubMed.
- M. F. Stephanopoulos, Acc. Chem. Res., 2013, 47, 783–792 CrossRef PubMed.
- T. R. Reina, S. Ivanova, M. Centeno and J. A. Odriozola, Catal. Today, 2015, 253, 149–154 CrossRef CAS.
- D.-W. Jeong, V. Subramanian, J.-O. Shim, W.-J. Jang, Y.-C. Seo, H.-S. Roh, J. H. Gu and Y. T. Lim, Catalysis letters, 2013, 143, 438–444 CrossRef CAS.
- Y. Zheng, Y. Jiao, Y. Zhu, Q. Cai, A. Vasile, L. H. Li, Y. Han, Y. Chen and S.-Z. Qiao, J. Am. Chem. Soc., 2017, 139, 3336–3339 CrossRef CAS PubMed.
- R.-Q. Zhang, T.-H. Lee, B.-D. Yu, C. Stamp and A. Soon, Phys. Chem. Chem. Phy., 2012, 14, 16552–16557 RSC.
- N. Cheng, S. Stambula, D. Wang, M. N. Banis, J. Liu, A. Riese, B. Xiao, R. Li, T.-S. Sham, L.-M. Liu, G. A. Botton and X. Sun, Nat. Comm., 2016, 7, 13638 CrossRef CAS.
- S. K. Sahoo, Y. Ye, S. Lee, J. Park, H. Lee, J. Lee and W. Han, ACS Ener. Lett., 2018, 4, 126–132 CrossRef.
- X. Mao, L. Zhang, G. Kour, S. Zhou, S. Wang, C. Yan, Z. Zhu and A. Du, ACS Appl. Mater. Interfa., 2019, 11, 17410–17415 CrossRef CAS PubMed.
- X. Mao, G. Kour, C. Yan, Z. Zhu and A. Du, J. Phys. Chem. C, 2019, 123, 3703–3710 CrossRef CAS.
- X. Mao, C. Ling, C. Tang, C. Yan, Z. Zhu and A. Du, J. Catal., 2018, 367, 206–211 CrossRef CAS.
- H. Liu, A. T. Neal, Z. Zhu, Z. Luo, X. Xu, X. Tománek and P. D. Ye, ACS Nano, 2014, 8, 4033–4041 CrossRef CAS PubMed.
- A. C.- Gomez, J. Phys. Chem. Let., 2015, 6, 4280–4291 CrossRef.
- J. Qiao, X. Kong, Z.-X. Hu, F. Yang and W. Ji, Nat. Comm., 2014, 5, 4475 CrossRef CAS PubMed.
- H. Liu, Y. Du, Y. Deng and D. Y. Peide, Chem. Soc. Rev., 2015, 44, 2732–2743 RSC.
- L. Li, Y. Yu, G. J. Ye, Q. Ge, X. Ou, H. Wu, D. Feng, X. H. Chen and Y. Zhang, Nature nanotechnology, 2014, 9, 372 CrossRef CAS PubMed.
- H. Tian, B. Deng, M. L. Chin, X. Yan, H. Jiang, S. J. Han, V. Sun, Q. Xia, M. Dubey, F. Xia and H. Wang, ACS Nano, 2016, 10, 10428–10435 CrossRef CAS PubMed.
- D. K. Sang, H. Wang, Z. Guo, N. Xie and H. Zhang, Adv. Funct. Mater., 2019, 29, 1903419 CrossRef CAS.
- Q. Li, Q. Zhou, L. Shi, Q. Chen and J. Wang, J. Mater. Chem. A, 2019, 7, 4291–4312 RSC.
- M. Akhtar, G. Anderson, R. Zhao, A. Alruqi, J. E. Mroczkowska, G. Sumanasekera and J. B. Jasinski, npj 2D Mater. Appl., 2017, 1, 1–13 CrossRef.
- J. Zhang, H. Shin and W. Lu, Chem. Comm., 2019, 55, 2601–2604 RSC.
- X. Ren, J. Zhou, X. Qi, X. Liu, Z. Huang, Z. Li, Y. Ge, S. Chander, D. Joice, S. Ponraj, S. Wang, J. Zhong and H. Zhang, Adv. Funct. Mater., 2017, 7, 1700396 Search PubMed.
- X.-X. Xue, S. Shen, X. Jiang, P. Sengdala, K. Chen and Y. Feng, J. Phys. Chem. Lett., 2019, 10, 3440–3446 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251 CrossRef CAS.
- J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671 CrossRef CAS PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- A. Hashmi and J. Hong, J. Phys. Chem. C, 2015, 119, 9198–9204 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- K. Mathew, R. Sundararaman, K. Letchworth-Weaver, T. Arias and R. G. Hennig, J. Chem. Phys., 2014, 140, 084106 CrossRef PubMed.
- R. Dronskowski and P. E. Blöchl, J. Phys. Chem. C, 1993, 97, 8617–8624 CrossRef CAS.
- F. Banhart, J. Kotakoski and A. V. Krasheninnikov, ACS Nano, 2010, 5, 26–41 CrossRef PubMed.
- Y. Singh, S. Back and Y. Jung, Phys. Chem. Chem. Phys., 2018, 20, 21095–21104 RSC.
- B. Garlyyev, J. Fichtner, O. Piqué, O. Schneider, A. S. Bandarenka and F. Calle-Vallejo, Chem. Sci., 2019, 10, 8060–8075 RSC.
- W.-L. Li, C. Ertural, D. Bogdanovski, J. Li and R. Dronskowski, Inorg. Chem., 2018, 57, 12999–13008 CrossRef CAS PubMed.
- F. Calle-Vallejo, A. Krabbe and J. M. García-Lastra, Chem. Sci., 2017, 8, 124–130 RSC.
- J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jonsson, J. Phys. Chem. B, 2004, 108, 17886–17892 CrossRef.
- I. C. Man, H.-Y. Su, F. Calle-Vallejo, H. A. Hansen, J. I. Martnez, N. G. Inoglu, J. Kitchin, T. F. Jaramillo, J. K. Nørskov and J. Rossmeisl, ChemCatChem, 2011, 3, 1159–1165 CrossRef CAS.
- S. C. Perry, D. Pangotra, L. Vieira, L.-I. Csepei, V. Sieber, L. Wang, C. P. de León and F. C. Walsh, Nat. Rev. Chem., 2019, 3, 442–458 CrossRef CAS.
- A. Kulkarni, S. Siahrostami, A. Patel and J. K. Nørskov, Chem. Rev., 2018, 118, 2302–2312 CrossRef CAS PubMed.
- A. Mahata and B. Pathak, Nanoscale, 2017, 9, 9537–9547 RSC.
- S. Siahrostami, A. Verdaguer-Casadevall, M. Karamad, D. Deiana, P. Malacrida, B. Wickman, M. Escudero-Escribano, E. Paoli, R. Frydendal and T. W. Hansen, et al. , Nat. Mater., 2013, 12, 1137–1143 CrossRef CAS PubMed.
- Y. Abghoui and E. Skúlason, J. Phys. Chem. C, 2017, 121, 24036–24045 CrossRef CAS.
- J. K. Nørskov, T. Bligaard, A. Logadottir, J. R. Kitchin, J. G. Chen, S. Pandelov and U. Stimming, J. Elec. Chem. Soc., 2005, 152, 23–26 CrossRef.
- A. Ziletti, A. Carvalho, D. K. Campbell, D. F. Coker and A. C. Neto, Phys. Rev. Lett., 2015, 114, 046801 CrossRef CAS PubMed.
- G. Wang, W. J. Slough, R. Pandey and S. P. Karna, 2D Materials, 2016, 3, 025011 CrossRef.
- Q. Zhou, Q. Chen, Y. Tong and J. Wang, Angew. Chem. Int. Ed., 2016, 55, 11437–11441 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Structural details of the transition metal-doped phosphorene SACs, dissolution potential results of the TM–Ph SACs, O2 adsorption details, projected density of states (PDOS) analysis of the TM–Ph SACs, projected density of states (PDOS) analysis of O2 binding to Fe–Ph SAC, bond length analysis for O2 binding on TM–Ph SACs, structural details of the ORR intermediate binding, charge transfer and ICOHP analysis, ORR free energy diagrams of Ir–Ph SAC of thickness 2ML and 3ML, AIMD simulation of active TM–Ph SACs, details of O2 interaction with P atoms of TM–Ph SACs. See DOI: 10.1039/d0na00209g |
| This journal is © The Royal Society of Chemistry 2020 |