Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Mechanism of CO2 conversion to methanol over Cu(110) and Cu(100) surfaces
Michael D.
Higham
 *ab,
Matthew G.
Quesne
*ab,
Matthew G.
Quesne
 ab and
C. Richard A.
Catlow
ab and
C. Richard A.
Catlow
 abc
abc
aResearch Complex at Harwell, Rutherford Appleton Laboratory, Harwell Oxford, Didcot, Oxon, OX11 0FA, UK. E-mail: highamm@cardiff.ac.uk
bCardiff University, School of Chemistry, Main Building, Park Place, Cardiff, CF10 3AT, UK
cKathleen Lonsdale Materials Chemistry, Department of Chemistry, University College London, 20 Gordon Street, London WC1H 0AJ, UK
First published on 4th May 2020
Abstract
Density functional methods are applied to explore the reaction mechanism for CO2 hydrogenation to methanol over low-index Cu surfaces, namely Cu(110) and Cu(100). A detailed reaction network is obtained, examining several different possible mechanistic routes, including methanol formation via formate and hydrocarboxyl bound intermediates, the role of formaldehyde and formic acid as stable intermediary reaction products, as well as exploring the possibility of CO2 dissociation and subsequent hydrogenation of the resultant CO. We find that, in contrast to the dominant Cu(111) facet, the Cu(110) and Cu(100) surfaces facilitate a moderate extent of CO2 activation, which results in lower activation barriers for initial elementary processes involving CO2 hydrogenation and dissociation, opening up reaction pathways considered unfeasible for Cu(111). Consequently, a wider variety of potential mechanistic routes to achieve methanol synthesis is observed and compared to Cu(111), illustrating the essential role of the Cu surface structure in catalytic activity, and providing insights into the mechanism of CO2 hydrogenation over Cu-based catalysts. In providing a thorough and detailed exploration of all of the possible mechanistic pathways for CO2 conversion to methanol, the present work represents a reference point for future studies investigating systems representative of the industrial Cu/ZnO catalyst, enabling a clear identification of the limitations of unsupported Cu catalysts, and thus allowing a more complete understanding of the role of the support material.
Introduction
Use of fossil fuels such as coal, oil, and gas, has long been established as a major cause of pollution and global warming, as it results in large quantities of CO2 and other pollutant gases being released into the atmosphere. As such, new technologies that aim to utilise atmospheric CO2 in order to reduce its environmental impact are essential in the transition from dependence on fossil fuels towards sustainable alternatives. One such avenue relies on the production of methanol (CH3OH) from CO2 derived from waste emissions and from atmospheric sources, and sustainably generated hydrogen (H2) obtained from efficient water splitting processes, powered by photocatalysis or electricity produced from renewable sources. As well as itself being a valuable industrial product, CH3OH derived from atmospheric CO2 could serve as a renewable, carbon neutral fuel source, essentially mirroring nature's photosynthetic carbon cycle.1 Moreover, as a highly energy dense combustible fuel, CH3OH can also be used to generate electricity via the direct methanol fuel cell2 which could ultimately replace the internal combustion engine. As such, catalytic methods for methanol synthesis are at the forefront in efforts to utilise waste CO2.Copper-based catalysts are the most widely used systems for the industrial conversion of CO2 to methanol, with the Cu/ZnO/Al2O3 catalyst being particularly widely used, having been in use since 1966, primarily for the catalytic conversion of syngas to methanol, when a new co-precipitation technique enabled the production of a highly efficient catalyst, considerably more so than earlier ZnO/Al2O3 catalysts, whilst also avoiding the rapidly sintering observed in earlier attempts to produce Cu-containing catalysts.3 In addition to the Cu/ZnO/Al2O3 catalyst being used for syngas conversion to methanol, the catalyst can also be used for CO2 hydrogenation. Indeed, previous experimental studies strongly suggest that CO2 is the key reactant for methanol production from syngas.3 However, despite this widespread use, much remains to be understood regarding the precise role of the components of the industrial catalyst, and how these roles manifest themselves in terms of the catalyst surface structure and the mechanism by which methanol conversion takes place. Initial hypotheses proposed a “synergistic” argument that supposed the existence of a property unique to the Cu/ZnO system that accounted for the considerably improved activity compared to its constituent components, as shown by extensive studies comparing catalytic activity against composition, and thus identifying an optimal Cu![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ZnO ratio.4,5 On the other hand, there is experimental evidence suggesting that maximising Cu surface area is the primary role of the support; indeed, such studies revealed a linear relationship between activity and Cu surface area for a wide range of different support materials,6 with Cu/SiO2 being observed to be the most active catalyst, but also suffering from rapid sintering, preventing its adoption as an industrial catalyst, and the low activity of unsupported Cu being attributed to a low surface area to mass ratio, compared to the supported catalysts. Evidently, there is much that remains unclear regarding the origin of the remarkable activity exhibited by Cu/ZnO catalysts.
ZnO ratio.4,5 On the other hand, there is experimental evidence suggesting that maximising Cu surface area is the primary role of the support; indeed, such studies revealed a linear relationship between activity and Cu surface area for a wide range of different support materials,6 with Cu/SiO2 being observed to be the most active catalyst, but also suffering from rapid sintering, preventing its adoption as an industrial catalyst, and the low activity of unsupported Cu being attributed to a low surface area to mass ratio, compared to the supported catalysts. Evidently, there is much that remains unclear regarding the origin of the remarkable activity exhibited by Cu/ZnO catalysts.
Previous computational studies7,8 examining unsupported Cu as a catalyst for CO2 hydrogenation to methanol have focused on the Cu(111) facet, as it is the most stable low-index surface and is the dominant surface for polycrystalline copper, as predicted from the surface energies for the low-index Cu surfaces via the Wulff method.9–11 Other higher index facets, resembling stepped defective pristine low-index surfaces and edge regions of polycrystalline nanoparticles, have also been the subject of similarly detailed experimental and computational studies, such as the Cu(211)12–14 and Cu(321) facets.15 Clearly, the high activity of such Cu surface morphologies reported in such studies provides valuable insights for understanding the experimentally observed activity of Cu, and indeed one might expect intuitively that such surfaces, featuring low coordinated Cu atoms, would be highly active. However, in polycrystalline Cu samples such surface structures are likely to account only for a very small fraction of total Cu surface area, being more reflective of Cu particle edges than surface planes which consist mostly of the low index Cu(111), Cu(100), and Cu(110) facets. Compared to Cu(111) and the previously mentioned higher index surfaces, considerably less attention has been devoted to the other low-index facets, namely Cu(110), and Cu(100); computational studies investigate the related forward and reverse water–gas shift reactions,16 but are not reported for the methanol synthesis reaction. The Cu(110) and Cu(100) facets are only slightly less stable than Cu(111) and form the remainder of the surface of the Wulff nanoparticle. Hence, it is of great interest to explore the reaction mechanism for methanol synthesis over the Cu(110) and Cu(100) surfaces, in order to assess more completely the role of Cu as a catalyst for this particular reaction. Previous experimental studies reveal that the Cu(100) and Cu(110) surfaces have significant activity towards methanol synthesis, and more so than the most stable Cu(111) facet, reflecting structure sensitivity of this catalytic process,17–20 and warranting a detailed mechanistic overview, which is moreover necessary for a comprehensive overview of the role of copper in this key reaction. Moreover, the insights obtained will pave the way for a greater understanding of the precise role of the ZnO support in the industrially relevant catalyst by understanding more fully the strengths and limitations of the unsupported Cu-only catalyst, investigating the extent to which Cu(110) and Cu(100) facets might be expected to contribute to methanol synthesis activity and exploring the overall reaction mechanism over these surfaces. In this study, 25 distinct elementary processes potentially involved in methanol synthesis over Cu(110) and Cu(100) are explored for each surface from a computational perspective, investigating CO2 activation, dissociation, and hydrogenation of both CO and CO2via a range of intermediate species. The results reveal that, unlike the dominant Cu(111) facet, Cu(110) and Cu(100) surfaces are capable of activating CO2 sufficiently so to reduce considerably activation barriers for CO2 hydrogenation and dissociation processes, compared to that calculated for Cu(111) by previous studies.7,8 Consequently, a greater variety of possible reaction mechanisms are relevant for CO2 hydrogenation over these low index surfaces. The calculations presented in this article shed light on possible means by which supported Cu catalysts may improve upon Cu-only catalysts by identifying elementary processes which provide a common bottleneck to CO2 hydrogenation for all low index Cu facets. The detailed investigation of several different possible reaction pathways for methanol synthesis presented in this study furthermore provides a foundation for future studies investigating other catalysts for methanol synthesis beyond the Cu-based catalysts which are the focus of our investigation. The complete mechanistic analysis presented here not only illuminates the mechanism for the experimentally reported CO2 conversion to methanol over unsupported Cu catalyst surfaces,17–20 but will additionally serve as a valuable reference study for future investigations concerning other, related catalysts, for the same process, enabling a clear identification of the limitations of unsupported Cu catalysts, and allowing deeper insights into the behaviour of complex multi-component catalyst, and the specific roles of individual component materials.
Computational details
All calculations were performed using plane-wave density functional theory (DFT) as implemented in the VASP code (version 5.4.4).21–24 Slab models for the Cu(110) and Cu(100) facets were constructed consisting of six Cu layers separated by 18 Å of vacuum, ensuring sufficient slab separation to avoid any interaction between surfaces in adjacent periodic images. The top four layers of the slab were allowed to relax, whilst the bottom two were fixed at their bulk lattice positions. Whilst previous computational works examining low-index Cu surfaces used smaller Cu slab models consisting of fewer Cu layers,7,8 it has been noted that greater slab thicknesses might be required to obtain properly converged surface energies,25 and it has been observed that for the minority Cu low-index surfaces, the calculated surface energy is more sensitive to the slab thickness than for the most stable Cu(111) facet. Hence, the 6-layer slab model employed in this study ensures that any such problems are avoided. A dipole correction was applied to the vacuum to eliminate any spurious electrostatic interaction originating from the asymmetric relaxation of the slab. For the purposes of modelling adsorption and reaction processes, for the Cu(110) surface model a p(3 × 3) supercell was used, whilst for the Cu(100) surface model a p(2 × 2) supercell was used, resulting in two slabs of comparable size (54 and 48 Cu atoms, respectively), and allowing for sufficient separation between adsorbates in adjacent periodic images. A Monkhorst–Pack k-point sampling scheme was used,26 with k-point meshes of (3 × 2 × 1) and (4 × 4 × 1) used for the Cu(110) and Cu(100) surface supercells, respectively, commensurate with the cell dimensions. Inner electrons were replaced by projector-augmented waves (PAW),27,28 and the valence states were expanded in plane-waves with a cut-off energy of 450 eV. The PBE exchange correlation functional was used throughout,29 with a dispersion correction applied using the D2 scheme devised by Grimme,30 in order to account for the weak van der Waals interactions that are key to determining the physisorption behaviour of species relevant to methanol synthesis, such as CO2. Additionally, no corrections were made to account for vibrational zero-point energies, since it is expected that any such contribution would be negligible relative to the calculated electronic energy, since in surface catalysis adsorption removes many of the degrees of freedom associated with reactions in vacuum.In order to investigate the elementary reaction processes taking place on the Cu(110) and Cu(100) surfaces during CO2 conversion, optimised geometries were obtained for all adsorbed reactants, products, and intermediates, with atomic forces converged to within 0.01 eV Å−1. In each case, electronic wavefunctions were converged such that the total energy was converged to within 10−5 eV. Transition states were identified using the climbing image nudged elastic bands (CI-NEB) method,31 with vibrational analysis confirming that a saddle point had indeed been located. For transition states not converged using the CI-NEB method, the improved dimer method (IDM)32,33 was applied to refine transition states with atomic forces converged to within 0.03 eV Å−1.
Results
CO2 adsorption and activation
For each of the three low-index Cu surface, Cu(111), Cu(110), and Cu(100), CO2 adsorption was explored, with the results collected in Table 1. In all cases, CO2 adsorption was modestly exothermic, with calculated adsorption energies being in the range of 0.14 eV to 0.39 eV, consistent with CO2 physisorption. The calculated CO2 adsorbate geometries reveal no significant changes compared to gas phase CO2, further supporting the presence of a physisorbed CO2 species.| Cu facet | E ads./eV | d (Cu–C)/Å | d (C–O)/Å | ∠ (O–C–O)/° |
|---|---|---|---|---|
| (111) | −0.353 | 3.41 | 1.18 | 179.45 |
| (110) | −0.148 | 3.49 | 1.18 | 179.40 |
| (100) | −0.391 | 3.43 | 1.18 | 179.20 |
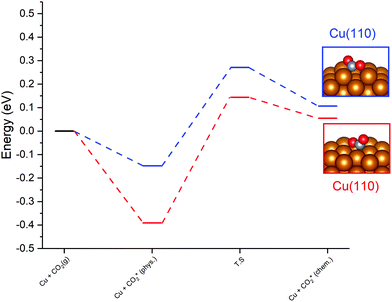
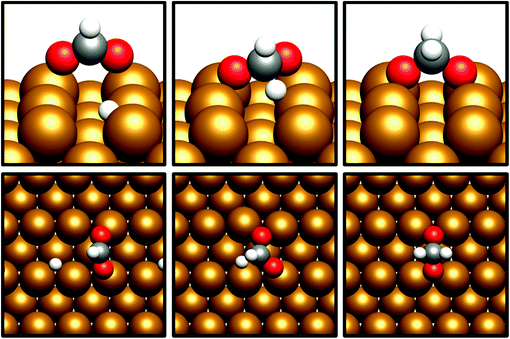
For the Cu(110) and Cu(100) facets, however, a second mode of CO2 adsorption was identified, featuring a significant distortion of the CO2 O–C–O angle (∠ (O–C–O) < 130°), implying a considerable weakening of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond and a degree of chemisorption behaviour with some electron transfer into the CO2 antibonding orbitals. For the Cu(111) facet, on the other hand, no such adsorption mode was identified. For both the Cu(110) and Cu(100) surfaces, a local minimum structure was identified, lying at a higher energy than the physisorbed species, but being only slightly unstable relative to gas phase CO2, by approximately 0.1 eV. The calculated energetics for the transition of physisorbed to chemisorbed CO2, along with calculated geometric data for the latter, are summarised in Table 2. For both the (110) and (100) surfaces, the chemisorbed CO2 molecule was found in a highly coordinated hollow surface site (see Fig. 1 for graphical depiction). In both cases, a distinct transition state was identified for the conversion of the physisorbed CO2 species to its chemisorbed counterpart, with activation energies of 0.42 eV and 0.54 eV being determined for the Cu(110) and Cu(100) surfaces, respectively, with a considerable reduction of approximately 1.5 Å in the Cu–C distance occurring during this transition, and an accompanying lengthening of the C–O bonds. Fig. 1 graphically summarises the relative energies associated with gas phase CO2, the physisorbed and chemisorbed CO2 species, and the transition state linking the two modes of adsorption.
O bond and a degree of chemisorption behaviour with some electron transfer into the CO2 antibonding orbitals. For the Cu(111) facet, on the other hand, no such adsorption mode was identified. For both the Cu(110) and Cu(100) surfaces, a local minimum structure was identified, lying at a higher energy than the physisorbed species, but being only slightly unstable relative to gas phase CO2, by approximately 0.1 eV. The calculated energetics for the transition of physisorbed to chemisorbed CO2, along with calculated geometric data for the latter, are summarised in Table 2. For both the (110) and (100) surfaces, the chemisorbed CO2 molecule was found in a highly coordinated hollow surface site (see Fig. 1 for graphical depiction). In both cases, a distinct transition state was identified for the conversion of the physisorbed CO2 species to its chemisorbed counterpart, with activation energies of 0.42 eV and 0.54 eV being determined for the Cu(110) and Cu(100) surfaces, respectively, with a considerable reduction of approximately 1.5 Å in the Cu–C distance occurring during this transition, and an accompanying lengthening of the C–O bonds. Fig. 1 graphically summarises the relative energies associated with gas phase CO2, the physisorbed and chemisorbed CO2 species, and the transition state linking the two modes of adsorption.
| Process no. | Cu facet | ΔE/eV | E a/eV | v/cm−1 | d (Cu–C)/Å | d (C–O)/Å | ∠ (O–C–O)/° |
|---|---|---|---|---|---|---|---|
| 1 | (110) | 0.254 | 0.419 | 190.97 | 1.998 | 1.27, 1.27 | 127.53 |
| 1 | (100) | 0.446 | 0.535 | 181.67 | 2.141 | 1.22, 1.33 | 128.45 |
Bader charge analysis was also performed to determine the extent to which the observed CO2 distortion is accompanied by charge transfer which might indicate the extent of activation. For both Cu(110) and Cu(100), a moderate degree of charge transfer was discovered for the bent chemisorbed CO2 species, with the respective excess Bader charges calculated as β = 0.77 and β = 0.76, compared to β = 0.07 and β = 0.06 for the physisorbed species. Hence, an increase in charge localisation of 0.70e− is evident as a result of the transition from the physisorbed to the chemisorbed CO2; in both cases the charge accumulation on CO2 was primarily localised on the C atom. For both Cu(110) and Cu(100), this charge accumulation on C was accompanied by slight oxidation of the Cu atoms coordinated with the activated CO2 species. Hence, charge transfer from the Cu surface to the adsorbate is demonstrated, in agreement with the proposal that electron transfer from the Cu surface to the CO2 antibonding orbitals is responsible for the resulting changes in CO2 adsorption geometry. Clearly, the chemisorbed bent CO2 species is activated by both of these low-index Cu facets, and can be assumed to promote subsequent reaction processes such as hydrogenation or dissociation to CO and O, which are explored later in this study.
The limited activation of CO2 over Cu(111) compared to other low-index surfaces has been documented in past experimental17,34 and computational35,36 studies, with both Yoshihara et al.17 and Wang et al.35 proposing that CO2 activation over low-index Cu surfaces follows the order Cu(110) > Cu(100) > Cu(111). This conclusion is consistent with the results obtained in this study, with no activation of CO2 detected for Cu(111), and a more kinetically accessible activated CO2 for Cu(110) compared to Cu(100). Whilst Wang et al. explored both periodic and cluster models to represent the Cu surfaces, it was found that the lack of inclusion of weak dispersion forces in their periodic approach (as the method devised by Grimme applied in the present work was not developed until two years after the publication of Wang et al.) limited the utility of the periodic slab model, as such interactions are key to modelling CO2 physisorption. However, the present work combines a periodic slab model (which more accurately represents the extended natures of real Cu surfaces than a cluster model) with a dispersion correction and arrives a largely similar conclusion in terms of the ordering of each of the Cu surfaces according to the extent to which they facilitate CO2 activation, corroborating the earlier computational results. Interestingly, previous computational studies investigating Cu(111) facets of an octahedral nanocluster, rather than a periodic surface, did identify a stable chemisorbed CO2 species, albeit with a more limited electron transfer of ∼0.4, as determined from Bader charge analysis.37 The enhanced CO2 adsorption and activation over such nanocluster facets can be attributed to the changes in electronic structure of metal atoms at nanoparticle edges, hence such behaviour is not observed for periodic Cu(111) surfaces or larger nanoparticle facets, reflecting the highly surface-sensitive nature of CO2 adsorption and activation on Cu facets. The results reported in the present study suggest a greater degree of activation than that reported by Wang et al. for the Cu(110) and Cu(100) facets, with a considerably greater deviation from the linear geometry of free CO2. Additionally, the Bader charge analysis confirms a modest degree of activation compared to previous computational studies exploring transition metal carbides which are known to be highly activating towards CO2;38 for physisorbed CO2, comparably small Bader charges were calculated for both the low-index Cu facets investigated in this study (β = 0.07 and β = 0.06, for Cu(110) and Cu(100), respectively), and metal carbides such as TiC, VC, ZrC and NbC (β = 0.06, β = 0.06, β = 0.12 and β = 0.07 for the facets of TiC, VC, ZrC and NbC, respectively, which exhibit the greatest extent of electron transfer to the physisorbed state38). However, for the chemisorbed species, the extent of charge transfer from the Cu substrate was considerably less than that calculated previously for the metal carbides, with the most activating carbide surfaces exhibiting Bader charge accumulation of β = 1.79, β = 1.12, β = 1.84 and β = 1.19 for TiC, VC, ZrC and NbC respectively, compared to only 0.7e− for both Cu(110) and Cu(100). For each of these metal carbides, the activated chemisorbed species is more stable than the physisorbed state; in particular, it is notable that the extent of electron transfer, as illustrated by the Bader charge analysis is strongly correlated with the stability of the chemisorbed state (Eads. = −3.05 eV, Eads. = −1.93 eV, Eads. = −3.32 eV and Eads. = −1.98 eV for TiC, VC, ZrC and NbC, respectively). In contrast with the metal carbides and in accordance with the observed trend correlating the extent of Bader charge accumulation on CO2 and the stability of the chemisorbed state, for the low-index Cu surfaces investigated in the present work, the chemisorbed state is slightly energetically unstable with respect to gas phase CO2, (as noted in Table 2) and thus expected to be a comparatively short-lived surface species before either undergoing subsequent reactive processes or reverting to the more stable physisorbed state. One can expect that CO2 desorption will more readily take place than any subsequent reaction process, given that it would appear to be kinetically unhindered, hence one might conclude that no further reaction, and indeed formation of methanol, would take place. However, it must be considered that the adsorption, activation, and desorption, of CO2, are essentially reversible processes, whereas it is likely that subsequent reaction processes, such as hydrogenation to formate or hydrocarboxyl will be considerably more exothermic, and thus irreversible (indeed this is reported in the present work). Hence, whilst CO2 adsorption may predominate, we cannot exclude at least partial, irreversible, consumption of CO2 to form hydrogenated intermediates, and ultimately methanol. Moreover, one the central aims of this study is to explore all mechanistic routes, hence it is essential to study subsequent reaction processes. Our results imply a significant degree of CO2 activation over low-index Cu surfaces, enabling the formation of a distinct local minimum adsorption geometry for Cu(110) and Cu(100), which may still enable CO2 to undergo hydrogenation to yield methanol. Indeed, even if the activated CO2 species are relatively short lived, and do not accumulate in appreciable quantity on the catalyst surface, this does not preclude such a species participating in subsequent elementary reaction processes as an intermediate between the more stable physisorbed CO2 species and the products of these processes (i.e. CO2 dissociation, or hydrogenation processes when H2 is present).
Consideration must also be given to previous experimental Raman, IR and HREELS studies, which suggest that Cu surface structure and annealing effects have a significant impact on whether the bent, activated CO2 species is observed, with such species being reported for rough Cu surface, but not for smooth annealed surfaces,39–41 while the results obtained in the present work only consider the pristine low-index Cu facets. However, rough surfaces will include a variety of facets and the observed activation of CO2 on such surfaces can be attributed to the two low index components.
Overall, there is considerable experimental evidence suggesting the possibility of an activated CO2 species being present on Cu surfaces, in agreement with the computational results presented here.17,34,39–41 Indeed, previous surface enhanced Raman spectroscopy (SERS) studies suggest the coexistence of both activated and non-activated CO2 species,39 reflecting the relatively close adsorption energies and low activation barriers to formation of the activated species calculated in the present work. As such, the remainder of this study will focus on only the Cu(110) and Cu(100) surfaces, which do exhibit the activated CO2 species, for subsequent dissociation and hydrogenation processes which are important for methanol synthesis.
H2 adsorption and dissociation
Given that CO2 activation appears to be exhibited by the Cu(110) and Cu(100) surfaces, the next prerequisite for CO2 hydrogenation is the dissociative adsorption of H2. Cu catalysts have long been known to be highly active towards H2 dissociation, which is consistent with the calculations performed in this study.42–45 The results in Table 3 show that for both Cu(110) and Cu(100), non-dissociative H2 physisorption was calculated to be very mildly exothermic, at −0.11 eV and −0.08 eV for Cu(110) and Cu(100), respectively. The most stable adsorption site for the H2 molecule is atop a Cu surface atom (Fig. 2), but other sites, namely bridging (short and long bridge sites for Cu(110)) and hollow adsorption sites, are close in energy. For both surfaces, the dissociated state was determined to have a lower energy with respect to the weakly physisorbed state, with adsorption energies of −0.32 eV for Cu(110) and −0.28 eV for Cu(100); in both cases, it can be seen that H2 dissociation is exothermic with respect to the physisorbed state by around 0.2 eV, consistent with the well-established role of Cu in facilitating H2 dissociation. For Cu(100), adsorbed H atoms had lower energies on surface hollow sites affording a highly coordinated adsorption environment, whereas for Cu(110), H atoms adsorbed at the short bridge sites were found to be most stable. Activation barriers were calculated for dissociation of physisorbed H2, with Ea calculated at 0.28 eV for Cu(110) and 0.52 eV for Cu(100), indicating that such a process is indeed energetically feasible. It is notable that the ease with which we expect H2 dissociation to occur correlates to high local hydrogen availability, facilitating CO2 hydrogenation. Previous computational studies investigating H2 dissociation as part of a study exploring the Cu(111) facet as a catalyst for CO2 hydrogenation to methanol did not consider H2 physisorption and the associated barrier for dissociation.8 However, it has been demonstrated that the inclusion of weak dispersion forces in simulations plays a key role in determining H2 physisorption behaviour;46 hence the inclusions of such a correction in the calculations in the present study is consistent with the observation of a weakly physisorbed H2 molecule preceding dissociation, accompanied by a modest activation barrier. Whilst the activation barrier for H2 dissociation may be greater than that for H2 desorption, it is clear from the calculated barriers for H2 dissociation that this process is energetically feasible, with a low barrier calculated for Cu(110) and a moderate barrier for Cu(100). Coupled with the exothermic H2 dissociation energy, it can be concluded that this overall process is under thermodynamic control, and that atomic H arising from H2 dissociation is likely to be present on the Cu surface, in line with the well-reported experimental observation of this process.42–45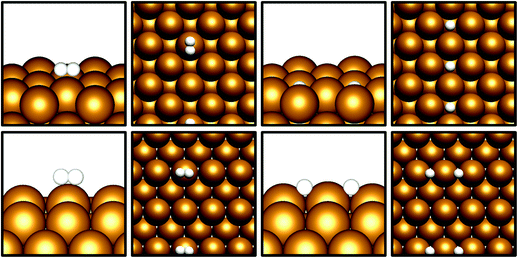 | ||
| Fig. 2 Graphical depiction from side and top view of physisorbed (left) and dissociated (right) H2, for Cu(100) (top) and Cu(110) (bottom). | ||
| Process no. | Cu facet | E ads. (phys.)/eV | ΔEdiss./eV | E a/eV | v/cm−1 |
|---|---|---|---|---|---|
| 2 | (110) | −0.113 | −0.210 | 0.284 | 811.542 |
| 2 | (100) | −0.083 | −0.197 | 0.517 | 1239.385 |
Pathways for CO2 conversion to methanol
Methanol synthesis from CO2 could take place via a variety of possible reaction pathways with a range of possible intermediates; the process necessarily involves the formation of three C–H bonds and one O–H bond, as well as the cleavage of one of the CO2 C–O bonds. However, there several different reaction pathways depending on the order in which these processes occur, giving rise to different intermediate species; the pathway featuring the most kinetically accessible and most stable intermediates will therefore be the most favourable. As such, this study considers several different approaches, involving direct hydrogenation of CO2* to either HCOO* or COOH*, as well as processes derived from CO2* dissociation and subsequent hydrogenation of the resulting CO*. Intermediate species considered include HCOOH*, H2CO*, H2COO*, H2COOH*, CH2OH*, and CH3O*, the latter two being the penultimate adsorbed species before methanol formation. The relation between these intermediates and the reaction processes linking them is summarised in Fig. 3. The subsequent sections will address each reaction process sequentially, before we finally consider H2O formation which is a by-product of methanol synthesis from CO2.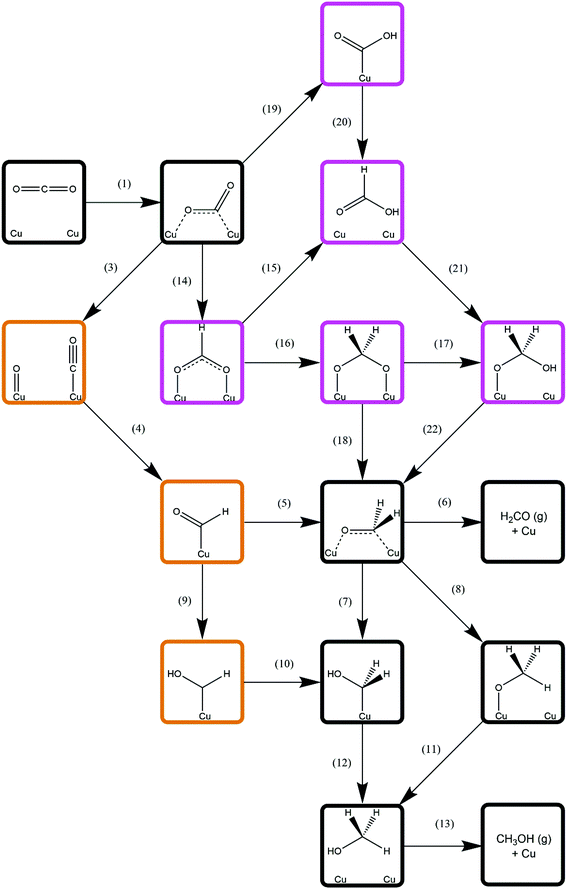 | ||
| Fig. 3 Simplified schematic depicting possible reaction pathways for methanol synthesis from CO2. For clarity, only processes involving C-containing species are show; H2 dissociation (process 2, Table 3) and elementary reaction processes involving H2O formation (processes 23–25, Table 9) are omitted and are common to all possible reaction pathways. Intermediates associated exclusively with CO2 hydrogenation are highlighted in purple; those associated exclusively with CO hydrogenation are highlighted in orange; and intermediates common to both pathways are indicated by black borders. Numbers adjacent to arrows representing elementary processes correspond to the process number labels for each unique process as listed in the results tables. | ||
CO2 dissociation to CO + O
We explore first the pathway involving CO2 dissociation, and indeed, past studies identified the presence of an activated CO2 species as a precursor to CO2 dissociation.39,47 Furthermore, a series of experimental studies utilising low-energy electron diffraction (LEED), Auger electron spectroscopy (AES) and ellipsometry techniques report CO oxidation to CO2 by pre-adsorbed surface oxygen (i.e. the reverse of CO2 dissociation) for all three low-index Cu surfaces.34,48–50 However, the absence of an activated, bent CO2 species for Cu(111) makes the reverse dissociation process unlikely for this surface, (which indeed is found to be the case from experimental34,51 and computational52 studies), but, owing to its formation on Cu(110) and Cu(100), CO2 dissociation to CO on these facets is clearly feasible. This notion is further corroborated by previous computational studies which provide evidence for the involvement of a bent CO2 intermediate in CO oxidation over Cu(110).36 Additionally, previous computational electrocatalysis studies exploring Cu(100) electrodes suggest that CO is a possible intermediate in not only methanol synthesis, but also the formation of higher alcohols and hydrocarbons.53,54 Whilst a detailed investigation of the formation of these products lies beyond the scope of the present work, the previous results nonetheless indicate that CO hydrogenation, and by extension CO2 dissociation, is worthy of investigation. Our calculated results for CO2 dissociation are tabulated in Table 4. For both cases, accessible transitions states were identified, with activation barriers of 0.79 eV and 0.71 eV calculated for Cu(110) and Cu(100), respectively. Whilst CO2 dissociation over Cu(100) was found to be very slightly exothermic (−0.08 eV), the corresponding process for Cu(110) was determined to be endothermic by 0.52 eV.| Process no. | Cu facet | ΔE/eV | E a/eV | v/cm−1 | d (C–O) (TS)/Å |
|---|---|---|---|---|---|
| 3 | (110) | 0.520 | 0.792 | 182.416 | 2.032 |
| 3 | (100) | −0.083 | 0.711 | 319.611 | 1.943 |
Clearly, the calculated activation barriers for CO2 dissociation make this possibility distinctly feasible. In particular, there is good agreement with experimental TPD studies conducted on Cu(100) which confirm that CO2 dissociation readily occurs.55 For the Cu(110) facet, the experimental perspective is less clear, with contradictory reports regarding the presence of adsorbed O originating from CO2 dissociation.51 Nonetheless, the calculated dissociation energies reproduce the relative order of the activities of these two Cu surfaces, with the Cu(100) facet being more active for CO2 dissociation than the Cu(110) surface. The calculated activation barriers agree well with previous computational studies,16 which identify both Cu(100) and Cu(110) as being active for CO2 dissociation, although the calculated activation barriers were determined to be lower in this study, more so for Cu(100). An important consideration is the overall thermodynamic driving force for CO2 dissociation; whilst not detecting any significant CO2 dissociation under UHV conditions over Cu(110), Nakamura et al.51 identify the thermodynamic driving force for this process as being strongly determined by the loss of translational and rotational entropy resulting from CO2 dissociative adsorption. However, it must be considered that under hydrogenation conditions, this effect may be mitigated by subsequent hydrogenation of CO to methanol and adsorbed O to water, which may then be desorbed to the gas phase. As such, the energetic barrier to CO2 dissociation is probably the more important factor, as at least according to the computational results derived in this study, such a process could quite feasibly form part of the overall reaction pathway for CH3OH formation over Cu(100) and Cu(110). Hence, in the following sections, possible hydrogenation pathways for methanol synthesis from both CO and CO2 will be considered.
CO hydrogenation to methanol
Having established the possibility of CO2 dissociation leading to the presence of CO on Cu(110) and Cu(100) surfaces, along with the feasibility of H2 dissociation to yield H*, hydrogenation of CO to yield methanol is now considered, with the calculated results being presented in Tables 5 and 6 for Cu(110) and Cu(100), respectively. Hydrogenation can take place at either O or C; the former process was investigated briefly and was found to be unfeasible, with high activation barriers of 1.66 eV for Cu(110) and 1.92 eV for Cu(100). As such, this process and subsequent hydrogenation of the resulting COH* intermediate was not considered as a possible mechanistic pathway for methanol synthesis. The latter process, with hydrogenation taking place at C, was, however, found to have much lower activation barriers for both of the Cu surfaces investigated. The first hydrogenation step yields a formyl HCO* species (process 4, Tables 5 and 6); the calculated activation energies were comparable with values of 1.08 eV (process 4, Table 5) and 1.11 eV (process 4, Table 6) obtained, along with endothermic reaction energies of 0.66 (process 4, Table 5) and 0.74 (process 4, Table 6), for Cu(110) and Cu(100), respectively.| Process no. | Elementary process | ΔE/eV | E a/eV | v/cm−1 |
|---|---|---|---|---|
| HCO* formation | ||||
| 4 | CO* + H* → HCO* | +0.660 | 1.076 | 1044.590 |
| H 2 CO formation, desorption and hydrogenation | ||||
| 5 | HCO* + H* → H2CO* | −0.597 | 0.109 | 644.746 |
| 6 | H2CO* → H2CO(g) | +0.986 | — | — |
| 7 | H2CO* + H* → CH2OH* | +0.087 | 0.963 | 927.927 |
| 8 | H2CO* + H* → CH3O* | −0.622 | 0.388 | 328.280 |
| HCOH formation and hydrogenation | ||||
| 9 | HCO* + H* → HCOH* | −0.095 | 0.496 | 1164.784 |
| 10 | HCOH* + H* → CH2OH* | −0.339 | 0.284 | 818.827 |
| CH 3 OH formation and desorption | ||||
| 11 | CH3O* + H* → CH3OH* | −0.004 | 0.960 | 926.043 |
| 12 | CH2OH* + H* → CH3OH* | −0.705 | 0.604 | 610.080 |
| 13 | CH3OH* → CH3OH(g) | +0.771 | — | — |
| Process no. | Elementary process | ΔE/eV | E a/eV | v/cm−1 |
|---|---|---|---|---|
| HCO* formation | ||||
| 4 | CO* + H* → HCO* | +0.737 | 1.116 | 959.849 |
| H 2 CO formation, desorption and hydrogenation | ||||
| 5 | HCO* + H* → H2CO* | −0.537 | 0.327 | 689.409 |
| 6 | H2CO* → H2CO(g) | +0.770 | — | λ |
| 7 | H2CO* + H* → CH2OH* | −0.258 | 0.649 | 985.000 |
| 8 | H2CO* + H* → CH3O* | −0.905 | 0.046 | 311.795 |
| HCOH formation and hydrogenation | ||||
| 9 | HCO* + H* → HCOH* | +0.067 | 0.673 | 1159.938 |
| 10 | HCOH* + H* → CH2OH* | −0.422 | 0.245 | 642.437 |
| CH 3 OH formation and desorption | ||||
| 11 | CH3O* + H* → CH3OH* | −0.148 | 0.698 | 1029.907 |
| 12 | CH2OH* + H* → CH3OH* | −0.829 | 0.597 | 586.857 |
| 13 | CH3OH* → CH3OH(g) | +0.613 | — | — |
At this point, there are two distinct possibilities for subsequent hydrogenation, which may either take place at C, yielding formaldehyde H2CO* (process 5, Tables 5 and 6), or at O, yielding a hydroxyformyl HCOH* intermediate (process 9, Tables 5 and 6). For both the Cu(110) and Cu(100), the formaldehyde option has a lower activation energy with values of 0.11 eV (process 5, Table 5) and 0.33 eV (process 5, Table 6), and exothermic corresponding reaction energies of −0.60 eV (process 5, Table 5) and −0.54 (process 5, Table 6). Whilst the activation barriers for HCOH* formation are higher at 0.50 eV (process 9, Table 5) and 0.67 eV (process 9, Table 6) for Cu(110) and Cu(100) respectively, they are low enough for the competing HCOH* intermediate to be kinetically accessible, and in both cases the reaction energies are small, with an exothermic −0.10 eV being calculated for Cu(110) and a slightly endothermic 0.07 eV calculated for Cu(100).
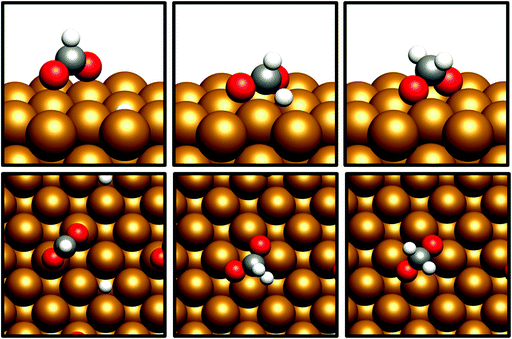
The desorption energy for formaldehyde was also calculated to determine how strongly the species is bound to the catalyst surfaces, and therefore whether it is sufficiently stable and long-lived to participate in subsequently elementary processes. The desorption energy was calculated to be endothermic by 0.99 eV for Cu(110) (process 6, Table 5) and 0.77 eV for Cu(100) (process 6, Table 6), indicating that formaldehyde is strongly bound to the catalyst surface in both cases. It is notable that the adsorption geometry for formaldehyde on both Cu facets considered shows considerable distortion from the usual planar geometry exhibited by the gas-phase molecule, indicating a strong degree of chemical binding to the surface rather than mere physisorption, and perhaps activating formaldehyde towards further hydrogenation to the CH2OH* and CH3O* intermediates which are precursors species for methanol (Fig. 4). Indeed, Bader charge analysis confirms a similar extent of electron transfer from the surface to formaldehyde as for CO2; the Cu(110) surface appears to be slightly more activating with a calculated Bader charge accumulation of β = 0.7, compared to β = 0.67 for Cu(100), relative to gas-phase formaldehyde. Evidently, formaldehyde is a viable intermediate species for methanol formation which can be expected to participate in further elementary reaction processes, rather than simply being desorbed to the gas phase.
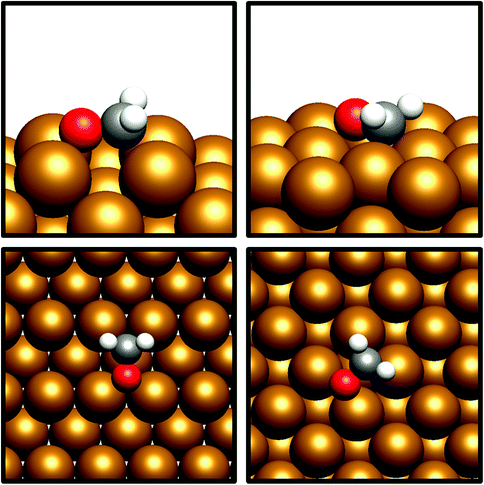 | ||
| Fig. 4 Graphical depiction of optimised formaldehyde adsorption geometry for Cu(100) (top) and Cu(110) (bottom), as seen from the side (left) and from the top (right). | ||
For formaldehyde conversion to methanol, the reaction may either proceed through a methoxy CH3O* intermediate, or a hydroxylmethylene CH2OH* intermediate, depending on whether the following hydrogenation process takes place at C or O. For both Cu(110) and Cu(100), the more kinetically feasible pathway involves CH3O* formation, with activation barriers of 0.39 eV and 0.05 eV and with corresponding reaction energies of −0.62 eV and −0.91 eV for the Cu(110) and Cu(100) surfaces respectively (process 8, Tables 5 and 6). The competing CH2OH* pathway, whilst still not excessively energetically unfeasible, gave considerably higher activation barriers of 0.96 eV and 0.65 eV (in both cases ∼0.6 eV greater than the corresponding activation energies for the CH3O* pathway) for the Cu(110) and Cu(100) surfaces, respectively. A similar shift is also seen for the reaction energies, with the calculated values being +0.09 eV and −0.25 eV for Cu(110) and Cu(100) (process 7, Tables 5 and 6). Hence, our calculations suggest that formaldehyde is a likely intermediate in methanol formation from CO, given its strong adsorption to both the (110) and (100) Cu surfaces and the relative ease by which formaldehyde undergoes further hydrogenation to yield CH3O*.
Hydrogenation of the HCOH* intermediate at C can also result in the formation of the CH2OH* intermediate, hence both the formaldehyde and HCOH* pathways can converge on this intermediate species. The energetics of HCOH* hydrogenation to CH2OH* are comparable for both the Cu(110) and Cu(100) surfaces, with respective activation energies of 0.28 eV and 0.25 eV, with corresponding reaction energies of −0.34 eV and −0.42 eV (process 10, Tables 5 and 6). It is notable that whilst the energetics for HCOH* formation are unfavourable compared to H2CO formation, subsequent formation of the CH2OH* intermediate is more energetically accessible from HCOH* than H2CO. Indeed, starting from HCO* hydrogenation and arriving at CH2OH*, the most energetically demanding step requires only 0.50 eV/0.67 eV for the HCOH* pathway, compared to 0.96 eV/0.65 eV for the H2CO pathway, for Cu(110)/Cu(100). Hence, at least for Cu(110), the HCOH* intermediate affords the most energetically accessible route to the CH2OH* intermediate, although the pathway involving formaldehyde and then methoxy before methanol formation is overall the lowest energy route.
We should note, however, that the CH2OH* intermediate, originating from either HCOH* or H2CO, must compete with the CH3O* intermediate, which can only originate from formaldehyde hydrogenation. For Cu(110), a moderately low activation barrier of 0.39 eV was calculated for formation of the latter species (process 8, Table 5), while a very low value of 0.05 eV is obtained for Cu(100) (process 8, Table 6), and the respective calculated reaction energies were determined to be exothermic for both Cu surfaces at −0.62 eV and −0.91 eV (process 8, Tables 5 and 6). Hence, we find that CH3O* formation is more energetically accessible than the isomeric CH2OH* intermediate, although for the Cu(110) surface, the highest energy barrier for CH2OH* formation from HCO* is comparable to the corresponding step for CH3O* formation (0.50 eV vs. 0.39 eV), whereas the differences for the Cu(100) surface are greater (0.65 eV vs. 0.33 eV).
Methanol formation may ultimately take place by the hydrogenation of either CH2OH* at C, or by CH3O* at O. For both Cu(110) and Cu(100), methanol formation from CH2OH* is less energetically hindered, with activation barriers calculated at 0.60 eV for both surfaces, and both processes are moderately exothermic with values of −0.71 eV and −0.82 eV calculated for Cu(110) and Cu(100) respectively (process 12, Tables 5 and 6). For methanol formation from CH3O*, the activation barrier is considerably higher for Cu(110) at 0.96 eV, compared to 0.70 eV for Cu(100), and both processes were determined to be only very slightly exothermic, with a reaction energy of <−0.01 eV for the Cu(110) surface and −0.15 eV for Cu(100) (process 11, Tables 5 and 6).
It is clear that for both Cu(110) and Cu(100) surfaces, there is competition between two pairs of intermediates, HCOH* and H2CO, and CH2OH* and CH3O*, which represent two different degrees of hydrogenation, and for both surfaces the overall most energy-demanding elementary process is the primary hydrogenation of CO to HCO, which precedes these competing processes, with activation barriers calculated at slightly greater than 1 eV. Given that all subsequent activation barriers are lower, it is reasonable to speculate that if this kinetic barrier can be overcome, then so should all subsequent, lower, barriers, and we might expect the reaction to proceed through a combination of several intermediate species.
Tables 5 and 6 give details of all of the elementary processes concerned with CO hydrogenation to methanol over Cu(110) and Cu(100), respectively. In both cases, the most energetically demanding processes are HCO* formation and subsequent hydrogenation at O to obtain the O–H bond present in the final product. For Cu(110), the activation barrier for hydrogenation of methoxy to methanol is slightly lower than for HCO* hydrogenation, whilst the inverse is true for Cu(100). We also note that the calculated activation barriers suggest a higher activity for CO hydrogenation over Cu(100) compared to Cu(110) for all elementary processes except for the initial hydrogenation of CO to HCO*, which in both cases is identified as the most energy-demanding step.
It is interesting that whilst for both Cu(110) and Cu(100), formaldehyde formation is more energetically favoured over HCOH* formation, the subsequent hydrogenation processes are invariably more energetically accessible for HCOH* than for formaldehyde. For Cu(110), formaldehyde is energetically favoured with an activation barrier of 0.11 eV (process 5, Table 5), compared to 0.50 eV for HCOH* (process 9, Table 5), yet the barriers for HCOH* hydrogenation to CH2OH* and then methanol are only 0.28 eV and 0.60 eV respectively (processes 10 and 12, Table 5). On the other hand, the most energetically accessible route for methanol formation via formaldehyde proceeds through CH3O* hydrogenation with a much higher activation barrier of 0.96. For Cu(100), this behaviour is similar but more subtle, with formaldehyde again being more energetically favoured over HCOH*, but at the cost of subsequent hydrogenation processes being more energetically hindered than those for HCOH*. These results suggest, therefore, that both HCOH* and formaldehyde could participate in methanol synthesis from CO hydrogenation.
As mentioned earlier, the strong calculated adsorption energy for H2CO is also notable on both surfaces. H2CO was calculated to bind more strongly to the catalyst surface than the product CH3OH (0.99 eV vs. 0.77 eV for Cu(110), 0.77 eV vs. 0.61 eV for Cu(100)), and furthermore, the binding energy was calculated to be greater than the activation energies determined for subsequent reaction processes leading to methanol formation. These results imply that the subsequent reaction of formaldehyde to undergo more extensive hydrogenation is kinetically favoured over formaldehyde desorption, indicating that formaldehyde is not a major by-product of CO hydrogenation.
CO2 hydrogenation – formate vs. hydrocarboxyl
Having already considered methanol formation via intermediate CO hydrogenation, the discussion now focuses on direct hydrogenation of CO2. There are two possible potential intermediates arising from this process: either hydrogenation takes place at the CO2 C atom, yielding a formate HCOO* intermediate (process 14, Tables 7 and 8), or at O, resulting in the formation of the hydrocarboxyl species COOH* (process 19, Tables 7 and 8). For both the Cu(110) and Cu(100) surfaces, formation of the HCOO* was kinetically preferred, with respective activation energies calculated at 0.25 eV and 0.40 eV, and corresponding reaction energies of −0.98 eV and −1.17 eV (process 14, Tables 7 and 8). In both cases, the most stable HCOO* coordination geometry was determined to consist of a bidentate orientation with both oxygen atoms positioned on top of surface Cu atoms (Fig. 5 and 6), although alternative diagonal on-top orientations and also those featuring the bidentate HCOO* intermediate adsorbed with both O atoms located between two surface Cu atoms were found to be only marginally less stable. Bidentate HCOO* formation involves CO2 hydrogenation, yielding initially a monodentate HCOO* adsorption geometry immediately following the transition state, which, by an essentially barrierless rotation, forms the bidentate species.| Process no. | Elementary process | ΔE/eV | E a/eV | v/cm−1 |
|---|---|---|---|---|
| HCOO* | ||||
| 14 | CO 2 * + H* → HCOO* | −0.978 | 0.246 | 702.298 |
| 15 | HCOO* + H* → HCOOH* | +0.349 | 0.938 | 1061.697 |
| 16a | HCOO* + H* → H2COO* (LB) | +0.230 | 1.056 | 877.380 |
| 17a | H2COO* + H* → OCH2OH* (LB) | +0.196 | 1.348 | 1146.997 |
| 18a | H2COO* → H2CO* + O* (LB) | +1.205 | 1.662 | 151.468 |
| 16b | HCOO* + H* → H2COO* (SB) | +0.668 | 1.789 | 822.753 |
| 17b | H2COO* + H* → OCH2OH* (SB) | −0.286 | 0.623 | 1041.733 |
| COOH* | ||||
| 19 | CO2* + H* → COOH* | −0.408 | 0.986 | 1261.956 |
| 20 | COOH* + H* → HCOOH* | −0.387 | 0.517 | 709.148 |
| 21 | HCOOH* → HCOOH(g) | +0.816 | — | — |
| HCOOH* hydrogenation | ||||
| 22 | HCOOH* + H* → OCH2OH* | −0.194 | 0.844 | 606.191 |
| OCH 2 OH* dissociation, H 2 CO desorption and hydrogenation | ||||
| 23 | OCH 2 OH* → H2CO* + OH* | +0.037 | 0.899 | 136.674 |
| 6 | H2CO* → H2CO(g) | +0.986 | — | — |
| 7 | H2CO* + H* → CH2OH* | +0.087 | 0.963 | 927.927 |
| 8 | H 2 CO* + H* → CH3O* | −0.622 | 0.388 | 328.280 |
| 11 | CH 3 O* + H* → CH3OH* | −0.004 | 0.960 | 926.043 |
| 12 | CH2OH* + H* → CH3OH* | −0.705 | 0.604 | 610.080 |
| 13 | CH 3 OH* → CH3OH(g) | +0.771 | — | — |
| Process no. | Elementary process | ΔE/eV | E a/eV | v/cm−1 |
|---|---|---|---|---|
| HCOO* | ||||
| 14 | CO2* + H* → HCOO* | −1.174 | 0.403 | 565.798 |
| 15 | HCOO* + H* → HCOOH* | +0.437 | 0.925 | 634.635 |
| 16 | HCOO* + H* → H2COO* | +0.272 | 1.163 | 868.135 |
| 17 | H2COO* + H* → OCH2OH* | −0.113 | 0.788 | 1185.234 |
| 18 | H2COO* → H2CO* + O* | +1.111 | 1.172 | 195.307 |
| COOH* | ||||
| 19 | CO 2 * + H* → COOH* | −0.160 | 0.941 | 1395.513 |
| 20 | COOH* + H* → HCOOH* | −0.392 | 1.109 | 972.935 |
| 21 | HCOOH* → HCOOH(g) | +0.554 | — | — |
| HCOOH* hydrogenation | ||||
| 22 | HCOOH* + H* → OCH2OH* | −0.029 | 0.813 | 729.629 |
| OCH 2 OH* dissociation, H 2 CO desorption and hydrogenation | ||||
| 23 | OCH 2 OH* → H2CO* + OH* | +0.337 | 0.826 | 160.058 |
| 6 | H2CO* → H2CO(g) | +0.770 | — | — |
| 7 | H 2 CO* + H* → CH2OH* | −0.258 | 0.649 | 985.000 |
| 8 | H2CO* + H* → CH3O* | −0.905 | 0.046 | 311.795 |
| 11 | CH3O* + H* → CH3OH* | −0.148 | 0.698 | 1029.907 |
| 12 | CH 2 OH* + H* → CH3OH* | −0.829 | 0.597 | 586.857 |
| 13 | CH 3 OH* → CH3OH(g) | +0.613 | — | — |
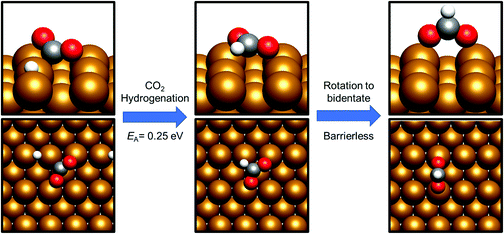
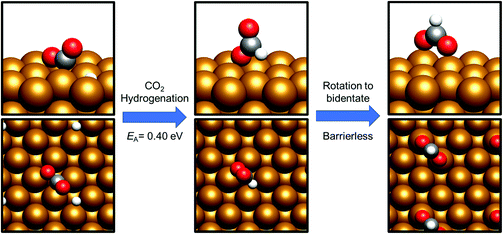
By contrast, COOH* formation involved higher activation barriers for hydrogenation, with Ea being calculated at 0.99 eV and 0.94 eV for Cu(110) and Cu(100) respectively, with the corresponding reaction energies obtained being −0.41 eV and −0.16 eV (process 19, Tables 7 and 8). Hence, the calculated activation barriers suggest that initial CO2 hydrogenation preferentially takes place at C, with low activation barriers associated with HCOO* formation for both Cu(110) and Cu(100).
HCOO* hydrogenation
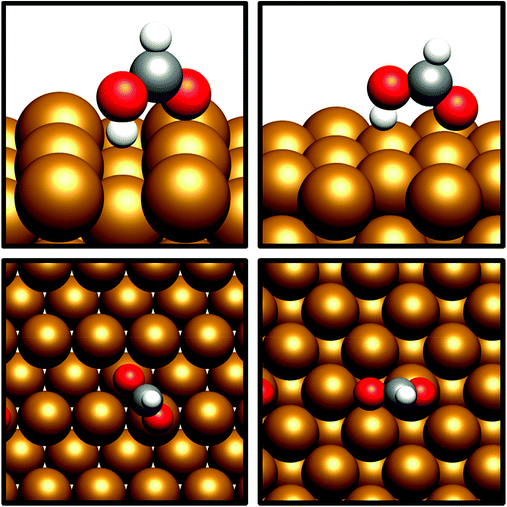
HCOO* can undergo subsequent hydrogenation to form either dioxymethylene, H2COO*, or formic acid, depending on whether hydrogenation takes place at C or O. HCOO* dissociation to HCO* and O* was briefly considered to test whether this process could offer a potential route to the HCO* intermediate identified in the preceding section; however, the process was found to be highly endothermic, with the elementary process HCOO* → HCO* + O* resulting in an energy change of >+1.5 eV for both Cu(110) and Cu(100). Clearly, any kinetic barrier associated must be greater than or equal to this energy change, rendering any such process kinetically and thermodynamically irrelevant. Of the two possible hydrogenation pathways, HCOOH formation has a slightly lower activation energy, although in both cases activation energies are moderately high: for H2COO* formation, the respective activation barriers for Cu(110) and Cu(100) are 1.06 eV and 1.16 eV, with corresponding endothermic reaction energies of +0.23 eV and +0.27 eV (process 16a, Table 7, and process 16, Table 8). On the other hand, the activation energies for HCOOH formation from HCOO* were slightly lower, at 0.94 eV and 0.93 eV for Cu(110) and Cu(100), respectively. In both cases, the process is mildly endothermic, with calculated energy changes of +0.35 eV and +0.27 eV for Cu(110) and Cu(100), respectively (process 15, Tables 7 and 8). HCOOH desorption is endothermic with respect to the gas phase, calculated at +0.55 eV for Cu(110) and +0.82 eV for Cu(100) (process 21, Tables 7 and 8), with the optimised adsorption geometry featuring HCOOH adsorbed with the carbonyl O atom atop a surface Cu site (Fig. 7).For H2COO*, an adsorption geometry consisting of both O atoms bridging two surface Cu atoms is of lower energy, in contrast to the on-top bidentate geometry on HCOO*; the lowest activation barrier for HCOO* hydrogenation was obtained where the adsorbate O coordination shifted during the hydrogenation process to reflect to difference in the preferred environment for the initial and final state (Fig. 8 and 9).
The behaviour is a little more complex for the Cu(110) surface, as two distinct perpendicular bidentate bridging sites are present, referred to as the short and long bridge sites. The longer bridge site is better able to accommodate both the H2COO* intermediate (by 0.39 eV), so whilst there is little difference between the stability of the HCOO* intermediate on the short and long bridge sites, H2COO* formation is only feasible at the long bridge site, with the calculated activation barrier for HCOO* formation at the short bridge site being much too high at 1.79 eV (process 16b, Table 7) to be relevant.
Further hydrogenation of H2COO* was also investigated, to form the hydroxyoxomethylene species, OCH2OH*, which for the Cu(110) surface, was found to have a high activation energy of 1.35eV for H2COO* in the more stable long bridge adsorption site and a reaction energy of +0.20 eV(process 17a, Table 7). However, for the less stable short bridge H2COO* adsorption geometry, a much lower activation energy of 0.62 eV was determined, with a corresponding reaction energy of −0.29 (process 17b, Table 7). This difference between the two different modes of H2COO* adsorption is probably attributable to the inherently greater stability of the long bridge site making the H2COO* intermediate at this site resistant to further hydrogenation. Hence, it would appear that formation of the OCH2OH* intermediate from HCOO* on the Cu(110) surface is kinetically challenging, given that for the short bridge adsorption mode, the first hydrogenation step is unfeasible, whilst for the long bridge site the second hydrogenation poses a potentially insurmountable barrier. For the Cu(100) surface, on the other hand, hydrogenation of H2COO* is kinetically feasible, with an activation barrier of 0.79 eV and reaction energy of −0.11 eV (process 17, Table 8). In contrast to the Cu(110) surface, HCOO* hydrogenation over Cu(100) presents a kinetically accessible reaction pathway to obtain the OCH2OH* intermediate.
Dissociation of the H2COO* species was also considered as a potential means to obtain H2CO, which has already been demonstrated to be a potential intermediate for methanol synthesis earlier in our discussion of the discussion on CO hydrogenation. For Cu(110), the calculated activation barrier Ea for dissociation of H2COO* at the most stable long bridge site was much too large, at 1.66 eV, with a corresponding ΔE of +1.20 eV (process 18a, Table 7). For Cu(100), the calculated activation energy is much smaller, but still potentially limiting at 1.17 eV, with a reaction energy of +1.10 eV (process 18, Table 8). For both surfaces, the strongly endothermic H2COO* dissociation energies reflect the stability of the H2COO* intermediate, particularly over Cu(110) as do the calculated activation barriers for hydrogenation processes, with only H2COO* hydrogenation over Cu(100) having a moderately low activation barrier compared to other less energetically feasible processes.
It is clear that for these elementary processes, the Cu(100) surface is considerably more active. It is likely that the difference in surface structure, in particular the packing and arrangement of surface Cu atoms, is responsible for this behaviour, with the H2COO* intermediate being too strongly bound on the Cu(110) surface due to the dimensions of the long bridge site being commensurate with that of the adsorbate. Hence, the intermediate is not especially active towards further hydrogenation when bound to Cu(110) in this manner.
COOH* hydrogenation
It is also possible to form HCOOH via the COOH* intermediate by hydrogenation taking place at C, with HCOOH being a common intermediate in both the formate and hydrocarboxyl reaction pathways. For Cu(110), the process is highly favourable, with only a moderate activation energy of 0.52 eV and an exothermic reaction energy of −0.39 eV (process 20, Table 7). The same process on Cu(100) is considerably less kinetically favoured, with an activation energy of 1.11 eV and reaction energy of −0.39 eV (process 20, Table 8).HCOOH hydrogenation
HCOOH has been identified as a possible product of both the formate and hydrocarboxyl pathways, and as mentioned earlier, desorption of HCOOH to the gas phase is moderately endothermic (+0.55 eV and +0.82 eV for Cu(110) and Cu(100), respectively, process 21, Tables 7 and 8). Hence, it is of interest to consider its subsequent hydrogenation to the OCH2OH* intermediate, which was also examined as a product of H2COO* hydrogenation in the formate pathway. The energetics of this process were found to be similar for both of the Cu surfaces, with moderate activation energies of 0.84 eV and 0.81 eV for the Cu(110) and Cu(100) surfaces, respectively. Both processes were modestly exothermic, with respective ΔE of −0.19 eV and −0.03 eV (process 22, Tables 7 and 8). Hence, it is clear that the HCOOH intermediate provides a more kinetically accessible route to OCH2OH* compared to the alternative H2COO* hydrogenation which was only determined to be feasible for Cu(100).OCH2OH* dissociation
The OCH2OH* intermediate is fully saturated and cannot accommodate any further hydrogenation. Cleavage of a C–O bond, necessary for obtaining the product methanol, was found to be unrealistic for intermediates arising from CO2 hydrogenation such as HCOO* and H2COO*. Hence, OCH2OH dissociation is the only remaining option for the requisite C–O bond cleavage, except of course via CO2 dissociation as discussed previously. There are two possible outcomes for OCH2OH* dissociation:| OCH2OH* → CH2OH* + O* |
| OCH2OH* → H2CO + OH* |
The first process yields the CH2OH* intermediate which has been shown in this study to react readily with co-adsorbed H* to generate the product methanol. However, for both Cu(110) and Cu(100), the dissociation was determined to have a high activation barrier of ∼2 eV, which is far too large for this process to be considered as a viable means to generate the CH2OH* intermediate. The alternative process, yielding formaldehyde, however, was found to be much more kinetically feasible and well within the bounds of accessibility, with comparable activation energies of 0.89 eV and 0.83 eV for the Cu(110) and Cu(100) facets, respectively. For both surfaces, the dissociation process was endothermic, with corresponding reaction energies of 0.04 eV and 0.34 eV (process 23, Tables 7 and 8). The product, formaldehyde, has already been identified in this study as an intermediate species for CO hydrogenation to methanol, and the different formaldehyde hydrogenation pathways have already been calculated. Hence H2CO originating from OCH2OH* dissociation during CO2 hydrogenation will undergo these elementary processes in much the same way.
As already discussed, since all other possibilities for C–O bond cleavage during CO2 hydrogenation to methanol (i.e. excluding dissociation of CO2 itself) can be ruled out as kinetically unfeasible on both Cu(110) and Cu(100) surfaces, we may deduce that OCH2OH* is a key intermediate common to both the HCOO* and COOH* reaction pathways. Furthermore, that the only calculated feasible dissociation process for OCH2OH* yields formaldehyde also necessitates H2CO as an essential intermediate. However, the processes leading to the OCH2OH* intermediate vary between the two Cu facets in question.
Reviewing the calculated values summarised in Tables 7 and 8, it can be seen that that the reaction pathway for which the most highly activated elementary processes is minimised is the formate pathway for Cu(110), and the hydrocarboxyl pathway for Cu(100), although in both cases, the most energy-demanding step for the lowest energy route is only slightly less energetically costly than that of the competing pathway. For Cu(100), the most energetically demanding step via the COOH* route is only 0.054 eV more accessible than that for the competing HCOO* pathway. For Cu(110), a similarly small difference is also observed, with the process with the higher activation energy, formate hydrogenation to formic acid, having a barrier which is only 0.048 eV higher that of than CO2 hydrogenation to COOH*. Hence, it is reasonable to expect both intermediates to be present and participating in methanol formation for both Cu(110) and Cu(100) surfaces.
H2O formation
The stoichiometry of the product methanol necessitates that CO2 hydrogenation yields water as a byproduct. Methanol formation via CO2 dissociation results in surface O* which may be converted to OH* and then finally to water; for direct CO2 hydrogenation, the calculations suggest that OH* arising from OCH2OH* dissociation is the main route by which water formation takes place. Hence, for both Cu(110) and Cu(100), the energetics for O* and OH* hydrogenation have been considered, with the results presented in Table 9.| Process no. | Elementary process | ΔE | E a/eV | v/cm−1 |
|---|---|---|---|---|
| (110) | ||||
| 24 | O* + H* → OH* | −0.951 | 0.632 | 1051.683 |
| 25 | OH* + H* → H2O* | +0.052 | 0.770 | 1215.664 |
| 26 | H2O* → H2O | +0.143 | — | — |
| (100) | ||||
| 24 | O* + H* → OH* | −1.147 | 0.486 | 784.975 |
| 25 | OH* + H* → H2O* | +0.022 | 0.757 | 403.908 |
| 26 | H2O* → H2O | +0.438 | — | — |
For both Cu(110) and Cu(100), O* hydrogenation is strongly exothermic, with respective reaction energies of −0.95 eV and −1.15 eV; the corresponding activation energies are modest at 0.63 eV and 0.49 eV (process 24, Table 9). Hydrogenation of OH* to yield water has slightly higher calculated activation barriers of 0.77 eV and 0.76 eV for Cu(110) and Cu(100), respectively. For both surfaces, the elementary process for H2O formation from OH was found to be almost thermoneutral, with negligibly endothermic energy changes of 0.05 eV and 0.02 eV (process 25, Table 9). The product H2O was found to be only fairly weakly adsorbed on both the Cu(110) and Cu(100) surfaces, hence it can be assumed to desorb readily to the gas phase, with desorption being endothermic by 0.14 eV over Cu(110), compared to 0.44 eV for Cu(100) (process 26, Table 9). Hence, water formation over both of the low index Cu surfaces considered will occur readily and the resultant water can be expected to desorb to the gas phase, facing competitive adsorption against both reactants CO2* and H*, as well as molecular intermediates such as H2CO and HCOOH, generated throughout the overall methanol synthesis reaction. As water is more weakly adsorbed on Cu(110) and Cu(100), competitive adsorption against the reactants and intermediates means that water formation and desorption can be considered as essentially irreversible.
Discussion
The calculations presented here show that a variety of different reaction pathways (summarised in Fig. 3) are potentially feasible for methanol formation over Cu(110) and Cu(100). Comparing the CO and CO2 reaction pathways, in both cases the activation barriers for CO2 dissociation were calculated to be somewhat higher than the most energy-demanding elementary processes for the CO2 pathways with the lowest activation energies, but not significantly so, with the CO2 dissociation barrier over Cu(110) being only 0.138 eV greater than the barrier for formate hydrogenation to formic acid; the discrepancy is even smaller for Cu(100) where hydrocarboxyl hydrogenation to formic acid is negligibly smaller than that of CO2 dissociation (0.007 eV). Hence, we might expect not only that methanol synthesis takes place via the formate and hydrocarboxyl intermediates identified for CO2 hydrogenation, but also via the CO mediated reaction pathway. Of all the intermediates explored, formaldehyde is the only common intermediate to all of the reaction pathways explored for both CO and CO2 hydrogenation. HCOOH is also identified as playing a key role for CO2 hydrogenation, featuring in the least kinetically demanding pathways for methanol synthesis via both HCOO* and COOH*, and for both of the Cu surfaces investigated. The reaction energy profile diagrams presented in Fig. 10 and 11 show the interrelation between the various possible reaction pathways. Indeed, for both Cu(110) and Cu(100), the pathways corresponding to CO hydrogenation are overall more energy demanding; however the most energy demanding individual processes for all possible pathways are comparable, further suggesting that several different pathways may be involved in the overall reaction.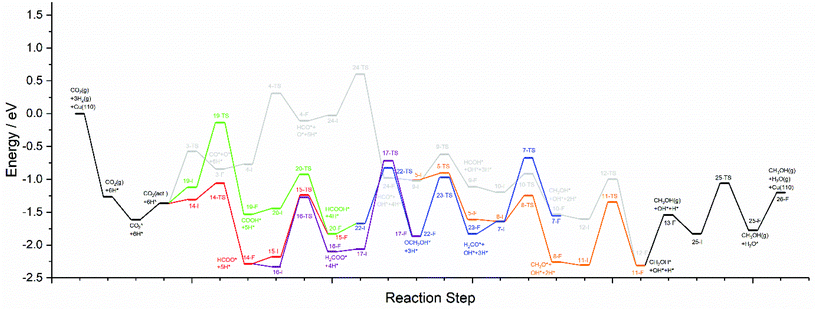 | ||
| Fig. 10 Reaction energy profile plots for CO2 hydrogenation to methanol over Cu(110). The various different reaction pathways are presented together to illustrate their interrelation. The processes indicated in black are common to all pathways. The processes indicated in grey correspond to CO2 dissociation and subsequent hydrogenation to HCO*, then HCOH*, then CH2OH*, and finally the product CH3OH*. The processes indicated in orange branch off from the grey pathway and correspond to HCO* hydrogenation to H2CO*, then CH3O*, and finally to the product CH3OH*. The green and red pathways correspond to CO2 hydrogenation to COOH* and HCOO*, converging at HCOOH* formation, subsequent hydrogenation of which to OCH2OH* being indicated by the blue pathway. The blue and orange pathways converge since H2CO* hydrogenation is common to both. Similarly, the blue and grey pathways converge since CH2OH* is a common intermediate to both. The purple pathway illustrates the alternative HCOO* hydrogenation to H2COO*, and its subsequent hydrogenation to OCH2OH*, hence the purple pathway converges with the blue pathway. All energetic minima and transition state are labelled with a number corresponding to the elementary processes detailed in Tables 4–9, with initial state, transition state and final state structure energies being indicated with the letters I, TS, and F, respectively. | ||
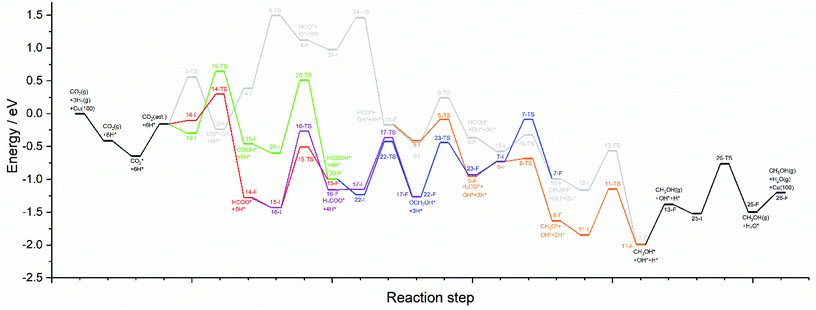 | ||
| Fig. 11 Reaction energy profile plots for CO2 hydrogenation to methanol over Cu(100). The various different reaction pathways are presented together to illustrate their interrelation. The processes indicated in black are common to all pathways. The processes indicated in grey correspond to CO2 dissociation and subsequent hydrogenation to HCO*, then HCOH*, then CH2OH*, and finally the product CH3OH*. The processes indicated in orange branch off from the grey pathway and correspond to HCO* hydrogenation to H2CO*, then CH3O*, and finally to the product CH3OH*. The green and red pathways correspond to CO2 hydrogenation to COOH* and HCOO*, converging at HCOOH* formation, subsequent hydrogenation of which to OCH2OH* being indicated by the blue pathway. The blue and orange pathways converge since H2CO* hydrogenation is common to both. Similarly, the blue and grey pathways converge since CH2OH* is a common intermediate to both. The purple pathway illustrates the alternative HCOO* hydrogenation to H2COO*, and its subsequent hydrogenation to OCH2OH*, hence the purple pathway converges with the blue pathway. All energetic minima and transition state are labelled with a number corresponding to the elementary processes detailed in Tables 4–9, with initial state, transition state and final state structure energies being indicated with the letters I, TS, and F, respectively. | ||
Although there are comparatively few previous computational studies exploring a detailed reaction network for methanol synthesis over Cu(110) and Cu(100), the previous theoretical studies focusing on the most stable Cu(111) facet can serve as a useful comparison to assess the activity of the remaining low-index surfaces explored in the present work, and to compare possible reaction pathways.7,8,56 The intermediates identified by Grabow et al.8 correspond to those identified in this study as being central to the CO2 hydrogenation mechanism, namely HCOO*, COOH*, HCOOH, H2CO and OCH2OH, and the preference for formic acid formation over dioxomethylene in the HCOO* pathway was also observed for Cu(110) and Cu(100), showing similarities to the activity of the Cu(111) surface.
A key difference between the results presented in this study, and that of Grabow et al., concerns CO2 dissociation to CO. Grabow et al. reported a very high activation barrier for CO2 dissociation over Cu(111), calculated to be 1.77 eV, thus making the possibility of CO and intermediates arising from its hydrogenation irrelevant for methanol synthesis. On the other hand, in the present work, it was found that CO2 dissociation is considerably less activated over Cu(110) and Cu(100), with an activation barrier of ∼1.1 eV for both of the minority facets, although it must be noted that this activation barrier is still slightly higher than any of those for the direct CO2 hydrogenation pathways. As discussed above, this finding is consistent with experimental evidence which suggests that Cu(111) is not especially active towards CO2 adsorption and that CO2 activation readily takes place over Cu(110) and Cu(100), along with the finding in the present work that no CO2 activation was observed over Cu(111), in contrast to the other low-index surfaces. On the other hand, computational studies conducted by Zhao et al.7 appear to report a bent activated CO2 species over Cu(111) (∠ (O–C–O) = 127.6°) comparable to those identified in this study over Cu(110) and Cu(100), although no appreciable discussion is devoted to the role of this species in the earlier study, which to suggested an Eley–Rideal type mechanism for CO2 hydrogenation invoking direct reaction of gas-phase CO2 with adsorbed H*, without exploring CO2 dissociation. However, both the works of Grabow and Zhao examine some of the same processes on Cu(111) as those associated with CO hydrogenation over Cu(110) and Cu(100) in the present study; Grabow et al. report that the activation barrier and reaction energy for CO* hydrogenation to HCO* over Cu(111) is comparable to that determined here for the remaining low index surfaces, i.e. moderately highly activated and considerably endothermic (Ea ∼1 eV, ΔE = 0.7 ± 0.1 eV). Both of these previous DFT studies suggest that HCOH* formation is considerably more kinetically demanding over Cu(111) compared to the activation barriers determined in this study for Cu(110) and Cu(100), although for HCOH* hydrogenation to H2CO* and H2COH* would appear to be facile on all three surfaces, i.e. for Cu(111) as reported by Zhao and Grabow, as well for Cu(110) and Cu(100) as reported in the present work. A similar agreement is seen for H2CO* hydrogenation to CH3O* and CH2OH*, with both processes being kinetically feasible over all three surfaces, with CH3O* formation having a lower activation barrier and being more exothermic. Further agreement between all three low index facets is observed with regards to methanol formation, with CH2OH* hydrogenation being less kinetically demanding and more exothermic than the corresponding process for CH3O*. Hence, it appears that the overall hydrogenation activity does have similarities for all three surfaces, except for the crucial initial CO2 dissociation and CO* hydrogenation processes, for which Cu(110) and Cu(100) would appear to perform considerably better than the dominant Cu(111) surface. The fact that only the early hydrogenation processes were found to be less activated over Cu(110) and Cu(100) can also be strongly connected to the observed activation of CO2 over these surface reported in the present work that was absent for Cu(111). Consequently, we suggest a methanol synthesis pathway utilising CO and its subsequent hydrogenation products as intermediates, given that polycrystalline Cu catalysts can be expected to exhibit surface environments resembling all three of the low index facets.
Comparing CO2 hydrogenation processes, it is also interesting to note that, compared to reports in previous computational works on Cu(111), the calculated kinetic barriers for CO2 hydrogenation over Cu(110) and Cu(100) reveal the minority low index surfaces to be considerably more active towards CO2 hydrogenation, both to COOH* and HCOO*; whilst HCOO* formation was reported by both Grabow and Zhao as being both kinetically and thermodynamically feasible over Cu(111), the calculations performed in this study reveal lower activation barriers and more exothermic reaction energies for both Cu(110) and Cu(100). The superior activity of the two minority low index facets towards COOH* formation is even more pronounced; Zhao et al. report this process to be mildly endothermic with a high activation barrier of 1.27 eV, whilst Grabow et al. consider the process to be wholly unfeasible, given that the reverse process (COOH* + * → CO2* + H*) was reported to be highly activated (Ea = 1.23 eV) and highly exothermic (ΔE = 0.55 eV), making CO2* hydrogenation to COOH* not kinetically feasible. By contrast, the calculated energetics for Cu(110) and Cu(100) presented in the present work suggest that COOH* formation is only moderately activated, with Ea < 1 eV for both surfaces, and in both cases the process is modestly exothermic. Once again, we find the pattern of initial reaction processes involving CO2 – in this case hydrogenation rather than dissociation having lower barriers over Cu(110) and Cu(100), compared to the more dominant Cu(111) surface.
For COOH* hydrogenation to formic acid, the behaviour exhibited between the three surfaces is more varied, with the process being kinetically facile over Cu(110) (Ea = 0.52 eV), moderately activated over Cu(111) (Ea = 0.76 ± 0.03 eV) according to Grabow and Zhao, and considerably more so over Cu(100) (Ea = 1.11 eV). Subsequent hydrogenation of HCOOH* to OCH2OH* was found to be only slightly less activated for Cu(110) and Cu(100) (Ea ∼0.82 eV) compared to Cu(111) (Ea = 0.97 ± 0.07 eV), and mildly exothermic for all three facets. Once again we find the pattern of initial elementary processes involving CO2 having lower energy barriers over Cu(110) and Cu(100), than Cu(111), but with similar behaviour observed between the three surfaces for subsequent elementary processes such as hydrogenation of intermediates like COOH*. This finding further supports the notion that the CO2 activation reported for the Cu(110) and Cu(100) is responsible for the main differences in activity compared to the non-CO2-activating Cu(111) facet.
Turning now to subsequent reactions for HCOO*, there is broad agreement between the previous studies on Cu(111) and the present work on the low-index surface that HCOO* dissociation to yield formyl is not possible, owing to the process on all surfaces being highly endothermic and as such much too kinetically unfeasible to be considered as a possible mechanism for C–O bond cleavage. We find the energetics of HCOO* hydrogenation to yield methanol to be similar for all three surfaces, with Grabow and Zhao agreeing that the process is moderately activated and modestly endothermic (Ea = 0.86 ± 0.05 eV, ΔE ∼0.2 eV) over Cu(111), comparable to the energetics reported for both Cu(110) and Cu(100) in this study (Ea ∼0.93 eV, ΔE = 0.4 ± 0.05 eV). For all three surfaces, this process is considerably more favourable than the competing hydrogenation to yield H2COO, with the two previous Cu(111) studies reporting activation barriers of at least 1.2 eV; lower activation barriers were obtained for Cu(110) and Cu(100) (Ea ∼1 eV), but nonetheless higher than for HCOOH* formation. On the other hand, whilst subsequent dissociation of H2COO* to H2CO* and O*, as well as further hydrogenation to yield OCH2OH*, were reported to be feasible over Cu(111) in the previous computational studies, for Cu(110) and Cu(100) the present work found the former to be much more highly activated. This behaviour is particularly pronounced for Cu(110), although for all three Cu surfaces the high kinetic barrier is probably associated with the process being highly endothermic in the first place, with calculated activation barriers being only slightly greater than the endothermic overall energy change associated with the process. Whilst we found the latter hydrogenation step to OCH2OH* to be potentially feasible over Cu(100), with comparable energetics to that reported for Cu(111) by Grabow and Zhao, for Cu(110) H2COO* hydrogenation is improbable owing to the high activation barrier of nearly 1.7 eV; this result can possibly be attributed to the high relative stability of the H2COO* adsorbate on Cu(110), which is responsible for both its comparative ease of formation compared to the same process taking place over Cu(111) and Cu(100), and its relative resistance to undergoing subsequent reaction processes. In any case, we find that for all three surfaces, methanol synthesis via HCOO* preferentially takes place via HCOOH* rather than H2COO*, although the exact limiting processes that makes H2COO* less favourable vary between the surfaces. This finding further reflects the notion that differences between activity of the three surfaces is largely connected to the process of CO2 activation, and that subsequent reaction processes involving intermediate species are largely similar for all of the Cu low-index facets.
For Cu(111), the previous computational studies suggest that whilst formation of the key formaldehyde intermediate is kinetically possible via either H2COO* or OCH2OH* dissociation (with the reaction pathway to the latter intermediate being overall lower in energy), the reverse process is essentially spontaneous, given that the activation barriers were determined to be almost equal to the endothermicity of the process. Whilst H2COO* dissociation was found to be similarly kinetically hindered, and almost spontaneous in the reverse, for Cu(110) and Cu(100), OCH2OH* dissociation, on the other hand, was determined to be a moderately activated and mildly endothermic (Ea ∼0.86, ΔE = +0.04 eV and +0.34 eV for Cu(110) and Cu(100), respectively), thus not suffering from the issue of the reverse process occurring spontaneously as was found to be the case for Cu(111). These results, in addition to the improvement in CO2 activation observed for Cu(110) and Cu(100), suggest superior activity of these surfaces compared to the dominant Cu(111) surface.
As can be seen from the review and comparison of the reaction network for the three surfaces, many of the most important differences between the Cu(110) and Cu(100) facets, and the Cu(111) surface, lie in the initial elementary processes involving CO2, rather than subsequent processes taking place later in the reaction pathway, which appear to be more similar between the three Cu surfaces. This observation provides strong evidence for the observed activation of CO2 for Cu(110) and Cu(100), but not Cu(111), being key to the improved activity of the former surfaces. It is of interest to consider the implications of this with respect to the role of the ZnO support in facilitating methanol synthesis in the industrially ubiquitous Cu/ZnO catalyst. Whilst the extent of activation of CO2 by Cu(110) and Cu(100) is modest, if the Bader charge analyses presented here and in previous works38 is to be used as a measure of activation, the calculated reaction energetics suggest considerable improvement in activity towards CO2 hydrogenation and dissociation compared to the non-activating Cu(111). Hence, whilst the ZnO support may potentially play a role in CO2 activation, Cu is likely to be involved, given that the present work shows that non-dominant low-index Cu facets can facilitate CO2 activation, and we would expect Cu coordination environments resembling those of the Cu(110) and Cu(100) facets to be present on Cu/ZnO catalysts. The presence of surface environments resembling the Cu(110) and Cu(100) facets may be linked to the role of the ZnO support in hindering sintering and allowing these higher energy surfaces to be expressed. However, as this work demonstrates, CO2 hydrogenation over Cu(110) and Cu(100) suffers from many of the same energetic bottlenecks at the Cu(111) surface for many subsequent elementary processes concerning formate hydrogenation. Indeed, recently experimental work57 suggests that interfacial Cu/ZnO sites could be key to facilitating formate activation, which would represent an avenue for improved catalytic activation that has not been observed for unsupported Cu catalysts.
Conclusions
The calculations presented in this work show that CO2 activation takes place over Cu(110) and Cu(100) surfaces and that these Cu facets show improved catalytic behaviour for CO2 dissociation and hydrogenation processes, compared to the more extensively studied dominant Cu(111) facet. Methanol synthesis via CO hydrogenation is not realistic for the Cu(111) surface due to the negligible extent of CO2 dissociation, whilst for Cu(110) and Cu(100) it remains a distinct possibility. Furthermore, methanol synthesis via both HCOO* and COOH* as intermediates, rather than just HCOO*, is shown to be possible over Cu(110) and Cu(100) owing to the significantly lower barrier to this initial hydrogenation process compared to Cu(111). Overall, the non-dominant Cu surfaces appear to offer considerably more flexibility in terms of possible reaction pathways to obtain the product methanol.Our analysis provides valuable insights into the importance of Cu surface structure and morphology in understanding fully the nature of Cu-based catalysts for methanol synthesis. It is intended that, based on the calculated activation barriers presented in the current work, future studies will further investigate the mechanism for methanol synthesis and the relative importance of the identified intermediates through microkinetic modelling studies. The data presented in this systematic study of the low-index surfaces of the unsupported copper catalyst will form the basis of future microkinetic work examining the improvement in rate-constants that can be expected in the next generation of industrially relevant supported catalysts. Moreover, this work will not only provide a basis for further investigation of low index Cu catalyst surfaces, but will inform future works exploring supported Cu catalysts and as such assist in furthering progress towards developing a more complete understanding of widely used industrial catalysts. More generally, our study has allowed a detailed exploration of the various mechanistic possibilities in the widely studied CO2 hydrogenation reaction. It is intended that the key elementary processes identified from our complete mechanistic analysis will facilitate future investigations into more complex multi-component catalyst systems that are representative of industrial catalysts, revealing new insights into the role of support materials and other components of such catalysts.
Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
The authors acknowledge the GCRF START project (ST/R002754/1) for funding support. Additionally, the authors acknowledge the support of the Supercomputing Wales project, which is part-funded by the European Regional Development Fund (ERDF) via Welsh Government, Science and Technology Facilities Council Scientific Computing Department's SCARF cluster, and the UK National Supercomputing Service ARCHER (accessed via membership of the Materials Chemistry Consortium which is funded by Engineering and Physical Sciences Research Council (EP/L000202)), for the provision of computational resources. The UK Catalysis Hub is thanked for resources and support provided via membership of the UK Catalysis Hub Consortium and funded by EPSRC (Grants EP/R026815/1).References
- G. A. Olah, A. Goeppert and G. K. S. Prakash, J. Org. Chem., 2009, 74, 487–498 CrossRef CAS PubMed.
- M. P. Hogarth and G. A. Hards, Platinum Met. Rev., 1996, 40, 150–159 CAS.
- K. C. Waugh, Catal. Lett., 2012, 142, 1153–1166 CrossRef CAS.
- J. B. Bulko, R. G. Herman, K. Klier and G. W. Simmons, J. Phys. Chem., 1979, 83, 3118–3122 CrossRef CAS.
- K. Klier, Appl. Surf. Sci., 1984, 19, 267–297 CrossRef CAS.
- M. Kurtz, N. Bauer, C. Büscher, H. Wilmer, O. Hinrichsen, R. Becker, S. Rabe, K. Merz, M. Driess, R. A. Fischer and M. Muhler, Catal. Lett., 2004, 92, 49–52 CrossRef CAS.
- Y. F. Zhao, Y. Yang, C. Mims, C. H. F. Peden, J. Li and D. Mei, J. Catal., 2011, 281, 199–211 CrossRef CAS.
- L. C. Grabow and M. Mavrikakis, ACS Catal., 2011, 1, 365–384 CrossRef CAS.
- G. Wulff, Z. Kristallogr. – Cryst. Mater., 1901, 449–530 CAS.
- G. D. Barmparis, Z. Lodziana, N. Lopez and I. N. Remediakis, Beilstein J. Nanotechnol., 2015, 6, 361–368 CrossRef PubMed.
- R. Tran, Z. Xu, B. Radhakrishnan, D. Winston, W. Sun, K. A. Persson and S. P. Ong, Sci. Data, 2016, 3, 160080 CrossRef CAS PubMed.
- M. Behrens, F. Studt, I. Kasatkin, S. Kuhl, M. Havecker, F. Abild-Pedersen, S. Zander, F. Girgsdies, P. Kurr, B.-L. Kniep, M. Tovar, R. W. Fischer, J. K. Norskov and R. Schlogl, Science, 2012, 336, 893–897 CrossRef CAS PubMed.
- F. Studt, M. Behrens, E. L. Kunkes, N. Thomas, S. Zander, A. Tarasov, J. Schumann, E. Frei, J. B. Varley, F. Abild-Pedersen, J. K. Nørskov and R. Schlögl, ChemCatChem, 2015, 7, 1105–1111 CrossRef CAS.
- F. Studt, M. Behrens and F. Abild-Pedersen, Catal. Lett., 2014, 144, 1973–1977 CrossRef CAS.
- J. L. C. Fajín, M. N. D. S. Cordeiro, F. Illas and J. R. B. Gomes, J. Catal., 2009, 268, 131–141 CrossRef.
- G. C. Wang and J. Nakamura, J. Phys. Chem. Lett., 2010, 1, 3053–3057 CrossRef CAS.
- J. Yoshihara and C. T. Campbell, J. Catal., 1996, 161, 776–782 CrossRef CAS.
- P. B. Rasmussen, M. Kazuta and I. Chorkendorff, Surf. Sci., 1994, 318, 267–280 CrossRef CAS.
- P. B. Rasmussen, P. M. Holmblad, T. Askgaard, C. V. Ovesen, P. Stoltze, J. K. Nørskov and I. Chorkendorff, Catal. Lett., 1994, 26, 373–381 CrossRef CAS.
- J. Nerlov and I. Chorkendorff, J. Catal., 1999, 181, 271–279 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B, 1996, 54, 169 CrossRef PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- W. Sun and G. Ceder, Surf. Sci., 2013, 617, 53–59 CrossRef CAS.
- H. Monkhorst and J. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- G. Kresse, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787 CrossRef CAS PubMed.
- G. Henkelman and H. Jónsson, J. Chem. Phys., 2000, 113, 9978 CrossRef CAS.
- G. Henkelman and H. Jónsson, J. Chem. Phys., 1999, 111, 7010–7022 CrossRef CAS.
- A. Heyden, A. T. Bell and F. J. Keil, J. Chem. Phys., 2005, 123, 224101 CrossRef PubMed.
- F. H. P. M. Habraken, E. P. Kieffer and G. A. Bootsma, Surf. Sci., 1979, 83, 45–59 CrossRef CAS.
- G. C. Wang, L. Jiang, Y. Morikawa, J. Nakamura, Z. S. Cai, Y. M. Pan and X. Z. Zhao, Surf. Sci., 2004, 570, 205–217 CrossRef CAS.
- S. Y. Liem and J. H. R. Clarke, J. Chem. Phys., 2004, 121, 4339–4345 CrossRef CAS PubMed.
- K. S. Rawat, A. Mahata and B. Pathak, J. Catal., 2017, 349, 118–127 CrossRef CAS.
- M. G. Quesne, A. Roldan, N. H. De Leeuw and C. R. A. Catlow, Phys. Chem. Chem. Phys., 2019, 21, 10750–10760 RSC.
- W. Akemann and A. Otto, Surf. Sci., 1992, 272, 211–219 CrossRef CAS.
- W. Akemann and A. Otto, Surf. Sci., 1993, 287–288, 104–109 CrossRef CAS.
- K. H. Ernst, D. Schlatterbeck and K. Christmann, Phys. Chem. Chem. Phys., 1999, 1, 4105–4112 RSC.
- G. Anger, A. Winkler and K. D. Rendulic, Surf. Sci., 1989, 220, 1–17 CrossRef CAS.
- G. Wiesenekker, G. J. Kroes, E. J. Baerends and R. C. Mowrey, J. Chem. Phys., 1995, 102, 3873–3883 CrossRef CAS.
- S. Kumar and B. Jackson, J. Chem. Phys., 1994, 100, 5956–5964 CrossRef CAS.
- J. A. White and D. M. Bird, Chem. Phys. Lett., 1993, 213, 422–426 CrossRef CAS.
- L. Álvarez-Falcón, F. Viñes, A. Notario-Estévez and F. Illas, Surf. Sci., 2016, 646, 221–229 CrossRef.
- H. J. Freund and R. P. Messmer, Surf. Sci., 1986, 172, 1–30 CrossRef CAS.
- F. H. P. M. Habraken, G. A. Bootsma, P. Hofmann, S. Hachicha and A. M. Bradshaw, Surf. Sci., 1979, 88, 285–298 CrossRef CAS.
- F. H. P. M. Habraken and G. A. Bootsma, Surf. Sci., 1979, 87, 333–347 CrossRef CAS.
- F. H. P. M. Habraken, C. M. A. M. Mesters and G. A. Bootsma, Surf. Sci., 1980, 97, 264–282 CrossRef CAS.
- J. Nakamura, J. A. Rodriguez and C. T. Campbell, J. Phys.: Condens. Matter, 1989, 1, SB149–SB160 CrossRef CAS.
- F. Muttaqien, Y. Hamamoto, I. Hamada, K. Inagaki, Y. Shiozawa, K. Mukai, T. Koitaya, S. Yoshimoto, J. Yoshinobu and Y. Morikawa, J. Chem. Phys., 2017, 147, 094702 CrossRef PubMed.
- W. Luo, X. Nie, M. J. Janik and A. Asthagiri, ACS Catal., 2016, 6, 219–229 CrossRef CAS.
- K. J. P. Schouten, Z. Qin, E. P. Gallent and M. T. M. Koper, J. Am. Chem. Soc., 2012, 134, 9864–9867 CrossRef CAS PubMed.
- P. B. Rasmussen, P. A. Taylor and I. Chorkendorff, Surf. Sci., 1992, 269–270, 352–359 CrossRef CAS.
- Y. Yang, C. A. Mims, D. H. Mei, C. H. F. Peden and C. T. Campbell, J. Catal., 2013, 298, 10–17 CrossRef CAS.
- B. Xie, R. J. Wong, T. H. Tan, M. Higham, E. K. Gibson, D. Decarolis, J. Callison, K. F. Aguey- Zinsou, M. Bowker, C. R. A. Catlow, J. Scott and R. Amal, Nat. Commun., 2020, 11, 1615 CrossRef PubMed.
| This journal is © The Royal Society of Chemistry 2020 |