Reactivity descriptors in acid catalysis: acid strength, proton affinity and host–guest interactions
Prashant
Deshlahra
 *a and
Enrique
Iglesia
*b
*a and
Enrique
Iglesia
*b
aDepartment of Chemical and Biological Engineering, Tufts University, Medford, MA 02155, USA. E-mail: prashant.deshlahra@tufts.edu
bDepartment of Chemical Engineering, University of California at Berkeley, Chemical Sciences Division, E.O. Lawrence Berkeley National Laboratory, Berkeley, CA 94720, USA. E-mail: iglesia@berkeley.edu
First published on 22nd June 2020
Abstract
Brønsted acids mediate chemical transformations via proton transfer to bound species and interactions between the conjugate anion and bound cationic intermediates and transition states that are also stabilized by van der Waals forces within voids of molecular dimensions in inorganic hosts. This Feature Article describes the relevant descriptors of reactivity in terms of the properties of acids and molecules that determine their ability to donate and accept protons and to reorganize their respective charges to optimize their interactions at bound states. The deprotonation energy (DPE) of the acids and the protonation energy (Eprot) of the gaseous analogs of bound intermediates and transition states reflect their respective properties as species present at non-interacting distances. These properties accurately describe the reactivity of acids of a given type, such as polyoxometalates (POM) with a given type of addenda atom but different central atoms and heterosilicates, for different families of reactions. They do not fully capture, however, differences among acid types (e.g., Mo and W POM, heterosilicates, mineral acids) for diverse types of chemical transformations (e.g., elimination, isomerization, dimerization, condensation). The incompleteness of such descriptors reflects their inability to describe how protonated molecular species and conjugate anions restructure their respective charges when present as a binding pair at interacting distances. Such interaction energies represent electrostatic forces that depend on charge distributions in the cations and anions and the ability to reorganize the distributions to maximize the interactions. In the case of deprotonation, the electrostatic and charge reorganization components of DPE for various acids solely reflect the ability of the conjugate anion to accept and distribute the negative charge, a characteristic unique of each type of solid acid and specifically of the composition of its extended conjugate anion framework. The energy required to accept and rearrange the positive charge in bound intermediates and transition states reflects, in turn, their respective ability to recover the ionic and covalent components of DPE, the energy required to detach proton from conjugate anions. The DPE components and the recovery fractions together lead to a modified DPE, which captures only the part of DPE that remains unrecovered by the ion-pair interactions at bound intermediates and transition states, as the unifying descriptor for broad families of acids and reactions. The electrostatic and charge reorganization energies involved in these general descriptors are placed in historical context by assessing their connections to the heuristics of hard–soft acid–base displacements. Further development of these concepts requires benchmarking and extension of electrostatic and reorganization components of energies for a more diverse set of reaction types and acid families and advancement of methods for more efficient calculations of electrostatic interactions. Reactivity descriptors must also account for dispersive interactions between host cavities and guest molecules, requiring a framework analogous to the one described here for ion-pair interactions; these dispersive interactions depend on the fit between their shapes and sizes as well as their “structural stiffness” that determines the ability to modify the shapes of molecules and voids to minimize free energy. Entropy considerations and estimates of their dependence on properties of catalysts and molecules are also required for accurately determining Gibbs free energies that ultimately determine reaction rates.
1. Introduction
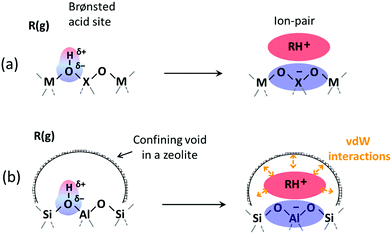
Solid Brønsted acids catalyze some of the most important chemical transformations of fossil and renewable feedstocks into valuable fuels and chemicals.1–7 Such materials contain protons, which act as active sites of varying acid strength, often residing within voids of molecular dimensions. Confinement effects can stabilize specific transition states and intermediates and provide significant control of molecular access to active sites.8–17 In such manners, the acid strength and the size and shape of the voids combine to determine reactivity, but the interactions that these two properties of solid acids mediate differ in origin and magnitude. Electrostatic and covalent effects are responsible for the consequences of acid strength on catalysis while weak concerted van der Waals forces, resulting from induced dipoles, account for the effects of confinement (Scheme 1).These different effects and consequences for catalysis are often conflated in mechanistic interpretations of observed reactivity and selectivity, in spite of the disparate contributions of these reactivity descriptors throughout the range of the very diverse solid acids, differing in composition and void structure, used in practice. Reactivity and binding properties of probe molecules are often attributed, inaccurately and imprecisely, to “acidity” differences.18–22 Fortuitous connections between binding energies and rates are inappropriately taken as evidence that the number and acid strength and the confining voids in solid acids constitute precise and inseparable measures of their “acidity”, even when the evidence contradicts these heuristics.16,23,24 Such a historical trajectory persists today, conjuring visions of universality in linear scaling relations, with a wish for simplicity thus used to replace the essential need for rigorous reactivity descriptors.
These descriptors must account for the independent effects of acid strength and confinement, but also for how separate descriptors of a catalyst and of the reacting molecules are insufficient to describe the stability of transition states and bound intermediates. These species determine reactivity and require their respective molecular fragments to interact with the surfaces of inorganic solids. In doing so, the locations of atoms and of electron density in guest and host species differ from those in their respective non-interacting states. As a result, the energy required to rearrange atoms and electrons must be considered in developing more accurate descriptors of reactivity. The requisite accuracy requires, in turn, that these descriptors become more specific for different types of acid catalysis and unavoidably less universal, thus requiring judicious choices between precision and simplicity, but also providing more insightful and diverse design criteria for catalyst optimization in return.
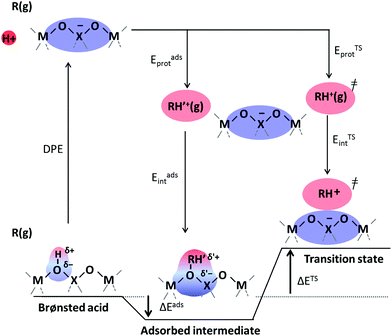
Brønsted acids transfer their protons, fully or in part, to molecules; in doing so, they enable the formation of cation–anion interacting pairs at the bound intermediates and transition states (TS) involved in the elementary steps that ultimately determine reactivity and selectivity (Scheme 1).10,25–29 Therefore, the deprotonation energy (DPE) of the solid, the only rigorous measure of acid strength, and the proton affinities, which reflect the energy associated with the formation of gaseous analogs of surface species from neutral molecules and isolated protons (Eprot), represent the independent, but incomplete, catalyst and molecular descriptors of reactivity. Born–Haber thermochemical cycles that express the energy change for the formation of kinetically-relevant intermediates or transition states from bare acids and gaseous molecules as a sum of the DPE of the solid (a property independent of the reactant molecules), the Eprot of the molecular analogs (a property independent of the solid), and the ion-pair interaction energies (Eint; Scheme 2), provide a conceptual framework for the analysis of activation barriers.11,12,19,23,24,29,30 The formation energy of ion-pair transition states is determined by the extent to which the energy required to remove the proton (DPE) can be recovered by interactions between the cationic organic moiety and the conjugate anion (Eint) at a TS. Such rigorous formalisms are based on the state function character of the thermodynamic properties that underpin transition state theory. They allow DPE and Eint to be dissected into components that depend on how protons and reactive cations differ in size and in the amount and location of their charges, which influence electrostatic interactions, charge relaxation in hosts and guests, van der Waals (vdW) contacts, and steric distortions of the bound species and the conjugate anion as they interact.13,15,30–35 These components have been assessed for diverse families of Brønsted acids and chemical reactions in recent studies that probe mechanistic details of these reactions and connections between reactivity and the properties of molecules and solid acids through experiment and theory.30,33,35–37
Here, we address the incomplete nature of the independent properties of the molecules and acid sites as descriptors for reactivity and selectivity and, in assessing such incompleteness, how host–guest interactions are essential, albeit less general, components of more accurate descriptors. The examples chosen mean to illustrate how the charge distribution in the cationic guests and the anionic hosts influence ion-pair interactions for acid sites of different strength, for the specific case of acids where the effects of dispersive interactions on the stability of bound intermediates and transition states do not vary significantly due to absence of confining voids. The matters of host–guest interactions involving dispersive and steric forces within confining voids are outside the scope and contents of this discourse.
Section 2 describes acid strength and proton affinity for diverse families of acids and reactants. Section 3 describes mechanistic details for several families of reactions catalyzed by Brønsted acids, chosen to establish how charge distributions in kinetically-relevant transition states and precursors influence rates and selectivity and to assess the merits and limitations of acid strength and proton affinity as independent descriptors. Section 4 illustrates how types of solid acids differ in the electrostatic and charge reorganization components that determine their DPE, but also in the binding of intermediates and transition states. These different components cause DPE to influence differently the stability of intermediates and transition states among these acids and thus their reactivity and, in the case of competing pathways with different DPE requirements, their selectivity. Section 5 illustrates how historical descriptors of acid–base interactions are relevant for solid acids and made quantitative by the treatments and concepts examined here.
2. Acid strength and proton affinity as separate descriptors of reactivity for active sites and molecular species involved in catalytic sequences
2.1. Families of Brønsted acids and their deprotonation energies
The strength of Brønsted acids reflects their ability to donate protons, a metric available for solid acids with well-defined structures from DFT-derived DPE values. These values merely reflect the stability of the conjugate anion, without residual interactions with the proton removed or with any molecular species. DPE values do not depend on the species that would ultimately accept the proton, whether such species are titrants, bound intermediates, or transition states; therefore, they represent the sole rigorous descriptor of the strength of a solid acid, irrespective of the purposes for which they are ultimately used; they describe a solid in isolation from its function as a catalyst and as a host for molecules.Fig. 1 shows several families of solid acids with known structures and includes materials with a broad range of acid strength and confining environments, such as polyoxometalates with Keggin structures (POM), heterosilicate zeotypes, and gaseous forms of mineral acids and liquid superacids consisting of Brønsted–Lewis pairs. Table 1 and Fig. 2 show DPE values of these acids obtained using different DFT functionals and cluster38 or periodic39,40 theoretical frameworks.
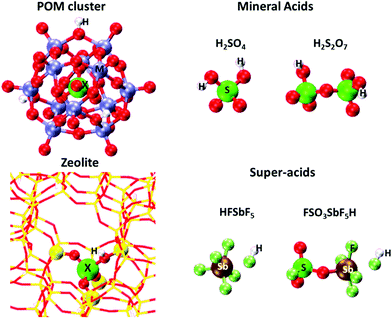 | ||
| Fig. 1 Optimized structures of a H3PMo12O40 POM cluster, a cluster representation of Al-MFI heterosilicate, and molecular Brønsted acids. The acid composition in POM and MFI is modified by changing the heteroatom (X) in POM and MFI and addenda atoms (M) in POM clusters. Adapted from data and methods reported in ref. 30, 41 and 42. | ||
| Index number | Acid identity | DPE values (kJ mol−1) | ||
|---|---|---|---|---|
| Periodic DFT | Cluster DFT | Other | ||
| a VASP39,40/PW91/USPP.30,33,41 b Gaussian38/PW91/Aug-cc-pvdz and 6-31G(d,p).30 c VASP/PW91/PAW.30 d Gaussian/B3LYP/6-311+G**.42 e Gaussian/G2(MP2).42 f VASP/RPBE/PAW/thermodynamic averaging and framework-dependent energy correction.43 g HF, QM-Pot method.44 h Gaussian/ωB97X-D/6-31G(d,p)/38 T-atom cluster.16 i Gaussian/ωB97X-D/6-311++G(3df, 3pd)/38 T-atom cluster.16 j VASP/PW91/USPP/128 T-atom cluster.33 | ||||
| POM clusters | ||||
| 1 | H2SW12O40 | 1068a | ||
| 2 | H3PW12O40 | 1081a | 1087c | |
| 3 | H4SiW12O40 | 1105a | ||
| 4 | H5AlW12O40 | 1117a | ||
| 5 | H6CoW12O40 | 1142a | ||
| 6 | H2SMo12O40 | 1095a | ||
| 7 | H3PMo12O40 | 1103a | 1109b | 1114c |
| 8 | H4SiMo12O40 | 1125a | ||
| 9 | H5AlMo12O40 | 1131a | ||
| 10 | H6CoMo12O40 | 1152a | ||
| POM clusters with all vicinal protons H-bonded to CH3OH monomers | ||||
| 1 | H2SW12O40 | 1084a | ||
| 2 | H3PW12O40 | 1113a | ||
| 3 | H4SiW12O40 | 1147a | ||
| 4 | H5AlW12O40 | 1164a | ||
| 5 | H6CoW12O40 | 1191a | ||
| 7 | H3PMo12O40 | 1136a | ||
| 8 | H4SiMo12O40 | 1167a | ||
| POM clusters with protonated CH3OH dimers on all vicinal protons | ||||
| 1 | H2SW12O40 | 1115a | ||
| 2 | H3PW12O40 | 1163a | ||
| 3 | H4SiW12O40 | 1207a | ||
| 4 | H5AlW12O40 | 1241a | ||
| 5 | H6CoW12O40 | 1252a | ||
| 7 | H3PMo12O40 | 1191a | ||
| 8 | H4SiMo12O40 | 1227a | ||
| Dehydrated POM clusters | ||||
| 2 | HPW12O39 | 1070a | ||
| 7 | HPMo12O39 | 1091a | ||
| Reduced POM clusters | ||||
| 7 | H5PMo12O40 | 1126a | ||
| Mineral acids | ||||
| 25 | H2SO4 | 1310a | 1313d | 1301e |
| 26 | H2S2O7 | 1203d | ||
| 27 | H2S3O10 | 1152d | ||
| 28 | H3PO4 | 1395a | 1384d | |
| Super acids | ||||
| 29 | FSO3SbF5H | 1106d | ||
| 30 | HSbF6 | 1108d | ||
| 31 | HC5(CN)5 | 1098d | ||
| 32 | HAlCl4 | 1111d | ||
| 33 | HAlBr4 | 1110d | ||
| Zeolites | ||||
| 35 | MFI, BEA, FER, MOR, CHA, FAU | 1201 ± 11f | 1170–1200g | |
| Heterosilicate clusters with MFI structure | ||||
| 37 | Al-MFI | 1186a | 1226h (1200)i | 1167j |
| 38 | Ga-MFI | 1195a | 1246h | 1178j |
| 39 | Fe-MFI | 1201a | 1242h | 1189j |
| 40 | B-MFI | 1251a | 1292h | 1214j |
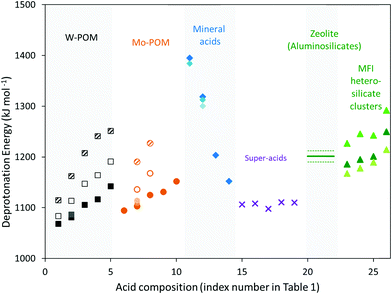 | ||
| Fig. 2 DPE values calculated for a proton on W-POM (squares) and Mo-POM (circles) clusters, when all vicinal protons on the same cluster are bare (closed symbols) or covered with H-bonded CH3OH monomers (open symbols) or protonated CH3OH dimers (shaded symbols), gas-phase molecular mineral acids (diamonds), super-acids (×), zeolites (horizontal line; dashed lines show uncertainty resulting from deviations in DPE values for different frameworks and Al atom locations43), and cluster forms of MFI heterosilicates (triangles) as a function of the acid composition represented by the index number shown in Table 1. Dark, medium and light shades of closed symbols reflect methods 1, 2 and 3 used to calculate DPE values, as shown in Table 1. | ||
POM clusters consist of a central tetrahedral oxo-anion encapsulated within a shell of octahedral metal-oxo species, with external cations acting to compensate the ionic charge at the center (Fig. 1). For WOx shells (W-POM), the DPE values for removing one proton increase monotonically (1068–1142 kJ mol−1)12,30,45,46 as the valence of the central atom decreases (S6+, P5+, Si4+, Al3+, Co2+) and as the number of balancing protons concomitantly increases. Similar trends are evident for Mo-POM clusters (DPE 1095–1152 kJ mol−1; Table 1), but the DPE values for Mo-POM clusters are larger than for W-POM clusters for any given central atom because MoOx shells can reorganize the negative charge imposed by the removal of the proton at a lesser energy cost.30,33,41,45 The DPE values of protons in POM clusters are sensitive to chemical modifications at vicinal locations. For example, DPE values decrease when vicinal OH groups recombine to form dehydroxylated clusters (and H2O) and increase when H-atoms reduce POM clusters upon cleavage of C–H bonds during oxidative dehydrogenations (Table 1).41 The DPE also increases as vicinal protons in a given cluster interact with bound species via H-bonding (1081 to 1113 kJ mol−1 as a CH3OH is H-bonded to each of the two vicinal protons in H3PW12O40 cluster; Table 1) or as some of the other protons in a POM cluster are transferred to bound molecules to form ion-pairs (1081 to 1163 kJ mol−1 as a protonated CH3OH dimer is formed at each of the two vicinal protons in H3PW12O40 cluster; Table 1).30,45 These trends reflect the concomitant increase in the anionic charge within such clusters as a result of such interactions, which lead to a stronger conjugate base and a higher energy cost for proton transfer. Such effects are ubiquitous on POM clusters, which act as polyprotic acids, but are absent on acids with protons that are isolated electronically, either by large distances or by an insulating interconnecting framework, as is the case for heterosilicates. The coverage dependence of DPE on polyprotic acids can, in turn, lead reactivity to vary with the coverage and the charge of bound species during catalysis. Thus, changes in identities of the central heteroatom and addenda atoms in oxide shells, dehydroxylation, H-atom addition and formation of bound species in systems with “interacting” protons lead to significant variation in DPE values for POM clusters (by ∼200 kJ mol−1).
DPE values for mineral oxo-acids (e.g. H2SO4, H3PO4) also increase as the valence of the central atom in their XO4 tetrahedra decreases,30,42 as in the case of POM clusters (Fig. 2 and Table 1). Similarly, the intermolecular dehydration of mineral acids (e.g., H2SO4 conversion to H2S2O7 or H2S3O10) decreases the DPE values (Fig. 1, 2 and Table 1),42 because the linked SO4 tetrahedra act as Lewis acids and accept electrons upon deprotonation, leading to more stable anions and weaker conjugate bases. DPE values for other strong acids containing Brønsted–Lewis acid site pairs (1098–1111 kJ mol−1; Fig. 1, 2 and Table 1)42 are smaller than for H2SO4 (1313 kJ mol−1), but larger than for some POM clusters (1081 kJ mol−1 for H3PW12O40). Thus, some POM clusters are stronger acids than Brønsted–Lewis site pairs that are denoted as “superacids” in their solvated liquid forms. The extent of dissociation of protons in condensed liquid acids, the property measured by acidity functions,47 however, would be enhanced by the solvating environments around the molecular groups. Thus, acid strength and solvation effects are conflated in empirical acidity scales and the two must be separated to decipher effects of the reactive site and the environment on reactivity and selectivity trends for broad classes of acids.
For POM clusters and mineral acids, DPE values derived from cluster and periodic DFT treatments are shown in Table 1. Cluster methods treat isolated molecules or clusters using wavefunctions consisting of linear combinations of basis functions localized at each atom. Periodic codes treat units (“supercells”) that repeat in all three dimensions and use non-local plane-waves as basis functions. For each acid, differences in DPE values between periodic and molecular methods are of the same order as those using different functionals, basis sets, or pseudopotentials for each method (Table 1; H3PMo12O40 DPE 1103 and 1114 kJ mol−1 from periodic PW91 method with US and PAW pseudopotentials, and 1109 from cluster method; H2SO4 DPE 1310 from periodic DFT, and 1301 and 1313 kJ mol−1 from B3LYP/6-31G** and G2(MP2) cluster methods, respectively). Thus, any inaccuracies caused by charged repeating units are accurately treated by the corrections implemented in periodic treatments.48,49
In contrast to acids of molecular or cluster character, zeolites contain extended crystals with many repeating units and precise DPE values for such systems represent a calculation challenge. For instance, the DPE for a proton balancing the AlO4− framework charge at the intersection between straight and sinusoidal channels in Al-MFI zeolite is 1668 kJ mol−1 from periodic DFT methods (without charge correction),43 1226 or 1186 kJ mol−1 from cluster or DFT methods for MFI clusters with 38 T-atoms (37 Si and one Al atom; Table 1),16 1167 kJ mol−1 for a 128 T-atom cluster using periodic DFT (Table 1),33 and 1200 kJ mol−1 for “QM-Pot” methods that treat local regions near protons using quantum mechanics (QM) and the more distant crystalline framework with classical interatomic potentials (Pot) parametrized by ab initio methods.44 These differences represent inaccuracies in correcting for interactions among periodic conjugate anions, as well as the possibility that the reference energies change significantly between charged and uncharged systems in the programs used to calculate the energies, instead of any expected composition or structure dependent DPE changes in these systems as discussed next.43
The energy of a periodic system with a net charge represents an infinite series of electrostatic interaction terms that does not converge to a finite value; therefore, charged supercells must include a uniform background charge in order to maintain charge neutrality. The corrections required to estimate the spurious interactions of atoms with this background charge and of dipole and quadrupole moments of isolated supercells with the periodic lattice of these moments to subtract them from DFT-derived energies.48,49 These corrections are accurate for POM and molecular acids because the atoms in each supercell are isolated electronically from vicinal supercells by a vacuum region. The dipole and quadrupole corrections, however, cannot be implemented for crystalline heterosilicates,50–52 because the electron density for atoms at the edges of each supercell extend beyond its boundaries, while the respective nuclei remain fully within the supercell.
QM-Pot methods can circumvent these specific artifacts in charged periodic systems,44,53,54 but the resulting energies depend sensitively on the shape and size of the QM cluster chosen, on the unrelaxed link atoms that are required to terminate such a cluster, and on the approximations used for “embedding” clusters in classical potentials. Analyses based on consistent treatments of such factors by using the same size of QM cluster and terminating Si–H bonds in CHA, FAU, MFI and MOR zeolites showed that DPE values are insensitive to the framework structure (1170–1200 kJ mol−1; Table 1 and Fig. 2), and close to energies derived solely from DFT by using large MFI clusters (1167 kJ mol−1 for 128 T atom MFI, Table 1).44 QM-Pot methods also showed that DPE values for proton forms of zeolites do not depend on the density of Al atoms in the framework, except for next nearest neighbor Al sites (protons at paired AlO4− tetrahedra linked by a single Si atom via Al–O–Si bridges).55
High-silica zeolites that contain only isolated tetrahedral AlO4− anions and charge-balancing protons within insulating silicate frameworks are compositionally uniform and free of central heteroatom changes and interactions of vicinal protons in polyprotic species that influence DPE in POM and mineral acids (Table 1 and Fig. 1). Consequently, DPE values could only be influenced by the local structure imposed by a given crystalline framework when Al is the heteroatom; the framework type determines the local Al–O–Si bond angles and the O–H bond lengths and vibrational frequencies. These effects were assessed for MFI, FER, MOR BEA, CHA and FAU frameworks.43 DPE values were calculated at each tetrahedral site for a given framework by ensemble averaging them at the four O-atoms in each AlO4 group; these DPE values are similar at each distinct crystallographic Al site for each given framework (within ±3, 5, 7, 22 kJ mol−1 for FER, BEA, MFI, MOR; CHA and FAU have only one Al location).43 The DPE values for each T-site did not scale monotonically with the different Al–O–Si bond angles, OH bond lengths, or frequencies at each location, indicating that DPE values are insensitive to the local Al structure that contains the charge-balancing proton.43,44,54,56 DPE values, however, varied by as much as 150 kJ mol−1 among frameworks and were larger (by more than 400 kJ mol−1) for MFI than values calculated from QM-Pot methods (1200 kJ mol−1)44 or from cluster models for MFI (1167–1226 kJ mol−1).43 These differences reflect inaccurate anion energies in periodic supercells that scale linearly with the density of framework atoms in each structure. These corrections were determined using the slope of linear dependence of DPE on framework density, and the difference between periodic DFT43 and QM-Pot44 values at one O-atom in MFI. These procedures lead to mean DPE values of 1201 ± 11 kJ mol−1 for all Al-atom T-site locations in MFI, FER, MOR BEA, CHA and FAU frameworks (Table 1 and Fig. 2).43
More recently, a re-examination of DPE calculations using QM-pot methods57 confirmed that these DPE estimates are insensitive to the Si–O–Al bond angles, but exhibit a dependence on the dielectric constant of zeolites, which, in turn, depends on framework densities. This framework density dependence is much weaker than periodic models as shown by 30 kJ mol−1 difference between DPE of MFI and FAU,57 which is much less than the corresponding difference of 150 kJ mol−1 in periodic models without dipole and quadrupole corrections.43 The effects were shown to reflect the energy of solvation of the positive charge in the detached proton located within the framework, which varies inversely with the dielectric constant in classical continuum solvation models. Such details were used to derive an intrinsic DPE corresponding to a proton that remains in the framework upon deprotonation at a distant location from the conjugate anion, which ultimately did not depend on framework density.57
Taken together, these calculations show that DPE values do not depend on the framework structure or the local structure at the T-site that stabilizes the protons in aluminosilicates and resolve discrepancies in periodic DFT calculations by correcting for inaccuracies in the reference state energy in such periodic DFT implementations. DPE values in such heterosilicate framework, however, depend strongly on the identity of the trivalent atom in heterosilicates and thus on composition, as is also the case for POM clusters and mineral acids (Table 1 and Fig. 2; 1226–1292 kJ mol−1 for MFI with Al, Ga, Fe, B heteroatoms using a 38-atom cluster in VASP). Such effects of composition reflect the ability of the conjugate anion to accept the negative charge, which depends on the electronegativity or Lewis acid strength of the central heteroatom in the acid.
The DPE of an acid fully describes its strength, independently of what reactants, transition states, or molecular probes ultimately interact with the proton in adsorption or catalysis. It represents a descriptor of the acid catalyst because the energies of bound intermediates and transition states relevant to reactivity depend on DPE (Scheme 2; ΔE = DPE + Eprot + Eint). The protonation energies (Eprot values), in contrast, depend only on the properties of the molecules that interact with the protons, irrespective of the properties of the protons; they reflect the energy of the reaction between a gaseous proton and a gaseous acceptor molecular species.
2.2. Molecules and their protonation energies
The energies involved in forming gaseous cations from neutral molecules represent their protonation energies (Eprot). These energies are relevant for chemical reactivity when the cations formed are faithful structural and chemical analogs for the relevant bound intermediates and transition states in a catalytic sequence, as depicted in the thermochemical cycle formalisms in Scheme 2. These energies are strictly molecular properties, with more negative Eprot values characteristic of more stable gaseous cations.30,33,58–63 Calorimetric measurements have shown that enthalpies of adsorption of several alcohol and nitrile species correlate with the proton affinity,64,65 providing a direct evidence that Eprot values are descriptors of energies of surface species, as inferred from kinetic measurements for several reactions in Section 3.Scheme 3 shows several types of bound cations including those formed upon protonation of bases often used to titrate acid sites as well as intermediates and transition states typically encountered in solid acid catalysis. Scheme 3 also shows gaseous analogs of these bound cations formed by protonation of neutral precursors. Ammonia and pyridine titrants accept protons to form bound ammonium and pyridinium cations, respectively, from strong Brønsted acids and H-bonded species with a partial proton transfer on weaker acids. Here, free ammonium and pyridinium cations represent the gaseous analogs of the respective bound species (Scheme 3, steps 1 and 2). H2O and CH3OH assist proton-hopping among O-atoms in the conjugate anions of acids through transition states that resemble H3O+ and CH3OH2+ cations, respectively; consequently, such cations represent their respective gaseous analogs of proton hopping transition states (Scheme 3, steps c and d).66 Gaseous analogs are similarly evident for the intermediates and transition states that mediate alkanol dehydration (Scheme 3, steps e and f), isomerization (step g) and oligomerization (step h) of alkenes, and monomolecular protolytic cracking (step i) and dehydrogenation (step j) of alkanes. Table 2 shows these catalyst-independent protonation energies (Eprot) for each of these species derived from cluster38 and periodic39,40 DFT calculations.
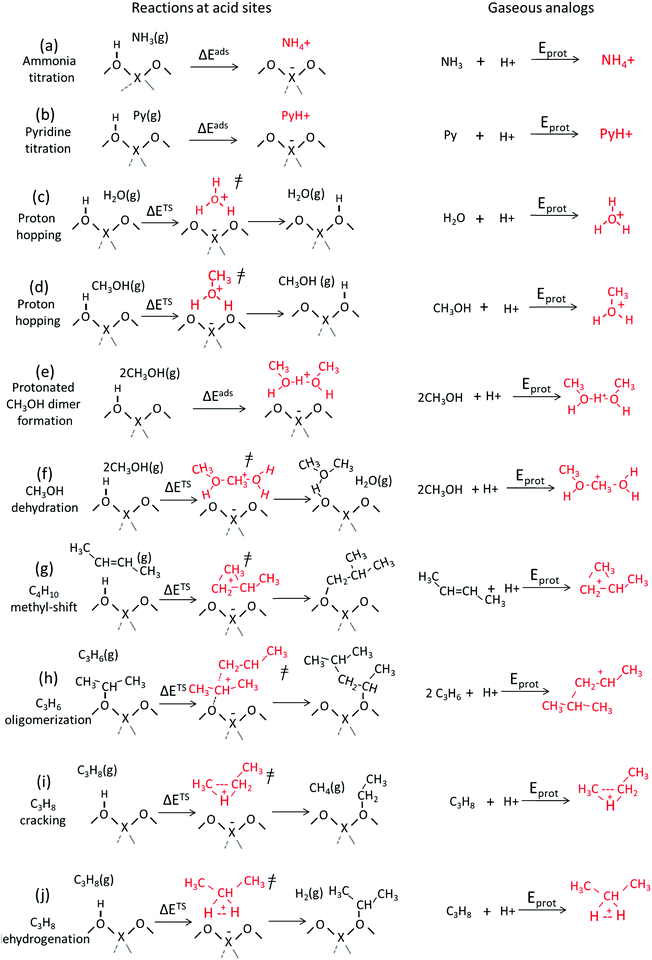 | ||
| Scheme 3 Examples of charged species and transition states mediating acid-catalyzed reactions and the formation of gaseous analogs of such species via addition of a proton to reactant molecules. | ||
| Molecule | Protonated species | DPE values (kJ mol−1) | ||
|---|---|---|---|---|
| Periodic DFT | Cluster DFT | Measuredf | ||
| a VASP, PW91, USPP.30,33 b Gaussian.59 c Gaussian.60 d Gaussian.61–63 e CHH+ and CHC+ cations illustrated in Scheme 3, steps i and j. f Measured values.65 | ||||
| N-Containing molecules | ||||
| NH3 | NH4+ | −884a | −887b | |
| C5H5N | C5H5NH+ | −964a | ||
| Oxygenates | ||||
| H2O | OH3+ | −717a | −718b | −724f |
| CH3OH | CH3OH2+ | −779a | −774f | |
| CH3OH-H+–CH3OH | −924a | |||
| CH3OH–CH3+–H2O | −815a | |||
| Alkanes | ||||
| CH4 | CH5+ (CHH+)e | −557c | ||
| C2H6 | CHC+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e e |
−622a | ||
CHH+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e e |
−607a | −607c | ||
| C3H8 | CHC+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e e |
−662a | −644d | |
CHH+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e e |
−628a | −610d | ||
| i-C4H10 | CHC+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e e |
−712a | −685d | |
CHH+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e e |
−708a | −631d | ||
| Alkenes | ||||
| C2H4 | CH3CH2+ (primary) | −671c | ||
| (CH2CH2)H+ (bridging) | −703a | −700c | ||
| C3H6 | CH3CH2CH2+ (primary) | −696a | ||
| CH3CH + CH3 (secondary) | −786a | |||
| Cyclopropyl | −748a | |||
| 1-C4H10 | Methylcyclopropyl | −787a | ||
| Cycloalkenes | ||||
| C6H10 | Ring contraction TS | −815a | ||
These Eprot values reflect the proton-accepting tendencies of the specific atoms that share the positive charge and thus depend on the specific reactions that occur when the protons are placed at different locations within a given acceptor. The N-atoms in NH3 and pyridine molecules are strongly basic and Eprot values are negative and large (−884 and −964 kJ mol−1 for NH3 and pyridine; Table 2), making such molecules essentially irreversible titrants of Brønsted acids at low temperatures (Scheme 3, steps a and b). Such cations mediate reactions such as selective catalytic reduction of NO using ammonia67,68 and pyridine synthesis.69 Oxygenates, alkenes and alkanes exhibit less negative Eprot values than NH3 (−779, −717, −703, −557 kJ mol−1, for CH3OH, H2O, C2H4 and CH4; Table 2). The replacement of H-atoms in hydrocarbons or oxygenates by stronger electron donors (e.g., CH3 groups) makes the protonated species more stable and Eprot values more negative (−717 and −779 kJ mol−1 for H2O and CH3OH; −557 and −607 kJ mol−1 for CH4 and C2H6; Table 2). Protonated H2O shuttles protons among the O-atoms in the oxoanions of solid acids, while protonated alkanols act as transition states for proton shuttling as well as H2O elimination during alkanol dehydration reactions and for the ultimate desorption of alkenes from the resulting bound alkoxides.12,70 The protonated alkanol dimers that mediate direct dehydration events and thus circumvent bound alkoxides as intermediates are more stable than protonated monomers (Scheme 3, steps d, e; Table 2, Eprot values −717, −779, −924, −815 kJ mol−1 for the formation of H3O+, CH3OH2+, CH3OH–H+–CH3OH, CH3OH–CH3+–H2O, respectively).12,70,71
In isomerization reactions, propene reactants from cyclopropyl cations that are more stable than primary cations but less stable than secondary cations (Eprot values −748, −696, −786 kJ mol−1; Table 2). These cyclopropyl cations mediate methyl shifts in alkene isomerization reactions (Scheme 3, step g) and become more stable when alkyl substituents are present at C-atoms connected to the C-atoms involved in the double bond (Eprot values −748 and −787 kJ mol−1 for cyclopropyl and methylcyclopropyl cations; Table 2).14,72 In monomolecular alkane rearrangements mediated by pentacoordinated carbonium ions, CHC+ and CHH+ three-atom charged moieties mediate cracking and dehydrogenation, respectively (Scheme 3, steps i and j).15,61–63 These alkane-derived carbonium ions are the least stable cations among the species included in Table 2.
The values of DPE for the acid and of Eprot for the gaseous analogs of bound species are descriptors of reactivity because they influence the energy required for H-transfer from the acid to the molecule. These descriptions are incomplete because the distribution of charge and the atomic arrangements in the conjugate anion and in the protonated molecules are different in their isolated form, used to calculate DPE and Eprot, from those when brought together in their interacting state. As a result, DPE and Eprot are incomplete descriptors, because the extent of reorganization differs among families of catalysts for a given reaction, preventing the formation energies of bound species from being uniquely related to these independent catalyst and molecular properties (Section 3). For instance, CH3OH dehydration activation energies are smaller on stronger acids for both Mo-POM and W-POM with different central atoms and MFI with different heteroatoms, but for a given DPE values, they are also lower for MFI than for Mo-POM or W-POM. Also, the formation energy of transition states on H3PW12O40 cluster is not a smooth function of Eprot as, for example, the transition state formation energies for H2O mediated proton shuttling is much lower than methyl shift in protonated C3H6 despite similar Eprot values to form H3O+ and cyclopropyl C3H7+ from respective molecules (Section 3). The origins of the incompleteness and more complete descriptors derived from accurate assessments of the components of interaction energies are discussed in Section 4.
3. Effects of DPE and Eprot on reactivity and selectivity for Brønsted acid catalyzed dehydration, isomerization and condensation reactions
The method of analysis described here separates the energy of bound species into terms that reflect the independent properties of catalysts and molecules and an additional term that describes how the conjugate anion and the bound cation interact through electrostatic effects and rearrangements made possible by the ability of the interacting species to reorganize their respective charge distributions and atomic arrangements. The methods used and the conclusions reached, described here for the specific example of catalytic transformations on Brønsted acids, affirm the more general tenet that molecular and catalyst descriptors characteristic of their non-interacting states can never provide descriptions of a universal character for reactions mediated by bound species.The thermochemical cycle in Scheme 2 depicts hypothetical steps that, when taken together, combine to give the energies of formation of kinetically-relevant transition states (ΔETS) and of bound species (ΔEads) from a bound proton and the gaseous reactants. These energies of formation are given by the sum of (i) the DPE of the solid acid; (ii) the protonation energies of the gaseous analogs of transition states and bound intermediates from a gaseous H+ and neutral precursors (ETSprot, Eadsprot); and (iii) the interaction energies between the conjugate anion formed in (i) and the protonated species formed in (ii) (ETSint, Eadsint) to give:
| ΔETS = DPE + ETSprot + ETSint | (1) |
| ΔEads = DPE + Eadsprot + Eadsint | (2) |
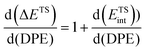 | (3) |
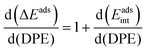 | (4) |
When the kinetically-relevant steps occur on bare surfaces, measured activation energies derived from rate constants represent the energy required to form the transition state from gaseous reactants (Ea = ΔETS). Bound species become the relevant precursors when such species are present at near saturation coverages and activation energies reflect the energy required to form the transition states but from bound species (Ea = ΔETS − ΔEads).12,30 In the latter case, eqn (1) and (2) indicate that activation energies reflect the combined effects of DPE and Eprot on the interacting transition state and the bound precursors:
| Ea = (ETSprot − Eadsprot) + (ETSint − Eadsint) | (5) |
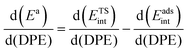 | (6) |
The selectivity to a given product for two parallel reactions from the same bound precursor occurring at any given surface coverage reflects the energy differences between their kinetically-relevant transition states, which, in turn, represent the combined differences in protonation energies and ion-pair interaction energies between the two transition states:
| Ea1 − Ea2 = (ETS1prot − ETS2prot) + (ETS1int − ETS2int) | (7) |
The sensitivity of the selectivity to DPE then merely represents the difference between sensitivities of the ion-pair interactions energies for the two transition states:
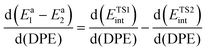 | (8) |
These treatments exploit the thermodynamic nature of transition state formalisms and the nature of the relevant state functions. They show that rates and selectivities depend on the catalyst-independent Eprot values of molecular analogs of bound intermediates and transition states, but also on Eint values, which represent the ability of each adsorbate–catalyst pair to restructure the placement of their electrons and atoms in order to minimize the free energy of each pair. These Eint values depend on DPE, through the distribution of charge in the anion, but also on the size/shape of the confining voids and on the charge distribution and size/shape of the molecules involved in each adsorbate–catalyst interacting pair. The unique character of each pair introduces significant challenges in defining a more complete descriptor by precluding any plausible claims to universality. In return, these interactions introduce a rich diversity of catalytic behaviors that transcends the narrow confines of formalisms based solely on the independent properties of catalysts and molecules.
These concepts and the limitations of such descriptors are illustrated here for several families of reactions on Mo-POM, W-POM, MFI and mineral acids, but the treatments and learnings are applicable beyond the chosen examples. Each reaction seeks to illustrate ancillary concepts and consequences; they include consequences for reactivity and selectivity for alkanol elimination, isomerization of alkanes and cycloalkanes, alkene dimerization, and alkanol–alkene Prins condensation. Alkanol eliminations are used to demonstrate how a given mechanism at different coverages of bound intermediates leads to two different rate constants, each one of which determined by barriers that reflect the energy of formation of the same ion-pair transition state but from two different bound intermediates that differ in charge, thus leading to different consequences of DPE for the two rate constants. The skeletal isomerization of alkanes and cycloalkanes is used to show how the charge distribution within the cationic moiety at an ion-pair transition state determines the sensitivity of activation barriers to DPE and how parallel rearrangements mediated by transition states with similar charge distributions render selectivities insensitive to DPE. Alkanol–alkene Prins condensation and alkene dimerization reactions are used to demonstrate how transition states that differ in net charge lead to weaker effects of DPE for those with lesser charge, which become favored on weaker acids. These illustrative examples demonstrate the effects of charges and their location in cations and anions at ion-pair transition states and in bound intermediates for acids of different strengths within the families of W-POM, Mo-POM, MFI and mineral acids, but exclude the effects of the “softness” of charge distributions.
3.1. Alkanol elimination reactions
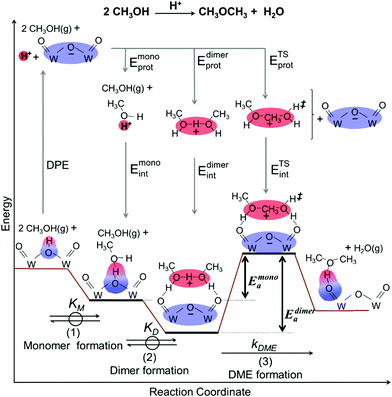
Methanol dehydration to dimethyl ether (DME) proceeds on solid Brønsted acids via either sequential or direct routes on POM clusters and zeolites, with relative contributions that favor sequential routes at high temperatures (>500 K) because of the entropy penalties of bimolecular pathways. DFT-derived Gibbs free energies of transition states for this reaction, together with spectroscopic evidence for bound intermediates during catalysis, indicate that direct routes prevail at the lower temperatures relevant in practice.12,73 This direct route involves quasi-equilibrated formation of H-bonded CH3OH monomers (KM, Scheme 4, step 1) and of protonated dimers (KD, Scheme 4, step 2) and dimer rearrangements that eliminate H2O in the kinetically-relevant step (kDME, Scheme 4, step 3),12,73 leading to turnover rates (v; per H+ measured by titration during catalysis) given by: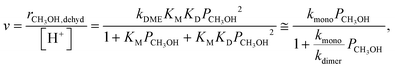 | (9) |
The kmono and kdimer parameters obtained by regressing rate data to the functional form of eqn (9) decreased exponentially as DPE values increased on both W-POM and Mo-POM clusters with different central atoms and on MFI with different heteroatoms (Fig. 3a), consistent with higher activation energies on the weaker acids.12,16 When DPE predominantly influences activation energies instead of entropies, the sensitivities of rate constants can be used to determine the effects of DPE on activation energies:
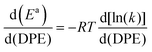 | (10) |
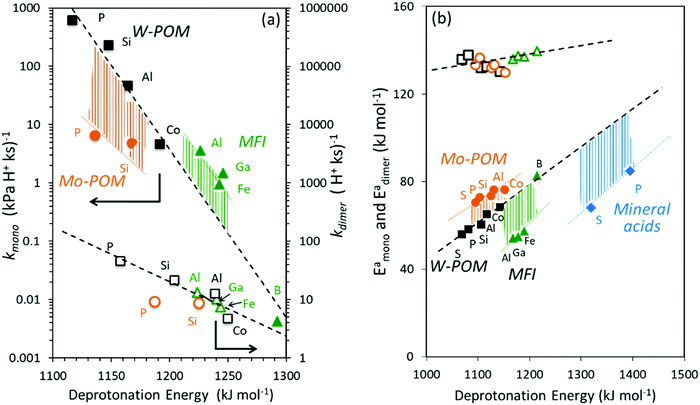 | ||
| Fig. 3 (a) Measured CH3OH dehydration rate constants at 433 K and (b) DFT-derived energies of direct DME formation transition states referenced to an adsorbed CH3OH monomer and a gaseous CH3OH (kmono, Eamono; closed symbols) and referenced to a protonated CH3OH dimer (kdimer, Eadimer; open symbols) as a function of DFT derived DPE values on W-POM (squares) and Mo-POM (circles) clusters and mineral acids (diamonds) with different central atoms (S, P, Si, Al, Co) and MFI heterosilicates (triangles) with different heteroatoms (Al, Ga, Fe, B). For abscissa in (a) the DPE values for clusters saturated with monomers and dimers are used for kmono and kdimer, respectively, due to the saturated nature of surfaces at measurement conditions (DPE values in Table 1 and Fig. 2). Adapted from data originally reported in ref. 12, 16 and 30 | ||
Larger alkanols also interact with protons to form H-bonded and ion-pairs intermediates and transition states; these species show charge distributions analogous to those for methanol but include monomolecular H2O elimination routes that form alkoxides (that desorb as alkenes) along with bimolecular routes, as in the case of methanol, to ethers. Ethanol dehydration to diethyl ether occurs via SN2 type substitution routes, either sequentially via bound ethoxy intermediates (also formed via SN2 type reactions) or directly via reactions of H-bonded ethanol with another ethanol. Bound ethoxy species can also form ethylene via E2 type elimination steps.70 H-bonded monomers, protonated ethanol dimers, and ethoxy species represent the prevalent bound intermediates at typical conditions of ethanol dehydration. The dehydration rate constants decrease with increasing DPE and for POM with Co central atoms are about 10-fold lower than P central atoms, consistent with lower reactivity for the weaker acid.70 This sensitivity of rate constants to DPE reflects more highly charged transition states than their relevant precursors, as discussed above for the case of CH3OH dehydration. The ratios of rate constants for SN2 and E2 pathways, however, are nearly identical among these solid acids and thus insensitive to DPE because both transition states are highly charged. Such acid-independent selectivities reflect the similar amounts and spatial distributions of charge for the transition states that mediate these two routes; as a result, the interaction energies at their respective transition states recover a similar fraction of the respective DPE for each cluster.70
These data show that the amount and distribution of charge at transition states and precursors determine the effects of DPE on reactivity and selectivity; these conclusions are confirmed next by describing transition state structures that mediate the isomerization of alkenes and cycloalkenes. For these reactions, activation energies depend on the energy required to form ion-pair transition states from a proton and a gaseous reactant, but the transition state structures for acyclic and cyclic alkenes differ in how they delocalize their positive charge; as a result, they recover the energy required to separate the proton to a different extent, leading to rate constant ratios that sense acid strength.
3.2. Skeletal isomerization of acyclic and cyclic alkenes
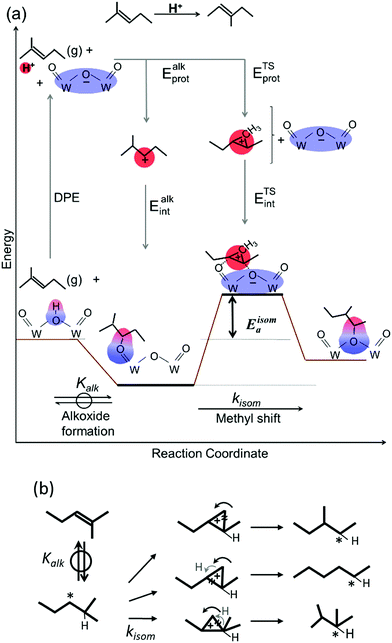
Skeletal isomerization of alkenes is carried out on bifunctional metal–acid catalysts with the metal function performing the quasi-equilibrated dehydrogenation of alkanes. The alkenes formed are protonated to give bound alkoxides and undergo methyl shifts mediated by cyclopropyl carbocations.11,14,74–76 Turnover rates are accurately described by: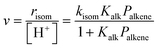 | (11) |
The interconversion of acyclic skeletal hexane isomers (n-hexane, 2-methylpentane, 3-methylpentane, 2,3-dimethybutane and 2,2-dimethybutane; Fig. 4a and b) is used here as an illustrative example,14 but the analysis and conclusions are general for isomerization of alkanes and alkenes of different chain length and also for their β-scission reactions.75,76 These skeletal rearrangements occur via cyclopropyl carbocations that mediate methyl shifts and the lengthening or shortening of backbones (Scheme 5). The cyclopropyl cations that mediate changes in the backbone length require the concerted transfer of a H-atom in order to transfer a primary methyl group to a location along the backbone (Scheme 5b).72 The cyclopropyl ion-pair transition states mediating the methyl shifts and the backbone length changes differ in the stability of their respective gaseous analogs, because of the different degrees of substitution of the C-atoms within cyclopropyl groups (Eprot values in Table 2); cations with alkyl groups attached to the CH2–CH2 moiety in the cyclopropyl group are more stable than those requiring concerted CH3- and H-shifts (Fig. 4a). The positive charge is located at the same position within the cyclopropyl moiety for all skeletal rearrangement events, causing all isomerization rate constants to decrease exponentially and to the same extent for all isomer products with increasing DPE on W-POM clusters with different central atoms (Fig. 4b); consequently, the ratios of these rate constants, a measure of selectivity, are insensitive to DPE. More explicitly, these DPE-independent selectivity ratios reflect transition states that not only have similar charges and charge locations, but also ones that recover, as a result, similar fractions of the DPE difference between stronger and weaker acids via interactions with conjugate anions. These ratios merely reflect the stability of the gaseous analogs of their respective transition states on all acids.14
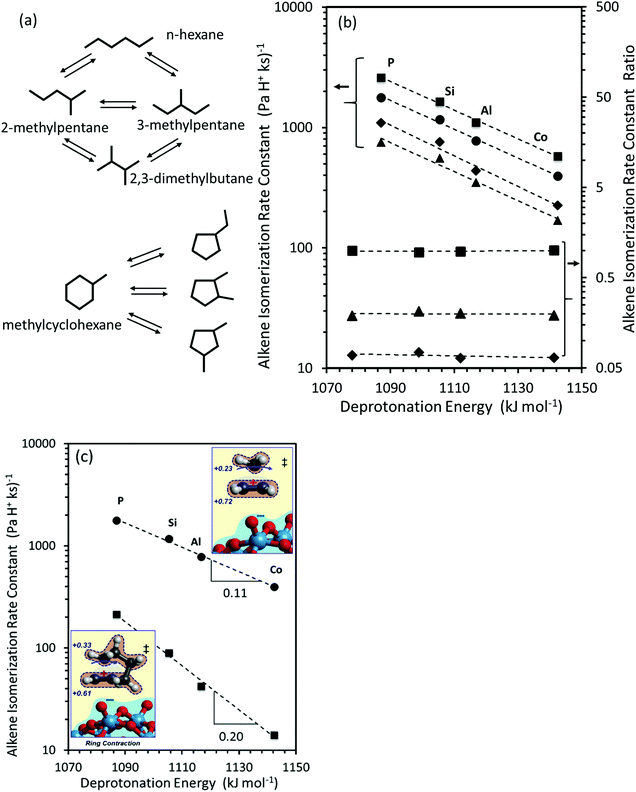 | ||
| Fig. 4 (a) Interconversion of hexane and methylcyclohexane and their skeletal isomers. (b) Measured isomerization rate constants for 2-methylpentane (circles), 3-methylpentane (squares), 2,3-dimethylbutane (diamonds) and n-hexane (triangles), and rate constant ratios for 3-methylpentane (squares), 2,3-dimethylbutane (diamonds) and n-hexane (triangles) isomerization to 2-methylpentane. (c) 2-methylpentane (circles) and methylcyclohexane (squares) isomerization rate constants, as a function of DFT derived DPE values on W-POM clusters with different central atoms (P, Si, Al, Co). Insets in (c) show charge distributions in methyl-shift and ring-contraction transition states. Data originally reported in ref. 14 and 74. | ||
The conversion of methylcyclohexane to alkyl cyclopentane isomers (Fig. 4a) also requires the shift of an alkyl group (instead of the methyl in n-alkenes) in protonated cycloalkyl cations, which causes a new C–C bond to form and the ring to contract. In this case, the alkyl groups with the more electron donating nature than methyl delocalize positive charge in the cyclopropyl center (insets in Fig. 4c; charge delocalization for methyl shift in cyclohexene is greater than in propene), leading to a more diffuse cation that recovers a smaller fraction of the differences in DPE among W-POM clusters with different central atoms, as discussed above for the case of methanol dehydration intermediates and transition states. The weaker recovery of DPE differences causes the energy of formation of ring-contraction transition states from bare protons and gaseous cycloalkenes to be more sensitive to acid strength than the interconversion among n-hexane isomers (Fig. 4c, −RTd(ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k)/d(DPE) values 0.11 ± 0.01 for 2-methylpent-2-ene isomerization, and 0.20 ± 0.01 methylcyclohexene isomerization).
k)/d(DPE) values 0.11 ± 0.01 for 2-methylpent-2-ene isomerization, and 0.20 ± 0.01 methylcyclohexene isomerization).
These differences show how charge distributions determine the strengths of these ion-pair interactions and thus how the stability of full ion-pair transition states sense DPE. In most cases acid-catalyzed reactions proceed via full ion-pair transition states,11,12,15,30,37 where protons are fully transferred to an organic moiety. When the charge distributions in different transition states are similar, the selectivities are independent of acid strength. Next, we discuss an example of exceptions where one of the two transition states relevant to selectivity does not form full ion-pair, which leads to selectivities that are sensitive to acid strengths.
3.3. Isobutanal–isobutene Prins condensation
The acid-catalyzed condensation of oxygenates leads to the formation of new C–C bonds and the removal of O-atoms, in processes that are essential to modify their volatility and energy density.35,77,78 Isobutanal–isobutene Prins condensation reactions on Brønsted acids occur via nucleophilic attack by the terminal C atom in the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond of gaseous isobutene at the carbonyl C atom of a H-bonded isobutanal molecule. This kinetically-relevant step forms alkoxy species with a new C–C bond, which undergo subsequent deprotonation and dehydration in kinetically-irrelevant steps to form 2,5-dimethyl-hexadiene (2,5DMH) isomers (Fig. 5a).77 Such reactions occur in parallel with the oligomerization of the alkene co-reactants, which involves the protonation of isobutene to form bound tert-butoxides that undergo nucleophilic attack at their tertiary C atom by the terminal C atom in the C
C bond of gaseous isobutene at the carbonyl C atom of a H-bonded isobutanal molecule. This kinetically-relevant step forms alkoxy species with a new C–C bond, which undergo subsequent deprotonation and dehydration in kinetically-irrelevant steps to form 2,5-dimethyl-hexadiene (2,5DMH) isomers (Fig. 5a).77 Such reactions occur in parallel with the oligomerization of the alkene co-reactants, which involves the protonation of isobutene to form bound tert-butoxides that undergo nucleophilic attack at their tertiary C atom by the terminal C atom in the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond of another isobutene to form alkoxy species; these alkoxy moieties deprotonate to form predominantly 2,4,4-trimethyl-pentene isomers (Fig. 5a).77 Isobutanal can bond to protons via H-bonding or by protonation to form 1-hydroxy-isobutoxide; isobutene can form a π-complex, an iso-butoxide, or a tert-butoxide at Brønsted acid sites, and each of these bound species can react with either isobutanal or isobutene to form dimer species.
C bond of another isobutene to form alkoxy species; these alkoxy moieties deprotonate to form predominantly 2,4,4-trimethyl-pentene isomers (Fig. 5a).77 Isobutanal can bond to protons via H-bonding or by protonation to form 1-hydroxy-isobutoxide; isobutene can form a π-complex, an iso-butoxide, or a tert-butoxide at Brønsted acid sites, and each of these bound species can react with either isobutanal or isobutene to form dimer species.
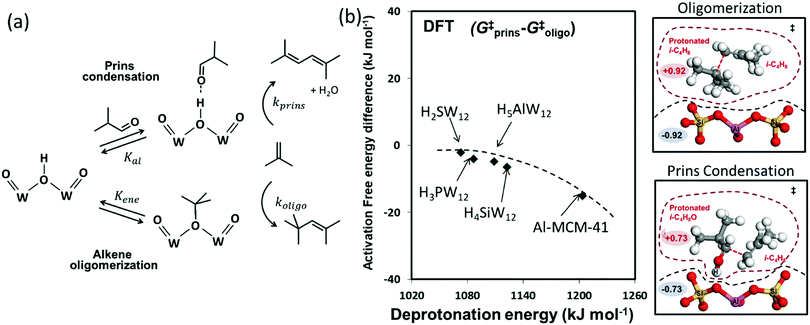 | ||
| Fig. 5 (a) The steps mediating Prins condensation and oligomerization reactions in isobutanal–isobutene mixtures on Brønsted acids. (b) Difference in DFT derived Gibbs free energy of activation between Prins condensation and oligomerization as a function of DPE on W-POM clusters and Al-MCM-41, and structures and charges of transition states on Al-MCM-41. Dashed curve represents trends. Adapted from data originally published in ref. 35 and 77 Molecular structures reproduced with permission from American Chemical Society. | ||
The elementary steps involved in the formation of these adsorbed species and in their C–C coupling, deprotonation and dehydration steps (Fig. 5a and Scheme 5 in ref. 77) lead to rate equations that accurately describe measured turnover rates for Prins condensation and oligomerization on W-POM clusters and mesoporous and microporous aluminosilicates:
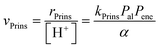 | (12) |
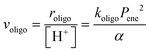 | (13) |
| α = 1 + KalPal + KenePene + Kal–enePalPene + Kal–alPal2 + Kene–enePene2 | (14) |
Taken together, these illustrative examples show that activation energies vary linearly with DPE (as shown by the semilogarithmic plots; Fig. 3a and 4b) on each family of Brønsted acids (e.g. W-POM clusters with different central atoms or MFI heterosilicates with different heteroatoms). The sensitivity of activation energies to DPE depends on the difference between individual sensitivities of transition states and precursors, which, in turn, depend on the charge distributions in these species. The activation energies for a series of reactions mediated by ion-pair transition states with similar charge distribution in the organic cation for an acid site with a given DPE depend on Eprot values of gaseous analogs of the cations (Fig. 4b).
Thus, DPE and Eprot are useful catalyst and molecular descriptors of reactivity, but, as we show next, these properties of isolated molecules and protons cannot fully describe reactivities because interaction energies also depend on the extent to which cations and anions are able to reorganize charge in order to maximize interactions at intermediates and transition states. More complete descriptors require that we account for how “soft” or “hard” the charge distributions are in the organic cations and the inorganic conjugate anions; these properties ultimately determine how much energy they require in order to reorganize their charge distribution as isolated species to adopt those present at their interacting distance in transition states.
3.4. Incompleteness of reactivity descriptors based solely on the independent properties of isolated molecular analogs and of solid acids
The incompleteness of the descriptors of non-interacting catalysts and molecules and the role of the “adjustments” made by the binding site and the bound molecule as they interact at intermediates and transition states are assessed first using the conversion of CH3OH to DME and H2O, for which the effects of DPE on measured rate constants kmono and kdimer and the DFT-derived activation energies were described in Section 3.1. These rearrangements are examined on different families of solid acids and they represent the system for which such effects were first identified and interpreted.30,33Fig. 3a shows that measured kmono values (per H+), which reflect the energy of formation of the DME transition state from a bound and a gaseous CH3OH precursor (Scheme 4), are smaller on Mo-based POM clusters than on W-based clusters of similar structure even when, through differences in central atom, the W and Mo acids have the same DPE value. Thus, for a given acid strength, defined as a property of a solid by its DPE, the DME formation transition states are more stable on W-POM than on Mo-POM clusters relative to their respective bound CH3OH monomer precursors. The kmono values on MFI heterosilicates also deviate from the reactivity-DPE trends defined by W-POM clusters for the same DPE. Such deviations arise in part because of confinement effects, but also from the different propensity of the two acid families to reorganize charge (Fig. 3a). The DFT-derived activation energies relevant to the magnitude of kmono (Eamono) are higher on Mo-POM clusters than on W-POM clusters at the same DPE (Fig. 3b), consistent with the lower kmono values measured on Mo-POM clusters. The DFT derived Eamono values on MFI heterosilicates and mineral acids (H2SO4, H3PO4) are smaller than predicted at the DPE of these acids using the trends from W-POM. These DFT calculations use PW91 functionals that lack any dispersion corrections; consequently, the energies reported in Fig. 3b do not include any of the attractive dispersion forces that characterize confinement effects in heterosilicates with voids of molecular dimensions. The isolated transition states and monomer precursors are independent of the acid, indicating that the Eprot values are identical for all acids (Scheme 4) and that these Eprot values do not account for the differences in activation energies among the different families of solid acids [Ea = (ETSprot − Eadsprot) + (ETSint − Eadsint); eqn (5)]. Instead, these different Eamono values on different acid families for the same DPE reflect different ETSint values for acids of similar intrinsic strength (i.e. DPE values). The kdimer values on all acid families lie along the same trend line (Fig. 3a and b), because the transition state and the precursor both involve full ion-pairs with similar charge distribution, which cause ETSint and Eadsint to differ from each other to the same extent for all acid families for a given DPE; as a result the effects on ETSint and Eadsint by each acid family cancel to give Eadimer values that become a single-valued function of DPE for all acids.
These data suggest that the formation energies of transition states and precursors from bare protons and gaseous reactants are not, in general, single-valued functions of DPE for Mo-POM, W-POM, MFI and mineral acids, but that the differences in the effects of DPE for the different acid families, in some cases, cancel, specifically when the transition state and the precursor that determine rate constants have similar charge distributions. Thus, the formation energies of surface species from bare protons are more sensitive than activation energies as probes of the incompleteness of any given reactivity descriptor. The formation energies of all transition states and precursors can be related to DPE, Eprot, and Eint values using respective thermochemical cycles that describe their formation (Schemes 2, 4 and eqn (1), (2)), thus allowing activation energy descriptors to be derived from differences between the cycles for the formation of transition states and their relevant precursors (eqn (5)). Next, we examine the effects of DPE and Eprot values as probes on the formation energies of transition states and reactive intermediates from bare protons in order to assess their relevance and completeness as reactivity descriptors.
Fig. 6a shows DFT-derived (PW91 functionals without dispersion corrections) formation energies for the DME transition state relative to bare protons and two gaseous CH3OH molecules, which determine the second-order DME dehydration rate constants, as a function of DPE on Mo-POM and W-POM clusters, MFI heterosilicates, and gaseous mineral acids (H2SO4, H3PO4). The transition state energies on Mo-POM are less negative, than on W-POM, but more negative on MFI and mineral acids. These results show that different families of acids stabilize the transition state to different extents, even when those acids are of similar intrinsic strength (the same DPE values); they also show that these differences arise from differences in ion-pair interactions in acids even without accounting for dispersion effects due to confinement (PW91 functionals do not include induced-dipole van der Waals contributions). The formation energies of the CH3OH monomer and dimer intermediates referenced to protons and gaseous reactants are also less negative on Mo-POM than on W-POM, but more negative on mineral acids, suggesting that the data shown in Fig. 6a are representative of how these different acid families stabilize reactive intermediates and transition states to different extents at any given DPE value and intrinsic acid strength.30
 | ||
| Fig. 6 (a) DFT (PW91) derived energies of DME formation transition states as a function of DPE values on W-POM (squares) and Mo-POM (circles) clusters and mineral acids (diamonds) with different central atoms (S, P, Si, Al, Co) and MFI heterosilicates (triangles) with different heteroatoms (Al, Ga, Fe, B) (b) formation energies of surface species at a Brønsted acid site on H3PW12O40 cluster as a function of the protonation energies of gaseous analogs of these species. Dashed lines represent trends for W-POM in (a) and CH3OH dimers and DME formation transition state (TS) in (b). Shaded regions and vertical arrows show deviations from trend lines. Adapted from data published and methods described originally in ref. 30 and 33 | ||
Fig. 6b shows the formation energies for surface intermediates and transition states involved in alkanol dehydration, alkene skeletal rearrangements, proton hopping and adsorption of basic molecules (all referenced to bare protons and gaseous reactants) on H3PW12O40 clusters (DPE = 1081 kJ mol−1) as a function of the Eprot values of the gaseous analogs of their respective bound intermediates and transition states (Eprot values in Table 2). These formation energies depend on Eprot and Eint values for an acid with a given DPE and would become a unique function of Eprot only if Eint values were similar for all intermediates and transition states on a given acid (Schemes 2–4; ΔE = DPE + Eprot + Eint, eqn (1) and (2)). The formation energies in Fig. 6b exhibit weak correlations with Eprot values but also show significant deviations from the trend line connecting the data for the full ion-pair CH3OH dimer and DME formation transition states (Fig. 6b), suggesting that Eint values are not similar for the different intermediates and transition states. For instance, the energy for the full ion-pair transition state that mediates ring contraction lies well above the trend-line in Fig. 6b, which suggests that its Eint value is less negative than the DME formation transition state because its more delocalized positive charge causes weaker effective electrostatic interactions with the negative charge at the conjugate anion (Section 3.2; Fig. 4). In contrast, CH3OH monomer intermediates and the H2O-mediated proton shuttle transition state (shown in Schemes 3 and 4) lie well below the trend line in Fig. 6b, suggesting that these species are much less charged than the full-ion pair transition states because the gaseous analogs of these species and their conjugate anions lower their energy by reorganizing their charge more effectively than full ion-pair transition states (as discussed in detail in Section 4). These observations show how and why DPE (Fig. 6a) and Eprot (Fig. 6b), the respective descriptors of their isolated forms, represent incomplete descriptors of reactivity because the adjustments made by the binding site and the bound molecule in minimizing their combined energy at their binding distances matter significantly for the stability of intermediates and transition states.
The origins of the different effects of DPE and Eprot on different types of acids reflect the nature of the interaction energies that mediate the binding of intermediates and transition states, as well as the nature of the electrostatic and charge reorganization energies of the bound species, including the protons that are transferred in forming ion-pairs, and of the inorganic conjugate anions. Such important properties of a solid acid, and of acids in general, are examined next in developing more complete descriptors of reactivity in acid catalysis. They ultimately depend on the electronegativity of the gaseous analogs of bound species and deprotonated acids, which determines how much charge they retain when interacting with a counterion, and their chemical “hardness” that reflects how resistant they are to charge reorganization.79,80
4. Influence of electrostatic interactions and charge reorganizations and the evolution towards more complete reactivity descriptors
The formation energies of ion-pair transition states and intermediates bound to acid sites from bare protons and gaseous reactants can be described by the thermochemical cycle depicted in Scheme 2. The resulting activation energies are obtained by subtracting the energy components in the cycles responsible for the formation of the transition state and of its kinetically-relevant bound precursor (eqn (5) and (6)).30DPE values are calculated by removing the H-atom in the acidic O–H as a H+, but from an O–H bond with a strong covalent character. As a result, the deprotonation of an O–H Brønsted acid requires significant charge reorganization in the conjugate anion upon H+ removal (Scheme 6).25,26,30,81 The transition states that mediate acid catalysis typically consist of fully-formed ion-pairs that are predominantly stabilized by electrostatic interactions with the conjugate anion; consequently, the charge distribution in the anion at the transition state differs markedly from that in the anionic component in the O–H group. This leads to only a small fraction of the energy required to reorganize charge upon deprotonation of the acid being recovered upon formation of ion-pair transition states; in contrast, the electrostatic component of the energy required to remove H+ from the O–H group is more fully recovered upon formation of the transition state or any protonated intermediate. The limited extent to which the charge reorganization component of deprotonation is recovered at the transition state renders ion-pair transition states less stable on acids for which reorganization energies for deprotonation required more energy (i.e. for more covalent O–H bonds).30
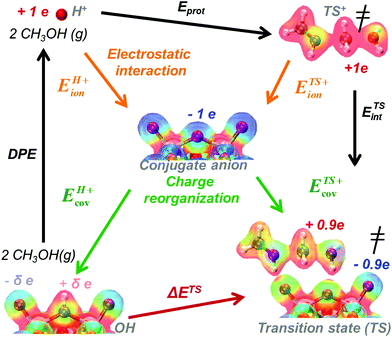 | ||
| Scheme 6 The energy of DME formation transition state referenced to a bare acid and two gaseous CH3OH molecules (ΔETS) described in terms of the acid's DPE, the gas-phase protonation energy (Eprot) and interaction energy (ETSint) of cationic transition state analog with its conjugate anion. DPE and ETSint reflect ion-pair interactions with electrostatic (ionic) and charge reorganization (covalent) components. Colors on electron distributions reflect electrostatic potentials (red = positive, electron deficient; blue = negative, electron rich). Adapted from results and methods in ref. 33. | ||
The charge reorganization and electrostatic components of the DPE represent intrinsic properties of solid acids and the extent to which these components are recovered upon formation of each transition state and bound intermediate differs among dehydration, isomerization and proton shuttling reactions.30,33 These DPE components for different families of acids and extents of recovery by reactive intermediates and transition states can be quantified through the use of Born–Haber thermodynamic cycles as described next.
DPE and ion-pair interaction energies are first dissected into their respective electrostatic and charge reorganization components to assess how the DPE components vary among acid families and what fraction of these components are recovered by different ion-pair transition states. All of these interactions involve the movement of an isolated full cation and an isolated full conjugate anion toward each other from non-interacting to interacting distances, as shown schematically in the Born–Haber thermochemical cycles (Schemes 2 and 4–6), and the extent of charge reorganization determines how much charge the bound species retain in their interacting state. We adopt a partitioning method based on Fajans’ characterization of the strength of ionic bonds as the strength of purely electrostatic interactions between full ions and charge reorganization as the presence of “partial covalency” in ionic bonds, because this approach successfully predicts trends in ionic and covalent nature in binary solids.82,83 Therefore, in what follows, the purely electrostatic interactions between full ions with charge distributions of their non-interacting states and interactions mediated by charge reorganization are referred to as “ionic” and “covalent” components, respectively.
The ionic component can be determined by numerical integration of classical electrostatic interactions between the DFT-derived charge distributions to assess the changes in energy when gaseous analogs of bound species and isolated conjugate anions approach each other from non-interacting distances and reach the location that gives the strongest electrostatic interaction, without allowing the locations of the atoms or the charges to relax from those in their respective isolated states. Such calculations are based on the Hellman–Feynman theorem,83,84 which posits that once electron distributions have been determined by quantum mechanics, energies and forces can be derived from entirely classical treatment of such distributions.85,86 The cation–anion distance considered here is defined as the distance between the O-atom of the acid from which the proton is removed and a reference atom near the charge center in the cation, such as a proton or a C-atom at the CH3+ group.30,33 Electrostatic interaction energies initially become more negative as cations and anions approach each other, but then less negative upon closer approach of their respective electron clouds because of electron–electron repulsion. The most negative electrostatic interaction energy is considered the ionic component of the total interaction energy between a cation and an anion. The most negative electrostatic interaction energy is considered as the ionic component of the total interaction energy between a cation and an anion. Thus, values for the ionic component of ion-pair interaction energies (e.g., ETS+ion) are negative. The values for the ionic components of DPE (i.e., EH+ion) are, however, positive because DPE, defined as the energy change upon separating H+ from its conjugate anion to non-interacting distances, is positive (see, e.g., Scheme 6). The covalent component of the interaction energy is obtained by subtracting its ionic component from the DFT-derived DPE or ion-pair interaction energies at the transition state (TS), with H+ and gaseous analog of transition state (TS+) as the respective cations.
Fig. 7 shows the ionic and covalent components of DPE as a function of the total DPE for POM clusters with Mo and W addenda atoms, for MFI crystalline heterosilicates, and for gaseous forms of mineral acids. The ionic components of DPE (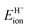 , 230–680 kJ mol−1) are smaller and more broadly distributed in magnitude than their respective covalent components (
, 230–680 kJ mol−1) are smaller and more broadly distributed in magnitude than their respective covalent components (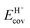 , 720–870 kJ mol−1) for DPE, as expected for the heterolytic nature of the cleavage of largely covalent O–H bonds in these acids. Such bonds are more ionic for silicates and mineral acids than for POM clusters; for POM clusters, they are more ionic for clusters with W than Mo addenda atoms. Acids with covalent components smaller or larger than the trends for W-POM in Fig. 7b also exhibit smaller or larger respective DME formation transition state energies in Fig. 6a; these trends confirm the hypothesis that the energy required for charge reorganization in the solid acid upon deprotonation remains largely unrecovered at ion-pair transition states. A rigorous accounting of the different extents of recovery for ionic and covalent components of DPE may lead to more complete reactivity descriptors than DPE alone.
, 720–870 kJ mol−1) for DPE, as expected for the heterolytic nature of the cleavage of largely covalent O–H bonds in these acids. Such bonds are more ionic for silicates and mineral acids than for POM clusters; for POM clusters, they are more ionic for clusters with W than Mo addenda atoms. Acids with covalent components smaller or larger than the trends for W-POM in Fig. 7b also exhibit smaller or larger respective DME formation transition state energies in Fig. 6a; these trends confirm the hypothesis that the energy required for charge reorganization in the solid acid upon deprotonation remains largely unrecovered at ion-pair transition states. A rigorous accounting of the different extents of recovery for ionic and covalent components of DPE may lead to more complete reactivity descriptors than DPE alone.
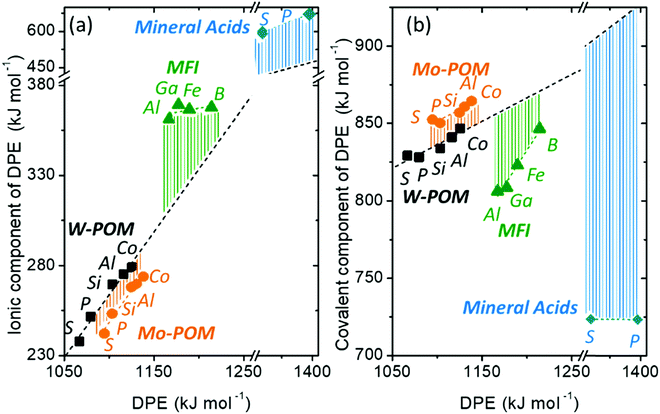 | ||
Fig. 7 (a) Ionic 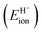 and (b) covalent and (b) covalent 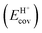 components of the DPE of POM, MFI and mineral acids as a function of DPE values from DFT (PW91). Shaded regions reflect differences between trends for W-POM and other acid families. DPE values of the compositions shown are listed in Table 1. Data published originally in ref. 30 and 33. components of the DPE of POM, MFI and mineral acids as a function of DPE values from DFT (PW91). Shaded regions reflect differences between trends for W-POM and other acid families. DPE values of the compositions shown are listed in Table 1. Data published originally in ref. 30 and 33. | ||
A more complete descriptor of the reactivity of acids based on DPE values must include the separate ionic and covalent components of DPE, an intrinsic property of a particular acid or type of acid, but also the extent to which each component is recovered at the transition state, typically a property of a reaction or a family of reactions. This is done here using the framework provided by the thermochemical cycles in Schemes 4–6 and the energy terms in eqn (1) and (2).30,33 The Eprot values in such cycles represent intrinsic properties of gaseous species and they are therefore independent of the acid used. The (ΔETS − Eprot) values (eqn (1)) depend on the properties of the solids, through their DPE values but also through the ability of each transition state to recover part of the energy required to remove the proton through interaction between transition state cation and conjugate anion (ETSint < 0):
| ΔETS − Eprot = DPE + ETSint. | (15) |
Fig. 8a shows DFT-derived (ΔETS − Eprot) values as a function of DPE for the transition states that mediate H2O-assisted H+ shuttling (Scheme 3), H2O elimination from CH3OH to form DME (Scheme 4 and Fig. 3), (non-productive) methyl shifts in C3H6-derived alkoxides (analogous to alkene isomerization transition states in Scheme 5 and Fig. 4), and cyclohexene ring contraction (analogous to ring-contraction in Fig. 4) on Mo and W POM clusters and on cluster models of heterosilicates with MFI-type frameworks. For an acid of a given strength and family, these (ΔETS − Eprot) values are much smaller for H2O assisted H+ shuttling transition state than cyclohexene ring contraction, indicative of ETSint values that are more negative because their transition states recover a larger fraction of the energy required to separate the proton from the conjugate anion (DPE) as a result of their smaller size and their more localized, and thus more “proton-like”, charge distribution.
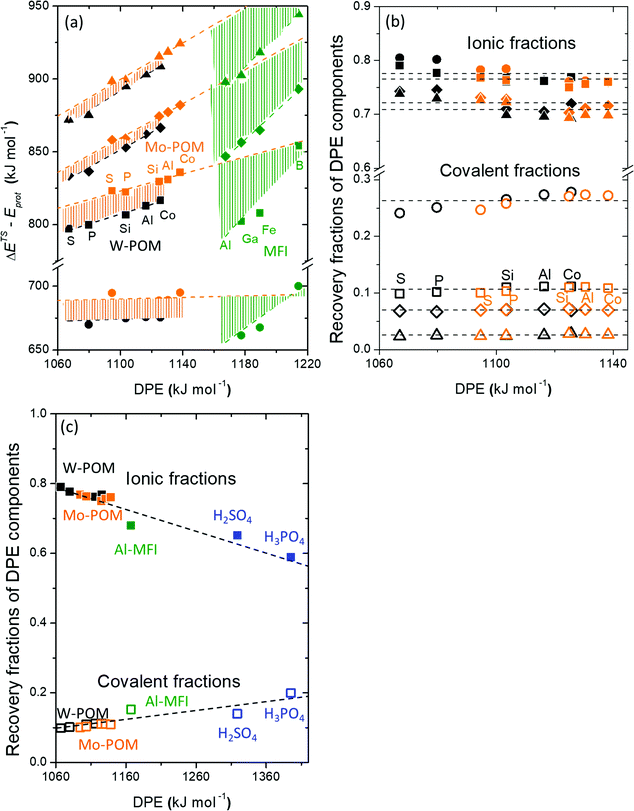 | ||
| Fig. 8 (a) Difference between DFT-derived transition state energies and gas-phase protonation energies (ΔETS − Eprot, Scheme 1), (b) fractions of ionic (closed symbols) and covalent (open symbols) DPE components recovered by transition state cations (fTSion, fTScov) for H2O assisted H+ shuttling (circles), DME formation (squares), C3H6 methyl-shift (diamonds) and C6H10 ring-contraction (triangles) on Mo (orange) and W (black) POM, and (c) fractions recovered by the DME formation transition state cation on Mo (orange) and W (black) POM, MFI (green), and mineral acids (blue) versus DPE. Shaded regions in (a) reflect offsets between best-fit lines. Horizontal dashed lines in (b) reflect averages over all POM clusters. Dashed lines in (c) reflect trends. Data and methods published originally in ref. 30 and 33. Parts (a), (b) reproduced with permission from American Chemical Society. | ||
DPE values for different families of solid acids (Mo-POM, W-POM, MFI heterosilicates) and ETSint values for different transition states (H+ shuttling, DME formation, methyl-shift, ring-contraction) can be dissected into their ionic and covalent components (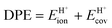 ;
; 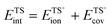 , Scheme 6):
, Scheme 6):
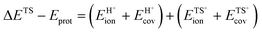 | (16) |
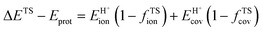 | (17) |
These fTSion and fTScov values reflect the ratios of respective ionic and covalent components of ion-pair interactions for transition states (ETSint) and protons (DPE):
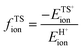 | (18) |
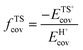 | (19) |
Eqn (15) suggests that (ΔETS − Eprot) values should depend on a modified DPE that reflects only the portion of DPE that is not recovered by ion-pair interactions between gaseous analogs of the transition state and conjugate anions (ΔETS − Eprot = DPE + ETSint; ETSint < 0). This modified DPE, in turn, reflects the ionic and covalent components of DPE and their fractions recovered by transition states (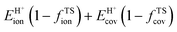 ; eqn (17)).30 When fTSion and fTScov values are insensitive to the specific DPE value or acids of a family type (Mo-POM, W-POM, MFI, mineral acid) and represent a unique property of a given type of transition state cation, these modified DPE values become a complete descriptor of reactivity and rigorously account for all relevant properties of the solid acid and of the reactive species involved in a given type of chemical transformation.
; eqn (17)).30 When fTSion and fTScov values are insensitive to the specific DPE value or acids of a family type (Mo-POM, W-POM, MFI, mineral acid) and represent a unique property of a given type of transition state cation, these modified DPE values become a complete descriptor of reactivity and rigorously account for all relevant properties of the solid acid and of the reactive species involved in a given type of chemical transformation.
Such requirements are examined next to determine whether these fTSion and fTScov values depend on the total DPE and for each type of acid and each of the four types of transition states in Fig. 8. Transition state cations recover significant fractions of the ionic components of DPE (fTSion, 0.6–0.8; Fig. 8b), but much smaller fractions of the (larger) covalent components of DPE (fTScov, 0.02–0.3; Fig. 8b), consistent with the full ion-pair character of these transition states. The ionic and covalent recovery fractions for these ion-pairs increase as the cations become smaller and approach the size of a proton (fI < fII < fIII < fIV, where I, II, III and IV represent transition states for cyclohexene ring contraction, methyl shift in propene, DME formation and H2O assisted proton shuttling, respectively; Fig. 8b). The fTSion and fTScov values for each transition state cation depend only weakly on DPE and are similar on Mo and W POM clusters for all four transition states (1060–1140 kJ mol−1 range of DPE values, Fig. 8b).
These fractions were also calculated for Al-MFI and for mineral acids for the DME formation transition state to include a broader range of DPE (1060–1400 kJ mol−1) and of acid families (Fig. 8c). Over this broader DPE range, these fTSion values decrease, while fTScov values increase with increasing DPE. Yet, the fTSion and fTScov values for the POM clusters, MFI and mineral acids lie on a trend line that is independent of the type of acid, thus rendering them intrinsic properties of the cationic species and specifically of their charge distribution. Such effects can be taken into account via recovery fractions that depend linearly on DPE (but are independent of families of acids) instead of constant values, as shown for the intermediates and transition state for CH3OH dehydration.30
The fTSion and fTScov values were not calculated for other heteroatoms in MFI and for other transition states due to computational limitations. The complex pore topologies of MFI and other zeolites require sampling of a large number of orientations in order to ensure optimum electrostatic interactions between the charge distributions determined from non-interacting states of the cation and the anion. Efficient sampling of these orientations would require methods more efficient than the direct numerical integration of charge distributions used here,30 such as those involving distributed multipole expansions.87
This dissection of DPE into ionic and covalent components and the grouping of types of reactions based on sizes or concentrated or diffuse nature of the charge distribution of their transition states lead to more complete descriptors of reactivity than the intrinsic acid strength (total DPE values). Such descriptors require that solid acids be described by their separate ionic and covalent components of DPE, and bound intermediates and transition states be described by their ability to recover a given fraction of the electrostatic and charge reorganization energies required to deprotonate the solid acid. These “recovery fractions” are essentially independent of the family of solid acids and depend only very weakly on DPE. For the small ranges of POM DPE values, the recovery fractions can be treated as unique values for each given type of transition state, reported here as the mean of such fractions calculated on all POM clusters. The fractions were not calculated explicitly for all MFI and TS combinations and were excluded from the mean values to check how accurately the fractions derived from POM can predict reactive properties of MFI. As a result, these fractions become a single-valued descriptor of transition state stability. These findings lead to a general descriptor in the form of an effective DPE value (eqn (17)); this combination of terms brings together the acid  and the transition state (fTSion,fTScov) properties in their most general form. The (ΔETS − Eprot) values are shown in Fig. 9 as a function of the general descriptor obtained using
and the transition state (fTSion,fTScov) properties in their most general form. The (ΔETS − Eprot) values are shown in Fig. 9 as a function of the general descriptor obtained using  ,
, 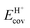 for each acid (Fig. 7) and fTSion, fTScov for each transition state. The single-valued character shown by these data indicate that the right-hand side of eqn (17) accurately separates the properties of the anion (the solid) and the cation (the reaction chemistry and its TS) and then combines them in order to predict TS stability and thus reactivity.
for each acid (Fig. 7) and fTSion, fTScov for each transition state. The single-valued character shown by these data indicate that the right-hand side of eqn (17) accurately separates the properties of the anion (the solid) and the cation (the reaction chemistry and its TS) and then combines them in order to predict TS stability and thus reactivity.
 | ||
| Fig. 9 Difference between DFT-derived (PW91) TS energies and gas-phase protonation energies (ΔETSint − Eprot, Scheme 1) for H+ shuttling (circles), CH3OH dehydration (squares), C3H6 methyl-shift (diamonds) and C6H10 ring-contraction (triangles) on Mo (orange) and W (black) POM and MFI (green), as a function of the modified DPE reflecting the sum of DPE and its compensation via ion-pair interactions.33 Reproduced with permission from American Chemical Society. | ||
The PW91 functionals used to obtain the energies of bound intermediates and transition states do not include van der Waals forces interactions (vdW). As a result, they lead to seemingly accurate and complete relations between the modified DPE values and DFT-derived activation energies for different types of chemical transformations not just on Mo and W POM clusters, but also on MFI heterosilicates that confine species within voids of molecular dimensions (Fig. 9). In actuality, the voids of molecular dimensions in crystalline heterosilicates provide an additional type of stabilization to bound intermediates and transition states through vdW contacts between the inorganic host and the guest molecules.31,32,88,89
A similar treatment was used to determine the effects of DPE components on the stability of bound intermediates that are essentially unchanged, such as H-bonded CH3OH monomers and full ion-pair protonated dimers.30 The gaseous analog for H-bonded monomers was considered to be a proton interacting electrostatically with a neutral CH3OH molecule, which recovered essentially all of the electrostatic component of proton–anion interaction reflected in DPE (fion values 1.0–0.95 on POM and mineral acids).30 This intermediate also recovered a large fraction of the charge reorganization component of the DPE (fcov 0.87–0.85), which is consistent with an essentially neutral H-bonded CH3OH monomer. In contrast, the protonated dimer recovers fractions similar to those recovered by the full ion-pair DME formation transition state, but only a very small part of the covalent component of DPE (fion values 0.74–0.68, fcov values 0.14–0.16 on POM for dimer). These data demonstrate that modified DPE values for neutral monomers and protonated dimers are able to describe the formation energies of these species, and the activation energies corresponding to the first-order and zero-order DME formation rate constants (Eamono and Eadimer, Scheme 4) can be described by the difference between the modified DPE of the transition state and the relevant precursor (Fig. 3).
Such analyses of recovery fractions by transition states and reactive intermediates need to be expanded to broader families of reactions to assess the extent of completeness of these descriptors. Some reactions (e.g., alkene–alkanal Prins condensations, Section 3.3) involve charges in the transition state that depend on acid strength, leading to full ion-pairs on strong acids, but to smaller charges on weaker acids. For such transition states the recovery fractions fion and fcov are likely to become stronger functions of DPE than the transition states in Fig. 8 that remain full ion-pairs for the entire DPE range.
Alkene isomerization and oligomerization reactions involve bound alkoxide intermediates and the full transfer of the proton to the bound alkenes (Sections 3.2 and 3.3); these alkoxides remain essentially neutral and replace the covalent O–H bond with a covalent C–O bond. The required charge reorganization and recovery fractions depend on the differences between strengths of C–O and O–H covalent bonds. Calculations of recovery fractions for such species over different acid families would reveal if these fractions remain a single-valued function of DPE, as is the case for DME formation transition states (in Fig. 8c).
The differences in ionic and covalent components lead to more complex property–function relations than those that simply use the intrinsic properties of the acid (DPE) and molecules (Eprot) in their isolated forms. Such complexity, however, increases the diversity of properties that can be used to modify reactivity and selectivity. These properties are single-valued properties of the isolated acids and molecules, but only within families of catalysts and reactions, because they reflect the intrinsic ability of the conjugate anion (the acid) and of the gaseous analogs of the bound species (the molecule) to reorganize charge. These concepts are embedded, in less quantitative form and for mineral and organic acids, within historical concepts of electronegativity and hard–soft acid–base chemistry. These formalisms treat the ability to donate and reorganize charge, but in a manner less amenable to quantitative predictions of reactivity predictors than the conceptual framework developed here. The heuristic and conceptual connections between these two approaches are described in more detail in the next section.
5. Historical evolution of descriptions of acid–base pairs in terms of electrostatics and charge reorganization
The partial covalency of bonds in ionic solids is typically described in terms of the indirect influence of the charge-to-size ratios of anions and cations on the ability to reorganize charge through polarization.82,83,90 The diverse shape and chemical identity of ions encountered in catalysis preclude accurate predictions from such methods, in spite of their heuristic value, thus requiring the development of energy-based descriptors of such properties.One such energy-based descriptor is derived from the sensitivity of the energy of a given acid or base (E), such as a proton or a group of atoms that constitutes the gaseous analog of a transition state or a conjugate anion, to a perturbation in their number of electrons (N):79,90
 | (20) |
Chemical strength and hardness are used routinely to describe reactivity trends in acid–base displacement reactions through Pearson's hard–soft acid–base (HSAB) theory,94,95 later developed into more quantitative form by Parr and Pearson using DFT-derived energies and their derivatives in eqn (20) together with energy minimizations via partial charge transfer between cations and anions.80,91 The HSAB principle states that for pairs with a given electronegativity difference between the acid and the base, hard acids interact more strongly with hard bases and soft acids with soft bases.91 Such treatments have enabled more complete descriptions of reactivity trends in displacement reactions by accounting for trends that differ from those predicted based solely on electronegativity differences.
Fig. 10 shows the DFT derived energy of a H-atom and the gaseous structural analog of a DME formation transition state as a function of the total charge of these species. The regression of these values to the functional form of eqn (20) gives the chemical strength and hardness values for each. The energy of the H-atom increases more strongly than that of the DME transition state when an electron is removed (slope of energy vs. number of electrons, Fig. 10); the proton is more electropositive than this transition state (μH0 = 7.2 V, μTS0 = 2.6 V). Consequently, it is expected to retain a less positive charge when it interacts with a given conjugate anion. The curvature of the relation between energy and number of electrons is also greater for a H-atom than the transition state, indicative of its higher chemical hardness and its stronger resistance to acquire a number of electrons larger than required for its minimum energy (ηH = 12.8 V e−1, ηTS = 4.5 V e−1). Next, we discuss how these properties are related to DPE and ion-pair interaction energies, using the DME formation transition states on POM and mineral acids as illustrative examples.
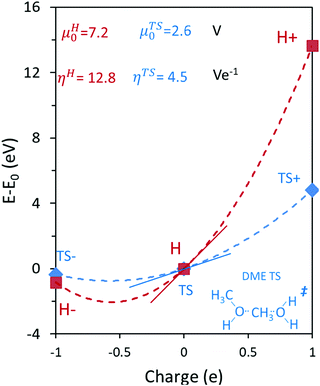 | ||
| Fig. 10 PW91 derived change in energy of H-atom and gaseous analog of DME formation transition state as a function of charge on the species. Dashed curves represent best fits to eqn (20). Solid lines represent local slopes. Derived from structures and methods in ref. 30. | ||
The chemical strength and hardness defined by eqn (20) represent properties of neutral atoms or groups of atoms that are useful in predicting how they interact and how much charge they acquire in their interacting state, as shown in Scheme 7 using hypothetical species A and B. Here, we examine the indirect connection between these properties and direct calculations of intrinsic acid strength (DPE) and of ion-pair interaction energies and their ionic and covalent components. In doing so, we consider H-atoms and structural analogs of transition states as Lewis acids (species A in Scheme 7) and POM clusters and mineral acids without one of their H-atoms as the Lewis bases (species B in Scheme 7) that undergo electron transfer and acid–base interactions to form either the Brønsted acids or the ion-pair transition states. Fig. 11a shows the chemical strength difference (μB0 − μA0, Scheme 7) between dehydrogenated POM clusters or mineral acids and a H-atom (μ0 − μH0) and between the acids (with one H-atom removed) and the DME formation transition state (μ0 − μTS0) as a function of DPE. Fig. 11b shows the relation between the chemical hardness of the acids (with one H-atom removed) and the DPE of each acid.
 | ||
| Scheme 7 Effects of chemical strength and hardness of species A and B on the nature of A + B – ion-pair interaction. | ||
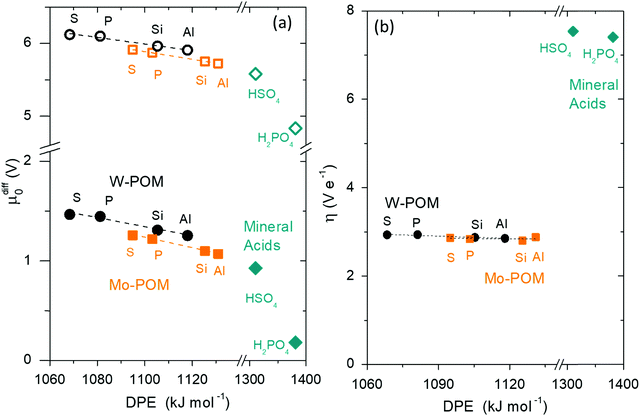 | ||
| Fig. 11 (a) Difference between chemical strengths of dehydrogenated POM clusters or mineral acids and H-atom (μ0 − μH0; closed symbols) or DME formation transition state (μ0 − μTS0; open symbols) and (b) chemical hardness (η) for POM clusters and mineral acids as a function of DPE. The μ0 and η values are obtained by regressing energies of neutral cation and anion forms (derived using methods and structures reported in ref. 30) to the form of eqn (20) (as illustrated in Fig. 10). | ||
A larger (positive) chemical strength difference between species B and A arises from a greater tendency for electron transfer from A to B (Scheme 7). This difference is more positive for the DME formation transition state than for H-atoms (Fig. 10a), consistent with the ion-pair nature of the transition state and with the essentially uncharged H-atoms in covalent OH bonds in Brønsted acids (Scheme 6 and Fig. 7, 8a). The chemical strength difference μ0 − μH0 decreases with increasing DPE for POM clusters, but is smaller for Mo-POM than W-POM (Fig. 11a) for a given value of the DPE, consistent with a covalent component of DPE that is larger for Mo-POM and increases with DPE (Fig. 7b), because species with similar electronegativity lead to a lower driving force for electron transfer (Scheme 7). These trends for POM clusters reflect solely their different chemical strength, because their hardness values are essentially the same for all POM clusters (Fig. 11b). In contrast, mineral acids have a lower covalent component of DPE than POM clusters (Fig. 7b), in spite of smaller chemical strength differences between HSO4 or H2PO4 species and H-atoms (Fig. 11c), because these species have a larger value of chemical hardness than POM clusters. Higher values of chemical hardness tend to favor electron transfer because they form concentrated charged species that interact strongly via electrostatic forces.79 Thus, strength and hardness combine to determine how strongly Lewis acids and bases interact; such effects are precisely reflected in a quantitative and systematic manner in the ionic and covalent components of DPE and ion-pair interactions described in Section 4.
These HSAB concepts for acid–base displacements in solvated pairs can be transferred to acid catalysis by considering the preference for bases (e.g., dehydrogenated POM clusters) to displace one another based on their interaction strengths with a given acid (e.g., H-atom or neutral form of DME transition state). Such displacement preferences can be determined by minimization of the total energy of the acid–base pair due to electron transfer resulting in change in energy of the acid and the base due to their chemical strength and hardness (eqn (20)) and the electrostatic interaction between the charged species.79 The base (dehydrogenate POM) that displaces another base in forming a pair with the acid (gaseous DME transition state) would form the more stable transition state.
The energy minimization in the implementation of HSAB concepts tend to omit electrostatic interactions or approximate them as spherical distributions of charges instead of the actual charge distributions in acids and bases.79 The charge reorganization and electrostatic interaction energies considered rigorously in our recent work provide descriptors that are direct and specific to the types of catalysts and reaction,30,33 which seem more useful than the indirect historical descriptors for the predictions of activation energies but the full extent of generality of these descriptors and relations to the historical concepts remain to be explored.
6. Outlook and conclusions
The concepts described in this Feature Article show how and why independent descriptors of acid catalysts and molecules in their respective isolated non-interacting state are insufficient to describe reactivity in acid catalysis, especially solid acid catalysts. Such inherent incompleteness merely reflects the nature of interaction energies at bound intermediates and transition states. These interactions cannot be captured, in general, solely by the ability of species to donate or accept a proton, because they also sense the ability of solid anions and organic cations to reorganize charge so as to minimize the energy of bound intermediates and transition states. These interactions reflect, in turn, how these charges are distributed throughout the isolated forms of these species, as well as the energy required to rearrange charges so as to optimize the overall free energy of the system.The electrostatic and charge reorganization components of the interactions between protons and conjugate anions solely reflect the ability of the anion to accept and distribute the negative charge. They are characteristics of each type of solid acid, with the relevant descriptions dictated by the amount of charge in the conjugate anions and the energy required to delocalize that charge (Mo-POM and W-POM clusters with different central atoms, silicates with different heteroatoms, mineral acids). The energy required to reorganize charge in bound species and transition states is captured by their respective ability to recover the ionic and covalent components of DPE, the energy required to remove the proton from the conjugate anion to non-interacting distances. The evidence provided here raises significant concerns about the accuracy and usefulness of linear scaling relations that purport to describe chemical reactivity solely on the basis of the properties of isolated molecular species and inorganic solid catalysts. It also casts serious doubts about the fidelity and relevance of experimental and theoretical metrics of acid strength based on the binding properties of any specific titrant molecule. The essential requirement to account for charge reorganization in anions and cations upon binding may seem onerous and indeed the incompleteness of independent descriptors brings forth unavoidable challenges into any attempts to “complete” them. Yet, the complexity inherent in the more realistic framework described here reveals design criteria and compositional diversity in a manner otherwise concealed by simplistic rules based on linear combinations of the properties of isolated molecules and solids on chemical reactivity.
These concepts have led to more complete descriptors of reactivity and, by necessity, to general rules that are inherently more granular, but they represent nothing more than the extension of heuristic concepts of chemical strength and hardness, in more quantitative and modern form, to acid–base catalysis by solids. They preserve our ability to transfer the isolated properties of molecules and solids into a prediction of how they would respond to the presence of each other within interacting distances, albeit with the requirements that solids and reactions must be judiciously but more granularly grouped into types or families.
The initial steps in our search for more complete descriptors, which we describe here for a few illustrative types of acids and reactions, must be followed by benchmarking and extensions of electrostatic and reorganization components of energies for more types of reactions and acid families. An appropriate path forward and outlook includes:
(i) Mapping relations between the properties of cations and anions used historically as descriptors of acids and bases and the electrostatic and charge reorganization components of their interaction energies,
(ii) Developing more efficient methods to calculate electrostatic interactions among charged species and to precisely account for electrostatic interactions among charged unit cells in periodic systems,
(iii) Incorporating non-covalent host–guest interactions, such as van der Waals forces, that become important especially within voids of molecular dimensions, as well as structure optimization methods that allow inorganic frameworks to relax, at an energy penalty, in order to minimize the free energy of confined host–guest pairs,
(iv) Including entropy considerations, because of their relevance to the Gibbs free energies required for reactivity estimates in transition state theory treatments, into the framework described here, which is currently based solely on electronic energy considerations.
6.1. Relations between the properties of cations and anions and the electrostatic and charge reorganization components of their interaction energies
All chemical bonds retain some level of covalency, even when denoted in practice as “ionic bonds”. Such covalency is typically associated with heuristics based on the size and charge of the atoms that share the chemical bond, because larger ions typically exhibit more deformable valence electron clouds, while smaller ions, with more localized charges, tend to distort the charge distribution in the counterion more effectively.82,83,90 Electron sharing, the signature of covalency, is therefore favored when cations are small and anions are large, because it requires anion charges to deform toward cations to form species that become less charged than full ion pairs.These heuristics, based solely on size and charge, suggest that small cations, such as protons, would form more covalent bonds with the conjugate anions than the larger and more diffuse cations that are characteristic of transition states. Such guiding principles do not consider shape or provide precise guidance about how to define size or charge for conjugate anions that consist of extended structures, such as in the case of solid acids. The combined electronegativity and hardness of reactive species and conjugate anions, determined from DFT-derived energies, taken together with HSAB principles, provide indirect energy-based descriptors of the distributions of charges and of their ability to reorganize.79,80,90–95 Our approach replaces such indirect properties with direct predictions of reactivity that can be generalized into a single “number”; this number combines the properties of isolated molecules and catalysts for families of reactions and types of acids. Electronegativity and hardness values are shown here for some acids and bases involved in acid catalysis to illustrate relations between the indirect historical descriptors and the interaction energies calculated directly. A more complete mapping of such relations for broader range of acids and reactions would be useful in developing more rigorous connections between intuitive historical descriptors and quantitative look-up tables for DPE components and recovery fractions that determine the modified DPE values.
6.2. Accurate and efficient methods for calculating electrostatic interactions in chemical bonds
Our framework uses electrostatic energies derived from numerical integration of Coulomb energy terms over grid-based charge densities; these methods scale poorly with the number of grid points, thus precluding the use of more detailed charge distributions in these calculations.87 Methods based on distributed moments of the charge distributions87,96 and adaptive algorithms that adjust between fine-grained and coarse-grained charge distributions based on the distances between interacting ions96 would enable better sampling of diverse molecular orientations for charge distributions that extend over larger distances and for complex topologies, such as those present in the nanometer-sized voids of crystalline heterosilicates.Precise estimates of electrostatic interactions among unit cells in periodic lattices are required for DFT-derived DPE values in crystalline heterosilicates,43 as well as in ancillary calculations such as H+ and OH− addition energies required to estimate acid–base properties in periodic solids.97 These estimates require, in turn, accurate estimates of dipole and quadrupole moments and their interactions for unit cells.48 These calculations exhibit spurious electrostatic interactions associated with electron clouds for atoms near cell boundaries that extend into vicinal supercells, while their nuclei, treated as point charges, remain entirely on one side of the boundary. These extraneous contributions can be minimized, and plausibly eliminated, by using quasi-spherical diffuse charges for nuclei, so that the smeared charges and the point charge look identical from outside the sphere,98 thus balancing the electrons that lie across cell boundaries. Such methods have been tried in attempts to calculate dipole moments in bound CO–CO pairs at Pt surfaces, by partitioning supercells into regions for each CO and assigning partial charges to each region.99 Such strategies would allow precise periodic DFT calculations of DPE values, which require the isolation of the negative charge at the conjugate anion framework upon removal of protons to non-interacting distances, thus avoiding large cluster calculations, QM-MM approaches requiring uncertain judgments about the required size of the QM region, or ad hoc corrections based on the framework density.43
6.3. Host–guest interactions in confining voids
The confinement of guest molecules within voids of molecular dimensions introduces non-covalent interactions that benefit from the right host–guest “fit” and from the ability of the guest and the host (such as crystalline heterosilicates) to reorganize their “shape” at an energy penalty that is compensated by an improvement in fit. These shape reorganization concepts are analogous to those that reorganize charge in the ion-pair interactions discussed in this Feature Article, in which case the charge reorganization incurs an energy penalty that is compensated by the more effective electrostatic interactions that result. In the reorganization of shape, also mediated by electron rearrangements required to distort chemical bonds, the benefits result from more effective van der Waals contacts, which reflect induced dipoles instead of net charges. These interactions depend on differences in shapes and sizes between the host and the guest, as well on their “structural stiffness,” just as the ion-pair interactions depend on electronegativity differences and “chemical hardness”. The adaptation of shapes in seeking energy minima was demonstrated for alkene oligomerization transition states of different sizes in aluminosilicate frameworks.34–37 The refinement and quantification of these effects will require metrics of structural stiffness based on energies, as well as further improvements in the handling of vdW interactions within DFT functionals.6.4. Entropy considerations and the kinetic relevance of elementary steps based on free energies
The framework for analysis described here uses the electronic energies of molecules and acids to determine the kinetic relevance of specific elementary steps and decides, on such basis, what energy and free energy differences determine reactivity for each illustrative reaction. The entropy component of the Gibbs free energies that determine reactivity did not affect conclusions about the effects of DPE on alkanol elimination rate constants on POM clusters,33,70 but such consistency may not extend to other types of solid acids and reactions, especially for confined systems, for which the enthalpic gains brought forth by van der Waals forces come at significant entropy losses, thus leading to compensation effects between activation enthalpies and entropies often observed in acid catalysis.100 Entropy effects are also relevant to the assessment of the kinetic relevance of elementary steps, because conclusions reached based solely on electronic energies can differ significantly from those based on the Gibbs free energies that determine the magnitude of rate constants and thus the kinetic relevance of specific elementary steps. Such probing of reaction coordinates and transition states based on free energies is challenging because vibrational entropies derived using harmonic oscillator formalisms are inaccurate for low-frequency modes that replace translational and rotational model of gas and liquid molecules upon their binding at surfaces; yet, such modes represent the largest contributions to the entropy of bound intermediates and transition states. More accurate entropy estimates require detailed sampling of the full potential energy surfaces for such modes,101 the replacement of such modes with hindered translators or rotors based on statistical mechanics,102ad hoc replacement of the entropy of such modes with a set fraction of the entropy of gaseous analogs,103,104 or empirical relations between entropy loss and “occupied volume” for molecules confined in pores.105 While such methods have been developed and implemented and compared for specific systems of adsorbates on metals or mobile species in pores, benchmarking and assessment of their accuracy for diverse reactions on Brønsted acids need to be performed in order to identify the most efficient methods that can accurately predict free energies and the relations of their entropy components to properties of molecules and acids for relevant families of reactions and types of acids.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, under contract number DE-AC05-76RL0-1830. We acknowledge Prof. Michele Sarazen (Princeton University), Dr William Knaeble (ExonnMobil), Dr Andrew Jones, Dr Robert Carr (ExonnMobil), Dr Stanley Hermann, Prof. Shuai Wang (Xiamen University), Prof. Rajamani Gounder (Purdue University), Prof. Matthew Neurock (University of Minnesota) for their technical and conceptual contributions to the findings described here and in previous jointly published articles. We thank Dr Andrew Hwang, Prof. Michele Sarazen, Mr Ari Fisher, Dr Biswanath Dutta, Mr Janik Hense, Mr Adam Twombly and Mr Husain Adamji for their review and proofreading of this article. Computational resources were provided by the Environmental Molecular Science Laboratory (EMSL) at Pacific Northwest National Laboratory (PNNL), a DOE Office of Science User Facility (Proposal Number 48772) and by Extreme Science and Engineering Discovery Environment (XSEDE; National Science Foundation award number ACI-1548562). EI acknowledges Theodore Vermeulen Chair Fund for support. PD acknowledges support from American Chemical Society Petroleum Research Fund (award number 57869-DNI5).References
- P. A. Jacobs and J. A. Martens, Studies in Surface Science and Catalysis, Elsevier, 1991, vol. 58, pp. 445–496 Search PubMed.
- A. Corma, Chem. Rev., 1995, 95, 559–614 CrossRef CAS.
- C. Martínez and A. Corma, Coord. Chem. Rev., 2011, 255, 1558–1580 CrossRef.
- K. Tanabe and W. F. Hölderich, Appl. Catal., A, 1999, 181, 399–434 CrossRef CAS.
- W. Vermeiren and J. P. Gilson, Top. Catal., 2009, 52, 1131–1161 CrossRef CAS.
- J. N. Chheda, G. W. Huber and J. A. Dumesic, Angew. Chem., Int. Ed., 2007, 46, 7164–7183 CrossRef CAS PubMed.
- M. Guisnet and L. Pinard, Catal. Rev., 2018, 60, 337–436 CrossRef CAS.
- E. G. Derouane and Z. l. Gabelica, J. Catal., 1980, 65, 486–489 CrossRef CAS.
- C. Hu, M. Hashimoto, T. Okuhara and M. Misono, J. Catal., 1993, 143, 437–448 CrossRef CAS.
- J. F. Haw, Phys. Chem. Chem. Phys., 2002, 4, 5431–5441 RSC.
- J. Macht, R. T. Carr and E. Iglesia, J. Am. Chem. Soc., 2009, 131, 6554–6565 CrossRef CAS PubMed.
- R. T. Carr, M. Neurock and E. Iglesia, J. Catal., 2011, 278, 78–93 CrossRef CAS.
- E. Iglesia, Consequences of Confinement for Catalysis within Voids of Molecular Dimensions, Proceedings of the 24th Solvay Conference on Chemistry, 2018, pp. 148–155.
- W. Knaeble, R. T. Carr and E. Iglesia, J. Catal., 2014, 319, 283–296 CrossRef CAS.
- R. Gounder and E. Iglesia, Chem. Commun., 2013, 49, 3491–3509 RSC.
- A. J. Jones, R. T. Carr, S. I. Zones and E. Iglesia, J. Catal., 2014, 312, 58–68 CrossRef CAS.
- F. Goltl, C. Michel, P. C. Andrikopoulos, A. M. Love, J. Hafner, I. Hermans and P. Sautet, ACS Catal., 2016, 6, 8404–8409 CrossRef CAS.
- A. Auroux and A. Gervasini, J. Phys. Chem., 1990, 94, 6371–6379 CrossRef CAS.
- C. Lee, D. J. Parrillo, R. J. Gorte and W. E. Farneth, J. Am. Chem. Soc., 1996, 118, 3262–3268 CrossRef CAS.
- M. Boronat and A. Corma, Catal. Lett., 2015, 145, 162–172 CrossRef CAS.
- G. Bourdillon, C. Gueguen and M. Guisnet, Appl. Catal., 1990, 61, 123–139 CrossRef CAS.
- D. Zhou, Y. Bao, M. Yang, N. He and G. Yang, J. Mol. Catal. A: Chem., 2006, 244, 11–19 CrossRef CAS.
- D. J. Parrillo, C. Lee, R. J. Gorte, D. White and W. E. Farneth, J. Phys. Chem., 1995, 99, 8745–8749 CrossRef CAS.
- R. J. Gorte, Catal. Lett., 1999, 62, 1–13 CrossRef CAS.
- R. A. Van Santen, Catal. Today, 1997, 38, 377–390 CrossRef CAS.
- V. B. Kazanskii, Acc. Chem. Res., 1991, 24, 379–383 CrossRef CAS.
- V. B. Kazansky and I. N. Senchenya, J. Catal., 1989, 119, 108–120 CrossRef.
- E. G. Derouane, J. C. Vedrine, R. R. Pinto, P. M. Borges, L. Costa, M. Lemos, F. Lemos and F. R. A. Ribeiro, Catal. Rev., 2013, 55, 454–515 CrossRef CAS.
- M. T. Aronson, R. J. Gorte and W. E. Farneth, J. Catal., 1986, 98, 434–443 CrossRef CAS.
- P. Deshlahra, R. T. Carr and E. Iglesia, J. Am. Chem. Soc., 2014, 136, 15229–15247 CrossRef CAS PubMed.
- F. Eder and J. A. Lercher, J. Phys. Chem. B, 1997, 101, 1273–1278 CrossRef CAS.
- A. Corma, J. Catal., 2003, 216, 298–312 CrossRef CAS.
- P. Deshlahra and E. Iglesia, ACS Catal., 2016, 6, 5386–5392 CrossRef CAS.
- M. L. Sarazen and E. Iglesia, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, E3900–E3908 CrossRef CAS PubMed.
- S. Wang and E. Iglesia, J. Catal., 2017, 352, 415–435 CrossRef CAS.
- M. L. Sarazen, E. Doskocil and E. Iglesia, ACS Catal., 2016, 6, 7059–7070 CrossRef CAS.
- M. L. Sarazen and E. Iglesia, ChemCatChem, 2018, 10, 4028–4037 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, M. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian Inc., Wallingford CT, 2009, vol. 27, p. 34.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558 CrossRef CAS PubMed.
- P. Deshlahra, R. T. Carr, S.-H. Chai and E. Iglesia, ACS Catal., 2015, 5, 666–682 CrossRef CAS.
- I. A. Koppel, P. Burk, I. Koppel, I. Leito, T. Sonoda and M. Mishima, J. Am. Chem. Soc., 2000, 122, 5114–5124 CrossRef CAS.
- A. J. Jones and E. Iglesia, ACS Catal., 2015, 5, 5741–5755 CrossRef CAS.
- M. Brändle and J. Sauer, J. Am. Chem. Soc., 1998, 120, 1556–1570 CrossRef.
- M. J. Janik, J. Macht, E. Iglesia and M. Neurock, J. Phys. Chem. C, 2009, 113, 1872–1885 CrossRef CAS.
- J. Macht, R. T. Carr and E. Iglesia, J. Catal., 2009, 264, 54–66 CrossRef CAS.
- L. P. Hammett and A. J. Deyrup, J. Am. Chem. Soc., 1932, 54, 2721–2739 CrossRef CAS.
- G. Makov and M. C. Payne, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 4014 CrossRef CAS PubMed.
- J. r. Neugebauer and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 16067 CrossRef CAS PubMed.
- L. Grajciar, C. O. Arean, A. Pulido and P. Nachtigall, Phys. Chem. Chem. Phys., 2010, 12, 1497–1506 RSC.
- C. Freysoldt, J. R. Neugebauer and C. G. Van de Walle, Phys. Rev. Lett., 2009, 102, 016402 CrossRef PubMed.
- F. Bruneval, J.-P. Crocombette, X. Gonze, B. Dorado, M. Torrent and F. Jollet, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 045116 CrossRef.
- J. Sauer and M. Sierka, J. Comput. Chem., 2000, 21, 1470–1493 CrossRef CAS.
- U. Eichler, M. Brändle and J. Sauer, J. Phys. Chem. B, 1997, 101, 10035–10050 CrossRef CAS.
- M. Sierka, U. Eichler, J. Datka and J. Sauer, J. Phys. Chem. B, 1998, 102, 6397–6404 CrossRef CAS.
- C. Lo and B. L. Trout, J. Catal., 2004, 227, 77–89 CrossRef CAS.
- M. Rybicki and J. Sauer, Catal. Today, 2019, 223, 86–93 CrossRef.
- M. J. Janik, R. J. Davis and M. Neurock, J. Catal., 2006, 244, 65–77 CrossRef CAS.
- K. A. Peterson, S. S. Xantheas, D. A. Dixon and T. H. Dunning, J. Phys. Chem. A, 1998, 102, 2449–2454 CrossRef CAS.
- D. H. Aue, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 487–508 CAS.
- P. M. Esteves, G. G. P. Alberto, A. Ramírez-Solís and C. J. A. Mota, J. Phys. Chem. A, 2000, 104, 6233–6240 CrossRef CAS.
- C. J. A. Mota, P. M. Esteves, A. Ramírez-Solís and R. Hernández-Lamoneda, J. Am. Chem. Soc., 1997, 119, 5193–5199 CrossRef CAS.
- P. M. Esteves, C. J. A. Mota, A. Ramírez-Solís and R. Hernández-Lamoneda, J. Am. Chem. Soc., 1998, 120, 3213–3219 CrossRef CAS.
- R. J. Gorte and S. P. Crossley, J. Catal., 2019, 375, 524–530 CrossRef CAS.
- C.-C. Lee, R. Gorte and W. Farneth, J. Phys. Chem. B, 1997, 101, 3811–3817 CrossRef CAS.
- J. A. Ryder, A. K. Chakraborty and A. T. Bell, J. Phys. Chem. B, 2000, 104, 6998–7011 CrossRef CAS.
- C. Paolucci, J. Di Iorio, F. Ribeiro, R. Gounder and W. Schneider, Advances in Catalysis, Elsevier, 2016, vol. 59, pp. 1–107 Search PubMed.
- C. Paolucci, A. A. Verma, S. A. Bates, V. F. Kispersky, J. T. Miller, R. Gounder, W. N. Delgass, F. H. Ribeiro and W. F. Schneider, Angew. Chem., Int. Ed., 2014, 53, 11828–11833 CrossRef CAS PubMed.
- C. H. McAteer, C. D. Brown and R. D. Davis Sr., Pyridine base synthesis, US Pat., 5780635, 1998 Search PubMed.
- W. Knaeble and E. Iglesia, J. Phys. Chem. C, 2016, 120, 3371–3389 CrossRef CAS.
- J. R. Di Iorio, A. J. Hoffman, C. T. Nimlos, S. Nystrom, D. Hibbitts and R. Gounder, J. Catal., 2019, 380, 161–177 CrossRef CAS.
- M. A. Natal-Santiago, R. Alcala and J. A. Dumesic, J. Catal., 1999, 181, 124–144 CrossRef CAS.
- A. J. Jones and E. Iglesia, Angew. Chem., Int. Ed., 2014, 53, 12177–12181 CrossRef CAS PubMed.
- W. Knaeble and E. Iglesia, J. Catal., 2016, 344, 817–830 CrossRef CAS.
- G. Noh, Z. Shi, S. I. Zones and E. Iglesia, J. Catal., 2018, 368, 389–410 CrossRef CAS.
- G. Noh, S. I. Zones and E. Iglesia, J. Phys. Chem. C, 2018, 122, 25475–25497 CrossRef CAS.
- S. Wang and E. Iglesia, ACS Catal., 2016, 6, 7664–7684 CrossRef CAS.
- S. Herrmann and E. Iglesia, J. Catal., 2018, 360, 66–80 CrossRef CAS.
- P. W. Ayers, R. G. Parr and R. G. Pearson, J. Chem. Phys., 2006, 124, 194107 CrossRef PubMed.
- R. G. Parr and R. G. Pearson, J. Am. Chem. Soc., 1983, 105, 7512–7516 CrossRef CAS.
- R. A. Van Santen and G. J. Kramer, Chem. Rev., 1995, 95, 637–660 CrossRef CAS.
- K. Fajans, Naturwissenschaften, 1923, 11, 165–172 CrossRef CAS.
- S. J. French, J. Chem. Educ., 1936, 13, 122 CrossRef CAS.
- R. P. Feynman, Phys. Rev., 1939, 56, 340 CrossRef CAS.
- Y. Ma and P. Politzer, J. Chem. Phys., 2004, 120, 8955–8959 CrossRef CAS PubMed.
- R. F. W. Bader, Chem. – Eur. J., 2006, 12, 2896–2901 CrossRef CAS PubMed.
- A. Volkov and P. Coppens, J. Comput. Chem., 2004, 25, 921–934 CrossRef CAS PubMed.
- G. Sastre and A. Corma, J. Mol. Catal. A: Chem., 2009, 305, 3–7 CrossRef CAS.
- A. J. Jones, S. I. Zones and E. Iglesia, J. Phys. Chem. C, 2014, 118, 17787–17800 CrossRef CAS.
- P. Geerlings and F. De Proft, Phys. Chem. Chem. Phys., 2008, 10, 3028–3042 RSC.
- R. S. Mulliken, J. Chem. Phys., 1934, 2, 782–793 CrossRef CAS.
- A. L. Allred and E. G. Rochow, J. Inorg. Nucl. Chem., 1958, 5, 264–268 CrossRef CAS.
- C. E. Housecroft and A. G. Sharpe, Inorganic Chemistry, Pearson, England, 2005, pp. 673–700 Search PubMed.
- R. G. Pearson, J. Am. Chem. Soc., 1963, 85, 3533–3539 CrossRef CAS.
- R. G. Pearson, Chemical hardness, Wiley Online Library, 1997 Search PubMed.
- G. A. Cisneros, M. Karttunen, P. Ren and C. Sagui, Chem. Rev., 2014, 114, 779–814 CrossRef CAS PubMed.
- S. Wang and E. Iglesia, J. Phys. Chem. C, 2016, 120, 21589–21616 CrossRef CAS.
- D. J. Griffiths, Introduction to electrodynamics, Prentice Hall, Upper Saddle River, N.J., 1999 Search PubMed.
- P. Deshlahra, J. Conway, E. E. Wolf and W. F. Schneider, Langmuir, 2012, 28, 8408–8417 CrossRef CAS PubMed.
- R. Gounder and E. Iglesia, Acc. Chem. Res., 2011, 45, 229–238 CrossRef PubMed.
- A. Bajpai, P. Mehta, K. Frey, A. M. Lehmer and W. F. Schneider, ACS Catal., 2018, 8, 1945–1954 CrossRef CAS.
- L. H. Sprowl, C. T. Campbell and L. Arnadottir, J. Phys. Chem. C, 2016, 120, 9719–9731 CrossRef CAS.
- C. T. Campbell and J. R. Sellers, Chem. Rev., 2013, 113, 4106–4135 CrossRef CAS PubMed.
- P. Deshlahra and E. Iglesia, J. Phys. Chem. C, 2014, 118, 26115–26129 CrossRef CAS.
- P. J. Dauenhauer and O. A. Abdelrahman, ACS Cent. Sci., 2018, 4, 1235–1243 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2020 |