Open Access Article
Open Access ArticleSurprising solvent-induced structural rearrangements in large [N⋯I+⋯N] halogen-bonded supramolecular capsules: an ion mobility-mass spectrometry study†‡
Ulrike
Warzok
a,
Mateusz
Marianski§
 b,
Waldemar
Hoffmann
b,
Waldemar
Hoffmann
 ab,
Lotta
Turunen¶
c,
Kari
Rissanen
ab,
Lotta
Turunen¶
c,
Kari
Rissanen
 c,
Kevin
Pagel
c,
Kevin
Pagel
 ab and
Christoph A.
Schalley
ab and
Christoph A.
Schalley
 *ad
*ad
aInstitut für Chemie und Biochemie, Freie Universität Berlin, Takustraße 3, 14195 Berlin, Germany. E-mail: c.schalley@fu-berlin.de
bFritz-Haber-Institut der Max-Planck-Gesellschaft, Faradayweg 4-6, 14195 Berlin, Germany
cDepartment of Chemistry, NanoScience Center, University of Jyväskylä, P. O. Box 35, 40014 Jyväskylä, Finland
dSchool of Life Sciences, Northwestern Polytechnical University, 127 Youyi Xilu, Xi'an, Shaanxi 710072, P. R. China
First published on 5th September 2018
Abstract
Coordinative halogen bonds have recently gained interest for the assembly of supramolecular capsules. Ion mobility-mass spectrometry and theoretical calculations now reveal the well-defined gas-phase structures of dimeric and hexameric [N⋯I+⋯N] halogen-bonded capsules with counterions located inside their cavities as guests. The solution reactivity of the large hexameric capsule shows the intriguing solvent-dependent equilibrium between the hexamer and an unprecedented pentameric [N⋯I+⋯N] halogen-bonded capsule, when the solvent is changed from chloroform to dichloromethane. The intrinsic flexibility of the cavitands enables this novel structure to adopt a pseudo-trigonal bipyramidal geometry with nine [N⋯I+⋯N] bonds along the edges and two pyridine binding sites uncomplexed.
Introduction
Supramolecular capsules have attracted continuous attention since Rebek introduced his famous hydrogen-bonded “tennis ball” in 1993.1 A plethora of examples have been described in the literature, which feature a broad range of different binding motifs such as hydrogen bonding,2 metal coordination,3 ion-pair interactions,4 or more recently, halogen bonding.5–8 Among these interactions, the strength and directionality of the halogen bond (XB) renders it exceptionally promising for the development of novel, structurally well-defined supramolecular complexes.9The halogen bond is a noncovalent interaction between a polarized halogen atom and a Lewis base.10 Positively charged iodonium ions are a special case of XB donor, as they can bind two Lewis bases in a three-center-four-electron bond.11,12 Since these two Lewis bases can be identical, building block synthesis for larger supramolecular assemblies is more easily achieved, as no attention needs to be paid to complementary couples of matching XB donors and acceptors. This renders iodonium ions excellent synthons for the self-assembly of novel supramolecular capsules.6,7,13
The structural analysis of large supramolecular capsules,14 as well as the investigation of their dynamic rearrangements in condensed phase are challenging.15,16 Self-assembly and self-sorting processes can be very fast, produce transient intermediates, or numerous products of low abundance. Standard condensed phase techniques, such as NMR, often struggle to provide information on the composition of these mixtures due to substantial signal superposition or fast dynamic processes averaging the signal positions. Moreover, the ability to target individual complexes in the mixture to conduct a detailed structural analysis is limited. However, these analytical shortcomings can be readily overcome by complementary gas-phase techniques.17
Electrospray ionization (ESI) is a soft ionization method capable of transferring even large noncovalent complexes from solution into the gas phase with minimal to no fragmentation.18 The transfer of ions into the gas phase interrupts the operation of underlying solution equilibria, thereby enabling their separation and subsequent analysis. Mass spectrometry (MS) offers a range of gas-phase experiments to investigate the structure and reactivity of a mass-selected ion of interest.19 Moreover, traditional MS experiments can be augmented with orthogonal separation techniques such as ion mobility spectrometry (IMS), which adds another dimension by separating analytes beyond their mass-to-charge (m/z) ratio. In a drift tube IMS (DT-IMS) experiment, ions are guided by a weak electric field through a drift tube filled with an inert buffer gas typically at pressures of a few millibars. During their migration, more extended ions are decelerated by a larger number of collisions with the buffer gas than compact ions of the same m/z and, as a result, leave the IMS cell after longer drift times. Consequently, the combination of IMS and MS to ion mobility-mass spectrometry (IM-MS) accomplishes ion separation not only based on their m/z, but also differences in charge, size, and shape.20 The drift time of an ion can be further converted to a collision cross section (CCS), which represents an intrinsic molecular property independent from instrumental parameters.21,22 Comparison of CCS values to reference experimental or theoretical values can provide quite detailed insight into the molecular structure. Hence, the characterization of supramolecular complexes in solution can largely benefit from gas-phase techniques such as MS and IMS.23
Theoretical modelling of large supramolecular complexes presents challenges due to their size and delicate balance of various forces governing their stability. Grimme et al. presented quantum chemical calculations on a neutral halogen-bonded, heterodimeric capsule using semi-empirical methods tailored for the treatment of such systems.24 Alternatively, composite methods, in which a more advanced quantum-mechanical treatment of the XB can be combined with a lower level of theory for the remaining framework of the capsules,25 offer a feasible solution to study larger complexes.
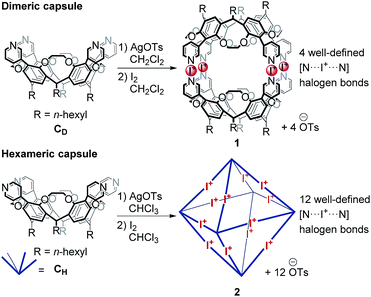
Recently, we reported the synthesis and characterization of dimeric and hexameric halogen-bonded capsules self-assembling from the different pyridyl-substituted resorcin[4]arene cavitands CD and CH and positively charged iodonium ions through coordinative [N⋯I+⋯N] halogen bonds (Scheme 1).6,7 Their syntheses follow a two-step protocol. First, the cavitands are reacted with silver(I) p-toluenesulfonate to yield the Ag(I)-containing capsules. Then, a reaction with molecular iodine leads to an [N⋯Ag+⋯N] → [N⋯I+⋯N] exchange reaction. The halogen-bonded capsules were characterized by NMR and diffusion ordered spectroscopy (DOSY), together with preliminary MS experiments.
Here, we focus on a detailed structural analysis of dimeric and hexameric halogen-bonded capsules 1 and 2 in the gas phase (Scheme 1). Collision cross sections derived from DT-IM-MS measurements in helium buffer gas (DTCCSHe) were compared with theoretical values obtained from structures optimized with composite density-functional theory (DFT) and semi-empirical calculations. The calculations confirm formation of highly regular complexes and provide insights into their anion-guest binding behaviour. We furthermore observe a selective, solvent-dependent rearrangement of the hexamer into new pentameric halogen-bonded capsules 3 upon a rather subtle change of the solvent from chloroform to dichloromethane. The capsules are thus responsive to a chemical stimulus. The novel structure has been identified to exhibit an unusual pseudo-trigonal bipyramidal geometry with nine [N⋯I+⋯N] bonds along the edges and two pyridines uncomplexed.
Material and methods
Sample preparation
For the assembly of the [N⋯I+⋯N] halogen-bonded dimeric capsule 1, the hexameric capsule 2, and the pentameric capsule 3 (1 mM), a solution of the corresponding cavitand CD (for 1, 1 eq.) or CH (for 2 and 3, 1 eq.) was first mixed with AgOTs (2.0 eq.), stirred for 1 h and subsequently treated with I2 (2.5 eq.), stirred for 20 min and centrifuged to remove precipitated AgI from the mixture. Dimeric and pentameric capsules (1, 3) were assembled and investigated using dichloromethane as the reaction and electrospray solvent; for the hexameric capsule 2, chloroform was used instead.6,7Electrospray ionization mass spectrometry
Positive-mode electrospray ionization quadrupole-time-of-flight high resolution mass spectrometric (ESI-Q-TOF-HRMS) experiments were performed with a Synapt G2-S HDMS (Waters Co., Milford, MA, USA) instrument. The following settings were used: flow rate 5–10 μL min−1, capillary voltage 3.3 kV, sample cone voltage 40 V, source offset 80 V, source temperature 90 °C, desolvation temperature 250 °C, nebulizer gas 6 bar, desolvation gas flow 500 L h−1. For collision-induced dissociation (CID), N2 was used as the collision gas. Fragmentation experiments were conducted in the trap cell of the Synapt G2-S HDMS instrument with collision energies of 2–25 V. Data acquisition and processing was carried out using MassLynx™ (version 4.1).Drift tube ion mobility-mass spectrometry
Measurements to obtain experimental collision cross sections (DTCCSHe) have been conducted on an in-house-constructed DT-IM-MS instrument (iMob), which is described in detail elsewhere.26 Briefly, ions are generated using a nano-electrospray ionization (nESI) source and subsequently pulsed into an ion mobility cell in which they travel under the influence of a weak electric field (10–15 V cm−1) through helium buffer gas (∼5 mbar). After ion separation in the ion mobility cell, the ions of interest are m/z-selected using a quadrupole mass filter and their arrival time distributions (ATDs) are recorded by measuring their time-dependent ion current. ATDs have been recorded at six different drift voltages (950–1200 V) and were fitted by Gaussian functions. The center of each Gaussian corresponds to the drift time of a single species and is further converted into a DTCCSHe using the Mason–Schamp equation.21,22Theoretical calculations
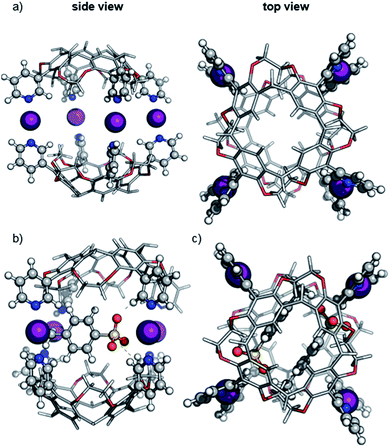
The size of the capsules under consideration prohibits full treatment at the density-functional theory level. To decrease the computational effort while maintaining the quantum mechanical description of the halogen bond, the multilayered ONIOM method was used as implemented in the Gaussian09 rev.D01 code.27 The DFT level of theory has been applied to the iodonium ions, the pyridine groups and the tosylate counterions (see Fig. 2), while the cavitand scaffold was described with the semi-empirical AM1 method.28To choose a suitable exchange-correlation density functional, we first evaluated the performance of commonly used methods on the [pyridine⋯I+⋯pyridine] model system. The structure has been optimized at the MP2 level of theory with a def2-TZVP basis set and the binding energy has been calculated. Next, the binding energy of various functionals in def2-type29 basis sets were computed (see ESI, Table S1‡) and compared with MP2/def2-QZVPP single-point energies. Among the tested methods, the PBE0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 hybrid exchange-correlation functional in a small def2-SVP basis set yields a small absolute error of 8.8 kJ mol−1 which promises a good balance between accuracy and tractability of calculations. Moreover, the comparison of geometric parameters of the [pyridine⋯I+ pyridine] model system optimized at the PBE0/def2-SVP level of theory with the corresponding MP2-optimized complex resulted only in very minor geometrical differences. Hereafter, we will refer to the ONIOM(PBE0/def2-SVP:AM1) method used in this work simply as DFT/AM1.
30 hybrid exchange-correlation functional in a small def2-SVP basis set yields a small absolute error of 8.8 kJ mol−1 which promises a good balance between accuracy and tractability of calculations. Moreover, the comparison of geometric parameters of the [pyridine⋯I+ pyridine] model system optimized at the PBE0/def2-SVP level of theory with the corresponding MP2-optimized complex resulted only in very minor geometrical differences. Hereafter, we will refer to the ONIOM(PBE0/def2-SVP:AM1) method used in this work simply as DFT/AM1.
The theoretical collision cross sections ™CCSHe were calculated using a trajectory method, as implemented in the Mobcal program.31 We used a uniform charge model for all atoms and adopted silicon parameters for the iodonium ions.
All calculated structures were optimized with the n-hexyl sidechains in a fully extended zigzag conformation. The CCS values derived from such arbitrary structures are likely to be overestimated by some constant increment per cavitand associated with the flexibility of the side chains. Therefore, we introduced a correction which was estimated as follows: a short molecular dynamics simulation was performed for a dimeric capsule for which the halogen-bonds were constrained to equilibrium bond lengths and angles, as derived from the [pyridine⋯I+⋯pyridine] model.32 Next, we extracted 30 random snapshots which featured n-hexyl chains in diverse orientations. The n-hexyl dihedral angles were translated to a pre-optimized capsule and the structure was again reoptimized at the DFT/AM1 level of theory. The geometry-optimized structures, which span several kJ mol−1 energy range, exhibit CCS values between 560 and 590 Å2 (see ESI, Fig. S9‡) with a mean of approximately 575 Å2, significantly below the 610 Å2 calculated for a dimer with fully extended side chains. To account for this inherent flexibility of the n-hexyl chains, we corrected all reported ™CCSHe values by an increment of (610–575 Å2)/2 cavitands ≈ 20 Å2 per cavitand.
Results and discussion
Structural analysis of halogen-bonded dimeric and hexameric capsules in the gas phase
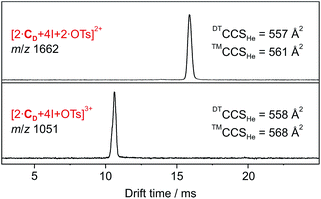 | ||
| Fig. 1 DT-IM-MS ATDs of ions derived from dimeric halogen-bonded capsule 1. Experimental DTCCSHe and theoretical ™CCSHe values are given. | ||
The optimized structure of the empty dimeric halogen-bonded capsule (Fig. 2a) reveals a slight helical twist of the two cavitands against each other to allow the formation of four linear [N⋯I+⋯N] bonds with an equilibrium N⋯I+ distance of 2.28 Å. The twist between two capsules is significantly smaller than that observed in the previously reported crystal structure for the silver-coordinated precursor capsule.6 The smaller twist can be attributed to the linearity of the halogen bonds with N–I–N angles close to 180 degrees, whereas the [N⋯Ag+⋯N] motif adopts an angle of 150–160 degrees.6,12
For calculations of capsular complexes with one tosylate counterion, several different starting structures were considered, which included positions of the anion inside and outside of the cavity (see ESI, Fig. S10‡). A tosylate ion inside the cavity has been found to be more stable, however, the energy preference is small (<4 kJ mol−1). In the optimized geometry, the tosylate anion does not interact with any iodonium ion directly, but rather with the cavitand through [Caryl–H⋯O−] interactions (Fig. 2b).33 The insertion of the second tosylate ion into the cavity leads to a cooperative stabilization of 35 kJ mol−1 – more than any other position around the capsule. Their antiparallel arrangement does not only reduce charge repulsion, but forms stabilizing van der Waals interactions between the two aromatic rings of the tosylates (Fig. 2c).
The predicted ™CCSHe values (corrected by 20 Å2 per cavitand; see above and ESI, Fig. S8‡) are 568 and 561 Å for the ions carrying one and two tosylate ions, respectively and agree well with experimental data (Fig. 1). We conclude that both anions bind cooperatively inside the cavity. The virtually identical collision cross sections suggest that already the first anion occupies the cavity.
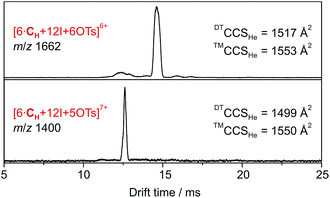 | ||
| Fig. 3 DT-IM-MS ATDs of ions derived from hexameric halogen-bonded capsule 2. Experimental DTCCSHe and theoretical ™CCSHe values are given. | ||
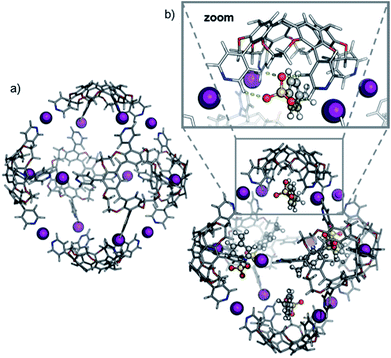
Accordingly, six spatially distributed binding pockets at such positions provide binding sites for six tosylates (Fig. 4b). The calculated ™CCSHe for the [6·CH + 12I + 6·OTs]6+ and [6·CH + 12I + 5·OTs]7+ ions of 1550 and 1553 Å2 are in good agreement with the experiment thus indicating that the hexameric capsule retains an intact octahedral geometry upon transfer into the gas phase with linear [N⋯I+···N] halogen bonds along all edges (Fig. 3). An anion-binding mode with tosylates bridging two adjacent pyridine rings of the same cavitand by multiple [Caryl–H⋯O−] interactions is proposed. It also appears to be well-suited in terms of size and shape complementarity of this host–guest complex.
Solvent-dependent formation of pentameric capsules
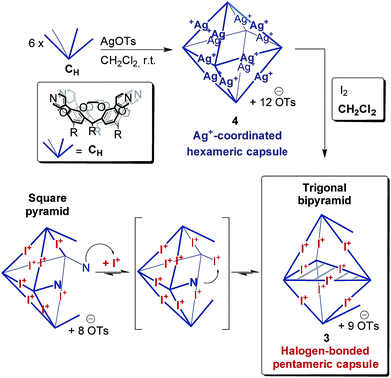
The corresponding ESI mass spectrum (90 μM in CH2Cl2) clearly shows the selective formation of a halogen-bonded pentamer 3 (Fig. 5). The almost exclusive appearance of pentameric species, instead of a non-specific distribution of oligomers, strongly suggests stable and well-defined structures to form. The signals can be assigned to charge states 6+ to 3+ and the most abundant signal of each charge state belongs to a complex with a formal [5·CH + 9I]9+ core to which a varying number of anions is attached. The most dominant peak at m/z 1602 belongs to the complex [5·CH + 9I + 4·OTs]5+. The observed exact mass and experimental isotope pattern agree with those simulated based on natural abundances. The mass spectrum furthermore exhibits ions which correspond to singly and doubly protonated species for each charge state accompanying the [5·CH + 9I + x·OTs](9−x)+ peaks, e.g. [5·CH + 9I + H + 5·OTs]5+ and [5·CH + 9I + 2H + 6·OTs]5+ ions at m/z 1637 and 1671. Considering possible pentameric assemblies which would maintain linear [N⋯I+⋯N] halogen bonds quickly makes clear that the formation of a complex which has all pyridine binding sites coordinated is impossible. Two possible candidates that maintain structural specificity, a bowl-shaped square pyramid and a pseudo-trigonal bipyramid, are possible (Scheme 2). In order to accommodate the geometrical constrains, both structures must feature uncomplexed pyridines, i.e. two for the pseudo-trigonal bipyramid and four for the square pyramid. Similarly, earlier studies by Aakeröy et al. demonstrated the formation of a heterodimeric halogen-bonded capsule in the solid state, in which one of four possible XBs is sacrificed in a fraction of the complexes due to steric congestion.8
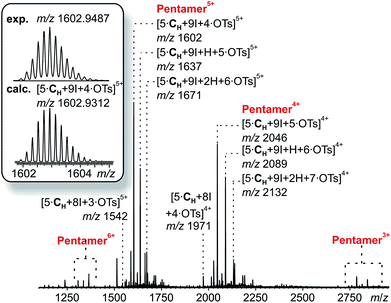 | ||
| Fig. 5 ESI-Q-TOF-HRMS spectrum of pentameric halogen-bonded capsule 3 (90 μM in CH2Cl2) with experimental and calculated isotopic pattern (inset). | ||
The two most prominent peaks for [5·CH + 9I + x·OTs](9−x)+ ions contain five and four tosylate counterions (x = 4, 5). This agrees with the trends observed for dimeric and hexameric [N⋯I+⋯N] capsules: each cavitand monomer offers one tosylate binding site within the capsule cavity. Upon ionization, the additional outer counterions are easily stripped off. In addition, the elimination of one of the inner tosylates can occur, but is energetically somewhat more demanding. This observation thus supports the assumption that the pentamer is a closed capsule and consequently speaks in favour of the bipyramidal structure. The 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 cavitand-to-iodonium stoichiometry observed in the prominent peaks of the mass spectrum is also in good agreement with the bipyramidal structure of the pentamer, as the square pyramid only requires eight [N⋯I+⋯N] halogen bonds, while the bipyramid bears nine. Capsule-derived complexes with singly coordinated I+ have not been observed, neither in this nor in our previous study.6 Consequently, the [N⋯I+⋯N] bond is likely much more stable than the hypothetical [N⋯I+] group. Furthermore, the observed single and double – but not triple or quadruple – protonation indicates the presence of two free pyridines as in the bipyramid rather than the four of the square pyramid. All these findings thus agree that the structure of the pentamer is that of a bipyramid that bears two non-coordinated pyridines. Nevertheless, low-abundant signals corresponding to ions with a formal [5·CH + 8I]8+ core, which appear at m/z 1542 and 1971, may indicate that the square pyramidal complex is present in solution at low concentrations. Therefore, the pseudo-trigonal bipyramidal pentameric [5·CH + 9I]9+ and the square pyramidal [5·CH + 8I]8+ complexes may exist in an equilibrium with each other. This equilibrium, however, is strongly shifted towards the pseudo-trigonal bipyramidal complex as this structure helps maximizing the number of halogen bonds within the pentamer (Scheme 2).
9 cavitand-to-iodonium stoichiometry observed in the prominent peaks of the mass spectrum is also in good agreement with the bipyramidal structure of the pentamer, as the square pyramid only requires eight [N⋯I+⋯N] halogen bonds, while the bipyramid bears nine. Capsule-derived complexes with singly coordinated I+ have not been observed, neither in this nor in our previous study.6 Consequently, the [N⋯I+⋯N] bond is likely much more stable than the hypothetical [N⋯I+] group. Furthermore, the observed single and double – but not triple or quadruple – protonation indicates the presence of two free pyridines as in the bipyramid rather than the four of the square pyramid. All these findings thus agree that the structure of the pentamer is that of a bipyramid that bears two non-coordinated pyridines. Nevertheless, low-abundant signals corresponding to ions with a formal [5·CH + 8I]8+ core, which appear at m/z 1542 and 1971, may indicate that the square pyramidal complex is present in solution at low concentrations. Therefore, the pseudo-trigonal bipyramidal pentameric [5·CH + 9I]9+ and the square pyramidal [5·CH + 8I]8+ complexes may exist in an equilibrium with each other. This equilibrium, however, is strongly shifted towards the pseudo-trigonal bipyramidal complex as this structure helps maximizing the number of halogen bonds within the pentamer (Scheme 2).
Theory confirms the individual cavitands to be sufficiently flexible to form a stable pseudo-trigonal bipyramidal pentameric capsule. Three cavitands in equatorial positions participate with all four pyridine groups in linear [N⋯I+⋯N] bonds (Fig. 6a). These cavitands are capped axially by the other two which bind in a somewhat distorted conformation. The two apical cavitands form only three [N⋯I+⋯N] bonds each and the fourth pyridine moiety remains unbound. In principle, two different configurational isomers of this pentameric capsule are possible: the two unbound pyridines can adopt an eclipsed or a gauche position relative to each other. This accounts for the complex 1H NMR of capsule 3; multiple sets of signals likely originate from a mixture of two different complexes that both have lower symmetry than the hexamer. Alike the hexameric capsule, tosylate ions can bind inside the cavity of the pentameric capsule above the upper rim of the cavitands stabilized by [Caryl–H⋯O−] interactions (Fig. 6b). In contrast to the hexameric capsules, the binding sites are not equivalent anymore; the tosylates prefer to populate the more remote apical cavitands first, and then bind to more crowded equatorial cavitands.
The ATD obtained for the [5·CH + 9I + 4·OTs]5+ ion in a DT-IM-MS experiment shows a single narrow peak which is consistent with the presence of a well-defined species in the gas phase (Fig. 7). The difference in size and shape of the two possible configurational isomers of capsule 3 is apparently not sufficient to differentiate the species in the ATD. The measured DTCCSHe for capsule 3 of 1286 Å2 is approximately 20% smaller than that of the hexameric capsule 2. The optimized structure of the pseudo-trigonal bipyramidal pentamer capsule, with four tosylates occupying the cavity, yielded a calculated ™CCSHe value of 1279 Å2 which is in excellent agreement with the experimental value.
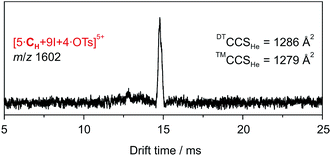 | ||
| Fig. 7 DT-IM-MS ATDs of ions derived from pentameric halogen-bonded capsule 3. Experimental DTCCSHe and theoretical ™CCSHe values are given. | ||
These results confirm the discovery of a new type of large, well-behaved supramolecular complex based on [N⋯I+⋯N] halogen bonds. This is the first example of a resorcinarene-based pentameric supramolecular capsule. The selective formation of pentameric capsules illustrates the possible interplay of preorganized, but inherently flexible cavitands and directional halogen bonds being modulated by a third factor – solvent effects. Solvent-induced transformations in discrete supramolecular assemblies have been described for numerous other systems and are most likely to arise from changes between protic/aprotic and polar/apolar solvents.16 However, examples which feature the change between two very similar solvents, as in our case chloroform and dichloromethane, are extremely rare which makes this finding especially intriguing.24
Self-assembly most often leads to the smallest possible, not too highly strained assembly in which all binding sites are coordinatively saturated. This is the best compromise between entropic (particle number) and enthalpic effects (avoiding strain and unsaturated binding sites). It is thus surprising that a solvent effect can be large enough to energetically overcome the energetic penalty associated with two pyridine binding sites remaining unsaturated. However, when considering all effects that come into play here, the hexamer → pentamer rearrangement appears reasonable: (i) Dichloromethane has a significantly higher polarity than chloroform as expressed in their dielectric constants ε of 8.93 and 4.81, respectively, and thus provides better solvation to the free pyridines. (ii) More pentamers can form from the same number of building blocks, increasing particle number and thus entropy. (iii) The formation of mixtures of isomers also contributes to a favourable entropy of the pentamer. (iv) Space filling34 of the voids between the encapsulated tosylates inside the capsules with solvent molecules likely contributes differently for the hexamer (larger voids) and the pentamer (smaller voids). Chloroform and dichloromethane differ in size and might therefore template the assembly of one complex or the other by providing a more optimal filling of this particular cavity.35 All these (and maybe more) effects help balancing the energetic penalty arising from leaving two binding sites open. We therefore propose an equilibrium between the hexameric and the pentameric capsules which is susceptible to the small shift in energetics associated with the solvent change.
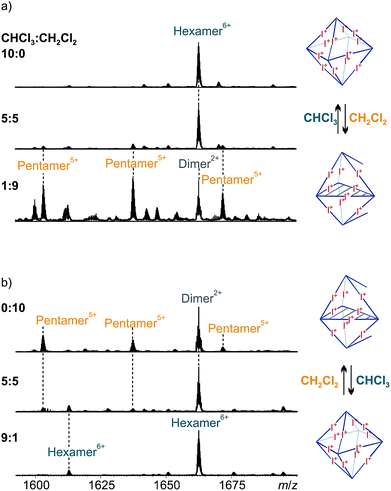
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9, the hexameric capsule vanishes and the pentamer prevails (Fig. 8a, bottom). Note that the remaining peak at m/z 1662 belongs to a dimeric ion which is likely an ionization artifact.
9, the hexameric capsule vanishes and the pentamer prevails (Fig. 8a, bottom). Note that the remaining peak at m/z 1662 belongs to a dimeric ion which is likely an ionization artifact.
The experiment can be carried out in the opposite direction as well. Starting from a clear solution (1 mM) of pentameric halogen-bonded capsule 3 in dichloromethane, dilution of the sample to 0.1 mM in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of chloroform and dichloromethane leads to a mixture of pentameric and hexameric complexes in a very similar ratio as observed in the first experiment (Fig. 8b, center). An increase of the amount of chloroform to 90% of the spray solvent gives exclusively hexameric complexes (Fig. 8b, bottom). These switching experiments indeed demonstrate the solvent-dependent equilibrium between the two capsules 2 and 3.
1 mixture of chloroform and dichloromethane leads to a mixture of pentameric and hexameric complexes in a very similar ratio as observed in the first experiment (Fig. 8b, center). An increase of the amount of chloroform to 90% of the spray solvent gives exclusively hexameric complexes (Fig. 8b, bottom). These switching experiments indeed demonstrate the solvent-dependent equilibrium between the two capsules 2 and 3.
A CID tandem MS experiment provides evidence that the hexamer–pentamer transition is solely taking place in solution. No gas-phase rearrangement leading preferentially from hexameric to pentameric complexes was observed (see ESI, Fig. S6 and S7‡).
These results emphasize the certainly unexpected solvent effects and clearly demonstrate the halogen-bonded hexameric capsule to be a stimuli-responsive assembly, which reacts to changes in its environment by substantial structural rearrangements.
Conclusions
The first study on the solution reactivity of large [N⋯I+⋯N] halogen-bonded capsules revealed a solvent-dependent rearrangement of the known hexameric capsule into a novel pentameric [N⋯I+⋯N] halogen-bonded capsule. While condensed phase methods could not provide detailed insight, the combination of ESI-MS, DT-IM-MS and theoretical calculations enabled us to elucidate the structure of this new [N⋯I+⋯N] halogen-bonded capsule. The complex possesses an unusual pseudo-trigonal bipyramidal geometry with nine [N⋯I+⋯N] bonds along the edges and two of the five incorporated cavitands partially uncomplexed. We demonstrate that this fascinating and rather unexpected equilibrium between the hexameric and the pentameric complex originates solely from a subtle change of solvent from chloroform to dichloromethane. This stimuli-responsive rearrangement is rationalized by a combination of microsolvation, space-filling, and different entropic contributions.Moreover, we provide first evidence for the anion guest-binding in the different [N⋯I+⋯N] halogen-bonded capsules by a combination of experimental and theoretical gas-phase methods. Each cavitand incorporated into the dimeric, pentameric and hexameric complexes is capable of binding one tosylate ion within the capsule's cavity, resulting in the binding of up to two, five and six anions, in 1, 3, and 2 respectively. Two different binding modes depending on the size of the complex were predicted by DFT-level calculations. Especially the binding in the less sterically crowded pentamers and hexamers is interesting. It shows the tosylate ions without interaction with the [N⋯I+⋯N] moieties, but rather between the two pyridine units and above the upper rim of the cavitand stabilized by [Caryl–H⋯O−] interactions. This agrees well with studies on similar, yet significantly less complex systems investigated by Erdélyi and coworkers.12 Furthermore, this is also in marked contrast to the anion binding of the silver-coordinated, dimeric precursor capsule, for which X-ray crystal structure analysis showed the anions to be located outside the cavity and in direct interaction with the silver cations.6
In conclusion, the large [N⋯I+⋯N] halogen-bonded capsules feature [Caryl–H⋯O−] interactions and halogen bonds as orthogonal noncovalent interactions which determine the assembly of the host and the guest binding. This underlines the potential for their application for the hierarchical self-assembly of supramolecular architectures in solution.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This project has been supported by the Deutsche Forschungsgemeinschaft (CRC 765).References
- R. Wyler, J. de Mendoza and J. Rebek, Angew. Chem., Int. Ed. Engl., 1993, 32, 1699–1701 CrossRef.
- J. Rebek, T. Heinz and D. M. Rudkevich, Nature, 1998, 394, 764–766 CrossRef.
- M. Fujita, S. Nagao and K. Ogura, J. Am. Chem. Soc., 1995, 117, 1649–1650 CrossRef PubMed.
- G. V. Oshovsky, D. N. Reinhoudt and W. Verboom, J. Am. Chem. Soc., 2006, 128, 5270–5278 CrossRef PubMed.
- (a) O. Dumele, B. Schreib, U. Warzok, N. Trapp, C. A. Schalley and F. Diederich, Angew. Chem., Int. Ed., 2017, 56, 1152–1157 CrossRef PubMed; (b) O. Dumele, N. Trapp and F. Diederich, Angew. Chem., Int. Ed., 2015, 54, 12339–12344 CrossRef PubMed.
- L. Turunen, U. Warzok, R. Puttreddy, N. K. Beyeh, C. A. Schalley and K. Rissanen, Angew. Chem., Int. Ed., 2016, 55, 14033–14036 CrossRef PubMed.
- L. Turunen, U. Warzok, C. A. Schalley and K. Rissanen, Chem, 2017, 3, 861–869 Search PubMed.
- C. B. Aakeröy, A. Rajbanshi, P. Metrangolo, G. Resnati, M. F. Parisi, J. Desper and T. Pilati, CrystEngComm, 2012, 14, 6366–6368 RSC.
- L. C. Gilday, S. W. Robinson, T. A. Barendt, M. J. Langton, B. R. Mullaney and P. D. Beer, Chem. Rev., 2015, 115, 7118–7195 CrossRef PubMed.
- (a) G. Cavallo, P. Metrangolo, R. Milani, T. Pilati, A. Priimagi, G. Resnati and G. Terraneo, Chem. Rev., 2016, 116, 2478–2601 CrossRef PubMed; (b) M. Erdélyi, Chem. Soc. Rev., 2012, 41, 3547–3557 RSC.
- (a) A.-C. C. Carlsson, M. Uhrbom, A. Karim, U. Brath, J. Gräfenstein and M. Erdélyi, CrystEngComm, 2013, 15, 3087–3092 RSC; (b) A.-C. C. Carlsson, J. Gräfenstein, A. Budnjo, J. L. Laurila, J. Bergquist, A. Karim, R. Kleinmaier, U. Brath and M. Erdélyi, J. Am. Chem. Soc., 2012, 134, 5706–5715 CrossRef PubMed; (c) S. B. Hakkert and M. Erdélyi, J. Phys. Org. Chem., 2015, 28, 226–233 CrossRef; (d) A.-C. C. Carlsson, K. Mehmeti, M. Uhrbom, A. Karim, M. Bedin, R. Puttreddy, R. Kleinmaier, A. A. Neverov, B. Nekoueishahraki, J. Gräfenstein, K. Rissanen and M. Erdélyi, J. Am. Chem. Soc., 2016, 138, 9853–9863 CrossRef PubMed.
- M. Bedin, A. Karim, M. Reitti, A.-C. C. Carlsson, F. Topić, M. Cetina, F. Pan, V. Havel, F. Al-Ameri, V. Sindelar, K. Rissanen, J. Gräfenstein and M. Erdélyi, Chem. Sci., 2015, 6, 3746–3756 RSC.
- L. Turunen, A. Peuronen, S. Forsblom, E. Kalenius, M. Lahtinen and K. Rissanen, Chem.–Eur. J., 2017, 23, 11714–11718 CrossRef PubMed.
- (a) D. Beaudoin, F. Rominger and M. Mastalerz, Angew. Chem., Int. Ed., 2016, 55, 15599–15603 CrossRef PubMed; (b) L. R. MacGillivray and J. L. Atwood, Nature, 1997, 389, 469–472 CrossRef; (c) T. Gerkensmeier, W. Iwanek, C. Agena, R. Fröhlich, S. Kotila, C. Näther and J. Mattay, Eur. J. Org. Chem., 1999, 2257–2262 CrossRef; (d) R. M. McKinlay, G. W. V. Cave and J. L. Atwood, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 5944–5948 CrossRef PubMed; (e) T. Schröder, R. Brodbeck, M. C. Letzel, A. Mix, B. Schnatwinkel, M. Tonigold, D. Volkmer and J. Mattay, Tetrahedron Lett., 2008, 49, 5939–5942 CrossRef; (f) O. Ugono, J. P. Moran and K. T. Holman, Chem. Commun., 2008, 1404–1406 RSC.
- R. Custelcean, Chem. Soc. Rev., 2014, 43, 1813–1824 RSC.
- W. Wang, Y.-X. Wang and H.-B. Yang, Chem. Soc. Rev., 2016, 45, 2656–2693 RSC.
- (a) S. Sato, Y. Ishido and M. Fujita, J. Am. Chem. Soc., 2009, 131, 6064–6065 CrossRef PubMed; (b) S. P. Black, D. M. Wood, F. B. Schwarz, T. K. Ronson, J. J. Holstein, A. R. Stefankiewicz, C. A. Schalley, J. K. M. Sanders and J. R. Nitschke, Chem. Sci., 2016, 7, 2614–2620 RSC; (c) N. K. Beyeh, M. Kogej, A. Ahman, K. Rissanen and C. A. Schalley, Angew. Chem., Int. Ed., 2006, 45, 5214–5218 CrossRef PubMed; (d) W. Hoffmann, K. Folmert, J. Moschner, X. Huang, H. von Berlepsch, B. Koksch, M. T. Bowers, G. von Helden and K. Pagel, J. Am. Chem. Soc., 2018, 140, 244–249 CrossRef PubMed.
- (a) D. Fujita, Y. Ueda, S. Sato, H. Yokoyama, N. Mizuno, T. Kumasaka and M. Fujita, Chem, 2016, 1, 91–101 CrossRef; (b) B. Baytekin, H. T. Baytekin and C. A. Schalley, Org. Biomol. Chem., 2006, 4, 2825–2841 RSC; (c) Analytical methods in supramolecular chemistry, ed. C. A. Schalley, Wiley-VCH, Weinheim, 2012 Search PubMed.
- (a) L. Cera and C. A. Schalley, Chem. Soc. Rev., 2014, 43, 1800–1812 RSC; (b) Z. Qi, T. Heinrich, S. Moorthy and C. A. Schalley, Chem. Soc. Rev., 2015, 44, 515–531 RSC.
- F. Lanucara, S. W. Holman, C. J. Gray and C. E. Eyers, Nat. Chem., 2014, 6, 281–294 CrossRef PubMed.
- C. Uetrecht, R. J. Rose, E. van Duijn, K. Lorenzen and A. J. R. Heck, Chem. Soc. Rev., 2010, 39, 1633–1655 RSC.
- E. S. Baker, B. H. Clowers, F. Li, K. Tang, A. V. Tolmachev, D. C. Prior, M. E. Belov and R. D. Smith, J. Am. Soc. Mass Spectrom., 2007, 18, 1176–1187 CrossRef PubMed.
- (a) P. Bonakdarzadeh, F. Topić, E. Kalenius, S. Bhowmik, S. Sato, M. Groessl, R. Knochenmuss and K. Rissanen, Inorg. Chem., 2015, 54, 6055–6061 CrossRef PubMed; (b) O. Jurček, P. Bonakdarzadeh, E. Kalenius, J. M. Linnanto, M. Groessl, R. Knochenmuss, J. A. Ihalainen and K. Rissanen, Angew. Chem., Int. Ed., 2015, 54, 15462–15467 CrossRef PubMed; (c) A. Kiesilä, L. Kivijärvi, N. K. Beyeh, J. O. Moilanen, M. Groessl, T. Rothe, S. Götz, F. Topić, K. Rissanen, A. Lützen and E. Kalenius, Angew. Chem., Int. Ed., 2017, 56, 10942–10946 CrossRef PubMed; (d) M. Petryk, A. Troć, B. Gierczyk, W. Danikiewicz and M. Kwit, Chem.–Eur. J., 2015, 21, 10318–10321 CrossRef PubMed; (e) J. Ujma, M. de Cecco, O. Chepelin, H. Levene, C. Moffat, S. J. Pike, P. J. Lusby and P. E. Barran, Chem. Commun., 2012, 48, 4423–4425 RSC; (f) C. Wang, X.-Q. Hao, M. Wang, C. Guo, B. Xu, E. N. Tan, Y.-Y. Zhang, Y. Yu, Z.-Y. Li, H.-B. Yang, M.-P. Song and X. Li, Chem. Sci., 2014, 5, 1221–1226 RSC; (g) M. Wang, C. Wang, X.-Q. Hao, X. Li, T. J. Vaughn, Y.-Y. Zhang, Y. Yu, Z.-Y. Li, M.-P. Song, H.-B. Yang and X. Li, J. Am. Chem. Soc., 2014, 136, 10499–10507 CrossRef PubMed.
- R. Sure and S. Grimme, Chem. Commun., 2016, 52, 9893–9896 RSC.
- (a) T. Vreven, K. S. Byun, I. Komáromi, S. Dapprich, J. A. Montgomery, K. Morokuma and M. J. Frisch, J. Chem. Theory Comput., 2006, 2, 815–826 CrossRef PubMed; (b) L. W. Chung, W. M. C. Sameera, R. Ramozzi, A. J. Page, M. Hatanaka, G. P. Petrova, T. V. Harris, X. Li, Z. Ke, F. Liu, H.-B. Li, L. Ding and K. Morokuma, Chem. Rev., 2015, 115, 5678–5796 CrossRef PubMed; (c) R. Wieczorek and J. J. Dannenberg, J. Am. Chem. Soc., 2003, 125, 8124–8129 CrossRef PubMed.
- (a) S. Warnke, C. Baldauf, M. T. Bowers, K. Pagel and G. von Helden, J. Am. Chem. Soc., 2014, 136, 10308–10314 CrossRef PubMed; (b) P. R. Kemper, N. F. Dupuis and M. T. Bowers, Int. J. Mass Spectrom., 2009, 287, 46–57 CrossRef.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Rana-singhe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. To-masi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 09, Revision rev.D01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- M. J. S. Dewar, E. G. Zoebisch, E. F. Healy and J. J. P. Stewart, J. Am. Chem. Soc., 1985, 107, 3902–3909 CrossRef.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef.
- M. F. Mesleh, J. M. Hunter, A. A. Shvartsburg, G. C. Schatz and M. F. Jarrold, J. Phys. Chem., 1996, 100, 16082–16086 CrossRef.
- Maestro Schrödinger Release 2017-4, Maestro, Schröding-er, LLC, New York, NY, 2017 Search PubMed.
- S. S. Zhu, H. Staats, K. Brandhorst, J. Grunenberg, F. Gruppi, E. Dalcanale, A. Lützen, K. Rissanen and C. A. Schalley, Angew. Chem., Int. Ed., 2008, 47, 788–792 CrossRef PubMed.
- S. Mecozzi and J. J. Rebek, Chem.–Eur. J., 1998, 4, 1016–1022 CrossRef.
- B. Kilbas, S. Mirtschin, R. Scopelliti and K. Severin, Chem. Sci., 2012, 3, 701–704 RSC.
Footnotes |
| † Dedicated to Prof. Helmut Schwarz on the occasion of his 75th birthday. |
| ‡ Electronic supplementary information (ESI) available. See DOI: 10.1039/c8sc03040e |
| § Currently at Hunter College, The City University of New York. |
| ¶ Currently at Department of Chemistry – BMC, Uppsala University. |
| This journal is © The Royal Society of Chemistry 2018 |