Open Access Article
Open Access ArticleStructural characterization of framework–gas interactions in the metal–organic framework Co2(dobdc) by in situ single-crystal X-ray diffraction†
Miguel I.
Gonzalez
 a,
Jarad A.
Mason
a,
Eric D.
Bloch
a,
Simon J.
Teat
b,
Kevin J.
Gagnon
b,
Gregory Y.
Morrison
b,
Wendy L.
Queen
a,
Jarad A.
Mason
a,
Eric D.
Bloch
a,
Simon J.
Teat
b,
Kevin J.
Gagnon
b,
Gregory Y.
Morrison
b,
Wendy L.
Queen
 cd and
Jeffrey R.
Long
cd and
Jeffrey R.
Long
 *aef
*aef
aDepartment of Chemistry, University of California, Berkeley, California 94720-1462, USA. E-mail: jrlong@berkeley.edu
bAdvanced Light Source, Lawrence Berkeley National Laboratory, Berkeley, California 94720, USA
cThe Molecular Foundry, Lawrence Berkeley National Laboratory, Berkeley, California 94720, USA
dÉcole Polytechnique Fédérale de Lausanne (EPFL), Institut des Sciences et Ingénierie Chimiques, CH 1051 Sion, Switzerland
eDepartment of Chemical and Biomolecular Engineering, University of California, Berkeley, California 94720-1462, USA
fMaterials Sciences Division, Lawrence Berkeley National Laboratory, Berkeley, California 94720 94720, USA
First published on 19th April 2017
Abstract
The crystallographic characterization of framework–guest interactions in metal–organic frameworks allows the location of guest binding sites and provides meaningful information on the nature of these interactions, enabling the correlation of structure with adsorption behavior. Here, techniques developed for in situ single-crystal X-ray diffraction experiments on porous crystals have enabled the direct observation of CO, CH4, N2, O2, Ar, and P4 adsorption in Co2(dobdc) (dobdc4− = 2,5-dioxido-1,4-benzenedicarboxylate), a metal–organic framework bearing coordinatively unsaturated cobalt(II) sites. All these molecules exhibit such weak interactions with the high-spin cobalt(II) sites in the framework that no analogous molecular structures exist, demonstrating the utility of metal–organic frameworks as crystalline matrices for the isolation and structural determination of unstable species. Notably, the Co–CH4 and Co–Ar interactions observed in Co2(dobdc) represent, to the best of our knowledge, the first single-crystal structure determination of a metal–CH4 interaction and the first crystallographically characterized metal–Ar interaction. Analysis of low-pressure gas adsorption isotherms confirms that these gases exhibit mainly physisorptive interactions with the cobalt(II) sites in Co2(dobdc), with differential enthalpies of adsorption as weak as −17(1) kJ mol−1 (for Ar). Moreover, the structures of Co2(dobdc)·3.8N2, Co2(dobdc)·5.9O2, and Co2(dobdc)·2.0Ar reveal the location of secondary (N2, O2, and Ar) and tertiary (O2) binding sites in Co2(dobdc), while high-pressure CO2, CO, CH4, N2, and Ar adsorption isotherms show that these binding sites become more relevant at elevated pressures.
Introduction
In situ X-ray diffraction using single crystals as solid-state matrices has emerged as a powerful approach toward the direct observation of molecules and their reactivity.1–5 The crystal lattice acts to both stabilize and align molecular guests, enabling their isolation and subsequent structural determination by crystallography. Amid many significant advances over the past two decades, these systems have found promising applications in the study of weakly interacting species, such as adsorbed gases,6–15 which have been traditionally difficult to characterize crystallographically. Considerable work in this area has focused on conducting in situ X-ray diffraction experiments to investigate host–guest interactions and guest reactivity in molecular flasks, macromolecular hosts designed to encapsulate molecular guests.1,3 Recognition that the chemistry of these systems extends to the capture and confinement of gas molecules has led to the characterization of a series of small gases within a molecular cavitand.15 Recent work has featured single-crystal-to-single-crystal reactions of gas molecules with transition metal complexes. As particularly striking examples, this solid–gas reactivity has been leveraged to follow the exchange of small molecules (N2, CO, NH3, C2H4, H2, and O2) on an iridium pincer complex12 and to isolate rhodium-alkane σ-complexes through the hydrogenation of their corresponding alkene complexes.16–18 Although these reports reinforce the growing utility of molecular single-crystal matrices, their general applicability remains limited by the scarcity of structures that retain crystallinity upon binding and reaction of the molecular guests.2 In addition, the tendency of molecules to pack closely in the crystalline state engenders only small or transient apertures in the crystal. This inability to support larger pore structures severely restricts the size of guests that can be incorporated.3 The need to develop new crystalline matrices to address these challenges outlines an opportunity for alternative materials to contribute to the advancement of the field.Metal–organic frameworks are a class of materials composed of inorganic clusters or metal ions connected in three dimensions by organic linkers. These materials exhibit the ability to adopt highly porous crystalline structures with well-defined pore architectures,19,20 leading to their extensive evaluation for applications in gas storage,21,22 gas separations,23,24 and catalysis.25–28 In contrast to the non-covalent interactions in molecular crystals, the coordinate-covalent bonds linking the inorganic and organic units in metal–organic frameworks give rise to their inherently greater thermal and chemical stability. Consequently, these materials are capable of maintaining porous structures that accommodate the removal, inclusion, exchange, or reaction of a more diverse selection of molecular guests over a wider range of conditions compared to molecular assemblies. In particular, frameworks that exhibit permanent and open porosity are uniquely suited to the study of gaseous species. Furthermore, these materials can be designed to facilitate explicit framework–guest interactions through synthetic control over pore size, shape, and functionality.
Indeed, research on metal–organic frameworks has increasingly relied on in situ diffraction experiments to provide critical insight into the contribution of the pore structure to adsorption behavior and reactivity.29–64 Such studies also complement and validate computational efforts focused on understanding and predicting the properties of these materials.46,65–68 Despite the greater accessibility, simplicity, and precision associated with single-crystal X-ray diffraction, the majority of work involving gases has been accomplished using powder X-ray and neutron diffraction methods.29–53,64 This primarily stems from the following challenges: (i) the difficulty in preparing single crystals of sufficient size and quality to be suitable for diffraction experiments, (ii) the tendency of some crystals to fracture under the evacuation or gas-dosing conditions, and (iii) the exceptionally high sensitivity to contaminants inherent to the small sample sizes used in single-crystal measurements (∼500 ng for a typical 200 μm wide single crystal). The third challenge is especially problematic in studying frameworks bearing metals with open coordination sites, due to the propensity of these sites to bind water over more weakly coordinating species. Nevertheless, several studies have proven to be successful in employing single-crystal X-ray diffraction experiments to observe framework–gas interactions.29,54,56,60–63,69
The M2(dobdc) series of metal–organic frameworks (M = MgII, MnII, FeII, CoII, NiII, CuII, ZnII, and CdII; dobdc4− = 2,5-dioxido-1,4-benzenedicarboxylate; also referred to as M-MOF-74 or CPO-27(M)) have been intensely studied due to their high density of exposed metal(II) sites, which can interact favorably with guest molecules.29–47,55,70,71 Much of the work evaluating the adsorption properties and reactivity of these materials has depended on powder X-ray or neutron diffraction for in situ characterization of gas binding.29,31–47 Comparatively few studies have been performed using single-crystal X-ray diffraction29,55 due to the intrinsic difficulty that accompanies in situ gas-dosing experiments on materials with open coordination sites and because only Co2(dobdc) and Zn2(dobdc) readily form single crystals. This work seeks to expand on these studies through techniques developed to dose gases into single crystals under rigorously air-free conditions. Herein, we report the direct structural characterization of CO, CH4, N2, O2, Ar, and P4 adsorption in single crystals of Co2(dobdc) (Fig. 1). The resulting structures confirm that each gas binds first to the exposed cobalt(II) site and allow the identification of secondary (for N2, O2, and Ar) and tertiary (for O2) binding sites within the framework. Remarkably, further inspection of CoII–gas distances reveals that binding occurs primarily through weak covalent (for CO) or non-covalent (for CH4, N2, O2, and Ar) interactions, which have never been observed by single-crystal X-ray diffraction. Finally, a combination of low- and high-pressure gas adsorption isotherms are used to evaluate the relationship between structure and adsorption behavior.
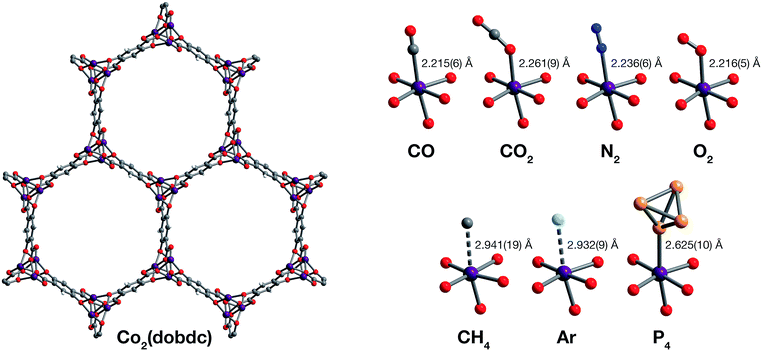 | ||
| Fig. 1 Structures determined by single-crystal X-ray diffraction. (Left) A portion of the crystal structure of Co2(dobdc) (dobdc4− = 2,5-dioxido-1,4-benzenedicarboxylate) at 296 K viewed along the c axis. (Right) First coordination spheres for CoII in the structures of CO, CO2,29 N2, O2, CH4, Ar, and P4 in Co2(dobdc) (at 150 K for CO2; at 100 K for N2, O2, CH4, and P4; at 90 K for CO and Ar); purple, red, gray, blue, light blue, light orange, and white spheres represent Co, O, C, N, Ar, P, and H atoms, respectively. Note that the O2 molecules bound to the CoII sites in Co2(dobdc)·5.9O2 were found to be disordered over two orientations with relative occupancies of 73(3)% and 27(3)% (Fig. S8†), but only one of these orientations (73(3)% occupancy) is shown for clarity. The structure of Co2(dobdc)·2.9CO2 has been reported previously29 and is shown here to facilitate comparisons. | ||
Experimental
Materials and methods
N,N-Dimethylformamide (DMF), ethanol, and methanol were obtained from commercial sources and used without further purification. Hexanes was deoxygenated by purging with Ar for 1 h and dried using a commercial solvent purification system designed by JC Meyer Solvent Systems. The compounds Co(NO3)2·6H2O and 2,5-dihydroxy-1,4-benzenedicarboxylic acid (H4dobdc) were purchased from Sigma-Aldrich and used as received. White phosphorus (P4) was prepared by heating red phosphorus under vacuum (∼80 μbar) in a flame-sealed borosilicate glass tube over a Bunsen burner flame. The crude white phosphorus was then purified by recrystallization from hexanes. Caution: white phosphorus is highly toxic and reacts violently with O2in air. Single crystals of Co2(dobdc) were synthesized using a slight modification to a previously published procedure.71 Briefly, a 100 mL Pyrex jar was charged with H4dobdc (198 mg, 1.00 mmol), Co(NO3)2·6H2O (970 mg, 3.34 mmol), and a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (v/v/v) mixture of DMF/ethanol/water (80 mL), and was then sealed with a Teflon cap. The resulting mixture was sonicated until all reactants were fully dissolved to form a violet solution. The reaction mixture was then placed in an oven that was preheated to 100 °C and kept at this temperature for 24 h, yielding violet needle-shaped single crystals. The crystals were soaked three times in 80 mL of DMF for 24 h at 120 °C, followed by soaking three times in 80 mL of methanol at 60 °C. The crystals were then stored in methanol in a 20 mL PTFE-capped vial prior to use for single-crystal X-ray diffraction experiments or gas-adsorption measurements. The Langmuir surface area of the sample used for gas adsorption measurements was determined to be 1400 ± 2 m2 g−1.
1 (v/v/v) mixture of DMF/ethanol/water (80 mL), and was then sealed with a Teflon cap. The resulting mixture was sonicated until all reactants were fully dissolved to form a violet solution. The reaction mixture was then placed in an oven that was preheated to 100 °C and kept at this temperature for 24 h, yielding violet needle-shaped single crystals. The crystals were soaked three times in 80 mL of DMF for 24 h at 120 °C, followed by soaking three times in 80 mL of methanol at 60 °C. The crystals were then stored in methanol in a 20 mL PTFE-capped vial prior to use for single-crystal X-ray diffraction experiments or gas-adsorption measurements. The Langmuir surface area of the sample used for gas adsorption measurements was determined to be 1400 ± 2 m2 g−1.
Single-crystal X-ray diffraction
All crystals were found to be obverse/reverse twins based on analysis of their diffraction patterns. For each structure, CELL_NOW72 was used to determine the orientation matrices. Raw data for both twin matrices were integrated and corrected for Lorentz and polarization effects using Bruker AXS SAINT73 software and corrected for absorption using TWINABS.74 TWINABS was used to produce a merged HKLF4 file for structure solution and initial refinement and an HKLF5 file for final structure refinement. The structures were solved using direct methods with SHELXS75,76 and refined using SHELXL75,77 operated in the OLEX2 interface.78 Thermal parameters were refined anisotropically for all non-hydrogen atoms. Disorder and thermal motion of the bound gas molecules required the use of displacement parameter (for Co2(dobdc)·1.2CO, Co2(dobdc)·5.9O2, Co2(dobdc)·3.8N2 Co2(dobdc)·2.0Ar, and Co2(dobdc)·1.3P4) and distance (for Co2(dobdc)·5.9O2, Co2(dobdc)·3.8N2, and Co2(dobdc)·1.3P4) restraints. All hydrogen atoms were refined using the riding model.
Gas adsorption
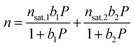 | (1) |
| bi = e−Si/ReEi·1000/RT | (2) |
The Langmuir parameter can be expressed using eqn (2), where Si is the site-specific integral entropy of adsorption in J mol−1 K−1; Ei is the site-specific differential enthalpy of adsorption in kJ mol−1, R is the gas constant in J mol−1 K−1, and T is the temperature in K. For all gases, isotherms were fit both independently for each temperature (Fig. S11, S13, S15, and S17†) and simultaneously for all temperatures (Fig. S12, S14, S16, and S18†).
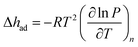 | (3) |
The Langmuir fits for each gas (fit independently for each temperature) were used to obtain the exact pressures that correspond to specific loadings at different temperatures (298, 308, and 318 K for N2, O2, and Ar; 293, 298, 303, 313, and 323 K for CH4). This was done at loading intervals of 0.05 mmol g−1. At each loading, the slope of the best-fit line to ln(P) versus 1/T was calculated to obtain the differential enthalpy.
Results and discussion
Structural characterization
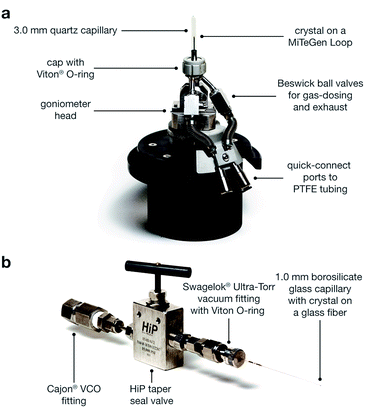
Two methods were developed for dosing gases into single crystals. The first involves using an environmental gas cell (Fig. 2a), which was designed and built at ALS beamline 11.3.1. Similar to other gas cells that have recently been developed,81,82 the cell allows the collection of single-crystal X-ray diffraction data on samples under vacuum or dosed with a desired gas. With this method, the structure of the framework can be monitored throughout the evacuation and gas dosing of the crystal. This capability affords appreciable flexibility, as the temperature, gas pressure, and time can be changed at each stage of the experiment in response to structural data. As a result, the gas cell is especially useful for studying unfamiliar samples that still require experimental conditions to be optimized. Alternatively, a single crystal can be inserted into a borosilicate capillary, which is then heated under vacuum and subsequently dosed using a manifold or gas adsorption analyzer. The capillary is then flame-sealed with the crystal kept under a specified pressure of gas that is lower than 1 bar. Unlike the gas cell, using capillaries requires the evacuation time and temperature and the gas-dosing pressure to be determined prior to data collection. Although less versatile, the capillary method benefits from higher sample throughput compared to the gas cell because diffraction experiments are only conducted on gas-dosed samples. Consequently, this method can be preferable for samples that have established activation parameters and gas adsorption properties.The metal–organic framework Co2(dobdc) crystallizes in the space group R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) , in which the special positions are exclusively situated along the one-dimensional helical chains of Co atoms, at the center of the organic linkers, and through the center of the hexagonal pores. This makes the framework particularly amenable to the crystallographic characterization of guest species as no crystallographic symmetry is enforced on sites above and within the vicinity of the coordinatively unsaturated cobalt(II) centers. This is evident in the exceptionally ordered structures of gases within Co2(dobdc) even in cases where the interactions are weak, as described previously29,33,40,55,68 and discussed below.
, in which the special positions are exclusively situated along the one-dimensional helical chains of Co atoms, at the center of the organic linkers, and through the center of the hexagonal pores. This makes the framework particularly amenable to the crystallographic characterization of guest species as no crystallographic symmetry is enforced on sites above and within the vicinity of the coordinatively unsaturated cobalt(II) centers. This is evident in the exceptionally ordered structures of gases within Co2(dobdc) even in cases where the interactions are weak, as described previously29,33,40,55,68 and discussed below.
Inspection of the structures of Co2(dobdc)·1.2CO, Co2(dobdc)·0.58CO, and Co2(dobdc)·2.0CH4 (Fig. 3), where only a single adsorption site is populated, shows that CO and CH4 first bind to the open coordination site of cobalt(II), confirming that this site has the greatest contribution to the adsorption of these gases in the material. Multiple adsorption sites could be located in the structures of Co2(dobdc)·3.8N2, Co2(dobdc)·5.9O2, Co2(dobdc)·2.0Ar, and Co2(dobdc)·1.3P4 (Fig. 3), which complicates the determination of the primary adsorption sites. Comparison of relative site occupancies, displacement parameters, and framework–guest distances, however, indicates that N2, O2, Ar, and P4 also bind primarily to the cobalt(II) sites. Remarkably, the secondary binding sites for N2, O2, and Ar were found to have nearly identical locations (Fig. S1 and S2†), close to the non-bridging carboxylate and phenoxide oxygen atoms of dobdc4−. Previous reports also identify the same secondary binding site in structures of CO2 (ref. 29) (Fig. 3) and H2O68 in Co2(dobdc) (Fig. S1 and S2†). The similarity of these binding pockets likely arises from a slightly polarizing environment generated by the partial negative charges on surrounding linker oxygen atoms. In other metal–organic frameworks, the linker carboxylate oxygen atoms have been shown to facilitate similar weak interactions with gases.52,54
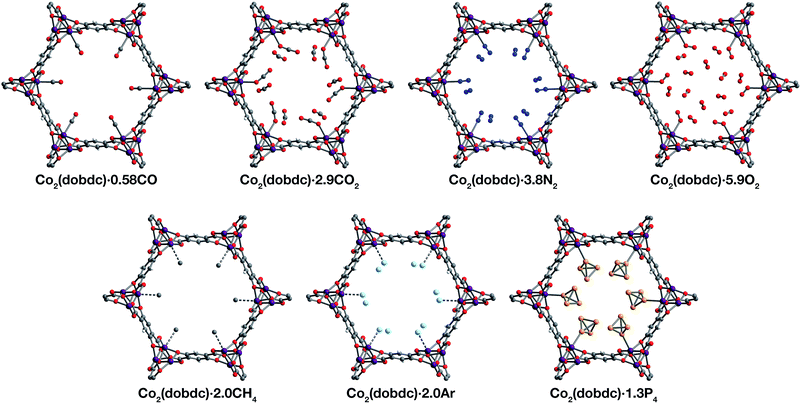 | ||
| Fig. 3 A portion of the crystal structures of Co2(dobdc)·0.58CO at 90 K, Co2(dobdc)·2.9CO2 at 150 K,29 Co2(dobdc)·5.9O2 at 100 K, Co2(dobdc)·3.8N2 at 100 K, Co2(dobdc)·2.0CH4 at 100 K, Co2(dobdc)·2.0Ar, and Co2(dobdc)·1.3P4 at 100 K viewed along the c axis, as determined by single-crystal X-ray diffraction; purple, red, gray, blue, light blue, light orange, and white spheres represent Co, O, C, N, Ar, P, and H atoms, respectively. Note that the O2 molecules bound to the CoII sites in Co2(dobdc)·5.9O2 were found to be disordered over two orientations with relative occupancies of 73(3)% and 27(3)% (Fig. S8†), but only one of these orientations (73(3)% occupancy) is shown for clarity. In the structure of Co2(dobdc)·1.3P4, the P4 molecules were found in two positions (Fig. S10†), one with P4 molecules coordinated to the CoII sites (45.5(10)% occupancy) and another 3.88(3) Å away from the CoII sites centers (20.6(10)% occupancy), but only the coordinated P4 molecules are shown for clarity. The structure of Co2(dobdc)·2.9CO2 has been reported previously29 and is shown here to facilitate comparisons. | ||
The structures of Co2(dobdc)·1.2CO at 100 K and Co2(dobdc)·0.58CO at 90 K (Fig. 3) were obtained under 1.00 bar of CO in the gas cell. In these structures, CO loading was found to be lower than one per cobalt(II) site, which likely results from slow diffusion of CO as the crystals were rapidly cooled after CO dosing. Nevertheless, both structures display Co–CCO distances of 2.215(6) Å (Fig. 1) and similar Co–C–O angles (175.7(12)° for Co2(dobdc)·1.2CO and 178.0(11)° for Co2(dobdc)·0.58CO). These distances and angles are comparable to those previously obtained from powder neutron diffraction at 10 K, Co–CCO distance = 2.18(2) Å and Co–C–O angle = 171(2)°.40 The long Co–CCO distance and deviation of the Co–C–O angle from 180° are both consistent with a weak interaction between cobalt(II) and CO with limited CoII–CO π backbonding. This is further supported by larger CO oxygen displacement parameters compared to carbon, which suggests that the bound CO is free to bend out of the axis along the CoII–CO bond. Surveying the Cambridge Crystal Structure Database (CCSD),83 single-crystal structures of cobalt carbonyl complexes with Co–CCO distances longer than 2.0 Å are unprecedented. Examples of cobalt(II)–carbonyl complexes are exceedingly rare and all exhibit a low-spin configuration with Co–CCO bond distances around 1.8 Å, which are typical to strong Co–CO bonds.84 The weak-field dobdc4− ligands in Co2(dobdc) impose a high-spin configuration for cobalt(II), which is maintained after binding CO.40 Population of the anti-bonding cobalt(II) orbitals makes the Co–CO σ interaction less favorable, lengthening the Co–CCO distance. This diminishes CoII–CO π back-donation by preventing overlap between the Co 3d and CO π* orbitals. Together, these interdependent effects manifest in the exceptionally weak and fully reversible M–CO interaction in Co2(dobdc), which has been shown to be a major advantage of Co2(dobdc) and its MgII, MnII, FeII, NiII, and ZnII analogs as prospective materials for industrial CO separations.40
X-ray analysis of a single crystal of Co2(dobdc) under 0.8 bar N2 at 100 K resulted in the structure of Co2(dobdc)·3.8N2 (Fig. 3). The structure shows that N2 binds to cobalt(II) through an end-on interaction with a Co–NN2 distance of 2.236(6) Å (Fig. 1). This distance is comparable with the Fe–NN2 distance of 2.30(1) Å obtained from the powder neutron diffraction structure of N2 in Fe2(dobdc).35 Deviation of the Co–N–N angle (170.2(9)°) from 180° also suggests minimal π back-donation from CoII to N2. Of the cobalt dinitrogen complexes reported in the CCSD,83 none have Co–NN2 distances greater than 2.0 Å and only one of these features cobalt in its +2 oxidation state.85 The long Co–NN2 distance in Co2(dobdc)·3.8N2 indicates a much weaker interaction between N2 and the high-spin cobalt(II) centers in Co2(dobdc) compared to the Co–N2 bonds formed in typical cobalt dinitrogen complexes.86–88 The Co–N2 bonds in these complexes are strengthened by significant Co–N2 π back-donation, whereas N2 can be thought to interact mainly through σ donation to cobalt(II) in Co2(dobdc). The secondary N2 binding sites in Co2(dobdc)·3.8N2 (Fig. 3 and S1†) display van der Waals interactions between N2 and the oxygen atoms of dobdc4−, with N⋯O contacts ranging from 3.44(2) to 3.771(2) Å (Fig. S2†). These sites are nearly identical to those located in the powder neutron diffraction structure of N2 in Fe2(dobdc).35 Full population of both binding sites to give four N2 molecules adsorbed per formula unit in Co2(dobdc) corresponds surprisingly well to the estimated number of N2 molecules adsorbed as a monolayer in the framework, which is ∼4.3 based on a Brunauer–Emmett–Teller (BET) fit to 77 K N2 adsorption isotherm data.29
To determine the structure of O2 in Co2(dobdc), data was collected on a single crystal dosed with 0.5 bar of O2 in a sealed capillary at 100 K. In the structure of Co2(dobdc)·5.9O2 (Fig. 3), O2 is found to bind end-on with a Co–OO2 distance of 2.216(5) Å (Fig. 1). Disorder of the O2 molecule results in two bent orientations with Co–O–O angles of 127.3(10)° and 128(3)° and relative occupancies of 73(3)% and 27(3)%, respectively (Fig. S8†). The Co–OO2 distance in Co2(dobdc)·5.9O2 is unusually long. Structures of cobalt dioxygen complexes in the CCSD83 and recently reported dioxygen adducts formed in other cobalt metal–organic frameworks,60,62 all show Co–OO2 distances that fall below 2.0 Å. This again suggests significant disparity between the Co–O2 interaction in Co2(dobdc) and those in molecular cobalt complexes, where O2 binding is characterized by electron transfer from one or two cobalt(II) centers to form superoxo or peroxo complexes, respectively.89,90 In addition to the long Co–OO2 distance, no significant difference in the average Co–O distances is apparent between cobalt(II) and dobdc4− in Co2(dobdc) (2.035(5) Å) and in Co2(dobdc)·5.9O2 (2.036(5) Å). This further implies that partial oxidation of cobalt(II) does not occur upon O2 binding, which is in contrast to partial oxidation of the iron(II) centers in Fe2(dobdc) to form either iron-superoxo species at 211 K or iron-peroxo species at 298 K.35 Like in Co2(dobdc)·3.8N2, the secondary bindings sites in Co2(dobdc)·5.9O2 feature O2 interacting with the dobdc4− oxygen atoms, with O⋯O contacts that range from 3.391(17) Å to 3.88(2) Å. Remarkably, tertiary binding sites for O2 can also be identified in the structure, where O2 interacts only with other O2 molecules adsorbed on the primary and secondary sites. Similar sites were also observed by powder neutron diffraction in the structure of O2 in Fe2(dobdc).35 Experimental observation of these sites is particularly helpful to computational efforts focused on understanding the contribution of gas–gas interactions to adsorption in metal–organic frameworks and other porous materials.46,65,68,91,92
The structure of Co2(dobdc)·2.0CH4 (Fig. 3) was obtained by cooling a single crystal of Co2(dobdc) under 1 bar of CH4 to 100 K in the gas cell. Although methane hydrogen atoms could not be located in the structure due to disorder and the difficulty in locating hydrogen atoms by X-ray diffraction, electron density corresponding to a methane carbon atom could be distinctly resolved above the framework cobalt sites with a CoII⋯CCH4 distance of 2.941(19) Å (Fig. 1). Significantly, this is the first M–CH4 interaction that has been characterized by single-crystal X-ray diffraction. The Co⋯CCH4 distance is comparable to distances characterized for metal–methane interactions in other metal–organic frameworks, which are generally close to 3 Å. The most relevant of these are from structures determined by powder neutron diffraction for CD4 in Fe2(dobdc) (Fe⋯CCD4 distance of 2.98(1) Å)66 and in Mg2(dobdc) (Mg⋯CCD4 distance of 3.04 Å).93 The long M⋯CCH4 distances in all of these structures are indicative of weak non-covalent interactions that stem from polarization of CH4 by the partial positive charge on the metal center. These distances contrast with the relatively short M⋯C distances (around 2.4–2.5 Å) in alkane σ-complexes, which involve donation from the alkane C–H σ bond to the metal center.16–18 Although the CoII–CH4 interaction in Co2(dobdc) and analogous noncovalent M–CH4 interactions should clearly be distinguished from the bonds formed in true metal–alkane σ-complexes, characterization of such weak M–CH4 interactions has become increasingly important in the evaluation of materials for natural gas storage.22
The inherent chemical stability of the noble gases has been thoroughly exploited for maintaining an inert environment for highly reactive species. As a result of this stability, isolation of molecular metal–noble gas species is exceedingly difficult. While no molecular metal–noble gas species other than metal–Xe94,95 have been characterized crystallographically, computational methods and experimental techniques such as photodissociation spectroscopy and mass spectrometry have been employed to study these species.95–101 Encouraged by the preceding results, attempts were made to characterize metal–Ar interactions, which have never been crystallographically observed, in Co2(dobdc). Under a pressure of 1.14 bar of Ar in the gas cell, no significant electron density could be observed over the cobalt(II) sites in Co2(dobdc) at 100 K. Upon cooling to 90 K, however, two binding sites for Ar were resolved, one directly above the metal center and another at a location similar to the secondary binding sites of N2 and O2 (Fig. 2 and S1†). It is highly improbable that Ar occupies these adjacent sites simultaneously, because the distance between Ar molecules in the two sites (2.71(3) Å) is much shorter than twice the van der Waals radius of Ar (3.76 Å). In agreement with this, refinement of the Ar site occupancies results in site occupancies of 60.6(1.3)% for Ar interacting with cobalt(II) and 39.3(1.6)% for the second site, which give an overall formula of Co2(dobdc)·2.0Ar. These observations suggest that both sites have comparable affinities for Ar, resulting in an equilibrium between the two. Similar adsorption behavior has been observed for Kr and Xe in Ni2(dobdc) and Mg2(dobdc).43,47 The interaction of Ar with the cobalt(II) centers in Co2(dobdc) is characterized by a Co–Ar distance of 2.932(9) Å (Fig. 1), which represents the first metal–Ar interaction observed by crystallography. This distance compares well with M–Kr and M–Xe distances in Ni2(dobdc) and Mg2(dobdc) (Ni–Kr = 3.03(3) Å and 3.26(15) Å, Mg–Kr = 3.23(3) Å, Ni–Xe = 3.01(2) Å and 3.395(7) Å, Mg–Xe = 3.14(2) Å) obtained by powder X-ray diffraction.43,47 The long distances between Ar, Kr, and Xe and the exposed metal sites in these frameworks is attributed to polarization induced by the partial positive charge on the metal centers. Like N2 and O2, Ar interacts with the dobdc4− oxygen atoms in its second binding site (Fig. S2†). Interactions between Ar and other noble gases with the linker oxygen atoms in other metal–organic frameworks have also been observed by both single-crystal10,54,69 and powder X-ray diffraction.43,47
Motivated by previous work demonstrating the confinement of white phosphorus within a supramolecular cage102 and a coordination solid,103 we envisioned that CoII–P4 species could be stabilized by leveraging the site-isolation of the open cobalt(II) coordination sites in Co2(dobdc). Heating activated single crystals of Co2(dobdc) in the presence of white phosphorus in a sealed vial at 80 °C resulted in adsorption of P4 molecules to give Co2(dobdc)·1.3P4 as determined by single-crystal X-ray diffraction. Initial refinement of the structure revealed clearly resolved P4 tetrahedron exhibiting η1-coordination to the cobalt(II) sites of the framework, with a CoII–PP4 distance of ∼2.6 Å. The P4 moiety, however, displayed highly prolate anisotropic displacement parameters and unusual P–P bond distances, long Papical–Pbasal bonds (∼2.6 Å) and short Pbasal–Pbasal bonds (∼2.0 Å), compared to the P–P bond distances in the crystal structure of P4 (2.190(5)–2.212(5) Å).104 Given the relatively long CoII–P bond distance and large displacement parameters, the apparent distortion of the coordinated P4 likely resulted from disorder of the P4 molecule rather than activation by the cobalt(II) center. Thus, the P4 molecule was modelled to be disordered over two positions with all P–P distances restrained to be similar. The revised structure reveals that P4 binds to only 45.5(10)% of the cobalt(II) sites with a long CoII–PP4 distance of 2.625(10) Å (Fig. 1 and 3). The relative distance between P4 molecules coordinated to adjacent cobalt(II) sites suggests that P4 cannot coordinate to each cobalt(II) center because this would lead to P⋯P contacts (2.53(3) Å) that are much shorter than twice the van der Waals radius of P (3.90 Å). Consequently, the rest of the adsorbed P4 populates a second site (20.6(10)% occupancy) 3.88 Å away from the cobalt(II) center (Fig. S10†), where steric congestion prevents closer approach of the P4 molecule to cobalt(II). Although rare, several molecular η1–P4 complexes have been prepared by employing transition metal precursors with an agostic interaction or weakly coordinated ligand that can be displaced by P4 under mild reaction conditions.105,106 In contrast to the long CoII–PP4 distance in Co2(dobdc)·1.3P4, molecular η1–P4 complexes reported in the CCSD83 possess much shorter metal–PP4 distances that range from 2.1622(8)–2.464(3) Å and contain electron-rich metals capable of π backbonding to P4. These comparisons imply that, similar to the CoII–CO and CoII–N2 interactions characterized in Co2(dobdc), the longer CoII–PP4 bond in Co2(dobdc)·1.3P4 arises from the inability of the high-spin cobalt(II) centers to effectively support π back-donation to P4. Notably, the weaker cobalt(II)–P4 complexes in Co2(dobdc) can be prepared and remain stable at much higher temperatures whereas most molecular η1–P4 complexes readily decompose at room temperature.105,106 This thermal stability is attributed to the site-isolation of these CoII–P4 species and their inability to decompose through oxidative addition of P4, due to the high-spin state and coordinative saturation of the framework cobalt(II) centers.
Gas adsorption
Low-pressure gas adsorption isotherms at different temperatures were collected for CH4, N2, O2, and Ar, while the isotherms for CO and CO2 were obtained from previous work29,40 to relate the adsorption properties of these gases to the corresponding structures (Fig. 4 and S11–S18†). To provide a quantitative comparison, the differential enthalpies of adsorption (Δhad), a measure of the average binding energy for an adsorbate at a specific surface coverage, were calculated from isotherm data at low coverage of each gas (Table 1). In agreement with the crystal structures, the differential enthalpies of adsorption, which range from −48.8(2) (for CO) to −17(1) kJ mol−1 (for Ar), indicate relatively weak Co–gas interactions compared to those characterized in molecular complexes. To place these values into context, −Δhad for CO in Co2(dobdc) is about one third of the bond dissociation energy for the first CO in CpCo(CO)2 (148(2) kJ mol−1; Cp− = cyclopentadienyl).108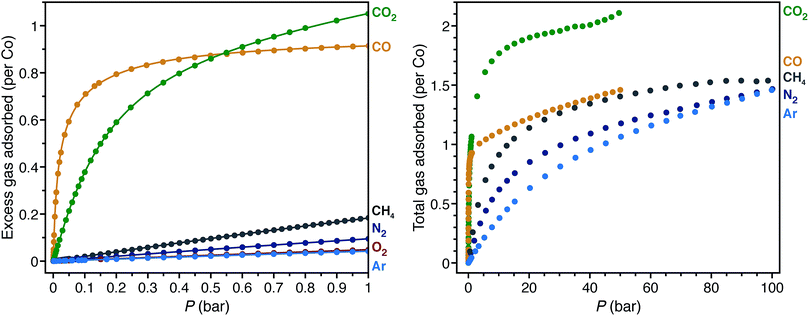 | ||
| Fig. 4 Low-pressure gas adsorption isotherms for CO (yellow),40 CO2 (green),29 CH4 (gray), N2 (dark blue), O2 (red), and Ar (light blue) at 298 K (left). High-pressure gas adsorption isotherms for CO (yellow),40 CO2 (green), CH4 (gray), N2(dark blue), and Ar (light blue) at 298 K (right). The filled circles and solid lines represent experimental data and corresponding Langmuir fits, respectively. | ||
| Gas | d(Co–Xgas) (Å) | Δda (Å) | −Δhadb (kJ mol−1) |
|---|---|---|---|
| a Δd = the Co–Xgas distance minus the sum of the ionic radius for high-spin cobalt(II)107 and the van der Waals radius of the coordinated atom. Δd was not calculated for CH4 because the Co⋯C distance is between Co and the central atom of CH4, not the coordinated hydrogen atoms, which makes it difficult to compare rigorously with the other gases. b Low-coverage differential enthalpies of adsorption were calculated at a loading of 0.5 mmol g−1 using independent Langmuir fits to low-pressure adsorption isotherms. c Although the structure of CO2 in Co2(dobdc) was collected at a higher temperature (150 K) compared to the other structures (90 and 100 K), the Co–OCO2 distance (2.23(4) Å) obtained at 10 K from powder neutron diffraction data shows that the Co–OCO2 distance does not shorten significantly at lower temperatures.29 | |||
| CO | 2.215(6) (Co–C) | −0.230(6) | 48.8(2)40 |
| CO2 | 2.261(9)29 (Co–O)c | −0.004(9) | 33.6(1)29 |
| N2 | 2.236(6) (Co–N) | −0.059(6) | 20.3(6) |
| O2 | 2.216(5) (Co–O) | −0.049(5) | 18.56(3) |
| CH4 | 2.941(19) (Co⋯C) | — | 19.21(9) |
| Ar | 2.932(9) (Co–Ar) | 0.307(9) | 17(1) |
The trend in −Δhad values, CO > CO2 > N2 > CH4 > O2 > Ar, shows no clear correlation with the Co–Xgas distances obtained by single-crystal X-ray diffraction. As an approximate method to account for differences in the van der Waals radii among coordinated atoms, the sum of the ionic radius for high-spin cobalt(II) and the van der Waals radius of the coordinated atom can be subtracted from the Co–Xgas distances to give the parameter Δd. More negative values for Δd should correspond to stronger interactions. With the exception of CO2 and CH4, the trend in Δd is consistent with that of −Δhad. In the structure of CO2 on Co2(dobdc) (Fig. 1), CO2 coordinated to the cobalt(II) sites tilts towards one of the linker oxygen atoms to give a CCO2⋯O distance of 3.29(7) Å.29 This indicates that both direct interaction of CO2 with the metal site and weak secondary interactions contribute to its enthalpy of adsorption. Conceivably, these additional interactions cause CO2 to be an outlier in the trend between Δd and −Δhad. Care should be exercised, however, in inferring relative binding strengths by comparing crystallographic distances. Overall, these results show that multiple factors contribute to the binding energy of a molecule and that interaction distances alone cannot adequately represent all of these factors, especially when considering different molecules. More reliable correlations can be drawn if distances are compared between the same molecule interacting with the same metal center.
The high-pressure adsorption isotherms for CO, CO2, CH4, N2, and Ar at 298 K (Fig. 4) show that secondary adsorption sites become relevant at higher pressures, as the uptake for all gases eventually exceeds one gas molecule per cobalt site with increasing pressure. Qualitative comparison of the isotherms suggests that the secondary adsorption sites for CO2 have the highest binding affinity with an uptake of ∼2 CO2 molecules per Co at 40 bar. This likely results from the favorable interaction between the partial positive charge on the CO2 carbon atom with linker oxygen atoms in the framework and intermolecular interactions between neighboring CO2 molecules (Fig. S2†). In contrast, CO, CH4, N2, and Ar have less pronounced adsorption at high pressures, with each showing an uptake of less than 1.5 molecules of gas per Co at 40 bar. Perhaps the most striking comparison lies between CO and CO2. As a polar molecule, CO has a stronger interaction with the cobalt(II) sites in the framework, which is clearly evident in its steeper low-pressure isotherm and more negative differential enthalpy of adsorption. At pressures beyond 0.55 bar, however, Co2(dobdc) adsorbs significantly larger amounts of CO2, demonstrating that distinct adsorption sites within a material can have considerably different selectivities depending on the nature of the gases adsorbed.
Conclusions
The foregoing results highlight the unique advantages of metal–organic frameworks as robust crystalline matrices that facilitate unhindered access of guest molecules, enabling for example the study of guest interactions with open metal coordination sites within the framework pores. Rigorously air-free gas-dosing methods were developed to overcome the challenges associated with studying weakly binding gases in single crystals. Through these methods, the interaction of CO, CH4, N2, O2, Ar, and P4 with the metal–organic framework Co2(dobdc) were directly observed by single-crystal X-ray diffraction. The resulting structures reveal the location of the primary, secondary (for N2, O2, and Ar) and tertiary (for O2) binding sites for these gases within the framework. Moreover, examination of the CoII–gas distances shows that these CoII–gas interactions are distinctly weak compared to those found in molecular complexes. These unique interactions arise from the square pyramidal coordination geometry and the high-spin electronic configuration enforced by the framework on cobalt(II). As a result, this work represents the first report of the structural characterization of such species by single-crystal X-ray diffraction. Finally, differential enthalpies of adsorption determined from low-pressure gas adsorption isotherms corroborate the weak binding affinities inferred from the relatively long CoII–gas distances observed in the single-crystal structures, while high-pressure gas adsorption isotherms at 298 K show significant contribution from secondary binding sites at pressures beyond 1 bar. Altogether, these results establish in situ single-crystal X-ray diffraction as a valuable technique, which imparts not only a practical understanding of gas adsorption in porous materials, but also new insights into the underlying interactions that give rise to their adsorption behavior.Ongoing efforts are focused on developing in situ single-crystal X-ray diffraction methods that can be routinely employed in the evaluation of metal–organic frameworks for specific applications, such as gas separations and gas storage. In particular, techniques are being explored to enable (i) mounting crystals that decompose in air, (ii) systematic determination of the dependence of site occupancies for multiple binding sites on guest loading, (iii) collection of diffraction data at lower temperatures to lessen thermal disorder, and (iv) structural assessment of the absorptive properties of these materials in the presence of gas mixtures. Furthermore, it can be envisioned that these techniques can be used to isolate and observe reactive intermediates in metal–organic frameworks, providing a way to determine the structures of species that have only been amenable to characterization by spectroscopy.
Acknowledgements
This work was supported through the Center for Gas Separations Relevant to Clean Energy Technologies, an Energy Frontier Research Center funded by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences under Award DE-SC0001015. This research used resources of the Advanced Light Source and the Molecular Foundry, which are supported by the Director, Office of Science, Office of Basic Energy Sciences, of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231. We thank Rebecca L. Siegelman, Julia Oktawiec, Dianne J. Xiao, James R. Nasiaka, Jason S. Lee, Kenji Sumida, David L. Rogow, and Dante Valdez for helpful discussions and experimental assistance.Notes and references
- M. Yoshizawa, J. K. Klosterman and M. Fujita, Angew. Chem., Int. Ed., 2009, 48, 3418–3438 CrossRef CAS PubMed.
- M. E. van der Boom, Angew. Chem., Int. Ed., 2011, 50, 11846–11848 CrossRef CAS PubMed.
- Y. Inokuma, M. Kawano and M. Fujita, Nat. Chem., 2011, 3, 349–358 CrossRef CAS PubMed.
- S. D. Pike and A. S. Weller, Philos. Trans. R. Soc., A, 2015, 373, 20140187 CrossRef PubMed.
- W. M. Bloch, N. R. Champness and C. J. Doonan, Angew. Chem., Int. Ed., 2015, 54, 12860–12867 CrossRef CAS PubMed.
- M. Albrecht, M. Lutz, A. Spek and G. van Koten, Nature, 2000, 406, 970–974 CrossRef CAS PubMed.
- M. Albrecht, M. Lutz, A. M. M. Schreurs, E. T. H. Lutz, A. L. Spek and G. Van Koten, J. Chem. Soc., Dalton Trans., 2000, 3797–3804 RSC.
- J. L. Atwood, L. J. Barbour and A. Jerga, Science, 2002, 296, 2367–2369 CrossRef CAS PubMed.
- A. O'Neil, C. Wilson, J. M. Webster, F. J. Allison, J. A. K. Howard and M. Poliakoff, Angew. Chem., 2002, 114, 3950–3953 CrossRef.
- S. Takamizawa, E.-I. Nakata, T. Saito and K. Kojima, CrystEngComm, 2003, 5, 411–413 RSC.
- O. V. Zenkina, E. C. Keske, R. Wang and C. M. Crudden, Angew. Chem., Int. Ed., 2011, 50, 8100–8104 CrossRef CAS PubMed.
- Z. Huang, P. S. White and M. Brookhart, Nature, 2010, 465, 598–601 CrossRef CAS PubMed.
- S. Takamizawa, T. Akatsuka and T. Ueda, Angew. Chem., Int. Ed., 2008, 47, 1689–1692 CrossRef CAS PubMed.
- J. Sundberg, L. J. Cameron, P. D. Southon, C. J. Kepert and C. J. McKenzie, Chem. Sci., 2014, 5, 4017–4025 RSC.
- C. M. Kane, A. Banisafar, T. P. Dougherty, L. J. Barbour and K. T. Holman, J. Am. Chem. Soc., 2016, 138, 4377–4392 CrossRef CAS PubMed.
- S. D. Pike, A. L. Thompson, A. G. Algarra, D. C. Apperley, S. A. Macgregor and A. S. Weller, Science, 2012, 337, 1648–1651 CrossRef CAS PubMed.
- S. D. Pike, F. M. Chadwick, N. H. Rees, M. P. Scott, A. S. Weller, T. Krämer and S. A. Macgregor, J. Am. Chem. Soc., 2015, 137, 820–833 CrossRef CAS PubMed.
- F. M. Chadwick, N. H. Rees, A. S. Weller, T. Krämer, M. Iannuzzi and S. A. Macgregor, Angew. Chem., Int. Ed., 2016, 55, 3677–3681 CrossRef CAS PubMed.
- M. Eddaoudi, J. Kim, N. Rosi, D. Vodak, J. Wachter, M. O'Keeffe and O. M. Yaghi, Science, 2002, 295, 469–472 CrossRef CAS PubMed.
- S. M. Cohen, Chem. Rev., 2012, 112, 970–1000 CrossRef CAS PubMed.
- L. J. Murray, M. Dincă and J. R. Long, Chem. Soc. Rev., 2009, 38, 1294–1314 RSC.
- J. A. Mason, M. Veenstra and J. R. Long, Chem. Sci., 2014, 5, 32–51 RSC.
- K. Sumida, D. L. Rogow, J. A. Mason, T. M. McDonald, E. D. Bloch, Z. R. Herm, T.-H. Bae and J. R. Long, Chem. Rev., 2012, 112, 724–781 CrossRef CAS PubMed.
- Z. R. Herm, E. D. Bloch and J. R. Long, Chem. Mater., 2014, 26, 323–338 CrossRef CAS.
- L. Ma, C. Abney and W. Lin, Chem. Soc. Rev., 2009, 38, 1248–1256 RSC.
- A. Corma, H. García and F. X. Llabrés i Xamena, Chem. Rev., 2010, 110, 4606–4655 CrossRef CAS PubMed.
- C. Wang, M. Zheng and W. Lin, J. Phys. Chem. Lett., 2011, 2, 1701–1709 CrossRef CAS.
- S. M. Cohen, Z. Zhang and J. A. Boissonnault, Inorg. Chem., 2016, 55, 7281–7290 CrossRef CAS PubMed.
- W. L. Queen, M. R. Hudson, E. D. Bloch, J. A. Mason, M. I. Gonzalez, J. S. Lee, D. Gygi, J. D. Howe, K. Lee, T. A. Darwish, M. James, V. K. Peterson, S. J. Teat, B. Smit, J. B. Neaton, J. R. Long and C. M. Brown, Chem. Sci., 2014, 5, 4569–4581 RSC.
- P. D. C. Dietzel, B. Panella, M. Hirscher, R. Blom and H. Fjellvåg, Chem. Commun., 2006, 959–961 RSC.
- P. D. C. Dietzel, R. E. Johnsen, H. Fjellvåg, S. Bordiga, E. Groppo, S. Chavan and R. Blom, Chem. Commun., 2008, 5125–5127 RSC.
- Y. Liu, H. Kabbour, C. M. Brown, D. A. Neumann and C. C. Ahn, Langmuir, 2008, 24, 4772–4777 CrossRef CAS PubMed.
- A. C. McKinlay, B. Xiao, D. S. Wragg, P. S. Wheatley, I. L. Megson and R. E. Morris, J. Am. Chem. Soc., 2008, 130, 10440–10444 CrossRef CAS PubMed.
- P. D. C. Dietzel, P. A. Georgiev, J. Eckert, R. Blom, T. Strässle and T. Unruh, Chem. Commun., 2010, 46, 4962–4963 RSC.
- E. D. Bloch, L. J. Murray, W. L. Queen, S. Chavan, S. N. Maximoff, J. P. Bigi, R. Krishna, V. K. Peterson, F. Grandjean, G. J. Long, B. Smit, S. Bordiga, C. M. Brown and J. R. Long, J. Am. Chem. Soc., 2011, 133, 14814–14822 CrossRef CAS PubMed.
- K. Sumida, J.-H. Her, M. Dincǎ, L. J. Murray, J. M. Schloss, C. J. Pierce, B. A. Thompson, S. A. FitzGerald, C. M. Brown and J. R. Long, J. Phys. Chem. C, 2011, 115, 8414–8421 CAS.
- E. D. Bloch, W. L. Queen, R. Krishna, J. M. Zadrozny, C. M. Brown and J. R. Long, Science, 2012, 335, 1606–1610 CrossRef CAS PubMed.
- W. L. Queen, E. D. Bloch, C. M. Brown, M. R. Hudson, J. A. Mason, L. J. Murray, A. J. Ramirez-Cuesta, V. K. Peterson and J. R. Long, Dalton Trans., 2012, 41, 4180–4188 RSC.
- S. J. Geier, J. A. Mason, E. D. Bloch, W. L. Queen, M. R. Hudson, C. M. Brown and J. R. Long, Chem. Sci., 2013, 4, 2054–2061 RSC.
- E. D. Bloch, M. R. Hudson, J. A. Mason, S. Chavan, V. Crocellà, J. D. Howe, K. Lee, A. L. Dzubak, W. L. Queen, J. M. Zadrozny, S. J. Geier, L.-C. Lin, L. Gagliardi, B. Smit, J. B. Neaton, S. Bordiga, C. M. Brown and J. R. Long, J. Am. Chem. Soc., 2014, 136, 10752–10761 CrossRef CAS PubMed.
- D. J. Xiao, E. D. Bloch, J. A. Mason, W. L. Queen, M. R. Hudson, N. Planas, J. Borycz, A. L. Dzubak, P. Verma, K. Lee, F. Bonino, V. Crocellà, J. Yano, S. Bordiga, D. G. Truhlar, L. Gagliardi, C. M. Brown and J. R. Long, Nat. Chem., 2014, 6, 590–595 CrossRef CAS PubMed.
- H. Furukawa, F. Gándara, Y.-B. Zhang, J. Jiang, W. L. Queen, M. R. Hudson and O. M. Yaghi, J. Am. Chem. Soc., 2014, 136, 4369–4381 CrossRef CAS PubMed.
- O. V. Magdysyuk, F. Adams, H.-P. Liermann, I. Spanopoulos, P. N. Trikalitis, M. Hirscher, R. E. Morris, M. J. Duncan, L. J. McCormick and R. E. Dinnebier, Phys. Chem. Chem. Phys., 2014, 16, 23908–23914 RSC.
- W. M. Bloch, A. Burgun, C. J. Coghlan, R. Lee, M. L. Coote, C. J. Doonan and C. J. Sumby, Nat. Chem., 2014, 6, 906–912 CrossRef CAS PubMed.
- E. D. Bloch, W. L. Queen, S. Chavan, P. S. Wheatley, J. M. Zadrozny, R. Morris, C. M. Brown, C. Lamberti, S. Bordiga and J. R. Long, J. Am. Chem. Soc., 2015, 137, 3466–3469 CrossRef CAS PubMed.
- J. S. Lee, B. Vlaisavljevich, D. K. Britt, C. M. Brown, M. Haranczyk, J. B. Neaton, B. Smit, J. R. Long and W. L. Queen, Adv. Mater., 2015, 27, 5785–5796 CrossRef CAS PubMed.
- S. K. Ghose, Y. Li, A. Yakovenko, E. Dooryhee, L. Ehm, L. E. Ecker, A.-C. Dippel, G. J. Halder, D. M. Strachan and P. K. Thallapally, J. Phys. Chem. Lett., 2015, 6, 1790–1794 CrossRef CAS PubMed.
- L. J. Murray, M. Dincǎ, J. Yano, S. Chavan, S. Bordiga, C. M. Brown and J. R. Long, J. Am. Chem. Soc., 2010, 132, 7856–7857 CrossRef CAS PubMed.
- K. Sumida, S. Horike, S. S. Kaye, Z. R. Herm, W. L. Queen, C. M. Brown, F. Grandjean, G. J. Long, A. Dailly and J. R. Long, Chem. Sci., 2010, 1, 184–191 RSC.
- M. T. Kapelewski, S. J. Geier, M. R. Hudson, D. Stück, J. A. Mason, J. N. Nelson, D. J. Xiao, Z. Hulvey, E. Gilmour, S. A. FitzGerald, M. Head-Gordon, C. M. Brown and J. R. Long, J. Am. Chem. Soc., 2014, 136, 12119–12129 CrossRef CAS PubMed.
- T. M. McDonald, J. A. Mason, X. Kong, E. D. Bloch, D. Gygi, A. Dani, V. Crocellà, F. Giordanino, S. O. Odoh, W. S. Drisdell, B. Vlaisavljevich, A. L. Dzubak, R. Poloni, S. K. Schnell, N. Planas, K. Lee, T. Pascal, L. F. Wan, D. Prendergast, J. B. Neaton, B. Smit, J. B. Kortright, L. Gagliardi, S. Bordiga, J. A. Reimer and J. R. Long, Nature, 2015, 519, 303–308 CrossRef CAS PubMed.
- Z. Hulvey, B. Vlaisavljevich, J. A. Mason, E. Tsivion, T. P. Dougherty, E. D. Bloch, M. Head-Gordon, B. Smit, J. R. Long and C. M. Brown, J. Am. Chem. Soc., 2015, 137, 10816–10825 CrossRef CAS PubMed.
- D. Gygi, E. D. Bloch, J. A. Mason, M. R. Hudson, M. I. Gonzalez, R. L. Siegelman, T. A. Darwish, W. L. Queen, C. M. Brown and J. R. Long, Chem. Mater., 2016, 28, 1128–1138 CrossRef CAS.
- J. Rowsell, E. C. Spencer, J. Eckert and J. Howard, Science, 2005, 309, 1350–1354 CrossRef CAS PubMed.
- P. D. C. Dietzel, Y. Morita, R. Blom and H. Fjellvåg, Angew. Chem., Int. Ed., 2005, 44, 6354–6358 CrossRef CAS PubMed.
- J. S. Anderson, A. T. Gallagher, J. A. Mason and T. D. Harris, J. Am. Chem. Soc., 2014, 136, 16489–16492 CrossRef CAS PubMed.
- M. I. Gonzalez, E. D. Bloch, J. A. Mason, S. J. Teat and J. R. Long, Inorg. Chem., 2015, 54, 2995–3005 CrossRef CAS PubMed.
- C. A. Trickett, K. J. Gagnon, S. Lee, F. Gándara, H.-B. Buergi and O. M. Yaghi, Angew. Chem., Int. Ed., 2015, 54, 11162–11167 CrossRef CAS PubMed.
- R. J. Marshall, S. L. Griffin, C. Wilson and R. S. Forgan, J. Am. Chem. Soc., 2015, 137, 9527–9530 CrossRef CAS PubMed.
- D. J. Xiao, M. I. Gonzalez, L. E. Darago, K. D. Vogiatzis, E. Haldoupis, L. Gagliardi and J. R. Long, J. Am. Chem. Soc., 2016, 138, 7161–7170 CrossRef CAS PubMed.
- D. A. Reed, D. J. Xiao, M. I. Gonzalez, L. E. Darago, Z. R. Herm, F. Grandjean and J. R. Long, J. Am. Chem. Soc., 2016, 138, 5594–5602 CrossRef CAS PubMed.
- A. T. Gallagher, M. L. Kelty, J. G. Park, J. S. Anderson, J. A. Mason, J. P. S. Walsh, S. L. Collins and T. D. Harris, Inorg. Chem. Front., 2016, 3, 536–540 RSC.
- P. M. Bhatt, Y. Belmabkhout, A. Cadiau, K. Adil, O. Shekhah, A. Shkurenko, L. J. Barbour and M. Eddaoudi, J. Am. Chem. Soc., 2016, 138, 9301–9307 CrossRef CAS PubMed.
- S. K. Elsaidi, M. H. Mohamed, C. M. Simon, E. Braun, T. Pham, K. A. Forrest, W. Xu, D. Banerjee, B. Space, M. J. Zaworotko and P. K. Thallapally, Chem. Sci., 2017, 8, 2373–2380 RSC.
- L.-C. Lin, K. Lee, L. Gagliardi, J. B. Neaton and B. Smit, J. Chem. Theory Comput., 2014, 10, 1477–1488 CrossRef CAS PubMed.
- K. Lee, W. C. Isley, A. L. Dzubak, P. Verma, S. J. Stoneburner, L.-C. Lin, J. D. Howe, E. D. Bloch, D. A. Reed, M. R. Hudson, C. M. Brown, J. R. Long, J. B. Neaton, B. Smit, C. J. Cramer, D. G. Truhlar and L. Gagliardi, J. Am. Chem. Soc., 2014, 136, 698–704 CrossRef CAS PubMed.
- K. Lee, J. D. Howe, L.-C. Lin, B. Smit and J. B. Neaton, Chem. Mater., 2015, 27, 668–678 CrossRef CAS.
- R. Mercado, B. Vlaisavljevich, L.-C. Lin, K. Lee, Y. Lee, J. A. Mason, D. J. Xiao, M. I. Gonzalez, M. T. Kapelewski, J. B. Neaton and B. Smit, J. Phys. Chem. C, 2016, 120, 12590–12604 CAS.
- X. Chen, A. M. Plonka, D. Banerjee, R. Krishna, H. T. Schaef, S. Ghose, P. K. Thallapally and J. B. Parise, J. Am. Chem. Soc., 2015, 137, 7007–7010 CrossRef CAS PubMed.
- W. Zhou, H. Wu and T. Yildirim, J. Am. Chem. Soc., 2008, 130, 15268–15269 CrossRef CAS PubMed.
- S. R. Caskey, A. G. Wong-Foy and A. J. Matzger, J. Am. Chem. Soc., 2008, 130, 10870–10871 CrossRef CAS PubMed.
- G. M. Sheldrick, CELL NOW V2008/2, Bruker AXS Inc, 2008 Search PubMed.
- Bruker Analytical X-ray Systems, Inc., SAINT and APEX 2 Software for CCD Diffractometers, Bruker Analytical X-ray Systems, Inc., Madison, WI, USA, 2000 Search PubMed.
- G. M. Sheldrick, TWINABS, Version 2012/1, University of Göttingen, 2012 Search PubMed.
- G. M. Sheldrick, Acta Crystallogr., A, Found. Crystallogr., 2008, 64, 112–122 CrossRef CAS PubMed.
- G. M. Sheldrick, SHELXS, University of Göttingen, Germany, 2014 Search PubMed.
- G. M. Sheldrick, SHELXL, University of Göttingen, Germany, 2014 Search PubMed.
- O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339–341 CrossRef CAS.
- E. W. Lemmon, M. L. Huber and M. McLinden, Reference Fluid Thermodynamic and Transport Properties-REFPROP Version 8.0, National Institute of Standards and Technology, Standard Reference Data Program, Gaithersburg, 2007 Search PubMed.
- E. W. Lemmon and R. Span, J. Chem. Eng. Data, 2006, 51, 785–850 CrossRef CAS.
- J. E. Warren, R. G. Pritchard, D. Abram, H. M. Davies, T. L. Savarese, R. J. Cash, P. R. Raithby, R. Morris, R. H. Jones and S. J. Teat, J. Appl. Crystallogr., 2009, 42, 457–460 CrossRef CAS.
- J. M. Cox, I. M. Walton, C. A. Benson, Y. S. Chen and J. B. Benedict, J. Appl. Crystallogr., 2015, 48, 578–581 CAS.
- C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 2016, 72, 171–179 CrossRef CAS PubMed.
- C. A. Ghilardi, S. Midollini and L. Sacconi, J. Organomet. Chem., 1980, 186, 279–287 CrossRef CAS.
- P. Fernández, A. Sousa-Pedrares, J. Romero, M. L. Durán, A. Sousa, P. Pérez-Lourido and J. A. García-Vázquez, Eur. J. Inorg. Chem., 2010, 814–823 CrossRef.
- B. A. MacKay and M. D. Fryzuk, Chem. Rev., 2004, 104, 385–402 CrossRef CAS PubMed.
- M. D. Fryzuk and S. A. Johnson, Coord. Chem. Rev., 2000, 200–202, 379–409 CrossRef CAS.
- N. Khoenkhoen, B. de Bruin, J. N. H. Reek and W. I. Dzik, Eur. J. Inorg. Chem., 2015, 567–598 CrossRef CAS.
- E. C. Niederhoffer, J. H. Timmons and A. E. Martell, Chem. Rev., 1984, 84, 137–203 CrossRef CAS.
- B. S. Tovrog, D. J. Kitko and R. S. Drago, J. Am. Chem. Soc., 1976, 98, 5144–5153 CrossRef CAS.
- J. B. DeCoste, M. H. Weston, P. E. Fuller, T. M. Tovar, G. W. Peterson, M. D. LeVan and O. K. Farha, Angew. Chem., Int. Ed., 2014, 53, 14092–14095 CrossRef CAS PubMed.
- S. T. Meek, S. L. Teich-McGoldrick and J. J. Perry, J. Phys. Chem. C, 2012, 116, 19765–19772 CAS.
- H. Wu, W. Zhou and T. Yildirim, J. Am. Chem. Soc., 2009, 131, 4995–5000 CrossRef CAS PubMed.
- K. Seppelt, Z. Anorg. Allg. Chem., 2003, 629, 2427–2430 CrossRef CAS.
- W. Grochala, Chem. Soc. Rev., 2007, 36, 1632–1655 RSC.
- D. Bellert and W. H. Breckenridge, Chem. Rev., 2002, 102, 1595–1622 CrossRef CAS PubMed.
- P. D. Carnegie, B. Bandyopadhyay and M. A. Duncan, J. Phys. Chem. A, 2008, 112, 6237–6243 CrossRef CAS PubMed.
- P. D. Carnegie, B. Bandyopadhyay and M. A. Duncan, J. Phys. Chem. A, 2011, 115, 7602–7609 CrossRef CAS PubMed.
- B. Bandyopadhyay and M. A. Duncan, Chem. Phys. Lett., 2012, 530, 10–15 CrossRef CAS.
- D. Lessen and P. J. Brucat, J. Chem. Phys., 1989, 90, 6296–6305 CrossRef CAS.
- R. N. Perutz and J. J. Turner, J. Am. Chem. Soc., 1975, 97, 4791–4800 CrossRef CAS.
- P. Mal, B. Breiner, K. Rissanen and J. R. Nitschke, Science, 2009, 324, 1697–1699 CrossRef CAS PubMed.
- W. Choi, H. Ohtsu, Y. Matsushita and M. Kawano, Dalton Trans., 2016, 45, 6357–6360 RSC.
- A. Simon, H. Borrmann and J. Horakh, Eur. J. Inorg. Chem., 1997, 130, 1235–1240 CAS.
- M. Peruzzini, L. Gonsalvi and A. Romerosa, Chem. Soc. Rev., 2005, 34, 1038 RSC.
- P. L. Luis, I. de los Rios and M. Peruzzini, Phosphorus Res. Bull., 2001, 12, 167–180 CrossRef CAS.
- R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767 CrossRef.
- B. Sztáray, L. Szepes and T. Baer, J. Phys. Chem. A, 2003, 107, 9486–9490 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Supplementary figures, crystallographic information, adsorption isotherms and fits, CCDC 1530119–1530126. For ESI and crystallographic data in CIF or other electronic format. See DOI: 10.1039/c7sc00449d |
| This journal is © The Royal Society of Chemistry 2017 |