Open Access Article
Open Access ArticleHalogen bonded Borromean networks by design: topology invariance and metric tuning in a library of multi-component systems†
Vijith
Kumar
 a,
Tullio
Pilati
a,
Giancarlo
Terraneo
a,
Tullio
Pilati
a,
Giancarlo
Terraneo
 a,
Franck
Meyer‡
a,
Pierangelo
Metrangolo
a,
Franck
Meyer‡
a,
Pierangelo
Metrangolo
 ab and
Giuseppe
Resnati
ab and
Giuseppe
Resnati
 *a
*a
aLaboratory of Nanostructured Fluorinated Materials (NFMLab), Department of Chemistry, Materials, and Chemical Engineering “Giulio Natta”, Politecnico di Milano, Via L. Mancinelli 7, 20131 Milano, Italy. E-mail: giuseppe.resnati@polimi.it
bVTT-Technical Research Centre of Finland, P. O. Box 1000, FI-02044 VTT, Finland
First published on 26th October 2016
Abstract
A library of supramolecular anionic networks showing Borromean interpenetration has been prepared by self-assembly of crypt-222, several metal or ammonium halides, and five bis-homologous α,ω-diiodoperfluoroalkanes. Halogen bonding has driven the formation of these anionic networks. Borromean entanglement has been obtained starting from all the four used cations, all the three used anions, but only two of the five used diiodoperfluoroalkanes. As the change of the diiodoperfluoroalkane, the cation, or the anion has a different relative effect on the metrics and bondings of the self-assembled systems, it can be generalized that bonding, namely energetic, features play here a less influential role than metric features in determining the topology of the prepared tetra-component cocrystals. This conclusion may hold true for other multi-component systems and may function as a general heuristic principle when pursuing the preparation of multi-component systems having the same topology but different composition.
Introduction
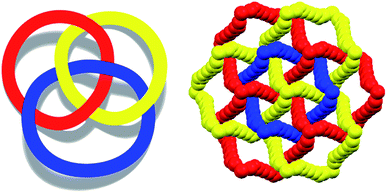
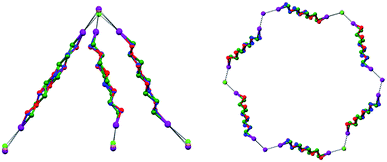
To control the topological features of self-assembled systems is a key issue in many different fields related to basic sciences1 and applied technologies.2 An example from application oriented studies is to avoid interpenetration and form metal–organic frameworks3 (MOFs) or covalent organic frameworks4 (COFs) with large voids, both compound classes being promising materials for gas storage5 and sensing,6 mixture separation,7 and catalysis.8 An example from basic investigations, is the development of heuristic principles to control the supramolecular connectivity in catenanes,9 rotaxanes,10 and knots,11 the field having contributed strongly, during the last decade or so, to the terrific progress in the design of recognition and self-assembly processes in solution and in solids.The Borromean rings12 (Fig. 1, left) constitute a particularly fascinating pattern of topological entanglement13 where complexity, structural integrity, and aesthetic beauty are present in the final architecture. The distinctive topological feature of Borromean links lies in their intrinsic mode of interpenetration: three mutually disjointed closed curves form a link, yet no two rings are linked; but if anyone is cut, the other two are free to separate.
This complex interwoven structure has inspired scientists from varied backgrounds14 and the first formation of discrete molecular Borromean rings was realized in 1997 by the effective manipulation of a DNA sequence.15 Subsequently, nanoscale Borromean rings were prepared by Stoddart et al. through the use, in concert, of metal coordination, supramolecular and dynamic covalent chemistry.16 Infinite Borromean networks are frequently17 based on two-dimensional (6,3) networks with undulating character.18 It seems that the presence of large empty frames in Borromean networks is an essential requirement for entanglement.19 Coordination chemistry16d,20 has frequently driven the formation of non-trivial links, Borromean systems included. Also hydrogen bonds,21 argentophilic22 and π–π interactions23 have been used, possibly in combination with coordination chemistry, to facilitate the formation and/or stabilization of the Borromean motif.
Halogen bonding (XB)24 has consolidated its role as a powerful tools in crystal engineering.25 The available halogen bonded synthons are very diversified and both neutral and ionic motifs have been used to achieve a great variety of supramolecular architectures.26 Halide anions have been recognized as very good XB acceptors and have been used to form several halogen bonded networks with different topologies.27 For instance, self-assembly of bromide or chloride anions with carbon tetrabromide affords acentric adamantanoid networks presenting interesting non-linear optical properties28 and chloride anion effectively templated redox-active ferrocene catenanes in solution and a surface-confined environment.29
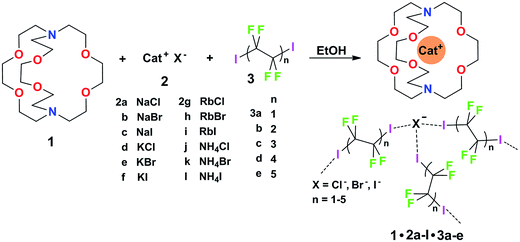
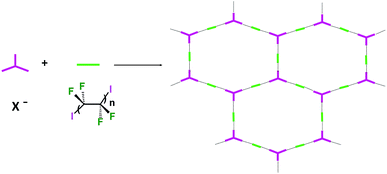
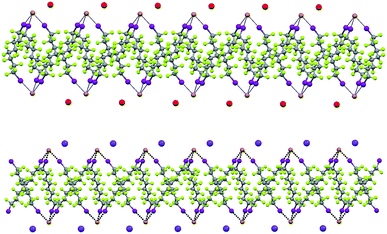
Some years ago we have demonstrated that self-assembly of 4,7,13,16,21,24-hexaoxa-1,10-diazabicyclo[8.8.8]hexacosane (crypt-222, 1), potassium iodide (2f), and α,ω-diiodoperfluoroalkanes (3a–d) lead to the cocrystals 1·2f·3a–d (Fig. 2).30 K+ cations are cryptated by 1 and the electron donor ability of I− anions is boosted. These anions behave as tridentate XB acceptors and interact with three different diiodoperfluoroalkyl chains 3a–d which work as bidentate and telechelic XB donors. (6,3) nets are formed where I− anions sit at the vertexes of the hexagonal frames and diiodoperfluoroalkanes form the sides (Fig. 3). In all four cocrystals these honeycomb nets produce layers which alternate with hydrocarbon layers formed by K+⊂crypt-222 and iodide anions sitting at the layer interfaces. While in 1·2f·3a,b the fluorous layer contains a single honeycomb net, in 1·2f·3c,d it contains three (6,3) nets showing Borromean entanglement supported by XB (Fig. 1, right).
Cocrystals 1·2·3 are obtained on self-assembly of three different chemical species (i.e., cryptand 1, salts 2, and diiodoperfluoroalkanes 3) and four components (i.e., 1, the cation and anion from salts 2, and 3) which can be varied independently. The numerous possibilities to vary the composition of these tetra-component cocrystals offer a unique opportunity to pursue the design and preparation of a library of different cocrystals wherein the halogen bonded supramolecular anions show Borromean entanglement. The challenge to prepare a library of cocrystals with Borromean interpenetration is a case of a quite general problem, i.e., how to change the composition of a multi-component and self-assembled system while maintaining unmodified its topology. It was expected that the change of only some of the dimensional and electronic characteristics in the items of a library of cocrystals 1·2·3 is compatible with the formation of nets showing Borromean entanglement. In other words, we expected that cocrystals “similar” to 1·2f·3c,d or 1·2f·3a,b would afford (6,3) nets with or without Borromean interpenetration, respectively. In order to assess the chemical meaning of such similarity, we prepared a library of cocrystals 1·2·3 containing Na+, or K+, or Rb+, or NH4+ cations, Cl−, or Br−, or I− anions, and two−, or four−, or six−, or eight−, or ten− carbon diiodoperfluoroalkanes 3 (Fig. 2).
Different anions and cations give rise to XBs and electrostatic attraction between opposite ions (the two strongest interactions in cocrystals 1·2·3) endowed with quite different strength. This allowed us to assess the relevance of the bonding features in determining the connectivity and the interpenetration in the formed cocrystals. In other words, this allowed us also to assess if the Borromean interpenetration tolerates non minor differences in the strength of interactions driving the cocrystals self-assembly.
As to the metric of cocrystals 1·2·3, our working hypothesis was that if the presence of large and void frames in a network is a prerequisite for its Borromean entanglement, diiodoperfluoroalkanes 3 were very promising candidates for obtaining a library of Borromean (6,3) cocrystals 1·2·3. 3a–e are expected to be the anion spacers in supramolecular anionic networks of cocrystals 1·2·3 (Fig. 3) and are also expected to behave as rigid and rod-like moieties,31 as it is typically the case for perfluoroalkyl derivatives. 3a–e are thus assumed to function as the most influential component in determining the metric of the networks. One or more of them were expected to be tailored to reliably afford (6,3) networks sized for Borromean interpenetration independent of the cation and anion nature and a library of Borromean cocrystals 1·2·3 should be accessible.
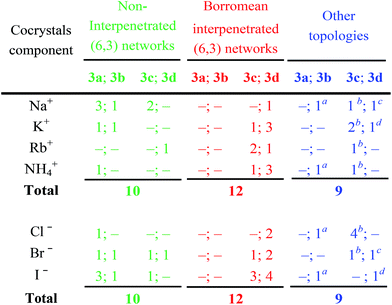
The structures of obtained multicomponent cocrystals 1·2a–l·3a–e determined via single crystal X-ray analyses (ESI, Tables S1–S5†) were numerous enough to map in the detail the overall architectural landscape as a function of the cocrystal composition and to identify the boundaries of the compositional space compatible with (6,3) net formation and Borromean entanglement (Table 1). Borromean entanglement is present in twelve of the obtained cocrystals and this topology was formed starting from all four cations, all three anions, and only two of the five diiodoperfluoroalkanes 3 which have been used. This proves that the architectural features responsible for the Borromean entanglement in cocrystals 1·2·3 are robust enough to hold up some variability in both the XB donor and acceptor modules, namely in both the metric and bonding features of the cocrystals. Considering the different relative effect that the change of the diiodoperfluoroalkane, the cation, or the anion has on metrics and bondings in cocrystals 1·2·3, it can be generalized that bonding, namely energetic, features play a less influential role than metrics in determining the topology of the multi-component systems under study. These conclusions may hold true for other multi-component systems and they may work as general heuristic principles when pursuing the preparation of multi-component cocrystals having the same topology but different composition.
Results and discussion
Preparation of cocrystals 1·2a–l·3a–e
To correlate reliably the structural differences in 1·2a–l·3a–e cocrystals with differences in the starting components, our preliminary experiments aimed at optimizing experimental conditions for the preparation of our cocrystals. The aim was to secure that the structure of the obtained systems was largely independent of the experimental conditions. This enabled us to draw general, robust, and safe conclusions on the composition vs. cocrystal topology relationships.We selected five sets of starting tectons as representative of different possible self-assemblies; the two sets 1/2a/3a and 1/2b/3b were expected to afford non-Borromean adducts for similarity with already reported cocrystals 1·2f·3a,b, while the three sets 1/2c/3d, 1/2h/3c, and 1/2j/3d were expected to afford Borromean adducts. We first monitored, with the NMR technique, ethanol solutions containing the pure tectons mentioned above in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5 ratio, namely the stoichiometry of a (6,3) network. 1H and 19F spectra of these solutions after some hours at room temperature, confirmed cation cryptation occurred quite rapidly under adopted conditions (ESI, paragraph S3†). We then evaporated solutions wherein the 1
1.5 ratio, namely the stoichiometry of a (6,3) network. 1H and 19F spectra of these solutions after some hours at room temperature, confirmed cation cryptation occurred quite rapidly under adopted conditions (ESI, paragraph S3†). We then evaporated solutions wherein the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 ratio was 1
3 ratio was 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5, 1
1.5, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, and 1
2, and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 in order to assess how dependent the formed cocrystal was on the adopted stoichiometry. These studies have been performed on a set of four systems. DSC and powder X-ray analyses of the cocrystals (isolated at 25% ca. conversion) proved that, within the tested compositional range, the formed cocrystal was not affected by the solution stoichiometry (ESI, paragraphs S4 and S5†). We finally tried cocrystals formation starting from 1
1 in order to assess how dependent the formed cocrystal was on the adopted stoichiometry. These studies have been performed on a set of four systems. DSC and powder X-ray analyses of the cocrystals (isolated at 25% ca. conversion) proved that, within the tested compositional range, the formed cocrystal was not affected by the solution stoichiometry (ESI, paragraphs S4 and S5†). We finally tried cocrystals formation starting from 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5 molar solutions of cation⊂crypt-222 halides and diiodoperfluoroalkanes. The analytical techniques mentioned above showed that the cocrystals formed after this protocol (at 25% ca. conversion) were the very same as in previous experiments where pure tectons 1, 2, and 3 were mixed in a 1
1.5 molar solutions of cation⊂crypt-222 halides and diiodoperfluoroalkanes. The analytical techniques mentioned above showed that the cocrystals formed after this protocol (at 25% ca. conversion) were the very same as in previous experiments where pure tectons 1, 2, and 3 were mixed in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5 ratio.
1.5 ratio.
Slow isothermal evaporation of the solvent from ethanol solutions of pure 1, 2, and 3 in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5 ratio was thus chosen as the standard protocol to prepare all the cocrystals. After 3–7 days at room temperature, colorless crystals were formed and IR analyses showed that νC–H stretchings were blue shifted with respect to pure starting 1 (typically at 2810–2970 cm−1 rather than at 2710–2940 cm−1), consistent with the presence of cation⊂crypt-222 halides (ESI, S6†). The presence of diiodoperfluoroalkanes in the isolated cocrystals was proven, among others, by the νC–F stretching peaks in the 1085–1200 cm−1 region. These peaks were red shifted, compared to pure tectons 3, suggesting involvement in XB formation⊂crypt-222 halides (1·2).32 These data indicate that, in all fifty two cases under study, halogen bonded cocrystals 1·2·3 were formed wherein the α,ω-diiodoperfluoroalkanes 3a–e are the XB donors and the anion of cryptated salts 1·2a–l are the acceptors.33 Melting points were different from starting tectons 1, 2, and 3 and from respective cation⊂crypt-222 halides (1·2). These data indicate that, in all fifty two cases under study, halogen bonded cocrystals 1·2·3 were formed wherein the α,ω-diiodoperfluoroalkanes 3a–e are the XB donors and the anion of cryptated salts 1·2a–l are the acceptors.
1.5 ratio was thus chosen as the standard protocol to prepare all the cocrystals. After 3–7 days at room temperature, colorless crystals were formed and IR analyses showed that νC–H stretchings were blue shifted with respect to pure starting 1 (typically at 2810–2970 cm−1 rather than at 2710–2940 cm−1), consistent with the presence of cation⊂crypt-222 halides (ESI, S6†). The presence of diiodoperfluoroalkanes in the isolated cocrystals was proven, among others, by the νC–F stretching peaks in the 1085–1200 cm−1 region. These peaks were red shifted, compared to pure tectons 3, suggesting involvement in XB formation⊂crypt-222 halides (1·2).32 These data indicate that, in all fifty two cases under study, halogen bonded cocrystals 1·2·3 were formed wherein the α,ω-diiodoperfluoroalkanes 3a–e are the XB donors and the anion of cryptated salts 1·2a–l are the acceptors.33 Melting points were different from starting tectons 1, 2, and 3 and from respective cation⊂crypt-222 halides (1·2). These data indicate that, in all fifty two cases under study, halogen bonded cocrystals 1·2·3 were formed wherein the α,ω-diiodoperfluoroalkanes 3a–e are the XB donors and the anion of cryptated salts 1·2a–l are the acceptors.
Thirty one out of the fifty two 1·2·3 adducts afforded samples suitable for single crystal X-ray analyses. Five cocrystals, specifically 1·2f·3a–d and 1·2c·3a had already been reported30a,33 and the remaining twenty six structures are discussed here.
Description of selected crystal structures
Diiodoperfluoroalkanes, the sides of the supramolecular anionic networks, function as bidentate and telechelic XB donors in all cocrystals but 1·2f·3e where some diiododecane units work as monodentate XB donors.
Halide anions, the network nodes, function as tetradentate XB acceptors in (4,4) nets (2 cocrystals) and in the discrete units present in 1·2f·3e. Halide anions work as tridentate XB acceptors in all other systems namely in those showing the presence of (6,3) networks (twenty two cocrystals), ribbons of juxtaposed squares (five cocrystals), and pearl-necklace arrangements (one cocrystal).
XB and the electrostatic attraction between cations and halide anions are strong interactions in cocrystals 1·2·3 and affect their structure, but also segregation34 of fluorous and hydrocarbon components is ubiquitous and highly influential in determining the overall crystal packing. Fluoroalkyl chains segregate from cryptated cations in by far the majority of the cocrystals and halide anions typically sit at the interface of segregated domains. For instance, alternating fluorocarbon and hydrocarbon layers are formed by the discrete adducts of 1·2f·3e (ESI, Fig. S10†), the pearl-necklaces of 1·2b·3d (ESI, Fig. S11†), and all (6,3) networks (ESI, Fig. S12†).
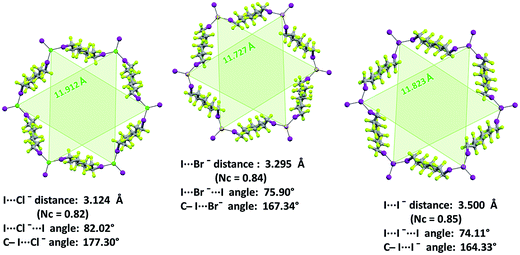
Similar to analogous systems,27 XBs are approximately on the extension of the C–I covalent bond, as expected for strong XBs (C–I⋯X− angles span the range 167.81–179.58°). I⋯X−⋯I angles are 76.68°, 74.60°, and 72.16° in 1·2a·3a, 1·2b·3a, and 1·2c·3a, respectively, and the resulting pyramidal arrangement around halides determines an egg tray shape in the (6,3) nets. The larger angle associated with the smaller halide allows for framing cavities of relatively constant size on halide change and the importance of this issue will be discussed in detail in one of the following paragraphs. Cryptated cations are sitting in these cavities. Fluorous layers in these systems formed by short-chain diiodoperfluorocarbons always contain a single honeycomb net.
The packings of all these cocrystals are nearly isostructural (Fig. 4), ten cocrystals being in the P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) space group. Notably, this space group is adopted also by the Borromean cocrystal 1·2j·3d where a water molecule completes the first coordination sphere35 of the chloride. A water molecule is present also in the coordination sphere of the bromide cocrystal 1·2h·3c, and this confirms that the tendency of 3c,d to form Borromean (6,3) networks is quite robust.
space group. Notably, this space group is adopted also by the Borromean cocrystal 1·2j·3d where a water molecule completes the first coordination sphere35 of the chloride. A water molecule is present also in the coordination sphere of the bromide cocrystal 1·2h·3c, and this confirms that the tendency of 3c,d to form Borromean (6,3) networks is quite robust.
XB features parallel those described above for non-interpenetrated (6,3) nets (ESI, Fig. S12–S16†). For instance, C–I⋯X− angles are quite linear and I⋯X−⋯I angles decrease when the weight of the halide increases (I⋯X−⋯I angles in 1·2j·3d, 1·2k·3d, and 1·2l·3d, are 83.15°, 78.73°, 74.92°, respectively). Moreover, the I⋯Br− separation in 1·2k·3d (326.1 pm which corresponds to a normalized contact36Nc of 0.83) is longer than the I⋯Cl− separation in 1·2j·3d (310.8 pm, Nc = 0.82) but shorter than the I⋯I− one in 1·2l·3d (347.3 pm, Nc = 0.84). This scale parallels the relative size of the different anions and is consistent with theoretical studies in the gas phase37 and some experimental studies38 in solution showing that, with a given XB donor, Cl− gives shorter and stronger XB than Br− which gives shorter and stronger XB than I−.
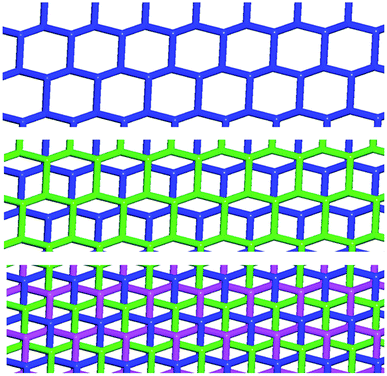
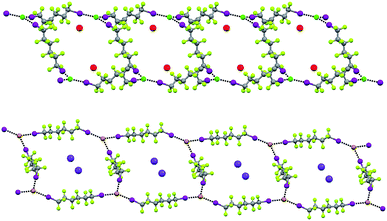
In Borromean systems a fluorous layer is formed by three translationally related honeycomb nets which entangle in a 2D → 2D fashion (Fig. 5 and 6). The chair-like shape of hexagonal frames, resulting from the pyramidal geometry at halide nodes and responsible for the egg tray arrangement of single nets, creates conditions for interpenetration. The typical stiffness of perfluoroalkyl chains,31 forming the sides of the hexagonal rings, helps in maintaining the large polymeric mesh of hexagonal frames which is a prerequisite for entanglement of three honeycomb nets.
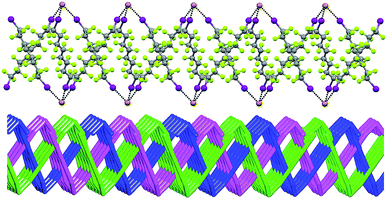 | ||
| Fig. 5 Top: Partial representation along the crystallographic a-axis (Mercury 3.8, ball and stick) of one undulating honeycomb net in 1·2e·3d. XBs are in black dotted lines. Colour codes as in Fig. 4. Bottom: Schematic view (approximately along the a-axis) of three entangled (6,3) networks in the same compound; three different colours have been used for the three different nets. | ||
The electrostatic attraction between cations and halide anions is a strong interaction in 1·2·3 cocrystals. On cation and anion change the separation of these charged species in the packing undergoes minor changes and the overall crystal packing remains quite constant. The convenient sizing of the cavities of the honeycomb grid is enabled primarily by the size of diiodoperfluoroalkane 3 and is tuned by the flexibility around the node of the hexagonal units. In fact, on X− change, minor changes are observed in X−⋯X− separations (they are 11.823, 11.727, and 11.912 Å in 1·2f·3d, 1·2e·3d, and 1·2d·3d, respectively), K+⋯K+ separations (they are 7.194, 7.163, and 7.202 Å for the same derivatives as above), and X−⋯K+ separations (they are 6.939, 6.913, and 7.126 Å for the same cocrystals as above). Differently, I⋯X−⋯I angles show remarkable variability when X− changes (they are 73.08° in 1·2f·3d, 75.92° in 1·2e·3d, and 82.02° in 1·2d·3d). These geometric features help in rationalizing the topological invariance in the Borromean systems on component change. Chloride anion is the smallest anion of the 1·2d–f·3d series and consistent with its ability to form strong XBs,37,38 XBs in the chloride cocrystal 1·2d·3d are shorter than in other halide cocrystals 1·2e,f·3d. In 1·2d·3d, hexagonal units large enough to ensure interpenetration are assembled by flattening the hexagonal frame relative to 1·2e,f·3d namely by widening I⋯X−⋯I angles which, for the chloride, are 82°, the widest angle of the series 1·2d–f·3d. In other words, the increased separation of perfluoroalkyl chains resulting from widening of the angles at the nodes in 1·2d·3d counterbalances contraction of the hexagonal frames resulting from the small chloride size and the short XBs it forms. For the same reasons I⋯Br−⋯I angles are smaller than I⋯I−⋯I angles. The isostructurality in the Borromean networks thus results from a fine balance between synthons size, strength, and flexibility (Fig. 7).
In the five cocrystals wherein linear ribbons are present (Fig. 9), the ratio of starting tectons 1, 2, and 3 is 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5 and halide anions function as tridentate XB acceptors, once again as in Borromean nets. These ribbons are formed by juxtaposed squares having anions at the vertexes, diiodoperfluoroalkanes at the sides, and cations hosted in the squares. The topology observed in these structures is related to the nearly planar and T shaped geometry adopted by the anions (Fig. 9). In all five structures the XB donor is the diiodoperfluorohexane 3c while the cation can be any one of the four used in this paper and the anion either a chloride or a bromide. This confirms that the combined action of the size of the diiodoperfluoroalkane modules 3 and the flexibility, namely the angles, at the nodes is quite influential for the topology adopted by supramolecular anions.
1.5 and halide anions function as tridentate XB acceptors, once again as in Borromean nets. These ribbons are formed by juxtaposed squares having anions at the vertexes, diiodoperfluoroalkanes at the sides, and cations hosted in the squares. The topology observed in these structures is related to the nearly planar and T shaped geometry adopted by the anions (Fig. 9). In all five structures the XB donor is the diiodoperfluorohexane 3c while the cation can be any one of the four used in this paper and the anion either a chloride or a bromide. This confirms that the combined action of the size of the diiodoperfluoroalkane modules 3 and the flexibility, namely the angles, at the nodes is quite influential for the topology adopted by supramolecular anions.
Finally, in 1·2a·3b, 1·2l·3b, and 1·2f·3e halide anions function as tetradentate XB acceptors. In the first cocrystal anions are connected into square and planar (4,4) networks hosting one cryptated cation at the center of the square frame (ESI, Fig. S19†). Similar but undulated (4,4) networks are present in 1·2l·3b while in 1·2f·3e iodide anions adopt a distorted tetrahedral geometry and assemble well defined supramolecular anions through short I⋯X XBs. These supra-anions further interact with each other to give infinite chains via loose C–I⋯I–C XBs (ESI, Fig. S10, S20 and S21†).
Topology of cocrystals 1·2·3 as a function of starting components
A detailed comparison of the topologies of halogen bonded supramolecular anions in sets of cocrystals containing given cations but different anions and/or diiodoperfluorocarbons, further indicates that the size of the cation influences the metric of the cocrystals but it does not affect it to the point of becoming the most influential factor for the topology adopted by the halogen bonded supramolecular anion. For instance, Na+⊂crypt-222, the smallest cryptated cation in the examined series,39 affords a supramolecular anion with Borromean interpenetration (i.e., 1·2c·3d) only when the large iodide anion is the XB acceptor and the long diiodoperfluorooctane 3d is the XB donor. Smaller XB acceptors, namely bromide and chloride anions, and shorter XB donors, e.g., diiodoperfluoroalkanes 3c or 3b, form non-interpenetrated (6,3) networks (e.g., 1·2a·3c, 1·2b·3c, and 1·2c·3b) when self-assembling with Na+⊂crypt-222.
In general, cations are very effective in determining recognition phenomena and the structure of templated systems,40 but the data described above consistently prove that in our systems, Borromean interpenetration appears only when the formation of hexagonal frames with large enough meshes is secured by the synergistic action of the size of the cation, the anion, and the diiodoperfluoroalkane, the size of the diiodoalkane playing the most influential role.
A pro-active role of halide anions in the formation of Borromean interpenetrated systems is related to their spherical nature which allows the I⋯X−⋯I angles to be wider for lighter halides in order to slightly flatten the (6,3) networks and to counterbalance the smaller size of the hexagonal frames formed by lighter halides. For instance, the I⋯X−⋯I angles are 73.47° for the iodide cocrystal 1·2l·3d, 78.73° for the bromide 1·2k·3d, and 83.15 for the chloride 1·2j·3d. In this way, the egg tray shaped supramolecular anion contains cavities conveniently sized for Borromean entanglement.
In the four cocrystals 1·2a·3c, 1·2d·3c, 1·2g·3c, and 1·2j·3c wherein chloride anion is paired with diiodoperfluorohexane 3c, the supramolecular anions are ribbons of squares (Fig. 9). In general, no chloride salt forms Borromean systems on self-assembly with diiodohexane 3c. This might be rationalized by considering that the flexibility described above at the halide nodes of supramolecular anions is not effective enough to afford adequately sized honeycomb frames on self-assembly of chloride anions, i.e., the smallest used halide, with diiodohexane 3c, i.e., the shortest diiodoalkane able to give Borromean (6,3) nets. In contrast, flexibility can afford adequately sized honeycomb frames on self-assembly of chloride anions with the longer diiodoperfluorooctane 3d (as it is the case in 1·2d·3d and 1·2j·3d).45
The presence of large cavities in a network is a prerequisite for Borromean entanglements. The size of the diiodoperfluorocarbon, which is the side of the network meshes, is the most important parameter in determining the meshes’ metric. The diiodobutane 3b and the diiododecane 3e are the outer borders of the metric window enabling Borromean interpenetration. In other words, the former compound is too short and the latter is too long to form (6,3) networks enabling Borromean interpenetration. Eight of the twelve systems showing this entanglement are formed by diiodoperfluorooctane 3d, namely its length seems better tailored to Borromean entanglement than diiodohexane 3c.
While the presence of fluorine atoms in tectons 3 does not contribute directly to the formation of Borromean systems, e.g., by forming specific attractive interactions or by determining the size of the cavities in the supramolecular anions, fluorine gives major indirect contributions to such a formation. First, the presence of fluorine enables compounds 3 to dependably function as rigid and rod-like tectons and thus to determine unvaryingly the spacing metric of halide anions. Second, it boosts the XB donor ability of iodine atoms and allows them to drive reliably the formation of supramolecular and halogen bonded anions. Strong and regularly linear XBs are formed. This interaction directionality translates the tectons’ geometry into a self-assembled architecture geometry, namely halide anions are typically pinned on the elongation of the diiodoperfluoroalkanes’ molecular axis. Third, the presence of fluorine atoms favors the formation of layers containing more than one supramolecular anionic network, a prerequisite for interpenetration. This is due to the fact that perfluoroalkyl derivatives have a strong tendency to segregate, and this tendency increases with the length of the fluoroalkyl chain.46 Interpenetration of the supramolecular anionic networks of a given layer is a way to increase segregation of their fluorous component while fulfilling the space filling requirements. Interestingly, thirteen cocrystals 1·2·3 contain interpenetrated supramolecular anions, one of them is formed by diiodobutane 3b, four by diiodohexane 3c, and eight by diiodooctane 3d. The relative frequency of interpenetration clearly parallels the relative tendency of diiodoperfluoroalkanes 3 to segregate47 and the indirect relevance of fluorine to Borromean interpenetration is confirmed.
Conclusions
Very few reports describe Borromean systems obtained by design,16 as most cases of this entanglement have been identified via topological analyses of structures in the Cambridge Structural Database.19 This highlights the great challenge related to the design and obtainment of this topology.Molecular interpenetration and entanglement are common phenomena in natural and human-made systems, spanning DNA and self-assembled coordination polymers.1,2,9–11 While the engineering of the benefits of these structural features in a system are still beyond routine approaches, the design and control of these features are particularly hot and timely in several fields of chemistry. We have reported here the XB driven self-assembly of a small library of nearly isostructural cocrystals containing supramolecular anionic networks endowed with Borromean interpenetration. XB has been confirmed as a reliable tool in the rational construction of entangled supramolecular assemblies with sophisticated topologies.48 The reported results contribute to the field of anion-templated assembly of interpenetrated and interlocked structures, a field that has strongly contributed to some recent progresses of supramolecular chemistry.29,44,49
Borromean networks have been obtained starting from all the four used cations and all the three used anions, but only the diiodoperfluorohexane 3c and -octane 3d. These results confirm the working hypotheses that some of the α,ω-diiodoperfluoroalkanes would afford regularly (6,3) networks with frames sized to enable for Borromean interpenetration and that this can occur independent from the used cation and anion.
Two key structural features of diiodoperfluoroalkanes 3 for the obtainment of the Borromean systems are: (a) the rigid and rod-like character of diiodoperfluoroalkyl derivatives 3, this character enabling 3c,d to space halide anions after a dependable and useful metric; (b) the tendency of perfluoroalkyl motifs to segregate from hydrocarbon motifs, this tendency favoring the formation of fluorous layers containing more than one anionic network and the Borromean entanglement of these networks. A third structural feature which also contributes to the library preparation is the spherical character of halide anions, which helps in adjusting the geometry of XBs around the halides, namely in tuning the degree of pyramidalization at the nodes of the networks in order to form honeycomb frames with a convenient size.
In conclusion, the change of cations and anions in cocrystals 1·2·3 substantially affects the bonding features, namely the energetic aspects, in the self-assembled systems while it causes minor modifications of their metrics. On the other hand, the change of the diiodoperfluoroalkane is the most influential element for the metric of cocrystals 1·2·3 and has a minor effect on cation–anion attraction and on XB, the two strong interactions in the cocrystals. Borromean interpenetration has been observed starting from all four cations, all three anions and only two of the five diiodoperfluoroalkanes. It thus seems that the metric features play a more influential role than energetic features in determining the topology of the tetra-component cocrystals described here. The applicability of this heuristic principle in the design and synthesis of other multi-component systems might be general and the usefulness of this principle in the self-assembly of crypt-111 (i.e., 4,10,15-trioxa-1,7-diazabicyclo[5.5.5]heptadecane), halide derivatives, and diiodoperfluoroalkanes is under assessment.
Acknowledgements
The authors would like to acknowledge the financial support of MIUR for grants PRIN 2010–2011 (projects no. 2010CX2TLM and no. 2010ERFKXL).Notes and references
-
(a) Y. Inokuma, T. Ukegawa, M. Hoshino and M. Fujita, Chem. Sci., 2016, 7, 3910–3913 Search PubMed
; (b) M. Frank, M. D. Johnstone and G. H. Clever, Chem.–Eur. J., 2016, 22, 14104–14125 Search PubMed
; (c) H. S. Scott, N. Ogiwara, K. J. Chen, D. G. Madden, T. Pham, K. Forrest, B. Space, S. Horike, J. J. Perry IV, S. Kitagawa and M. J. Zaworotko, Chem. Sci., 2016, 7, 5470–5476 Search PubMed
; (d) J. F. Ayme, J. E. Beves, C. J. Campbell and D. A. Leigh, Angew. Chem., Int. Ed., 2014, 53, 7823–7827 Search PubMed
; (e) S. Zhang, H.-J. Sun, A. D. Hughes, R.-O. Moussodia, A. Bertin, Y. Chen, D. J. Pochan, P. A. Heiney, M. L. Klein and V. Percec, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 9058–9063 Search PubMed
; (f) M. W. Hosseini, Acc. Chem. Res., 2005, 38, 313–323 Search PubMed
.
-
(a) R. Tang, S. Zhou, Z. Cheng, G. Yu, Q. Peng, H. Zeng, G. Guo, Q. Li and Z. Li, Chem. Sci., 2016 10.1039/c6sc02956f
; (b) H. J. Sun, S. Zhang and V. Percec, Chem. Soc. Rev., 2015, 44, 3900–3923 Search PubMed
; (c) S. Y. Zhang, W. Shi, P. Cheng and M. J. Zaworotko, J. Am. Chem. Soc., 2015, 137, 12203–12206 Search PubMed
; (d) Y. Horibe, J. Yang, Y. H. Cho, X. Luo, S. B. Kim, Y. S. Oh, F. T. Huang, T. Asada, M. Tanimura, D. Jeong and S. W. Cheong, J. Am. Chem. Soc., 2014, 136, 8368–8373 Search PubMed
; (e) S. Honda, T. Yamamoto and Y. Tezuka, J. Am. Chem. Soc., 2010, 132, 10251–10253 CrossRef CAS PubMed
; (f) E. R. Kay, D. A. Leigh and F. Zerbetto, Angew. Chem., Int. Ed., 2007, 46, 72–191 Search PubMed
.
-
(a) Y. C. Tan and H. C. Zeng, Chem. Commun., 2016, 52, 11591 RSC
; (b) B. Volosskiy, K. Niwa, Y. Chen, Z. Zhao, N. O. Weiss, X. Zhong, M. Ding, C. Lee, Y. Huang and X. Duan, ACS Nano, 2015, 9, 3044–3049 Search PubMed
; (c) K. M. Choi, H. M. Jeong, J. H. Park, Y.-B. Zhang, J. K. Kang and O. M. Yaghi, ACS Nano, 2014, 8, 7451–7457 CrossRef CAS PubMed
; (d) N. Stock and S. Biswas, Chem. Rev., 2012, 112, 933–969 Search PubMed
; (e) D. Zhao, D. J. Timmons, D. Yuan and H.-C. Zhou, Acc. Chem. Res., 2011, 44, 123–133 Search PubMed
; (f) O. K. Farha and J. T. Hupp, Acc. Chem. Res., 2010, 43, 1166–1175 CrossRef CAS PubMed
.
-
(a) S. Dalapati, E. Jin, M. Addicoat, T. Heine and D. Jiang, J. Am. Chem. Soc., 2016, 138, 5797–5800 Search PubMed
; (b) P. J. Waller, F. Gándara and O. M. Yaghi, Acc. Chem. Res., 2015, 48, 3053–3063 Search PubMed
.
-
(a) D. Alezi, Y. Belmabkhout, M. Suyetin, P. M. Bhatt, Ł. J. Weseliński, V. Solovyeva, K. Adil, I. Spanopoulos, P. N. Trikalitis, A.-H. Emwas and M. Eddaoudi, J. Am. Chem. Soc., 2015, 137, 13308–13318 Search PubMed
; (b) A. J. Graham, D. R. Allan, A. Muszkiewicz, C. A. Morrison and S. A. Moggach, Angew. Chem., 2011, 50, 11138–11141 Search PubMed
.
-
(a) D. J. Wales, J. Grand, V. P. Ting, R. D. Burke, K. J. Edler, C. R. Bowen, S. Mintova and A. D. Burrows, Chem. Soc. Rev., 2015, 44, 4290–4321 Search PubMed
; (b) J.-S. Qin, D.-Y. Du, W.-L. Li, J.-P. Zhang, S.-L. Li, Z.-M. Su, X.-L. Wang, Q. Xu, K.-Z. Shao and Y.-Q. Lan, Chem. Sci., 2012, 3, 2114–2118 Search PubMed
.
-
(a) K. Raatikainen and K. Rissanen, Chem. Sci., 2012, 3, 1235–1239 Search PubMed
; (b) R. Matsuda, T. Tsujino, H. Sato, Y. Kubota, K. Morishige, M.Takata and S. Kitagawa, Chem. Sci., 2010, 1, 315–321 Search PubMed
.
-
(a) Z. Zhang, Y. Chen, S. He, J. Zhang, X. Xu, Y. Yang, F. Nosheen, F. Saleem, W. He and X. Wang, Angew. Chem., Int. Ed., 2014, 53, 12517–12521 CAS
; (b) L. Meng, Q. Cheng, C. Kim, W.-Y. Gao, L. Wojtas, Y.-S. Chen, M. J. Zaworotko, X. P. Zhang and S. Ma, Angew. Chem., Int. Ed., 2012, 51, 10082–10085 Search PubMed
.
-
(a) T. Sawada, M. Yamagami, K. Ohara, K. Yamaguchi and M. Fujita, Angew. Chem., Int. Ed., 2016, 55, 4519–4522 Search PubMed
; (b) K. J. Hartlieb, A. K. Blackburn, S. T. Schneebeli, R. S. Forgan, A. A. Sarjeant, C. L. Stern, D. Cao and J. F. Stoddart, Chem. Sci., 2014, 5, 90–100 Search PubMed
; (c) N. H. Evans and P. D. Beer, Chem. Soc. Rev., 2014, 43, 4658–4683 Search PubMed
; (d) R. Hovorka, G. Meyer-Eppler, T. Piehler, S. Hytteballe, M. Engeser, F. Topic, K. Rissanen and A. Lützen, Chem.–Eur. J., 2014, 20, 13253–13258 Search PubMed
.
-
(a) A. Vidonne, T. Kosikova and D. Philp, Chem. Sci., 2016, 7, 2592–2603 Search PubMed
; (b) J. D. Crowley, S. M. Goldup, A.-L. Lee, D. A. Leigh and R. T. McBurney, Chem. Soc. Rev., 2009, 38, 1530–1541 Search PubMed
; (c) J. P. Sauvage and C. D. Buchecker, Molecular Catenanes, Rotaxanes and Knots: A Journey Through the World of Molecular Topology, Wiley-VCH, Weinheim, 1999 Search PubMed
.
-
(a) K. E. Horner, M. A. Miller, J. W. Steed and P. M. Sutcliffe, Chem. Soc. Rev., 2016 10.1039/c6cs00448b
; (b) V. Marcos, A. J. Stephens, J. Jararnillo-Garcia, A. L. Nussbaumer, S. L. Woltering, A. Valero, J.-F. Lemonnier, I. J. V. Yrezabal and D. A. Leigh, Science, 2016, 352, 1555–1559 Search PubMed
; (c) J. F. Ayme, J. E. Beves, C. J. Campbell and D. A. Leigh, Chem. Soc. Rev., 2013, 42, 1700–1712 RSC
.
-
(a) C. D. Pentecost, N. Tangchaivang, S. J. Cantrill, K. S. Chichak, A. J. Peters and J. Fraser Stoddart, J. Chem. Educ., 2007, 84, 855–859 CrossRef CAS
; (b) C. A. Schalley, Angew. Chem., Int. Ed., 2004, 43, 4399–4401 Search PubMed
.
- R. S. Forgan, J. P. Sauvage and J. F. Stoddart, Chem. Rev., 2011, 111, 5434–5464 Search PubMed
.
- G. Natarajan, A. Mathew, Y. Negishi, R. L. Whetten and T. Pradeep, J. Phys. Chem. C, 2015, 119, 27768–27785 Search PubMed
.
-
(a) C. Mao, W. Sun and N. C. Seeman, Nature, 1997, 386, 137–138 Search PubMed
; (b) N. C. Seeman, Acc. Chem. Res., 1997, 30, 357–363 Search PubMed
.
-
(a) C. R. Yates, D. Benitez, S. I. Khan and J. F. Stoddart, Org. Lett., 2007, 9, 2433–2436 Search PubMed
; (b) A. J. Peters, K. S. Chichak, S. J. Cantrill and J. F. Stoddart, Chem. Commun., 2005, 3394–3396 Search PubMed
; (c) K. S. Chichak, A. J. Peters, S. J. Cantrill and J. Fraser Stoddart, J. Org. Chem., 2005, 70, 7956–7962 Search PubMed
; (d) S. J. Cantrill, K. S. Chichak, A. J. Peters and J. F. Stoddart, Acc. Chem. Res., 2005, 38, 1–9 Search PubMed
; (e) K. S. Chichak, S. J. Cantrill, A. R. Pease, S. H. Chiu, G. W. V. Cave, J. L. Atwood and J. F. Stoddart, Science, 2004, 304, 1308–1312 CrossRef CAS PubMed
.
- Q. X. Yao, X. H Jin, Z. F. Ju, H. X. Zhang and J. Zhang, CrystEngComm, 2009, 11, 1502–1504 Search PubMed
.
-
(a) X. L. Zhang, C. P. Guo, Q. Y. Yang, W. Wang, W. S. Liu, B. S. Kang and C. Y. Su, Chem. Commun., 2007, 4242–4244 Search PubMed
; (b) X. Q. Lu, M. Pan, J. R. He, Y. P. Cai, B. S. Kang and C. Y. Su, CrystEngComm, 2006, 8, 827–829 Search PubMed
.
-
(a) L. Carlucci, G. Ciani, D. M. Proserpio, T. G. Mitina and V. A. Blatov, Chem. Rev., 2014, 114, 7557–7580 Search PubMed
; (b) L. Carlucci, G. Ciani and D. M. Proserpio, Coord. Chem. Rev., 2003, 246, 247–289 Search PubMed
.
- M. Pan and C. Y. Su, CrystEngComm, 2014, 16, 7847–7859 Search PubMed
.
-
(a) N. N. Adarsh and P. Dastidar, Cryst. Growth Des., 2010, 10, 483–487 Search PubMed
; (b) Y. B. Men, J. Sun, Z. T. Huang and Q. Y. Zheng, Angew. Chem., Int. Ed., 2009, 48, 2873–2876 CrossRef CAS PubMed
.
- L. Dobrzanska, H. G. Raubenheimer and L. J. Barbour, Chem. Commun., 2005, 5050–5052 Search PubMed
.
- M. P. Suh, H. J. Choi, S. M. So and B. M. Kim, Inorg. Chem., 2003, 42, 676–678 Search PubMed
.
-
(a) G. Cavallo, P. Metrangolo, R. Milani, T. Pilati, A. Priimagi, G. Resnati and G. Terraneo, Chem. Rev., 2016, 116, 2478–2601 Search PubMed
; (b) G. Berger, J. Soubhye and F. Meyer, Polym. Chem., 2015, 6, 3559–3580 RSC
; (c) C. Robertson, R. N. Perutz, L. Brammer and C. A. Hunter, Chem. Sci., 2014, 5, 4179–4183 RSC
; (d) G. R. Desiraju, P. S. Ho, L. Kloo, A. C. Legon, R. Marquardt, P. Metrangolo, P. Politzer, G. Resnati and K. Rissanen, Pure Appl. Chem., 2013, 85, 1711–1713 Search PubMed
.
-
(a) C. B. Aakeröy, T. K. Wijethunga, J. Benton and J. Desper, Chem. Commun., 2015, 51, 2425–2428 RSC
; (b) P. Metrangolo, G. Resnati, T. Pilati and S. Biella, in Halogen Bonding. Fundamentals and Applications, ed. P. Metrangolo and G. Resnati, Springer-Verlag, Berlin, Heidelberg, 2008, vol. 126, pp. 105–136 Search PubMed
.
-
(a) C. C. Robertson, R. N. Perutz, L. Brammer and C. A. Hunter, Chem. Sci., 2014, 5, 4179–4183 Search PubMed
; (b) P. Metrangolo, F. Meyer, T. Pilati, G. Resnati and G. Terraneo, Angew. Chem., Int. Ed., 2008, 47, 6114–6127 Search PubMed
; (c) P. Metrangolo and G. Resnati, Chem.–Eur. J., 2001, 7, 2511–2519 Search PubMed
.
-
(a) J. Marti-Rujas, L. Meazza, G. K. Lim, G. Terraneo, T. Pilati, K. D. M. Harris, P. Metrangolo and G. Resnati, Angew. Chem., Int. Ed., 2013, 52, 13444–13448 Search PubMed
; (b) C. B. Aakeröy, M. Baldrighi, J. Desper, P. Metrangolo and G. Resnati, Chem.–Eur. J., 2013, 19, 16240–16247 Search PubMed
; (c) P. Metrangolo, T. Pilati, G. Terraneo, S. Biella and G. Resnati, CrystEngComm, 2009, 11, 1187–1196 Search PubMed
.
- S. V. Lindeman, J. Hecht and J. K. Kochi, J. Am. Chem. Soc., 2003, 125, 11597–11606 Search PubMed
.
- N. H. Evans, H. Rahman, A. V. Leontiev, N. D. Greenham, G. A. Orlowski, Q. Zeng, R. M. J. Jacobs, C. J. Serpell, N. L. Kilah, J. J. Davis and P. D. Beer, Chem. Sci., 2012, 3, 1080–1089 Search PubMed
.
-
(a) R. Liantonio, P. Metrangolo, F. Meyer, T. Pilati, W. Navarrini and G. Resnati, Chem. Commun., 2006, 1819–1821 Search PubMed
; (b) R. Liantonio, P. Metrangolo, T. Pilati and G. Resnati, Cryst. Growth Des., 2003, 3, 355–361 Search PubMed
.
-
(a) P. Metrangolo, T. Pilati, G. Resnati and A. Stevenazzi, Chem. Commun., 2004, 1492–1493 Search PubMed
; (b) G. Gattuso, A. Pappalardo, M. F. Parisi, I. Pisagatti, F. Crea, R. Liantonio, P. Metrangolo, W. Navarrini, G. Resnati, T. Pilati and S. Pappalardo, Tetrahedron, 2007, 63, 4951–4958 Search PubMed
.
-
(a) P. Cardillo, E. Corradi, A. Lunghi, S. V. Meille, M. T. Messina, P. Metrangolo and G. Resnati, Tetrahedron, 2000, 56, 5535–5550 Search PubMed
; (b) M. T. Messina, P. Metrangolo, W. Navarrini, S. Radice, G. Resnati and G. Zerbi, J. Mol. Struct., 2000, 524, 87–94 Search PubMed
.
- G. Cavallo, P. Metrangolo, T. Pilati, G. Resnati, M. Ursini and G. Terraneo, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2013, 69, m387–m388 Search PubMed
.
-
(a) Y.-C. Wu, P. Leowanawat, H.-J. Sun, B. E. Partridge, M. Peterca, R. Graf, H. W. Spiess, X. Zeng, G. Ungar, C.-S. Hsu, P. A. Heiney and V. Percec, J. Am. Chem. Soc., 2015, 137, 807–819 CrossRef CAS PubMed
; (b) H. Takezawa, T. Murase, G. Resnati, P. Metrangolo and M. Fujita, J. Am. Chem. Soc., 2014, 136, 1786–1788 CrossRef CAS PubMed
.
- K. B. James, Acc. Chem. Res., 2005, 38, 671–678 Search PubMed
.
- The normalized contact Nc is defined as the ratio DXY/(rX + rY), where DXY is the experimental distance between the halogen bonded iodine atoms X and halide anions Y and rX and rY are the van der Waals radius for iodine and the Pauling ionic radius of the halide anion Y, respectively. Nc is a useful indicator of the relative interaction strength, more useful than the XB distance itself, because it allows distances between different interacting sites to be compared.
- R. D. Walsh, J. M. Smith, T. W. Hanks and W. T. Pennington, Cryst. Growth Des., 2012, 12, 2759–2768 Search PubMed
.
-
(a) R. Tepper, B. Schulze, M. Jäger, C. Friebe, D. H. Scharf, H. Görls and U. S. Schubert, J. Org. Chem., 2015, 80, 3139–3150 Search PubMed
; (b) M. Cametti, K. Raatikainen, P. Metrangolo, T. Pilati, G. Terraneo and G. Resnati, Org. Biomol. Chem., 2012, 10, 1329–1333 Search PubMed
; (c) M. G. Sarwar, B. Dragisic, S. Sagoo and M. S. Taylor, Angew. Chem., Int. Ed., 2010, 49, 1674–1677 Search PubMed
.
- It is interesting to observe that smaller cations seem more prone than larger cations to afford samples of cocrystals 1·2·3 suitable for single crystal X-ray analyses. The mean volumes of Na+⊂crypt-222, K+⊂crypt-222, Rb+⊂crypt-222, and NH4+⊂crypt-222 in 1·2·3 cocrystals (measured via the volumes of polyhedra defined by the eight heteroatoms of crypt-222 1 in cocrystals 1·2·3) are 24.404, 28.547, 32.494, and 34.469 Å3, respectively. A correlation clearly exists between the volume of the supramolecular cation cat+⊂crypt-222 and the volume of the non-cryptated cation afforded by salts 2. When using 3a–d, the same set of cocrystals was tried for all cations, but sodium, potassium, ammonium, and rubidium afforded ten, seven, seven, and five single crystalline adducts, respectively.
-
Supramolecular Chemistry, ed. J. W. Steed and J. L. Atwood, Wiley, Chichester, 2nd edn, 2009, pp. 105–222 Search PubMed
.
-
(a) P. A. Gale and T. Gunnlaugsson, Chem. Soc. Rev., 2010, 39, 3595–3596 Search PubMed
; (b) Anion Receptor Chemistry, ed. J. L. Sessler, P. A. Gale and W. S. Cho, Royal Society of Chemistry, Cambridge, UK, 2006 Search PubMed
; (c) Special issue: Anion Coordination Chemistry II, ed. P. A. Gale, Coord. Chem. Rev., 2006, vol. 250, pp. 2917–3244 Search PubMed
.
-
(a) N. G. White and M. J. MacLachlan, Chem. Sci., 2015, 6, 6245–6249 Search PubMed
; (b) B. Hasenknopf, J. M. Lehn, B. O. Kneisel, G. Baum and D. Fenske, Angew. Chem., Int. Ed. Engl., 1996, 35, 1838–1840 Search PubMed
.
-
(a) T. U. Connell, S. Sandanayake, G. N. Khairallah, J. M. White, R. A. J. O'Hair, P. S. Donnelly and S. J. Williams, Dalton Trans., 2013, 42, 4903–4907 Search PubMed
; (b) M.-O. M. Piepenbrock, G. O. Lloyd, N. Clarke and J. W. Steed, Chem. Rev., 2010, 110, 1960–2004 Search PubMed
; (c) P. Diaz, D. Michael, P. Mingos, R. Vilar, A. J. P. White and D. J. Williams, Inorg. Chem., 2004, 43, 7597–7604 Search PubMed
; (d) D. Rais, J. Yau, D. Michael, P. Mingos, R. Vilar, A. J. P. White and D. J. Williams, Angew. Chem., Int. Ed., 2001, 40, 3464–3467 Search PubMed
.
- For selective halide anions templated synthesis of catenane and rotaxanes under XB control see:
(a) J. M. Mercurio, R. C. Knighton, J. Cookson and P. D. Beer, Chem.–Eur. J., 2014, 20, 11740–11749 CrossRef CAS PubMed
; (b) M. J. Langton, S. W. Robinson, I. Marques, V. Félix and P. D. Beer, Nat. Chem., 2014, 6, 1039–1043 Search PubMed
; (c) A. Caballero, F. Zapata, N. G. White, P. J. Costa, V. Fèlix and P. D. Beer, Angew. Chem., Int. Ed., 2012, 51, 1876–1880 CrossRef CAS PubMed
.
- It is also interesting to observe that the heavier, namely more polarizable, the halide anion is, the more likely the obtainment of Borromean interpenetration becomes. Eight, nine, and fourteen single cocrystals 1·2·3 were obtained starting from chloride, bromide, and iodide anions, respectively, and one fourth, one third, and a half of these cocrystals present Borromean interpenetration, respectively.
-
(a) V. Ojogun, B. L. Knutson, S. Vyas and H. J. Lehmler, J. Fluorine Chem., 2010, 131, 784–790 CrossRef CAS PubMed
; (b) E. D. Wolf, P. Ruelle, J. V. D Broeke, B. J. Deelman and G. van Koten, J. Phys. Chem. B, 2004, 108, 1458–1466 Search PubMed
; (c) L. E. Kiss, I. Kövesdi and J. Rábai, J. Fluorine Chem., 2001, 108, 95–109 Search PubMed
.
- Four, eleven, and eleven cocrystal 1·2·3 have been formed by 3b, 3c, and 3d, respectively. The probability to form interpenetrated anionic networks is thus 25% for 3b, 36% for 3c, and 73% for 3d.
-
(a) M. C. Pfrunder, A. S. Micallef, L. Rintoul, D. P. Arnold, K. J. P. Davy and J. McMurtrie, Cryst. Growth Des., 2012, 12, 714–724 CrossRef CAS
; (b) P. Metrangolo, F. Meyer, T. Pilati, D. M. Proserpio and G. Resnati, Chem.–Eur. J., 2007, 13, 5765–5772 Search PubMed
.
- P. D. Beer, M. R. Sambrook and D. Curiel, Chem. Commun., 2006, 2105–2117 Search PubMed
.
Footnotes |
| † Electronic supplementary information (ESI) available: Materials and methods, NMR, DSC, powder and single crystal X-ray data. CCDC 1505909–1505934. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c6sc04478f |
| ‡ Present address: Laboratory of Biopolymers and Supramolecular Nanomaterials, Université Libre de Bruxelles, Boulevard du Triomphe, 1050 Bruxelles, Belgium. |
| This journal is © The Royal Society of Chemistry 2017 |