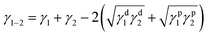Open Access Article
Open Access ArticleExcellent mechanical performance and enhanced dielectric properties of OBC/SiO2 elastomeric nanocomposites: effect of dispersion of the SiO2 nanoparticles†
Xing Zhao,
Lu Bai*,
Rui-Ying Bao,
Zheng-Ying Liu,
Ming-Bo Yang and
Wei Yang
and
Wei Yang *
*
College of Polymer Science and Engineering, Sichuan University, State Key Laboratory of Polymer Materials Engineering, Chengdu, 610065, Sichuan, China. E-mail: slulu_1116@163.com; weiyang@scu.edu.cn; Fax: +86 28 8546 0130; Tel: +86 28 8546 0130
First published on 29th September 2017
Abstract
Two kinds of fumed SiO2 nanoparticles with the same average diameter but distinct surface characteristics (hydrophilic A200 and hydrophobic R974) were incorporated into an ethylene-α-olefin block copolymer (OBC) to prepare high-performance thermoplastic elastomeric nanocomposites via simple melt mixing. Hydrophilic A200 exhibits a particular chain-like distribution while hydrophobic R974 shows a homogenous dispersion in the nanocomposites. The rheological percolation threshold of OBC/A200 nanocomposites was much lower than that of OBC/R974 nanocomposites, showing a more developed nanoparticle network in OBC/A200 nanocomposites. Thermodynamic analysis revealed that the particular chain-like distribution of A200 and more developed network structure are due to the selective localization of hydrophilic A200 in the melt. The reinforcement effect of hydrophilic A200 in OBC/A200 nanocomposites is always higher than that of hydrophobic R974 in OBC/R974 nanocomposites at the same filler loading, and even better, the increments in the tensile modulus of OBC/A200 nanocomposites are almost four times higher than that of OBC/R974 nanocomposites at the same silica loading. Besides, the dielectric permittivity of the OBC/A200 composite at low frequency was also higher than that of the OBC/R974 composite with the same loading of filler at the same frequency. These results provide guidance for the preparation of high-performance elastomeric nanocomposites with both excellent mechanical performance and enhanced dielectric properties.
Introduction
In recent years, nanofiller modified thermoplastic elastomers have emerged as a novel class of nanocomposites and have attracted considerable interest. Especially, functional thermoplastic elastomer nanocomposites with high conductivity, dielectric properties, flame-retardant performance and so on, have achieved significant progress.1–8 The matrices for thermoplastic elastomer nanocomposites include styrenic block copolymers, thermoplastic polyolefins, thermoplastic polyurethanes and thermoplastic copolyesters, etc.7–10 These thermoplastic elastomers generally show both good processability and high elasticity which impart a favorable application prospect to their nanocomposites.High-performance thermoplastic elastomer nanocomposites have been developed with the addition of a variety of inorganic fillers such as silica nanoparticles (NPs), graphene, carbon black, carbon nanotubes, ceramics and other nanomaterials.10–16 However, these nanomaterials are generally poorly dispersed within the matrix in the form of aggregates. It has been widely accepted that a homogeneous and uniform dispersion of NPs is one of the keys to achieve excellent reinforcement in physical and functional performance of thermoplastic elastomer nanocomposites.17,18 Many efforts have been devoted to improve the dispersion of nanomaterials by mixing methods, surface modification of nanomaterials and other methods.19–22
Fumed silica NP was one of the most widely used nano fillers for nanocomposites because of the high specific surface area, high thermal stability and high mechanical strength.23–28 Abundant silanols exist on the surface of silica NPs,29 which lead to the dispersion of silica NPs in the form of aggregates in the matrix due to the powerful NP–NP interaction and hydrogen bonding interactions. Thus, silica NPs are generally modified with different functional groups in order to achieve uniform dispersion by increasing NP–matrix interaction and decreasing NP–NP interaction.30,31 Except for reinforcement for thermoplastic elastomers, silica NPs are also utilized to fabricate dielectric composite materials. It has been reported that the addition of silica NPs in polymer can obtain high-k polymer composites which provide an ideal solution to combine the dielectric property of fillers and low-temperature process-ability of polymer matrix.32 However, high filler loadings reduces processability of the composites and even leads to a decrease in dielectric permittivity because NPs trend to agglomerate at high filler loading. In this regard, homogenous dispersion of silica NPs is still an important issue for preparation of high-k polymer composites.
Recently, a novel class of ethylene-α-olefin copolymers, olefin block copolymers (OBCs), which consist of alternating hard segments (crystallizable ethylene-α-olefin blocks with extremely low levels α-olefin comonomer) and soft segments (amorphous ethylene-α-olefin blocks with high levels of α-olefin comonomer) have been synthesized by the chain shuttling technology.33–35 Based on this technology, the produced OBCs feature excellent elastomeric property, good processability, outstanding heat resistance and high thermal stability. Moreover, OBCs exhibit better crystallization ability, higher crystallization temperature (Tc) and melting temperature (Tm), compared with ethylene-α-olefin random copolymers (ORCs, one of the most widely used elastomeric polymers), resulting in a significantly promising applications at relative higher temperatures.36,37 With these advantages, OBCs are chosen as the matrix to prepare multi-functional thermoplastic elastomer nanocomposites.37–39 In our previous work, the mechanical properties of OBC were enhanced by introduction of multi-walled carbon nanotubes (MWCNTs).37 An extremely uniform dispersion of MWCNTs in OBC through melt mixing was achieved due to the selective localization of MWCNTs caused by lower affinity towards the hard blocks of OBC. As the result, the mechanical properties of OBC were evidently improved.
In the present study, to impart enhanced mechanical and dielectric performances of OBC-based nanocomposites, two kinds of fumed silica NPs with the same average diameter but distinct surface characteristics (hydrophilic and hydrophobic) were incorporated into OBC via simple melt mixing. Scanning electron microscope (SEM) and transmission electron microscope (TEM) were carried out to characterize the different dispersion states of different silica NPs in the solid state, and rheological measurements along with thermodynamic analysis were performed to reveal the different dispersion states of silica NPs in the molten state. A chain-like dispersion of hydrophilic silica nanoparticles (A200) was achieved since the A200 NPs exhibit different affinity towards the different blocks of OBC, while hydrophobic R974 NPs dispersed randomly in OBC. As a result, the two series of OBC-based nanocomposites exhibit distinctly different mechanical and dielectric properties.
Experimental
Materials
OBC (Infuse 9500), synthesized by chain shuttling polymerization technology, consisting of nearly amorphous soft segments and crystallizable hard segments, with a total octene content of 38%, was purchased from Dow Chemical Co. (Midland, MI, USA). The weight-average molecular mass (Mw), polydispersity (Mw/Mn) and density of OBC are 82![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 g mol−1, 2.3 and 0.878 g cm−3, respectively. Two kinds of fumed silica NPs produced by Evonik Degussa, with distinct surface characteristics but the same average diameter of 12 nm were used. One is hydrophilic silica NPs, A200, with a hydroxyl density of 2.5 –OH per nm2 and the other is hydrophobic silica NPs, R974, synthesized by the replacement of methyl for half of hydroxyl present on surface of A200, namely, with a methyl density of 1.25 –CH3 per nm2.
600 g mol−1, 2.3 and 0.878 g cm−3, respectively. Two kinds of fumed silica NPs produced by Evonik Degussa, with distinct surface characteristics but the same average diameter of 12 nm were used. One is hydrophilic silica NPs, A200, with a hydroxyl density of 2.5 –OH per nm2 and the other is hydrophobic silica NPs, R974, synthesized by the replacement of methyl for half of hydroxyl present on surface of A200, namely, with a methyl density of 1.25 –CH3 per nm2.
Sample preparation
OBC-based nanocomposites filled with R974 and A200 respectively, were prepared by simple melt mixing in the mixer of a torque rheometer (XSS-300, Shanghai Kechuang Rubber Plastics Machinery Set Ltd, Shanghai, PR China) with a rotational speed of 50 rpm at 150 °C for 5 min. The resulted samples were designated as OBC–R-x and OBC–A-x respectively, where R and A refer to the two kinds of fumed SiO2 NPs, and x stands for the volume fraction of silica in the composites. After compounding, all the composites were compression molded into sheets with a thickness of about 1.2 mm at 150 °C for 3 min under a pressure of 10 MPa.Characterization
Results and discussion
Dispersion of silica nanoparticles in OBC/SiO2 nanocomposites
The dispersion states of both SiO2 NPs in OBC matrix were observed by SEM and TEM. The SEM images of the nanocomposites with relatively low (5 vol%) and high (15 vol%) contents of SiO2 are shown in Fig. 1a–f. In the whole field of vision, no large aggregates can be found in neither OBC/A200 nor OBC/R974 nanocomposites. A200 SiO2 NPs show a greater degree of connection in OBC/A200 nanocomposites as indicated in Fig. 1a, c and e, while single R974 NP and their small aggregates are uniformly dispersed in the matrix as shown in Fig. 1b, d and f because of the poor NP–NP interactions.40 The dispersion was also examined by TEM. Fig. 1g confirms that a chain-like network structure was formed in OBC/A200 nanocomposites, while R974 NPs were irregularly dispersed in OBC/R974 nanocomposites as shown in Fig. 1h. The reason for the chain-like dispersion in OBC/A200 will be analyzed in detail in the following section. | ||
| Fig. 1 Typical SEM micrographs of nanocomposites (a) OBC–A-5, (b) OBC–R-5, (c and e) OBC–A-15, (d and f) OBC–R-15, and typical TEM images of nanocomposites (g) OBC–A-5, (h) OBC–R-5. | ||
Dielectric properties
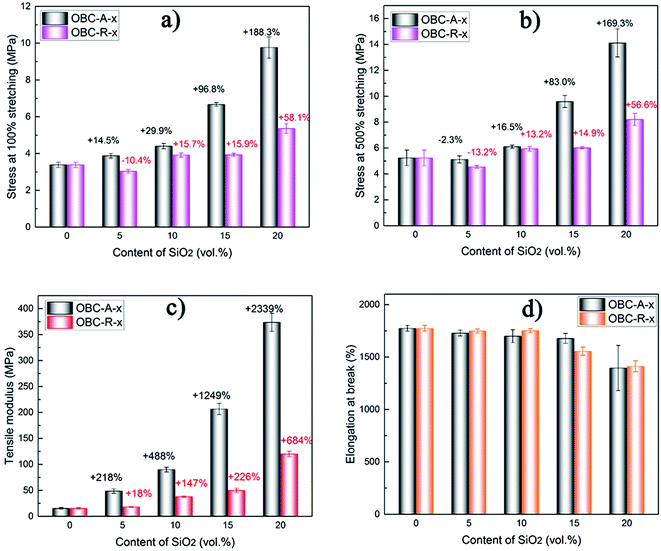
Fig. 2 depicts the dielectric permittivity and loss tangent of OBC/A200 and OBC/R974 nanocomposites with different content of SiO2 as a function of frequency from 100 Hz to 107 Hz. In the low frequency ranges, the dielectric permittivity of OBC/A200 nanocomposites decreased sharply with the increasing of frequency owing to remarkable dielectric relaxation from 100 to 103 Hz. In the high frequency ranges, dielectric permittivity of OBC/A200 nanocomposites gradually become stable, because the dipoles do not have time to align in the direction of applied external field.41 The dielectric permittivity of OBC/R974 nanocomposites shows a substantial independence of frequencies. The dielectric loss of both OBC/A200 and OBC/R974 nanocomposites is quite low, always lower than 1 in the entire range of frequencies even when the content of SiO2 is as high as 20 vol%.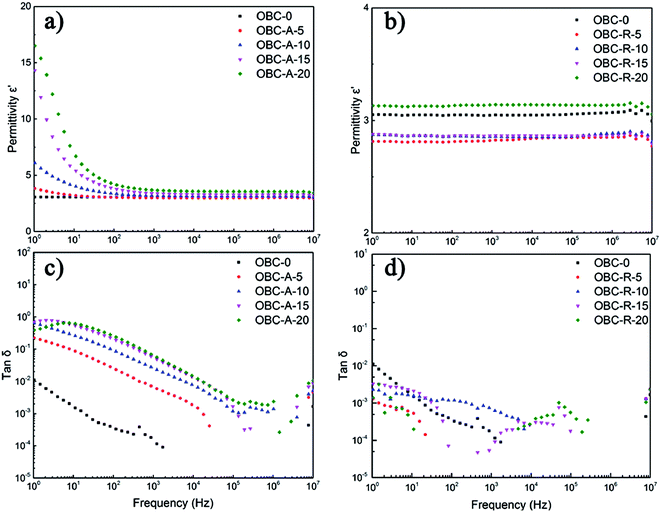 | ||
| Fig. 2 Frequency responses of (a and b) the dielectric constant, (c and d) dielectric loss of OBC/A200 and OBC/R974 nanocomposites, respectively. | ||
The dielectric permittivity and loss tangent at 1 Hz of OBC/A200 and OBC/R974 nanocomposites are summarized as a function of SiO2 content in Fig. 3. The dielectric permittivity of OBC/A200 nanocomposites continuously increased from 3.1 to 16.5 with increasing SiO2 content. However, the dielectric permittivity for OBC/R974 nanocomposites shows very slight change with the increasing of SiO2 content. The dielectric loss tangent of all OBC/A200 nanocomposites is higher than that of pure OBC, while the dielectric loss tangent of all OBC/R974 nanocomposites shift to a lower value compared with pure OBC as shown in Fig. 3b.
 | ||
| Fig. 3 (a) Dielectric permittivity and (b) dielectric loss for OBC/R974 and OBC/A200 nanocomposites at 1 Hz. | ||
The different performances in dielectric properties for two series of nanocomposites can be ascribed to the different surface characteristics and the distinct dispersion states of SiO2 nanoparticles. The surface of A200 NPs possesses more polar hydroxyl groups, resulting in effective orientation polarization within the nanocomposites due to the inherent dipolar nature of hydroxyl groups, which directly results in an obvious increase in dielectric permittivity for OBC/A200 nanocomposites at low frequency due to the accumulation of mobile charges at the interface between samples and electrodes. However, the polarization of hydroxyls on surface of R974 NPs was weaken by the numerous methyl surrounding hydroxyls. The addition of silica generally leads to improved dielectric permittivity. However, the groups on the surface of nanoparticles increase free volume at the interface between nanoparticles and matrix, which reduces the dielectric permittivity of the composite.42 It is also probable reason here. The continuous chain-like distribution of hydrophilic SiO2 (A200) in the nanocomposites resulting in easier shift of charge carriers to dissipate energy, which would be the main reason for the increase of dielectric loss after the addition of SiO2 (A200). In this regard, compared with pure OBC, the dielectric loss of OBC/R974 nanocomposites decreases owing to the irregularly-dispersed state of hydrophobic SiO2 NPs (R974) in OBC/R974 nanocomposites. The weak connection between R974 NPs generates little polarization loss.
Rheological behaviors
Dynamical rheological measurements were utilized widely to characterize the filler network and the phase morphology in polymer composites. It has been admitted that particle-filled polymers can manifest a liquid–solid transition because of the existence of filler network structure within the composites.43,44 The large-scale relaxation of polymer chains in the composites is prominently restricted by the presence of network structure.45,46 Thus, rheological properties can reflect the dispersion states of NPs in composites. The storage modulus (G′) and loss tangent (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ, defined as the ratio of storage modulus to loss modulus) as a function of frequency measured at 150 °C are shown in Fig. 4. It is obvious that the two series of nanocomposites show significantly different rheological properties and the differences can only stem from the different dispersion states of SiO2 NPs with distinct surface characteristics. Fig. 4a shows that with increasing loading of SiO2 NPs, the storage modulus of both series of nanocomposites increase gradually, resulting from the restriction of polymer chain relaxation in the presence of rigid particles and formation of inter-connected SiO2 network. When the content of SiO2 is as high as 10 vol%, the frequency-dependent of G′ in low-frequency region is significantly depressed. It should be noted that the storage modulus of OBC/A200 nanocomposites is always higher than that of OBC/R974 nanocomposites at the same loading level of SiO2 NPs and the same frequency. The emergence of plateau in the low frequency region of storage modulus vs. frequency curve indicates the formation of developed interconnected SiO2 network structure. Typically, the slopes in the low frequency region of lg
δ, defined as the ratio of storage modulus to loss modulus) as a function of frequency measured at 150 °C are shown in Fig. 4. It is obvious that the two series of nanocomposites show significantly different rheological properties and the differences can only stem from the different dispersion states of SiO2 NPs with distinct surface characteristics. Fig. 4a shows that with increasing loading of SiO2 NPs, the storage modulus of both series of nanocomposites increase gradually, resulting from the restriction of polymer chain relaxation in the presence of rigid particles and formation of inter-connected SiO2 network. When the content of SiO2 is as high as 10 vol%, the frequency-dependent of G′ in low-frequency region is significantly depressed. It should be noted that the storage modulus of OBC/A200 nanocomposites is always higher than that of OBC/R974 nanocomposites at the same loading level of SiO2 NPs and the same frequency. The emergence of plateau in the low frequency region of storage modulus vs. frequency curve indicates the formation of developed interconnected SiO2 network structure. Typically, the slopes in the low frequency region of lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) G′ ∼ lg
G′ ∼ lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ω curve of OBC–A-5 nanocomposite is 0.157, tremendously lower than that of lg
ω curve of OBC–A-5 nanocomposite is 0.157, tremendously lower than that of lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) G′ ∼ lg
G′ ∼ lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ω curve of OBC–R-5 (0.582), confirming that the formation of developed network structure containing interconnected hydrophilic SiO2 NPs in the composites. These results are perfectly consistent with SEM observation as well as the above discussed dielectric properties.
ω curve of OBC–R-5 (0.582), confirming that the formation of developed network structure containing interconnected hydrophilic SiO2 NPs in the composites. These results are perfectly consistent with SEM observation as well as the above discussed dielectric properties.
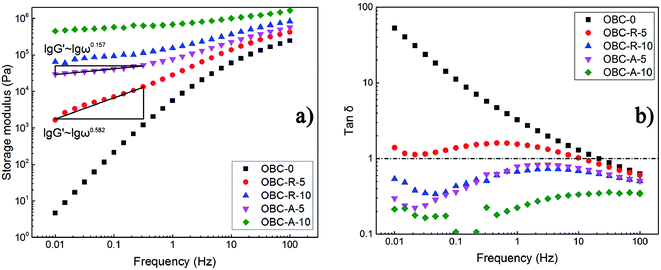 | ||
| Fig. 4 Logarithmic plots of (a) the storage modulus and (b) the loss tangent as a function of frequency. | ||
Loss tangent (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) also characterizes the viscoelastic behavior of materials. In general, a higher value of tan
δ) also characterizes the viscoelastic behavior of materials. In general, a higher value of tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ indicates larger viscosity of the material and a lower value of tan
δ indicates larger viscosity of the material and a lower value of tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ implies that the material exhibits greater elasticity and less loss of energy under the dynamic deformation. Fig. 4b demonstrates the loss tangent (tan
δ implies that the material exhibits greater elasticity and less loss of energy under the dynamic deformation. Fig. 4b demonstrates the loss tangent (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) of OBC/A200 and OBC/R974 nanocomposites with different content of SiO2 as a function of frequency. Obviously, the tan
δ) of OBC/A200 and OBC/R974 nanocomposites with different content of SiO2 as a function of frequency. Obviously, the tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ of OBC–A-5 is much lower than 1, whereas that of OBC–R-5 is higher than 1, suggesting a significantly solid-like behavior of OBC/A200 nanocomposites. This result also indicates that a developed interconnected network structure was formed at a low loading of hydrophilic SiO2 (A200) in the nanocomposites, while the hydrophobic SiO2 (R974) in OBC/R974 nanocomposites presents a separately-dispersed state as shown in Fig. 1.
δ of OBC–A-5 is much lower than 1, whereas that of OBC–R-5 is higher than 1, suggesting a significantly solid-like behavior of OBC/A200 nanocomposites. This result also indicates that a developed interconnected network structure was formed at a low loading of hydrophilic SiO2 (A200) in the nanocomposites, while the hydrophobic SiO2 (R974) in OBC/R974 nanocomposites presents a separately-dispersed state as shown in Fig. 1.
Thermodynamics analysis
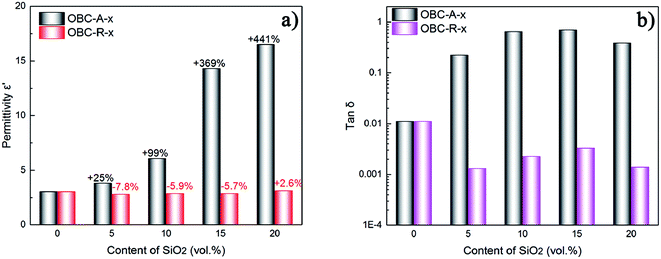
Thermodynamics governs the distribution of the filler in OBC at the equilibrium state and classical thermodynamics can be used to predict the preferential distribution of fillers in OBC.37 As is known, different from ORC mainly containing random ethylene-α-octene copolymer, OBC consists of alternating hard segments (polyethylene-rich domains) and soft segments (ethylene-α-octene-rich domains).47 These two kinds of domains present different surface energy (γ), due to the different chain sequences in the domains. Thus, the affinity between SiO2 NPs and different domains is possibly the foremost reason for the peculiar chained distribution of hydrophilic SiO2 in OBC/A200 nanocomposites. Therefore, classical thermodynamics were used to calculate the affinity of different SiO2 NPs to different domains of OBC.The estimation of the interfacial tension between two components can be calculated from surface tension using the well-known equation of Wu:48
Because of the long polyethylene segments and random ethylene-α-octene segments of OBC, we describe the surface tension of polyethylene-rich domains and ethylene-α-octene-rich domains by that of polyethylene and ethylene-octene copolymers (ORCs), respectively. In previous work, it has been proved that the content of octene has little effect on the surface tension of ORCs, thus the use of surface tension of ORC with 39% octene content to describe the surface tension of ethylene-α-octene-rich domains of OBC with 38% octene content is comparatively reasonable.37 The surface tension values of the materials at 190 °C (higher than the melting point of OBC) were used. The values of surface tension, as well as its dispersion components and polar components are listed in Table 1. The interfacial tension between different SiO2 NPs and different rich domains of OBC was calculated using the geometric mean equation and the values of all possible pairs are listed in Table 2.
| Materials | Total (γ) | Surface tension (mN m−1) | |
|---|---|---|---|
| Dispersion component (γd) | Polar component (γp) | ||
| a According to Liu et al.40b According to Liu et al.40c Described with that of ethylene-olefin random copolymers.49d Described with that of polyethylene.50 | |||
| R974a | 41.81 | 34.34 | 7.47 |
| A200b | 77.3 | 36.5 | 40.8 |
| Ethylene-α-octene-rich domainsc | 17.5 | 15.6 | 1.9 |
| Polyethylene-rich domainsd | 25.9 | 25.9 | 0 |
| System | Pairs | Interfacial tension (γ1–2) (mN m−1) |
|---|---|---|
| OBC/A200 | A200/ethylene-α-octene-rich domains | 29.5 |
| A200/polyethylene-rich domains | 41.7 | |
| OBC/R974 | R974/ethylene-α-octene-rich domains | 5.5 |
| R974/polyethylene-rich domains | 8.1 |
As is known, hydrophilic SiO2 NPs, A200, tend to gather together to form aggregates due to the high interfacial tension and abundant hydroxy groups. On the contrary, hydrophobic SiO2 NPs, R974, are more likely to disperse in the polymer matrix in the separately-dispersed state because of the relatively low interfacial tension.51 However, an unexpected result happened in our work that A200 presented a peculiar chained distribution in OBC/A200 nanocomposites instead of gathering into large aggregates. This phenomenon can be explained with the results from the thermodynamic analysis. As can be seen in Table 2, in OBC/A200 nanocomposites, the interfacial tension between A200 NPs and ethylene-α-octene-rich domains is much smaller than that between A200 NPs and polyethylene-rich domains, namely, A200 shows higher affinity to ethylene-α-octene-rich domains. It indicates that after melt mixing, the interconnected A200 NPs are inclined to distribute along the ethylene-α-octene chain segments, resulting in a chained distribution of A200 NPs in the nanocomposites. In comparison, the interfacial tension between R974 NPs and ethylene-α-octene-rich domains is close to that between R974 NPs and polyethylene-rich domains, which indicates that R974 NPs do not show a selective localization in the different domains of OBC. These results indicated by thermodynamic analysis are in good agreement with SEM and TEM observations.
Mechanical properties
In this study, we incorporated SiO2 NPs with distinct surface characteristics into OBC, with the purpose of getting a high-performance nanocomposites. Considering that the peculiar chained distribution of A200 NPs and the interconnected network structure are hopeful to improve mechanical properties of nanocomposites, some of the typical mechanical properties of thermoplastic elastomer nanocomposites are further characterized. The representative uniaxial tensile stress–strain curves for OBC and its nanocomposites are presented in Fig. S1.† The average values of tensile modulus, elongation at break, stress at 100% and 500% stretching of two series of nanocomposites are plotted versus the content of SiO2 NPs in Fig. 5.As shown in Fig. S1,† the stress–strain curves of pure OBC and its nanocomposites are quite different. Pure OBC shows a continuously increasing stress at low strains and strain-hardening at the late stage. However, nearly all of nanocomposites evidently exhibit a yield plateau or necking phenomenon at low strains. This phenomenon can be attributed to the incorporation of fumed SiO2 NPs which restricts the segmental motion of the matrix in elastic deformation stage. After yield point, the restricted chain segments begin to move, showing strain-softening. It should be noted that OBC/A200 nanocomposites exhibit more obvious strain-softening compared with OBC/R974 nanocomposites, probably due to the more stable interconnected A200 network structure.
In Fig. 5a and b, the stress at a certain stretching (100% and 500%) of both series of nanocomposites, show a significantly increasing tendency with increasing content of SiO2 NPs. The stress at a certain stretching mainly depends on the network structure of the fillers in the nanocomposites. With the increasing content of SiO2 NPs in both OBC/A200 and OBC/R974 composites, the net-work structure of the SiO2 NPs become more and more perfect, which improve the stress. Comparing OBC/A200 with OBC/R974 nanocomposites, the network structure of SiO2 is well-developed more easily in OBC/A200 due to the peculiar chain-like structure of SiO2. Thus, the stress at 100% and 500% stretching of OBC/A200 nanocomposites is always much higher than that of OBC/R974 nanocomposites. In addition, the tensile modulus of both series of nanocomposites increases, and the percentages of reinforcement in the tensile modulus of OBC/A200 are almost four times as much as those of OBC/R974 at the same content of SiO2 as seen in Fig. 5c. Therefore, we can conclude that the greatly enhanced mechanical properties for OBC/A200 nanocomposites over OBC/R974 nanocomposites is primarily due to the peculiar chained distribution and interconnected network of A200 NPs in OBC/A200 nanocomposites. This particular chain structure can hinder the aggregations of hydrophilic SiO2, and impel SiO2 to present a peculiar chained distribution in OBC/A200 nanocomposites, showing a significantly reinforcement effect in the nanocomposites. Typically, larger stress and tensile modulus were achieved in OBC/A200 nanocomposites compared with OBC/R974 nanocomposites.
In Fig. 5d, the tensile elongation at break of OBC/A200 and OBC/R974 nanocomposites are both higher than 1300% even when the content of SiO2 is high as 20 vol%, and the tensile elongations at break of both series of nanocomposites are close at the same content of SiO2. According to previous studies,52,53 the large elongation at break of OBC stems from the long and flexible chain segments (soft blocks) between crystals (hard blocks), which can be stretched easily.54
Thus, a new elastomeric nanocomposite with excellent mechanical strength and toughness, and improved dielectric properties was developed. With these advantages, this new material holds potential to be utilized in fields such as dielectric elastomers, toughening agents for dielectric materials, electrically-driven deformation materials and flexible damping devices.
Conclusions
OBC/A200 and OBC/R974 nanocomposites were prepared through one-step melt compounding method and the effect of the distinct different surface characteristics of the two kinds of fumed nano-silica nanoparticles on the structure and performance of OBC based nanocomposites was investigated. The hydrophilic silica (A200) with more silanols dispersed in OBC in a peculiar chain-like structure while the hydrophobic silica (R974) NPs dispersed separately in OBC. Selective localization of hydrophilic silica (A200) due to the higher affinity towards the soft blocks of OBC dominates the peculiar chain-like distribution of hydrophilic silica in OBC composites while the hydrophobic silica NPs exhibit close affinity towards both the soft blocks and hard blocks of OBC. The percolation threshold of OBC/A200 nanocomposites is lower than that of OBC/R974 nanocomposites due to the peculiar chain-like distribution and inter-connected SiO2 in OBC/A200 nanocomposites. The OBC/A200 nanocomposites exhibit enhanced dielectric permittivity with low dielectric loss. The percentages of reinforcement in stress at a certain stretching of OBC/A200 nanocomposites are always higher than that of OBC/R974 nanocomposites at the same silica loading, and even better, the percentages of reinforcement in tensile modulus of OBC/A200 nanocomposites are almost four times higher than that of OBC/R974 nanocomposites at the same silica loading.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (NNSFC Grants 51422305, 21374065 and 51503132), Sichuan Provincial Science Fund for Distinguished Young Scholars (2015JQO003).References
- W. L. Hu, R. R. Wang, Y. F. Lu and Q. B. Pei, J. Mater. Chem. C, 2014, 2, 1298–1305 RSC
.
- K. Shehzad, A. A. Hakro, Y. Zeng, S. H. Yao, Y. Xiao-Hong, M. Mumtaz, K. Nadeem, N. S. Khisro and Z. M. Dang, Appl. Nanosci., 2015, 5, 969–974 CrossRef CAS
.
- H. G. Wu, P. J. Yao, N. Y. Ning, L. Q. Zhang, H. C. Tian, Y. P. Wu and M. Tian, RSC Adv., 2016, 6, 32932–32939 RSC
.
- O. S. Kwon, D. Lee, S. P. Lee, Y. G. Kang, N. C. Kim and S. H. Song, RSC Adv., 2016, 6, 59970–59975 RSC
.
- F. Jiang, Y. Q. Zhang, C. Fang, Z. K. Wang and Z. G. Wang, RSC Adv., 2014, 4, 60079–60085 RSC
.
- F. Memarian, A. Fereidoon and M. G. Ahangari, RSC Adv., 2016, 6, 101038–101047 RSC
.
- S. T. Liu, M. Tian, B. Y. Yan, Y. Yao, L. Q. Zhang, T. Nishi and N. Y. Ning, Polymer, 2015, 56, 375–384 CrossRef CAS
.
- T. Li, L. F. Ma, R. Y. Bao, G. Q. Qi, W. Yang, B. H. Xie and M. B. Yang, J. Mater. Chem. A, 2015, 3, 5482–5490 CAS
.
- E. Helal, L. G. Amurin, D. J. Carastan, R. R. de Sousa Jr, E. David, M. Frechette and N. R. Demarquette, Polymer, 2017, 113, 9–26 CrossRef CAS
.
- L. Y. Ma, B. Yu, X. D. Qian, W. Yang, H. F. Pan, Y. Q. Shi, L. Song and Y. Hu, Polym. Adv. Technol., 2014, 25, 605–612 CrossRef CAS
.
- S. M. Lai, C. K. Wang and H. F. Shen, J. Appl. Polym. Sci., 2005, 97, 1316–1325 CrossRef CAS
.
- O. Malay, O. Oguz, C. Kosak, E. Yilgor, I. Yilgor and Y. Z. Menceloglu, Polymer, 2013, 54, 5310–5320 CrossRef CAS
.
- L. Flandin, A. Chang, S. Nazarenko, A. Hiltner and E. Baer, J. Appl. Polym. Sci., 2000, 76, 894–905 CrossRef CAS
.
- K. S. Lam, Y. W. Wong, L. S. Tai, Y. M. Poon and F. G. Shin, J. Appl. Phys., 2004, 96, 3896–3899 CrossRef CAS
.
- D. Ponnamma, K. K. Sadasivuni, M. Strankowski, P. Moldenaers, S. Thomas and Y. Grohens, RSC Adv., 2013, 3, 16068–16079 RSC
.
- Y. J. Chen, Y. Li, D. H. Xu and W. T. Zhai, RSC Adv., 2015, 5, 82034–82041 RSC
.
- D. F. Eckel, M. P. Balogh, P. D. Fasulo and W. R. Rodgers, J. Appl. Polym. Sci., 2004, 93, 1110–1117 CrossRef CAS
.
- L. Bokobza, Polymer, 2007, 48, 4907–4920 CrossRef CAS
.
- C. Xu, K. Ohno, V. Ladmiral and R. J. Composto, Polymer, 2008, 49, 3568–3577 CrossRef CAS
.
- Y. Y. Huang and E. M. Terentjev, Polymers, 2012, 4, 275–295 CrossRef
.
- Z. M. Dang, M. S. Zheng and J. W. Zha, Small, 2016, 12, 1688–1701 CrossRef CAS PubMed
.
- S. K. Kumar, N. Jouault, B. Benicewicz and T. Neely, Macromolecules, 2013, 46, 3199–3214 CrossRef CAS
.
- J. P. Sharma and S. S. Sekhon, Bull. Mater. Sci., 2013, 36, 629–634 CrossRef CAS
.
- H. R. Jung, D. H. Ju, W. J. Lee, X. W. Zhang and R. Kotek, Electrochim. Acta, 2009, 54, 3630–3637 CrossRef CAS
.
- M. Battistella, M. Cascione, B. Fiedler, M. H. G. Wichmann, M. Quaresimin and K. Schulte, Composites, Part A, 2008, 39, 1851–1858 CrossRef
.
- X. Chen, J. Gug and M. J. Sobkowicz, Compos. Sci. Technol., 2014, 95, 8–15 CrossRef CAS
.
- P. M. Gore, S. Zachariah, P. Gupta and K. Balasubramanian, RSC Adv., 2016, 6, 105180–105191 RSC
.
- N. Katiyar and K. Balasubramanian, RSC Adv., 2015, 5, 4376–4384 RSC
.
- K. M. S. Meera, R. M. Sankar, J. Paul, S. N. Jaisankar and A. B. Mandal, Phys. Chem. Chem. Phys., 2014, 16, 9276–9288 RSC
.
- E. Barna, B. Bommer, J. Kursteiner, A. Vital, O. von Trzebiatowski, W. Koch, B. Schmid and T. Graule, Composites, Part A, 2005, 36, 473–480 CrossRef
.
- M. I. Aranguren, E. Mora, J. V. Degroot and C. W. Macosko, J. Rheol., 1992, 36, 1165–1182 CrossRef CAS
.
- K. Deshmukh, M. B. Ahamed, K. K. Sadasivuni, D. Ponnamma, M. A. A. AlMaadeed, R. R. Deshmukh, S. K. K. Pasha, A. R. Polu and K. Chidambaram, J. Appl. Polym. Sci., 2017, 134, 11 CrossRef
.
- D. J. Arriola, E. M. Carnahan, P. D. Hustad, R. L. Kuhlman and T. T. Wenzel, Science, 2006, 312, 714–719 CrossRef CAS PubMed
.
- H. P. Wang, D. U. Khariwala, W. Cheung, S. P. Chum, A. Hiltner and E. Baer, Macromolecules, 2007, 40, 2852–2862 CrossRef CAS
.
- V. C. Gibson, Science, 2006, 312, 703–704 CrossRef CAS PubMed
.
- F. Zuo, C. Burger, X. M. Chen, Y. M. Mao, B. S. Hsiao, H. Y. Chen, G. R. Marchand, S. Y. Lai and D. Chiu, Macromolecules, 2010, 43, 1922–1929 CrossRef CAS
.
- T. Li, J. H. Pu, L. F. Ma, R. Y. Bao, G. Q. Qi, W. Yang, B. H. Xie and M. B. Yang, Polym. Chem., 2015, 6, 7160–7170 RSC
.
- S. D. Wu, H. Li, G. S. Huang and J. R. Wu, RSC Adv., 2014, 4, 19024–19033 RSC
.
- Z. Z. Tong, B. Zhou, J. Huang, J. T. Xu and Z. Q. Fan, RSC Adv., 2014, 4, 15678–15688 RSC
.
- X.-Q. Liu, Y. Wang, W. Yang, Z.-Y. Liu, Y. Luo, B.-H. Xie and M.-B. Yang, J. Mater. Sci., 2012, 47, 4620–4631 CrossRef CAS
.
- J. Y. Kim, W. H. Lee, J. W. Suk, J. R. Potts, H. Chou, I. N. Kholmanov, R. D. Piner, J. Lee, D. Akinwande and R. S. Ruoff, Adv. Mater., 2013, 25, 2308–2313 CrossRef CAS PubMed
.
- T. C. Mo, H. W. Wang, S. Y. Chen, R. X. Dong, C. H. Kuo and Y. C. Yeh, J. Appl. Polym. Sci., 2007, 104, 882–890 CrossRef CAS
.
- M. Abdel-Goad, P. Potschke, D. H. Zhou, J. E. Mark and G. Heinrich, J. Macromol. Sci., Part A: Pure Appl.Chem., 2007, 44, 591–598 CrossRef CAS
.
- L. J. Romasanta, M. A. Lopez-Manchado and R. Verdejo, Eur. Polym. J., 2013, 49, 1373–1380 CrossRef CAS
.
- R. Krishnamoorti, A. S. Silva, M. A. Modi and B. Hammouda, Macromolecules, 2000, 33, 3803–3809 CrossRef CAS
.
- P. Thareja and S. Velankar, Rheol. Acta, 2007, 46, 405–412 CrossRef CAS
.
- H. E. Park, J. M. Dealy, G. R. Marchand, J. A. Wang, S. Li and R. A. Register, Macromolecules, 2010, 43, 6789–6799 CrossRef CAS
.
- S. Wu, J. Macromol. Sci., Rev. Macromol. Chem. Phys., 1974, C10, 1–73 Search PubMed
.
- C. G. Ma, M. Q. Zhang and M. Z. Rong, J. Appl. Polym. Sci., 2007, 103, 1578–1584 CrossRef CAS
.
- S. Asai, K. Sakata, M. Sumita and K. Miyasaka, Polym. J., 1992, 24, 415–420 CrossRef CAS
.
- M. Parvinzadeh, S. Moradian, A. Rashidi and M. E. Yazdanshenas, Appl. Surf. Sci., 2010, 256, 2792–2802 CrossRef CAS
.
- S. Bensason, E. V. Stepanov, S. Chum, A. Hiltner and E. Baer, Macromolecules, 1997, 30, 2436–2444 CrossRef CAS
.
- J. Minick, A. Moet, A. Hiltner, E. Baer and S. P. Chum, J. Appl. Polym. Sci., 1995, 58, 1371–1384 CrossRef CAS
.
- H. P. Wang, S. P. Chum, A. Hiltner and E. Baer, J. Appl. Polym. Sci., 2009, 113, 3236–3244 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra08074c |
| This journal is © The Royal Society of Chemistry 2017 |