Hierarchical design of synthetic gel composites optimized to mimic the impact energy dissipation response of brain tissue
Bo
Qing
 a and
Krystyn J.
Van Vliet
*ab
a and
Krystyn J.
Van Vliet
*ab
aDepartment of Biological Engineering, Massachusetts Institute of Technology, 77 Massachusetts Avenue, Cambridge, MA 02139, USA
bDepartment of Materials Science and Engineering and Department of Biological Engineering, Massachusetts Institute of Technology, 77 Massachusetts Avenue, Cambridge, MA 02139, USA. E-mail: krystyn@mit.edu
First published on 9th August 2016
Abstract
Synthetic polymer gels that accurately mimic key mechanical properties of brain tissue are valuable tools for evaluating protective equipment and understanding injury mechanisms, for example in response to concentrated mechanical impact events. Here, we employ impact indentation to investigate the response of brain tissue from three species (mice, rats, and pigs), quantified in terms of penetration resistance, energy dissipation capacity, and energy dissipation rate. We identify measurable variations in these three metrics among the different animal models, suggesting that a highly tunable materials system is required to capture the full impact response of specific brain models. To achieve enhanced tunability of energy dissipation, we engineer bilayered polymer composites based on polydimethylsiloxane (PDMS) elastomers and swollen organogels. This bilayer design leverages the key properties of each individual layer to decouple the penetration resistance and energy dissipation characteristics of the composite material. Additionally, we demonstrate that by sequentially tuning the stiffness and thickness of the top layer, all three of these impact response metrics can be optimized to match that of porcine brain tissue. Together, these results suggest that the mechanical behavior of composite gels under impact loading can be modulated to mimic different brain tissues and brain injury models with high fidelity.
Design, System, ApplicationDesign of a polymeric system that mechanically mimics brain tissue presents several challenges. For applications such as ballistic testing and robotic surgery optimization, the tissue simulant should replicate viscoelastic properties of brain and must also exhibit structural stability in ambient air; the latter constraint excludes biocompatible hydrogels. Here, we synthesize simple bilayered composites comprising a silicone-based elastomer atop a swollen silicone organogel, and find that this hierarchical structure enables the decoupling of the penetration resistance and energy dissipation characteristics of the material. The extent to which we can decouple these parameters is constrained by the properties of each individual layer, since only intermediate responses can be achieved. By varying the stiffness of the top elastomeric layer, the impact response of the composite can be tuned to attain the desired penetration resistance. Next, by varying the thickness of the top layer, which negligibly affects penetration resistance within the range studied here, the energy dissipation response can be optimized to also match that of the target tissue. This hierarchical approach greatly widens the design space for soft-tissue simulant materials and can be translated to other biological and structural applications that require precise, independent modulation of elastic and viscous or energy dissipative properties. |
I. Introduction
Traumatic brain injury (TBI) caused by a focal impact to the head negatively affects millions of individuals each year in the United States.1 Athletes and soldiers are two subpopulations exposed frequently to adverse impact events ranging from head collisions to ballistic attacks, and are thus susceptible to TBI. Synthetic tissue simulant materials capable of mimicking the mechanical deformation of brain tissue under such insults are valuable tools for developing protection strategies that effectively dissipate the mechanical energy. These mechanical brain surrogates can serve as test media for assessing new protective helmets, enabling the prediction of injury severity both experimentally and computationally.2–4 However, the soft matter employed to date, such as ballistic gelatin3,5 and Roma Plastilina #1 ballistic clay,6 are poor representations of the mechanical response of this so-called soft tissue – as the brain is one of the most compliant organs in the body.7 The Young's elastic modulus of ballistic gelatin, an environmentally unstable hydrogel derived from denatured collagen, is approximately 100 kPa,3 which is mechanically comparable to muscle tissue8 but approximately three orders of magnitude stiffer than brain tissue.9 Roma Plastilina #1 ballistic clay, an oil-based modeling clay, is even stiffer than ballistic gelatin with a Young's elastic modulus on the order of 1 MPa,10 and also exhibits notable temperature sensitivity that introduces undesirable testing variation.11 Therefore, there remains a critical need for a class of tissue simulant materials that more accurately replicates the deformation response of brain tissue under impact loading, specifically in terms of penetration resistance and impact energy dissipation. Moreover, there exists a need to understand quantitatively how the impact response can vary as a function of species for biological tissues, or as a function of molecular composition and structure for synthetic polymers.A recent study of individual polydimethylsiloxane (PDMS) organogels as potential tissue simulant candidates indicated a wide range of mechanical tunability, but failed to fully reflect the complex rate-dependent behavior of brain tissue.12 The elastic and viscoelastic properties of such PDMS organogels can be tuned systematically by adjusting parameters such as the concentration of chemical crosslinkers, molecular weight of polymer chains, and amount of solvent loading.13–15 However, a significant limitation of those organogels was that each of these composition parameters influenced both the penetration resistance and energy dissipation characteristics of the impacted material. As a result, independent modulation of each of these properties has not been achieved.12 To address this problem, we here extended that monolithic system to create a simple bilayered composite, by bonding a highly compliant PDMS elastomer (CY52-276 Dow Corning®) with a PDMS organogel. Our objective was to introduce hierarchical structure into the synthetic material, chiefly to decouple these impact dissipation characteristics but also noting that biological tissues naturally exhibit complex hierarchical structures that influence their mechanical properties at different time and length scales.16–18 We chose to build on the existing PDMS organogels because this polymer is environmentally stable in air, easily manufactured, and cost effective – all of which are important features of a practical tissue simulant material for applications including ballistic testing and robotic surgery optimization.3,19
Using a computational finite element model, we have shown that a bilayered composite provides additional design parameters that potentially enable the decoupling of penetration resistance from impact energy dissipation.20 Here, we aimed to further validate those computational predictions and demonstrate experimentally that the bilayered composite can indeed be optimized to fully match the impact response of brain tissue – among the most mechanically compliant tissue comprising biological organs. First, we quantified the penetration resistance, energy dissipation capacity, and energy dissipation rate of hydrated brain tissues harvested from mice, rats, and pigs via impact indentation, a technique that applies concentrated impact loads with corresponding strain energy densities approaching ballistic conditions.21 We then synthesized variations of the bilayered PDMS composite and conducted impact indentation experiments to explore whether and how the layer stiffness and thickness modulated the impact response metrics over a range of impact velocities. With this understanding of how the properties of each layer modulate the material's overall impact response, we designed and optimized a bilayered composite to match the impact response of porcine brain tissue, which is considered the most suitable animal model among these three mammalian species for analogy to human brain tissue.22
II. Materials and methods
Tissue harvesting
Whole brains were harvested from two healthy rodent models (infant mice, adult rats) and one healthy porcine model (adult pigs). A total of six mouse brains, three rat brains, and four pig brains were collected from Boston Children's Hospital, the Division of Comparative Medicine at MIT, and a local stockyard in Massachusetts, respectively. All experiments involving animals followed the University IACUC protocol and the NIH guidelines for animal care. After excision, brains were sliced into several sections of 6 mm thickness along different anatomical directions and immediately stored in Hibernate®-A medium on ice. All subsequent characterization experiments were conducted with the tissues immersed in the same medium at room temperature, as the mechanical properties of tissue depend strongly on their hydration state and the goal of this study was to characterize the mechanical response of these tissues to impact loading in near-physiological conditions.23,24 The total post-mortem time elapsed between animal death and mechanical characterization of the prepared brain tissue slices varied between 3 and 48 h. Over this duration, the brain slices maintained their structural integrity, and measured impact properties did not vary detectably.Fabrication of bilayered polymer composites
The bilayered polymer composite consisted of a viscoelastic PDMS organogel beneath a more compliant PDMS elastomer. The PDMS organogel was a chemically crosslinked PDMS network (formed from vinyl-terminated PDMS and tetrafunctional silane crosslinkers) swollen in a non-reactive methyl-terminated PDMS solvent. Full processing details for the organogel, developed by Mrozek and Lenhart et al., have been reported earlier.15 Each polymer composite in the present study included a organogel layer of 5 mm thickness and the same composition: 60 vol% 1.1 kg mol−1 solvent with 2.25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 silane
1 silane![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) vinyl stoichiometry. The silicone rubber that served as the top layer was a commercial grade of PDMS called CY52-276 (Dow Corning®). Similar to the more commonly known Sylgard® 184, CY52-276 is a two-component silicone kit comprising a prepolymer base (Part A) and a catalyst (Part B), which allows for facile variation of elastomer stiffness based on the relative amount of each component in the mixture. However, CY52-276 produced fully cured elastomers with a lower shear elastic modulus G ∼ 1 kPa that we confirmed via macroscale rheometry and was necessary for mimicking brain tissue compliance; Sylgard® 184 is considerably stiffer at concentrations required for full polymerization. The thickness of the compliant top silicone layer was controlled by the volume of mixture that was prepared, and these samples were cured at 80 °C overnight. Because the top and bottom layer were both PDMS-based, oxygen plasma treatment of each layer enabled complete bonding. It has been shown previously that oxidation at the surface of PDMS layers creates covalent siloxane bonds from exposed silanol groups.25,26 Immediately after exposure to oxygen plasma (30 s, 30 W), the two layers were pressed together to form a bilayered polymer composite.
vinyl stoichiometry. The silicone rubber that served as the top layer was a commercial grade of PDMS called CY52-276 (Dow Corning®). Similar to the more commonly known Sylgard® 184, CY52-276 is a two-component silicone kit comprising a prepolymer base (Part A) and a catalyst (Part B), which allows for facile variation of elastomer stiffness based on the relative amount of each component in the mixture. However, CY52-276 produced fully cured elastomers with a lower shear elastic modulus G ∼ 1 kPa that we confirmed via macroscale rheometry and was necessary for mimicking brain tissue compliance; Sylgard® 184 is considerably stiffer at concentrations required for full polymerization. The thickness of the compliant top silicone layer was controlled by the volume of mixture that was prepared, and these samples were cured at 80 °C overnight. Because the top and bottom layer were both PDMS-based, oxygen plasma treatment of each layer enabled complete bonding. It has been shown previously that oxidation at the surface of PDMS layers creates covalent siloxane bonds from exposed silanol groups.25,26 Immediately after exposure to oxygen plasma (30 s, 30 W), the two layers were pressed together to form a bilayered polymer composite.
Rheology
Shear rheology experiments were conducted using a parallel plate rheometer (Anton Paar MCR 501, 10 mm diameter plate) to characterize the stiffness of the CY52-276 silicone. After the PDMS cured, a surgical punch was used to cut out samples with the appropriate diameter while they were immersed in 150 mM NaCl phosphate buffered saline (PBS) containing 3% Pluronic® F108. Because some mixtures produced highly compliant and adhesive gels, this surfactant facilitated clean detachment of the silicone from the container.27 Frequency sweep measurements were conducted at 1% shear strain in the linear viscoelastic regime. The total thickness of each sample was determined by the gap height at which the instrument first detected contact, and the storage modulus G′ at 1 Hz was used to quantify and compare the stiffness of the CY52-276 layers.Impact indentation
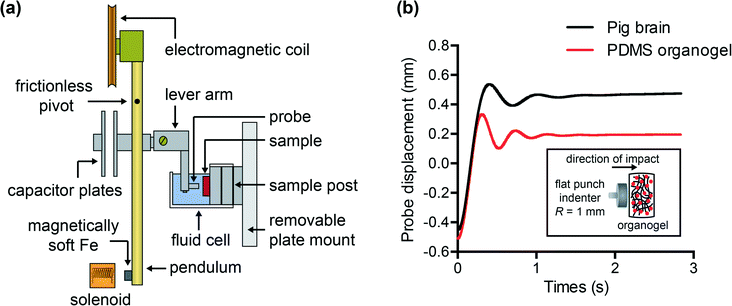
To characterize and compare the dynamic response of brain tissues and polymer gels under concentrated impact loading, impact indentation experiments were conducted at 25 °C using a pendulum-based instrumented nanoindenter as described in previous work.12 The experimental configuration is illustrated in Fig. 1(a), highlighting the ability to conduct tests in fully hydrated conditions.28 Electromagnetic interactions between a conductive coil at the top of the pendulum and a stationary magnetic plate behind the coil (not shown) apply the load, causing the pendulum to move about a frictionless pivot. The parallel plate capacitor measures indenter displacement as the pendulum moves. Activating the solenoid causes the pendulum to swing back and maintain its position. After the electromagnetic coil current increases to the desired amount, deactivating the solenoid releases the “loaded” pendulum such that the probe swings into the sample at an impact velocity that increases with increasing electromagnetic coil current (stored energy).Fig. 1(b) illustrates examples of recorded probe displacement obtained from one porcine brain sample and the viscoelastic PDMS organogel at the same impact velocity of 4.2 mm s−1. With this raw displacement profile and the corresponding velocity profile, we can compute key impact energy dissipation response parameters such as the maximum penetration depth xmax, energy dissipation capacity K, and dissipation quality factor Q.21 To quantify xmax, we must first determine the impact velocity vin, which is the maximum probe velocity immediately prior to contact and thus defines the contact position x0. After setting the displacement profile relative to the contact position, we calculate xmax as the deformation at which the probe velocity first decreases to zero. The calculation of K is less straightforward because we need to account for the inherent damping of the pendulum itself.29,30 We define K as the energy dissipated by the sample Esd normalized by the sum of dissipated and restored sample energies (Esd + Esr) in the first impact cycle:
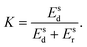 | (1) |
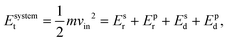 | (2) |
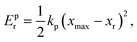 | (3) |
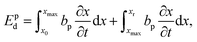 | (4) |
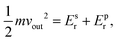 | (5) |
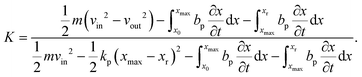 | (6) |
In this study, we employed a stainless steel cylindrical flat punch probe with a radius of 1 mm for impact on all materials. This probe connected to a lever arm attached to the pendulum, which allowed for lowering of the probe into the fluid cell. Each sample was adhered to an aluminum sample post also within the fluid cell. Due to the adhesive nature of these PDMS surfaces, the synthetic polymers adhered readily to the sample post. However, a thin layer of low-viscosity cyanoacrylate adhesive (Loctite® 4013) was required to attach brain tissue (of 6 mm thickness) to the sample post. In this configuration, loading occurred in the horizontal direction, normal to the sample surface. For annotation purposes, the “top” layer of a composite gel corresponds to the layer that experiences direct contact with the probe. During mechanical testing, brain tissue was immersed in Hibernate-A CO2-independent media to preserve tissue integrity and synthetic polymers were immersed in PBS + 3% Pluronic® F108 to reduce probe adhesion; these solutions have similar viscosity. Separate experiments were conducted previously in air and in fluid on non-adhesive samples, to confirm that the presence of fluid caused negligible damping; this verified that testing in fluid did not influence the measured energy dissipation properties.21
III. Results and discussion
How do brain tissues from different species respond to concentrated impact loading?
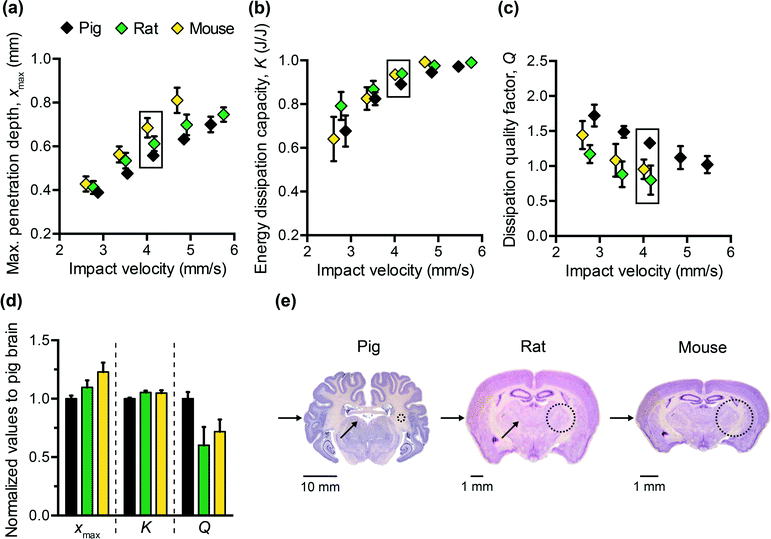
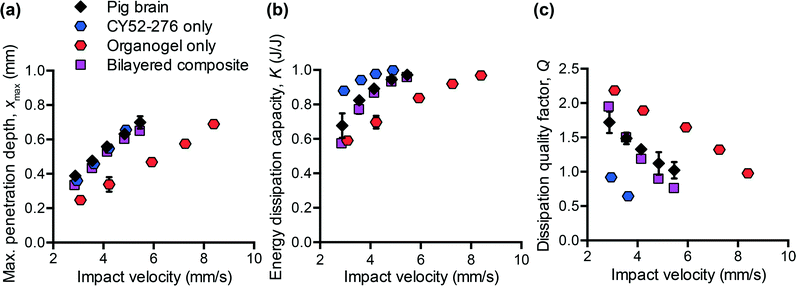
To design polymers as mechanically biofidelic brain tissue simulants, we first studied the impact response of animal brain tissue under loading conditions relevant to mechanical insult and injury. Additionally, because numerous animal models of traumatic brain injury exist, each with its own strengths and weaknesses,31,32 we hypothesized that we would detect species-to-species variation in terms of the three impact energy dissipation parameters of interest. We conducted impact indentation experiments on brain slices obtained from infant mice, adult rats, and adult pigs. Fig. 2(a–c) shows the measured xmax, K, and Q, respectively, for each species at impact velocities between 2 and 6 mm s−1. Because brain is highly compliant (low elastic moduli as compared with other biological organs such as heart or bone), impact velocities greater than 6 mm s−1 tended to penetrate the sample so deeply that the pendulum motion was impeded physically by the electromagnetic coil contacting with the stationary magnetic plate. Although the velocities investigated here are on the order of only mm s−1, the corresponding impact strain energy densities, which range from 0.5 kJ m−3 to 3.5 kJ m−3 due to the small size of the probe, are comparable to ballistic strain energy densities.33 We observed all brain tissues to exhibit the following trends: as the impact velocity increased, the probe penetrated into the sample further, the sample dissipated more energy and this energy was dissipated at a quicker rate. Compared to previous impact loading studies on other soft tissues, brain tissue was similar to liver tissue in terms of penetration resistance and was much more dissipative than either liver or heart tissue.12 Note that all experiments on tissues were conducted in aqueous fluid at 25 °C. Previous studies of brain tissue macroscale rheology have noted decreased stiffness (specifically, shear storage modulus) at 37 °C as compared to the ambient room temperature of interest here,34 and such increased compliance may potentially and slightly reduce xmax and increase K. Future work includes extending the impact indentation instrumentation to enable characterization of such tissues at 37 °C.Additionally, we identified detectable differences in the magnitude of all three impact response parameters when comparing brain tissue from different species (Fig. 2(a–c)). Impact velocities were not necessarily identical because the control parameter is the electromagnetic coil current (related directly to a pre-load on the cocked pendulum) and the magnitude of the corresponding velocity may vary slightly due to the pendulum swing distance calibration conducted for each set of experiments. To highlight the species-to-species variation, we normalized the magnitudes of each impact response parameter to that of porcine brain and conducted one-way ANOVA. Fig. 2(d) shows normalized data corresponding to an impact velocity of approximately 4 mm s−1 (boxed data points in Fig. 2(a–c)). A statistically significant distinction was identified among the three species for xmax, K, and Q (p-values < 0.001) at this impact velocity, and also at the other impact velocities considered (not shown). These variations in mechanical properties among species were anticipated, due to species-dependent differences in structure and composition. Histological staining of coronal brain sections in Fig. 2(e) indicates several key differentiating features such as brain size, degree of convolution in the outer cerebral cortex, and the ratio of white to gray matter. Of the three species considered herein, porcine brain is the most similar to human brain, as both are gyrencephalic (highest degree of convolution) and consist of roughly 60% white and 40% gray matter.35,36 In contrast, rodent brains are lissencephalic (not convoluted) and contain only roughly 10% white matter.37 Several studies have reported the stiffness of white matter to be greater and the stress relaxation times to be longer, as compared to gray matter from the same species.9,38–40 Our observations are consistent with those findings, in that porcine brain was more resistant to penetration (lower xmax) and dissipated energy more slowly (higher Q) than both types of rodent brains. These data do not resolve why the impact response of rat and mouse brains differs, but we note that the animal ages for each cohort also differed and may reflect differences in the maturity of the brain structure and composition (rats aged 6 to 18 months, and mice aged 3 weeks). Additionally, we note that the relatively smaller dimensions of mouse brain tissue constrained the measurement positions near the sample center to be within 1 to 2 mm from the tissue perimeter. As this distance is similar to the probe contact radius, it is possible that the closer proximity of those measurements to the sample edge could have contributed to increased penetration depths in mouse brain tissue (as compared with larger tissue samples from porcine brain that were located at least 10 mm from sample perimeters).
From Fig. 2(d), we also observed that the impact response parameters varied to different degrees among species. For example, at an impact velocity of 4 mm s−1, the mean penetration depth xmax of mouse brain was 23% greater than that of pig brain (with a 95% confidence interval of this difference ranging from 19 to 27%), whereas the mean impact dissipation capacity K of mouse brain was only 5% greater than that of pig brain (with a 95% confidence interval of this difference ranging from 4 to 6%). This contrast could be problematic when developing mechanically biofidelic tissue simulant materials that are capable of mimicking multiple animal models, because the primary limitation of existing materials is the strong coupling between penetration resistance and energy dissipation. If the material is well-matched to the penetration depth exhibited by the target soft tissue, but not well-matched to the targeted magnitude of K, further tuning to approximate the brain tissue K would be at the expense of a change in xmax. As a result, the implications of the differences among species are twofold: first, they highlight the importance of selecting an appropriate animal model for brain injury because differences in anatomy and structure translate to a difference in mechanical behavior; second, they prompt the need for a more tunable materials system to afford such variation in and decoupling of these metrics.
How does the bilayered composite design offer enhanced tunability?
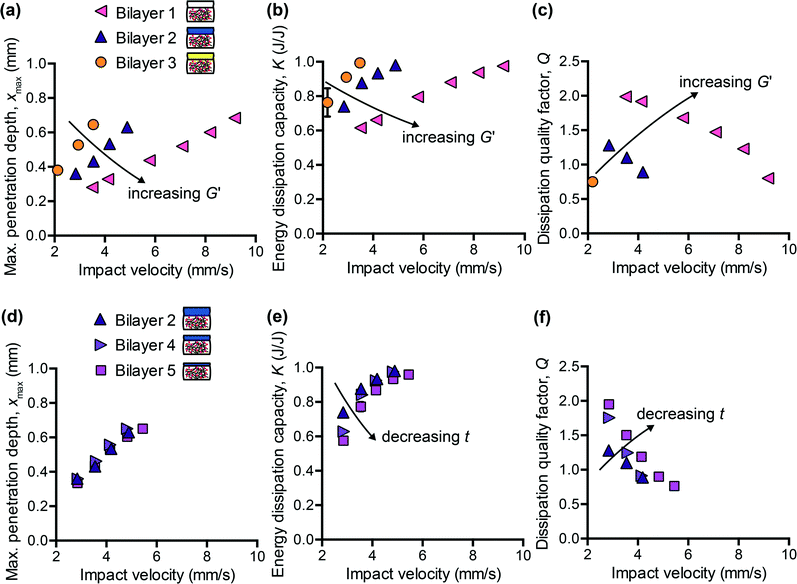
Motivated by the need to decouple energy dissipation capacity and penetration resistance in synthetic polymers, and by the inherent hierarchical structure of many biological tissues, we sought to investigate whether a simple bilayer composite could provide the necessary tunability to match the impact response of brain tissue with respect to all three impact energy dissipation metrics. As in all composites, the goal was to leverage key properties of different materials to optimize overall performance. Using a previously characterized PDMS organogel12 as a starting point, which did not reflect the energy dissipation characteristics of brain tissue, we added a more compliant PDMS elastomer (CY52-276 Dow Corning®) as a top layer. One advantage of multiple layers is the introduction of two new tunable parameters: the thickness and the stiffness of the top layer. Although we could also adjust the mechanical properties of the PDMS organogel, we chose to maintain one molecular composition of the bottom layer for all composites and focused on how the addition of the top layer modulated the overall penetration resistance and energy dissipation characteristics of the composite.We first considered the effects of varying the stiffness of the top layer, while maintaining the layer thickness constant. Fig. 3(a–c) shows the measured impact response for three bilayered composites at a range of impact velocities. The storage modulus G′ of the CY52-276 layer of bilayer 1, 2, and 3 was 4.75 kPa, 1 kPa, and 0.85 kPa, respectively; the top layer thickness t was 2.6 mm and the overall sample thickness was 8 mm. As expected, a bilayered composite with a stiffer top layer exhibited lower xmax (Fig. 3(a)). Additionally, K decreased and Q increased with increasing stiffness of the top layer (Fig. 3(b and c)). These results reflect the fact that increasing the crosslinking density of the PDMS top layer leads to higher elastic moduli but also lower surface adhesion.41,42 This effect was especially pronounced for the silicone formulations studied here. During the impact event, the rebound velocity vout is expected to decrease if adhesive forces inhibit the pendulum from retracting; eqn (6) implies that K will then effectively increase. Because more energy is dissipated during the first impact cycle, the overall energy dissipation rate will also increase, corresponding to a lower Q value. Although we reduced molecular interactions between the probe and sample surface by conducting experiments in PBS containing 3% Pluronic® F108, adhesion is likely still a non-negligible mechanism of energy dissipation in these material systems.
Next, we maintained G′ of the CY52-276 layer constant at 1 kPa and explored the effects of varying only the thickness. Bilayer 2, 4, and 5 consisted of a 2.6 mm, 0.9 mm, and 0.7 mm thick top layer, respectively. Tuning the thickness of the top layer, within the range studied here, negligibly affected the penetration resistance of the composite (Fig. 3(d)). Interestingly, the measured xmax of these three composites was also identical to that of the CY52-276 PDMS material itself (Fig. 4(a)). Note that this monolithic CY52-276 sample was also of stiffness of 1 kPa but was made thicker (5 mm), to minimize contributions from the finite thickness effect.43 This indicates that the penetration resistance of the bilayered composite is governed strongly by the stiffness of the top layer, when the top layer is more compliant than the bottom layer. To support this conclusion, we also conducted impact indentation experiments on a thin CY52-276 monolayer (0.9 mm thick) adhered directly to the aluminum sample post. We found xmax to be the same magnituede for the thin monolayer and thick monolayer at impact velocities under 4 mm s−1, and observed a finite thickness effect only at the higher impact velocities. The contributions from the underlying aluminum substrate were sufficiently small (considerably less than the differences in xmax between bilayer 1 and 2) that it is understandable that the viscoelastic PDMS organogel substrate of kPa stiffness did not detectably influence the composite's overall resistance to penetration at the loading conditions investigated here.
 | ||
| Fig. 4 Comparison of the impact response of a bilayered composite to that of the individual layer components and the target porcine brain tissue: (a) maximum penetration depth, (b) energy dissipation capacity, and (c) dissipation quality factor as a function of impact velocity. The composition of the bilayered composite corresponds to that of bilayer 5 from Fig. 3. This composite gel reasonably approximated the impact response of porcine brain tissue for all three metrics, whereas the individual layers alone did not. Data are represented as mean ± standard deviation, and error bars may appear smaller than data symbols. | ||
Separately, varying only the thickness of the top layer, while maintaining its composition and thus mechanical properties constant, detectably altered the energy dissipation characteristics of the composite (Fig. 3(e and f)). As the thickness decreased, K decreased and Q increased – trends that were particularly evident at the lower impact velocities. Bilayer 5, which included the thinnest top layer among these samples, responded most similarly to the monolithic PDMS organogel, suggesting that the bottom PDMS organogel layer dominated the composite's overall energy dissipation response. When comparing Fig. 3(a–c) with Fig. 3(d–f), the differences among bilayers 2, 4, and 5 were not as pronounced as those among bilayers 1, 2, and 3. Therefore, these data demonstrate the means to first coarsely tune the composite system (by adjusting the stiffness of the top layer) and then finely tune (by adjusting the thickness of the top layer) toward an overall targeted energy dissipation response. Also, because xmax is independent of top layer thickness whereas K and Q are not, we are able to decouple the composite's penetration resistance from its energy dissipation characteristics – an important feature that was lacking in previous polymer simulant materials. However, we note that the extent to which we can decouple xmax from K and Q is still bound by the properties of each individual layer. For example, with the bilayered composites studied here, it would not be straightforward to achieve a magnitude of xmax exceeding that of the PDMS organogel and also a magnitude of K less than that of the PDMS organogel. Nonetheless, for compliant biological tissues such as brain tissue, which exhibit both substantial penetration and high energy dissipation capacity, the tunability accessible within this system is sufficient.
Can a bilayered composite gel be optimized to match the impact response of adult porcine brain?
With the improved tunability of this bilayered PDMS composite, we next considered whether the impact response of adult porcine (pig) brain could be replicated over a range of loading conditions. Porcine brain was chosen as the target in this study because it was the closest representation of human brain that is readily accessible for replicate experiments, such that adverse tissue preservation steps (such as freezing that can alter tissue structure) are not required. The first objective of our optimization process was to identify a composition of CY52-276 PDMS with mechanical stiffness that resulted in the same penetration resistance as porcine brain. We iteratively characterized the storage modulus G′ (at 1 Hz) of this polymer for different prepolymer![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) initiator-catalyst ratios, and measured the corresponding xmaxvia impact indentation. If penetration resistance was too low compared to that of brain tissue, we synthesized a more compliant CY52-276 by increasing the volume fraction of prepolymer, and vice versa. These steps were iterated to establish the composition and stiffness required to achieve the target penetration depth over the range of velocities of interest. For adult porcine brain tissue, a CY52-276 layer with G′ = 1 kPa (6
initiator-catalyst ratios, and measured the corresponding xmaxvia impact indentation. If penetration resistance was too low compared to that of brain tissue, we synthesized a more compliant CY52-276 by increasing the volume fraction of prepolymer, and vice versa. These steps were iterated to establish the composition and stiffness required to achieve the target penetration depth over the range of velocities of interest. For adult porcine brain tissue, a CY52-276 layer with G′ = 1 kPa (6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 prepolymer to initiator-catalyst v/v) was needed. The next objective of our optimization process was to tune the thickness of the CY52-276 layer such that the bilayered composite exhibited the same K and Q as porcine brain over a range of impact velocities. Recall that varying the thickness of the top layer incurred negligible effects on xmax, so if we met our second objective, this composite would be expected to recapitulate all three energy dissipation metrics. Following the trends in Fig. 3(e and f), we used a thinner CY52-276 layer to decrease K and increase Q, and iteratively identified a top layer thickness of 0.7 mm and stiffness of 1 kPa reflected the penetration resistance, energy dissipation capacity, and energy dissipation rate of porcine brain tissue over a range of impact velocities.
5 prepolymer to initiator-catalyst v/v) was needed. The next objective of our optimization process was to tune the thickness of the CY52-276 layer such that the bilayered composite exhibited the same K and Q as porcine brain over a range of impact velocities. Recall that varying the thickness of the top layer incurred negligible effects on xmax, so if we met our second objective, this composite would be expected to recapitulate all three energy dissipation metrics. Following the trends in Fig. 3(e and f), we used a thinner CY52-276 layer to decrease K and increase Q, and iteratively identified a top layer thickness of 0.7 mm and stiffness of 1 kPa reflected the penetration resistance, energy dissipation capacity, and energy dissipation rate of porcine brain tissue over a range of impact velocities.
Fig. 4 illustrates that neither of the individual components of this bilayer exhibited all of these impact energy dissipation properties, such that the bilayer provided a unique composite response. The PDMS organogel failed to replicate any of the three metrics of porcine brain. Although the CY52-276 PDMS monolayer exhibited the same penetration resistance as porcine brain (Fig. 4(a)), its energy dissipation characteristics were noticeably different (Fig. 4(b and c)). When we combined these two materials in a simple bilayer, xmax was similar to that of the monolithic CY52-276, but both K and Q were modified to intermediary values that reflected those of porcine brain.
Fig. 4 demonstrates clearly our primary design objective of a simple composite that serves as a mechanical surrogate for porcine brain tissue under concentrated impact loading. However, we also note that this mechanical impact response indicated mechanisms of energy dissipation that motivate further study. Upon closer examination of the rate dependence in Fig. 4, we found the bilayered composite to behave similarly to the bottom organogel at the lowest impact velocity in terms of K and Q. However, as the impact velocity increased, the energy dissipation response of the composite deviated from that of the organogel and approached that of the CY52-276. One may have initially predicted the opposite trend, because higher impact velocities translate to greater penetration depths (very close to the total thickness of the top layer when using the highest impact velocity), which should lead to a greater contribution from the underlying organogel. We thus posit that adhesion between the impacting probe and top layer strongly modulated impact energy dissipation, despite the fact that these experiments on the PDMS bilayers were conducted in saline that included a surfactant to reduce probe-sample adhesion. Experiments on brain tissues intentionally did not include this surfactant. Greater penetration depths also imply a greater contact area between the probe and sample surface when interfacial wetting occurs between the probe and impacted polymer, promoting adhesive interactions that would increase K and decrease Q.44 Although the bilayered composite mechanically mimicked porcine brain during these impact indentation experiments, and thus met our primary goal of tunability and parameter decoupling, we note that in the wider context of certain tissue surrogate applications (e.g., assessment of a new protective helmet subjected to ballistic tests), the simulant polymer may not directly come into contact with the fired projectiles. In those cases and applications, the adhesive nature of the CY52-276 surface would no longer contribute significantly to impact energy dissipation. Finally, we note that soft tissues may also exhibit stickiness, and the extent of probe-tissue adhesion depends on the molecular composition of the tissue, the impacting probe, and the surrounding medium. Future work in this area could include using computational modeling to distinguish the relative contributions of surface adhesion affecting the impact energy dissipation response.
IV. Summary and outlook
Our goals in this study were to characterize the dynamic impact response of various brain tissues, and to identify a simple, manufacturable polymer system capable of generating the same response with material stability in room-temperature air. Impact indentation experiments provided a means to quantify the penetration resistance, energy dissipation capacity, and energy dissipation rate of tissues and simulant gels in fully hydrated conditions. Brain tissue from all three animal models was highly susceptible to penetration and highly dissipative when compared to other soft tissues characterized in previous studies. Additionally, we observed slight but detectable species-to-species variation in all three impact response metrics, which may be attributed to the structural and compositional differences among mouse, rat, and pig brains. We thus designed and fabricated PDMS-based bilayered composites, and demonstrated that such an approach leverages the key properties of each component to facilitate the independent tuning of penetration resistance and energy dissipation. We deliberately chose to limit the number of composite layers to two because tissue surrogate applications ideally use materials that are simple, cost effective, and easily manufactured at large scales. Additional layers or compositionally graded soft matter could certainly be introduced for situations that require even more tunability than our current system, though not required and beyond the scope of the present focus on mammalian brain tissue. With only two layers, we showed that we could optimize the impact response of the composite gel to match that of porcine brain by independently modulating the stiffness and thickness of the more compliant top layer. In summary, these findings provide the design principles required to synthesize a physical surrogate of brain tissue for use in material modeling or in testing of protective strategies, by enabling accurate predictions of mechanical deformation of brain tissue under concentrated impact loading.Acknowledgements
This research was supported by the U.S. Army through the Institute for Soldier Nanotechnologies under Contract W911NF-07-D-0004. We gratefully acknowledge R. Mrozek and J. Lenhart (Army Research Laboratory) for synthesizing the organogel. We thank M. Sahin (Boston Children's Hospital) and J. Haupt (MIT) for supplying the rodent brain tissues. We appreciate helpful discussions with J. Maloney and A. Mijailovic (MIT) on interpreting impact response measurements. B. Q. acknowledges the National Defense Science and Engineering Graduate Fellowship.References
- J. D. Voss, J. Connolly, K. A. Schwab and A. I. Scher, Update on the epidemiology of concussion/mild traumatic brain injury, Curr. Pain Headache Rep., 2015, 19, 32 CrossRef PubMed.
- M. J. Thali, B. P. Kneubuehl, U. Zollinger and R. Dirnhofer, The skin-skull-brain model: a new instrument for the study of gunshot effects, Forensic Sci. Int., 2002, 125, 178–189 CrossRef CAS PubMed.
- T. F. Juliano, A. M. Forster, P. L. Drzal, T. Weerasooriya, P. Moy and M. R. VanLandingham, Multiscale mechanical characterization of biomimetic physical associating gels, J. Mater. Res., 2006, 21, 2084–2092 CrossRef CAS.
- J. C. Roberts, T. P. Harrigan, E. E. Ward, T. M. Taylor, M. S. Annett and A. C. Merkle, Human head–neck computational model for assessing blast injury, J. Biomech., 2012, 45, 2899–2906 CrossRef CAS PubMed.
- G. J. Appleby-Thomas, P. J. Hazell, J. M. Wilgeroth, C. J. Shepherd, D. C. Wood and A. Roberts, On the dynamic behavior of three readily available soft tissue simulants, J. Appl. Phys., 2011, 109, 084701 CrossRef.
- A. C. Merkle, E. E. Ward, J. V. O'Connor and J. C. Roberts, Assessing behind armor blunt trauma (BABT) under NIJ standard-0101.04 conditions using human torso models, J. Trauma, 2008, 64, 1555–1561 CrossRef PubMed.
- N. D. Leipzig and M. S. Shoichet, The effect of substrate stiffness on adult neural stem cell behavior, Biomaterials, 2009, 30, 6867–6878 CrossRef CAS PubMed.
- Y. Yoshikawa, T. Yasuike, A. Yagi and T. Yamada, Transverse elasticity of myofibrils of rabbit skeletal muscle studied by atomic force microscopy, Biochem. Biophys. Res. Commun., 1999, 256, 13–19 CrossRef CAS PubMed.
- S. Budday, R. Nay, R. de Rooij, P. Steinmann, T. Wyrobek, T. C. Ovaert and E. Kuhl, Mechanical properties of gray and white matter brain tissue by indentation, J. Mech. Behav. Biomed. Mater., 2015, 46, 318–330 CrossRef PubMed.
- C. Hernandez, M. F. Buchely and A. Maranon, Dynamic characterization of Roma Plastilina No. 1 from drop test and inverse analysis, Int. J. Mech. Sci., 2015, 100, 158–168 CrossRef.
- J. E. Seppala, Y. Heo, P. E. Stutzman, J. R. Sieber, C. R. Snyder, K. D. Rice and G. A. Holmes, Characterization of clay composite ballistic witness materials, J. Mater. Sci., 2015, 50, 7048–7057 CrossRef CAS.
- Z. I. Kalcioglu, R. A. Mrozek, R. Mahmoodian, M. R. VanLandingham, J. L. Lenhart and K. J. Van Vliet, Tunable mechanical behavior of synthetic organogels as biofidelic tissue simulants, J. Biomech., 2013, 46, 1583–1591 CrossRef PubMed.
- S. K. Patel, S. Malone, C. Cohen, J. R. Gillmor and R. H. Colby, Elastic modulus and equilibrium swelling of poly(dimethylsiloxane) networks, Macromolecules, 1992, 25, 5241–5251 CrossRef CAS.
- L. E. Roth, D. A. Vega, E. M. Valles and M. A. Villar, Viscoelastic properties of networks with low concentration of pendant chains, Polymer, 2004, 45, 5923–5931 CrossRef CAS.
- R. A. Mrozek, P. J. Cole, K. J. Otim, K. R. Shull and J. L. Lenhart, Influence of solvent size on the mechanical properties and rheology of polydimethylsiloxane-based polymeric gels, Polymer, 2011, 52, 3422–3430 CrossRef CAS.
- S. Nicolle, P. Vezin and J. F. Palierne, A strain-hardening bi-power law for the nonlinear behaviour of biological soft tissues, J. Biomech., 2010, 43, 927–932 CrossRef CAS PubMed.
- A. Gautieri, S. Vesentini, A. Redaelli and M. J. Buehler, Hierarchical structure and nanomechanics of collagen microfibrils from the atomistic scale up, Nano Lett., 2011, 11, 757–766 CrossRef CAS PubMed.
- A. A. Zadpoor, Nanomechanical characterization of heterogeneous and hierarchical biomaterials and tissues using nanoindentation: the role of finite mixture models, Mater. Sci. Eng., C, 2015, 48, 150–157 CrossRef CAS PubMed.
- D. C. Duffy, O. J. A. Schueller, S. C. Brittain and G. M. Whitesides, Rapid prototyping of microfluidic switches in poly(dimethyl siloxane) and their actuation by electro-osmotic flow, J. Micromech. Microeng., 1999, 9, 211–217 CrossRef CAS.
- R. Mahmoodian and B. Qing, et al., Multiscale computational design of synthetic gels as simulants of soft-tissue impact response, J. Biomech. Search PubMed , under review.
- Z. I. Kalcioglu, M. Qu, K. E. Strawhecker, T. Shazly, E. Edelman, M. R. VanLandingham, J. F. Smith and K. J. Van Vliet, Dynamic impact indentation of hydrated biological tissues and tissue surrogate gels, Philos. Mag., 2011, 91, 1339–1355 CrossRef CAS.
- P. Sauleau, E. Lapouble, D. Val-Laillet and C. H. Malbert, The pig model in brain imaging and neurosurgery, Animal, 2009, 3, 1138–1151 CrossRef CAS PubMed.
- D. M. Ebenstein and L. A. Pruitt, Nanoindentation of soft hydrated materials for application to vascular tissues, J. Biomed. Mater. Res. A, 2004, 69, 222–232 CrossRef CAS PubMed.
- S. Nicolle and J. F. Palierne, Dehydration effect on the mechanical behaviour of biological soft tissues: observations on kidney tissues, J. Mech. Behav. Biomed. Mater., 2010, 3, 630–635 CrossRef CAS PubMed.
- D. C. Duffy, J. C. McDonald, O. J. A. Scheuller and G. M. Whitesides, Rapid prototyping of microfluidic systems in poly(dimethylsiloxane), Anal. Chem., 1998, 70, 4974–4984 CrossRef CAS PubMed.
- M. A. Eddings, M. A. Johnson and B. K. Gale, Determining the optimal PDMS-PDMS bonding technique for microfluidic devices, J. Micromech. Microeng., 2008, 18, 067001 CrossRef.
- C. G. P. H. Schroen, M. A. C. Stuart, K. van der Voort Maarschalk, A. van der Padt and K. van't Riet, Influence of preadsorbed block copolymers on protein adsorption: surface properties, layer thickness, and surface coverage, Langmuir, 1995, 11, 3068–3074 CrossRef CAS.
- G. Constantinides, Z. I. Kalcioglu, M. McFarland, J. F. Smith and K. J. Van Vliet, Probing mechanical properties of fully hydrated gels and biological tissues, J. Biomech., 2008, 41, 3285–3289 CrossRef PubMed.
- G. Constantinides, C. A. Tweedie, D. M. Holbrook, P. Barragan, J. F. Smith and K. J. Van Vliet, Quantifying deformation and energy dissipation of polymeric surfaces under localized impact, Mater. Sci. Eng., A, 2008, 489, 403–412 Search PubMed.
- G. Constantinides, C. A. Tweedie, N. Savva, J. F. Smith and K. J. Van Vliet, Quantitative impact testing of energy dissipation at surfaces, Exp. Mech., 2009, 49, 511–522 CrossRef CAS.
- Y. Xiong, A. Mahmood and M. Chopp, Animal models of traumatic brain injury, Nat. Rev. Neurosci., 2013, 14, 128–142 CrossRef CAS PubMed.
- D. M. Morales, N. Marklund, D. Lebold, H. J. Thompson, A. Pitkanen, W. L. Maxwell, L. Longhi, H. Laurer, M. Maegele, E. Neugebauer, D. I. Graham, N. Stocchetti and T. K. McIntosh, Experimental models of traumatic brain injury: do we really need to build a better mousetrap?, Neuroscience, 2005, 136, 971–989 CrossRef CAS PubMed.
- J. G. Snedeker, M. Barbezat, P. Niederer, F. R. Schmidlin and M. Farshad, Strain energy density as a rupture criterion for the kidney: impact tests on porcine organs, finite element simulation, and a baseline comparison between human and porcine tissues, J. Biomech., 2005, 38, 993–1001 CrossRef CAS PubMed.
- M. Hrapko, J. A. van Dommelen, G. W. Peters and J. S. Wismans, The influence of test conditions on characterization of the mechanical properties of brain tissue, J. Biomech. Eng., 2008, 130, 031003–031013 CrossRef CAS PubMed.
- S. Herculano-Houzel, The human brain in numbers: a linearly scaled-up primate brain, Front. Hum. Neurosci., 2009, 3, 31 Search PubMed.
- D. W. Howells, M. J. Porritt, S. S. J. Rewell, V. O'Collins, E. S. Sena, H. B. van der Worp, R. J. Traystman and M. R. Macleod, Different strokes for different folks: the rich diversity of animal models of focal cerebral ischemia, J. Cereb. Blood Flow Metab., 2010, 30, 1412–1431 CrossRef CAS PubMed.
- E. C. Bush and J. M. Allman, The scaling of white matter to gray matter in cerebellum and neocortex, Brain Behav. Evol., 2003, 61, 1–5 CrossRef.
- J. A. W. van Dommelen, T. P. J. van der Sande, M. Hrapko and G. W. M. Peters, Mechanical properties of brain tissue by indentation: interregional variation, J. Mech. Behav. Biomed. Mater., 2010, 3, 158–166 CrossRef CAS PubMed.
- T. Kaster, I. Sack and A. Samani, Measurement of the hyperelastic properties of ex vivo brain tissue slices, J. Biomech., 2011, 44, 1158–1163 CrossRef CAS PubMed.
- F. Pervin and W. W. Chen, Dynamic mechanical response of bovine gray matter and white matter brain tissues under compression, J. Biomech., 2009, 42, 731–735 CrossRef PubMed.
- J. Chen, K. E. Wright and M. A. Birch, Nanoscale viscoelastic properties and adhesion of polydimethylsiloxane for tissue engineering, Acta Mech. Sin., 2014, 30, 2–6 CrossRef CAS.
- L. Cai, T. E. Kodger, R. E. Guerra, A. F. Pegoraro, M. Rubinstein and D. A. Weitz, Soft poly(dimethylsiloxane) elastomers from architecture-driven entanglement free design, Adv. Mater., 2015, 27, 5132–5140 CrossRef CAS PubMed.
- J. A. C. Santos, L. M. Rebelo, A. C. Araujo, E. B. Barros and J. S. de Sousa, Thickness-corrected model for nanoindentation of thin films with conical indenters, Soft Matter, 2012, 8, 4441 RSC.
- A. R. Savkoor and G. A. D. Briggs, The effect of tangential force on the contact of elastic solids in adhesion, Proc. R. Soc. London, Ser. A, 1977, 356, 103–114 CrossRef.
| This journal is © The Royal Society of Chemistry 2016 |