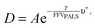Porosity in metal–organic framework glasses

Abstract

The porosity of a glass formed by melt-quenching a metal–organic framework, has been characterized by positron annihilation lifetime spectroscopy. The results reveal porosity intermediate between the related open and dense crystalline frameworks ZIF-4 and ZIF-zni. A structural model for the glass was constructed using an amorphous polymerization algorithm, providing additional insight into the gas-inaccessible nature of porosity and the possible applications of hybrid glasses.

---

Metal–organic frameworks (MOFs) remain the subject of intense research across chemistry, engineering, materials and biological domains. Their chemically tunable porosities are intrinsic to the potential for application in, for example, gas storage and separation, drug delivery and catalysis.^1,2 The maturing field has seen notable advances in changing the porosity-linked properties of MOFs through utilization of defects,³ and also their physical state of matter. This latter category of non-crystalline or amorphous MOFs⁴ includes glasses, obtained by melt-quenching of the liquids formed upon melting these hybrid structures.⁵ The porosity, or ‘free-volume’ within these MOF glasses has not yet been quantified, and is extremely important given the possible application of hybrid glasses in ionic, electronic or thermal conduction,^6–8 alongside the more familiar membrane and sieving applications.

Positron Annihilation Lifetime Spectroscopy (PALS) has been used to identify internal porosity in dense polymers,^9,10 Nafion,¹¹ microporous polymers,¹² porous aromatic frameworks,¹³ zeolites¹⁴ and activated carbons, with good agreement with the cavity sizes measured by small-angle neutron scattering (SANS), ellipso-metric porosimetry (EP) and gas sorption (e.g. BET).¹⁵

The technique involves the generation of positrons (the anti-matter counterpart of an electron, with identical mass, spin = 1/2 and charge = +1), with a range of energies able to penetrate dense matter that otherwise would be inaccessible to gas. Positrons slow to thermal energies through inelastic collisions and positron–phonon interactions, and once thermalized, the positron will either annihilate as a free particle, a trapped particle or in a bound state with an electron called positronium. The triplet ground state of positronium, ortho-positronium (o-Ps), annihilates by a mechanism known as pick-off whereby the o-Ps localizes in pockets of free volume and eventually annihilates with an electron from the surrounding matter. The time to annihilation, or o-Ps lifetime, is measured by birth and death gamma rays.⁹ The lifetime of o-Ps has been directly correlated with the pore size (the lifetime being shortened if the pick-off electron is nearby) while the number of annihilations has been directly correlated with the relative number of pores.¹⁶

The application of PALS to crystalline MOF-5 provided both information complimentary to standard gas sorption analysis, but moreover offers unique insights into internal pore structure, including defects.¹⁷ PALS has also been used to rationalise the absence of porosity in the theoretically porous Zn-HKUST-1 MOF. In this case, the surface of the activated material was found to be unstable; this collapsed crystal surface formed a barrier which prevented gas molecules from accessing the interior.¹⁸ Correlations between gas permeability and the free volume, measured by PALS, in mixed matrix membranes have also been reported.^12,19

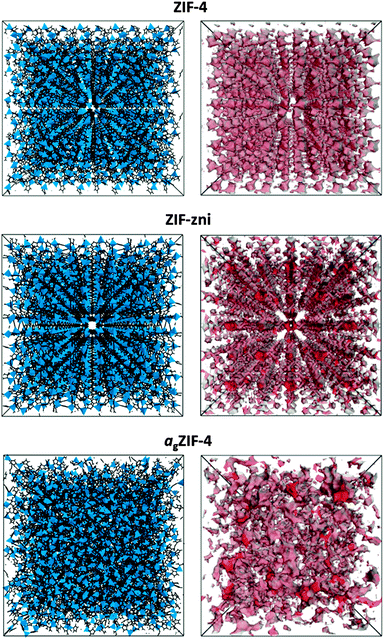
Motivated by the ability to probe the internal structures of the newly reported melt-quenched MOF-glasses,⁵ here we report the application of PALS to a glass formed by melt-quenching of ZIF-4, a three-dimensional metal–organic framework of composition Zn(C₃H₃N₂)₂.²⁰ Prior to melting at 573 °C, recrystallization to a known dense framework of identical chemical composition, ZIF-zni, is observed.⁵ The porosities of ZIF-4, ZIF-zni and the resultant melt quenched glass (a_gZIF-4), shown in Fig. 1, were all probed by PALS in this work.

Fig. 1 Structures for ZIF-4 (4 × 4 × 4 supercell, CCDC 602538), ZIF-zni (4 × 4 × 4 supercell, CCDC 120379) and a_gZIF-4 (2062 Zn atoms). Left: Atomic structures with ligands in black and zinc in blue. Right: Accessible porosity shown as a red Connolly surface, using a probe of 1 Å in diameter.

To provide comparison with the experimental data, the Polymatic code²¹ was used to simulate the atomic structure of a_gZIF-4, using force fields developed by Hu et al.²² Polymatic is a generalised polymerisation algorithm for amorphous polymers that incorporates automated bond-formation and annealing schemes. Five models were obtained in order to sample different regions of configuration space, and were formed by building an array of Zn(C₃H₃N₂)₂ repeat-units and allowing the closest ‘reactive pairs’ to form a bond. An average of 98% of reactions were completed, yielding computationally derived models with an average density of 1.417 g cm⁻³ (or, in terms of tetrahedral atoms per unit volume, 4.277 Zn nm⁻³), which is in good agreement with the experimentally determined density of 1.625 g cm⁻³ (or 4.905 Zn nm⁻³). The algorithm does not require density as an input and therefore the predicted density is purely an outcome of the dynamics, reactions and equilibration cycles. A representative configuration for a_gZIF-4, together with the crystallographic unit cells of ZIF-4 and ZIF-zni, is displayed in Fig. 1. The porosity of each structure was generated using BIOVIA based on ‘hard-sphere’ surface mapping across the internal surface.²³

Samples of ZIF-4, ZIF-zni and a_gZIF-4 were synthesized using previously established procedures.⁵²²NaCl, which was sealed in a thin mylar envelope, was used as the source of positrons. The samples were packed into a 2 mm thick cell surrounding the positron source. The o-Ps lifetime measurements were taken under vacuum (1 × 10⁻⁵ Torr) at 298 K using an EG&G Ortec spectrometer at a rate of 4.5 × 10⁶ counts per sample. The lifetimes are converted to pore sizes by using the quantum-based formulation¹⁶ with a spherical pore geometry for ZIF-4 and a_gZIF4, and a square channel geometry for ZIF-zni based on visual inspection of the structures.

For ZIF-4, two distinct cavity sizes were detected by PALS (Fig. 2). The experimentally determined smaller cavity size of ca. 3.3 Å is in excellent agreement with the value of 3.3 Å calculated from the solved crystal structure, whilst the size of the larger cavity appears slightly overestimated by PALS, at 6.2 Å compared to 5.1 Å. For ZIF-zni, PALS yields pores of 6.6 and 3.8 Å, compared to the crystal structure with pores of 5.5 and 3.0 Å, the latter of which exists in very small quantities.

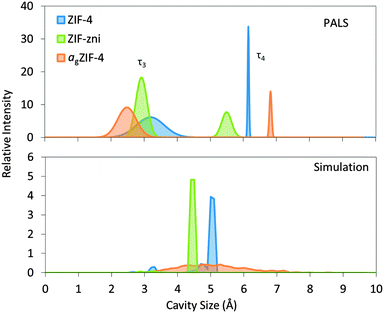Fig. 2 Pore size distributions measured with PALS and simulated with Zeo++^24,25 for ZIF-4, ZIF-zni and a_gZIF-4. PALS results for the third and fourth components (τ₃ and τ₄) are represented as Gaussian distributions which correspond to the small and large cavities, respectively.

The results from PALS appear to overestimate the pore sizes of the crystalline phases, which perhaps suggests imperfections in the models used for channel geometries.

Such overestimations are however less with a_gZIF-4, where the distribution of pore sizes is larger than for crystalline ZIF-4 and ZIF-zni. a_gZIF-4 contains the smallest and the largest pore sizes according to both PALS and simulation. The large and small cavity sizes were detected at 6.9 and 2.6 Å respectively which compare well with the largest and smallest cavities of 6.4 and 2.6 Å from simulation.

Experimental N₂ sorption isotherms have demonstrated that ZIF-zni and a_gZIF-4 show no significant N₂ uptake.⁵ ZIF-4 however, undergoes a phase transition at ca. 35 kPa. This structural change, involving rotation of the imidazolate linkers, facilitates N₂ adsorption and is also referred to as a ‘gate-opening’ mechanism.²⁶ The PALS experimental data provide further rationalization of the dense nature of both ZIF-zni and a_gZIF-4, indicating that the small cavities could prohibit access into the structure by N₂ (3.64 Å diameter).

Pore volume fraction as a function of probe size was calculated for the simulated structures (Fig. 3). For a point-size probe, all cavities are accessible which is represented by a pore volume fraction of unity. As the probe diameter increases, a certain amount of cavities become inaccessible which is shown as a drop in pore volume fraction. There is a sharp drop observed for ZIF-4 and ZIF-zni where a large amount of cavities become inaccessible with a slight increase in probe size, a typical feature for crystalline frameworks. a_gZIF-4 is markedly different with a gradual decline in pore volume fraction highlighting the amorphous nature of the framework. In addition, a tail at large probe diameter is observed for a_gZIF-4 where there remains a significant fraction of cavities capable of hosting the larger probes up to 7 Å. Considering this adjustment of porosity, a_gZIF-4 may be a valuable precursor material for fabricating amorphous carbons with a particular morphology. For example, thermally-rearranged (TR) polymers have proven excellent gas and vapour separation membranes due to their optimal combination of large cavities connected with smaller size-selective windows.²⁷

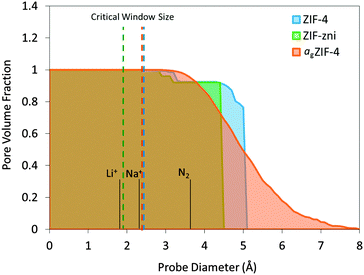Fig. 3 Pore volume fraction calculated for ZIF-4, ZIF-zni and a_gZIF-4 with a range of probe diameters. Dashed lines represent the critical window size for free transport according to the Voronoi representation using Zeo++.^24,25 Note that ZIF-4 undergoes a pressure-induced phase transition, which is not reflected in this scheme.

Critical window size is defined as the maximum probe size that can transport through a unit cell from one side to the other, i.e. the smallest constriction along a connected channel. This is calculated analytically using Zeo++ which can map the pore channels from the nodes of a Voronoi network (a graph representation of the void space for a given arrangement of atoms in a periodic space). This is indicated by dashed lines in Fig. 3. The critical window sizes are smaller than 3 Å, which correspond well with the smallest cavity sizes found by PALS and confirm the expected inaccessibility of N₂ (3.64 Å diameter). Given the observed flexibility of the imidazolate linkers in the ZIF family,²⁸ the window sizes may well increase under high pressures but given the restricted degrees of freedom, the expected change is minimal. Even without any flexibility these candidates may be capable of transporting ions such as lithium (1.8 Å diameter) and sodium (2.32 Å diameter), ignoring any electrostatic, physical adsorption and chemical absorption effects.

Whilst the cavity sizes vary slightly upon the sequence of transitions from ZIF-4 to ZIF-zni to a_gZIF-4, the combination of cavity size and number of cavities can appear significant when compared to the range of materials previously studied by PALS (Fig. 4a). Interestingly, both crystalline materials and a_gZIF-4 possess cavities of a diameter between those of conventional polymers (e.g. polycarbonate and polysulfone) and classical inorganic zeolites, though lower than open framework MOFs. Such results reflect the hybrid nature of these materials with the possession of both inorganic and organic components.

Fig. 4 (a) Comparison of PALS results for a range of materials including polymers, zeolites, MOFs and the present study of ZIF glasses. Only the cavity diameters for the fourth component (τ₄) are displayed where multi-modal distributions exist. (b) Relative diffusivity predicted from Cohen and Turnbull equation with arbitrary penetrant radii of 0.6 and 1.4 Å. Ref. in Table SI-2 (ESI†).

Cohen and Turnbull derived a generalised theory for transport through amorphous materials that was later related to the fractional free volume measured by PALS, here defined as FFV_PALS.^29–31 Diffusivity (D) can be related to FFV_PALS in the following way,

where A is an empirical constant related to temperature and various properties of the penetrant, γ is a geometric factor related to the overlapping of free volume elements and ν* is the minimum volume required to allow penetrant diffusion. As a simplification, the model is used here to postulate the diffusion properties of the ZIF glass compared with other materials. With all parameters held constant, diffusivity is calculated for two arbitrary scenarios of ν*(=1 and 10 ų), equivalent to radii of 0.6 and 1.3 Å for small ions, plotted in Fig. 4b. It can be seen that the difference in diffusivity between two penetrants of different molecular volumes can be maximized with a_gZIF-4 and materials within the same range of FFV_PALS. Zeolite MFI-100 sits within this range and was shown to have good ion transport properties in seawater. Porous aromatic frameworks, which also sit in this range of FFV_PALS, have been shown to have good lithium ion transport and carbon dioxide capture properties. Therefore a_gZIF-4 may be considered a promising candidate for transport, sensing, capture or release of small ions or molecules.

Aside from providing further information on the porosity of MOF glasses, this work has important consequences for the potential applications for glasses made from MOFs, (i.e. in both gas transport and conductive settings). Notably, TR polymers,³² lie close to a_gZIF-4 in terms of the largest cavity diameter. These TR polymers have been shown to possess free volume structures in the glassy state that enable molecular and ionic transport surpassing that of conventional polymers. Existing literature in the TR domain, which focuses on the effect of chain flexibility on physical and transport properties,³³ may provide direction for further research into the potential uses of melt-quenched MOF glasses such as a_gZIF-4.

AWT and CMD acknowledges the CSIRO Julius Career Award for support. CMD is supported by the Australian Research Council (DE40101359). TDB Acknowledges Trinity Hall (University of Cambridge) for funding.

Notes and references

1. H. Furukawa, K. E. Cordova, M. O'Keeffe and O. M. Yaghi, Science, 2013, 341, 974–986.
2. J. E. Mondloch, M. J. Katz, W. C. Isley III, P. Ghosh, P. Liao, W. Bury, G. W. Wagner, M. C. Hall, J. B. DeCoste, G. W. Peterson, R. Q. Snurr, C. J. Cramer, J. T. Hupp and O. K. Farha, Nat. Mater., 2015, 14, 512–516.
3. Z. L. Fang, B. Bueken, D. E. De Vos and R. A. Fischer, Angew. Chem., Int. Ed., 2015, 54, 7234–7254.
4. T. D. Bennett and A. K. Cheetham, Acc. Chem. Res., 2014, 47, 1555–1562.
5. T. D. Bennett, J. C. Tan, Y. Z. Yue, E. Baxter, C. D. Ducati, N. Terril, H. Y. Yeung, Z. Zhou, W. Chen, S. Henke, A. K. Cheetham and G. N. Greaves, Nat. Commun., 2015, 6, 8079.
6. S. Horike, W. Chen, T. Itakura, M. Inuaki, D. Umeyama, H. Asakura and S. Kitagawa, Chem. Commun., 2014, 50, 10241–10243.
7. H. Kato and T. Kasuga, Mater. Lett., 2012, 79, 109–111.
8. C. Sanchez, B. Julian, P. Belleville and M. Popall, J. Mater. Chem., 2005, 15, 3559–3592.
9. M. R. Tant and G. L. Wilkes, Polym. Eng. Sci., 1981, 21, 874–895.
10. N. Petzetakis, C. M. Doherty, A. W. Thornton, X. C. Chen, P. Cotanda, A. J. Hill and N. P. Balsara, Nat. Commun., 2015, 6, 7529.
11. Z. Chai, C. Wang, H. Zhang, C. M. Doherty, B. P. Ladewig, A. J. Hill and H. Wang, Adv. Funct. Mater., 2010, 20, 4394–4399.
12. C. H. Lau, P. T. Nguyen, M. R. Hill, A. W. Thornton, K. Konstas, C. M. Doherty, R. J. Mulder, L. Bourgeois, A. C. Y. Liu, D. J. Sprouster, J. P. Sullivan, T. J. Bastow, A. J. Hill, D. L. Gin and R. D. Noble, Angew. Chem., Int. Ed., 2014, 53, 5322–5326.
13. K. Konstas, K. F. Taupitz, D. R. Turner, D. F. Kennedy and M. R. Hill, CrystEngComm, 2014, 16, 8937–8940.
14. B. Zhu, C. M. Doherty, X. Hu, A. J. Hill, L. Zou, Y. S. Lin and M. Duke, Microporous Mesoporous Mater., 2013, 173, 78–85.
15. D. W. Gidley, H.-G. Peng and R. S. Vallery, Annu. Rev. Mater. Res., 2006, 36, 49–79.
16. S. J. Tao, J. Chem. Phys., 1972, 56, 5499–5510.
17. M. Liu, A. G. Wong-Foy, R. S. Vallery, W. E. Frieze, J. K. Schnobrich, D. W. Gidley and A. J. Matzger, Adv. Mater., 2010, 22, 1598–1601.
18. J. I. Feldblyum, M. Liu, D. W. Gidley and A. J. Matzger, J. Am. Chem. Soc., 2011, 133, 18257–18263.
19. H. Jeazet, T. Koschine, C. Staudt, K. Raetzke and C. Janiak, Membranes, 2013, 3, 331–353.
20. K. S. Park, Z. Ni, A. P. Cote, J. Y. Choi, R. D. Huang, F. J. Uribe-Romo, H. K. Chae, M. O'Keeffe and O. M. Yaghi, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 10186–10191.
21. L. Abbott, K. Hart and C. Colina, Theor. Chem. Acc., 2013, 132, 1–19.
22. Z. Hu, L. Zhang and J. Jiang, J. Chem. Phys., 2012, 136, 244703.
23. M. L. Greenfield and D. N. Theodorou, Macromolecules, 1993, 26, 5461–5472.
24. M. Haranczyk, C. H. Rycroft, R. L. Martin and T. F. Willems, Zeo++: High-throughput analysis of crystalline porous materials, v0.2.2, Lawrence Berkeley National Laboratoy, Berkeley, 2012.
25. T. F. Willems, C. H. Rycroft, M. Kazi, J. C. Meza and M. Haranczyk, Microporous Mesoporous Mater., 2012, 149, 134–141.
26. T. D. Bennett, S. Cao, J. C. Tan, D. A. Keen, E. G. Bithell, P. J. Beldon, T. Friscic and A. K. Cheetham, J. Am. Chem. Soc., 2011, 133, 14546–14549.
27. H. B. Park, C. H. Jung, Y. M. Lee, A. J. Hill, S. J. Pas, S. T. Mudie, E. van Wagner, B. D. Freeman and D. J. Cookson, Science, 2007, 318, 254–258.
28. E. O. Beake, M. T. Dove, A. E. Phillips, D. A. Keen, M. G. Tucker, A. L. Goodwin, T. D. Bennett and A. K. Cheetham, J. Phys.: Condens. Matter, 2013, 25, 395403.
29. M. H. Cohen and D. Turnbull, J. Chem. Phys., 1959, 31, 1164–1169.
30. D. Turnbull and M. H. Cohen, J. Chem. Phys., 1961, 34, 120–125.
31. B. D. Freeman and A. J. Hill, Structure and Properties of Glassy Polymers, American Chemical Society, Washington, DC, 1998.
32. S. Kim and Y. M. Lee, J. Nanopart. Res., 2012, 14, 949.
33. M. Calle and Y. M. Lee, Macromolecules, 2011, 44, 1156–1165.

---

Footnote

† Electronic supplementary information (ESI) available: PALS and simulation details. See DOI: 10.1039/c5cc10072k

---